Abstract
This study investigates the influence of vacancy engineering and nitrogen doping on the structural, electronic, and optical properties of T-graphene fragments (TFs) using density functional theory (DFT) and time-dependent DFT (TD-DFT). A central vacancy and five pyridinic nitrogen doping configurations are explored to modulate the optoelectronic behavior. All systems are thermodynamically stable, exhibiting tunable HOMO–LUMO gaps, orbital distributions, and charge transfer characteristics. Optical absorption spectra show redshifts and enhanced oscillator strengths in doped variants, notably v-NTF2 and v-NTF4. Nonlinear optical (NLO) analysis reveals significant enhancement in both static and frequency-dependent responses. v-NTF2 displays an exceptionally high first-order hyperpolarizability (⟨β⟩ = 1228.05 au), along with a strong electro-optic Pockels effect (β (−ω; ω, 0)) and second harmonic generation (β (−2ω; ω, ω)). Its third-order response, γ (−2ω; ω, ω, 0), also exceeds 1.2 × 105 au under visible excitation. Conceptual DFT descriptors and energy decomposition analysis further supports the observed trends in reactivity, charge delocalization, and stability. These findings demonstrate that strategic nitrogen doping in vacancy-engineered TFs is a powerful route to tailor electronic excitation, optical absorption, and nonlinear susceptibility. The results offer valuable insight into the rational design of next-generation carbon-based materials for optoelectronic, photonic, and NLO device applications.
1. Introduction
Graphene [1] has set the benchmark for two-dimensional materials with its unique honeycomb structure and extraordinary properties [2,3,4,5,6], but carbon’s remarkable versatility opens the door to a rich variety of 2D frameworks. Driven by the quest for new functionalities, researchers have explored non-hexagonal carbon lattices that promise novel electronic and structural behaviors. Enyashin et al. [7] suggested twelve new nonhexagonal 2D carbon structures, including T-graphene, which has a tetragonal (square-like) pattern with sp2-hybridized carbon atoms. Liu et al. [8] first proposed T-graphene in two forms: planar and buckled. These forms show different electronic behaviors. The planar type is metallic, while the buckled type behaves like graphene with Dirac-like fermions and high Fermi velocity, making it semi-metallic. Both forms are dynamically stable, but planar T-graphene is more stable below 900 K, while buckled T-graphene has stability issues below 940 K. Sheng et al. [9] showed theoretically that boron–nitrogen pair doping can open T-graphene’s band gap, enabling a transition from semi-metallic to semiconducting behavior suitable for nanoelectronics. Additionally, computational studies indicate that non-hexagonal rings in 2D carbon allotropes like T-graphene significantly enhance the electronic component of thermal conductivity compared to graphene [10]. T-graphene finds potential applications in different fields, such as hydrogen storage [9,11,12], gas sensors [13,14,15], current rectification and spintronics [16], electrode in ion batteries [17,18,19,20], optoelectronics [21], etc. Wang et al. [22] studied T-graphene nanoribbons (T-GNRs), finding that zigzag T-GNRs are always metallic while armchair T-GNRs can switch between metallic and semiconducting depending on their width. Dai et al. [23] used theoretical methods to show that these nanoribbons can display negative differential resistance and linear current–voltage behavior.
Confinement of 2D materials into zero-dimensional (0D) nanostructures, such as finite fragments or ultra-small nanoflakes, can lead to enhanced optical and electronic responses owing to edge effects, discrete energy levels, and increased surface-to-volume ratios [24,25,26]. T-graphene fragments (TFs), derived from finite-sized cutouts of the infinite T-graphene sheet, offer a rich platform to investigate size- and shape-dependent electronic and optoelectronic behavior [27]. Deb et al. [27] used a first-principles approach to study the electronic and optical properties of planar TFs, with a particular focus on their nonlinear optical (NLO) response. Their results demonstrate strong, tunable NLO behavior under external fields, highlighting TFs as promising candidates for NLO applications. Additionally, alkali metal doping offers a promising strategy to enhance the NLO response of nanomaterials by breaking centrosymmetry. Recent DFT studies on TFs reveal that Li, Na, and K doping significantly improves their stability and first hyperpolarizability, identifying these complexes as potential candidates for advanced nanoscale NLO applications [28]. Unlike hexagonal graphene Fs, TFs inherently possess structural asymmetry and strain fields even in their pristine form, resulting in localized π-electron behavior and intrinsic bandgap opening without external perturbation. TG flakes have also emerged as promising candidates for hydrogen storage, with studies showing that Li decoration significantly alters their electronic properties. DFT results indicate that external electric fields can reversibly modulate hydrogen adsorption on Li-decorated TG, enabling controllable storage and release [29]. Furthermore, the effects of B and N doping on TFs have been investigated, demonstrating size-dependent stability, distinct vibrational characteristics, semiconducting behavior, and potential applications in CO gas sensing, nanosensors, and rectifying devices [15,30]. Additionally, analysis of singlet–triplet gaps, symmetries, and transition dipoles of low-lying excited states indicates that TFs are photoluminescent materials. Despite the optically forbidden HOMO–LUMO transitions and large optical gaps, these features suggest the intriguing possibility of singlet exciton fission into multiple triplet excitons [31].
Non-hexagonal ring structures can develop naturally during graphene growth or be introduced through electron irradiation [32,33]. Biphenylene, a planar carbon sheet with tetragons, hexagons, and octagons, has been synthesized in the laboratory [34]. Although planar T-graphene has not yet been experimentally synthesized, the successful synthesis of biphenylene suggests that it could be made in the future.
Tailoring the electronic structure of finite size fragments is commonly achieved through defect engineering, such as by introducing vacancies or heteroatoms [35,36,37], with vacancies also acting as active sites for functionalization. Among doping strategies, nitrogen doping is especially effective for modulating electronic density, enhancing charge transport, and tuning optical transitions [38,39], as its higher electronegativity introduces localized donor or acceptor levels and alters electronic distribution. Nitrogen doping in graphene-based systems has already demonstrated enhancements in optical properties [40,41,42].
Despite these developments, the understanding of how vacancy engineering and nitrogen doping collectively influence the linear and nonlinear optical responses of TF remains limited. There exists a pressing need to comprehensively examine the interplay between geometry, electronic structure, and optical activity in these systems, particularly in the ultraviolet (UV) range, where they exhibit strong absorption [27,32]. Transition dipole moments, oscillator strengths, and charge transfer excitations in TFs are expected to vary significantly with dopant placement and defect topology, offering a rational strategy to tune properties like light-harvesting efficiency, polarizability, and hyperpolarizability.
In this context, the present work aims to systematically investigate the structural, electronic, and optical properties of pristine, vacancy-induced, and nitrogen-doped TFs using DFT and time-dependent DFT (TD-DFT) approaches. Key global reactivity descriptors are analyzed to evaluate thermodynamic and kinetic stability [43,44,45,46,47,48]. Special emphasis is placed on the HOMO–LUMO gap, absorption spectra, oscillator strengths, transition dipole moments, and light-harvesting efficiencies to reveal structure–property relationships critical for optoelectronic and NLO applications. Our findings demonstrate that strategic nitrogen doping in the vacancy-engineered TF framework modulates the system’s stability in a site-dependent manner while enabling fine-tuning of the UV absorption profile and NLO responses, offering valuable insight into the design of next-generation carbon-based photonic materials.
2. Computational Methodology
Density functional theory (DFT) has been employed to carry out the structural optimization of the systems using the Gaussian 16 computational package [49]. All vacancy-induced pristine and nitrogen-doped TFs have been fully relaxed without imposing any symmetry constraints. The meta-hybrid M06-2X [50] functional has been used for its proven accuracy in capturing noncovalent interactions, charge transfer, and electronic correlation effects in low-dimensional systems. It has been employed in combination with the 6-311+G(d,p) basis set, which provides triple-zeta valence quality along with diffuse and polarization functions [51]. Frequency calculations have been performed to characterize the nature of the stationary points. The presence of only real vibrational frequencies confirms that the optimized structures have reached true local minima on the potential energy surface. Energy decomposition analysis (EDA) using the MULTIWFN program [52] has been carried out to analyze the total interaction energy by separating it into key contributions, such as electrostatic, steric, and quantum effects. To explore the optical absorption characteristics of the systems, time-dependent density functional theory (TDDFT) has been applied.
To evaluate the thermodynamic stability of the pristine, vacancy-engineered, and nitrogen-functionalized TFs, the cohesive energy per atom () has been calculated using the relationships
Here, , , , , , and represent the total energies of the pristine TF, vacancy-induced TF, nitrogen-doped TFs, and isolated hydrogen, carbon, and nitrogen atoms, respectively. , , and correspond to the number of hydrogen, carbon, and nitrogen atoms in each system.
3. Results and Discussion
In this work, a central vacancy has been introduced in the TF by removing all carbon atoms forming the central tetragonal ring, followed by hydrogen passivation of the resulting edge carbon atoms to stabilize the structure. This modified configuration is referred to as v-TF. Subsequently, nitrogen has been introduced as a dopant in five different configurations: pyridinic-N4 inner edge-doped TF (v-NTF1), pyridinic-N4 corner-doped TF (v-NTF2), pyridinic-N4 outer edge-doped TF (v-NTF3), pyridinic-N8 corner-distributed TF (v-NTF4), and pyridinic-N8 edge-distributed TF (v-NTF5). Figure 1 depicts the optimized geometries of vacancy-engineered pristine and nitrogen-doped TFs. The creation of a central vacancy in TGF profoundly alters its structural integrity by disrupting the delocalized π-system and breaking local symmetry, leading to noticeable out-of-plane distortions. This structural perturbation renders both the v-TF and v-NTFs distinctly non-planar, in sharp contrast to the flat topology of the parent TGF. Remarkably, v-NTF4 featuring symmetrically distributed pyridinic-N8 dopants at the corners preserves near-planarity, suggesting that a balanced dopant arrangement can effectively compensate for vacancy-induced strain. In stark contrast, v-NTF5 exhibits a significantly buckled architecture, likely driven by edge-localized nitrogen doping that enhances structural asymmetry and induces considerable geometric deformation.
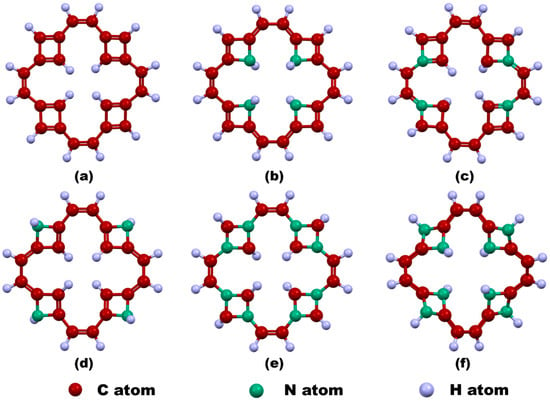
Figure 1.
Geometry-optimized configurations of vacancy-induced TFs: (a) v-TF and nitrogen-doped variants, (b) v-NTF1, (c) v-NTF2, (d) v-NTF3, (e) v-NTF4, and (f) v-NTF5.
3.1. Electronic Structure and Stability
The calculated cohesive energies () and HOMO–LUMO gaps () for pristine, vacancy-induced, and nitrogen-doped TFs are summarized in Table 1. Negative cohesive energy values across all structures confirm their thermodynamic stability and indicate the feasibility of synthesizing these quantum dots under experimental conditions. These negative values also imply that the systems are energetically stable and will not spontaneously dissociate into their constituent atoms. Among all configurations, pristine TF exhibits the most negative cohesive energy (−6.751 eV/atom), highlighting its exceptional stability, which can be attributed to the continuous sp2-hybridized carbon framework and delocalized π-electron system. It also shows a moderate of 3.642 eV, consistent with previous reports employing the B3LYP functional [27]. Introducing a central vacancy (v-TF) reduces both the (−6.017 eV/atom) and (3.622 eV), reflecting reduced stability as a result of disrupted conjugation and local strain. Nitrogen doping into the vacancy framework leads to diverse electronic responses depending on the dopant configuration. Notably, v-NTF1 and v-NTF3 exhibit slightly improved stability (−6.034 and −6.031 eV/atom) and enhanced energy gaps (3.680 and 4.009 eV), suggesting that well-placed nitrogen atoms can reinforce structural integrity while widening the gap through favorable C–N bonding and orbital reorganization. In contrast, v-NTF2 shows both the lowest (2.957 eV) and reduced stability (−5.848 eV/atom), indicating electronic delocalization and local distortion. Interestingly, v-NTF4 and v-NTF5 demonstrate significantly wider (4.800 and 5.544 eV) despite their relatively lower (−5.751 and −5.953 eV/atom). This suggests that specific nitrogen doping configurations, particularly those with symmetric or edge-distributed nitrogen atoms, can induce orbital localization or reduce frontier orbital overlap, thereby widening the energy gap. The reduced structural stability in these cases may arise from accumulated strain and electronic repulsion among closely positioned nitrogen atoms, especially at the corners. These findings demonstrate that nitrogen doping is an effective strategy for modulating the electronic structure of vacancy-containing TFs. Although defects may reduce stability, appropriate dopant configurations can restore structural integrity and alter the , enabling the design of materials with tailored optoelectronic properties. The broad range of values observed further suggests that the optical response of these systems can be systematically tuned through controlled structural modifications. Notably, plays a critical role in determining the NLO behavior of molecular systems, as it directly influences the polarizability and hyperpolarizability responses. Smaller values typically enhance charge transfer interactions between donor and acceptor orbitals, thereby increasing the first- and second-order NLO coefficients. Therefore, the tunability of in TFs not only affects their linear optical properties but also governs their NLO responses. This correlation offers a deeper understanding of the structure–property relationship in TFs and provides a rational basis for designing NLO-active materials with tailored functionalities.

Table 1.
Cohesive energy per atom () along with the HOMO-LUMO energy gap () of TF, vacancy-induced TF, and NTFs.
Furthermore, the HOMO–LUMO isosurface plots (Figure 2) have been analyzed to reveal the impact of vacancy creation and nitrogen doping on the electronic structure of TFs. In v-TF, both frontier molecular orbitals are moderately delocalized around the vacancy site, reflecting retained π-conjugation and moderate orbital overlap. For v-NTF1 and v-NTF3, nitrogen doping leads to asymmetric but partially delocalized frontier orbitals, suggesting enhanced orbital overlap and slight stabilization, consistent with their moderate band gaps. Conversely, v-NTF2 exhibits a highly localized LUMO, indicating potential charge trapping and a reduced band gap, which could impact electronic conductivity. Notably, v-NTF4 and v-NTF5 show highly symmetric yet spatially separated HOMO and LUMO densities, suggesting reduced orbital overlap and enhanced gap widening. These patterns support a dopant-driven modulation of the electronic structure, where both the position and distribution of nitrogen atoms critically influence charge delocalization, energy gap tuning, and, ultimately, the suitability of TFs for optoelectronic applications.
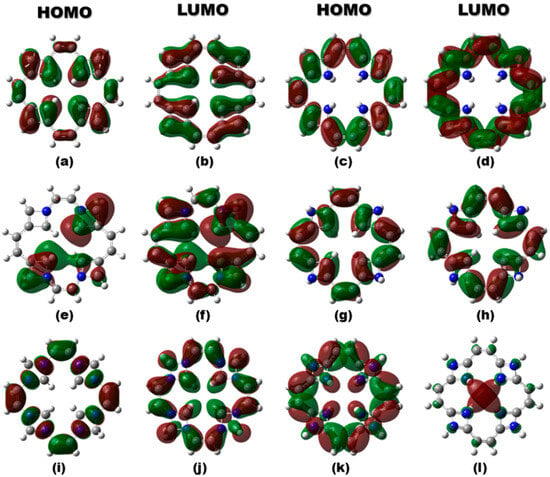
Figure 2.
HOMO and LUMO isosurfaces of v-TF and nitrogen-doped TFs: (a,b) v-TF, (c,d) v-NTF1, (e,f) v-NTF2, (g,h) v-NTF3, (i,j) v-NTF4, and (k,l) v-NTF5. Green and brown lobes represent the positive and negative phases of molecular orbitals.
3.2. Chemical Reactivity Parameters
Conceptual density functional theory (CDFT) provides a rigorous framework for assessing molecular reactivity and stability through global descriptors. In this study, adiabatic ionization potential () and electron affinity () have been computed from total energy differences between charged and neutral species, offering more accurate estimates than orbital-based approximations. These quantities are evaluated using the following expressions:
where and are assigned to be the energies of , and electron systems, respectively.
IP refers to the energy required to remove an electron from a system, while EA denotes the energy released upon electron addition. The calculated IP and EA (Table 2) values reveal a strong dependence on structural modification in TFs. Pristine TF exhibits a high IP (6.483 eV) and moderate EA (2.017 eV), indicating good electronic stability. Vacancy introduction reduces IP (v-TF: 5.048 eV), reflecting weaker electron binding. Among the doped systems, IP follows the trend v-NTF3 (6.711) > v-NTF4 (6.410) > v-NTF1 (6.346) > v-NTF5 (5.591) > v-NTF2 (4.420), while EA shows v-NTF2 (2.649) > v-NTF3 (2.016) > v-NTF1 (1.848) > v-NTF4 (0.941) > v-NTF5 (−0.760). v-NTF2 exhibits the strongest electron-accepting character, as indicated by its highest electron affinity, while v-NTF3 demonstrates the highest ionization potential, reflecting its superior resistance to electron loss and enhanced electronic stability. These trends suggest that nitrogen doping modulates IP and EA significantly, enabling fine-tuning of reactivity and charge transport behavior through dopant positioning and structural engineering.

Table 2.
Ionization potential (), electron affinity (), chemical hardness (), chemical potential (), and electrophilicity index (ω) of TF, vacancy-induced TF, and NTFs.
Based on the calculated IP and EA, the global reactivity descriptors, such as chemical hardness () [53], chemical potential (), electronegativity (χ) [54,55], and electrophilicity index (ω) [44,45], can be subsequently derived using the following equations:
These chemical reactivity descriptors for pristine, vacancy-induced, and nitrogen-doped TFs are summarized in Table 2. These descriptors provide insight into each system’s ability to resist or accept charge, offering a measure of electronic stability and reactivity. Chemical hardness of the studied systems decreases in the order of v-NTF5 > v-NTF4 > v-NTF3 > v-NTF1 > TF > v-TF > v-NTF2, indicating a gradual increase in chemical softness. Conversely, the electrophilicity index increases in the order of v-NTF5 < v-NTF4 < v-TF < v-NTF1 < TF < v-NTF3 < v-NTF2, suggesting that softer systems are more prone to accepting electronic charge. According to the maximum hardness and minimum electrophilicity principles (MHP and MEP) [56,57], the most stable systems should exhibit high η and low ω. However, the observed trends deviate from these principles, suggesting that other physical factors, such as dopant position, local orbital interactions, and geometric distortion, play an equally important role in determining stability. For instance, v-NTF5, although the hardest and least electrophilic system, has a negative electron affinity and shallow chemical potential, indicating poor ability to accommodate additional charge, likely due to electronic repulsion near the edge-distributed nitrogen sites. On the other hand, v-NTF2, with the highest ω and lowest η, is chemically soft and highly reactive, but this comes at the cost of structural and electronic stability due to charge localization and disrupted conjugation. Among the nitrogen-doped variants, v-NTF3 emerges as the most balanced system, characterized by a notably high η (4.695 eV), a significantly negative (−4.364 eV), and a moderate electrophilicity index η (2.028 eV). This balance suggests good electronic stability, strong electron-withdrawing capacity, and controlled reactivity. The observed trends show that systems with lower η and higher ω tend to exhibit enhanced charge transfer character and reduced energy gaps, which are beneficial for NLO responses. In contrast, higher η correlates with greater stability but diminished optical activity. Thus, controlled tuning of η and ω through vacancy engineering and nitrogen doping provides a rational strategy for designing TFs with tailored electronic and optical functionalities.
3.3. Energy Decomposition Analysis
To better understand the underlying factors influencing the stability of pristine, vacancy-induced, and nitrogen-doped TFs, energy decomposition analysis (EDA) has been performed using the EDA-SBL scheme [58]. The total interaction energy (E) has been partitioned into three physically meaningful components: electrostatic (Eelec), steric (Ester), and quantum (Equan) contributions. The electrostatic component, comprising classical Coulomb interactions, has contributed attractively to the system’s stability. The steric term, arising from the Weizsäcker kinetic energy, has remained strongly repulsive and generally larger than the quantum term, which has originated from electron correlation and the Pauli exclusion principle. Despite its repulsive nature, the steric effect has been significant due to its magnitude. The corresponding values have been summarized in Table S1. The pristine TF has exhibited the most stabilizing electrostatic energy (−54,067.448 eV), balanced by steric (23,507.196 eV) and quantum (1854.016 eV) contributions, resulting in the most favorable total interaction energy (−28,706.237 eV). Vacancy creation in v-TF has led to a reduction in all three components, producing less negative total energy (−24,676.581 eV), consistent with disrupted conjugation and reduced structural stability. Nitrogen doping has partially recovered the interaction strength. v-NTF1 and v-NTF3 have shown comparable total energies (−26,482.069 and −26,481.793 eV), with slightly enhanced electrostatic and quantum contributions relative to v-TF, indicating stabilization through favorable dopant positioning. Meanwhile, v-NTF2 has demonstrated slightly lower stability (−26,474.240 eV), attributed to an increased quantum term (1943.602 eV), likely due to localized electronic effects near the corner doping sites. Among the doped systems, v-NTF4 and v-NTF5 have exhibited the most favorable interaction energies (−28,274.649 and −28,283.493 eV), approaching that of pristine TF. These configurations have combined strong electrostatic stabilization with higher steric and quantum contributions, suggesting effective charge redistribution and enhanced structural balance due to symmetric or edge-distributed nitrogen arrangements. Overall, EDA has revealed that while vacancy formation has diminished structural stability, strategically implemented nitrogen doping, particularly in symmetric or edge-focused geometries, has effectively counterbalanced this effect through increased electrostatic and quantum stabilization.
3.4. Linear Optical Properties
TD-DFT calculations have been carried out, considering the lowest 20 singlet excited states, to explore the electronic excitation behavior and optical properties of pristine, vacancy-engineered, and nitrogen-doped TFs. Key parameters, including the maximum absorption wavelength (λmax), excitation energy (ΔE), oscillator strength (f0), transition dipole moments (µe), dominant singlet–singlet transitions (S0 → Sₙ) corresponding to the highest oscillator strengths, and corresponding light-harvesting efficiency (ηλ), have been summarized in Table 3, and the corresponding absorption spectra have been depicted in Figure 3. These results have provided insight into how structural modifications have influenced the optical response and charge transfer characteristics of the TF framework.

Table 3.
Vertical excitation parameters of pristine TF, vacancy-induced TF (v-TF), and nitrogen-doped TF (NTF): excitation wavelength (λ), excitation energy (ΔE), oscillator strength (f0), excited-state dipole moment (µe), nature of the electronic transition, and light-harvesting efficiency (ηλ) for both the first excited state (S1) and the most optically active singlet excited state (with the highest f0).
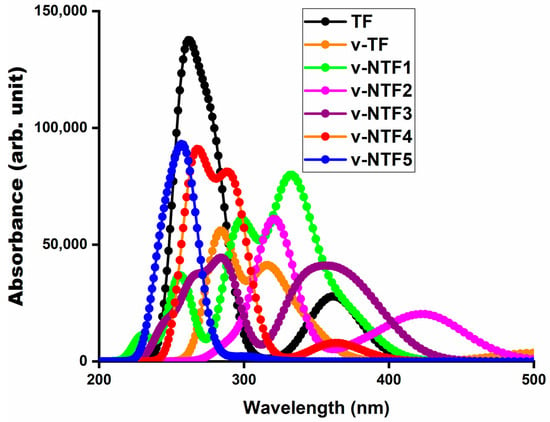
Figure 3.
UV-visible absorption spectra of TF, vacancy-induced TF, and NTFs.
Analysis of the absorption spectra has revealed that all systems exhibit their strongest absorption peaks in the ultraviolet region, with λmax values ranging from 243.46 nm to 321.53 nm. The trend in maximum absorption wavelength has followed the order of v-NTF5 < TF < v-TF < v-NTF3 < v-NTF4 < v-NTF1 < v-NTF2. This progression has indicated a systematic shift of absorption toward longer wavelengths or the lower-energy region of the electromagnetic spectrum, reflecting a redshift from the pristine TF to the vacancy-modified (v-TF) and most nitrogen-doped systems. However, v-NTF5 has deviated from this trend, exhibiting a noticeable blue shift, likely due to more localized excitation and a larger energy gap. The most pronounced redshift of the highest peak is observed for v-NTF2 (~63 nm), which is associated with a strong charge transfer transition and the lowest excitation energy (ΔE = 3.856 eV). This redshift is indicative of enhanced π-conjugation and orbital reorganization due to vacancy and dopant effects. Notably, v-NTF1 and v-NTF2 exhibit polarized π → π* excitations with partial intramolecular charge transfer character, with transitions like S0 → S8 (v-NTF1) and S0 → S7 (v-NTF2), primarily involving H → L + 2 (86%) and H-3 → L + 2 (74%), respectively. These transitions are accompanied by moderate to high oscillator strengths (f0 ≈ 0.78–0.81), reflecting allowed excitations with efficient transition dipole coupling. The corresponding transition dipole moments are also appreciably large (μe = 7.145 and 7.304 for v-NTF1 and v-NTF2, respectively), indicating strong polarization between the ground and excited states and supporting the partially delocalized nature of the excitations. These features contribute to intense and allowed optical transitions, in agreement with earlier findings in sulfur-doped GFs [59], where higher μe values have been found to correlate with enhanced oscillator strengths and greater absorption intensities.
In contrast, v-NTF5 shows the shortest λmax (243.46 nm), the highest ΔE (5.093 eV), and the lowest f0 (0.308), suggesting localized excitation and poor optical responsiveness. The dominant excited-state transition in this case is S0 → S16, corresponding to a π → π* excitation with a relatively low transition dipole moment (μe = 3.991 D), confirming limited orbital overlap and inefficient charge polarization. These factors weaken the excitation probability and the overall light–matter interaction. As observed in related studies, the absorption peaks with the highest oscillator strength generally correspond to the most intense transitions in the spectra. In our case, this trend is preserved across most systems. Moreover, for structures like v-NTF3 and v-NTF4, although the absorptions remain in the UV region, the observed redshifts and moderate oscillator strengths suggest moderate optical activity with potential for controlled photoexcitation. The major transitions in these cases are S0 → S9 (λmax = 286.08 nm, f0 = 0.568) for v-NTF3 and S0 → S6 (λmax = 292.13 nm, f0 = 0.536) for v-NTF4, both assigned as π → π* in nature. The transition dipole moments remain moderate (μe ≈ 5.8 D), reflecting partially delocalized excitations with some charge transfer character.
Additionally, the first singlet excited states (S0 → S1) for all systems have been examined, and they consistently show very low oscillator strengths (f0 ≈ 0.000–0.001), indicating that these are optically forbidden or dark transitions. While these transitions do not contribute significantly to the absorption spectrum, their energetic positions are crucial for understanding the onset of electronic excitation and may play a role in non-radiative processes, such as internal conversion or intersystem crossing.
Given that all TF derivatives absorb strongly in the UV region, their utility may extend to NLO applications, particularly frequency-doubling or UV-based photonic devices. Given that all TF systems exhibit strong absorption in the ultraviolet region, the light-harvesting efficiency (ηλ), using the relationship , becomes a key metric for evaluating their photoresponse as it is highly sensitive to the oscillator strength () of electronic transitions. Systems like TF, v-NTF1, and v-NTF2 exhibit large () values and high ηλ, indicating strong UV-photon absorption—desirable for applications in UV photodetectors, NLO devices, and energy-harvesting platforms.
The convergence of ηλ values toward unity in these systems reflects efficient orbital overlap and extended π-conjugation induced by vacancy and dopant engineering. This trend aligns with established findings in donor-acceptor systems, where higher is linked to stronger π-delocalization and charge transfer efficiency. Transition dipole moment analysis further reinforces this understanding, as higher μe values are consistently associated with allowed, polarized transitions. Thus, tuning and ηλ via structural modifications highlights the promise of these TFs for high-performance UV-active optoelectronic and photonic technologies.
3.5. Nonlinear Optical Properties
The presence of delocalized electrons in TFs is known to significantly enhance NLO responses, which motivated us to explore the NLO properties of v-TFs and v-NTFs. The strength of a system’s optical response is fundamentally governed by its electronic characteristics, which depend not only on linear polarizability (⟨α⟩) but also on higher-order responses, such as first-order (⟨β⟩) and second-order (⟨γ⟩) hyperpolarizabilities. Understanding these properties is crucial for the rational design of advanced optoelectronic and photonic materials.
Accordingly, we have computed both static and frequency-dependent ⟨α⟩, ⟨β⟩, and ⟨γ⟩ values for all vacancy-modified and nitrogen-doped configurations using the following expressions [60]:
Here, , , and denote the components of the linear polarizability and the first- and second-order hyperpolarizability tensors, respectively. Among these, and correspond to the second- and third-order NLO response coefficients. The corresponding data are presented in Tables S2–S4 (Supporting Information). The variation of these NLO parameters across different doping patterns and defect structures is illustrated in Figure 4. For comparative insight, we also refer to earlier reported values of pristine TF, which reveal that certain doped structures exhibit significantly enhanced NLO responses. These observations highlight the crucial role of defect engineering and dopant positioning in shaping the NLO behavior of TFs. Additionally, the interaction of molecular dipole moments with external electromagnetic fields can significantly influence NLO responses. To capture these effects, we have investigated the dynamic NLO behavior of the studied systems under two laser excitation frequencies, ω = 0.0428 au and ω = 0.0856 au, corresponding to wavelengths of approximately 1064 nm and 532 nm, respectively. These frequencies are widely employed in experimental NLO setups as they represent the fundamental and second harmonic of the Nd: YAG laser. The lower frequency (ω = 0.0428 au) lies in the near-infrared region and is ideal for probing off-resonant optical responses, whereas the higher frequency (ω = 0.0856 au), located in the visible region, is better suited for exploring resonance-enhanced effects. By evaluating the systems under both excitation conditions, we provide a comprehensive assessment of their frequency-dependent NLO performance, enhancing the relevance of our findings for practical photonic and optoelectronic applications. Notably, the pristine TF, reported in previous literature, exhibits zero polarizability due to its perfect centrosymmetry and absence of a permanent dipole moment [27]. Such high symmetry leads to complete cancellation of dipole vectors, resulting in no net polarization and hence no contribution to polarizability or hyperpolarizabilities. However, the introduction of a central vacancy breaks this symmetry and redistributes the electron density, thereby inducing finite polarizability in the modified systems. Further enhancement is observed upon nitrogen doping, where the dopant atoms introduce electronic asymmetry and localized charge polarization. As a result, all studied v-TFs and v-NTFs display nonzero polarizability values, which vary according to the nature and position of the dopants. Among the configurations, v-NTF2 exhibits the highest static polarizability (α (0; 0) = 388.543 au), suggesting significant electron delocalization. This is followed by v-TF and v-NTF1. At the lower laser frequency (ω = 0.0428 au), v-NTF2 maintains the highest dynamic polarizability (413.057 au), while at the higher frequency (ω = 0.0856 au), v-NTF1 shows the maximum value (422.475 au). These results highlight the frequency-dependent nature of the polarizability and the differential sensitivity of each system to optical excitation. In contrast, v-NTF5 consistently displays the lowest polarizability across all regimes, indicating a more localized and less responsive electron distribution. An examination of the static ⟨β⟩ values reveals that all of the vacancy-modified and nitrogen-doped systems exhibit nonzero first-order hyperpolarizabilities, highlighting the role of symmetry breaking induced by defect formation and dopant incorporation. Among them, v-NTF2 stands out with an exceptionally large β value of 1228.048 au, indicative of strong ICT and pronounced second-order NLO activity. This enhancement is likely due to its highly asymmetric nitrogen doping and extended electronic delocalization. v-NTF4 also shows a significantly higher β (162.629 au) compared to the other systems, emphasizing the critical influence of dopant configuration on NLO performance. In contrast, systems like v-TF, v-NTF1, v-NTF3, and v-NTF5 exhibit very low β values (<2 au), suggesting minimal second-order NLO contributions. Notably, the first-order hyperpolarizability demonstrates a direct correlation with linear polarizability and an inverse relationship with the HOMO–LUMO energy gap. In this context, β trends closely follow the variations in band gaps, with systems with lower (such as v-NTF2 and v-NTF4) displaying markedly enhanced β responses. Remarkably, the β value of v-NTF2 (1228.048 au) significantly exceeds many previously reported carbon-based systems, including graphene quantum dots (1–200 au) [61], graphdiyne (0.13 au) [62], sumanene (135.43 au) and its BH/NH analogues (59–744 au) [63], T-graphene (6–780 au) [27], 6-6-12-graphyne oligomers (697.92 au) [64], phagraphene Fs (~600 au) [65], except one (~F6), superalkali M3O on graphenylene (114–1040 au) [66], and graphitic carbon nitride derivatives, such as C18N27H8 and C30N44H12 (103–1130 au) [67]. For reference, urea, commonly used as a benchmark organic NLO molecule, has an experimentally measured ⟨β⟩ of 0.33 × 10−30 esu (38.20 au) [68], indicating that v-NTF2 and v-NTF4 far exceed this value, further showcasing their strong potential for NLO applications. Inspection of the β tensor components shows that the first-order hyperpolarizability is predominantly governed by z-axis contributions, notably, βzyy, βzzz, and βzxx. This directional dominance indicates efficient charge redistribution along the molecular z-axis, characteristic of asymmetric systems exhibiting strong intramolecular charge transfer. Such an anisotropic response is a hallmark of effective second-order NLO materials, reinforcing the directional nature of the polarization under an external electric field. The observed trend in static hyperpolarizability (⟨β⟩) among the studied systems is consistent with the predictions of the two-level model, which relates β to the key optical parameters via the expression
where is the oscillator strength, is the change in dipole moment between ground and excited states, and ΔE is the excitation energy. According to this model, systems with strong charge transfer transitions, moderate to large , and low excitation energies are expected to exhibit enhanced β responses.
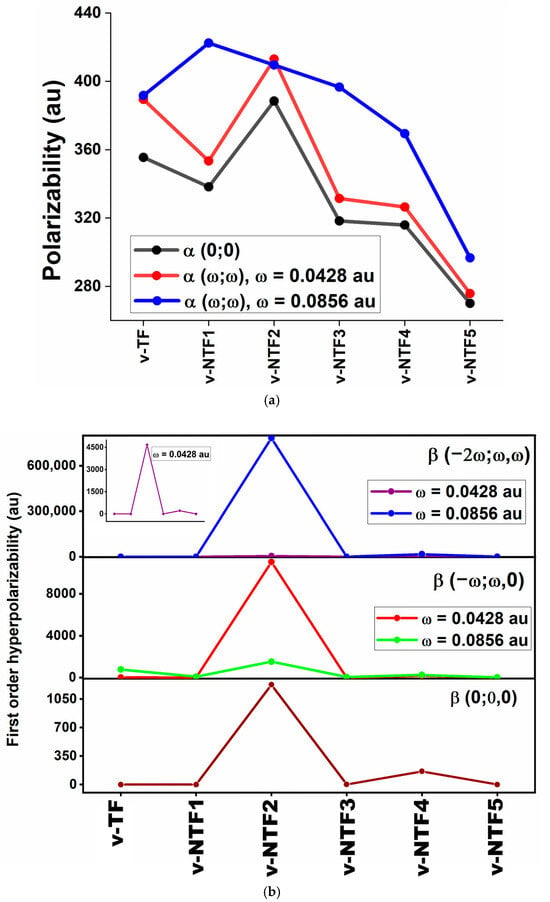
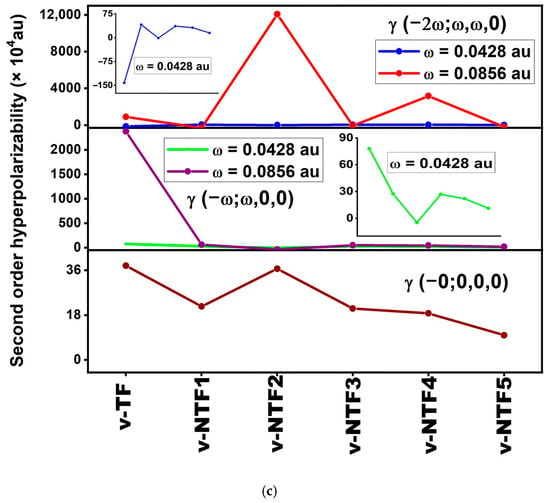
Figure 4.
Static and frequency-dependent (a) polarizability, (b) first-order hyperpolarizability, and (c) second-order hyperpolarizability of vacancy-induced TF and NTFs.
This correlation is clearly observed in v-NTF2, which shows the highest β (1228.048 au), consistent with its lowest ΔE, strong charge transfer character, and reasonable oscillator strength (Table 3). A similar trend is noted for v-NTF4, which also shows a substantial β (162.629 au). In contrast, other systems with higher excitation energies and weaker or localized transitions exhibit minimal β values. These results validate the applicability of the two-level model and emphasize the importance of electronic asymmetry and transition characteristics in tuning the NLO response of TFs.
The application of incident photon frequencies gives rise to two essential NLO phenomena: the electro-optical Pockels effect (EOPE), described by β (−ω; ω, 0), and second harmonic generation (SHG), represented by β (−2ω; ω, ω). These properties are critical in evaluating the frequency-dependent NLO performance of a material under external optical fields. As summarized in Table S3, the studied vacancy-induced and nitrogen-doped TFs show wide variation in their dynamic hyperpolarizabilities depending on both the system’s configuration and the frequency applied. Among all structures, v-NTF2 exhibits exceptionally large values for both β (−ω; ω, 0) and β (−2ω; ω, ω), particularly at ω = 0.0856 au, where it reaches a peak β (−2ω; ω, ω) exceeding 7.8 × 105 au. This remarkable enhancement clearly indicates the presence of strong resonance-assisted charge transfer transitions and efficient nonlinear photon interactions. Similarly, v-NTF4 demonstrates substantial values for both EOPE and SHG responses, especially at a visible frequency, signifying a highly polarizable charge distribution enabled by its symmetric dopant configuration. In contrast, systems like v-NTF3 and v-NTF1 show moderate enhancements, while v-TF displays a sharp increase in dynamic β only under visible excitation, suggesting frequency-sensitive NLO switching behavior. To further understand the third-order NLO behavior of vacancy-modified and nitrogen-doped TFs under applied optical fields, we have evaluated the dynamic second-order hyperpolarizability γ at two standard excitation frequencies (ω = 0.0428 and 0.0856 au). These quantities correspond to two essential optical processes: the DC–Kerr effect, characterized by γ (−ω; ω, 0, 0), and third-harmonic generation (THG), described by γ (−2ω; ω, ω, 0). As shown in Table S4, the dynamic γ responses vary significantly across the studied systems, indicating a strong dependence on both frequency and the underlying electronic structure. Among the doped systems, v-NTF2 displays a strikingly large γ (−2ω; ω, ω, 0) at visible excitation (ω = 0.0856 au), surpassing 1.2 × 105 au. This exceptional third-order response reflects intense ICT characteristics and potential resonance enhancement associated with low-lying excited states and strong π-delocalization. Similarly, v-NTF4 also shows enhanced THG at this frequency, reinforcing the role of dopant distribution and symmetry in modulating nonlinear susceptibility. In contrast, systems like v-NTF1, v-NTF3, and v-NTF5 exhibit small and even negative γ values in certain cases, suggesting weak or destructive interference in nonlinear polarization, possibly due to cancellation effects or localized excitations. Notably, the γ (−ω; ω, 0, 0) values for most systems are positive and increase with frequency, particularly for v-TF and v-NTF3, implying their suitability for DC–Kerr-based modulation. However, the emergence of negative γ values at higher excitation frequencies in v-NTF2 and v-NTF1 suggests possible non-resonant destructive contributions or complex field–molecule interactions that may alter third-order susceptibilities.
Frequency-dependent NLO analysis shows that applied optical fields significantly modulate the α, β, and γ responses of vacancy-engineered and nitrogen-doped TFs. Systems like v-NTF2 and v-NTF4 exhibit strong second- and third-order NLO behavior, making them promising for frequency conversion, optical switching, and photonic applications. These findings highlight the role of structural design and excitation tuning in optimizing TFs for advanced nonlinear optical technologies.
4. Conclusions
Remarkably, the interplay between vacancy defects and nitrogen doping in TFs has been shown to profoundly influence their structural integrity, electronic structure, and optical functionalities. Through comprehensive DFT and TD-DFT analyses, we have demonstrated that introducing a central vacancy disrupts the inherent symmetry of the pristine TF, enabling new pathways for tuning its optoelectronic behavior. Subsequent pyridinic nitrogen doping at specific edge and corner sites further modulates the HOMO–LUMO gap, charge transfer characteristics, and orbital localization, all of which are crucial for enhancing the optical response. Among the doped configurations, v-NTF2 stands out due to its exceptional nonlinear optical performance, characterized by a significantly high first-order hyperpolarizability and strong dynamic responses under visible light excitation. The observed enhancement is closely tied to the asymmetric electron distribution and efficient intramolecular charge transfer facilitated by targeted dopant positioning. These trends are well-supported by conceptual DFT descriptors and energy decomposition analysis, affirming the role of dopant symmetry and defect topology in governing reactivity and stability. Taken together, our findings not only deepen the understanding of structure–property relationships in TFs but also present a rational strategy for designing frequency-dependent NLO-active carbon nanomaterials. This approach holds considerable promise for future applications in UV photodetectors, electro-optic modulators, and advanced photonic devices.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/chemistry7040126/s1, Table S1. Energy decomposition analysis of TF, vacancy-induced TF, and NTFs, Table S2. Static and frequency-dependent polarizabilities of vacancy-induced TF and NTFs, Table S3. First-order static and frequency-dependent hyperpolarizabilities of vacancy-induced TF and NTFs, Table S4. Second-order static and frequency-dependent hyperpolarizabilities of vacancy-induced TF and NTFs.
Author Contributions
Conceptualization, J.D. and P.K.C.; data curation, J.D.; formal analysis, J.D.; funding acquisition, P.K.C.; investigation, J.D.; methodology, J.D. and P.K.C.; project administration, P.K.C.; resources, J.D. and P.K.C.; software, J.D.; supervision, P.K.C.; validation, J.D. and P.K.C.; visualization, J.D.; writing—original draft, J.D.; writing—review and editing, P.K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Department of Science and Technology, India, grant number: SR/S2/JCB-09/2009.
Data Availability Statement
The data that support the findings of this study are included in the article and its Supplementary Materials.
Acknowledgments
J.D. thanks the Anusandhan National Research Foundation for the National Post Doctoral Fellowship (File No.: PDF/2023/000629). P.K.C. would like to thank the Department of Science and Technology, New Delhi, for the J. C. Bose National Fellowship.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb Carbon: A Review of Graphene. Chem. Rev. 2009, 110, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The Rise of Graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.N.R.; Sood, A.K.; Subrahmanyam, K.S.; Govindaraj, A. Graphene: The New Two-Dimensional Nanomaterial. Angew. Chem. Int. Ed. 2009, 48, 7752–7777. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The Electronic Properties of Graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Enyashin, A.N.; Ivanovskii, A.L. Graphene Allotropes. Phys. Status Solidi (B) 2011, 248, 1879–1883. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.; Huang, Q.; Guo, L.; Chen, X. Structural and Electronic Properties of Graphene: A Two-Dimensional Carbon Allotrope with Tetrarings. Phys. Rev. Lett. 2012, 108, 225505. [Google Scholar] [CrossRef]
- Sheng, X.-L.; Cui, H.-J.; Ye, F.; Yan, Q.-B.; Zheng, Q.-R.; Su, G. Octagraphene as a Versatile Carbon Atomic Sheet for Novel Nanotubes, Unconventional Fullerenes, and Hydrogen Storage. J. Appl. Phys. 2012, 112, 074315. [Google Scholar] [CrossRef]
- Tong, Z.; Pecchia, A.; Yam, C.; Dumitrică, T.; Frauenheim, T. Ultrahigh Electron Thermal Conductivity in T-Graphene, Biphenylene, and Net-Graphene. Adv. Energy Mater. 2022, 12, 2200657. [Google Scholar] [CrossRef]
- Ye, X.-J.; Liu, C.-S.; Zhong, W.; Zeng, Z.; Du, Y.-W. Metalized T Graphene: A Reversible Hydrogen Storage Material at Room Temperature. J. Appl. Phys. 2014, 116, 114304. [Google Scholar] [CrossRef]
- El Kassaoui, M.; Lakhal, M.; Benyoussef, A.; El Kenz, A.; Loulidi, M.; Mounkachi, O. Improvement of the Hydrogen Storage Performance of T-Graphene-like Two-Dimensional Boron Nitride upon Selected Lithium Decoration. Phys. Chem. Chem. Phys. 2022, 24, 15048–15059. [Google Scholar] [CrossRef]
- Liu, C.S.; Jia, R.; Ye, X.J.; Zeng, Z. Non-hexagonal symmetry induced functional T graphene for the detection of carbon monoxide. J. Chem. Phys. 2013, 139, 034704. [Google Scholar] [CrossRef]
- Shamim, S.U.D.; Siddique, A.; Dash, B.K.; Ahmed, T.; Shaha, S.; Islam, M.; Piya, A.A. Exploring the Sensing Performance of T-Graphene, T-Boron Nitride, and Their Lateral Heterostructure for Toxic CO, NO, NO2, and SO2 Gas Molecules. Langmuir 2025, 41, 8726–8739. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, A.; Paria, S.; Jana, D. Tetragonal graphene nanodot as carbon monoxide gas sensor and current rectification device. J. Phys. Chem. Solids 2018, 123, 172–182. [Google Scholar] [CrossRef]
- Chowdhury, S.; Majumdar, A.; Jana, D. Search for magnetism in transition metal atoms doped tetragonal graphene: A DFT approach. J. Magn. Magn. Mater. 2017, 441, 523–530. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Dai, X.; Chen, G.; Liu, G. A Record-High Ion Storage Capacity of T-Graphene as Two-Dimensional Anode Material for Li-Ion and Na-Ion Batteries. Appl. Surf. Sci. 2020, 527, 146849. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Y.; Liu, N.; Li, J.; Ouyang, C. Theoretical Prediction of T-Graphene as a Promising Alkali-Ion Battery Anode Offering Ultrahigh Capacity. Phys. Chem. Chem. Phys. 2020, 22, 3281–3289. [Google Scholar] [CrossRef] [PubMed]
- Yadav, N.; Dhilip Kumar, T.J. Si Doped T-Graphene: A 2D Lattice as an Anode Electrode in Na Ion Secondary Batteries. New J. Chem. 2022, 46, 9718–9726. [Google Scholar] [CrossRef]
- Yadav, N.; Dhilip Kumar, T.J. Ab Initio Characterization of N Doped T-Graphene and Its Application as an Anode Material for Na Ion Rechargeable Batteries. Sustain. Energy Fuels 2021, 5, 4060–4068. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Nandy, A.; Chakrabarti, A.; Jana, D. Optical properties and magnetic flux-induced electronic band tuning of a T-graphene sheet and nanoribbon. Phys. Chem. Chem. Phys. 2017, 19, 21584–21594. [Google Scholar] [CrossRef]
- Wang, X.Q.; Li, H.D.; Wang, J.T. Structural stabilities and electronic properties of planar C4 carbon sheet and nanoribbons. Phys. Chem. Chem. Phys. 2012, 14, 11107–11111. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.J.; Yan, X.H.; Xiao, Y.; Guo, Y.D. Electronic and transport properties of T-graphene nanoribbon: Symmetry-dependent multiple Dirac points, negative differential resistance and linear current-bias characteristics. Euro. Phys. Lett. 2014, 107, 37004. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Z.; Zhao, G.; Wang, F. Quantum Confinement Effect on the Electronic and Optical Properties of Two-Dimensional Halide Perovskites. Comput. Mater. Sci. 2023, 230, 112524. [Google Scholar] [CrossRef]
- Huang, Y.C.; Chang, C.P.; Lin, M.F. Magnetic and Quantum Confinement Effects on Electronic and Optical Properties of Graphene Ribbons. Nanotechnology 2007, 18, 495401. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, C.M.; Yang, L.; Chou, M.Y. Quantum Confinement and Electronic Properties of Silicon Nanowires. Phys. Rev. Lett. 2004, 92, 236805. [Google Scholar] [CrossRef]
- Deb, J.; Paul, D.; Sarkar, U. Density Functional Theory Investigation of Nonlinear Optical Properties of T-Graphene Quantum Dots. J. Phys. Chem. A 2020, 124, 1312–1320. [Google Scholar] [CrossRef]
- Sarwar, S.; Yaqoob, J.; Khan, M.U.; Hussain, R.; Zulfiqar, S.; Anwar, A.; Assiri, M.A.; Imran, M.; Ibrahim, M.M.; Mersal, G.A.M.; et al. Deciphering the Role of Alkali Metals (Li, Na, K) Doping for Triggering Nonlinear Optical (NLO) Properties of T-Graphene Quantum Dots: Toward the Development of Giant NLO Response Materials. ACS Omega 2022, 7, 24396–24414. [Google Scholar] [CrossRef]
- Saedi, L.; Alipour, E.; Javanshir, Z.; Vahabi, V. Reversible Hydrogen Adsorption on Li-Decorated T-Graphene Flake: The Effect of Electric Field. J. Mol. Graphics Model. 2019, 87, 192–196. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Pal, P.; Chowdhury, S.; Jana, D. First Principles Raman Study of Boron and Nitrogen Doped Planar T-Graphene Clusters. Mater. Res. Express 2015, 2, 095603. [Google Scholar] [CrossRef]
- Nazir, A.; Shukla, A. Computational Study of Geometry, Electronic Structure, and Low-Lying Excited States of Linear T-Graphene Quantum Dots. J. Phys. Chem. Solids 2025, 207, 112912. [Google Scholar] [CrossRef]
- Lahiri, J.; Lin, Y.; Bozkurt, P.; Oleynik, I.I.; Batzill, M. An Extended Defect in Graphene as a Metallic Wire. Nat. Nanotechnol. 2010, 5, 326–329. [Google Scholar] [CrossRef]
- Kotakoski, J.; Krasheninnikov, A.V.; Kaiser, U.; Meyer, J.C. From Point Defects in Graphene to Two-Dimensional Amorphous Carbon. Phys. Rev. Lett. 2011, 106, 105505. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejčí, O.; Dimosthenous, S.; Kachel, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene Network: A Nonbenzenoid Carbon Allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef]
- Chen, K.; Wang, W.; Chen, L.; Dao, D.V.; Park, J.; Rajendiran, R.; Lee, I.-H.; Li, O.L. Oxygen Vacancy Defect Tungsten-Oxide-Quantum-Dot-Modified Nitrogen-Doped Graphene with Interfacial Tiny Primitives to Boost Oxygen Reduction Reaction. J. Alloys Compd. 2022, 908, 164588. [Google Scholar] [CrossRef]
- Feng, J.; Xu, S.; Xia, C.; Song, N.; Dong, H.; Yu, L.; Dong, L. Density Functional Theory Study of the Relationship between N-Dopants and Vacancy Defects on Graphene Quantum Dots for Oxygen Reduction Electrocatalysis. ACS Appl. Nano Mater. 2024, 7, 21578–21589. [Google Scholar] [CrossRef]
- Zhu, J.; Mu, S. Defect Engineering in Carbon-Based Electrocatalysts: Insight into Intrinsic Carbon Defects. Adv. Funct. Mater. 2020, 30, 2001097. [Google Scholar] [CrossRef]
- Martins, G.; Galvan, A.L.S.; Valenga, M.G.P.; Cardozo Martins, T.A.; Bergamini, M.F.; Marcolino-Junior, L.H. Nitrogen-Doped Graphene Quantum Dots (N-GQDs): A Promising Material for the Development of Electrochemical Immunosensors. ACS Appl. Nano Mater. 2025, 8, 5908–5918. [Google Scholar] [CrossRef]
- Carolan, D.; Rocks, C.; Padmanaban, D.B.; Maguire, P.; Svrcek, V.; Mariotti, D. Environmentally Friendly Nitrogen-Doped Carbon Quantum Dots for next Generation Solar Cells. Sustain. Energy Fuels 2017, 1, 1611–1619. [Google Scholar] [CrossRef]
- Feng, J.; Guo, Q.; Song, N.; Liu, H.; Dong, H.; Chen, Y.; Yu, L.; Dong, L. Density Functional Theory Study on Optical and Electronic Properties of Co-Doped Graphene Quantum Dots Based on Different Nitrogen Doping Patterns. Diam. Relat. Mater. 2021, 113, 108264. [Google Scholar] [CrossRef]
- Jabed, M.A.; Zhao, J.; Kilin, D.; Yu, T. Understanding of Light Absorption Properties of the N-Doped Graphene Oxide Quantum Dot with TD-DFT. J. Phys. Chem. C 2021, 125, 14979–14990. [Google Scholar] [CrossRef]
- Chan, S.-C.; Cheng, Y.-L.; Chang, B.K.; Hong, C.-W. DFT Calculation in Design of Near-Infrared Absorbing Nitrogen-Doped Graphene Quantum Dots. Phys. Chem. Chem. Phys. 2022, 24, 1580–1589. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chattaraj, P.K. Conceptual Density Functional Theory Based Electronic Structure Principles. Chem. Sci. 2021, 12, 6264–6279. [Google Scholar] [CrossRef] [PubMed]
- Chattaraj, P.K.; Sarkar, U.; Roy, D.R. Electrophilicity Index. Chem. Rev. 2006, 106, 2065–2091. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpály, L.v.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Deb, J.; Paul, D.; Sarkar, U.; Ayers, P.W. Characterizing the Sensitivity of Bonds to the Curvature of Carbon Nanotubes. J. Mol. Model. 2018, 24, 249. [Google Scholar] [CrossRef] [PubMed]
- Ghara, M.; Pan, S.; Deb, J.; Kumar, A.; Sarkar, U.; Chattaraj, P.K. A Computational Study on Structure, Stability and Bonding in Noble Gas Bound Metal Nitrates, Sulfates and Carbonates (Metal = Cu, Ag, Au). J. Chem. Sci. 2016, 128, 1537–1548. [Google Scholar] [CrossRef]
- Paul, D.; Sarkar, U.; Ayers, P.W. Impact of Confining Hydrogen Molecule inside Fullerenes: A Glance through DFT Study. J. Mol. Model. 2025, 31, 23. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Account. 2007, 120, 215–241. [Google Scholar]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2011, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The Density Functional Viewpoint. J. Chem. Phys. 1978, 68, 3801–3807. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Ayers, P.W. The Physical Basis of the Hard/Soft Acid/Base Principle. Faraday Discuss. 2007, 135, 161–190. [Google Scholar] [CrossRef]
- Parr, R.G.; Chattaraj, P.K. Principle of Maximum Hardness. J. Am. Chem. Soc. 1991, 113, 1854–1855. [Google Scholar] [CrossRef]
- Miranda-Quintana, R.A.; Chattaraj, P.K.; Ayers, P.W. Finite Temperature Grand Canonical Ensemble Study of the Minimum Electrophilicity Principle. J. Chem. Phys. 2017, 147, 124103. [Google Scholar] [CrossRef]
- Liu, S. Steric Effect: A Quantitative Description from Density Functional Theory. J. Chem. Phys. 2007, 126, 244103. [Google Scholar] [CrossRef]
- Zhao, F.; Zhang, T.; Sui, S.; Chen, Z. Influence on the Optical and Electronic Properties of Graphene Quantum Dots Originating from the S-Doping Site: A Theoretical Investigation. J. Phys. Chem. A 2025, 129, 4357–4363. [Google Scholar] [CrossRef]
- Kurtz, H.A.; Stewart, J.J.P.; Dieter, K.M. Calculation of the nonlinear optical properties of molecules. J. Comput. Chem. 1990, 11, 82–87. [Google Scholar] [CrossRef]
- Yamijala, S.S.; Mukhopadhyay, M.; Pati, S.K. Linear and Nonlinear Optical Properties of Graphene Quantum Dots: A Computational Study. J. Phys. Chem. C 2015, 119, 12079–12087. [Google Scholar] [CrossRef]
- Li, X. Design of novel graphdiyne-based materials with large second-order nonlinear optical properties. J. Mater. Chem. C 2018, 6, 7576–7583. [Google Scholar] [CrossRef]
- Armaković, S.; Armaković, S.J.; Šetrajčić, J.P.; Holodkov, V. Aromaticity, Response, and Nonlinear Optical Properties of Sumanene Modified with Boron and Nitrogen Atoms. J. Mol. Model. 2014, 20, 2538. [Google Scholar] [CrossRef]
- Nath, S.; Bandyopadhyay, A.; Sen, S.; Jana, D. First Principles Investigation of Structural, Electronic and Optical Properties of Synthesized Radiaannulene Oligomers for 6,6,12-Graphyne. J. Phys. Chem. Solids 2021, 153, 109990. [Google Scholar] [CrossRef]
- Ghosh, M.; Nath, S.; Sen, S.; Jana, D. Nonlinear Optical Response and Characteristic Raman Spectra of Phagraphene Quantum Dots. Phys. Scr. 2023, 98, 045109. [Google Scholar] [CrossRef]
- Song, Y.-D.; Wang, Q.-T.; Gao, W.-W.; He, Z.; Wu, Y. Theoretical Study of Electronic and Nonlinear Optical Properties of Novel Graphenylene-Based Materials with Donor–Acceptor Frameworks. J. Mol. Model. 2022, 28, 165. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.J.; Gu, F.L. Tuning the Nonlinear Optical Response of Graphitic Carbon Nitride by Doping Li Atoms. J. Phys. Chem. C 2018, 122, 26635–26641. [Google Scholar] [CrossRef]
- Khan, M.U.; Khalid, M.; Ibrahim, M.; Braga, A.A.C.; Safdar, M.; Al-Saadi, A.A.; Janjua, M.R.S.A. First Theoretical Framework of Triphenylamine-Dicyanovinylene Based Nonlinear Optical Dyes: Structural Modification of π-Linkers. J. Phys. Chem. C 2018, 122, 4009–4018. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).