Density Functional Theory Simulations of Skaergaardite (CuPd) with a Self-Consistent Hubbard U-Correction
Abstract
1. Introduction
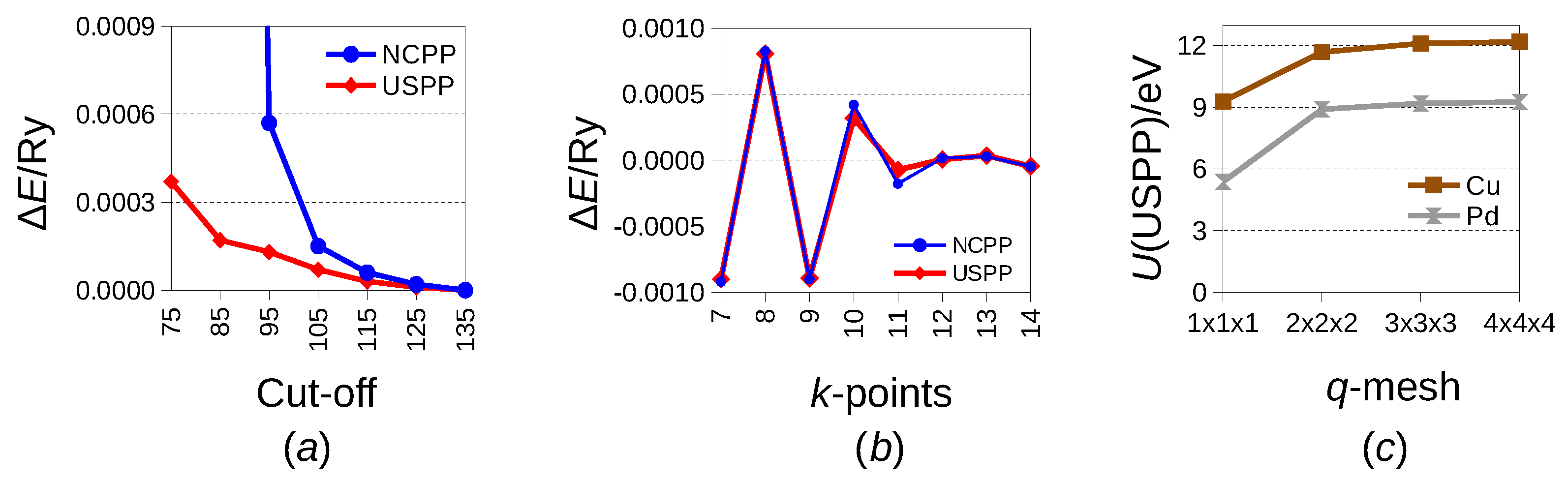
2. Materials and Methods
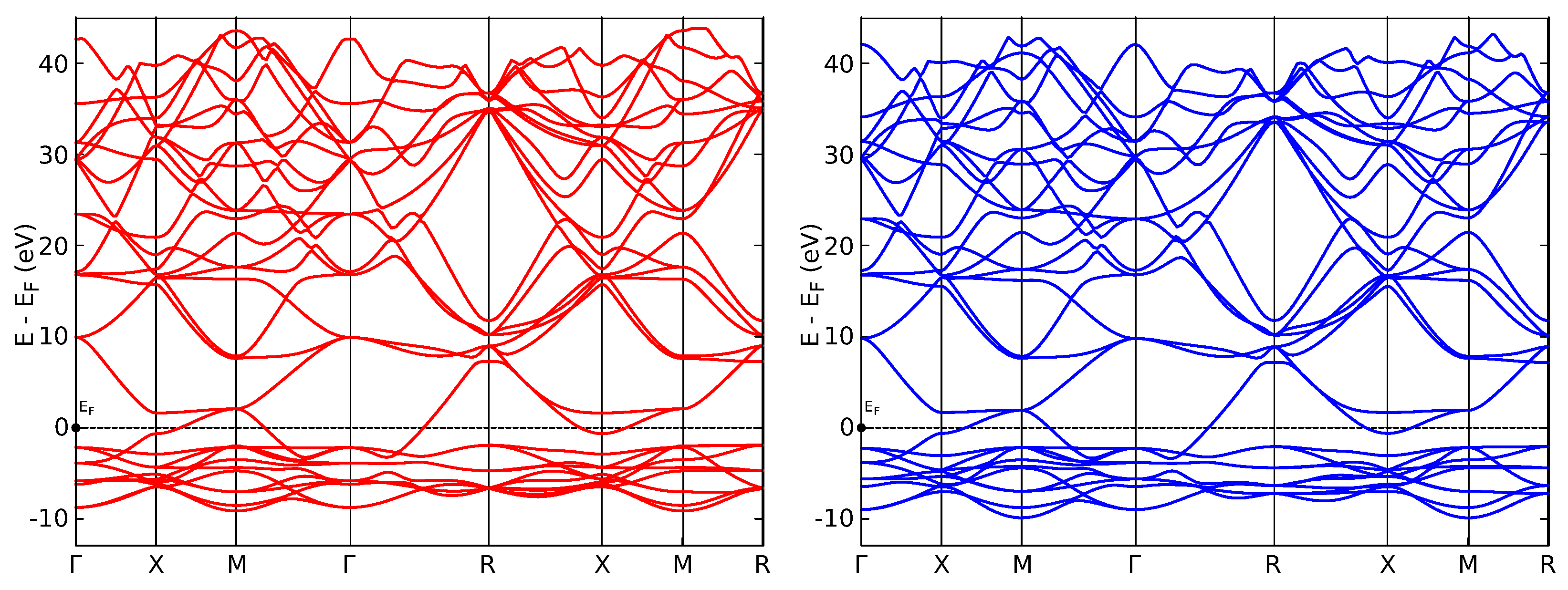
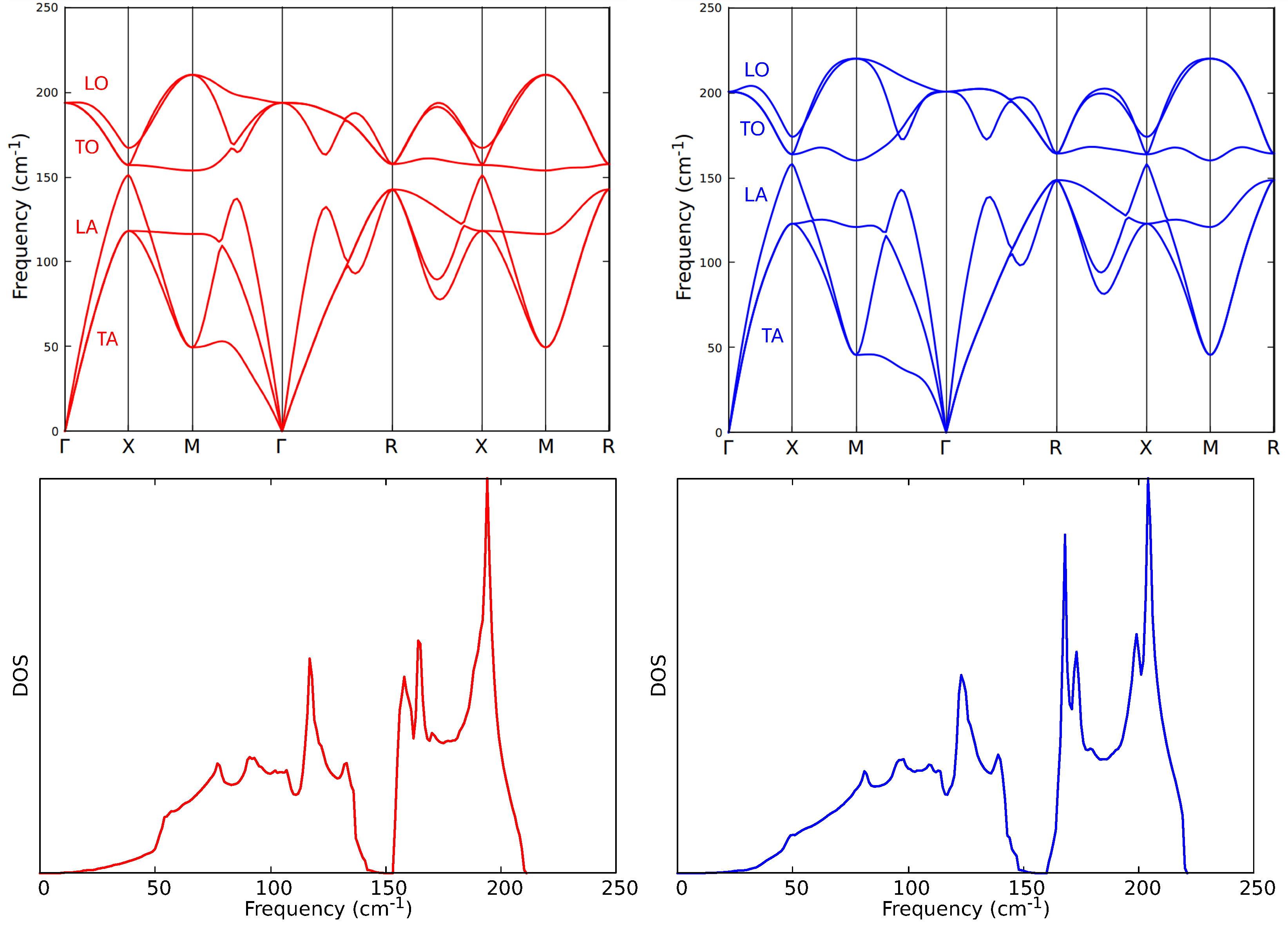
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, Z.; Palmore, G.T.R.; Sun, S. Electrochemical reduction of CO2 catalyzed by metal nanocatalysts. Trends Chem. 2019, 1, 739–750. [Google Scholar] [CrossRef]
- Wang, X.; Kariuki, N.; Vaughey, J.T.; Goodpaster, J.; Kumar, R.; Myers, D. Bimetallic Pd–Cu oxygen reduction electrocatalysts. J. Electrochem. Soc. 2008, 155, B602. [Google Scholar] [CrossRef]
- Woldu, A.R.; Huang, Z.; Zhao, P.; Hu, L.; Astruc, D. Electrochemical CO2 reduction (CO2RR) to multi-carbon products over copper-based catalysts. Coord. Chem. Rev. 2022, 454, 214340. [Google Scholar] [CrossRef]
- Jiang, T.-W.; Jiang, K.; Cai, W.-B. Electrochemical CO2 reduction on Pd-based electrodes: From mechanism understanding to rational catalyst design. J. Mater. Chem. A 2024, 12, 21515–21530. [Google Scholar] [CrossRef]
- Mustafa, A.; Shuai, Y.; Lougou, B.G.; Wang, Z.; Razzaq, S.; Zhao, J.; Shan, J. Progress and perspective of electrochemical CO2 reduction on Pd-based nanomaterials. Chem. Eng. Sci. 2021, 245, 116869. [Google Scholar] [CrossRef]
- Ma, S.; Sadakiyo, M.; Heima, M.; Luo, R.; Haasch, R.T.; Gold, J.I.; Yamauchi, M.; Kenis, P.J.A. Electroreduction of carbon dioxide to hydrocarbons using bimetallic CuPd catalysts with different mixing patterns. J. Am. Chem. Soc. 2017, 139, 47–50. [Google Scholar] [CrossRef]
- Xing, M.; Guo, L.; Hao, Z. Theoretical insight into the electrocatalytic reduction of CO2 with different metal ratios and reaction mechanisms on palladium–copper alloys. Dalton Trans. 2019, 48, 1504. [Google Scholar] [CrossRef]
- Mun, Y.; Lee, S.; Cho, A.; Kim, S.; Han, J.W.; Lee, J. Cu-Pd alloy nanoparticles as highly selective catalysts for efficient electrochemical reduction of CO2 to CO. Appl. Catal. B 2019, 246, 82–88. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Wang, H.-B.; Zhang, F.-F.; Li, J.-W.; Hu, X.-Z.; Yan, S.-W.; Bai, Y.-M.; Zhang, X.; Shen, G.-R.; Yin, P.-F.; et al. Nanocavity enriched CuPd alloy with high selectivity for CO2 electroreduction toward C2H4. Rare Met. 2024, 43, 1513–1523. [Google Scholar] [CrossRef]
- Nie, S.; Wu, L.; Liu, Q.; Wang, X. Entropy-derived synthesis of the CuPd Sub-1nm alloy for CO2-to-acetate electroreduction. J. Am. Chem. Soc. 2024, 146, 29364–29372. [Google Scholar] [CrossRef]
- Piper, J. Diffusion of hydrogen in copper-palladium alloys. J. Appl. Phys. 1966, 37, 715–720. [Google Scholar] [CrossRef]
- Petriev, I.S.; Pushankina, P.D.; Andreev, G.A. Investigation of low-temperature hydrogen permeability of surface modified Pd–Cu membranes. Membr. Membr. Technol. 2023, 5, 360–369. [Google Scholar] [CrossRef]
- Rivera, D.J.; Muhich, C.L. Preventing H2S poisoning of dense Pd membranes for H2 purification using an electric-field: An Ab initio study. Surf. Sci. 2023, 733, 122303. [Google Scholar] [CrossRef]
- Lewis, F.A. The palladium-hydrogen system: Structures near phase transition and critical points. Int. J. Hydrogen Energy 1995, 20, 587–592. [Google Scholar] [CrossRef]
- Zhang, K.; Way, J.D. Palladium-copper membranes for hydrogen separation. Sep. Purif. Technol. 2017, 186, 39–44. [Google Scholar] [CrossRef]
- Subramanlan, P.R.; Laughlin, D.E. Phase equilibrium of Cu-Pd. J. Phase Equilibria 1991, 12, 231–240. [Google Scholar] [CrossRef]
- Geng, F.; Boes, J.R.; Kitchin, J.R. First-principles study of the Cu-Pd phase diagram. Calphad 2017, 56, 224–229. [Google Scholar] [CrossRef]
- Mukundan, V.; Yin, J.; Joseph, P.; Luo, J.; Shan, S.; Zakharov, D.; Zhong, C.-J.; Malis, O. Nanoalloying and phase transformations during thermal treatment of physical mixtures of Pd and Cu nanoparticles. Sci. Technol. Adv. Mater. 2014, 15, 025002. [Google Scholar] [CrossRef]
- Kamakoti, P.; Sholl, D.S. A comparison of hydrogen diffusivities in Pd and CuPd alloys using density functional theory. J. Membr. Sci. 2003, 225, 145–154. [Google Scholar] [CrossRef]
- Rudashevsky, N.S.; McDonald, A.M.; Cabri, L.J.; Nielsen, T.F.D.; Stanley, C.J.; Kretzer, Y.L.; Rudashevsky, V.N. Skaergaardite, PdCu, a new platinum-group intermetallic mineral from the Skaergaard intrusion, Greenland. Mineral. Mag. 2004, 68, 615–632. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. Crystal Structures, 2nd ed.; Interscience Publishers: New York, NY, USA, 1963; Volume 1, pp. 85–237. Available online: https://rruff.geo.arizona.edu/AMS/minerals/Skaergaardite (accessed on 30 March 2025).
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- thermo_pw Is an Extension of the Quantum ESPRESSO Package. Available online: http://qeforge.qe-forge.org/gf/project/thermo_pw/ (accessed on 30 March 2025).
- Perdew, P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. Lond. A 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Timrov, I.; Marzari, N.; Cococcioni, M. Hubbard U-parameters from density-functional perturbation theory. Phys. Rev. B 2018, 98, 085127. [Google Scholar] [CrossRef]
- Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D.; De Vita, A.; Payne, M.C. Thermal Contraction and Disordering of the Al(110) Surface. Phys. Rev. Lett. 1999, 82, 3296–3299. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1652, 65, 349–354. [Google Scholar] [CrossRef]
- Jain, E.; Gitanjali, P.; Chouhan, S.S.; Sanyal, S.P. Structural, electronic, elastic and thermal properties of some transition metal CuX (X = Sc and Pd) intermetallics: A FP-LAPW study. Comput. Mater. Sci. 2014, 52, 3315–3321. [Google Scholar] [CrossRef]
- Benmakhlouf, A.; Daoud, S.; Bouarissa, N.; Allaoui, O. Elastic constants and thermophysical properties of CuPd: First-principles study. Rev. Mex. Fís. 2025, 71, 020501. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 0-471-41526-X. [Google Scholar]
- Napoli, M.; Maris, A. Reference data for Skaergaardite; University of Bologna: Bologna, Italy, 2025. [Google Scholar] [CrossRef]
- Dahal, S.; Kafle, G.; Kaphle, G.C.; Adhikari, N.P. Study of electronic and magnetic properties of CuPd, CuPt, Cu3Pd, and Cu3Pt: Tight binding linear muffin-tin orbitals approach. J. Inst. Sci. Technol. 2014, 19, 137–144. [Google Scholar] [CrossRef]
- Takizawa, S.; Blügel, S.; Terakura, K.; Oguchi, T. Theoretical study of the structural stability of CuPd and CuPt alloys: Pressure-induced phase transition of CuPt alloy. Phys. Rev. 1991, 43, 947. [Google Scholar] [CrossRef]
- Pakdel, S.; Olsen, T.; Thygesen, K.S. Effect of Hubbard U-corrections on the electronic and magnetic properties of 2D materials: A high-throughput study. npj Comput. Mater. 2025, 11, 18. [Google Scholar] [CrossRef] [PubMed]
- Miiller, A.P.; Brockhouse, B.N. Anomalous Behavior of the Lattice Vibrations and the Electronic Specific Heat of Palladium. Phys. Rev. Lett. 1968, 20, 798–801. [Google Scholar]
- Buhrer, W.; Schneider, T.; Gläser, W. Phonon dispersion in copper. Solid State Commun. 1966, 4, 443–446. [Google Scholar] [CrossRef]
- Fultz, B.; Anthony, L.; Nagel, L.J.; Nicklow, R.M.; Spooner, S. Phonon densities of states and vibrational entropies of ordered and disordered Ni3Al. Phys. Rev. B 1995, 52, 3315–3321. [Google Scholar]


| USPP | NCPP | EXP | EXP | EXP | FP-LAPW [33] | USPP [34] | |||
|---|---|---|---|---|---|---|---|---|---|
| PBE-GGA+U | PBE-GGA+U | CuPd | Cu | Pd | PBE-GGA | WC-GGA | PBEsol-GGA | PBE-GGA | |
| a/Å | 3.0531 | 3.0343 | 2.988 [21] | 3.6150 [21] | 3.8898 [21] | 3.0145 | 2.9663 | 2.9560 | 3.002 |
| /Å | 2.6440 | 2.6275 | 2.588 | ||||||
| V/Å3 | 28.459 | 27.937 | 26.677 | ||||||
| /kg m3 | 9918.15 | 10,125.67 | 10,303.04 a | ||||||
| /GPa | 199.78 | 178.18 | 176.2 [35] | 234.1 [35] | 184.03 | 217.54 | 208.66 | 181.07 | |
| /GPa | 163.88 | 154.13 | 124.9 [35] | 176.1 [35] | 144.12 | 173.72 | 185.01 | 150.40 | |
| /GPa | 100.01 | 95.12 | 81.4 [35] | 71.2 [35] | 60.87 | 94.11 | 69.47 | 97.10 | |
| B/GPa | 173.51 | 162.15 | 158.85 | 184.92 | 188.84 | 160.04 | |||
| E/GPa | 131.77 | 118.37 | 108.00 a | 130.21 | |||||
| G/GPa | 48.51 | 43.50 | 38.97 a | 47.70 | |||||
| 0.3583 | 0.3581 | 0.386 a | 0.365 | ||||||
| /m s−1 | 4900.72 | 4663.84 | 4586.79 a | 4635 | |||||
| /m s−1 | 2211.66 | 2074.43 | 2078.34 a | 2138 | |||||
| /m s−1 | 2363.54 | 2191.36 | 2343.30 a | 2408 | |||||
| /K | 290.41 | 287.56 | 291.49 a | 301 | |||||
| USPP | NCPP | |||||
|---|---|---|---|---|---|---|
| Degeneracy | - | Cu | Pd | - | Cu | Pd |
| 2 | −8.766 | 4d 0.48 | 3d 0.52 | −9.009 | 3d 0.45 | 4d 0.55 |
| 1 | −6.219 | 5s 0.54 | 4s 0.46 | −6.485 | 4s 0.94 | – |
| 3 | −5.829 | 4d 0.21 | 3d 0.79 | −5.638 | 3d 0.74 | 4d 0.26 |
| 2 | −3.891 | 4d 0.52 | 3d 0.48 | −3.841 | 3d 0.55 | 4d 0.45 |
| 3 | −2.188 | 4d 0.79 | 3d 0.21 | −2.263 | 3d 0.26 | 4d 0.74 |
| 3 | +9.909 | 4p 0.63 | 5p 0.36 | +9.801 | n.a. | n.a. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Napoli, M.; Maris, A. Density Functional Theory Simulations of Skaergaardite (CuPd) with a Self-Consistent Hubbard U-Correction. Chemistry 2025, 7, 56. https://doi.org/10.3390/chemistry7020056
Napoli M, Maris A. Density Functional Theory Simulations of Skaergaardite (CuPd) with a Self-Consistent Hubbard U-Correction. Chemistry. 2025; 7(2):56. https://doi.org/10.3390/chemistry7020056
Chicago/Turabian StyleNapoli, Martino, and Assimo Maris. 2025. "Density Functional Theory Simulations of Skaergaardite (CuPd) with a Self-Consistent Hubbard U-Correction" Chemistry 7, no. 2: 56. https://doi.org/10.3390/chemistry7020056
APA StyleNapoli, M., & Maris, A. (2025). Density Functional Theory Simulations of Skaergaardite (CuPd) with a Self-Consistent Hubbard U-Correction. Chemistry, 7(2), 56. https://doi.org/10.3390/chemistry7020056






