Fully Conjugated Heteroatomic Non- and Quasi-Alternant Polyradicals
Abstract
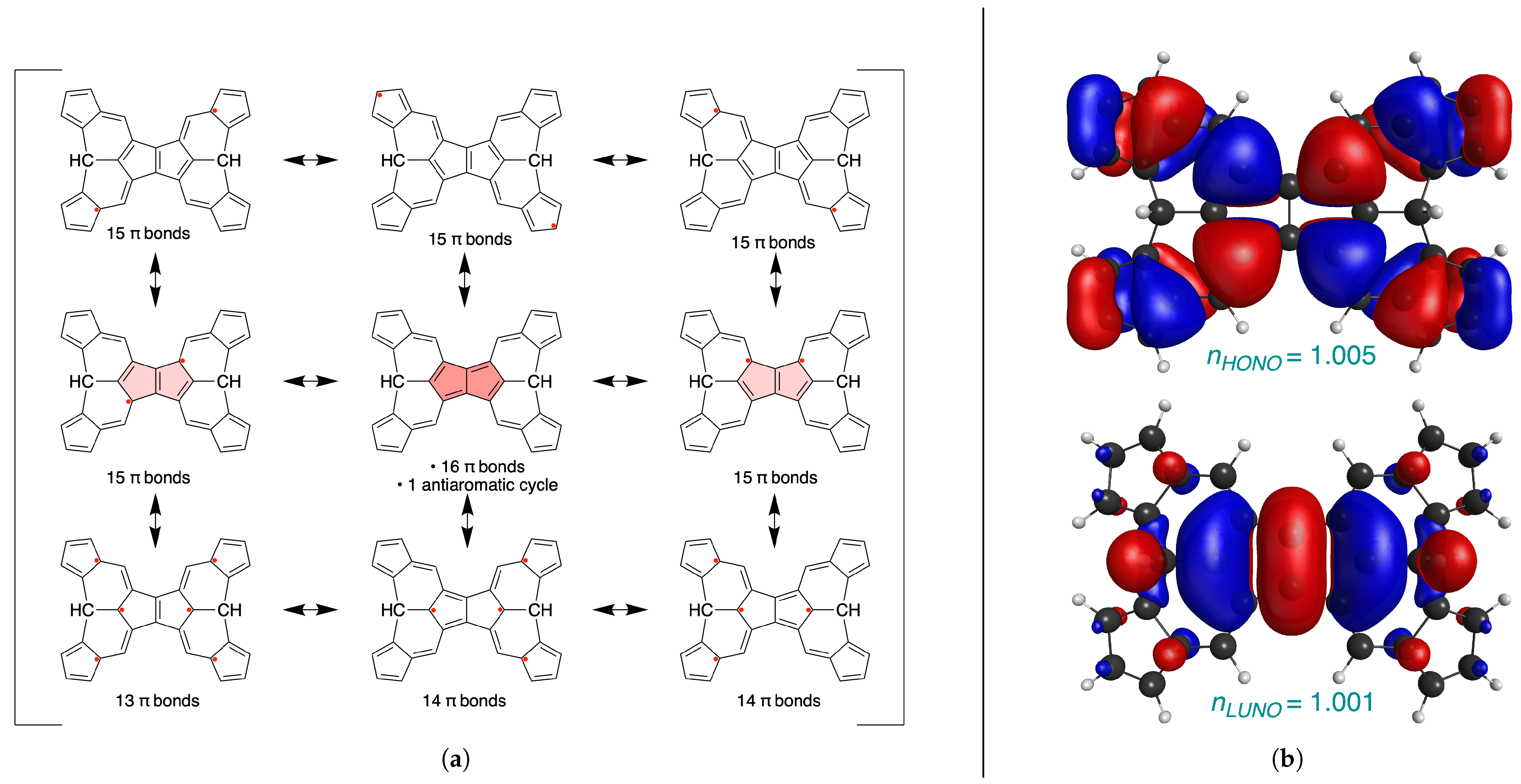
1. Introduction
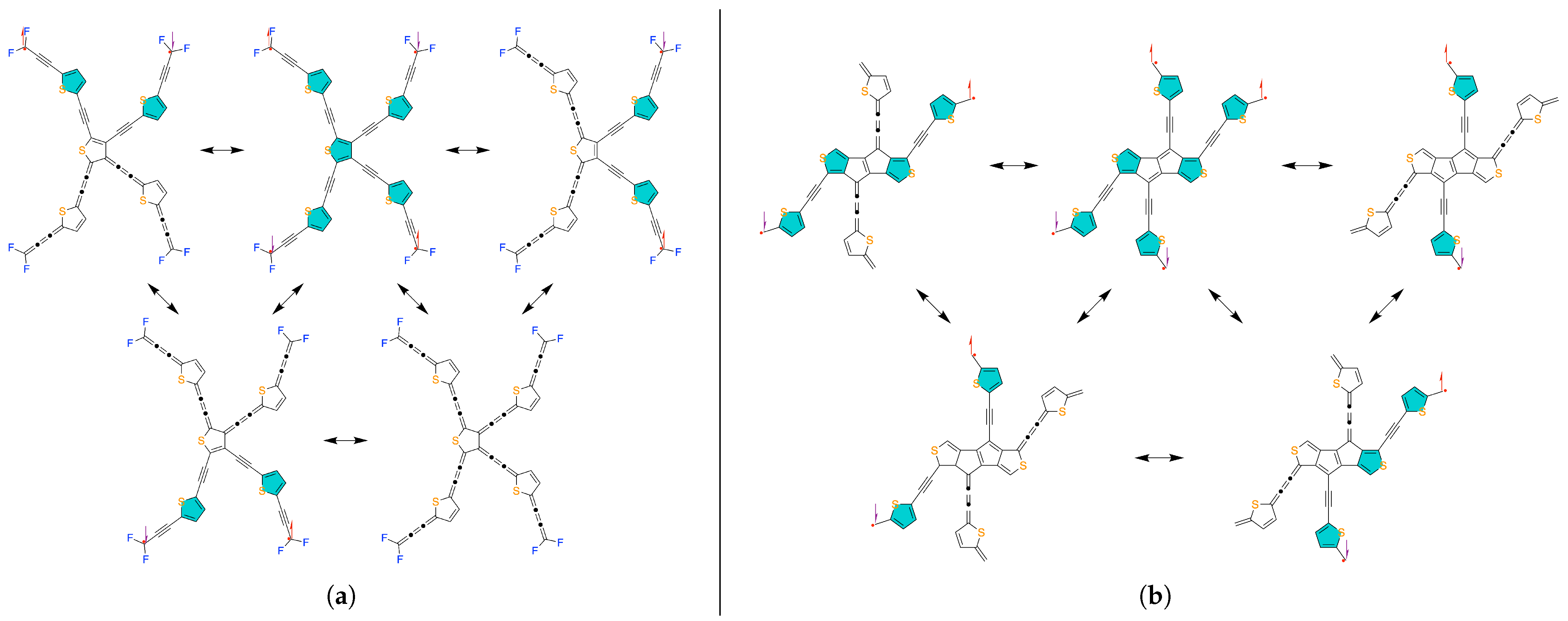
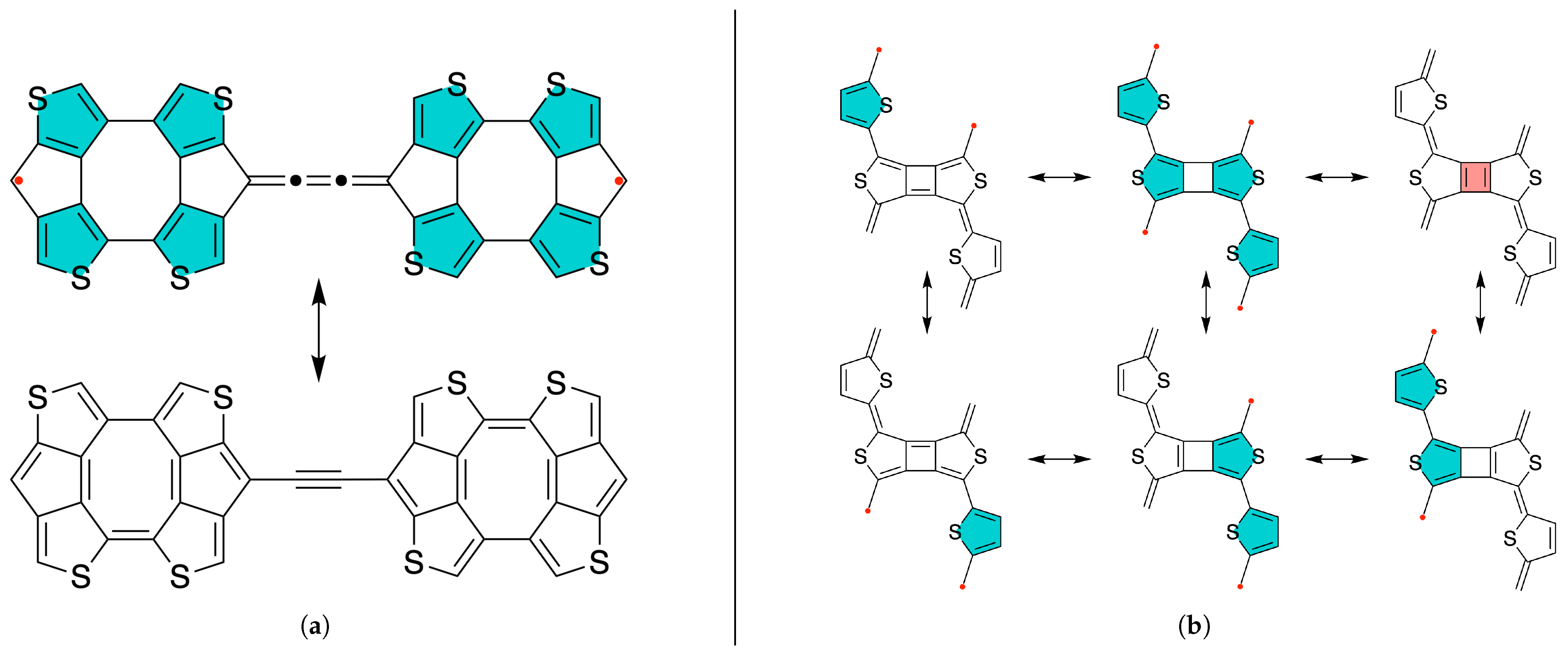
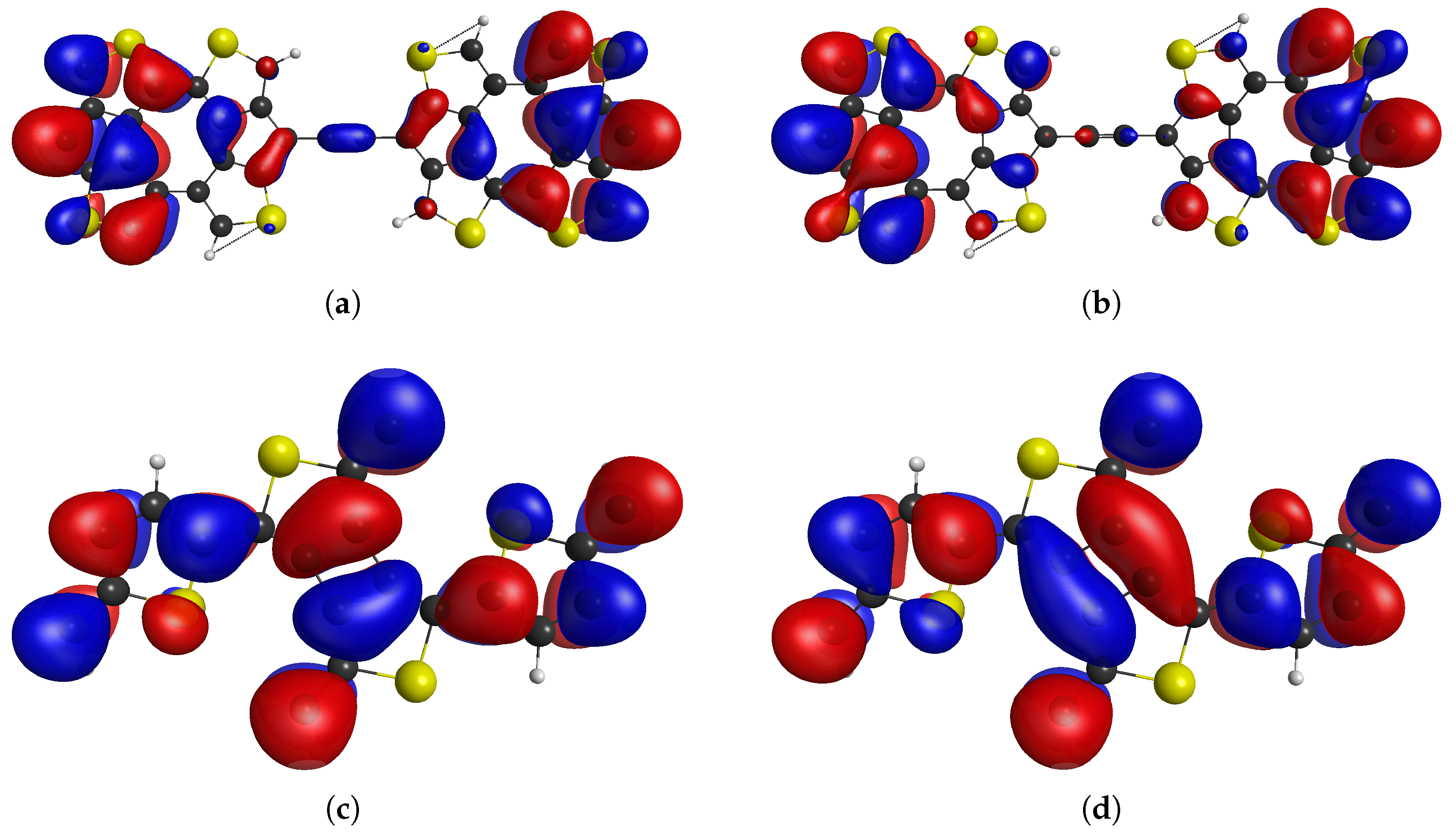
2. Results and Discussion
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zimmerman, P.M.; Zhang, Z.; Musgrave, C.B. Singlet fission in pentacene through multi-exciton quantum states. Nat. Chem. 2010, 2, 648–652. [Google Scholar] [CrossRef]
- Guo, Z.; Park, S.; Yoon, J.; Shin, I. Recent progress in the development of near-infrared fluorescent probes for bioimaging applications. Chem. Soc. Rev. 2014, 43, 16–29. [Google Scholar] [CrossRef]
- Hu, X.; Wang, W.; Wang, D.; Zheng, Y. The electronic applications of stable diradicaloids: Present and future. J. Mater. Chem. C 2018, 6, 11232–11242. [Google Scholar] [CrossRef]
- Okamoto, Y.; Tanioka, M.; Muranaka, A.; Miyamoto, K.; Aoyama, T.; Ouyang, X.; Kamino, S.; Sawada, D.; Uchiyama, M. Stable Thiele’s Hydrocarbon Derivatives Exhibiting Near-Infrared Absorption/Emission and Two-Step Electrochromism. J. Am. Chem. Soc. 2018, 140, 17857–17861. [Google Scholar] [CrossRef] [PubMed]
- Morita, Y.; Nishida, S.; Murata, T.; Moriguchi, M.; Ueda, A.; Satoh, M.; Arifuku, K.; Sato, K.; Takui, T. Organic tailored batteries materials using stable open-shell molecules with degenerate frontier orbitals. Nat. Mater. 2011, 10, 947–951. [Google Scholar] [CrossRef] [PubMed]
- Minami, T.; Nakano, M. Diradical Character View of Singlet Fission. J. Phys. Chem. Lett. 2012, 3, 145–150. [Google Scholar] [CrossRef]
- Varnavski, O.; Abeyasinghe, N.; Aragó, J.; Serrano-Pérez, J.J.; Ortí, E.; López Navarrete, J.T.; Takimiya, K.; Casanova, D.; Casado, J.; Goodson, T.I. High Yield Ultrafast Intramolecular Singlet Exciton Fission in a Quinoidal Bithiophene. J. Phys. Chem. Lett. 2015, 6, 1375–1384. [Google Scholar] [CrossRef]
- Lombardi, F.; Lodi, A.; Ma, J.; Liu, J.; Slota, M.; Narita, A.; Myers, W.K.; Müllen, K.; Feng, X.; Bogani, L. Quantum units from the topological engineering of molecular graphenoids. Science 2019, 366, 1107–1110. [Google Scholar] [CrossRef]
- Cheng, W.; Chen, H.; Liu, C.; Ji, C.; Ma, G.; Yin, M. Functional organic dyes for health-related applications. VIEW 2020, 1, 20200055. [Google Scholar] [CrossRef]
- Betkhoshvili, S.; Poater, J.; Moreira, I.d.P.R.; Bofill, J.M. Leap from Diradicals to Tetraradicals by Topological Control of π-Conjugation. J. Org. Chem. 2024, 89, 19–14006. [Google Scholar] [CrossRef]
- Betkhoshvili, S.; de P. R. Moreira, I.; Poater, J.; Bofill, J.M. Pathway to Polyradicals: A Planar and Fully π-Conjugated Organic Tetraradical(oid). J. Phys. Chem. Lett. 2024, 15, 5243–5249. [Google Scholar] [CrossRef] [PubMed]
- Betkhoshvili, S.; de P., R.; Moreira, I.; Poater, J.; Bofill, J.M. Algorithmic Design of Metal-Free Fully π-Conjugated Organic Polyradicals with Any Ground-State Multiplicity. J. Phys. Chem. C 2025, 129, 4464–4480. [Google Scholar] [CrossRef]
- Ovchinnikov, A.A. Multiplicity of the ground state of large alternant organic molecules with conjugated bonds. Theor. Chim. Acta 1978, 47, 297–304. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C. Some Studies in Molecular Orbital Theory I. Resonance Structures and Molecular Orbitals in Unsaturated Hydrocarbons. J. Chem. Phys. 1950, 18, 265–274. [Google Scholar] [CrossRef]
- Salem, L. The Molecular Orbital Theory of Conjugated Systems; Benjamin Inc.: New York, NY, USA, 1966. [Google Scholar]
- Wade, L.G.; Simek, J.W. Organic Chemistry; Always Learning; Pearson: London, UK, 2022. [Google Scholar]
- Ruedenberg, K.; Sundberg, K.R. MCSCF Studies of Chemical Reactions: Natural Reaction Orbitals and Localized Reaction Orbitals. In Quantum Science: Methods and Structure. A Tribute to Per-Olov Löwdin’; Calais, J.L., Goscinski, O., Linderberg, J., Öhrn, Y., Eds.; Springer: Boston, MA, USA, 1976; pp. 505–515. [Google Scholar] [CrossRef]
- Cheung, L.M.; Sundberg, K.R.; Ruedenberg, K. Dimerization of carbene to ethylene. J. Am. Chem. Soc. 1978, 100, 8024–8025. [Google Scholar] [CrossRef]
- Cheung, L.M.; Sundberg, K.R.; Ruedenberg, K. Electronic rearrangements during chemical reactions. II. Planar dissociation of ethylene. Int. J. Quantum Chem. 1979, 16, 1103–1139. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Sigbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. J. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Johnson, R.P.; Schmidt, M.W. The sudden polarization effect: MC-SCF calculations on planar and 90° twisted methylenecyclopropene. J. Am. Chem. Soc. 1981, 103, 3244–3249. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M.; Almlöf, J.; Heiberg, A.; Roos, B.O. The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule. J. Chem. Phys. 1981, 74, 2384–2396. [Google Scholar] [CrossRef]
- Feller, D.F.; Schmidt, M.W.; Ruedenberg, K. Concerted dihydrogen exchange between ethane and ethylene. SCF and FORS calculations of the barrier. J. Am. Chem. Soc. 1982, 104, 960–967. [Google Scholar] [CrossRef]
- Ruedenberg, K.; Schmidt, M.W.; Gilbert, M.M.; Elbert, S. Are atoms intrinsic to molecular electronic wavefunctions? I. The FORS model. J. Chem. Phys. 1982, 71, 41–49. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Lowdin, P.O. Present Situation of Quantum Chemistry. J. Phys. Chem. 1957, 61, 55–68. [Google Scholar] [CrossRef]
- Yamaguchi, K. The electronic structures of biradicals in the unrestricted Hartree-Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Clar, E. The Aromatic Sextet; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Anglada, J.M.; Poater, J.; Moreira, I.d.P.R.; Bofill, J.M. Controlling the Diradical Character of Thiele Like Compounds. J. Org. Chem. 2023, 88, 8553–8562. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Seth, M.; Ziegler, T. Range-Separated Exchange Functionals with Slater-Type Functions. J. Chem. Theory Comput. 2012, 8, 901–907. [Google Scholar] [CrossRef]
- Förster, A.; Franchini, M.; van Lenthe, E.; Visscher, L. A Quadratic Pair Atomic Resolution of the Identity Based SOS-AO-MP2 Algorithm Using Slater Type Orbitals. J. Chem. Theory Comput. 2020, 16, 875–891. [Google Scholar] [CrossRef]
- Förster, A.; Visscher, L. Double Hybrid DFT Calculations with Slater Type Orbitals. J. Comput. Chem. 2020, 41, 1660–1684. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Barca, G.M.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent Developments in the General Atomic and Molecular Electronic Structure System. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef] [PubMed]
- Zahariev, F.; Xu, P.; Westheimer, B.M.; Webb, S.; Galvez Vallejo, J.; Tiwari, A.; Sundriyal, V.; Sosonkina, M.; Shen, J.; Schoendorff, G.; et al. The General Atomic and Molecular Electronic Structure System (GAMESS): Novel Methods on Novel Architectures. J. Chem. Theory Comput. 2023, 19, 7031–7055. [Google Scholar] [CrossRef] [PubMed]
- Siegbahn, P.; Heiberg, A.; Roos, B.; Levy, B. A Comparison of the Super-CI and the Newton-Raphson Scheme in the Complete Active Space SCF Method. Phys. Scr. 1980, 21, 323–327. [Google Scholar] [CrossRef]
- Pulay, P.; Hamilton, T.P. UHF Natural Orbitals for Defining and Starting MC-SCF Calculations. J. Chem. Phys. 1988, 88, 4926–4933. [Google Scholar] [CrossRef]
- Bofill, J.M.; Pulay, P. The Unrestricted Natural Orbital–Complete Active Space (UNO–CAS) Method: An Inexpensive Alternative to the Complete Active Space–Self-Consistent-Field (CAS–SCF) Method. J. Chem. Phys. 1989, 90, 3637–3646. [Google Scholar] [CrossRef]
- Tóth, Z.; Pulay, P. Comparison of Methods for Active Orbital Selection in Multiconfigurational Calculations. J. Chem. Theory Comput. 2020, 16, 7328–7341. [Google Scholar] [CrossRef]


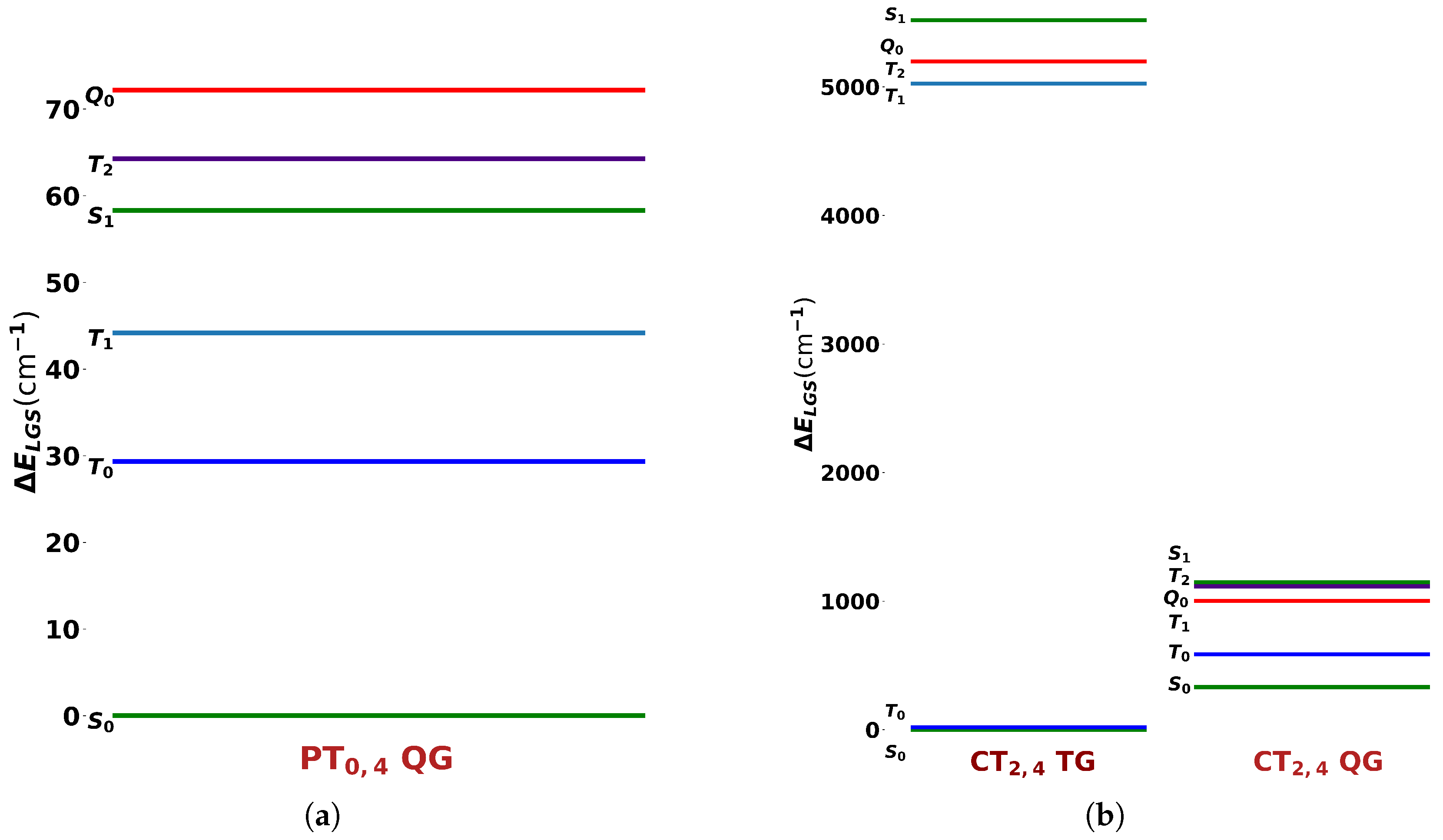
| State | Symmetry | HONO − 1 | HONO | LUNO | LUNO + 1 | from GS (cm−1) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.050 | 1.043 | 0.958 | 0.948 | 0.00 | |||||
| A | 1.037 | 1.012 | 0.989 | 0.962 | 29.34 | |||||
| A | 1.024 | 1.017 | 0.983 | 0.975 | 44.18 | |||||
| A | 1.018 | 1.010 | 0.993 | 0.979 | 58.31 | |||||
| A | 1.011 | 1.008 | 0.991 | 0.990 | 64.25 | |||||
| A | 1.000 | 1.000 | 1.000 | 0.999 | 72.21 | |||||
| State | Symmetry | HONO − 1 | HONO | LUNO | LUNO + 1 | from GS (cm−1) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | 1.848 | * | 1.012 | * | 0.990 | N | 0.160 | 0.00 | ||
| N | 1.852 | * | 1.001 | * | 1.001 | N | 0.157 | 18.84 | ||
| 1.097 | 1.075 | 0.934 | 0.898 | 5197.44 | ||||||
| 1.017 | 1.000 | 1.000 | 0.985 | 5197.44 | ||||||
| 1.017 | 1.000 | 1.000 | 0.985 | 5197.44 | ||||||
| 1.025 | 1.012 | 1.011 | 0.954 | 5517.36 | ||||||
| State | Symmetry | HONO − 1 | HONO | LUNO | LUNO + 1 | from GS (cm−1) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.202 | 1.002 | 0.999 | 0.799 | 0.00 | ||||||
| 1.129 | 1.000 | 1.000 | 0.872 | 254.64 | ||||||
| 1.006 | 1.000 | 1.000 | 0.995 | 671.30 | ||||||
| 1.006 | 1.000 | 1.000 | 0.995 | 671.33 | ||||||
| N/A * | ||||||||||
| 1.025 | 1.012 | 1.011 | 0.954 | 817.11 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betkhoshvili, S.; Poater, J.; Moreira, I.d.P.R.; Bofill, J.M. Fully Conjugated Heteroatomic Non- and Quasi-Alternant Polyradicals. Chemistry 2025, 7, 45. https://doi.org/10.3390/chemistry7020045
Betkhoshvili S, Poater J, Moreira IdPR, Bofill JM. Fully Conjugated Heteroatomic Non- and Quasi-Alternant Polyradicals. Chemistry. 2025; 7(2):45. https://doi.org/10.3390/chemistry7020045
Chicago/Turabian StyleBetkhoshvili, Sergi, Jordi Poater, Ibério de P. R. Moreira, and Josep Maria Bofill. 2025. "Fully Conjugated Heteroatomic Non- and Quasi-Alternant Polyradicals" Chemistry 7, no. 2: 45. https://doi.org/10.3390/chemistry7020045
APA StyleBetkhoshvili, S., Poater, J., Moreira, I. d. P. R., & Bofill, J. M. (2025). Fully Conjugated Heteroatomic Non- and Quasi-Alternant Polyradicals. Chemistry, 7(2), 45. https://doi.org/10.3390/chemistry7020045









