py.Aroma: An Intuitive Graphical User Interface for Diverse Aromaticity Analyses

Abstract

The nucleus-independent chemical shift (NICS) criterion plays a significant role in evaluating (anti-)aromaticity. While being readily accessible even for non-computational chemists, adding ghost atoms for multi-points NICS evaluations poses a significant challenge. In this article, I introduce py.Aroma 4, a freely available and open-source Python package designed specifically for analyzing (anti-)aromaticity. Through its user-friendly graphical interface, py.Aroma simplifies and enhances aromaticity analyses by offering key features such as HOMA/HOMER index computation, Gaussian-type input file generation for diverse NICS calculations and corresponding output processing, NMR spectra plotting, and computational supporting information (SI) generation for scientific manuscripts. Additionally, NICS_⊥ is suggested for evaluating (anti-)aromaticity for non-planar or tilted rings. Pre-compiled executables for macOS and Windows are freely available online. Facilitate accessibility for users lacking programming experience or time constraints.

1. Introduction

The concept of (anti-)aromaticity has risen to prominence as a fundamental concept in both organic and inorganic chemistry, governing the stability and reactivity of cyclic molecules. Since the early conceptual work of aromaticity by August Kekulé, the understanding of this phenomenon has undergone significant expansion [1,2]. According to classic definition as introduced by Hückel, an aromatic molecule must be cyclic and planar with [4n + 2] (n = 0, 1, 2, …) continuous π-electrons conjugation throughout the ring. Conversely, Hückel anti-aromatic molecules have [4n] π-electrons [3,4]. Möbius aromaticity, introduced by Heilbronner in 1964, stands in contrast to Hückel’s aromaticity [5]. While Hückel’s rule associates aromaticity with [4n + 2] π-electrons, molecules with Möbius topology require [4n] π-electrons to be aromatic and [4n + 2] π-electrons to be anti-aromatic [6]. As (anti-)aromaticity is not directly observable, numerous criteria have been developed to assess its presence and its magnitude in molecules, based on structural, energetic, and reactivity characteristics [7,8,9,10,11,12]. Among these, the harmonic oscillator model of aromaticity (HOMA) [8] and nucleus-independent chemical shift (NICS) [13,14,15,16] are two of the most widely employed methods.

NICS calculations represent a magnetic-based criterion for assessing (anti-)aromaticity. This approach aims to evaluate the “degree of shielding” experienced by a hypothetical non-interacting probe atom placed at the position of interest within the induced magnetic field, usually in the center of the ring and/or at some distance away from it. While experimentally unrealizable due to the inherent presence of nuclei and/or electrons in all atoms, theoretical computations can employ dummy atoms, which have no nucleus and no basis functions (such as the “Bq” atom in Gaussian), to approximate this NICS probe and offer valuable insights into its (anti-)aromatic character. The “single-point (SP) NICS” approach, pioneered by Schleyer et al., utilizes a single NICS probe placed at a specific location to quantify and assign (anti-)aromaticity. The NICS value is defined as the reverse value of magnetic shielding; thus, negative NICS values generally indicate shielding from the induced ring current and are associated with aromatic character. Conversely, positive NICS values indicate deshielding and are typically associated with nonaromatic or antiaromatic character [13]. In recent years, NICS has evolved into multi-point methods, offering a more detailed picture of a molecular induced magnetic field. These methods involve placing NICS probes across various regions, including NICS scan [17], NICS-XY-scan [18,19,20], 2D/3D NICS (as recognized as iso-chemical shielding surface, ICSS) [21,22,23,24,25,26,27,28,29], and integrated NICS [30,31]. However, manually adding hundreds to thousands of NICS probes or placing them on tilted/disordered rings without fitting the ring plane is impractical. Each NICS probe calculation requires evaluating the shielding tensor at that specific point. This is because the shielding effect depends on the probe’s position relative to the π-electrons and nuclei in the ring. Placing probes arbitrarily for tilted/disordered rings without fitting the ring plane can lead to inaccurate NICS values, thus leading to overestimation or underestimation of the (anti-)aromaticity. For the hundreds or thousands of probes needed for multi-points NICS calculations, manually adding individual probes is time-consuming and inefficient, especially for large systems. Additionally, analyzing the results from numerous scattered probes can be challenging and difficult to interpret, making it hard to extract meaningful trends.

Here, this paper presents py.Aroma, a user-friendly program package designed specifically for analyzing aromaticity. py.Aroma offers a suite of functionalities for aromaticity analyses, minimizing user investment and simplifying the workflow through its intuitive GUI. This interface allows users to readily access clear visualizations and detailed feedback on their analyses. Furthermore, py.Aroma automates the detection of cyclic systems within the analyzed molecule, alleviating the need for users to manually provide atom numbering. This feature significantly streamlines the analysis process, particularly for complex molecules with multiple cycles.

2. Methods

While several existing programs and projects provide functionalities for NICS computations, they often function as standalone tools or lack user-friendly graphical interfaces (GUIs) (

Table 1. Comparison of py.Aroma with some programs having functionalities for aromaticity analyses. (○: supported by the program by default; —: not supported by the program)

Program	Detect Cycle?	BLA	HOMA, HOMER	POAV	NICS					NMR	GUI
					SP	XY-Scan	2D	3D	INICS
Aroma	—	—	—	—	—	○	—	—	—	—	○
Predi-XY	—	—	—	—	—	○	—	—	—	—	—
Multiwfn	—	○	○ 1	—	○ 2	—	○	○	○	○	—
py.Aroma	○	○	○	○	○	○	○	○	○	○	○

¹ HOMER is not supported by default. ² Cartesian coordinates of ghost atoms cannot be saved to the input file; manual typing is required.

) [32,33,34]. py.Aroma is written in Python 3.11 and offers a comprehensive array of functionalities for aromaticity analysis, including: bond length alternation (BLA) analyses, HOMA and HOMER indices computation, generation of input files for diverse NICS calculations (single-point NICS, NICS-XY-scan, 2D/3D NICS, and integrated NICS: INICS [31]) via commercially available Gaussian software, and extraction of shielding tensors from corresponding output files. As additional functions, py.Aroma allows users to access π-orbital axis vector (POAV) [35,36,37] analysis and create supporting information (SI) for scientific manuscripts. Figure S1 provides a detailed illustration of py.Aroma’s workflow, encompassing these functionalities and technical components.

To achieve its extensive functionality, py.Aroma relies on several third-party libraries: PyQt6 [38] powers the graphical user interface, ensuring user-friendly interactions. NumPy [39] and Matplotlib [40] handle mathematical computations, generate visualizations, and provide interactive 3D molecular structures. NetworkX [41] facilitates the automatic identification of chord-less cycles within molecular structures. OpenPyxl [42] enables users to save BLA, INICS, and 2D NICS results in .xlsx format for further visualization and analysis using external software.

Pre-compiled executables of py.Aroma for macOS and Microsoft Windows can be downloaded from https://wongzit.github.io/program/pyaroma/download (accessed on 18 December 2024), and the complete source code is openly accessible on https://github.com/wongzit/pyAroma (accessed on 18 December 2024). A detailed user manual and examples files are provided within the GitHub repository, guiding users through installation, operation, and advanced features of py.Aroma.

3. Usage

Upon launching py.Aroma, users are presented with a menu bar providing access to the program setting panel, online user manual, py.Aroma homepage, and contact developer via e-mail feature (Figure 1). The user needs to select the desired file to initiate an aromaticity analysis. py.Aroma supports three primary file types: (1) chemical file format (.xyz, .pdb, .mol2); (2) Gaussian input file (.gjf, .com); and (3) Gaussian output file (.log, .out).

The specific functionalities available within the interface are contingent upon the selected file type (Figure S1). This paper delineates a selection of prominent functionalities of py.Aroma. All geometry optimizations herein were performed using the density functional theory (DFT) ωB97X-D [43] functional, along with the 6-31G(d) [44,45] basis set, and NMR calculations were done at the B3LYP/6-31+G(d) [46,47] level of theory without further statement. Gaussian 16 B.01 [48] served as the computational platform for all calculations.

3.1. Compute HOMA and HOMER Index

HOMA stands as a widely recognized and successful metric for quantifying aromaticity [49]. The HOMA index is defined as follows:

$$\mathrm{H}\mathrm{O}\mathrm{M}\mathrm{A}=1-{\displaystyle \frac{\alpha }{n}}{\sum }_{i=1}^n{\left(R_i-R_{\mathrm{o}\mathrm{p}\mathrm{t}}\right)}^2,$$

(1)

where R_i indicates for i-th bond of examined cycle and R_opt stands for the optimal bond length. py.Aroma employs the default HOMA parameters α and R_opt, as sourced from Refs. [8,50,51,52]. It has been reported that the HOMA index works exceptionally well as an index of molecular similarity, as long as the reference molecule is modified [53]. Thus, users retain the flexibility to modify these parameters within the program settings panel to tailor their analyses. In 2023, Arpa and Durbeej proposed the Harmonic Oscillator Model of Excited-state aRomaticity (HOMER) as a valuable extension to the established HOMA method for ground-state molecules [12]. This timely development aligns with the growing research interest in excited-state properties, and the HOMER index has gained support in the py.Aroma program.

As a geometry-based method, HOMA/HOMER calculations are accessible across all file types supported by py.Aroma. Upon molecular structure reading, the chordless_cycle function in the NetworkX library automatically identifies all cyclic subunits within the molecular geometry. Subsequently, py.Aroma computes the HOMA/HOMER index for each detected ring, providing a comprehensive assessment of aromaticity distribution within the molecule (Figure 2).

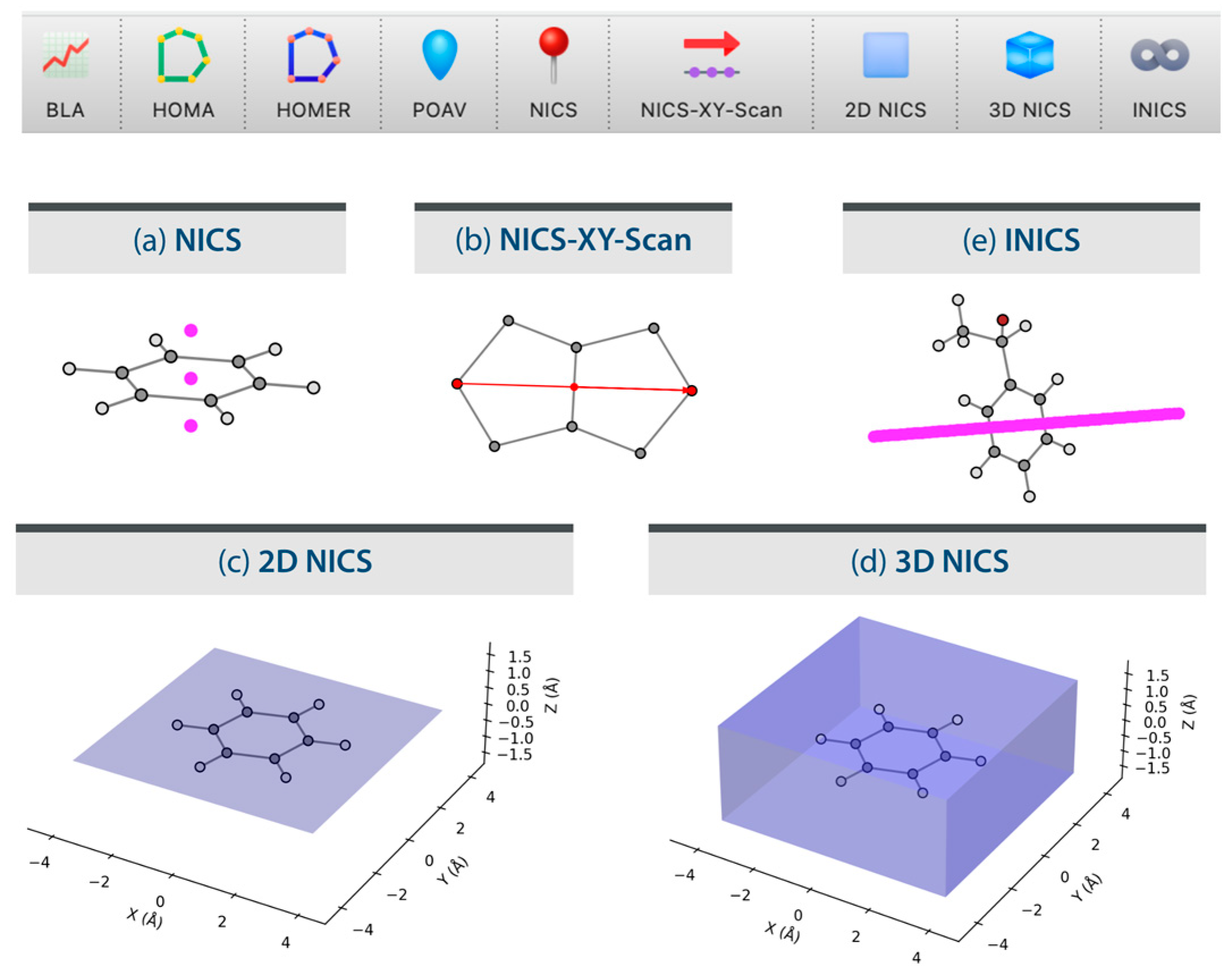
3.2. Generate Gaussian Input Files for NICS Calculations

NICS remains the most prominent computational tool for evaluating aromaticity. A negative NICS index signifies aromatic character, while a positive value indicates antiaromaticity. Values close to zero suggest nonaromaticity or weak (anti-)aromaticity [54]. To determine that, NICS calculations require placing “dummy atoms” (in Gaussian, Bq atom), which are the NICS probes, at examined positions. py.Aroma streamlines this process by enabling users to add ghost atoms for all cyclic subunits with a single click (Figure 3a). This process is achieved by employing the following steps: (1) plane fitting: py.Aroma utilizes the least squares method to identify the plane that best fits the chosen cycle; (2) coordinate projection: atoms within the cycle are projected onto the fitted plane; (3) normal vector calculation: the normal vector of the fitted plane is determined based on the projected positions; and (4) ghost atom placement: Cartesian coordinates for ghost atoms are computed using the normal vector and the center coordinates of the chosen cycle.

Beyond single-point NICS analyses, py.Aroma allows users to efficiently generate input files for multi-point NICS calculations (Figure 3b–e). Before saving the files, users can customize calculation methods (e.g., NMR method, computational level, charge, spin multiplicity, etc.) through a build-in calculation setup window (Figure S2).

3.3. Process Gaussian Output Files for NICS Calculations

py.Aroma can process Gaussian output files generated from NICS calculations, allowing users to readily access, confirm, and analyze the results. Notably, several studies have highlighted the ZZ component of the shielding tensor, such as NICS(0)_ZZ or NICS(1)_ZZ, as a more accurate descriptor of aromaticity compared with the traditional NICS(0) definition [55]. However, NICS_ZZ applying ZZ components solely reflect the out-of-plane shielding under the specific condition of a planar system aligned parallel to the XY plane. For planar systems aligned differently, such as parallel to the XZ or YZ plane, the out-of-plane component would be captured by the YY or XX component of the shielding tensor, respectively. While individual XX, YY, and ZZ components of the shielding tensor are readily accessible within the Gaussian output file, extracting the out-of-plane component directly becomes challenging for non-planar or tilted ring systems deviating from the Cartesian planes. This limitation necessitates alternative approaches for accurately assessing aromaticity in such systems. To overcome this limitation, the py.Aroma offers the NICS_⊥ calculation. This quantity represents the pseudo-ZZ component of the shielding tensor, providing a more generalizable measure of out-of-plane magnetic susceptibility and aromaticity across diverse molecular geometries. This alternative metric is computed by the unit normal vector of the ring plane and the shielding tensors extracted from the Gaussian output file (Figure 4a). For a ring defined by specific atoms, the best-fit plane is determined using the least squares method, with the equation of the plane given in Equation (2) (Figure 4b). The unit normal vector n of the fitted plane is obtained according to Equation (3):

$$ax+by+cz+d=0$$

(2)

$$\mathit{n}=\left(a,b,c\right),\sqrt{a^2+b^2+c^2}=1$$

(3)

According to vector and tensor operations, the tensor σ_⊥ perpendicular to a given ring is calculated as Equation (4), where σ is the original tensor, n is the column unit vector perpendicular to the defined ring, and n^T is the transpose of n. Thus, the NICS_⊥ tensor perpendicular to a given ring is calculated as Equation (5):

$${\sigma }_{\perp }={\mathit{n}}^{\mathrm{T}}\sigma \mathit{n}$$

(4)

$${\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\perp }={a^2\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{X}\mathrm{X}}+ba{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{Y}\mathrm{X}}+ca{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{Z}\mathrm{X}}+ab{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{X}\mathrm{Y}}+b^2{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{Y}\mathrm{Y}}+cb{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{Z}\mathrm{Y}}+ac{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{X}\mathrm{Z}}+bc{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{Y}\mathrm{Z}}+c^2{\mathrm{N}\mathrm{I}\mathrm{C}\mathrm{S}}_{\mathrm{Z}\mathrm{Z}}$$

(5)

Figure 4. (a) An example of shielding tensors from the NICS output. (b) The best-fit plane is marked in a rectangle for a phenyl ring in [7]cycloparaphenylene.

Figure 4. (a) An example of shielding tensors from the NICS output. (b) The best-fit plane is marked in a rectangle for a phenyl ring in [7]cycloparaphenylene.

To validate the accuracy and reliability of the pseudo-ZZ component, NICS_⊥, a case study was conducted utilizing [8]cycloparaphenylene ([8]CPP) as the subject molecule (Figure 5a). For comparison, a similar calculation was performed on the linear derivative, [8]paraphenylene ([8]LPP), employing the same methodology (Figure 5b). In the case of [8]LPP, the examined ring (fifth phenyl ring from the left) lies perfectly within the XY plane. Consequently, the calculated NICS(1)_ZZ value at the B3LYP/6-31+G(d) level of theory of −24.06 directly reflects its pronounced out-of-plane aromaticity [44,45,56,57]. Conversely, the ring of interest in [8]CPP is not aligned parallel to any of the Cartesian planes. In the case of a non-planar system like this, directly extracting the ZZ component from the output file (−6.52 and −3.90 for NICS(1)_ZZ and NICS(−1)_ZZ [58], respectively) would not accurately reflect its local aromaticity compared with [8]LPP. For a more direct comparison of out-of-plane aromaticity between [8]CPP and [8]LPP, the NICS(1)_⊥ metric calculated using the py.Aroma was employed. This metric specifically assesses the pseudo-ZZ component of the shielding tensor, providing a more generalizable measure for non-planar geometries. The calculated NICS(±1)_⊥ values by Bq atoms 81 and 82 within [8]CPP were −25.66 and −20.92, respectively. These large negative values identical to that of [8]LPP (–24.06) indicate a significant out-of-plane aromaticity comparable with that observed in [8]LPP, highlighting the effectiveness and accuracy of NICS_⊥ for characterizing aromaticity in non-planar and tilted systems. A comprehensive investigation of the aromaticity based on the NICS metric of all phenyl rings in [8]CPP and [8]LPP is provided in the Supplementary Materials (Table S1).

py.Aroma demonstrates a capacity for the recognition of multi-points NICS calculation types directly from the output file names (Figure S1). This capability enables the program to deliver tailored visualizations and analyses for diverse NICS methods (Figure 6): For NICS-XY-scan calculations, py.Aroma generates informative scan traces, visually depicting the evolution of NICS values along a specified axis or trajectory (Figure 6b). In 2D NICS calculations, py.Aroma constructs 2D heatmaps, effectively capturing the spatial distribution of NICS values across a molecular plane (Figure 6c). For 3D NICS outputs, py.Aroma enables users to export shielding tensors into Gaussian .cube files. These files seamlessly integrate with numerous visualization software packages, further empowering the exploration and analysis of 3D NICS patterns (Figure 6d).

Although NICS and its derivatives have played a significant role in evaluating aromaticity and have been widely applied since their initial definition in 1996, careful attention must be given to the reliability of result interpretation. Previous studies have reported instances where NICS indices fail, not only in complexes, transition-metal clusters, and weak interaction systems, but also in certain organic molecules [59,60,61,62,63,64,65]. Therefore, it is important to use multiple descriptors to assess aromaticity and reach a comprehensive conclusion.

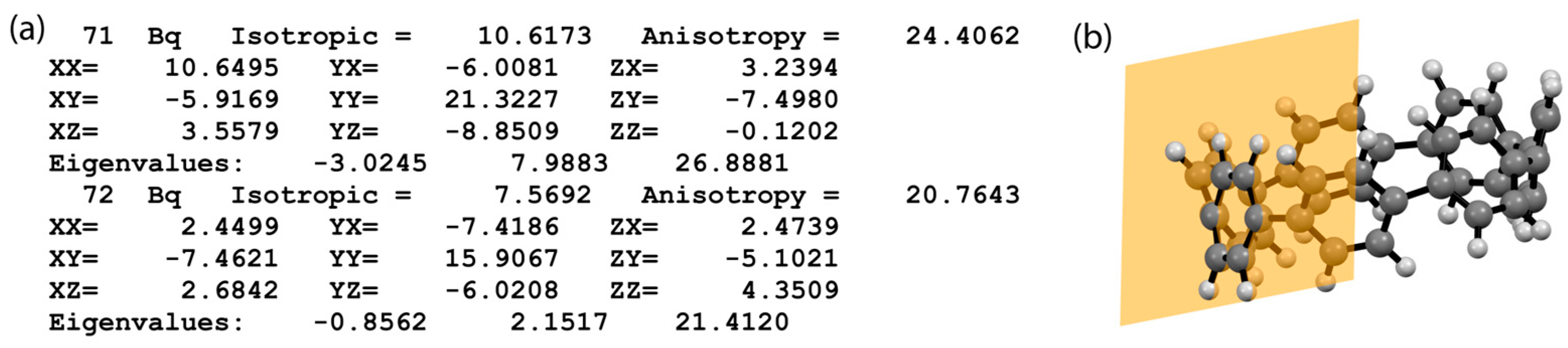
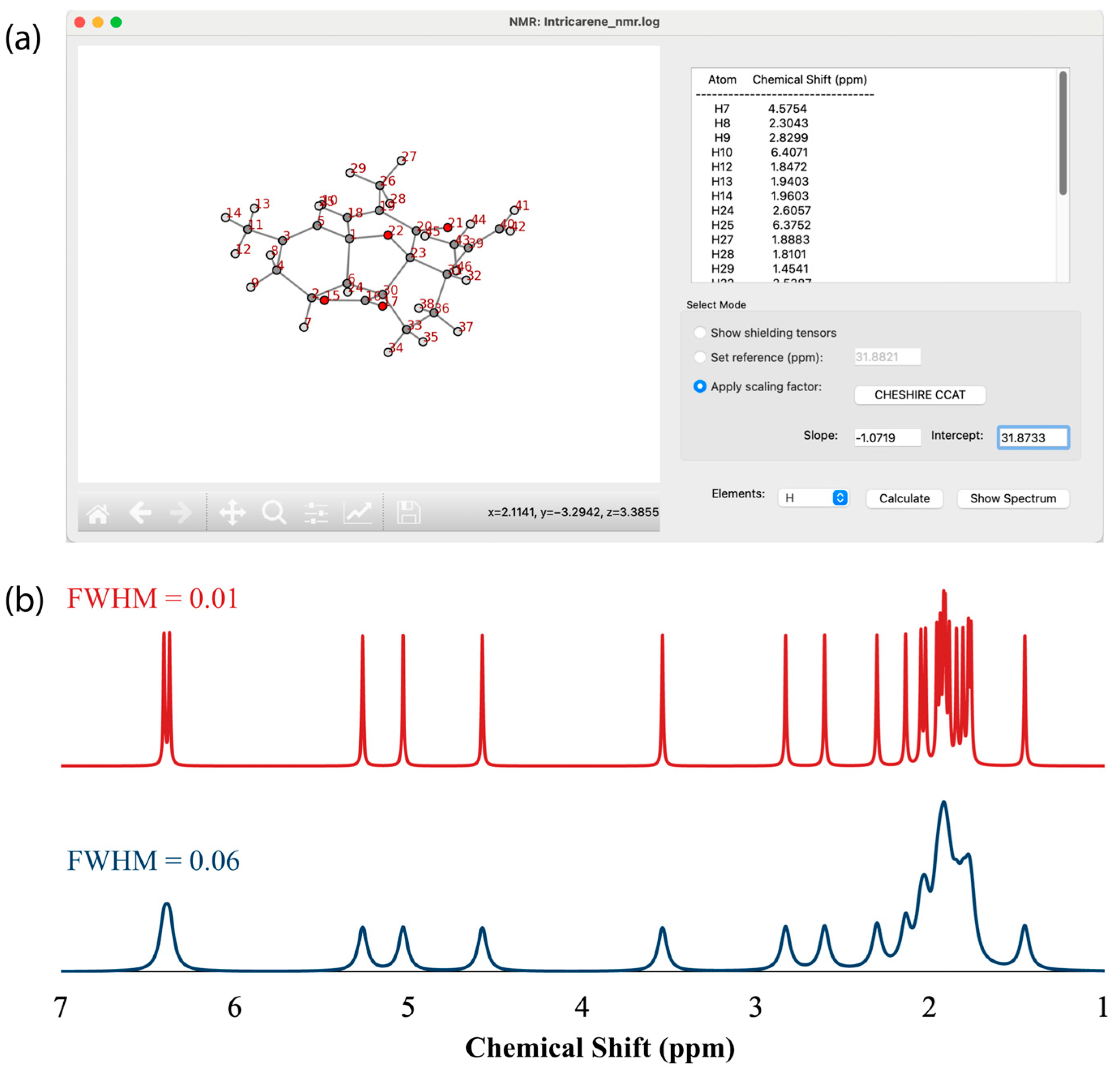
3.4. NMR Spectrum

While NICS calculations remain its core functionality, py.Aroma also provide an NMR plotting module, allowing users to enrich their research. The NMR module within py.Aroma facilitates the generation of informative NMR spectra based on the extracted shielding tensors. Three modes are available: (1) direct visualization: this mode generates an NMR spectrum where individual peaks correspond directly to the calculated shielding tensors, providing a straightforward representation of the magnetic environment surrounding each nucleus; (2) chemical shift referencing: users can designate a specific peak as a reference, prompting the program to adjust all other peaks on the spectrum based on their respective chemical shifts relative to the chosen reference; and (3) scaled chemical shift analysis: py.Aroma allows users to apply scaling factors [66,67] to the shielding tensors before generating the spectrum (Figure 7a).

To achieve a realistic representation of NMR spectra, py.Aroma employs the Lorentzian function (Equation (6)) to broaden the theoretical peaks with a user-defined line width. This convolution accounts for natural line-broadening phenomena typically observed in real-world NMR experiments.

$$L\left(x\right)={\displaystyle \frac{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}}{2\pi }}{\displaystyle \frac{1}{{(x-x_i)}^2+0.25\times {\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}}^2}}$$

(6)

The full width at half maximum (FWHM) determines the peak shape, and it is set to 0.01 in py.Aroma by default (Figure 7b).

3.5. Generate Computational Supporting Information

The generation of comprehensive and well-formatted supporting information (SI) stands as a critical task in manuscript preparation for computational chemistry research. This often involves manipulating and summarizing huge amount of output files, manually extracting key data such as optimized geometries, and compiling them into a standardized format. Recognizing this significant burden, py.Aroma incorporates an SI module to streamline this process. Previously, a pioneering tool offered a similar solution for automated SI generation [70]. However, its website seems to have been removed [71], which prompted the integration of this functionality within py.Aroma to ensure availability and accessibility for the scientific community. The SI module seamlessly activates when a Gaussian output file without ghost atoms is opened in py.Aroma. Based on the job type (e.g., opt, sp, freq, etc.), the program automatically extracts and formats pertinent information for inclusion in the SI file. This includes:

• Routine section: identifies the computational method and basis set employed.
• Charge and spin multiplicity: specifies the electronic configuration of the system.
• Point group: characterizes the molecule’s symmetry.
• Electronic energy: provides the optimized ground-state energy in hartree units.
• Cartesian coordinates: compiles the atomic positions of the optimized geometry.
• Number of imaginary frequencies (freq jobs only): indicates vibrational stability or instability.
• Thermal parameters (freq jobs only): summarizes relevant thermodynamic properties, including zero-point energy, thermal energy, enthalpy, and free energy.

Furthermore, py.Aroma allows users to edit the SI output format by choosing between .txt and .xlsx files, catering to different preferences and software compatibility. While py.Aroma is designed to simplify workflows and assist researchers in preparing SI, the program serves as a tool to support, not replace critical scientific judgment. It is important to analyze and interpret the generated data thoughtfully.

4. Conclusions

This work introduces py.Aroma, a user-friendly Python program designed to streamline and enhance aromaticity analyses. The program facilitates various calculations and visualizations related to aromaticity, including HOMA/HOMER indices, single-point and multi-points NICS calculations, NMR spectrum visualization, and bond length alternation analyses. Its intuitive graphical interface minimizes entry barriers, making it accessible to both computational and experimental chemists. While the current version only supports Gaussian input and output files, I am actively developing functionalities for additional computational packages, such as ORCA [72,73]. I remain open to suggestions for further enhancements and believe that py.Aroma will prove to be a valuable tool for the broader chemistry community.