Abstract
The dn number or configuration is a very useful parameter in transition metal chemistry because it conveys information about the expected properties of a d-block metal complex, including its shape, magnetism, thermodynamic stability, kinetic lability, and spectroscopic properties. The dn number can be determined from either the oxidation state (OS) or valence number (VN) of the metal centre, and since, in most cases, these are numerically equal, the derived dn value is the same. However, examples are discussed where the OS and VN are not equal, which results in unavoidable ambiguities in dn values. Following a discussion of these examples, a revised definition of dn is proposed based on the occupation of the frontier molecular orbitals of the complex.
1. Introduction
The importance of the d-block or transition elements in, for example, synthesis, catalysis, biological inorganic chemistry, and in numerous solid-state materials would be hard to overstate, and understanding their chemistry is, therefore, both a central pillar of any undergraduate chemistry course and essential to many research programmes (Appendix A Note 1). In seeking to understand and explain the chemistry of these elements, an appreciation of the characteristics of electrons in d orbitals is obviously indispensable, and most textbooks and undergraduate courses begin with an account of Crystal Field Theory (CFT) before progressing to a more detailed treatment using Ligand Field Theory (LFT), the latter being essentially a molecular orbital (MO) description of transition metal complexes. Several current and many older texts offer a detailed explication of both CFT and LFT, which will be no more than briefly adumbrated here, but a key feature of any analysis is the nature and extent of d orbital splitting in a crystal/ligand field and the number of electrons formally assigned to the d orbitals (Appendix A Note 2) [1,2,3,4,5]. This latter feature is generally enumerated as n in the term dn, and it is widely accepted that assigning a dn number is particularly useful for rationalising many of the properties of transition metal complexes. There are, nevertheless, some intrinsic ambiguities in dn assignments in some instances, not least because of certain differences in how n is determined according to the oxidation state (OS) and the Covalent Bond Classification (CBC) methods. The primary objective of this article will be to discuss these ambiguities and offer some suggestions on how to resolve them with a principal focus on how this topic is taught at the undergraduate level whilst recognising that many of the basic principles are relevant to several current areas of research.
2. A Definition of the dn Number and Why It Is a Useful Parameter
A general definition of the dn number can be ascertained from the following representative literature quotes:
- ‘The dn configuration is the number of electrons that are housed in metal d orbitals that are either primarily non-bonding or have metal–ligand antibonding character.’ (Appendix A Note 3) [6,7].
- ‘The number of d-electrons generally describes the number of electrons not involved in the primary metal–ligand bonding interactions.’ [8].
- ‘…in the dn configuration using the definition that this quantity refers to electrons in d-based molecular orbitals that are not considered to be bonding.’ [9].
- ‘…the dn configuration corresponds to the number of electrons in d-based molecular orbitals that are formally localised on the metal after bond formation, i.e., those that are not components of metal–ligand bonding orbitals.’ [9].
The key distillate from these four definitions is that the electrons included in the dn number should not be involved in significant metal–ligand bonding interactions or, to put it another way, should reside only in orbitals that are non-bonding or metal–ligand antibonding. However, the adjective ‘primary’ and the adverb ‘primarily’ employed in the first two quotes are inherently subjective, with the consequence that the assignment of a dn number remains open to interpretation, at least in some circumstances. Whilst there is a general consensus on the usefulness of dn for the great majority of complexes, divergences arise in determining the value of n in two broad areas, namely: (a) when the oxidation state (OS) and valence number (VN) of the metal in the complex are not the same and (b) when a dn number has been determined computationally that differs from the value assigned using either OS or VN methods (Appendix A Note 4) [10,11,12,13] (Appendix A Note 5) [14,15,16,17]. In the sections that follow, many of the general areas of divergence will be discussed before concluding with some final observations and a proposed, modified definition of the dn number.
Before proceeding, however, it is important to reiterate that a dn configuration is a very useful heuristic, especially in an educational setting, because it allows the following features (the list is not exhaustive) to be readily understood, interpreted, rationalised, and, in some cases, predicted, at least to a first approximation:
- (i)
- The magnetic properties of complexes based on the number of unpaired electrons present, which includes a consideration of whether the complex is low spin or high spin according to the relative magnitude of the crystal field splitting energy (Δ) vs. the electron pairing energy (P) (Appendix A Note 6).
- (ii)
- The expectation that d0 complexes should not be susceptible to oxidation at the metal centre.
- (iii)
- The observation that many four-coordinate d8 metal complexes are square planar, whereas four-coordinate d10 and d0 complexes are almost invariably tetrahedral (Appendix A Note 7) [18].
- (iv)
- The observation that octahedral coordination is particularly favourable for metals with a d6 or a d3 configuration.
- (v)
- Whether or not complexes are kinetically labile or inert with respect to ligand substitution reactions according to the magnitude of the crystal/ligand field stabilisation energy (CFSE/LFSE) and the derived crystal/ligand field activation energy.
- (vi)
- The rationalisation of trends in lattice energies and hydration energies according to the magnitude of the CFSE/LFSE.
- (vii)
- The mechanisms of homogeneous catalysis by late transition metal complexes, which frequently involve interchange between d6, d8 and d10 species.
- (viii)
- Jahn-Teller distortions from idealised geometries for particular dn configurations; for example, d9 octahedral complexes.
- (ix)
- The interpretation of the electronic spectra of complexes using qualitative Orgel or more quantitative Tanabe–Sugano diagrams.
- (x)
- The isolobal principle and the fragment orbital analysis from which it is derived [19].
Detailed explanations of features (i)–(ix) can be found in the texts cited in refs. [1,2,3,4,5] (and in other standard inorganic chemistry texts) whilst ref. [19] provides a comprehensive description of the isolobal principle (x).
3. Crystal Field Theory and Ligand Field Theory
Despite its vintage and well-known limitations, the starting point for understanding the properties of d orbitals and their associated electrons in transition metal chemistry is usually Crystal Field Theory (CFT). In outline, the basis of CFT considers a metal ion to be surrounded by a collection of ligands arranged in a particular geometry, providing an electrostatic field that gives rise to a characteristic splitting of the valence d orbitals resulting from coulombic repulsions between the metal d electrons and the ligand lone pairs. In the simplest and the most commonly first taught example, an octahedral coordination geometry results in the splitting of the five d orbitals into two groups, one containing three orbitals at lower energy and the other containing two orbitals at higher energy. These orbitals are then allocated the symmetry labels t2g and eg taken from the character table for the Oh point group in this instance. This arrangement of two groups of orbitals in an octahedral crystal field is illustrated in Figure 1a, which also highlights the term Δoct that denotes the energy separation between them, usually termed the crystal field splitting energy or parameter. The value of n in the dn number, which indicates the occupancy of these orbitals, is then normally assigned according to Equation (1) where m is the Group number of the metal in the periodic table and OS is the oxidation state; for example, n for the complex [Fe(OH2)6]3+ is 8 − 3 = 5; i.e., Fe(III) is therefore assigned a d5 configuration (Appendix A Note 5) [14,15,16,17] (Appendix A Note 8).
n = m − OS
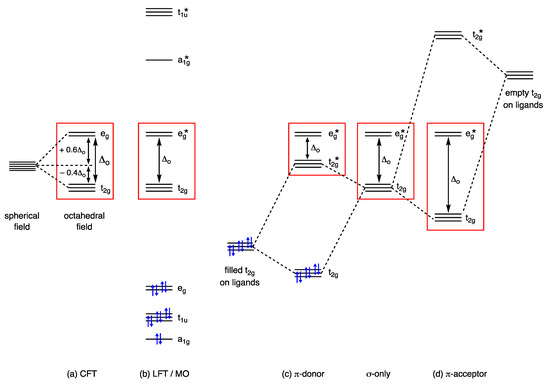
Figure 1.
Qualitative energy level diagrams for idealised octahedral transition metal complexes derived from (a) CFT and (b) LFT/MO. Diagrams (c) and (d) illustrate the consequences for the t2g orbitals of π bonding from π donor and π acceptor ligands, respectively. The orbitals enclosed in the red boxes are generally treated as metal-based, and the number of electrons that occupy these orbitals, n, is expressed in the term dn. The electrons in blue are in orbitals that are formally associated with the ligands. More details on these diagrams can be found in refs. [1,2,3,4,5].
The concept of the Crystal Field Stabilisation Energy (CFSE, sometimes referred to as Ligand Field Stabilisation Energy or LFSE) is then derived from the energies of the t2g and eg orbitals relative to a hypothetical spherical field (Figure 1a) and this is widely used to explain and rationalise the features outlined in points (i) and (iv)–(vi) listed in Section 2.
Useful though the CFT model is, its treatment of the interaction between the metal ion and the ligands as purely electrostatic ignores any covalency in the metal–ligand bonding. This shortcoming is generally addressed using an LFT/MO approach, which results, for an octahedral complex, in the qualitative molecular orbital energy level diagram illustrated in Figure 1b. The MO diagram shown in Figure 1b and its derivation will not be discussed in detail except to note that the part of it highlighted in the red box corresponds to the d orbital splitting arrangement obtained from CFT, as a comparison with Figure 1a reveals. The crucial difference, however, is that the eg orbitals of the CFT approach are labelled eg* in the LFT/MO diagram since they are now metal–ligand σ antibonding in character and are, therefore, no longer the pure d orbitals of the CFT model. This point is made explicitly in the following quote taken from ref. [1]: ‘The main difference between the MO and the crystal field results is that the eg* orbitals, as they are obtained in the MO treatment, are not pure metal d orbitals.’ [original emphasis]. Nevertheless, these eg* orbitals are closer in energy to the metal d orbitals than they are to the ligand-based orbitals since the elements through which the ligands are bonded to the metal are usually more electronegative than the metals to which they are bonded, such that the ligand orbitals lie at lower energy than the metal orbitals. Although this is something of an oversimplification (as discussed in Section 11), the usual approach adopted for electron accounting purposes is for the a1g, t1u and eg orbitals (see Figure 1b) to accommodate the ligand-based electrons, leaving the metal-based electrons to occupy the t2g and eg* orbitals. Accordingly, using the example above, an Fe(III) complex would still be designated as d5.
The diagram shown in Figure 1b represents an octahedron in which only metal–ligand σ bonding has been considered such that, whilst the eg* orbitals now incorporate some ligand character (and are σ antibonding as noted above), the t2g orbitals are non-bonding and therefore remain as pure metal d orbitals. As soon as any metal–ligand π bonding is considered, however, these t2g orbitals become involved, in a manner shown qualitatively for π donors and π acceptors in Figure 1c and d respectively. Accordingly, they can no longer be considered as pure metal d orbitals but, for the same reasons as outlined above for the eg* orbitals, they remain close in energy to the metal d orbitals from which they were derived (Appendix A Note 9) [5]. It therefore still makes sense to assign a dn number based on the combined occupancy of these metal-based t2g and eg orbitals whilst recognising that neither are any longer pure metal d orbitals, nor can they be described as non-bonding orbitals. Although the precise arrangement and labelling of the frontier orbitals will change depending on the coordination geometry of the metal and the point group of the complex, the same OS-based principles for determining the dn number apply for a range of coordination numbers and geometries.
The brief outline of CFT and LFT given above reveals how the dn number is usually determined using the OS method, but the value of this term in relation to the points listed in Section 2 is that (for an octahedron) the t2g and eg orbitals (shown in the red boxes of Figure 1) are also the frontier orbitals and therefore play a central rôle in the chemistry of the complex. For complexes with other geometries, the frontier orbitals will have different symmetry labels, but in each case, they will have the same symmetries as the d-orbitals from which they are derived.
Before leaving this section on the CFT and LFT/MO approaches to understanding transition metal chemistry, we note that it has been argued that, for highly covalent compounds, a sd/sd2 hybridisation model derived from a Natural Bond Order (NBO) Theory analysis is intuitively more useful from a teaching perspective than LFT derived MO diagrams [20] (Appendix A Note 10) [21,22]. This hybridisation approach considers only ns and (n − 1)d orbitals (on the basis that the np orbitals are deemed too high in energy to be available for bonding) and makes use of a three-centre, four-electron (3c,4e) model involving sd or sd2 hybrid orbitals at the metal centre to describe much of the metal–ligand bonding [23]. However, since this sd/sd2 hybridisation approach does not differ from the CFT/LFT analysis in terms of how to determine the dn number, it will not be considered further in this article.
4. Covalent Bond Classification
Having outlined a simple CFT/LFT approach to determining dn which explicitly employs the OS of the metal as shown in Equation (1), there is an alternative methodology for assigning the dn number, which, in certain circumstances, results in a different value of n. This is the Covalent Bond Classification (CBC) method, which focusses on what is termed the Valence Number (VN) instead of the OS, and it is therefore important to establish where and why the CBC and OS approaches differ [24,25,26].
The CBC methodology categorises compounds in terms of a central element, M, bound to L, X and Z ligands, which formally donate two, one and zero electrons, respectively, to the M centre and leads to a description of the type MLlXxZz, where the subscripts l, x and z refer to the number of each of the L, X and Z ligands. Full details of the history and application of the CBC method are set out in the papers of Green and Parkin listed in refs. [24,25,26] and will not be reproduced here except with regard to what is defined as the Equivalent Neutral Class (ENC), which is used to render any charged complexes (and neutral complexes containing both L and Z ligands) in terms of an equivalent neutral format according to the transformations set out in Scheme 1.
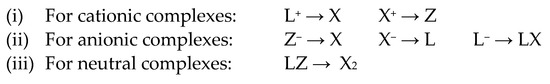
Scheme 1.
Transformations used to assign an ENC within the CBC framework [24,25,26].
The ENC feature within the CBC method is important since the resulting neutral MLlXxZz designation leads directly to the assignment of the VN according to Equation (2), from which the value of n in the dn number is then determined using Equation (3) where m is the metal’s Group number in the periodic table.
VN = x + 2z
n = m − VN
For the great majority of mononuclear complexes, VN and OS are numerically equal, and the dn number assigned to the complex is, therefore, the same whichever method is used, but as shown in Figure 2, the derived dn numbers do differ in some circumstances [24,26]. Thus, for the example compounds 1–5, the dn numbers are the same, whereas for compounds 6–10, they are not. Specifically, complexes where OS ≠ VN occur when: (i) σ Z (and sometimes π Z) ligands are present; (ii) the ligands are formally cationic; (iii) the metal is in a negative oxidation state; (iv) the complexes are binuclear and contain metal–metal bonds. It is these differences and how they may be reconciled, which are the principal focus of the discussions that follow, but first, the ambiguities in the dn assignment for carbene and alkene ligand complexes are considered as these illustrate that a one-to-one mapping of ligands via either OS or VN is not always chemically defensible, which can therefore be a source of divergent dn assignments (Appendix A Note 11).
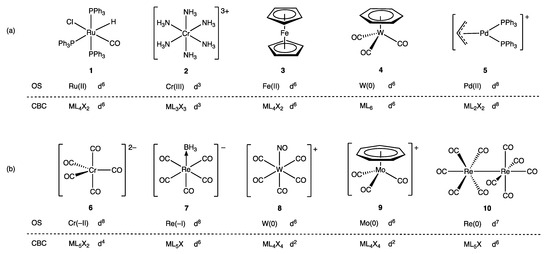
Figure 2.
Comparison of dn assignments using the OS method and the CBC method (via ENC and then VN). (a) For complexes 1–5, the methods are in agreement on dn assignments. The OS for complexes 1–5 is assigned by assuming PPh3, CO and NH3 are neutral, and H, Cl, η3-C3H3 and η5-C5H5 are formally negatively charged. According to the CBC method for complexes 1–5: H and Cl are X ligands, η5-C5H5 is L2X, η3-C3H3 is LX, η6-C6H6 is L3, and all other ligands are L. To obtain the ENC for 2 and 5, the transformation L+ → X is required (see Scheme 1). (b) For complexes 6–10, the OS and CBC methods are not in agreement regarding dn assignments. The OS for complexes 6–10 is assigned by assuming CO and BH3 are neutral, and the linear NO (in 8) [27] and η7-C7H7 (in 9) are formally positively charged (but see Section 8 regarding ambiguities in assigning the charge to η7-C7H7 ligands). According to the CBC method for complexes 6–10: BH3 is Z, NO is X3, η7-C7H7 is L2X3, Re(CO)5 is X, and all other ligands are L. To obtain the ENC for 6 and 8, the transformations required are L− → LX and Z− → X, respectively, whereas to obtain the ENC for 9, the transformation L+ → X is necessary (see Scheme 1).
5. Carbene and Alkene Complexes
Metal carbene complexes provide a useful illustration of potential ambiguities in the assignment of a dn number. Such complexes have traditionally been categorised as either Fischer or Schrock carbenes (Appendix A Note 11) [23,28], which are distinguished by the nature of the metal-carbon bonding, as shown generically in Figure 3. Thus, in classical, heteroatom-stabilised Fischer carbene complexes such as 11 (Figure 4), the carbene carbon is electrophilic, which is rationalised on the basis that carbene ligands are good σ donors (and moderate π acceptors) derived from singlet carbenes (Figure 3a); accordingly, they are treated as neutral, L-type ligands and have no consequence when determining the OS or VN of the metal. In contrast, in Schrock carbenes such as 12 (Figure 4), the carbene carbon is nucleophilic, the ligand being formally derived from a triplet carbene fragment (Figure 3b); they are therefore treated as dianionic ligands for the purposes of determining the metal OS and as X2 ligands within the CBC framework.
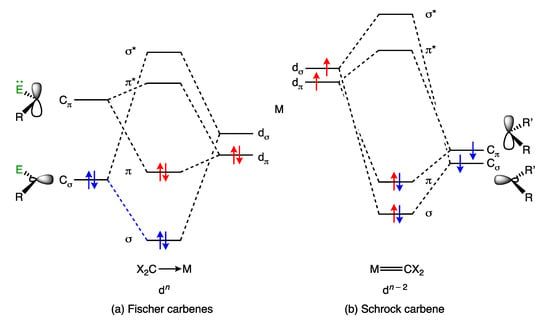
Figure 3.
Qualitative bonding schemes for (a) Fischer carbenes and (b) Schrock carbenes. Traditional Fischer carbenes are moderate π acceptors but also have heteroatom substituents, E (e.g., OMe), capable of forming a π bonding interaction with the vacant p orbital on the carbene C atom. Schrock carbenes have shorter M–C separations than Fischer carbenes, consistent with a greater degree of M=C double bond character. This figure is adapted from ref. [29]; see also ref. [9].
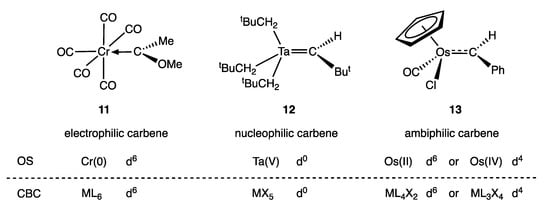
Figure 4.
Classical examples of metal carbenes that conform to the Fischer (11) and Schrock (12) extremes. The carbene ligand in 11 is shown bonded to the metal with an arrow to highlight its classification as an L-type ligand, and the carbene ligand in 12 is shown double-bonded to the metal to highlight its classification as an X2-type ligand. The carbene ligand in 13 does not conform with the Fischer-Schrock classification.
It is important to recognise, however, that Fischer and Schrock carbenes are effectively two extremes at the ends of a continuum in terms of the properties of a general CR2 ligand, and many instances are known of carbene ligands that fall between these extremes. Thus, carbene complexes such as 13 have been described as ambiphilic [30], and Fischer-type carbenes are known that do not have heteroatom substituents [31,32]. Moreover, within this smorgasbord of examples must be included not only complexes of Arduengo’s N-heterocyclic carbenes (NHCs) [33] and Bertrand’s cyclic alkyl amino carbenes (CAACs) [34], but also, the Grubbs’ ruthenium complexes (typically incorporating the carbene ligand, CHPh). Grubbs’ carbenes are often considered to be intermediate between the Fischer and Schrock extremes, although, as argued in ref. [35], they are rather closer to the latter type than to the former.
It is clear that the substituents on the carbene ligand greatly affect the nature of the metal-carbene complex, but it is important to recognise that the metal centre to which the carbene is bonded also has a profound effect. This is obvious when comparing the known carbene complexes of Zr with those of Pd, but it is also clear that the ancillary ligands can decisively control the properties of the carbene ligand as illustrated by the electrophilic vs. nucleophilic nature of the CF2 ligand in the complexes [RuCl2(CF2)(CO)(PPh3)2] and [Ru(CF2)(CO)2(PPh3)2] respectively [36,37] (Appendix A Note 12) [38,39].
How, then, should metal carbenes that are situated between the Fischer-Schrock extremes be classified (i.e., L vs. X2) and what dn number should be assigned? It is possible that the classification of all the ‘in-between’ carbene complexes could be arbitrated by computational studies and a single value of dn assigned on a case-by-case basis. More generally, however, this dichotomy exposes a fundamental limitation in the simple dn model (as well as within the OS and CBC models) by offering a binary choice between two values that represent the extremes of a chemical continuum, a point made, albeit not in relation to dn numbers, by the authors of ref. [35], viz., ‘Of course, loss of detail is the inevitable result when undertaking a discrete classification where nature offers a continuum of variation.’
Similar arguments can be made for compounds with carbyne/alkylidyne (CR) ligands and also for metal alkene complexes according to the nature of the alkene substituents and the metal centre to which the alkene is bound [8,23]. For example (see Figure 5), C2H4 may be considered as an L ligand in 14, whereas C2(CN)4 can be treated as a dianionic or X2 ligand (i.e., part of a metallacyclopropane) in 15 as evidenced, in each case, by the C–C bond lengths indicated. In complex 16, however, the C2H4 ligand is described as ‘intermediate along the continuum between the Ti(II)-ethylene and Ti(IV)-metallacyclopropane limiting structures.’ [40] (Appendix A Note 13) [41].
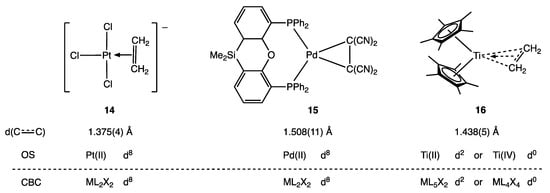
Figure 5.
Examples of metal alkene complexes that represent the π complex (14) and metallacyclopropane (15) extremes, and 16, which is described as intermediate in character.
Thus, in the case of metal carbene and metal alkene complexes (and in other classes of compounds, including metal carbynes, metal alkynes and some of those discussed below) it is apparent that a limitation of the dn formalism results from it being a digital assignment applied to what are analogue chemical bonding systems (Appendix A Note 14) [42]. Coherent MO bonding schemes for metal carbenes and metal alkenes that apply across the Fischer/Schrock and metal-alkene/metallacyclopropane ranges all have two components comprising σ donation and π back-donation (according to the classic Dewar-Chatt-Duncanson (DCD) model described in all standard texts), the relative contributions of each being controlled by the nature of the metal fragment and the ligand substituents [1,2,3,4,5,19,23].
We note that similar arguments for carbene and alkene ligands to those outlined above have been presented by Parkin in ref. [9] in terms of an LZ’ designation where Z’ denotes a varying degree of ligand π acceptor character. Thus, a minimal Z component is consistent with a simple L ligand, whereas a substantial Z component leads to a ligand designation of LZ, which transforms [Scheme 1 (iii)] to X2.
6. σ Acceptor (σ Z) Ligands: Boranes
As noted in Section 4, a circumstance where the OS and CBC methods diverge in the assignment of the dn number arises for complexes that contain Z ligands. For the situation where one σ Z ligand is coordinated to the metal (π Z ligands are discussed in the following section), the OS-derived dn number determined using Equation (1) becomes dn−2 according to Equation (3) where VN is employed, as exemplified in complex 7 (Figure 2), which contains the σ Z BH3 ligand. This difference arises because, in the OS approach, a Z ligand is usually considered as neutral and, therefore, has no effect on the OS, whereas Equation (2) reveals that the VN increases by two for each Z ligand present (since the metal uses two further electrons to bond to the Z ligand) with the consequences for the value of n in dn then evident from Equation (3). It should be noted, however, that if the Z ligand is treated as a dianionic group, the OS- and CBC-derived dn numbers would then be in agreement.
Examples of σ Z ligands are commonly encountered in a range of ambiphilic ligands, and the discrepancy in dn values that arises from using an OS or VN determination can be appreciated with reference to the examples shown in Figure 6 (Appendix A Note 15) [43]. Thus, the gold complex 17 is observed to be square planar with a short Au–B bond distance of 2.309(8) Å and significant pyramidalisation around the B atom, all of which are consistent with a d8 configuration at a Au(III) centre. However, Mössbauer spectroscopy and MO calculations support a Au(I) d10 configuration for complex 17 [44]. In addition, the anionic platinum complex 18 has recently been reported, which is isoelectronic with 17 and also square planar but with a substantially shorter Pt–B bond distance of 2.219(2) Å. Whilst this is consistent with a Pt(II) d8 configuration, the X-ray photoelectron spectrum of 18 and MO calculations support a Pt(0) d10 assignment [45]. Furthermore, the gold complexes 19a and 19b each contain a P,B-chelate but with different B substituents that result in the Lewis acidity of the borane function in 19b being considerably greater than in 19a, as reflected in the Au–B bond distance being much shorter in 19b [2.663(8) Å] than in 19a [2.995(8) Å] albeit both rather long and therefore weak [46].
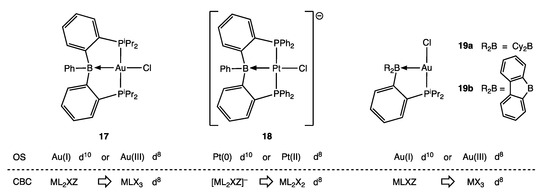
Figure 6.
Examples of metal complexes (17–19) with chelating P,B-ambiphilic ligands.
The large variation in M–B bond distances for the complexes 17, 18, 19a and 19b (which span almost 0.8 Å), depending on the nature of M and the B-substituents R, indicates that the strength of the M→BR3 interaction varies considerably, as shown in Figure 7, with attendant consequences for the determination of the dn configuration of M; this is reminiscent of the situation with Fischer/Schrock carbene ligands discussed in Section 5. We note that Hill has recognised these complexities and, in order to address the problem, has advocated that the formulae of complexes containing a M → BR3 bond be written with an associated (M → B)n descriptor to indicate the presence of the BR3 ligand [47]. Following Hill’s suggestion (which has been criticised by Parkin [6]), more generally, a formula for a compound containing one Z ligand would be presented as [MLlXxZ] (M → Z)n where n is the n in dn determined using Equation (1), assuming the Z ligand to be neutral. As Hill states, this descriptor is analogous to one proposed by Enemark and Feltham (and widely used) for metal nitrosyl complexes (see below) [48,49] (Appendix A Note 16).
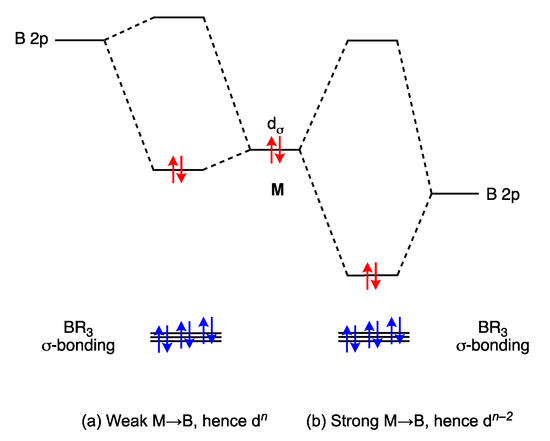
Figure 7.
Qualitative bonding schemes for metal complexes of σ Z ligands, such as BR3, showing the two extremes that differ in their assigned dn number. The electrons, originally associated with M are depicted in red and those originally associated with BR3 are in blue. In (a), the M → B interaction is weak, consistent with an OS-derived dn designation, whereas in (b), the M → B interaction is much stronger for which a CBC-derived dn−2 descriptor is more appropriate. The BR3 ligand represented in (a) can be classified as a Z ligand, whereas in (b) it can be classified as X2.
As a further example, a recent paper has offered a detailed computational and spectroscopic analysis of a terminal iron(III) nitride complex P3BFe(N) where P3B is the boratrane ligand, tris(o-di-isopropylphosphinophenyl)borane [50]. This complex is described as a Fe(III) d5 complex and, to quote more specifically, ‘The unusual d5-configuration is stabilized by significant delocalisation (≈50%) of the unpaired electron onto the axial boron and nitrogen ligands, with a majority of the spin residing on boron.’ We highlight this OS-derived d5 configuration, with the subsequent description of the single unpaired electron being delocalised onto both B and N atoms, since it contrasts with a CBC approach which would seek to assign a specific X and/or Z designation to each of these ligating atoms (B and N) and derive a dn number on that basis. The merits of each approach will be discussed further in Section 12.
Finally in this section, we note that the issues associated with ambiphilic ligand complexes have received detailed attention from Karen, McArdle and Takats, who discuss several more examples, together with related SO2 complexes, where they compare and contrast the OS and CBC approaches to σ Z ligands [14].
7. π Acceptor (π Z) Ligands: CO
Having examined the situation where the metal is bonded to the Z ligand through a σ bond (σ Z ligands), it is important to address how the OS and CBC approaches deal with π acceptor ligands (π Z ligands) and the extent to which the π Z component should be considered in the determination of the dn number. This matter is usefully exemplified by considering the homologous series of isoelectronic, metal hexacarbonyl complexes [M(CO)6]Q where Q varies from −2 to +3 [9,26].
For the situation where M is a 5d element, taking the two complexes at the ends of this series, [Hf(CO)6]2− and [Ir(CO)6]3+, the extent of π back-donation from the metal d orbitals (the t2g set in a regular octahedron) into the CO π* orbitals decreases very substantially from the Hf complex to the Ir complex, as shown by computational studies, and evidenced by an increase of almost 500 cm−1 in the νCO stretching frequency on progressing from [Hf(CO)6]2− to [Ir(CO)6]3+. Figure 8 shows the trend in the νCO stretching frequency together with the σ bonding and π back-bonding contributions for each complex in the series [9,51,52,53,54] (Appendix A Note 17) [55].
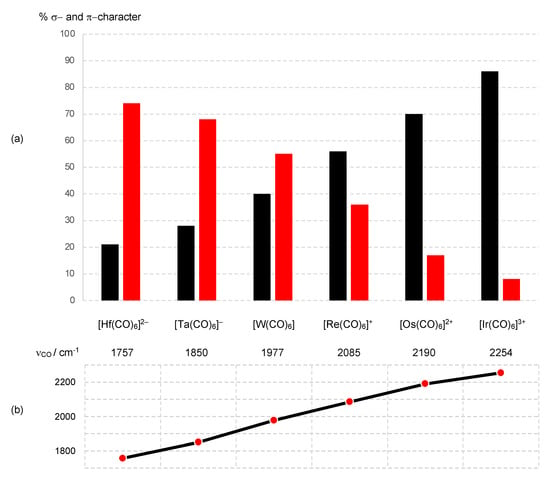
Figure 8.
(a) A plot of the M–CO bonding contributions of (in black) the σ bonding (a1g + t1u + eg) and (in red) the π back-bonding (t2g) for the 3rd row d-block [M(CO)6]Q species. For the Hf, Ta and W complexes, π back-bonding predominates, while for the Re, Os and Ir complexes, σ bonding is dominant. (b) IR stretching frequencies for the CO bands (T1u) for the [M(CO)6]Q species showing a regular trend across the series. Carbonyl complexes with νCO greater than in free CO (2143 cm−1) are usually termed ‘non-classical’ metal carbonyls. Data are taken from ref. [51].
From an OS perspective, the oxidation state of the metal M for the series [M(CO)6]Q is numerically equal to Q, and each complex would be assigned a d6 configuration according to Equation (1). However, it is argued in ref. [9] that in circumstances where the π back-donation is deemed significant, a (CO)6 ligand combination should be classified not simply as L6 but rather, with an incorporated Z component (on the basis of symmetry considerations), as L6Z3. This L6Z3 designation then transforms under the ENC rules [Scheme 1 (iii)] to L3X6. Specifically, for [Hf(CO)6]2−, this [ML6]2− species would be considered as [ML6Z3]2− and since Z− is equivalent to X [Scheme 1 (ii)], this becomes ML6X2Z. Then, because LZ is equivalent to X2 [Scheme 1 (iii)], the final MLXZ designation of [Hf(CO)6]2− is ML5X4 from which, according to Equation (3), a d0 assignment follows (Appendix A Note 18). If one ignores (reasonably) the π back-bonding in [Ir(CO)6]3+, a CBC-derived d6 configuration is obtained ([ML6]3+ transforms to ML3X3, leading to d6 where M = Ir), which therefore begs the question, at what point is the π Z component deemed sufficiently large for it to be taken into account in assigning the dn number?
A descriptive answer to this question is offered in the following text taken from ref. [9].
Thus, the t2g orbitals transform from being classified as largely non-bonding in [Ir(CO)6]3+ to bonding in [Hf(CO)6]2−. This progression is necessarily accompanied by a decrease in the dn configuration using the definition that this quantity refers to electrons in d-based molecular orbitals that are not considered to be bonding.
It is further suggested that the π Z component should be explicitly included for metal carbonyl anions, which therefore implies that the transition from d6 to d0 in the [M(CO)6]Q series should occur between [W(CO)6] and the anionic [Ta(CO)6]− [9]. However, as the plot shown in Figure 8 demonstrates, the switch in the relative importance of the σ L and π Z components of the M–CO bonding actually occurs between cationic [Re(CO)6]+ and [W(CO)6]. Thus, for [W(CO)6], the reasonable assumption of significant π back-bonding (see Figure 8) would result in an ENC of ML3X6 (see above), which has a d0 configuration, in contrast to the more usually encountered classification of ML6, which is d6. For the cationic species [Re(CO)6]+, [Os(CO)6]2+ and [Ir(CO)6]3+, the data in Figure 8 are in accord with a d6 assignment. We note that this matter has previously received detailed consideration in refs. [9,26], to which we will return in Section 12.
The trend towards increasing π back-donation from [Ir(CO)6]3+ to [Hf(CO)6]2− shown in Figure 8 is readily understood in terms of the increasing electron richness of the metal centre, which is illustrated in the qualitative MO diagram shown in Figure 9 (Appendix A Note 19) [56]. Thus, for [Ir(CO)6]3+, the lowering in energy of the occupied metal t2g level due to π back-bonding is negligible as a consequence of a 3+ charge, which results in a large energy separation between the metal t2g orbitals and the π* orbitals (of t2g symmetry) on the CO ligands. [Ir(CO)6]3+ is therefore often classed as a ‘non-classical’ metal carbonyl, and the frontier t2g orbitals are essentially non-bonding. By contrast, for [Hf(CO)6]2−, the lowering in energy of the occupied metal t2g level due to π back-bonding is substantial because of the negative charge on the complex leading to the energy of the metal t2g orbitals and CO π* orbitals being significantly closer. Moreover, as shown in Figure 9, because Hf is early and Ir is late in the d-block, the filled HOMO (t2g) energy level will be energetically more accessible for [Hf(CO)6]2− than for [Ir(CO)6]3+, consistent with the experimental observation that metal carbonyl anions are much more readily oxidised than non-classical metal carbonyl cations [51,52] (Appendix A Note 20) [57].
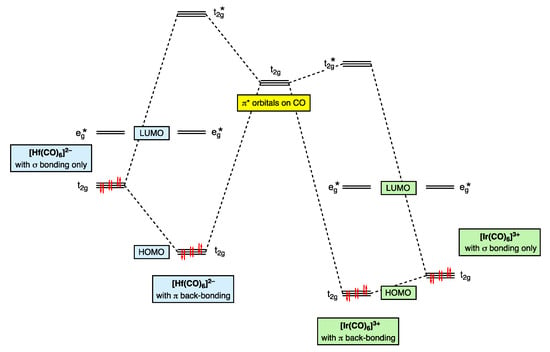
Figure 9.
A qualitative MO energy level diagram showing the effect on the HOMO (t2g) of π back-bonding to the π* orbitals on CO for the metal hexacarbonyl species [Hf(CO)6]2− and [Ir(CO)6]3+ [52]. Note that for [Hf(CO)6]2−, the electrons in the filled HOMO (t2g) remain more energetically accessible, consistent with the much greater susceptibility of metal carbonyl anions to oxidation compared to metal carbonyl cations.
8. Cationic Ligands: Linear NO and Tropylium
It is well recognised that there are difficulties in finding a consistent description of the bonding in metal nitrosyl complexes using simple models, and this has led to much discussion over several decades. Moreover, although this debate has generally been a topic primarily of academic interest, the potential applications of metal nitrosyls, including in medicine, have recently attracted considerable attention [58,59].
Only a brief mention will be made here of the categorisation of complexes containing nitrosyl (NO) ligands because this topic is considered in more detail in refs. [9,60]. The OS method treats linear NO ligands as NO+ and bent NO ligands as NO− with the consequent impact on the dn number. This classification has been criticised as simplistic based on structural and computational evidence, which shows that there are exceptions to such assignments and several examples where the M–N–O angle lies between the expected extremes of 180° (for NO+) and ~120° (for NO−). As a result, Enemark and Feltham proposed the {MNO}n notation (cited earlier) where the value of n is the dn number of the complex when the NO ligands are treated as NO+ [48,49] (Appendix A Note 16). Nevertheless, the NO+/NO− classification remains a topic of continued interest, as demonstrated in the recent publications by Klüfers et al. concerning whether or not a range of {CoNO}8 complexes should be classified as Co(III)–NO− or Co(I)–NO+ [61,62] (Appendix A Note 21) [63,64,65,66,67,68].
Whatever the issues around an OS-derived classification of the NO ligand, the CBC method explicitly requires that the π Z component be considered in the MLlXxZz designation for linear NO complexes when assigning the ENC and VN (and hence the dn number) since the N–O π* orbitals are both the LUMO and the HOMO, which therefore have the same energy (see Figure 10) [26].
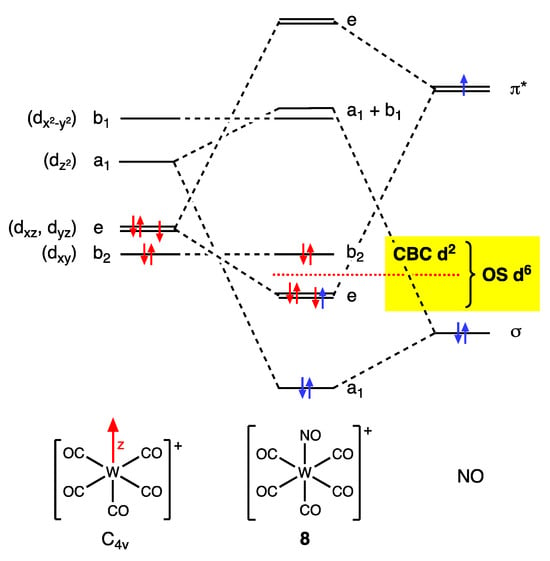
Figure 10.
A qualitative MO diagram for the C4v-symmetric, mononitrosyl complex 8, which is isoelectronic with the Oh-symmetric [W(CO)6]. Complex 8 has six electrons in the HOMO and HOMO-1, and two vacant low-lying orbitals (LUMO and LUMO+1); the frontier orbitals of 8 all have the same symmetry as d-orbitals and are similar to the t2g and eg orbitals of [W(CO)6]. The size of the e-b2 energy gap is a function of the back-bonding interactions with the π* orbitals on CO and NO. The CBC method judges this gap to be sufficiently large for only the two b2 electrons to be counted in the dn determination, part of the evidence cited in support of which is the very short W–N bond length [9], whereas the OS method leads to all six of the (e + b2) electrons being counted in the dn assignment (see yellow highlight).
As set out in some detail in ref. [9] (Appendix A Note 22) [26,65], the precise CBC description of coordinated NO ligands depends on their number and the symmetry of the complex in which they reside. Thus, mononitrosyls are designated as X3, dinitrosyls [as a (NO)2 group in an octahedral complex] are designated L2X2 for trans or LX4 for cis, and tetranitrosyls [as a (NO)4 group in a tetrahedral complex] are together designated L6, which leads to the (sometimes substantial) differences in the dn assignments based on CBC and OS methods illustrated in Figure 11 for complexes 20–23.
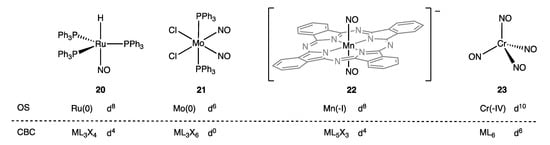
Figure 11.
dn configurations for some linear nitrosyl complexes 20–23 calculated from OS (assigning linear NO as NO+) and the CBC method (VN and hence dn according to the NO-group assignments noted in the text that are, respectively: 20, X3; 21, LX4; 22, L2X2; 23, L6) (Appendix A Note 23) (Appendix A Note 24) [69].
In the case of the cycloheptatrienyl ligand, for the purposes of assigning a dn number using the OS formalism, it is treated as either [C7H7]3− or [C7H7]+ since both are aromatic systems with 10π and 6π electrons respectively (Appendix A Note 25). In contrast, in the CBC method, the π Z component associated with the C7H7 ligand leads to a singular assignment as an L2X3 ligand in all cases, and the variance between the two approaches is clear from a comparison of complexes 24 and 25 (Figure 12). From an OS perspective, the η7-C7H7 ligand is judged to be [C7H7]3− in 24 and [C7H7]+ in 25. This is not an arbitrary judgement since the highly electropositive Ti centre in 24 makes [C7H7]3− a chemically reasonable choice and is in line with MO calculations [70], whereas the alternative [C7H7]+ assignment for 25 is consistent with both its chemistry and its XPS spectrum and is supported by DFT calculations [71]. Both OS and CBC methods, therefore, agree on the d0 configuration assigned to 24 (Figure 12), but a marked difference is seen for 25, which would be assigned a d2 configuration using the CBC method, whereas the OS-derived configuration is d6. More generally, the exclusive L2X3 classification for the η7-C7H7 ligand within the CBC framework will give rise to a dn number consistent with the OS approach where it is appropriate to consider the ligand as [C7H7]3−, but the OS method will result in a dn+4 assignment where it is deemed more appropriate to consider the ligand as [C7H7]+.
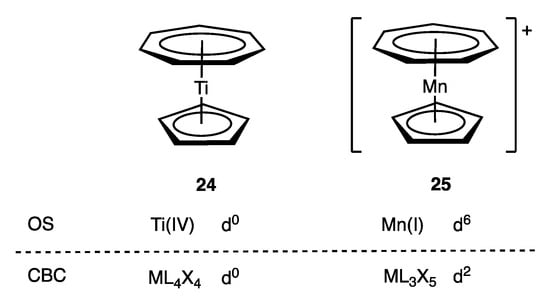
Figure 12.
dn configurations for C7H7 complexes calculated from OS (assigning C7H7 as [C7H7]3− in 24 and [C7H7]+ in 25) and CBC method (assigning C7H7 as L2X3).
The issue of alternative η7-C7H7 assignments was also discussed in ref. [60] in relation to [Mo(η7-C7H7)(CO)3]+ (9 in Figure 2), where it was argued that since this species displays tropylium-like chemistry for the C7H7 ligand, a [C7H7]+ assignment is preferred leading to a d6 configuration for 9 rather than the d2 configuration derived using the CBC method.
Cationic ligands are not common, but many examples are nevertheless known (in addition to [NO]+ and [C7H7]+) for which the assignment of a dn number using the OS method is generally straightforward [72,73,74,75,76]. However, it is important to recognise that the CBC method treats cationic ligands rather differently since, in general, an L+ designation transforms to X according to Scheme 1 (i), which then has consequences for the assignment of a dn number (Appendix A Note 26).
9. Negative Oxidation States
How the OS and CBC methods deal with negative oxidation states is a matter we have considered before and will not reprise in detail here, but the contrast in the two approaches is illustrated by the difference between the derived dn assignments for [Fe(CO)4]2− (26) and [Fe(CO)6]2+ (27) shown in Figure 13 [60]. In terms of the OS description, 26 is a tetrahedral, d10-Fe(–II) complex, whereas 27 is an octahedral, d6-Fe(II) species. The OS description clearly signals that these two iron carbonyl species would be expected to have very different chemistries, which they certainly do: the dicationic 27 has been characterised as a ‘superelectrophile’ whilst the dianionic 26 is a powerful nucleophile that is readily oxidised [77,78]. According to the CBC method, 26 [using L− → LX, Scheme 1 (ii)] and 27 [using L+ → X, Scheme 1 (i)] are both members of the same ENC of ML4X2 from which a d6 configuration follows [9] (Appendix A Note 27).
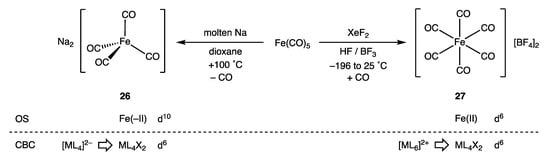
Figure 13.
OS and CBC descriptors and derived dn assignments for [Fe(CO)4]2− (26) and [Fe(CO)6]2+ (27). Both of these complexes can be prepared from Fe(CO)5 but under strikingly different conditions; contrast the potent reducing agent required for the preparation of 26 with the potent oxidising agent employed in the preparation of 27 (Appendix A Note 28).
10. Compounds Containing Metal–Metal Bonds
Figure 14 highlights a selection of binuclear metal complexes (28–30) that feature unsupported metal–metal bonds along with the OS and CBC derived dn configurations. The binuclear complex [Mn2(CO)10] (28) has previously been discussed [60], but in brief, the OS method views 28 as a Mn(0) compound comprising two d7-Mn(CO)5 fragments that are linked by a σ2 Mn–Mn single bond. In contrast, the CBC method treats both Mn centres as ML5X since each Mn(CO)5 unit is counted as an X ligand as far as the other Mn centre is concerned, resulting in a VN of 1 and a derived d6 configuration for each Mn according to Equation (3) [24,25,26].
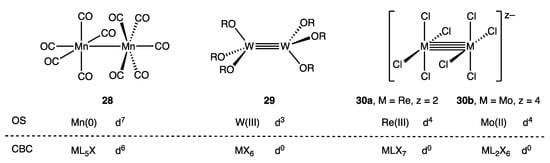
Figure 14.
Unsupported metal–metal bonded species with M–M bond orders of 1 (28), 3 (29) and 4 (30a and 30b) and the dn counts for each metal centre determined by OS and CBC methods.
Similarly, using the OS method, the ditungsten complex W2(OtBu)6 (29) features two W(III) centres linked by a σ2π4 W≡W triple bond formed by combination of two d3-W(OtBu)3 fragments whilst the classic dirhenium(III) complex [Re2Cl8]2− (30a) features a σ2π4δ2 Re≣Re quadruple bond arising from the combination of two d4-[ReCl4]− units [2,79,80,81]. In contrast, it is assumed, based on the treatment of [Mn2(CO)10] outlined above, that the CBC method would classify the metal centres in 29 as MX6 and in 30a as MLX7 (consistent with a standard assignment of their valence) resulting in a d0 configuration in each case based on the VN numbers of 6 and 7 respectively. The discrepancy between the two methods is quite general, such that within the CBC framework, compounds containing metal–metal bonds will have dn numbers for each metal centre that are reduced in direct proportion to the metal–metal bond order compared to the dn numbers derived from an OS analysis.
Much of the chemical literature, especially for those compounds with metal–metal multiple bonds, adopts the OS approach of counting the M–M bonding electrons as part of the dn count in large part because they are predominantly localised on the metal centres rather than on the ligands [79]. Our preference is the OS approach since we contend that it gives a greater insight into the chemistry of dimetallic complexes. For example, the observation that the species [Cl4Mo≣MoCl4]4− (30b) is readily oxidised chemically or electrochemically can be understood in terms of its OS description as a d4-d4 Mo(II) complex [82,83] but less readily in terms of the alternative CBC description as a d0-d0 complex. Similarly, the dimolybdenum complex 31 undergoes the reaction shown in Figure 15 to give 32, which has been characterised as an oxidative addition of the peroxide RO–OR to the d3-d3 Mo(III) complex 31 to give compound 32 containing two d2 Mo(IV) centres linked by a Mo=Mo double bond, albeit with two bridging alkoxides [84]. Such a rationalisation does not naturally emerge from a d0-d0 configuration that would be assigned to both 31 and 32 according to the CBC method, although one could characterise the reaction shown in Figure 15 as a Mo≡Mo/RO–OR bond metathesis reaction [85]. It should nevertheless be stated in any OS-based discussion concerning dn numbers for M–M bonded compounds that some of the dn electrons are involved in M–M bonding, the number of which is equal to the M–M bond order (at least to a first approximation), a caveat that is unnecessary when using the CBC approach (Appendix A Note 29) [86].
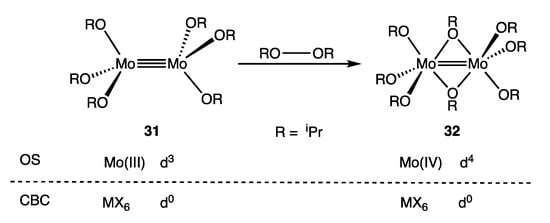
Figure 15.
Addition of di-isopropyl peroxide across the Mo≡Mo bond in 31 to give the Mo=Mo bonded 32.
There are numerous examples of binuclear compounds with formal metal–metal bonds (single or multiple), which contain bridging (μ) ligands that are not considered here (apart from 32 above) since, in many cases, debates continue regarding the actual magnitude of the bond order [26]. Likewise, cluster compounds that incorporate metal–metal bonds are best described using cluster bonding models such as Polyhedral Skeletal Electron Pair Theory (PSEPT), sometimes referred to as the Wade-Mingos rules, since the OS and dn number of individual metal centres within the cluster are less meaningful, especially as the number of the metal atoms in the cluster increases (Appendix A Note 30) [87].
11. Inverted Ligand Fields
The dn configuration of the anionic complex [Cu(CF3)4]− (33) has been the source of much, and at times strenuous, debate for over a decade [88]. The application of OS and CBC methods is apparently straightforward for this species, and, as shown in Figure 16, both methods agree on a d8 assignment, which is consistent with the observed square planar geometry at the Cu centre. However, based on computational analysis of the frontier orbitals in 33, it has been suggested that the resonance structures denoted as 33* in Figure 16 are a more accurate representation of the bonding with an attendant d10 Cu(I) description.
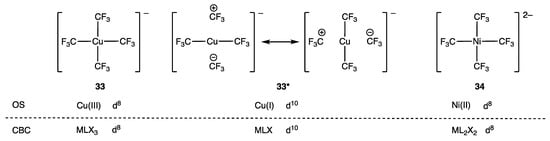
Figure 16.
Complexes (33) (including the resonance structures denoted as 33*) and (34) for which the dn assignment has been the subject of debate centred on inverted ligand fields.
The conventional ordering of the orbitals in a square planar complex has the HOMO and LUMO localised primarily on the metal, which is a consequence of the energy of the orbitals on the ligands being lower than the energy of the metal valence orbitals; Figure 17a illustrates this for the LUMO in a normal D4h ligand field. It is argued, however, that the CF3 ligands in a complex such as 33 provide an inverted ligand field such that the HOMO and LUMO are localised primarily on the ligand due to the energy of the ligand orbitals being higher than the energy of the metal valence orbitals; Figure 17b illustrates this for the LUMO in an inverted D4h field. It is notable that for the inverted ligand field, the electrons in the b1g orbital are included in the dn count, although this runs counter to the definitions of the dn number given in Section 2 since this b1g orbital is a σ bonding orbital.
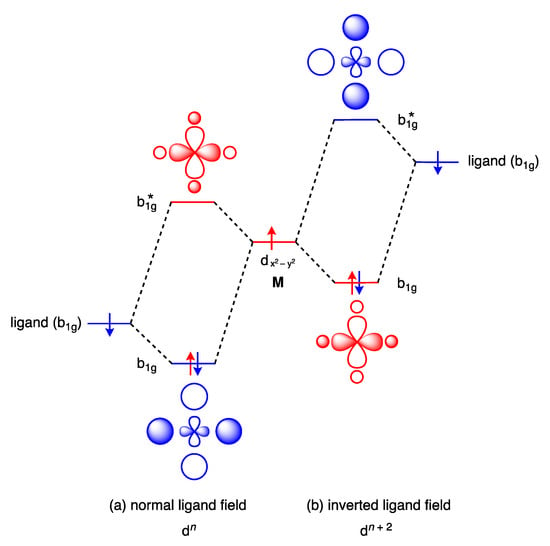
Figure 17.
Qualitative MO diagrams showing how the energy of the ligand donor orbital relative to the metal acceptor orbital determines the nature of the LUMO (b1g*) in a complex with D4h symmetry. In a normal ligand field (a), e.g., in [Pt(NH3)4]2+, the LUMO has substantial metal d-character, while in an inverted field (b), e.g., in [Cu(CF3)4]−, the LUMO has substantial ligand character. From these diagrams, it can be appreciated that a dn configuration in a normal ligand field (a) could become a dn+2 configuration in an inverted ligand field (b). This diagram is a modified version of the one presented in ref. [89]; see also ref. [9].
The debate over whether 33 should be treated as d10 Cu(I) or d8 Cu(III) has even been referred to as the ‘Oxidation State Wars’, and a recent analysis provided by Klein et al. has led to the interesting suggestion that [Cu(CF3)4]− could be described as having a quasi-d10 configuration (based on their computational analysis) but a formal-d8 configuration [90]. There seems to be little debate in a recent publication regarding a d8-Ag(III) assignment for the complex [Ag(CF3)4]− [91].
The analogous square planar nickel(II) complex 34 is isoelectronic with 33 and would be assigned a d8 configuration by applying simple OS or CBC rules. However, computational and spectroscopic analysis of 34 has led to the suggestion [92] that it is better physically described as a d9 metal complex. In our view, this is a problematic assignment because when employing a conventional use of the dn term, a d9 assignment for mononuclear complex 34 would carry the implication that it is paramagnetic, which it is not, although we note that the authors rationalize the observed diamagnetism as being due to anti-ferromagnetic coupling between an electron on the metal and an electron delocalized over all four CF3 ligands.
Another example related to compound 33 is the fluorogold complex 35 (Figure 18), which is a well-characterised square planar, d8 Au(III) (or trivalent MLX3) species. More recently, the oxo-gold (36) and nitrido-gold (37) complexes have also been described. These complexes are ostensibly examples of d7 Au(IV)/MLX4 and d6 Au(V)/MLX5 species, respectively, but a computational analysis suggests that both 36 and 37 are best treated as d8 Au(III) species, with one and two unpaired electrons localised on the O and N ligands respectively. This is illustrated in Figure 18 using dots to indicate the salient electrons on the F/O/N atoms, and it is argued that 36 and 37 are further examples of inverted ligand field complexes where the frontier orbitals are ligand-based [93].
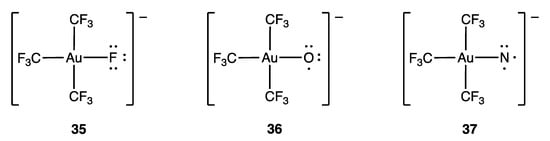
Figure 18.
Lewis structures for the anionic gold(III) complexes [AuX(CF3)3]− (35, X = F; 36, X = O; 37, X = N).
In general, inverted ligand field complexes can be viewed as a subset of complexes that feature non-innocent ligands where neither the formal oxidation state nor the MLlXxZz descriptor (and associated dn number) reflect the electronic structure evident from a detailed analysis of experimental (e.g., spectroscopic data) or computational studies.
12. Concluding Discussion and a Modified Definition of dn
The dn configuration of a transition metal complex is a unifying concept that pervades much of d-block chemistry, from organometallic/coordination chemistry and catalysis to bioinorganic chemistry and solid-state materials. Indeed, the great strength of the dn heuristic lies in its simplicity and its amenability to useful generalisations that help to rationalise many of the properties of d-block metal complexes, such as those listed in Section 2. Nevertheless, there are some fundamental ambiguities associated with how a dn number is determined, which arise for the following reasons: (a) dn values can be intrinsically ambiguous where they denote one or other extreme in a metal–ligand bonding scheme that is actually a continuum (see Section 5 for examples); (b) in circumstances where spectroscopic and/or computational results indicate a dn value that differs from dn values determined according to OS- or CBC-derived rules (see Section 11); and (c) where differences arise between OS and CBC methodologies (despite the fact that the rules of each method are internally self-consistent).
There is no general resolution for any ambiguities in the assignment of a dn number associated with reasons (a) and (b) since they reflect the inherent limitations of the simple dn model. With regard to reason (c), for the most part, OS- and CBC-derived dn numbers determined using either Equation (1) or Equation (3) are the same. However, as set out in Section 4, and the following sections, and addressed in refs. [6,24,25,26], the OS and CBC methods do differ in their dn assignment for the following categories:
- (i)
- (ii)
- Complexes containing cationic ligands (Section 8).
- (iii)
- Complexes in which the metal is in a negative oxidation state (Section 9).
- (iv)
- Complexes with metal–metal bonds (Section 10).
That such differences should occur is not unexpected given that simple or approximate models, by their very nature, will not be applicable in all situations, and the fact that two such models might diverge in certain instances is unsurprising. Having said this, we draw attention to the text below taken from ref. [6].
However, whereas oxidation numbers depend on how one chooses to deconstruct the molecule, the dn configuration is a function of the molecule and must be independent of how one decides to deconstruct it. As such, a system of evaluating molecules that results in different dn configurations for the same molecule according to the preference of the author is unsatisfactory.[original emphasis]
Considering the first sentence, it is true that there are some circumstances where ambiguities arise in determining an oxidation state. More fundamentally, however, the statement, ‘…the dn configuration is a function of the molecule and must be independent of how one decides to deconstruct it.’, is one we would question since, as we have argued above and will discuss further below, any definition of dn is necessarily somewhat subjective and, therefore, comes with inevitable uncertainties that are inherent in any approximate model. With regard to the second sentence in the above-quoted text, we are inclined to agree and, accordingly, propose the following definition for dn:
The dn number of a transition metal complex is assigned based on the number of electrons that occupy the frontier orbitals, which have the same symmetry as metal d-orbitals.
This broader definition removes any reference to dn electrons having to be in orbitals that are primarily non-bonding (or antibonding) and recognises (a) the fact that dn is itself something of a misnomer since the electrons of interest occupy molecular orbitals that, whilst they have the same symmetry as d orbitals, are not d atomic orbitals and (b) that dn is effectively a mnemonic for the number of electrons in the frontier orbitals of the complex, i.e., those electrons that are involved in the chemistry of the complex. In addition, we argue that this definition of dn has the following advantages for mononuclear complexes:
- (1)
- It removes the issues around the subjective interpretation of the terms ‘primary’ or ‘primarily’ with regard to whether or not electrons reside in bonding orbitals (see Section 2).
- (2)
- It preserves the useful link between the value of dn and the structural and chemical properties listed in Section 2.
- (3)
Points (1) and (2) are self-explanatory and require no further comment. The essence of point (3) is that, according to the proposed definition of dn, we start by determining a dn number based on the metal OS and then subsequently add whatever caveats are necessary in relation to the compound of interest. For example, compounds with σ Z ligands are assigned an OS-derived dn number, following which, it is made clear in any discussion that two of these electrons are associated, whether strongly or weakly, with the M→Z bond (see Section 6) (Appendix A Note 31). Likewise, for compounds with π Z ligands, such as in the homologous series [M(CO)6]Q, a d6 assignment is preferred, followed by an indication of the extent of any π back-donation from the metal to the CO π* orbitals, in line with the discussion presented in Section 7. Moreover, a d6 assignment preserves the link with the expected redox chemistry of metal carbonylate anions that are easily oxidised [54,94,95] (Appendix A Note 32) [96]. A similar caveat was discussed in Section 10 regarding an OS-derived dn number for metal–metal bonded compounds and those electrons associated with the M–M bonding (Appendix A Note 33).
Much of the discussion above highlights a salient and important difference between the OS and CBC approaches, which is that the former is (obviously) based on the oxidation state, whereas the latter employs valence. Thus, if one accepts Sidgwick’s original definition for the valence of an atom as the number of electrons that the atom uses in bonding, then in complexes such as [Hf(CO)6]2− and [Re2Cl8]2−, it is inevitable that the value of n in the term dn will decrease to zero since all of the metal-based electrons are involved in bonding (π back-bonding or metal–metal bonding) to some degree [10,11,12,13,97]. Furthermore, in using the OS method, an OS is first determined and the dn number is assigned directly from the application of Equation (1). Any judgement about the validity of this dn number then follows according to the nature of the compound, based on specific experimental and/or spectroscopic data and the insights afforded by computational studies, as illustrated with the examples given in Section 6, Section 7, Section 8, Section 9 and Section 10 above. In contrast, the CBC method requires rather less judgement and fewer caveats, but in the case of π Z ligands, the judgement required is made before a dn number is assigned.
In conclusion, we emphasise that simple models will always have limitations, and any expectation that they will be applicable in all circumstances is chimerical [60]. It is nevertheless important to recognise the great value of the OS and CBC methodologies for the systematisation and classification of, particularly, transition metal compounds, in both teaching and research contexts, despite the limitations they each may have. In this regard, as we have done before [60], we will quote Frenking, Schwerdtfeger, and co-workers who offer the apposite apothegm: ‘Chemical bonding models are not right or wrong, they are more or less useful’ [98].
OS assignments continue to attract discussion (and sometimes controversy) in the chemical literature, but whatever one’s preference in terms of OS vs. CBC, we close with a final recommendation that is in line with a broadly similar statement made by Parkin in ref. [9]. Namely, in any discussion where the dn number is being used to gain some insight into the chemistry of a particular compound, it is important, for reasons that must now be obvious, to specify whether n has been determined using the OS or CBC method and also to what extent any assignment derives from spectroscopic and/or computational insights (Appendix A Note 34) [99,100].
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We would like to thank the following people who have made helpful comments during the preparation of this article: Robert H. Crabtree (Yale University, USA), Gernot Frenking (Philipps-Universität Marburg, Germany), Jonathan Rourke (University of Cardiff, UK) and Mark J. Winter (University of Sheffield, UK).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Notes
- The terms ‘transition elements’ and ‘d-block elements’ will be considered as fungible in this article without concern as to whether certain elements merit inclusion within those categories or not. Thus, arguments, for example, about whether the Group 12 elements are best described as transition elements or main group elements will be left to others.
- For a selection of current texts which cover both CFT and LFT, see refs. [1,2,3,4,5].
- This statement is taken from ref. [6] which makes specific reference to the text by Jean [7].
- The definitions of oxidation state and valence are different (although often confused), as has been made clear in refs. [10,11,12,13].
- For more detail on how to assign an oxidation state, see ref. [14] and for an abbreviated summary, see ref. [15]. See also the IUPAC ‘Gold Book’ definitions of oxidation state [16] and the related term, oxidation number [17]. For the purposes of this article, the distinction between oxidation state and oxidation number is unimportant.
- Many discussions of whether a given compound will be high spin or low spin (where there is a distinction to be made) focus on the magnitude of Δ and the factors which affect it (the nature of the ligand, the row in the periodic table in which the metal resides and the metal oxidation state) and the pairing energy (P) associated with placing two electrons in the same orbital. With regard to the pairing energy, in ref. [5], the exchange energy associated with each of the different possible electron configurations is evaluated, which is a rather more rigorous approach.
- There are a few exceptions to this generalisation, such as certain square planar d10 Ag(I) complexes, which have been known for over 50 years. However, they are rare, and the planar geometry is normally associated either with a rigidity inherent in the chelating ligands or as a result of the geometry being crystallographically imposed. See, for example, ref. [18].
- In neutral gas-phase atoms, ns orbitals are populated in addition to (n − 1)d orbitals as reflected in the electronic configurations often presented in periodic tables; for example, the ground state electronic configuration of Fe is written as 4s2 3d6. In metal complexes, however, the (n − 1)d orbitals are generally lower in energy than the ns orbitals such that all the valence electrons are allocated to the d orbitals. Within the CFT (and LFT) models, Fe(0) is therefore designated as d8 and Fe(III), for example, as d5.
- This general point is captured for the t2g and eg orbitals in the following quote taken from ref. [5]: ‘Taken together, the 2eg and the 1t2g are described as the metal-based orbitals.’ [the numbers in front of eg and t2g reflect the numbering of the orbitals in the diagram presented in ref. [5] and are of no consequence for the argument presented here].
- For more details on NBO Theory, see refs. [21,22].
- For the purposes of this article, the terms carbene and alkylidene will be treated as synonymous, and the term carbene will be used throughout.
- That the treatment of CF2 carbene ligands is of more than just academic interest is evident from some of their important applications described in refs. [38,39].
- For a more general article on this topic, see ref. [41].
- The gradation from M(η2-H2) to M(H)2 represents the simplest continuum in bonding from ML to MX2 (and hence a dn to dn−2 transition); see ref. [42] and refs. therein.
- Neutral ambiphilic ligands of the type considered here are multidentate ligands which contain a Z-type boron centre attached to, usually, one, two or three S- or P-donor sites, each one of which can be labelled as an L ligand. For a review of this general topic, see ref. [43].
- More generally, {MNO}n may be written as {M(NO)x}n to accommodate poly-nitrosyl complexes. As stated in the text, the values of n in the expressions {MNO}n (or {M(NO)x}n) and dn are the same if the NO ligand is treated as NO+. Alternatively, the value of n in the expression {MNO}n can be determined by adding the value of n in the dn number of the complex without the NO ligands to the number of electrons present in the NO π* orbitals; one per NO.
- For a computational study which considers the 3d element series, [Ti(CO)6]2− to [Fe(CO)6]2+, see ref. [55].
- It is worth noting that were the π Z interaction ignored in [Hf(CO)6]2−, an initial CBC assignment of [ML6]2− becomes, according to the transformation L− → LX, ML6X2 from which a d2 configuration would result based on Equation (3), but see ref. [9] for a more detailed discussion of how to consider this transformation in species where there is undoubtedly a significant π component.
- Versions of Figure 9 appear in most inorganic chemistry textbooks, but they do not generally take into account the following: (i) the interactions between the metal t2g orbitals and the filled π bonding orbitals on the CO, which also have t2g symmetry, (ii) the effect that the positive charge has on increasing the strength of the M–CO σ bonding and hence the increasing energy of the eg* orbitals and (iii) the mutual σ/π bond-strengthening known as the synergic effect. One text that does consider these matters in more detail is ref. [56], specifically, p. 862.
- An interesting approach referred to as Charge Distribution via Reporters (CDVR) can be found in ref. [57] which bears on some of the issues discussed in this section, although not specifically the dn number.
- For further recent examples of papers by Klüfers et al. that deal with the bonding in metal nitrosyls, see refs. [63,64] and for an interesting discussion about how to consider the NO ligand in the complex [TpMe2]NiNO (where [TpMe2] is the tris(3,5-dimethylpyrazolyl)hydroborato ligand), see refs. [65,66]. For a recent paper which considers how to estimate charge distribution in metal nitrosyl complexes, see ref. [67] and for a discussion of the factors which affect the linear vs. bent (or intermediate) geometries in the cationic species [MCl(NO)2(PPh3)2]+ (M = Ru, Os), see ref. [68].
- The CBC approach to dealing with poly-nitrosyl compounds is also briefly considered in refs. [26,65].
- [Mn(CO)(NO)3] and [FeX(NO)3] (X = Cl, Br, I) are examples of M(NO)3 complexes which have C3v symmetry with a pseudo tetrahedral geometry at the metal centre. They are d10 complexes according to the OS method [Mn(-III) and Fe(-II), respectively]. We are not aware that an MLX assignment has been proposed for the M(NO)3 unit, but it is expected that the d6 configuration that the CBC method suggests for other [M(CO)n(NO)4–n] complexes also holds for [Mn(CO)(NO)3] which leads to an ML5X designation, and the classification of a M(NO)3 group in a tetrahedral geometry of L4X; [FeX(NO)3] will then be d6-ML4X2.
- The electronic structure of the paramagnetic complex 22 has been reported as d6 with, in addition, two electrons occupying a doubly degenerate HOMO, which is localised on the NO ligands, see ref. [69].
- The reason why the Hückel 4n + 2 condition for aromaticity matters in this context is that within the OS formalism, ligands are generally removed from the metal centre not only in accordance with the ionic approximation set out in refs. [14,15,16,17] but also in their closed-shell configuration.
- NO and C7H7 are treated somewhat differently due to the inclusion of the Z component. Thus, NO is initially designated as LXZ, which, since LZ is equivalent to X2 [Scheme 1 (iii)], becomes X3. C7H7 is initially classified as L3XZ, which, again because LZ is equivalent to X2, becomes L2X3.
- The problem disappears if the equivalent neutral class formalism is abandoned for complexes in negative oxidation states whereby [Fe(CO)4]2− would be considered simply as [FeL4]2− in which the two additional electrons would convert d8-FeL4 to d10-[FeL4]2−.
- The addition of a haloalkane RX to 26 (Collman’s Reagent) to give the versatile intermediate species [RFe(CO)4]− is a pivotal reaction for the synthetic applications of [Fe(CO)4]2− and can be viewed as involving two electrons from the Fe centre in 26 to form the Fe–R bond in [RFe(CO)4]−; effectively, an SN2 reaction. In terms of OS, this process is readily understood as an oxidation of a d10-Fe(-II) to give a d8-Fe(0) species. By contrast, in terms of the CBC, this reaction involves a transformation of a d6-ML4X2 to a d8-ML5 species, which is less easily reconciled with electronic changes at the Fe centre.
- A computational study which contrasts the number of electrons actually associated with metal–metal bonding with a simplistic accounting based on the M–M bond order is reported in ref. [86].
- For a general article on PSEPT, see ref. [87].
- This suggestion is in accord with the (M → B)n descriptor proposed by Hill in ref. [47] and discussed in Section 6.
- If the significant vs. insignificant π back-bonding judgment is to be evidenced by the position of the νCO bands in the vibrational spectra, then complications will arise with substituted metal carbonyls. For example, the νCO bands for cis-[Cr(CO)2(dmpe)2] (dmpe = Me2PCH2CH2PMe2) occur at 1856 and 1798 cm−1, which are in the vicinity of the νCO (T1u) bands for [V(CO)6]−. See ref. [96].
- In line with this suggestion, and following the point made in (Appendix A Note 31), it may be noted that metal–metal bonded binuclear compounds are sometimes written with a similar type of descriptor to indicate the metal–metal bond order, for example, [Mo2(CO)6(η-C5H5)2] (M–M) and [Mo2(CO)4(η-C5H5)2] (M≡M).
- See, for example, refs. [99,100].
References
- Cotton, F.A.; Wilkinson, G.; Gaus, P.L. Basic Inorganic Chemistry, 3rd ed.; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Cotton, F.A.; Wilkinson, G.; Murillo, C.A.; Bochmann, M. Advanced Inorganic Chemistry, 6th ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Housecroft, C.E.; Sharpe, A.G. Inorganic Chemistry, 5th ed.; Pearson: London, UK, 2018. [Google Scholar]
- Weller, M.T.; Overton, T.L.; Rourke, J.P.; Armstrong, F.A. Inorganic Chemistry, 7th ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Keeler, J.; Wothers, P. Chemical Structure and Reactivity: An Integrated Approach, 2nd ed.; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Parkin, G. A Simple Description of the Bonding in Transition-Metal Borane Complexes. Organometallics 2006, 25, 4744–4747. [Google Scholar] [CrossRef]
- Jean, Y. Molecular Orbitals of Transition Metal Complexes; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Hartwig, J. Organotransition Metal Chemistry: From Bonding to Catalysis; University Science Books: Sausalito, CA, USA, 2010. [Google Scholar]
- Parkin, G. Impact of the Coordination of Multiple Lewis Acid Functions on the Electronic Structure and vn Configuration of a Metal Centre. Dalton Trans. 2022, 51, 411–427. [Google Scholar] [CrossRef]
- Parkin, G. Valence, Oxidation Number, and Formal Charge: Three Related but Fundamentally Different Concepts. J. Chem. Ed. 2006, 83, 791–799. [Google Scholar] [CrossRef]
- Smith, D.W. Valence, Covalence, Hypervalence, Oxidation State and Coordination Number. J. Chem. Ed. 2005, 82, 1202–1204. [Google Scholar] [CrossRef]
- Norman, N.C.; Pringle, P.G. Hypervalence: A Useful Concept or One That Should Be Gracefully Retired? Chemistry 2022, 4, 1226–1249. [Google Scholar] [CrossRef]
- Norman, N.C. Periodicity and the s- and p-Block Elements, 2nd ed.; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Karen, P.; McArdle, P.; Takats, J. Toward a Comprehensive Definition of Oxidation State (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 1017–1081. [Google Scholar] [CrossRef]
- Karen, P.; McArdle, P.; Takats, J. Comprehensive Definition of Oxidation State (IUPAC Recommendations 2016). Pure Appl. Chem. 2016, 88, 831–839. [Google Scholar] [CrossRef]
- McNaught, A.D.; Wilkinson, A. (Eds.) 1997. IUPAC. Compendium of Chemical Terminology, 2nd ed.; the “Gold Book”. Oxidation State. Available online: https://goldbook.iupac.org/terms/view/O04365 (accessed on 10 July 2023).
- McNaught, A.D.; Wilkinson, A. (Eds.) 1997. IUPAC. Compendium of Chemical Terminology, 2nd ed.; The “Gold Book”. Oxidation Number. Available online: https://goldbook.iupac.org/terms/view/O04363 (accessed on 10 July 2023).
- Young, A.G.; Hanton, L.R. Square Planar Silver(I) Complexes: A Rare but Increasingly Observed Stereochemistry for Silver(I). Coord. Chem. Rev. 2008, 252, 1346–1386. [Google Scholar] [CrossRef]
- Albright, T.A.; Burdett, J.K.; Whangbo, M.H. Orbital Interactions in Chemistry, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Fekl, U. Covalent d-Block Organometallics: Teaching Lewis Structures and sd/sd2 Hybridisation Gives Students Additional Explanations and Powerful Predictive Tools. J. Chem. Ed. 2021, 98, 3189–3206. [Google Scholar] [CrossRef]
- Landis, C.R.; Weinhold, F. 18-Electron Rule and the 3c/4e Hyperbonding Saturation Limit. J. Comput. Chem. 2016, 37, 237–241. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO Analysis and How is it Useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- Crabtree, R.H. The Organometallic Chemistry of the Transition Metals, 7th ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Green, M.L.H. A New Approach to the Formal Classification of Covalent Compounds and Elements. J. Organomet. Chem. 1995, 500, 127–148. [Google Scholar] [CrossRef]
- Green, M.L.H.; Parkin, G. Application of the Covalent Bond Classification Method for the Teaching of Inorganic Chemistry. J. Chem. Ed. 2014, 91, 807–816. [Google Scholar] [CrossRef]
- Parkin, G. Classification of Organometallic Compounds. Comprehensive Organometallic Chemistry III; Elsevier: Amsterdam, The Netherlands, 2007; Volume 1, pp. 1–57. [Google Scholar]
- Bohnenberger, J.; Feuerstein, W.; Himmel, D.; Daub, M.; Breher, F.; Krossing, I. Stable Salts of the Hexacarbonyl Chromium(I) Cation and its Pentacarbonyl-Nitrosyl Chromium(I) Analogue. Nat. Commun. 2019, 10, 624. [Google Scholar] [CrossRef]
- Grubbs, R.H.; Trnk, T.M.; Sandford, M.S. Fundamentals of Molecular Catalysis; Kurosawa, H., Yamamoto, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Montgomery, C.D. Fischer and Schrock Carbene Complexes: A Molecular Modeling Exercise. J. Chem. Ed. 2015, 92, 1653–1660. [Google Scholar] [CrossRef]
- Esteruelas, M.A.; González, A.I.; López, A.M.; Oñate, E. An Osmium-Carbene Complex with Fischer–Schrock Ambivalent Behavior. Organometallics 2003, 22, 414–425. [Google Scholar] [CrossRef]
- Casey, C.P.; Vosejpka, P.C.; Askham, F.R. Amphiphilic Carbene Complexes: Both Electrophiles and Nucleophiles Attack the Carbene Carbon of C5H5(CO)2Re:CHR. J. Am. Chem. Soc. 1990, 112, 3713–3715. [Google Scholar] [CrossRef]
- Santamaría, J.; Aguilar, E. Beyond Fischer and Schrock Carbenes: Non-Heteroatom-Stabilized Group 6 Metal Carbene Complexes—A General Overview. Org. Chem. Front. 2016, 3, 1561–1588. [Google Scholar] [CrossRef]
- Hopkinson, M.N.; Richter, C.; Schedler, M.; Glorius, F. An Overview of N-Heterocyclic Carbenes. Nature 2014, 510, 485–496. [Google Scholar] [CrossRef]
- Soleilhavoup, M.; Bertrand, G. Cyclic (Alkyl)(Amino)Carbenes (CAACs): Stable Carbenes on the Rise. Acc. Chem. Res. 2015, 48, 256–266. [Google Scholar] [CrossRef]
- Occhipinti, G.; Jensen, V.R. Nature of the Transition Metal Carbene Bond in Grubbs Olefin Metathesis Catalysts. Organometallics 2011, 30, 3522–3529. [Google Scholar] [CrossRef]
- Clark, G.R.; Hoskins, S.V.; Jones, T.C.; Roper, W.R. Oxidation State Control of the Reactivity of a Transition Metal-Carbon Double Bond. Synthesis, X-Ray Crystal Structure, and Reactions of the Zerovalent Difluorocarbene Complex [Ru(=CF2)(CO)2(PPh3)2]. J. Chem. Soc. Chem. Commun. 1983, 13, 719–721. [Google Scholar] [CrossRef]
- Clark, G.R.; Hoskins, S.V.; Roper, W.R. Difluorocarbene Complexes of Ruthenium Derived from Trifluoromethyl Compounds. RuCl2(CF2)(CO)(PPh3)2, RuCl2(CFNMe2)(CO)(PPh3)2 and the Structure of Ru(CF3)(HgCF3)(CO)2(PPh3)2. J. Organomet. Chem. 1982, 234, C9–C12. [Google Scholar] [CrossRef]
- Fu, X.-P.; Xue, X.-S.; Zhang, X.-Y.; Xiao, Y.-L.; Zhang, S.; Guo, Y.-L.; Leng, X.; Houk, K.N.; Zhang, X. Controllable Catalytic Difluorocarbene Transfer Enables Access to Diversified Fluoroalkylated Arenes. Nat. Chem. 2019, 11, 948–956. [Google Scholar] [CrossRef]
- Zhou, W.; Pan, W.-J.; Chen, J.; Zhang, M.; Lin, J.-H.; Cao, W.; Xiao, J.-C. Transition-Metal Difluorocarbene Complexes. Chem. Commun. 2021, 57, 9316–9329. [Google Scholar] [CrossRef]
- Cohen, S.A.; Auburn, P.R.; Bercaw, J.E. Structure and Reactivity of Bis(pentamethylcyclopentadienyl)(ethylene)titanium(II), a Simple Olefin Adduct of Titanium. J. Am. Chem. Soc. 1983, 105, 1136–1143. [Google Scholar] [CrossRef]
- Jerabek, P.; Schwerdtfeger, P.; Frenking, G. Dative and Electron-Sharing Bonding in Transition Metal Compounds. J. Comput. Chem. 2019, 40, 247–264. [Google Scholar] [CrossRef]
- Crabtree, R.H. Dihydrogen Complexation. Chem. Rev. 2016, 116, 8750–8769. [Google Scholar] [CrossRef]
- Bouhadirab, G.; Bourissou, D. Complexes of Ambiphilic Ligands: Reactivity and Catalytic Applications. Chem. Soc. Rev. 2016, 45, 1065–1079. [Google Scholar] [CrossRef]
- Sircoglou, M.; Bontemps, S.; Mercy, M.; Saffon, N.; Takahashi, M.; Bouhadir, G.; Maron, L.; Bourissou, D. Transition-Metal Complexes Featuring Z-Type Ligands: Agreement or Discrepancy between Geometry and dn Configuration? Angew. Chem. Int. Ed. 2007, 46, 8583–8586. [Google Scholar] [CrossRef]
- Kameo, H.; Tanaka, Y.; Shimoyama, Y.; Izumi, D.; Matsuzaka, H.; Nakajima, Y.; Lavedan, P.; Le Gac, A.; Bourissou, D. Square-Planar Anionic Pt0 Complexes. Angew. Chem. Int. Ed. 2023, 62, e202301509. [Google Scholar] [CrossRef]
- Bontemps, S.; Bouhadir, G.; Miqueu, K.; Bourissou, D. On the Versatile and Unusual Coordination Behavior of Ambiphilic Ligands o-R2P(Ph)BR’2. J. Am. Chem. Soc. 2006, 128, 12056–12057. [Google Scholar] [CrossRef]
- Hill, A.F. An Unambiguous Electron-Counting Notation for Metallaboratranes. Organometallics 2006, 25, 4741–4743. [Google Scholar] [CrossRef]
- Enemark, J.H.; Feltham, R.D. Stereochemical Control of Valence, III. The {CoNO}8 Group in Ligand Fields C4v, C2v, and Cs Symmetry. J. Am. Chem. Soc. 1974, 96, 5004–5005. [Google Scholar] [CrossRef]
- Enemark, J.H.; Feltham, R.D. Principles and Structure, Bonding and Reactivity for Metal Nitrosyl Complexes. Coord. Chem. Rev. 1974, 13, 339–406. [Google Scholar] [CrossRef]
- Schild, D.J.; Nurdin, L.; Moret, M.-E.; Oyala, P.H.; Peters, J.C. Characterisation of a Proposed Terminal Iron(III) Nitride Intermediate of Nitrogen Fixation Stabilized by a Trisphosphine-Borane Ligand. Angew. Chem. Int. Ed. 2022, 61, e202209655. [Google Scholar] [CrossRef]
- Frenking, G.; Fernández, I.; Holzmann, N.; Pan, S.; Krossing, I.; Zhou, M. Metal–CO Bonding in Mononuclear Transition Metal Carbonyl Complexes. JACS Au 2021, 1, 623–645. [Google Scholar] [CrossRef]
- Frenking, G. Understanding the Nature of the Bonding in Transition Metal Complexes: From Dewar’s Molecular Orbital Model to an Energy Partitioning Analysis of the Metal-Ligand Bond. J. Organomet. Chem. 2001, 635, 9–23. [Google Scholar] [CrossRef]
- Bach, C.; Willner, H.; Aubke, F.; Wang, C.; Rettig, S.J.; Trotter, J. Cationic Iridium(III) Carbonyl Complexes: [Ir(CO)6]3+ and [Ir(CO)5Cl]2+. Angew. Chem. Int. Ed. Engl. 1996, 35, 1974–1976. [Google Scholar] [CrossRef]
- Ellis, J.E.; Chi, K.-M. Synthesis, Isolation, and Characterisation of [K(cryptand 2.2.2)]2[Hf(CO)6], the First Substance to Contain Hafnium in a Negative Oxidation State. Structural Characterisation of [K(cryptand 2.2.2)]2[M(CO)6].Pyridine (M = Ti, Zr, and Hf). J. Am. Chem. Soc. 1990, 112, 6022–6025. [Google Scholar] [CrossRef]
- van der Lubbe, S.C.C.; Vermeeren, P.; Fonseca Guerra, C.; Bickelhaupt, F.M. The Nature of Nonclassical Carbonyl Ligands Explained by Kohn-Sham Molecular Orbital Theory. Chem. Eur. J. 2020, 26, 15690–15699. [Google Scholar] [CrossRef]
- Purcell, K.F.; Kotz, J.C. Inorganic Chemistry; W. B. Saunders Company Ltd.: London, UK, 1977. [Google Scholar]
- Wolczanski, P.T. Flipping the Oxidation State Formalism: Charge Distribution in Organometallic Complexes as Reported by Carbon Monoxide. Organometallics 2017, 36, 622–631. [Google Scholar] [CrossRef]
- Stepanenko, I.; Zalibera, M.; Schaniel, D.; Telser, J.; Arion, V.B. Ruthenium-Nitrosyl Complexes as NO-Releasing Molecules, Potential Anticancer Drugs, and Photoswitches Based on Linkage Isomerism. Dalton Trans. 2022, 51, 5367–5393. [Google Scholar] [CrossRef]
- Gouveia Júnior, F.S.; de Moraes Silveira, J.A.; Holanda, T.M.; Marinho, A.D.; Ridnour, L.A.; Wink, D.A.; Bezerra de Siqueira, R.J.; Azul Monteiro, H.S.; Silva de Sousa, E.H.; de França Lopes, L.G. New Nitrosyl Ruthenium Complexes with Combined Activities for Multiple Cardiovascular Disorders. Dalton Trans. 2023, 52, 5176–5191. [Google Scholar] [CrossRef]
- Norman, N.C.; Pringle, P.G. In Defence of Oxidation States. Dalton Trans. 2022, 51, 400–410. [Google Scholar] [CrossRef]
- Ampßler, T.; Monsch, G.; Popp, J.; Riggenmann, T.; Salvador, P.; Schröder, D.; Klüfers, P. Not Guilty on Every Count: The “Non-Innocent” Nitrosyl Ligand in the Framework of IUPAC’s Oxidation-State Formalism. Angew. Chem. Int. Ed. 2020, 59, 12381–12386. [Google Scholar] [CrossRef]
- Popp, J.; Riggenmann, T.; Schröder, D.; Ampßler, T.; Salvador, P.; Klüfers, P. Bent and Linear {CoNO}8 Entities: Structure and Bonding in a Prototypic Class of Nitrosyls. Inorg. Chem. 2021, 60, 15980–15996. [Google Scholar] [CrossRef]
- Popp, J.; Klüfers, P. Bond Strength of a Diatomic Acceptor Ligand: A Reliable Measure of its Antibond Occupation and its Charge? Eur. J. Inorg. Chem. 2022, 32, e202200374. [Google Scholar] [CrossRef]
- Schröder, D.; Klüfers, P. Bonding in PdCl(NO) and Related Nitrosylmetal Species of the Enemark-Feltham {MNO}10 Type. Z. Anorg. Allg. Chem. 2023, 649, e202200338. [Google Scholar] [CrossRef]
- Landry, V.K.; Pang, K.; Quan, S.M.; Parkin, G. Tetrahedral Nickel Nitrosyl Complexes with Tripodal [N3] and [Se3] Donor Ancillary Ligands: Structural and Computational Evidence that a Linear Nitrosyl is a Trivalent Ligand. Dalton Trans. 2007, 8, 820–824. [Google Scholar] [CrossRef]
- Tomson, N.C.; Crimmin, M.R.; Petrenko, T.; Rosebrugh, L.E.; Sproules, S.; Boyd, W.C.; Bergman, R.G.; DeBeer, S.; Toste, F.D.; Wieghardt, K. A Step Beyond the Feltham-Enemark Notation: Spectroscopic and Correlated ab Initio Computational Support for an Antiferromagnetically Coupled M(II)-(NO)− Description of Tp*M(NO) (M = Co, Ni). J. Am. Chem. Soc. 2011, 133, 18785–18801. [Google Scholar] [CrossRef]
- D’Arpino, A.A.; Cundari, T.R.; Wolczanski, P.T.; MacMillan, S.N. Transition Metal Nitrosyls: Statistics, Charge Estimates via CDVR, and Studies of Tetradentate Chelate Diamides (pddi)M and (pddi)MNO (M = Cr, Fe, and Co). Organometallics 2023, 42, 2747–2761. [Google Scholar] [CrossRef]
- Mingos, D.M.P. A Theoretical Analysis of Ambivalent and Ambiphilic Lewis Acids/Bases with Symmetry Signatures. Coord. Chem. Rev. 2015, 293–294, 2–18. [Google Scholar] [CrossRef]
- Tangen, E.; Conradie, J.; Svadberg, A.; Ghosh, A. Understanding the Unexpected Linearity of the trans-{Mn(NO)2}8 Unit in a Phthalocyanine Complex: Some Thoughts on Dinitrosylheme Intermediates in Biology. J. Inorg. Biochem. 2005, 99, 55–59. [Google Scholar] [CrossRef]
- Menconi, G.; Kaltsoyannis, N. Nature of the Transition Metal-Cycloheptatrienyl Bond. Computational Studies of the Electronic Structure of [M(h7-C7H7)(h5-C5H5)] (M = Groups 4-6). Organometallics 2005, 24, 1189–1197. [Google Scholar] [CrossRef]
- Basse, R.; Vanicek, S.; Höfer, T.; Kopacka, H.; Wurst, K.; Muller, T.; Schwartz, H.A.; Olthof, S.; Casper, L.A.; Nau, M.; et al. Cationic Cycloheptatrienyl Cyclopentadienyl Manganese Sandwich Complexes: Tromancenium Explored with High-Power LED Photosynthesis. Organometallics 2021, 40, 2736–2749. [Google Scholar] [CrossRef]
- Goedken, V.L.; Vallarino, L.M.; Quagliano, J.V. Cationic Ligands. Coordination of the 1,1,1 -Trimethylhydrazinium Cation to Nickel(II). Inorg. Chem. 1971, 10, 2682–2685. [Google Scholar] [CrossRef]
- Feil, C.M.; Hettich, T.D.; Beyer, K.; Sondermann, C.; Schlindwein, S.H.; Nieger, M.; Gudat, D. Comparing the Ligand Behavior of N-Heterocyclic Phosphenium and Nitrosyl Units in Iron and Chromium Complexes. Inorg. Chem. 2019, 58, 6517–6528. [Google Scholar] [CrossRef]
- Malchau, C.; Loose, F.; Mees, Y.; Duppe, J.; Sun, Y.; Niedner-Schatteburg, G.; Thiel, W.R. Electronic Properties of a Cationic Triphenylphosphine Ligand Decorated with a (η5-C5H5)Fe Group in Late-Transition-Metal Complexes. Organometallics 2020, 39, 3335–3343. [Google Scholar] [CrossRef]
- Schroers, J.P.; Kliemann, M.N.; Kollath, J.M.A.; Tauchert, M.E. How Cationic Metalloligands Affect the Coordination of Lewis Basic Ligands in RhI Complexes. Organometallics 2021, 40, 3893–3906. [Google Scholar] [CrossRef]
- Maser, L.; Vogt, M.; Langer, R. Cationic Ligands Between σ-Donation and Hydrogen-Bridge-Bond-Stabilisation of Ancillary Ligands in Coinage Metal Complexes with Protonated Carbodiphosphoranes. Dalton Trans. 2022, 51, 17397–17404. [Google Scholar] [CrossRef]
- Finze, M.; Bernhardt, E.; Willner, H.; Lehmann, C.W.; Aubke, F. Homoleptic, σ-Bonded Octahedral Superelectrophilic Metal Carbonyl Cations of Iron(II), Ruthenium(II), and Osmium(II). Part 2: Syntheses and Characterizations of [M(CO)6][BF4]2 (M = Fe, Ru, Os). Inorg. Chem. 2005, 44, 4206–4214. [Google Scholar] [CrossRef]
- Collman, J.P. Disodium Tetracarbonylferrate—A Transition Metal Analog of a Grignard Reagent. Acc. Chem. Res. 1975, 8, 342–347. [Google Scholar] [CrossRef]
- Cotton, F.A.; Murillo, C.A.; Walton, R.A. (Eds.) Multiple Bonds between Metal Atoms, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Falvello, L.R.; Foxman, B.M.; Murillo, C.A. Fitting the Pieces of the Puzzle: The d bond. Inorg. Chem. 2014, 53, 9441–9456. [Google Scholar] [CrossRef]
- Krapp, A.; Lein, M.; Frenking, G. The Strength of the s-, p-, and d-bonds in Re2Cl82–. Theor. Chem. Acc. 2008, 120, 313–320. [Google Scholar] [CrossRef]
- Carlin, R.T.; Osteryoung, R.A. Electrochemistry of Molybdenum Chloride Dimers in a Basic Ambient-Temperature Molten Salt. Inorg. Chem. 1988, 27, 1482–1488. [Google Scholar] [CrossRef]
- Nuzzo, R.G.; Simon, H.J.; San Filippo, J., Jr. Selective Reduction of Sulfoxides. J. Org. Chem. 1977, 42, 568–569. [Google Scholar] [CrossRef]
- Chisholm, M.H.; Kirkpatrick, C.C.; Huffman, J.C. Reactions of Metal–Metal Multiple Bonds. 7. Addition of the Halogens Chlorine, Bromine and Iodine and Diisopropyl Peroxide to Hexaisopropoxydimolybdenum (M≡M). Dinuclear Oxidative-Addition Reactions Accompanied by Metal–Metal Bond-Order Changes from 3 to 2 to 1. Inorg. Chem. 1981, 20, 871–876. [Google Scholar]
- Norman, N.C.; Pringle, P.G. Reply to the ‘Comment on “In Defence of Oxidation States”’ by J. C. Green. Dalton Trans. 2022, 51, 748–749. [Google Scholar] [CrossRef]
- Gatti, C.; Lasi, D. Source Function Description of Metal–Metal Bonding in d-Block Organometallic Compounds. Faraday Discuss. 2007, 135, 55–78. [Google Scholar] [CrossRef]
- Mingos, D.M.P. Polyhedral Skeletal Electron Pair Approach. Acc. Chem. Res. 1984, 17, 311–319. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alvarez, S.; Mealli, C.; Falceto, A.; Cahill III, T.J.; Zeng, T.; Manca, G. From Widely Accepted Concepts in Coordination Chemistry to Inverted Ligand Fields. Chem. Rev. 2016, 116, 8173–8192. [Google Scholar] [CrossRef]
- Walroth, R.C.; Lukens, J.T.; MacMillan, S.N.; Finkelstein, K.D.; Lancaster, K.M. Spectroscopic Evidence for a 3d10 Ground State Electronic Configuration and Ligand Field Inversion in [Cu(CF3)4]1−. J. Am. Chem. Soc. 2016, 138, 1922–1931. [Google Scholar] [CrossRef]
- Leach, I.F.; Havenith, R.W.A.; Klein, J.E.M.N. Revisiting Formal Copper(III) Complexes: Bridging Perspectives with Quasi-d10 Configurations. Eur. J. Inorg. Chem. 2022, 27, e202200247. [Google Scholar] [CrossRef]
- Demonti, L.; Tabikh, H.; Saffon-Merceron, N.; Nebra, N. Safe Entry to Ag(I)/Ag(III) Mixed Valence Salts Containing the Homoleptic Ag(III) Anion [Ag(CF3)4]−. Eur. J. Inorg. Chem. 2023, 26, e202300042. [Google Scholar] [CrossRef]
- Shreiber, S.T.; DiMucci, I.M.; Khrizanforov, M.N.; Titus, C.J.; Nordlund, D.; Dudkina, Y.; Cramer, R.E.; Budnikova, Y.; Lancaster, K.M.; Vicic, D.A. [(MeCN)Ni(CF3)3]− and [Ni(CF3)4]2−: Foundations Toward the Development of Trifluoromethylations at Unsupported Nickel. Inorg. Chem. 2020, 59, 9143–9151. [Google Scholar] [CrossRef]
- Pérez-Bitrián, A.; Alvarez, S.; Baya, M.; Echeverría, J.; Martín, A.; Orduna, J.; Menjón, B. Terminal Au–N and Au–O Units in Organometallic Frames. Chem. Eur. J. 2023, 29, e202203181. [Google Scholar] [CrossRef]
- Ellis, J.E. Adventures with Substances Containing Metals in Negative Oxidation States. Inorg. Chem. 2006, 45, 3167–3186. [Google Scholar] [CrossRef]
- Ellis, J.E. Metal Carbonyl Anions: From [Fe(CO)4]2− to [Hf(CO)6]2− and Beyond. Organometallics 2003, 22, 3322–3338. [Google Scholar] [CrossRef]
- Connor, J.A.; McEwen, G.K.; Rix, C.J. Ditertiary Alkylphosphine Derivatives of the Group VI Metal Carbonyls and their Oxidation with Iodine. J. Chem. Soc. Dalton Trans. 1974, 6, 589–595. [Google Scholar] [CrossRef]
- Sidgwick, N.V. The Electronic Theory of Valence; Oxford University Press: Oxford, UK, 1927. [Google Scholar]
- Zhao, L.; Pan, S.; Holzmann, N.; Schwerdtfeger, P.; Frenking, G. Chemical Bonding and Bonding Models in Main-Group Chemistry. Chem. Rev. 2019, 119, 8781–8845. [Google Scholar] [CrossRef]
- Gimferrer, M.; Aldossary, A.; Salvador, P.; Head-Gordon, M. Oxidation State Localised Orbitals: A Method for Assigning Oxidation States Using Optimally Fragment-Localised Orbitals and a Fragment Orbital Localisation Index. J. Chem. Theory Comput. 2022, 18, 309–322. [Google Scholar] [CrossRef]
- Rupf, S.M.; Pan, S.; Moshtaha, A.L.; Frenking, G.; Malischewski, M. Structural Characterization and Bonding Analysis of [Hg{Fe(CO)5}2]2+[SbF6]−2. J. Am. Chem. Soc. 2023, 145, 15353–15359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).