Conformational Preference of Flavonols and Its Effect on the Chemical Properties Involved in Radical Scavenging Activity
Abstract
:1. Introduction
2. Materials and Methods
2.1. DFT Calculation
2.2. Conformational Search in the Gas Phase or Aqueous Environment
2.3. Calculation of the Bond Dissociation Energy (BDE)
2.4. Computation of pKa
2.5. Computation of IE
3. Results and Discussion
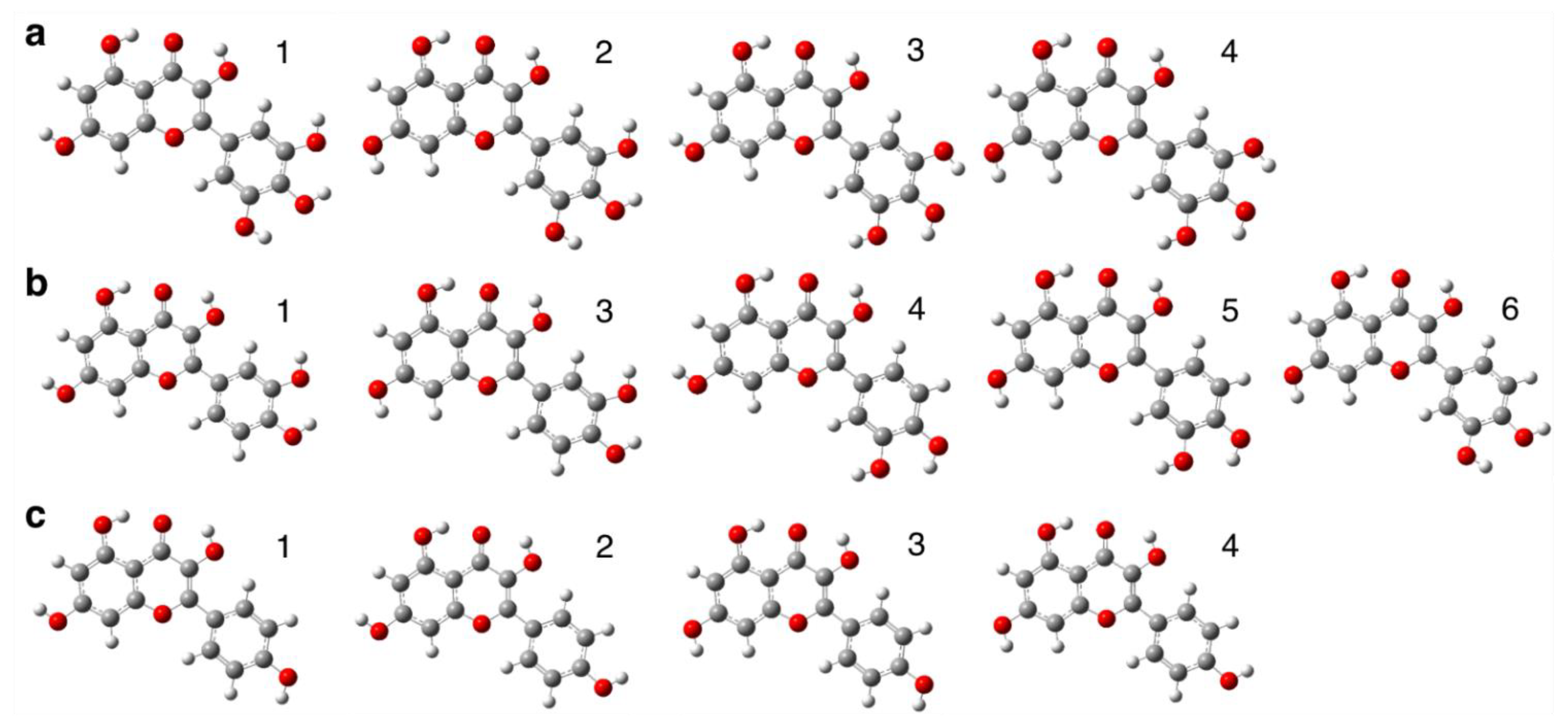
3.1. Conformational Search of Each Flavonol Molecule in the Gas Phase
3.2. Conformational Search of Each Flavonol Molecule in the Aqueous Environment
3.3. BDE and ΔGo of the Reaction of Scavenger with HOO• for O-H Bond in Each Hydroxy Group
3.4. Calculated pKa for Each Hydroxy Group
3.5. Calculated IE in the Aqueous Environment
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dröge, W. Free Radicals in the Physiological Control of Cell Function. Physiol. Rev. 2002, 82, 47–95. [Google Scholar] [CrossRef]
- Halliwell, B. Biochemistry of Oxidative Stress. Biochem. Soc. Trans. 2007, 35, 1147–1150. [Google Scholar] [CrossRef]
- Pacher, P.; Beckman, J.S.; Liaudet, L. Nitric Oxide and Peroxynitrite in Health and Disease. Physiol. Rev. 2007, 87, 315–424. [Google Scholar] [CrossRef]
- Genestra, M. Oxyl Radicals, Redox-Sensitive Signalling Cascades and Antioxidants. Cell. Signal. 2007, 19, 1807–1819. [Google Scholar] [CrossRef]
- Lushchak, V.I. Free Radicals, Reactive Oxygen Species, Oxidative Stresses and Their Classifications. Ukr. Biochem. J. 2015, 87, 11–18. [Google Scholar] [CrossRef]
- Riley, P.A. Free Radicals in Biology: Oxidative Stress and the Effects of Ionizing Radiation. Int. J. Radiat. Biol. 1994, 65, 27–33. [Google Scholar] [CrossRef]
- Sainz, R.M.; Lombo, F.; Mayo, J.C. Radical Decisions in Cancer: Redox Control of Cell Growth and Death. Cancers 2012, 4, 442–474. [Google Scholar] [CrossRef]
- Dozor, A.J. The Role of Oxidative Stress in the Pathogenesis and Treatment of Asthma. Ann. N. Y. Acad. Sci. 2010, 1203, 133–137. [Google Scholar] [CrossRef]
- Zhou, R.; Tardivel, A.; Thorens, B.; Choi, I.; Tschopp, J. Thioredoxin-Interacting Protein Links Oxidative Stress to Inflammasome Activation. Nat. Immunol. 2010, 11, 136–140. [Google Scholar] [CrossRef]
- Rochette, L.; Lorin, J.; Zeller, M.; Guilland, J.-C.; Lorgis, L.; Cottin, Y.; Vergely, C. Nitric Oxide Synthase Inhibition and Oxidative Stress in Cardiovascular Diseases: Possible Therapeutic Targets? Pharmacol. Ther. 2013, 140, 239–257. [Google Scholar] [CrossRef]
- Galano, A.; Raúl Alvarez-Idaboy, J. Computational Strategies for Predicting Free Radical Scavengers’ Protection against Oxidative Stress: Where Are We and What Might Follow? Int. J. Quantum Chem. 2019, 119, e25665. [Google Scholar] [CrossRef]
- Kumar, N.; Goel, N. Phenolic Acids: Natural Versatile Molecules with Promising Therapeutic Applications. Biotechnol. Rep. 2019, 24, e00370. [Google Scholar] [CrossRef]
- Pham-Huy, L.A.; He, H.; Pham-Huy, C. Free Radicals, Antioxidants in Disease and Health. Int. J. Biomed. Sci. 2008, 4, 89–96. [Google Scholar]
- Sanchez-Moreno, C. Review: Methods Used to Evaluate the Free Radical Scavenging Activity in Foods and Biological Systems. Food Sci. Technol. Int. 2002, 8, 121–137. [Google Scholar] [CrossRef]
- Re, R.; Pellegrini, N.; Proteggente, A.; Pannala, A.; Yang, M.; Rice-Evans, C. Antioxidant Activity Applying an Improved ABTS Radical Cation Decolorization Assay. Free Radic. Biol. Med. 1999, 26, 1231–1237. [Google Scholar] [CrossRef]
- Goupy, P.; Dufour, C.; Loonis, M.; Dangles, O. Quantitative Kinetic Analysis of Hydrogen Transfer Reactions from Dietary Polyphenols to the DPPH Radical. J. Agric. Food Chem. 2003, 51, 615–622. [Google Scholar] [CrossRef]
- Platzer, M.; Kiese, S.; Herfellner, T.; Schweiggert-Weisz, U.; Miesbauer, O.; Eisner, P. Common Trends and Differences in Antioxidant Activity Analysis of Phenolic Substances Using Single Electron Transfer Based Assays. Molecules 2021, 26, 1244. [Google Scholar] [CrossRef]
- Prior, R.L.; Cao, G. Analysis of Botanicals and Dietary Supplements for Antioxidant Capacity: A Review. J. AOAC Int. 2000, 83, 950–956. [Google Scholar] [CrossRef]
- Evelson, P.; Travacio, M.; Repetto, M.; Escobar, J.; Llesuy, S.; Lissi, E.A. Evaluation of Total Reactive Antioxidant Potential (TRAP) of Tissue Homogenates and Their Cytosols. Arch. Biochem. Biophys. 2001, 388, 261–266. [Google Scholar] [CrossRef]
- Frankel, E.N.; Meyer, A.S. The Problems of Using One-Dimensional Methods to Evaluate Multifunctional Food and Biological Antioxidants. J. Sci. Food Agric. 2000, 80, 1925–1941. [Google Scholar] [CrossRef]
- Prior, R.L.; Wu, X.; Schaich, K. Standardized Methods for the Determination of Antioxidant Capacity and Phenolics in Foods and Dietary Supplements. J. Agric. Food Chem. 2005, 53, 4290–4302. [Google Scholar] [CrossRef]
- Spiegel, M. Current Trends in Computational Quantum Chemistry Studies on Antioxidant Radical Scavenging Activity. J. Chem. Inf. Model. 2022, 62, 2639–2658. [Google Scholar] [CrossRef]
- Galano, A.; Alvarez-Idaboy, J.R. A Computational Methodology for Accurate Predictions of Rate Constants in Solution: Application to the Assessment of Primary Antioxidant Activity. J. Comput. Chem. 2013, 34, 2430–2445. [Google Scholar] [CrossRef]
- Dzib, E.; Cabellos, J.L.; Ortíz-Chi, F.; Pan, S.; Galano, A.; Merino, G. Eyringpy: A Program for Computing Rate Constants in the Gas Phase and in Solution. Int. J. Quantum Chem. 2019, 119, e25686. [Google Scholar] [CrossRef]
- Alvarez-Idaboy, J.R.; Galano, A. On the Chemical Repair of DNA Radicals by Glutathione: Hydrogen vs Electron Transfer. J. Phys. Chem. B 2012, 116, 9316–9325. [Google Scholar] [CrossRef]
- Vo, Q.V.; Bay, M.V.; Nam, P.C.; Mechler, A. Is Indolinonic Hydroxylamine a Promising Artificial Antioxidant? J. Phys. Chem. B 2019, 123, 7777–7784. [Google Scholar] [CrossRef]
- Rauter, A.P.; Ennis, M.; Hellwich, K.-H.; Herold, B.J.; Horton, D.; Moss, G.P.; Schomburg, I. Nomenclature of Flavonoids (IUPAC Recommendations 2017). Pure Appl. Chem. 2018, 90, 1429–1486. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, Y.; Diao, T.; Zeng, W.; Zuo, Y. Experimental and Theoretical Study on Antioxidant Activity of the Four Anthocyanins. J. Mol. Struct. 2020, 1204, 127509. [Google Scholar] [CrossRef]
- Spiegel, M.; Andruniów, T.; Sroka, Z. Flavones’ and Flavonols’ Antiradical Structure–Activity Relationship—A Quantum Chemical Study. Antioxidants 2020, 9, 461. [Google Scholar] [CrossRef]
- Rice-Evans, C.A.; Miller, N.J.; Paganga, G. Structure-Antioxidant Activity Relationships of Flavonoids and Phenolic Acids. Free Radic. Biol. Med. 1996, 20, 933–956. [Google Scholar] [CrossRef]
- Xie, H.J.; Mou, W.S.; Lin, F.R.; Xu, J.H.; Lei, Q.F. Radical Scavenging Activity of Myricetin. Acta Physico-Chimica Sin. 2013, 29, 1421–1432. [Google Scholar] [CrossRef]
- Nakanishi, I.; Ohkubo, K.; Shoji, Y.; Fujitaka, Y.; Shimoda, K.; Matsumoto, K.; Fukuhara, K.; Hamada, H. Relationship between the Radical-Scavenging Activity of Selected Flavonols and Thermodynamic Parameters Calculated by Density Functional Theory. Free Radic. Res. 2020, 54, 535–539. [Google Scholar] [CrossRef]
- Fiorucci, S.; Golebiowski, J.; Cabrol-Bass, D.; Antonczak, S. DFT Study of Quercetin Activated Forms Involved in Antiradical, Antioxidant, and Prooxidant Biological Processes. J. Agric. Food Chem. 2007, 55, 903–911. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Cagnina, S.; Rotureau, P.; Fayet, G.; Adamo, C. The Ammonium Nitrate and Its Mechanism of Decomposition in the Gas Phase: A Theoretical Study and a DFT Benchmark. Phys. Chem. Chem. Phys. 2013, 15, 10849. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Galano, A.; Alvarez-Idaboy, J.R. Kinetics of Radical-Molecule Reactions in Aqueous Solution: A Benchmark Study of the Performance of Density Functional Methods. J. Comput. Chem. 2014, 35, 2019–2026. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. How Well Can New-Generation Density Functionals Describe the Energetics of Bond-Dissociation Reactions Producing Radicals? J. Phys. Chem. A 2008, 112, 1095–1099. [Google Scholar] [CrossRef]
- Carreon-Gonzalez, M.; Vivier-Bunge, A.; Alvarez-Idaboy, J.R. Thiophenols, Promising Scavengers of Peroxyl Radicals: Mechanisms and Kinetics. J. Comput. Chem. 2019, 40, 2103–2110. [Google Scholar] [CrossRef]
- Gotō, H.; Ōsawa, E. An Efficient Algorithm for Searching Low-Energy Conformers of Cyclic and Acyclic Molecules. J. Chem. Soc. Perkin Trans. 2 1993, 2, 187–198. [Google Scholar] [CrossRef]
- Goto, H.; Osawa, E. Corner Flapping: A Simple and Fast Algorithm for Exhaustive Generation of Ring Conformations. J. Am. Chem. Soc. 1989, 111, 8950–8951. [Google Scholar] [CrossRef]
- Matsui, T.; Baba, T.; Kamiya, K.; Shigeta, Y. An Accurate Density Functional Theory Based Estimation of PKa Values of Polar Residues Combined with Experimental Data: From Amino Acids to Minimal Proteins. Phys. Chem. Chem. Phys. 2012, 14, 4181. [Google Scholar] [CrossRef]
- Galano, A.; Pérez-González, A.; Castañeda-Arriaga, R.; Muñoz-Rugeles, L.; Mendoza-Sarmiento, G.; Romero-Silva, A.; Ibarra-Escutia, A.; Rebollar-Zepeda, A.M.; León-Carmona, J.R.; Hernández-Olivares, M.A.; et al. Empirically Fitted Parameters for Calculating PKa Values with Small Deviations from Experiments Using a Simple Computational Strategy. J. Chem. Inf. Model. 2016, 56, 1714–1724. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Rimarčík, J.; Lukeš, V.; Klein, E.; Ilčin, M. Study of the Solvent Effect on the Enthalpies of Homolytic and Heterolytic N–H Bond Cleavage in p-Phenylenediamine and Tetracyano-p-Phenylenediamine. J. Mol. Struct. THEOCHEM 2010, 952, 25–30. [Google Scholar] [CrossRef]


| Conf. Index | Myricetin | Quercetin | Kaempferol | |||
|---|---|---|---|---|---|---|
| Probability | ωC3-C2-C1′-C2′ | Probability | ωC3-C2-C1′-C2′ | Probability | ωC3-C2-C1′-C2′ | |
| g-1 | 0.534 | 0.1 | 0.475 | −1.2 | 0.385 | 9.4 |
| g-2 | 0.354 | 0.0 | 0.257 | −3.8 | 0.310 | −10.9 |
| g-3 | 0.075 | 11.1 | 0.143 | 4.9 | 0.161 | 13.9 |
| g-4 | 0.035 | −13.3 | 0.082 | 171.8 | 0.144 | 13.2 |
| g-5 | - | - | 0.023 | 168.1 | - | - |
| g-6 | - | - | 0.019 | 167.6 | - | - |
| Molecule | A1 and C | A2 | B1, B2, and B3 |
|---|---|---|---|
| myricetin | I.A1 ≈ 0° and C ≈ 0° II.(A1 ≈ 180° and C ≈ 0°) or (A1 ≈ 0° and C ≈ 180°) | I.A2 ≈ 0° II.A2 ≈ 180° | I.B1 ≈ 0° and B2 ≈ 0° and B3 ≈ 0° II.B1 ≈ 180° and B2 ≈ 180° and B3 ≈ 180° III.others |
| quercetin | I.A1 ≈ 0° and C ≈ 0° II.(A1 ≈ 180° and C ≈ 0°) or (A1 ≈ 0° and C ≈ 180°) | I.A2 ≈ 0° II.A2 ≈ 180° | I.B1 ≈ 0° and B2 ≈ 0° II.B1 ≈ 180° and B2 ≈ 180° |
| kaempferol | I.A1 ≈ 0° and C ≈ 0° II.(A1 ≈ 180° and C ≈ 0°) or (A1 ≈ 0° and C ≈ 180°) | I.A2 ≈ 0° II.A2 ≈ 180° | I.B2 ≈ 0° II.B2 ≈ 180° |
| Conf. Index | Myricetin | Quercetin | Kaempferol | |||
|---|---|---|---|---|---|---|
| Probability | ωC3-C2-C1′-C2′ | Probability | ωC3-C2-C1′-C2′ | Probability | ωC3-C2-C1′-C2′ | |
| w-1 | 0.368 (g-2) † | 27.0 | 0.390 (g-2) | −27.8 | 0.295 (g-2) | −29.5 |
| w-2 | 0.181 (g-4) | −25.4 | 0.183 (g-3) | 26.6 | 0.290 (g-1) | 31.0 |
| w-3 | 0.165 (g-1) | 27.0 | 0.108 (g-6) | 151.5 | 0.209 (g-3) | 30.6 |
| w-4 | 0.125 (none) | 25.4 | 0.103 (g-5) | 152.8 | 0.192 (g-4) | 29.9 |
| w-5 | 0.094 (g-3) | 26.6 | 0.087 (g-4) | 153.5 | - | - |
| w-6 | 0.052 (none) | 25.7 | 0.043 (none) | 152.3 | - | - |
| w-7 | - | - | 0.037 (none) | 153.0 | - | - |
| w-8 | - | - | 0.035 (none) | 27.4 | - | - |
| Conf. Index/Position | Myricetin | Quercetin | Kaempferol |
|---|---|---|---|
| BDE (ΔGo) † | BDE (ΔGo) | BDE (ΔGo) | |
| g-1/O3 | 86.7 (8.1) ‡ | 86.4 (8.0) | 87.2 (8.1) |
| g-2/O3 | 87.1 (8.4) | 86.4 (7.6) | 87.0 (7.7) |
| g-3/O3 | 87.7 (8.0) | 86.7 (7.8) | 87.5 (8.1) |
| g-4/O3 | 88.0 (8.4) | 87.1 (7.9) | 87.3 (7.8) |
| g-5/O3 | - | 87.3 (7.7) | - |
| g-6/O3 | - | 87.5 (8.1) | - |
| mean of ΔGo | 8.2 ± 0.2 | 7.8 ± 0.2 | 7.9 ± 0.2 |
| g-1/O5 | 103.5 (24.1) | 103.6 (24.0) | 103.8 (24.0) |
| g-2/O5 | 104.4 (24.9) | 103.6 (23.6) | 103.6 (23.7) |
| g-3/O5 | 103.9 (24.0) | 104.5 (24.7) | 104.6 (24.7) |
| g-4/O5 | 103.9 (25.8) | 104.0 (24.3) | 104.6 (24.7) |
| g-5/O5 | - | 104.0 (25.9) | - |
| g-6/O5 | - | 103.8 (25.7) | - |
| mean of ΔGo | 24.7 ± 0.7 | 24.7 ± 0.8 | 24.3 ± 0.4 |
| g-1/O7 | 96.6 (17.1) | 95.9 (19.5) | 96.4 (17.3) |
| g-2/O7 | 96.4 (16.8) | 96.5 (17.4) | 96.4 (17.3) |
| g-3/O7 | 96.5 (17.4) | 96.2 (17.1) | 95.9 (16.7) |
| g-4/O7 | 95.8 (16.9) | 96.3 (16.6) | 96.0 (16.8) |
| g-5/O7 | - | 95.7 (15.9) | - |
| g-6/O7 | - | 96.2 (17.0) | - |
| mean of ΔGo | 17.1 ± 0.2 | 17.2 ± 1.1 | 17.0 ± 0.2 |
| g-1/O3‘ | 84.5 (8.4) | 84.0 (6.5) | - |
| g-2/O3′ | 84.6 (8.6) | 83.9 (6.0) | - |
| g-3/O3′ | 84.5 (6.1) | 84.1 (6.2) | - |
| g-4/O3′ | 84.1 (5.8) | 83.1 (5.0) | - |
| g-5/O3′ | - | 82.7 (4.5) | - |
| g-6/O3′ | 82.8 (4.4) | ||
| mean of ΔGo | 7.2 ± 1.3 | 5.4 ± 0.8 | - |
| g-1/O4′ | 76.2 (0.4) | 81.8 (3.2) | 89.8 (10.2) |
| g-2/O4′ | 76.2 (0.5) | 81.7 (2.7) | 89.9 (10.0) |
| g-3/O4′ | 75.5 (−0.7) | 81.2 (5.1) | 89.7 (9.6) |
| g-4/O4′ | 75.7 (−2.7) | 81.2 (2.4) | 89.9 (9.4) |
| g-5/O4′ | - | 80.9 (1.9) | 90.3 (8.7) |
| g-6/O4′ | - | 81.1 (1.8) | |
| mean of ΔGo | −0.6 ± 1.3 | 2.9 ± 1.1 | 9.8 ± 0.3 |
| g-1/O5′ | 84.6 (8.6) | - | - |
| g-2/O5′ | 84.8 (8.8) | - | - |
| g-3/O5′ | 84.5 (6.0) | - | - |
| g-4/O5′ | 84.2 (5.9) | - | - |
| g-5/O5′ | - | - | - |
| g-6/O5′ | - | - | - |
| mean of ΔGo | 7.3 ± 1.4 | - | - |
| Conf. Index/Position | Myricetin | Quercetin | Kaempferol |
|---|---|---|---|
| w-1/O3 | 8.1 | 8.6 | 8.6 |
| w-2/O3 | 8.4 | 8.5 | 8.6 |
| w-3/O3 | 8.2 | 8.4 | 8.6 |
| w-4/O3 | 8.5 | 8.4 | 8.6 |
| w-5/O3 | 8.2 | 8.4 | - |
| w-6/O3 | 8.3 | 8.5 | - |
| w-7/O3 | - | 8.5 | - |
| w-8/O3 | - | 8.4 | - |
| mean | 8.3 ± 0.1 | 8.5 ± 0.1 | 8.6 ± 0.0 |
| w-1/O5 | 8.7 | 8.6 | 8.7 |
| w-2/O5 | 8.8 | 8.6 | 8.7 |
| w-3/O5 | 9.0 | 8.7 | 8.7 |
| w-4/O5 | 8.7 | 8.6 | 8.7 |
| w-5/O5 | 8.6 | 8.5 | - |
| w-6/O5 | 8.5 | 8.7 | - |
| w-7/O5 | - | 8.6 | - |
| w-8/O5 | - | 8.5 | - |
| mean | 8.7 ± 0.2 | 8.6 ± 0.1 | 8.7 ± 0.0 |
| w-1/O7 | 7.5 | 7.5 | 7.4 |
| w-2/O7 | 7.5 | 7.4 | 7.5 |
| w-3/O7 | 7.3 | 7.4 | 7.4 |
| w-4/O7 | 7.5 | 7.5 | 7.4 |
| w-5/O7 | 7.4 | 7.4 | - |
| w-6/O7 | 7.3 | 7.4 | - |
| w-7/O7 | 7.5 | 7.4 | - |
| w-8/O7 | 7.5 | 7.5 | - |
| mean | 7.4 ± 0.1 | 7.4 ± 0.0 | 7.4 ± 0.0 |
| w-1/O3′ | 8.2 | 8.4 | - |
| w-2/O3′ | 8.1 | 8.3 | - |
| w-3/O3′ | 8.2 | 8.1 | - |
| w-4/O3′ | 8.0 | 8.1 | - |
| w-5/O3′ | 8.1 | 8.2 | - |
| w-6/O3′ | 8.0 | 8.0 | - |
| w-7/O3′ | - | 8.0 | - |
| w-8/O3′ | - | 7.9 | - |
| mean | 8.1 ± 0.1 | 8.1 ± 0.1 | |
| w-1/O4′ | 6.8 | 7.6 | 8.4 |
| w-2/O4′ | 6.7 | 7.6 | 8.4 |
| w-3/O4′ | 6.7 | 7.4 | 8.5 |
| w-4/O4′ | 6.6 | 7.4 | 8.4 |
| w-5/O4′ | 6.6 | 7.5 | - |
| w-6/O4′ | 6.4 | 7.3 | - |
| w-7/O4′ | - | 7.3 | - |
| w-8/O4′ | - | 7.2 | - |
| mean | 6.6 ± 0.1 | 7.4 ± 0.1 | 8.4 ± 0.0 |
| w-1/O5′ | 8.2 | - | - |
| w-2/O5′ | 8.0 | - | - |
| w-3/O5′ | 8.1 | - | - |
| w-4/O5′ | 7.9 | - | - |
| w-5/O5′ | 8.0 | - | - |
| w-6/O5′ | 7.9 | - | - |
| w-7/O5′ | - | - | - |
| w-8/O5′ | - | - | - |
| mean | 8.0 ± 0.1 |
| Conf. Index | Myricetin | Quercetin | Kaempferol |
|---|---|---|---|
| w-1 | 111.93 | 111.72 | 111.15 |
| w-2 | 111.75 | 111.45 | 111.44 |
| w-3 | 111.13 | 111.60 | 111.55 |
| w-4 | 111.78 | 111.65 | 111.50 |
| w-5 | 111.63 | 111.41 | - |
| w-6 | 110.97 | 111.55 | - |
| w-7 | - | 111.48 | - |
| w-8 | - | 111.44 | - |
| mean | 111.5 ± 0.4 | 111.5 ± 0.1 | 111.2 ± 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondo, H.X.; Takano, Y. Conformational Preference of Flavonols and Its Effect on the Chemical Properties Involved in Radical Scavenging Activity. Chemistry 2022, 4, 1123-1135. https://doi.org/10.3390/chemistry4040076
Kondo HX, Takano Y. Conformational Preference of Flavonols and Its Effect on the Chemical Properties Involved in Radical Scavenging Activity. Chemistry. 2022; 4(4):1123-1135. https://doi.org/10.3390/chemistry4040076
Chicago/Turabian StyleKondo, Hiroko X., and Yu Takano. 2022. "Conformational Preference of Flavonols and Its Effect on the Chemical Properties Involved in Radical Scavenging Activity" Chemistry 4, no. 4: 1123-1135. https://doi.org/10.3390/chemistry4040076
APA StyleKondo, H. X., & Takano, Y. (2022). Conformational Preference of Flavonols and Its Effect on the Chemical Properties Involved in Radical Scavenging Activity. Chemistry, 4(4), 1123-1135. https://doi.org/10.3390/chemistry4040076






