hERG Blockade Prediction by Combining Site Identification by Ligand Competitive Saturation and Physicochemical Properties
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. SILCS-MC Docking for Training Set of 163 Compounds
3.2. Application of SILCS-MC Predictive Models to Validation Sets
3.3. Molecular Conformation and Atomic GFE Contribution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Redfern, W.; Carlsson, L.; Davis, A.; Lynch, W.; MacKenzie, I.; Palethorpe, S.; Siegl, P.; Strang, I.; Sullivan, A.; Wallis, R. Relationships between preclinical cardiac electrophysiology, clinical QT interval prolongation and torsade de pointes for a broad range of drugs: Evidence for a provisional safety margin in drug development. Cardiovasc. Res. 2003, 58, 32–45. [Google Scholar] [CrossRef]
- Priest, B.; Bell, I.M.; Garcia, M. Role of hERG potassium channel assays in drug development. Channels 2008, 2, 87–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Bruin, M.L.; Pettersson, M.; Meyboom, R.H.; Hoes, A.W.; Leufkens, H.G. Anti-HERG activity and the risk of drug-induced arrhythmias and sudden death. Eur. Heart J. 2005, 26, 590–597. [Google Scholar] [CrossRef] [PubMed]
- Ray, W.A.; Murray, K.T.; Meredith, S.; Narasimhulu, S.S.; Hall, K.; Stein, C.M. Oral erythromycin and the risk of sudden death from cardiac causes. N. Engl. J. Med. 2004, 351, 1089–1096. [Google Scholar] [CrossRef] [PubMed]
- Killeen, M.J. Drug-induced arrhythmias and sudden cardiac death: Implications for the pharmaceutical industry. Drug Discov. Today 2009, 14, 589–597. [Google Scholar] [CrossRef]
- Nachimuthu, S.; Assar, M.D.; Schussler, J.M. Drug-induced QT interval prolongation: Mechanisms and clinical management. Ther. Adv. Drug Saf. 2012, 3, 241–253. [Google Scholar] [CrossRef] [Green Version]
- Onakpoya, I.J.; Heneghan, C.J.; Aronson, J.K. Post-marketing withdrawal of 462 medicinal products because of adverse drug reactions: A systematic review of the world literature. BMC Med. 2016, 14, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Jamieson, C.; Moir, E.M.; Rankovic, Z.; Wishart, G. Medicinal chemistry of hERG optimizations: Highlights and hang-ups. J. Med. Chem. 2006, 49, 5029–5046. [Google Scholar] [CrossRef]
- Roden, D.M. Drug-induced prolongation of the QT interval. N. Engl. J. Med. 2004, 350, 1013–1022. [Google Scholar] [CrossRef] [Green Version]
- Fermini, B.; Fossa, A.A. The impact of drug-induced QT interval prolongation on drug discovery and development. Nat. Rev. Drug Discov. 2003, 2, 439–447. [Google Scholar] [CrossRef]
- Garrido, A.; Lepailleur, A.; Mignani, S.M.; Dallemagne, P.; Rochais, C. hERG toxicity assessment: Useful guidelines for drug design. Eur. J. Med. Chem. 2020, 195, 112290. [Google Scholar] [CrossRef] [PubMed]
- Strauss, D.G.; Gintant, G.; Li, Z.; Wu, W.; Blinova, K.; Vicente, J.; Turner, J.R.; Sager, P.T. Comprehensive in vitro proarrhythmia assay (CiPA) update from a cardiac safety research consortium/health and environmental sciences institute/FDA meeting. Ther. Innov. Regul. Sci. 2019, 53, 519–525. [Google Scholar] [CrossRef] [PubMed]
- Vicente, J.; Zusterzeel, R.; Johannesen, L.; Mason, J.; Sager, P.; Patel, V.; Matta, M.K.; Li, Z.; Liu, J.; Garnett, C. Mechanistic model-informed proarrhythmic risk assessment of drugs: Review of the “CiPA” initiative and design of a prospective clinical validation study. Clin. Pharmacol. Ther. 2018, 103, 54–66. [Google Scholar] [CrossRef]
- Chi, K.R. Revolution dawning in cardiotoxicity testing. Nat. Rev. Drug Discov. 2013, 12, 565. [Google Scholar] [CrossRef] [PubMed]
- Colatsky, T.; Fermini, B.; Gintant, G.; Pierson, J.B.; Sager, P.; Sekino, Y.; Strauss, D.G.; Stockbridge, N. The comprehensive in vitro proarrhythmia assay (CiPA) initiative—Update on progress. J. Pharmacol. Toxicol. Methods 2016, 81, 15–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aronov, A.M. Predictive in silico modeling for hERG channel blockers. Drug Discov. Today 2005, 10, 149–155. [Google Scholar] [CrossRef]
- Villoutreix, B.O.; Taboureau, O. Computational investigations of hERG channel blockers: New insights and current predictive models. Adv. Drug Deliv. Rev. 2015, 86, 72–82. [Google Scholar] [CrossRef]
- Jing, Y.; Easter, A.; Peters, D.; Kim, N.; Enyedy, I.J. In silico prediction of hERG inhibition. Future Med. Chem. 2015, 7, 571–586. [Google Scholar] [CrossRef]
- Kalyaanamoorthy, S.; Barakat, K.H. Development of safe drugs: The hERG challenge. Med. Res. Rev. 2018, 38, 525–555. [Google Scholar] [CrossRef]
- Song, M.; Clark, M. Development and evaluation of an in silico model for hERG binding. J. Chem. Inf. Model. 2006, 46, 392–400. [Google Scholar] [CrossRef]
- Thai, K.-M.; Ecker, G.F. A binary QSAR model for classification of hERG potassium channel blockers. Bioorg. Med. Chem. 2008, 16, 4107–4119. [Google Scholar] [CrossRef]
- Hemmerich, J.; Ecker, G.F. In silico toxicology: From structure–activity relationships towards deep learning and adverse outcome pathways. WIREs Comput. Mol. Sci. 2020, 10, e1475. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Sun, H.; Liu, H.; Li, D.; Li, Y.; Hou, T. ADMET evaluation in drug discovery. 16. Predicting hERG blockers by combining multiple pharmacophores and machine learning approaches. Mol. Pharm. 2016, 13, 2855–2866. [Google Scholar] [CrossRef] [PubMed]
- Wacker, S.; Noskov, S.Y. Performance of machine learning algorithms for qualitative and quantitative prediction drug blockade of hERG1 channel. Comput. Toxicol. 2018, 6, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Braga, R.C.; Alves, V.M.; Silva, M.F.B.; Muratov, E.; Fourches, D.; Tropsha, A.; Andrade, C.H. Tuning HERG out: Antitarget QSAR models for drug development. Curr. Top. Med. Chem. 2014, 14, 1399–1415. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seierstad, M.; Agrafiotis, D.K. A QSAR model of hERG binding using a large, diverse, and internally consistent training set. Chem. Biol. Drug Des. 2006, 67, 284–296. [Google Scholar] [CrossRef] [PubMed]
- Kratz, J.M.; Schuster, D.; Edtbauer, M.; Saxena, P.; Mair, C.E.; Kirchebner, J.; Matuszczak, B.; Baburin, I.; Hering, S.; Rollinger, J.M. Experimentally validated hERG pharmacophore models as cardiotoxicity prediction tools. J. Chem. Inf. Model. 2014, 54, 2887–2901. [Google Scholar] [CrossRef] [PubMed]
- Yamakawa, Y.; Furutani, K.; Inanobe, A.; Ohno, Y.; Kurachi, Y. Pharmacophore modeling for hERG channel facilitation. Biochem. Biophys. Res. Commun. 2012, 418, 161–166. [Google Scholar] [CrossRef]
- Cavalli, A.; Poluzzi, E.; De Ponti, F.; Recanatini, M. Toward a pharmacophore for drugs inducing the long QT syndrome: Insights from a CoMFA study of HERG K+ channel blockers. J. Med. Chem. 2002, 45, 3844–3853. [Google Scholar] [CrossRef]
- Munawar, S.; Windley, M.J.; Tse, E.G.; Todd, M.H.; Hill, A.P.; Vandenberg, J.I.; Jabeen, I. Experimentally validated pharmacoinformatics approach to predict hERG inhibition potential of new chemical entities. Front. Pharmacol. 2018, 9, 1035. [Google Scholar] [CrossRef]
- Pagadala, N.S. Computational prediction of hERG blockers using homology modelling, molecular docking and QuaSAR studies. Results Chem. 2021, 3, 100101. [Google Scholar] [CrossRef]
- Rajamani, R.; Tounge, B.A.; Li, J.; Reynolds, C.H. A two-state homology model of the hERG K+ channel: Application to ligand binding. Bioorg. Med. Chem. Lett. 2005, 15, 1737–1741. [Google Scholar] [CrossRef]
- Farid, R.; Day, T.; Friesner, R.A.; Pearlstein, R.A. New insights about HERG blockade obtained from protein modeling, potential energy mapping, and docking studies. Bioorg. Med. Chem. 2006, 14, 3160–3173. [Google Scholar] [CrossRef]
- Durdagi, S.; Deshpande, S.; Duff, H.J.; Noskov, S.Y. Modeling of open, closed, and open-inactivated states of the hERG1 channel: Structural mechanisms of the state-dependent drug binding. J. Chem. Inf. Model. 2012, 52, 2760–2774. [Google Scholar] [CrossRef] [PubMed]
- Cavalluzzi, M.M.; Imbrici, P.; Gualdani, R.; Stefanachi, A.; Mangiatordi, G.F.; Lentini, G.; Nicolotti, O. Human ether-à-go-go-related potassium channel: Exploring SAR to improve drug design. Drug Discov. Today 2020, 25, 344–366. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.-M.; Yu, M.-S.; Kazmi, S.R.; Oh, S.Y.; Rhee, K.-H.; Bae, M.-A.; Lee, B.H.; Shin, D.-S.; Oh, K.-S.; Ceong, H. Computational determination of hERG-related cardiotoxicity of drug candidates. BMC Bioinf. 2019, 20, 67–73. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhao, J.; Wang, Y.; Fan, Y.; Zhu, L.; Yang, Y.; Chen, X.; Lu, T.; Chen, Y.; Liu, H. Prediction of hERG K+ channel blockage using deep neural networks. Chem. Biol. Drug Des. 2019, 94, 1973–1985. [Google Scholar] [CrossRef]
- Czodrowski, P. hERG me out. J. Chem. Inf. Model. 2013, 53, 2240–2251. [Google Scholar] [CrossRef]
- Konda, L.S.K.; Praba, S.K.; Kristam, R. hERG liability classification models using machine learning techniques. Comput. Toxicol. 2019, 12, 100089. [Google Scholar] [CrossRef]
- Ryu, J.Y.; Lee, M.Y.; Lee, J.H.; Lee, B.H.; Oh, K.-S. DeepHIT: A deep learning framework for prediction of hERG-induced cardiotoxicity. Bioinformatics 2020, 36, 3049–3055. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, L.; Jiang, S.; Wang, Y.; Zou, J.; Fu, H.; Yang, S. Capsule networks showed excellent performance in the classification of hERG blockers/nonblockers. Front. Pharmacol. 2020, 10, 1631. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, Y.; Chen, X.; Hua, Y.; Xing, G.; Deng, C.; Liang, L.; Lu, T.; Chen, Y.; Liu, H. Reducing hERG Toxicity Using hERG Classification Model and Fragment-growing Network. ChemRxiv 2021. [Google Scholar] [CrossRef]
- Chavan, S.; Abdelaziz, A.; Wiklander, J.G.; Nicholls, I.A. A k-nearest neighbor classification of hERG K+ channel blockers. J. Comput. Aided Mol. Des. 2016, 30, 229–236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siramshetty, V.B.; Chen, Q.; Devarakonda, P.; Preissner, R. The Catch-22 of predicting hERG blockade using publicly accessible bioactivity data. J. Chem. Inf. Model. 2018, 58, 1224–1233. [Google Scholar] [CrossRef]
- Gadaleta, D.; Mangiatordi, G.F.; Catto, M.; Carotti, A.; Nicolotti, O. Applicability domain for QSAR models: Where theory meets reality. Int. J. Quant. Struct.-Prop. Relat. 2016, 1, 45–63. [Google Scholar] [CrossRef]
- Schyman, P.; Liu, R.; Wallqvist, A. General purpose 2D and 3D similarity approach to identify hERG blockers. J. Chem. Inf. Model. 2016, 56, 213–222. [Google Scholar] [CrossRef]
- Wang, W.; MacKinnon, R. Cryo-EM structure of the open human ether-à-go-go-related K+ channel hERG. Cell 2017, 169, 422–430.e410. [Google Scholar] [CrossRef] [Green Version]
- Dickson, C.J.; Velez-Vega, C.; Duca, J.S. Revealing molecular determinants of hERG blocker and activator binding. J. Chem. Inf. Model. 2019, 60, 192–203. [Google Scholar] [CrossRef]
- Helliwell, M.V.; Zhang, Y.; El Harchi, A.; Du, C.; Hancox, J.C.; Dempsey, C.E. Structural implications of hERG K+ channel block by a high-affinity minimally structured blocker. J. Biol. Chem. 2018, 293, 7040–7057. [Google Scholar] [CrossRef] [Green Version]
- Negami, T.; Araki, M.; Okuno, Y.; Terada, T. Calculation of absolute binding free energies between the hERG channel and structurally diverse drugs. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Munawar, S.; Vandenberg, J.I.; Jabeen, I. Molecular Docking Guided Grid-Independent Descriptor Analysis to Probe the Impact of Water Molecules on Conformational Changes of hERG Inhibitors in Drug Trapping Phenomenon. Int. J. Mol. Sci. 2019, 20, 3385. [Google Scholar] [CrossRef] [Green Version]
- Perissinotti, L.; Guo, J.; Kudaibergenova, M.; Lees-Miller, J.; Ol’khovich, M.; Sharapova, A.; Perlovich, G.L.; Muruve, D.A.; Gerull, B.; Noskov, S.Y. The pore-lipid interface: Role of amino-Acid determinants of lipophilic access by ivabradine to the hERG1 pore domain. Mol. Pharmacol. 2019, 96, 259–271. [Google Scholar] [CrossRef] [PubMed]
- Zangerl-Plessl, E.-M.; Berger, M.; Drescher, M.; Chen, Y.; Wu, W.; Maulide, N.; Sanguinetti, M.; Stary-Weinzinger, A. Toward a Structural View of hERG Activation by the Small-Molecule Activator ICA-105574. J. Chem. Inf. Model. 2019, 60, 360–371. [Google Scholar] [CrossRef] [PubMed]
- Kudaibergenova, M.; Guo, J.; Khan, H.M.; Zahid, F.; Lees-Miller, J.; Noskov, S.Y.; Duff, H.J. Allosteric Coupling Between Drug Binding and the Aromatic Cassette in the Pore Domain of the hERG1 Channel: Implications for a State-Dependent Blockade. Front. Pharmacol. 2020, 11, 914. [Google Scholar] [CrossRef] [PubMed]
- Kalyaanamoorthy, S.; Lamothe, S.M.; Hou, X.; Moon, T.C.; Kurata, H.T.; Houghton, M.; Barakat, K.H. A structure-based computational workflow to predict liability and binding modes of small molecules to hERG. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef]
- Wan, H.; Selvaggio, G.; Pearlstein, R.A. Toward in vivo-relevant hERG safety assessment and mitigation strategies based on relationships between non-equilibrium blocker binding, three-dimensional channel-blocker interactions, dynamic occupancy, dynamic exposure, and cellular arrhythmia. PLoS ONE 2020, 15, e0234946. [Google Scholar] [CrossRef]
- Schewe, M.; Sun, H.; Mert, Ü.; Mackenzie, A.; Pike, A.C.; Schulz, F.; Constantin, C.; Vowinkel, K.S.; Conrad, L.J.; Kiper, A.K. A pharmacological master key mechanism that unlocks the selectivity filter gate in K+ channels. Science 2019, 363, 875–880. [Google Scholar] [CrossRef]
- Creanza, T.M.; Delre, P.; Ancona, N.; Lentini, G.; Saviano, M.; Mangiatordi, G.F. Structure-Based Prediction of hERG-Related Cardiotoxicity: A Benchmark Study. J. Chem. Inf. Model. 2021, 61, 4758–4770. [Google Scholar] [CrossRef]
- Guvench, O.; MacKerell, A.D., Jr. Computational fragment-based binding site identification by ligand competitive saturation. PLoS Comput. Biol. 2009, 5, e1000435. [Google Scholar] [CrossRef] [Green Version]
- Faller, C.E.; Raman, E.P.; MacKerell, A.D.; Guvench, O. Site Identification by Ligand Competitive Saturation (SILCS) simulations for fragment-based drug design. In Fragment-Based Methods in Drug Discovery; Springer: New York, NY, USA, 2015; pp. 75–87. [Google Scholar]
- Lakkaraju, S.K.; Raman, E.P.; Yu, W.; MacKerell, A.D., Jr. Sampling of Organic Solutes in Aqueous and Heterogeneous Environments using Oscillating μex Grand Canonical-like Monte Carlo-Molecular Dynamics Simulations. J. Chem. Theory Comput. 2014, 10, 2281–2290. [Google Scholar] [CrossRef] [Green Version]
- Raman, E.P.; Yu, W.; Guvench, O.; MacKerell, A.D. Reproducing crystal binding modes of ligand functional groups using Site-Identification by Ligand Competitive Saturation (SILCS) simulations. J. Chem. Inf. Model. 2011, 51, 877–896. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raman, E.P.; Yu, W.; Lakkaraju, S.K.; MacKerell, A.D., Jr. Inclusion of Multiple Fragment Types in the Site Identification by Ligand Competitive Saturation (SILCS) Approach. J. Chem. Inf. Model. 2013, 53, 3384–3398. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Jo, S.; Lakkaraju, S.K.; Lind, C.; Yu, W. Identification and characterization of fragment binding sites for allosteric ligand design using the site identification by ligand competitive saturation hotspots approach (SILCS-Hotspots). Biochim. Biophys. Acta Gen. Subj. 2020, 1864, 129519. [Google Scholar] [CrossRef] [PubMed]
- Goel, H.; Hazel, A.; Ustach, V.D.; Jo, S.; Yu, W.; Mackerell, A. Rapid and Accurate Estimation of Protein-Ligand Relative Binding Affinities using Site-Identification by Ligand Competitive Saturation. Chem. Sci. 2021, 12, 8844–8858. [Google Scholar] [CrossRef] [PubMed]
- Goel, H.; Yu, W.; Ustach, V.D.; Aytenfisu, A.H.; Sun, D.; MacKerell, A.D. Impact of electronic polarizability on protein-functional group interactions. Phys. Chem. Chem. Phys. 2020, 22, 6848–6860. [Google Scholar] [CrossRef]
- Ustach, V.D.; Lakkaraju, S.K.; Jo, S.; Yu, W.; Jiang, W.; MacKerell, A.D., Jr. Optimization and Evaluation of Site-Identification by Ligand Competitive Saturation (SILCS) as a Tool for Target-Based Ligand Optimization. J. Chem. Inf. Model. 2019, 59, 3018–3035. [Google Scholar] [CrossRef]
- Raman, E.P.; Lakkaraju, S.K.; Denny, R.A.; MacKerell, A.D., Jr. Estimation of relative free energies of binding using pre-computed ensembles based on the single-step free energy perturbation and the site-identification by Ligand competitive saturation approaches. J. Comput. Chem. 2017, 38, 1238–1251. [Google Scholar] [CrossRef]
- Yu, W.; Lakkaraju, S.K.; Raman, E.P.; Fang, L.; MacKerell, A.D., Jr. Pharmacophore Modeling Using Site-Identification by Ligand Competitive Saturation (SILCS) with Multiple Probe Molecules. J. Chem. Inf. Model. 2015, 55, 407–420. [Google Scholar] [CrossRef]
- Yu, W.; Lakkaraju, S.K.; Raman, E.P.; MacKerell, A.D., Jr. Site-Identification by Ligand Competitive Saturation (SILCS) assisted pharmacophore modeling. J. Comput. Aided Mol. Des. 2014, 28, 491–507. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Jo, S.; Lakkaraju, S.K.; Weber, D.J.; MacKerell, A.D., Jr. Exploring protein-protein interactions using the Site-Identification by Ligand Competitive Saturation (SILCS) methodology. Proteins Struct. Funct. Bioinf. 2019, 87, 289–301. [Google Scholar] [CrossRef]
- Jo, S.; Xu, A.; Curtis, J.E.; Somani, S.; MacKerell, A.D. Computational Characterization of Antibody-Excipient Interactions for Rational Excipient Selection using the Site Identification by Ligand Competitive Saturation (SILCS)-Biologics Approach. Mol. Pharm. 2020, 17, 4323–4333. [Google Scholar] [CrossRef] [PubMed]
- Somani, S.; Jo, S.; Thirumangalathu, R.; Rodrigues, D.; Tanenbaum, L.M.; Amin, K.; MacKerell, A.D., Jr.; Thakkar, S.V. Toward biotherapeutics formulation composition Engineering using site-identification by ligand competitive saturation (SILCS). J. Pharm. Sci. 2021, 110, 1103–1110. [Google Scholar] [CrossRef] [PubMed]
- Goel, H.; Hazel, A.; Yu, W.; Jo, S.; MacKerell, A.D. Application of site-identification by ligand competitive saturation in computer-aided drug design. New J. Chem. 2022, 46, 919–932. [Google Scholar] [CrossRef]
- Mousaei, M.; Kudaibergenova, M.; MacKerell, A.D., Jr.; Noskov, S. Assessing hERG1 blockade from Bayesian machine-learning-optimized site identification by ligand competitive saturation simulations. J. Chem. Inf. Model. 2020, 60, 6489–6501. [Google Scholar] [CrossRef] [PubMed]
- Kramer, J.; Obejero-Paz, C.A.; Myatt, G.; Kuryshev, Y.A.; Bruening-Wright, A.; Verducci, J.S.; Brown, A.M. MICE models: Superior to the HERG model in predicting Torsade de Pointes. Sci. Rep. 2013, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Sinha, N.; Sen, S. Predicting hERG activities of compounds from their 3D structures: Development and evaluation of a global descriptors based QSAR model. Eur. J. Med. Chem. 2011, 46, 618–630. [Google Scholar] [CrossRef] [PubMed]
- Perissinotti, L.L.; De Biase, P.M.; Guo, J.; Yang, P.-C.; Lee, M.C.; Clancy, C.E.; Duff, H.J.; Noskov, S.Y. Determinants of isoform-specific gating kinetics of hERG1 channel: Combined experimental and simulation study. Front. Physiol. 2018, 9, 207. [Google Scholar] [CrossRef]
- Asai, T.; Adachi, N.; Moriya, T.; Oki, H.; Maru, T.; Kawasaki, M.; Suzuki, K.; Chen, S.; Ishii, R.; Yonemori, K. Cryo-EM structure of K+-bound hERG channel complexed with the blocker astemizole. Structure 2021, 29, 203–212.e204. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Vanommeslaeghe, K.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chemical Computing Group ULC. Molecular Operating Environment MOE 2020.09; Chemical Computing Group ULC: Montreal, QC, Canada, 2022. [Google Scholar]
- Grisoni, F.; Ballabio, D.; Todeschini, R.; Consonni, V. Molecular descriptors for structure–activity applications: A hands-on approach. In Computational Toxicology; Springer: New York, NY, USA, 2018; pp. 3–53. [Google Scholar]
- Mao, J.; Akhtar, J.; Zhang, X.; Sun, L.; Guan, S.; Li, X.; Chen, G.; Liu, J.; Jeon, H.-N.; Kim, M.S. Comprehensive strategies of machine-learning-based quantitative structure-activity relationship models. Iscience 2021, 24, 103052. [Google Scholar] [CrossRef] [PubMed]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors. John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pearlman, D.A.; Charifson, P.S. Are Free Energy Calculations Useful in Practice? A Comparison with Rapid Scoring Functions for the p38 MAP Kinase Protein System†. J. Med. Chem. 2001, 44, 3417–3423. [Google Scholar] [CrossRef] [PubMed]
- Kalyaanamoorthy, S.; Barakat, K.H. Binding modes of hERG blockers: An unsolved mystery in the drug design arena. Expert Opin. Drug Discov. 2018, 13, 207–210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Seebohm, G.; Sanguinetti, M.C. Position of aromatic residues in the S6 domain, not inactivation, dictates cisapride sensitivity of HERG and eag potassium channels. Prac. Natl. Acad. Sci. USA 2002, 99, 12461–12466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanguinetti, M.C.; Tristani-Firouzi, M. hERG potassium channels and cardiac arrhythmia. Nature 2006, 440, 463–469. [Google Scholar] [CrossRef]
- Saxena, P.; Zangerl-Plessl, E.-M.; Linder, T.; Windisch, A.; Hohaus, A.; Timin, E.; Hering, S.; Stary-Weinzinger, A. New potential binding determinant for hERG channel inhibitors. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Sanguinetti, M.C.; Chen, J.; Fernandez, D.; Kamiyat, K.; Mitchesonf, J.; Sanchez-Chapulaş, J.A. Physicochemical basis for binding and voltage-dependent block of hERG channels by structurally diverse drugs. In The hERG Cardiac Potassium Channel: Structure, Function and Long QT Syndrome; John Wiley & Sons: Hoboken, NJ, USA, 2005; p. 159. [Google Scholar]
- Gillman, K.W.; Parker, M.F.; Silva, M.; Degnan, A.P.; Tora, G.O.; Lodge, N.J.; Li, Y.-W.; Lelas, S.; Taber, M.; Krause, R.G. Design, optimization, and in vivo evaluation of a series of pyridine derivatives with dual NK1 antagonism and SERT inhibition for the treatment of depression. Bioorg. Med. Chem. Lett. 2013, 23, 407–411. [Google Scholar] [CrossRef]
- Durdagi, S.; Subbotina, J.; Lees-Miller, J.; Guo, J.; Duff, H.J.; Noskov, S.Y. Insights into the molecular mechanism of hERG1 channel activation and blockade by drugs. Curr. Med. Chem. 2010, 17, 3514–3532. [Google Scholar] [CrossRef]
- Choe, H.; Nah, K.H.; Lee, S.N.; Lee, H.S.; Lee, H.S.; Jo, S.H.; Leem, C.H.; Jang, Y.J. A novel hypothesis for the binding mode of HERG channel blockers. Biochem. Biophys. Res. Comm. 2006, 344, 72–78. [Google Scholar] [CrossRef]
- Miranda-Quintana, R.A.; Bajusz, D.; Rácz, A.; Héberger, K. Extended similarity indices: The benefits of comparing more than two objects simultaneously. Part 1: Theory and characteristics. J. Cheminformatics 2021, 13, 32. [Google Scholar] [CrossRef] [PubMed]
- Miranda-Quintana, R.A.; Rácz, A.; Bajusz, D.; Héberger, K. Extended similarity indices: The benefits of comparing more than two objects simultaneously. Part 2: Speed, consistency, diversity selection. J. Cheminformatics 2021, 13, 33. [Google Scholar] [CrossRef] [PubMed]
- Dunn, T.B.; Seabra, G.M.; Kim, T.D.; Juárez-Mercado, K.E.; Li, C.; Medina-Franco, J.L.; Miranda-Quintana, R.A. Diversity and Chemical Library Networks of Large Data Sets. J. Chem. Inf. Model. 2021, in press. [Google Scholar] [CrossRef] [PubMed]
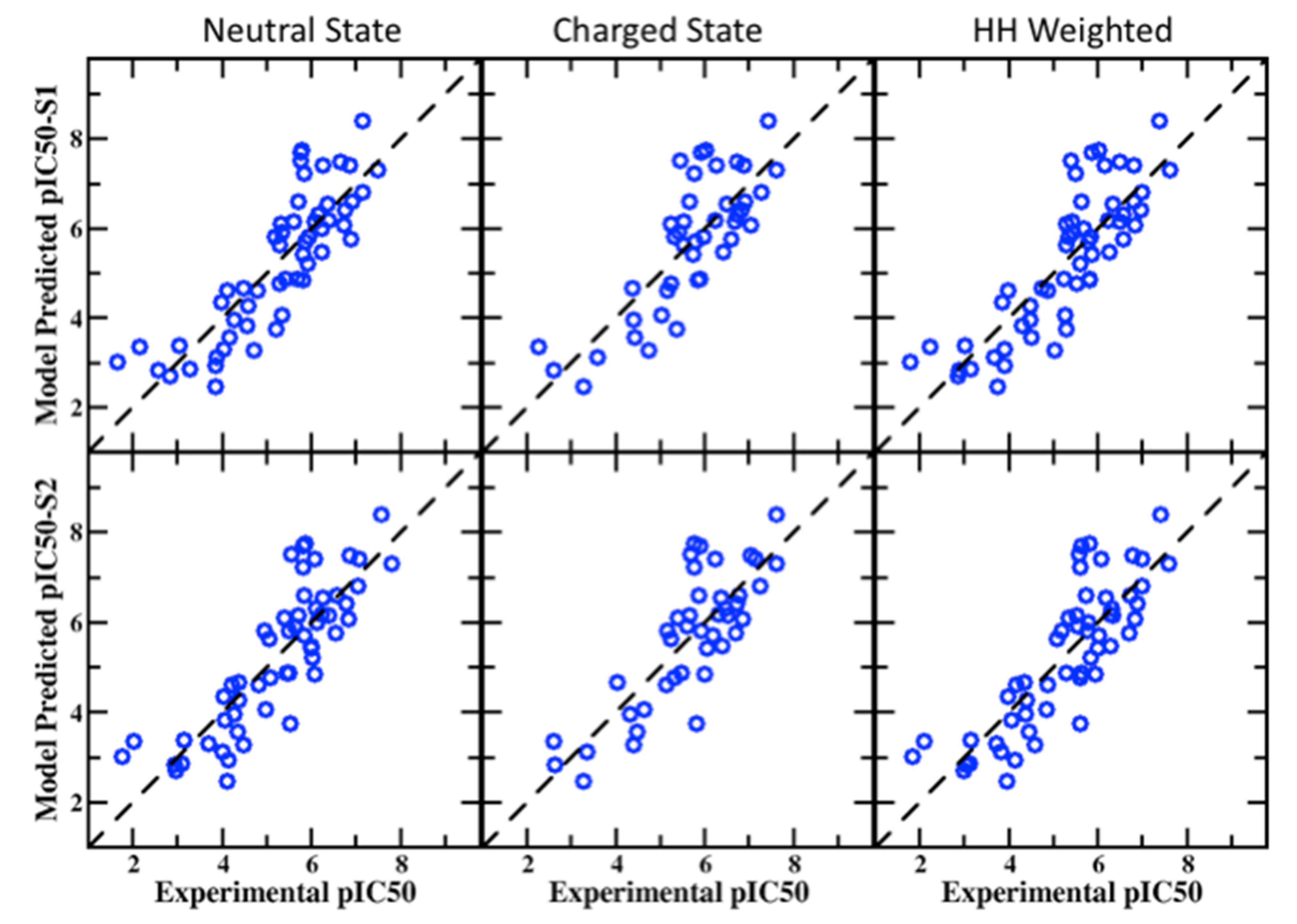
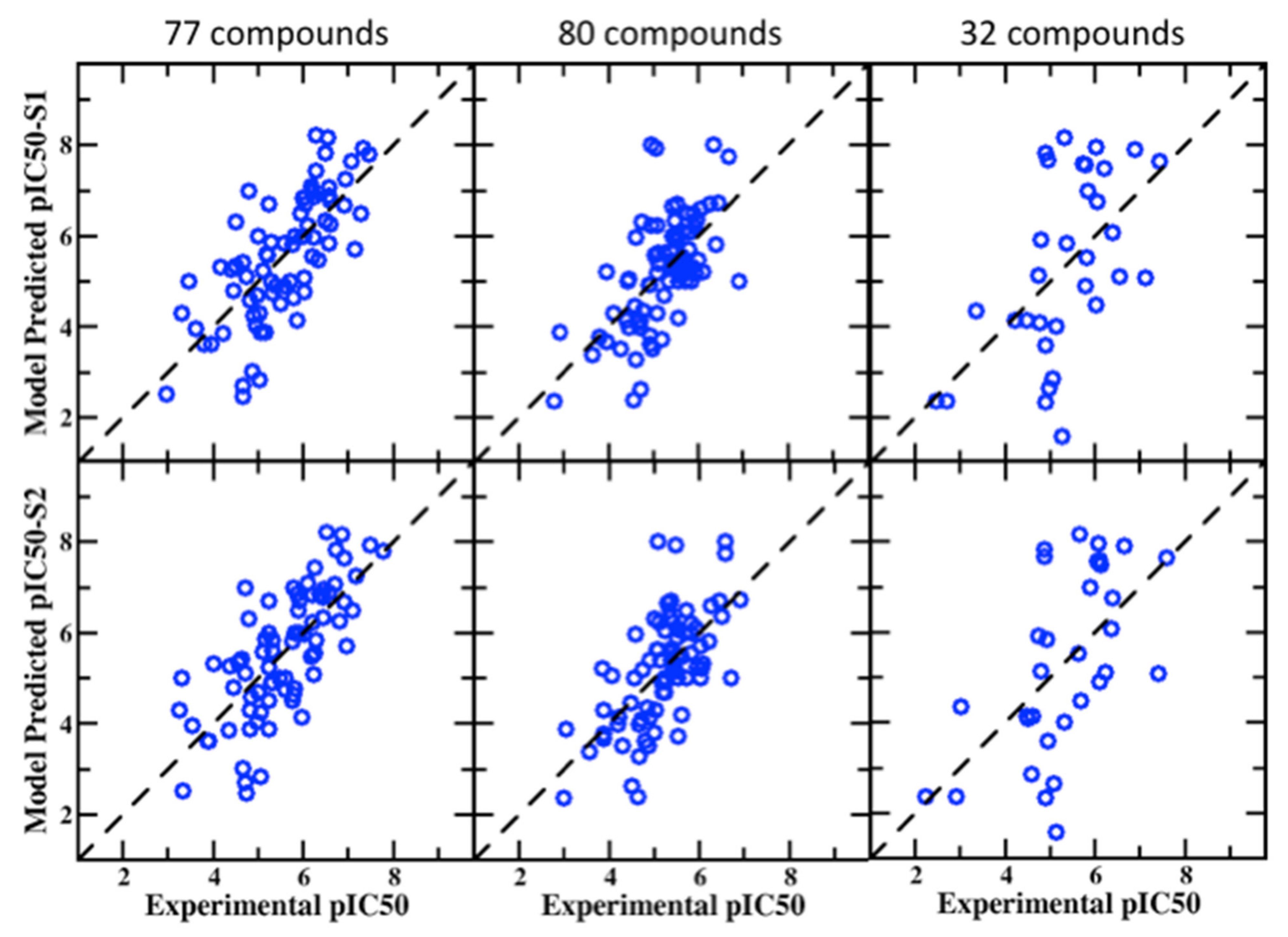
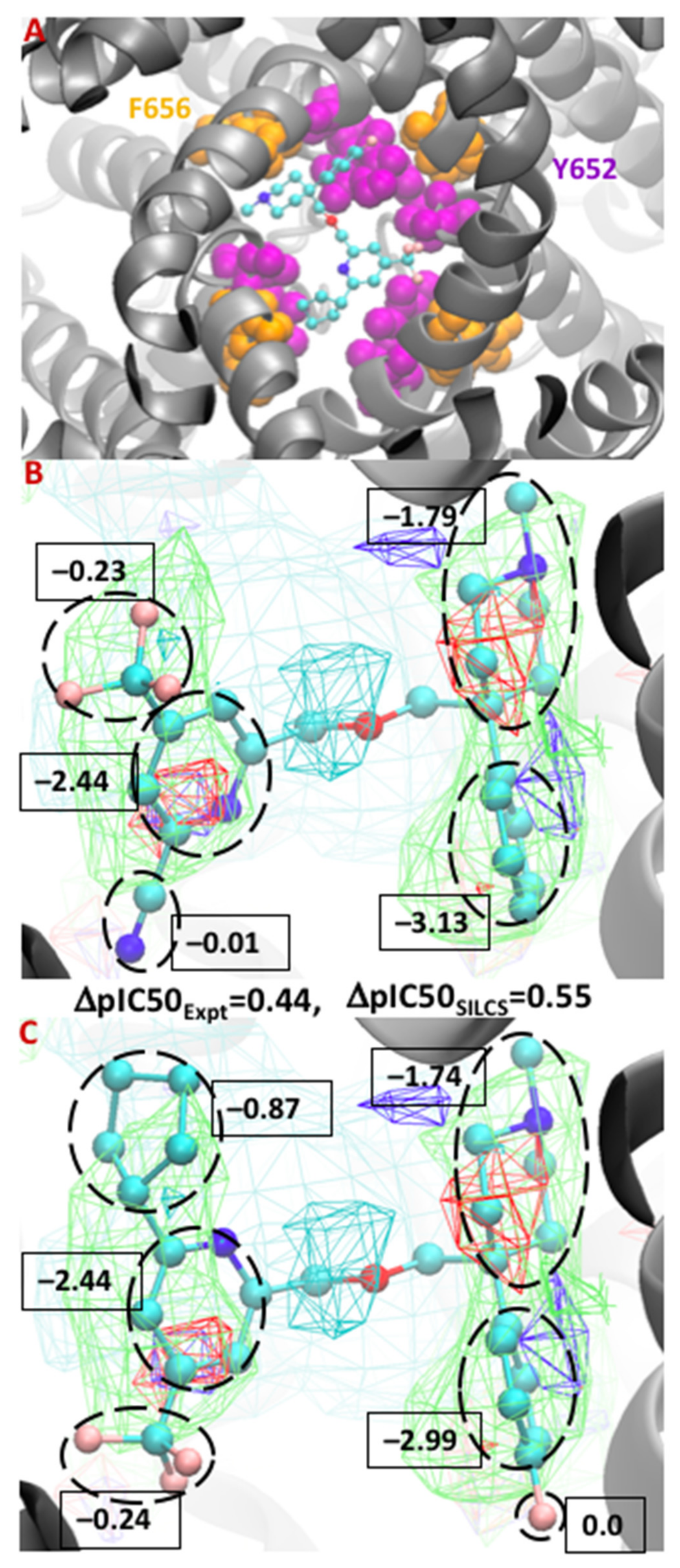
| MUE | R | PI | PC | |
|---|---|---|---|---|
| S1 | 0.836 | 0.108 | 0.097 | 0.524 |
| S2 | 1.109 | 0.044 | 0.034 | 0.509 |
| BML S1 | 0.903 | 0.453 | 0.456 | 0.643 |
| BML S2 | 0.840 | 0.408 | 0.362 | 0.605 |
| Docking Scores | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Neutral State | Charged State | HH Weighted | ||||||||||
| MUE | R | PI | PC | MUE | R | PI | PC | MUE | R | PI | PC | |
| S1 | 1.600 | 0.055 | 0.098 | 0.546 | 1.560 | 0.057 | 0.108 | 0.516 | 1.494 | 0.134 | 0.2 | 0.573 |
| S2 | 1.745 | 0.099 | 0.114 | 0.546 | 1.759 | 0.092 | 0.179 | 0.542 | 1.682 | 0.15 | 0.187 | 0.573 |
| BML S1 | 1.050 | 0.640 | 0.642 | 0.734 | 1.036 | 0.480 | 0.380 | 0.635 | 0.872 | 0.705 | 0.680 | 0.749 |
| BML S2 | 1.349 | 0.611 | 0.579 | 0.708 | 1.329 | 0.476 | 0.443 | 0.653 | 1.179 | 0.632 | 0.619 | 0.722 |
| PPM + Docking Scores | ||||||||||||
| S1 | 0.733 | 0.819 | 0.827 | 0.812 | 0.764 | 0.784 | 0.778 | 0.785 | 0.752 | 0.814 | 0.820 | 0.805 |
| S2 | 0.709 | 0.825 | 0.825 | 0.815 | 0.743 | 0.792 | 0.787 | 0.794 | 0.721 | 0.824 | 0.828 | 0.816 |
| BML S1 | 0.696 | 0.841 | 0.852 | 0.833 | 0.739 | 0.804 | 0.796 | 0.792 | 0.702 | 0.835 | 0.843 | 0.822 |
| BML S2 | 0.669 | 0.844 | 0.847 | 0.826 | 0.704 | 0.815 | 0.763 | 0.780 | 0.693 | 0.834 | 0.818 | 0.811 |
| PPM | ||||||||||||
| MLR | 0.734 | 0.819 | 0.832 | 0.816 | 0.764 | 0.784 | 0.781 | 0.786 | 0.763 | 0.809 | 0.818 | 0.804 |
| Docking Scores | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 77 Compounds | 80 Compounds | 32 Compounds | ||||||||||
| MUE | R | PI | PC | MUE | R | PI | PC | MUE | R | PI | PC | |
| S1 | 1.298 | 0.416 | 0.442 | 0.641 | 1.550 | −0.078 | 0.066 | 0.511 | 1.888 | 0.235 | 0.267 | 0.589 |
| S2 | 1.567 | 0.441 | 0.456 | 0.643 | 1.845 | −0.014 | 0.143 | 0.549 | 2.055 | 0.227 | 0.297 | 0.607 |
| BML S1 | 0.888 | 0.625 | 0.647 | 0.732 | 0.922 | 0.516 | 0.510 | 0.672 | 1.720 | 0.313 | 0.207 | 0.560 |
| BML S2 | 1.185 | 0.646 | 0.659 | 0.738 | 1.345 | 0.532 | 0.541 | 0.686 | 1.904 | 0.363 | 0.392 | 0.613 |
| Docking Scores + PPM | ||||||||||||
| S1 | 0.824 | 0.692 | 0.721 | 0.757 | 0.803 | 0.519 | 0.565 | 0.691 | 1.341 | 0.566 | 0.592 | 0.692 |
| S2 | 0.822 | 0.691 | 0.707 | 0.749 | 0.796 | 0.529 | 0.575 | 0.699 | 1.315 | 0.562 | 0.549 | 0.679 |
| BML S1 | 0.789 | 0.713 | 0.738 | 0.766 | 0.724 | 0.624 | 0.629 | 0.722 | 1.341 | 0.558 | 0.539 | 0.663 |
| BML S2 | 0.775 | 0.722 | 0.745 | 0.771 | 0.711 | 0.648 | 0.642 | 0.725 | 1.320 | 0.585 | 0.560 | 0.681 |
| PPM | ||||||||||||
| MLR | 0.822 | 0.691 | 0.707 | 0.749 | 0.816 | 0.516 | 0.568 | 0.690 | 1.382 | 0.540 | 0.576 | 0.679 |
| Docking Scores | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test 1 (100 Compounds) | Test 3 (155 Compounds) | Test 4 (73 Compounds) | ||||||||||
| MUE | R | PI | PC | MUE | R | PI | PC | MUE | R | PI | PC | |
| S1 | 1.132 | 0.034 | −0.001 | 0.503 | 1.021 | −0.125 | −0.161 | 0.464 | 0.888 | −0.088 | −0.073 | 0.476 |
| S2 | 1.330 | −0.019 | −0.071 | 0.489 | 1.127 | −0.156 | −0.206 | 0.442 | 0.889 | −0.159 | −0.136 | 0.445 |
| BML S1 | 1.008 | 0.242 | 0.247 | 0.608 | 0.868 | 0.092 | 0.105 | 0.555 | 1.084 | 0.061 | 0.094 | 0.534 |
| BML S2 | 1.108 | 0.236 | 0.219 | 0.60 | 0.897 | 0.063 | 0.077 | 0.537 | 0.842 | 0.022 | −0.002 | 0.500 |
| Docking Scores + PPM | ||||||||||||
| S1 | 0.886 | 0.396 | 0.429 | 0.643 | 0.541 | 0.412 | 0.475 | 0.659 | 0.468 | 0.454 | 0.469 | 0.659 |
| S2 | 0.937 | 0.325 | 0.329 | 0.595 | 0.541 | 0.413 | 0.474 | 0.658 | 0.470 | 0.444 | 0.463 | 0.658 |
| BML S1 | 0.868 | 0.419 | 0.428 | 0.654 | 0.542 | 0.412 | 0.473 | 0.659 | 0.468 | 0.445 | 0.447 | 0.651 |
| BML S2 | 0.866 | 0.416 | 0.43 | 0.656 | 0.543 | 0.412 | 0.481 | 0.660 | 0.468 | 0.445 | 0.449 | 0.651 |
| PPM | ||||||||||||
| MLR | 0.872 | 0.415 | 0.442 | 0.658 | 0.739 | 0.542 | 0.475 | 0.659 | 0.469 | 0.444 | 0.459 | 0.656 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goel, H.; Yu, W.; MacKerell, A.D., Jr. hERG Blockade Prediction by Combining Site Identification by Ligand Competitive Saturation and Physicochemical Properties. Chemistry 2022, 4, 630-646. https://doi.org/10.3390/chemistry4030045
Goel H, Yu W, MacKerell AD Jr. hERG Blockade Prediction by Combining Site Identification by Ligand Competitive Saturation and Physicochemical Properties. Chemistry. 2022; 4(3):630-646. https://doi.org/10.3390/chemistry4030045
Chicago/Turabian StyleGoel, Himanshu, Wenbo Yu, and Alexander D. MacKerell, Jr. 2022. "hERG Blockade Prediction by Combining Site Identification by Ligand Competitive Saturation and Physicochemical Properties" Chemistry 4, no. 3: 630-646. https://doi.org/10.3390/chemistry4030045
APA StyleGoel, H., Yu, W., & MacKerell, A. D., Jr. (2022). hERG Blockade Prediction by Combining Site Identification by Ligand Competitive Saturation and Physicochemical Properties. Chemistry, 4(3), 630-646. https://doi.org/10.3390/chemistry4030045







