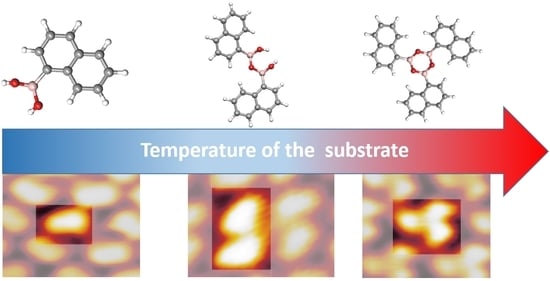
On-Surface Synthesis of Boroxine-Based Molecules
Abstract
:1. Introduction
2. Materials and Methods
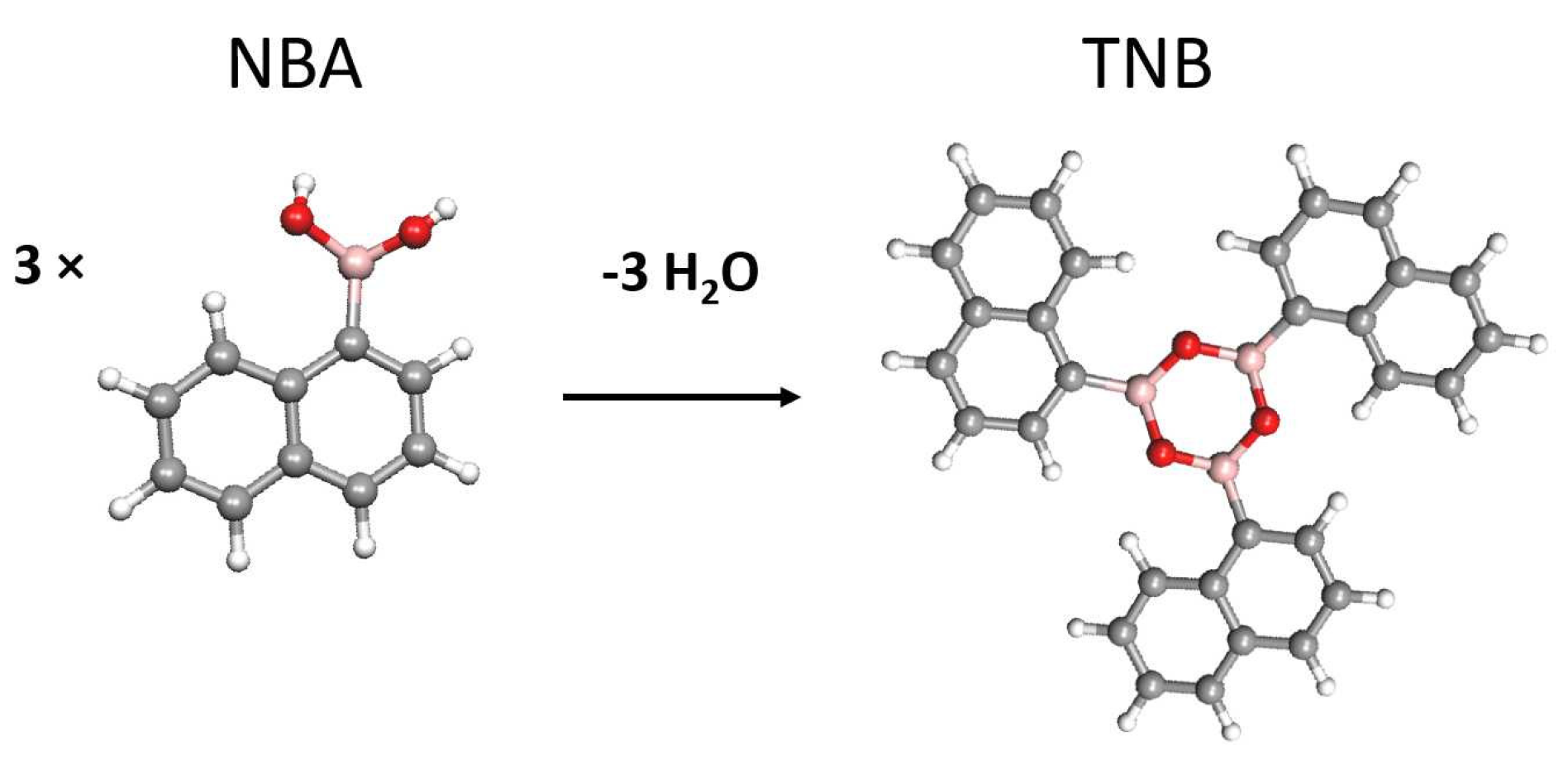
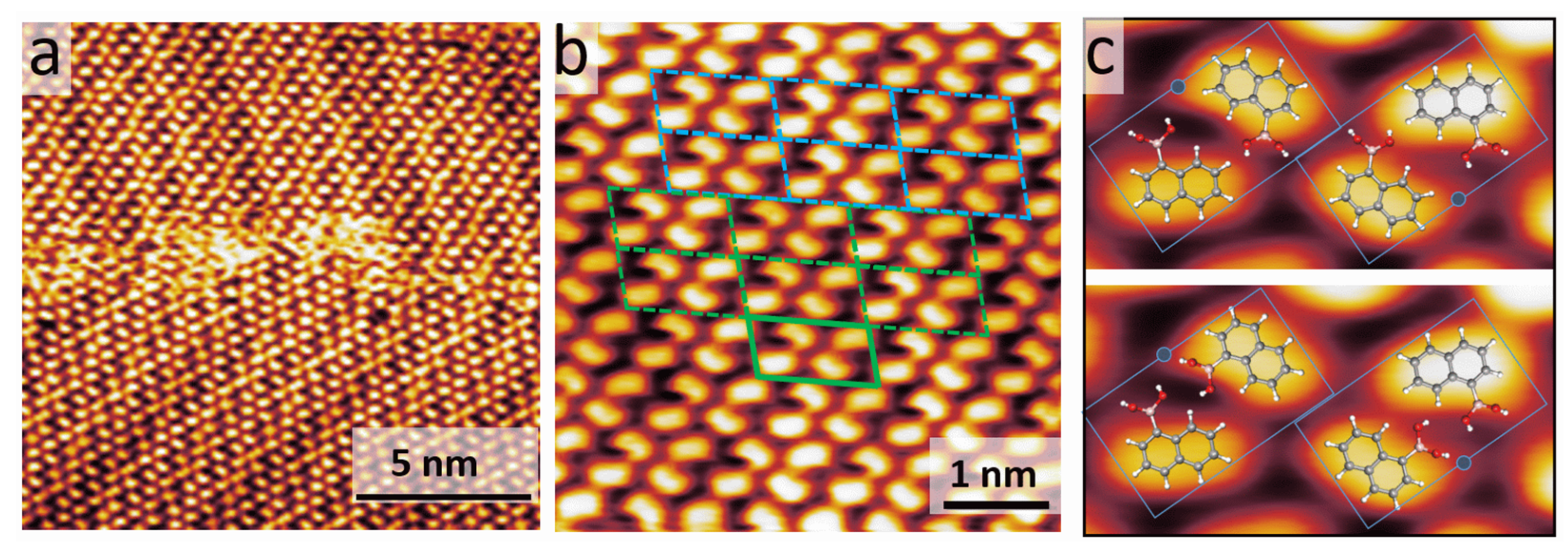
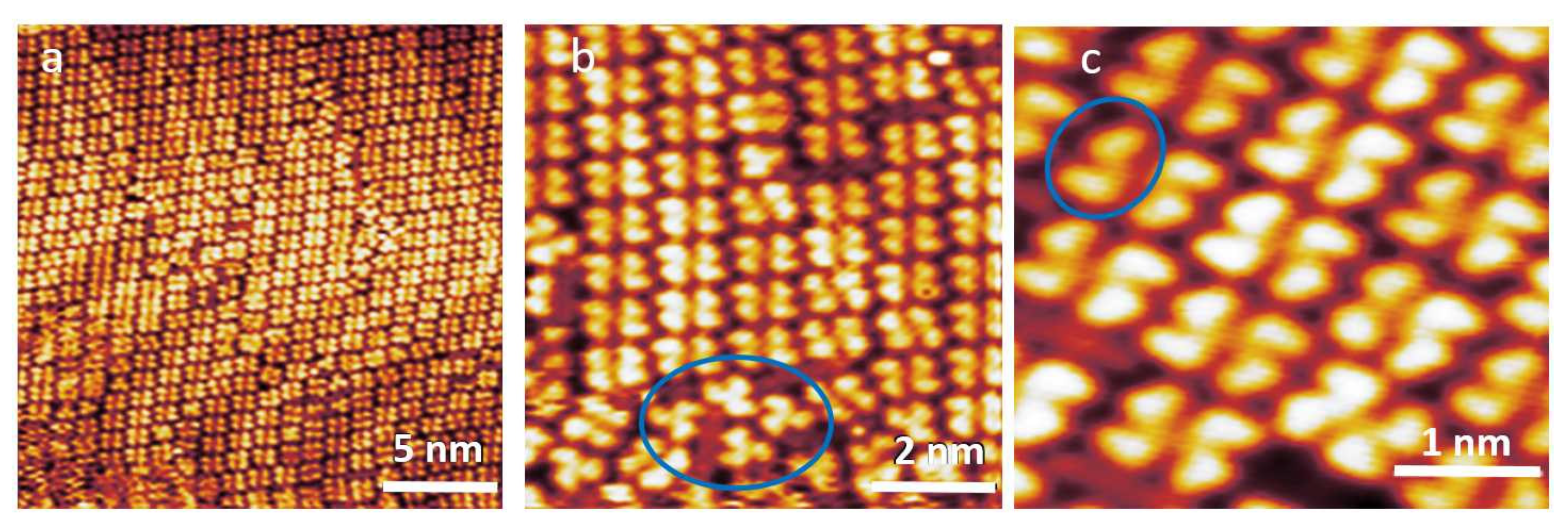
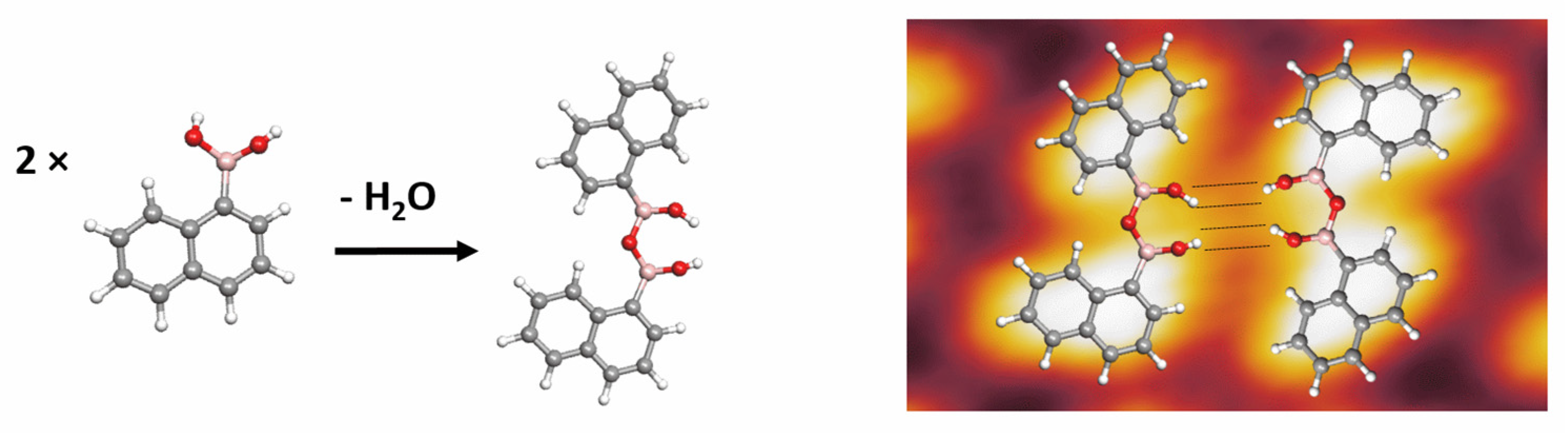
3. Results and Discussion
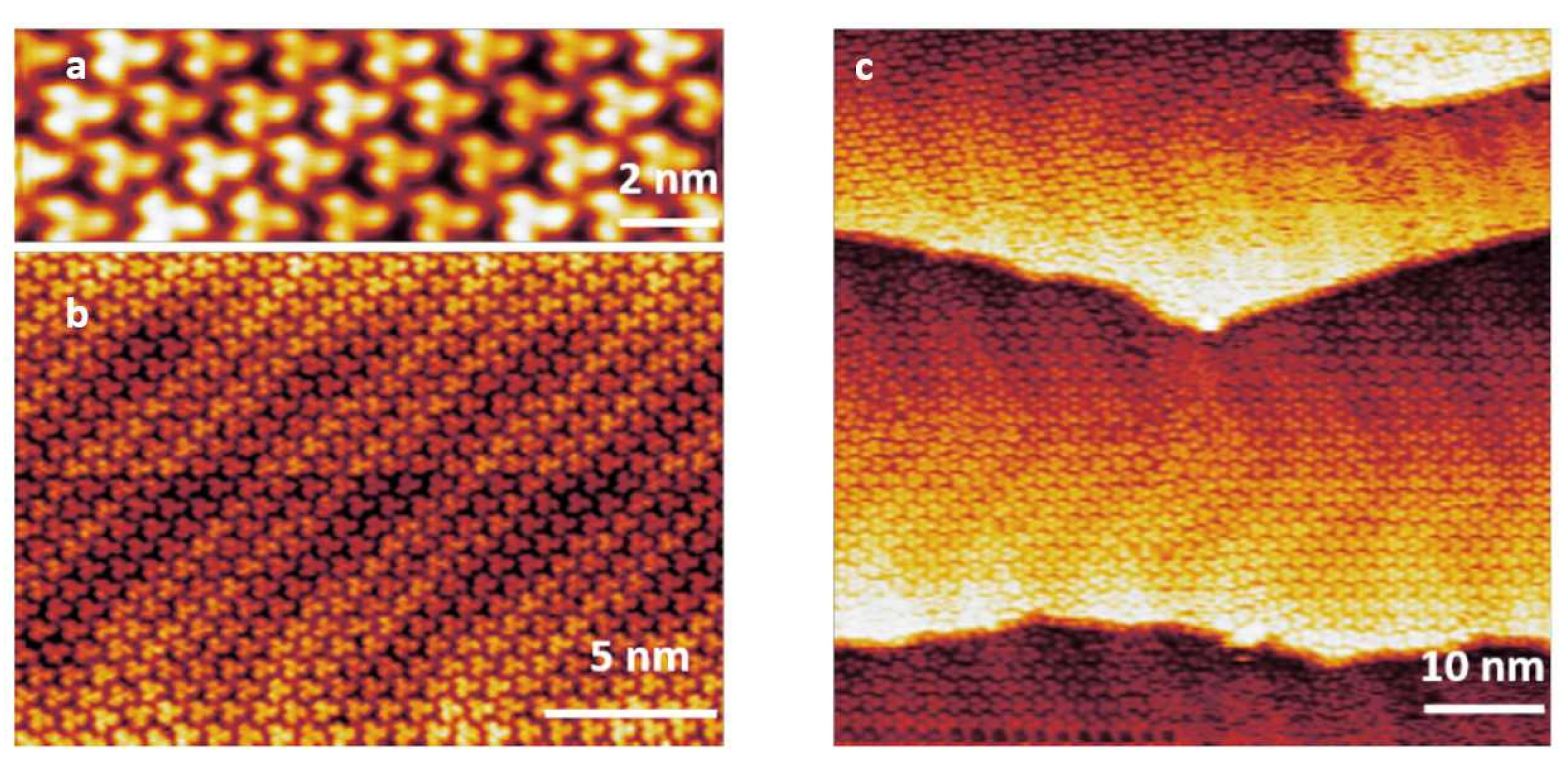
3.1. STM
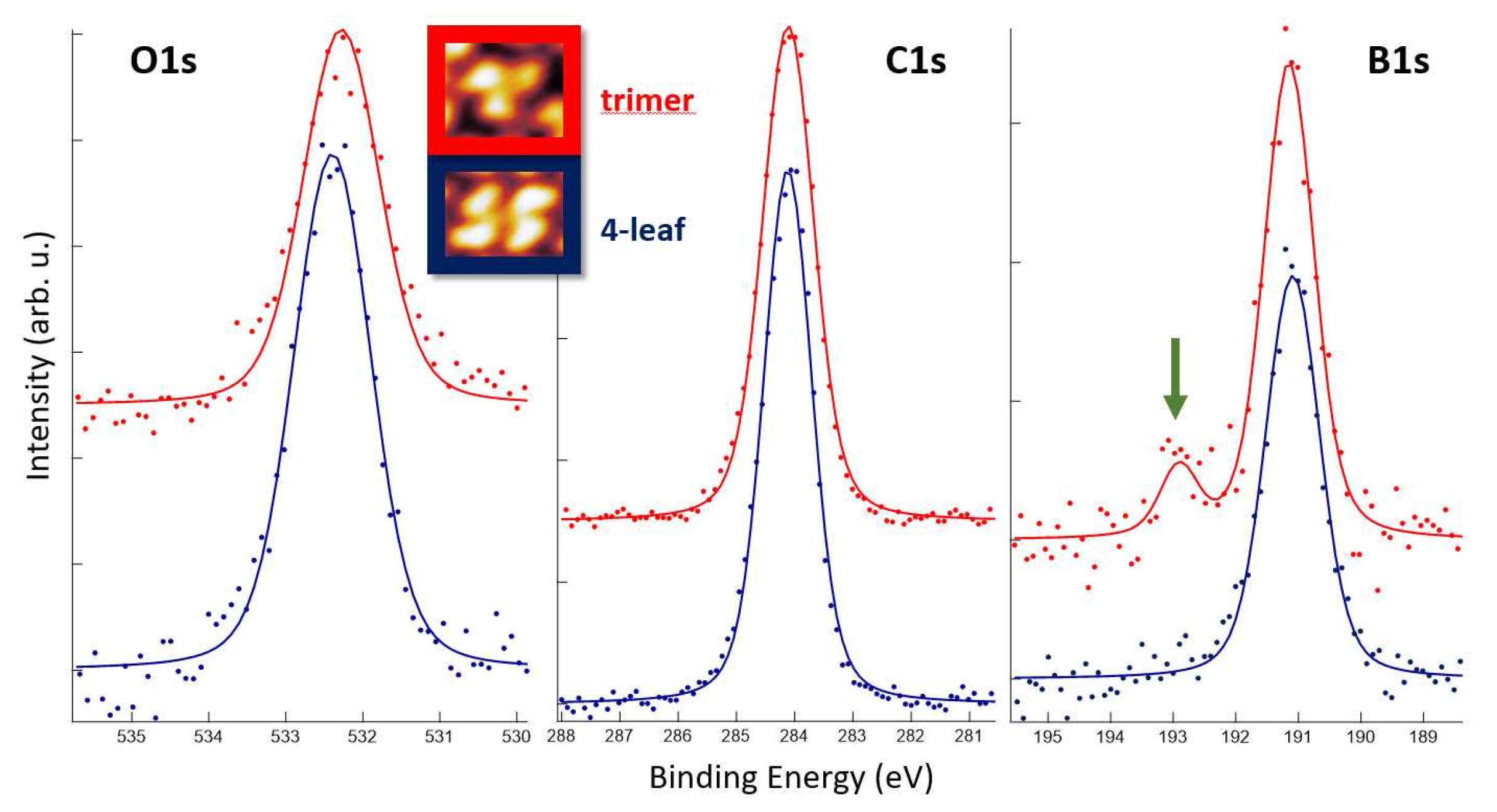
3.2. XPS
3.3. NEXAFS
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bartels, L. Tailoring molecular layers at metal surfaces. Nat. Chem. 2010, 2, 87–95. [Google Scholar] [CrossRef]
- Barth, J. V Molecular architectonic on metal surfaces. Annu. Rev. Phys. Chem. 2007, 58, 375–407. [Google Scholar] [CrossRef] [Green Version]
- Di Giovannantonio, M.; Tomellini, M.; Lipton-Duffin, J.; Galeotti, G.; Ebrahimi, M.; Cossaro, A.; Verdini, A.; Kharche, N.; Meunier, V.; Vasseur, G.; et al. Mechanistic Picture and Kinetic Analysis of Surface-Confined Ullmann Polymerization. J. Am. Chem. Soc. 2016, 138, 16696–16702. [Google Scholar] [CrossRef] [Green Version]
- Clair, S.; De Oteyza, D.G. Controlling a Chemical Coupling Reaction on a Surface: Tools and Strategies for On-Surface Synthesis. Chem. Rev. 2019, 119, 4717–4776. [Google Scholar] [CrossRef]
- Grill, L.; Hecht, S. Covalent on-surface polymerization. Nat. Chem. 2020, 12, 115–130. [Google Scholar] [CrossRef]
- Côté, A.P.; Benin, A.I.; Ockwig, N.W.; Matzger, A.J.; Yaghi, O.M. Porous, Crystalline, Covalent Organic Frameworks. J. Low Temp. Phys. 2004, 427, 155303. [Google Scholar] [CrossRef] [Green Version]
- Waller, P.J.; Gándara, F.; Yaghi, O.M. Chemistry of Covalent Organic Frameworks. Acc. Chem. Res. 2015, 48, 3053–3063. [Google Scholar] [CrossRef]
- Ma, L.; Wang, S.; Feng, X.; Wang, B. Recent advances of covalent organic frameworks in electronic and optical applications. Chinese Chem. Lett. 2016, 27, 1383–1394. [Google Scholar] [CrossRef]
- Feng, X.; Ding, X.; Jiang, D. Covalent organic frameworks. Chem. Soc. Rev. 2012, 41, 6010. [Google Scholar] [CrossRef]
- Zwaneveld, N.A.A.; Pawlak, R.; Abel, M.; Catalin, D.; Gigmes, D.; Bertin, D.; Porte, L. Organized formation of 2D extended covalent organic frameworks at surfaces. J. Am. Chem. Soc. 2008, 130, 6678–6679. [Google Scholar] [CrossRef]
- Dienstmaier, F.; Gigler, A.M.; Goetz, A.J.; Knochel, P.; Bein, T.; Lyapin, A.; Reichlmaier, S.; Heckl, W.M.; Lackinger, M. Synthesis of Well-Ordered COF Monolayers: Surface Growth of Nanocrystalline Precursors versus Direct On-Surface Polycondensation. ACS Nano 2011, 5, 9737–9745. [Google Scholar] [CrossRef]
- Dienstmaier, J.F.; Medina, D.D.; Dogru, M.; Knochel, P.; Bein, T.; Heckl, W.M.; Lackinger, M. Isoreticular two-dimensional covalent organic frameworks synthesized by on-surface condensation of diboronic acids. ACS Nano 2012, 6, 7234–7242. [Google Scholar] [CrossRef]
- Colson, J.W.; Dichtel, W.R. Rationally synthesized two-dimensional polymers. Nat. Chem. 2013, 5, 453–465. [Google Scholar] [CrossRef]
- Clair, S.; Abel, M.; Porte, L. Growth of boronic acid based two-dimensional covalent networks on a metal surface under ultrahigh vacuum. Chem. Commun. 2014, 50, 9627–9635. [Google Scholar] [CrossRef] [Green Version]
- Plas, J.; Ivasenko, O.; Martsinovich, N.; Lackinger, M.; De Feyter, S. Nanopatterning of a covalent organic framework host–guest system. Chem. Commun. 2016, 52, 68–71. [Google Scholar] [CrossRef] [Green Version]
- Toffoli, D.; Stredansky, M.; Feng, Z.; Balducci, G.; Furlan, S.; Stener, M.; Ustunel, H.; Cvetko, D.; Kladnik, G.; Morgante, A.; et al. Electronic properties of the boroxine–gold interface: Evidence of ultra-fast charge delocalization. Chem. Sci. 2017, 8, 3789–3798. [Google Scholar] [CrossRef] [Green Version]
- Costantini, R.; Stredansky, M.; Cvetko, D.; Kladnik, G.; Verdini, A.; Sigalotti, P.; Cilento, F.; Salvador, F.; De Luisa, A.; Benedetti, D.; et al. ANCHOR-SUNDYN: A novel endstation for time resolved spectroscopy at the ALOISA beamline. J. Electron. Spectros. Relat. Phenomena 2018, 229, 7–12. [Google Scholar] [CrossRef]
- Cossaro, A.; Floreano, L.; Verdini, A.; Casalis, L.; Morgante, A. Comment on “local methylthiolate adsorption geometry on Au(111) from photoemission core-level shifts”. Phys. Rev. Lett. 2009, 103, 119601. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989; ISBN 9780195092769. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R. Development of the Colle- Salvetti correlation energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Triguero, L.; Pettersson, L.; Ågren, H. Calculations of near-edge X-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory. Phys. Rev. B-Condens. Matter Mater. Phys. 1998, 58, 8097–8110. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ellis, D.E.; Ros, P. Self-consistent molecular Hartree—Fock—Slater calculations I. The computational procedure. Chem. Phys. 1973, 2, 41–51. [Google Scholar] [CrossRef]
- Guerra, C.F.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- Rettig, S.J.; Trotter, J. Crystal and molecular structure of phenylboronic acid, C6H5B(OH)2. Can. J. Chem. 1977, 55, 3071–3075. [Google Scholar] [CrossRef]
- Fournier, J.H.; Maris, T.; Wuest, J.D.; Guo, W.; Galoppini, E. Molecular tectonics. Use of the hydrogen bonding of boronic acids to direct supramolecular construction. J. Am. Chem. Soc. 2003, 125, 1002–1006. [Google Scholar] [CrossRef]
- Stredansky, M.; Sala, A.; Fontanot, T.; Costantini, R.; Africh, C.; Comelli, G.; Floreano, L.; Morgante, A.; Cossaro, A. On-surface synthesis of a 2D boroxine framework: A route to a novel 2D material? Chem. Commun. 2018, 54, 3971–3973. [Google Scholar] [CrossRef]
- Minkov, I.; Gel’mukhanov, F.; Friedlein, R.; Osikowicz, W.; Suess, C.; Öhrwall, G.; Sorensen, S.L.; Braun, S.; Murdey, R.; Salaneck, W.R.; et al. Core excitations of naphthalene: Vibrational structure versus chemical shifts. J. Chem. Phys. 2004, 121, 5733–5739. [Google Scholar] [CrossRef]
- Dri, C.; Fronzoni, G.; Balducci, G.; Furlan, S.; Stener, M.; Feng, Z.; Comelli, G.; Castellarin-Cudia, C.; Cvetko, D.; Kladnik, G.; et al. Chemistry of the Methylamine Termination at a Gold Surface: From Autorecognition to Condensation. J. Phys. Chem. C 2016, 120, 6104–6115. [Google Scholar] [CrossRef]
- Toffoli, D.; Ponzi, A.; Bernes, E.; De Simone, M.; Grazioli, C.; Coreno, M.; Stredansky, M.; Cossaro, A.; Fronzoni, G. Correlation effects in B1s core-excited states of boronic-acid derivatives: An experimental and computational study. J. Chem. Phys. 2019, 151, 134306. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turco, E.; Stredansky, M.; Costantini, R.; Martinez, J.A.; Dell’Angela, M.; Zerbato, E.; Toffoli, D.; Fronzoni, G.; Morgante, A.; Floreano, L.; et al. On-Surface Synthesis of Boroxine-Based Molecules. Chemistry 2021, 3, 1401-1410. https://doi.org/10.3390/chemistry3040101
Turco E, Stredansky M, Costantini R, Martinez JA, Dell’Angela M, Zerbato E, Toffoli D, Fronzoni G, Morgante A, Floreano L, et al. On-Surface Synthesis of Boroxine-Based Molecules. Chemistry. 2021; 3(4):1401-1410. https://doi.org/10.3390/chemistry3040101
Chicago/Turabian StyleTurco, Elia, Matus Stredansky, Roberto Costantini, Javier A. Martinez, Martina Dell’Angela, Elena Zerbato, Daniele Toffoli, Giovanna Fronzoni, Alberto Morgante, Luca Floreano, and et al. 2021. "On-Surface Synthesis of Boroxine-Based Molecules" Chemistry 3, no. 4: 1401-1410. https://doi.org/10.3390/chemistry3040101
APA StyleTurco, E., Stredansky, M., Costantini, R., Martinez, J. A., Dell’Angela, M., Zerbato, E., Toffoli, D., Fronzoni, G., Morgante, A., Floreano, L., & Cossaro, A. (2021). On-Surface Synthesis of Boroxine-Based Molecules. Chemistry, 3(4), 1401-1410. https://doi.org/10.3390/chemistry3040101