Topological Analysis of Magnetically Induced Current Densities in Strong Magnetic Fields Using Stagnation Graphs

Abstract

Stagnation graphs provide a useful tool to analyze the main topological features of the often complicated vector field associated with magnetically induced currents. Previously, these graphs have been constructed using response quantities appropriate for modest applied magnetic fields. We present an implementation capable of producing these graphs in arbitrarily strong magnetic fields, using current-density-functional theory. This enables us to study how the topology of the current vector field changes with the strength and orientation of the applied magnetic field. Applications to CH${}_4$, C${}_2$H${}_2$ and C${}_2$H${}_4$ are presented. In each case, we consider molecular geometries optimized in the presence of the magnetic field. The stagnation graphs reveal subtle changes to this vector field where the symmetry of the molecule remains constant. However, when the electronic state and symmetry of the corresponding equilibrium geometry changes with increasing field strength, the changes to the stagnation graph are extensive. We expect that the approach presented here will be helpful in interpreting changes in molecular structure and bonding in the strong-field regime.

1. Introduction

The topology and properties of magnetically induced currents have been widely studied using linear response techniques [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] and a number of programs have been developed to both calculate the induced currents and analyze their main features [18,20,21,22,23]. An essential requirement is to ensure gauge–origin independence of the calculated currents; this has been achieved by a range of methods including: the individual gauge for localized orbitals (IGLO) method [24], the continuous set of gauge transformations (CSGT) approach [6,25,26], the continuous transformation of the gauge origin of the current density (CTOCD) method [8,10,14,15,27,28,29,30] and using London atomic orbitals (LAOs) [18,31] (also known as gauge-including atomic orbitals (GIAOs)). The physical current density is a rich source of chemical information [21,26,32,33,34,35,36,37]; its topology reflects the chemical structure of the molecule and its interaction with the applied magnetic field. Its features have been used as a criterion to assess the aromaticity of molecules [38], give insight into electron delocalization [39,40,41,42] and to probe hydrogen bond strengths [43,44,45]. The magnetically induced currents can also be directly related to magnetic response properties via the induced current susceptibility, a tensor describing the derivative of the induced current with respect to the applied magnetic field. Evaluating this response quantity at a zero magnetic field and using the Biot-Savart law leads directly to magnetic susceptibilities and NMR shielding constants. Furthermore, ring-current models have long been used to rationalize NMR chemical shifts in molecules [21,32,46,47,48,49].

The magnetically induced current is a relatively complicated vector field, and as such, tools for its analysis and interpretation of its main features in a simple manner are highly desirable. Approaches that analyze the induced currents by integration are well developed, see, for example, the GIMIC program [18,41]. Recently, we presented an implementation of these techniques in the context of the current-density-functional theory (CDFT), allowing applications to systems in arbitrarily strong magnetic fields [50]. Somewhat less attention has been given to topological approaches, which employ concepts from vector field analysis to analyze the topology of the vector field and provide insight into the magnetic behaviour of the system.

A few groups have pursued a topological analysis following early work on the mathematical characterization of stagnation points in vector fields by Reyn [51]. In particular, see the work of Keith and Bader [26], as well as works by Pelloni, Faglioni, Zanasi and Lazzeretti [52,53,54,55] for applications to molecular systems. These studies demonstrate how the location and classification of stagnation points (points in space at which the current density $\mathbf{j}$ has a magnitude of zero, i.e., $\left|\mathbf{j}\right|=0$) to produce stagnation graphs can distill the main features of the complicated current vector field into simpler plots that can be easily visualized without suffering from issues, such as occlusion, that often make the direct visualization of dense 3D vector fields challenging.

In the present work, we extend these techniques to analyze magnetically induced currents in strong magnetic fields at the CDFT level. This allows us to identify the main features and topology of induced currents as a function of the applied magnetic field strength and its direction relative to the molecular frame. In Section 2, we outline the necessary theoretical background to calculate the magnetically induced current densities in strong fields; detailing how the current density is determined in Section 2.1 and how its topological characteristics may be classified in Section 2.2. In Section 3, we describe the computational approach used to locate and classify stagnation points and construct stagnation graphs. The results are presented in Section 4 for applications to the CH${}_4$, C${}_2$H${}_2$ and C${}_2$H${}_4$ molecules at their ground state equilibrium geometries over a range of field strengths, obtained using a recently developed implementation of geometrical gradients for calculations using LAOs [56]. The changes in the stagnation plots with the applied field strength are carefully examined and analyzed in Section 5. Conclusions and directions for future work are discussed in Section 6.

2. Theoretical Background

2.1. Magnetically Induced Current Densities

In the presence of a uniform magnetic field $\mathbf{B}$, the non-relativistic electronic Hamiltonian is given by

$$\widehat{\mathcal{H}}={\widehat{\mathcal{H}}}_0+\frac{1}{2}(\mathbf{B}\times {\mathbf{r}}_O)·\widehat{\mathbf{p}}+\mathbf{B}·\widehat{\mathbf{s}}+\frac{1}{8}(\mathbf{B}\times {\mathbf{r}}_O)·(\mathbf{B}\times {\mathbf{r}}_O),$$

(1)

where ${\widehat{\mathcal{H}}}_0$ is the zero–field Hamiltonian, $\widehat{\mathbf{p}}$ the momentum operator ($-ı\nabla$), $\widehat{\mathbf{s}}$ the spin operator and ${\mathbf{r}}_O$ the position relative to some gauge–origin $\mathbf{O}$. Since $\nabla ·\mathbf{B}=0$ for a uniform magnetic field, the magnetic field may be represented by a vector potential $\mathbf{A}$ such that $\mathbf{B}=\nabla \times \mathbf{A}$; in the Coulomb gauge, this vector potential is defined to have a divergence of zero, $\nabla ·\mathbf{A}=0$. Therefore, for a uniform magnetic field, the vector potential depends on the gauge–origin as

$${\mathbf{A}}_O\left(\mathbf{r}\right)=\frac{1}{2}\mathbf{B}\times (\mathbf{r}-\mathbf{O}),$$

(2)

and a change of the position of the gauge–origin $\mathbf{O}\to \mathbf{G}$ is a gauge transformation,

$${\mathbf{A}}_G\left(\mathbf{r}\right)={\mathbf{A}}_O\left(\mathbf{r}\right)-\nabla {\mathbf{A}}_O\left(\mathbf{G}\right)·\mathbf{r}.$$

(3)

This gauge–transformation corresponds to a unitary transform of the Hamiltonian,

$${\widehat{\mathcal{H}}}^{\prime }=exp(ı{\mathbf{A}}_O\left(\mathbf{G}\right)·\mathbf{r})\widehat{\mathcal{H}}exp(-ı{\mathbf{A}}_O\left(\mathbf{G}\right)·\mathbf{r}),$$

(4)

the eigenfunctions of which, $\psi$, therefore undergo a compensating unitary transformation

$${\psi }^{\prime }=exp(ı{\mathbf{A}}_O\left(\mathbf{G}\right)·\mathbf{r})\psi ,$$

(5)

under which observables of the system remain gauge–origin invariant. This gauge–origin dependence of the wavefunction cannot be properly represented in a finite basis except by explicitly including the gauge–origin; this is the approach taken using LAOs [31], which comprise a standard Gaussian-type basis function ${\phi }_a$ centred on $\mathbf{R}$ and multiplied by a field-dependent complex phase factor,

$${\omega }_a\left(\mathbf{r}\right)={\phi }_a\left(\mathbf{r}\right)exp\left(-\frac{ı}{2}\mathbf{B}\times (\mathbf{R}-\mathbf{O})·\mathbf{r}\right)$$

(6)

which yields wavefunctions that are correct to first order in the magnetic field and properties that are gauge–origin invariant [57]. Utilizing an LAO basis, the effects of the magnetic field can be treated in a non-perturbative manner, allowing the behaviour of the systems in the magnetic fields of arbitrary strength to be examined [58,59].

The magnetically induced physical current density $\mathbf{j}$ is a continuous vector field in three dimensions and may be written as the sum of the diamagnetic current density ${\mathbf{j}}_d$ and paramagnetic current density ${\mathbf{j}}_p$ [59,60],

$$\begin{array}{cc}\hfill {\mathbf{j}}_d\left(\mathbf{r}\right)& =-\mathbf{A}\left(\mathbf{r}\right)\sum _{\sigma }{\rho }_{\sigma }\left(\mathbf{r}\right)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathbf{j}}_p\left(\mathbf{r}\right)& =\frac{ı}{2}\sum _{\sigma }\sum _i\left(\nabla {\varphi }_{i\sigma }\left(\mathbf{r}\right){\varphi }_{i\sigma }^{\ast }\left(\mathbf{r}\right)-{\varphi }_{i\sigma }\left(\mathbf{r}\right)\nabla {\varphi }_{i\sigma }^{\ast }\left(\mathbf{r}\right)\right)\hfill \end{array}$$

(8)

where ${\rho }_{\sigma }$ is the $\sigma$-spin density, and ${\varphi }_{i\sigma }$ are the $\sigma$-spin occupied molecular orbitals.

Through the non-perturbative inclusion of magnetic field effects, the magnetically induced current density can be evaluated without the need for linear response calculations; in a basis of LAOs, the one–particle density matrix $D_{ab}^{\sigma }$ computed at the Hartree–Fock (HF) or CDFT levels [59,60,61] may be used to evaluate the diamagnetic and paramagnetic current densities as

$$\begin{array}{cc}\hfill {\mathbf{j}}_d\left(\mathbf{r}\right)& =-\mathbf{A}\left(\mathbf{r}\right)\sum _{\sigma }\sum _{ab}{D}_{ab}^{\sigma }{\omega }_a\left(\mathbf{r}\right){\omega }_b^{\ast }\left(\mathbf{r}\right)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\mathbf{j}}_p\left(\mathbf{r}\right)& =\frac{ı}{2}\sum _{\sigma }\sum _{ab}{D}_{ab}^{\sigma }\left(\nabla {\omega }_a\left(\mathbf{r}\right){\omega }_b^{\ast }\left(\mathbf{r}\right)-{\omega }_a\left(\mathbf{r}\right)\nabla {\omega }_b^{\ast }\left(\mathbf{r}\right)\right),\hfill \end{array}$$

(10)

each of which are individually gauge–origin dependent; however, the physical current density $\mathbf{j}={\mathbf{j}}_d+{\mathbf{j}}_p$ is gauge–origin invariant and can be computed at arbitrary field strengths.

2.2. Topological Characteristics

The magnetically induced current density $\mathbf{j}\left(\mathbf{r}\right)$ is a three-dimensional vector field with a topological structure that may be characterized in terms of its singularities, otherwise referred to as stagnation points, at which $\left|\mathbf{j}\right|=0$. The collection of these points for a system with magnetically induced currents is its stagnation graph, which describes the topological structure of the vector field [6,36,37,51,62]. The Cartesian components of the current density $j_{\alpha }\left(\mathbf{r}\right)$ at position $\mathbf{r}$ around a stagnation point ${\mathbf{r}}_0$ may be described by the second–order Taylor expansion

$$j_{\alpha }\left(\mathbf{r}\right)=\sum _{\beta }(r_{\beta }-r_{0\beta }){\left.\frac{\partial j_{\alpha }}{\partial r_{\beta }}\right|}_{{\mathbf{r}}_0}+\frac{1}{2}\sum _{\beta \gamma }(r_{\beta }-r_{0\beta })(r_{\gamma }-r_{0\gamma }){\left.\frac{{\partial }^2{j}_{\alpha }}{\partial r_{\beta }\partial r_{\gamma }}\right|}_{{\mathbf{r}}_0},$$

(11)

in which the zeroth–order term is, by definition, zero. Taking only the first–order approximation, the current density in the region of the singular point can be described by the linear equation [54,63,64,65,66,67]:

$$\mathbf{j}=\mathbf{J}\mathbf{d},J_{\alpha \beta }={\left.\frac{\partial j_{\alpha }}{\partial r_{\beta }}\right|}_{{\mathbf{r}}_0},\mathbf{d}=\mathbf{r}-{\mathbf{r}}_0,$$

(12)

where $\mathbf{j}$ is the current density at $\mathbf{r}$, and $\mathbf{J}$ is the Jacobian matrix with elements $J_{\alpha \beta }$ comprising the first derivative of $j_{\alpha }$ with respect to $r_{\beta }$.

It can be shown that the local behaviour of the current may be characterized by the eigenvalues ${\eta }_i$ of the Jacobian matrix [51]. The number of non-zero eigenvalues of $\mathbf{J}$ is denoted by the rank r, whilst the excess of eigenvalues with a positive real component over those with a negative real component is denoted the signature s – together the ordered pair $(r,s)$ can be used to characterize the stagnation point [22,52,53,54,64,65]. Given that, at points where the current density is zero, the identity $\nabla ·\mathbf{j}=0$ must be satisfied, the only possible $(r,s)$ combinations for a three-dimensional vector field are $(3,\pm 1)$, $(2,0)$ and $(0,0)$. In addition, a topological index i may be defined at a stagnation point where $\mathbf{J}$ has two non–zero eigenvalues as

$$\begin{array}{c}\hfill i=\left\{\begin{array}{cc}+1\hfill & {\eta }_1={\eta }_2^{\ast },{\eta }_3=0\hfill \\ -1\hfill & {\eta }_1=-{\eta }_2,{\eta }_3=0\hfill \end{array}\right.\end{array}$$

(13)

The resulting classifications are summarized in

Table 1. The classification of stagnation points by their topological characteristics.

$(\mathit{r},\mathit{s})$	i	${\mathit{\eta }}_{\mathit{i}}$ Conditions	Magnetotropicity	Classification
$(3,\pm 1)$		${\eta }_1,{\eta }_2,{\eta }_3\in \mathbb{R}$		isolated singularity: saddle
$(3,\pm 1)$		${\eta }_3\in \mathbb{R},{\eta }_1={\eta }_2^{\ast }$	$\mathbf{B}·(\nabla \times \mathbf{j})>0$	isolated singularity: paramagnetic focus
$(3,\pm 1)$		${\eta }_3\in \mathbb{R},{\eta }_1={\eta }_2^{\ast }$	$\mathbf{B}·(\nabla \times \mathbf{j})<0$	isolated singularity: diamagnetic focus
$(2,0)$	$-1$	${\eta }_1,{\eta }_2\in \mathbb{R},{\eta }_3=0$		stagnation line: saddle
$(2,0)$	$+1$	$\mathfrak{Re}\left({\eta }_1\right),\mathfrak{Re}\left({\eta }_2\right)=0,{\eta }_3=0$	$\mathbf{B}·(\nabla \times \mathbf{j})>0$	stagnation line: paramagnetic vortex
$(2,0)$	$+1$	$\mathfrak{Re}\left({\eta }_1\right),\mathfrak{Re}\left({\eta }_2\right)=0,{\eta }_3=0$	$\mathbf{B}·(\nabla \times \mathbf{j})<0$	stagnation line: diamagnetic vortex
$(0,0)$		${\eta }_1,{\eta }_2,{\eta }_3=0$		branching point

and will be used throughout this work [22,54,65,66,67].

3. Computational Methods

Previous works [22,65] have suggested using Newton–Raphson approaches to search for stagnation points, which occur at the nodes of the current density $\mathbf{j}$. In particular, these optimization schemes only use first-order information to search the three-dimensional current-density vector field from a grid of arbitrarily chosen starting points [22]. Here, we present an alternative choice of the objective function in stagnation point searches in Section 3.1 before outlining an approach allowing for full second-order trust-region optimization, which benefits from quadratic convergence in the vicinity of stagnation points, in Section 3.2. Our approach to selecting an initial grid of starting points for the search and their subsequent refinement to produce clear stagnation graphs is detailed in Section 3.3.

3.1. Selecting an Appropriate Objective Function

The purpose of the stagnation point search is to locate the set of points $\left\{\mathbf{r}\right\}$ at which the objective function

$$\left|\mathbf{j}\left(\mathbf{r}\right)\right|={\left[j_x^2\left(\mathbf{r}\right)+j_y^2\left(\mathbf{r}\right)+j_z^2\left(\mathbf{r}\right)\right]}^{\frac{1}{2}}.$$

(14)

is zero. Such points can be located by searching for stationary points in $\left|\mathbf{j}\right|$ and selecting those at which $\left|\mathbf{j}\right(\mathbf{r}\left)\right|=0$. Previous works have suggested optimizing $\left|\mathbf{j}\right(\mathbf{r}\left)\right|$ directly via the Newton–Raphson approach, which requires only evaluation of the objective function and its first derivative [22,65]. However, it is clear that $\left|\mathbf{j}\right(\mathbf{r}\left)\right|$ will exhibit cusps at the stagnation points. To demonstrate this, we consider an example of the ethene molecule oriented in the $yz$-plane with the two carbon nuclei equidistant from the origin along the z-axis in Figure 1. Plotting $\left|\mathbf{j}\right|$ along the line $-2.5\le y\le 2.5$ bohr at $z=2.3$ bohr, we expect to observe three stagnation points in line with the plots of Ref. [54] when a field of 0.1 $B_0$ is applied parallel to the C–C bond axis ($B_0=ħe^{-1}{a}_0^{-2}=2.3505\times {10}^{5}T$). These points are clearly visible in Figure 1a; however, it can also be seen in Figure 1a that the expected cusps are present at the stagnation points along this line. The first derivative of Equation (14) may be readily evaluated as

$$\frac{\partial \left|\mathbf{j}\right|}{\partial r_{\alpha }}=\frac{j_x}{\left|\mathbf{j}\right|}\frac{\partial j_x}{\partial r_{\alpha }}+\frac{j_y}{\left|\mathbf{j}\right|}\frac{\partial j_y}{\partial r_{\alpha }}+\frac{j_z}{\left|\mathbf{j}\right|}\frac{\partial j_z}{\partial r_{\alpha }},$$

(15)

and the singularities associated with the factors $1/\left|\mathbf{j}\right|$ at the stagnation points are clearly present in Figure 1b, with the total derivative of the objective function being discontinuous at these points. In practice, we find that, using this objective function, the cusps associated with the stagnation points can be approached to a sufficient proximity that the optimization can be terminated; however, the rate of convergence is somewhat hindered.

A full second-order approach, in which the issues associated with the singularities of $\left|\mathbf{j}\right(\mathbf{r}\left)\right|$ are avoided, may be straightforwardly formulated by considering at alternative objective function, ${\left|\mathbf{j}\left(\mathbf{r}\right)\right|}^2$. Figure 2 shows plots of ${\left|\mathbf{j}\right|}^2$ and its first derivative in the same region plotted for $\left|\mathbf{j}\right|$ and its derivatives in Figure 1; it can be seen that this objective function is continuous, and both the gradient and the Hessian of this function are well defined at the stagnation points. This objective function, its gradient and its Hessian may then be evaluated as

$$\begin{array}{cc}\hfill {\left|\mathbf{j}\right|}^2& =j_x^2+j_y^2+j_z^2\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \frac{{\partial \left|\mathbf{j}\right|}^2}{\partial r_{\alpha }}& =\sum _{\gamma }\left(\frac{\partial j_{\gamma }}{\partial r_{\alpha }}{j}_{\gamma }+j_{\gamma }\frac{\partial j_{\gamma }}{\partial r_{\alpha }}\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\left|\mathbf{j}\right|}^2}{\partial r_{\alpha }\partial r_{\beta }}& =\sum _{\gamma }\left(\frac{{\partial }^2{j}_{\gamma }}{\partial r_{\alpha }\partial r_{\beta }}{j}_{\gamma }+2\frac{\partial j_{\gamma }}{\partial r_{\alpha }}\frac{\partial j_{\gamma }}{\partial r_{\beta }}+j_{\gamma }\frac{{\partial }^2{j}_{\gamma }}{\partial r_{\alpha }\partial r_{\beta }}\right).\hfill \end{array}$$

(18)

The gradient components are displayed in Figure 2b and are well behaved as expected.

Figure 2. (a) The value of ${\left|\mathbf{j}\right|}^2$; (b) The Cartesian gradient components ${\partial }_{\gamma }{\left|\mathbf{j}\right|}^2$ and its magnitude plotted from $y=-2.5$ to $2.5$ bohr at $z=2.3$ bohr in the ethene molecule in the $yz$-plane with a magnetic field of $0.1B_0$ along the z-axis.

Figure 2. (a) The value of ${\left|\mathbf{j}\right|}^2$; (b) The Cartesian gradient components ${\partial }_{\gamma }{\left|\mathbf{j}\right|}^2$ and its magnitude plotted from $y=-2.5$ to $2.5$ bohr at $z=2.3$ bohr in the ethene molecule in the $yz$-plane with a magnetic field of $0.1B_0$ along the z-axis.

Furthermore, the Hessian may be readily evaluated affording full second-order optimization at a modest cost. The required partial derivatives with respect to the position may be evaluated in terms of the LAOs and density matrices as

$$\begin{array}{cc}\hfill j_{\alpha }& =\frac{ı}{2}\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{\partial {\omega }_a}{\partial r_{\alpha }}{\omega }_b^{\ast }-{\omega }_a\frac{\partial {\omega }_b^{\ast }}{\partial r_{\alpha }}\right)-A_{\alpha }\sum _{\sigma ab}{D}_{ab}^{\sigma }{\omega }_a{\omega }_b^{\ast }\hfill \\ \hfill \frac{\partial j_{\alpha }}{\partial r_{\beta }}& =\frac{ı}{2}\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{{\partial }^2{\omega }_a}{\partial r_{\alpha }\partial r_{\beta }}{\omega }_b^{\ast }+\frac{\partial {\omega }_a}{\partial r_{\alpha }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\beta }}-\frac{\partial {\omega }_a}{\partial r_{\beta }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\alpha }}-{\omega }_a\frac{{\partial }^2{\omega }_b^{\ast }}{\partial r_{\alpha }\partial r_{\beta }}\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & -A_{\alpha }\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{\partial {\omega }_a}{\partial r_{\beta }}{\omega }_b^{\ast }+{\omega }_a\frac{\partial {\omega }_b^{\ast }}{\partial r_{\beta }}\right)-\frac{1}{2}{\epsilon }_{\alpha \gamma \beta }{B}_{\gamma }\sum _{\sigma ab}{D}_{ab}^{\sigma }{\omega }_a{\omega }_b^{\ast }\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \frac{{\partial }^2{j}_{\alpha }}{\partial r_{\beta }\partial r_{\gamma }}& =\frac{ı}{2}\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{{\partial }^3{\omega }_a}{\partial r_{\alpha }\partial r_{\beta }\partial r_{\gamma }}{\omega }_b^{\ast }+\frac{{\partial }^2{\omega }_a}{\partial r_{\alpha }\partial r_{\beta }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\gamma }}+\frac{{\partial }^2{\omega }_a}{\partial r_{\alpha }\partial r_{\gamma }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\beta }}+\frac{\partial {\omega }_a}{\partial r_{\alpha }}\frac{{\partial }^2{\omega }_b^{\ast }}{\partial r_{\beta }\partial r_{\gamma }}\right.\hfill \\ \hfill & -\left.\frac{{\partial }^2{\omega }_a}{\partial r_{\beta }\partial r_{\gamma }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\alpha }}-\frac{\partial {\omega }_a}{\partial r_{\beta }}\frac{{\partial }^2{\omega }_b^{\ast }}{\partial r_{\alpha }\partial r_{\gamma }}-\frac{\partial {\omega }_a}{\partial r_{\gamma }}\frac{{\partial }^2{\omega }_b^{\ast }}{\partial r_{\alpha }\partial r_{\beta }}-{\omega }_a\frac{{\partial }^3{\omega }_b^{\ast }}{\partial r_{\alpha }\partial r_{\beta }\partial r_{\gamma }}\right)\hfill \\ \hfill & -\frac{1}{2}{\epsilon }_{\alpha \gamma \beta }{B}_{\gamma }\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{\partial {\omega }_a}{\partial r_{\gamma }}{\omega }_b^{\ast }+{\omega }_a\frac{\partial {\omega }_b^{\ast }}{\partial r_{\gamma }}\right)-\frac{1}{2}{\epsilon }_{\alpha \beta \gamma }{B}_{\beta }\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{\partial {\omega }_a}{\partial r_{\beta }}{\omega }_b^{\ast }+{\omega }_a\frac{\partial {\omega }_b^{\ast }}{\partial r_{\beta }}\right)\hfill \\ \hfill & -A_{\alpha }\sum _{\sigma ab}{D}_{ab}^{\sigma }\left(\frac{{\partial }^2{\omega }_a}{\partial r_{\beta }\partial r_{\gamma }}{\omega }_b^{\ast }+\frac{\partial {\omega }_a}{\partial r_{\beta }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\gamma }}+\frac{\partial {\omega }_a}{\partial r_{\gamma }}\frac{\partial {\omega }_b^{\ast }}{\partial r_{\beta }}+{\omega }_a\frac{{\partial }^2{\omega }_b^{\ast }}{\partial r_{\beta }\partial r_{\gamma }}\right)\hfill \end{array}$$

(21)

These derivatives have been implemented in the Quest program [23]. The correctness of each contribution was verified by finite-difference calculations with respect to $r_{\alpha }$.

3.2. Optimization Algorithm

To locate the stagnation points, ${\left|\mathbf{j}\right|}^2$ was minimized with respect to $\mathbf{r}$ using a trust region approach. Using this method, a quadratic model of the objective function

$$\begin{array}{c}\hfill m_k({\mathbf{r}}_k+\mathbf{d})={\left|\mathbf{j}\right|}_k^2+{\mathbf{d}}^T{\mathbf{g}}_k+\frac{1}{2}{\mathbf{d}}^T{\mathbf{H}}_k\mathbf{d}\end{array}$$

(22)

is constructed around each point visited in the optimization ${\mathbf{r}}_k$. Here, $\mathbf{d}$ defines the step taken from the point ${\mathbf{r}}_k$, and ${\left|\mathbf{j}\right|}_k^2$, ${\mathbf{g}}_k$ and ${\mathbf{H}}_k$ are the objective function, its gradient and Hessian at ${\mathbf{r}}_k$, respectively,

$${\left|\mathbf{j}\right|}_k^2={\left|\mathbf{j}\left({\mathbf{r}}_k\right)\right|}^2{\mathbf{g}}_k={\left.\frac{{\partial \left|\mathbf{j}\right|}^2}{\partial r_{\alpha }}\right|}_{{\mathbf{r}}_k}{\mathbf{H}}_k={\left.\frac{{\partial }^2{\left|\mathbf{j}\right|}^2}{\partial r_{\alpha }\partial r_{\beta }}\right|}_{{\mathbf{r}}_k}$$

(23)

To ensure progress in the optimization, the step $\mathbf{d}$ is determined by solving the trust-region subproblem

$$\underset{\mathbf{d}}{min}{m}_k({\mathbf{r}}_k+\mathbf{d}){,\mathrm{subject}\mathrm{to}\left|\right|\mathbf{d}\left|\right|}_2\le {\Delta }_k,$$

(24)

where ${\Delta }_k$ is the trust-radius. The step cannot exceed the trust region, in which the quadratic model is expected to be reliable. At each iteration, the accuracy of the step from the quadratic model is monitored using the ratio of the actual change in ${\left|\mathbf{j}\right|}^2$ to that predicted by the quadratic model. If the step does not produce a sufficient decrease in ${\left|\mathbf{j}\right|}^2$, the trust-radius is reduced. Alternatively, if the model is particularly accurate (as would be the case if it was close to a stationary point for example), then the trust-radius may be increased; if the model is reasonably accurate, the trust-radius is kept the same. This approach is detailed in Algorithm 1, where the ratio used to control the trust-radius is denoted ${\gamma }_k$. At each step, we solve the trust–region subproblem Equation (24) using the Steihaug-Toint truncated conjugate gradient algorithm [68].

Algorithm 1 Trust Region optimization

${\Delta }_0=0.1$ for$k=0,1,2,\dots$do     obtain ${\mathbf{d}}_k$ by solving Equation (24)     ${\gamma }_k=\frac{|\mathbf{j}\left({\mathbf{r}}_k\right){|}^2-{\left|\mathbf{j}({\mathbf{r}}_k+{\mathbf{d}}_k)\right|}^2}{m_k\left({\mathbf{r}}_k\right)-m_k({\mathbf{r}}_k+{\mathbf{d}}_k)}$     if ${\gamma }_k<0.25$ then         ${\Delta }_{k+1}=\mathsf{max}(0.25{\Delta }_k,1.0\times {10}^{-8})$     else if ${\gamma }_k>0.75$ and $\left|\right|{\mathbf{d}}_k\left|\right|={\Delta }_k$ then         ${\Delta }_{k+1}=\mathsf{min}(2{\Delta }_k,0.3)$     else         ${\Delta }_{k+1}={\Delta }_k$     end if     ${\mathbf{r}}_{k+1}={\mathbf{r}}_k+{\mathbf{d}}_k$ end for

In practice, we observe rapid convergence from a wide range of starting points, with quadratic convergence in the local region. The optimization is terminated when the following convergence criteria are satisfied: the maximum value of the gradient ${\nabla \left|\mathbf{j}\right|}^2$ is ⩽2 $\times {10}^{-6}$ au, its root-mean-square is ⩽${10}^{-6}$ au, and its Euclidian norm is ⩽${10}^{-8}$ au, the norm of the change in $\mathbf{r}$ is ⩽$3\times {10}^{-5}$ au and its maximum value ⩽$6\times {10}^{-4}$ au and the norm of the change in ${\left|\mathbf{j}\right|}^2$ is ⩽${10}^{-8}$ au. This allows us to clearly distinguish the required stagnation points in the current-density vector field.

3.3. Initial Point Selection

A key aspect of making a stagnation point search computationally tractable is how the initial points for the optimizations are selected. Few details in this regard are discussed in previous studies of stagnation plots [22,65]. In the present work, the stagnation point search is carried out after a converged CDFT calculation from initial points defined using an atom-centred quadrature grid, with angular coordinates given by the eleventh degree Lebedev quadrature [69] and radial coordinates given by the LMG method [70] with threshold on the relative error of the radial integral of ${10}^{-2}$. This grid is of the type used in DFT calculations but is much sparser than would be required for a full numerical integration of quantities, such as the electron density and its gradient. It does, however, retain a similar structure to the full DFT integration grid, with more points found close to the nuclei and less points as the distance from the nuclei increases. This structure provides a set of starting points that are well placed to resolve the details of often more complex stagnation lines in the vicinity of nuclei whilst also sampling those further away. In the present work, we initiate stagnation point searches from this initial grid of points.

Typically, plotting the converged points reveals the structure of the stagnation graph, but points may be relatively sparsely placed along the stagnation lines. In order to increase the number of stagnation points located, a second refinement stage is carried out. The path between stagnation points from the initial search that are separated by $1.5$ bohr or less is divided into segments of approximately $0.1$ bohr and a new initial point created at the midpoint of each segment. Once these points are generated, they are filtered to remove any points that are within $0.05$ bohr of another point in the set. Optimizations are then carried out from these points to refine the stagnation graph. This strategy was effective at locating a larger number of singular points, particularly along stagnation lines, whilst minimizing the computational cost. Finally, since ${\left|\mathbf{j}\right|}^2$ decays towards zero as we move away from the molecule, stagnation points in regions of negligible charge density ($\rho <{10}^{-3}$ au) are discarded to leave only those of interest within the molecular volume.

4. Results

To test the efficiency of this new implementation and investigate how the current vector field topology and associated stagnation graph changes in the presence of strong magnetic fields, we study three small molecules: CH${}_4$, C${}_2$H${}_2$ and C${}_2$H${}_4$. For each case, we consider fields of magnitude $\left|\mathbf{B}\right|=0.0-0.2B_0$ and optimize the molecular geometries using the analytic gradient implementation of Ref. [56] at the cTPSS/u-aug-cc-pVTZ level. Here, the prefix u- indicates that the basis set is used in its uncontracted form; uncontracted basis sets are used to provide greater flexibility to describe the response of the wavefunction to the magnetic field. The spherical-harmonic form of these Gaussian basis functions are used throughout.

To aid the efficiency of the calculations density-fitting is used for all calculations, with the AutoAux auxiliary basis set. This autogenerated auxiliary basis set is generated following the approach outlined in Ref. [71] and provides a conservative auxiliary basis set constructed by considering the product space of the primary orbital basis. This choice helps to ensure that the results are consistent over a wide range of field strengths. Here, we note that the TZ quality basis set employed should be sufficiently accurate to describe systems in field strengths $\left|\mathbf{B}\right|\le 0.2B_0$—see, for example, Refs. [50,72] for discussion of this point.

The stagnation plots are visualized along with the nuclear framework using the QMole tool, built using the Plotly python package [73], and are shown in the following subsections in static form; html files are provided as Supporting Information, which allow the reader to explore the plots in 3D using any modern web browser.

4.1. CH${}_4$

The energy and main geometrical parameters for the equilibrium structure of CH${}_4$, optimized in magnetic fields of $\left|\mathbf{B}\right|=0.05B_0$, $0.10B_0$, $0.15B_0$ and $0.20B_0$ aligned in the lowest energy orientation parallel to one of the C–H bonds, are presented in

Table 2. Equilibrium geometries of CH${}_4$ at the magnetic field strengths considered in this work, optimized with the cTPSS functional and in the u-aug-cc-pVTZ basis. In all cases, the magnetic field is aligned parallel to one of the C–H bonds.

$\left|\mathit{B}\right|$ / ${\mathit{B}}_0$	Energy / ${\mathit{E}}_{\mathbf{h}}$	R${}_{\mathbf{C}}-\mathbf{H}$ / bohr	∢ H–C–H / Degree	Point Group
0.00	−40.541554	2.0638	109.5	T${}_{\mathrm{d}}$
0.05	−40.536608	2.0631, 2.0632	109.4, 109.5	C${}_3$
0.10	−40.522124	2.0614, 2.0615	109.3, 109.6	C${}_3$
0.15	−40.499129	2.0585, 2.0604	109.2, 109.8	C${}_3$
0.20	−40.469243	2.0543, 2.0620	108.9, 110.0	C${}_3$

. It can be seen that, as expected for a closed-shell molecule, the energy exhibits diamagnetic behaviour and increases with field strength.

In the absence of a magnetic field, the equilibrium geometry of CH${}_4$ has the familiar T${}_{\mathrm{d}}$ point group with all C–H bond lengths and H–C–H bond angles equal. Upon the application of a magnetic field, the point group symmetry of the molecule becomes that of the molecule and magnetic field combined; this usually lowers the symmetry of the system since, of the symmetry operations at zero field, only rotation axes parallel to the field, mirror planes perpendicular to the field and inversion centres remain [74]. In the case of CH${}_4$ with a magnetic field applied parallel to one of the C–H bonds, the only symmetry element remaining is the three-fold rotation axis parallel to the field; hence, the point group is reduced to C${}_3$.

It can be seen in Table 2 that, with an applied magnetic field, the optimized geometry distorts away from the tetrahedral structure to a lower symmetry arrangement; the length of the C–H bond along the C${}_3$ axis becomes distinct from that of the other bonds. Similarly, the H–C–H angles involving the axial H become distinct from those involving only non-axial H atoms. In Table 2, these quantities are reported in pairs, with the first value corresponding to the axial case and the second the non-axial case.

It can be seen that the axial C–H bond becomes compressed with increasing field strength, reducing in length by ∼$0.5$ pm at $\left|\mathbf{B}\right|=0.20B_0$ relative to zero field. The trend for the non-axial bonds is less clear since their length remains approximately constant over this range of field strengths. In addition, the axial H–C–H angles become slightly more acute and the non-axial H–C–H angles become slightly more obtuse with increasing field strength, with the non-axial H–C–H angles being around 1.1${}^{\circ }$ smaller than the axial H–C–H angles at $\left|\mathbf{B}\right|=0.2B_0$.

The CH${}_4$ stagnation plots in the range $\left|\mathbf{B}\right|=0.05-0.2B_0$ are shown in Figure 3. The stagnation plot at $\left|\mathbf{B}\right|=0.05B_0$ closely resembles the plot presented in Ref. [54], with saddle lines coloured blue, para- and dia-tropic vortex lines coloured red and green, respectively, and branching points coloured purple. The latter are located close to the C${}_3$ axis as expected. The similarity with Ref. [54] confirms the accuracy of the present implementation for locating the stagnation points and also that the classifications in Table 1 are correctly implemented.

In general, the structures of the stagnation plots display only minor changes with increasing field strength in this range. However, two trends with increasing field strength may be observed; the outer saddle and diatropic vortex lines dilate to have a slightly larger radius around the carbon atom, whilst simultaneously, the inner paratropic vortex and saddle lines contract towards the carbon atom with increasing field strength. The stagnation plots reflect the fact that, as the field strength increases, the induced current becomes more intense and compact around the carbon atom.

4.2. C${}_2$H${}_2$

In

Table 3. Equilibrium geometries of C${}_2$H${}_2$ at the magnetic field strengths considered in this work, optimized with the cTPSS functional and in the u-aug-cc-pVTZ basis. In all cases, the magnetic field is aligned perpendicular to the C–C bond.

$\left|\mathit{B}\right|$ / ${\mathit{B}}_0$	Energy / ${\mathit{E}}_{\mathbf{h}}$	R${}_{\mathbf{C}}-\mathbf{C}$ / bohr	R${}_{\mathbf{C}}-\mathbf{H}$ / bohr	∢ H–C–C / Degree	Point Group
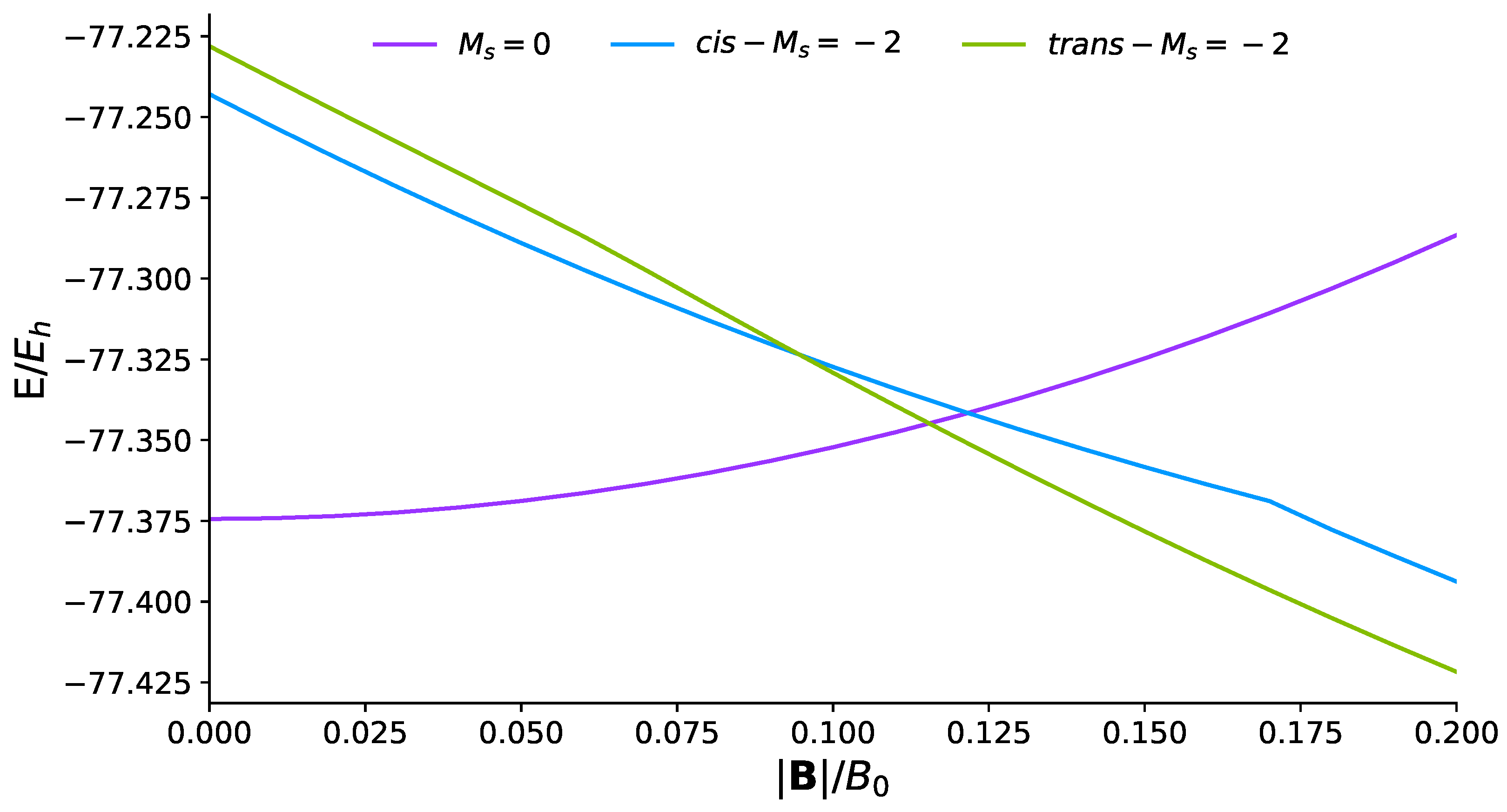
0.00	−77.374420	2.2727	2.0136	180.0	D${}_{\infty \mathrm{h}}$
0.05	−77.368853	2.2722	2.0123	180.0	C${}_{2\mathrm{h}}$
0.10	−77.352224	2.2703	2.0085	180.0	C${}_{2\mathrm{h}}$
0.15	−77.378285	2.5974	2.0679	118.5	C${}_{\mathrm{i}}$
0.20	−77.421742	2.6106	2.0658	115.8	C${}_{\mathrm{i}}$

, the energies and main geometrical parameters for the equilibrium structures of C${}_2$H${}_2$, optimized in magnetic fields of $\left|\mathbf{B}\right|=0.05B_0$, $0.10B_0$, $0.15B_0$ and $0.20B_0$ aligned in the lowest energy orientation perpendicular to the C–C bond, are presented. Over the range of fields considered, the ground state of the molecule changes from that with $M_{\mathrm{s}}=0$ to $M_{\mathrm{s}}=-2$; this occurs at a field strength of around $0.12B_0$. Consistent with Ref. [75], the equilibrium geometry of C${}_2$H${}_2$ in the lowest energy triplet state at zero field has a cis structure, with both hydrogen atoms on the same side of the C–C bond. However, at a field strength of around $0.10B_0$, the trans structure in which the two hydrogen atoms are on either side of the C–C bond becomes lower in energy than the cis structure; hence, the $M_{\mathrm{s}}=-2$ state has a trans equilibrium geometry at $\left|\mathbf{B}\right|>0.1B_0$, where it is the ground state. The energies of the optimized $M_{\mathrm{s}}=0$, cis-$M_{\mathrm{s}}=-2$ and trans-$M_{\mathrm{s}}=-2$ states are summarized in Figure 4.

The equilibrium geometry of the $M_{\mathrm{s}}=0$ state of C${}_2$H${}_2$ remains linear whilst it is the ground state; however, the presence of the magnetic field leads to a reduction in symmetry from D${}_{\infty }\mathrm{h}$ to C${}_{2\mathrm{h}}$ since only the two-fold rotation axis parallel to the field, the mirror plane perpendicular to the field and the inversion centre are retained. It can be seen in Table 3 that, as the field strength increases, both the C–C and C–H bonds contract slightly. In comparison, the trans-$M_{\mathrm{s}}=-2$ state has an electronic configuration in which an $\alpha$-spin electron in a bonding orbital has been excited to an anti-bonding orbital and undergone a spin flip to a $\beta$-spin electron. In the stronger fields considered here, the favorable interaction of the unpaired $\beta$-electrons with the external magnetic field is sufficient to make the $M_{\mathrm{s}}=-2$ states lower in energy than the $M_{\mathrm{s}}=0$ state, whilst in the stronger fields, the trans conformation is favored over the cis. Consistent with these changes in occupation, the C–C bond lengthens significantly, and the C–H bonds also lengthen but to a lesser extent. The H–C–C bond angle becomes 118.5${}^{\circ }$ at 0.15 $B_0$ and becomes more acute with the increasing field. In the presence of the field, the trans-$M_{\mathrm{s}}=-2$ state adopts an orientation such that the field lies in the molecular plane, and the point group symmetry of the system is reduced from C${}_{2\mathrm{h}}$ in the absence of a field to C${}_i$.

The stagnation plots for C${}_2$H${}_2$ are presented in Figure 5. The plot at $\left|\mathbf{B}\right|=0.05B_0$ exhibits the same features as that obtained from response calculations in Ref. [76]. In addition to the classes of the stagnation point identified for CH${}_4$, isolated saddle nodes are visible in the plane containing the internuclear axis and perpendicular to the applied field. The stagnation graph at $0.10B_0$ has a very similar structure to that at $0.05B_0$. The picture at $0.15B_0$ and $0.20B_0$ is entirely different since the stagnation graph of the ground state at this field strength contains no stagnation lines but only isolated paratropic vortices and saddle points. These features will be discussed further in Section 5.

To illustrate how the stagnation plots neatly summarize the topology of the magnetically induced current vector field, contour plots of $\left|\mathbf{j}\right|$ in the $xz$ and $yz$ planes of Figure 5b are presented in Figure 6. On the left, the darkest blue features in the $xz$-plane, representing the smallest $\left|\mathbf{j}\right|$, show where the stagnation lines are located. The stagnation line perpendicular to the C–C bond and passing through its midpoint and those that form loops encircling the nuclei can both be seen in Figure 6a. On the right, the darkest blue features in the $yz$-plane capture the central diatropic vortex line displayed as a ring around the C–C bond midpoint in Figure 5. In addition, the points intersecting the bond axis are clearly represented, along with the four isolated saddle node stagnation points. This demonstrates that the stagnation plots accurately and succinctly capture the main features of the topology of the complicated vector field associated with the magnetically induced current.

4.3. C${}_2$H${}_4$

The energy and main geometrical parameters for the equilibrium structure of C${}_2$H${}_4$, optimized in magnetic fields of $\left|\mathbf{B}\right|=0.05B_0$, $0.10B_0$, $0.15B_0$ and $0.20B_0$ aligned in the lowest energy orientation parallel to the C–C bond, are presented in

Table 4. Equilibrium geometries of C${}_2$H${}_4$ at the magnetic field strengths considered in this work, optimized with the cTPSS functional and in the u-aug-cc-pVTZ basis. In all cases, the magnetic field is aligned parallel to the C–C bond.

$\left|\mathit{B}\right|$ / ${\mathit{B}}_0$	Energy / ${\mathit{E}}_h$	R${}_{\mathbf{C}}-\mathbf{C}$ / bohr	R${}_{\mathbf{C}}-\mathbf{H}$ / bohr	∢ H–C–H / Degree	Point Group
0.00	−78.633815	2.5150	2.0532	116.5	D${}_{2\mathrm{h}}$
0.05	−78.628954	2.5146	2.0523	116.2	C${}_{2\mathrm{h}}$
0.10	−78.614244	2.5133	2.0497	115.2	C${}_{2\mathrm{h}}$
0.15	−78.589425	2.5110	2.0457	113.7	C${}_{2\mathrm{h}}$
0.20	−78.554391	2.5084	2.0407	111.5	C${}_{2\mathrm{h}}$

. In this orientation, the zero-field point group of D${}_{2\mathrm{h}}$ is reduced to C${}_{2\mathrm{h}}$ in a magnetic field since only the two-fold rotation axis along the C–C bond parallel to the field, the mirror plane perpendicular to the field and the centre of inversion remain. Consistent with this symmetry, all of the C–H bonds remain equivalent even with increasing field strength. Between $\left|\mathbf{B}\right|=0.05B_0$ and $0.20B_0$, the C–C and C–H bonds are compressed by ∼0.3 and ∼0.7 pm, respectively, whilst at the same time, the H–C–H bond angles become more acute, reducing by 5${}^{\circ }$ over this range of field strengths.

The stagnation plots for C${}_2$H${}_4$ are presented in Figure 7. As for CH${}_4$, the plot at $\left|\mathbf{B}\right|=0.05B_0$ exhibits the same features as that obtained from response calculations in Ref. [54]. The structure of the stagnation graph remains similar for all the field strengths considered here; as such, only that at $\left|\mathbf{B}\right|=0.05B_0$ is presented in Figure 7.

5. Discussion

Stagnation graphs of the kind presented in Figure 3, Figure 5 and Figure 7 provide convenient spatial descriptions of the magnetically induced current densities in molecules, with which various magnetic properties can be predicted. Analysis of the stagnation graphs obtained by response calculations for CH${}_4$, C${}_2$H${}_2$ and C${}_2$H${}_4$ has been presented in Refs. [54,76]. We now examine how this analysis changes over the range of fields considered in the present work.

In the diamagnetic CH${}_4$ molecule, the current flow around the edges of the molecule in the low-density regions is diatropic and perpendicular to $\mathbf{B}$. At the centre of these rings of diatropic current flow is the C${}_3$ rotation axis of the molecule and along which lies a diatropic vortex line. Approaching regions of the molecule in which the charge density is greater, the structure of the magnetically induced current density becomes more complex with multiple individual circulations or toroidal vortices. At the centre of each lies a paratropic or diatropic vortex line for paratropic or diatropic vortices, respectively; these branch from the axial vortex line above the carbon atom and converge to the axial vortex line below the carbon atom such that they form closed loops. In the same region, saddle lines form a closed loop between the branching points on the axial vortex line and lie at the points of zero current flow between adjacent vortices.

As described in Section 4, it can be seen in Figure 3 that the structure of the stagnation graph in CH${}_4$ remains generally similar with increasing magnetic field strength; however, the outer ring of saddle and diatropic vortex lines around the carbon atom dilate, whilst the inner ring of saddle and paratropic vortex lines contract with increasing field strength. This may be confirmed by considering the current densities at different field strengths; streamlines of the current in the $xy$ plane perpendicular to the magnetic field and at a height of $z=-0.2$ bohr relative to the carbon atom at the origin in CH${}_4$ at $\left|\mathbf{B}\right|=0.1B_0$ and $0.2B_0$ are shown in Figure 8a,b, respectively. At the higher field strength, the magnitude of the current flow around the toroidal vortices becomes larger, resulting in the diatropic stagnation lines moving further from the nucleus. At the same time, the paratropic vortices are compressed towards the nucleus; hence the paratropic vortex lines moving towards the nucleus.

As presented in Section 4, the ground state of the C${}_2$H${}_2$ molecule changes between $\left|\mathbf{B}\right|=0.10B_0$ and $0.15B_0$ from $M_{\mathrm{s}}=0$ to $M_{\mathrm{s}}=-2$ and the equilibrium geometry changes from a linear structure to adopt a trans conformation. The stagnation graph changes completely, with only a few isolated stagnation points remaining. The pattern of stagnation points at this geometry and field strength may be understood by considering the magnitude of the current density in the plane of the molecule; this is presented in Figure 9a, where the stagnation points can be clearly identified. Since the $M_{\mathrm{s}}=-2$ state of C${}_2$H${}_2$ is not closed shell and has a different number of $\alpha$ and $\beta$ electrons, the current density of each is not necessarily the same. This can be seen clearly in Figure 9b,c, depicting the norm of the $\alpha$ and $\beta$ current densities, respectively. In the $\alpha$ case, a line of zero current density loops between the two carbon nuclei and around each, whilst in the $\beta$ case, separate lines of zero current density appear to encircle each of the carbon nuclei and a line of zero current density at the midpoint of the C–C bond parallel to the magnetic field is visible.

The overall stagnation graph describes points where the magnitude of the total current density is zero; since this is a non-negative quantity by definition, at each stagnation point, the magnitudes of both the $\alpha$ and $\beta$ current densities must vanish. The total stagnation graph, therefore, represents the intersection of the sets of stagnation points that would be obtained for the $\alpha$ and $\beta$ spin currents independently. Since the topology of the $\alpha$ and $\beta$ spin currents are significantly different, the intersection of their stagnation points results in a small number of points, which are visible in Figure 9a and located in Figure 5c,d.

For C${}_2$H${}_4$, the stagnation graph exhibits very little change between $\left|\mathbf{B}\right|=0.05B_0$ and $0.20B_0$. This may be rationalized by noting that the symmetry of the molecule does not change with increasing field strength in the range studied here. The relationship between a molecule’s symmetry elements, particularly mirror planes, and its stagnation graph has been discussed in detail in Refs. [52,53,54], where it is shown that the presence and position of stagnation lines can be determined from mirror planes. Whilst the equilibrium C–C and C–H bond lengths and the H–C–H bond angles change with increasing field strength, the symmetry of the molecule remains constant, and as such, the features present in the stagnation graph remain the same, notwithstanding distortions with increasing field strength similar to those in CH${}_4$.

Previous studies of stagnation graphs have mainly focused on small molecules with high symmetry and have used first-order methods to determine the location of stagnation points [22,52,53,54,65]. We expect that the second-order optimization approach for locating the stagnation points presented here should allow stagnation graphs to be mapped-out efficiently for more complex systems. As demonstrated with C${}_2$H${}_2$, this approach allows the changes in the stagnation graph to be examined as the symmetry of the molecule and its state changes, which is expected to become essential to study systems in stronger magnetic fields [56].

6. Conclusions

A second-order optimization method for mapping out the stagnation graphs of molecular systems has been presented. In this approach, stagnation points are located by minimizing ${\left|\mathbf{j}\right|}^2$, which, in contrast to $\left|\mathbf{j}\right|$, has well-defined first and second derivatives, enabling the stagnation graph to be elucidated efficiently and robustly for general systems.

In contrast to previous work in this area [52,53,54,76], the magnetic field effects are here treated in a non-perturbative manner, allowing stagnation graphs to be computed at arbitrary field strengths and the effect of varying field strength on the characteristics of the stagnation graphs to be examined. Furthermore, the changes in the stagnation graph arising due to the effect of the magnetic field on the equilibrium geometry of the molecules has been accounted for by optimizing the molecular geometries at each field strength using the implementation of Ref. [56] before computing the stagnation graphs. This approach has been applied to study the stagnation graphs of three small molecules: CH${}_4$, C${}_2$H${}_2$ and C${}_2$H${}_4$, which have previously been considered using response calculations [54,76], across a range of magnetic field strengths. In weak fields, the results obtained with the present approach are consistent with these earlier results, indicating the reliability of the implementation.

Upon increasing the field strength, we observe that the extent to which the stagnation graphs change depends strongly on the how the symmetry of the molecular structure and electronic state are affected by the magnetic field. In cases where the electronic state and molecular symmetry remain the same as in the absence of a field, only subtle changes to the stagnation graphs are observed, such as contractions and dilations of the radii of closed stagnation line loops. These changes can be explained by considering the magnitude of the current densities, which generally increase with increasing field strength, increasing the radii of toroidal vortices and increasing the distance between their corresponding vortical stagnation lines.

In cases where increasing the field strength results in a change in the electronic state and an accompanying change in the symmetry of the molecular geometry, much more extensive changes to the stagnation graph are observed. For example, the change in the ground state of C${}_2$H${}_2$ from $M_{\mathrm{s}}=0$ to $M_{\mathrm{s}}=-2$ at increasing field strength completely alters the molecular structure, symmetry and hence the stagnation graph. The structure of the stagnation graph was rationalized by considering the individual $\alpha$ and $\beta$ spin current densities, with the stagnation points for the total current being the intersection of the stagnation points for the $\alpha$ and $\beta$ spin currents individually.

We expect that the second-order approach for determining stagnation plots presented in this work will become a useful tool for understanding the electronic structure of more complex molecules in strong magnetic fields. The present implementation allows flexibility to study stagnation graphs for a wide range of uniform magnetic fields in a non-perturbative manner and to resolve their $\alpha$ and $\beta$-spin contributions. In the present work, only small molecules with up to two carbon atoms have been considered; in later work, we will apply this method to study current densities in more diverse molecular systems, such as homo- and heterocyclic aromatic molecules and aromatic systems, for which the stagnation graphs are known to show a wider range of features [66]. In future work, we will also consider the generalization of this approach to non-uniform magnetic fields, as described in Ref. [77]. As noted by Pelloni and Lazzeretti [76], the interaction between toroidal vortices and the gradient of non-uniform magnetic fields can be examined with the aid of stagnation graphs, and these may provide useful insight into these effects on nuclear magnetic shielding as well as more exotic properties, such as molecular anapole moments.