Recent Progress in Two-Dimensional Nanomaterials for Laser Protection
Abstract
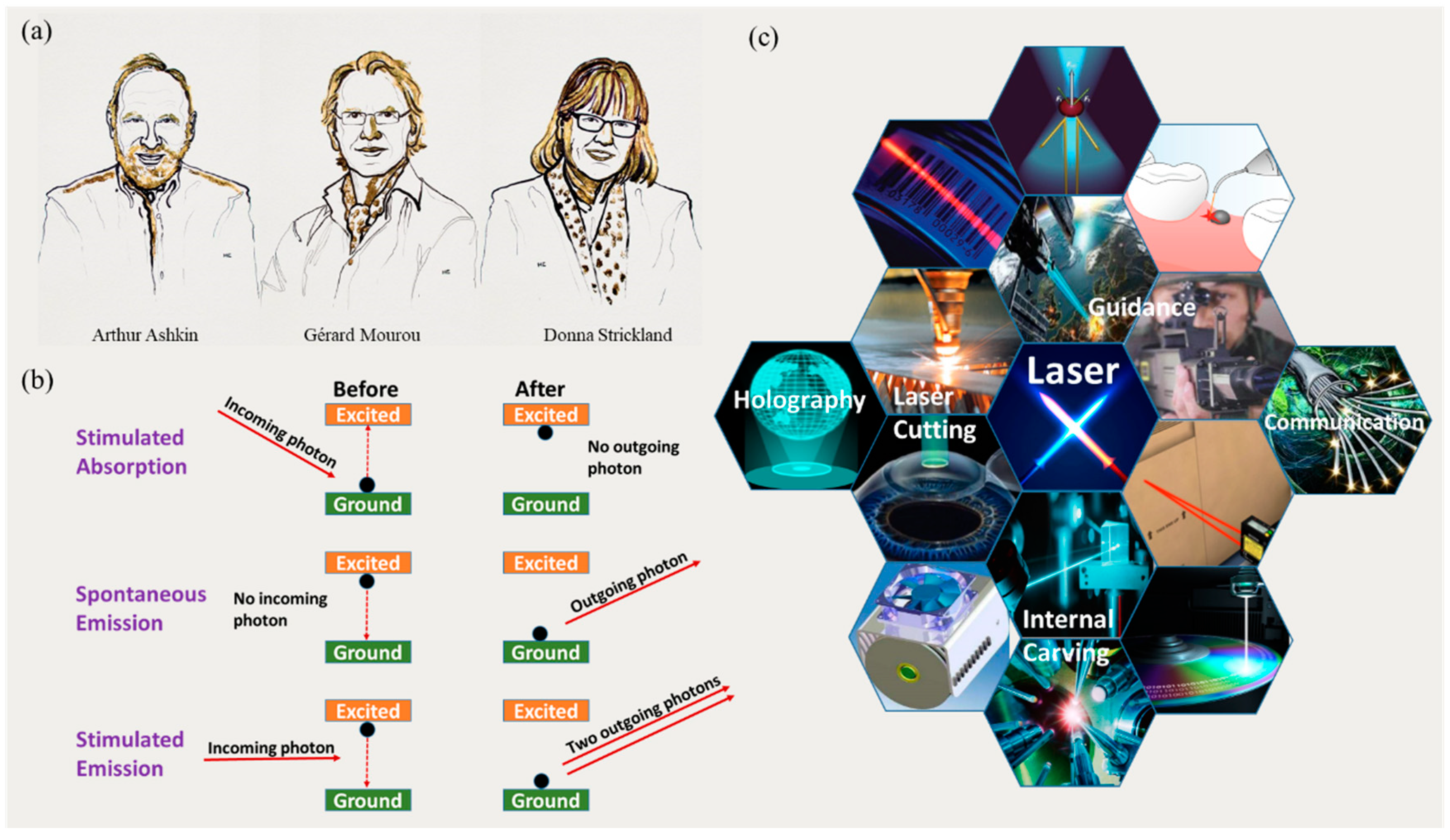
1. Introduction
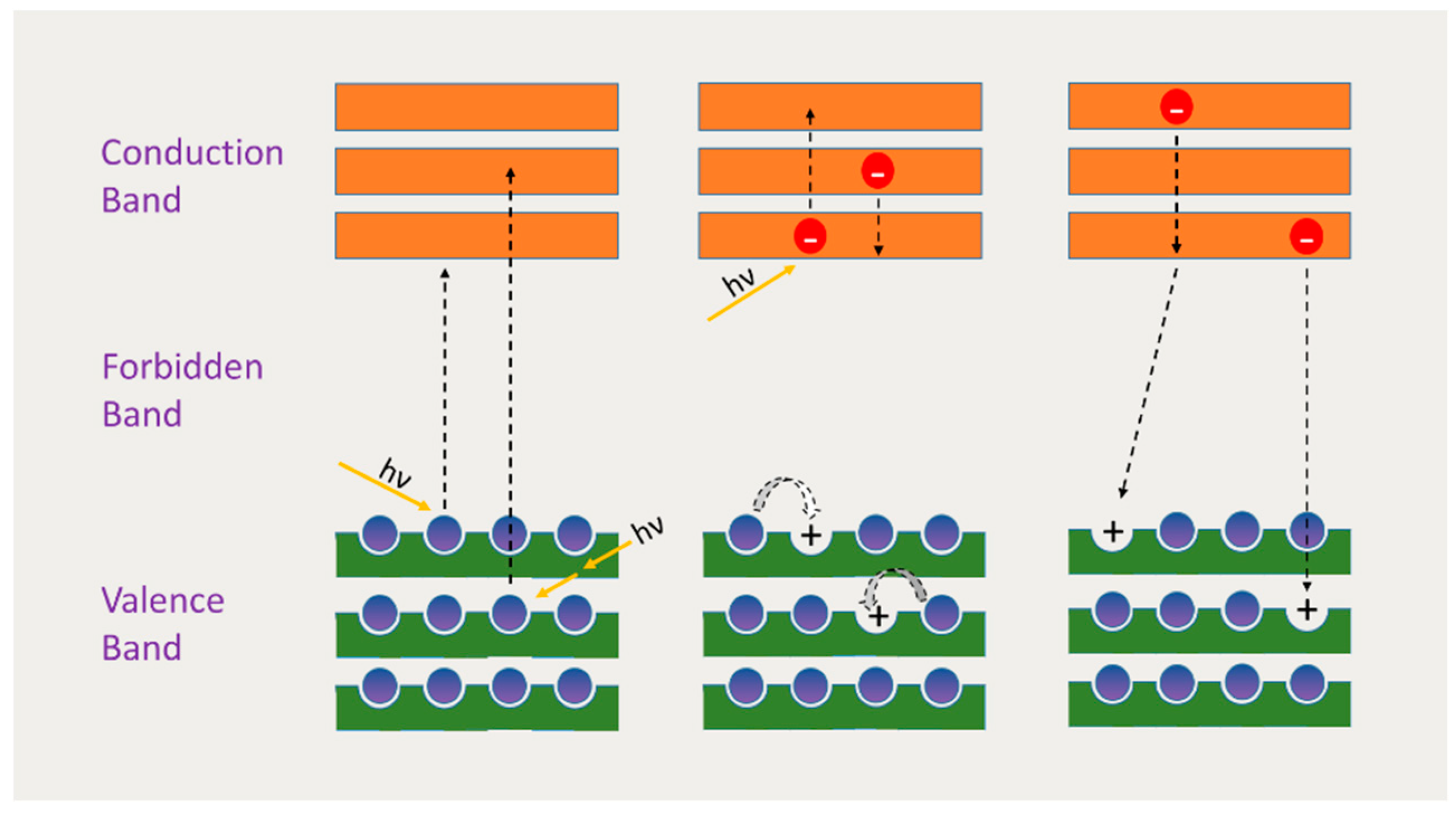
2. Optical Limiting Mechanisms
2.1. Reverse Saturable Absorption
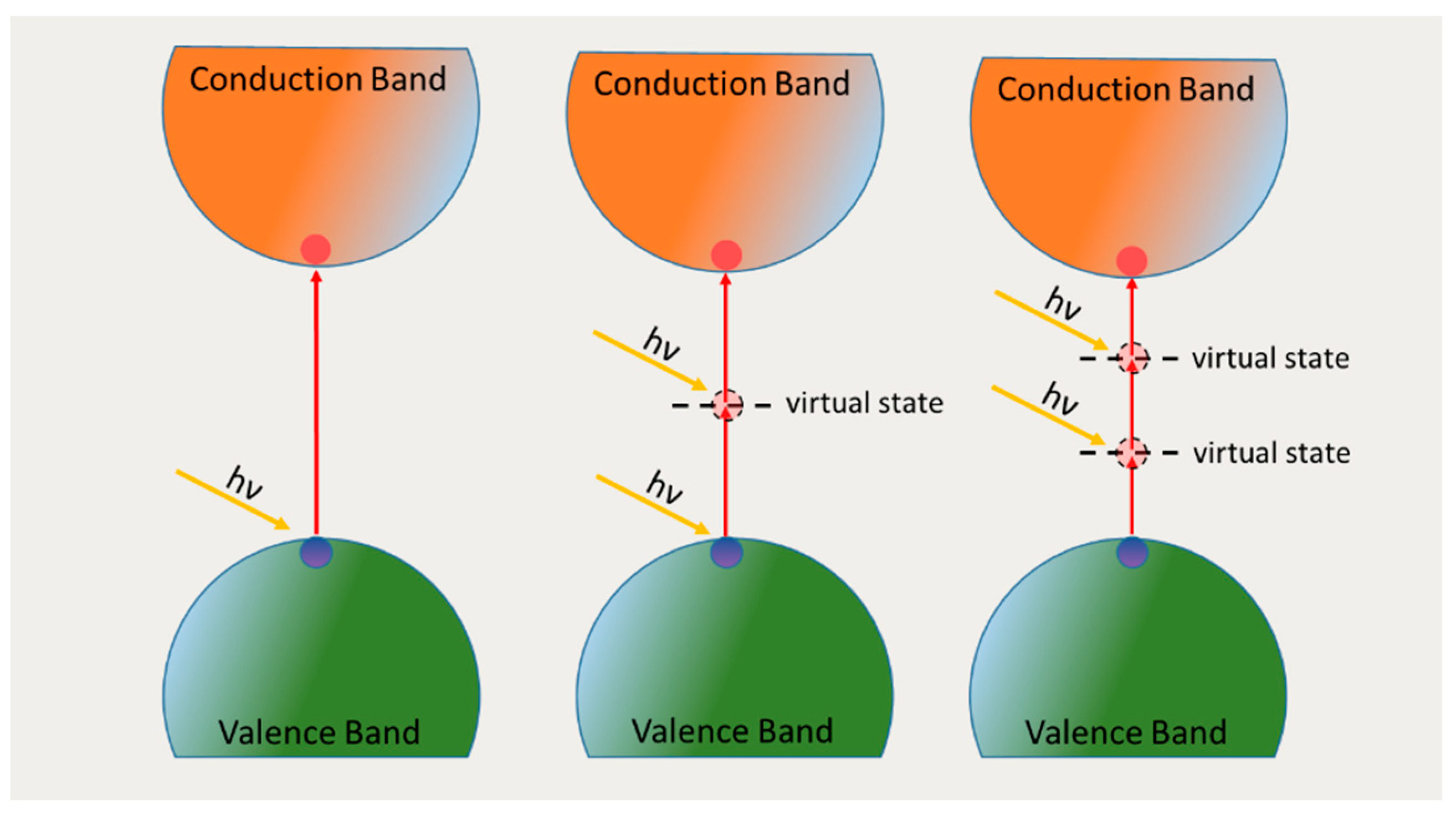
2.2. Multi-Photon Absorption
2.3. Free-Carrier Absorption
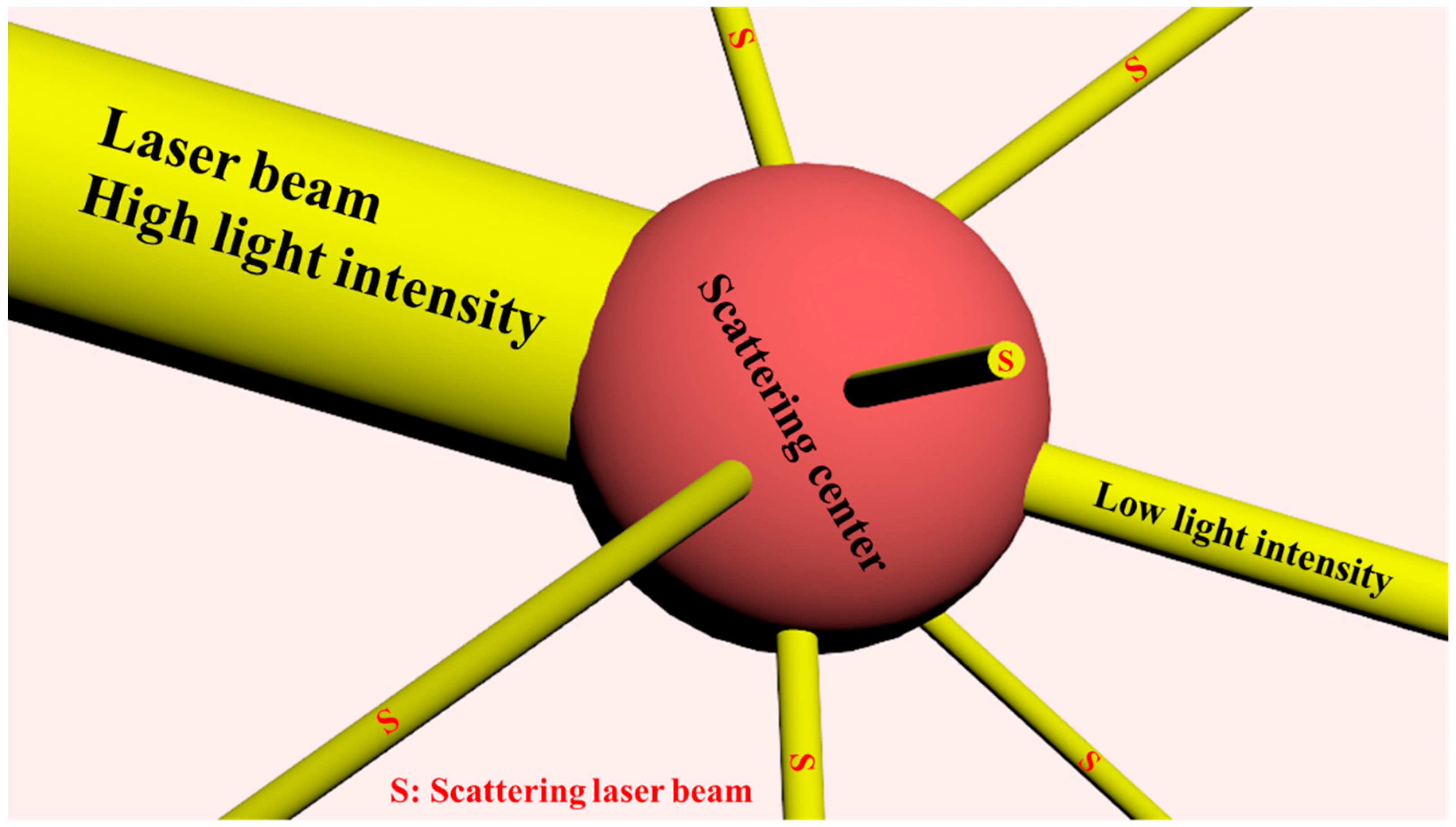
2.4. Nonlinear Scattering
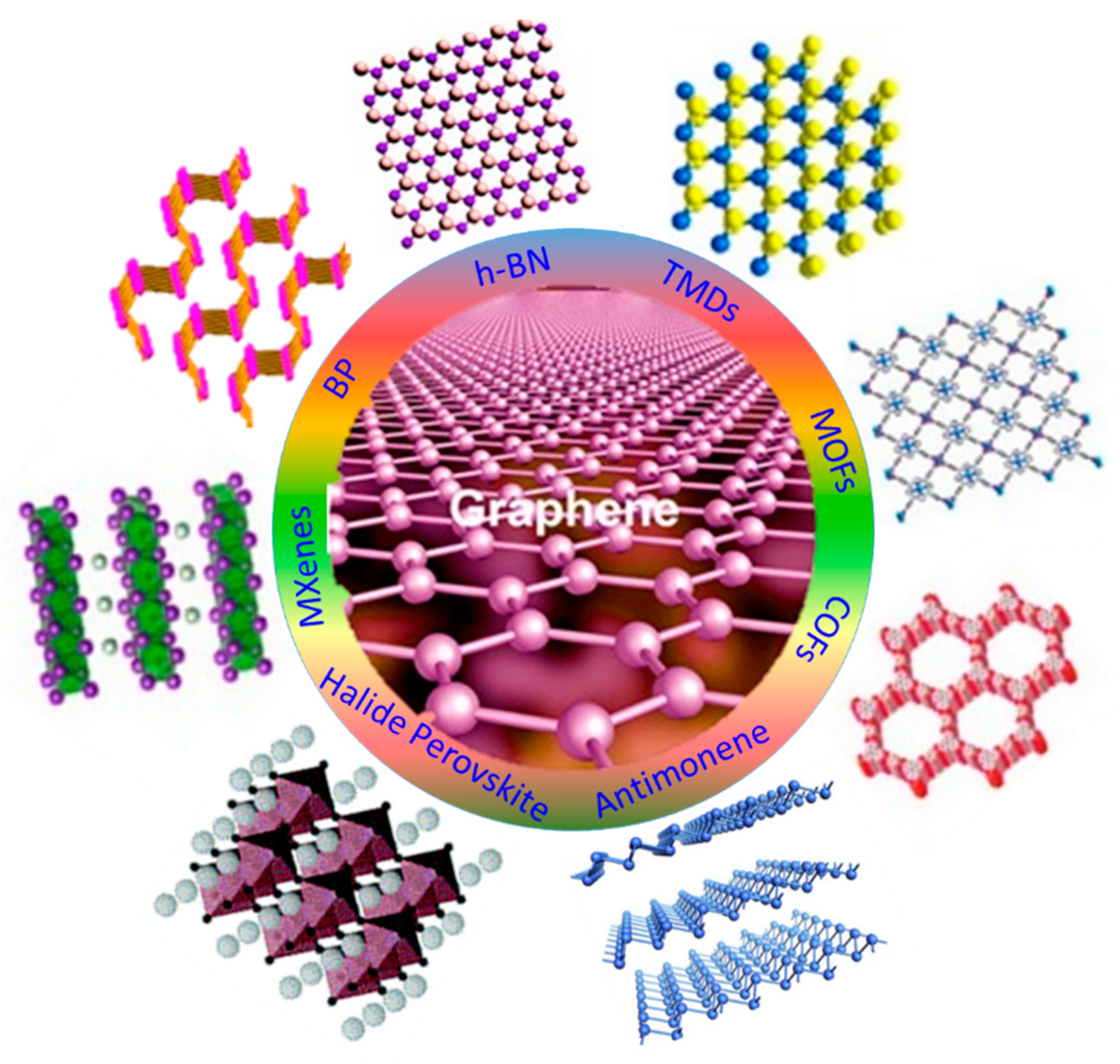
3. Two-Dimensional (2D) Nanomaterials for Optical Limiting
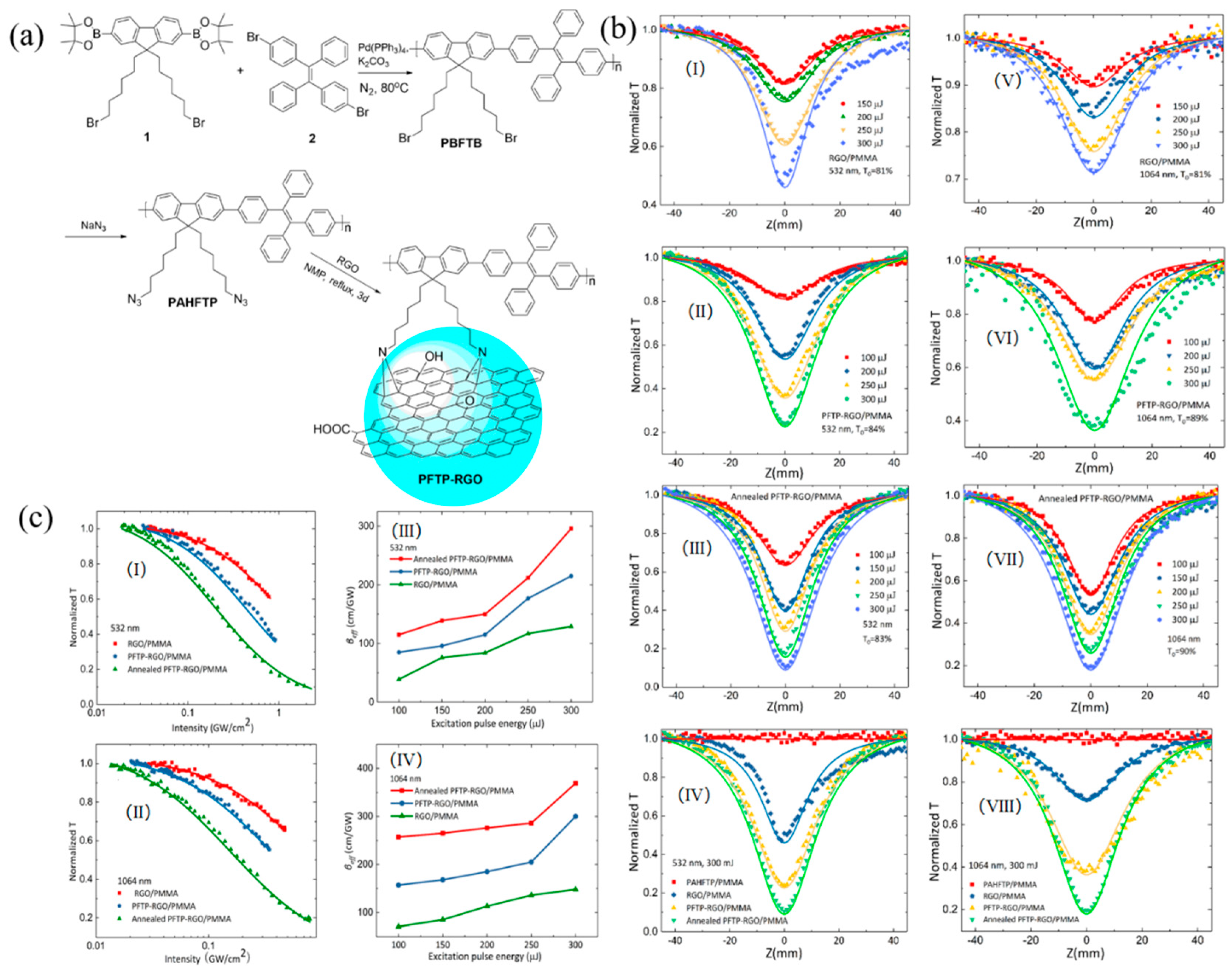
3.1. Graphene
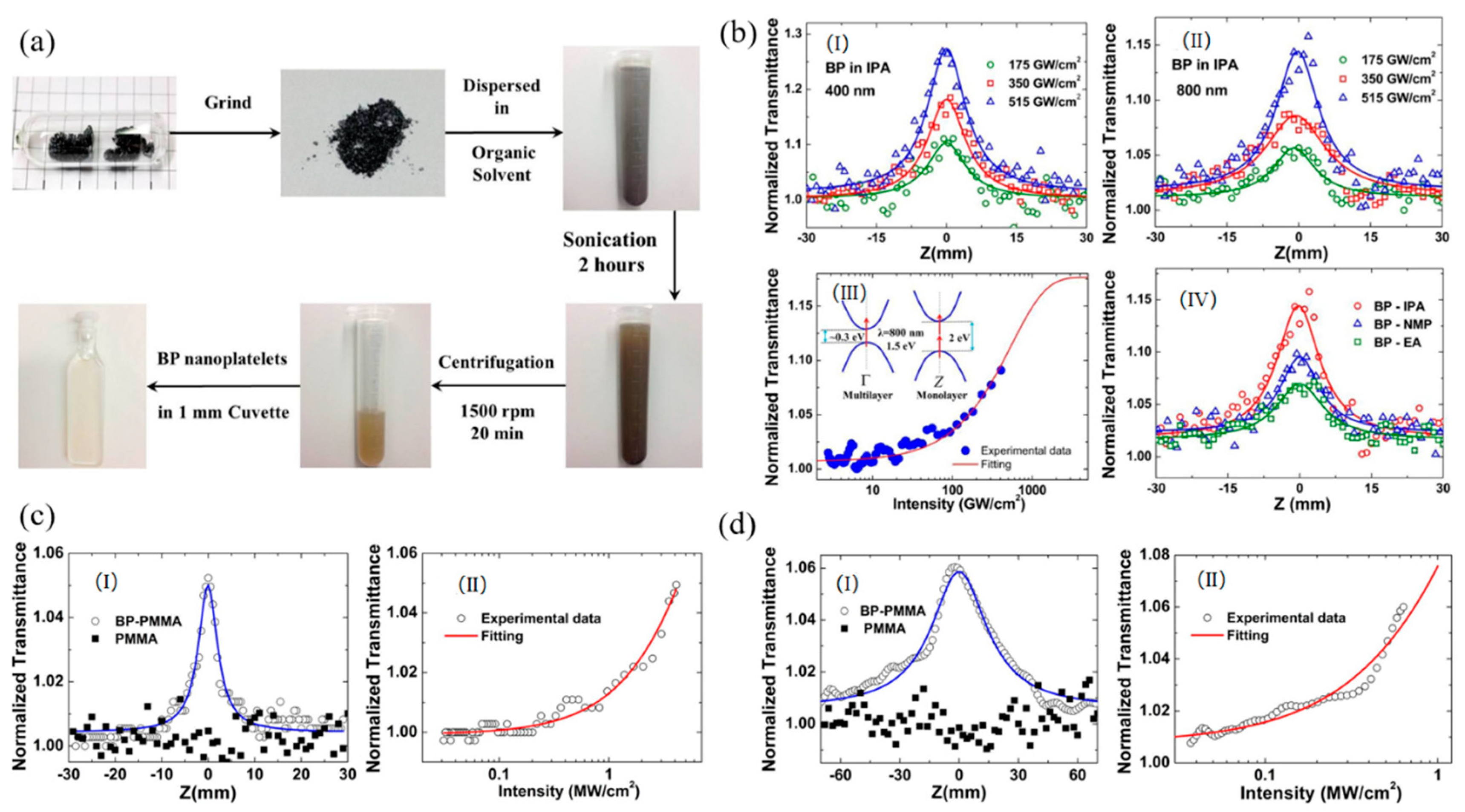
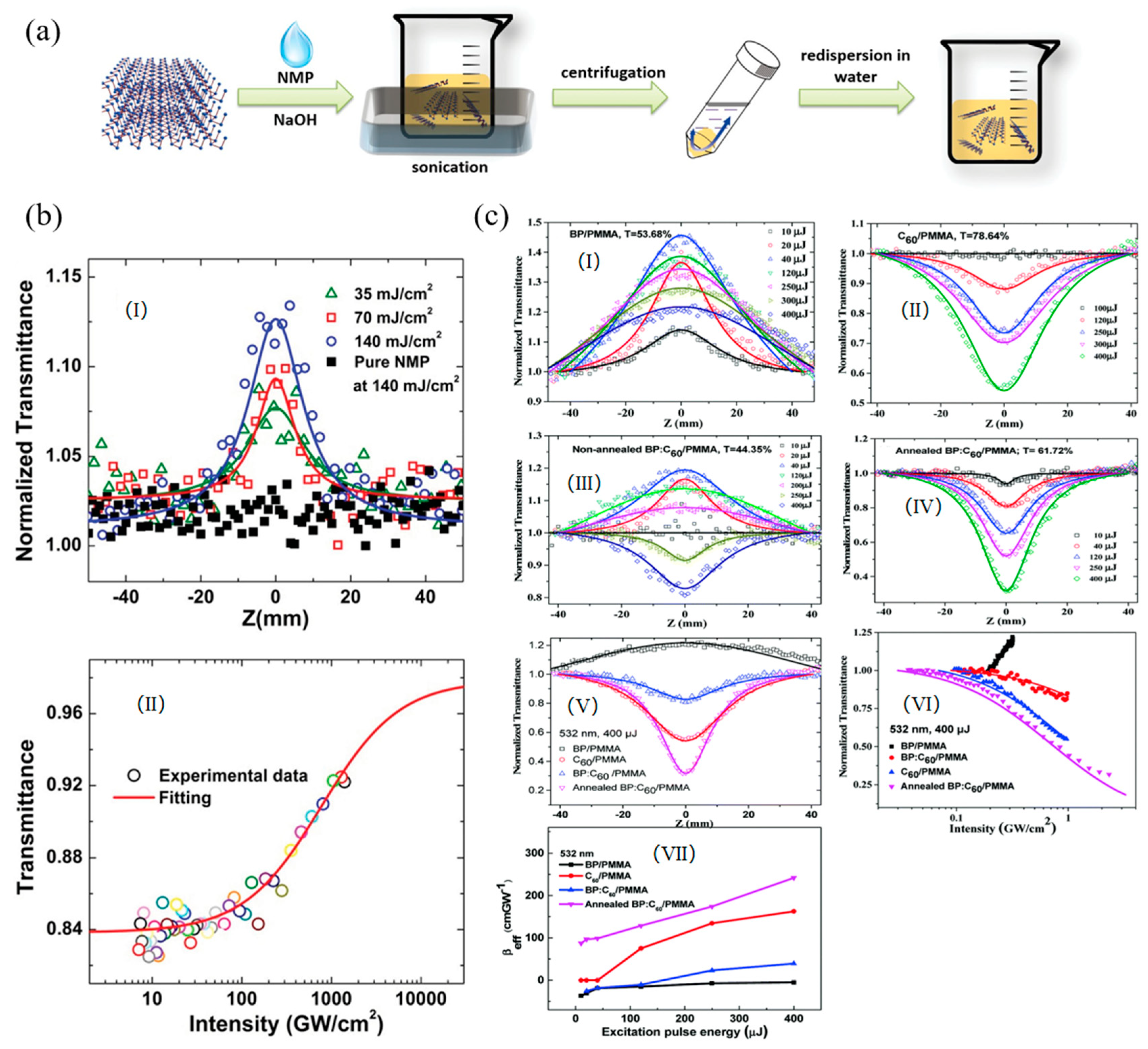
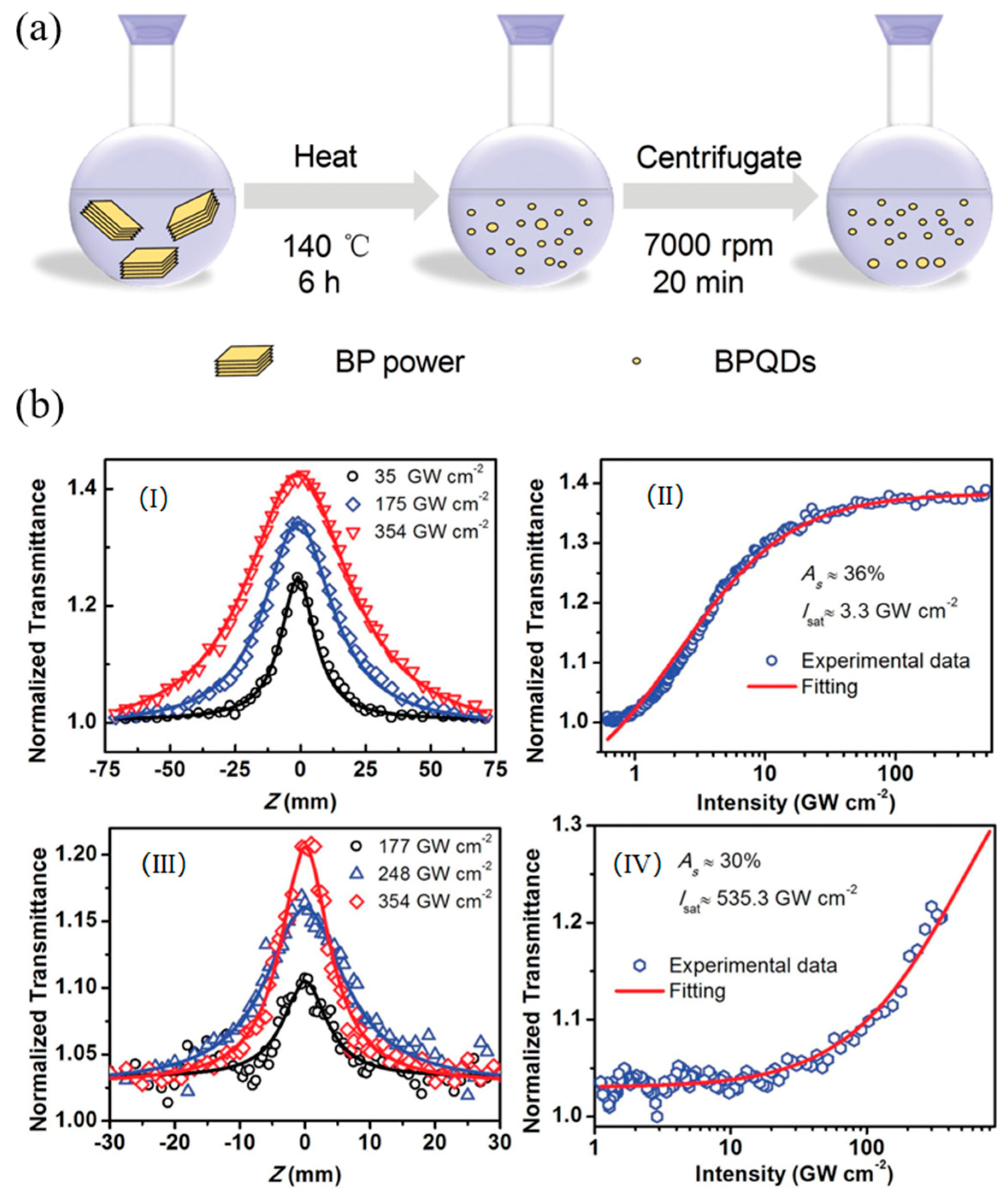
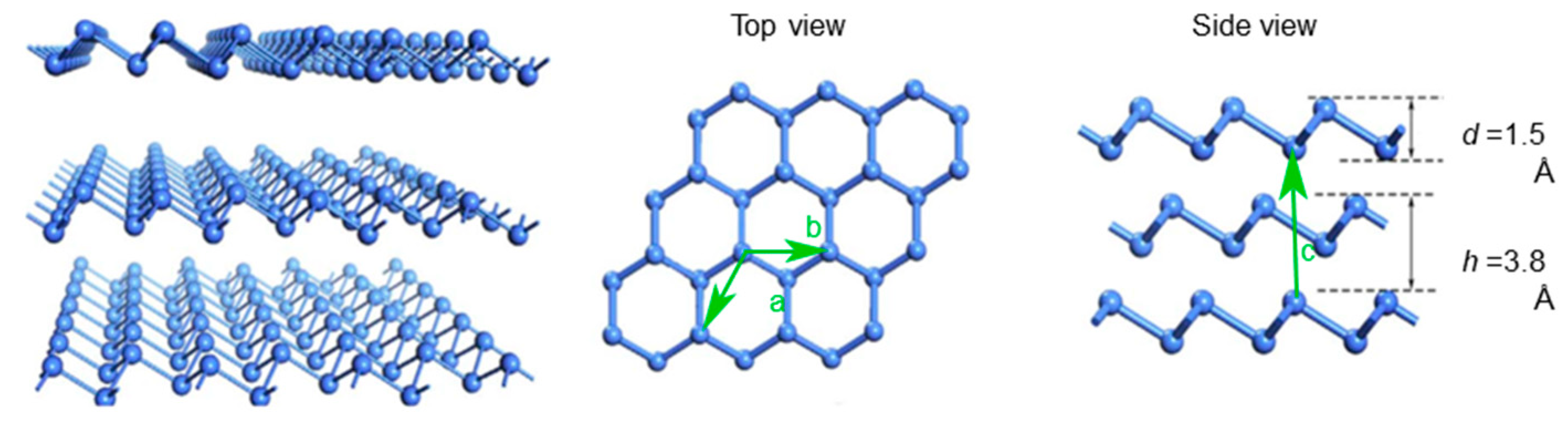
3.2. Black Phosphorus
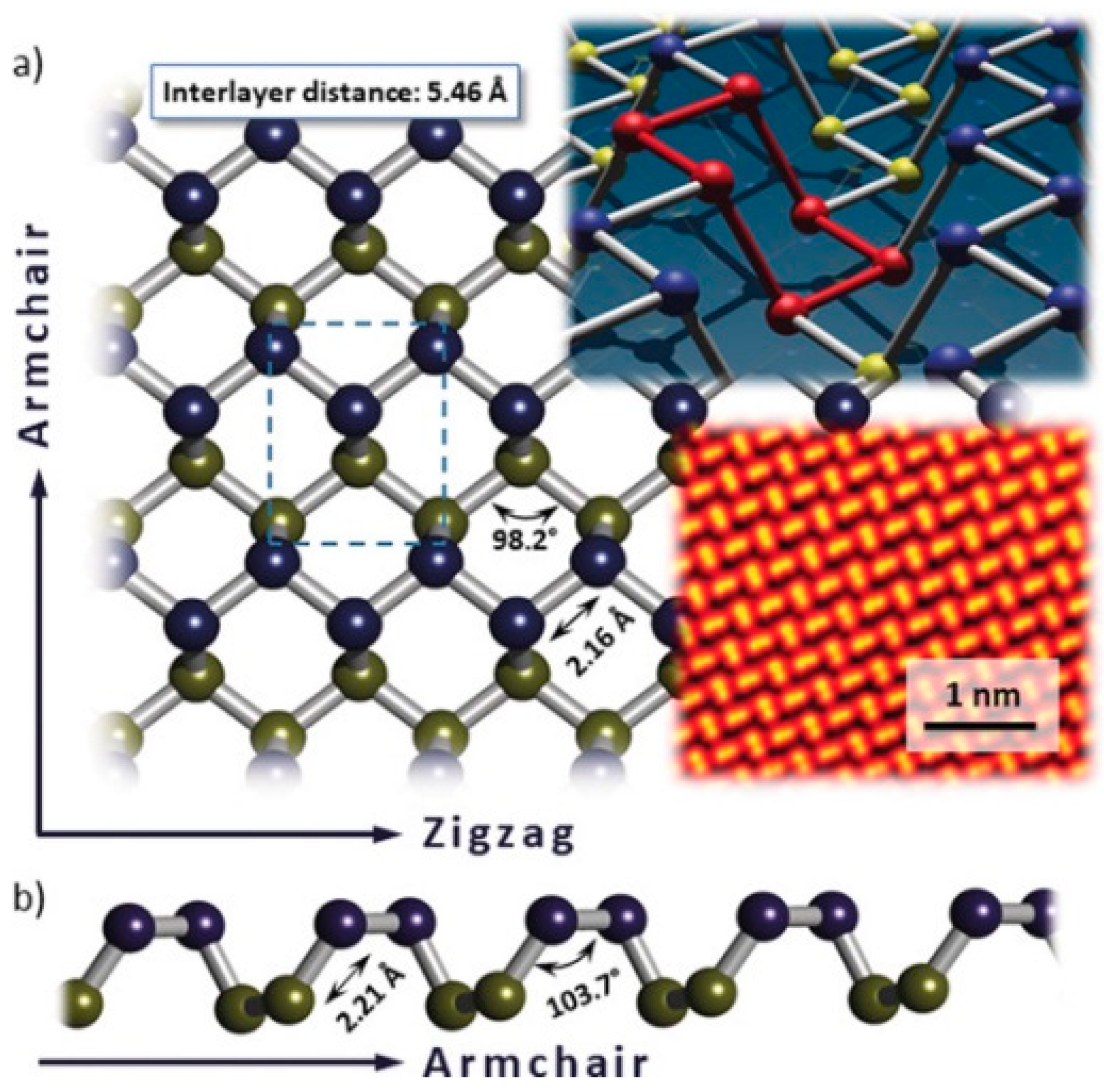
3.3. Antimonene
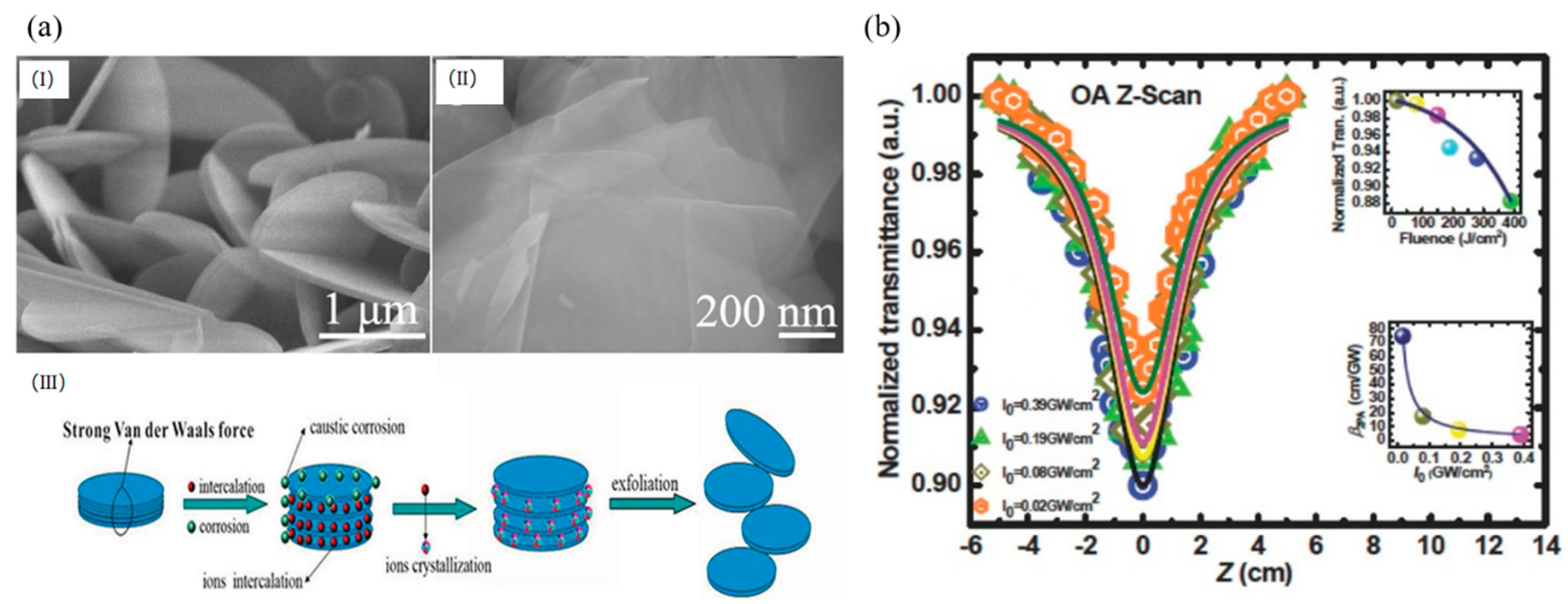
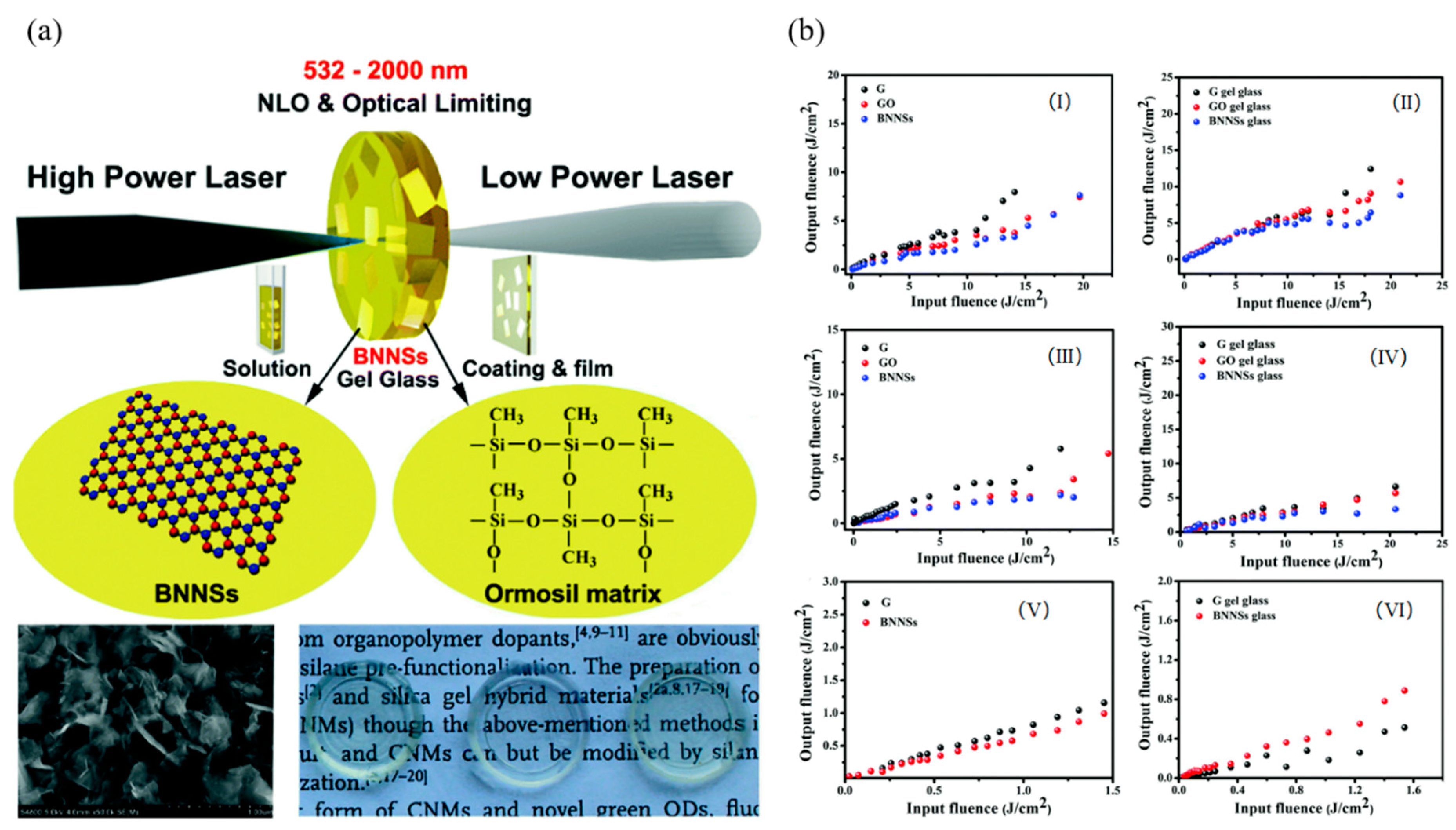
3.4. Hexagonal Boron Nitride Sheets (h-BN)
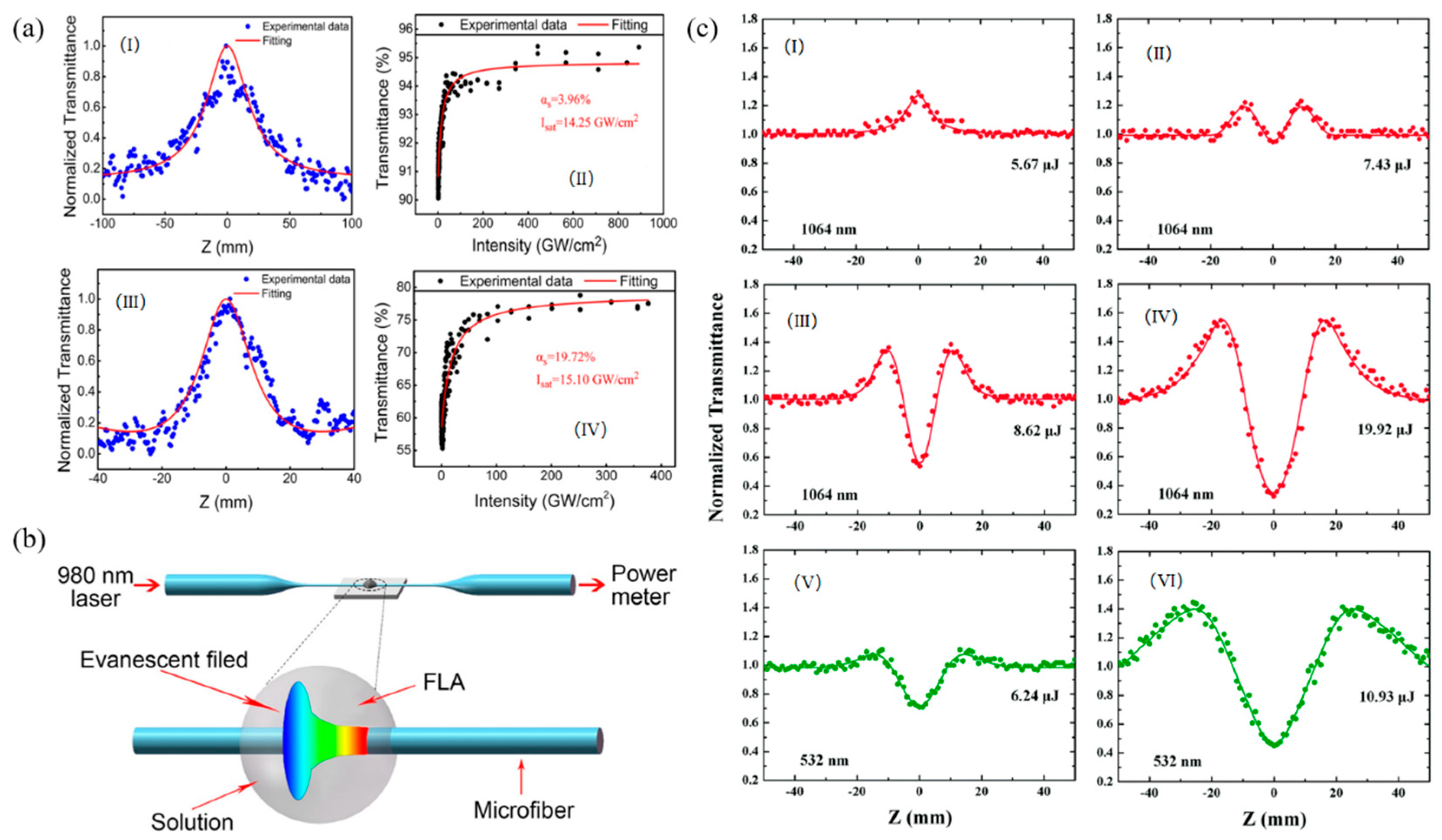
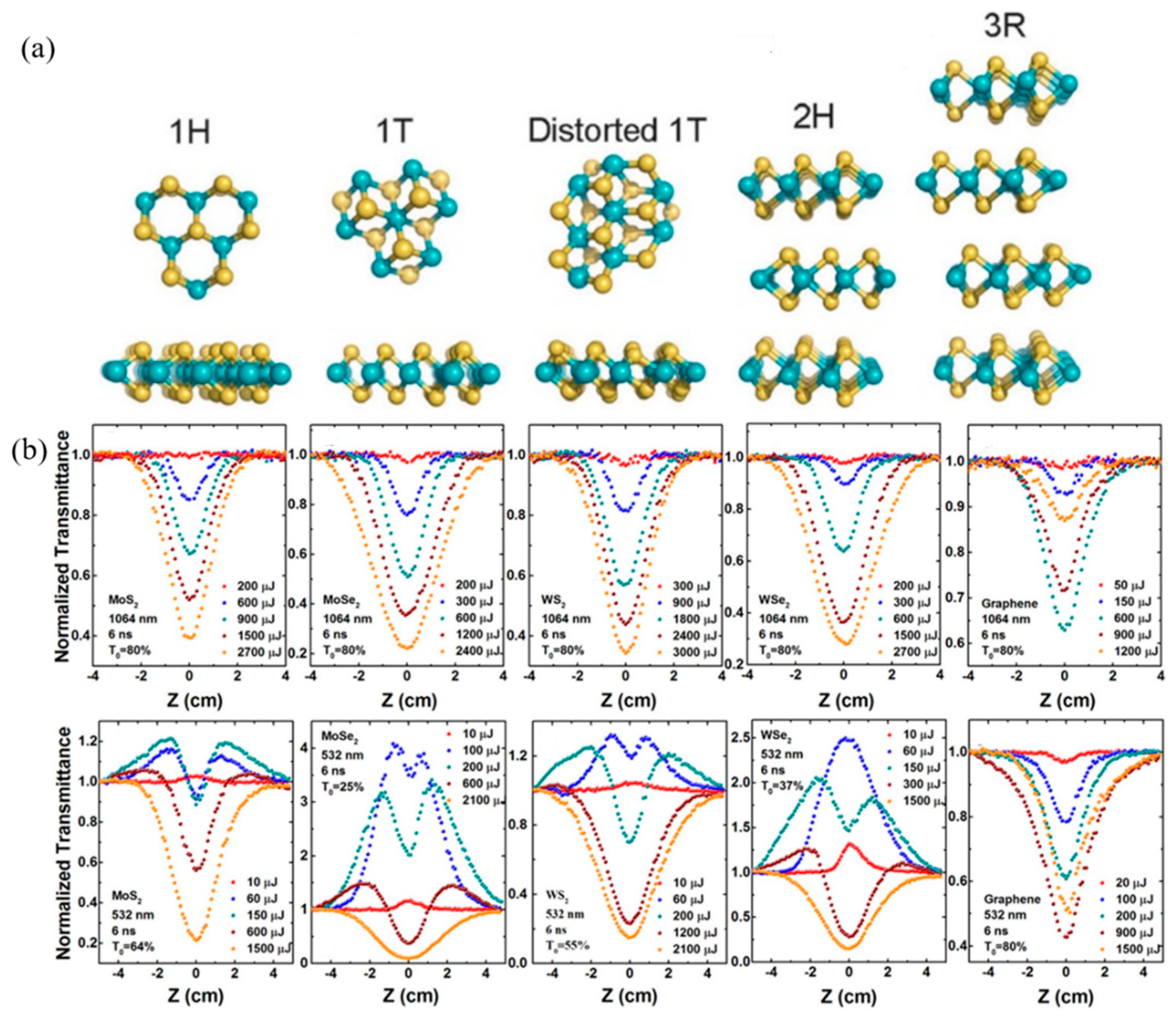
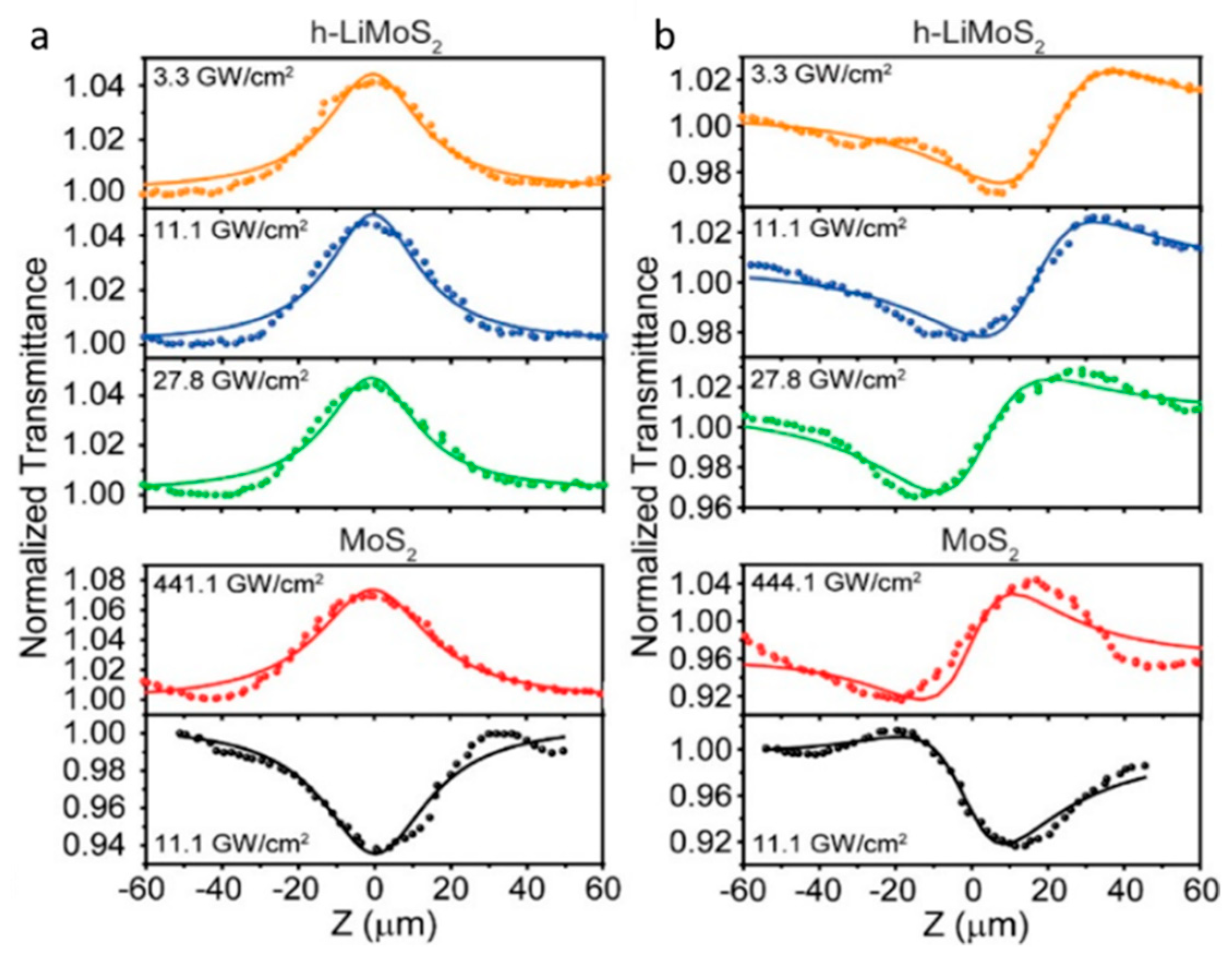
3.5. Transition Metal Dichalcogenides (TMDs)
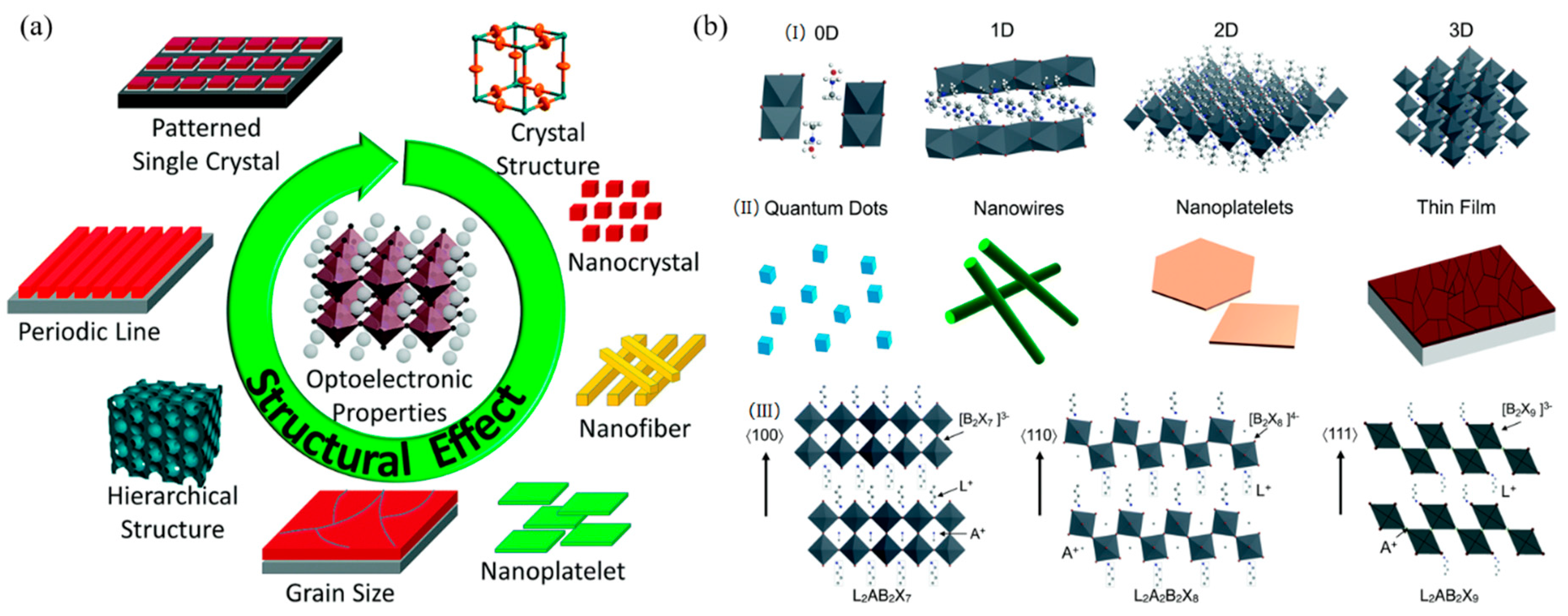
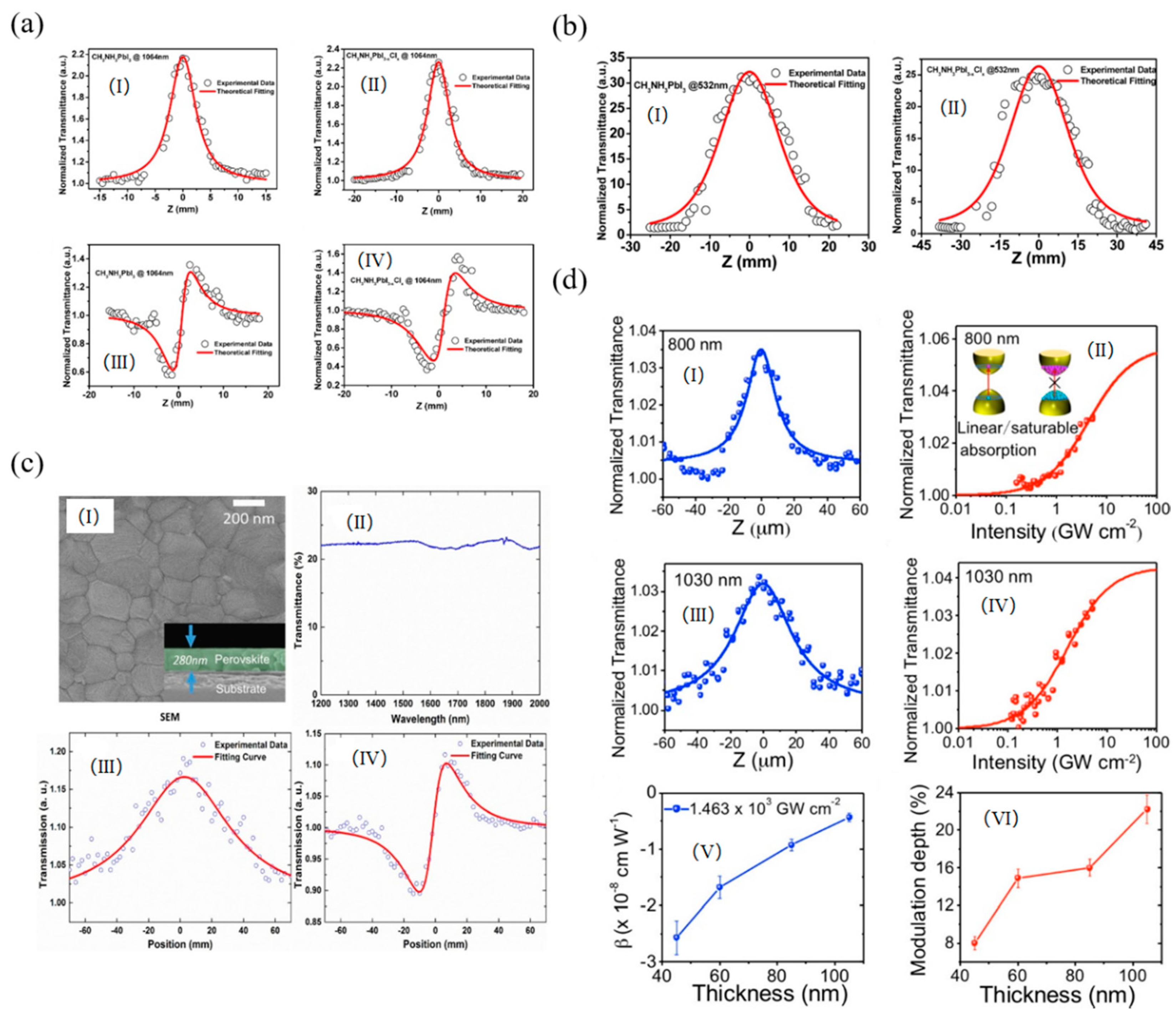
3.6. Halide Perovskites
4. Conclusion and Perspectives
Funding
Conflicts of Interest
References
- Ashkin, A. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef] [PubMed]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical Levitation by Radiation Pressure. Appl. Phys. Lett. 1971, 19, 283–285. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Desbois, J.; Gires, F.; Turnois, P. A new approach to picosecond laser pulse analysis shaping and coding. IEEE J. Quant. Electron. 1973, 9, 213–218. [Google Scholar] [CrossRef]
- The Nobel Prize in Physics 2018. NobelPrize.org. Nobel Media AB. Available online: https://www.nobelprize.org/prizes/physics/2018/press-release/ (accessed on 2 October 2018).
- Ashkin, A. Trapping of Atoms by Resonance Radiation Pressure. Phys. Rev. Lett. 1978, 40, 729–732. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical trapping and manipulation of viruses and bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M. Internal cell manipulation using infrared laser traps. Proc. Natl. Acad. Sci. USA 1989, 86, 7914–7918. [Google Scholar] [CrossRef]
- Ashkin, A.; Schütze, K.; Dziedzic, J.M.; Euteneuer, U.; Schliwa, M. Force generation of organelle transport measured in vivo by an infrared laser trap. Nature 1990, 348, 346–348. [Google Scholar] [CrossRef]
- Block, S.M.; Blair, D.F.; Berg, H.C. Compliance of bacterial flagella measured with optical tweezers. Nature 1989, 338, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Abbondanzieri, E.A.; Greenleaf, W.J.; Shaevitz, J.W.; Landick, R.; Block, S.M. Direct observation of base-pair stepping by RNA polymerase. Nature 2005, 438, 460–465. [Google Scholar] [CrossRef] [PubMed]
- Perkins, T.T.; Quake, S.R.; Smith, D.E.; Chu, S. Relaxation of a single DNA molecule observed by optical microscopy. Science 1994, 264, 822–826. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef]
- Sekundo, W.; Kunert, K.S.; Blum, M. Small incision corneal refractive surgery using the small incision lenticule extraction (SMILE) procedure for the correction of myopia and myopic astigmatism: Results of a 6 month prospective study. Br. J. Ophthalmol. 2011, 95, 335–339. [Google Scholar] [CrossRef]
- Lin, F.; Xu, Y.; Yang, Y. Comparison of the visual results after SMILE and femtosecond laser-assisted LASIK for myopia. J. Refract. Surg. 2014, 30, 248–254. [Google Scholar] [CrossRef] [PubMed]
- Pert, G.J. Output characteristics of amplified-stimulated-emission lasers. J. Opt. Soc. Am. B 1994, 11, 1425–1435. [Google Scholar] [CrossRef]
- Wang, H.; Yu, H.; Zhou, X.; Kan, Q.; Yuan, L.; Chen, W.; Wang, W.; Ding, Y.; Pan, J. High-power InGaAs/GaAs quantum-well laser with enhanced broad spectrum of stimulated emission. Appl. Phys. Lett. 2014, 105, 141101. [Google Scholar] [CrossRef]
- Apkarian, V.A. Stimulated emission as a major channel for the depopulation of laser-excited states in condensed media. Chem. Phys. Lett. 1984, 108, 150–154. [Google Scholar] [CrossRef]
- Hutchin, R.A. A New Physical Model for the Vacuum Field Based on Einstein’s Stimulated Emission Theory. Opt. Photon. J. 2015, 5, 109–112. [Google Scholar] [CrossRef]
- Johar Shakir, Q.J.; Patel, A.R. The use of lasers in periodontology. Int. J. Curr. Res. 2017, 9, 44806–44809. [Google Scholar]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Spangler, C.W. Recent development in the design of organic materials for optical power limiting. J. Mater. Chem. 1999, 9, 2013–2020. [Google Scholar] [CrossRef]
- Leite, R.C.C.; Porto, S.P.S.; Damen, T.C. The Thermal Lens Effect as a Power-Limiting Device. Appl. Phys. Lett. 1967, 10, 100–101. [Google Scholar] [CrossRef]
- Zhang, H. Ultrathin Two-Dimensional Nanomaterials. ACS Nano 2015, 9, 9451–9469. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Cao, X.; Wu, X.J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.H.; et al. Recent Advances in Ultrathin Two-Dimensional Nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, Z.; Zhang, Z.; Niu, W.; Li, C.; Yang, N.; Chen, B.; Zhang, H. Two-Dimensional Metal Nanomaterials: Synthesis, Properties, and Applications. Chem. Rev. 2018, 118, 6409–6455. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Gao, S.; Xie, Y. Atomically-thick two-dimensional crystals: Electronic structure regulation and energy device construction. Chem. Soc. Rev. 2014, 43, 530–546. [Google Scholar] [CrossRef]
- Acerce, M.; Voiry, D.; Chhowalla, M. Metallic 1T phase MoS2 nanosheets as supercapacitor electrode materials. Nat. Nanotechnol. 2015, 10, 313–318. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Yu, G.; Pan, L.; Liu, N.; McDowell, M.T.; Bao, Z.; Cui, Y. Stable Li-ion battery anodes by in-situ polymerization of conducting hydrogel to conformally coat silicon nanoparticles. Nat. Commun. 2013, 4, 1943. [Google Scholar] [CrossRef]
- Zhang, M.; Zhu, Y.; Wang, X.; Feng, Q.; Qiao, S.; Wen, W.; Chen, Y.; Cui, M.; Zhang, J.; Cai, C.; et al. Controlled Synthesis of ZrS2 Monolayer and Few Layers on Hexagonal Boron Nitride. J. Am. Chem. Soc. 2015, 137, 7051–7054. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lin, C.; Zhang, F.X.; Jin, J. Phase Transformation Guided Single-Layer β-Co(OH)2 Nanosheets for Pseudocapacitive Electrodes. ACS Nano 2014, 8, 3724–3734. [Google Scholar] [CrossRef] [PubMed]
- Roy-Mayhew, J.D.; Aksay, I.A. Graphene materials and their use in dye-sensitized solar cells. Chem. Rev. 2014, 114, 6323–6348. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lau, S.P.; Yan, F. Functionalized graphene and other two-dimensional materials for photovoltaic devices: Device design and processing. Chem. Soc. Rev. 2015, 44, 5638–5679. [Google Scholar] [CrossRef]
- Wan, X.; Long, G.; Huang, L.; Chen, Y. Graphene—A promising material for organic photovoltaic cells. Adv. Mater. 2011, 23, 5342–5358. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Pei, S.; Ma, L.; Cheng, H.M. 25th anniversary article: Carbon nanotube- and graphene-based transparent conductive films for optoelectronic devices. Adv. Mater. 2014, 26, 1958–1991. [Google Scholar] [CrossRef]
- Puzzo, D.P.; Helander, M.G.; O’Brien, P.G.; Wang, Z.; Soheilnia, N.; Kherani, N.; Lu, Z.; Ozin, G.A. Organic light-emitting diode microcavities from transparent conducting metal oxide photonic crystals. Nano Lett. 2011, 11, 1457–1462. [Google Scholar] [CrossRef]
- Wu, T.L.; Yeh, C.H.; Hsiao, W.T.; Huang, P.Y.; Huang, M.J.; Chiang, Y.H.; Cheng, C.H.; Liu, R.S.; Chiu, P.W. High-Performance Organic Light-Emitting Diode with Substitutionally Boron-Doped Graphene Anode. ACS Appl. Mater. Interfaces 2017, 9, 14998–15004. [Google Scholar] [CrossRef]
- Kim, J.S.; Jeon, P.J.; Lee, J.; Choi, K.; Lee, H.S.; Cho, Y.; Lee, Y.T.; Hwang, D.K.; Im, S. Dual Gate Black Phosphorus Field Effect Transistors on Glass for NOR Logic and Organic Light Emitting Diode Switching. Nano Lett. 2015, 15, 5778–5783. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, G.; Chen, Y.; Zeng, L.J.; Zhu, C.X.; Neoh, K.G.; Wang, C.; Kang, E.T. Conjugated polymer-grafted reduced graphene oxide for nonvolatile rewritable memory. Chem. Eur. J. 2011, 17, 13646–13652. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Zhang, B.; Cao, Y.; Chen, Y. Solution-processable poly(N-vinylcarbazole)-covalently grafted MoS2 nanosheets for nonvolatile rewritable memory devices. Nanoscale 2017, 9, 2449–2456. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Zhuang, X.; Liu, B.; Wang, L.; Gu, L.; Song, S.; Zhang, B.; Chen, Y. In Situ Synthesis and Characterization of Poly(aryleneethynylene)-Grafted Reduced Graphene Oxide. Chem. Eur. J. 2016, 22, 2247–2252. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Zhang, B.; Cao, Y.; Yang, X.; Gu, J.; Chen, Y. Conjugated polymer covalently modified graphene oxide quantum dots for ternary electronic memory devices. Nanoscale 2017, 9, 10610–10618. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Hu, J.; Zhu, S.; Lu, J.; Zhu, H. Synergistically Enhanced Optical Limiting Property of Graphene Oxide Hybrid Materials Functionalized with Pt Complexes. ACS Appl. Mater. Interfaces 2017, 9, 33029–33040. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Y.; Chen, Y.; Wang, J.; Zhang, B.; Zhang, J.; Blau, W.J. Graphene oxide covalently functionalized with zinc phthalocyanine for broadband optical limiting. Carbon 2011, 49, 1900–1905. [Google Scholar] [CrossRef]
- Chen, Y.; Bai, T.; Dong, N.; Fan, F.; Zhang, S.; Zhuang, X.; Sun, J.; Zhang, B.; Zhang, X.; Wang, J.; et al. Graphene and its derivatives for laser protection. Prog. Mater. Sci. 2016, 84, 118–157. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, N.; Jiang, P.; Wang, K.; Wang, J.; Chen, Y. Reduced Graphene Oxide Chemically Modified with Aggregation-Induced Emission Polymer for Solid-State Optical Limiter. Chem. Eur. J. 2018, 24, 19317–19322. [Google Scholar] [CrossRef]
- Shi, M.; Dong, N.; He, N.; Wan, Y.; Cheng, H.; Han, M.; Wang, J.; Chen, Y. MoS2 nanosheets covalently functionalized with polyacrylonitrile: Synthesis and broadband laser protection performance. J. Mater. Chem. C 2017, 5, 11920–11926. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Zhou, L.; Zhang, J.; Li, F.; Li, K.; Yang, H. An all-liquid crystal based high-performance laser protection system via linear/nonlinear dual-mechanisms. Chem. Commun. 2018, 54, 397–400. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Liang, X.; Le, Z.; Xiao, J.; Yu, L.; Li, F.; Cao, H.; Li, K.; Yang, Z.; et al. Unconventional High-Performance Laser Protection System Based on Dichroic Dye-Doped Cholesteric Liquid Crystals. Sci. Rep. 2017, 7, 42955. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Self-activating liquid crystal devices for smart laser protection. Liq. Cryst. 2016, 43, 2062. [Google Scholar] [CrossRef]
- Wang, K.; Szydlowska, B.M.; Wang, G.; Zhang, X.; Wang, J.J.; Magan, J.J.; Zhang, L.; Coleman, J.N.; Wang, J.; Blau, W.J. Ultrafast Nonlinear Excitation Dynamics of Black Phosphorus Nanosheets from Visible to Mid-Infrared. ACS Nano 2016, 10, 6923–6932. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.W.; Liu, S.; Zeng, B.W.; Huang, H.; Xiao, J.; Li, J.B.; Long, M.Q.; Xiao, S.; Yu, X.F.; Gao, Y.L.; et al. Ultraviolet saturable absorption and ultrafast carrier dynamics in ultrasmall black phosphorus quantum dots. Nanoscale 2017, 9, 4683–4690. [Google Scholar] [CrossRef]
- Huang, J.; Dong, N.; Zhang, S.; Sun, Z.; Zhang, W.; Wang, J. Nonlinear Absorption Induced Transparency and Optical Limiting of Black Phosphorus Nanosheets. ACS Photon. 2017, 4, 3063–3070. [Google Scholar] [CrossRef]
- Lu, L.; Tang, X.; Cao, R.; Wu, L.; Li, Z.; Jing, G.; Dong, B.; Lu, S.; Li, Y.; Xiang, Y.; et al. Broadband Nonlinear Optical Response in Few-Layer Antimonene and Antimonene Quantum Dots: A Promising Optical Kerr Media with Enhanced Stability. Adv. Opt. Mater. 2017, 5, 1700301. [Google Scholar] [CrossRef]
- Karamanis, P.; Otero, N.; Pouchan, C. Unleashing the quadratic nonlinear optical responses of graphene by confining white-graphene (h-BN) sections in its framework. J. Am. Chem. Soc. 2014, 136, 7464–7473. [Google Scholar] [CrossRef]
- Subrata, B.; Chandra, S.T.; Soumya, V.; Arup, K.K.; Udit, C.; Pathik, K.; Pulickel, M.A. Nonlinear Optical Properties and Temperature Dependent Photoluminescence in hBN-GO Heterostructure 2D Material. J. Phys. Chem. C 2017, 121, 8060–8069. [Google Scholar]
- Saouma, F.O.; Stoumpos, C.C.; Wong, J.; Kanatzidis, M.G.; Jang, J.I. Selective enhancement of optical nonlinearity in two-dimensional organic-inorganic lead iodide perovskites. Nat. Commun. 2017, 8, 742. [Google Scholar] [CrossRef]
- Walters, G.; Sutherland, B.; Hoogland, S.; Shi, D.; Comin, R.; Sellan, D.; Bake, O.; Sargent, E. Two-Photon Absorption in Organometallic Bromide Perovskites. ACS Nano 2015, 9, 9340–9346. [Google Scholar] [CrossRef]
- Wei, T.-C.; Mokkapati, S.; Li, T.-Y.; Lin, C.-H.; Lin, G.-R.; Jagadish, C.; He, J.-H. Nonlinear Absorption Applications of CH3NH3PbBr3 Perovskite Crystals. Adv. Funct. Mater. 2018, 28, 1707175. [Google Scholar] [CrossRef]
- Nie, Z.; Trovatello, C.; Pogna, E.A.A.; Dal Conte, S.; Miranda, P.B.; Kelleher, E.; Zhu, C.; Turcu, I.C.E.; Xu, Y.; Liu, K.; et al. Broadband nonlinear optical response of monolayer MoSe2 under ultrafast excitation. Appl. Phys. Lett. 2018, 112, 031108. [Google Scholar] [CrossRef]
- Yin, J.; Chen, H.; Lu, W.; Liu, M.; Li, I.L.; Zhang, M.; Zhang, W.; Wang, J.; Xu, Z.; Yan, P.; et al. Large-area and highly crystalline MoSe2 for optical modulator. Nanotechnology 2017, 28, 484001. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, K.; Roy, N.; Philip, R.; Park, T.J. Anomalous growth of multi-phased and multi-dimensional Manganese oxide–Metal (Fe, Co and Ni) oxide nanostructures: Synthesis and optical limiting properties. J. Alloys Comp. 2014, 611, 82–90. [Google Scholar] [CrossRef]
- Anand, B.; Kaniyoor, A.; Swain, D.; Baby, T.T.; Venugopal Rao, S.; Sankara Sai, S.S.; Ramaprabhu, S.; Philip, R. Enhanced optical limiting and carrier dynamics in metal oxide-hydrogen exfoliated graphene hybrids. J. Mater. Chem. C 2014, 2, 10116–10123. [Google Scholar] [CrossRef]
- Ren, H.; Shehzad, F.K.; Zhou, Y.; Zhang, L.; Iqbal, A.; Long, Y. Incorporation of Keplerate-type Mo-O based macroanions into Zn2Al-LDH results in the formation of all-inorganic composite films with remarkable third-order optical nonlinearity. Dalton. Trans. 2018, 47, 6184–6188. [Google Scholar] [CrossRef]
- Zhu, G.; Long, Y.; Ren, H.; Zhou, Y.; Zhang, L.; Shi, Z.; Shehzad, F.K.; Asif, H.M. Notable Third-Order Optical Nonlinearities Realized in Layer-by-Layer Assembled Composite Films by Intercalation of Porphyrin/Polyoxometalate into Layered Double Hydroxide. J. Phys. Chem. C 2016, 120, 22549–22557. [Google Scholar] [CrossRef]
- Medishetty, R.; Zareba, J.K.; Mayer, D.; Samoc, M.; Fischer, R.A. Nonlinear optical properties, upconversion and lasing in metal-organic frameworks. Chem. Soc. Rev. 2017, 46, 4976–5004. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, L.; Liu, S.; Zhang, Y.; He, Z.; Li, W.; Zhang, F.; Shi, Y.; Lü, W.; Li, Y.; et al. Ultrathin Metal-Organic Framework: An Emerging Broadband Nonlinear Optical Material for Ultrafast Photonics. Adv. Opt. Mater. 2018, 6, 1800561. [Google Scholar] [CrossRef]
- Cao, Y.; Tian, X.; Gu, J.; Liu, B.; Zhang, B.; Song, S.; Fan, F.; Chen, Y. Covalent Functionalization of Black Phosphorus with Conjugated Polymer for Information Storage. Angew. Chem. Int. Ed. 2018, 57, 4543–4548. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, Z.; Zhang, L.; Zheng, X.; Xiao, L.; Jia, S.; Wang, J. A novel electrically controllable volatile memory device based on few-layer black phosphorus. J. Mater. Chem. C 2018, 6, 2460–2466. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, T.L.; Xiao, L.; Kolaczkowski, M.A.; Zhang, L.; Klivansky, L.M.; Altoe, V.; Tian, B.; Guo, J.; Peng, X.; et al. Facile integration of low-cost black phosphorus in solution-processed organic solar cells with improved fill factor and device efficiency. Nano Energy 2018, 53, 345–353. [Google Scholar] [CrossRef]
- Shirk, J.S.; Pong, R.G.S.; Flom, S.R.; Heckmann, H.; Hanack, M. Effect of Axial Substitution on the Optical Limiting Properties of Indium Phthalocyanines. J. Phys. Chem. A 2000, 104, 1438–1449. [Google Scholar] [CrossRef]
- Chen, Y.; Hanack, M.; Araki, Y.; Ito, O. Axially modified gallium phthalocyanines and naphthalocyanines for optical limiting. Chem. Soc. Rev. 2005, 34, 517–529. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hanack, M.; Blau, W.J.; Dini, D.; Liu, Y.; Lin, Y.; Bai, J. Soluble axially substituted phthalocyanines: Synthesis and nonlinear optical response. J. Mater. Sci. 2006, 41, 2169–2185. [Google Scholar] [CrossRef]
- Tutt, L.W.; Boggess, T.F. A review of optical limiting mechanisms and devices using organics, fullerenes, semiconductors and other materials. Prog. Quant. Electron. 1993, 17, 299–338. [Google Scholar] [CrossRef]
- O’Flaherty, S.M.; Hold, S.V.; Cook, M.J.; Torres, T.; Chen, Y.; Hanack, M.; Blau, W.J. Molecular engineering of peripherally and axially modified phthalocyanines for optical limiting and nonlinear optics. Adv. Mater. 2003, 15, 19–32. [Google Scholar] [CrossRef]
- He, G.S.; Tan, L.S.; Zheng, Q.D.; Prasad, P.N. Multiphoton Absorbing Materials: Molecular Designs, Characterizations, and Applications. Chem. Rev. 2008, 108, 1245–1330. [Google Scholar] [CrossRef]
- Boggess, T.F.; Bohnert, K.M.; Mansour, K.; Moss, S.C.; Boyd, I.W.; Smirl, A.L. Simultaneous measurement of the two-photon coefficient and free-carrier cross section above the bandgap of crystalline silicon. IEEE J. Quant. Electron. 1986, 22, 360–368. [Google Scholar] [CrossRef]
- Feng, M.; Zhan, H.; Chen, Y. Nonlinear optical and optical limiting properties of graphene families. Appl. Phys. Lett. 2010, 96, 033107. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Blau, W.J. Carbon nanotubes and nanotube composites for nonlinear optical devices. J. Mater. Chem. 2009, 19, 7425–7443. [Google Scholar] [CrossRef]
- Wang, J.; Hernandez, Y.; Lotya, M.; Coleman, J.N.; Blau, W.J. Broadband Nonlinear Optical Response of Graphene Dispersions. Adv. Mater. 2009, 21, 2430–2435. [Google Scholar] [CrossRef]
- Belousova, I.M.; Mironova, N.G.; Scobelev, A.G.; Yur’ev, M.S. The investigation of nonlinear optical limiting by aqueous suspensions of carbon nanoparticles. Opt. Commun. 2004, 235, 445–452. [Google Scholar] [CrossRef]
- Lei, W.; Liu, G.; Zhang, J.; Liu, M. Black phosphorus nanostructures: Recent advances in hybridization, doping and functionalization. Chem. Soc. Rev. 2017, 46, 3492–3509. [Google Scholar] [CrossRef] [PubMed]
- Abate, Y.; Akinwande, D.; Gamage, S.; Wang, H.; Snure, M.; Poudel, N.; Cronin, S.B. Recent Progress on Stability and Passivation of Black Phosphorus. Adv. Mater. 2018, 30, 1704749. [Google Scholar] [CrossRef] [PubMed]
- Castellanos-Gomez, A.; Vicarelli, L.; Prada, E.; Island, J.O.; Narasimha-Acharya, K.L.; Blanter, S.I.; Groenendijk, D.J.; Buscema, M.; Steele, G.A.; Alvarez, J.V.; et al. Isolation and characterization of few-layer black phosphorus. 2D Mater. 2014, 1, 025001. [Google Scholar] [CrossRef]
- Hirsch, A.; Hauke, F. Post-Graphene 2D Chemistry: The Emerging Field of Molybdenum Disulfide and Black Phosphorus Functionalization. Angew. Chem. Int. Ed. 2018, 57, 4338–4354. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.B.; Miao, L.L.; Guo, Z.N.; Qi, X.; Zhao, C.J.; Zhang, H.; Wen, S.C.; Tang, D.Y.; Fan, D.Y. Broadband nonlinear optical response in multi-layer black phosphorus: An emerging infrared and mid-infrared optical material. Opt. Express. 2015, 23, 11183–11194. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zhang, H.; Lu, S.; Wang, Z.; Tang, S.; Shao, J.; Sun, Z.; Xie, H.; Wang, H.; Yu, X.-F.; et al. From Black Phosphorus to Phosphorene: Basic Solvent Exfoliation, Evolution of Raman Scattering, and Applications to Ultrafast Photonics. Adv. Funct. Mater. 2015, 25, 6996–7002. [Google Scholar] [CrossRef]
- Shi, M.; Huang, S.; Dong, N.; Liu, Z.; Gan, F.; Wang, J.; Chen, Y. Donor-acceptor type blends composed of black phosphorus and C60 for solid-state optical limiters. Chem. Commun. 2018, 54, 366–369. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Guo, Z.; Huang, H.; Xiao, Q.; Zhang, H.; Yu, X.-F. Solvothermal Synthesis and Ultrafast Photonics of Black Phosphorus Quantum Dots. Adv. Opt. Mater. 2016, 4, 1223–1229. [Google Scholar] [CrossRef]
- Ji, J.; Song, X.; Liu, J.; Yan, Z.; Huo, C.; Zhang, S.; Su, M.; Liao, L.; Wang, W.; Ni, Z.; et al. Two-dimensional antimonene single crystals grown by van der Waals epitaxy. Nat. Commun. 2016, 7, 13352. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yan, Z.; Li, Y.; Chen, Z.; Zeng, H. Atomically thin arsenene and antimonene: Semimetal-semiconductor and indirect-direct band-gap transitions. Angew. Chem. Int. Ed. 2015, 54, 3112–3115. [Google Scholar] [CrossRef]
- Zhang, S.L.; Xie, M.Q.; Li, F.Y.; Yan, Z.; Li, Y.F.; Kan, E.; Liu, W.; Chen, Z.F.; Zeng, H.B. Semiconducting Group 15 Monolayers: A Broad Range of Band Gaps and High Carrier Mobilities. Angew. Chem. Int. Ed. 2016, 128, 1698–1701. [Google Scholar] [CrossRef]
- Wang, G.; Pandey, R.; Karna, S.P. Atomically thin group v elemental films: Theoretical investigations of antimonene allotropes. ACS Appl. Mater. Interfaces 2015, 7, 11490–11496. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Zhang, X.; Li, L. Strain-driven band inversion and topological aspects in Antimonene. Sci. Rep. 2015, 5, 16108. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Tian, W.C.; Wang, W.L.; Yao, D.X. Two-Dimensional Pnictogen Honeycomb Lattice: Structure, On-Site Spin-Orbit Coupling and Spin Polarization. Sci. Rep. 2015, 5, 11512. [Google Scholar] [CrossRef]
- Song, Y.; Liang, Z.; Jiang, X.; Chen, Y.; Li, Z.; Lu, L.; Ge, Y.; Wang, K.; Zheng, J.; Lu, S.; et al. Few-layer antimonene decorated microfiber: Ultra-short pulse generation and all-optical thresholding with enhanced long term stability. 2D Mater. 2017, 4, 045010. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, M.; Wang, Z.; Han, K.; Liu, X.; Xu, X. Excellent nonlinear absorption properties of β-antimonene nanosheets. J. Mater. Chem. C 2018, 6, 2848–2853. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, F.; Wu, Y.; Hao, X.; Wang, Z.; Xu, X. One-Step Exfoliation and Hydroxylation of Boron Nitride Nanosheets with Enhanced Optical Limiting Performance. Adv. Opt. Mater. 2016, 4, 141–146. [Google Scholar] [CrossRef]
- Chang, C.W.; Okawa, D.; Majumdar, A.; Zettl, A. Solid-State Thermal Rectifier. Science 2006, 314, 1121–1124. [Google Scholar] [CrossRef] [PubMed]
- Golberg, D.; Costa, P.M.F.J.; Lourie, O.; Mitome, M.; Bai, X.D.; Kurashima, K.; Zhi, C.Y.; Tang, C.C.; Bando, Y. Direct Force Measurements and Kinking under Elastic Deformation of Individual Multiwalled Boron Nitride Nanotubes. Nano Lett. 2007, 7, 2146–2151. [Google Scholar] [CrossRef]
- Chen, Y.; Zou, J.; Campbell, S.J.; Le Caer, G. Boron nitride nanotubes: Pronounced resistance to oxidation. Appl. Phys. Lett. 2004, 84, 2430–2432. [Google Scholar] [CrossRef]
- Kumbhakar, P.; Kole, A.K.; Tiwary, C.S.; Biswas, S.; Vinod, S.; Taha-Tijerina, J.; Chatterjee, U.; Ajayan, P.M. Nonlinear Optical Properties and Temperature-Dependent UV-Vis Absorption and Photoluminescence Emission in 2D Hexagonal Boron Nitride Nanosheets. Adv. Opt. Mater. 2015, 3, 828–835. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, Y.; Sun, X.; Liu, S.; Ma, F.; Zhao, G.; Hao, X.; Zhou, S. Ultra-broadband nonlinear optical response of two-dimensional h-BN nanosheets and their hybrid gel glasses. Nanoscale 2018, 10, 4276–4283. [Google Scholar] [CrossRef] [PubMed]
- Dong, N.; Li, Y.; Feng, Y.; Zhang, S.; Zhang, X.; Chang, C.; Fan, J.; Zhang, L.; Wang, J. Optical Limiting and Theoretical Modelling of Layered Transition Metal Dichalcogenide Nanosheets. Sci. Rep. 2015, 5, 14646. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.F.; Liu, J.W.; Fu, L.; Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 2014, 346, 1344–1347. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, S.-C.; Ali, M.N.; Felser, C.; Yan, B. Prediction of Weyl semimetal in orthorhombic MoTe2. Phys. Rev. B 2015, 92, 161107. [Google Scholar] [CrossRef]
- Qi, Y.; Naumov, P.G.; Ali, M.N.; Rajamathi, C.R.; Schnelle, W.; Barkalov, O.; Hanfland, M.; Wu, S.C.; Shekhar, C.; Sun, Y.; et al. Superconductivity in Weyl semimetal candidate MoTe2. Nat. Commun. 2016, 7, 11038. [Google Scholar] [CrossRef]
- Shirodkar, S.N.; Waghmare, U.V. Emergence of ferroelectricity at a metal-semiconductor transition in a 1T monolayer of MoS2. Phys. Rev. Lett. 2014, 112, 157601. [Google Scholar] [CrossRef]
- Tan, S.J.; Abdelwahab, I.; Ding, Z.; Zhao, X.; Yang, T.; Loke, G.Z.; Lin, H.; Verzhbitskiy, I.; Poh, S.M.; Xu, H.; et al. Chemical Stabilization of 1T’ Phase Transition Metal Dichalcogenides with Giant Optical Kerr Nonlinearity. J. Am. Chem. Soc. 2017, 139, 2504–2511. [Google Scholar] [CrossRef]
- Chen, K.; Schunemann, S.; Song, S.; Tuysuz, H. Structural effects on optoelectronic properties of halide perovskites. Chem. Soc. Rev. 2018, 47, 7045–7077. [Google Scholar] [CrossRef] [PubMed]
- Shi, E.; Gao, Y.; Finkenauer, B.P.; Akriti; Coffey, A.H.; Dou, L. Two-dimensional halide perovskite nanomaterials and heterostructures. Chem. Soc. Rev. 2018, 47, 6046–6072. [Google Scholar] [CrossRef]
- Manser, J.S.; Christians, J.A.; Kamat, P.V. Intriguing Optoelectronic Properties of Metal Halide Perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef] [PubMed]
- Cheng, P.; Zhan, X. Stability of organic solar cells: Challenges and strategies. Chem. Soc. Rev. 2016, 45, 2544–2582. [Google Scholar] [CrossRef] [PubMed]
- Ju, M.G.; Dai, J.; Ma, L.; Zeng, X.C. Lead-Free Mixed Tin and Germanium Perovskites for Photovoltaic Application. J. Am. Chem. Soc. 2017, 139, 8038–8043. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Gao, P.; Grätzel, M.; Nazeeruddin, M.K. Organohalide lead perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 2448–2463. [Google Scholar] [CrossRef]
- Seo, J.; Noh, J.H.; Seok, S.I. Rational Strategies for Efficient Perovskite Solar Cells. Acc. Chem. Res. 2016, 49, 562–572. [Google Scholar] [CrossRef]
- Yang, W.S.; Park, B.W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H.; et al. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef]
- Sha, W.E.I.; Ren, X.; Chen, L.; Choy, W.C.H. The efficiency limit of CH3NH3PbI3 perovskite solar cells. Appl. Phys. Lett. 2015, 106, 221104. [Google Scholar] [CrossRef]
- Sutherland, B.R.; Sargent, E.H. Perovskite photonic sources. Nat. Photon. 2016, 10, 295–302. [Google Scholar] [CrossRef]
- Zhang, R.; Fan, J.; Zhang, X.; Yu, H.; Zhang, H.; Mai, Y.; Xu, T.; Wang, J.; Snaith, H.J. Nonlinear Optical Response of Organic–Inorganic Halide Perovskites. ACS Photon. 2016, 3, 371–377. [Google Scholar] [CrossRef]
- Jiang, G.; Miao, L.; Yi, J.; Huang, B.; Peng, W.; Zou, Y.; Huang, H.; Hu, W.; Zhao, C.; Wen, S. Ultrafast pulse generation from erbium-doped fiber laser modulated by hybrid organic–inorganic halide perovskites. Appl. Phys. Lett. 2017, 110, 161111. [Google Scholar] [CrossRef]
- Li, P.; Chen, Y.; Yang, T.; Wang, Z.; Lin, H.; Xu, Y.; Li, L.; Mu, H.; Shivananju, B.N.; Zhang, Y.; et al. Two-Dimensional CH3NH3PbI3 Perovskite Nanosheets for Ultrafast Pulsed Fiber Lasers. ACS Appl. Mater. Interfaces 2017, 9, 12759–12765. [Google Scholar] [CrossRef] [PubMed]
| Wavelength Range | Energy (J) × 10−19 | Pathological Effect |
|---|---|---|
| 180–400 nm (UV) | 4.95–9.90 | Photochemical cataract and keratitis |
| 400–780 nm (visible light) | 2.54–4.95 | Retinal photochemical damage or burn |
| 780–1400 nm (near IR) | 1.40–2.54 | Cataract or retinal burns |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, B.; Chen, Y. Recent Progress in Two-Dimensional Nanomaterials for Laser Protection. Chemistry 2019, 1, 17-43. https://doi.org/10.3390/chemistry1010004
Liu Z, Zhang B, Chen Y. Recent Progress in Two-Dimensional Nanomaterials for Laser Protection. Chemistry. 2019; 1(1):17-43. https://doi.org/10.3390/chemistry1010004
Chicago/Turabian StyleLiu, Zhiwei, Bin Zhang, and Yu Chen. 2019. "Recent Progress in Two-Dimensional Nanomaterials for Laser Protection" Chemistry 1, no. 1: 17-43. https://doi.org/10.3390/chemistry1010004
APA StyleLiu, Z., Zhang, B., & Chen, Y. (2019). Recent Progress in Two-Dimensional Nanomaterials for Laser Protection. Chemistry, 1(1), 17-43. https://doi.org/10.3390/chemistry1010004





