Abstract
In various applications, IoT temporal data play a crucial role in accurately predicting future trends. Traditional models, including Rolling Window, SVR-RBF, and ARIMA, suffer from a potential accuracy decrease because they generally use all available data or the most recent data window during training, which can result in the inclusion of noisy data. To address this critical issue, this paper proposes a new forecasting technique called Adaptive Holt–Winters (AHW). The AHW approach utilizes two models grounded in an exponential smoothing methodology. The first model is trained on the most current data window, whereas the second extracts information from a historical data segment exhibiting patterns most analogous to the present. The outputs of the two models are then combined, demonstrating enhanced prediction precision since the focus is on the relevant data patterns. The effectiveness of the AHW model is evaluated against well-known models (Rolling Window, SVR-RBF, ARIMA, LSTM, CNN, RNN, and Holt–Winters), utilizing various metrics, such as RMSE, MAE, p-value, and time performance. A comprehensive evaluation covers various real-world datasets at different granularities (daily and monthly), including temperature from the National Climatic Data Center (NCDC), humidity and soil moisture measurements from the Basel City environmental system, and global intensity and global reactive power from the Individual Household Electric Power Consumption (IHEPC) dataset. The evaluation results demonstrate that AHW constantly attains higher forecasting accuracy across the tested datasets compared to other models. This indicates the efficacy of AHW in leveraging pertinent data patterns for enhanced predictive precision, offering a robust solution for temporal IoT data forecasting.
1. Introduction
The Internet of Things (IoT) is an emerging technology that involves globally connected intelligent devices accessible via the Internet. These devices, sometimes called sensors, are designed to collect data and react to stimuli from their surroundings. IoT has applications in various domains, including intelligent residences, smart buildings, environmental monitoring networks, power consumption measurement systems, safety and surveillance solutions, commercial applications, and healthcare technologies [1]. The anticipated economic impact of IoT across various sectors is expected to reach USD 6.2 trillion by 2025 [2].
There are various types of sensors, each designed to measure specific data. Some have been engineered to monitor atmospheric conditions, including temperature, humidity, precipitation, and wind velocity. Alternatively, other sensors can detect movement, illumination levels, mechanical operations, force exertion, and water depth, among other parameters. The vast quantities of data these sensors produce can be utilized in various applications and decision-making processes [3,4]. Consequently, analyzing these data as efficiently as possible is crucial to ensure that the most precise decisions are made in specific critical applications. These devices collect measurements/readings from a particular environment, with each reading linked to its corresponding acquisition date and time. Over a designated timeframe, these measurements accumulate, and the resulting dataset is subsequently classified as time series data.
Using time series data will enhance and streamline business processes while extracting valuable insights to improve operational trends, identify anomalies, and uncover seasonal patterns [3]. Nevertheless, such vast quantities of diverse data types exacerbate the 3Vs of big data (variety, volume, and velocity), posing significant challenges in data analysis [5]. Analyzing IoT data involves scrutinizing various datasets to uncover trends, patterns, correlations, and novel insights from the accumulated information. This analysis employs diverse machine learning and data mining techniques to extract knowledge, resulting in models capable of predicting new values with high accuracy [6]. Subsequently, these models adapt to the latest data inputs, enhancing their predictive accuracy. However, such models typically utilize all available data or a recent direct window of data for training. Consequently, the trained data may incorporate irrelevant patterns that do not reflect the current situation, potentially diminishing the overall forecasting accuracy or requiring extended processing times.
IoT forecasting is one of the main challenges that IoT technology is facing because of the limited computational resources, connectivity, streaming, etc. Therefore, many forecasting models have been proposed to address these limitations. These models have been adapted for use in the IoT field, and they include lightweight, energy-efficient, real-time forecasting in edge devices. Memory-efficient forecasting techniques [7], frequency-aware lightweight models [8], and compressed recurrent neural networks [9] are examples of these models and are used in different domains, including smart agriculture, healthcare, industrial monitoring, etc. These models maintain accuracy while reducing model complexity, making them ideal for the limitations of IoT platforms.
This study concentrates on IoT time series data forecasting models because specific applications require both rapidity and accuracy, necessitating highly precise predictions within short timeframes [10,11]. We introduce an innovative adaptive technique founded on the Holt–Winters forecasting model, namely “AHW”. This approach seeks to predict a spectrum of values by analyzing historical trends and identifying the most relevant patterns from previous data points. It combines these extracted similar data windows with the Holt–Winters model to create and train a forecasting system that includes past information. AHW aims to achieve high forecasting accuracy and minimize the time required for prediction processes.
The remainder of this paper is structured as follows. Section 2 examines existing IoT data forecasting models. Section 3 provides a comprehensive description of the proposed IoT data forecasting model. Section 4 describes the implementation and evaluation of the proposed model. Section 5 concludes the paper and summarizes the key findings and implications of the proposed approach.
2. Related Work
The prediction of IoT data remains a significant challenge in the IoT field. Numerous applications rely on these predictions to initiate certain actions, and many forecasting models have been specifically designed for these types of data.
The Auto-Regressive Integrated Moving Average (ARIMA) model stands out as a prominent approach for such forecasting. Utilizing a collection of historical time series data, ARIMA was developed and trained to forecast future values [12]. The primary objective of ARIMA is to identify and highlight autocorrelations within previously collected data. The ARIMA model comprises two primary components. The first is the autoregressive (AR) element, which utilizes a linear combination of past values to predict a range of future values for the variable in question. This component was used when there was a correlation between the measured values. The second component is the moving average (MA), which, unlike the AR element, does not rely on previous forecasting values. Instead, it utilizes the errors generated from past predictions in the regression process and considers them as a weighted moving average of the previous forecast errors. The MA component is beneficial when there is minimal correlation within the data. A significant drawback of ARIMA is its reliance on expert input to compute and set up the necessary parameters for achieving highly precise forecasts [13,14,15]. Despite this limitation, ARIMA is regarded as a superior model compared to other time series forecasting techniques, owing to its ability to identify the most suitable model for a given time series. When dealing with low correlation data, ARIMA employs a constant mean, resulting in predictions that closely align with the mean value. Conversely, ARIMA adjusts the mean for correlated data to reflect this correlation, producing highly accurate predictions [14]. The ARIMA model separates data into various components, such as seasonality and trends, and develops a model for each element. ARIMA’s effectiveness is also constrained when handling variables with nonlinear interrelationships. Furthermore, ARIMA models face challenges in scenarios where the assumption of constant error variance may not hold in real-world applications. ARIMA has several variants, one of which integrates the Generalized Autoregressive Conditional Heteroskedasticity (GRACH) model. This ARIMA-GRACH hybrid effectively addresses the issue of a constant standard deviation error. Nonetheless, optimizing the GRACH model and identifying its ideal parameters remains a formidable task [16].
The Rolling Window (sliding window) (RW) regression model is another forecasting approach. The RW model is regarded as the most straightforward prediction technique, owing to its lack of intricate calculations. The RW regression model employs a set of previous values known as a window to forecast a series of future values. Once a prediction is made, the window shifts forward in one step, incorporating the predicted value before generating the next forecast. This model can incorporate various statistical methods, including machine learning techniques. RW can deliver remarkably precise results without requiring prior experience [17]. The popularity of the RW model stems from its ability to generate reliable predictions efficiently, and it is favored for its rapid calculations that yield highly precise predictions. The model forecasts were derived from a statistical representation of the preceding data window. This window is split into two parts: training and prediction samples. The model is then fitted using a training sample and various statistical methods to forecast future data. The accuracy of these predictions was subsequently assessed using a prediction sample to determine the model’s suitability [18]. However, the RW regression model’s reliance on the most recent data window for training may incorporate patterns that are not relevant to the current conditions, potentially compromising the forecasts’ overall accuracy.
The Long Short-Term Memory Network (LSTM) is another approach that stands out for its complexity. LSTM employs a distinct set of memory elements called gates to address vanishing gradients. It regulates the network by determining when to acquire and discard previous historical data from the memory unit or when to refresh the memory with newly generated information. Therefore, network training requires only the present state and a few preceding states. LSTM’s remarkable ability to recognize patterns and dependencies across numerous steps [3] has made it a widely adopted technique, renowned for delivering highly precise predictions [19]. To handle time series information with extended dependencies, LSTM is purposefully designed to identify and utilize long-term patterns in sequential data, such as in natural language processing (NLP) applications where the sequence of words plays a crucial role. Nevertheless, LSTM employs intricate calculations that require high-performance computing resources and is time-consuming in model generation, posing a challenge for certain real-time applications where time is critical.
The Recurrent Neural Network (RNN), a deep learning technique, is another commonly employed approach for accurately forecasting time series data. Fischer and Krauss [20] incorporated gradient-boosted trees alongside random forest algorithms as an additional predictive method. Their analysis revealed that both gradient-boosted trees and random forests exhibit superior predictive capabilities compared to deep learning-based approaches. Furthermore, they highlighted the intricate nature of neural network training using deep learning methodologies. Lee and Yoo [21] introduced internal layers to the RNN structure to fine-tune the threshold levels of values. Their innovative framework demonstrated an improvement in the accuracy of the predicted outcomes. Choi [22] introduced a combined approach for predicting time series data in financial markets. Their method integrated LSTM and ARIMA models to forecast stock market price trends using time series data. Ghofrani et al. [23] introduced another combined approach utilizing Bayesian Neural Network (BNN) and clustering techniques. Their method incorporated K-means clustering to select the most suitable training data while employing a BNN for the predictive model. This integrated approach yielded the most precise results compared to alternative models. While RNNs offer certain benefits, they involve intricate computations that demand substantial processing power and are time intensive. This makes them unsuitable for real-time applications, where speed is essential.
Hybrid models have also been proposed to combine different types of algorithms. Ratnayaka et al. [24] introduced a combined approach utilizing ARIMA and an Artificial Neural Network (ANN) to predict share prices, examining time series data to discern value trends. Horelu et al. [25] employed the Hidden Markov Model (HMM) to address short-term value-pattern dependencies while using a Recurrent Neural Network (RNN) for long-term dependencies. It should be emphasized that the complex computations involved in ANNs require significant processing power and are time-consuming to develop. In contrast, ARIMA requires statistical analysis and data science expertise to correctly set up the model’s key parameters [15]. These factors make such combined approaches difficult to implement in practical applications.
Support Vector Regression (SVR), a variant of the Support Vector Machine (SVM), is another approach used for forecasting. The efficacy of SVR depends on the chosen kernel function, and consequently, selecting more suitable kernel functions will improve SVR precision. Researchers have proposed numerous kernel functions, with linear kernel functions utilized for linear challenges. The RBF kernel function exhibited superior capability in addressing nonlinear issues. SVR-RBF employs spatial mapping and feature extraction techniques to convert nonlinear problems into linear problems for resolution. Furthermore, SVR-RBF can be mapped onto an infinite-dimensional space to derive solutions [26]. The forecasting accuracy of the SVR and SVR-RBF regression models may be compromised because of their reliance on the most recent historical data or the entire dataset during training. This is because both approaches incorporate patterns not representative of the current conditions.
The Holt–Winters method, also known as triple exponential smoothing, is another renowned and swift forecasting technique. Developed by Charles C. Holt and Peter Winters, it is considered one of the most uncomplicated yet powerful predictive models available. It employs basic forecasting calculations, thus eliminating the need for sophisticated resources and lengthy operation times. Three essential components are required for this approach, including trend, level, and seasonality, as shown in Equation (1) [27]:
where t is the elapsed time, is the smoothed level, b(t) is the smoothed seasonal index at t, and is the number of periods in the seasonal cycle. Although this approach can adapt to changing trends and patterns, it is constrained by the seasonal components [27]. The Holt–Winters regression model utilizes the preceding direct set of values or the entire historical dataset during training. This approach may lead to the inclusion of data patterns in the training set that are no longer relevant to the current situation, potentially reducing the accuracy of model forecasts. Ryan Kristianto [28] proposed a new model for time series data prediction by optimizing the Holt–Winters algorithm using the strength points in the Fruit Fly Optimization function. This model used the Fruit Fly Optimization function to specify the values of Alpha, Beta, and Gamma, the smoothing parameters of the level, trend, and seasonal, respectively, of the Holt–Winters algorithm, and achieved a higher accuracy than the Holt–Winters model. Neda et al. [29] proposed a spatial-temporal Holt–Winters method for forecasting short-term temperature data using ERA5 reanalysis data. Holt–Winters is used to capture the seasonality of data with a high degree of accuracy, taking into consideration the trend and seasonality of the data.
Many pattern-matching techniques have been proposed. Heshan and Qingshan [30] proposed a pattern matching of time series. They used it in the trend prediction, an evaluation method proposed for the actual trend of time series data, to evaluate the experiment results. A simulated series is used as the imputed pattern, which enhances the trend prediction accuracy. Yi-Liang [31] proposed a day-ahead solar power forecasting technique using pattern analysis and state transition. The proposed method utilizes historical photovoltaic power generation as input data for the model. The model contains two main parts: the first is the pattern analysis to evaluate the similarity of the daily time series data using the Euclidean distance followed by grouping using the k-means time series clustering algorithm. The second part is the state transition, which calculates the state transitions between two consecutive days. Nitya and Aleena [32] proposed a pattern recognition and prediction technique in time series data using retrieval augmented techniques. They used the OpenAI CLIP model to find visual similarity among visual time series patterns. Then, they used the top-most similar patterns from these extracted data windows in the time series predictions. Bo Cao et al. [33] proposed a probability forecasting method of the wind power ramp event using the time series similarity search algorithm. The proposed algorithm used the similarity search technology with an empirical probability forecasting method; however, this method requires a large amount of historical data to extract the template pattern and evaluate the probability of the ramp occurrence.
Faisal Saeed et al. [34] proposed a graph-based transformer model for energy load forecasting called SmartFormer. This model captures the inter-series dependencies and predicts the load using the graph structure. It can represent various temporal patterns and reduce the redundant information inside a data stream. They integrated the neural network components into the proposed transformer layers, allowing the fusion of the sequence encodings and graph aggregation processes. The proposed model works efficiently on multivariate data but has performance problems when forecasting univariate data.
Lightweight forecasting models are essential in the IoT field because of the limited resources of the sensors; therefore, many studies have addressed this challenge. Aitian Ma et al. [35] proposed an extremely slow resource multivariate time series forecasting called MixLinear. They modeled the intra-segment and inter-segment variations in the time domain to extract the frequency variations from the latent space in the frequency domain. This allows for predicting long-term future values by extracting trends and patterns from historical data. Rémi and Hugo [36] proposed a temporal linear network forecasting method for time series data. The model captures the temporal and future dependencies in multivariate data. They performed some successive transformations to create structured weight dependencies to develop a regularization process. They achieved the interpretability of linear models while achieving higher performance using the structured parameter space. Chaolv et al. [37] proposed a simple model by integrating two parts, the first one is the encoder of the historical time series feature into a hidden space with a linear layer called Timester with a backbone forecaster called Bonster, which uses other backbones to predict the noise components based on the historical observations of variables.
Existing studies have utilized the immediately preceding set of values or the entire historical dataset for training purposes. Consequently, the training data may encompass various patterns unrelated to the current context, potentially compromising the overall prediction accuracy. Furthermore, utilizing the entirety of historical data in the training phase can be exhaustive, particularly when dealing with vast datasets. For this purpose, numerous current prediction models (such as LSTM, RNN, SmartFormer, and ANN) utilize complex computations that demand powerful computing capabilities and substantial time to produce the model. This lengthy process may prove problematic in certain near-real-time scenarios where time is a crucial element [3].
The abovementioned challenges prompted this study to introduce a novel “AHW” approach. AHW addresses the previous issues and provides solutions with the following objectives: (1) employing the immediate preceding window of data to construct a prediction model using uncomplicated, rapid computations; (2) utilizing historical measured values (excluding the most recent ones) based on similarity criteria to develop an additional forecasting model using simple, swift calculations; and (3) combining the two aforementioned prediction models to create an improved model that enhances overall forecasting precision.
3. The Proposed AHW Forecasting Method
This section introduces a novel, fast data mining technique for forecasting designed to enable near-real-time data analytics processes. The proposed method (AHW) is an innovative adaptation of the Holt–Winters approach that utilizes all of the previously stored historical data within the aforementioned data schema. AHW identifies the historical data pattern that most closely matches the current data window and incorporates this into the forecasting process. This approach, which combines the historically closest window with the most recent data, yields a swift, precise, and effective outcome compared to the Holt–Winters technique. AHW is based on the Holt–Winters approach owing to its exceptional accuracy in forecasting seasonal time series data. AHW can generate predictions through rapid and straightforward calculations, which is crucial for applications where time is critical. Figure 1 illustrates the AHW forecasting methodology.
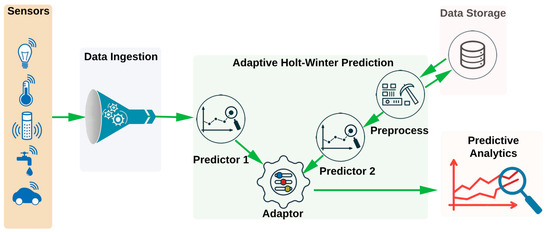
Figure 1.
The proposed AHW forecasting model.
AHW identifies an ideal window size, which is a benchmark for subsequent window sizes. The dataset determines the perfect window size, ensuring each window encompasses at least one complete seasonal cycle of data points. Including more seasonal cycles in the window enhances the precision of the comparison. A larger dataset helps reduce the impact of data irregularities and exceptional occurrences. In the second step, once the window size is determined, a mean curve is computed utilizing all preceding windows in the historical dataset. This average window serves as a benchmark for comparison, enabling the identification of disparities between the current and average windows and facilitating error estimation. The third step involves calculating the level for the average window using Equation (2). This calculation is utilized to ascertain the level difference between the current and average windows. Subsequently, the mean level for each window in the historical database was determined. The system then stores the disparity between the average window’s level and the current window in the database.
Here, t represents a point in the time series, n denotes the final point, and xt denotes the current point. The modified root mean square error (RMSE), presented in Equation (3), is determined by comparing the average window with the current window, taking into consideration the disparity between the levels, as illustrated in Equation (3).
In this formula, t represents a specific moment in the time series, and n denotes the final point in the window. Variable xt signifies the present point in the historical window, and yt indicates the current point in the average window. The value L represents the disparity between the two levels for the average and recent windows. The traditional RMSE equation is better modified to capture the similarity between two different windows of data; these windows can exhibit identical oscillatory behavior (wave patterns) but at various levels. Therefore, adding the level difference calculated in Equation (2) to the traditional RMSE equation will help to identify the closest wave patterns regarding the level difference. Once the RMSE between the two windows is determined, the database records this value. Additionally, details about the window, including its current level, are logged in the historical records.
After completing all the preceding computations outlined in Algorithm 1, the database is cataloged with the essential information. This indexing process is crucial for swiftly identifying the nearest window from the entire historical dataset. This ensures that the closest window is readily available for forecasting purposes, eliminating the need to reprocess all data for each prediction. This enhanced speed represents a significant contribution to the AHW model.
When a fresh set of data (newly recorded values stored in the database) becomes available for predicting subsequent value(s), the following procedure, as outlined in Algorithm 2, is implemented. The first step is to compute the mean level for the final data window and subsequently determine the variance between this level value and the average window level, mirroring the approach utilized in the preprocessing stages. The second step involves calculating the RMSE between the average and most recent windows while considering the level disparities as delineated in Equation (3).
Once the RMSE value was obtained, the next step was identifying the most similar window from the preprocessed database. This was achieved by comparing the RMSE of the current window with the RMSE values stored for each historical window in the database. The window with the closest RMSE value was deemed the optimal match, possessing the most comparable values to the present window. This optimal window can then be utilized in the subsequent forecasting process.
| Algorithm 1. Preprocess Historical Data |
| Input HistoricalData dataset WindowSize ← Select Window Size (includes at least one seasonal data) AvgWindow ← Zero Array HistoricalDataLength ← HistoricalData.length For i ← 0 to HistoricalDataLength −1 do CurrWindow ← HistoricalData[i, WindowSize] For jl ← 0 to WindowSize −1 do AvgWindow[j] ← AvgWindow[j] + CurrWindow[i] End For add WindowSize to i End For AvgLevel ← 0 For i← 0 to AvgWindow.length −1 do AvgWindow[j] ← AvgWindow[j]/(HistoricalDataLength/WindowSize) AvgWindowLevel ← AvgWindowLevel + AvgWindow[j] End For AvgWindowLevel ← AvgWindowLevel/AvgWindow.length For i ← 0 to HistoricalDataLength−1 do HistWindow ← HistoricalData[i, WindowSize] HistWindowLength ← HistWindow.length HistWindowLevel ← 0 HistWindowRMSE ← 0 For j ← 0 to HistWindowLength −1 do HistWindowLevel ← HistWindowLevel + HistWindow[j] End For HistWindowLevel ← HistWindowLevel/HistWindowLength HistWindowLevelDiff ← HistWindowLevel-AvgWindowLevel For j ← 0 to HistWindowLength −1 HistWindowRMSE ← HistWindowRMSE + SquareRoot((HistWindow[j] + HistWindowLevelDiff −AvgWindow[j])2) End For Store i, HistWindowRMSE in StoredWindowsInfo Database add WindowSize to i End For |
| Algorithm 2. Data Forecasting |
| Input LatestWindowData dataset, AvgWindow, AvgWindowLevel, HistoricalData dataset, WindowSize LatestWindowLevel ← 0 LatestWindowLength ← LatestWindowData.length For i ← 0 to LatestWindowLength −1 do LatestWindowLevel ← LatestWindowLevel + LatestWindowData [i] End For LatestWindowLevel ← LatestWindowLevel/LatestWindowLength LatestWindowLevelDiff ← LatestWindowLevel-AvgWindowLevel LatestWindowRMSE ← 0 For i ← 0 to LatestWindowLength −1 do LatestWindowRMSE ← LatestWindowRMSE + SquareRoot((LatestWindowData[i] +LatestWindowLevelDiff-AvgWindow[i])2) End For ClosestWindow ← ∞ ClosestWindowRMSEDiff ← ∞ For i ← 0 to StoredWindowsInfo.length −1 do If Absolute(StoredWindowsInfo[i].RMSE − LatestWindowRMSE) is less than ClosestWindowRMSEDiff ClosestWindow ← i ClosestWindowRMSEDiff ← Absolute(StoredWindowsInfo[i].RMSE − LatestWindowRMSE) End For ClosestWindowData ← HistoricalData[i × WindowSize, (i + 1) × WindowSize] Calculate trend, level, seasonality for LatestWindowData. LatestWindowDataTraining ← LatestWindowData [0, 0.8 × LatestWindowLength] LatestWindowDataAddapting ← LatestWindowData[0.8 × LatestWindowLength +1, LatestWindowLength] ClosestWindowDataTraining ← ClosestWindowData[0, 0.8 × ClosestWindowData.length] LatestPredict ← Use LatestWindowDataTraining to predict LatestWindowDataAddapting using Holt–Winters equation ClosestPredict ← Use ClosestWindowDataTraining to predict ClosestWindowDataAddapting using Holt–Winters equation LatestWindowDiff ← 0 TotalDiff ← 0 For i ← 0 to LatestWindowDataAddapting.length −1 do LatestWindowDiff ← LatestWindowDiff + Absolute(LatestPredict[i] − LatestWindowDataAddapting[i]) TotalDiff←TotalDiff + Absolute(LatestPredict[i] − LatestWindowDataAddapting[i]) + Absolute(ClosestPredict[i] − LatestWindowDataAddapting[i]) End For LatestPercent ← LatestWindowDiff/TotalDiff PredictNewDataLatest ← Use LatestWindowData and Holt–Winters equation PredictNewDataClosest ← Use ClosestWindowData and Holt–Winters equation For i ← 0 to PredictNewDataLatest.length −1 do FinalPredictedData[i] ← (PredictNewDataLatest × LatestPercent) + (PredictNewDataClosest × 1 − LatestPercent) End For Return FinalPredictedData |
After extracting the nearest window from the historical database, the latest window of sensed values will be analyzed to determine trend, level, and seasonality. The data were subsequently divided into two segments: learning and adaptation. Our studies revealed that allocating 80% of the data for learning and 20% for adapting yielded optimal results, although utilizing different percentages did not markedly impact the accuracy. We employ 80% of the data to forecast the remaining 20% using Equation (4) (Holt–Winters formula):
F represents the newly forecasted value, and t denotes the present time value. The variable m signifies the number of periods, Lt indicates the series level, bt represents the trend value, and St represents the estimated seasonal element. Finally, s denotes the seasonality length, which is equivalent to the number of periods within a season. Once the forecast values are calculated using Equation (4) for the most recent data window, an identical procedure is applied to the set of historically similar values identified and extracted from the existing dataset.
The outcome of the preceding stages will yield predicted values utilizing the most recent window of values, FNew, and predicted values employing the historical data window, FOld. Each segment of the predicted data constituted 20% of the forecasted values. An adaptive procedure is necessary to determine the optimal proportion of FNew and FOld that most closely aligns with the actual 20% from the original dataset, utilizing Equations (5) and (6). Here, Newt represents the latest predicted data point derived from FNew, and Actt denotes the present actual data point. Similarly, Oldt represents the current predicted data point generated by FOld.
In the final stage, the most suitable adaptive proportion of the dataset is utilized in the prediction procedure to determine the ultimate forecasted value (FFinal), as shown in Equation (7).
When the actual data falls between FNew and FOld, FFinal is adjusted using PNew and POld, considering both FNew and FOld. However, if the actual data lie above or below FNew or FOld, the percentage value for the nearest predicted value is set to one, whereas the other is set to zero. This adaptation process enhances the accuracy of the final predicted value compared to the Holt–Winters method, thus fulfilling the research’s primary objective of improving precision.
4. Results and Discussions
To validate the AHW method outlined in the preceding section, we applied it and evaluated its performance against established forecasting and prediction techniques. These include Holt–Winters (HW), ARIMA, Rolling Window (RW), Support Vector Regression with Radial Basis Function (SVR-RBF), LSTM, CNN, and RNN. For ARIMA, we used the values p = 0, d = 1, and q = 2, which obtained the best prediction results (by experiments). Focusing on accuracy as the key metric, our analysis encompassed two forecasting levels for each dataset: monthly and daily. Throughout our trials, we maintained a fixed seasonal period of 12 monthly forecasts and 365 daily forecasts.
4.1. Datasets
Table 1 illustrates the utilization of five well-known real datasets: (1) the National Climatic Data Center (NCDC) [38], (2) Basel City-H [39], (3) Basel City-S [39], (4) IHEPC-GI [40], and (5) IHEPC-GI [40].

Table 1.
Datasets used in the evaluation part.
4.2. Evaluation Results
DB1: The first dataset is the temperature feature provided by the National Climatic Data Center (NCDC) [38]. The National Center for Environmental Information (NCEI) collects and disseminates environmental data, including climate information, for public use. We used sub-hourly data collected from 234 stations distributed across the region. Each station was equipped with sensors that recorded measurements every five minutes. This dataset comprises 258,212,798 sensed values, spanning from 1 January 2006 to 27 April 2021. The recorded data encompassed various climatic parameters, such as temperature, radiation, surface temperature, humidity, and soil moisture.
In our experiment, we chose the temperature feature that presented the most diverse range of data. We used a window size of 48 for the monthly forecasting dataset and 365 for the daily forecasting dataset. The monthly forecasting level yielded RMSE/MAE values of 1.9475/1.6849 for AHW, 1.9768/1.6935 for HW, 15.5199/12.8402 for ARIMA, 9.3381/8.2183 for RW (window size = 3), 9.3731/8.2422 for SVR-RBF, 8.7299/6.8039 for LSTM, 4.7751/3.7358 for CNN, and 5.8109/4.3654 for RNN as displayed in Figure 2a. For the daily dataset, the RMSE/MAE results were 4.4756/3.5597 for AHW, 4.5802/3.6736 for HW, 15.4917/12.7306 for ARIMA, 10.2243/8.6567 for RW (window size = 30), 11.6265/9.2091 for SVR-RBF, 18.2412/15.3383 for LSTM, 11.1932/9.5714 for CNN, and 14.3404/11.8075 for RNN as illustrated in Figure 2b.
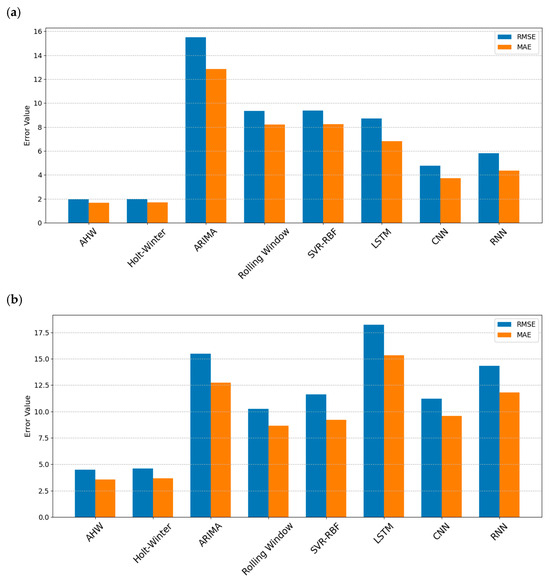
Figure 2.
Comparative evaluation of RMSE and MAE across eight forecasting methods on the NCDC temperature dataset (DB1): (a) monthly prediction; (b) daily prediction.
DB2/DB3: The second and third datasets are the weather data for Basel City, Switzerland [39], generated by the NASA Meteoblue Climatology Website. The dataset comprises various climatic parameters, including temperature, humidity, soil moisture, and wind speed. Measurements were taken hourly from 1 January 1985 to 31 July 2021, resulting in 320,664 data points. We derived two separate datasets for experimental purposes by extracting two specific features from the Basel City dataset.
For the second dataset, humidity values were used. A window size of 24 was employed for the monthly forecasting dataset, whereas the daily forecasting dataset utilized a window size of 730. The RMSE/MAE values for the monthly forecasting level are as follows: AHW at 4.1468/3.2923, HW at 5.9863/5.2783, ARIMA at 10.3617/9.1388, RW (window size = 3) at 5.8854/4.8770, SVR-RBF at 5.8243/4.8217, LSTM at 5.7443/4.7792, CNN at 30.2965/28.0841, and RNN at 34.2855/32.2153. The RMSE/MAE values for the daily dataset: AHW achieved 8.4530/6.8796, HW recorded 12.8838/10.9986, ARIMA yielded 13.3860/11.2767, RW (window size = 30) reached 9.0113/7.3990, SVR-RBF attained 8.8738/7.3050, LSTM recorded 10.0217/8.2478, CNN yielded 8.6207/7.1614, and RNN achieved 13.9162/11.5179.
For the third dataset, we extracted the soil moisture column and used the same window size as that of DB2. The RMSE/MAE results for monthly forecasting: AHW achieves 0.0341/0.0294, HW yields 0.0409/0.0357, ARIMA produces 0.0402/0.0347, RW with a 3-unit window size reaches 0.0446/0.0340, SVR-RBF attains 0.0409/0.0354, LSTM 0.0381/0.0299, CNN 0.0349/0.0301, and RNN 0.0445/0.0338. For the daily dataset, the following RMSE values were obtained: AHW records 0.0335/0.0312, HW shows 0.0460/0.0383, ARIMA demonstrates 0.0386/0.0317, RW utilizing a 30-unit window size exhibits 0.0481/0.0368, SVR-RBF registers 0.0440/0.0378, LSTM 0.0889/0.0803, CNN 0.0714/0.0607, and RNN 0.0479/0.0405.
The fourth and fifth datasets were derived from Individual Household Electric Power Consumption (IHEPC) data [40]. This collection consists of measurements of electrical power usage from a residence in Sceaux, France. The dataset encompasses 2,075,259 readings obtained between December 2006 and November 2010. In our study, we extracted two distinct features from the IHEPC dataset, resulting in the creation of two separate datasets.
For the fourth dataset, we used the global intensity column. A window size of 12 was used for the monthly forecasting dataset. The daily forecasting dataset was set to 365. The monthly forecasting results show RMSE/MAE values of 0.4407/0.3797 for AHW, 0.4712/0.3824 for HW, 1.8456/1.6420 for ARIMA (p = 0, d = 1, q = 0), 0.9934/0.6929 for RW (window size = 3), 2.1026/1.9031 for SVR-RBF, 4.9962/4.4495 for LSTM, 1.4564/1.1902 for CNN, and 2.4722/2.3042 for RNN. For the daily dataset, the RMSE/MAE values as follows: AHW 1.3022/0.9168, HW 1.3204/0.9968, ARIMA (p = 0, d = 1, q = 0) 2.3290/1.9667, RW (window size = 30) 1.4283/1.0932, SVR-RBF 4.7298/4.3824, LSTM 1.5365/1.1786, CNN 1.4132/1.0770, and RNN 1.4738/1.1259.
For the fifth dataset, we selected a global reactive power column. We used the same window size as previously described. For monthly forecasting, the RMSE/MAE values were as follows: AHW at 0.0218/0.0159, HW at 0.0218/0.0159, ARIMA (p = 0, d = 1, q = 0) at 0.0224/0.0162, RW (window size = 3) at 0.0277/0.0198, SVR-RBF at 0.0218/0.0197, LSTM at 0.0219/0.0190, CNN at 0.0282/0.0181, and RNN at 0.0353/0.0311. In the daily dataset, the results were as follows: AHW 0.0397/0.0278, HW 0.0416/0.0296, ARIMA (p = 0, d = 1, q = 0) 0.0415/0.0283, RW (window size = 30) 0.0400/0.0279, SVR-RBF 0.1333/0.1187, LSTM 0.0405/0.0300, CNN 0.0417/0.0287, and RNN 0.0399/0.0287.
As summarized in Table 2, our proposed AHW method outperformed the alternative forecasting model for all datasets studied.

Table 2.
Forecasting performance comparison.
To show that the observed performance gains are truly meaningful, a statistical significance test was performed by calculating the p-value using a paired t-test on per-window RMSE between the proposed solution data and the other models, including Holt–Winters, ARIMA, Rolling Window, SVR-RBF, LSTM, CNN, and RNN, as shown in Table 3. All the p-values calculated between AHW and the other models are less than 0.05 (significance level) for all datasets on all seasons (monthly and daily). However, a few forecasting models showed p-value slightly more than 0.05 (specifically, in 4 out of 70 experiments) with different datasets. These occurred in the Global Intensity dataset at the monthly forecasting level for the Rolling Window method and in the Global Reactive Power dataset at the monthly forecasting level for three forecasting models, including SVR-RBF, LSTM, and RNN.

Table 3.
Forecasting Statistical Significance (p-values) comparison.
Table 4 lists the runtime performance findings. The proposed AHW model primarily demonstrates viable and, in most cases, greater computational efficiency compared to the tested deep learning models, such as LSTM, CNN, and RNN. For example, for NCDC temperature, AHW takes 0.456 s for monthly forecasts, which is notably quicker than LSTM (8.086 s), CNN (7.294 s), and RNN (6.785 s). AHW has demonstrated a consistent trend that holds across all datasets and features for monthly forecasting. For the daily feature level, AHW’s forecasting time increases as anticipated due to the large data size and higher granularity; however, it remains notably faster than the deep learning models. For example, for Basel City Humidity (day), AHW takes 9.655 s, which is noticeably less than LSTM (348.504 s), CNN (401.139 s), and RNN (374.756 s). Hence, AHW scales comparatively well in terms of computational cost as the data granularity increases.

Table 4.
Runtime performance comparison.
The Holt–Winters and ARIMA models are considered lighter models and require less time to perform forecasting. Hence, both models have demonstrated better runtime performance than the AHW model. However, AHW performance is lower because it conducts the Holt–Winters calculations twice (once for the latest window and once for the historical window) and requires more calculations to find the closest window. Additionally, AHW has an “adaptive” component, which involves extra computations. However, this increase is typically minor and could be defensible by potential improvements in forecasting accuracy, as shown in Table 2.
The reason the “Rolling Window” model has the lowest forecasting times across all scenarios (0.0002 s to 0.0003 s) is that it employs the rolling window approach, which involves taking a historical average or a fixed window size, a computationally trivial operation. However, its accuracy is likely to be calculatedly lower than that of more sophisticated models, such as AHW.
SVR-RBF performs better than AHW because it is a mixed model that depends on the specific dataset and features. Additionally, SVR-RBF possesses non-linear capabilities and the ability to incorporate multiple features. These are simpler than the calculations performed by AHW, which make SVR-RBF faster. However, this performance is considered negligible in comparison to the forecasting accuracy obtained by AHW, as shown in Table 2.
Although AWH hypothetically adds a slight overhead compared to static models like ordinary Holt–Winters, it does not seem to significantly hinder its applicability and efficiency, particularly when considering the substantial computational cost savings compared to deep learning models, as well as the excellent accuracy performance that AHW demonstrated across all datasets. Hence, the AHW model is considered a robust model for time series forecasting, where accurate predictions are critical.
5. Conclusions
The Internet of Things (IoT) is crucial in various fields. One of the primary challenges lies in utilizing IoT-generated data for analytical purposes, making the forecasting processes of IoT data a vital component in making informed decisions. To this end, this study introduced an innovative technique known as AHW, which is derived from the Holt–Winters forecasting model. The newly developed AHW approach produced a pair of distinct models. The first model was developed using the most suitable data pattern from prior historical records of the current values. The second model was constructed using the most recent set of values. Subsequently, an adaptation process was introduced to equilibrate the forecasting procedure between the historical model and the model based on the latest value set. This process employed adaptive calculations and comparisons with the validation data subset to yield greater accuracy than that achieved by the Holt–Winters model. This study utilized five datasets from real-world scenarios for empirical assessment, including the temperature data from the National Climatic Data Center (NCDC), humidity and soil moisture measurements from the Basel City environmental dataset, and global intensity and global reactive power from the Individual Household Electric Power Consumption (IHEPC).
The evaluation results demonstrated that AHW constantly attains higher forecasting accuracy across the tested datasets compared to the models (ARIMA, Rolling Window, SVR-RBF, LSTM, RNN, CNN, and the Holt–Winters), utilizing various metrics, such as RMSE, MAE, p-value, and time performance. This indicates the efficacy of AHW in leveraging pertinent data patterns for enhanced predictive precision, offering a robust solution for temporal IoT data forecasting. The limitation of the proposed technique is that it only deals with periodic seasonal data; however, a lot of IoT applications deal with this type of data, especially for environmental IoT applications and other applications such as intelligent residences, smart buildings, power consumption measurement systems, safety, and surveillance solutions.
Author Contributions
Conceptualization, S.S. and G.A.-N.; methodology, S.S.; software, S.S.; validation, S.S. and G.A.-N.; formal analysis, S.S. and G.A.-N.; investigation, S.S. and G.A.-N.; resources, S.S.; data curation, S.S. writing—original draft preparation, S.S. and G.A.-N.; writing—review and editing, S.S. and G.A.-N.; visualization, S.S.; supervision, G.A.-N.; project administration, G.A.-N.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data derived from public domain resources.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zeinab, K.A.M.; Elmustafa, S.A.A. Internet of Things Applications, Challenges and Related Future Technologies. World Sci. News. 2017, 67, 2. [Google Scholar]
- Mohammadi, M.; Al-Fuqaha, A.; Sorour, S.; Guizani, M. Deep learning for IoT big data and streaming analytics: A survey. IEEE Commun. Surv. Tutor. 2018, 20, 2923–2960. [Google Scholar] [CrossRef]
- Xie, X.; Wu, D.; Liu, S.; Li, R. IoT data analytics using deep learning. arXiv 2017, arXiv:1708.03854. [Google Scholar]
- Hassan, S.A.; Syed, S.S.; Hussain, F. Communication Technologies in IoT Networks. In Internet of Things; Springer: Cham, Switzerland, 2017; pp. 13–26. [Google Scholar] [CrossRef]
- Kaur, N.; Sood, S.K. Efficient Resource Management System Based on 4Vs of Big Data Streams. Big Data Res. 2017, 9, 98–106. [Google Scholar] [CrossRef]
- Wazurkar, P.; Bhadoria, R.S.; Bajpai, D. Predictive analytics in data science for business intelligence solutions. In Proceedings of the 2017 7th International Conference on Communication Systems and Network Technologies (CSNT), Nagpur, India, 11–13 November 2017; pp. 367–370. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, Y.; Chen, P.; Shu, Y.; Rao, Z.; Pan, L.; Yang, B.; Guo, C. LightGTS: A Lightweight General Time Series Forecasting Model. arXiv 2025, arXiv:2506.06005. [Google Scholar] [CrossRef]
- Xu, Z.; Zeng, A.; Xu, Q. FITS: Modeling time series with 10k parameters. arXiv 2023, arXiv:2307.03756. [Google Scholar] [CrossRef]
- Huang, J.; Li, J.; Oh, J.; Kang, H. LSTM with spatiotemporal attention for IoT-based wireless sensor collected hydrological time-series forecasting. Int. J. Mach. Learn. Cybern. 2023, 14, 3337–3352. [Google Scholar] [CrossRef]
- Virmani, C.; Choudhary, T.; Pillai, A.; Rani, M. Applications of Machine Learning in Cyber Security. In Handbook of Research on Machine and Deep Learning Applications for Cyber Security; IGI Global: Hershey, PA, USA, 2020; pp. 83–103. [Google Scholar] [CrossRef]
- Marjani, M.; Nasaruddin, F.; Gani, A.; Karim, A.; Hashem, I.A.T.; Siddiqa, A.; Yaqoob, I. Big IoT data analytics: Architecture, opportunities, and open research challenges. IEEE Access 2017, 5, 5247–5261. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wu, F.; Fan, W.; Tang, J.; Liu, H. Multi-dimensional joint prediction model for IoT sensor data search. IEEE Access 2019, 7, 90863–90873. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Sen, P.; Roy, M.; Pal, P. Application of ARIMA for forecasting energy consumption and GHG emission: A case study of an Indian pig iron manufacturing organization. Energy 2016, 116, 1031–1038. [Google Scholar] [CrossRef]
- Calheiros, R.N.; Masoumi, E.; Ranjan, R.; Buyya, R. Workload prediction using ARIMA model and its impact on cloud applications’ QoS. IEEE Trans. Cloud Comput. 2014, 3, 449–458. [Google Scholar] [CrossRef]
- Kane, M.J.; Price, N.; Scotch, M.; Rabinowitz, P. Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 outbreaks. BMC Bioinform. 2014, 15, 276. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.A.; Akber, A.; Xu, Y. Sliding window regression-based short-term load forecasting of a multi-area power system. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Zivot, E.; Wang, J. Rolling analysis of time series. In Modeling Financial Time Series with S-Plus®; Springer: New York, NY, USA, 2003; pp. 299–346. [Google Scholar] [CrossRef]
- Brownlee, J. Long Short-term Memory Networks with Python: Develop Sequence Prediction Models with Deep Learning. In Machine Learning Mastery; Jason Brownle: West Point, MS, USA, 2017. [Google Scholar]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Lee, S.I.; Yoo, S.J. A Deep Efficient Frontier Method for Optimal Investments; Department of Computer Engineering, Sejong University: Seoul, Republic of Korea, 2017. [Google Scholar] [CrossRef]
- Choi, H.K. Stock price correlation coefficient prediction with ARIMA-LSTM hybrid model. arXiv 2018, arXiv:1808.01560. [Google Scholar]
- Ghofrani, M.; Carson, D.; Ghayekhloo, M. Hybrid clustering-time series-bayesian neural network short-term load forecasting method. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Rathnayaka, R.M.K.T.; Seneviratna, D.M.K.N.; Jianguo, W.; Arumawadu, H.I. A hybrid statistical approach for stock market forecasting based on artificial neural network and ARIMA time series models. In Proceedings of the 2015 International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC), Nanjing, China, 30 October–1 November 2015; pp. 54–60. [Google Scholar] [CrossRef]
- Horelu, A.; Leordeanu, C.; Apostol, E.; Huru, D.; Mocanu, M.; Cristea, V. Forecasting techniques for time series from Sensor Data. In Proceedings of the 2015 17th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 21–24 September 2015; pp. 261–264. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, J.; He, Y.; Zhang, Y.; Xiong, G.; Liu, Y. Short-term load forecasting based on integration of SVR and stacking. IEEE Access 2020, 8, 227719–227728. [Google Scholar] [CrossRef]
- Khalid, A.; Sarwat, A.I. Unified univariate-neural network models for lithium-ion battery state-of-charge forecasting using minimized akaike information criterion algorithm. IEEE Access 2021, 9, 39154–39170. [Google Scholar] [CrossRef]
- Kristianto, R.P. Modeling of time series data prediction using fruit fly optimization algorithm and triple exponential smoothing. In Proceedings of the 2019 4th International Conference on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 20–21 November 2019; pp. 407–412. [Google Scholar]
- Akrami, N.; Li, Y.; Dey, P.; Dev, S. Spatial-Temporal-TES: Reanalysis Dataset Based Short-Term Temperature Forecasting System. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 1763–1768. [Google Scholar]
- Guan, H.; Jiang, Q. Pattern matching of time series and its application to trend prediction. In Proceedings of the 2008 2nd International Conference on Anti-Counterfeiting, Security and Identification, Guiyang, China, 20–23 August 2008; pp. 41–44. [Google Scholar]
- Hu, Y.L. Day-Ahead Solar Power Forecasting with Pattern Analysis and State Transition. In Proceedings of the 2021 3rd Global Power, Energy and Communication Conference (GPECOM), Antalya, Turkey, 5–8 October 2021; pp. 148–153. [Google Scholar]
- Singh, N.; Swetapadma, A. Pattern Recognition and Prediction in Time Series Data Through Retrieval-Augmented Techniques. In Proceedings of the 2024 International Conference on Electrical Electronics and Computing Technologies (ICEECT), Greater Noida, India, 29–31 August 2024; pp. 1–6. [Google Scholar]
- Cao, B.; Chang, L.; Gong, X.; Barrera, J.L.C.; Levy, T.; Kilpatrick, R. Probability forecasting of wind power ramp events using a time series similarity search algorithm. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 972–976. [Google Scholar]
- Saeed, F.; Rehman, A.; Shah, H.A.; Diyan, M.; Chen, J.; Kang, J.M. SmartFormer: Graph-based transformer model for energy load forecasting. Sustain. Energy Technol. Assess. 2025, 73, 104133. [Google Scholar] [CrossRef]
- Ma, A.; Luo, D.; Sha, M. MixLinear: Extreme Low Resource Multivariate Time Series Forecasting with 0.1 K Parameters. arXiv 2024, arXiv:2410.02081. [Google Scholar]
- Genet, R.; Inzirillo, H. A Temporal Linear Network for Time Series Forecasting. arXiv 2024, arXiv:2410.21448. [Google Scholar]
- Zeng, C.; Tian, Y.; Zheng, G.; Gao, Y. How Much Can Time-related Features Enhance Time Series Forecasting? arXiv 2024, arXiv:2412.01557. [Google Scholar]
- Diamond, H.J.; Karl, T.R.; Palecki, M.A.; Baker, C.B.; Bell, J.E.; Leeper, R.D.; Easterling, D.R.; Lawrimore, J.H.; Meyers, T.P.; Helfert, M.R.; et al. U.S. Climate Reference Network after one decade of operations: Status and assessment. Bull. Am. Meteor. Soc. 2013, 94, 489–498. [Google Scholar] [CrossRef]
- Meteoblue. Weather History Download Basel [Online]. Available online: https://www.meteoblue.com/en/weather/archive/export/basel_switzerland_2661604 (accessed on 5 June 2024).
- UCI. Repository of Machine Learning Database [Online]. Available online: http://archive.ics.uci.edu/ml/datasets/Individual+household+electric+power+consumption (accessed on 5 March 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).