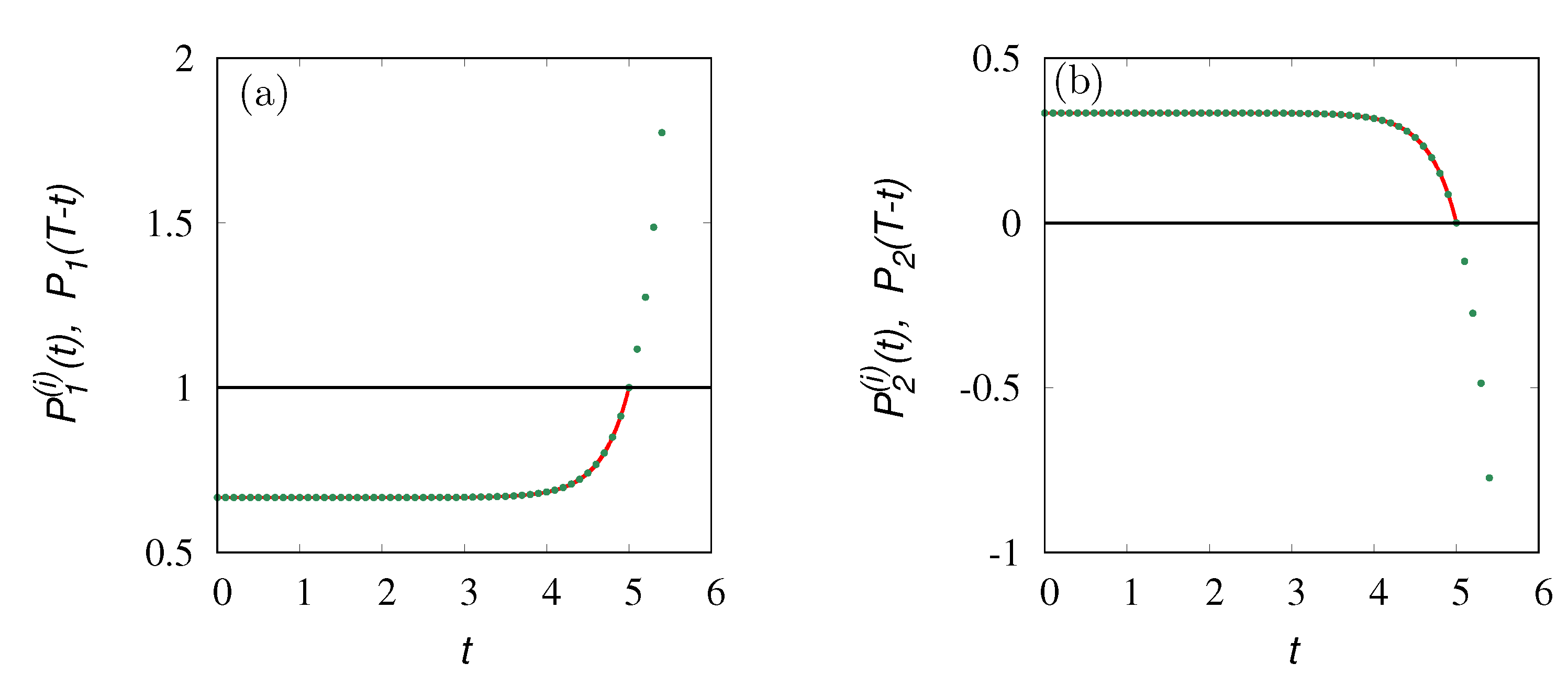1. Introduction
The origin and nature of irreversible behavior is one of the major physical problems that has concerned physics since its ancient formulation (Aristotle’s physics is indeed a form of irreversible physics where dissipation—as in the motion of a massive particle in a fluid medium—is accounted for [
1]). With the rise of mechanics and its conservative description (culminating with the Hamiltonian formalism and the Liouville theorem), the issue of irreversibility has been turned into the problem of deriving the irreversible/dissipative behavior as an epistemic emergent property of conservative Hamiltonian dynamics [
2,
3,
4,
5]. This was indeed the central issue in the famous Boltzmann–Zermelo dispute [
6], further elaborated on by generations of physicists (see [
4,
7] and references therein). The pioneering works by Albert Einstein on the role of quantum effects on macroscopic thermodynamic properties (specific heats, Brownian motion, etc.) [
8,
9] indicated that a consistent theory of irreversibility should necessarily take into account quantum effects either in the form of radiative transitions [
10,
11,
12] or interactions with the zero-point field [
13]; see also [
14]. With this physical background, the theory of irreversible thermodynamics has been developed essentially as a continuous thermodynamic theory, in which all the microscopic mechanisms are embedded into the phenomenological constitutive equations for the fluxes.
The classical formulation of the theory of irreversible processes is essentially based on the Onsager–Machlup linear relation between fluxes and thermodynamic forces [
15,
16], further elaborated on by Green and many other authors [
17,
18]. This theory is essentially grounded in parabolic transport equations for the concentration fields and to equilibrium Gaussian distributions. The intrinsic asymmetry of parabolic models in treating space and time variables (first order in time, second order in space) leads to the paradox of infinite propagation velocity, as immediately follows from the non-compactly supported nature of the diffusional Green function for any time
[
19].
This problem has been addressed by Carlo Cattaneo who proposed a hyperbolic transport model to solve it, nowadays referred to as the Cattaneo heat equation [
19,
20]. The Cattaneo heat equation, independently of its intrinsic relevance, has represented a major stimulus in thermodynamic research in order to extend the theory beyond the assumptions of the parabolic models (corresponding to what is commonly referred to as “the theory of irreversible processes” [
18]), generalizing the representation of entropy production rate beyond the equilibrium ansatz, thus developing a more general framework referred to as “extended thermodynamics” [
21,
22]. Specifically, the rate of entropy production has been generalized by Ingo Müller and Tommaso Ruggeri to include an additional quadratic dependence on the fluxes that superimpose to the expression deriving from equilibrium thermodynamics, and definitely vanishing at equilibrium. Further insights on the thermodynamic analysis of the Cattaneo equation can be found in Refs. [
23,
24,
25], and a detailed flux-based model of both heat and mass transport in multicomponent systems leading to the Cattaneo equation has been recently developed in Ref. [
26]. We return to a more careful discussion on the analyses developed in Refs. [
23,
24,
25] in
Section 3, connecting it to the stochastic interpretation of the Cattaneo equation.
The field of irreversible thermodynamics has been developed via several different theories: classical irreversible thermodynamics, rational thermodynamics, internal variable thermodynamics, rational extended thermodynamics, GENERIC (General Equation for Non-Equilibrium Reversible-Irreversible Coupling) formalism, conservative–dissipative formalism. We refer to Refs. [
27,
28,
29,
30,
31,
32,
33] and references therein for a thorough analysis and discussions of these approaches. The common denominator of these theories is the continuous formulation via smooth fields (of position and time) of the thermodynamic problem by choosing an appropriate set of non-equilibrium variables and internal degrees of freedom (the choice being different from theory to theory), deriving their corresponding evolution equations consistently with thermodynamic principles. This can be referred to as a top-down approach, typical of the striving for generality in thermodynamic, in which the formal structure of the theory is derived from basic principles (first and second principles of thermodynamics, objectivity, etc.), the functional forms of the equations for the continuous fields chosen in order to satisfy these principles, and subsequently their physical validity (and agreement with experiments), is put in relation to specific classes of physical systems (for fluids, it can be compressible/incompressible, Newtonian/viscoelastic, simple liquids/polymeric liquids/suspensions, normal fluids/superfluids, etc.). In this way, i.e., in pursuing a mathematical continuous-field approach, some, more subtle, physical pre-conditions and requirements may be unwittingly violated.
With specific reference to the extended thermodynamics by Müller and Ruggeri, while this extension has marked a major advance in thermodynamic modeling of a variety of physical phenomena, motivating the conviction that the hyperbolic theory is not only physically consistent (with the principles of relativity as regards the boundedness of propagation velocity), but also necessary in order to account for the experimental observations (e.g., as regards heat transfer [
34,
35,
36]), especially at the microscale [
22,
37], the hyperbolic foundation of extended irreversible thermodynamics grounded on the Cattaneo equation is characterized by a conceptual and mathematical shortcoming, namely, the lack of positivity of the Cattaneo heat equation in spatial dimensions higher than one. In the one-dimensional case Mark Kac proved the stochastic foundation of the Cattaneo model, and thus, its positivity [
38].
The issue of positivity has been pointed out in Refs. [
39,
40], and it has represented the main motivation for analyzing a stochastic interpretation of transport models in higher dimensions via the concept of generalized Poisson–Kac (GPK) processes [
40,
41], that subsequently has been extended to encompass also anomalous diffusional effects [
42,
43].
The starting principle, in the analysis in Massimiliano Giona and colleagues [
40] of transport models, referred to as the principle of stochastic consistency, is indeed quite simple: the transport models expressed in the form of integro-differential equations for the concentrations of the transported entities should indeed derive from the micro/mesoscopic stochastic equations of motion at the particle/molecular level as their statistical description (generalized Fokker–Planck equations). In this way, the fulfillment of positivity is automatically ensured from probability theory. This is not the case in continuous models, no matter how detailed or elaborate they are. For instance, consider the elegant multicomponent theory elaborated in Ref. [
26]. Numerical simulations provided in Ref. [
26] refer to one-dimensional models with Dirichlet and Neumann boundary conditions, for which the Cattaneo equation is stochastically consistent, and positivity is generically ensured, paying attention to the expression for the boundary conditions (see [
44] for a thorough analysis of this issue). In higher dimensions, and for generic boundary conditions, the problem of negative concentrations may arise.
The principle of stochastic consistency corresponds to a bottom-up approach, starting from micro/mesoscopic models of the system (theoretically derived and/or experimentally verified), expressed in the form of stochastic differential equations (in order to account for the effects of thermal and possibly quantum fluctuations/transitions), aimed at deriving out of them continuous field equations for the irreversible processes under investigation. In this way, the definition of the internal variables acquires a direct physical meaning, as it is not subject to a modeling choice at a thermodynamic macroscopic level, but follows from the description of the microscopic physics, deriving either from experiments or from fundamental statistical physical or molecular modeling. The validity/accuracy of the resulting thermodynamic model, thus, rests entirely on the validity/accuracy of the underlying microscopic model from which it has been derived. This provides a two-way scrutiny of the microscopic physics also via macroscopic/thermodynamic experiments, and consequently a deeper understanding of the fundamental mechanisms involved.
In the first part of the present article, we carefully analyze the issue of positivity for transport operators associated with mass and heat transfer, as this represents a foundational principle in any thermodynamic theory of irreversible processes, at the same level of physical importance of the positivity of entropy production rates in out-of-equilibrium conditions. As follows from the Pawula theorem [
45], the positivity constraint is not restricted to models possessing finite propagation velocity, as it embraces the whole theory of Markovian processes. Indeed, the Pawula theorem can be invoked for the generalizations of Boltzmannian kinetic theory (Burnett, super-Burnett equations) beyond the classical 5-modes expansion [
46], in order to understand some potential shortcomings of these approaches as regards the positivity of the solutions. Starting from the pioneering work by Harold Grad on the 13-modes expansion of the Boltzmann equation [
47], it becomes clear that more refined truncation approximations of the kinetic Boltzmann equation may produce more accurate results (for rarefied systems) at the cost of losing the positivity requirement or providing related unphysical phenomena [
48,
49]. Turning back to the Cattaneo equation, while it is possible to derive it via a truncated expansion (see, e.g., [
50]), the lack of positivity of its solutions does not stem from the truncation approximation: the same truncation in one-dimensional spatial problems provides a consistent model as regards positivity and stochastic consistency, while in higher spatial dimensions this is not the case.
Indeed positivity, or more accurately the lack of positivity, is one of the most distinctive alarm bells of the lack of a correct thermodynamic behavior. We address this issue with the aid of a problem raised by Jos Uffink [
51], and further elaborated in Ref. [
52], in connection with the analysis irreversibility and thermodynamic behavior developed by Michael Mackey [
53,
54].
The stochastic alternative to the Cattaneo model in higher dimensions is expressed by GPK models [
40,
41,
55,
56] characterized by Markovian transition rates, that reduce to the Cattaneo equation in the one-dimensional case assuming a two-velocity simplification. This class of models put forward a representation issue, consisting of the feature that the resulting concentration fields of continuous thermodynamic theories may be functions not only of space and time variables, but also of other internal degrees of freedom, such as velocities or velocity orientations, in order to account for the Markovian nature of the transition process. This case bears similarities with the kinetic foundation of transport theory, grounded in the Boltzmann equation, in which the one-particle density function—the dynamics of the lower moments of which determines mass, momentum, and energy balances—depends explicitly on the particle velocity [
57].
The above observations bring attention to the representation issue in continuous theories of irreversible thermodynamics, as in general the concentration fields involved in these equations may depend also on additional internal variables, and this dependence cannot be neglected. The analysis of this topic represents the second part of this article, where we consider two interesting case studies motivated by microfluidic applications and by the analysis of chemical physical processes at microscale. The first problem is represented by the interaction of diffusing particles with a solid boundary where adsorption/chemical reaction takes place. If the hydrodynamic interactions are accounted for, the effective diffusion coefficient depends on the particle position and it vanishes as the particle approaches the surface [
58,
59]. But even if the diffusivity is assumed to be constant, a subtle issue of stochastic consistency of the parabolic model arises due to the interplay between a stochastic model possessing unbounded propagation velocity (the Wiener model associated with the parabolic diffusion equation) and ordinary reactive events possessing a finite transition rate and/or a finite probability of occurrence.
The second case study is represented by mass-transport phenomena in complex viscoelastic flows in which any consistent model for mass transport should necessarily account for the internal degrees of freedom associated with the viscoelastic relaxation of the solvent fluid [
60,
61,
62].
The article is organized as follows.
Section 2 succinctly reviews the problem of the positivity of the Cattaneo equation and its stochastic solution in terms of generalized Poisson–Kac processes.
Section 3 addresses the issue of positivity in a broader thermodynamic context, providing a physical interpretation of the Uffink counterexample to the Mackey theory of irreversibility. The case of a one-dimensional Poisson–Kac dynamics (Cattaneo equation) under time-reversal is explicitly analyzed. The representation issue originated by the formulation of GPK processes is also analyzed.
This significant aspect is further exemplified with the aid of problems deriving from chemical–physical/hydrodynamic phenomena at the microscale.
Section 4 addresses the problems of diffusing particles undergoing adsorption or chemical reactions at a solid surface, as the parabolic model in this case suffers some delicate issues of stochastic consistency, in that it cannot be represented by means of a stochastic dynamics with ordinary annihilation rates. Conversely, hyperbolic models are intrinsically suited for elegantly handling these problems.
Section 5 addresses another physical problem leading to interesting representation issues for continuous concentration fields, related to diffusion in viscoelastic fluids, the rheological properties of which are accounted for and impact, via fluctuation–dissipation relations, the transport properties of the diffusing solute.
2. Positivity Constraint and Stochastic Representation: The Case of the Cattaneo Equation
The positivity of the concentrations of individual entities (atoms, molecules, photons) is a logical consistency principle associated with their ontological definition, marking the difference between particle-based and field-based physics. The concept of “concentration” is intrinsically associated with a counting process, and with the ontological principle that an individual entity either can be or cannot be, but it cannot “negatively be”. This principle is naturally transferred to the evolution equations for the concentrations. In this meaning it takes priority over any other physical principle, such as the thermodynamic constraints associated with the second principle. Moreover, if concentrations were negative, also the formulation of entropic inequalities would in general fail. The typical example is provided by the diffusion equation on the real line
with
(the positivity of
D is indeed a thermodynamic constraint, ensuring the existence and boundedness of the solutions of Equation (
1) for
, i.e., summable, initial conditions),
, equipped with regularity conditions at infinity,
An entropy function for the diffusion equation is given by the Boltzmann–Gibbs entropy
:
for which one obtains
that is strictly greater than or equal to zero provided that
Fortunately, Equation (
4) is ensured by the extremum principle for the parabolic diffusion equation [
63], provided that
. However, in dealing with more complex transport equations, in which the expression for the fluxes has been obtained from continuous thermodynamic theories, the fulfillment of the positivity constraint is far from being guaranteed. A typical example is provided by the Cattaneo equation. Consider the Cattaneo equation for a concentration field
,
,
characterized by two parameters, the diffusivity
D [m
2/s], and the relaxation time
[s], out of which the characteristic velocity
,
can be defined. The inclusion of the first term on the left-hand side of Equation (
5) with
determines the hyperbolic character of Equation (
5), that is characterized by a constant propagation velocity
expressed by Equation (
6).
For one-dimensional spatial problems, Equation (
5) specializes as
The reduction of Equations (
5)–(
7) is mathematically trivial, but its physical implications are much subtler that it may seem.
For
, the Cattaneo equation reduces to the parabolic diffusion equation, which admits a straight interpretation in terms of stochastic dynamics: Equation (
5) corresponds, for
, to the Fokker–Planck equation for the probability density function (coinciding, modulo an irrelevant multiplicative factor, with the concentration
), associated with the Wiener-driven Langevin equation:
where
is the particle position vector at time
t and
is the increment in the time interval
of the 3-dimensional Wiener process
(we use capital-letter notation, such as
, for the process, and lower-case notation, for instance
, for a realization of it).
Motivated by this strong connection between stochastic models of motion and transport equations (we return to this issue in
Section 4) it has been natural to search for a stochastic interpretation of the Cattaneo equation. This was provided by Kac in 1974 [
38] (although the original manuscript dates to the early 1950s, and almost at the same time Sheldon Goldstein published an analogous contribution on persistent random walks [
64,
65]), in terms of quite a simple process defined by the parity transition of an ordinary Poisson counting process
,
characterized by the transition rate
.
The stochastic model defined by Equation (
9) is characterized by a constant velocity
, in which the direction of motion is inverted accordingly to the parity of
. Consequently, the transition time
, i.e., the time interval between two inversions in the direction of motion, is itself a random variable characterized by an exponential distribution with density
,
. The position
of the particle at time
t is not a Markovian process, but a Markovian embedding of it can be achieved by considering the joint variable
with
, attaining values
.
In this way, defining the partial probability densities,
the Chapman–Kolmogorov equation applied to
permits derivation of the balance equations for
:
The Cattaneo equation (
7) for the overall density
is recovered from Equation (
11), setting
,
. Due to its stochastic origin, the one-dimensional Cattaneo equation is consistent with the positivity requirement, in that if
, then the
solution of Equation (
7) is non-negative for any
.
The extension of this property to higher dimensions is not possible. In spatial dimensions higher than one, the Cattaneo equation does not admit any stochastic interpretation, in that there is no stochastic process possessing the Cattaneo equation as the evolution equation for its probability density function. Moreover, it has been shown in Ref. [
39] that, starting from two-dimensional spatial problems, the Green function of the Cattaneo equation attains negative values.
This result can be checked by considering the fundamental solution of the one-dimensional
, and of the three-dimensional
Cattaneo equation, corresponding to the response of the Cattaneo equation to an impulsive forcing both in space and time [
66]. In one-dimensional spatial problems, the Cattaneo equation (
7), admits the fundamental solution [
66]
where
is the modified Bessel function of the first kind and order 0, and
is the Heaviside step function of arguments
. In a similar way, the fundamental solution of the Cattaneo equation (
5) in
is given by [
66]
where
is the Dirac delta function of argument
,
is the modified Bessel function of the first kind and order 1 of argument
, and
represents the continuous, non-impulsive part of the fundamental solution, defined by Equation (
13).
Figure 1 depicts the fundamental solutions of the Cattaneo equation in one and three dimensions. In the one-dimensional case,
is always non-negative, consistent with the positivity requirement (
Figure 1a). Conversely, the regular, non-impulsive part of the three-dimensional fundamental solution
in
displays negative values (
Figure 1b).
The lack of positivity is a major physical problem in all the cases in which the concentration corresponds to the specific content of intrinsically non-negative physical entities, such as in mass and thermal transport problems.
The only exception is represented by momentum transfer, i.e., the equations of hydrodynamics, as the hydrodynamic mean-field velocity is the first-order moment of a probability distribution function (see, e.g., the classical kinetic analysis based on the Boltzmann equation), and consequently no requirement of positivity for the momentum-transfer equations is dictated by fundamental principles. In the case of momentum transfer, the natural extension of the Newtonian paradigm is to consider constitutive equations of a viscoelastic nature for the shear stress tensor as a function of the deformation tensor, characterized by finite non-vanishing relaxation times [
67,
68]. In this way, the finite propagation velocity of the shear stresses can be accounted for, as discussed in Ref. [
62] (see also [
61]). Nevertheless, in dealing with hydrodynamics, this represents a second-order problem with respect to the commonly assumed hypothesis of incompressibility for liquid flows, corresponding to the solenoidal condition for the velocity field, as the latter implies an infinite convective velocity in the propagation of density and pressure perturbations (infinite sound velocity). A way to overcome this issue is addressed in Ref. [
69], where a dynamic formulation of the pressure contribution is proposed.
3. Positivity Constraint and Irreversibility
As addressed in
Section 2, the condition of positivity is structural and fundamental whenever mass and thermal balances are concerned. To perform a mass balance means essentially to count the number of molecules (particles) that are present in infinitesimal volume elements. A negative number of atoms (and similarly a negative value of a probability or a probability density) is an alarm bell that something in the theory is deeply incorrect, and it can hardly be justified as acceptable even in a non-classical quantum interpretation of fluctuations (as claimed, e.g., by Richard Feynman [
70]). The occurrence of negative probabilities in quantum mechanics was also addressed by Paul Dirac [
71] as a consequence of the quantum formalism to be essentially conceived in a “hypothetical quantum world”, while in the “actual world” (i.e., in the physical phenomenology and reality) transition probabilities should be always considered as positive quantities. In any case, one should avoid a misinterpretation of this strange quantum fall-out as regards probabilities, with respect to the meaning of probabilities in statistical physics. In stochastic modeling, we use probability densities for particle distributions in space as a normalized representation for concentrations. But as far as the concentration of entities is concerned, its strict non-negative nature is an a priori concept related to just the counting of discrete entities, that ultimately is based on the positivity of mass for molecules and particles, and on the non-existence of antiparticles for massless photons (as the antiparticle of a photon is essentially a photon itself).
The positivity of the evolution equations for mass/temperature is, therefore, a fundamental constraint in the balance equations of any theory of irreversible phenomena. In the remainder of this article, we explain why the positivity constraint is actually as fundamental as the fulfillment of the second principle of thermodynamics dictating the positivity of entropy production rates. Specifically, we consider the Mackey theory of irreversibility [
53,
54].
In a series of works [
53,
54], Mackey addressed in detail the properties a dynamical system should possess in order to exhibit thermodynamic behavior. The analysis is based on the Markov operator associated with the dynamics, mapping densities into densities. For instance, if one considers the Langevin dynamics, Equation (
8), the evolution equation for densities is the parabolic diffusion equation,
, and the corresponding Markov operator
, continuously parametrized with respect to
, is
such that
. The proper space for studying the properties of Markov operators is the space of functions
in the domain
(corresponding to the physical region where transport occurs), equipped with the
-norm
. In general, a Markov operator is any linear operator
, parametrized with respect to time
, such that for any
,
the following conditions are met:
Probability conservation:
The time domain of definition of the Markov operator can be either in the case of invertible systems, or for non-invertible ones.
As a criterion for a proper thermodynamic behavior, Mackey chose the increase of the Kullback conditional entropy with respect to the equilibrium density. More precisely, assume that the Markov operator admits an equilibrium density
, such that
. The conditional entropy,
, of
with respect to
is defined by
and, according to Mackey, a system possesses a proper thermodynamic behavior if the conditional entropy
is a monotonically increasing function of
t, vanishing at equilibrium. Based on this reasonable definition, Mackey was able to show that if the Markov operator is invertible, then
i.e., the conditional entropy does not increase, remaining constant at the value dictated by the initial density
. This is the case in a dynamical system defined by a system of ordinary differential equations. Consequently, “non-invertibility in system dynamics, as reflected in an evolution of densities via a non-invertible Markov operator, is necessary for the entropy to increase as the system evolves” ([
54], p. 33).
This formulation has been questioned by Uffink [
51], and elaborated further in Ref. [
52]. Specifically, Uffink considered a 2-state Markov chain, which, as is known, possesses a proper thermodynamic behavior. Indicating with
and
the probability of the two states, and
, we have
with
. In this case,
, and since
possesses bounded eigenvalues:
,
, the inverse operator
,
, can be defined, and consequently
is invertible, apparently in contradiction with Mackey’s result. More specifically, consider the forward dynamics Equation (
19) up to a given time
, and then define
.
A similar phenomenology arises in the case of Poisson–Kac processes, as well as in the case of any GPK or extended Poisson–Kac process [
43] possessing Einsteinian (the mean square displacement is, in the long term, a linear function of time) or anomalous diffusive behavior (the mean square displacement is, in the long term, a nonlinear function of time). The reason for this essentially lies in the spectral properties of these processes [
52,
72], as the eigevalues of their evolution operators possess bounded real part (in the case of parabolic models, the real part of the ordered eigenvalue sequence diverges to minus infinity, causing
to be a semigroup with respect to time
t, and thus, a non-invertible operator).
In order to make a definite example, consider the simplest two-velocity Poisson–Kac model in non-dimensional form, defined in a closed domain
, equipped with periodic boundary conditions. The dynamics for the partial densities
corresponds to Equation (
11) with
. The Poisson–Kac process possesses a proper thermodynamic behavior. The entropy function in this case can be defined as
By making use of Equation (
11) in the case
equipped with periodic boundary conditions and unit values for
and
(corresponding just to the non-dimensional formulation of the Poisson–Kac process), one obtains
and the definition of the entropy
is analogous, modulo an additive constant, to the Kullback conditional entropy, as the equilibrium partial densities
are uniform in
.
In this case,
, the eigenfunctions of
are just the periodic Fourier imaginary exponentials
, with the associated eigenvalues
,
, where
,
for
and
, for
,
, with
. The closed-form solution of Equation (
11) in this case takes the expression
where the expressions for
,
are reported in
Appendix A.
As for Markov chains, the dynamics of Poisson–Kac processes is invertible: by considering the time reversal
and inverting the direction of the velocity, which corresponds to the transformation
, where
refer to the time-reversal dynamics satisfying the equations
As in the case of the Markov chain, integrate the dynamics up to a given time instant , and then, starting from the profiles at , perform the time-reversal to obtain , .
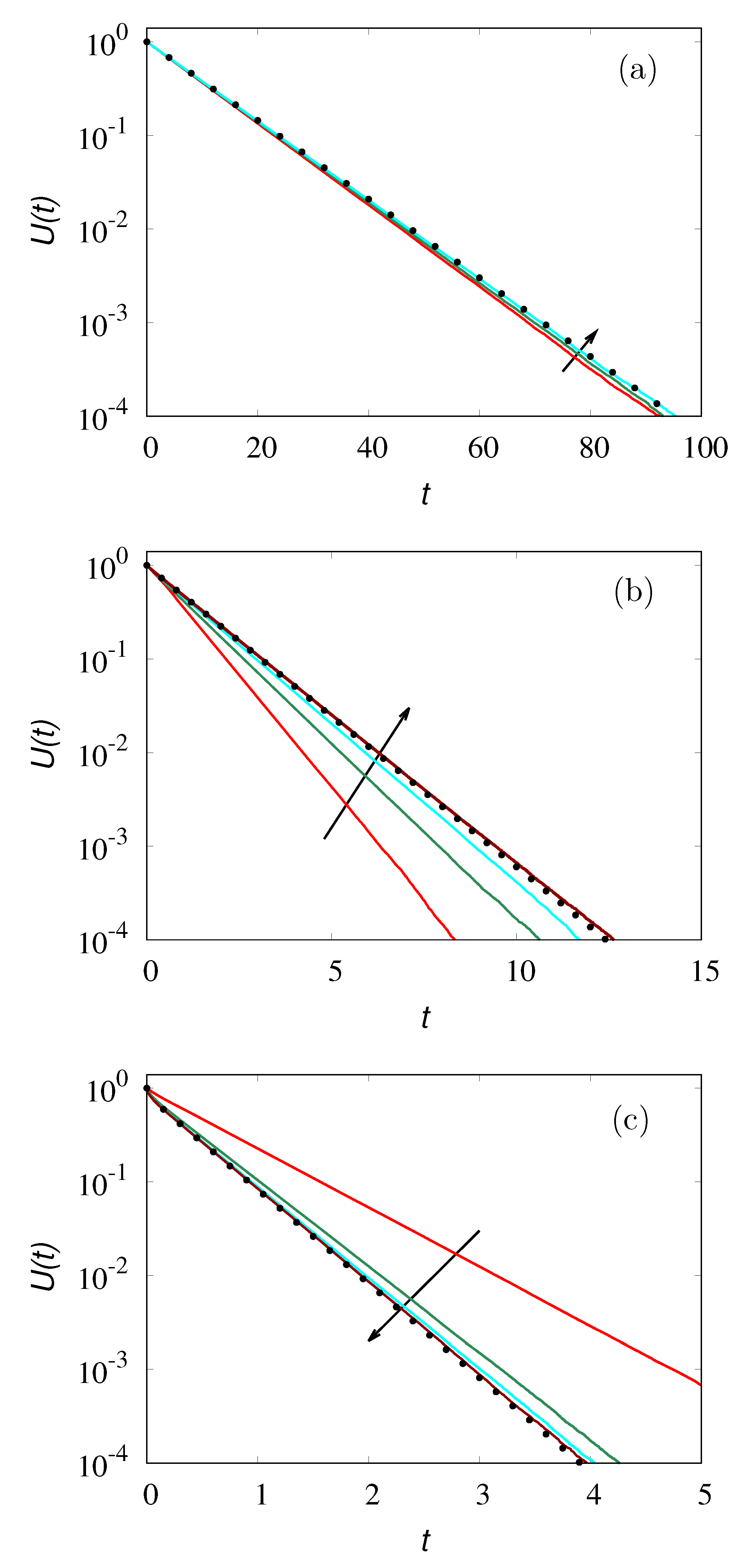
Figure 2 depicts the result of the time-reversal operation, i.e., the quantities
,
, for the 2-state Markov chain starting from
,
,
,
, integrating up to
.
As expected, for
the inverse dynamics correctly reproduce backwardly the forward trajectory up to the initial configuration. For
, the quantities
either attain negative values or values greater than 1. A similar case occurs for the Poisson–Kac dynamics.
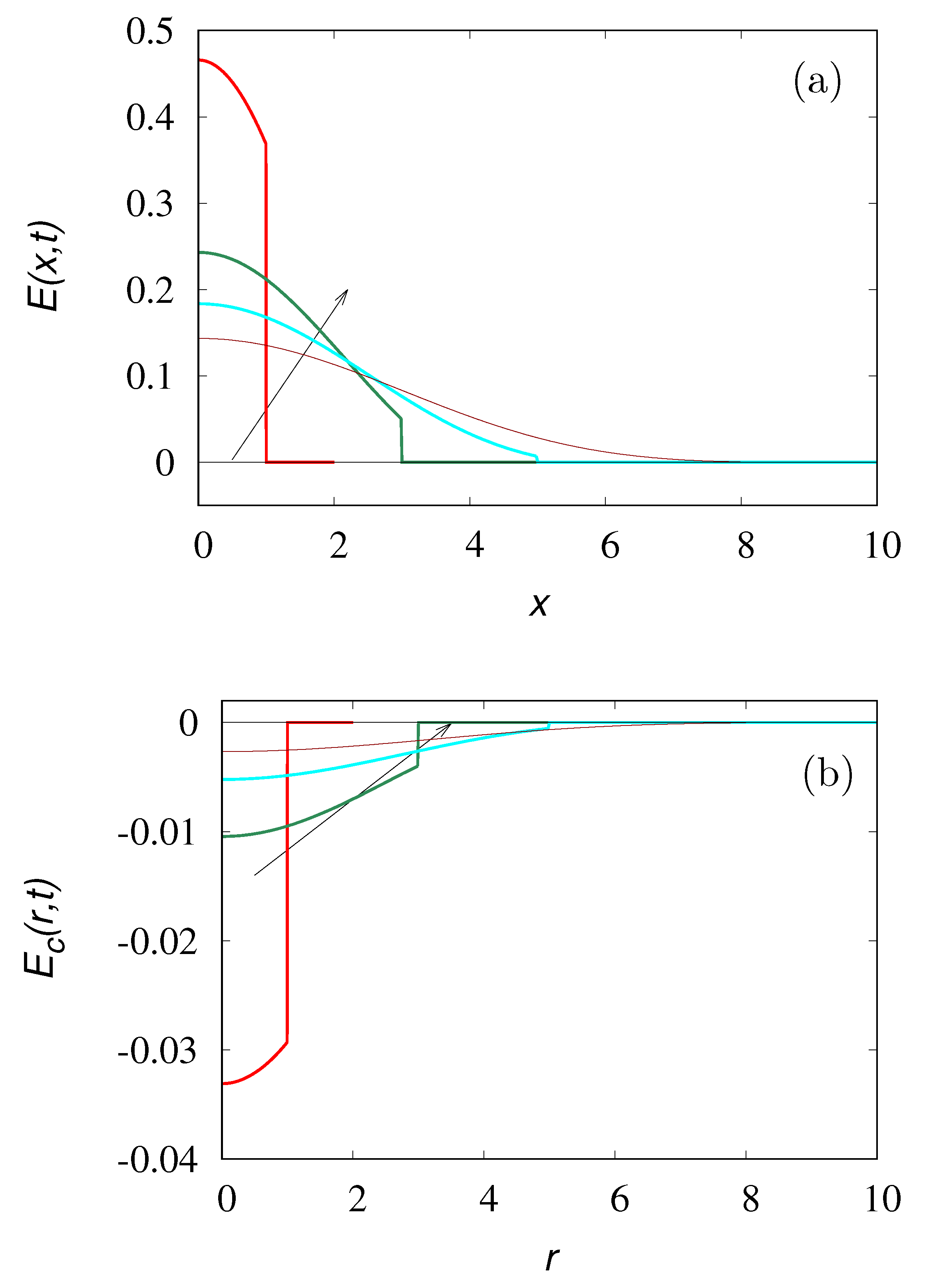
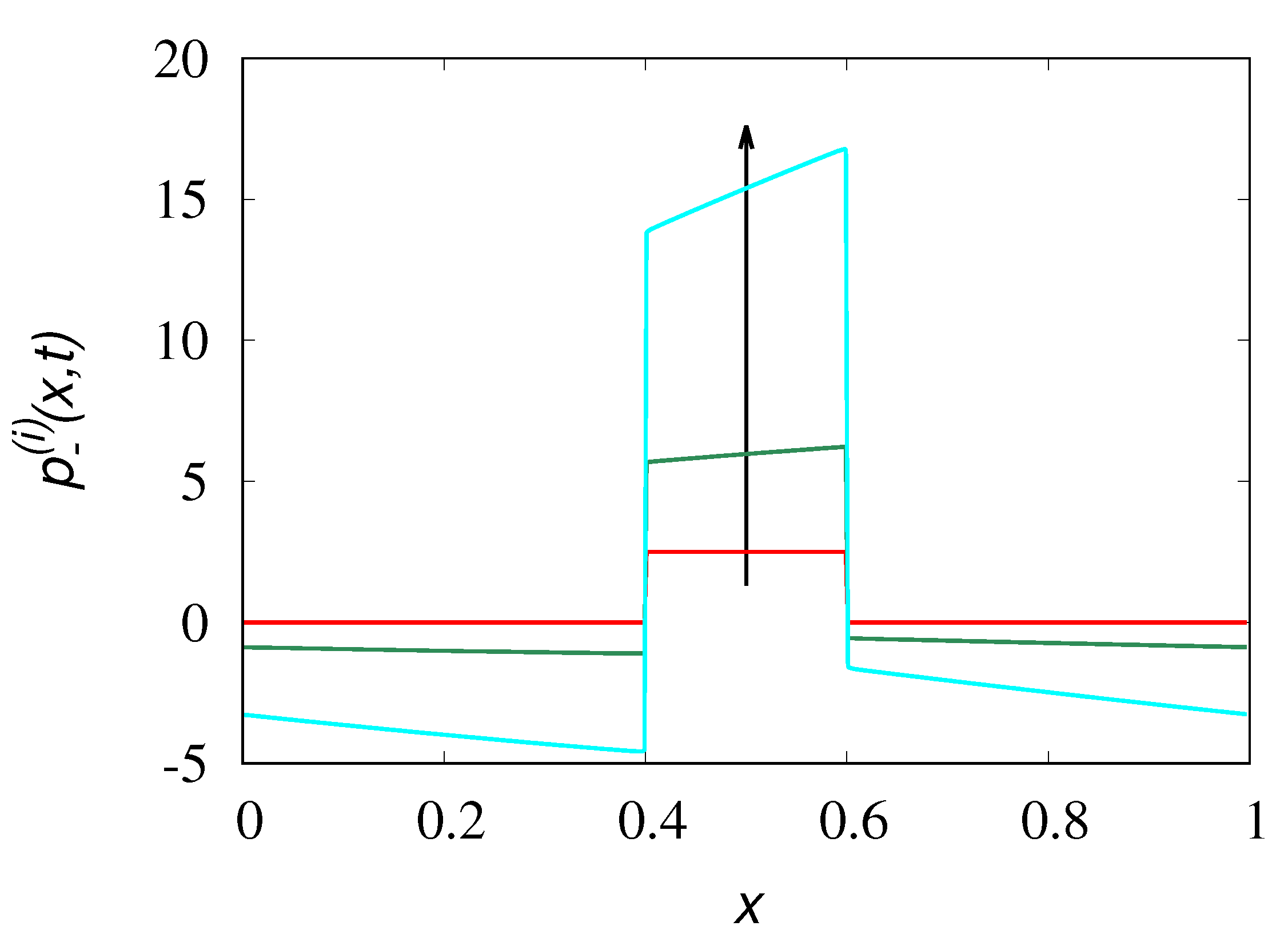
Figure 3 displays the partial density
obtained from Equation (
22), starting from the initial distributions
for
and zero otherwise, with
and
at various time instants. The stopping time was set equal to
.
The profiles of the time-reversed dynamics
(lines) at several values of time
are depicted in
Figure 4 against the results of stochastic simulations (symbols) for
. As expected from the spectral structure of the Poisson–Kac processes the time-reversed dynamics correctly reproduces backwardly the concentration patterns up to
. At later times, the concentration profiles attain negative values, as depicted in
Figure 5, reproducing correctly the initial profile at
.
This result is not surprising, and provides a conclusive answer to Uffink’s objection to Mackey’s theory. For
, the time-reversal defines an operator
that is no longer a Markov operator, as the positivity condition (
15) is not met. In both the cases considered, as well as in all the cases in which the eigenvalues of the Markov operator possess bounded real parts, the positivity constraint (i.e., its failure for the time-reversed operator
) indicates that the time-reversed dynamics does not exist as a probabilistic model (i.e., that
exists as a mathematical operator but it is not a Markov operator), and moreover, that the theory developed by Mackey fully applies to all these cases.
The above analysis indicates the thermodynamic importance of the positivity constraints, and how they can be applied to discriminate between thermodynamic and non-thermodynamic behavior of dynamical systems.
For this reason, in developing higher-dimensional transport models generalizing the Cattaneo heat transfer equation and ensuring the positivity constraint, a safe approach is to obtain them from micro/mesoscopic stochastic models of motion. If one generalizes the original Kac’s approach from one-dimensional to higher-dimensional problems, the natural mass/heat transport model is represented (in the linear case) by generalized Poisson–Kac processes, the probabilistic description of which involves the joint probability density
, parametrized with respect to particle velocity
and defined by the integro-differential equation
with
and
,
. Equation (
24) corresponds to a linear Boltzmann equation, and an open question is to obtain simplified evolution equations for the marginal density
other than the long-term parabolic diffusion equation. This means that thermodynamic theories and transport equations should necessarily include in their formulations the presence of additional degrees of freedom (in this case, the velocity variable
) and develop the theory accordingly. The model may also include additional physical effects, becoming nonlinear in the densities
[
37,
41]. Another even more drastic representation issue emerges in the study of mass transport in complex fluids, as outlined in
Section 5.
The above analysis permits the framing of some further observations on the thermodynamic consistency of the Cattaneo model, that admit a broader range of validity. Limiting the analysis to the one-dimensional case (which is the only stochastically consistent case), some criticisms developed in Refs. [
23,
24,
25] find a natural explanation. The one-dimensional Cattaneo equation is indeed thermodynamically consistent (see, e.g., the discussion in Ref. [
25]) as regards the existence of a monotonically non-decreasing entropy function (expressed by Equation (
20), provided that the entropy is properly defined in terms of its natural internal variables (
,
). In the one-dimensional case, one can always express
in terms of the overall density
and flux
, but whenever higher-dimensional generalized Poisson–Kac processes are considered this is no longer possible. Nevertheless, these processes still have an explicit representation of the entropy function in terms of the system of partial densities [
73].
When considering problems in bounded domains the boundary conditions should be defined consistently with their hyperbolic nature [
23,
44], otherwise lack of positivity may follow from the incorrect modeling of the boundary effects.
The work by Miles Rubin [
24] addresses a remarkable effect of the hyperbolic Cattaneo model, namely, that the flux may locally be directed from a region at lower concentration to a region at higher concentration. More precisely, it may happen at some point,
and
, that
and
, i.e., the flux
is locally directed towards increasing concentration
. For instance, this can be achieved at
if
is a monotonically increasing function of
x while
. In the work by Rubin, this has been considered as a thermodynamic inconsistency, owing to the Clausius formulation of the second law of thermodynamics, and for this reason the author proposes a nonlinear modification of the Cattaneo model. This problem is still matter of discussion in the recent literature as the “dilemma of hyperbolic heat conduction” [
74].
This phenomenon, albeit of transient nature (i.e., occurring for timescales of the order ), and associated with highly particular and extreme initial conditions, is indeed not thermodynamically inconsistent. The reason for this apparently strong claim stems from three major observations. First of all, as discussed above, an entropy function exists which ensures that thermodynamics and the second principle is fulfilled. Secondly, the Clausius principle holds in a thermodynamic context for macroscopically observable processes, i.e., for macroscopic timescales, that in the case of the Cattaneo model correspond to timescales larger than the reciprocal of the transition rate . But the most interesting observation is that if the Clausius formulation is interpreted as a fundamental law of nature (at the same level of the principles of relativity) that should be applied for any , this is in contradiction with the finite propagation velocity of any physical process.
We consider the Clausius formulation adapted to mass transport, albeit its thermal counterpart is conceptually identical. Since the foundations of the theory of extended thermodynamics in the formulation due to Müller and Ruggeri heavily rely on relativistic principles, it is interesting to address further this subtle issue. Actually, a major result in the theory of relativistic kinetics has been proved by Richard Dudley [
75], showing that any relativistically consistent stochastic process cannot be Markovian. For instance, in the Poisson–Kac model
, the particle position is not a Markovian process, as one needs the local orientation
for obtaining a Markovian embedding of it. This determines the need of the two partial densities,
, for a statistical description of the process.
The upper bound for the velocity of propagation (dictated by the velocity of light in vacuo), and the occurrence of a non-vanishing diffusivity, imply a finite correlation time. In the case of the Cattaneo model, and of its Poisson–Kac stochastic counterpart, this just means that should also be bounded. But for any process possessing a bounded correlation time, it is always possible to prepare the system such that locally the flux may go from lower to higher concentration gradients.
In this sense, this result applies to more general systems even beyond the relativistic case, under the condition that the velocity autocorrelation function is a regular function of time. To make the simplest example consider the case of Brownian particles using the Stokes–Langevin formulation:
where
m is the particle mass,
the Stokes friction factor,
, with
the Boltzmann constant,
the temperature, and
the distributional derivative of a Wiener process.
In this case, the velocity autocorrelation function is exponential
,
, and out of Equation (
25) the Fokker–Planck equation for the density
can be straightforwardly derived. Next, consider an ensemble of such particles in a box, for instance,
, with reflective boundary conditions at
, and the following initial condition:
where
is a Gaussian distribution with respect to
v with zero mean and squared variance
. Equation (
26) implies that all the particles are initially located in the right half of the domain with non-negative initial velocities. These initial conditions are well posed from the mathematical point of view. Due to the correlations in velocity, at the early stages of the process the particle ensemble will move preferentially from the region of lower concentration
to the region of higher concentration. This phenomenon is depicted in
Figure 6, where the data and the concentration profiles are obtained from the stochastic simulations of Equations (
25) and (
26), (setting
a.u.,
), using an ensemble of
particles.
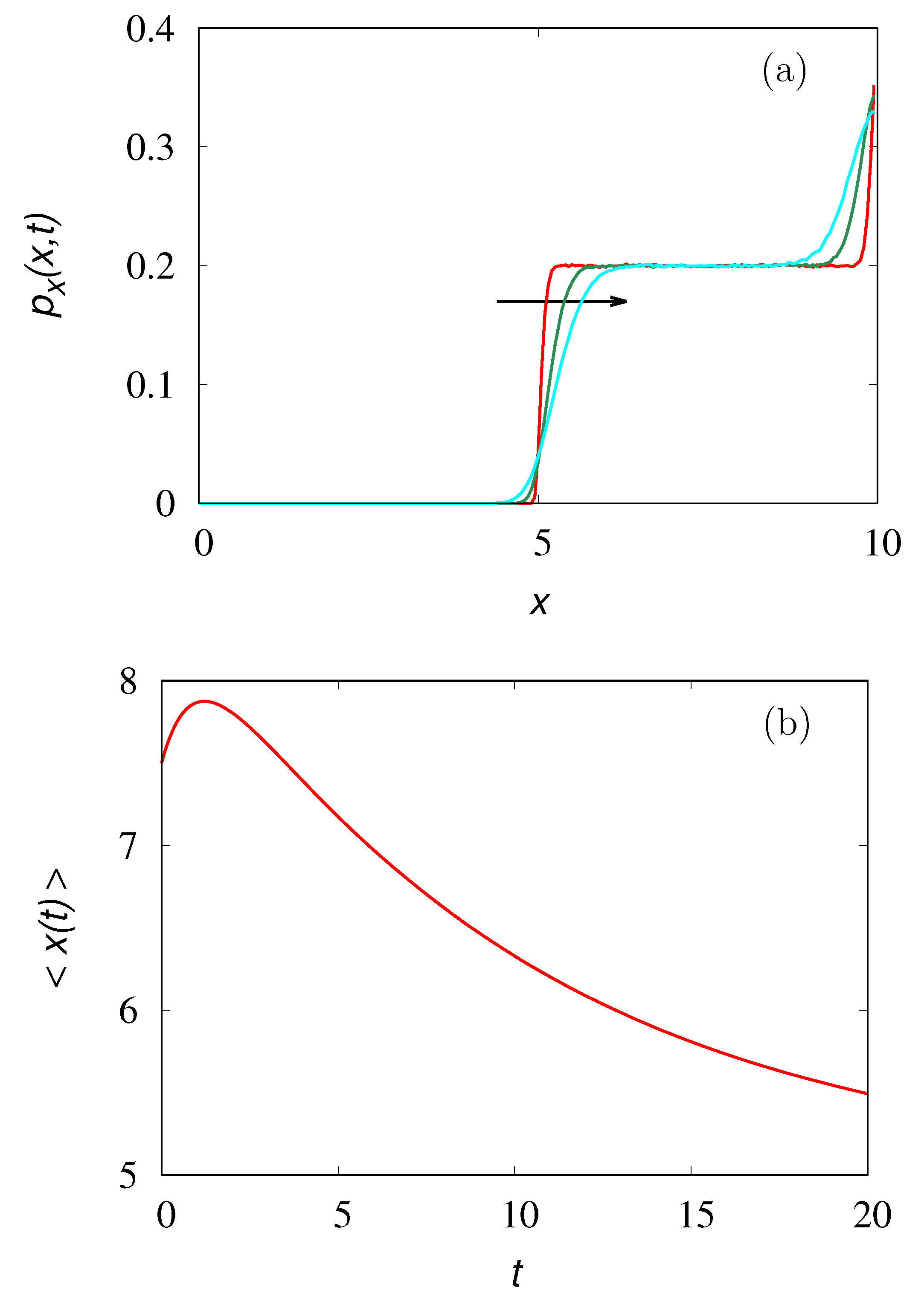
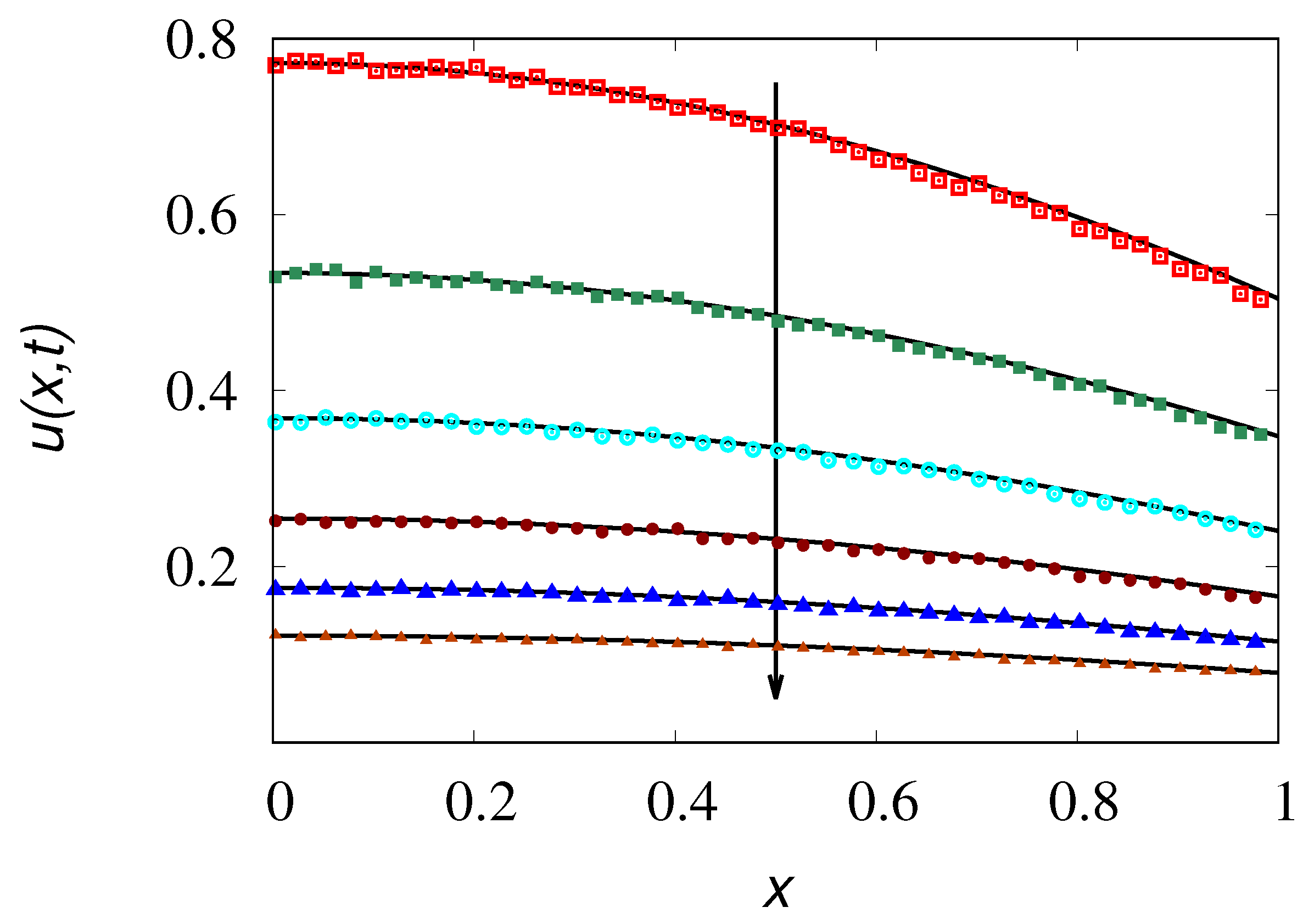
Figure 6a depicts the spatial concentration profiles, i.e., the marginal density
at the early stages of the process, while
Figure 6b shows the mean particle position,
, as a function of time
t.
As can be observed, in the early stages particles move towards the region of higher concentration, as indicated by the increasing behavior of up to , i.e., for timescales of the order of magnitude of the correlation time. Subsequently, fluctuational effects restore the normal diffusive behavior, tending towards homogenization, and thus, .
This example is obviously a “gedanken” experiment. The initial conditions of the form of Equation (
26) are practically never met in physical phenomenology, as it would imply the action of a sort of Maxwell demon to prepare initially the system in this way. But this is not the issue. The main point is that this behavior is still thermodynamically conceivable without violating the second law, and indicates the subtle role played by finite propagation velocity. The same behavior occurs for the Cattaneo model, and this observation can be extended from mass transport to thermal transport with some attention.
4. Coupling Transport with Interfacial Phenomena: Stochastic Consistency at Work
The requirement of stochastic consistency can be used to explore another class of chemical–physical problems, involving the occurrence of chemical reactions at an interface, the prototypical model of which is represented by a diffusing solute performing a chemical reaction at an interface possessing zero measure. This problem highlights a subtle pathology of the parabolic models when considered in the light of a microscopic stochastic model for the process.
Consider a solute, the concentration of which is
, diffusing in a closed domain, for instance,
, and performing at
a surface chemical reaction (modeled as a first-order reaction), while the other boundary,
, is impermeable to mass transport. Assuming the classical parabolic model for diffusion, one has
equipped with the boundary condition,
where the constant
(isothermal conditions are considered) accounts for the “rate” of the surface chemical reaction. This meaning of
is further addressed below. The initial condition is uniform inside the system,
.
In a non-dimensional setting,
,
,
, one has
where
represents the mass-transfer Biot number. For the sake of notational simplicity, we will indicate the non-dimensional variables
and
just as
x and
t. Equation (
29) is a linear problem, admitting a closed-form solution:
where
,
are the roots of the cardinal eigenvalue equation,
. The fraction of solute
within the system at time
t is given by
The non-dimensional concentration
can be interpreted probabilistically as the probability density of finding the solute particles in the system, the dynamics of which is expressed by the Langevin Equation (
8):
where
is the increment of a Wiener process in the time interval
. While the boundary condition at
corresponds to a reflection in particle motion, problems arise in expressing the reactive boundary condition at
for finite and non-vanishing values of
(and consequently of
). This stems from the fact that
is not a rate, as it possesses the physical dimension of a velocity [m/s]. Consequently, the reactive boundary condition does not correspond to an ordinary Markov process for a solute particle touching the reactive boundary and being annihilated at it with some probability.
As is known [
76,
77], it is possible to provide an algorithmic solution to this problem. Consider the numerical simulation of Equation (
32) adopting a time step
, i.e.,
, where
, and
,
are independent and identically distributed random variables sampled from a normal distribution (with zero mean and unit variance). If
touches or crosses the reactive boundary at
, the particle reacts (it is annihilated) with probability
(in the non-dimensional formulation,
), otherwise it is reflected back.
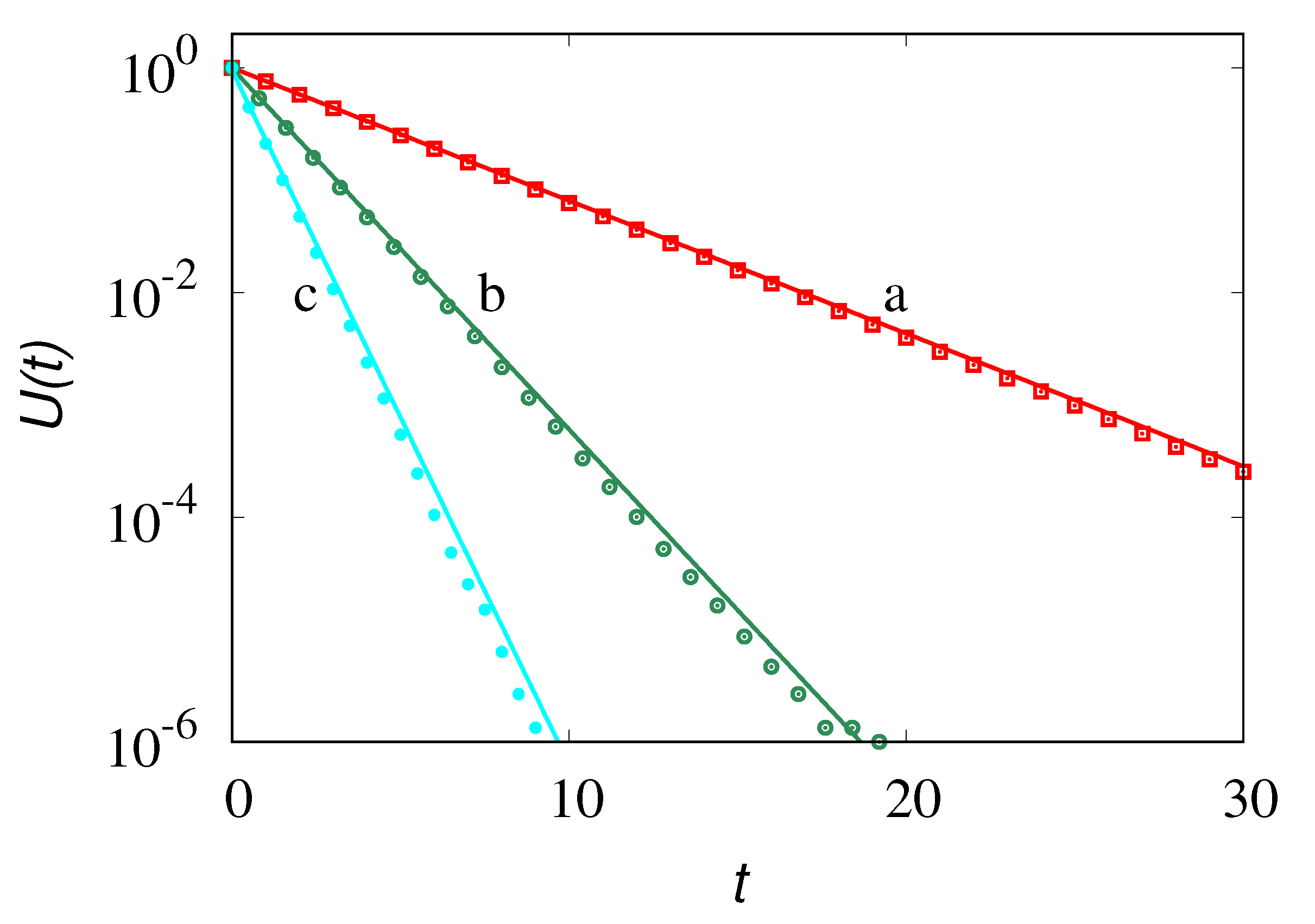
Figure 7 shows the results of stochastic simulations using Equation (
33) for an ensemble of
particles with
compared with the analytical result for
(
31).
However, the application of Equation (
33) to the discretized approximation of the Langevin equation (
32) represents an algorithmic solution of the dynamics that does not correspond to any stochastic process evolving in a continuous space-time and performing ordinary reactive events (i.e., possessing a finite rate). For this reason, one can state that the parabolic model of a diffusing species performing a surface chemical reaction at a solid interface violates the requirement of stochastic consistency, providing a pathological case that can be referred to as the paradox of surface chemical reactions.
Actually, this paradox finds an explanation if one consider the properties of the trajectories of Wiener processes, and their intersections with lower-dimensional manifolds (in this case the reactive interface): if a Wiener process crosses an interface at time
, in the neighborhood of
, a Cantor set (Cantor dust) of intersections occurs, the fractal dimension of which is
[
78], justifying the rescaling of
by a factor proportional to
.
This problem finds a straightforward and elegant solution considering models of transport possessing finite propagation velocity. For simplicity, consider the case of a Poisson–Kac process:
where
,
, so that the effective diffusivity
equals 1, equipped with the following initial and boundary conditions at
:
The reactive events occurring at
are described by means of the probability
, corresponding to the annihilation probability for a particle touching the reactive interface. Consequently, the reactive boundary condition at
becomes, in the hyperbolic setting,
indicating that a fraction
of the incoming flux of particles
is reflected back. Equation (
34), equipped with the boundary conditions (
35) and (
36), admits a consistent stochastic representation, independent of the algorithmic temporal resolution
.
Figure 8 depicts the temporal evolution for
obtained from the stochastic simulations of the hyperbolic model (
34)–(
36) with
,
for several values of the annihilation probability
. The stochastic simulation is rather simple: initially the particles are randomly and uniformly distributed in
, with equal probability of positive and negative velocity directions. Each particle performs a Poisson–Kac dynamics:
, where
is a Poisson counting process with transition rate
. If a particle reaches
it is reflected back, if it reaches
it is annihilated (removed from the ensemble) with probability
.
By varying from to the whole spectrum of physical situations can be described, from complete reflection () to total annihilation once the reactive boundary is touched ().
The parabolic model (
29) can be recovered in the Kac limit, letting
be arbitrarily large, still assuming
, and defining the annihilation probability
in terms of
and the Biot number
. To obtain this relation, consider the expression
for the flux in the hyperbolic model. Enforcing the reactive boundary condition Equation (
36), one has
In the Kac limit (
,
),
, where
is the overall density, so that Equation (
37) provides
This boundary condition should be compared with the boundary condition Equation (
29) of the parabolic model, indicating that the group
should coincide with
, i.e.,
that corresponds to the feature that
decreases as
to vanishing values in the Kac limit. Equation (
39) is indicating the intrinsic pathology of the parabolic Kac limit in the presence of interfacial effects (surface chemical reactions, adsorption phenomena). Given
, for large but finite
s, the annihilation probability
progressively decreases, still attaining non-vanishing values (ensuring the occurrence of the chemical reaction). However, in the limit
, one has
(and
means that the incoming flux at the interface is totally reflected and no reaction occurs), indicating that the Kac limit is a singular limit in the presence of interfacial phenomena. In this sense, the parabolic model (
29) is a singular and physically pathological limit of the hyperbolic Poisson–Kac dynamics.
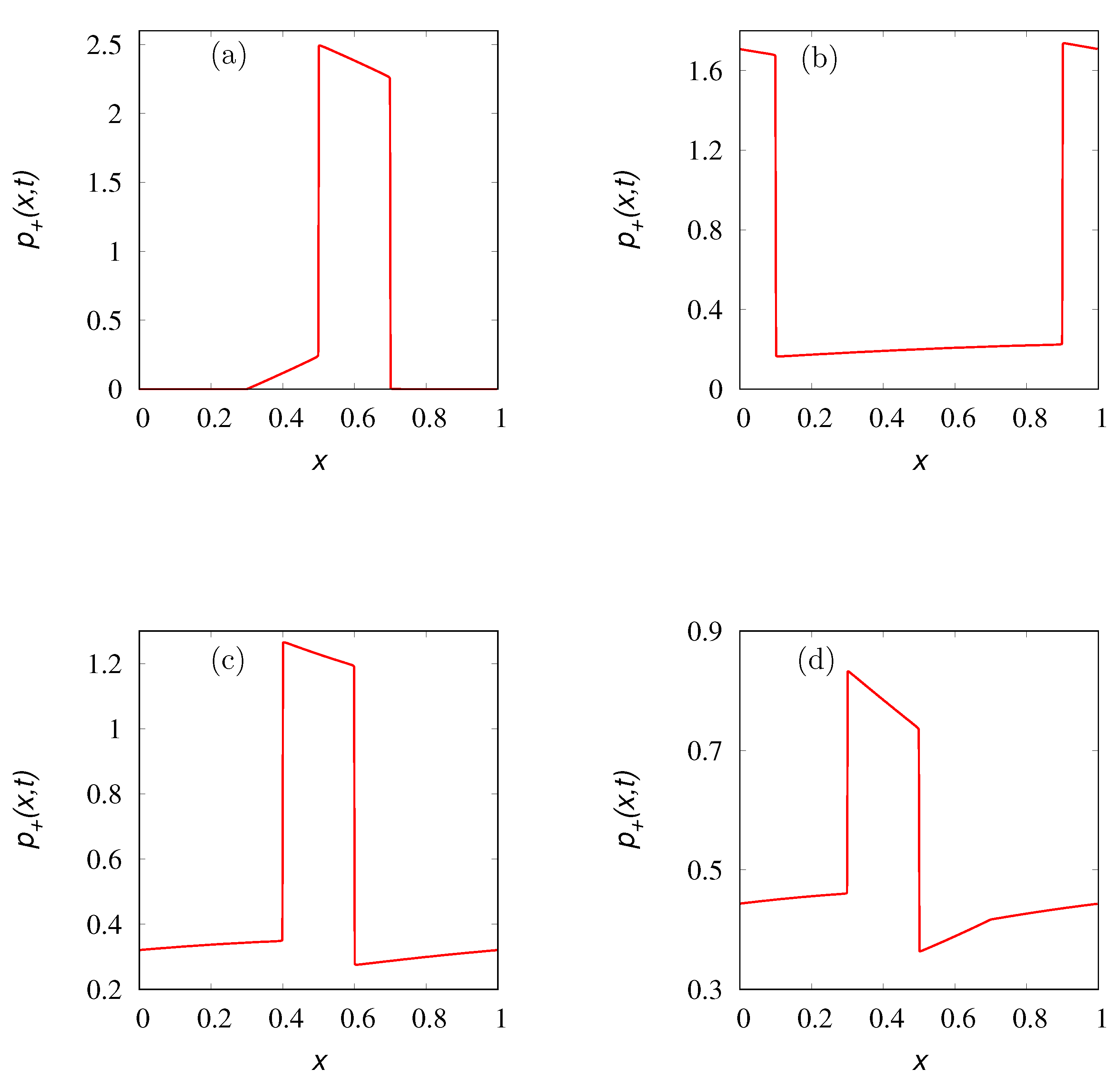
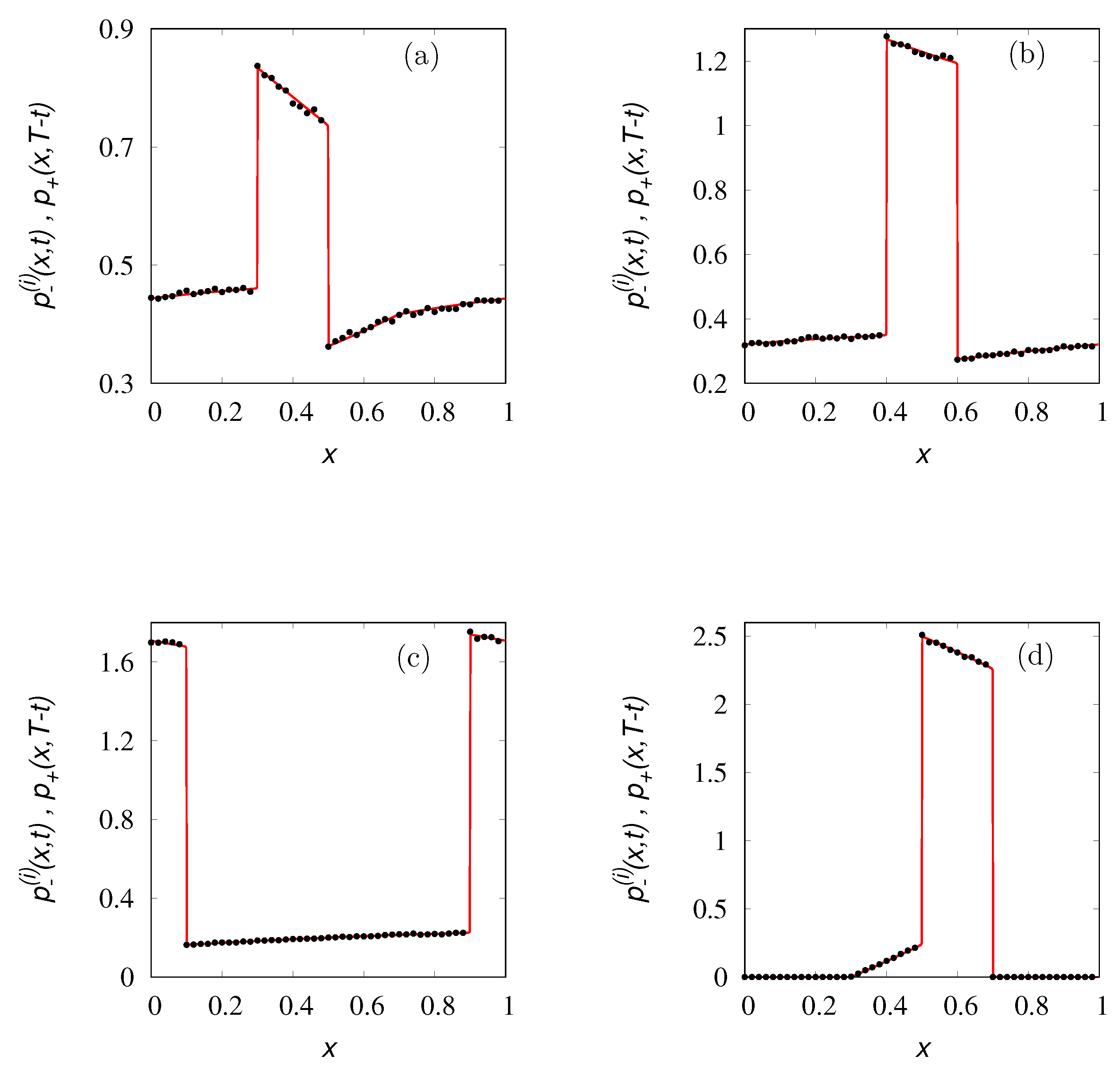
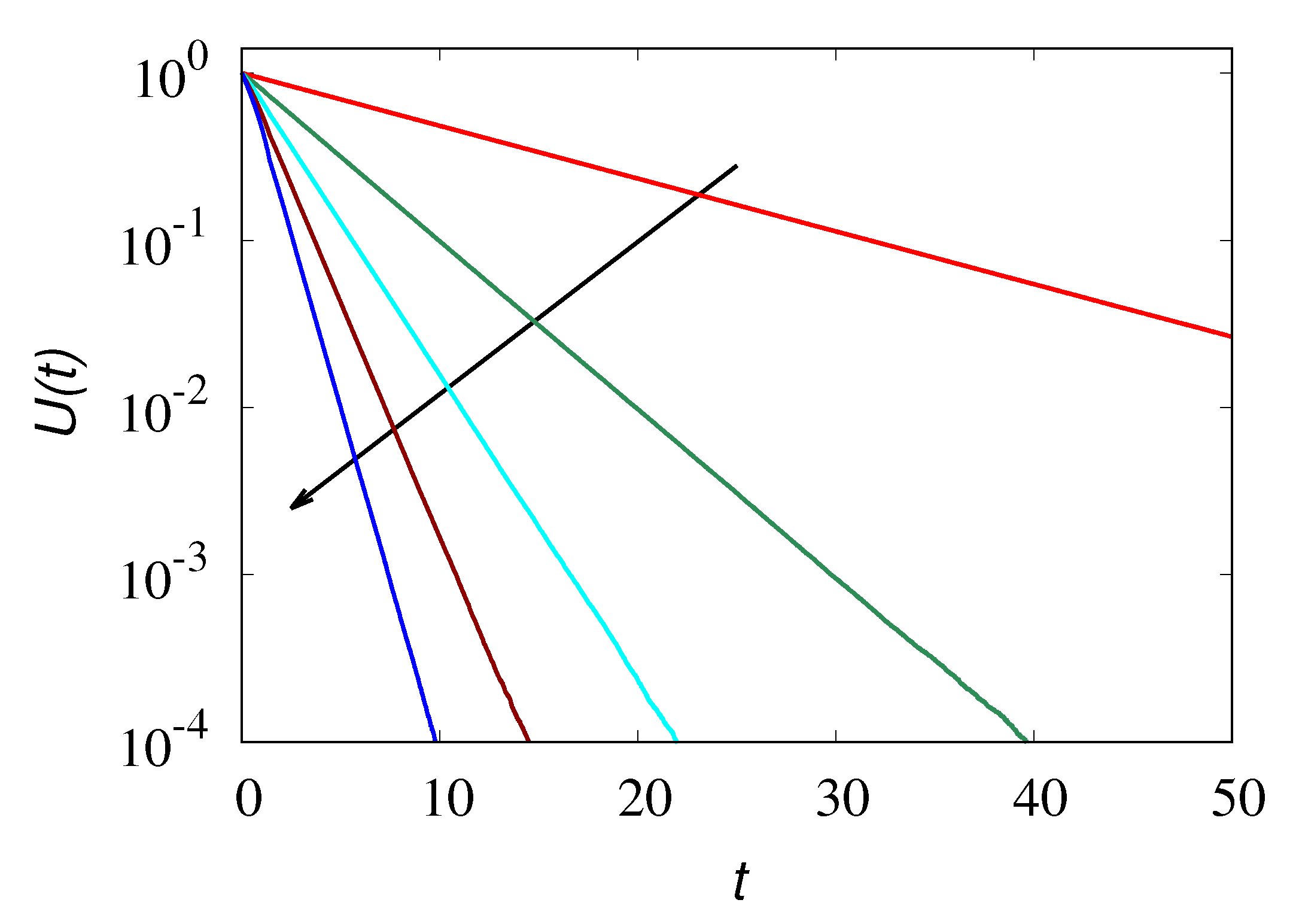
To exemplify the above analysis of the Kac limit for large but finite values of
,
Figure 9 depicts the behavior of
obtained from the stochastic simulations of the hyperbolic transport model at three different values of
for increasing values of
, compared with the corresponding results of the parabolic model (
29)–(
31). The behavior of the concentration profiles at different time instants for
is depicted in
Figure 10 compared with the parabolic result Equation (
30).
The number of particles used in the stochastic simulations reported in
Figure 9 is
, while
for the concentration profiles depicted in
Figure 10.
As expected, the results of the hyperbolic model (
34)–(
36) converge to those of its parabolic limit (
30) and, by taking a large enough value of
, the difference between the two settings becomes immaterial.
5. From Equations of Motion to Continuous Models of Transport
In classical transport theories, as well in the extended formulation of thermodynamic theories of irreversible phenomena, we are used to considering concentration fields of transported entities as smooth functions of spatial and temporal t coordinates, and consequently to develop thermodynamic analyses of their consistency starting from this formal setting.
However, there are cases when a coherent and accurate formulation of the transport equations requires the introduction of additional internal variables, the dynamics of which accounts for the physical response of the system. This phenomenon was discussed in
Section 3 in relation to hyperbolic model of transport associated with GPK processes in order to enforce the requirement of finite propagation velocity. In the current Section, we consider an even more fundamental situation associated with the constitutive properties of a fluid medium.
The main purpose of this paragraph is to show how the definition of the auxiliary variables follows naturally from the microscopic dynamics of the transported entities, and this approach may complement the continuous models of extended thermodynamics to define the relevant auxiliary variable from the underlying microscopic physics.
Specifically, let us consider the transport of micrometric (or nanometric) particles in viscoelastic and polymeric fluid possessing non-Newtonian rheological properties. Let us stress that this problem is completely different (by nature and length scales involved) from the dynamics of a polymer in a polymeric solution considered in classical polymer dynamics [
79,
80,
81], where an overdamped approximation for the dynamics of the polymer is considered, leading to a Smoluchowski equation in the presence of hydrodynamic interactions at the level of Kuhn segments (i.e., at the molecular scale) [
79]. As regards fluid–particle interactions for nano- and micrometric particles, the fluid can be treated as a continuous medium defined by its rheological properties (the linear response regime is explicitly considered). This is the case for the so-called microbead rheology, and a similar approach has been discussed in Refs. [
82,
83], which admits significant applications at the cellular level related to the motion of endosomes, lipidic particles in the cytoplasmatic medium, that corresponds to a highly complex viscoelastic fluid [
84,
85]. It is also worth noting that the treatment of viscoelasticity is a classical achievement of thermodynamic theories [
61,
86], but as to our knowledge its mass-transport implications have never been considered accurately enough.
The parabolic modeling of transport is explicitly considered in order to focus on the strictly rheological nature of problem. The extension to the hyperbolic setting is straightforward. Macroscopic transport equations in generic fluids can be developed from micro/mesoscopic stochastic equations of motion. Indeed, the basic paradigm of this approach is expressed by the theory of Brownian motion: (i) express particle dynamics accounting for mean-field hydrodynamic interactions and stochastic thermal fluctuations; (ii) define the intensity of velocity fluctuations from equilibrium properties at constant temperature; and finally, (iii) make the overdamped approximation so that the statistical description of the process can be expressed exclusively in terms of the spatial concentration of the diffusing species, without any accounting for the particle velocities.
The same approach can be extended to transport in any real complex fluid once its rheological properties are specified [
67]. Below, we consider the case of a viscoelastic fluid, neglecting for simplicity the effects of fluid inertia on particle hydromechanics [
62]. In the linear viscoelastic case, the particle equations of motion can be written in terms of a friction kernel
, accounting for the memory effects in the viscoelastic response [
60]:
where
represents the stochastic thermal forcing. Setting
,
,
,
. Particle motion is described by the system of equations
where “*” indicates convolution. The kernel
can be obtained from the rheological properties of the fluid medium, and it is, therefore, a well defined physical property. For a spherical particle of mass
m and radius
,
, where the viscosity kernel
corresponds to the linear response function of the fluid. Actually,
can be obtained for polymeric fluids from the structural properties of the polymeric molecules [
79]. In linear viscoelasticity,
can be expressed as the linear combination of exponentially decaying functions of time [
67,
68]:
characterized by the relaxation rates
,
. Setting
, Equation (
41) can be rewritten as
where
,
, are distributional derivatives of independent Wiener processes. Observe that in Equation (
44) the thermal forcing term entering Equation (
41) has been redistributed among the internal
-degrees of freedom, as a fluctuating contribution acting directly on
would determine the divergence of
for
, and ultimately the absence of any equilibrium behavior. In Equation (
44), the coefficients
should be determined from fluctuation–dissipation relations (second Kubo fluctuation dissipation theorem [
60]), expressing the autocorrelation function of
in terms of the dissipative memory kernel:
and from the equilibrium property
. After some algebra, this provides the values of
[
87]:
From Equation (
44) the explicit representation of
can be obtained, namely,
where
are the filtered increments of a Wiener process through a low-pass filter with a pole at
.
From the above analysis, it follows that the Fokker–Planck equation associated with Equations (
41)–(
44) represents the rational and correct way to express mass balance in the viscoelastic medium. Specifically, the associated Fokker–Planck equation involves the joint density
, and it takes the form
No way exists to reduce in general Equation (
49) for
, e.g., via an overdamped approximation, to an equation exclusively expressed with respect to the marginal concentration field
:
although in the case of a microbead confined by an optical trap a partial overdamped approximation can be performed, eliminating the velocity variable by expressing it as a function of the internal degrees of freedom
,
.
This means that a correct formulation of the transport problem in a viscoelastic medium should involve the solution of the
-dimensional parabolic model equipped with suitable boundary conditions describing the specific case study under consideration. The problem of mass transport in viscoelastic media, treated rigorously starting from the equations of motion coupled with fluctuation–dissipation relations, opens up interesting issues as regards the representation formalism in thermodynamic theories and the possibility of obtaining reduced models. This problem indicates the need for introducing additional variables accounting for the history of the process (the
variables), that cannot be projected out in a consistent way. If
N is sufficiently large,
(10), the direct solution of Equation (
49) becomes unfeasible and the only way to study the process is to return to the direct simulation of the stochastic Lagrangian Equations (
41)–(
44).
One can draw a general conclusion from the above analysis of particle mass transport in viscoelastic fluids. The bottom-up approach starts from a model of interaction at micro/mesoscales of the system with the environment (in the present case, the system is the particle ensemble and the environment is the fluid), expressed by the friction kernel
, and of the thermal effects (the fluctuation–dissipation theorem). Once this microscopic description is defined, providing a reliable and accurate description for the microphysics, the macroscopic transport equations follow together with the definition, induced by the microphysics, of the relevant degrees of freedom. As in the case of the Poisson–Kac processes, the internal degrees of freedom introduced from the stochastic equations of motion are indeed “internal coordinates” parametrizing the concentration field. This marks the difference with respect to the thermodynamic definition of internal variables that corresponds to continuous scalar/vector/tensor fields of the space-time variable
[
31], and makes this approach conceptually similar to the formulation of the evolution equations in kinetic theory [
46].
6. Conclusions
There are two main issues addressed in this article. First of all, the physical relevance of the positivity condition for the evolution equations of concentrations, without which any analysis of irreversibility based on entropic constraints loses its meaning.
The example of the statistical properties of Poisson–Kac processes under time reversal is paradigmatic, as soon as this process is irreversible. This process is irreversible not because the time-reversed operator, , , of its Markov operator cannot be defined ( exists in a mathematical and physical sense), but because is no longer a Markov operator due to its lack of positivity: does not map (positive) densities into (positive) densities. The backward evolution of , starting from any initial distribution , traces back its previous history up to a given time instance , corresponding to the time instant at which either the forward or the backward densities attain at some point vanishing values, and afterwards the densities start to become negative. Once the densities become negative, any definition of entropy based on the average of their logarithms loses its meaning. This case study shows the significance of ensuring the positivity condition, and this can be safely achieved if the macroscopic transport model admits a stochastic interpretation, i.e., if it represents the statistical description of some micro/mesoscopic stochastic model of motion or interaction. This leads, for processes possessing finite propagation velocity and Markovian or semi-Markovian transitions, to a statistical description expressed in the form of integro-differential evolution equations for the associated densities.
The second main issue, involving either stochastic consistency or representation problems, originates by the description of microscopic phenomena expressed, e.g., in the form of chemical–physical interactions (surface chemical reactions) or hydrodynamic models (particle motion in complex viscoelastic fluids).
The case of surface reactions is particularly interesting as it shows that parabolic transport models can hardly cope with event-based phenomena such as surface reactions occurring at an interface. Indeed, it is possible to provide an algorithmic strategy to address this class of problems in numerical simulations, assuming kinetic processes to be dependent on the time resolution adopted in the particle motion, but this strategy leads to a singular limit for . For these problems, the hyperbolic approach provides a consistent formal setting for accommodating interfacial events occurring with finite rates and non-vanishing probabilities. This indicates once again that bounded velocities imply also finite transition rates in order to avoid the occurrence of singular limits.
In terms of the thermodynamic representation of the evolution equations, an even harder problem is provided by transport (diffusion) processes in complex fluids. The case of viscoelastic fluids has been analyzed, starting from the Brownian motion rationale, in order to derive the transport equations from the microscopic/mesoscopic dynamics. In this case, due to the memory effects associated with the complex response of the fluid medium, it is practically impossible to project out the relaxation degrees of freedom of the medium in order to obtain transport equations expressed exclusively in term of the concentration fields of the diffusing species. This leads to higher-dimensional transport models that necessarily account also for the evolution of the memory degrees of freedom in the particle dynamics (the variables
,
introduced in
Section 5) the solution of which, for sufficiently large
N, becomes unfeasible, leading to direct stochastic simulations being the only reasonable alternative to tackle these problems.
The bottom-up approach to the definition of the internal degrees of freedom provides a robust and consistent approach to obtain macroscopic transport models from the underlying microscopic equations of motion. In this article, we have considered the case of microdynamics possessing either Markovian transition rates (as for Poisson–Kac and generalized Poisson–Kac processes) or a Markovian embedding characterized by a Markovian dynamics for the auxiliary variables (particle motion in a viscoelastic fluid). The same approach can be straightforwardly extended to more complex microdynamics possessing, e.g., semi-Markov transition rates [
42,
43,
88]. The latter problem is of physical interest in cold-atom physics [
89], and it can hardly be tackled directly from continuous theories without an a priori characterization of the semi-Markov properties of the microdynamics.