Abstract
We develop a Green’s functions scattering method for systems with Chern–Simons plane boundary layers on dielectric half-spaces. The Casimir pressure is derived by evaluation of the stress tensor in a vacuum slit between two half-spaces. The sign of the Casimir pressure on a Chern–Simons plane layer separated by a vacuum slit from the Chern–Simons layer at the boundary of a dielectric half-space is analyzed for intrinsic and glass substrates.
1. Introduction
Quantum interaction between macroscopic bodies in the ground state is studied via the Casimir effect [1,2]—various reviews and books are dedicated to the subject [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The Lifshitz formula [25] determines the interaction between two dielectric half-spaces separated by a vacuum slit; it determines interaction due to fluctuations in the relevant case when transverse electric (TE) and transverse magnetic (TM) polarizations of the electromagnetic field do not mix after reflection from flat boundaries of dielectrics. In this case, the Casimir pressure is attractive for dielectric half-spaces separated by a vacuum slit [26].
Nevertheless, there exist systems with plane boundaries and Casimir repulsive pressure. The Casimir pressure is repulsive for three dielectric media with plane-parallel boundaries when the inequality for dielectric permittivities holds [27] with the frequency; here, the medium with a dielectric permittivity fills the space between dielectrics with permittivities and . The experiment [28] has demonstrated that the sign of the Casimir–Lifshitz force can indeed be changed from attractive to repulsive by a suitable selection of interacting materials immersed in a fluid. The contribution of surface modes in three-layered systems guaranteeing repulsion has been investigated in Ref. [29], where it was demonstrated that at short separations, surface modes play a decisive role in the Casimir repulsion. The repulsive critical Casimir forces emerging in a critical binary liquid mixture near the critical temperature can be used to counteract attraction due to fluctuating Casimir–Lifshitz forces [30].
Another possibility to obtain the Casimir repulsion is to study the interaction between plates with dielectric, diamagnetic and magnetodielectric properties [31,32,33,34,35]. The pressure between a perfectly conducting plate and an infinitely permeable plate is derived by Timothy Boyer [36]; the pressure is purely repulsive in this case: its magnitude is that of the Casimir pressure between two perfectly conducting plates [2]. Casimir pressure and repulsion between metamaterials were investigated in Refs. [37,38,39,40].
One can also obtain Casimir repulsion in systems with plane-parallel Chern–Simons layers [41,42]. There is a mixing of TE and TM polarizations of the electromagnetic field after reflection from the Chern–Simons layer [42]. The general result for the Casimir energy of two arbitrary Chern–Simons layers in vacuum is expressed through nondiagonal reflection matrices on the basis of TE and TM polarizations [42]. This structure of reflection matrices leads to the Casimir attraction or the Casimir repulsion in systems with plane-parallel Chern–Simons layers in vacuum and at the boundaries of dielectrics, depending on the parameters of the layers [41,42,43,44]. The Monte Carlo method was used to calculate the Casimir energy of interacting Chern–Simons layers in vacuum in Refs. [45,46].
Maxwell–Chern–Simons (2 + 1) space-time dimensional Abelian electrodynamics with the Chern–Simons term was considered in Ref. [47]; there is a massive spin-1 excitation in this case. The constant of the Chern–Simons action is dimensionless in the (3 + 1) case. The study of the Casimir energy in systems with Chern–Simons terms in (3 + 1) dimensions was started in Refs. [48,49] in the framework of rigid, nonpenetrable boundary conditions.
Physical systems are known to be described by the Chern–Simons action with a quantized constant of the action. In the low-energy effective theory of topological insulators, the term proportional to , with and the electric and magnetic fields, respectively, is added to the standard electromagnetic energy density; integration of this term over the volume of the topological insulator yields boundary Chern–Simons action. Chern–Simons boundary action is defined in this case by a dimensionless quantized parameter a: , , where is a fine structure constant of quantum electrodynamics and n is an integer number [50]. The Casimir effect for topological insulators was studied in Refs. [51,52,53,54,55,56].
In the non-dispersive case, Chern insulators [57,58,59] are described by the Chern–Simons action with a quantized parameter , where C is a Chern number equal to the winding number of a map from a two-dimensional torus to a two-dimensional unit sphere. The Casimir effect for Chern insulators was investigated in Refs. [42,60,61].
For quantum Hall layers in an external magnetic field, the quantized parameter of the Chern–Simons action characterizing Hall plateaus takes the values , where is an integer or a fractional number [43,62,63].
Recently, the formalism based on Green’s functions scattering has been worked out [3,64]; in this approach, one evaluates the Casimir pressure in an explicit gauge-invariant derivation. The formalism yields gauge-invariant results for electric and magnetic Green’s functions by construction. Note that due to disregard of gauge invariance, the electric and the magnetic Green’s functions for the Lifshitz problem (two dielectric half-spaces separated by a vacuum slit) obtained in the book [4] contradict the result for the Casimir–Polder potential of a polarizable neutral atom located between two dielectric half-spaces [3,64].
The Casimir–Polder potential of a neutral anisotropic atom added to a multi-body system is expressed in the second-order perturbation theory in terms of electric Green’s functions for this system [3,65,66,67,68]. The Casimir–Polder potential of an anisotropic atom is repulsive at distances close to the hole in a plane conductor or grooves of a diffraction grating when the atomic polarizaibility is aligned in a direction perpendicular to the conductor [69,70] or a diffraction grating [71], in cylindrical and other geometries [72,73,74,75,76]. Note that the repulsion of the point charge from the axisymmetric conductor with an opening is present in electrostatics [77]. The curvature-induced repulsive effect on the lateral Casimir–Polder force is studied in Refs. [78,79,80]. The fundamental limits on the Casimir–Polder repulsive and attractive forces have been determined in Ref. [81].
The Casimir–Polder potential of a neutral anisotropic atom in the presence of a single Chern–Simons plane layer has been derived in Ref. [82]. The symmetric part of the polarizability for a nonmagnetic ground-state molecule yields potential proportional to the Casimir–Polder potential in front of a perfectly conducting plane; the asymmetric part of the polarizability also contributes to the Casimir–Polder potential [82]. Chiral media are actively studied in the Casimir effect [83,84]; the Casimir–Polder potential of a molecule with an isotropic chiral polarizability interacting with a chiral medium has been studied in Ref. [85]. Charge–parity violating effects [86] for the Casimir–Polder potential in the presence of a Chern–Simons layer have been studied in Ref. [87]: the Chern–Simons layer induces Casimir–Polder interaction both with a molecule that is not chiral but has an electric–magnetic cross polarizability and with a molecule having an anisotropic, asymmetric chiral polarizability. Recently, the formalism of Green’s functions scattering has been applied to derive analytic results for the Casimir–Polder potentials of an anisotropic neutral atom in the presence of Chern–Simons plane boundary layers on dielectric half-spaces and in vacuum [88]. A novel three-body vacuum parity effect has been discovered in the system Chern–Simons layer–atom–Chern–Simons layer, which manifests as different values of the Casimir–Polder potential after a 180 degree rotation of one of the layers [88].
In this paper, we develop a Green’s functions scattering method and derive the Casimir pressure in geometries with Chern–Simons plane boundary layers on dielectric substrates by evaluation of the Casimir fluctuation pressure via vacuum stress tensor [3,4,25,64,89]. We proceed as follows. In Section 2, we derive expressions for the field of a point dipole in vacuum in terms of electric and magnetic fields. Then, we derive electric and magnetic Green’s functions in a slit between two dielectric substrate half-spaces covered by Chern–Simons layers. The Casimir pressure is expressed in terms of electric and magnetic Green’s functions through evaluation of the vacuum stress tensor in the slit. In Section 3, we study the sign of the Casimir pressure on a Chern–Simons plane layer separated by a vacuum slit from the Chern–Simons layer at the boundary of a dielectric half-space for intrinsic and glass substrates. Connection between representations of the Casimir energy in the local polar basis and the local basis of TE and TM polarizations in momentum space is established in Appendix A.
The magnetic permeability of materials throughout the text. We use for the reduced Planck constant, ħ, and the speed of light, c, and Heaviside–Lorentz units.
2. Casimir Pressure in the System of Two Dielectric Half-Spaces with Chern–Simons Boundary Layers
Consider the volume charge density ) and the current density () of a dipole source at the point [82]:
where is an electric dipole moment vector, , t denotes time, the Latin letter indices denote the space components and is the three-dimensional Dirac delta function. The four-current density (1)–(2) satisfies the continuity equation .
The Weyl formula, [90]
valid for , can be substituted into the solution of equations for scalar () and vector ) potentials:
to find electric and magnetic fields from a dipole source (1)–(2) in free space. As a result, electric and magnetic fields propagating upwards from the dipole source (1)–(2) in free space have the form [3]
where , , and .
We start from a solution of the diffraction problem of a dipole field when the dielectric medium is filling the half-space . Scalar and vector functions defining the half-space or diffraction from it are denoted by index 1. A homogeneous dielectric half-space is characterized by a frequency dispersion of a dielectric permittivity at every point. In addition, there is a Chern–Simons plane layer at the boundary . The Chern–Simons layer at is described by the action
with a dimensionless parameter , the Levi-Civita symbol, the electromagnetic four-potential, , the Greek letter indices take Minkowski space-time values, and over space-time coordinates.
Consider an upward propagation of the electromagnetic field from a point dipole (1)–(2). In the presence of a dielectric medium for , one writes the solution of the Maxwell equations for in the form
The transmitted fields for are written in the form
where and . Vector functions and are found from the transversality of the reflected and transmitted fields and the boundary conditions imposed on the fields:
Boundary conditions (18)–(19) have been used to describe the diffraction of a plane electromagnetic wave in a medium with a piecewise constant axion field [91] and in a medium with Chern–Simons layers [92].
Boundary conditions (14)–(19) can be imposed in cylindrical coordinates in a local orthogonal basis in momentum space so that , :
The solution of the transversality conditions (20)–(21) and boundary conditions (22)–(25) imposed at yields
where the Fresnel reflection coefficients
and
depend on the dielectric permittivity of the half-space .
Electric and magnetic fields propagating downwards from the dipole source (1)–(2) in free space have the form [3]
where .
The next step is to find a solution of the diffraction problem of a dipole field when the medium is filling half-space . Scalar and vector functions defining the half-space or diffraction from it are denoted by index 2. A homogeneous dielectric half-space is characterized by a frequency dispersion of a dielectric permittivity at every point. There is a Chern–Simons plane layer characterized by a dimensionless parameter at the boundary .
In the presence of a dielectric medium for , one adds the reflected parts of fields to a solution (31)–(32) and writes the solution of the Maxwell equations for in the form
For , one writes the transmitted fields in the form
where and . Vector functions and are found from the transversality of the reflected and transmitted fields and the boundary conditions imposed on the fields:
It is convenient to write boundary conditions (38)–(43) in cylindrical coordinates in a local orthogonal basis in momentum space so that , :
and get
where Fresnel reflection coefficients , and depend on the dielectric permittivity of the half-space . The local matrix R resulting from Equations (26), (27), (50) and (51) is defined as follows:
The solution of a diffraction problem when both half-spaces are present simultaneously and the point dipole is located at , can be derived as follows. Denote the upper dielectric half-space () by index 1 and the lower dielectric half-space () by index 2. The Chern–Simons boundary layers at and are defined by the parameters and as before (Figure 1). From (53) and the solutions for the diffraction cases considered above, we define local matrices and for reflection of the tangential components of the electric field from media above and below the point dipole, respectively:
Tangential local components of the electric field in the interval from the point dipole (1)–(2) are expressed in terms of , after the summation of multiple reflections from media with indices 1 and 2:
where I is the identity matrix. From Equation (55), we define four matrices:
and write components of the electric field in a cylindrical local system of coordinates explicitly from Formulas (21), (44), (55) and (56)–(59):
where , , , () are components of the four matrices (56)–(59).
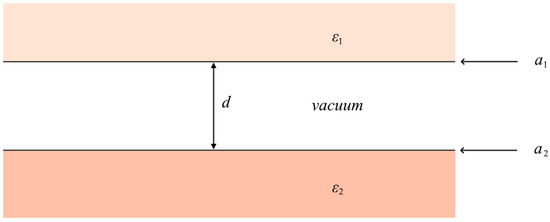
Figure 1.
Two dielectric half-spaces with Chern–Simons boundary layers are separated by a distance d. The permittivity of the upper dielectric half-space is ; the permittivity of the lower dielectric half-space is . The upper Chern–Simons boundary layer is defined by ; the lower Chern–Simons boundary layer is defined by .
For convenience, we rewrite and in a cylindrical system of coordinates:
The scattered part of the electric field at the point from the source (1)–(2) at the point for is given by
The rotation formulas between a cylindrical local basis and a Cartesian basis for every given are standard:
where and denote the Cartesian components of an electric dipole moment vector.
The Cartesian components of the scattered electric Green’s functions are expressed in terms of components of the reflected electric Green’s functions in a cylindrical local basis from (66)–(69) for :
In Equations (70)–(72), we omit nondiagonal contributions to scattered Green’s functions in a cylindrical local basis proportional to either , or since integrals over angle equal zero for these terms for coinciding arguments .
The components of the scattered electric Green’s functions in a cylindrical local basis entering (70)–(72) are found from (60)–(64):
After integration over the polar coordinates, we express scattered electric Green’s functions for coinciding arguments in terms of matrix elements of matrices (56)–(59) [88]:
Scattered magnetic Green’s functions can be evaluated from reflected electric Green’s functions:
The components of the scattered magnetic Green’s functions in a cylindrical local basis are found from (78) and (73)–(75):
The Cartesian components of the scattered magnetic Green’s functions are evaluated in complete analogy to the evaluation of the Cartesian components of the scattered electric Green’s functions.
For every and the coinciding arguments of the reflected local Green’s functions , these identities hold:
The Casimir pressure P equals the component of the fluctuation stress tensor in a slit between half-spaces; it is expressed in terms of the scattered electric and magnetic Green’s functions:
We use Formulas (70)–(72), identities (82)–(83) and the Wick rotation to express the Casimir pressure in terms of the reflection matrices and :
where “Tr” defines the trace operation and .
The corresponding Casimir energy on a unit surface has the form
The equivalence of the Casimir energy (86) to the result for the Casimir energy obtained within the scattering approach [43] is proved in Appendix A.
3. Casimir Interaction in Systems with Chern–Simons Layers on Realistic Substrates
The scattering approach yields finite expressions for the Casimir energy of several interacting objects; it has been applied to diffraction gratings [93,94,95,96], spheres, cylinders and other geometries [97,98,99,100,101,102,103,104,105,106,107]. Planes with conductivity have also been studied in the framework of the scattering approach in Refs. [3,108,109,110,111,112]. The experiment [113] has confirmed the (2 + 1) finite temperature polarization operator approach in the description of graphene layers and the strong temperature dependence of the Casimir pressure for interacting layers of graphene [108].
The Casimir energy of two Chern–Simons layers in vacuum for arbitrary Chern–Simons constants and was derived in Ref. [42] in the framework of the scattering approach. For , the Casimir force is repulsive over an interval , where [41,43]. For , the Casimir force is always attractive for two Chern–Simons layers in vacuum [42].
Suppose there is a quantization of Chern–Simons parameters and as in quantum Hall systems: , , where m and n are integer numbers and is a fine structure constant. The Casimir repulsion for two half-spaces covered by Chern–Simons layers was studied for , intrinsic and glass substrate materials in Refs. [43,44]. In Ref. [43], it was shown that for two substrate half-spaces separated by a vacuum slit, the Casimir repulsion can be achieved at the maximum distance nm for , and for two substrate half-spaces, the Casimir repulsion can be achieved at the maximum distance nm for . It was demonstrated in Ref. [44] that for two substrate half-spaces separated by a vacuum slit, the Casimir repulsion can be realized at the maximum distance nm between half-spaces; the maximum distance at which the Casimir repulsion occurs in this system corresponds to Chern–Simons constants or . In Ref. [44], it was shown that the minimum of the Casimir energy with nm is achieved for integer . The Casimir interaction of Chern–Simons layers in the presence of realistic substrate materials was not studied for small enough and different values of and or for geometries different from two half-space substrates with boundary Chern–Simons layers.
In this Section, we study the Casimir interaction of Chern–Simons layers for small enough values of and and explore the transition between the regimes of Casimir attraction and repulsion in the presence of a realistic dielectric substrate. Consider the Chern–Simons plane layer defined by the constant separated by a vacuum slit of width d from a dielectric half-space characterized by a dielectric permittivity and the boundary Chern–Simons layer defined by the constant (Figure 2). We emphasize that in this case. We evaluate the Casimir energy in this system for two dielectric substrate materials: intrinsic and glass. For the dielectric permittivity of intrinsic , the model from Ref. [114] is used. For glass, we use data from [115] to evaluate dielectric permittivity at imaginary frequencies. We apply Equation (86) to evaluate the Casimir energy.
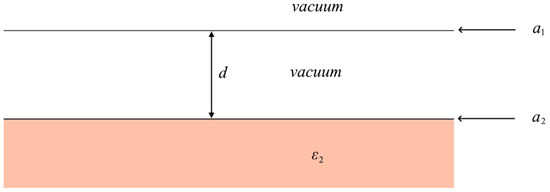
Figure 2.
The Chern–Simons layer defined by is separated by a distance d from a dielectric half-space, with the boundary Chern–Simons layer defined by . The permittivity of a dielectric half-space is .
The Casimir energy for the substrate and Chern–Simons layers with is presented in Figure 3; the minimum of the energy is at the distance nm. For , , the minimum is at the distance nm; for , , the minimum is at the distance nm.
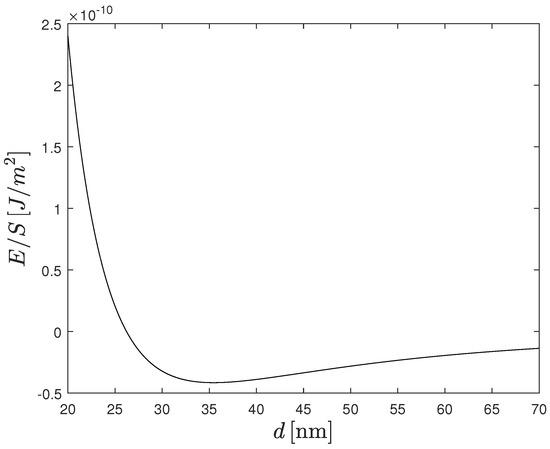
Figure 3.
The Casimir energy (86) as a function of a distance d between the Chern–Simons layer defined by and the Chern–Simons layer defined by at the boundary of intrinsic half-space substrate.
The Casimir energy for the glass substrate and Chern–Simons plane layers with , is shown in Figure 4; the minimum of the energy is at the distance nm. For , , the minimum is at the distance nm; for , , the minimum is at the distance nm; for , , the minimum is at the distance nm; for , , the minimum is at the distance nm. For , , there is no minimum of the Casimir energy: the Casimir repulsion occurs at all distances between the Chern–Simons layers.
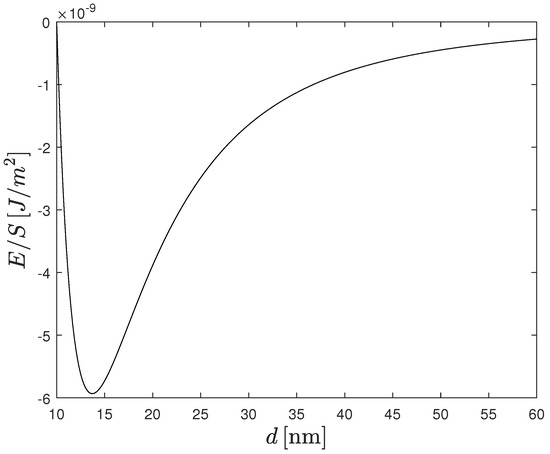
Figure 4.
The Casimir energy (86) as a function of a distance d between the Chern–Simons layer defined by and the Chern–Simons layer defined by at the boundary of glass half-space substrate.
4. Discussion and Summary
The Green’s functions scattering method [3,64] is explicitly gauge-invariant by construction; it is based on a direct evaluation of electric and magnetic Green’s functions and the fluctuation stress tensor in a vacuum slit between objects. In Refs. [3,64], the Casimir pressure is derived for flat geometries and boundary conditions when there is no mixing between transverse electric and transverse magnetic polarizations after reflection from flat boundaries. In Ref. [88] and in this paper, the method is generalized to systems with Chern–Simons plane layers; in this case, there is mixing between the transverse electric and transverse magnetic polarizations after reflection from the Chern–Simons layers.
In the present paper, the Casimir pressure is derived for dielectric half-spaces with Chern–Simons plane-parallel boundary layers via evaluation of the fluctuation stress tensor in a vacuum slit. Section 2, presents derivation of the Casimir pressure (85) expressed in terms of reflection matrices through evaluation of the fluctuation stress tensor in a vacuum slit. The fluctuation stress tensor is expressed through electric and magnetic Green’s functions in a vacuum slit. We start from evaluation of the electric Green’s functions in a vacuum slit [88]. The derivation of the magnetic Green’s functions and the stress tensor in a vacuum slit is new. To our knowledge, the Casimir pressure expressed in terms of nondiagonal reflection matrices has not been previously derived through evaluation of the vacuum stress tensor. In Appendix A, we prove the equivalence of the Casimir energy (86) to the result for the Casimir energy obtained with the scattering approach [43].
The Casimir pressure on a Chern–Simons plane layer separated by a vacuum slit from the boundary Chern–Simons layer on intrinsic or glass half-spaces has remarkable properties for experimental study. In Section 3, we concentrate on the case of quite small parameters , for the boundary Chern–Simons layers: the case that is easier to implement experimentally. The case of relatively small and different values of , was not investigated before. The geometry of the Chern–Simons plane layer separated by a vacuum slit from a dielectric half-space with the boundary Chern–Simons layer was not studied before. It is convenient to consider quantum Hall quantization of the parameters , , where m and n are integer numbers. For , the Casimir pressure is repulsive at all separations for the substrate; however, there exists a minimum of the Casimir energy in this case for the substrate. For and integers , there is a minimum of the Casimir energy both for the and substrates; the Casimir pressure is attractive when the separation between the layers is greater than the separation at the position of the minimum of the energy, and it is repulsive at shorter separations. We find the positions of the minimum of the Casimir energy for and for the intrinsic substrate and for and integers for the glass substrate.
The results obtained in this paper demonstrate that intrinsic and glass are natural substrate materials for the study of transitions from an attractive regime of the Casimir pressure to a repulsive one. The positions of the minimum of the Casimir energy are found at experimentally realizable distances between the layers for quite small integer numbers of quantization parameters for both Chern–Simons layers, which is important for experimental realization of the repulsive Casimir force.
Author Contributions
Both authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received financial support from a grant from the Russian Science Foundation (RSF project Nº 22-13-00151).
Data Availability Statement
Data are contained within the article.
Acknowledgments
Research was performed at the Research park of the St. Petersburg State University Computing Center, Russia.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Representations of the Casimir Energy in Two Bases
Here, we prove the equivalence of the Casimir energy (86) to the result for the Casimir energy obtained with the scattering approach [43,44]. In the present paper, we use the local polar basis vectors and in momentum space; in Ref. [43], the local basis vectors and of the TE and TM polarizations in momentum space have been used. The amplitudes of the incident electric fields in the two bases are related by the matrix :
The amplitudes of the reflected electric field are expressed through the amplitudes of the incident field by the matrix R defined in Equation (53):
The amplitudes of the reflected electric field in the two bases are related by the transition matrix :
One immediately finds the relation between the reflection matrices in the two bases:
The transformation matrices for a reflection from the upper half-space have the form
For a reflection from the lower half-space, the transformation matrices have the form
From (53), (54), (A4) and (A5)–(A8), we obtain reflection matrices in agreement with the scattering approach [43]:
One can write the product of the reflection matrices from the upper and the lower half-spaces:
The equality of the trace operations in two different bases follows:
where L is a positive integer number. The equivalence of the Casimir energy (86) to the result for the Casimir energy obtained with the scattering approach [43] follows from the equality (A12).
References
- Casimir, H.B.G.; Polder, D. The influence of retardation on the London–van der Waals forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wetensch. B 1948, 51, 793–795. Available online: https://dwc.knaw.nl/DL/publications/PU00018547.pdf (accessed on 1 February 2024).
- Marachevsky, V.N.; Sidelnikov, A.A. Green functions scattering in the Casimir effect. Universe 2021, 7, 195. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics. Part 2: Theory of Condensed States; Butterworh–Heinemann Ltd/Elsevier Ltd.: Oxford, UK, 1980. [Google Scholar] [CrossRef]
- Barash, Y.S.; Ginzburg, V.L. Electromagnetic fluctuations in matter and molecular (Van-der-Waals) forces between them. Sov. Phys. Usp. 1975, 18, 305–322. [Google Scholar] [CrossRef]
- Barash, Y.S.; Ginzburg, V.L. Some problems in the theory of van der Waals forces. Sov. Phys. Usp. 1984, 27, 467–491. [Google Scholar] [CrossRef]
- Plunien, G.; Müller, B.; Greiner, W. The Casimir effect. Phys. Rep. 1986, 134, 87–193. [Google Scholar] [CrossRef]
- Bordag, M.; Mohideen, U.; Mostepanenko, V.M. New developments in the Casimir effect. Phys. Rep. 2001, 353, 1–205. [Google Scholar] [CrossRef]
- Santangelo, E.M. Evaluation of Casimir energies through spectral functions. Theor. Math. Phys. 2002, 131, 527–542. [Google Scholar] [CrossRef]
- Milton, K.A. The Casimir effect: Recent controversies and progress. J. Phys. A Math. Gen. 2004, 37, R209–R277. [Google Scholar] [CrossRef]
- Jaffe, R.L. Casimir effect and the quantum vacuum. Phys. Rev. D 2005, 72, 021301(R). [Google Scholar] [CrossRef]
- Scheel, S.; Buhmann, S.Y. Macroscopic quantum electrodynamics—Concepts and applications. Acta Phys. Slovaca 2008, 58, 675–809. Available online: http://www.physics.sk/aps/pub.php?y=2008&pub=aps-08-05 (accessed on 1 February 2024). [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Rodriguez, A.; Capasso, F.; Johnson, S. The Casimir effect in microstructured geometries. Nat. Photon. 2011, 5, 211–221. [Google Scholar] [CrossRef]
- Marachevsky, V.N. The Casimir effect: Medium and geometry. J. Phys. A Math. Theor. 2012, 45, 374021. [Google Scholar] [CrossRef]
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys. 2016, 88, 045003. [Google Scholar] [CrossRef]
- Woods, L.M.; Krüger, M.; Dodonov, V.V. Perspective on some recent and future developments in Casimir interactions. Appl. Sci. 2021, 11, 293. [Google Scholar] [CrossRef]
- Lu, B.-S. The Casimir effect in topological matter. Universe 2021, 7, 237. [Google Scholar] [CrossRef]
- Elizalde, E. Ten Physical Applications of Spectral Zeta Functions; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Kirsten, K. Spectral Functions in Mathematics and Physics; Chapman & Hall/CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Fursaev, D.; Vassilevich, D. Operators, Geometry and Quanta: Methods of Spectral Geometry in Quantum Field Theory; Springer Science+Business Media B.V.: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Buhmann, S.Y. Dispersion Forces I. Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir–Polder and van der Waals Forces; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Dispersion Forces II. Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Zh. Eksp. Teor. Fiz. 1955, 29, 94–110. (In Russian) English translation: Sov. Phys. JETP 1956, 2, 73–83. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/2/1/p73?a=list (accessed on 1 February 2024).
- Renne, M.J. Microscopic theory of retarded van der Waals forces between macroscopic dielectric bodies. Physica 1971, 56, 125–137. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. General theory of van der Waals’ forces. Sov. Phys. Usp. 1961, 4, 153–176. [Google Scholar] [CrossRef]
- Munday, J.N.; Capasso, F.; Parsegian, V.A. Measured long-range repulsive Casimir–Lifshitz forces. Nature 2009, 457, 170–173. [Google Scholar] [CrossRef] [PubMed]
- Pirozhenko, I.; Lambrecht, A. Repulsive Casimir forces and the role of surface modes. Phys. Rev. A 2009, 80, 042510. [Google Scholar] [CrossRef]
- Schmidt, F.; Callegari, A.; Daddi-Moussa-Ider, A.; Munkhbat, B.; Verre, R.; Shegai, T.; Käll, M.; Löwen, H.; Gambassi, A.; Volpe, G. Tunable critical Casimir forces counteract Casimir–Lifshitz attraction. Nat. Phys. 2023, 19, 271–278. [Google Scholar] [CrossRef]
- Tomaš, M.S. Casimir force between dispersive magnetodielectrics. Phys. Lett. A 2005, 342, 381–388. [Google Scholar] [CrossRef][Green Version]
- Geyer, B.; Klimchitskaya, G.L.; Mostepanenko, V.M. Thermal Casimir interaction between two magnetodielectric plates. Phys. Rev. B 2010, 81, 104101. [Google Scholar] [CrossRef]
- Inui, N. Thickness dependence of the Casimir force between a magnetodielectric plate and a diamagnetic plate. Phys. Rev. A 2011, 84, 052505. [Google Scholar] [CrossRef]
- Brevik, I.; Parashar, P.; Shajesh, K.V. Casimir force for magnetodielectric media. Phys. Rev. A 2018, 98, 032509. [Google Scholar] [CrossRef]
- Shelden, C.; Spreng, B.; Munday, J.N. Enhanced repulsive Casimir forces between gold and thin magnetodielectric plates. Phys. Rev. A 2023, 108, 032817. [Google Scholar] [CrossRef]
- Boyer, T.H. Van der Waals forces and zero-point energy for dielectric and permeable materials. Phys. Rev. A 1974, 9, 2078–2084. [Google Scholar] [CrossRef]
- Rosa, F.S.S.; Dalvit, D.A.R.; Milonni, P.W. Casimir–Lifshitz theory and metamaterials. Phys. Rev. Lett. 2008, 100, 183602. [Google Scholar] [CrossRef]
- Rosa, F.S.S.; Dalvit, D.A.R.; Milonni, P.W. Casimir interactions for anisotropic magnetodielectric metamaterials. Phys. Rev. A 2008, 78, 032117. [Google Scholar] [CrossRef]
- Yannopapas, V.; Vitanov, N.V. First-principles study of Casimir repulsion in metamaterials. Phys. Rev. Lett. 2009, 103, 120401. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Zhou, J.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Repulsive Casimir force in chiral metamaterials. Phys. Rev. Lett. 2009, 103, 103602. [Google Scholar] [CrossRef] [PubMed]
- Markov, V.N.; Pis’mak, Y.M. Casimir effect for thin films in QED. J. Phys. A Math. Gen. 2006, 39, 6525–6532. [Google Scholar] [CrossRef]
- Marachevsky, V.N. Casimir effect for Chern–Simons layers in the vacuum. Theor. Math. Phys. 2017, 190, 315–320. [Google Scholar] [CrossRef]
- Marachevsky, V.N. Casimir interaction of two dielectric half spaces with Chern–Simons boundary layers. Phys. Rev. B 2019, 99, 075420. [Google Scholar] [CrossRef]
- Marachevsky, V.N. Chern–Simons boundary layers in the Casimir effect. Mod. Phys. Lett. A 2020, 35, 2040015. [Google Scholar] [CrossRef]
- Pavlovsky, O.; Ulybyshev, M. Casimir energy calculations within the formalism of noncompact lattice QED. Int. J. Mod. Phys. A 2010, 25, 2457–2473. [Google Scholar] [CrossRef]
- Pavlovsky, O.V.; Ulybyshev, M.V. Casimir energy in noncompact lattice electrodynamics. Theor. Math. Phys. 2010, 164, 1051–1063. [Google Scholar] [CrossRef]
- Milton, K.A.; Ng, Y.J. Maxwell–Chern–Simons Casimir effect. Phys. Rev. D 1990, 42, 2875–2880. [Google Scholar] [CrossRef]
- Elizalde, E.; Vassilevich, D.V. Heat kernel coefficients for Chern–Simons boundary conditions in QED. Class. Quantum Gravity 1999, 16, 813–822. [Google Scholar] [CrossRef][Green Version]
- Bordag, M.; Vassilevich, D.V. Casimir force between Chern–Simons surfaces. Phys. Lett. A 2000, 268, 75–80. [Google Scholar] [CrossRef][Green Version]
- Qi, X.-L.; Li, R.; Zang, J.; Zhang, S.-C. Inducing a magnetic monopole with topological surface states. Science 2009, 323, 1184–1187. [Google Scholar] [CrossRef] [PubMed]
- Grushin, A.G.; Cortijo, A. Tunable Casimir repulsion with three-dimensional topological insulators. Phys. Rev. Lett. 2011, 106, 020403. [Google Scholar] [CrossRef] [PubMed]
- Grushin, A.G.; Rodriguez-Lopez, P.; Cortijo, A. Effect of finite temperature and uniaxial anisotropy on the Casimir effect with three-dimensional topological insulators. Phys. Rev. B 2011, 84, 045119. [Google Scholar] [CrossRef]
- Chen, L.; Wan, S. Casimir interaction between topological insulators with finite surface band gap. Phys. Rev. B 2011, 84, 075149. [Google Scholar] [CrossRef]
- Chen, L.; Wan, S. Critical surface band gap of repulsive Casimir interaction between three-dimensional topological insulators at finite temperature. Phys. Rev. B 2012, 85, 115102. [Google Scholar] [CrossRef]
- Martín-Ruiz, A.; Cambiaso, M.; Urrutia, L.F. A Green’s function approach to the Casimir effect on topological insulators with planar symmetry. Europhys. Lett. 2016, 113, 60005. [Google Scholar] [CrossRef]
- Fialkovsky, I.; Khusnutdinov, N.; Vassilevich, D. Quest for Casimir repulsion between Chern–Simons surfaces. Phys. Rev. B 2018, 97, 165432. [Google Scholar] [CrossRef]
- Weng, H.; Yu, R.; Hu, X.; Dai, X.; Fang, Z. Quantum anomalous Hall effect and related topological electronic states. Adv. Phys. 2015, 64, 227–282. [Google Scholar] [CrossRef]
- Liu, C.-X.; Zhang, S.-C.; Qi, X.-L. The quantum anomalous Hall effect: Theory and experiment. Annu. Rev. Cond. Matter. Phys. 2016, 7, 301–321. [Google Scholar] [CrossRef]
- Ren, Y.; Qiao, Z.; Niu, Q. Topological phases in two-dimensional materials: A review. Rep. Prog. Phys. 2016, 79, 066501. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Lopez, P.; Grushin, A.G. Repulsive Casimir effect with Chern insulators. Phys. Rev. Lett. 2014, 112, 056804. [Google Scholar] [CrossRef] [PubMed]
- Muniz, Y.; Farina, C.; Kort-Kamp, W.J.M. Casimir forces in the flatland: Interplay between photoinduced phase transitions and quantum Hall physics. Phys. Rev. Res. 2021, 3, 023061. [Google Scholar] [CrossRef]
- Tse, W.-K.; MacDonald, A.H. Quantized Casimir force. Phys. Rev. Lett. 2012, 109, 236806. [Google Scholar] [CrossRef] [PubMed]
- Ezawa, Z.F. Quantum Hall Effects: Field Theoretical Approach and Related Topics; World Scientific: Singapore, 2008. [Google Scholar] [CrossRef]
- Marachevsky, V.N.; Sidelnikov, A.A. Gauge-invariant derivation of the Casimir–Lifshitz pressure. Phys. Part. Nucl. Lett. 2023, 20, 1114–1116. [Google Scholar] [CrossRef]
- Barton, G. Quantum-electrodynamic level shifts between parallel mirrors: Analysis. Proc. R. Soc. Lond. A 1987, 410, 141–174. [Google Scholar]
- Brevik, I.; Lygren, M.; Marachevsky, V.N. Casimir–Polder effect for a perfectly conducting wedge. Ann. Phys. 1998, 267, 134–142. [Google Scholar] [CrossRef]
- Messina, R.; Dalvit, D.A.R.; Maia Neto, P.A.; Lambrecht, A.; Reynaud, S. Dispersive interactions between atoms and nonplanar surfaces. Phys. Rev. A 2009, 80, 022119. [Google Scholar] [CrossRef]
- Bender, H.; Stehle, C.; Zimmermann, C.; Slama, S.; Fiedler, J.; Scheel, S.; Buhmann, S.Y.; Marachevsky, V.N. Probing atom-surface interactions by diffraction of Bose-Einstein condensates. Phys. Rev. X 2014, 4, 011029. [Google Scholar] [CrossRef]
- Levin, M.; McCauley, A.P.; Rodriguez, A.W.; Homer Reid, M.T.; Johnson, S.G. Casimir repulsion between metallic objects in vacuum. Phys. Rev. Lett. 2010, 105, 090403. [Google Scholar] [CrossRef] [PubMed]
- Eberlein, C.; Zietal, R. Casimir–Polder interaction between a polarizable particle and a plate with a hole. Phys. Rev. A 2011, 83, 052514. [Google Scholar] [CrossRef]
- Buhmann, S.Y.; Marachevsky, V.N.; Scheel, S. Impact of anisotropy on the interaction of an atom with a one-dimensional nano-grating. Int. J. Mod. Phys. A 2016, 31, 1641029. [Google Scholar] [CrossRef]
- Milton, K.A.; Abalo, E.K.; Parashar, P.; Pourtolami, N.; Brevik, I.; Ellingsen, S.A. Casimir–Polder repulsion near edges: Wedge apex and a screen with an aperture. Phys. Rev. A 2011, 83, 062507. [Google Scholar] [CrossRef]
- Milton, K.A.; Parashar, P.; Pourtolami, N.; Brevik, I. Casimir–Polder repulsion: Polarizable atoms, cylinders, spheres, and ellipsoids. Phys. Rev. D 2012, 85, 025008. [Google Scholar] [CrossRef]
- Milton, K.A.; Abalo, E.K.; Parashar, P.; Pourtolami, N.; Brevik, I.; Ellingsen, S.A. Repulsive Casimir and Casimir–Polder forces. J. Phys. A Math. Theor. 2012, 45, 374006. [Google Scholar] [CrossRef]
- Shajesh, K.V.; Schaden, M. Repulsive long-range forces between anisotropic atoms and dielectrics. Phys. Rev. A 2012, 85, 012523. [Google Scholar] [CrossRef]
- Marchetta, J.J.; Parashar, P.; Shajesh, K.V. Geometrical dependence in Casimir–Polder repulsion. Phys. Rev. A 2021, 104, 032209. [Google Scholar] [CrossRef]
- Savin, V.P.; Koksharov, Y.A. Electrostatic repulsion between an uncharged or slightly charged conductor and a point charge. J. Electrost. 2022, 120, 103769. [Google Scholar] [CrossRef]
- Nogueira, E.C.M.; Queiroz, L.; Alves, D.T. Sign inversion in the lateral van der Waals force. Phys. Rev. A 2022, 105, 062816. [Google Scholar] [CrossRef]
- Queiroz, L.; Nogueira, E.C.M.; Alves, D.T. Sign inversion in the lateral van der Waals force between an anisotropic particle and a plane with a hemispherical protuberance: An exact calculation. J. Phys. A Math. Theor. 2023, 56, 115301. [Google Scholar] [CrossRef]
- Alves, D.T.; Queiroz, L.; Nogueira, E.C.M.; Peres, N.M.R. Curvature-induced repulsive effect on the lateral Casimir–Polder–van der Waals force. Phys. Rev. A 2023, 107, 062821. [Google Scholar] [CrossRef]
- Venkataram, P.S.; Molesky, S.; Chao, P.; Rodriguez, A.W. Fundamental limits to attractive and repulsive Casimir–Polder forces. Phys. Rev. A 2020, 101, 052115. [Google Scholar] [CrossRef]
- Marachevsky, V.N.; Pis’mak, Y.M. Casimir–Polder effect for a plane with Chern–Simons interaction. Phys. Rev. D 2010, 81, 065005. [Google Scholar] [CrossRef]
- Jiang, Q.-D.; Wilczek, F. Chiral Casimir forces: Repulsive, enhanced, tunable. Phys. Rev. B 2019, 99, 125403. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir force between ideal metal plates in a chiral vacuum. Eur. Phys. J. Plus 2020, 135, 271. [Google Scholar] [CrossRef]
- Butcher, D.T.; Buhmann, S.Y.; Scheel, S. Casimir–Polder forces between chiral objects. New J. Phys. 2012, 14, 113013. [Google Scholar] [CrossRef]
- Khriplovich, I.B. Parity Nonconservation in Atomic Phenomena; Gordon and Breach Science Publishers S.A: Philadelphia, PA, USA, 1991. [Google Scholar]
- Buhmann, S.Y.; Marachevsky, V.N.; Scheel, S. Charge-parity-violating effects in Casimir–Polder potentials. Phys. Rev. A 2018, 98, 022510. [Google Scholar] [CrossRef]
- Marachevsky, V.N.; Sidelnikov, A.A. Casimir–Polder interaction with Chern–Simons boundary layers. Phys. Rev. D 2023, 107, 105019. [Google Scholar] [CrossRef]
- Brown, L.S.; Maclay, G.J. Vacuum stress between conducting plates: An image solution. Phys. Rev. 1969, 184, 1272–1279. [Google Scholar] [CrossRef]
- Weyl, H. Ausbreitung elektromagnetischer Wellen uber einen Leiter. Ann. Der Phys. 1919, 365, 481–500. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Hehl, F.W. Measuring a piecewise constant axion field in classical electrodynamics. Phys. Lett. A 2005, 341, 357–365. [Google Scholar] [CrossRef]
- Pis’mak, D.Y.; Pis’mak, Y.M.; Wegner, F.J. Electromagnetic waves in a model with Chern–Simons potential. Phys. Rev. E 2015, 92, 013204. [Google Scholar] [CrossRef] [PubMed]
- Lambrecht, A.; Marachevsky, V.N. Casimir interaction of dielectric gratings. Phys. Rev. Lett. 2008, 101, 160403. [Google Scholar] [CrossRef] [PubMed]
- Lambrecht, A.; Marachevsky, V.N. Theory of the Casimir effect in one-dimensional periodic dielectric systems. Int. J. Mod. Phys. A 2009, 24, 1789–1795. [Google Scholar] [CrossRef]
- Antezza, M.; Chan, H.B.; Guizal, B.; Marachevsky, V.N.; Messina, R.; Wang, M. Giant Casimir torque between rotated gratings and the θ = 0 anomaly. Phys. Rev. Lett. 2020, 124, 013903. [Google Scholar] [CrossRef]
- Marachevsky, V.N. The Casimir effect for diffraction gratings, symmetry breaking and geometric transitions. Phys. Part. Nucl. Lett. 2023, 20, 255–258. [Google Scholar] [CrossRef]
- Emig, T.; Graham, N.; Jaffe, R.L.; Kardar, M. Casimir forces between arbitrary compact objects. Phys. Rev. Lett. 2007, 99, 170403. [Google Scholar] [CrossRef]
- Rahi, S.J.; Emig, T.; Graham, N.; Jaffe, R.L.; Kardar, M. Scattering theory approach to electromagnetic Casimir forces. Phys. Rev. D 2009, 80, 085021. [Google Scholar] [CrossRef]
- Emig, T.; Jaffe, R.L.; Kardar, M.; Scardicchio, A. Casimir interaction between a plate and a cylinder. Phys. Rev. Lett. 2006, 96, 080403. [Google Scholar] [CrossRef]
- Canaguier-Durand, A.; Maia Neto, P.A.; Cavero-Pelaez, I.; Lambrecht, A.; Reynaud, S. Casimir interaction between plane and spherical metallic surfaces. Phys. Rev. Lett. 2009, 102, 230404. [Google Scholar] [CrossRef] [PubMed]
- Canaguier-Durand, A.; Gérardin, A.; Guérout, R.; Maia Neto, P.A.; Nesvizhevsky, V.V.; Voronin, A.Y.; Lambrecht, A.; Reynaud, S. Casimir interaction between a dielectric nanosphere and a metallic plane. Phys. Rev. A 2011, 83, 032508. [Google Scholar] [CrossRef]
- Bordag, M.; Nikolaev, V. Casimir force for a sphere in front of a plane beyond proximity force approximation. J. Phys. A Math. Theor. 2008, 41, 164002. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I. Vacuum energy between a sphere and a plane at finite temperature. Phys. Rev. D 2010, 81, 085023. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I.G. On the Casimir entropy for a ball in front of a plane. Phys. Rev. D 2010, 82, 125016. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Rahi, S.J.; Emig, T. Three-body Casimir effects and nonmonotonic forces. Phys. Rev. A 2009, 80, 022519. [Google Scholar] [CrossRef]
- Graham, N.; Shpunt, A.; Emig, T.; Rahi, S.J.; Jaffe, R.L.; Kardar, M. Electromagnetic Casimir forces of parabolic cylinder and knife-edge geometries. Phys. Rev. D 2011, 83, 125007. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Emig, T.; Noruzifar, E.; Zandi, R. Effect of curvature and confinement on the Casimir–Polder interaction. Phys. Rev. A 2015, 91, 012516. [Google Scholar] [CrossRef]
- Fialkovsky, I.V.; Marachevsky, V.N.; Vassilevich, D.V. Finite-temperature Casimir effect for graphene. Phys. Rev. B 2011, 84, 035446. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir and Casimir–Polder forces in graphene systems: Quantum field theoretical description and thermodynamics. Universe 2020, 6, 150. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Casimir–Polder effect for a stack of conductive planes. Phys. Rev. A 2016, 94, 012513. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Thermal Casimir and Casimir–Polder interactions in N parallel 2D Dirac materials. 2D Mater. 2018, 5, 035032. [Google Scholar] [CrossRef]
- Antezza, M.; Fialkovsky, I.; Khusnutdinov, N. Casimir–Polder force and torque for anisotropic molecules close to conducting planes and their effect on CO2. Phys. Rev. B 2020, 102, 195422. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of an unusual thermal effect in the Casimir force from graphene. Phys. Rev. Lett. 2021, 126, 206802. [Google Scholar] [CrossRef]
- Lambrecht, A.; Pirozhenko, I.; Duraffourg, L.; Andreucci, P. The Casimir effect for silicon and gold slabs. Europhys. Lett. 2007, 77, 44006. [Google Scholar] [CrossRef]
- Palik, E.D. (Ed.) Handbook of Optical Constants of Solids; Academic Press/Elsevier Inc.: Cambridge, MA, USA, 1997; Available online: https://www.sciencedirect.com/book/9780125444156/handbook-of-optical-constants-of-solids (accessed on 1 February 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).