Three-Dimension Calculation for the Scattering Problem for Non-Spherical Potential

Abstract

The interaction of the ²³⁸U with a neutron is studied. Correct accounting for the non-spherical shape of the uranium nucleus is in focus. The optical potential is used as a model. It is shown that the spherically symmetric and non-spherical potentials give different scattering patterns, in particular different resonance features of the cross-section. The possibility of using the method as an extension of the particle–rotor model of the nucleus is illustrated.

1. Introduction

Progress in the use of numerical methods results in the need for the fullest possible inclusion of all possible aspects of nuclear interactions. The possibility of accounting for the non-spherical form of nuclear interaction, along with other necessary components, has recently been included in software packages for calculating nuclear reactions [1,2,3,4]. In a number of studies, the calculation of the interaction is based on the use of the time-dependent Hartree–Fock approximation [3] or the calculation of classical trajectories [4]. If the equation for stationary states with realistic deformed potential has been solved, then the coupled channel procedure [5] is strongly important for the description of the scattering at the selected states.

Therefore, on one hand, the non-sphericity effect is incorporated into the calculations, and on the other hand, the calculation of the interaction is based on approximate, sometimes not even quantum mechanical, schemes. New effects arising from scattering by a non-spherical potential within quantum mechanics are considered in the present work.

The mechanism of the “shape of the nucleus” in the few-body problem is well developed [6,7]. However, this area of science, which has received significant results in the description of the nucleon interaction, the simplest elements and some simple cluster nuclei, is still far from being widely used due to obvious difficulties.

The particle–rotor model of the nucleus (PRMN) [5] and its more developed models [8,9,10,11,12] are a trend that is not directly related to the description of scattering but coincides in many respects with this paper. There are a number of nuclei that can be thought of as a rotating axially symmetric quantum rotor model plus a single nucleon. Some of the nuclear states are described within formalism that is practically equivalent to that presented, for example, in Refs. [10,13]. Here, the states of the ¹¹Be and ¹³C nuclei are studied as ¹⁰Be and ¹²C plus a neutron, respectively. However, the historical evolution of this trend, namely the use of the coupled channels method, led to ambiguous (not quite straightforward) features in the interpretation of the results. In particular, this is a description of levels with a certain total spin, angular momentum, etc. These quantities are not constants of motion in the case of non-spherical fields. In this work, such an interpretation is not applicable. The solution is used as a sum over the constant of motion, i.e., the projection of the angular momentum onto the axis of rotation. The question of the correspondence of the results obtained is open.

Nucleon–nucleus scattering is considered below to be the interaction of a point particle with an axially symmetric field. The interaction of a neutron with the ²³⁸U is chosen as a neutral example. It is one of the most widely used reactions in nuclear power. The interaction is described by the optical potential, which is one of the most popular simple ones. The potential parameters are taken from Ref. [14]. The aim of this work was not to describe the properties of the nucleus within the PRMN. However, due to the similarity of formalism, the presented results can also be interpreted as a representation of a new model for describing some properties of the ²³⁹U nucleus in the future, as well as other nuclei with similar structures.

2. Materials and Methods

2.1. Equation for a Potential with Axial Symmetry

The equation for the neutron interaction with a nucleus in the center-of-mass system, $\left(H_0+V-E\right)\mathsf{\Psi }\left(\mathit{r}\right)=0,$ with a zero impact parameter was written for the scattered wave $\mathsf{{\rm X}}\left(\mathit{r}\right),\mathsf{\Psi }=e^{i\mathit{k}\mathit{r}}+\mathsf{{\rm X}}$ in the following form:

$$\left(H_0+V-E\right)\mathsf{{\rm X}}\left(\mathit{r}\right)=-V{e}^{i\mathit{k}\mathit{r}},$$

where H₀ is the free Hamiltonian, V is the interaction potential, E is the interaction energy (in the system center-of-mass), $\mathit{k}$ is the wave vector corresponding to the incident plane wave. The coordinate system is rotated so that the potential does not depend on the azimuthal angle $\phi$ of the spherical coordinate system. We assumed that the wave vector lied in the ZOX plane (plane where $\phi =0$), making an angle ${\theta }^{\prime }$ with the OZ axis (polar axis, $\theta =0$). The above equation can be written in the form of an expansion in terms of a set of orthogonal wave functions, which are the eigenfunctions of the $\widehat{l_3}$ operator:

$$\mathsf{\Psi }=\sum _{m^{\prime }}\frac{{\psi }_{m^{\prime }}\left(r,\theta \right)e^{i{m}^{\prime }\phi }}{\sqrt{2\pi }}=\frac{1}{\sqrt{2\pi }}\left(e^{i\mathit{k}\mathit{r}}+\sum _{m^{\prime }}{\chi }_{m^{\prime }}{e}^{i{m}^{\prime }\phi }\right),$$

where $\widehat{l_3}$ is the operator of the third component of the angular momentum $\widehat{l_3}{e}^{i{m}^{\prime }\phi }=m^{\prime }{e}^{im{\prime }^{\phi }}$, m is its eigenvalue. Substituting this expansion into the original equation, multiplying both sides by $\frac{e^{-im\phi }}{\sqrt{2\pi }}$ and integrating over the angle $\phi$, we obtain a set of equations:

$$\left[H_{0,r\theta }+\frac{m^2}{r^2{\sin }^2\theta }+V\left(r,\theta \right)-E\right]{\chi }_m=-V\left(r,\theta \right)F\left(r,\theta ,{\theta }^{\prime },m\right),$$

where $F\left(r,\theta ,{\theta }^{\prime },m\right)=\frac{1}{2\pi }{\int }_0^{2\pi }{e}^{ikr\cos \tilde{\theta }\left(\theta ,{\theta }^{\prime },\phi \right)}{e}^{-im\phi }d\phi$, $H_{0,r\theta }$ is the Hamilton operator corresponding to free motion in the two-dimensional space of the half-plane with fixed $\phi =\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$ and $\tilde{\theta }$ is the angle between the wave vector and the radius vector $\overrightarrow{r}$.

The function $F$ is expressed in terms of the Bessel function of the first kind. In the selected coordinate system, the following expression was used:

$$F\left(r,\theta ,{\theta }^{\prime },m\right)=e^{ikr\cos \theta \cos {\theta }^{\prime }+\frac{\pi }{2}m}{J}_m\left(kr\sin \theta \sin {\theta }^{\prime }\right).$$

2.2. Numerical Model

A numerical scheme for solving two-dimensional differential equations in the scattering problem was used. The solution was based on the finite element method, matrix sweep. The result was the scattering amplitude $f\left(\theta ,\phi \right)$ at distances where $\mathsf{\Psi }\left(\overrightarrow{r}\right)$ is the asymptotic equivalent to the following expression:

$$e^{ikr\cos \tilde{\theta }}+f\left(\theta ,\phi \right)\frac{e^{ikr}}{r}.$$

The two-dimension scattering program was modified. Previously, it was used to calculate the resonant diffraction of molecules, as well as preliminary calculations of scattering by a non-spherical nucleus; basic details can be found in Refs. [15,16,17].

The optical theorem [18] is valid for each angle ${\theta }^{\prime }$; in this case, it has the following form:

$${\sigma }_{{\theta }^{\prime }}=\int {\left|f\left(\theta ,\phi \right)\right|}^{2}d\mathsf{\Omega }~\mathrm{I}\mathrm{m}f\left(\theta ={\theta }^{\prime },\phi =0\right),$$

where ${\sigma }_{{\theta }^{\prime }}$ is the scattering cross-section (with $\mathsf{\Omega }$ being the solid angle). Its confirmation was a criterion for the accuracy of the calculations.

Assuming that the angle ${\theta }^{\prime }$ can take any values and taking into account the symmetry equation for ${\theta }^{\prime }$ and $\pi -{\theta }^{\prime }$, the final cross-section of scattering on the axially symmetric potential can be written by averaging over this angle:

$$\sigma ={\int }_0^{\frac{\pi }{2}}{\sigma }_{{\theta }^{\prime }}\sin {\theta }^{\prime }d{\theta }^{\prime }\approx \sum C_j{\sigma }_{{{\theta }_j}^{\prime }}\sin {{\theta }_j}^{\prime }\mathsf{\Delta }{\theta }^{\prime },$$

where $C_j$ is the factor for numerical integration.

The described algorithm was applied to scattering of a neutron at a ²³⁸U nucleus. The potential of the nucleus–neutron interaction could be considered axially symmetric in a fairly good approximation, and the higher deformation parameters, except ${\beta }_2$, could be neglected.

For simplicity, we assumed that the shape of the nucleus was a spheroid with the ratio between the semi-major and semi-minor axes $(a-b)/R_0=1.06{\beta }_2$, where $R_0$ is the radius of the nucleus [19]. The sign of the deformation parameter was considered to be positive for the uranium isotope with a mass of 238 [20]. Two models, namely oblate and prolate spheroids, were used in this study.

The optical potential, which was called global by the authors, was taken as the initial one. It showed good agreement between the calculations and the experimental data [14]. The Wood–Saxon potential with an energy-dependent depth is used in this study, the width of the potential well is considered constant. For the present study, the width parameter is considered depending on the polar angle, and the circle is converted to an ellipse on the plane. The parameters of this ellipse were calculated so that the volume of the spheroid obtained by rotating the ellipse was equal to the volume of the ball. The radius of the ball was determined according to the standard formula $R_0=r_0{A}^{\frac{1}{3}}$, with the parameter $r_0$ derived from Ref. [14] and A being the atomic mass number.

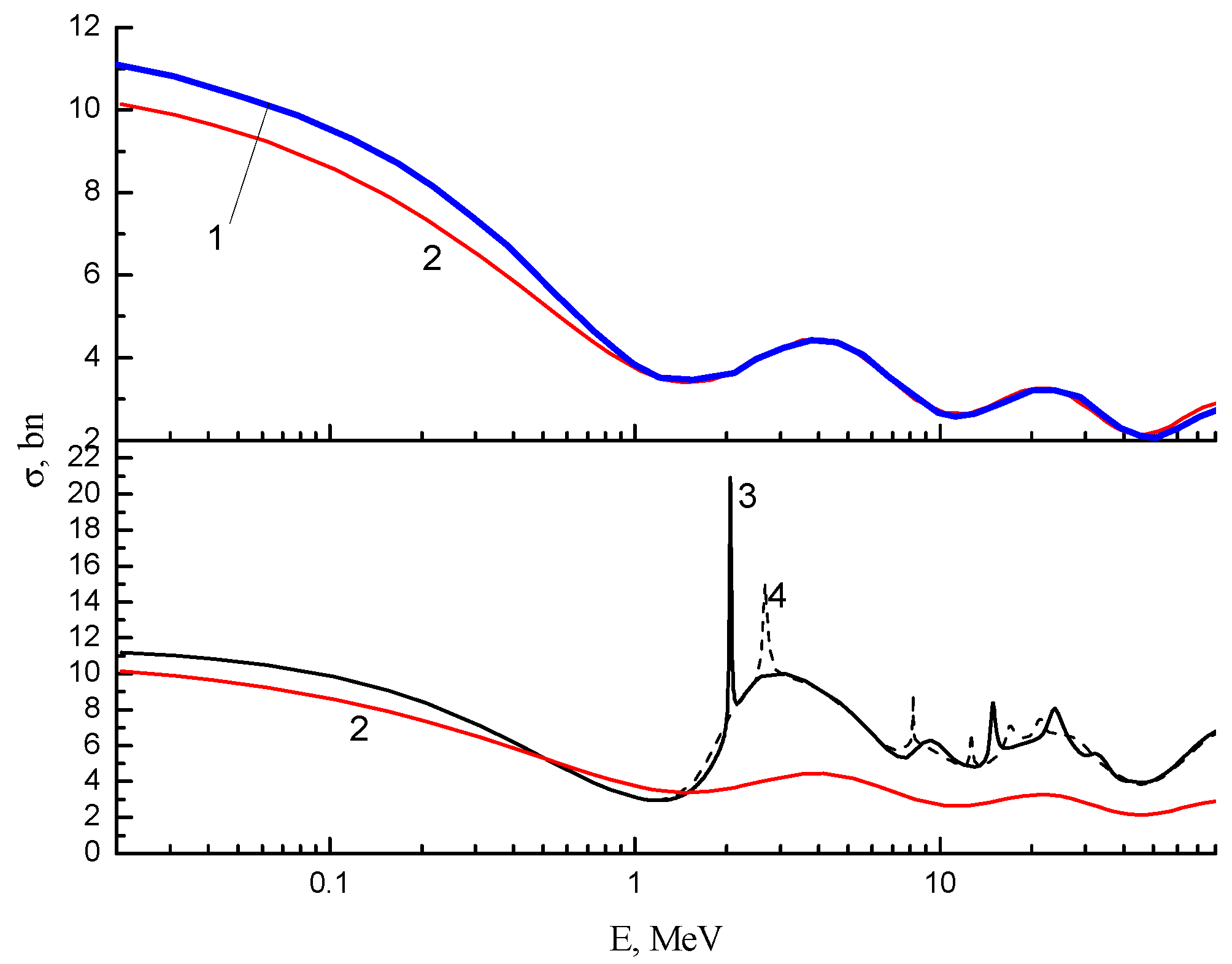
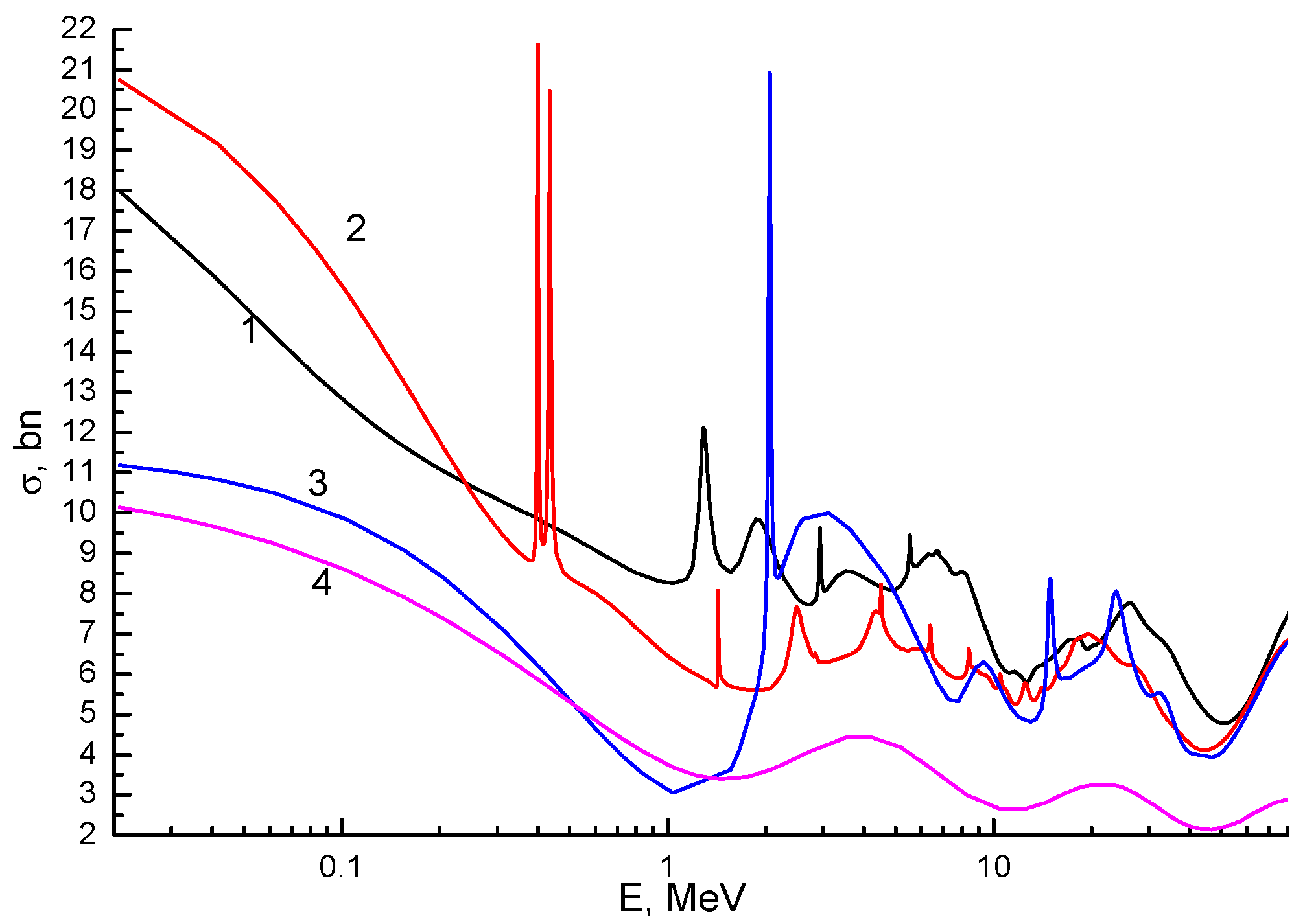
3. Results

The following control and research calculation with the optical potential is performed:

$$V+i\left(W+U\right),$$

where $V$ is the real potential, and $W$ and $U$ are the imaginary surface and volume absorption potentials taken from Ref. [14], respectively. The results shown in Figure 1 provide a satisfactory agreement between the cross-sections calculated and given in Ref. [14]. Some difference at low energies is apparently explained by the fact that in Ref. [14], the Hauser–Feshbach theory is included in the calculation of the elastic cross-section. Figure 1 shows different contributions from different parts of the potential. The above calculations demonstrate that the main contribution is made by the real potential, as well as by the imaginary volume and surface absorption ones. Further, the spin-orbital ls-interaction (V_ls) is not taken into account in the calculations; its contribution does not significantly change the results.

The scattering of a neutron on uranium as on an axially symmetric nucleus is a little more difficult when in accordance with the above algorithm. Individual solutions are found for different angles ${\theta }^{\prime }$. The examples of such calculations are illustrated in Figure 2.

Figure 3 shows the results of calculating the averaged cross-sections for neutron scattering on ²³⁸U.

Two models are presented: spherically symmetric potential and axially symmetric potential. The latter is used in two versions, for positive and negative internal quadrupole moments. The cross-section for scattering at the optical potential without the ls-interaction calculated in the first model is chosen as the control cross-section, which is in good agreement with the experimental one.

All scatter plots at the real potential quite differ from the control one. However, the cross-sections for scattering at axially symmetric potentials do not have pronounced maxima and minima, in contrast to the cross-section for the spherically symmetric potential. In particular, the scattering cross-section shifted by 2.5 bn on the prolate axially symmetric potential in the region above 0.3 MeV satisfactorily fits the control cross-section.

If the imaginary potential is included in the calculation (Figure 4), the cross-section decreases, and the resonances do not contribute, as for the centrally symmetric potential.

When real potentials, as well as full optical potentials, are used, there is a significant difference in the graphs for the models of the prolate (Figure 4, upper) and oblate (Figure 4, lower) spheroids. These calculations provide quite a simple mechanism for determining the deformation sign for some nuclei. It is possible to draw the following conclusion for the ²³⁸U and ²³⁵U nuclei based only on the available data. The calculations for ²³⁸U presented above also correspond quite well to ²³⁵U, and there is an insignificant difference in the potential depth (correction ≈ 5%) and width (less than a percent) due to the mass difference. Consequently, scattering by the 235 and 238 isotopes of uranium is described by similar potentials. Proceeding from the same cross-sections, the same sign of ${\beta }_2$ follows. Otherwise, the cross-sections would be significantly different.

The resonances are well seen in the scattering cross-section at the real potential. They come from the interaction of nuclear and centrifugal barriers. The latter has an analogue in the case of axial symmetry:

$$\frac{m^2}{r^2{\sin }^2\theta },$$

This barrier of a more complex shape than in the case of the spherically symmetric potential gives rise to quasi-stationary states. Some of them are interpreted as states of the ²³⁹U nucleus within the PRMN. In particular, the bright double resonance at 0.3 MeV can correspond to certain states in the region of 5 MeV, if the methodology used in studies such as that in Ref. [10] is followed.

Figure 5 shows the results of calculating the cross-sections for different m channels at different values of ${\theta }^{\prime }$. The sum of all of them, ${\sum }_{m=0,\pm 1\pm 2\dots }{\sigma }_m$, results in plots similar to those shown in Figure 2. For example, Figure 5, left, displays the terms for Figure 2, most upper left, and Figure 5, right, displays the terms for Figure 2, most upper right.

It can be seen that individual resonances appear in individual m-channels. Thus, the double resonance at 0.3 MeV is actually the result of the addition of resonances at $m=1$ and $m=2$, and the resonance contributes at angles $\theta ~\pi /4$ and completely disappears at $\theta ~\pi /2$. Resonances for different third projections of the angular momentum appear differently in the averaged cross-section. For example, this is the resonance at $E=1.4$ MeV and $m=2$; its contribution to the total cross-section is large precisely at $\theta ~\pi /2$. Or vice versa, the contribution of the resonance at $E=4.3$ MeV and $m=4$ disappears through addition and subsequent averaging. The used matrix sweep method is sensitive enough to resonances [21]; therefore, the proposed method can be effective as an extension of the PRMN. The question of interpreting the results in generally accepted terms, as well as the question of the applicability of such concepts in the problem with the absence of spherical symmetry, remains open.

4. Discussion

A method for resolving nuclear physics problems based on the improved algorithm is developed. This method is available for the solution for scattering in an axially symmetric field as a set of two-dimensional independent fields.

Cross-sections for elastic scattering of a neutron by ²³⁸U are found. The cross-sections for centrally symmetric and axially symmetric potentials are significantly different. At the same time, the curves of the cross-sections in the case of axially symmetric real potentials are smoother than the centrally symmetric ones; there are no significant drops, which exist for the centrally symmetric real potential. This gives a hope for describing the elastic scattering process with a decrease in the contribution of imaginary potentials.

Cross-section resonances or quasi-stationary states can be used within an approach similar to the particle-rotor model of the nucleus. An important difference would be in the classification. A new description could be based on the third component of angular moment and optimal angle of position.