Abstract
In this paper, we discuss quantum formalisms that do not use the axiom of choice. We also consider the fundamental problem that addresses the (in)correctness of having the complex numbers as the base field for Hilbert spaces in the København interpretation of quantum theory, and propose a new approach to this problem (based on the Lefschetz principle). Rather than a theorem–proof paper, this paper describes two new research programs on the foundational level, and focuses on basic open questions that arise in these programs.
1. Introduction
The København interpretation over the complex number has proved its uncanny effectiveness since it was conceived almost a century ago. On the algebraic level, states are solutions of a Schrödinger-type first-order differential equation such as
and linear combinations of solutions are also solutions. Here, represents the wave function, t denotes the time, denotes the quantum state, H is the Hamiltonian, and the cap defines the operator. Equations such as Equation (1) were developed in a complex model, giving it an assumed complex nature. On the other hand, the superposition principle for linear combinations can be applied over any field, and equations such as Equation (1)—or rather, the physical behavior they describe—can also be developed over other fields. The set of all solutions forms a vector space over a commutative field, or more generally, over a division ring.
The fact that every polynomial in one variable with complex coefficients has a complex root, yields the essential property that square complex matrixes always have eigenvalues, and, on the level of observables (see Section 3), this is actually a key property. Also, because the real subfield is of degree 2, the inner product used in the København description (see Section 3) allows one to have a normalization process and probability theory at one’s disposal.
Finally, the elegance and simplicity of the model adds to its value. This side of the story together with the previous point, forms the main “obstacle” in considering other København models over different (algebraically closed) fields, or even more general algebraic structures. In mathematics, for instance, for quite a while, algebraic geometers solely systematically worked over the complex numbers, due to the very same reasons quantum physicists use virtually solely : for its beauty and effectiveness (algebraically closed) and simply because it works (so why even bother?). Only when people such as André Weil started to consider and study algebraic geometry over finite fields in a systematic way, it turned out that this brave new algebraic geometry was as interesting as (and arguably even more interesting than) the “old” theory, and eventually even added further understanding of complex algebraic geometry.
This very discussion is one of the leading threads in this paper, and motivates us to introduce a conjectural Lefschetz quantum principle here.
Then, if one assumes to work over , then the so-called axiom of choice (AC) is often implicitly used in the mathematical machinery used to describe quantum physics. But since the philosophical discussion underlying quantum physics—including its many famous thought experiments—is very important for the theory, and since mathematics—even basic linear algebra—is so different without AC, we investigate what happens to quantum theory if one does not rely on AC.
We refer to the essay [1] for a deeper philosophical discussion on this matter.
The paper is organized as follows. Section 2 mathematically discusses the axiom of choice. Section 3 briefly describes the author’s approach to general quantum theories (over division rings) and we pay particular attention to finite fields and the minimal model. In Section 4, we develop a conjectural Lefschetz principle for quantum theory, and to that end, we first mathematically discuss the classical Lefschetz principle. In the final Section, we discuss the impact of not accepting AC on measurements and probabilities, and devise a number of thought experiments.
2. Axiom of Choice: Mathematical Discussion
We start this Section with a first formal formulation of the axiom of choice:
Let us look at a first illuminating example. Suppose each is a subset of the positive integers ; then, one could define as the smallest number in . The function that assigns to each the element is called a choice function. In this case, we do not need to invoke AC in order to fulfil the desired property. But in case we define as the set of nonempty subsets of the reals , no such choice function is known.
2.1. Russel’s Socks
Bertrand Russell gave a particularly entertaining example where one has to invoke the axiom of choice in order to define a choice function.Suppose one has an infinite collection of pairs of socks, where we assume that in one pair of socks, there is no way to distinguish between the socks. Then, in order to select one sock from each pair, one needs to invoke AC. Note that if one had started from pairs of shoes instead of socks, one could have defined a choice function (“select the left shoe”).
2.2. Choice Functions and Cartesian Products
In terms of choice functions, one can formulate AC as follows:
Certainly, each such choice function f defines an element of the Cartesian product of the sets in , so that we can give another equivalent statement:
2.3. Vector Spaces
The equivalent formulation that is of interest in the context of the present paper is the following:
Obviously, in the context of quantum theory, such results are of high importance.
Note that upon accepting AC, one can show that the size of a basis of a given vector space is independent of the choice of basis, and this size yields a notion of dimension.
3. København Interpretations beyond
In classical quantum theory, following the København interpretation—in some papers called actual quantum theory (AQT)—the state space is a Hilbert space (provided with the standard inner product). More precisely:
- (HS) A physical quantum system is represented by a Hilbert space , with the standard inner product and allowed to be nonfinite.
- (IP) The standard inner product sends to (or ), where is the complex conjugate of ; complex conjugation is an involutory automorphism of the field .
- (PS) Up to complex scalars, pure states (wave functions) are represented by nonzero vectors in ; usually, one considers normalized vectors.
- (TE) Time evolution operators are represented by linear operators of that preserve , that is, unitary operators. If is finite, unitary operators correspond to nonsingular complex -matrices U such that , where is the identity operator.
- (OB) Measuring an observable A in a system described by the wave function amounts to collapsing into one of the orthogonal eigenvectors of the Hermitian operator A, yielding as measurement the corresponding eigenvalue .
- (TP) Composite product states correspond to tensor products ; if a state in is not a product state, it is entangled.
- (BR) One follows Born’s rule, which says that if an observable A with discrete spectrum is measured, then the measurement will be one of the eigenvalues of A (this is OB), and the probability of measuring an eigenvalue is , where is the normalized wave function of the system, and is the projection onto the eigenspace of A corresponding to . If the eigenspace is 1-dimensional and is the normalized eigenvector which spans the eigenspace, one has that is the probability that the measurement will be made.
- (⋯).
The rest of this Section, gives a brief description of the approach given by the author in Ref. [2], which unifies all known modal quantum theories (over finite fields , algebraically closed fields, general division rings with involution).
This is by far the most mathematically technical Section of the paper, so let us first describe the central ideas. The key subsections for understanding the general picture are Section 3.1 and Section 3.2. The main idea is that one replaces by a general division ring—that is, a not necessarily commutative field—(see Section 3.1) and that one replaces the inner product by a so-called “-Hermitian form,” which is a natural generalization of the inner product (with much leg room, see Section 3.2) in the København formalism. Two natural choices are made: we first consider quantum theories over algebraically closed fields (in Section 3.3, Section 3.4 and Section 3.5); the fact that is algebraically closed is a highly important feature in the classical mathematical description of quantum theory, since the very fact that each nonconstant complex polynomial in one variable has a root is crucial for OB and BR. So, one needs to investigate quantum theories over general algebraically closed fields. In particular, we describe “complex-like theories” which share many features with classical quantum theory, and which lie at the base of our proposed quantum Lefschetz principle. This being said, we also consider quantum theories over finite fields (in Section 3.6), because those give rise to finite models, and hence arguably approach actual quantum problems in a more natural way.
3.1. The General Setting
A division ring is a field for which the multiplication is not necessarily commutative. Sometimes, division rings are called “skew fields”, but we prefer the name “division rings”. In Ref. [2], we described a general København approach, in which all known classical and modal quantum theories are united within one and the same framework. The main philosophy is that instead of the field of the complex numbers or finite fields, the underlying coordinatizing structures are generalized to division rings, so that we consider generalized Hilbert spaces over division rings instead of complex Hilbert spaces or their finite field analogons. Certainly, one has to have a suitable alternative for the classical inproducts, and this is perfectly possible if we provide the division rings with a so-called involution (see Section 3.2 just below).
3.2. Standard -Hermitian Forms
A “division ring with involution” is a division ring with an involutory anti-automorphism. If k is a division ring with involution , the standard -Hermitian form on the right vector space is given by
where and .
Remark 1.
In the case that , one obtains a form that is usually called symmetric; it is not a proper Hermitian form, but often still comes in handy in some situations (for example, in cases of field reduction, “real Hilbert spaces” have often been considered in quantum theory; see, e.g., the papers by William Wootters and his collaborators [3,4]).
We propose to describe all classical and modal quantum theories within one and the same framework, under the umbrella of “General Quantum Theories” (GQTs), as follows:
From now on, we propose to depict a physical quantum system in a general Hilbert space with k a division ring with involution .
Following Ref. [2], we speak of a standard GQT if given an involution , the general Hilbert space comes with the standard -Hermitian form. As some fields such as the real numbers and the rational numbers do not admit nontrivial involutions, they only can describe “improper” quantum systems.
3.3. Algebraically Closed Fields
Let k be any algebraically closed field in characteristic 0. It is well known that upon accepting the axiom of choice, there exists an involution in , where denotes the automorphism group of k and denotes its multiplicative group. Now, consider the set
One can immediately show that , endowed with the addition and multiplication coming from k, is also a field. Following Ref. [5]:
Theorem 1.
[-Analogy—algebraically closed version in characteristic 0] Let k be any algebraically closed field in characteristic 0. Let γ be an involution in . Then, is not a square in . Suppose is such that . Then, and .
So, each element of k has a unique representation as , with and i a fixed solution of . Fields that have index 2 in their algebraic closure are called real-closed fields, and can always be constructed as a of some involution . Real-closed fields share many properties with the reals : each such field is elementarily equivalent to the reals, which by definition means that they have the same first-order properties as the reals. We call a GQT complex-like if it is defined over an algebraically closed field k with nontrivial involution , where the elements of k are represented in Theorem 1 with respect to the field .
Remark 2.
The analogy goes even further: once we have defined as above, and we represent each element x in k as (which can be done by Theorem 1), it can be shown that the automorphism σ is given by
3.4. Extension of Quantum Theories
If one considers a GQT over a field k in characteristic 0, the following fundamental question arises:
Is embeddable in a complex-like theory (or in any other GQT, for that matter)?
Here, the notion of “embeddable” is straightforward: if k comes with the involution , we want to have a field extension for which ℓ is algebraically closed, and an involution of ℓ for which the restriction of to k precisely is . Since any GQT depends only on the Hermitian matrix of the -Hermitian form with respect to a chosen basis (with suitable adaptation to the infinite-dimensional case), it is clear that if the aforementioned GQT comes with the matrix A over k, then the same matrix A defines a -Hermitian form over ℓ which induces the initial form over k.
Observation 1.
If the dimension of the Hilbert space is fixed, then any GQT over k (and with respect to γ) is part of the GQT over ℓ (with involution ).
Section 3.4.1 clarifies on the reason why an extension theory is desired.
3.4.1. Comparison Theory
Any two fields k and of the same characteristic are contained (as a subfield) in a field ℓ. The following construction is quite a simple one: Let ℘ be the prime field in both k and (isomorphic to in characteristic 0 and to in characteristic ), generated by 0 and 1. Then, put and , with S (resp. ) a basis over ℘ of k (resp. ) consisting of algebraic and transcendental elements over ℘. Then, is “the” desired field. Obviously, such a field ℓ with the extension property is not unique, since ℓ can be extended indefinitely (for instance, by adding transcendental elements to ℓ). If we have formulated a suitable extension formalism for general quantum theories (over algebraically closed fields), one would be able to evaluate problems formulated over k and in one and the same theory formulated over ℓ (and any of its extensions). In that way, if the characteristic of the fields is fixed, we could look at a quantum theoretical setting prepared over different fields k and as being two guises of the same story: just extend the GQTs over k and to the appropriate GQT over ℓ. Since it is sometimes preferable to use algebraically closed fields, we want essentially that the following diagram commutes (see Figure 1), after the map is applied, which associates with each couple (where is a field or division ring, and an involution of ) the corresponding standard general quantum theory. (Of course, the same approach can be also applied to nonstandard GQTs.)
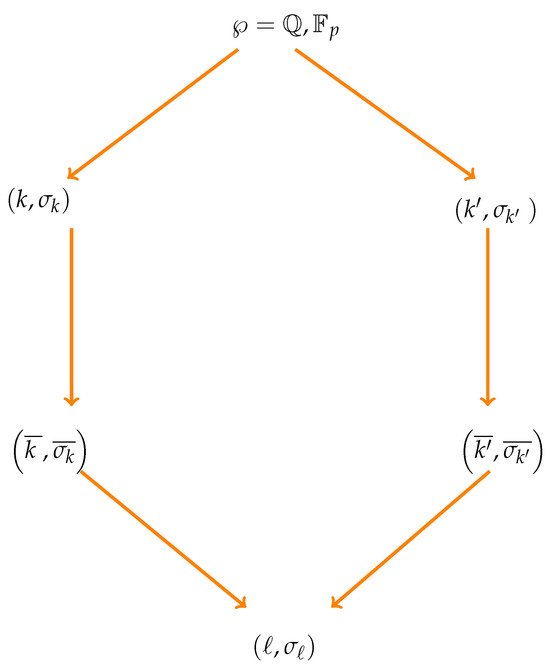
Figure 1.
Extension diagram. Each arrow stands for an extension of fields/division rings with involution. On top, the prime field is written down (without involution). In the end, we want to end up with a GQT which induces and . See text for details.
3.4.2. Schnor’s Result on Involutions
The bad news is that a general comparison dream cannot hold, as was shown in Ref. [2]. However, the result is true as soon as one assumes k to be algebraically closed to begin with, by a result of Schnor [6] (which says that if is a field extension of algebraically closed fields, and is an involution of k, then there exists an involution of ℓ that fixes k and induces in k).
Theorem 2
(Embedding Theorem of Quantum Theories [2]). Any GQT over an algebraically closed field k with involution γ is embeddable in a GQT over ℓ, where ℓ is any algebraically closed field extension of k.
In particular, this is also true for AQT: we can embed AQT in an infinite number of “nonisomorphic” GQTs over algebraically closed fields in characteristic 0, and this adds an infinite number of layers to the theory, which can be used in various situations (such as quantum coding schemes).
3.5. The Minimal Model:
Recall the following basic result:
Theorem 3.
Let k be any field. If k is not finite, then , where is an algebraic closure of k; if k is finite, is countable.
It is important to note that the statement relies on the axiom of choice.
Since is the unique prime field in characteristic 0, each field of characteristic 0 contains , and hence, each algebraically closed field k in characteristic 0 contains the algebraically closed field as well. By Theorem 3, is countable, and hence, it is also minimal with respect to being algebraically closed.
Observation 2.
The set of GQTs over can be considered as the set of minimal models (over algebraically closed fields) in characteristic 0.
The point is that, due to Theorem 2, any minimal GQT can be embedded in a GQT over any given algebraically closed field in characteristic 0. And also, if k is algebraically closed in characteristic 0 and we consider a GQT over k with involution , one observes that fixes the prime field , and so it also fixes the algebraic closure . (Note that the induced action might be trivial, in which case the induced quantum theory over is orthogonal/symmetric.)
Actually, we can do a bit better.
Observation 3.
Each GQT over an algebraically closed field k in characteristic 0 induces a general quantum theory over .
Proof.
Suppose is the involutory automorphism which comes with . As shown above, the automorphism fixes . If would fix elementwise, then one obtains a nontrivial element of order 2 in the Galois subgroup (where the latter denotes the automorphism group of which fixes its subfield elementwise), which is a contradiction, since this Galois group is known (using Ref. [5]) to be torsion-free (that is, it contains no nontrivial elements of finite order). □
We have obtained the following agreeable picture:
From this important point of view, it feels more natural to consider quantum theory coordinatized by the algebraic closure, , of the rational numbers. In fact, as the rational numbers are dense in the real numbers, the expression,
shows that every element of can be seen as a limit of Cauchy sequences in ; in other words:
Observation 4
(Universality of the Minimal Model). Classical quantum theory can be approximated by modal quantum theory over , while the latter is countable, algebraically closed, and contained in every division ring (and in particular: field) in characteristic 0.
3.6. Finite Fields
In Ref. [7], modal quantum theory (MQT) was introduced as a finite “toy model” for AQT, in which the underlying field is replaced by a finite field (where q is an arbitrary prime power). Inner products in the usual formal sense are not defined on vector spaces over a finite field, and hence, this aspect is not covered in Ref. [7]. The latter means that the very notion of “orthogonal states” does not occur in that approach. In Ref. [8], vector spaces are considered over finite fields, , with p a prime, for which the following property holds:
The reason is straightforward: besides the many similarities between and , we have a natural Hermitian bilinear form at our disposal that shares important aspects with the inner product . In Ref. [2], it is shown that there is no need at all for restricting the theory to primes with the aforementioned property. Let us give a quick overview.
- Let q be any prime power; then, up to isomorphism has a unique extension of degree 2, namely . The mapsends each element of to itself, while being an involutory automorphism of .
- Let n be any positive integer different from 0; then, if is the n-dimensional vector space over , define for and in V,
- For , one finds that
The following observation is taken from Ref. [2].
Observation 5.
The linear -matrices U which preserve the form , precisely are unitary matrices: -matrices U for which is the -identity matrix, where .
Classical quantum theory compares with MQT over finite fields as follows.
Remark 3
(-analogy—finite fields version). In this model of QT, plays the role of , the role of , γ the role of complex conjugation, and the role of inner product. By choosing any element κ in , we can represent each element of uniquely as
with . So, viewed from this representation, the situation at least looks “somewhat classical”.
3.7. The Base Field in Fixed Characteristic: Quantum Lefschetz Formalism
If we agree that in the København interpretation we need an algebraically closed field ℓ for describing amongst others a theory of observables based on eigenvalues and eigenvectors, one still needs to decide about the characteristic of the theory. Once a characteristic is fixed, another fundamental question emerges:
The very question as of which base field is needed in the Københaving interpretation has a long history, and has been considered in many papers. In Appendix A, a short overview of some papers that consider the “base field question” is given and those are compared to the GQT-approach proposed in Ref. [2] by the author of this paper. It is instructive as well to refer to Refs. [9,10,11,12] (considered in Ref. [2]) to list other relevant studies.
The discussion of the current subsection motivates us to introduce a quantum Lefschetz formalism in Section 4.
4. Quantum Lefschetz Principle A
In this Section, the quantum Lefschetz principle is introduced. Basically, we propose a way to compare different quantum theories over algebraically closed fields.
We first explain the mathematics of the Lefschetz principle.
4.1. Lefschetz Principle
The principle in its most naive but perhaps straightforward form, states the following:
Actually, the naive formulation of the main principle is even stronger: to check whether a statement about an algebraic variety over an algebraically closed field ℓ in characteristic 0 is true, it is sufficient to check it over (whatever that means). Solomon Lefschetz, in his book [13], states:
(Recall the discussion in Section 1 concerning the “choice of ”.) As Abraham Seidenbergh remarks in his paper [14], the situation is not quite as simple as Lefschetz claims. Seidenbergh describes the following beautiful yet simple example: consider two curves defined by equations and in the projective plane over the algebraically closed field k of characteristic 0. In the complex case, it is known that such curves meet in at least one point: there exist numbers , such that
According to Lefschetz, one could conclude the same for k. Indeed, assume that k is the algebraic closure of a field that is finitely generated over and contained in , and hence, that k is a subfield of (see Theorem 4 below). One then concludes that the curves have a point in common (because they have a point in common over ). Only now, the situation has changed: the property one was set to obtain was that the curves have a point in common over k, but now, one can only conclude that the curves have a point in common in some extension field of k inside of .
So, more precise statements are needed in order to grasp the Lefschetz principle in depth. The essence of the principle becomes much clearer if one first looks at the (precise) “baby” version:
Theorem 4
(Baby Lefschetz Principle). Let k be a field of characteristic 0 that is finitely generated over the field of rationals . Then, there is an isomorphism of fields,
from k to a subfield of the field of complex numbers .
This statement, although simple, is quite powerful once one considers its consequences. Lefschetz observed that every equation over an algebraically closed field ℓ of characteristic 0 is defined by a finite number of coefficients, which generate a field , which is finitely generated over , and whence Theorem 4 applies. The idea is very deep: although one starts in any algebraically closed field of characteristic 0, the typical problems that occur in the theory of algebraic varieties involve only finite data, and using Theorem 4, one obtains a principle that transfers the problem to the complex numbers. Unfortunately, as one has seen just above, Lefschetz’s initial version was not precise. Alfred Tarski came up with a solution in Ref. [15]:
Theorem 5
(Minor Lefschetz Principle). The theory of algebraically closed fields of characteristic 0 admits quantifier elimination, and therefore, all models are elementary equivalent.
For more clarity, let us also provide the following equivalent formulation.
Theorem 6
(Minor Lefschetz Principle, version 2). If an elementary sentence holds for one algebraically closed field of characteristic 0, then it holds for every algebraically closed field of characteristic 0.
We recall the notion of elementary sentence for the convenience of the reader. Let ℓ be any field. An atomic formula relative to ℓ is an expression of the form , where f is a polynomial with coefficients in ℓ. By a formula (again relative to ℓ), we mean an expression built up in a finite number of steps from atomic formulae by means of conjunction, negation, and quantifiers of the form “there exists an x such that,” where x varies over an algebraically closed field L containing ℓ. An elementary sentence (relative to ℓ) then is a formula involving no free parameters.
Another interesting variation of Lefschetz’s principle reads as follows:
Theorem 7
(Algebraic Lefschetz Principles). Let Φ be a sentence in the language for rings, where are constants and are binary functions. The followings are equivalent:
- Φ is true over every algebraically closed field in characteristic 0;
- Φ is true over some algebraically closed field in characteristic 0;
- Φ is true over algebraically closed fields in characteristic for arbitrarily large primes p;
- Φ is true over algebraically closed fields in characteristic for sufficiently large primes p.
Unfortunately, although the Minor Lefschetz Principle is quite general (and even still more general versions are known), not every statement carries over just like that. For example, the statement that the cardinality (number of rational points) of every variety is at most that of the continuum is true over , but certainly this is not true over algebraically closed fields with greater cardinality than .
4.2. Algebraically Closed Fields in Quantum Theory
Even if we agree to work with algebraically closed fields as the base field to describe quantum theory in the København interpretation, why would we have to use the complex numbers? For every prime number p (including 0) and every cardinal number , there is an algebraically closed field ℓ, which lives in characteristic p, and for which . And even if the field is not algebraically closed, there is a number of valuable quantum theories around that have much in common with classical quantum theory, while still behaving differently. For instance, as William Wootters explained to me [16], quantum theory over the reals contains mysterious features that have not been explained to this day. If we write a prepared state relative to an othonormal eigenbase as , and each as , then only the real vector contains the information about probabilities. Is there an underlying physical reason?
Remark 4.
Suppose we write each as ( real). Then, all states that “probability project” on are exactly of the form for which for all k (while the sum up to 1). So, the states are precisely the points of a so-called 2-dimensional Clifford torus.
In each of the approaches we have seen in Section 3.7, either it is (sometimes implicitly) assumed that the reals are contained in ℓ, or a number of properties are assumed that in the end hold for a København theory over the complex numbers (but not necessarily characterize the field uniquely as the complex numbers). We propose a completely different approach. If one starts from any given algebraically closed field ℓ—for instance, in characteristic 0 to fix ideas—then a reasoning similar to that of Lefschetz might enable us to transfer the entire quantum theory described in the language of the København interpretation over ℓ, to the København interpretation over . So, a sufficiently subtle Lefschetz theory in the spirit of the previous theorems might give us an answer.
Question 1.
Can we develop a Lefschetz principle for quantum theory, so as to show that one can indeed consider the complex numbers as a suitable field of coordinates?
An answer would largely settle the base field question in quantum theory. For instance, how much of complex quantum theory can be described in first-order logic over (plus some appropriate induction principle)?
Currently, we are developing an answer to this fundamental question.
Remark 5
(Automorphisms of and codes). The most commonly used automorphism of in quantum theory is complex conjugation, but there are many other automorphisms in all models of Zermelo–Fraenkel set theory plus AC. In fact, there are so many that the structure of is very hard to understand. On the other hand, in models without AC, it is consistent to say that —that is, that standard complex conjugation is the only nontrivial automorphism of . Surprisingly, the immense size and complexity of (upon accepting AC) is virtually never used in quantum theory, while for instance, in quantum coding theory, it would be a powerful tool. But even if , unexpected results can be obtained. The projective semilinear group acts on the (-dimensional) state space , and can select states based on the occurrence of fixed points; if , one can understand and control the action much better in this context. In such a model, one can show that for each automorphism φ of the state space (that is, each element of ), at least one of φ or is an element of the projective general linear group, and so has fixed points as the field is algebraically closed. This is a remarkable property in the context of selection processes, and hence also of quantum codes. Developing these codes is a subject of a forthcoming study [17].
Note that the proposed quantum Lefschetz principle is one step in the larger program of investigating (and comparing) GQTs as alternative languages to describe quantum theory through the København formalism. Other fundamental questions arise, such as to whether general covariance in general relativity survives in all GQTs, or what the fate of the Heisenberg principle is in GQT. The latter problem in GQTs over finite fields is discussed in Ref. [18].
5. Eigenvalues, Eigenvectors, and Probabilities
We start this Section with a construction taken from Ref. [19], of weird vector spaces upon not accepting AC.
5.1. A Particular Example [19]
Let S be a set. Then, is defined as
where , and where we have identified with a map .
Now, let be a collection of Russell’s socks (upon not accepting AC); see Section 2.1. (Actually, a stronger version of Russell’s socks is assumed here, as in §1.1 in Ref. [19].) Let be the set of all socks, and define
In Ref. [19], it is shown that is an irreflexive complex Hilbert space, so an operator on cannot be equal to its adjoint, and the usual Hilbert space formalism of quantum theory fails. In Ref. [19], it is argued that such Hilbert spaces have to be taken into account through the following thought experiment.
5.1.1. Identical Particles
Before describing the thought experiment suggested in Ref. [19], we recall some statements about identical particles. We say that two particles are considered identical if all their intrinsic properties such as mass, spin, charge, etc., are exactly the same. The configuration space of N identical particles is defined by
Here, the particles live in ; denotes the Cartesian product ; is the subspace of points for which at least two “coordinates” (in ) are the same (mathematical explanation: to remove singularities; physical explanation: identical particles cannot occupy the same “location” in space, in the sense that no projection on coordinate axes may coincide); and finally, is the symmetric group on N letters (which has to be divided out since one cannot distinguish between the particles). The fundamental group of gives information about the continuous trajectories between the particles.
Example 1.
Let and (two particles moving on a line). Then, is homeomorphic to the space , in which particles and are identified, and where Δ is defined by the line . So, we obtain the half-plane defined by .
Finally, a particle that follows Fermi–Dirac statistics is called a fermion; generally, such particles have a half-odd integer spin.
5.1.2. Thought Experiment
View as an assembly of identical noninteracting spin- particles that obey the Fermi–Dirac statistics. Its Hilbert space is defined as
and is isomorphic to . The family of all particles is viewed as the compound system of the distinguishable assemblies. Their Fock space is
The spaces and are counter examples to several assertions in Hilbert space theory [19]:
- Both spaces do not admit an infinite orthonormal (Schauder, see Section 5.2) eigenbase, so there is no way to choose a mode of observation (in the sense of Bohr’s complementarity interpretation); there is no Hamel base either;
- As the vector space duals of and are different from and , there is no notion of a self-adjoint operator in both and .
5.2. Schauder Bases
In infinite-dimensional Hilbert spaces, quantum theorists mostly use Schauder bases instead of Hamel bases. Hamel bases are the usual bases considered in linear algebra, but Schauder bases are somewhat different. We say that is a Schauder basis of the infinite-dimensional Hilbert space , if each vector can be represented as a tuple in with at most a countable number of nonzero coefficients. (Each vector can be obtained as a convergent series of vectors generated by seen as a Hamel base of a subspace of , so that the subspace generated by as a Hamel base is dense in ). We say that a Hilbert space is separable if it contains a countable Schauder basis. It can be shown that all infinite-dimensional separable Hilbert spaces are isometrically isomorphic to , cf. Ref. [20]. Note also that by Baire categoricity, one can show that the Hamel dimension of a complex Hilbert space is always finite or uncountable. Here, “Hilbert” is important. Suppose is an orthonormal basis of and let be a subset. Then , but it is not expressible relative to as a Hamel basis.
In spaces with a Schauder base , Born’s probability formalism works perfectly. Note that if is an infinite-dimensional Hilbert space, the dimension refers to its dimension with respect to a Hamel basis, and that the “Schauder dimension” can be different than the usual Hamel dimension.
If one considers an observable A in an infinite-dimensional Hilbert space, the orthonormal eigenbase of A is also considered to be a Schauder base.
5.3. Projector Operators
A Hermitian operator of a Hilbert space is called a projector (operator) if . (It is a dichotomy operator since it only allows two possible outcomes.) Now, consider a Hilbert space , and let be the observable that projects any vector onto the subspace A of . Let be a Schauder eigenbase of (taken that it exists). Then, , where A is generated by the eigenvectors in A and B is generated by the eigenvectors in . Let a quantum system be prepared in the state . Upon projecting onto A, respectively B, one obtains vectors and , respectively, and we can write:
Now expand and in the Schauder base of A and of , respectively, induced by to obtain and . Then, the probability of measuring the eigenvalue (“YES”) and the probability of measuring (“NO”) are given by
Note that if is the projector operator onto the eigenvector , then can be straightforwardly described as
5.4. Double Slit Experiments: A Variation in Quantum Theory without AC
The double slit experiment by Thomas Young does not need an introduction: it features a light beam fired in a straight line through a panel with two disjoint rectangular slits on a screen. Classical physics expects a diffraction pattern on the screen, and that is what actually happens. But if the intensity of the laser beam is turned down so that individual photons are sent through the slits one at the time, eventually the same diffraction pattern appears, as if interference still does occur. Although the particles are measured as a single pulse in a single position, a probability wave describes the probability of observing the particle at a specific point in the plane of the screen. Born’s rule gives us the probability distribution for finding an electron at specific places of the screen. Once an electron hits the screen and is detected, the wave function collapses and the outcome can be described through the eigenvalues of an observable matrix.
Although the following thought experiment is not directly related to the double slit experiment, it still shares some of its (even unexpected) characteristics.
So, let be a (generalized) Hilbert space over some field k in a model of Zermelo–Fraenkel without AC, which allows (Schauder) bases and of different cardinalities. This field may not be the complex numbers, but in the context of modal quantum theories, one should still consider this possibility. Anyway, due to Ref. [21], we know that exists. Note that necessarily is infinite-dimensional (in the sense that it is not finite-dimensional). Now, let be a second Hilbert space over k, and consider . Let be the projector operator of onto ; this is an observable with eigenvalues 0 and 1, and acts on as the identity. Now, consider a state in . After measuring , collapses into a state in which is a superposition.
A question arises:
Question 2.
What is the probability that a state is contained in ? As has no well-defined dimension, we have no idea how “big” is with respect to .
But we can do better.
Thought Experiment: AC Black Box Measurements
Suppose a quantum system is prepared in a state in the (possibly generalized) Hilbert space over the field k. We assume that upon not accepting the axiom of choice, admits Schauder bases of different cardinalities. Now, we are going to perform a measurement corresponding to the Hermitian operator A. Before making the measurement, we do not know whether AC holds true or not; this can only—in general—be observed after the measurement has been made. (There is a black box that returns the value “0” or “1”.) After the measurement, one obtains an eigenvalue with probability . If AC holds in the underlying mathematical theory, this outcome is standard. If AC does not hold, could have been measured with a different probability (by the formalism below (Section 5.5), for instance, could be infinitely small).
5.5. New Born Formalism and Higher Schauder Bases
Let S be an uncountable set, and suppose is a set of positive real numbers. Suppose as a limit is also real. Then, in any model of Zermelo–Fraenkel with AC, it can be shown that only at most a countable number of elements in are different from zero. The proof uses the property that a countable union of finite sets is also countable—a property that fails miserably when AC is not around. So, it makes sense to define higher Schauder bases as follows. One says that is a higher Schauder basis of the infinite-dimensional Hilbert space if all vectors of can be represented by a unique -tuple in which an uncountable number of nonzero entries is allowed and so that such vectors also occur. It follows that is not countable. Consider a state . For Born’s formalism to work, the condition
needs to be fulfilled. Upon accepting the axiom of choice, it is straightforward to show that Equation (20) implies that only a countable number of entries in is nonzero, and so in , one can still consider those states which make sense within the quantum-theoretical setting. In Zermelo–Fraenkel set theory without choice, however, there are models in which Equation (20) is true, with an uncountable number of entries being nonzero [22]. In this formalism, one only considers the state vectors for which (before normalization). (If one would work over an algebraically closed field ℓ of characteristic 0 which is different from , then we ask that is contained in the real-closed subfield which is defined relative to the choice of complex conjugation.)
Question 3.
Does this formalism cover the quantum-theoretical situations that are not possible over classical Schauder bases?
We suspect that the answer to this question, and also to the next question, is “yes.”
Question 4.
Does it make sense to introduce nonstandard probabilities (e.g., infinitely small probabilities) in this context?
5.6. Blass’s Theorem and Ineffective Observables
In Ref. [23], Andreas Blass showed in Zermelo–Fraenkel set theory, that if every vector space has a basis, then AC also holds. Blass starts with a set of disjoint nonempty sets (), picks an arbitrary field k, and constructs the field extension , where . Then, a particular subfield K of is constructed and is interpreted as a vector space over K. In , Blass considers the K-subspace V spanned by X. Assuming that V has a basis, a choice function on is then constructed. However, it does not follow that AC is deducible from the statement that every ℓ-vector space has a basis, with ℓ a specified, fixed field. On the other hand, k, , and K live in the same characteristic, so one has the following stronger statement.
Theorem 8
(Blass’s Theorem, version 2). Let p be any prime, or 0. Then, in Zermelo–Fraenkel set theory, AC is deducible from the assertion that every vector space over a field of characteristic p has a basis.
For quantum theory, the importance is obvious: in the classical København formalism, observables (Hermitian operators) collapse into one of the vectors of an orthogonal eigenbase, and the corresponding eigenvalue is the resulting observed value. Upon not accepting AC and using models of Zermelo–Fraenkel theory without AC, it is not excluded that some Hilbert spaces over (or some other field) do not have a base, so that the formalism of Hermitian observables fails, or needs to be adapted at the very least. In any case, by Theorem 8, one may suppose that the characteristic of k is 0. For instance, let be the set of orthonormal eigenvectors of some given observable B (which cannot be maximal by assumption), and let be the subspace of generated by over k (either as a Hamel base or as a Schauder base). By taking a state outside of , no measurement can be performed using the state .
Remark 6
(Quantum Lefschetz Principle B). Is a candidate for this formalism? If not, in view of first-order logic, one may switch to another algebraically closed field for which Blass’s Theorem does work (as such, ending up with ineffective observables).
6. Conclusions
This paper focused on two basic aspects of quantum theory. First of all, modal quantum theories were considered, and a research program was proposed that aims to understand (once and for all) which underlying coordinatizing algebraic structure (among division rings), including the complex numbers, yields the best language to describe quantum theory through the København interpretation. In order to describe this program, we briefly explained general quantum theory (described over division rings) in Section 3 and detailed a number of aspects that are not available in standard classical quantum theory. The main point is that one replaces the field of complex numbers by a general division ring (for which the product is not necessarily commutative) and that one replaces inner products by suitable -Hermitian forms, which act as natural generalizations of inner products in the København formalism. We considered quantum theories over algebraically closed fields in more detail, because being algebraically closed is the very feature that gives rise to a suitable theory of observables, and to Born’s rule in the classical setting. In particular, we described “complex-like theories” which share many features with classical quantum theory. (We also considered quantum theories over finite fields in some detail.) The new material in Section 3 is put forward in Section 3.4.1 and Section 3.5. Next, we proposed a quantum Lefschetz principle, which describes a conjectural way to compare different quantum theories over the various algebraically closed fields. Finally, in Section 5, we investigated the impact of (not assuming) the axiom of choice on the mathematical description of quantum theory and its physical applications. We first considered a thought experiment suggested in Ref. [19] (involving Russell’s socks) and described new thought experiments in which probabilities of measurements become dependent on whether one assumes the axiom of choice, or not. We then introduced the new concept of higher Schauder bases and a subsequent new Born rule formalism. We ended the paper with remarks about quantum theories that give rise to ineffective observables, and about quantum coding schemes in classical quantum theory in models that do not satisfy the axiom of choice.
The first questions that need to be resolved at this point (in quantum Lefschetz theory) are: (A) What part of quantum theory over the complex numbers can be recovered through its first order logic?; (B) What part of quantum theory over the complex numbers can be recovered through GQT over (refinement of the universality result Observation 4; this is an alternative approach to (A))? As to quantum theory without the axiom of choice, the first questions that naturally arise are: (C) further development of the formalism of higher Schauder bases (with and without choice), and (D) devising the automorphic codes in models without the axiom of choice (see Remark 5).
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The author wishes to thank Karl Svozil, Bill Wootters, and the anonymous referees for a number of interesting and helpful communications.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Comparing Theories
Appendix A.1. Barret/Hardy Approaches
- Both Hardy [24] and Barret [25] see states as probability vectors in some vector space V, and as the probability entries are real numbers (contained in the interval ), V is assumed to be a real vector space. This means that the underlying algebraic structure is assumed to contain the field of real numbers.In the unifying viewpoint of GQTs [2], probabilities are manifestations of the Hermitian form (through the generalized Born rule, e.g.), and the field or division ring one uses as underlying algebraic structure (whatever it is).
- In Ref. [24], two integer parameters K and N emerge, for which the identity holds. If one considers underlying algebraic structures such as the real numbers , the complex numbers or the quaternions , only confirms the aforementioned identity. Hardy concludes that this—at least intuitively—points towards the complex numbers, without providing a formal proof [26]. However, the identity was not considered in the entire realm of fields and division rings in characteristic 0—only over the set . (On the other hand, assuming the probabilities to be rational numbers in would also yield more flexibility for V.) Barret’s generalized probabilistic theories are based on Hardy’s axiomatic approach, so Barret ends up with the complex numbers as well.In our approach of GQTs [2], we also work with vector spaces, but any division ring (with involution) is allowed to be the coordinatizing agent, so as to find unifying behavior in this universe of quantum theories. The no-cloning result of Ref. [2], for instance, solely follows from the concept of linearity/superposition and is applicable for all division rings, hence also fields and algebraically closed fields, such as in particular (we refer to Refs. [27,28] for the initial no-cloning results over the complex numbers). The study in Ref. [2] shows that no-cloning is not a particular instance at all of quantum theory represented in the framework of complex numbers.
Appendix A.2. Cassinelli–Lahti Approach
In Ref. [29], a program is outlined for an axiomatic reconstruction of quantum mechanics based on the statistical duality of states and considerations of symmetry. The authors discuss the choice of the complex numbers in Section 4 in Ref. [29]. In their viewpoint of orthomodular spaces and because of the use of Solér’s theorem, one is again coordinatizing over a member of . The authors personally prefer the complex numbers for reasons of elegance. (At this point, it is important to recall the dangers of the elegance aspect, see Section 1.)
References
- Braeckman, J.; Thas, K. De Invloed van Esthetiek op ons “Onafhankelijk” Denken; Ghent University: Ghent, Belgium, 2023. [Google Scholar]
- Thas, K. General quantum theory—unification of classical and modal quantum theories. J. Phys. A Math. Gen. 2020, 53, 395304. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement sharing in real-vector-space quantum theory. Found. Phys. 2012, 42, 19–28. [Google Scholar] [CrossRef]
- Wootters, W.K. Optimal information transfer and real-vector-space quantum theory. In Quantum Theory: Informational Foundations and Foils; Chiribella, G., Spekkens, R.W., Eds.; Springer Science+Business Media B.V.: Dordrecht, The Netherlands, 2016; pp. 21–43. [Google Scholar] [CrossRef]
- Artin, E.; Schreier, O. Algebraische Konstruktion reeller Körper. Abh. Math. Semin. Univ. Hambg. 1927, 5, 85–99. [Google Scholar] [CrossRef]
- Schnor, B. Involutions in the group of automorphisms of an algebraically closed field. J. Algebra 1992, 152, 520–524. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M.D. Modal quantum theory. Found. Phys. 2012, 42, 918–925. [Google Scholar] [CrossRef]
- Lev, F.M. Introduction to a quantum theory over a Galois field. Symmetry 2010, 2, 1810–1845. [Google Scholar] [CrossRef]
- Aerts, D.; Daubechies, I. Physical justification for using the tensor product to describe two quantum systems as one joint system. Helv. Phys. Acta 1978, 51, 661–675. [Google Scholar] [CrossRef]
- Baez, J.C. Division algebras and quantum mechanics. Found. Phys. 2012, 42, 819–855. [Google Scholar] [CrossRef]
- Cassinelli, G.; Lahti, P. A theorem of Solér, the theory of symmetry and quantum mechanics. Int. J. Geom. Methods Mod. Phys. 2012, 9, 1260005. [Google Scholar] [CrossRef]
- Solér, P.M. Characterization of Hilbert spaces by orthomodular spaces. Commun. Algebra 1995, 23, 219–243. [Google Scholar] [CrossRef]
- Lefschetz, S. Algebraic Geometry; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar] [CrossRef]
- Seidenberg, A. Comments on Lefschetz’s principle. Am. Math. Month. 1958, 65, 685–690. [Google Scholar] [CrossRef]
- Tarski, A. A Decision Method for Elementary Algebra and Geometry; RAND Corporation: Santa Monica, CA, USA, 1957; Available online: https://www.rand.org/pubs/reports/R109.html (accessed on 14 August 2023).
- Wootters, W.K.; (Williams College, Williamstown, US). Personal communication, 2023.
- Thas, K. Involutory Quantum Codes (Working Title); Ghent University: Ghent, Belgium, 2023. [Google Scholar]
- Thas, K. Quantum Theory over Finite Fields Is Falsifiable through the Heisenberg Principle; Ghent University: Ghent, Belgium, 2023. [Google Scholar]
- Brunner, N.; Svozil, K.; Baaz, M. The axiom of choice in quantum theory. Math. Log. Quart. 1996, 42, 319–340. [Google Scholar] [CrossRef]
- Loaiza, M. A short introduction to Hilbert Space theory. J. Phys. Conf. Ser. 2017, 839, 012002. [Google Scholar] [CrossRef]
- Läuchli, H. Auswahlaxiom in der Algebra. Comment. Math. Helv. 1962, 37, 1–18. [Google Scholar] [CrossRef]
- MATHEMATICS. Uncountable Series without Axiom of Choice; Stack Exchange Inc.: New York, NY, USA, 2014; Available online: https://math.stackexchange.com/questions/1042030/uncountable-series-without-axiom-of-choice (accessed on 14 August 2023).
- Blass, A. Existence of bases implies the axiom of choice. Contemp. Math. 1984, 31, 31–33. [Google Scholar] [CrossRef]
- Hardy, L. Quantum theory from five reasonable axioms. arXiv 2021, arXiv:quant-ph/0101012. [Google Scholar] [CrossRef]
- Barret, J. Information processing in generalized probabilistic theories. Phys. Rev. A 2007, 75, 032304. [Google Scholar] [CrossRef]
- Hardy, L.; (Perimeter Institute for Theoretical Physics, Waterloo, ON, Canada). Personal communication, 2019.
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. The no-cloning theorem. Phys. Today 2009, 62, 76–77. [Google Scholar] [CrossRef]
- Cassinelli, G.; Lahti, P. Quantum mechanics: Why complex Hilbert space? Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20160393. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).