Abstract
A new version of the Abrasion–Ablation Monte Carlo for Colliders model with the Minimum Spanning Tree clusterization algorithm (AAMCC-MST) is used to simulate O–O collisions at the LHC, accounting for the presence of alpha-clustered states in O. The yields of He, Li, Be, B, C and N spectator nuclei are calculated taking into account the pre-equilibrium clusterization of spectator matter and short-range correlations (SRC) between nucleons in O. The impact of -clustering and SRC on the production of spectator neutrons and deuterons is investigated. The results on the production of spectator nucleons and fragments can help in evaluating the performance of Zero Degree Calorimeters in future studies of O–O collisions at the LHC.
1. Introduction
Proton–proton and nucleus–nucleus collisions are the main subjects of the research program at the Large Hadron Collider (LHC) at the European Organization for Nuclear Research (CERN) in Geneva, Switzerland. Over the years pp, p–Pb, Xe–Xe and Pb–Pb interactions were studied in A Large Ion Collider Experiment (ALICE) [1] at the LHC. The ALICE measurements covered a broad set of observables related to Quantum Chromodynamics (QCD), the theory of strong interactions, to understand, in particular, the dependence of the observables on the masses of colliding species. As discussed [2,3], in future LHC runs ALICE and other experiments may benefit from studies of smaller volumes of hot and dense nuclear matter created in O–O collisions to understand the emerging collectivity in interactions of light nuclei in comparison to the already studied interactions of heavy species.
An interesting feature of O consists of a possible presence of intranuclear He clusters, as suggested by the numbers of neutrons and protons contained in O. The nucleons can be arranged to form four intranuclear -clusters in O. Tetrahedral configurations of -clusters were considered for O [4,5] to match the spherical symmetry of the ground states of this nucleus. The coexistence of the clustered states with non-clustered ones is expected. The contribution of the clustered states to the O ground state was evaluated to be below 30% [6].
As reported recently for calculations with a multi-phase transport model (AMPT) [7], the global properties of O–O collisions, such as initial energy density and final charged-particle multiplicity, remain similar in modelling with -clustered structure of O and the harmonic oscillator non-clustered density profile of O. However, as shown in Refs. [8,9,10], a kind of snapshot of the overlap zone of colliding nuclei can be made by exploring the relativistic O–O collisions to reveal the intranuclear clustering in O despite the global spherical symmetry of the tetrahedral state. The cluster structure of initial O may impact the eccentricity of the overlap zone [11], the triangular flow of , K, p and [8,9], and the nuclear modification factor for D-mesons [12].
As known, nuclear matter outside the interaction zone of colliding nuclei remains relatively cold and forms spectator matter. Much less attention has been paid so far to a possible impact of the presence of -clustered states in O on the production of spectator fragments in O–O collisions. One can expect that a part of -clusters from O survive in collisions and thus form He spectators. The data on fragmentation of 2–200A GeV O in nuclear emulsion [13] confirm such expectations. In these measurements the events of O fragmentation in collisions with light (CNO: carbon, nitrogen, oxygen) and heavy nuclei (AgBr: silver, bromine) were distinguished, but in both cases the events containing He as spectator nuclear fragments were the most frequent ones [13]. This was understood as the experimental evidence for the formation of -clusters as building blocks of initial O nuclei.
It is important to find out whether the tetrahedral geometry of -clustered states in O [4,5] is consistent with enhanced production of He as spectators. The first comparison of the measurements [13] with results of an early version of our Abrasion-Ablation Monte Carlo for Colliders model with the Minimum Spanning Tree clusterization algorithm (AAMCC-MST), which took into account the pre-equilibrium clusterization of spectator matter [14], but neglected the -clustering in initial O, was presented in Ref. [15]. As found [15], the yields of He nuclei were underestimated by the model. Therefore, in our next study [16], the tetrahedral configuration of -clustering in O was introduced and various parameters of AAMCC-MST were tuned to describe the data [13] on the probabilities to produce specific elements (H, He, Li, Be, B, C and N) as spectator nuclei and also on the multiplicity distributions of He spectator fragments. In particular, on the basis of comparison with the data [13], the contribution of the clustered states to the ground state of O was estimated at the level of 30% [16].
The -clustering in nuclei is not the only phenomenon responsible for the correlations between intranuclear nucleons. The impact of short-range nucleon-nucleon correlations (SRC) [17] on the momentum distributions of spectator nucleons in fragmentation of O, Ca and Pb nuclei was investigated in detail in Ref. [18]. As shown by modelling ultracentral Pb–Pb collisions, the average numbers of spectator deuterons calculated for such collisions are affected by including SRC in AAMCC-MST [19]. Therefore, it is also necessary to evaluate the influence of SRC on the production of spectator nucleons and fragments in O–O collisions in AAMCC-MST modelling taking into account the presence of the tetrahedral -clustered states in O.
In the present paper, a new version of the AAMCC-MST model is used to simulate O–O collisions at the LHC. As described in Section 2, the model takes into account the admixture of -clustered states and SRC in O [16] and also pre-equilibrium clusterization of spectator matter [14,19]. Multiplicity distributions of spectator neutrons and deuterons as well as yields of secondary nuclei calculated for O–O collisions at the nucleon-nucleon center-of-mass energy, TeV are presented in Section 3. General features of O–O fragmentation at the LHC and the sensitivity of results to the choice of various calculation options are discussed in Conclusions, Section 4.
2. Modelling O–O Collisions in AAMCC-MST
A new version of AAMCC-MST model (for the source code see [20]) is used in the present study to model the production and decay of spectator matter in collisions of relativistic O nuclei. Each collision event is simulated with AAMCC-MST in several stages.
The modelling of an O–O collision starts with sampling positions of nucleons in both colliding nuclei. Three options were used for this procedure. The first option denoted hereafter as “no clustering, SRC” represents non-clustered O with the positions of nucleons taken from pre-sampled nucleon configurations provided in Ref. [17] where the short-range nucleon-nucleon correlations were taken into account.
The second option denoted as “clustered, step-like SRC” represents the clustered state of O. The centres of four -clusters are arranged first in the vertices of a tetrahedron [4,5,7] assuming its random orientation. In its turn, two parametrizations of the radial nucleon density distribution inside the -clusters, , are used with r defined as the radial distance from the cluster center. The first one is the harmonic oscillator (HO) parametrization based on the HO intranuclear potential in H: with , and fm, defining, respectively, the periphery-to-center ratio of and its periphery diffuseness. The second one is the Woods-Saxon (WS) parametrization , with fm as the cluster radius, and fm as the skin depth. The parameters of both distributions are taken to fit the radial density distribution of He [6,21]. The length of the edges of the tetrahedron with the centres of -clusters in its vertices was taken as fm and 4 fm for HO and WS distributions, respectively. In both cases with 30% of the clustered configurations mixed with 70% of non-clustered ones, the RMS (root mean square) charge radius of fm [22] for O is reproduced. The mixed radial distributions of protons and neutrons were assumed to be the same, and the resulting nucleon density distributions are shown in Figure 1 with the RMS radius for nucleons fm calculated as the average from 5000 nucleon configurations generated for O. The assumption of the equality of neutron and proton distributions can be questioned even in O with the same numbers of protons and neutrons, ; see Ref. [23] for details. However, fm and fm were extracted, respectively, in Refs. [24,25] from nucleus-nucleus reaction cross sections at low and intermediate collision energies. Comparing these values with the measured RMS charge radius fm [22], one can conclude that the difference between the RMS radii for protons and neutrons is actually quite small (<0.2 fm).
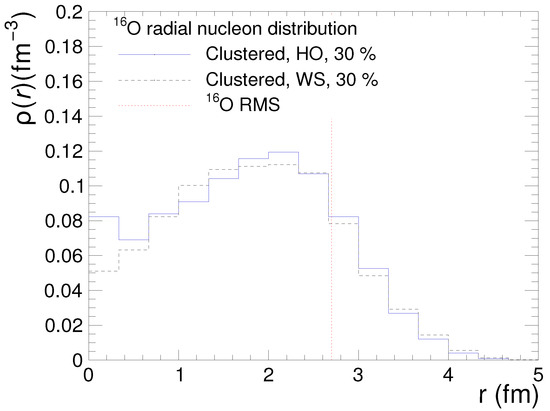
Figure 1.
Radial density distributions of nucleons for two options of clustered states (30%) mixed with non-clustered contributions (70%) in initial O. The RMS radius of O calculated for the resulting distributions is equal to 2.69 fm, and it is shown by a red dotted vertical line. See text for details.
The short-range nucleon-nucleon correlations in the second option are modelled by a step-like function differently with respect to SRC introduced in the first option following Ref. [17]. Here the minimum separation distance between nucleons (∼0.8 fm) is implemented in the Gibbs sampling algorithm [26] to sample the positions of nucleons in O.
The third option to sample the positions of nucleons in the clustered O is based on the same algorithm as the second option, but without accounting for SRC. It is denoted as “clustered, no SRC”. Since the probability of the clustered states in O is estimated below 30% [6], the non-clustered states were also sampled according to the HO parametrization of the O density following Ref. [27] with and fm. The outputs of the Monte Carlo modelling with the second or third options and without clustering were combined in the certain proportions (30% and 70%, respectively) to obtain final results.
Participant nucleons are removed from the initial nuclei at the abrasion stage modelled with the Glauber Monte Carlo (GlauberMC) model [28]. The sizes and shapes of spectator prefragments representing the remnants of both colliding nuclei are defined at the end of the abrasion stage.
The total excitation energy for each of the prefragments is calculated at the next stage of modelling with AAMCC-MST. Following the study of ALADIN Collaboration [29], a phenomenological parabolic dependence of the average excitation energy , per prefragment nucleon on the relative prefragment mass is used: . Here is the prefragment mass and A is the mass of the initial nucleus. The parameter values, MeV and 8 MeV, were used in our previous calculations [16], and the results were compared to the data [13]. It was found [16] that the results were less sensitive to than to the contribution of the clustered states. The calculations with MeV and the contribution of the clustered states of 30% demonstrated better agreement with the measured multiplicity distribution of He fragments. Therefore, this set of parameters is used also in the present study. Following the calculation of for each prefragment, the pre-equilibrium clusterization of the prefragments is modelled by means of the MST-clustering algorithm described in Refs. [14,19].
Finally, the decays of multiple excited nuclear fragments resulting from pre-equilibrium MST clusterization are simulated by means of the Fermi break-up model implemented in the Geant4 toolkit version 9.2 [30] and supplemented with photon evaporation model from the version 10.4.
3. Results
In Ref. [3] O–O collisions were modelled at TeV. So, the same collision energy for future oxygen runs at the LHC is assumed in the present study. Three options for the nuclear density distribution of O (see Section 2) are used in calculations.
3.1. Production of Spectator Neutrons at the LHC
Some of the experiments at the LHC are capable of detecting spectator neutrons by forward hadronic calorimeters. In particular, the ALICE experiment is equipped with Zero Degree Calorimeters [31] to detect spectator neutrons for the measurements of collision centrality [32] and collider luminosity [33] in Pb–Pb collisions because at least one neutron is emitted in each event. It is interesting to investigate whether these methods can be applied also to O–O collisions. The multiplicity distributions of spectator neutrons from O–O collisions at TeV are calculated with three options for the density distribution in O; see Figure 2.
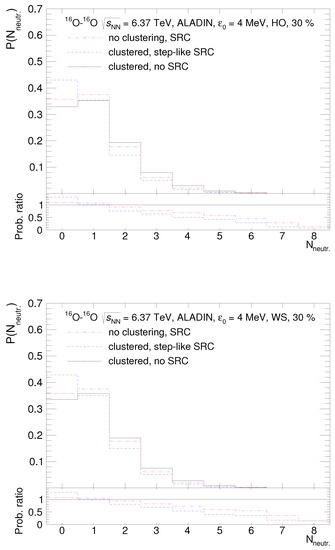
Figure 2.
Multiplicity distributions of spectator neutrons from O–O collisions at TeV calculated with accounting for SRC (dash-dotted red and dotted blue histograms) and for 30% of -clustering (dotted blue and solid black histograms) in O. The nuclear density in -clusters is taken on the basis of the harmonic oscillator model (top) and the Woods–Saxon distribution (bottom). The parameter MeV is used in all cases. Ratios between calculations with different options are presented in bottom panels. See text for details.
As shown in Figure 2, the multiplicity distributions, , of spectator neutrons calculated with three different options for nuclear density in O are generally consistent with each other and the distributions obtained with different parameterizations of the nuclear density of -clusters (HO and WS) are also in agreement regarding shape. However, the events with large numbers of spectator neutrons are essentially suppressed with accounting for SRC, because more neutrons remain bound in spectator nuclear fragments.
Spectator neutrons are absent in a large fraction of the simulated events: in ∼33% of events modelled without SRC and in ∼43% with SRC. This means that in contrast to Pb–Pb collisions, where spectator neutrons are emitted in ∼100% of events, less than 70% of O–O events will be triggered by the forward neutron calorimeters at the LHC.
3.2. Production of Spectator Deuterons at the LHC
As shown in Ref. [19], the production of deuterons in ultracentral Pb–Pb collisions at the Super Proton Synchrotron (SPS) at CERN was enhanced in calculations with accounting for SRC. A similar effect can be expected in modelling O–O collisions at the LHC. The multiplicity distributions of spectator deuterons calculated with three nuclear density options for O are presented in Figure 3.
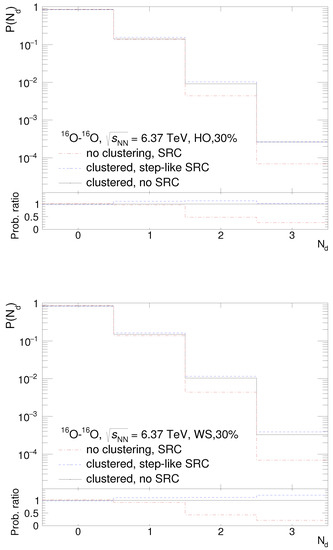
As shown in Figure 3, in ∼85% of O fragmentation events spectator deuterons are absent, while in the rest of events (∼14%) a single spectator deuteron is produced in calculations with all considered density parametrizations. The calculated obtained with different nuclear density parametrizations in O diverge noticeably only for much less frequent (∼1%) multiple deuteron production, for and 3 for both density parametrizations (HO and WS) implemented for -clusters in O. In the absence of clustering in O, events with and 3 are further suppressed. This indicates the sensitivity of double- and triple-deuteron events to the presence of clustering in O.
3.3. Production of Spectator Nuclei at the LHC
In Figure 4, the probabilities to produce specific spectator nuclei in O–O collisions at the LHC are presented. The probabilities were calculated with accounting for SRC for HO and WS parametrizations of the nucleon density inside -clusters in O, and they are ordered according to charge-to-mass ratios of the respective nuclei. The masses were taken from the nuclear data tables [34]. The 30% contribution of the clustered states in O is assumed in all calculations.
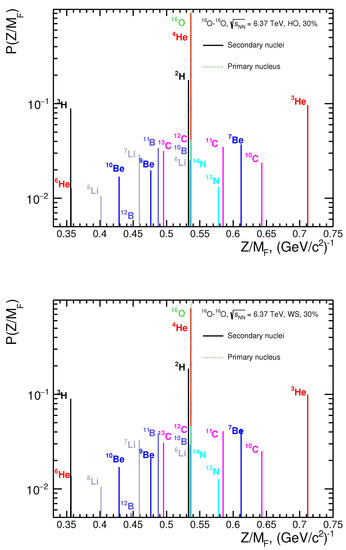
Figure 4.
Probabilities to produce spectator nuclei with given charge-to-mass ratio in O–O collisions at TeV. The probabilities were calculated with the -cluster density parametrization based on harmonic oscillator parametrization (top) and Woods-Saxon distribution (bottom). The value of for O is marked by a dashed line.
As seen in Figure 4, all possible elements (H, He, Li, Be, B, N and C) are produced as spectator nuclei after removing participant nucleons from initial O. Spectator nuclei are produced with similar probabilities in calculations with HO and WS parametrizations of the nucleon density inside -clusters. One can note that the production of spectator nuclei with enhanced neutron (He and B) or proton (C) content is also possible. Such nuclei are produced in events with the dominant abrasion of protons with respect to neutrons and vice versa.
In contrast to the calculations with the previous version of the AAMCC-MST model [15], which predicted H as the most frequent spectator fragment, the production of He dominates according to the present version of AAMCC-MST, see Figure 4. This is explained by accounting for -clustered states in initial O in the present calculations. At the same time, the present calculations demonstrate the absence of O and N spectator nuclei seen with the previous AAMCC-MST version [15]. The production of these nuclei is suppressed since the ALADIN parameterization [29] used in the present study delivers higher prefragment excitation energy in comparison to the hybrid parameterization used in the previous calculations [15]. As shown [16], the description of experimental data [13] on fragmentation of is improved with the ALADIN parameterization also used in the present work.
Finally, one can note that the yields of stable spectator nuclei such as H, He, Li, B, C and N are of special interest because their ratios are close to the ratio for O nuclei accelerated at the LHC. As seen from Figure 4, the probability to produce at least one of these nuclei approaches 1, and the respective cross section is close to the total hadronic cross section b. These nuclei can propagate in the vicinity of O beam nuclei in the magnetic field of the LHC, pass through the collimators of the collider and stay in the beam. According to Ref. [35], the integrated luminosity of nb is expected in a 40 hour run in total for all four experiments at the LHC. Therefore, about nbnb of spectator nuclei will be produced and can potentially circulate in the LHC along with initially injected 6 bunches of ions each with of O in total. Therefore, some He–O, Li–O, ...N–O events could potentially contaminate at the level of 1–10% the data on O–O collisions to be collected in future LHC runs. As pointed out in Ref. [35], this transmutation effect needs further investigations.
4. Conclusions
In the present paper, the new version of Abrasion–Ablation Monte Carlo for Colliders (AAMCC-MST) model tuned [16] to describe the data [13] on the fragmentation of 2–200A GeV O has been employed to model the production of spectator nucleons and nuclear fragments in O–O collisions at the LHC. In total, three options for O nuclear density distribution were used in calculations: (1) without considering -clustering but with accounting for SRC; (2) with accounting for -clustering and SRC; and (3) with accounting for -clustering but without considering SRC. In addition, with options (2) and (3) two distributions of the nuclear density in -clusters were used: the harmonic oscillator and Woods–Saxon distributions.
The multiplicity distributions of spectator neutrons and deuterons calculated for O–O collisions at the LHC with different options generally consistent with each other. In all cases, the fraction of events without spectator neutrons turned out to be significant (33–43%). Therefore, forward neutron calorimeters presently installed at the LHC are expected to be less effective in the measurements of collision centrality in O–O collisions. As follows from the calculations, the probabilities of events with two or three spectator deuterons are sensitive to accounting for the short-range nucleon–nucleon correlations in O.
The inclusion of -clustering in O enhances the production of He and makes it the most frequent spectator fragment in O–O collisions. The calculated yields of spectator fragments with equal numbers of protons and neutrons (H, He, Li, B, C and N) as in O, may help to evaluate their impact on LHC components. These secondary nuclei could propagate close to the beam nuclei, hit superconducting magnets or contaminate O–O events.
Author Contributions
Methodology I.P. and A.S.; software A.S., S.S. and R.N.; analysis A.S.; model validation R.N.; supervision I.P.; writing—original draft preparation A.S.; writing—review and editing R.N., S.S. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to Yury Tchuvil’sky and Dmitry Rodkin for discussions of -clustering effects in light nuclei.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AAMCC | Abrasion–Ablation Monte Carlo for Colliders |
| ALICE | A Large Ion Colider Experiment |
| AMPT | A Multi-Phase Transport model |
| CERN | European Organization for Nuclear Research |
| CNO | carbon, nitrogen, oxygen |
| GlauberMC | Glauber Monte Carlo |
| HO | harmonic oscillator |
| LHC | Large Hadron Collider |
| MST | Minimum Spanning Tree |
| QCD | Quantum Chromodynamics |
| RMS | root mean square |
| SPS | Super Proton Synchrotron |
| SRC | short-range correlations |
References
- ALICE Collaboration. The ALICE experiment—A journey through QCD. arXiv 2022, arXiv:2211.04384. [CrossRef]
- Report from Working Group 5: Future physics opportunities for high-density QCD at the LHC with heavy-ion and proton beams. In Physics at the HL-LHC and Perspectives for the HE-LHC; CERN Yellow Report, CERN-2019-007; Dainese, A., Mangano, M., Andreas, B., Meyer, A.B., Nisati, A., Salam, G., Vesterinen, M.A., Eds.; CERN: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Brewer, J.; Mazeliauskas, A.; van der Schee, W. Opportunities of OO and pO collisions at the LHC. arXiv 2021, arXiv:2103.01939. [Google Scholar] [CrossRef]
- Bijker, R.; Iachello, F. Evidence for tetrahedral symmetry in 16O. Phys. Rev. Lett. 2014, 112, 152501. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.B.; Dong, G.X.; Gao, Z.C.; Chen, Y.S.; Shen, C.W. Tetrahedral symmetry in the ground state of 16O. Phys. Lett. B 2019, 790, 498–501. [Google Scholar] [CrossRef]
- Zuker, A.P.; Buck, B.; McGrory, J.B. Structure of 16O. Phys. Rev. Lett. 1968, 21, 39–43. [Google Scholar] [CrossRef]
- Behera, D.; Mallick, N.; Tripathy, S.; Prasad, S.; Mishra, A.N.; Sahoo, R. Predictions on global properties in O+O collisions at the Large Hadron Collider using a multi-phase transport model. Eur. Phys. J. A 2022, 58, 175. [Google Scholar] [CrossRef]
- Lim, S.H.; Carlson, J.; Loizides, C.; Lonardoni, D.; Lynn, J.E.; Nagle, J.L.; Orjuela Koop, J.D.; Ouellette, J. Exploring new small system geometries in heavy ion collisions. Phys. Rev. C 2019, 99, 044904. [Google Scholar] [CrossRef]
- Li, Y.-A.; Zhang, S.; Ma, Y.-G. Signatures of α-clustering in 16O by using a multiphase transport model. Phys. Rev. C 2020, 102, 054907. [Google Scholar] [CrossRef]
- Bally, B.; Brandenburg, J.D.; Giacalone, G.; Heinz, U.; Huang, S.; Jia, J.; Lee, D.; Lee, Y.-J.; Li, W.; Loizides, C.; et al. Imaging the initial condition of heavy-ion collisions and nuclear structure across the nuclide chart. arXiv 2022, arXiv:2209.11042. [Google Scholar] [CrossRef]
- Broniowski, W.; Bożek, P.; Rybczyński, M.; Ruiz Arriola, E. Flow in collisions of light nuclei. Nucl. Phys. A 2021, 1005, 121763. [Google Scholar] [CrossRef]
- Katz, R.; Prado, C.A.G.; Noronha-Hostler, J.; Suaide, A.A.P. System-size scan of D meson RAA and vn using PbPb, XeXe, ArAr, and OO collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2020, 102, 041901. [Google Scholar] [CrossRef]
- El-Nagdy, M.S.; Abdelsalam, A.; Badawy, B.M.; Zarubin, P.I.; Abdalla, A.M.; Nabil Yasin, M.; Saber, A.; Mohamed, M.M.; Ahmed, M.M. Channels of projectile fragmentation of 16O nucleus in nuclear emulsion. J. Phys. Commun. 2018, 2, 035010. [Google Scholar] [CrossRef]
- Nepeivoda, R.; Svetlichnyi, A.; Kozyrev, N.; Pshenichnov, I. Pre-equilibrium clustering in production of spectator fragments in collisions of relativistic nuclei. Particles 2022, 5, 40–51. [Google Scholar] [CrossRef]
- Svetlichnyi, A.; Nepeivoda, R.; Kozyrev, N.; Pshenichnov, I. Secondary nuclei from 16O fragmentation at the LHC. PoS 2022, EPS-HEP2021, 310. [Google Scholar] [CrossRef]
- Svetlichnyi, A.; Savenkov, S.; Nepeivoda, R.; Kozyrev, N.; Pshenichnov, I. Smoking gun of nuclear clusterization in collisions of light relativistic nuclei. Phys. At. Nucl. 2022, 85, 958–964. [Google Scholar] [CrossRef]
- Alvioli, M.; Drescher, H.J.; Strikman, M. A Monte Carlo generator of nucleon configurations in complex nuclei including nucleon–nucleon correlations. Phys. Lett. B 2009, 680, 225–230. [Google Scholar] [CrossRef]
- Alvioli, M.; Strikman, M. Beam fragmentation in heavy ion collisions with realistically correlated nuclear configurations. Phys. Rev. C 2011, 83, 044905. [Google Scholar] [CrossRef]
- Kozyrev, N.; Svetlichnyi, A.; Nepeivoda, R.; Pshenichnov, I. Peeling away neutron skin in ultracentral collisions of relativistic nuclei. Eur. Phys. J. A 2022, 58, 184. [Google Scholar] [CrossRef]
- Abrasion-Ablation Monte Carlo for Colliders Repository. Available online: https://github.com/Spectator-matter-group-INR-RAS/AAMCC (accessed on 15 March 2023).
- Dumbrajs, O. Analyticity and model-independent determination of the nuclear charge density. Phys. Rev. C 1980, 21, 1677–1679. [Google Scholar] [CrossRef]
- Angeli, I.; Marinova, K. Table of experimental nuclear ground state charge radii: An update. At. Data Nucl. Data Tables 2013, 99, 69–95. [Google Scholar] [CrossRef]
- Shukla, A.; Åberg, S.; Patra, S.K. Nuclear structure and reaction properties of even–even oxygen isotopes towards drip line. J. Phys. G 2011, 38, 095103. [Google Scholar] [CrossRef]
- Ozawa, A.; Suzuki, T.; Tanihata, I. Nuclear size and related topics. Nucl. Phys. A 2001, 693, 32–62. [Google Scholar] [CrossRef]
- Liatard, E.; Bruandet, J.F.; Glasser, F.; Kox, S.; Chan, T.U.; Costa, G.J.; Heitz, C.; Masri, Y.E.; Hanappe, F.; Bimbot, R.; et al. Matter distribution in neutron-rich light nuclei and total reaction cross-section. Europhys. Lett. (EPL) 1990, 13, 401–404. [Google Scholar] [CrossRef]
- Owen, A.B. Monte Carlo Theory, Methods and Examples. 2013. Available online: https://artowen.su.domains/mc (accessed on 15 March 2023).
- Loizides, C.; Nagle, J.; Steinberg, P. Improved version of the PHOBOS Glauber Monte Carlo. arXiv 2014, arXiv:1408.2549. [Google Scholar] [CrossRef]
- Loizides, C.; Kamin, J.; D’Enterria, D. Improved Monte Carlo Glauber predictions at present and future nuclear colliders. Phys. Rev. C 2018, 97, 054910. [Google Scholar] [CrossRef]
- Botvina, A.S.; Mishustin, I.N.; Begemann-Blaich, M.; Hubele, J.; Imme, G.; Iori, I.; Kreutz, P.; Kunde, G.J.; Kunze, W.D.; Lindenstruth, V.; et al. Multifragmentation of spectators in relativistic heavy-ion reactions. Nucl. Phys. A 1995, 584, 737–756. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Inst. Meth. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Puddu, G.; Arnaldi, R.; Chiavassa, E.; Cicaló, C.; Cortese, P.; De Falco, A.; Dellacasa, G.; Ferretti, A.; Floris, M.; Gagliardi, M.; et al. The zero degree calorimeters for the ALICE experiment. Nucl. Inst. Meth. A 2007, 581, 397–401. [Google Scholar] [CrossRef]
- ALICE Collaboration. Centrality determination of Pb-Pb collisions at sNN = 2.76 TeV with ALICE. Phys. Rev. C 2013, 88, 044909. [Google Scholar] [CrossRef]
- ALICE Collaboration. ALICE luminosity determination for Pb-Pb collisions at sNN=5.02 TeV. arXiv 2022, arXiv:2204.10148. [CrossRef]
- Kondev, F.G.; Wang, M.; Huang, W.J.; Naimi, S.; Audi, G. The NUBASE2020 evaluation of nuclear physics properties. Chin. Phys. C 2021, 45, 030001. [Google Scholar] [CrossRef]
- Bruce, R.; Alemany-Fernández, R.; Bartosik, H.; Jebramcik, M.A.; Jowett, J.M.; Schaumann, M. Studies for an LHC pilot run with oxygen beams. In Proceedings of the 12th International Particle Accelerator Conference: IPAC2021, Campinas, Brazil, 24–28 May 2021; Lin, L., Byrd, J.M., Neuenschwander, R., Picoreti, R., Schaa, V.R.W., Eds.; JACoW Publishing: Geneva, Switzerland, 2021; pp. 53–56. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).