Abstract
In this paper, we investigate the modified symmetric teleparallel gravity or gravity, where Q is the nonmetricity, to study the evolutionary history of the universe by considering the functional form of , where and n are constants. Here, we consider the parametrization form of the deceleration parameter as (with the parameters at , , and the redshift, z), which provides the desired property for a sign flip from a decelerating to an accelerating phase. We obtain the solution of the Hubble parameter by examining the mentioned parametric form of q, and then we impose the solution in Friedmann equations. Employing the Bayesian analysis for the Observational Hubble data (OHD), we estimated the constraints on the associated free parameters with the current Hubble parameter to determine if this model may challenge the CDM ( cold dark matter with the cosmological constant, ) limitations. Furthermore, the constrained current value of the deceleration parameter shows that the present universe is accelerating. We also investigate the evolutionary trajectory of the energy density, pressure, and EoS (equation-of-state) parameters to conclude the accelerating behavior of the universe. Finally, we try to demonstrate that the considered parametric form of the deceleration parameter is compatible with gravity.
1. Introduction
Recently, several cosmological observations [,,,,,] have supported the late-time cosmic acceleration expansion of the universe. However, based on the same cosmological observation, it is estimated that dark energy (DE) and dark matter (DM) cover up 95–96% of the universe’s composition, comprising mysterious dark components, the so-called dark matter and dark energy, whereas baryonic matter covers up 4–5% of the content of the universe. Presently, general relativity (GR) is believed to be the most successful theory of gravitation, and its few gravitational tests have been discussed in Ref. []. However, it cannot provide a satisfactory explanation for the dark energy and dark matter problem; hence, it may not be regarded as the ultimate gravitational force theory for dealing with the current cosmological problems. Several alternative approaches have been proposed in the literature over the last several decades to overcome the current cosmological problems. Nowadays, the modified theory of gravity is the most admirable candidate to solve the current difficulties (the DE and DM problem) of the universe. One of the most prominent schemes to address the dark content issue of the universe is the modification of GR called the theory of gravity, where R is the Ricci scalar []. Some other modified theories are also developed to solve this issue, such as the theory, where is the torsion [,]; the theory [,]; the theory, where is the matter Lagrangian density [,]; the theory, where G is the Gauss–Bonnet invariant [,]; and many more.
Jimenez et al. [] recently proposed a novel proposal by considering a modification of the symmetric teleparallel equivalent to GR called gravity, where Q is a nonmetricity scalar. The nonmetricity, Q, of the metric geometrically characterizes the variation in the length of a vector in parallel transport, and it represents the primary geometric variable explaining the features of a gravitational interaction. Recently, several studies were conducted on gravity. Mandal et al. studied cosmography [] and the energy condition [] in nonmetric gravity. For the purpose of examining an accelerated expansion of the universe with the recent observations, Lazkoz et al. [] examined several gravity models. Furthermore, Solanki et al. [] studied the effect of bulk viscosity in the accelerating expansion of the universe in gravity. Esposito et al. [] examined exact isotropic and anisotropic cosmological solutions using reconstruction techniques. Moreover, gravity easily overcomes the limits set by Big Bang Nucleosynthesis (BBN) []. Many other studies have been completed within the context of the gravity theory [,,,,,]. Although various theoretical approaches exist to explain the phenomenon of cosmic acceleration, none are definitively known as the appropriate one. The current model of late-time cosmic acceleration is known as reconstruction. This is the inverse method of locating a suitable cosmological model. There are two kinds of reconstruction: parametric reconstruction and non-parametric reconstruction. The parametric reconstruction relies on estimating the model parameters from various observational data. It is also known as the model-dependent approach. The main idea is to assume a specific evolution scenario and then determine the nature of the matter sector or the exotic component that is causing the alleged acceleration. Several authors have used this method to find a suitable solution [,,].
In this paper, we consider the parametrization form of the deceleration parameter in terms of the redshift, z, as (with the parameters and ), which provides the desired property for the sign flip from a decelerating to an accelerating phase and investigate the Friedmann–Lemaître–Robertson–Walker (FLRW) universe in the framework of nonmetric gravity by using the functional form of as , where and n are arbitrary constants. The present paper is arranged as follows. In Section 2, we start with the basic gravity formalism and develop the field equation for the FLRW line element. In Section 3, we adopt the parametric form of a deceleration parameter and then find the Hubble solution. In Section 4, we estimate the constraints on the associated free parameters by employing the Bayesian analysis for the Observational Hubble data (OHD). Then, we check the evolutionary trajectory of the energy density, pressure, and the equation-of-state (EoS) parameters to conclude the accelerating behavior of the universe in Section 5. Lastly, we conclude our result in Section 6.
2. Gravity Formalism
The most generic action of nonmetric gravity is given by []
where f is an arbitrary function of nonmetricity scalar Q, is the matter Lagrangian density, and g is a determinant of the metric tensor, , where four-dimensional tensor indices are denoted by lower-case Greek letters and take the values 0 (time), 1, 2, 3 (space).
The definition of nonmetricity tensor in gravity is
and the corresponding traces are
Moreover, the superpotential tensor is given by
Hence, the nonmetricity scalar can be obtained as
The gravitational field equation derived by varying the action (1) with regard to the metric tensor is presented below:
where and .
Similarly, by varying the action (1) with regard to the connection, the following result can be obtained:
We shall consider a spatially flat FLRW universe throughout the investigation, whose metric is given by
Here, is a cosmic scale factor. The nonmetricity scalar obtained for the above FLRW metric, where is the Hubble parameter, and the dot denotes the time derivative. In this case, the energy-momentum tensor of a perfect fluid, , where p and are pressure and energy density, respectively, and denotes the four-velocity vector of the fluid.
Using the preceding Friedmann equations in the context of gravity, one may now study possible cosmological applications.
3. Parametrization of the Deceleration Parameter
The parametrization of the deceleration parameter q plays a significant role in determining the nature of the universe’s expanding rate. In this regard, some research employed various parametric forms of deceleration parameters, while other research investigated non-parametric forms. These methods have been widely discussed in the literature to characterize the concerns with cosmological investigations, such as the initial singularity problem, the problem of all-time decelerating expansion, the horizon problem, Hubble tension, and so on [,,]. Motivated by this fact, in this paper, we consider the simplest parametric form of the deceleration parameter q in terms of redshift z as []
where indicates the present value of deceleration parameter, and depicts the variation in the deceleration parameter as a function of z. Certainly, one of the most well-liked parametrizations of the dark energy equation of state served as inspiration for this parametric form for [], and it seems to be versatile enough to fit the behavior of a broad class of accelerating models.
The derivative of the Hubble parameter with respect to time t is . Then, there exists a relation between the Hubble parameter and the deceleration parameter in virtue of an integration:
where x is a changing variable. By using Equation (11) in Equation (12), we obtained the Hubble parameter in terms of redshift z as
where is the current Hubble constant (at ). Furthermore, utilizing the relationship between redshift and the universe’s scale factor , we may describe the relationship between cosmic time and redshift as
Using Equations (13) and (14) in Fridemann equations, we obtained the energy density , pressure p, and equation of state parameter in terms of redshift z as
respectively. The behavior and essential cosmological properties of the model described in Equation (11) are wholly dependent on the model parameters . In the next section, we constraint the model parameter by using the recent observational datasets to investigate the behavior of the cosmological parameters.
4. Observational Constraints and Cosmological Applications
Now, one can deal with the various observational datasets to constraint the parameters , . In order to study the observational data, we use the standard Bayesian technique, and to obtain the posterior distributions of the parameters, we employ a Markov Chain Monte Carlo (MCMC) method. Moreover, we use the emcee package to perform the MCMC analysis. Here, in this study, we used the Hubble measurements (i.e., Hubble data) to complete the stimulation. The following likelyhood function is used to find the best fits of the parameters;
where is the pseudo chi-squared function []. The functions for various datasets are discussed below.
Cosmic Chronometer (CC) Sample
Recently, a list of Hubble measurements in the redshift range were compiled by Singirikonda and Desai []. This dataset was measured from the differential ages of galaxies [,,,]. The complete list of datasets is presented in Ref. []. To estimate the model parameters, we use the chi-squerd function which is given by
where , represents the Hubble parameter with the model parameters, observed Hubble parameter values, respectively. is the standard deviation obtained from observations. The marginalized constraining results are displayed in Figure 1. In Figure 2, the profile of our model against Hubble data is shown.
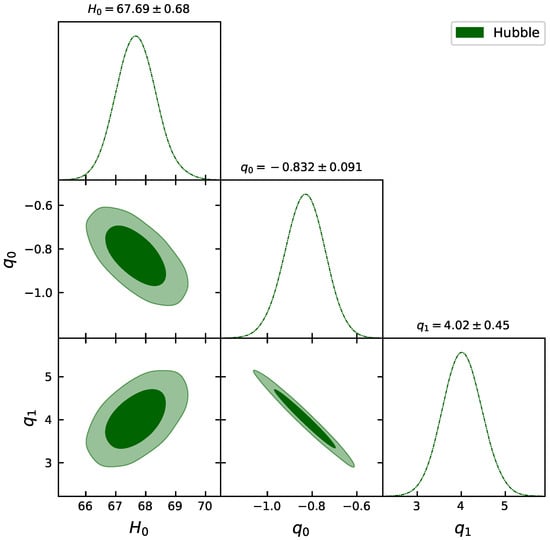
Figure 1.
The marginalized constraints on the coefficients in the expression of Hubble parameter, , in Equation (13) are shown by using the Hubble sample [].
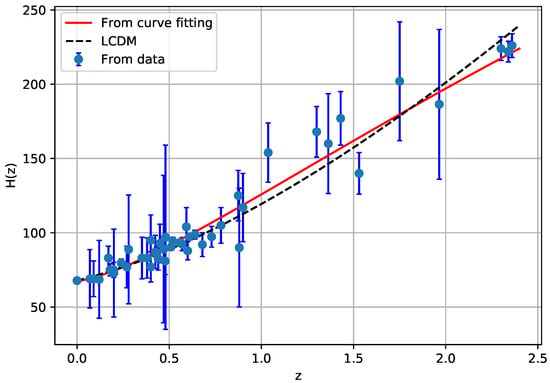
Figure 2.
The evolution of Hubble parameter, , with respect to redshift z. The red line represents our model and dashed line indicates the CDM model with the pressureless matter parameter, [] and the dark energy density parameter, []. The dots show the Hubble dataset with error bars [].
5. Cosmological Parameters
One of the cosmological parameters that is significant in explaining the state of the expansion of our universe is the deceleration parameter q. When the value of the deceleration parameter is strictly less than zero, it shows the accelerating behavior of the universe, and when it is non-negative, the universe decelerates. Furthermore, the observational data employed in this study revealed that our current universe is in an accelerating phase, with the present value of the deceleration parameter becoming . This type of result is seen in the existing literature [,].
Figure 3 indicates that the energy density of the universe increases with a redshift and still seems to as the universe expands, but Figure 4 demonstrates that the pressure decreases with the redshift and has large negative values throughout the cosmic evolution. The present cosmic acceleration induces this isotropic pressure behavior.
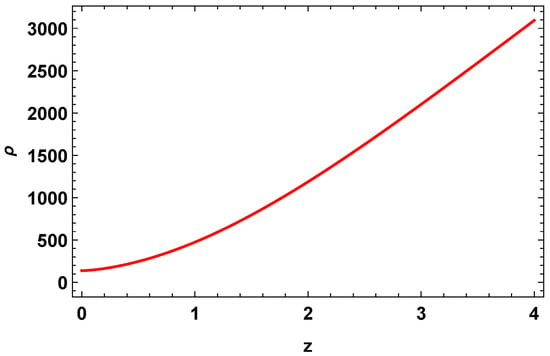
Figure 3.
Evolution trajectory of the energy density, (15), versus z with constraint values from the Hubble datasets [] and , .
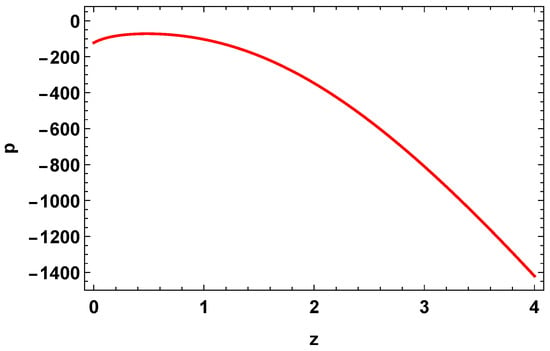
Figure 4.
Evolution trajectory of the pressure, p (16), versus z with constraint values from the Hubble datasets [] and , .
The EoS parameter w is also helpful in categorizing the decelerating and accelerating behavior of the universe, and it is defined as . The EoS categorizes three possible states for the accelerating universe which are the quintessence era, phantom era, and cosmological constant . Figure 5 shows the evolutionary trajectory of the EoS parameter, and it can be seen that the whole trajectory lies in the quintessence era. From Figure 5, One can see that and the current value of the EoS parameter is . Our result aligned with some of the studies [,], which indicates an accelerating phase.
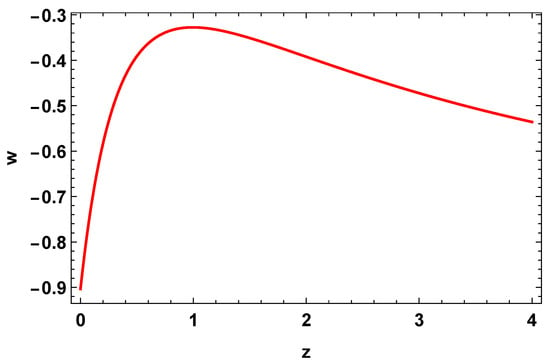
Figure 5.
Evolution trajectory of the equstion-of-state parameter, w (17), versus z with constraint values from the Hubble datasets [] and , .
6. Conclusions
The current scenario of the accelerated expansion of the universe has grown increasingly fascinating over time. Numerous dynamical DE models and modified gravity theories have been employed in various ways to find a suitable description of the accelerating universe. In this paper, we explored the accelerated expansion of the universe by adopting the parametric form of the deceleration parameter in the framework of gravity, where Q is the nonmetricity scalar depicted in the gravitational interaction.
We have examined the functional form of as , where and n are the arbitrary constants, and the parametrization form of the deceleration parameter as , where are the model parameters. By utilizing the above parametric form, we find out the solution of the Hubble parameter as . Furthermore, we used the Hubble datasets containing 31 data points to determine the best-fit values for the model parameters as , , and . Here, the shows the current value of the deceleration parameter, which depicts that the present expansion of the universe is accelerating. We analyzed the evolution of the various cosmological parameters corresponding to these best-fit values of the model parameters. The EoS parameter exhibits negative behavior and lies in the quintessence era, which depicts that the present universe is in an accelerating phase. Figure 3 indicates that the energy density of the universe increases with a redshift and still seems to as the universe expands, but Figure 4 demonstrates that the pressure decreases with the redshift and has large negative values throughout the cosmic evolution. Lastly, we conclude that the considered parametric form of the deceleration parameter in the framework of gravity theory plays an important role in driving the universe’s accelerated expansion.
Author Contributions
Conceptualization, G.N.G.; data curation, S.M.; formal analysis, P.K.S.; investigation, G.N.G.; methodology, G.N.G.; project administration, P.K.S.; software, G.N.G. and S.M.; supervision, P.K.S.; validation, P.K.S.; visualization, S.M.; writing—original draft, G.N.G.; writing—review and editing, S.M. and P.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
G.N.G. acknowledges the University Grants Commission (UGC), New Delhi, India, for awarding the Junior Research Fellowship (UGC-Ref. No.: 201610122060). S.M. acknowledges the Department of Science & Technology (DST), Govt. of India, New Delhi, for awarding the INSPIRE Fellowship (File No. DST/INSPIRE Fellowship/2018/IF180676). P.K.S. acknowledges the the Council of Scientific & Industrial Research (CSIR), New Delhi, India, for the financial support to carry out the Research project [No.03(1454)/19/EMR-II, Dt. 2 August 2019] and the Inter-University Centre for Astronomy and Astrophysics (IUCAA), Pune, India, for providing support through the visiting Associateship program.
Data Availability Statement
The data used can be found in the references cited.
Acknowledgments
Thanks to Department of Mathematics, Birla Institute of Technology and Science-Pilani, Hyderabad Campus, India, for providing DST-FIST lab, where the data simulation work is done.
Conflicts of Interest
The author declare no conflict of interest.
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. et al. [The Supernova Cosmology Project] Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, J.C.; Jha, S.; Kirshner, P.R.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z > 1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Dark energy anisotropic stress and large scale structure formation. Phys. Rev. D 2006, 73, 083502. [Google Scholar] [CrossRef]
- Daniel, S.F.; Caldwell, R.R.; Cooray, A.; Melchiorri, A. Large scale structure as a probe of gravitational slip. Phys. Rev. D 2008, 77, 103513. [Google Scholar] [CrossRef]
- Corda, C. Interferometric detection of gravitational waves: The definitive test for general relativity. Int. J. Mod. Phys. D 2009, 18, 2275–2282. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1–8. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Myrzakulov, R. Accelerating universe from F(T) gravity. Eur. Phys. J. C 2012, 71, 1752. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.I.; Odintsov, S.D. f(R, T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Moraes, P.H.R.S.; Sahoo, P. Wormholes in R2-gravity within the f(R, T) formalism. Eur. Phys. J. C 2018, 78, 46. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. f(R, Lm) gravity. Eur. Phys. J. C 2010, 70, 373–379. [Google Scholar] [CrossRef]
- Jaybhaye, L.V.; Solanki, R.; Mandal, S.; Sahoo, P.K. Cosmology in f(R, Lm) gravity. Phys. Lett. B 2022, 831, 137148. [Google Scholar] [CrossRef]
- Elizalde, E.; Myrzakulov, R.; Obukhov, V.V.; Sáez-Gómez, D. ΛCDM epoch reconstruction from F(R, G) and modified Gauss–Bonnet gravities. Class. Quantum Grav. 2010, 27, 095007. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Finite-time future singularities in modified Gauss-Bonnet and F(R, G) gravity and singularity avoidance. Eur. Phys. J. C 2010, 67, 295–310. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T. Coincident general relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Mandal, S.; Wang, D.; Sahoo, P.K. Cosmography in f(Q) gravity. Phys. Rev. D 2020, 102, 124029. [Google Scholar] [CrossRef]
- Mandal, S.; Sahoo, P.K.; Santos, J.R.L. Energy conditions in f(Q) gravity. Phys. Rev. D 2020, 102, 024057. [Google Scholar] [CrossRef]
- Lazkoz, R.; Lobo, F.S.N.; Ortiz-Baños, M.; Salzano, V. Observational constraints of f(Q) gravity. Phys. Rev. D 2019, 100, 104027. [Google Scholar] [CrossRef]
- Solanki, R.; Mandal, S.; Sahoo, P.K. Cosmic acceleration with bulk viscosity in modified f(Q) gravity. Phys. Dark Univ. 2021, 32, 100820. [Google Scholar] [CrossRef]
- Esposito, F.; Carloni, S.; Cianci, R.; Vignolo, S. Reconstructing isotropic and anisotropic f(Q) cosmologies. Phys. Rev. D 2022, 105, 084061. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Gakis, V.; Saridakis, E.N.; Basilakos, S. New models and Big Bang Nucleosynthesis constraints in f(Q) gravity. arXiv 2022, arXiv:2205.11445. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.; Olmo, G.J.; Rubiera-Garcia, D. Coupling matter Q in modified gravity. Phys. Rev. D 2018, 98, 084043. [Google Scholar] [CrossRef]
- Frusciante, N. Signatures of f(Q) gravity in cosmology. Phys. Rev. D 2021, 103, 044021. [Google Scholar] [CrossRef]
- Khyllep, W.; Paliathanasis, A.; Dutta, J. Cosmological solutions and growth index of matter perturbations in f(Q) gravity. Phys. Rev. D 2021, 103, 103521. [Google Scholar] [CrossRef]
- Ayuso, I.; Lazkoz, R.; Salzano, V. Observational constraints on cosmological solutions of f(Q) theories. Phys. Rev. D 2021, 103, 063505. [Google Scholar] [CrossRef]
- Gadbail, G.; Mandal, S.; Sahoo, P.K. Reconstruction of ΛCDM universe in f(Q) gravity. Phys. Lett. B 2022, 835, 137509. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R. Model-independent reconstruction of f(Q) non-metric gravity. Phys. Lett. B 2022, 832, 137229. [Google Scholar] [CrossRef]
- Mukherjee, A. Acceleration of the universe: A reconstruction of the effective equation of state. Mon. Not. R. Astron. Soc. 2016, 460, 273–282. [Google Scholar] [CrossRef]
- Arora, S.; Parida, A.; Sahoo, P.K. Constraining effective equation of state in f(Q,T) gravity. Eur. Phys. J. C 2021, 81, 555. [Google Scholar] [CrossRef]
- Gadbail, G.N.; Arora, S.; Kumar, P.; Sahoo, P.K. Interaction of divergence-free deceleration parameter in Weyl-type f(Q,T) gravity. Chin. J. Phys. 2022, 79, 246–255. [Google Scholar] [CrossRef]
- Banerjee, N.; Das, S. Acceleration of the universe with a simple trigonometric potential. Gen. Relativ. Gravit. 2005, 37, 1695–1703. [Google Scholar] [CrossRef]
- Cunha, J.V.; Lima, J.A.S. Transition redshift: New kinematic constraints from supernovae. Mon. Not. R. Astron. Soc. 2008, 390, 210–217. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Nájera, A. Dynamical dark energy models in the light of gravitational-wave transient catalogues. J. Cosmol. Astropart. Phys. 2022, 03, 060. [Google Scholar] [CrossRef]
- Wang, Y.-T.; Xu, L.-X.; Lu, J.-B.; Gui, Y.-X. Reconstructing dark energy potentials from parameterized deceleration parameters. Chin. Phys. B 2010, 19, 019801. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, A. Observational constraints on the acceleration of the Universe. Phys. Rev. D 2006, 73, 083506. [Google Scholar] [CrossRef]
- Hobson, M.P.; Jaffe, A.H.; Liddle, A.R.; Mukherjee, P.; Parkison, D. (Eds.) Bayesian Methods in Cosmology; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Singirikonda, H.; Desai, S. Model comparison of ΛCDM vs Rh=ct using cosmic chronometers. Eur. Phys. J. C 2020, 80, 694. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. J. Cosmol. Astropart. Phys. 2010, 02, 008. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z2. Mon. Not. R. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef]
- Gao, L.-Y.; Zhao, Z.-W.; Xue, S.-S.; Zhang, X. Relieving the H0 tension with a new interacting dark energy model. J. Cosmol. Astropart. Phys. 2021, 07, 005. [Google Scholar] [CrossRef]
- Mamon, A.A.; Das, S. A divergence-free parametrization of deceleration parameter for scalar field dark energy. Int. J. Mod. Phys. D 2016, 25, 1650032. [Google Scholar] [CrossRef]
- Hanafy, W.E.; Nashed, G.G.L. Phenomenological reconstruction of f(T) teleparallel gravity. Phys. Rev. D 2019, 100, 083535. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, A. Reconstruction of the deceleration parameter and the equation of state of dark energy. Phys. Rev. D 2007, 75, 043520. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).