The World through My Eyes: Fostering Students’ Understanding of Basic Optics Concepts Related to Vision and Image Formation
Abstract
1. Introduction
2. Research Background
2.1. Optics in Early Physics Education
2.2. Widespread Learning Difficulties in Introductory Optics: A Brief Overview
- light propagation (see [13]),
2.2.1. Learning Difficulties Regarding the Process of Vision
2.2.2. Learning Difficulties Regarding Image Formation by Converging Lenses
- the introduction of the ray model of light (and corresponding ray diagrams) from the beginning, and
- the focus on a mathematical description at too early a stage of teaching
2.3. Phenomenological Approaches in Science Education
2.4. A Phenomenological Approach to Introductory Optics: The Erlangen Teaching–Learning Sequence
2.4.1. Vision and Brightness
2.4.2. Refraction and Apparent Depth
2.4.3. The Look through a Prism
2.4.4. The Images of Converging Lens
2.5. Situational Interest
3. Research Questions
- RQ1:
- How does the phenomenological teaching approach to introductory optics affect students’ situational interest in optics compared to traditional instruction?
- RQ2:
- Which differences appear in students’ learning gains regarding the conceptual understanding of introductory optics topics, namely:
- (a)
- the process of vision,
- (b)
- refraction and apparent depth, and
- (c)
- image formation,
when comparing the phenomenological teaching approach and traditional instruction in German secondary schools?
4. Methods
4.1. Study Design and Sample
4.2. Interventions
4.3. Instrument
- P1:
- Scale to assess students’ situational interest in optics (only post-test); for details, see Section 4.3.1.
- P2:
- Concept inventory to assess students’ conceptual understanding of introductory optics topics (pre-test and post-test); for details, see Section 4.3.2.
4.3.1. Assessment of Students’ Situational Interest
4.3.2. Assessment of Students’ Conceptual Understanding of Introductory Optics
4.4. Data Analysis
5. Results
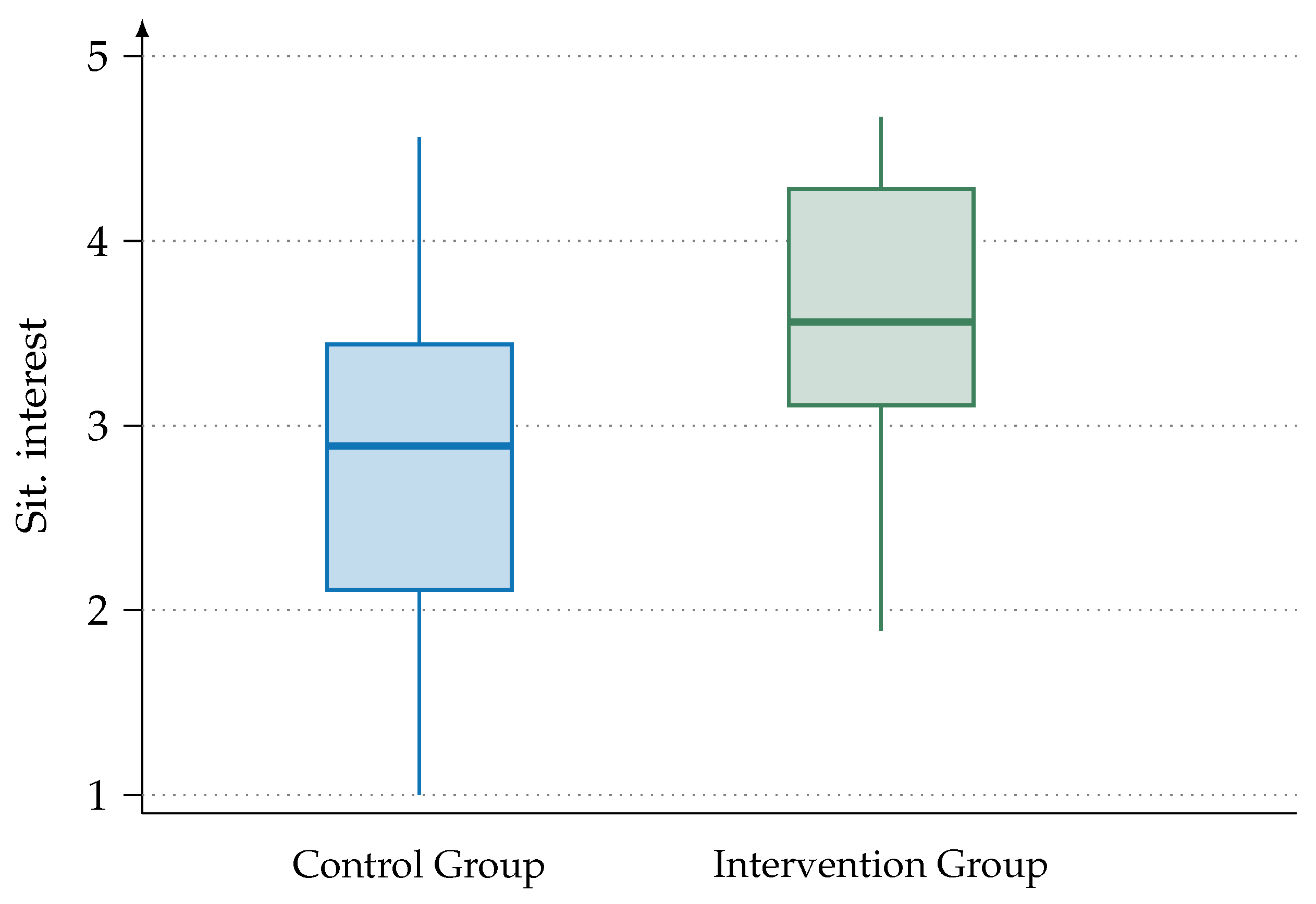
5.1. Results regarding RQ1
5.2. Results regarding RQ2
6. Discussion
6.1. Discussion of RQ1
6.2. Discussion of RQ2
7. Conclusion
7.1. Limitations
7.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hubber, P. Year 12 students’ mental models of the nature of light. Res. Sci. Educ. 2006, 36, 419–439. [Google Scholar] [CrossRef]
- Grosslight, L.; Unger, C.; Jay, E.; Smith, C. Understanding models and their use in science: Conceptions of middle and high school students and experts. J. Res. Sci. Teach. 1991, 28, 799–822. [Google Scholar] [CrossRef]
- Andersson, B.; Kärrqvist, C. How Swedish pupils, aged 12–15 years, understand light and its properties. Eur. J. Sci. Educ. 1983, 5, 387–402. [Google Scholar] [CrossRef]
- Galili, I.; Hazan, A. Learners’ knowledge in optics: Interpretation, structure and analysis. Int. J. Sci. Educ. 2000, 22, 57–88. [Google Scholar] [CrossRef]
- Haagen-Schützenhöfer, C.; Hopf, M. Design-based research as a model for systematic curriculum development: The example of a curriculum for introductory optics. Phy. Rev. Phy. Educ. Res. 2020, 16, 1571–1594. [Google Scholar] [CrossRef]
- Jones, D.; Zollman, D. Understanding vision: Students’ use of light and optics resources. Eur. J. Phys. 2014, 35, 055023. [Google Scholar] [CrossRef][Green Version]
- Grebe-Ellis, J. Das Auge Täuscht Sich Nicht—Phänomenologische Forschung am Beispiel der Optik. 2020. Available online: https://www.physikdidaktik.uni-wuppertal.de/fileadmin/physik/didaktik/Forschung/Grebe-Ellis-PhänomenologischeForschungOptik.pdf (accessed on 1 September 2022).
- Guesne, E. Light. In Children’s Ideas in Science; Driver, R., Guesne, E., Tiberghien, A., Eds.; Open University Press: Milton Keynes, UK, 1985; pp. 10–32. Available online: https://vdocuments.mx/childrens-ideas-in-science.html (accessed on 1 September 2022).
- de Hosson, C.; Kaminski, W. Historical controversy as an educational tool: Evaluating elements of a teaching-learning sequence conducted with the text “Dialogue on the Ways that Vision Operates”. Int. J. Sci. Educ. 2007, 29, 617–642. [Google Scholar] [CrossRef]
- Selley, N.J. Children’s ideas on light and vision. Int. J. Sci. Educ. 1996, 18, 713–723. [Google Scholar] [CrossRef]
- Bendall, S.; Goldberg, F.; Galili, I. Prospective elementary teachers’ prior knowledge about light. J. Res. Sci. Teach. 1993, 30, 1169–1187. [Google Scholar] [CrossRef]
- La Rosa, C.; Mayer, M.; Patrizi, P.; Vicentini-Missoni, M. Commonsense knowledge in optics: Preliminary results of an investigation into the properties of light. Eur. J. Sci. Educ. 1984, 6, 387–397. [Google Scholar] [CrossRef]
- Galili, I. Students’ conceptual change in geometrical optics. Int. J. Sci. Educ. 1996, 18, 847–868. [Google Scholar] [CrossRef]
- Singh, A.; Butler, P.H. Refraction: Conceptions and knowledge structure. Int. J. Sci. Educ. 1990, 12, 429–442. [Google Scholar] [CrossRef]
- Kaltakci-Gurel, D.; Eryilmaz, A.; McDermott, L.C. Identifying pre-service physics teachers’ misconceptions and conceptual difficulties about geometrical optics. Eur. J. Phys. 2016, 37, 045705. [Google Scholar] [CrossRef]
- Goldberg, F.M.; McDermott, L.C. An investigation of student understanding of the real image formed by a converging lens or concave mirror. Am. J. Phys. 1987, 55, 108–119. [Google Scholar] [CrossRef]
- Galili, I.; Bendall, S.; Goldberg, F. The effects of prior knowledge and instruction on understanding image formation. J. Res. Sci. Teach. 1993, 30, 271–301. [Google Scholar] [CrossRef]
- Goldberg, F.; Bendall, S.; Galili, I. Lenses, pinholes, screens, and the eye. Phys. Teach. 1991, 29, 221–224. [Google Scholar] [CrossRef]
- Tao, P. Developing understanding of image formation by lenses through collaborative learning mediated by multimedia computer-assisted learning programs. Int. J. Sci. Educ. 2004, 26, 1171–1197. [Google Scholar] [CrossRef]
- Perales Palacios, F.J.; Nevas Cazorla, F.; Cervantes Madrid, A. Misconceptions on geometric optics and their association with relevant educational variables. Int. J. Sci. Educ. 1989, 11, 273–286. [Google Scholar] [CrossRef]
- Annenberg Learner. Minds of Our Own. Can We Believe Our Eyes? Available online: https://www.learner.org/series/minds-of-our-own/1-can-we-believe-our-eyes/ (accessed on 1 September 2022).
- John, M.; Molepo, J.M.; Chirwa, M. South African learners’ conceptual understanding about image formation by lenses. Euras. J. Math. Sci. Techn. Educ. 2016, 13, 1723–1736. [Google Scholar] [CrossRef]
- Haagen-Schützenhöfer, C.; Hopf, M. Schülervorstellungen zur geometrischen Optik. In Schülervorstellungen und Physikunterricht; Schecker, H., Wilhelm, T., Hopf, M., Duit, R., Eds.; Springer Spektrum: Berlin/Heidlberg Germany, 2018; pp. 89–114. [Google Scholar] [CrossRef]
- Uwamahoro, J.; Ndihokubwayo, K.; Ralph, M.; Ndayambaje, I. Physics students’ conceptual understanding of geometric optics: Revisited analysis. Int. J. Sci. Educ. Techn. 2021, 30, 706–718. [Google Scholar] [CrossRef]
- Rice, T.; Feher, E. Pinholes and images: Children’s conceptions of light and vision. Sci. Educ. 1987, 71, 629–639. [Google Scholar] [CrossRef]
- Greca, I.M.; Moreira, M.A. Mental models, conceptual models, and modelling. Int. J. Sci. Educ. 2000, 22, 1–11. [Google Scholar] [CrossRef]
- Spiecker, H.; Bitzenbauer, P. Phenomenological optics with self-made liquid lenses in the physics classroom. Phys. Educ. 2022, 57, 045012. [Google Scholar] [CrossRef]
- Maier, G. Optik der Bilder; Verlag der Kooperative Dürnau: Dürnau, Germany, 1986. [Google Scholar]
- Maier, G. An Optics of Visual Experience; Adonis Press: Hillsdale, NY, USA, 2011. [Google Scholar]
- Østergaard, E.; Dahlin, B.; Hugo, A. Doing phenomenology in science education: A research review. Stud. Sci. Educ. 2008, 44, 93–121. [Google Scholar] [CrossRef]
- Moran, D. Introduction to Phenomenology; Routledge: London, UK, 2000. [Google Scholar] [CrossRef]
- Wagenschein, M. Rettet die Phänomene! In Fragen der Freiheit: Seminar für Freiheitliche Ordnung; Bad Boll: Eckwälden, Germany, 1976; pp. 50–65. Available online: http://www.martin-wagenschein.de/en/2/2-1-3-8.htm#retour204 (accessed on 1 September 2022).
- Wagenschein, M. Save the phenomena. The primacy of unmediated experience. In Context #20; The Nature Institute: Ghent, NY, USA, 2008; Available online: https://www.natureinstitute.org/article/martin-wagenschein/save-the-phenomena-the-primacy-of-unmediated-experience (accessed on 1 September 2022).
- Grusche, S. Phenomenon-based learning and model-based teaching: Do they match? J. Phys. Conf. Ser. 2019, 1287, 012066. [Google Scholar] [CrossRef]
- von Mackensen, M. Klang, Helligkeit und Wärme; Bildungswerk Beruf und Umwelt: Kassel, Germany, 1992. [Google Scholar]
- Grebe-Ellis, J. Phänomenologische Optik: Eine “Optik der Bilder”. Teil 1: Erkenntnistheoretische, experimentiermethodische und didaktische Merkmale eines nichtreduktionistischen Zugangs zur Optik. Chim. Didact. 2006, 32, 137–186. Available online: https://www.physikdidaktik.uni-wuppertal.de/fileadmin/physik/didaktik/Forschung/Publikationen/Grebe-Ellis/Grebe-Ellis_Phaeno_Optik_1.pdf (accessed on 1 September 2022).
- Lukenchuk, A. Traversing the chiasms of lived experiences: Phenomenological illuminations for practitioner research. Educ. Act. Res. 2006, 14, 423–435. [Google Scholar] [CrossRef]
- Dvořák, L. A do-it-yourself optical bench. Phys. Teach. 2011, 49, 452–454. [Google Scholar] [CrossRef]
- Uchida, S. A Variable focal length lens made from a food preservation lid. Phys. Teach. 2019, 57, 173–175. [Google Scholar] [CrossRef]
- Lin, H.-S.; Hong, Z.-R.; Chen, Y.-C. Exploring the developement of college students’ situational interest in learning science. Int. J. Sci. Educ. 2013, 35, 2152–2173. [Google Scholar] [CrossRef]
- Schraw, G.; Flowerday, T.; Lehman, S. Increasing situational interest in the classroom. Educ. Psych. Rev. 2001, 13, 211–224. [Google Scholar] [CrossRef]
- Flowerday, T.; Schraw, G. Teacher beliefs about instructional choice: A phenomenological study. J. Educ. Psych. 2000, 92, 634–645. [Google Scholar] [CrossRef]
- Palmer, D.H. Student interest generated during and inquiry skills lesson. J. Res. Sci. Teach. 2009, 46, 147–165. [Google Scholar] [CrossRef]
- Blankenburg, J.S.; Höffler, T.N.; Parchmann, I. Fostering today what is needed tomorrow: Investigating students’ interest in science. Sci. Educ. 2016, 100, 364–391. [Google Scholar] [CrossRef]
- Swarat, S.; Ortony, A.; Revelle, W. Activity matters: Understanding student interest in school science. J. Res. Sci. Teach. 2012, 49, 515–537. [Google Scholar] [CrossRef]
- Dreyhaupt, J.; Mayer, B.; Kreis, O.; Öchsner, W.; Muche, R. Cluster-randomized studies in educational research: Principles and methodological aspects. GMS J. Medic. Educ. 2017, 34, Doc26. [Google Scholar] [CrossRef]
- Winkelmann, J. Auswirkungen auf den Fachwissenszuwachs und auf Affektive Schülermerkmale durch Schüler- und Demonstrationsexperimente im Physikunterricht; Logos Verlag: Berlin, Germany, 2015. [Google Scholar]
- Cronbach, L.J. Coefficient alpha and the internal structure of tests. Psychometrika 1951, 16, 297–334. [Google Scholar] [CrossRef]
- Taber, K.S. The use of Cronbach’s alpha hhen developing and reporting research instruments in science education. Res. Sci. Educ. 2018, 48, 1273–1296. [Google Scholar] [CrossRef]
- Fromme, B. Fehlvorstellungen bei Studienanfängern: Was bleibt vom Unterricht der Sekundarstufe I? PhyDid B-Didakt. Phys.-Beiträge DPG-Frühjahrstagung 2018, 205–215. Available online: https://ojs.dpg-physik.de/index.php/phydid-b/article/view/835 (accessed on 1 September 2022).
- Hettmannsperger, R.; Müller, A.; Scheid, J.; Kuhn, J.; Vogt, P. KTSO-A: Konzepttest-Strahlenoptik–Abbildungen. Entwicklung eines Konzepttestszur Erfassung von Konzepten der Lichtausbreitung, Streuung und der Entstehung reeller Bilder im Bereich der Strahlenoptik. Prog. Sci. Educ. 2021, 4, 11–35. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Development of a test instrument to investigate secondary school students’ declarative knowledge of quantum optics. Eur. J. Sci. Math. Educ. 2021, 9, 57–79. [Google Scholar] [CrossRef]
- Zenger, T.; Bitzenbauer, P. Exploring German secondary school students’ conceptual knowledge of density. Sci. Educ. Int. 2022, 33, 86–92. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P.; Girnat, B. Assessing learners’ conceptual understanding of introductory group theory using the CI2GT: Development and analysis of a concept inventory. Educ. Sci. 2022, 12, 376. [Google Scholar] [CrossRef]
- Aslanides, J.S.; Savage, C.M. Relativity concept inventory: Development, analysis, and results. Phys. Rev. Phys. Educ. Res. 2013, 9, 010118. [Google Scholar] [CrossRef]
- Rost, J. Allgemeine Standards für die Evaluationsforschung. In Evaluation Psychologischer Interventionsmaßnahmen. Standards und Kriterien: Ein Handbuch; Hager, W., Patry, J.-L., Brezing, H., Eds.; Verlag Hans Huber: Bern, Switzerland, 2000; pp. 129–140. [Google Scholar]
- Nachar, N. The Mann-Whitney U: A test for assessing whether two independent samples come from the same distribution. Tutor. Quantit. Meth. Psych. 2008, 4, 13–20. [Google Scholar] [CrossRef]
- Hake, R.R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. Am. J. Phys. 1998, 66, 64–74. [Google Scholar] [CrossRef]
- Coletta, V.P.; Steinert, J.J. Why normalized gain should continue to be used in analyzing preinstruction and postinstruction scores on concept inventories. Phys. Rev. Phys. Educ. Res. 2020, 16, 010108. [Google Scholar] [CrossRef]
- Veith, J.; Bitzenbauer, P.; Girnat, B. Exploring learning difficulties in abstract algebra: The case of group theory. Educ. Sci. 2022, 12, 516. [Google Scholar] [CrossRef]
- Hartig, J.; Rakoczy, K. Mehrebenenanalyse. In Handbuch Statistik, Methoden und Evaluation; Holling, H., Schmitz, B., Eds.; Hogrefe Verlag GmbH & Co., KG: Göttingen, Germany, 2010; pp. 538–547. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Palmer, D.H.; Dixon, J.; Archer, J. Identifying underlying causes of situational interest in a science course for preservice elementary teachers. Sci. Educ. 2016, 100, 1039–1061. [Google Scholar] [CrossRef]
- Palmer, D.; Dixon, J.; Archer, J. Using situational interest to enhance individual interest and science-related behaviours. Res. Sci. Educ. 2017, 47, 731–753. [Google Scholar] [CrossRef]
- Bortz, J.; Döring, N. Forschungsmethoden und Evaluation für Human- und Sozialwissenschaftler; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Germann, P.J. Directed-inquiry approach to learning science process skills: Treatment effects and aptitude-treatment interactions. J. Res. Sci. Teach. 1989, 26, 237–250. [Google Scholar] [CrossRef]
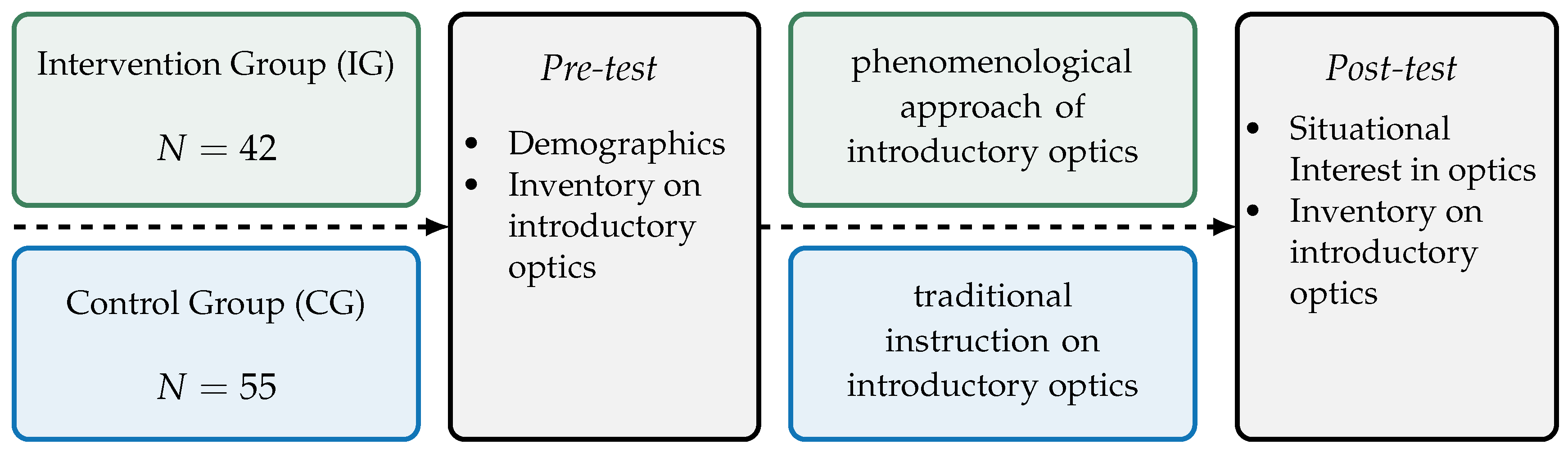



| Total Sample | Intervention Group (IG) (Phenomenological Approach) | Control Group (CG) (Traditional Instruction) | |
|---|---|---|---|
| Students | 97 | 42 | 55 |
| Teachers | 3 | 2 | 1 |
| Classes | 4 | 2 | 2 |
| Gender | |||
| males | 51 | 19 | 32 |
| females | 40 | 22 | 18 |
| not specified | 6 | 1 | 5 |
| Phenomenological Approach to Optical Concepts, IG | Traditional Optics Teaching, CG |
|---|---|
| Consistent treatment of the process of vision along the entire sequence. | The process of vision as an introductory topic. |
| Transmitter–receiver concept of vision. | Transmitter–receiver concept of vision. |
| Model-free treatment of apparent depth, refraction, and image formation. | Use of the ray model of light for the explanation of light refraction and for geometrical construction of image positions. |
| Experimental determination of dependencies between object width, image width, and focal length of a converging lens | Mathematical description of image formation using the thin lens formula. |
| Domain | Descriptors | Items |
|---|---|---|
| Process of vision | Light propagation, visibility of objects, sender-emission-receiver-concept, shadow. | 1, 2, 3, 4, 14, 15 |
| Refraction and apparent depth | Apparent depth, definition of light refraction, distinction between refraction and reflection. | 5, 6, 7, 8, 9 |
| Image formation by a converging lens | Real images of the converging lens, image size, brightness of images. | 10, 11, 12, 13 |
| Item 2: Which of the following objects/animals can you see in a completely darkened room? | |||||
|---|---|---|---|---|---|
| □ | A glowing firefly. | ||||
| □ | A white sheet of paper. | ||||
| □ | A bicycle reflector. | ||||
| □ | The eyes of a cat. | ||||
| □ | □ | □ | □ | □ | |
| Very sure | Sure | Undecided | Unsure | Guessed | |
| Item 9: Comment on the following statement of a classmate: I do not believe that light propagates in a straight line. If light falls obliquely on a water surface, its direction of propagation changes. | |||||
|---|---|---|---|---|---|
| □ | I agree with the classmate. Light does not propagate in a straight line. | ||||
| □ | I do not agree with the classmate. When light hits a water surface, it is reflected. | ||||
| □ | I agree with the classmate. When light hits a water surface, it always passes through in a straight line. | ||||
| □ | I do not agree with the student. The light is refracted at the water surface, but then it propagates in a straight line again. | ||||
| □ | □ | □ | □ | □ | |
| Very sure | Sure | Undecided | Unsure | Guessed | |
| Item 10: What can you say about the image of an object produced by a converging lens on a screen? | |||||
|---|---|---|---|---|---|
| □ | The image is upside down and side-inverted. | ||||
| □ | The image is upright and real. | ||||
| □ | The image is upside down and black and white. | ||||
| □ | The image is upright and in color. | ||||
| □ | □ | □ | □ | □ | |
| Very sure | Sure | Undecided | Unsure | Guessed | |
| Group | Median | SD | Mann–Whitney-U | p | r | |
|---|---|---|---|---|---|---|
| Pre-test | CG | 5.00 | 2.54 | , | - | |
| IG | 4.00 | 2.49 | ||||
| Post-test | CG | 7.00 | 3.02 | , | < | 0.27 |
| IG | 8.00 | 3.24 |
| (CG) | 0.08 | 0.21 | 0.11 | 0.17 |
| (IG) | 0.27 | 0.30 | 0.47 | 0.36 |
| Median (CG) | 0.20 | 0.25 | 0.00 | 0.24 |
| Median (IG) | 0.25 | 0.29 | 0.50 | 0.39 |
| Mann–Whitney U | , , | , , | , , | , , |
| r | - | - | 0.61 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebald, J.; Fliegauf, K.; Veith, J.M.; Spiecker, H.; Bitzenbauer, P. The World through My Eyes: Fostering Students’ Understanding of Basic Optics Concepts Related to Vision and Image Formation. Physics 2022, 4, 1117-1134. https://doi.org/10.3390/physics4040073
Sebald J, Fliegauf K, Veith JM, Spiecker H, Bitzenbauer P. The World through My Eyes: Fostering Students’ Understanding of Basic Optics Concepts Related to Vision and Image Formation. Physics. 2022; 4(4):1117-1134. https://doi.org/10.3390/physics4040073
Chicago/Turabian StyleSebald, Janika, Kai Fliegauf, Joaquin M. Veith, Henrike Spiecker, and Philipp Bitzenbauer. 2022. "The World through My Eyes: Fostering Students’ Understanding of Basic Optics Concepts Related to Vision and Image Formation" Physics 4, no. 4: 1117-1134. https://doi.org/10.3390/physics4040073
APA StyleSebald, J., Fliegauf, K., Veith, J. M., Spiecker, H., & Bitzenbauer, P. (2022). The World through My Eyes: Fostering Students’ Understanding of Basic Optics Concepts Related to Vision and Image Formation. Physics, 4(4), 1117-1134. https://doi.org/10.3390/physics4040073





