Abstract
The Ermakov–Milne–Pinney equation is ubiquitous in many areas of physics that have an explicit time-dependence, including quantum systems with time-dependent Hamiltonian, cosmology, time-dependent harmonic oscillators, accelerator dynamics, etc. The Eliezer and Gray physical interpretation of the Ermakov–Lewis invariant is applied as a guiding principle for the derivation of the special relativistic analog of the Ermakov–Milne–Pinney equation and associated first integral. The special relativistic extension of the Ray–Reid system and invariant is obtained. General properties of the relativistic Ermakov–Milne–Pinney are analyzed. The conservative case of the relativistic Ermakov–Milne–Pinney equation is described in terms of a pseudo-potential, reducing the problem to an effective Newtonian form. The non-relativistic limit is considered to be well. A relativistic nonlinear superposition law for relativistic Ermakov systems is identified. The generalized Ermakov–Milne–Pinney equation has additional nonlinearities, due to the relativistic effects.
1. Introduction
The Ermakov–Milne–Pinney (EMP) equation [1,2,3]
where C is a real constant usually taken as positive, and the dot stays for the time derivative, of the x-coordinate, is a ubiquitous nonlinear non-autonomous ordinary differential equation with many applications, in particular in problems related to the time-dependent harmonic oscillator or in connection with exact solutions of the one-dimensional time-independent Schrödinger equation. In more generality, applications of the EMP equation appear in cosmological models [4,5,6], Bose-Einstein condensates [7,8], photonic lattices [9], accelerator dynamics [10,11], gravitational wave propagation [12], higher order spin models [13], quantum plasmas [14], limit cycles [15], dynamical symmetries [16], magneto-gasdynamics [17], time-dependent non-Hermitian quantum system [18,19], supersymmetric systems [20], noncommutative quantum mechanics [21], etc. Historical notes can be found e.g., in [22,23]. We note that the name of the EMP equation is not yet a consensus in the literature. For instance, sometimes it can be referred just as Pinney equation.
Diverse generalizations of the EMP equation have been proposed, as for instance allowing to have a dependence on time [8,23], the inclusion of dissipation [24,25], unbalanced systems of EMP equations with different frequency functions [26], modified nonlinearities [27], stochastic differential equations with additive noise [28]. Following the generalization trend, it would be relevant to extend the EMP equation into the special relativity domain, with potential applications for the dynamics of charged particles in high energy density fields [29]. To date only a few results weakly related to special relativistic EMP equations are available, in connection with the Dirac equation [30] and the relativistic isotropic two-dimensional time-dependent harmonic oscillator [31]. Naturally, the relativistic extension is not straightforward due to the intrinsic extra nonlinearity imposed by the presence of the Lorentz factor. Moreover, the intimate connection between the EMP equation and the time-dependent harmonic oscillator raises the question of what defines the relativistic harmonic oscillator. In this regard, the relativistic motion immediately induces anharmonicities even in the case of a quadratic potential with a frequency-amplitude dependence [32,33]. Here we follow the approach of many authors [34,35,36,37,38,39,40,41,42,43], adopting the spinless Salpeter equation [44] with a quadratic external potential as our definition of relativistic harmonic oscillator. The choice is due to its simplicity, where just the Newtonian kinetic energy is replaced by its special relativistic counterpart. This version of the relativistic harmonic oscillator model has been recently experimentally probed [45].
The present work proposes a systematic approach towards the relativistic EMP equation and beyond, using as a simple guiding principle the Eliezer and Gray [46] physical interpretation of the Ermakov–Lewis associated first integral for the isotropic two-dimensional time-dependent harmonic oscillator. The reason is that the Eliezer and Gray method based on the conservation of the angular momentum of an auxiliary planar motion provides the standard physical reasoning behind the conservation of the Ermakov invariant [47,48]. Moreover, the extension of the Ray–Reid Ermakov systems [47] to the relativistic domain will be also obtained. In brief, a relativistic extension of the celebrated EMP equation and extensions is proposed (which obviously has no direct relation to special solutions of Klein-Gordon, Dirac or similar relativistic partial differential equations).
This paper is organized as follows. In Section 2, we review the Eliezer and Gray interpretation. In Section 3, we consider the relativistic isotropic two-dimensional time-dependent harmonic oscillator and follow the Eliezer and Gray method, to identify a relativistic EMP equation together with the associated conservation law. From the structure of the dynamical equations, the appropriate relativistic Ray–Reid system will be also derived, as well as with the corresponding first integral. Section 4 provides an alternative derivation based on a dynamical rescaling of time parameter. Section 5 and Section 6 deal with basic properties of the relativistic EMP equation, mainly in the autonomous case. Section 7 is dedicated to a nonlinear superposition law relating the solutions of the relativistic EMP system. Finally, Section 8 is reserved to the conclusions and extra remarks.
2. The Eliezer and Gray Physical Interpretation
We briefly reproduce the Eliezer and Gray physical interpretation [46] of the Ermakov-Lewis invariant, which will serve us as a guidance for a relativistic generalization of the EMP system. Consider the Lagrangian
with the corresponding auxiliary plane motion
where has the Cartesian components , and the EMP equation
where J is a real constant. In terms of polar coordinates , where , the equations of motion become
Equation (6) implies the constancy of the angular momentum
assuming for simplicity a unit mass. Combining Equations (5) and (7) we derive Equation (4). Considering the equation for the component of the auxiliary motion together with Equation (4), the constancy of the Ermakov–Lewis invariant I, given by
is directly verified, along trajectories. Expressing in terms of polar coordinates, one has
Therefore, the invariance of I is equivalent to the invariance of the angular momentum of the auxiliary plane motion.
For reference, it is worth considering the Ray–Reid (RR) generalization [47] of the EMP system and invariant, namely
where are arbitrary functions of the indicated arguments. The RR first integral for Equations (10) and (11) is
One can directly verify that along trajectories.
3. A Relativistic Ermakov–Milne–Pinney System
Proceeding in strict analogy with the non-relativistic (NR) case, consider the equations of motion for the 2-dimensional (2D) relativistic unit rest mass time-dependent harmonic oscillator, which can be derived [49,50] from the Lagrangian
where c is the speed of light and . The Euler-Lagrange equations are
which can be disentangled as
where . The equations of motion agree with findings in [31]. As with the NR case, employing cylindrical coordinates , we have the conserved angular momentum expressed as
Moreover, we get the Lorentz factor expressible in terms of as
The NR formal limit yields also from Equation (19). Using the angular momentum to eliminate the angular velocity, we obtain
From the identity , it becomes self-evident that the quantity
is a first integral, since
in complete analogy with the Ermakov–Lewis invariant for the NR problem. It can be also directly verified that along the trajectories of the system (20) and (21). The invariant has the same physical interpretation of the NR Ermakov invariant in terms of the conservation of the angular motion of the associated auxiliary 2D motion. In this context, it is justified to interpret Equations (20) and (21) as the (special) relativistic EMP system. Equation (21) is a relativistic EMP equation (REMP), and the first integral in Equation (22) is the relativistic Ermakov–Lewis invariant of the problem. Obviously, in the formal limit one recovers the NR case. Understanding the Lorentz factor in the sense of Equation (19), the relativistic EMP system is a pair of nonlinear second-order ordinary differential equations for . Unlike the NR case, the equation for x is not uncoupled.
To recapitulate, we have just used the standard Lagrangian for the special relativistic two-dimensional motion [51,52,53,54], in the particular case where the particle is under the influence of a force linear in position (a quadratic potential) as seen in a fixed local inertial frame with respect to which the motion is observed [49,50].
In passing, we write the Hamiltonian , associated with (13),
which is not a constant of motion in the non-conservative case where is a time-dependent function. Even in the autonomous case where , the nature of and the invariant in Equation (22) are different: the former is energy-like, while the latter is angular momentum-like.
From the structure of Equations (20) and (21) and after some trial and error, it is possible to identify a relativistic Ray–Reid (RRR) system, namely
where and the Lorentz factor is understood as a function of . The invariant for Equations (25) and (26) is
It can be verified that along trajectories. It is apparent that Equations (25)–(27) define a RRR system and its invariant, showing a complete symmetry between the x and y variables and recovering the RR system and invariant in the formal NR limit , as shown by comparison with Equations (10)–(12). A derivation provided by a dynamical rescaling of time will be described in the next Section.
Although our treatment has as motivation the relativistic time-dependent harmonic oscillator, it is clear that the invariants shown in Equations (22) and (27) do not depend on . Therefore, one is authorized to allow for more general functional dependencies of , e.g., in Equations (25) and (26), maintaining the constancy of the RRR invariant. Similar remarks apply to the NR case [55,56,57]. Notice that Equations (25) and (26) do not have a Lagrangian structure in general.
4. Derivation from a Dynamical Rescaling of Time
Let us start with the dynamical system
where a prime denotes derivative with respect to the independent variable : , and where can be anything in the same spirit as it is in the last Section. In the same way as for the RR system, it is obvious that (28) possess the invariant
If we now move to a new independent variable t defined by
then it can be checked after some algebra that the RRR system (25) and (26) is recovered, with , and that the invariant (29) transforms into (27). The procedure gives a more transparent derivation of the RRR system from a dynamical rescaling of time starting from the RR system.
It is worthwhile discussing Lorentz invariance. In the same sense as the Newtonian harmonic oscillator is obviously not Galilean invariant, the relativistic harmonic oscillator is not Lorentz invariant. In this respect we remember that the symmetry group of the NR Ermakov system is the group [58], which has no relation with the Galilean group. Moreover, notice that the force equation where are the components of the relativistic momentum is relativistic only “in a certain sense", quoting [49], since time has been kept as entirely distinct from the spatial coordinates. Nevertheless, a fully covariant interpretation is possible, regarding (13) as the Lagrangian for a charged particle under a scalar electrostatic potential which is a quadratic function of the spatial coordinates, in the instant inertial frame with respect the motion is observed. In this context, a fully covariant formalism could be easily performed following the standard approach [49,50,51,52,53,54] starting with the Lagrangian (here, m is the amss and q is the charge of the particle, A is the vector potential and is the scalar potential of the electromagnetic field) in the two-spatial dimensions case, with together with . This is the Lagrangian (13) assuming unit rest mass without loss of generality. In addition, the relativistic harmonic oscillator and REMP equations reproduce the Newtonian systems in the limit , where u is a measure of the maximal velocity of the problem. For instance, if is the amplitude of the motion under a linear force , the relativistic effects become negligible provided . The case of a very strong external field acting on a charged particle [29] is a suitable system to probe the relativistic effects. In this context, since the non-relativistic Ermakov system has found applications in accelerator physics [11], the relativistic version has potential applications for charged particle motions under high-intensity external fields.
Notice that the derivation of Equations (20) and (21) containing the REMP equation, together with the relativistic Ermakov–Lewis invariant (22), follows a very different route compared to the RRR system (25) and (26) and associated invariant (27). To obtain the REMP equation, the starting point was the relativistic Lagrangian for the 2D time-dependent harmonic oscillator, together with polar coordinates, exactly the same as the procedure for the NR EMP system but then with the special relativistic Lagrangian. On the other hand, the RRR system can be considered “relativistic” only in the ad hoc sense that it reduces to the NR RR system in the limit where c is some reference velocity, since its derivation does not starts from any physical relativistic Lagrangian. In the same context, the use of a dynamical rescaling of time clearly has not a relativistic spirit. First, the factor in Equation (30) is defined in terms of the particle velocity, not the relative velocity between two inertial frames. Second, it is obviously not a Lorentz transformation since the space variables are kept the same. Third, we had not the objective of setting a sort of symmetry transformation for the Equation (28). Rather, the goal was the use of a non-invariance transformation towards the derivation of the RRR system. Although at the moment there is lack of a physical interpretation of the RRR system, which as discussed is relativistic only in a formal sense, we think it is worthwhile to present it since it has a striking analogy with the traditional RR system, being a non-trivial pair of coupled nonlinear second-order ordinary differential equations possessing an exact invariant.
5. The Case
For a vanishing angular momentum, one has so that it can be chosen , without loss of generality. In this case, and Equation (20) becomes
which is the equation for a 1D relativistic time-dependent harmonic oscillator [59].
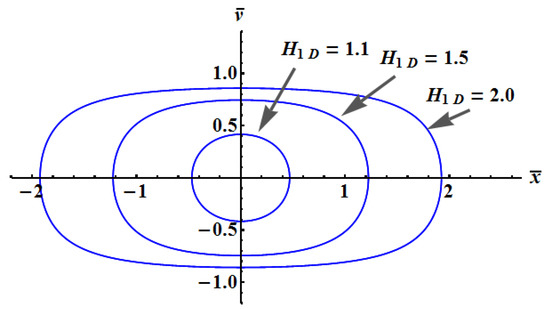
In the case of a constant frequency , obviously the energy is conserved. In terms of rescaled variables , the corresponding first integral is
with phase-space contour plots shown in Figure 1. Clearly, only bounded trajectories are admissible, as expected. The return points are located at . In rescaled coordinates, the NR limit corresponds to circular trajectories in phase-space, . For larger values of , the return points are also larger, implying more relativistic effects and increasing anharmonicity, as seen in Figure 1.
It is instructive to rewrite the conservation law in a Newtonian form,
where the (pseudo)potential is defined by
shown in Figure 2. In the NR limit, the variable is limited to small values, so that with , while larger values of correspond to enhanced relativistic effects and anharmonicity. The quantity provides a kind of transfer of the nonlinearity from the kinetic energy term to an anharmonic (pseudo)potential term, but seemingly has not a physical interpretation.
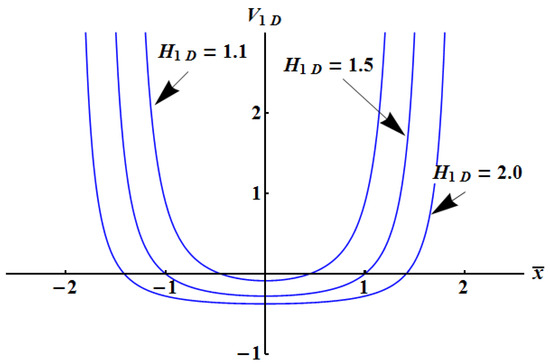
Figure 2.
Pseudo-potential from Equation (34) and different values of , as indicated.
The conserved energy can be used for the quadrature of the motion in terms of elliptic functions. For this purpose, we set
where A is the amplitude of the motion, and define
After some algebra, Equation (33) gets the form:
which can be immediately integrated yielding
where is an integration constant and are incomplete elliptic integrals of the first and second kind [60],
Using MATHEMATICA, one gets a series solution,
recovering the Newtonian result in the limit of small amplitude (which is also the non-relativistic limit). Similarly, the period T for which is
Approximate periodic solutions for the 1D conservative relativistic harmonic oscillator can also be found in [61].
6. Relativistic Conservative Ermakov–Milne–Pinney Equation
The REMP equation defined in Equation (21) with does not have collapsing () solutions due to the inverse cubic term. For instance, suppose and the rescaling , so that
The energy first integral is
Then one immediately concludes that .
Rewriting in a Newtonian form yields
with a (pseudo)potential defined by
shown in Figure 3. It is possible to show that , where is the equilibrium point of V,
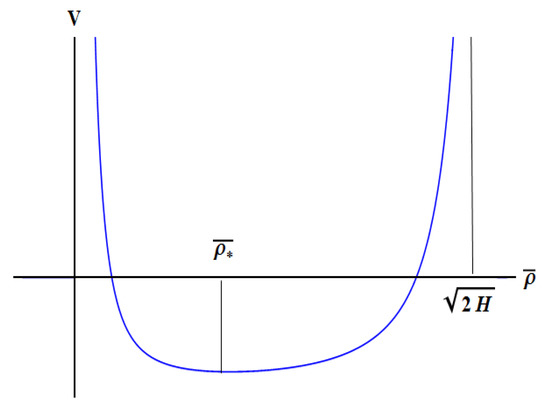
Figure 3.
Pseudo-potential V from Equation (45).
The return points correspond to , similarly to Figure 2, with stable oscillations around . Elementary algebra shows that the condition for periodic motions () is equivalent to
or, sufficiently small angular momentum. In the NR limit one has disregarding terms, so that the periodicity condition can be shown to be automatically satisfied. The characteristic function F is shown in Figure 4. A numerical investigation shows that the periodicity condition is always meet, for meaningful initial conditions , as expected.
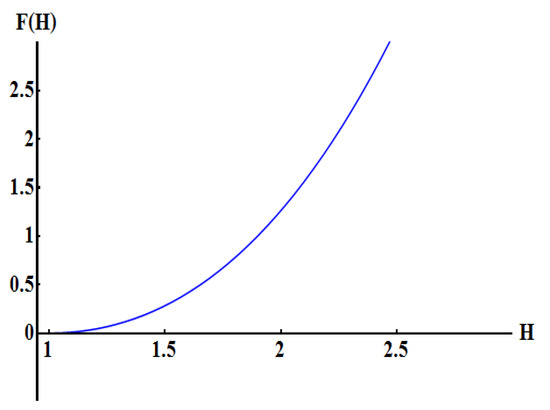
Figure 4.
Characteristic function from Equation (47) for .
7. Nonlinear Superposition Law
Let us assume that is a particular solution of the REMP Equation (21). Introducing the new variables
where is given by Equation (19) converts the relativistic Ermakov–Lewis invariant (22) into
being formally the same as the energy first integral for a 1D conservative NR harmonic oscillator. A quadrature yields
or
since , adopting and where is a constant phase. The nonlinear superposition law (51) generalizes the Newtonian result [55] to the relativistic context. For a specific application, the solution to be found numerically for a particular function.
8. Conclusions
In this paper, a considerable progress is made for the generalization of Ermakov systems towards the special relativity domain. The Eliezer and Gray physical interpretation of the Ermakov–Lewis invariant, was used as a guide for the derivation of the relativistic analog of the EMP equation, together with the corresponding first integral for the relativistic planar time-dependent harmonic oscillator. General aspects of the relativistic EMP equation have been addressed, and a nonlinear superposition law was derived. Despite the successful results, it is still possible to derive other classes of relativistic Ermakov systems, not arising from the correspondence with the Eliezer and Gray physical interpretation. For instance, symmetry principles can be a guiding principle, although the group structure of non-relativistic Ermakov systems obviously tends to be broken in the relativistic domain. In the same footing, to carry to the relativistic domain the linearization of standard Ermakov systems would be a probably unfeasible task. Finally, an intriguing question remains about the RRR system defined by Equations (25) and (26). If one starts from the Lagrangian (13) adding an Ermakov term to the potential V, we find precisely the system (25) and (26), where are suitable related to U, but with a factor instead of on all terms of the right-hand side. In this case, the quantity in Equation (27) would be not conserved, and no other first integral in direct correspondence with the non-relativistic RR invariant would be available. In other words, the Hamiltonian structure from (non-relativistic) RR systems [56] is almost immediately translated to the relativistic context, except for an ad hoc modification of the factor power, as long as one prefers to keep the existence of a RR invariant. In future works it is worthwhile to see how one can actually solve the new relativistic Ermakov systems with an explicit time-dependence. For this purpose, the search for quasi-exact solutions [62] can be a fruitful approach.
Funding
This research was funded by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).
Conflicts of Interest
The author declares no conflict of interest.
References
- Ermakov, V.P. Second-order differential equations. Conditions of complete integrability. Appl. Anal. Discrete Math. 2008, 2, 123–145. [Google Scholar]
- Milne, W.E. The numerical determination of characteristic numbers. Phys. Rev. 1930, 35, 863–867. [Google Scholar] [CrossRef]
- Pinney, E. The nonlinear equation y′′(x)+p(x)y(x)+cy−3(x)=0. Proc. Amer. Math. Soc. 1950, 1, 681. [Google Scholar]
- Hawkins, R.M.; Lidsey, J.E. Ermakov-Pinney equation in scalar field cosmologies. Phys. Rev. D 2002, 66, 023523. [Google Scholar] [CrossRef]
- Rosu, H.C.; Mancas, S.C.; Chen, P. Barotropic FRW Cosmologies with Chiellini damping. Phys. Lett. A 2015, 379, 882–887. [Google Scholar] [CrossRef][Green Version]
- Paliathanasis, A.; Tsamparlis, M.; Basilakos, S.; Capozziello, S. Scalar-tensor gravity cosmology: Noether symmetries and analytical solutions. Phys. Rev. D 2014, 89, 063532. [Google Scholar] [CrossRef]
- Haas, F. Anisotropic Bose-Einstein condensates and completely integrable dynamical systems. Phys. Rev. A 2002, 65, 033603. [Google Scholar] [CrossRef]
- Herring, G.; Kevrekidis, P.G.; Williams, F.; Christodoulakis, T.; Frantzeskakis, D.F. From Feshbach-resonance managed Bose-Einstein condensates to anisotropic universes: Applications of the Ermakov-Pinney equation with time-dependent nonlinearity. Phys. Lett. A 2007, 367, 140–148. [Google Scholar] [CrossRef]
- Rodríguez-Lara, B.M.; Aleahmad, P.; Moya-Cessa, H.M.; Christodoulides, D.N. Ermakov–Lewis symmetry in photonic lattices. Opt. Lett. 2014, 39, 2083–2085. [Google Scholar] [CrossRef]
- Courant, E.D.; Snyder, H.S. Theory of the alternating-gradient synchrotron. Ann. Phys. 1958, 3, 1–48. [Google Scholar] [CrossRef]
- Qin, H.; Davidson, R.C. Symmetries and invariants of the oscillator and envelope equations with time-dependent frequency. Phys. Rev. ST Accel. Beams 2006, 9, 054001. [Google Scholar] [CrossRef]
- Geralico, A.; Landolfi, G.; Ruggeri, G.; Soliani, G. Novel approach to the study of quantum effects in the early Universe. Phys. Rev. D 2004, 69, 043504. [Google Scholar] [CrossRef]
- Fring, A.; Frith, T. Metric versus observable operator representation, higher spin models. Eur. Phys. J. Plus 2018, 133, 57. [Google Scholar] [CrossRef]
- Haas, F.; Bret, A. Nonlinear low-frequency collisional quantum Buneman instability. EPL (Europhysics Letters) 2012, 97, 26001. [Google Scholar] [CrossRef]
- Llibre, J.; Pérez-Chavela, E. Limit cycles for a class of second order differential equations. Phys. Lett. A 2011, 375, 1080–1083. [Google Scholar] [CrossRef]
- Haas, F.; Goedert, J. On the linearization of the generalized Ermakov systems. J. Phys. A Math. Gen. 1999, 32, 2835–2844. [Google Scholar] [CrossRef]
- Rogers, C.; Schief, W.K. The pulsrodon in 2+1-dimensional magneto-gasdynamics: Hamiltonian structure and integrability. J. Math. Phys. 2011, 52, 083701. [Google Scholar] [CrossRef]
- Dey, S.; Fring, A.; Gouba, L. Milne quantization for non-Hermitian systems. J. Phys. A Math. Theor. 2015, 48, 40FT01. [Google Scholar] [CrossRef][Green Version]
- Fring, A.; Frith, T. Mending the broken PT-regime via an explicit time-dependent Dyson map. Phys. Lett. A 2017, 381, 2318–2323. [Google Scholar] [CrossRef][Green Version]
- Cen, J.; Fring, A.; Frith, T. Time-dependent Darboux (supersymmetric) transformations for non-Hermitian quantum systems. J. Phys. A Math. Theor. 2019, 52, 115302. [Google Scholar] [CrossRef]
- Dey, S.; Fring, A. Noncommutative quantum mechanics in a time-dependent background. Phys. Rev. D 2014, 90, 084005. [Google Scholar] [CrossRef]
- Cariñena, J.F.; de Lucas, J. A nonlinear superposition rule for solutions of the Milne-Pinney equation. Phys. Lett. A 2008, 372, 5385–5389. [Google Scholar] [CrossRef][Green Version]
- Morris, R.M.; Leach, P.G.L. The effects of symmetry-breaking functions on the Ermakov-Pinney equation. Appl. Anal. Discrete Math. 2017, 11, 62–73. [Google Scholar] [CrossRef]
- Haas, F. The damped Pinney equation and its applications to dissipative quantum mechanics. Physica Scripta 2010, 81, 025004. [Google Scholar] [CrossRef]
- Guha, P.; Ghose-Choudhury, A. Nonlocal transformations of the generalized Liénard type equations and dissipative Ermakov-Milne-Pinney systems. Int. J. Geom. Meth. Mod. Phys. 2019, 16, 1950107. [Google Scholar] [CrossRef]
- Athorne, C. On solving a class of unbalanced Ermakov- Pinney systems. J. Phys. A Math. Gen. 2001, 34, L563–L566. [Google Scholar] [CrossRef]
- Reid, J.L. An exact solution of the nonlinear differential equation ÿ+p(t)y=qm(t)/y2m−1. Proc. Am. Math. Soc. 1971, 27, 61–62. [Google Scholar]
- Cervantes-López, E.; Espinoza, P.B.; Gallegos, A.; Rosu, H.C. Ermakov–Ray–Reid systems with additive noise. Physica A 2015, 439, 44–47. [Google Scholar] [CrossRef]
- Hartemann, F.V. High-Field Electrodynamics; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Thylwe, K.-E.; McCabe, P. Bohr-Sommerfeld quantization condition for Dirac states derived from an Ermakov-type invariant. J. Math. Phys. 2013, 54, 052301. [Google Scholar] [CrossRef]
- Petrov, S.V. Classical dynamics of the relativistic oscillator. Eur. J. Phys. 2016, 37, 065605. [Google Scholar] [CrossRef]
- Guerrero, J.; Aldaya, V. A perturbative approach to the relativistic harmonic oscillator. Mod. Phys. Lett. A 1999, 14, 1689–1699. [Google Scholar] [CrossRef]
- Beléndez, A.; Pascual, C.; Méndez, D.I.; Neipp, C. Solution of the relativistic (an)harmonic oscillator using the harmonic balance method. J. Sound Vib. 2008, 311, 1447–1456. [Google Scholar] [CrossRef]
- Edery, A.; Laporte, P. First and second-order relativistic corrections to the two and higher-dimensional isotropic harmonic oscillator obeying the spinless Salpeter equation. J. Phys. Commun. 2018, 2, 025024. [Google Scholar] [CrossRef]
- Poszwa, A. Relativistic generalizations of the quantum harmonic oscillator. Acta Phys. Pol. A 2014, 126, 1226–1234. [Google Scholar] [CrossRef]
- Znojil, M. Harmonic oscillations in quasi-relativistic regime. J. Phys. A Math. Gen. 1996, 29, 2905–2918. [Google Scholar] [CrossRef]
- Balasubramanya, M.K. The action variable and frequency of a relativistic harmonic oscillator. Theor. Math. Phys. 2010, 162, 341–346. [Google Scholar] [CrossRef]
- Gold, L. Note on the relativistic harmonic oscillator. J. Franklin Inst. 1957, 264, 25–27. [Google Scholar] [CrossRef]
- Harvey, A.L. Relativistic harmonic oscillator. Phys. Rev. D 1972, 6, 1474–1476. [Google Scholar] [CrossRef]
- Teychenné, D.; Bonnaud, G.; Bobin, J.-L. Oscillatory relativistic motion of a particle in a power-law or sinusoidal-shaped potential well. Phys. Rev. E 1994, 49, 3253–3263. [Google Scholar] [CrossRef] [PubMed]
- Chargui, Y. On an approximation of the two-body spinless Salpeter equation. Eur. Phys. J. Plus 2018, 133, 543. [Google Scholar] [CrossRef]
- Llibre, J.; Makhlouf, A. On the periodic solutions of the relativistic driven harmonic oscillator. J. Math. Phys. 2020, 61, 012501. [Google Scholar] [CrossRef]
- Li, Z.-F.; Liu, J.-J.; Lucha, W.; Ma, W.-G.; Schöberl, F.F. Relativistic harmonic oscillator. J. Math. Phys. 2005, 46, 103514. [Google Scholar] [CrossRef]
- Salpeter, E.E. Mass corrections to the fine structure of hydrogen-like atoms. Phys. Rev. 1952, 87, 328–343. [Google Scholar] [CrossRef]
- Fujiwara, K.M.; Geiger, Z.A.; Singh, K.; Senaratne, R.; Rajagopal, S.V.; Lipatov, M.; Shimasaki, T.; Weld, D.M. Experimental realization of a relativistic harmonic oscillator. New J. Phys. 2018, 20, 063027. [Google Scholar] [CrossRef]
- Eliezer, C.J.; Gray, A. A note on the time-dependent harmonic oscillator. SIAM J. Appl. Math. 1976, 30, 463–468. [Google Scholar] [CrossRef]
- Ray, J.R.; Reid, J.L. More exact invariants for the time-dependent harmonic oscillator. Phys. Lett. A 1979, 71, 317–318. [Google Scholar] [CrossRef]
- Mancas, S.C.; Rosu, H.C. Ermakov-Lewis invariants and Reid systems. Phys. Lett. A 2014, 378, 2113–2117. [Google Scholar] [CrossRef][Green Version]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics; Addison Wesley: San Francisco, CA, USA, 2002; p. 316. [Google Scholar]
- Hand, L.N.; Finch, J.D. Analytical Mechanics; Cambridge University Press: Cambridge, MA, UK, 1998; p. 551. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 1975; p. 48. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley: New York, NY, USA, 1962; p. 408. [Google Scholar]
- Corben, H.C.; Stehle, P. Classical Mechanics; John Wiley: New York, NY, USA, 1960; p. 297. [Google Scholar]
- Arya, A. Introduction to Classical Mechanics; Benjamin Cummings: San Francisco, CA, USA, 1997; p. 694. [Google Scholar]
- Reid, J.L.; Ray, J.R. Ermakov systems, nonlinear superposition, and solutions of nonlinear equations of motion. J. Math. Phys. 1980, 21, 1583–1587. [Google Scholar] [CrossRef]
- Haas, F.; Goedert, J. On the Hamiltonian structure of Ermakov systems. J. Phys. A Math. Gen. 1996, 29, 4083–4092. [Google Scholar]
- Goedert, J.; Haas, F. On the Lie symmetries of a class of generalized Ermakov systems. Phys. Lett. A 1998, 239, 348–352. [Google Scholar] [CrossRef]
- Leach, P.G.L. Generalized Ermakov systems. Phys. Lett. A 1991, 158, 102–106. [Google Scholar] [CrossRef]
- Martin, J.; Bouquet, S. Search for first integrals in relativistic time-dependent Hamiltonian systems. J. Math. Phys. 1994, 35, 181–189. [Google Scholar] [CrossRef]
- Milne-Thomson, L.M. Elliptic integrals. In Handbook of Mathematical Functions; Abramowitz, M., Stegun, I.A., Eds.; Dover Publications: New York, NY, USA, 1972; p. 589. [Google Scholar]
- Mickens, R.E. Periodic solutions of the relativistic harmonic oscillator. J. Sound Vib. 1998, 212, 905–908. [Google Scholar] [CrossRef]
- Fring, A.; Tenney, R. Time-independent approximations for time-dependent optical potentials. Eur. Phys. J. Plus 2020, 135, 163. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).