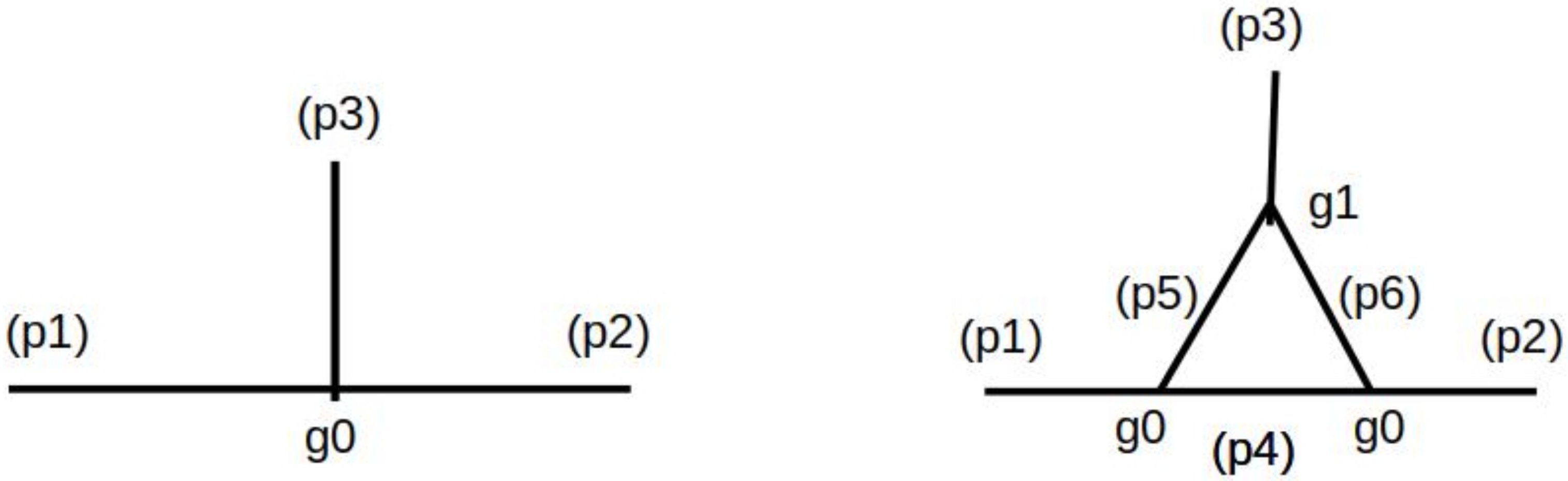Abstract
In this work, we provide an overview of the recent investigations on the non-extensive Tsallis statistics and its applications to high energy physics and astrophysics, including physics at the Large Hadron Collider (LHC), hadron physics, and neutron stars. We review some recent investigations on the power-law distributions arising in high energy physics experiments focusing on a thermodynamic description of the system formed, which could explain the power-law behavior. The possible connections with a fractal structure of hadrons is also discussed. The main objective of the present work is to delineate the state-of-the-art of those studies and show some open issues that deserve more careful investigation. We propose several possibilities to test the theory through analyses of experimental data.
PACS:
12.38.Mh; 13.60.Hb; 24.85.+p; 25.75.Ag
1. Introduction
An interesting description of hadronic systems in the hot and in the dense regimes, known as quark-gluon plasma (QGP), has been developed in recent years. Although motivated by the large amount of information that emerged from high energy physics (HEP) experiments, the consequences of those advances are far-reaching, since they may be present in any Yang–Mills field (YMF) theory. Here, we will give a short review of those developments, discuss the experimental evidence of the new theoretical approach, and present some applications to HEP, hadron physics, and astrophysics.
Before entering in the main subject of this work, let us summarize the three fundamental theories that form the foundations for the developments that will be discussed below. These three theories are: the YMF; the fractal geometry; and the non-extensive statistics proposed by Constantino Tsallis.
The Yang–Mills field theory is a prototype theory for describing most of the physical phenomena. It was proposed by Yang and Mills in the early 1950s [1] and was incorporated in the description of interacting fields that is known as Standard Model: it was incorporated into the electro-weak theory in the 1960s and in quantum chromodynamics (QCD) in the 1970s. Basically, it describes the propagation of undulatory fields in space and time, as well as the interaction between those fields. One of the fundamental properties of physics laws is the renormalization group invariance, and all the four known fundamental interactions show this feature as an essential aspect of its structure. At least three of them can be described by YMF, but for the gravitational interaction, a YMF version has also been proposed.
The simplest non-Abelian gauge field theory whose Lagrangian density includes bosons and fermions is given by
where is the field strength of the gauge field, and is the covariant derivative, with being the structure constants of the group, and the matrices of the group generators. In these expressions, with the spacetime coordinates, are the color group indices with the number of colors, g is the coupling constant, are the Dirac matrices, and , are flavor indices with the number of quark flavors. and A represent, respectively, the fermion and the vector fields. The YMF was shown to be renormalizable in ref. [2]. The asymptotic properties of the beta function of Yang–Mills theories, and particularly of QCD, were studied later, leading to the novel phenomenon of asymptotic freedom [3]. A comprehensive description of YMF can be found in, e.g., ref. [4].
Fractal is the name given by Benoit Mandelbrot to systems that present a geometry that is very different from the Euclidean one, although it has strong connections with natural phenomena as we observe them. Therefore, fractal geometry has been used to describe many natural shapes that can be observed in everyday life. The main aspect of a fractal is that it presents a fine structure with an undetermined number of components that are also fractals similar to the original system but at a different scale. This aspect is known as self-similarity. One important characteristic of fractals is the fractal dimension, which describes how the measurable aspects of the system change with scale. Contrary to the usual quantities in Euclidean geometry, where measurements with higher precision give a better evaluation of the same value for the measured quantity, in fractals, an increase of the resolution of the measurement will give a different value. This aspect is described by attributing a fractional dimension to the topological dimension of the system. The classical example is the coastline of an island, which has different lengths when measured with different precision.
A direct consequence of the self-similarity and the scaling properties with a fractional dimension is the power-law behavior of distributions observed for fractals. Thus, probability distributions are described by
with A being constant, an exponent related to the fractal dimension, and x is any random variable. The impressive ubiquity of fractals in physical systems, but also in mathematical iterative formulas, gives to the fractal theory an importance that can be noticed in many different areas, as physics, biology, sociology, and engineering. A nice introductory account of the applications of fractals can be found in refs. [5,6], and a comprehensive description of fractal geometry can be found in ref. [7].
The Tsallis statistics is a generalization of the Boltzmann–Gibbs (B-G) statistics, where the entropy is given by
where is the probability of x to be observed, q is the entropic index that quantifies how Tsallis entropy departs from the extensive B-G statistics, and is the Boltzmann constant. In the above expression, we used the q-logarithm function, defined as
A direct consequence of the entropic form defined above is the non-additivity of entropy, since for two independent systems, A and B, the entropy of the combined system, is
As the B-G statistics is recovered, the entropic form becomes additive and .
Another consequence is that often the probability distributions obtained in the non-extensive thermodynamics that result from the Tsallis entropic form are described in terms of the q-exponential function
which has found wide applicability in the last few years; see, e.g., refs. [8,9]. However, the full understanding of this statistics has not been accomplished yet. A comprehensive description of Tsallis Statistics and its applications can be found in refs. [10,11,12].
2. Objectives
The main objective of this work is to give a short review of the recent advances in the understanding of the fractal structures present in Yang–Mills fields, in particular QCD, and on its main implication, namely the need of Tsallis statistics to describe the thermodynamics aspects of the fields. We will obtain the entropic index of the Tsallis statistic as a function of the field fundamental parameters.
The main features of the fractal structure, which are summarized by the fractal dimension or fractal spectrum, will be discussed. We will show how the Tsallis statistics entropic index is related to the fractal structure that is represented as a thermofractal. Then, focusing in QCD and in high energy collisions (HEC), we shall obtain the effective coupling constant in terms of the entropic index, q, thereby relating the coupling to the field parameters by an analytical expression. We will show how the power-law behavior observed in momentum distributions measured at high energy collisions is naturally explained by the thermofractal structure. We will mention several experimental observations that can be easily described by the theory cited above.
The paper is organized as follows: In Section 3, we give a short description of Yang–Mills field theory, emphasizing the renormalization group invariance of the theory and evidencing the fractal structures present in the fields. We also show how the thermodynamic aspects of the Yang–Mills fields reflect the fractal structure in a way similar to the thermofractals, which were introduced to show how Tsallis statistics can emerge in thermodynamic systems, and study its main thermodynamic quantities. In Section 4, we describe the main experimental findings that give support to the theory presented here, and we study some applications of the theory to HEP, hadron physics, and astrophysics. Finally, in Section 5, we present a summary of the paper and our conclusions.
3. Theoretical Method
3.1. The Fractal Structures in Yang–Mills Fields
As mentioned above, one of main aspects of the YMF theory, mathematically described by Equation (1), is that it is renormalizable. It means that vertex functions that are regularized to avoid the ultra-violet (UV) divergence are related to the renormalized vertex functions to which renormalized parameters, and , are associated by [13,14]
where is the irreducible truncated vertex function for a particular set of operators, p is the momentum, m the mass, g the coupling constant, D the space-time dimension, and is a scale transformation parameter, i.e., .
We denote with a bar the renormalized quantities. This property is described by the renormalization group equation, also known as Callan-Symanzik (C-S) equation, which is given by [15,16]:
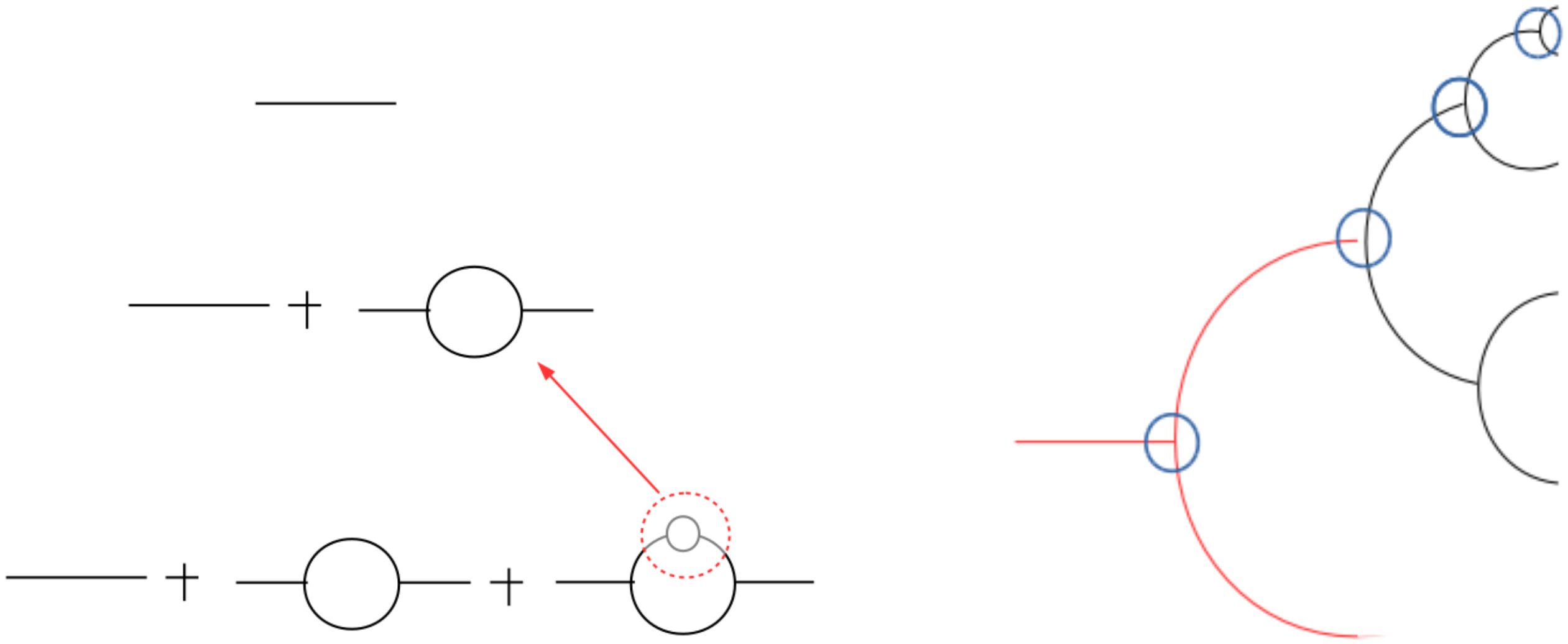
where M is the scale parameter, and the beta function is defined as , and is the anomalous dimension. As it is shown in the left panel of Figure 1, renormalization group invariance means that, after proper scaling, the loop in a higher order graph in the perturbative expansion is identical to a loop in lower orders. This is a direct consequence of the C-S equation, and it is of fundamental importance in what follows.
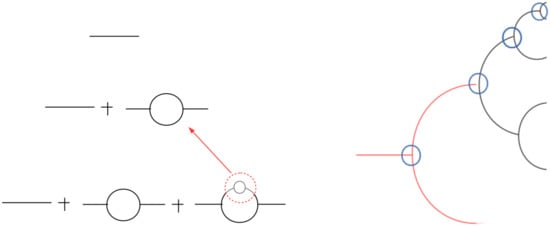
Figure 1.
Left panel: Diagrams showing the scaling properties of Yang–Mills fields. It is shown the loops at different orders in the perturbative expansion. Right panel: Diagrams of multiparticle production in collisions. The initial parton (first black line from the left) may be considered as a constituent of another parton (first red line from the left). The effective vertex couplings, which are given by the second expression in Equation (22) are indicated by circles. The figure in the left panel is taken from ref. [17].
The C-S equation is a specific case, for QCD, of a general equation representing renormalization group invariance, and can be applied to any system where that symmetry is present, thereby all calculations made for the hadronic case apply in a similar form to the Electro-Weak fields. Let us now analyze the possibility of fractal structures to be formed by the Yang–Mills fields.
On the other hand, the scaling symmetry is one of the key ingredients in a fractal system, but not the only one. If we want to show that YMF can form fractal structures, it is important to show that, beside the scaling symmetry it presents an internal structure. The combination between the scaling property and the internal structure will give rise to the self-similarity, a distinguishing aspect of fractals. We will use the perturbative method and the concept of effective parton, that is, a one-particle irreducible representation of the associated quantum field, to show that the effective parton can be understood as a complex system with internal structure. This internal structure will lead to the formation of fractal structures.
It is clear that the fractal structures may be more easily identified in the strongly interacting systems governed by QCD, and in fact, evidences of the fractal structure can be found in the literature already a long time ago. In the 1950’s the existing experimental data on HEC evidenced the formation of a system in thermodynamic equilibrium. Indeed, Fermi proposed a thermodynamic model to describe hadronic collisions at high energies [18]. The main issue then was to explain how a short-lived system (half-life of a few fm/c) could reach equilibrium so fast. This system was called fireball.
A few years later, Hagedorn [19] proposed his self-consistent thermodynamics (SCT) theory that was able to explain several features of hot hadronic systems. His starting point was a rather weird definition for fireballs, stating that:
“A fireball is (*) a statistical equilibrium (hadronic black-body radiation) of an undetermined number of all kinds of fireballs, each o which, in turn, is considered to be (goto *)”.
Notice how the definition of fireball given by Hagedorn resembles that of fractals.
Let us introduce in this section the formalism that will allow us to understand the fractal structure of gauge theories. We will consider that at any scale the system can be described as an ideal gas of particles with different masses, i.e masses might change with the scale. The time evolution of an initial partonic state is given by
where H is the Hamiltonian of the system. The state can be written as , where is a state with n interactions in the vertex function. Each proper vertex gives rise to a term in the Dyson series, and at time t the partonic state is given by
where is the Hamiltonian with the interaction neglected, g represents the coupling constant, and , while runs over all possible terms with n interaction vertices. Let us introduce states of well-defined number of effective partons, , so that
Therefore, , where is the scattering matrix, while and are the mass and momentum of the i partonic state, and represents all relevant quantum numbers necessary to completely characterize the partonic state. These states can be understood as a quantum gas of particles with different masses. Let us remark at this point that the number of particles in the state is not directly related to n, since high order contributions to the N particles states can be important. The rule is , where is the number of particles created or annihilated at each interaction. In Yang–Mills field theory, . We remark that 3- and 4-point contributions are not considered in our approach, since they cannot be renormalized at each order individually, cf. ref. [20].
Let us study the probability to find a state with one parton with mass between and , and momentum between and . This is given by
There are three factors in the rhs of this equation. The first one, , is related to the probability that an effective parton with energy between E and at time will evolve in such a way that at time t it will generate an arbitrary number of secondary effective partons in a process with n interactions. This factor can be written as , where is the probability distribution of the initial particle, and is the probability that exactly n interactions will occur in the elapsed time. The second bracket is the probability to get the configuration with N particles after n interactions, i.e.,
Finally, the last bracket in Equation (12) can be calculated statistically, leading to the following result [17]:
with
where is the Euler Gamma function, is the four-momentum of particle j inside the system of N particles, and is the energy of that particle. Note that we are not assuming a fixed value for the mass of particle j, where , so that and are variables that may change independently of each other. By combining all these results in Equation (12), one finally obtains
where is a parameter that, together with the parameter , determine the characteristics of the thermofractal. Its meaning will be elucidated below. We used, in Equation (16), that for N sufficiently large and , one can approximate . Notice that the total energy of the system formed in high energy collisions is of the order of tens of TeV, while the momentum range considered in most experiments is of the order of tens of MeV. Therefore, we can consider , where this identification of x is motivated in Section 3.2.
As we will show below, the distributions and can be obtained from considerations about self-similarity. Let us mention that relativistic corrections do not play the role of mass variations, as any relativistic correction should keep the rest mass invariant. Notice that going from one level to the next level of the hierarchy of subsystems does not correspond to a Lorentz transformation, but instead to a scale transformation. Then, the four-momenta do not provide themselves the self-similar properties of the system.
3.2. Self-Similarity and Fractal Structure
Due to scale invariance, the energy distribution of a parton, as given by Equation (16), must depend on the ratio , and this ratio must be invariant when we go from one level in the fractal structure to the other. For instance, let us consider that the system with energy E, in which the parton with energy appears as one among N constituents, is itself a parton inside a larger system with energy . Then, the scale invariance, when expressed in terms of the variable , gives
Expressing Equation (16) in terms of this scale-free variable, we have
On the other hand, self-similarity implies that
since the effective partons at any scale have the same probability distribution in terms of the scale-free variable. This relation imposes a strong condition to the probability distribution in Equation (18), since both distributions, in the left-hand side and in the right-hand side, must have the same shape. It is straightforward to conclude that they must follow a power-law function of the form
Substituting the ansatz above into Equation (18), it can be shown that [17]
where , while represents the fraction of total number of degrees of freedom (d.o.f.) of the state that is involved in each interaction, and is a reduced scale, while is the renormalization energy scale of the theory. This probability distribution is a power-law function, and it will be derived, as well, in Section 3.4 for thermofractals, cf. refs. [21,22,23]. An interesting interpretation of the entropic index q arises: it is related to the number of internal d.o.f. in the fractal structure, and the distribution of Equation (21) describes how the energy received by the initial parton flows to its internal d.o.f.. In the context of the theory developed in this section, this probability describes how the energy flows from the initial parton to the partons that appear at higher perturbative orders. Since new orders are associated to new vertices, this suggests that this distribution plays the role of an effective coupling constant in the vertex function, i.e.,
The situation is schematized in the right panel of Figure 1, where the vertex functions that are responsible for the scaling properties of the theory in multiparticle production (see Section 3.6) are shown.
3.3. Effective Coupling and -Function
The C-S equation together with the renormalized vertex functions were used to derive the beta function of QCD, which allowed it to show that QCD is asymptotically free [3,24]. The result at the one-loop approximation is
where and are directly related to the QCD field parameters, as described by the Yang–Mills Lagrangian in Equation (1). Quantitatively, the parameters and are related to the number of colors and flavors by and . In this section, we will study the beta function derived with our ansatz, and compare with that in QCD.
Let us consider a vertex in two different orders, as depicted in Figure 2. The vertex function at first order, i.e., at scale , is
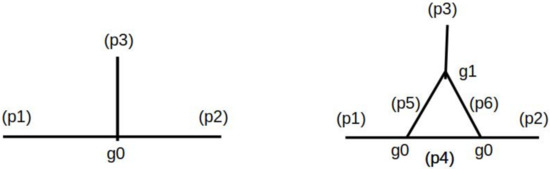
Figure 2.
Vertex functions at scale (left) and (right). Taken from ref. [17].
The next order in the perturbative approximation is given by the vertex with one additional loop at scale , which results in a vertex function
By comparing this expression with , one can identify the effective coupling as
where
The indexes refer to each of the particles created or absorbed during the process as described in the Feynman diagram in Figure 2. The symbol represents the set of quantum numbers necessary to fully characterize the particles, as spin, color, and flavor. The scaling properties of Yang–Mills fields allow us to relate to by an appropriate scale, . From dimensional analysis, the scaling behavior turns out to be . Using these considerations and from the C-S equation, it results that
where and are the anomalous dimensions. In order to compare with the QCD results, we will study the behavior of at , where is a scaling factor. From Equation (22), one has
and, substituting it into Equations (26) and (27), one can calculate the beta function in the one loop approximation. By considering the asymptotic limit , one obtains
with . Finally, by comparing with the QCD result, Equation (23), one can make the identification
where, in the last equality, we used . This result leads to , leading to an excellent agreement with the current experimental data analyses, as it will be discussed in Section 4. Notice that this analysis also predicts that there is some dependence of q on the number of flavors. It would be interesting that this prediction being confronted with experimental q-fits studies.
We notice that the scaling properties used here are necessary conditions to allow the renormalization of the quantum field theory after regularization and are present independently of the renormalization scale used; hence, our results are valid at any value for the scale chosen. In our approach, it becomes evident that the number of flavors gives the scaling dimension of the theory, and it is an essential part of the renormalization procedure, no matter what is the scale used to fix the theory after regularization.
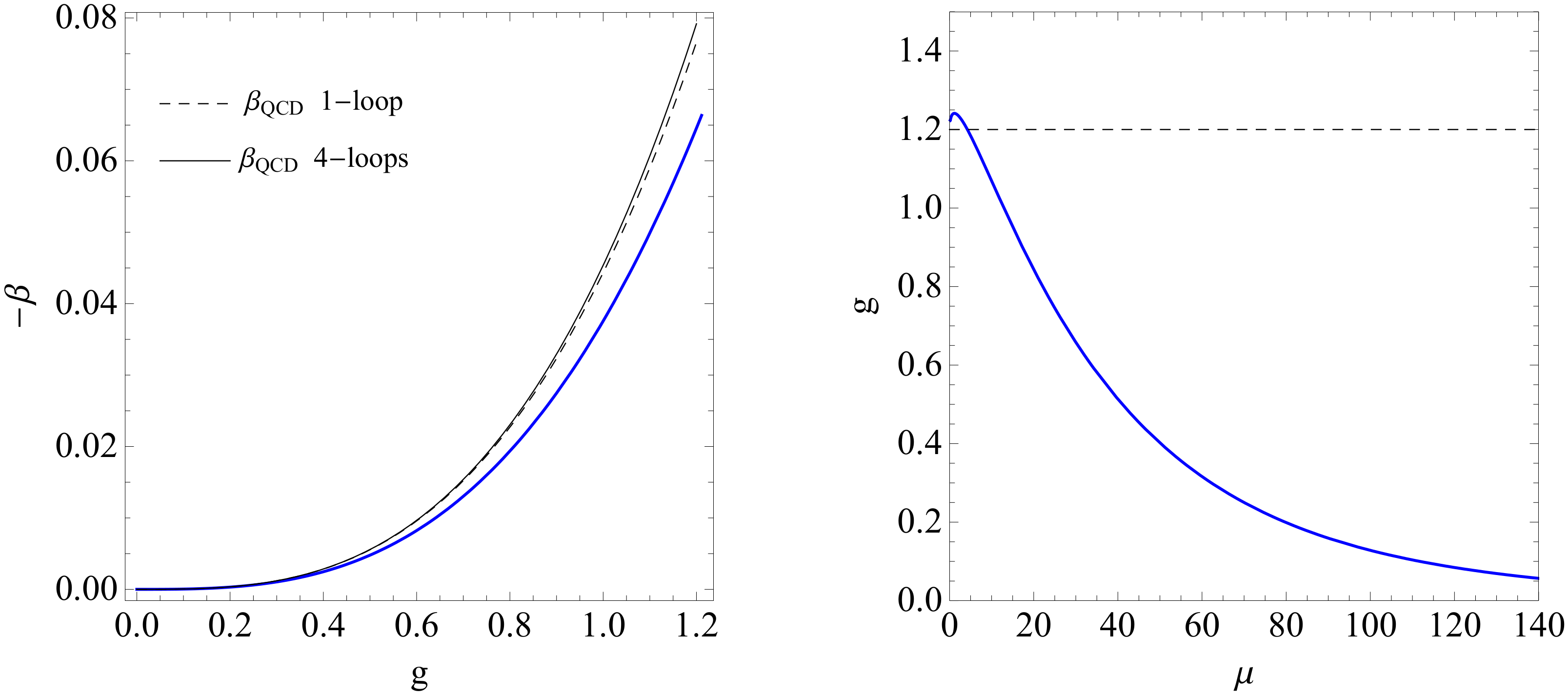
In Figure 3, we display the plots showing the behaviors of the beta function as a function of g, and of the coupling g as a function of . The results obtained here give a strong basis for the interpretation of previous experimental and phenomenological studies on QCD in terms of non-extensive statistics and thermofractals.
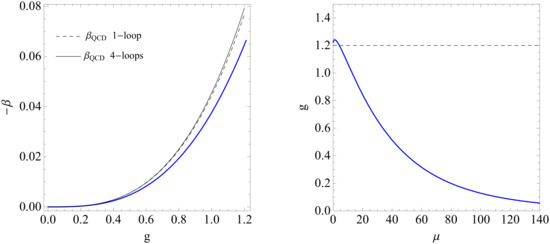
Figure 3.
Left panel: Behavior of beta function against effective coupling, as given by Equation (30). We display also the result from Quantum Chromodynamics (QCD) in one-loop [3] and four-loop [25] approximation. Right panel: Effective coupling as a function of the scale , as calculated by Equation (29). Taken from ref. [17].
Finally, one can see from the result of Equation (30) that values of lead to negative(positive) values of the beta function, i.e., . While we will mainly focus on the case in this manuscript, values are also allowed by the present description, and this corresponds to a YMF with a positive beta function as it follows from Equation (30); this is the case of quantum electrodynamics (QED). This illustrates the fact that the present formalism might have an impact not only in QCD physics but also in research fields like atomic and condensed matter physics.
3.4. Thermofractals
So far, we have shown that, in principle, fractal structures are possible to be formed in YMF. What we have to consider now is the evidence that such structures are really present in the physical systems, and if they play a relevant role in the evolution of those systems in time and in the interactions with other fields. It is easy to observe that evidence of such fractal structure was noticed long time ago.
The Hagedorn’s SCT gave predictions for some quantities that could be easily accessed experimentally. In particular, it predicted the transverse momentum distribution of the particles produced in the decay of the fireball, given by
where g is a constant, V is the volume of the system, , and y is the rapidity. Another prediction was the hadron mass spectrum, given by
where , while and are the parameters.
One interesting aspect of the theory was the prediction of a limiting temperature for the fireball, known today as Hagedorn temperature, , which is numerically equal to the parameter , i.e., . The comparison between theory and experiment brought a sudden recognition of the importance of Hagedorn’s theory, and its impact in HEP is notorious. Frautschi proposed a similar theory-based exclusively in hadron structure, stating that “hadrons are made of hadrons”, again using self-reference [26]. With this so-called bootstrap model, he obtained the same hadron mass spectrum formula shown in Equation (33).
The success of SCT prompted the development of ideal gas models for hadronic systems, the hadron resonance gas (HRG) models [27,28,29,30,31,32,33,34,35,36,37], that were able to explain many features of high energy collisions and hadron physics. Before that, an important paper [38] had explained, through Dyson–Schwinger expansion, how a strongly interacting system could behave under some conditions as an ideal gas of resonant particles.
Another important consequence of SCT came with the advent of the quark structure of hadrons, that was used in ref. [39], to propose that Hagedorn temperature was not a limiting temperature but a transition temperature between the confined quark and the deconfined quark regimes of hadronic matter. The last phase is known as QGP and is one of the most interesting issues in nowadays nuclear physics. Despite its initial success and its important consequences, with the results coming from accelerators able to deliver particles at higher energies than those from existing at that time, it was found that SCT was not able to explain correctly the outcome of the new HEP data. Indeed, Hagedorn himself proposed, in substitution to this thermodynamics theory, an empirical model based on QCD [40]. Since his theory gave so much correct information about hadronic systems, the question imposes itself is: what went wrong with Hagedorn’s theory?
A possible answer to this question is based on the special fractal structure found for YMF, and hence to QCD, which implies in the non-extensive thermodynamics that hadronic systems, and supposedly hadron, may present [21]. Such a fractal structure would result in fractional dimension of the phase-space of the compound particles of the system. Preliminary analysis of such idea lead to a fractal dimension that is compatible with the results from intermittency analyses.
The self-similarity is an evident feature of fireballs and hadrons according to their definitions by Hagedorn and Frautschi, respectively, as described above. However, many other evidences point to the self-similar structure of hadrons: fractal dimension has been identified through the analysis of intermittence in experimental distributions obtained in HEP experiments [41,42,43,44,45,46,47,48,49,50]; a parton distribution function (PDF) that describes the proton structure based on fractal properties was shown to fit experimental data rather well [51]; direct evidences of self-similarity in experimental data has been observed [52], but the so-called z-scaling [53,54] might be related to fractal structures, as well.
The emergence of the non-extensive behavior has been attributed to different causes. These include long-range interactions, correlations and memory effects [55], temperature fluctuations, and finite size of the system, among others. We will show in this section that a natural derivation of non-extensive statistics in terms of thermofractals [17,21] is possible. These are systems in thermodynamical equilibrium presenting the following properties:
- Total energy is given by , where F is the kinetic energy, and E is the internal energy of N constituent subsystems, so that .
- The constituent particles are thermofractals. This means that the energy distribution is self-similar or self-affine, i.e., at level n of the hierarchy of subsystems, is equal to the distribution in any other level, with being a scale-free variable that can be given by in the case of thermofractals of the type-I, or for thermofractals of the type-II.
- At some level of the fractal structure, the internal energy fluctuation is small enough to be disregarded. In this case, the internal energy is considered to be equal to the component mass m.
We denote by and the B-G and thermofractal distributions, respectively. It is possible to show that thermofractals results in energy distributions of the kind
with the negative sign in the exponent corresponding to the type-II thermofractal, while the positive sign corresponds to the type-I. The main difference between thermofractals of type-I and of type-II is the character of the distribution: type-I presents a distribution without cut-off, while type-II requires a cut-off because of the negative sing in the argument of the q-exponential function. As we will see below, q is the entropic index of the Tsallis statistics, while is a scale variable. In what follows, we will consider only the thermofractals of type-I, but the type-II can be derived in the same way [17]. The energy distribution according to B-G statistics is given by
where A is a normalization constant. In the case of thermofractals, the phase space must include the momentum d.o.f. of free particles, as well as internal d.o.f. . Then, the internal energy is where is an exponent to be determined, and one has [21]
with and . This expression relates the distributions at level 0 and 1 of the subsystem hierarchy. After integration, and by imposing self-similarity, i.e.,
the simultaneous solution of Equations (36) and (37) is obtained with [22]
We find that the distribution of thermofractals obeys Tsallis statistics with and . Observe that q is related to the number of d.o.f. that are relevant to the description of the system, and the fact that q is different from unit means that this number is finite. In this aspect, thermofractals can be considered as examples of small systems with finite d.o.f.. In the rest of this manuscript, we will study the connection between thermofractals and quantum field theory, and in particular to QCD.
3.5. Non-Extensive Self-Consistent Thermodynamics
The non-extensive self-consistent thermodynamics (NESCT) is a generalization of the SCT theory by imposing the self-consistency principle from Hagedorn in the non-extensive statistics from Tsallis [56]. The basic ingredients are the two forms of partition function for fireballs proposed by Hagedorn, only this time using the Tsallis q-exponential factor in Equation (38), i.e.,
which leads to
where , and is the density of states of the fireballs as a function of its energy, and
which is the partition function for an ideal gas of fermions and bosons with mass m. The sum in n results from the expansion of the logarithm function, and is related to the fermionic and bosonic mass spectra. In the case , which will be used here, is the hadron mass spectrum.
Since fireballs are thermofractals and present self-similarity, the following weak-constraint must hold:
The main task now is to find functions and that satisfy the equality above and simultaneously let the two forms of partition function identical to each other. This can be achieved [56,57] by choosing
and
where m is the mass of the components of the thermofractal and E is the total energy of the system. With those functions both forms of partition function result in
with
From here, one can see that there is a singularity at , and, therefore, the limiting temperature is found. The singularity at has the same nature as the limiting temperature in Hagedorn’s self-consistent thermodynamics [19], and indicates a limiting temperature for hadronic systems, also known as Hagedorn’s temperature. This limiting temperature was interpreted by Cabbibo and Parisi [39] as the critical temperature for the phase-transition between confined and deconfined regimes of quark matter.
Therefore, it is possible to generalize Hagedorn’s self-consistency principle within Tsallis statistics and as a result one gets a new hadron mass spectrum formula, given by Equation (43), the limiting temperature resulting from the singularity in Equation (45), now expressed in terms of the Tsallis temperature, but also a universal entropic index, q, which is characteristics of any hadronic system. The universality of hadroproduction processes in HEP implies that the value of q is the same disregard the colliding objects (leptons to hadrons to nuclei), a feature already stressed, cf. e.g., refs. [58,59], and widely discussed [60]. It is worthy of mention that both T and q are parameters in the hadron mass spectrum; therefore, they are related to the hadronic structure.
As in the case of the Hagedorn’s theory, cf. Equation (32), here also, the way to test experimentally the predictions of the theory is through the transversal momentum distribution, given by
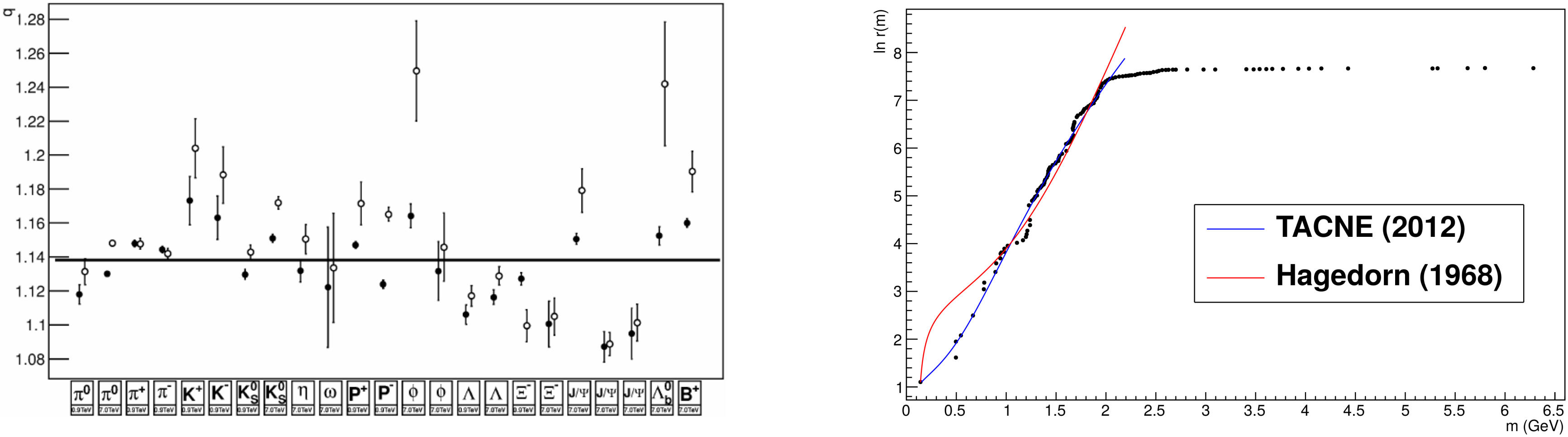
Once the parameters T and q are determined by fitting of Equation (47) to data on distribution, the entire thermodynamics of hot hadronic systems is determined. The extension of the Hagedorn theory to non-extensive statistics, which is characterized by the probability distribution Equation (39), allowed to reproduce the distribution of all the species produced in collisions with a high accuracy, leading to the result [61,62]
(see left panel of Figure 4).Other reactions like , , or collisions show the same behavior [60] (see, e.g., ref. [63], for a recent review). Moreover, the power-law behavior for the hadron spectrum predicted by this extension, cf. Equation (43), can be compared with the hadron spectrum from the Particle Data Group (PDG) [60]. This comparison, as displayed in the right panel of Figure 4, leads to an important improvement with respect to the exponential distribution proposed by Hagedorn, specially at the lowest masses, cf. ref. [61]. Observe that the hadron spectrum given by Equation (43) is valid up to , and we consider above this limit. Similarly the Regge trajectories may relax from the straight lines (see ref. [64] and references therein)). Notice that it would be possible to consider an approximation in the extension of the Hagedorn theory to non-extensive statistics, by using that the product of the functions in Equations (39) and (43) in the partition function can be expressed as
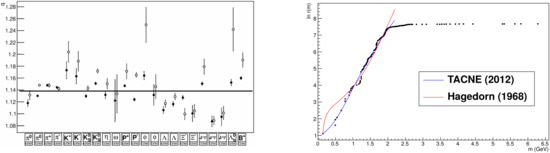
Figure 4.
Left panel: Entropic index, q, obtained from a fit of the abundance of different hadron species in collisions using Tsallis statistics, cf. refs. [61,62]. Right panel: Cumulative hadron spectrum, as a function of the hadron mass. The dots stand for the PDG result [60]. We display also he result by using the non-extensive self-consistent thermodynamics (blue) and the result predicted by Hagedorn (red), cf. ref. [61].
This leads to a good fit of observables as long as .
Finally, let us mention that it is possible to obtain any thermodynamics quantity and compare it to Lattice QCD (LQCD) results. A comparison between the results from NESCT and LQCD data has shown also a good agreement between both calculations [65], in this case without any adjustable parameter. Apart from these considerations, there are many other applications in which Tsallis statistics play an important role. This includes high energy collisions [62,66,67,68], hadron models [69], hadron mass spectrum [61], neutron stars [70], LQCD [65], non-extensive statistics [22,56,57], and many others. In the rest of the manuscript, we will see that the power-law behavior of Tsallis statistics leads, in fact, to important phenomenological consequences in these fields.
The theory presented here can be extended to collisions, as long as collective motion of the QGP fluid is taken into account [71]. The analyses of experimental data from HEP give room to some small variation of the entropic index, q, and for the temperature, , with collision energy and/or particle species [72], and the variation is larger for small multiplicity events. The variation can, in principle, be due to non-equilibrium processes, where perturbative QCD should be applied. In fact, as the multiplicity increases, the results seem to be independent from collision energy, and remain valid for , , and collision [73]. The use of non-extensive thermodynamics is important for the precise determination of the character of the phase transition between confined and deconfined states of the QCD matter [74,75].
We mentioned above that q and are related to the number of d.o.f. in the system. In the context of the fractal structure exhibited by the YMF, q is related to the number of relevant d.o.f. involved in the transfer of energy and momentum between interacting systems. Thus, regarding the general applicability of the theory, we observe that the most complex case was considered here, i.e., the case where the full phase-space is occupied and all possible field configurations, for both fermions and bosons, are allowed. These conditions seem to be valid for QGP, but for simpler systems, where the total quantum numbers are restricted enough or when topology does not allow the complete phase space to be occupied, as it may happen in, e.g., deep inelastic scattering or in high energy particles scattering, the q value may change accordingly. Recent experimental data show, indeed, that for high multiplicity events the q value tends to a universal value in good agreement with the one found here [76]. This universality is also manifest when considering other effects like e.g. eccentricity and flows [77].
3.6. Multiparticle Production
An interesting physical situation in which the scaling properties emerge is in multiparticle production in collisions [78]. We show in the right panel of Figure 1 a typical diagram in which two partons are created in each vertex. When effective masses and charges are used, the line of the respective field in Feynman diagrams represents an effective particle. An irreducible graph represents an effective parton, and the vertices are related to the creation of an effective parton. Due to the complexity of the system, it is desirable a statistical description in which the summation of all the diagrams becomes equivalent to an ideal gas of particles with different masses [38,79]. Another example is given by the hadron structure: As in the case of multiparticle production, too many complex graphs should be considered when studying the hadron at a high resolution. This is why calculations are typically limited either to the first leading orders, or to LQCD methods.
3.7. Non-Extensive Thermodynamics of Thermofractals
As we have seen above, the properties of the YMF can lead to the formation of fractal structures, and the thermofractal systems show us that the thermodynamics formalism that describes YMF fractal structure is the Tsallis statistics. In QCD, such fractal aspects appear in the generalized version of Hagedorn’s thermodynamics, which was described by the NESCT approach. In this section, we will describe some of the main aspects of the thermofractal system, since most of its characteristics are important for applications in hadron models and on the description of massive objects, as neutron stars, through the Tsallis statistics. We will present here the thermodynamics of a free quantum gas of bosons and fermions at finite temperature and chemical potential within Tsallis statistics.
We will define two versions of the q-exponential and q-logarithm functions as follows:
where in stands for , and stands for . The two versions of the functions in Equation (50), denoted by and , are in general needed when considering finite chemical potential. Notice that and , where and were defined in Equations (4) and (6), respectively. Then, the grand-canonical partition function for a non-extensive ideal quantum gas is given by [57]
where , the particle energy is , with m being the mass and the chemical potential, for bosons and fermions, respectively, and is the step function. Note that and , so that Tsallis statistics reduces to B-G statistics in the limit . As originally introduced in the literature, the and functions do not satisfy the Kubo-Martin-Schwinger (KMS) relations and show a break in the second derivatives at the Fermi surface (see ref. [80] and references therein). This issue was solved in ref. [57] by the introduction of some terms in the average number of particles, , and average energy, , that appear by taking the derivatives of the partition function of Eq. (51) with respect to and T, after performing the momentum integral. Later on, this gap was studied in detail in the search for physical significance [81,82].
The thermodynamics of Tsallis statistics which follows from Equation (51) has been used to successfully describe the thermodynamics of QCD in the confined phase by using the hadron resonance gas approach, with applications in high energy physics [57], hadron physics [83], and neutron stars [70].
4. Application and Results
In this section, we will describe how the theory presented in Section 3 can describe many aspects of QCD as observed in different physical situations, in particular in HEP. The main result we obtained from the theory is an analytic formula for the effective coupling constant in the non-perturbative regime, which follows as a consequence of the fractal structure. The effects of fractality of the YMF extend to other aspects, as the power-law behavior of the HEC distribution, which are described by Tsallis statistics and allow to access experimentally the value of the entropic index, q, that results to be in very good agreement with the value found by the theory. We describe some aspects of the coupling constants and beta-function.
4.1. Transverse Momentum Distributions
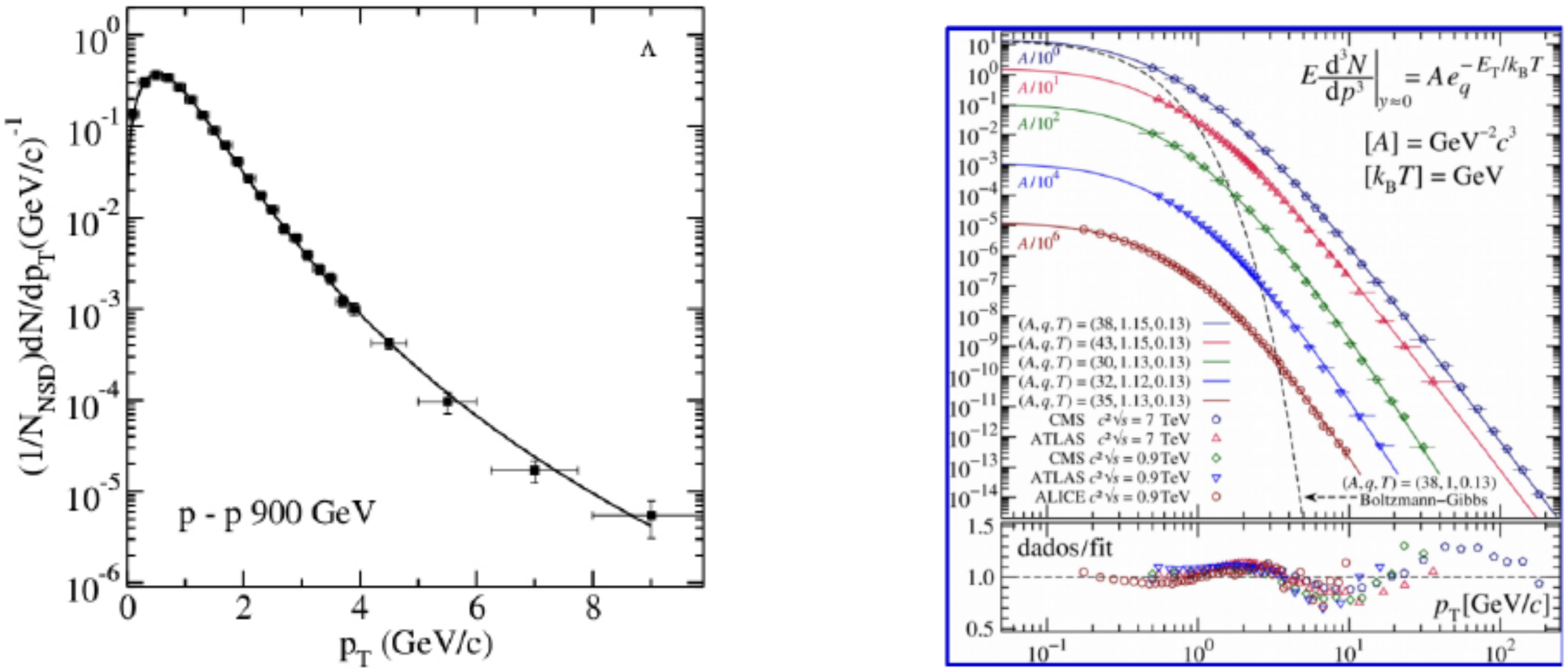
The predictions of NESCT have been compared with HEP experimental data for distributions (Equation (47)), showing a good agreement between calculation and data [61,66,84,85,86], resulting in and MeV. In addition, the hadron mass spectrum formula has been used to describe the known hadronic states, resulting again in a very good agreement with data and leading to values of q and T very similar to those obtained with analysis [61]. An example of fitting to distribution is shown in Figure 5 (left).
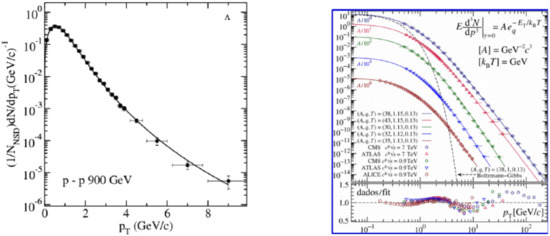
Figure 5.
Left panel: An example of fit of the calculated distribution to experimental data. Right panel: Fitting of the distribution formula to experimental data. Notice that the formula can fit well data over 15 orders of magnitude.
Careful fittings of distribution power-law formulas to high statistics data have shown some oscillations in the ratio between calculated and experimental data, which has already being attributed to fractal aspects of the hadronic interaction [87], as shown in Figure 5 (right). Notice also the wide range of experimental data that can be fitted with power-law formula. This may indicate that there are non-equilibrium events that are produced without the formation of a thermodynamically equilibrated system, but the multiplicity for such events must be smaller than 5. More investigations in this direction would be welcome.
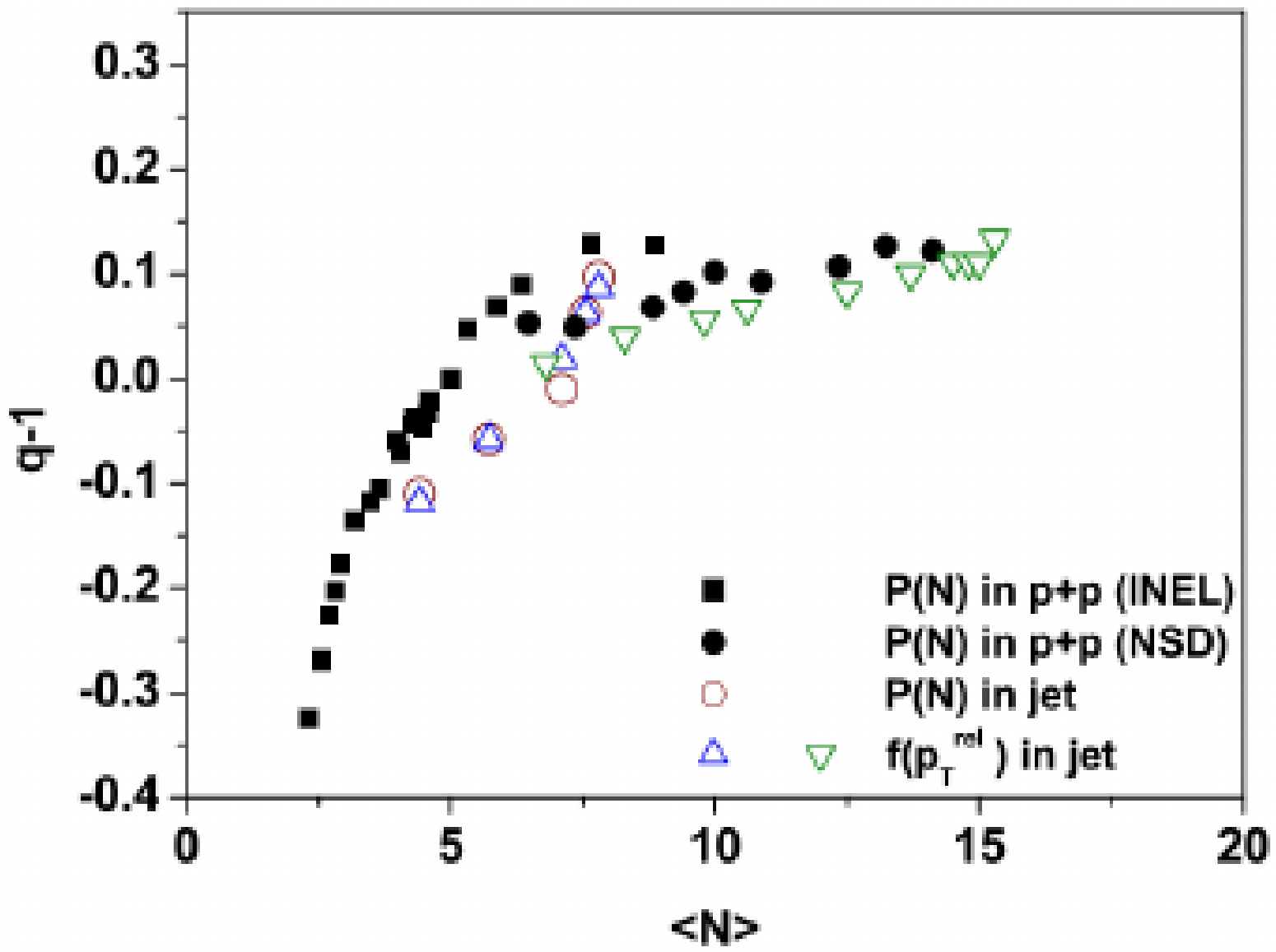
It is interesting the fact that the distributions for all particles produced in collisions at different energies can be described by roughly the same values for the parameters T and q of the non-extensive thermodynamics, as shown in ref. [61], cf. left panel of Figure 4. However, a study of the best fitted values for those parameters as a function of the multiplicity has shown that the parameters can be considered constant only for events with multiplicity larger than 5 or 6, as shown in the Figure 6.
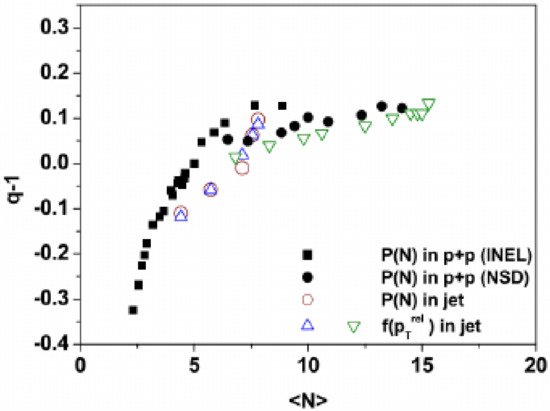
Figure 6.
Behavior of the parameter q as a function of multiplicity. It indicates the self-similarity between the system formed at high energy collisions and the jets produced by that system. In addition, it may indicate the region of multiplicity where particle production without the formation of an equilibrated system is relevant. Figure taken from ref. [88].
Another interesting aspect of the results shown in the Figure above is that there is a clear self-similarity in the distributions of particles and jets in relation to the beam direction, but there is also the same distribution for particles forming a jet in relation to the jet direction [88]. This is maybe the most direct experimental evidence of self-similarity in HEP and should be studied in more detail and with better statistics.
4.2. Rapidity Distributions
The use of the non-extensive thermodynamics allows a simple description of most of the data from HEP. In addition to the distribution described with just two parameters that have the same value for any secondary particle and any collision energy, also the rapidity distribution can be described by a simple model which includes other two parameters to describe the movement of two fireballs going apart after the collision. The two parameters are the position and width of two Gaussian functions describing the movement of those two fireballs. The two Gaussians are supposed to present some symmetries, so they can be described by only two parameters. Such model was presented in ref. [62], and the results show that the parameters for those Gaussian are also approximately constant for different collision energies for the range considered in that work, as shown in figures below. In the same work, predictions for particle production in collisions at 13 GeV were made, but, up to now, those predictions were not confronted with experimental data.
4.3. Intermittency
One of the most used techniques to unveil fractal dimensions from measured distributions is the intermittency method, that we briefly describe below. Consider the collision of two systems, each of which may be a lepton, a hadron, or a nucleus. Let be the rapidity (y) distribution of particles produced in an event at high energy. We focus our attention on a narrow window of width . The averaging over many similar windows is a process that can be considered later for the purpose of increasing the experimental statistics but should be put aside for the present. Let k denote the number of particles detected in in one event. Obviously, k will fluctuate from event to event. Let be the number of times that the multiplicity k recurs in events. Note that is not normalized, so it is not a distribution. Define [41,42]
where
The normalized moments are
where is the momentum order. Another useful quantity is defined by [43]
where
The probability
represents the probability to have an event with particles in the window with width . For sufficiently small, the behavior of this probability with is
The moments or depends on as
where is known as fractal spectrum. In addition,
therefore, . Note that we can make the identification
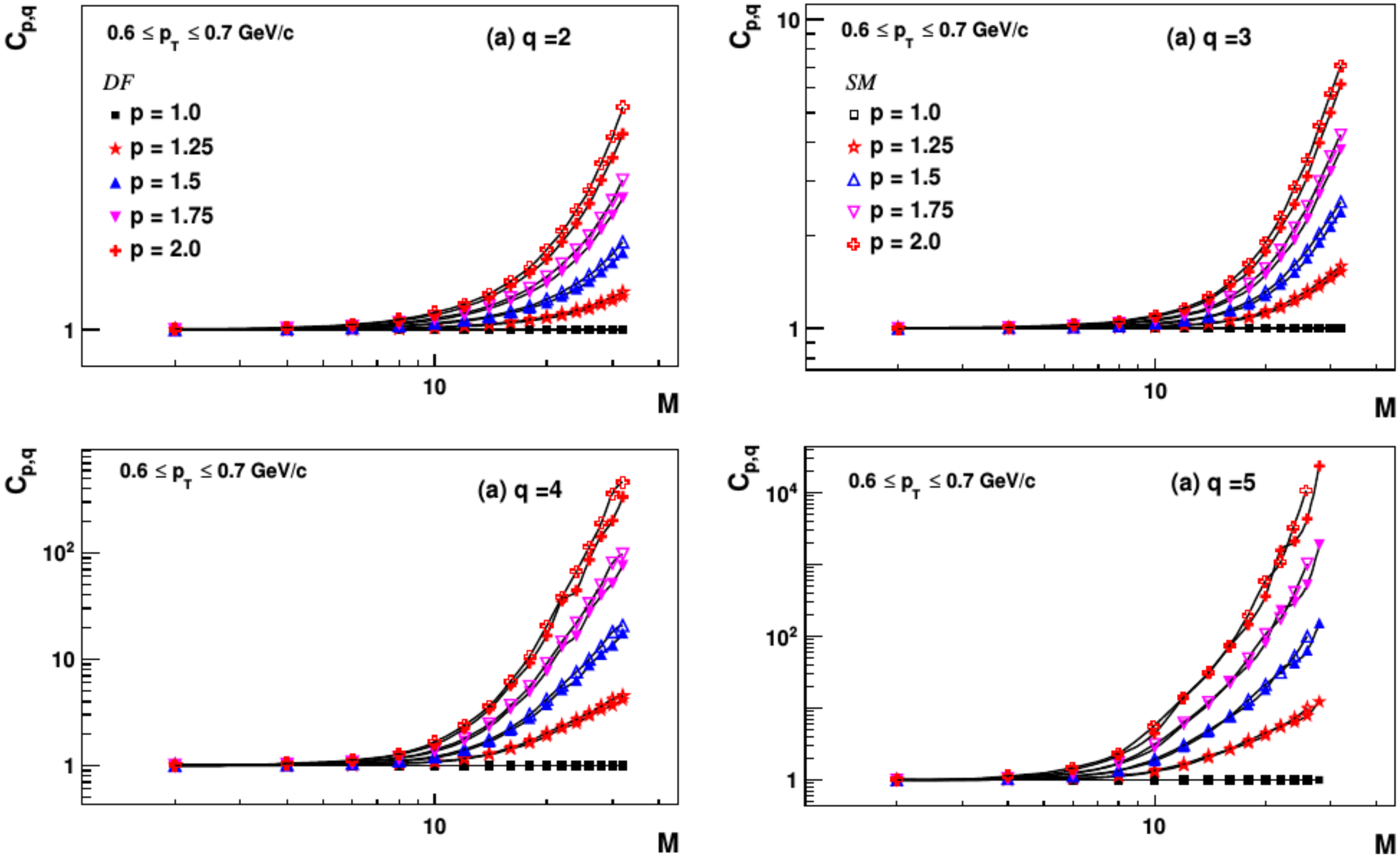
where is the Hausdorff dimension at order q. The advantage of the second momentum is that it is not calculated for each event, but to a collection of events. A nice description of the experimental approach to the relevant quantities is given in [89]. A typical result of such analysis is shown in Figure 7 and Figure 8. In Figure 7, the cumulative moments (also called fractality moments) are displayed as functions of , where is the number of bins in which the range of momenta is considered in the distribution, and is the bin width. The -dependence of seems to be close to a power-law behavior in , so that one can also define the scaling exponent as
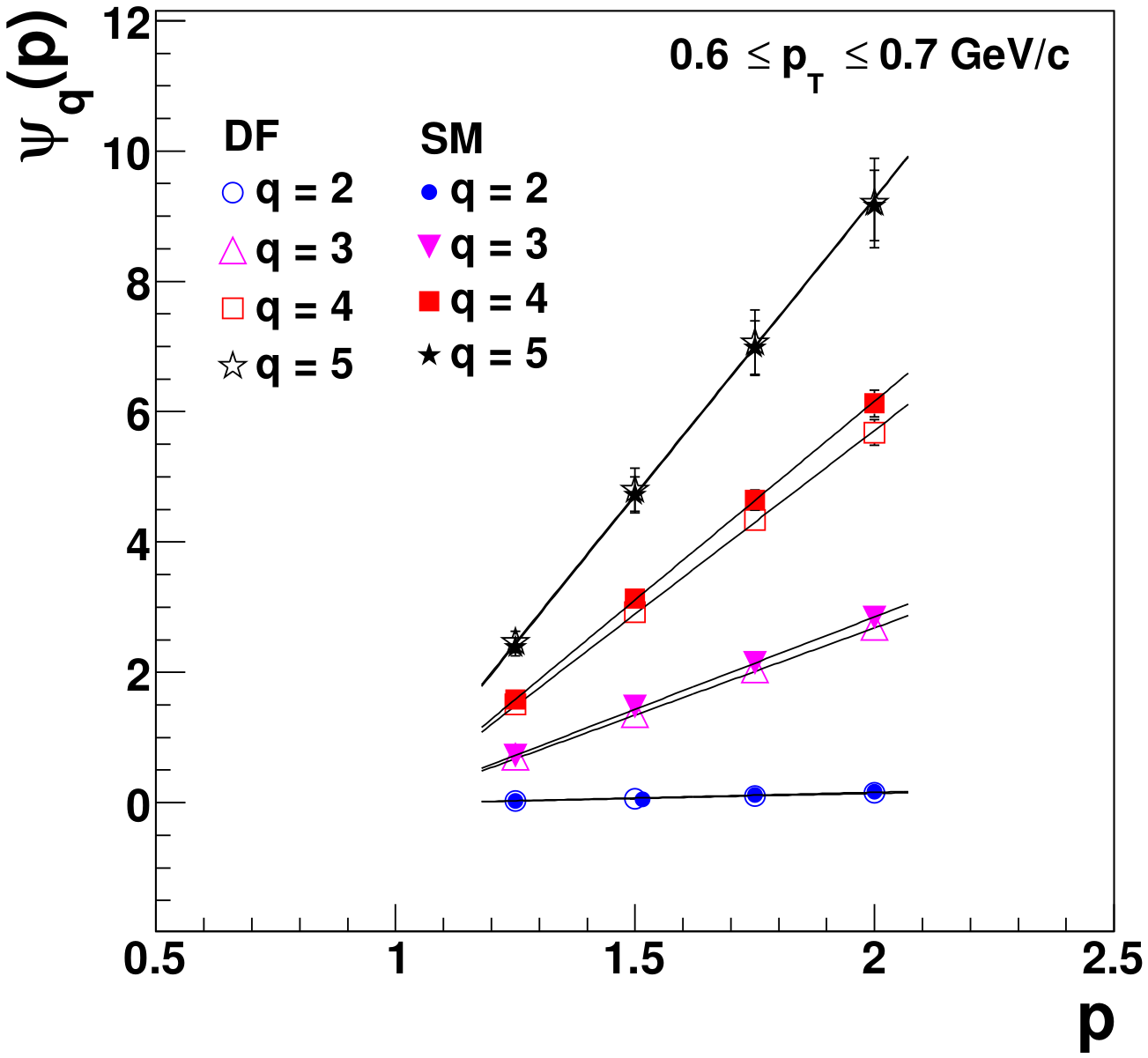
which is referred to as erraticity. In Figure 8 it is shown that the dependence of with the momentum is linear for each value of q.
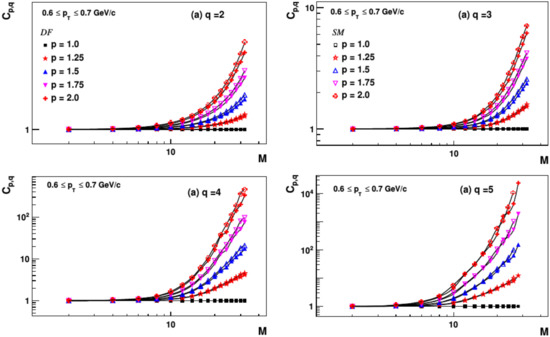
Figure 7.
Analysis of moments in intermittency study for the window , cf. ref. [90].
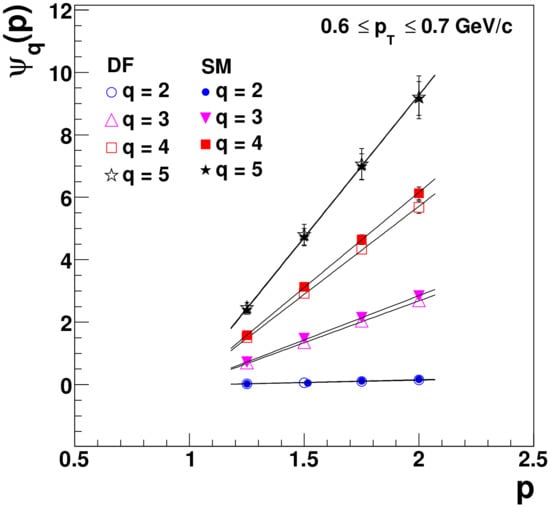
Figure 8.
defined in Equation (62) as a function of the momentum in intermittency study for the window , cf. ref. [90].
From the thermofractal structure one can obtain the fractal dimension of hadrons, what was done in ref. [21], resulting in , a value that is close to that resulting from intermittence analysis, around [91,92,93,94,95,96]. For a more complete description of intermittency and its application to HEP, see refs. [49,50].
4.4. Tsallis Statistics and QCD Thermodynamics
The thermodynamics of QCD in the confined phase can be studied within the HRG approach, which is based on the assumption that physical observables in this phase admit a representation in terms of hadronic states which are treated as non-interacting and point-like particles [27]. These states are taken as the conventional hadrons listed in the review by the PDG [60]. Within this approach, the partition function is then given by [57,70]
where is the partition function of a non-extensive ideal quantum gas given by Equation (51), q is the entropic index, and refers to the chemical potential for the i-th hadron.
The thermodynamic functions can be obtained from Equation (63) by using the standard thermodynamic relations. There are different proposals for the conditions determining the transition line between the confined and the deconfined regimes of QCD. Using the arguments of [29], the phase transition line in the diagram, with the baryonic chemical potential, can be determined by the condition , where the brakets stand for thermal expectation values. A different method based on the entropy density has been proposed in [97]. The result for the chemical freeze-out line is displayed in Figure 9 (left). The transition line determines the region where the confined states exist (below the line), and the region where one expects to find the quark-gluon plasma (above the line). We observe in this figure that the freeze-out line spams over the region of with a maximum value for corresponding to a null critical temperature. The curves show an inflection for which is related to the sharp increase in the baryon density as the baryonic chemical potential approaches the proton/neutron mass . A similar behavior is observed in Boltzmann–Gibbs statistics. For the effective temperature is for , which is not in full agreement with the value found in the analysis of the -distributions [61]. This disagreement can be related to the value adopted for , which still must be checked by analysis of experimental data with the non-extensive statistic. In order to provide an estimate of the sensitivity of the value of when changing q it is worth mentioning that the effective temperature for a slightly smaller value of the entropic index, , is , which is in much better agreement with the -distribution analysis. We also display in Figure 9 (right) the Equation of State (EoS) for hadronic matter at finite baryonic chemical potential. It it remarkable that becomes larger in Tsallis statistics as compared to B-G statistics (see a discussion in [57,70]). These thermodynamic studies lead to the natural value , which is in accordance with many previous analysis, like the results from collisions and the beta function of QCD studied above.
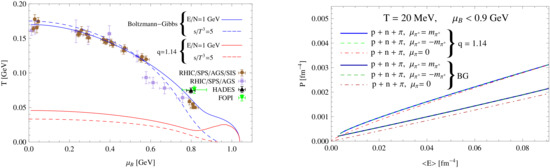
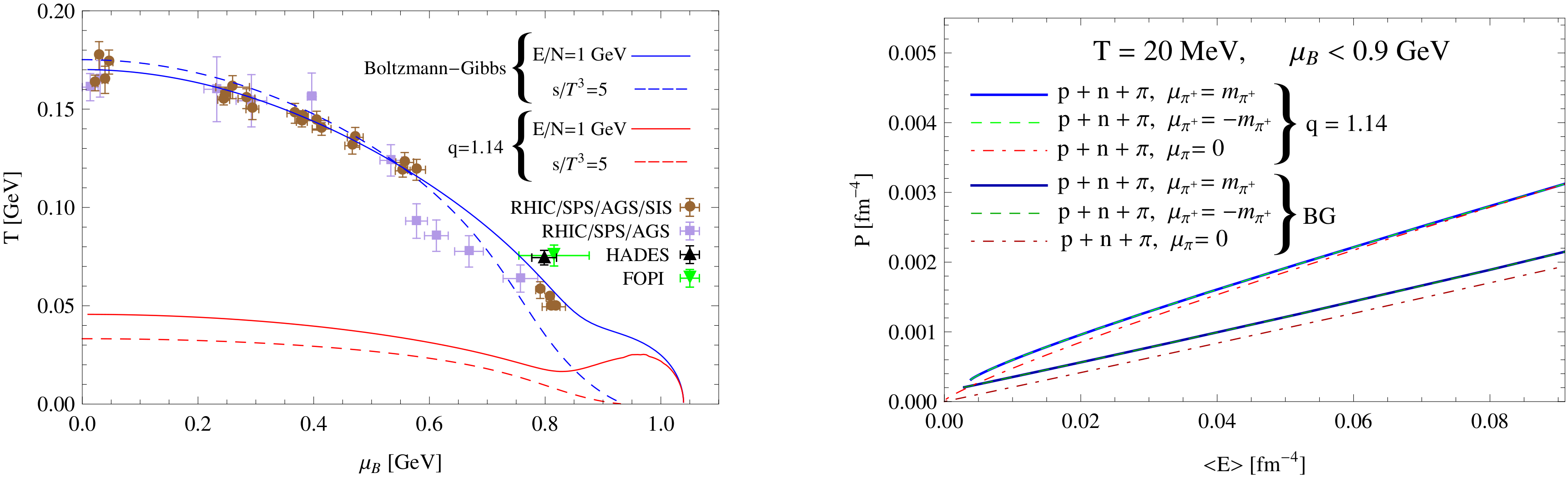
Figure 9.
Left panel: Chemical freeze-out line obtained by assuming (continuous lines) and (dashed lines). We plot the result by using Boltzmann–Gibbs statistics, and Tsallis statistics with . Experimental data are taken from: Relativistic Heavy Ion Collider (RHIC) /SPS /Alternating Gradient Synchrotron (AGS) /SIS, [98], RHIC/SPS/AGS [99],HADES [100], and FOPI [101]. Right panel: EoS of hadronic matter. Figure taken from ref. [57].
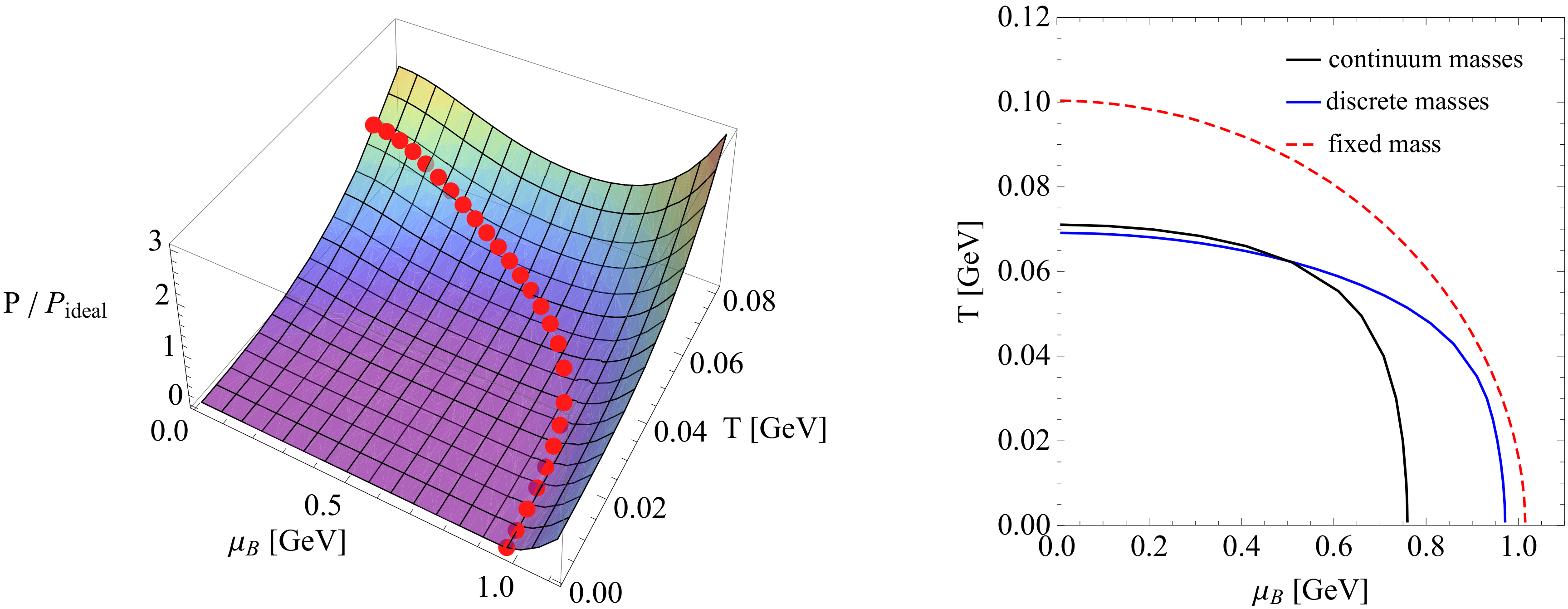
The QCD thermodynamics has been studied, as in ref. [83], by using Tsallis statistics within the Massachusetts Institute of Technology (MIT) bag model. This allowed to investigate the underlying fractal structure of hadrons, leading to the emergence of non-extensivity of the hadronic thermodynamics. The thermodynamic quantities have been studied in the approximation of fixed mass for all bag constituents, but also within the discrete mass approximation given by the PDG spectrum [60], as well as the continuum spectrum provided by the NESCT through Equation (43). The conclusion is that the continuum spectrum scenario fully applied the hypothesis that the hadron bag is an ideal gas of strongly interacting particles, and this corresponds to the picture of the hadrons as thermofractals. It is displayed in Figure 10 the regime in the phase space in which the proton exists as a bound particle, i.e., . The results in the three scenarios mentioned above are displayed in the left panel of this figure.
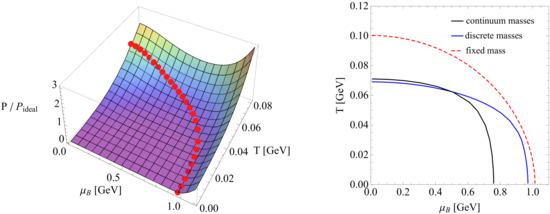
Figure 10.
Left panel: Pressure (normalized to the ideal gas limit) as a function of temperature and baryonic chemical potential in the case of a non-extensive gas with particles with discrete masses. Red dots indicate the region where the gas total energy inside a volume is equal the proton mass, i.e., . Right panel: Temperature as a function of baryonic chemical potential for a non-extensive gas within the constraint . For comparison, the results are displayed in three different scenarios: (i) continuum masses, (ii) discrete masses, and (iii) fixed mass. It is considered the value in both panels. Left panel taken from ref. [83].
4.5. Discussion
The theoretical method developed above allows us to understand on solid grounds the emergence of Tsallis statistics in HEC. The predictions of the theory find support on experimental data available, and can explain, in a single theoretical framework, many aspects of the HEP and of the hadronic systems. The effective coupling obtained from considerations about scale symmetry of the YMF shows how four-momentum imparted to one effective parton is distributed among its internal d.o.f., which are, themselves, associated to new effective partons created in the interactions between the fields.
The description of the results from high energy collisions by thermodynamics methods is interesting by itself because of possible applications in Astrophysics and in Cosmology. In fact, a description of baryogenesis in the early universe must necessarily take into account the properties of the phase transition between confined and deconfined regimes of the hadronic matter.
The extension of the NESCT to systems with finite chemical potential [57] has allowed the application of the thermodynamics properties of hadrons to the study of neutron stars (NS) [70,102]. While high energy collisions take place at high temperatures and low chemical potentials, protoneutron and NS are characterized by high chemical potentials and low temperatures, in a completely different region of the QCD phase diagram. When applied to describe these compact objects, the Tsallis statistics results on a very small change in the main macroscopic properties, as maximum mass and radius, but we found that the internal temperature of the stars decreases with the increase of the q-value (taken within a reasonable range) and, around the star central densities the temperature decreases by approximately 25% in average. This aspect may have important consequences when the star evolves from a hot and lepton rich object to a cold and deleptonized compact star. Moreover, the direct Urca process is substantially affected by non-extensivity, with probable consequences on the cooling rates of the stars. Notice that some authors have considered to study NS [102]. However, in this case the stellar maximum masses decrease with respect to the B-G statistic analysis, so that in subsequent studies the case only was taken into account. Besides NS constituted of hadrons, strange stars constituted of deconfined quarks were analyzed with a simple model [69]. The conclusions discussed above were all corroborated and the construction of the QCD phase diagram first order transition has shown that the limiting curve is quite sensitive to non-extensivity. An investigation with a model that allows the calculation of the critical end point (CEP) remains to be done.
The interpretation of the power-law distributions by the thermofractal structure offers the possibility to connect such structure to QCD properties, as shown in ref. [21]. Finally using the blast-wave approach to the expansion of the quark-gluon plasma, one can extend the present thermodynamics theory so as to apply to the problem of high energy nucleus-nucleus collisions, as well, for which there is a large number of accurate data [103].
Finally, the hadron structure can benefit from the theory presented here. In fact, some models have already used Tsallis statistics as a way to introduce the fractal aspects of the QCD in the description of hadron structure [83].
5. Conclusions
In this work, we reviewed the applications of Tsallis statistics to HEP, hadron physics, and astrophysics. We have investigated the structure of a thermodynamical system presenting fractal properties showing that it naturally leads to Tsallis non-extensive statistics. Based on the scaling properties of gauge theories and thermofractal considerations, we have shown that renormalizable field theories lead to fractal structures, and these can be studied with Tsallis statistics. By using a recurrence formula that reflects the self-similar features of the fractal, we have computed the effective coupling and the corresponding beta function. The result turns out to be in excellent agreement with the one-loop beta function of QCD. Moreover, the entropic index, q, has been determined completely in terms of the fundamental parameters of the field theory. Finally, the result for q is shown to be in good agreement with the value obtained by fitting Tsallis distributions to experimental data. These results give a solid basis from QCD to the use of non-extensive thermodynamics to study properties of strongly interacting systems and, in particular, to use thermofractal considerations to describe hadrons. In the last part of the manuscript we have discussed the experimental results on transverse momentum and rapidity distributions in collisions that provide a solid basis to study the role of Tsallis in HEP, as well as a discussion of some applications including the QCD thermodynamics, the QCD phase diagram and the physics of proto(neutron) stars.
From what was discussed here, one can see that there are still many open questions regarding the description of HEP data by power-law distributions. The main problem is to verify to what extent the idea of fractal structure can describe experimental data. In this regard, not only the distributions must be carefully analyzed, but also other quantities, mainly the fractal dimension that can be accessed through intermittency analysis. Although this analyses are still performed for HEP collisions on emulsion, no such analysis was performed with LHC data. Aside intermittency, the study of the parameters T and q as a function of multiplicity can shed some light on the discussion about the nature of the power-law distributions: is it due to a thermodynamical system in equilibrium or is it motivated by QCD aspects? If it is shown with accuracy that for multiplicities larger than 5 or 6 the values are constant, as predicted by the thermodynamical theory, this would favor the thermodynamics interpretation. The same analysis would allow for a discussion on the self-similarity in experimental data, as already discussed above.
One should keep in mind that the value for the entropic index, , obtained from the QCD parameters is a constant related to the fundamental parameters of the QCD, namely the number of colors and number of flavors. However, the assumption that the configuration space for any effective parton is completely available holds only under some special situations, as those found in HEP collisions. Whenever further constraints in the possible color and flavor, or even topological restrictions of the momentum space, are present, the number of d.o.f. will vary and therefore also the value for q observed in those situations. The effects of constraints are more evident when the particle multiplicity is small, or when experimental setup is such that just specific particle configurations are selected. Such cases can happen at low energy collisions and in very peripheral collisions.
The rapidity distribution can be further analyzed, and the predictions made for collisions at 13 GeV can be compared with the data already measured at that energy. In addition, the theory can be extended to account for nucleus-nucleus collision, with the inclusion of the blast-wave model in the thermodynamical description, allowing for the analysis of data. In summary, the interesting analysis that could be made with recent experimental data are (initially for but eventually also for ):
- Analysis of distribution with high statistics, obtaining the behavior of T and q as a function of multiplicity for different particles.
- Investigation of self-similarity in jet and secondary particle distributions.
- Investigation of the rapidity distribution as predicted with the theory, and also of the distributions for 13 GeV.
- Investigation of intermittency in HEP data from LHC.
These and other issues will be addressed in a forthcoming publication.
Author Contributions
Conceptualization, A.D.; methodology, A.D., E.M. and D.P.M.; software, A.D. and E.M.; validation, A.D. and E.M.; formal analysis, A.D. and E.M.; investigation, A.D., E.M. and D.P.M.; resources, A.D. and E.M.; data curation, A.D. and E.M.; writing—original draft preparation, A.D., E.M. and D.P.M.; writing—review and editing, A.D., E.M. and D.P.M.; visualization, A.D. and E.M.; supervision, A.D.; project administration, A.D. and E.M.; funding acquisition, A.D., E.M. and D.P.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research of A.D. and D.P.M. were funded by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq-Brazil) and by Project INCT-FNA Proc. No. 464898/2014-5, and by FAPESP under grant 2016/17612-7 (A.D.). The work of E.M. is funded by the Spanish MINEICO under Grant FIS2017-85053-C2-1-P, by the FEDER Andalucía 2014-2020 Operational Programme under Grant A-FQM-178-UGR18, by Junta de Andalucía under Grant FQM-225, by the Consejería de Conocimiento, Investigación y Universidad of the Junta de Andalucía and European Regional Development Fund (ERDF) under Grant SOMM17/6105/UGR, and by the Spanish Consolider Ingenio 2010 Programme CPAN under Grant CSD2007-00042. The research of E.M. is also supported by the Ramón y Cajal Program of the Spanish MINEICO under Grant RYC-2016-20678.
Acknowledgments
We would like to thank Constantino Tsallis for suggesting us to write this review.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, C.N.; Mills, R.L. Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 1954, 96, 191–195. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M. Regularization and renormalization of gauge fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- Politzer, H.D. Asymptotic freedom: an approach to strong interactions. Phys. Rep. 1974, 14, 129–180. [Google Scholar] [CrossRef]
- ’t Hooft, G. 50 Years of Yang–Mills Theory; World Scientific: Hackensack, NJ, USA, 2005. [Google Scholar]
- Batty, M.; Longley, P. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK, 1994. [Google Scholar]
- West, G. Scale, The Universal Laws of Life, Growth, and Death in Organisms, Cities, and Companies; Penguin Books: New York, NY, USA, 2018. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1983. [Google Scholar]
- Tempesta, P. Group entropies, correlation laws and zeta functions. Phys. Rev. E 2011, 84, 021121. [Google Scholar] [CrossRef] [PubMed]
- Kalogeropoulos, N. Groups, nonadditive entropy and phase transitions. Int. J. Mod. Phys. B 2014, 28, 1450162. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive statistical mechanics: a brief review of its present status. Anais da Academia Brasileira de Ciências 2002, 74, 3. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Dyson, F.J. The S-matrix in quantum electrodynamics. Phys. Rev. 1949, 75, 1736–1755. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Low, F.E. Quantum electrodynamics at small distances. Phys. Rev. 1954, 95, 1300–1312. [Google Scholar] [CrossRef]
- Callan, C.G., Jr. Broken scale invariance in scalar field theory. Phys. Rev. D 1970, 2, 1541–1547. [Google Scholar] [CrossRef]
- Symanzik, K. Small distance behavior in field theory and power counting. Commun. Math. Phys. 1970, 18, 227–246. [Google Scholar] [CrossRef]
- Deppman, A.; Megias, E.; Menezes, D.P. Fractals, non-extensive statistics and QCD. Phys. Rev. D 2020, 101, 034019. [Google Scholar] [CrossRef]
- Fermi, E. High-energy nuclear events. Prog. Theor. Phys. 1950, 5, 570–583. [Google Scholar] [CrossRef]
- Hagedorn, R. Statistical thermodynamics of strong interactions at high energies. Nuovo Cim. Suppl. 1965, 3, 147–186. [Google Scholar]
- Prochazka, V.; Zwicky, R. Finiteness of two- and three-point functions and the renormalization group. Phys. Rev. D 2017, 95, 065027. [Google Scholar] [CrossRef]
- Deppman, A. Thermodynamics with fractal structure, Tsallis statistics and hadrons. Phys. Rev. D 2016, 93, 054001. [Google Scholar] [CrossRef]
- Deppman, A.; Frederico, T.; Megias, E.; Menezes, D.P. Fractal structure and non-extensive statistics. Entropy 2018, 20, 633. [Google Scholar] [CrossRef]
- Deppman, A.; Megias, E. Fractal structure in gauge fields. Physics 2019, 1, 103. [Google Scholar]
- Gross, D.J.; Wilczek, F. Asymptotically free gauge theories. II. Phys. Rev. D 1974, 9, 980–993. [Google Scholar] [CrossRef]
- Czakon, M. The Four-loop QCD beta-function and anomalous dimensions. Nucl. Phys. B 2005, 710, 485–498. [Google Scholar] [CrossRef]
- Frautschi, S.C. Statistical bootstrap model of hadrons. Phys. Rev. D 1971, 3, 2821–2834. [Google Scholar] [CrossRef]
- Hagedorn, R. How We Got to QCD Matter from the Hadron Side: 1984. Lect. Notes Phys. 1985, 221, 53–76. [Google Scholar]
- Yukalov, V.I.; Yukalova, E.P. Thermodynamics of strong interactions. Phys. Part. Nucl. 1997, 28, 37–65. [Google Scholar] [CrossRef][Green Version]
- Cleymans, J.; Redlich, K. Chemical and thermal freezeout parameters from 1A to 200A GeV. Phys. Rev. C 1999, 60, 054908. [Google Scholar] [CrossRef]
- Agasian, N.O. Nonperturbative vacuum and condensates in QCD below thermal phase transition. Phys. Lett. B 2001, 519, 71–77. [Google Scholar] [CrossRef]
- Tawfik, A. QCD phase diagram: a comparison of lattice and hadron resonance gas model calculations. Phys. Rev. D 2005, 71, 054502. [Google Scholar] [CrossRef]
- Megias, E.; Ruiz Arriola, E.; Salcedo, L.L. Trace anomaly, thermal power corrections and dimension two condensates in the deconfined phase. Phys. Rev. D 2009, 80, 056005. [Google Scholar] [CrossRef]
- Huovinen, P.; Petreczky, P. QCD equation of state and hadron resonance gas. Nucl. Phys. A 2010, 837, 26–53. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Jakovac, A.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. The QCD equation of state with dynamical quarks. JHEP 2010, 11, 077. [Google Scholar] [CrossRef]
- Bazavov, A. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Megias, E.; Ruiz Arriola, E.; Salcedo, L.L. The Polyakov loop and the hadron resonance gas model. Phys. Rev. Lett. 2012, 109, 151601. [Google Scholar] [CrossRef] [PubMed]
- Noronha-Hostler, J.; Noronha, J.; Greiner, C. Hadron mass spectrum and the shear viscosity to entropy density ratio of hot hadronic matter. Phys. Rev. C 2012, 86, 024913. [Google Scholar] [CrossRef]
- Dashen, R.; Ma, S.K.; Bernstein, H.J. S Matrix formulation of statistical mechanics. Phys. Rev. 1969, 187, 345–370. [Google Scholar] [CrossRef]
- Cabibbo, N.; Parisi, G. Exponential hadronic spectrum and quark liberation. Phys. Lett. B 1975, 59, 67–69. [Google Scholar] [CrossRef]
- Hagedorn, R. Multiplicities, pT distributions and the expected hadron → quark - gluon phase transition. Riv. Nuovo Cim. 1983, 6, 1–50. [Google Scholar] [CrossRef]
- Bialas, A.; Peschanski, R.B. Moments of rapidity distributions as a measure of short range fluctuations in high-energy collisions. Nucl. Phys. B 1986, 273, 703–718. [Google Scholar] [CrossRef]
- Bialas, A.; Peschanski, R.B. Intermittency in multiparticle production at high energy. Nucl. Phys. B 1988, 308, 857–867. [Google Scholar] [CrossRef]
- Hwa, R.C. Fractal measures in multiparticle production. Phys. Rev. D 1990, 41, 1456. [Google Scholar] [CrossRef]
- Hwa, R.C.; Pan, J.C. Fractal behavior of multiplicity fluctuations in high-energy collisions. Phys. Rev. D 1992, 45, 1476–1483. [Google Scholar] [CrossRef]
- Hegyi, S.; Csorgo, T. On the intermittency signature of quark - gluon plasma formation. Phys. Lett. B 1992, 296, 256–260. [Google Scholar] [CrossRef]
- Hegyi, S. Monofractal density fluctuations and scaling laws for count probabilities and combinants. Phys. Lett. B 1993, 318, 642–647. [Google Scholar] [CrossRef]
- Dremin, I.M.; Hwa, R.C. Quark and gluon jets in QCD: Factorial and cumulant moments. Phys. Rev. D 1994, 49, 5805–5811. [Google Scholar] [CrossRef] [PubMed]
- Sarkisyan, E.K.G. Description of local multiplicity fluctuations and genuine multiparticle correlations. Phys. Lett. B 2000, 477, 1–12. [Google Scholar] [CrossRef]
- Kittel, W.; de Wolf, E. Soft Multihadron Dynamics; World Scientific: Singapore, 2005. [Google Scholar]
- De Wolf, E.A.; Dremin, I.M.; Kittel, W. Scaling laws for density correlations and fluctuations in multiparticle dynamics. Phys. Rept. 1996, 270, 1–141. [Google Scholar] [CrossRef]
- Lastovicka, T. Selfsimilar properties of the proton structure at low x. Eur. Phys. J. C 2002, 24, 529–533. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Multiplicity fluctuations due to the temperature fluctuations in high-energy nuclear collisions. Phys. Rev. C 2009, 79, 054903. [Google Scholar] [CrossRef]
- Tokarev, M.V.; Zborovský, I.; Kechechyan, A.O.; Dedovich, T.G. Verification of z-scaling in p+p, p¯+p and Au + Au collisions at RHIC, Tevatron and LHC. Phys. Part. Nucl. 2020, 51, 141–171. [Google Scholar] [CrossRef]
- Tokarev, M.; Kechechyan, A.; Zborovský, I. Validation of z -scaling for negative particle production in Au + Au collisions from BES-I at STAR. Nucl. Phys. 2020, 993, 121646. [Google Scholar] [CrossRef]
- Borland, L. Ito-Langevin equations within generalized thermostatistics. Phys. Lett. A 1998, 245, 67. [Google Scholar] [CrossRef]
- Deppman, A. Self-consistency in non-extensive thermodynamics of highly excited hadronic states. Physica A 2012, 391, 6380–6385. [Google Scholar] [CrossRef]
- Megias, E.; Menezes, D.P.; Deppman, A. Non extensive thermodynamics for hadronic matter with finite chemical potentials. Physica A 2015, 421, 15–24. [Google Scholar] [CrossRef]
- Sarkisyan, E.K.G.; Sakharov, A.S. On similarities of bulk observables in nuclear and particle collisions. arXiv 2004, arXiv:arXiv:hep-ph/0410324. [Google Scholar]
- Sarkisyan, E.K.G.; Sakharov, A.S. Multihadron production features in different reactions. AIP Conf. Proc. 2006, 828, 35–41. [Google Scholar]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; [Particle Data Group]; et al. Review of particle physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Marques, L.; Andrade-II, E.; Deppman, A. Nonextensivity of hadronic systems. Phys. Rev. D 2013, 87, 114022. [Google Scholar] [CrossRef]
- Marques, L.; Cleymans, J.; Deppman, A. Description of high-energy pp collisions using Tsallis thermodynamics: transverse momentum and rapidity distributions. Phys. Rev. D 2015, 91, 054025. [Google Scholar] [CrossRef]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S. Tsallis-thermometer: a QGP indicator for large and small collisional systems. J. Phys. G 2020, 47, 105002. [Google Scholar] [CrossRef]
- Fazio, S.; Fiore, R.; Jenkovszky, L.; Lavorini, A. Exclusive diffractive production of real photons and vector mesons in a factorized Regge-pole model with non-linear Pomeron trajectory. Phys. Rev. D 2012, 85, 054009. [Google Scholar] [CrossRef]
- Deppman, A. Properties of hadronic systems according to the nonextensive self-consistent thermodynamics. J. Phys. G 2014, 41, 055108. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis distribution in proton-proton collisions at s = 0.9 TeV at the LHC. J. Phys. G 2012, 39, 025006. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. From QCD-based hard-scattering to nonextensive statistical mechanical descriptions of transverse momentum spectra in high-energy pp and pp¯ collisions. Phys. Rev. D 2015, 91, 114027. [Google Scholar] [CrossRef]
- Rybczynski, M.; Wlodarczyk, Z. Similarities in multiparticle production processes in pp collisions as imprints of nonextensive statistics. Symmetry 2020, 12, 1339. [Google Scholar] [CrossRef]
- Cardoso, P.H.G.; Nunes da Silva, T.; Deppman, A.; Menezes, D.P. Quark matter revisited with non-extensive MIT bag model. Eur. Phys. J. A 2017, 53, 191. [Google Scholar] [CrossRef]
- Menezes, D.P.; Deppman, A.; Megias, E.; Castro, L.B. Non-extensive thermodynamics and neutron star properties. Eur. Phys. J. A 2015, 51, 155. [Google Scholar] [CrossRef]
- Grigoryan, S. Using the Tsallis distribution for hadron spectra in pp collisions: Pions and quarkonia at s = 5–13000 GeV. Phys. Rev. D 2017, 95, 056021. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Marques, L.; Mogliacci, S.; Paradza, M.W. On the precise determination of the Tsallis parameters in proton–proton collisions at LHC energies. J. Phys. G 2018, 45, 055001. [Google Scholar] [CrossRef]
- Sharma, N.; Cleymans, J.; Hippolyte, B.; Paradza, M. A Comparison of p-p, p-Pb, Pb-Pb collisions in the thermal model: multiplicity dependence of thermal parameters. Phys. Rev. C 2019, 99, 044914. [Google Scholar] [CrossRef]
- Azmi, M.D.; Bhattacharyya, T.; Cleymans, J.; Paradza, M. Energy density at kinetic freeze-out in Pb–Pb collisions at the LHC using the Tsallis distribution. J. Phys. G 2020, 47, 045001. [Google Scholar] [CrossRef]
- Biro, G.; Barnafoldi, G.G.; Biro, T.S.; Urmossy, K.; Takacs, A. Systematic analysis of the non-extensive statistical approach in high energy particle collisions - experiment vs. theory. Entropy 2017, 19, 88. [Google Scholar] [CrossRef]
- Acharya, S. Charged-particle production as a function of multiplicity and transverse spherocity in pp collisions at s=5.02 and 13 TeV. Eur. Phys. J. C 2019, 79, 857. [Google Scholar] [CrossRef]
- Castorina, P.; Iorio, A.; Lanteri, D.; Spousta, M.; Satz, H. Universality in hadronic and nuclear collisions at high energy. Phys. Rev. C 2020, 101, 054902. [Google Scholar] [CrossRef]
- Konishi, K. A Simple Algorithm for QCD Jets: An Introduction to Jet Calculus. Phys. Scr. 1979, 19, 195–202. [Google Scholar] [CrossRef]
- Venugopalan, R.; Prakash, M. Thermal properties of interacting hadrons. Nucl. Phys. A 1992, 546, 718–760. [Google Scholar] [CrossRef]
- Biró, T.S.; Shen, K.M.; Zhang, B.W. Non-extensive quantum statistics with particle–hole symmetry. Physica A 2015, 428, 410–415. [Google Scholar] [CrossRef][Green Version]
- Rozynek, J.; Wilk, G. An example of the interplay of nonextensivity and dynamics in the description of QCD matter. Eur. Phys. J. A 2016, 52, 294. [Google Scholar] [CrossRef]
- Rożynek, J.; Wilk, G. Dynamical nonextensivity or nonextensive dynamics? Eur. Phys. J. ST 2020, 229, 751–758. [Google Scholar] [CrossRef]
- Andrade, E.; Deppman, A.; Megias, E.; Menezes, D.P.; Nunes da Silva, T. Bag-type model with fractal structure. Phys. Rev. D 2020, 101, 054022. [Google Scholar] [CrossRef]
- Sena, I.; Deppman, A. Systematic analysis of pT -distributions in p + p collisions. Eur. Phys. J. A 2013, 49, 17. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. Transverse momentum distributions in proton–proton collisions at LHC energies and Tsallis thermodynamics. J. Phys. G 2014, 41, 065001. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. The Tsallis distribution at large transverse momenta. Eur. Phys. J. C 2015, 75, 430. [Google Scholar] [CrossRef]
- Rybczynski, M.; Wlodarczyk, Z.; Wilk, G. On the possibility of q-scaling in high energy production processes. J. Phys. G 2012, 39, 095004. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Self-similarity in jet events following from pp collisions at LHC. Phys. Lett. B 2013, 727, 163–167. [Google Scholar] [CrossRef]
- Agababyan, N.M. Self-affine fractality in π+p and K+p collisions at 250 GeV/c. Phys. Lett. B 1996, 382, 305–311. [Google Scholar] [CrossRef]
- Gupta, R. A Monte Carlo study of multiplicity fluctuations in Pb-Pb collisions at LHC energies. arXiv 2015, arXiv:arXiv:1501.03773. [Google Scholar]
- Ajinenko, I.V. Intermittency patterns in π+p and K+p collisions at 250 GeV/c. Phys. Lett. B 1989, 222, 306. [Google Scholar] [CrossRef]
- Albajar, C. Multifractal analysis of minimum bias events in s=630 GeV p¯p collisions. Z. Phys. C 1992, 56, 37–46. [Google Scholar]
- Sarkisyan, E.K.; Gelovani, L.K.; Sakharov, G.I.; Taran, G.G. Fractal analysis of pseudorapidity fluctuations in 4.5 A GeV/c C- (Ne, Cu) central collisions. Phys. Lett. B 1993, 318, 568–574. [Google Scholar] [CrossRef]
- Rasool, M.H.; Ahmad, M.A.; Ahmad, S. Multifractal study and multifractal specific heat of singly charged particles produced in 32S–Em interactions at 200 A GeV. Chaos, Solitons & Fractals 2015, 81(A), 197–202. [Google Scholar]
- Singh, G.; Jain, P.L. Multifractal analysis of 197Au-emulsion collisions at 10.6A GeV. Phys. Rev. C 1994, 50, 2508–2515. [Google Scholar] [CrossRef]
- Ghosh, D.; Deb, A.; Chattopadhyay, R.; Sarkar, S.; Jafry, A.K.; Lahiri, M.; Das, S.; Purkait, K.; Biswas, B.; Roychoudhury, J. Evidence of multifractal nature of target-evaporated slow particles produced in ultrarelativistic heavy ion interactions. Phys. Rev. C 1998, 58, 3553–3559. [Google Scholar] [CrossRef]
- Tawfik, A. A Universal description for the freezeout parameters in heavy-ion collisions. Nucl. Phys. A 2006, 764, 387–392. [Google Scholar] [CrossRef][Green Version]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Hadron production in central nucleus-nucleus collisions at chemical freeze-out. Nucl. Phys. A 2006, 772, 167–199. [Google Scholar] [CrossRef]
- Agakishiev, G. Hyperon production in Ar+KCl collisions at 1.76A GeV. Eur. Phys. J. A 2011, 47, 21. [Google Scholar] [CrossRef]
- Lopez, X. Subthreshold production of Σ(1385) baryons in Al+Al collisions at 1.9A GeV. Phys. Rev. C 2007, 76, 052203. [Google Scholar] [CrossRef]
- Lavagno, A.; Pigato, D. Nonextensive statistical effects in protoneutron stars. Eur. Phys. J. A 2011, 47, 52. [Google Scholar] [CrossRef]
- Feal, X.; Pajares, C.; Vazquez, R.A. Thermal behavior and entanglement in Pb-Pb and p-p collisions. Phys. Rev. C 2019, 99, 015205. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).