1. Introduction
The Severe Acute Respiratory Syndrome Coronavirus-2 (SARS-CoV-2) has caused the COVID-19 pandemic disease. The virus of diameter 70–90 nm [
1] is transmitted from human to human, primarily being carried by virus-laden fluid particles ejected from the mouth of infected individuals. In general, COVID-19 infection has multiple mode of transmission. It may spread by respiratory droplets and aerosols [
2,
3,
4], via direct contact such as hand shake or trough indirect contact via contaminated surfaces [
2]. The infectious dose for SARS-CoV-2 is not known. Extrapolating from studies of other viruses where more data are available, one might expect the threshold to vary from a few tens to a few thousand virus exemplars [
5]. From these data, it is also likely that the larger the dose of virus an individual is exposed to, the higher the likelihood of infection occurring. Whether the disease severity correlates with the size of the infectious dose is also unclear. However, based on animal experiments performed with a variety of viruses [
6], it is reasonable to assume that this is the case. SARS-CoV-2 can remain infective in aerosols for 3 h and on surfaces for 72 h in laboratory conditions [
2]. However, evidence about acquiring the infection via contaminated surfaces is scarce [
7].
Fluid particles responsible for the respiratory transmission are represented by aerosol and droplets [
2,
3,
4]. In this context, aerosol particles may contain exemplars of virus pathogen, epithelial and other cells or remnants of those, natural electrolytes and other substances from mucus and saliva, and water which typically evaporates quite fast, depending on the relative humidity of the surrounding air. Staying in the air for a long enough time (minutes or hours), aerosol particles of dimensions ≲5
m can be inhaled and airborne transferred over long distance in an indoor environment [
8,
9]. Large droplets ≳200
m stay airborne only for few seconds. Their movement mainly follows ballistic trajectories and to less extend the ambient air flow. Such droplets settle to the ground or other surrounding surface. Smaller droplets, say ≲5
m would evaporate in less than 3 s, at typical indoor relative humidity
. Since the sedimentation time of such a droplet is about 30 s, it would evaporate completely before reaching the background. Actually, the evaporation time for water droplets smaller than 80
m does not exceed their sedimentation time [
3]. The drying process would leave residuals of droplets after drying to moisture in equilibrium with ambient air. These residuals, so called droplet nuclei, are also airborne transferred aerosols. Aerosols particles (≲10
m) can float on the air and spread a significant distance (
m [
3]) following air flow streams, in particular after being dried [
3,
10].
The number density, velocity, and size distributions of fluid particles ejected in the course of expiratory events have important implications for transmission [
3,
10,
11,
12]. A single sneeze action can generate
fluid particles moving with velocities up to 20 m/s [
11]. Coughing generates 10–100 fewer droplets than sneezing at lower velocity ≲10 m/s [
10]. Along with coughing and sneezing, speaking also plays a significant role in spreading the virus contained particles [
12]. In particular, as it is normally done continuously over a longer period of time, the contribution into virus transmission can be significant. Moreover, the rate of particle production in the course of normal human speech is in positive correlation with the loudness (amplitude) of vocalization, ranging from approximately 1 to 50 particles per second [
12]. Needless to say, that SARS-CoV-2 infected individuals can spread the disease before the onset of clinical symptoms and the infection will be mostly transmitted in course of speaking generated virus-laden particles. Measured ejected particle size spans four orders of magnitude from ≃0.1 to ≃1000
m [
12,
13].
Face cover masks are currently treated as the best accepted personal protective equipment (PPE) in mitigating aerosol dispersal. In conditions of gradual softening of the pandemic outbreak measures, in many places, public has been asked or even obliged to wear masks. Thus, face masks, in some sense, become a norm in our lives. However, wearing face masks may become uncomfortable in some situations, like, for example, in summer heat, while staying on beaches or at hotel swimming pools, doing exercises in gyms, etc. Also, if an individual has a chronic respiratory condition such as asthma or chronic obstructive pulmonary disease (COPD), covering her/his mouth and nose can be especially challenging. The material barrier of the mask makes it harder to take in air. It also traps some carbon dioxide as it is exhaled, which means that one ends up breathing in air that is warmer and moister. Unfortunately, that sensation of having trouble breathing in a mask might get even worse in summer time. Many people with chronic lung conditions find it harder to breathe in hot, humid air (though some others fare worse when the weather is cold and dry).
The focus of the paper is understanding the physics that underpins the effectiveness of a possible non-material personal defense against airborne pathogens like SARS-CoV-2. The barrier of such non-material protection is supposed to be created by a flow of well directed, slightly inclined, down stream of air which screens the front of the open face in the manner of an air curtain. The protection mechanism is driven by the dragging of virus-laden airborne particles inside the width of the flow and as a consequence displacing them away from their primary trajectories. Our study shows that such, potentially portable, air curtain can provide both inward and outward protection and serve as an effective personal protective equipment (PPE) mitigating from human to human transmission of virus infection like COVID-19.
The structure of the paper is as follows. In
Section 2, we describe the main elements of the setup of a potentially portable air curtain to be used as PPE from airborne transmission of virus infection like COVID-19. In
Section 3, we investigate how the fluid particles gain their velocities being dragged by an air flow in different regimes of the flow layer over bodies. In
Section 4, we discuss the protection mechanism of the air barrier and validate its efficiency. In
Section 5, we conclude and comment upon the results of our study.
2. Air Curtain as PPE to Mitigate Airborne Virus Transmission
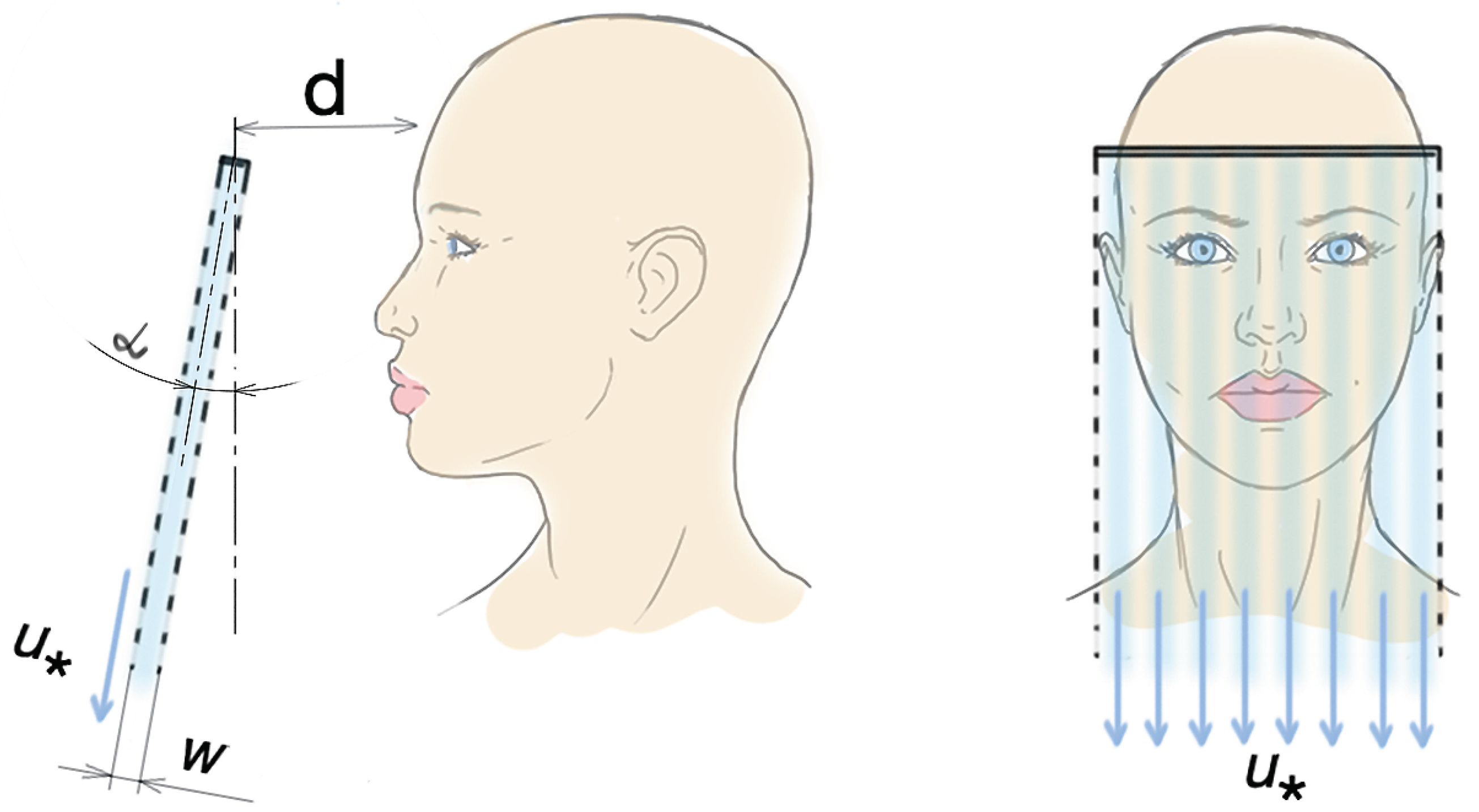
We want to consider a portable air curtain as a sort of dynamical PPE from exposure of a recipient’s mouth, nose and conjunctiva to virus-laden fluid particles injected by infected individuals. The air curtain is supposed to be created as a flow of well directed downward stream of air across the front of the open face, as schematically shown in
Figure 1. This air stream should provide a kind of dynamical barrier which steadily displaces inward running virus-laden aerosolized particles that would otherwise be inhaled by an uninfected person. In this setup, the outward protection is also provided by stimulation of a ground settling of outgoing virus-laden particles expelled by an infected person, so that sedimentation on surfaces located substantially bellow the typical level of the face openings would proceed faster than in usual conditions of indoors air background streams. One assumes that the curtain is formed out of surrounding air and streamed downwards in a way that the flow lines do not cross the plane of the face. For a sufficient downward bending of the barrier penetrating inward running particles, the plane of the air curtain should be inclined at a small angle
with respect to the vertical plane, as illustrated in
Figure 1.
We assume that an appropriately designed system can create such a stream across the entire height and width of the protected face. As a rough example of a particular realization, one can imagine that the air flow is injected from the edge of a brim equipped with a properly designed and instrumented air outlet which streams the air in a way that it forms a thin air barrier of the horizontal shape defined by the geometry of the edge of the brim. A good coverage can be already provided with dimensions and shape used for brims of the more-or-less standard baseball caps. For the instrumentation, we rely on current development of technology for construction of portable, low noisy and low consuming pumping units, which will be able to create an air curtain of about 1 cm thick with stable flow velocity ≲10 m/s across an area of typical face dimensions.
In the current study, we investigate the effectiveness of a portable air curtain in inward and outward protection from transmission of respiratory infections such as COVID-19. The protection effectiveness, in conditions of a typical parameters appropriate for creation of individual air curtain, mostly depends upon the ability of the air flow to band downward trajectories of the fluid particles containing influenza, in a way to prevent them coming into contact with the face surface of an uninfected individual.
In our setup, the degree of banding of the trajectories is defined by the effectiveness of the air flow, streamed at certain velocity
and angle
, to drag the fluid particles (aerosol and droplets) along the lines of the stream (see
Figure 1), while they are crossing the air curtain in transverse direction, thus being immersed for some time into the flow. The drag force excreted to a particle by moving media is defined as the component of the force parallel to the direction of the motion of the flow of the media (For a review see [
14,
15]). This force depends on the properties of the media, which is, in our case, the air at atmospheric pressure, its velocity, the size of a particle immersed into the media and its material properties. At a given velocity of the media, which we take
m/s for our benchmark setup, the particles of different sizes will gain their velocity in different regimes defined by the hydrodynamic conditions of the flow layer over the body of the particles. These regimes are investigated in the following section.
3. Dragging of Virus-Laden Aerosols and Droplets by Air Flow
In case a particle velocity vector
is different from the air velocity vector,
, the drug force exerted by the gas is given by Newtonian force
where
is the density of the flow,
is the maximal area of a body in the plane perpendicular to the flow direction and
is the drug (resistance) coefficient. The drug coefficient of a body depends on the velocity and the viscosity of the drugging media (gas or liquid) and is defined by the Reynolds number
where
D and
are the dimension of the body and the dynamical viscosity of media. The Reynolds number totally defines the mode of the flow layer over the body and thus the law of resistance. Depending on the value of
one defines the three regimes’ flow layers over the a body, namely, the laminar regime (
), the intermediate regime, i.e., a transition from laminar to turbulent (
), and the turbulent regime (
) [
14,
15]. The equation describing the resistance (drugging) response of a media to transport of a particle depends on the regime of the flow laying over the particle, thus it depends on the Reynolds number.
As discussed above, the size of particles ejected by a speaking, coughing or sneezing person spans the range between 0.1
m and ≃1000
m depending on the circumstances of the ejection. Further, we assume that the particles are spherical with smallest size 100 nm [
12,
13]. In our task, to understand the regimes of movement of particles with different sizes, we estimate their Reynolds numbers in a steady state flow of air at atmospheric pressure and velocity
m/s, when a particle is initially at rest,
. Throughout the paper, we use for the air density
and for its dynamical viscosity
. For a particle of size
m the Reynolds number is
, which implies that sub-micron particles should move in laminar regime. Bigger particles, namely those of the size between
and
m, for which
, should move in an intermediate regime. Eventually, particles with dimension
exceeding
will be drugged in a turbulent, so-called, auto-model regime.
Let us study in detail the drugging of the aerosol particles by a steady air flow in these three regimes.
For the laminar regime, the drug (resistance) coefficient of a hard spherical body obeys the Stocks formula
.
Therefore, the resistance force for a Stocks particle reads
In the range of Reynolds numbers between 1 and 700, for the dependence a number of empirical approximations are used. For the turbulent regime the drug coefficient is constant, in particular, for a hard spherical body, .
Let us consider the drugging of a disperse particle by a steady state one dimensional flow of media of density
propagating along the
x axis. We model the particle by a hard spherical body of diameter
D made out of material of density
, so that the mass of the particle is given by
Assume, that at
the particle with initial velocity
gets injected into the flow and let us evaluate the velocity of the particle with time
. The equation of motion can be expressed as follows
In Stocks regime (
), which implies
Equation (
6) can be reduced to the form
In front of the derivative in Equation (
8), is the dynamical relaxation time in Stocks regime, which indicates the estimate of time scale needed for a drugged particle to reach the velocity of the flow. Further, for the flow of constant velocity
, one can reduce the equation of motion to the dimensionless form
where
and
. Solving in Equation (
10), we arrive to
where
is set for the initial condition.
In the intermediate regime of flow layer over a particle, the drug (resistance) coefficient
is given by the Klyachko formula [
15]
often used as a good empirical approximation.
Using
instead of
and introducing a new variable
, one can re-write the equation of motion (
6) as follows
where
is a time scale so that
and
is a distance scale. Integrating this equation at initial conditions set to
and
one arrives to
Finally, after introduction of new variables
and
, the solution takes the following form
where
. We notice, that the relaxation time is given by
Finally, in the turbulent regime of flow layer over a particle, when
, the drug coefficient is just a constant
[
14,
15]. Thus, the equation of motion (
6) takes the form
where the coefficient
has a dimension of length. Introducing the characteristic time as
One can rewrite Equation (
17) in following form
where we use
. The solution of Equation (
19), with initial condition
, is given by following expression
4. Discussion
Using the result of
Section 3, one can estimate the effectiveness of the individual air flow barrier in providing inward and outward protection.
In our benchmark setup, described in
Section 2, we use the barrier formed by downward stream of air with width
cm, which is well localized in
cm away from the surface of a protected face and provides a constant flow velocity
m/s across vertical and horizontal dimensions of the face, as shown in
Figure 1. For the current theoretical study, to some extend, the distance
d is an arbitrary parameter. The choice of its value can be regulated by other factors, not directly related to the effectiveness of the PPE under study. The plane of the barrier is inclined at an angle
with respect to the vertical plane (see
Figure 1). The value of
will be discussed bellow.
A susceptible individual, while walking indoors, through an environment containing virus-laden particles, has a high risk of exposure to the infection through the openings of his face. The particles themselves, being airborne-transmitted, experience motion due to the environmental low speed background air flows with maximal velocity
m/s [
3]. Assuming the maximal indoor walking speed
m/s, one infers that an inward running particle, entering horizontally under the exterior plane of the air curtain, will cross the width of the barrier within
ms. Actually,
is the time available for the particle to gain velocity
aligned with the direction of the barrier air flow, due to its drag force. In course of drugging, within the inclined air barrier, the particle will gain a horizontal outward velocity in amount of
. Thus, the inward (horizontally) running particle velocity will be reduced by
or even inverted in its direction, depending on the value of the inclination angle
. If the gained vertical velocity is high enough to displace the particle down, namely sufficiently away from a potential contact with mucus and conjunctiva of the host’s face, the effectiveness of the protection is treated as justified. The fractional velocity gained by the particle, in different laying over regimes, is given by Formulas (
11), (
15) and (
20).
As we have discussed in the introduction, the airborne virus transmission is associated with droplets smaller than about 100
m that are suspended and transported in an air current [
8,
9]. These droplets can evaporate in a few seconds [
8,
9], so that droplet nuclei may be formed. Sometimes, a vapour-rich, buoyant turbulent expiratory jet can slow down this evaporation [
16]. The droplet nuclei size spans range from sub-microns to about 10
m. Thus, as argued in
Section 3, at a chosen velocity of the barrier flow, the gas-particles motion of this droplets size range is driven by Stocks and intermediate regimes.
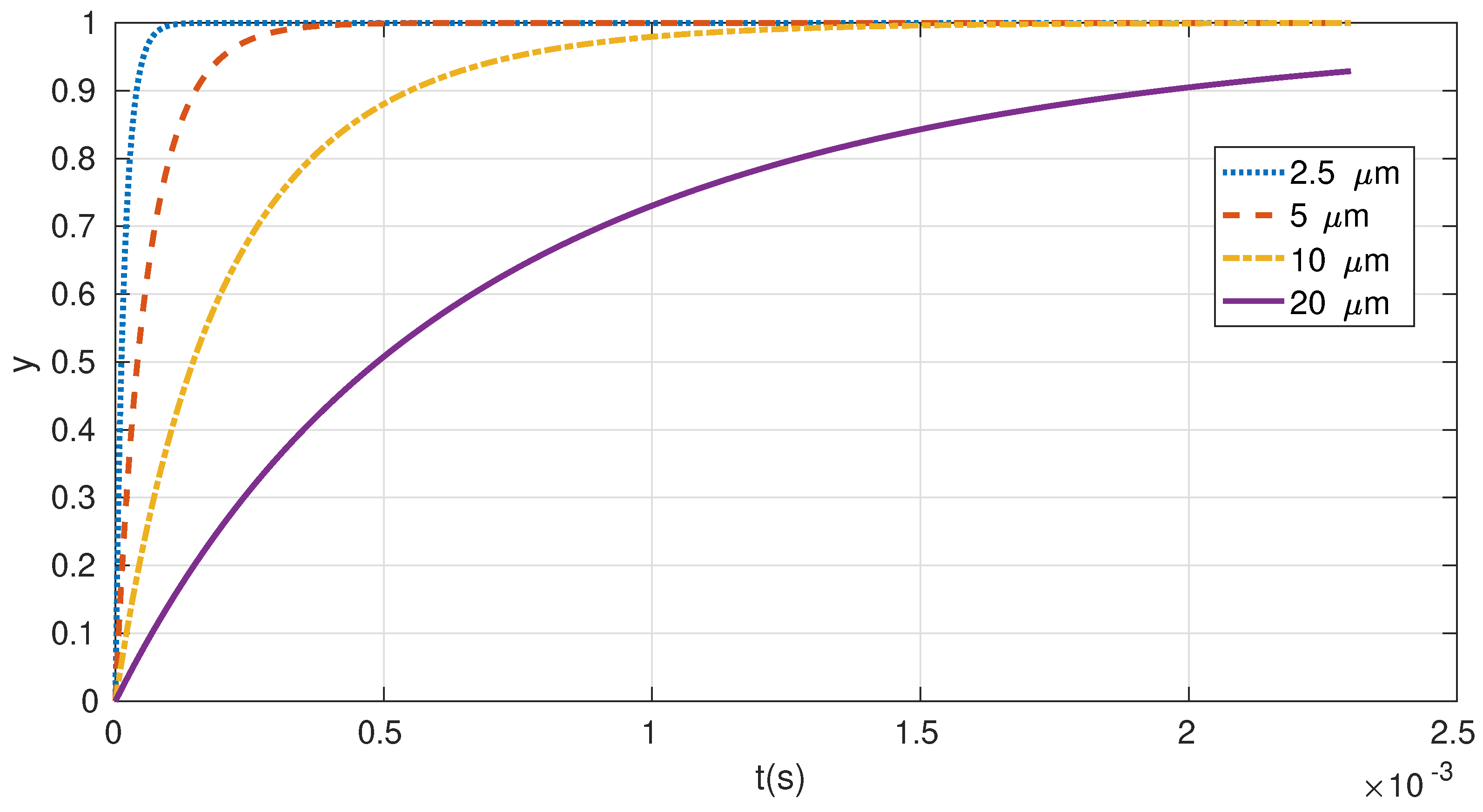
The smallest aerosols, up to size
m, should move in the Stocks regime with a fractional velocity gaining rate given by Equation (
11). For the above benchmark parameters of the barrier, the temporal progress of the fractional velocity gain is displayed in
Figure 2. One can see that the biggest Stocks driven aerosol particles will reach 90% of the barrier’s flow velocity,
m/s, within 16
s (the corresponding rate is indicated by the solid line plotted for particle size
m). Let us adjust the inclination angle in a way that the outward horizontal velocity gaining component would compensate for the inward running velocity, so that
. This implies that
, so that
. We can naturally assume that such compensation is maintained with accuracy up to the background speed of the indoor air,
m/s. Thus, the particle being immersed into the air barrier will be able to leave its width in about
ms, which can be mapped into the variation of the inclination angle,
. Herewith, the vertical component of the particle velocity will reach
m/s and hence the particle would be displaced
cm downward. Thus, we expect that the particle will sweep out downward, to avoid a potential contact with the face openings of the host. If the host is moving with lower velocity,
can be negative, so that an inward running particle will even be reflected in addition to the downward displacement described above. Similar reflection might take place in the case of bigger inclination angle; however, in practice, it is better to maintain it at an optimal value
to minimize spurious horizontal contributions of the barrier flow into the environmental background air streaming.
Bigger aerosols, up to 20
m, which might still be suspended in the indoor environment for a long time [
3], will be moved in an intermediate regime in Equation (
15) at slower time progress of the velocity gain, as shown in
Figure 3. Again, as one can see, the airborne aerosols in an intermediate barrier dragging regime will be accelerated up to 90% of the barrier’s flow velocity within less than in 2 ms. The corresponding rate is indicated by the solid line plotted for particle size 20
m. Since the velocity gain is still fast enough, i.e., the full acceleration will be achieved well before the elapsing of
, all arguments given in the above paragraph are valid for the biggest still airborne transmittable particles. These particles will be successfully displaced (≳44 cm) from trajectories potentially crossing the face.
The analysis above testifies that the air barrier is able to effectively mitigate inward propagation of airborne transmitted virus-laden fluid particles of all possible sizes.
We note that smaller particles, ≤5
m, might carry higher concentration of the virus than larger ones [
17,
18] and moreover can be transported deep into the lungs, avoiding defence of the upper respiratory system [
19,
20]. Also, small aerosols inoculation has been shown to cause more severe symptoms than bigger particles administered by intranasal inoculation and the dose of influenza required for inoculation by small aerosols route is 2–3 orders of magnitude lower than that required by intranasal inoculation [
17].
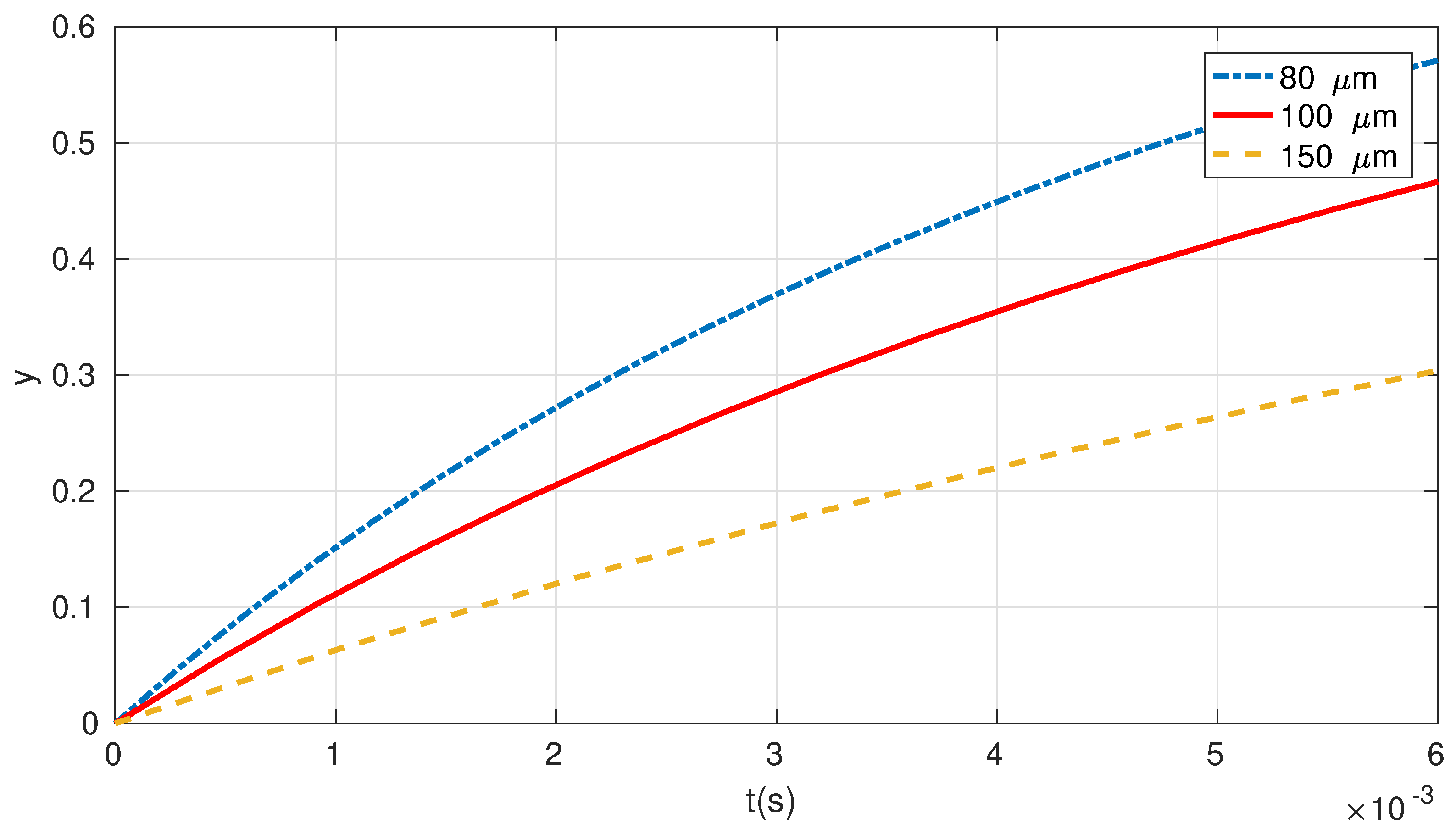
The protection is effectivity degraded for droplets which still can be transformed into airborne aerosols through evaporation, namely whose sedimentation time starts to exceed their evaporation time. Thus the smallest size droplets 80
m which will still be able to reach the ground before evaporation [
3] gain half of the velocity of the barrier stream within
. This is indicated in
Figure 4, by the dashed dotted line, i.e., a particle of such dimension starts to move with velocity
m/s after 5 ms. Therefore, the expected downward displacement will amount to
cm. 100
m and 150
m droplets will be displaced by
cm and
cm respectively. Although, the displacements are not enough, except, probably, for 80
m droplets, such particles, being displaced by the air barrier, proceed to fall freely in still air following their equation of motion, which is defined by gravity
and kinematic time scale given in Equation (
9). For example, a 80
m droplet should reach its terminal velocity
m/s within
ms and hence would meet the ground after
s from the moment it was expelled at a hight of
m. A bigger droplet, of 150
m size, will terminate its acceleration at
m/s, which implies its sedimentation time
s. Therefore, we believe that it is very likely that droplets of such sizes being moved down by the air barrier will proceed to settle to the ground instead of coming in a contact with the host’s face. However, one should say, that the definitive conclusion on the effectivity of this kind of stimulating sedimentation can be established in numerical simulations.
Outward protection is also an important issue in the COVID-19 pandemic, since SARS-CoV-2 transmission may occur earlier in the course of infection, from asymptomatic and minimal symptomatic hosts, which may expel fluid particles in the range from aerosol size up to a few millimeters. In the case of the air curtain, the outward protection, for outgoing droplets, is provided due to a kind of stimulation of ground settling of outgoing particles described above. Moreover, bigger outgoing droplets, of about ≳1 mm size, will be moved by the barrier gas-particle flow with respect to the auto-model regime in Equation (
20), with the kinematic time scale given by Equation (
18). This implies that, within
s (for
mm), the droplet will reach half of the speed of the barrier, namely
m/s, to be pointed almost vertically down. Thus it will be ground settled directly around infected individual within 0.3 s instead of following its ballistic trajectory which can spread 1–2 m along horizontal direction in violent expiratory events like coughing and sneezing [
16,
21,
22]. Since outgoing aerosols are also displaced by the air barrier, up to 0.5 m downwards, we believe that it will suppress the aerosols transport over long distances with indoor air flow. However, again, for definite answer, numerical simulations, like for example [
3], would be required.
5. Concluding Remarks
In the current respiratory COVID-19 pandemic, airborne virus-laden aerosols are considered as the primary route of transmission of of SARS-CoV-2 pathogen. Staying in the air for a long enough time (minutes or hours), aerosol particles can be transferred over long distance in an indoor environment [
8,
9] to be inhaled by a susceptible host. Face cover masks are currently treated as the best accepted PPE in mitigating aerosol dispersal. Thus, iregarding mitigation of the virus transmission, face masks have become a norm in our everyday lives. However, wearing face masks may become uncomfortable in some situations like in summer heat, while staying on beaches or at hotel swimming pools, doing exercises in gyms, etc. Moreover, the material barrier of masks or respirators makes it harder to take in air, which might be not be acceptable for an individual with a chronic respiratory condition like asthma, COPD, etc.
Therefore, we performed the study of a PPE based on non-material protective barrier created by a flow of well directed down stream of air across the front of an open face. Unlike in the case of material based protection, such as face masks and respirators, which trap virus-laden fluid particles via the combined effects of diffusion, inertial impaction, interception, and electrostatic attraction [
23], the air curtain PPE dynamically displaces the trajectories of infected particles that would otherwise be inhaled by an uninfected individual from reaching the surface and the openings of the host’s protected face. In our analytical study of the benchmark setup we demonstrated that the inward protection effectiveness of the air barrier is very high for airborne aerosols of all possible sizes.
For the sake of fairness and consistency, one should say that, unlike in the case of material-based face covers, the air barrier does not provide the trapping of outward going fluid particles. However, instead, it stimulates the ground settling of big droplets very close to the infected host and displaces exhaled aerosols up to 0.5 m downwards and hence, very likely, suppresses the airborne transport of the infection over long distances with indoor air flow. Moreover, while a mask’s material can significantly reduce the velocity of the through flow jet during expiratory events, presence of the same material leads to an increase of pressure in the region between the mask and the face and hence results in an increased perimeter leakage in the form of side jets, as shown analytically and numerically in [
24] and investigated experimentally in [
25]. The impact of this process depend on fluid structure, the structural design of the mask as well as the permeability of the mask’s material. The leakage jets that are ejected from the perimeter can be turbulent and highly directed (see, for example, the flow visualizations presented in [
25]), potentially serving as effective dispersers of respiratory aerosols in transverse directions. Spasmodic expiratory events such as coughing and sneezing that generate high transient expulsion velocities will significantly diminish the outward protection effectiveness of face masks [
25]. The air barrier does not suffer from the above disadvantages just because there is no physical cover material which otherwise would cause overpressure and perimeter leakage. Instead, the air barrier’s stream can substantially spoil the structures of jets generated by spasmodic expiratory events. The details of the outgoing fluid structure interaction with the air barrier is a matter of numerical modeling, in a manner of [
24], and as well as, perhaps, experimental studies developed in [
25] and other dedicated publications.
Our theoretical study of the benchmark setup is aimed to focus the attention of relevant community on the principal ability of a potentially portable air curtain to serve as an effective PPE in mitigation of the human to human transmission of respiratory virus infection like COVID-19. For an equipment realization and instrumentation we rely on the current development of technology for construction of portable, low noisy and low consuming air steaming engines. However, some general attractive every day life advantages of the air curtain PPE may be elucidated already now. Indeed, there is no necessity of hand washing and disinfection like in case of putting on and taking off the face masks. Instead, it is supposed that the air streaming equipment can be simply powered on and off. This also means that the face washing procedure, which is also important for the removal of sedimented pathogens in the vicinity of mucus and conjunctiva, is much more simplified compared to the wearing of face masks, respirators or face shields. It is difficult to manage to cover the mouth and nose with a flexed elbow or tissue, when coughing or sneezing with a face mask or respirator on, in particular if a face shield as a PPE is installed as well. It is clear that this is not the case for an air curtain PPE-wearing individual. The interior of the inner instrumentation of the equipment can be disinfected by installing a miniature interior UV source to be activated while the protecting device is taken off, so that the unit is self-disinfected. Although the stream of the barrier is formed out of surrounding air which itself can contain virus-laden fluid particles, their trajectories will always lie along the plain of the barrier and hence will never come in a contact with mucus or conjunctiva of the protected face. Thus, there is no need to instrument the device with a kind of on-flight disinfection equipment.