Abstract
We study Gaussian wave beam and wave packet types of solutions to the linearized cold plasma system in a toroidal domain (tokamak). Such solutions are constructed with help of Maslov’s complex germ theory (short-wave or semi-classical asymptotics with complex phases). The term “semi-classical” asymptotics is understood in a broad sense: asymptotic solutions of evolutionary and stationary partial differential equations from wave or quantum mechanics are expressed through solutions of the corresponding equations of classical mechanics. This, in particular, allows one to use useful geometric considerations. The small parameter of the expansion is where is the wavelength and L the dimension of the system. In order to apply the asymptotic algorithm, we need this parameter to be small, so we deal only with high-frequency waves, which are in the range of lower hybrid waves used to heat the plasma. The asymptotic solution appears to be a Gaussian wave packet divided by the square root of the determinant of an appropriate Jacobi matrix (“complex divergence”). When this determinant is zero, focal points appear. Our approach allows one to write out asymptotics near focal points. We also claim that this approach is very practical and leads to formulas that can be used for numerical simulations in software like Wolfram Mathematica, Maple, etc. For the particular case of high-frequency beams, we present a recipe for constructing beams and packets and show the results of their numerical implementation. We also propose ideas to treat the more difficult general case of arbitrary frequency. We also explain the main ideas of asymptotic theory used to obtain such formulas.
1. Introduction
The equations describing the propagation of an electromagnetic wave in a tokamak plasma are more manageable when the frequencies of the electric field are much higher than the electron cyclotron frequency in the plasma. In this framework, an application of asymptotic methods is quite appealing, if we consider the exact formulation [1,2,3,4,5,6,7]. We show in this paper how to work it out, under the assumption that the frequency of the wave is significantly higher than the electron cyclotron frequency, with wavelength varying among m and 1 m, i.e., for a frequency of the order of terahertz.
This analysis is particularly useful in order to predict the behavior of a broadband terahertz (THz) pulse in a non-uniform and dispersive plasma. This is mainly oriented toward a new plasma diagnostic system based on THz time-domain spectroscopy that simultaneously provides high time resolution and THz bandwidth coverage, allowing an analysis of wide ranges of plasma density variations without incurring opacity. Moreover, a possible application of high-power and -frequency sources for reactors like ITER (International Thermonuclear Experiment Reactor) and DEMO ( Demo project will pave the way for commercial fusion electricity) (characterized by high beta due to the high temperature of the plasma) would allow the use of the first or second harmonic of the electron cyclotron resonance in extraordinary wave polarization from the outboard side of the torus. This could avoid the complication, for the wave accessibility to the plasma center, of a launching from the high field side of the tokamak. Heating and current drive systems are extremely relevant matters in a thermonuclear plasma, magnetically confined in tokamak devices, as they provide a tool to reach, sustain, and control burning conditions. Due to the high intensity of the confinement magnetic field, devices such as ITER or DEMO will require a higher frequency for the electron cyclotron resonance heating (ECRH) at fundamental harmonics.
On the other hand, experimental plasma physics has relied on a variety of diagnostics tools to probe physical features like temperature and density. One of the most important diagnostic techniques is based on the use of electromagnetic waves, and terahertz bandwidth pulses can be used as a very sensitive probe of widely-varying plasma parameters. Therefore, low- and high-power (≥1 MW) RF (Radio Frequency) sources with output frequency in the THz range would be necessary in order to reach this goal [8]. The propagation of the THz pulse (monochromatic or bandwidth pulse) in a magnetically-confined plasma in tokamak structures can be conveniently studied by solving the Maxwell-fluid system of equations via asymptotic techniques.
Asymptotic methods are powerful mathematical techniques to solve the Maxwell equations in strongly anisotropic and dispersive media like magnetically-confined plasma; they mostly rely on the WKB (Wentzel-Kramers-Brillouin)expansion of the field without explicitly solving the coupled partial differential equations by numerical methods. In a tokamak plasma (i.e., confined by an external magnetostatic field), Maxwell equations must be coupled with the linearized equations of the electron and ion fluid elements (essentially the mass and momentum conservation equations) having neglected the thermal and collisional effects on the wave propagation, which for this particular kind of waves is a well-justified hypothesis. Asymptotic techniques applied to the propagation of the electromagnetic pulse highlight very well the geometric characteristic of the wave propagation and allow putting in evidence the singular points like cut-offs, mode conversions, geometrical reflections (caustics), etc. In view of the application to the ITER and DEMO, we study the propagation of an electric field. The corresponding asymptotic expansions is given.
In tokamak reactors, the use of high-frequency waves excited by antennas located outside the plasma and accommodated in the ports of the vessel is crucial for both diagnostic (terahertz (THz) pulse, which allows studying wide ranges of plasma density variations [9]) and (or) plasma heating (high-power frequency waves for plasma heating in fusion-oriented devices like ITER and DEMO [8]). For this reason, the knowledge of the propagation of the electric field inside the plasma assumes a crucial role in planning the experiments and interpreting the results. The Maxwell equations describing the propagation of an electromagnetic wave in a plasma, in the presence of an external magnetic field, have an easily worked form when the frequencies of the electric field are much higher than the ion cyclotron frequencies in the plasma, because the cold plasma assumption is well satisfied for the plasma dielectric tensor. This last assumption can be naively justified considering that the wavelength of the electromagnetic wave involved in the process satisfies the following inequality , where L is the variation scale length of the macroscopic plasma parameters, i.e., density and confining magnetic field.
In this framework, it is quite appealing to try to apply asymptotic methods using the formulation as given in [10,11,12,13]. We study the propagation of Gaussian wave packets and Gaussian beams inside the tokamak under the assumption of its localization and use the theory in [10] for finding the asymptotic form of the electric field using the small expansion parameter . In view of the application to the plasma heating in tokamaks, we take the wavelengths in the interval m < < 1 m corresponding to the microwave frequency interval typical of the lower hybrid waves (LWH) used for plasma heating.
In the special case of high frequencies, namely much greater than , the analysis becomes significantly simpler. The reason is that the initial system of equations is reduced to a treatable scalar equation. This allows us to construct explicit formulas for Gaussian packets and beams, which are given in Section 3. These formulas may be implemented numerically using software like Wolfram Mathematica, Maple, etc. We also underline that the formulas are elementary. Their understanding and practical use do not require any special knowledge of differential geometry, analysis, pseudo-differential calculus, asymptotic methods, etc.
In the general case (frequencies less than ), the reduction to a scalar case becomes quite a complicated task. This reduction can be done with the help of the trick proposed in [13] called scalarization. Its idea is to study a system whose Hamiltonian is a determinant of the matrix principal symbol. The reduced Hamiltonian system is very cumbersome, and so far, we have no explicit formulas for Gaussian packets and beams. The main steps of the scalarization are described in Section 4.
In Section 5, we give a brief description of the general theory. In the other sections, we present the results and outline the main proofs of the proposed algorithms. For the details, the reader should look at the papers where this material is explained in more detail.
2. Linearized System of Plasma Equations
In this section, we write out the cold plasma linearized system of equations. This system is reduced to a dimensionless form containing a small parameter. Such a form is standard for using Maslov’s asymptotic theory and methods [14,15,16,17]. With the help of this approach, one can describe Gaussian beams and packets in a tokamak region (see [11,12,18]). For references concerning physics of electromagnetic waves in plasma, see [19,20,21,22,23,24,25,26].
Let us consider an ionized gas consisting of electrons and protons. Let and be the charges of the electron and the proton and their masses. In the cold plasma model, the particles are described by their densities , , functions of coordinate and the time t, and by their velocities fields , , three-dimensional vector functions of x and t: for . The expression of the current is The densities satisfy the continuity equation , where , is the scalar product: . Then:
We make a hypothesis that the magnetic field applied to the plasma is much stronger than the magnetic field generated by the motion of the charges. The equation for the electric field is obtained after eliminating the magnetic field :
where c is the speed of light, is the electric constant, and ∧ is the vector product. This equation is coupled with Newton’s equation for the two types of charged particles:
This system is nonlinear because . We linearize it by omitting terms from and from (1). Then, using these linearized equations and (1), we can rewrite (2) and (3) in the form:
By passing to dimensionless variables, we put Equation (4) in a different framework with small parameter . To do this, we define the following objects. Let be squared frequencies of protons and electrons and be squared plasma frequency. We introduce the characteristic size L of the problem, the time , the beam frequency , the beam wavelength , the electric field , and the magnetic field . The typical tokamak radius is about 0.9 m, so we put m. Let be the cyclotron frequencies of the charges.
Introduce dimensionless parameters and also . The parameter h is assumed to be small. Then, in the dimensionless variables , where , , , , , after omitting primes, Equation (4) becomes:
In order to use semi-classical methods [14,15,16], we need to re-write Equation (5) in a standard form. We introduce the new variable and the unknown vector-column function with 12 components. Then, one has the “standard” form:
where:
As soon as we have presented the system of equations in the standard form, we can use the algorithm (see [14,15,17]) for constructing its solutions in a form of Gaussian wave packets and Gaussian beams.
3. Gaussian Packets and Beams for High Frequencies
In this section, we assume that the characteristic wavelength is high enough ( Hz). In this case, the part is negligible, which significantly simplifies the consideration. The case of lower frequencies leads to much more complicated constructions, and we discuss it in Section 4. We are interested in solutions associated with the “electric mode”. They can be described with the help of one of two Hamiltonian systems:
Let us denote by the trajectory of, say, Hamiltonian system issued from the point :
The projection of this trajectory is the ray . We assume that the point is placed outside of the tokamak camera and choose the vector k in such a form that intersects with the positive parameter (time) t. Note that before meeting the tokamak camera, (as well as ) is just the straight line:
Due to this assumption and conservation of the Hamiltonian on , we have .
Remark 1.
One can construct the trajectoriesdefined by the Hamiltonianand starting from the same point. Then, the trajectoriesandare the same curves in the phase space. They only differ in orientation with respect to time t. That is why we restrict ourselves only to.
3.1. Gaussian Beams
By Gaussian beams, we understand the stationary solutions of the Equation (6) localized in the neighborhood of rays . Now, we construct a diagonal matrix with complex entries having positive imaginary part: . Let be 3D unit orthogonal vectors such that and M is the matrix consisting of the vector columns ,: . The choice of M is not unique, and along with the parameters , it characterizes the structure of Gaussian beams.
We construct now the matrix and denote by the matrix solution to the Cauchy problem for variational system as follows:
where arguments of the matrix-functions are and is the unit matrix.
Later on, we will use letter for time and call it “the proper” time. Note that depend also on , so we omit this dependence to simplify notation.
The matrices have the following properties (see [14], §7–§8, Chapter II, §2, Chapter IV):
(1) for each : , .
(2) for each : Indeed, both sides are the vector solutions for the variational system, and we have and due to the definition of the matrices B and C and trajectory . This implies the equalities .
(3) For any fixed , one has if and only if . The point where (or which is the same ) is the focal one on the Gaussian beam. In what follows, we assume that there are no focal points. However, we also show graphically what happens in the situation with focal points without showing the formulas (see [17]).
(4) One can define the complex continuous function putting and the complex symmetric matrix with degenerate nonnegative imaginary part , having rank two.
Let us fix some neighborhood of the ray ; due to the assumption , we can define the solution to the equation:
which says that is a point on the ray such that the vector is perpendicular to in . Now, we can construct the phase S, which is a function of variables and all parameters omitted to simplify the notation:
the “phase of the polarization” (the Berry phase) by the formula:
and vector amplitudes by the formulas:
The vector functions , are arbitrary smooth functions on the trajectory, which together with vector p organize the right-oriented orthogonal basis : , .
Let us introduce two 12-vector functions:
where and:
The Gaussian beam is a solution of Equation (5) as follows.
Theorem 1.
There is an asymptotic solution to (5) of the form:
3.2. Gaussian Wave Packets
Let be a complex symmetric matrix with the strictly positive imaginary part and be a 2D complex vector column with the components . Let be a complex symmetric matrix with the strictly positive imaginary part and 12-vector functions be equal to zero outside a neighborhood of . Now, we construct an initial value of of a special form:
with a Gaussian wave packet localized in a neighborhood of the point . We want to construct the asymptotic solution of Equation (5) to the special Cauchy problem:
Let us define complex matrices and as solutions to the Cauchy problem (12). Then, the matrix is symmetric and has a positive imaginary part (compare with the case of Gaussian beams from Section 3.1). These two properties are implied by the following equalities (see [14] §7,8, Chapter II):
and . Furthermore, and are preserved with time t because the elements of these matrices are the skew inner product of the solutions to a linear variational Hamiltonian system.
Now, we introduce the complex phase of the Gaussian packet:
Theorem 2.
Remark 2.
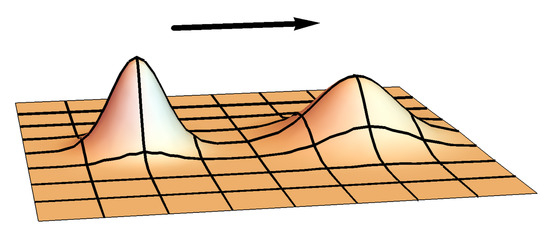
1. For each time t, the matrixis symmetric and nondegenerate, and its imaginary part is positive (see [14]). Due to these properties of the matrices B and C, the following estimates are true:
whereare positive constants. This means that the function Ψ is localized like a Gaussian function in a neighborhood of the pointmoving along the ray(see Figure 1).

Figure 1.
Gaussian wave packet.
2. The first scalar factor in (23) depends on the parameters ofof the rayand the parametersof the Gaussian packet. The second, vector factor depends on the parameters of the ray(also on the plasma frequency and the magnetic field) and do not depend on the parametersof the Gaussian packet.
3. If, then one can change P by k, X by, B by, and C by, whereis theunit matrix andis the matrix of second derivatives of, which is equal to:
3.3. Numerical Simulation
Let us choose values of physical parameters that are typical for real tokamaks. We consider our system in a toroidal domain (the tokamak) with major and minor radii as follows: = 0.90 m, a = 0.3 m. We assume that the magnetic field in the toroidal coordinates has the form:
We also assume that and . Let and be the characteristic cyclotron frequency for electrons and protons. Their numerical values are , ,
Using software like Wolfram Mathematica, Maple, etc., it is possible to visualize the trajectories of the Gaussian beams by applying the asymptotic formulas. The geometry and the magnetic field are those defined in the text, together with the other parameters. For this simulation, we chose also m, . The boundary of the torus is located at m; the focal point: m.
The trajectory in the tokamak is shown in Figure 2. The asymptotic solution till the entrance in the tokamak is in Figure 3.
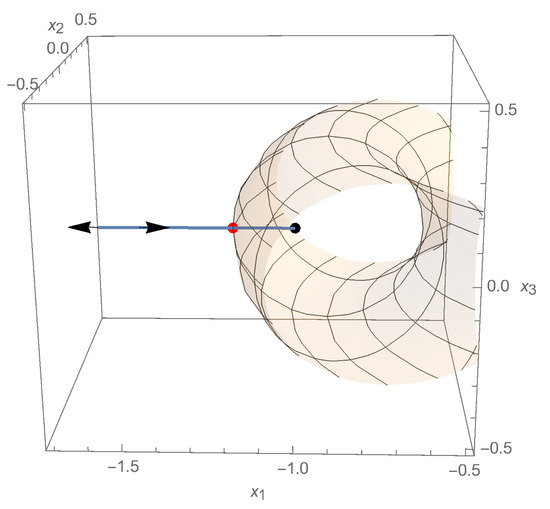
Figure 2.
The ray enters the torus and then leaves in the opposite direction. The right arrow indicates the initial direction of the ray. The left arrow is the direction of the ray after the reflection. The focal point (marked with a thick black dot) is the right end of the ray. The intersection of the ray with the border is marked with a thick red dot. The distance is in meters. The ray lies on the line .

Figure 3.
(a) Modulus of the wave function before entering the plane : . (b) Real part of the wave function on the line before entering the tokamak: .
We underline that our method also allows one to treat the case with focal points (see [12]). In this case, the formula is more complicated than the one given in Theorem 1, and it contains the Airy function; we do not present it here. Nevertheless, this formula is still constructive from the viewpoint of numerical calculations. The result of calculations in a neighborhood of the focal point is presented in Figure 4. However, it should be noted that for the physical values of the parameters in real tokamaks, the trajectories have no focal points. They go through the tokamak since their energy is quite large. For further details, we refer the reader to [11,12].

Figure 4.
In a neighborhood of the focal point. (a) Modulus of the wave function in the plane : . Focal point (). (b) Real part of the wave function on the line : . Focal point ().
4. The Case of Lower Frequencies
Now, we turn to the general case, when the characteristic frequency is not assumed to be large. The main difficulty is that we cannot say anymore that in Equations (6), (7), and (8), the part with is negligible.
This case was studied in [12], and it is much more complicated than the case described above. We describe it here in less detail, just mentioning the main underlying ideas and methods.
We recall that the algorithm [10,27] for constructing semi-classical asymptotics starts from finding eigenvalues and eigenvectors of the principal symbol matrix . The eigenvalues (which are the functions of p and x) are called modes or effective Hamiltonians, and they define the classical systems to be studied. In the high-frequency case, we actually deal with the matrix , and the eigenvalues and eigenvectors can be calculated explicitly. The former associated with the electric mode are Hamiltonians given by (9), and the corresponding eigenvectors are given by (17).
In the general case, such straightforward calculations are impossible. Hence, first of all, we reduce the -system to the system by eliminating , , and . As a result, we arrive at the equation as follows:
where are some real-valued functions of x and . Therefore, the reduction took place, but the price we paid was that the spectral problem was reduced to a problem for an operator pencil. Note that in the literature, usually, one goes the opposite way: reducing an operator pencil to a spectral problem (see [27]). Unfortunately, the formulas for are quite cumbersome, and one cannot write an explicit formula for eigenvalues of . Of course, we could use the Cardano formula, but it leads to Hamiltonians that are impossible to work with. On the other hand, the determinant , which is a product of effective Hamiltonians , could be calculated by means of arithmetic operations. Choose some effective Hamiltonian, say, , and denote . Then, the Gaussian beams and packets are associated with the trajectories of the Hamiltonian system H lying on the zero energy level . Assume that in a domain of interest in the phase space, . Then, one can use the Maupertuis–Jacobi principle stating that the solution of the system with Hamiltonians H and lying on the zero energy coincide up to the time reparameterization. One can also calculate the semi-classical correction entering the transport equation without the knowledge of H. This procedure helps to scalarize the initial vector problem and reduces it to studying a classical system with the Hamiltonian:
Remark 3.
Studying the Hamiltonian of Equation (27) may be interesting not only for tokamak studies. It can be useful in other applications of plasma physics, e.g., in cosmology.
Note that this Hamiltonian has three degrees of freedom, but in the case of a tokamak, due to the symmetry of the magnetic field, it can be reduced to a two degrees of freedom system. Such a system is generically non-integrable, but one can try to apply averaging methods to obtain an integrable system.
If the system is integrable, one can construct different types of asymptotic solutions of (5). Firstly, it is Gaussian beams, which are associated with trajectories of the Hamiltonian system. However, also, one can try to find spectral series associated with Liouville tori according to [10]. We plan to treat this problem in the future.
As we have said, this system is quite cumbersome. We did not construct Gaussian beams for real tokamaks. Instead, we constructed such solutions for a model example when the magnetic field is:
and the Hamiltonian system becomes integrable. For further details, we refer the reader to [13].
5. The Maslov Complex Germ Theory in a Short-Wave Approximation
In this section, we give an introduction to the asymptotic methods applied to the linear systems of partial differential equations in view of the applications to the plasma problems treated in the previous sections.
5.1. Linear System of Partial Differential Equations with a Small Parameter
Let us view a multidimensional system of linear partial differential equations as an equation, defined by a matrix whose elements are differential operators. We study the system of equations for m-vector-column functions in space with coordinates presented in the form:
or:
These systems with first-order (Schrödinger-type equation) and second-order (wave-type equation) derivatives by t are treated in similar ways in our context. If we move to the stationary case by replacing the operator by parameter E dual to t, we arrive at the spectral problems:
related to Equations (28) and (29).
Here, is the matrix-operator with elements in a form of differential scalar operators:
We introduce coordinates dual to . The complex-valued matrix with components is called the matrix symbol of the operator . The components in turn can be viewed as scalar symbols of operators .
Numbers over x and denote the order of application for the operator of multiplication by x and for differential operator . For example, in the one-dimensional case (), if , then . The variables t and h are treated as parameters.
Remark 4.
This brief account covers the basic notions of differential operators (i.e., operators defined by symbols, which are polynomial in p). For a more complete description of differential and pseudodifferential operators (i.e., operators defined by symbols of more general classes than polynomials in p), see [15].
We assume that for the symbol , the following expansion is true:
We want to construct some asymptotic solutions to Equations (28), (29). In the semi-classical theory, the typical form of the ansatz (outside of focal points and caustics) is:
and sums of such functions (the so-called WKB ansatz). The function if real defines the oscillatory (in the limit ) property of the asymptotics. In the complex case, the imaginary part of should be nonnegative () to define asymptotics that does not tend to infinity as . In points where , the asymptotic function is decreasing to zero with infinite order by h. For example, in the one-dimensional case, if , we have the plane wave; if , we have the wave packet for each t centered at point and oscillating and simultaneously decreasing as the Gaussian function. Vector function defines the amplitude part of the asymptotic solution. One can consider series , but we restrict ourselves only to the principal part of the amplitude, which gives a reasonably accurate description of the underlying physical process.
Let us discuss the effect of many dimensions in Systems (28) and (29). In order to apply the approximation methods to the system of equations, we should diagonalize the zero-order matrix . The matrix splits the space into the eigenspaces (which obviously depend on coordinates p, x), and acts on each of them as a multiplication by a scalar. In a similar way, the operator acts as a scalar differential operator on vector functions from these eigenspaces. Then, for the differential equation with the principal part being a scalar operator, the method of the complex germ (see [14,15,17]) is applied.
Reducing in this way the problem to the scalar case, we can obtain then the oscillatory part of asymptotic approximation, i.e., the function , which will be different for each eigenspace.
Then, the amplitude part of the asymptotic solution should be obtained. At this step, the non-diagonal perturbations would play their part in asymptotics construction.
5.2. Step 1. Factorization to Modes (Diagonalization of the Main Symbol )
Consider the main symbol , and assume that for each , there exists a real-valued eigenvalue with multiplicity k for each and such that the distance between and other eigenvalues is greater than some positive number . We assume that the corresponding invariant subspace consists only of eigenvectors (i.e., the matrix does not have non-trivial Jordan blocks corresponding to this eigenvalue). Such functions are known as effective Hamiltonians. They give rise to solutions (of the initial problem (28) or (29)) called modes or terms.
Considering all effective Hamiltonians that satisfy the assumptions given above, we obtain a solution of the original problem as a sum of modes.
The situation when the multiplicity k changes with is called the mode conversion. There is no general theory for this case, and there are very few examples where this problem has been solved.
Remark 5.
For plasma system, we mainly consider the mode corresponding to electromagnetic waves. For this case, we have.
We fix the basis in eigenspace corresponding to eigenvalue such that:
and assume that all vectors are smooth with respect to . We denote as the matrix consisting of vector-column . It is well known from linear algebra that there is a set of eigenvectors of adjoint complex-valued matrix with the same (real-valued) eigenvalue H, such that:
where the scalar product of vectors is defined by and is the Kronecker delta. Vectors and form a biorthogonal system. We can also construct the eigenvectors of transposed matrix with the same eigenvalue H and introduce the matrix consisting of vector-column . Then, (35) is equivalent to a matrix equality:
where is the unit matrix. Note that Condition (35) (or (36)) does not give the unique choice of the vectors , and one can always take any nondegenerate smooth matrix and construct the products and , which have the same properties as and . In the case, when is self-adjoint, it is natural to choose , then the system consists of orthonormal vectors, and the matrix should be the unitary one.
Remark 6.
There is no mathematical prescription for how to fix a choice of χ except the easiness of the answer or some physical reasons. For instance, if the matrixis real, then sometimes (but not always!), it is possible to choose χ as a real-valued matrix, then σ should be an orthogonal matrix.
Now, we present some solution of the original Equations (28) and (29) in the form:
where w is a new unknown -D column-vector function with components and is some pseudodifferential operator that gives just small corrections. The function w should satisfy the “reduced” equation with diagonal leading term:
or:
Here, is a “correcting” operator, and the matrix symbol L is:
where:
while is a (complex) inner product in complex Euclidean space.
The WKB ansatz for w has the form:
where is a vector function of length k. The m–D vector solution of Equation (28) or Equation (29) is obtained by the action of the operator (37) on w.
Remark on the Choice of Eigenvector System
Let us discuss the question of choosing the matrix . As we said above, this choice is not unique, although the final formula is unique modulo small correction. The various choices of simultaneously change the operator and in turn the vector-amplitude a. However, the formulas for the amplitude a could have a quite complicated form especially in hydrodynamic problems. It can happen that it is difficult to justify the boundedness of a in time t and study the stability problem of the solution. That is why although the choice of is not very important from the theoretical point of view, it is important in applications.
One of the recipes for how to normalize the matrix is the following. Assume that the leading term of the original system is conservative and that there exists the matrix operator such that the functional:
is preserved in time t. We substitute (37) into this form and obtain:
Using the formulas from the operator analysis, we find the principal symbol of the operator . It is , and we require:
where is the unit matrix. This condition could be used to choose the vectors . We stress that the last condition does not change if one multiplies the matrix by any smooth unitary matrix . Finally we say that the last condition could be used in the case when the full original system is not conservative; just its principal term can have such a property.
5.3. Step 2. Hamilton–Jacobi Equation, Hamiltonian System, Lagrangian Submanifolds, Complex Germ, and Transport Equations
5.3.1. Short-Wave Asymptotics with Real Phases: Hamilton–Jacobi Equation, Hamiltonian System, Lagrangian Manifolds
In order to construct some WKB-type solution of the form of (43) for Equation (38) or (39), one should find the solution of the Hamilton–Jacobi equation:
if we consider (38), or the equation:
if we consider (39).
We can move from Equation (39) to (38) by applying the square root operation. Inverting the direction of the time corresponds to a different choice of the branch of the root. Therefore, we will consider the problem in terms of (38) and will not explicitly write formulas in the notation of Problem (39).
The theory of Hamilton–Jacobi equations includes the following geometric objects. Every smooth function of defines the smooth n-dimensional surface in the space of values . This surface is Lagrangian, which means that the differential form in restricted to it is zero. Conversely, every Lagrangian surface (often called the Lagrangian manifold), which is nicely (i.e., diffeomorphically) projectable on the coordinate space , uniquely defines the function such that .
Let be the Lagrangian manifold defined by the function . It can be included in the one-parameter family of Lagrangian manifolds where for time , we have , and is defined by translation of by the Hamiltonian system:
In the coordinate notation, this family can be defined as:
where multidimensional parameter is the coordinate of and coordinate functions , are the solutions of Hamiltonian Equation (49).
Lagrangian manifold is nicely projectable on ; so are , at least for times t sufficiently close to . This means that the Jacobian . Hence, the unique function can be defined satisfying condition and for which . It can be defined by the formula:
where the function is the solution of the equation:
which is defined because . This function is the solution of (47) with initial condition .
In many physically-important situations, the phase function becomes multivalued after some period of time when manifolds become not nicely projectable on . In this case, the amplitude function in (43) becomes infinite. This fact is related to the appearance of focal points that can form curves or surfaces known in geometrical optics as caustics. It does not mean that the solution becomes infinite. It means that the form of asymptotics (43) becomes inappropriate in the vicinity of focal points. Analytically, focal points can be described by means of the Jacobian . For each focal point at the time t, we have .
Unlike the phase function , the Lagrangian manifold almost always exists regardless of the presence of focal points and caustics. Following Maslov’s method, we should go to (partial) momentum representation:
where y is n-dimensional variable where at the position, we have coordinate or coordinate . For example, for , it can be , , , . The atlas on the Lagrangian manifold can be introduced such that for each chart from it, there is coordinate y of the type defined above for which this chart can be uniquely projected on the space of values of y. Functions S and corresponding to domains where both x- and y-representation are valid are related by the Legendre transformation.
From the point of view of classical mechanics, moving from coordinate to corresponds to canonical transformation, which is defined by rotation by angle in the plane . Returning from y-presentation to usual x-presentation is the compensation of this transformation in quantum or wave mechanics, which according to V. A. Fock [28] (and the ideas of P. Dirac), is defined by the unitary operator (quantization of canonical transformation) that acts on (55). Rotation by corresponds to the h-Fourier transform, so the unitary operator is its inverse, defined by formula:
Here, I is the list of increasing integer numbers consisting of indices i for which transition from to presentation was made. Number is the length of I. Product is the dot product of vectors formed by taking i-components, , from vectors p, x. For example, for , , we have , , , .
Then, some gluing procedure should be applied to functions w corresponding to different charts of the Lagrangian manifold. This procedure consists of introducing factors by which local functions w should be multiplied to be compatible in intersections of charts. These factors are defined using the notion of the Maslov index.
5.3.2. Short-Wave Asymptotics with Complex Phases: Isotropic Manifolds with the Complex Germ
The use of the WKB method leads to the appearance of the Hamilton–Jacobi equation and the Hamiltonian system, for which it is required to find complex solutions. Such solutions may not exist at all. However, given the fact that the solution rapidly decays outside the set of zeros of the imaginary part of the phase S, we can restrict ourselves to considering an isotropic (a low-dimensional Lagrangian) manifold, at each point of which there is an n-dimensional complex plane (tangent to an imagined complex manifold).
In more detail, a manifold is isotropic, if its dimension is less than n, and it has the property that the restriction of differential form to it is equal to zero. The projection of the isotropic manifold onto is the set in the neighborhood of which the asymptotic solution is localized. The function S in points near this projection will be defined up to the quadratic term with a positive imaginary part. It means that the asymptotic solution in this case decays as a Gaussian function in the transverse direction of projection. This allows us to solve Equation (47) with error up to .
The counterpart of the full dimensionality of the Lagrangian submanifold in the isotropic case is the smooth assignment of some complex n-dimensional plane to each point of the isotropic submanifold (see Figure 5). This object is called the complex germ (see [14]).
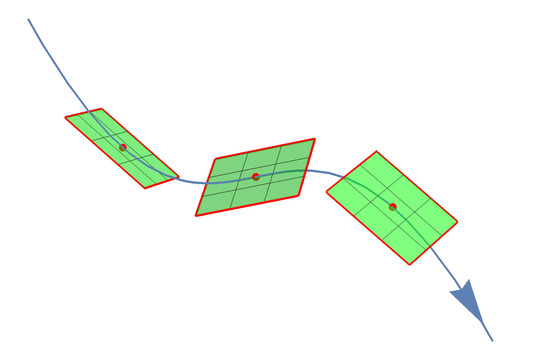
Figure 5.
One-dimensional isotropic submanifold with complex planes attached to each point.
Remark 7.
Such structures are called vector bundles. Here, the base space is the isotropic submanifold. The fiber at each point of the base space here is the n-dimensional complex vector space.
Remark 8.
Here, we make some notes about the definition of the complex germ. The space tangent to the phase spaceat the pointis the spaceagain. We then complexify this tangent spaces at all points (which gives us the spaceat each point). Let α be the coordinate in this submanifold. Then, the complex germ is the smooth assignmentof the n-dimensional complex subspace of the complexified tangent spaceto each point α on the isotropic submanifold. The complex subspaceshould have the following properties: (1) it should contain the complexified tangent space to the isotropic submanifold; (2) the bilinear prolongation of the real formto the complex spaceshould restrict to zero on; (3) the sesquilinear prolongation of the real formto the complex spacedivided by i should restrict to the nonnegative defined form onwith complexified tangent space to the isotropic submanifold as its kernel. Property (1) says that the complex germ over the isotropic submanifold should in some sense extend the isotropic submanifold to the n-dimensional structure. Property (2) says thatshould be zero onas in the Lagrangian case. Property (3) is the geometrical counterpart of the inequality.
The isotropic submanifold with the complex germ should (in the time-dependent case) be translated by the dynamics of Hamiltonian Equation (49) or (in the stationary case) be invariant under this translation.
We will be concerned with zero-dimensional isotropic submanifolds in the time-dependent case (Gaussian wave packets) and with one-dimensional isotropic submanifolds in the time-independent case (Gaussian beams).
The complex germ mathematical structure is more complicated than the Lagrangian submanifold, but the dynamics and calculations are much simpler in this case.
The isotropic submanifold is moved by Hamiltonian Equation (49), and the complex germ dynamics is described by the variational system along trajectory for n-sized square matrices , :
where we should put and as arguments of , , , . Matrix B corresponds to coordinate p, and matrix C corresponds to coordinate x. Then, in order to obtain the dynamics of the complex germ, we should build the matrix of coordinate columns of some n basis vectors of the complex germ at the initial time and solve the variational system, which will give us the basis vectors of the complex germ for other times.
We want to construct solution w in a form of a Gaussian wave packet, so we put on the function the initial condition:
defining the Gaussian packet in the vicinity of the point with momentum and with matrix with a positive defined imaginary part. Value is a real constant. Then, we should find the trajectory of Hamiltonian Equation (49) with initial conditions , and solve variational Equation (57) along this trajectory with initial conditions , , where is the unit matrix of size n.
We define the phase S in the form:
5.3.3. Transport Equation and the Solution of the Equation on the Eigenspace
5.3.4. Construction of the Solution of the Equation
The solution u of Equation (28) corresponding to the eigenspace with eigenvalue H with initial condition is given by the expression:
The solution of (28) with the initial condition being the superposition of initial conditions corresponding to different eigenspaces is given by combination of solutions for each eigenspace. We remind that for each eigenspace, functions H and matrices L will be different; hence, the equations for S and A will be different.
Remark 9.
The function:
is the solution of the parabolic Fock–Leontovich equation (see [1]).
5.3.5. Stationary Case
Here, we describe stationary solutions of the Gaussian beam-types corresponding to one-dimensional isotropic manifolds (i.e., curves). They should be invariant under Hamiltonian Equation (49), so they should be its trajectories , . The complex germ over this trajectory should be also invariant under the Hamiltonian system. It means that it is defined by the matrix function:
which should include the derivative of the trajectory radius vector as its column, and it should be the solution of the variational Equation (57). The matrix should be nonnegative and should have rank for every t. The last condition is satisfied if it is satisfied for initial time . Let be the solution of transport Equation (60).
We assume that the trajectory is not closed, i.e., it is homeomorphic to real line . Such a case takes place in our plasma system. For the case of closed curve questions of invariance of the complex germ and the functions S and A under, making turnings around the curve should be considered.
Then, we define the phase function S by:
where is the solution of the equation:
Then, the stationary solution of (30) corresponding to asymptotic spectral value is:
In the case when there is a focal point , i.e., the point where , the general theory [10,14,15] proposes integral representation of the asymptotical solution near this point in a form of the Fourier transform. There is also more effective representation in the form of the special Airy function [12,29].
6. Conclusions
The paper presented an algorithm for constructing Gaussian wave packets and Gaussian wave beams with focal points based on the example of plasma physics equations. The algorithm was based on the Maslov canonical operator in a situation with complex phases (the Maslov complex germ theory) and on geometric objects, which are curves in phase space, defining oscillations along the “axes” of the beams, and the complex planes added to them, which determine the decay along the normal direction to these axes. The former were determined with the help of the trajectories of a suitable Hamiltonian system and the latter with the help of the variational system. Another necessary object, the amplitude of the Gaussian packet or beam, was found as a result of the integration of the scalar (or sometimes the vector) transport equation. Hamiltonian systems, variational equations, and transport equations were determined by the symbols of the original system of equations under study, that is by matrix-valued functions defining the differential operators of the original system. The eigenvalues, which are effective Hamiltonians, determined the corresponding Hamiltonian systems, and the corrections to them (matrix, in the case when the effective Hamiltonians have multiplicity greater than one) determined the transport equations (in particular, the Berry phase). For wave packets and wave beams in the absence of focal points (turning points) on the “axes” of the beams, there were relatively simple effective formulas that could be easily implemented using Mathematica or MATLAB. The formulas presented contained, in particular, the solutions obtained using the method of the parabolic Fock–Leontovich equation, while part of the solution of the latter moved into the complex phase, which is more convenient for the numerical implementation of formulas for wave Gaussian beams. In addition, the Maslov complex germ theory allows one to construct asymptotic solutions in situations with focal points (turning points).
Author Contributions
A.Y.A.: Application of the theory to physics problems, S.Y.D.: General theory, A.I.K.: Calculation of Gaussian packets, program, B.T.: Methodology.
Funding
The work is supported by the Russian Science Foundation (Project No. 16-11-10282).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Babich, V.M.; Buldyrev, V.S. Asymptotic Methods in Short-Wavelength Diffraction Theory; Alpha Science International: Oxford, UK, 2009. [Google Scholar]
- Popov, M.M. A new method of computing wave fields in the high-frequency approximation. J. Sov. Math. 1982, 20, 1869–1882. [Google Scholar] [CrossRef]
- Popov, M.M. A new method of computation of wave fields using Gaussian beams. Wave Motion 1982, 4, 85–97. [Google Scholar] [CrossRef]
- Babich, V.M.; Ulin, V.V. Complex ray solutions and eigenfunctions concentrated in a neighborhood of a closed geodesic. J. Sov. Math. 1982, 20, 1749–1753. [Google Scholar] [CrossRef]
- Babich, V.M.; Ulin, V.V. Complex space-time ray method and “quasiphotons”. J. Sov. Math. 1984, 24, 269–273. [Google Scholar] [CrossRef]
- Ralston, J. Gaussian beams and the propagation of singularities. Stud. Partial. Differ. Equ. 1982, 23, C248. [Google Scholar]
- Kravtsov, Y.A.; Berczynski, P. Gaussian beams in inhomogeneous media: A review. Stud. Geophys. Geod. 2007, 51, 1–36. [Google Scholar] [CrossRef]
- Ceccuzzi, S.; Dattoli, G.; Palma, E.D.; Doria, A.; Gallerano, G.P.; Giovenale, E.; Mirizzi, F.; Spassovsky, I.; Ravera, G.; Surrenti, V.; et al. CARM: A THz source for plasma heating. In Proceedings of the 2013 38th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Mainz, Germany, 1–6 September 2013. [Google Scholar] [CrossRef]
- Kolner, B.H.; Buckles, R.A.; Conklin, P.M.; Scott, R.P. Plasma Characterization With Terahertz Pulses. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 505–512. [Google Scholar] [CrossRef]
- Fedoryuk, M.V.; Maslov, V.P. Semi-Classical Approximation in Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Dobrokhotov, S.Y.; Cardinali, A.; Klevin, A.I.; Tirozzi, B. Maslov complex germ and high-frequency Gaussian beams for cold plasma in a toroidal domain. Dokl. Math. 2016, 94, 480–485. [Google Scholar] [CrossRef]
- Anikin, A.Y.; Dobrokhotov, S.Y.; Klevin, A.I.; Tirozzi, B. Gaussian Packets and Beams with Focal Points in Vector Problems of Plasma Physics. Theor. Math. Phys. 2018, 196, 1059–1081. [Google Scholar] [CrossRef]
- Anikin, A.Y.; Dobrokhotov, S.Y.; Klevin, A.I.; Tirozzi, B. Scalarization of stationary semiclassical problems for systems of equations and its application in plasma physics. Theor. Math. Phys. 2017, 193, 1761–1782. [Google Scholar] [CrossRef]
- Maslov, V.P. The Complex WKB Method for Nonlinear Equations I: Linear Theory; Birkhäuser: Basel, Switzerland, 1994. [Google Scholar]
- Maslov, V.P. Operational Methods; Mir Publishers: Moscow, Russia, 1976. [Google Scholar]
- Belov, V.V.; Dobrokhotov, S.Y.; Tudorovskiy, T.Y. Operator separation of variables for adiabatic problems in quantum and wave mechanics. J. Eng. Math. 2006, 55, 183–237. [Google Scholar] [CrossRef]
- Belov, V.V.; Dobrokhotov, S.Y. Semiclassical Maslov asymptotics with complex phases. I. General approach. Theor. Math. Phys. 1992, 92, 843–868. [Google Scholar] [CrossRef]
- Cardinali, A.; Dobrokhotov, S.Y.; Klevin, A.; Tirozzi, B. Gaussian beams for a linearized cold plasma confined in a torus. J. Instrum. 2016, 11. [Google Scholar] [CrossRef]
- Leble, S.B. Nonlinear Waves in Waveguides; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar] [CrossRef]
- Cairns, R.A.; Fuchs, V. Calculation of a wave field from ray tracing. Nucl. Fusion 2010, 50, 095001. [Google Scholar] [CrossRef]
- Pereverzev, G.V. Paraxial WKB description of short wavelength eigenmodes in a tokamak. Phys. Plasmas 2001, 8, 3664–3672. [Google Scholar] [CrossRef]
- Mazzucato, E. Propagation of a Gaussian beam in a nonhomogeneous plasma. Phys. Fluids Plasma Phys. 1989, 1, 1855–1859. [Google Scholar] [CrossRef]
- Gerwin, R.A. Initial Value Solution of Maxwell’s Equations in Cold Plasma. Am. J. Phys. 1962, 30, 711–715. [Google Scholar] [CrossRef]
- Freidberg, J.P. Ideal MHD; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Brambilla, M. Kinetic Theory of Plasma Waves: Homogeneous Plasmas; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Stix, T.H. Waves in Plasmas; American Institute of Physics: College Park, MD, USA, 1992. [Google Scholar]
- Shkalikov, A.A. Operator Pencils Arising in Elasticity and Hydrodynamics: The Instability Index Formula. In Recent Developments in Operator Theory and Its Applications; Birkhäuser: Basel, Switzerland, 1996; pp. 358–385. [Google Scholar] [CrossRef]
- Fock, V.A. On the canonical transformation in classical and quantum mechanics. Acta Phys. Acad. Sci. Hung. 1969, 27, 219–224. [Google Scholar] [CrossRef]
- Klevin, A.I. Asymptotic eigenfunctions of the “bouncing ball” type for the two-dimensional Schrödinger operator with a symmetric potential. Theor. Math. Phys. 2019, 199, 849–863. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).