Abstract
Obligations in the Next-Generation Access Control (NGAC) standard enable the development of security-intensive workflow systems where access privileges evolve over time. However, specifying obligations for dynamic access requirements poses challenges, with errors having the potential to cause significant harm to the authorization state in NGAC applications. To identify and rectify such errors, our work aims to verify obligations by translating NGAC policies into logical formulas in SMTs (Satisfiability Modulo Theories). A primary challenge lies in the formalization of procedural obligations into declarative SMT formulas, given the potential for interference among administrative actions within an obligation. To address this issue, this paper analyzes all conflicts among obligation actions and formalizes them as logical formulas for the correct SMT-based verification of obligations in NGAC policies. We implemented the approach using the cvc5 solver and applied it to real-world systems. The results illustrate the successful formalization and verification of access control requirements.
1. Introduction
Obligations associated with access privileges play a crucial role in establishing accountability and maintaining privacy, which rely on the meticulous execution of security procedures by both the system and the user [1]. While access control primarily governs authorized user access to specific resources, data, or services, it fails to guarantee the proper execution of obligatory actions. A common practice is to incorporate obligations into access control policies rather than embedding them directly into system functionality. This is exemplified in the XACML 3.0 standard [2] and its associated extension [3], the Usage Control model [4], and the Next-Generation Access Control (NGAC) standard [5].
In traditional obligation models [1,6,7,8], the system and user obligations linked to access events typically do not alter access privileges upon execution. The authorization components of access control remain immutable in the face of obligatory actions, such as sending email notifications. In contrast, NGAC integrates administrative actions within obligations to handle dynamic access control requirements that modify the authorization elements and access privileges during runtime. We refer to the collective authorization elements at a specific moment in NGAC as a “configuration,” encompassing assignment, association, and prohibition relationships among associated users, user attributes, objects, obligation attributes, and access rights. An initial configuration and a set of administrative obligations define an NGAC policy. An obligation consists of a sequence of conditional actions that modify the configuration’s assignment, association, prohibition relationships, or other elements. Access privileges are determined by applying the decision procedure to the given configuration. When a permitted access event occurs under the initial configuration, it triggers associated obligations to modify the initial configuration, thereby transforming the initial configuration into a new one. Consequent obligation-associated access events can further update this new configuration. In this way, administrative obligations enable the implementation of workflow systems with changing access privileges.
However, the specification of administrative obligations for dynamic access requirements can be complex and error-prone. The obligations can transform the initial configuration into possible configurations through different event sequences. As discussed in the NGAC standard specification, due to complex run-time configuration and privilege changes, the application of NGAC has the potential to cause “grave harm to the authorization state through error or intent” [5]. Therefore, ensuring that administrative obligations are correctly implemented to meet dynamic access requirements is very important.
To verify NGAC policies, in our prior work, we developed an approach to formalizing the access decision procedure, individual configurations, and obligations as SMT (Satisfiability Modulo Theory) formulas [9]. The obligation formalization assumes that the actions within each obligation are independent—the execution of one action will not affect other actions. In other words, it cannot capture interdependencies between actions, such that one action’s postcondition falsifies the next action’s precondition or cancels the postcondition of a preceding action. However, it is critical to accurately formalize sequences of administrative actions as SMT formulas for SMT-based verification of NGAC policies.
To address this issue, this paper presents a thorough examination of the interdependencies inherent to administrative actions and formalizes them as SMT formulas to facilitate SMT-based verification of NGAC policies. To this end, we formalize the logical preconditions and postconditions of individual actions and the conflicting conditions among administrative actions within each obligation. To our knowledge, no prior work on NGAC, ARBAC, UCON+, or any other access control model has formally studied or encoded intra-obligation dependencies in a form that is verification-capable. This is the first formal approach to verifying dynamic, obligation-driven access control policies with intra-obligation dependencies that modify the permission state at runtime. Unlike other access control verification efforts, which primarily focus on static policies or administrative policies that can be modified by administrators, our work represents a novel approach to the formal verification of obligation-enabled dynamic access control.
Specifically, our contributions include the following:
- 1.
- A complete formalization of all built-in NGAC administrative actions, specifying precise preconditions and postconditions for each in SMT logic.
- 2.
- The first comprehensive study of obligatory actions’ interdependencies, conflicts, and verification, a topic that was not studied in prior research. It enables SMT-based verification that supports intradependency-aware reachability analysis of complex obligations.
- 3.
- An implementation in POMA (POlicy Machine Analyzer) [10], our open-source toolkit for visualizing, testing, and verifying NGAC policies, integrated with the cvc5 SMT solver [11].
- 4.
- A demonstration with real-world case studies that the proposed research enables the detection of semantic errors and policy safety violations that were previously unverifiable due to the dependence on subtle interactions between sequential actions.
The remainder of this paper is organized as follows: Section 2 reviews related work. Section 3 provides the preliminaries to make the paper self-contained. Section 4 describes the SMT-based approach to NGAC policy verification. Section 5 elaborates on the interdependence analysis of administrative actions. Section 6 presents the case studies, and Section 7 concludes this paper.
2. Related Work
We review related work in the areas of obligation models, verification of administrative access control policies, and SMT-based policy verification.
2.1. Obligation Models
Traditional obligation models focus on conditional access and non-administrative tasks (e.g., sending an email), rather than administrative changes to the authorization elements. Park and Sandhu [8] introduce obligations as requirements that have to be fulfilled by the subject after access is allowed. They describe two kinds of obligations: pre-obligations and ongoing obligations. Pre-obligation is a predicate that verifies that certain activities were performed before the main activity, while ongoing is a requirement that has to be satisfied continuously. Irwin et al. [1] propose a formal metamodel for capturing a system and its possible state from the perspective of obligations, where obligations are some actions that the subject must take in the future. As these obligations are based on specific actions that the user should take but may not take, they are unenforceable (e.g., the reviewer is required to submit a review of the paper by the deadline but may not do so). While XACML provides a syntax for obligation specification, the execution and interpretation of obligations are left to the policy execution engine or application. Li et al. [3] have extended XACML to support practical obligation specification by enriching the obligation syntax and semantics. The obligations are modeled as state machines communicating with access control systems. Margheri et al. [12] present obligations as additional actions connected to the access control system that must be executed by the Policy Enforcement point and usually correspond to logging, sending a message, or executing a command (e.g., sending an email, compressing a file, etc.). The UCON+ model [13], an extension to UCON, uses obligations in session transitions represented as different phases of access: pre-, ongoing, and post-access. The obligations are represented as additional, non-administrative actions that must be performed with access decisions. Furthermore, Shopp et al. [14] present the formal specifications for the UCON+ model, which uses obligations as directives that must be carried out before or after access is approved. Interestingly, their obligations can change attributes that may affect further access states (for example, to prohibit concurrent access to more than five users). However, such changes still cannot be considered administrative as they modify the environment and not the access policy.
2.2. Verification of Administrative Access Control Policies
Access control models fall into two categories: administrative and non-administrative. A non-administrative policy specifies the authorization elements with an access decision procedure. It remains unchanged during execution and may be updated offline by an administrator. For example, role-based access control (RBAC) specifies access privileges in terms of user–role assignment (URA), role–role assignment (RRA), and permission–role assignment (PRA). These assignments do not change at runtime. An administrative policy includes administrative operations to change the non-administrative counterpart. For example, Administrative RBAC (ARBAC) adds administrative commands to RBAC to update the URA, RRA, and PRA relations in an RBAC policy.
A substantial amount of work has been carried out on the verification of administrative attribute-based access control (ABAC) and RBAC policies. Jha et al. [15] have investigated the specification and verification of separation of duty (SoD) constraints in an ABAC model based on access control rules defined over subject, object, and environment attributes. They addressed the SoD enforcement with respect to the modifications of attributes and rules. Jha et al. [16] have also proposed ADABAC (Administrative ABAC) and used Alloy to analyze certain safety and liveness properties. They have further proposed AMABAC, an administrative model for the rule-based ABAC model, and used the datalog-based tool Z to verify AMABAC policies [17]. AMABAC provides administrative relations and commands for managing the subject, object, and environment attributes and access control rules. Users can apply individual commands manually to modify the policy elements and, thus, the access privileges.
Table 1 shows the main methods based on the ARBAC97 model [18]. They deal with administrative changes to URA but not RRA or PRA. iRR (Initial Role-to-Role assignments) means the corresponding method considers the initial role hierarchy before any administrative changes are made. A method without iRR does not handle role hierarchies at all. O stands for obligation-containing policies.

Table 1.
Verification methods for ARBAC.
Our work is comparable to the above studies, as NGAC is more general than RBAC and ARBAC. In NGAC, roles in RBAC correspond to user attributes, and URA (or RRA) maps to NGAC’s user–user attribute (or user attribute–user attribute) assignment. PRA is similar to NGAC’s association relation. However, this work offers the first comprehensive analysis of privilege-changing policies through administrative obligations, a problem not addressed in the previous literature. Our approach not only applies to the URA, RRA, and PRA of ARBAC but also extends to NGAC’s unique features, such as object attribute hierarchies and obligations. Additionally, we verify systematic access control requirements of who can do what and when, rather than merely focusing on user–role relations as in previous studies.
One key distinction between NGAC and administrative access control lies in how NGAC encapsulates a series of administrative commands into a module (e.g., obligation), automatically triggered by a matching access event. In contrast, administrative access control typically addresses individual administrative commands. Consequently, the proposed verification approach must diverge from existing research by addressing sequences of administrative commands. Notably, the interdependency analysis of administrative commands within an NGAC obligation poses a unique challenge not encountered in previous work.
2.3. Policy Verification with SMT
There are also works on the verification of non-administrative ABAC policies using SMT. Such verification involves only a static policy (similar to the initial configuration in NGAC without administrative obligations). Margheri et al. [12] introduced a comprehensive framework leveraging SMT to specify, analyze, and enforce attribute-based access control (ABAC) policies. This framework’s core is a specially designed language named the Formal Access Control Policy Language (FACPL). The framework can automatically verify properties using the authorizations mandated by individual policies and the relationships between multiple policies. FACPL can be translated into the SMT formulas without losing its semantic meaning. Arkoudas et al. [24] introduced SMT-based formal theories and logical frameworks for expressing and verifying access control policies. The authors reduce access adjudication to logical formulas and provide analyses on consistency, coverage, and change impact. Although the frameworks distinguish between policy administrators and policy users, only the administrators can manually change the access privileges. Zelkova [25] is a tool that encodes statically defined AWS policies as logical formulas and then uses SMT solvers to query the properties of these policies, providing users with a mechanism to detect misconfigurations of their policies. Notably, Zelkova is an at-scale industry software invoked millions of times daily. Zelkova does not consider policy changes made by administrators or any form of dynamic evolution of the access policy state.
2.4. Testing of Access Control Policies
This paper differs from testing NGAC policies [10] and obligations [6,7]. Policy testing is an alternate approach for quality assurance of access control policies. Unlike verification, policy testing aims to find errors by executing the policy with a set of test cases (i.e., access requests). The policy is faulty if the policy decision for any request is incorrect. Recent research has focused on test generation methods and policy mutation analysis [26]. Policy mutation is the widely applied approach for evaluating the effectiveness of these methods. It creates a set of mutants of a correct policy and then exercises each mutant against the tests generated by a testing method. A mutant is a modified version of the original policy where a policy element is mutated according to a fault model of representative types of errors. A mutant is said to be killed if at least one test fails; otherwise, it is a live mutant. The effectiveness of the testing method is indicated by the ratio between the total number of mutants killed and the total number of non-equivalent mutants [27]. Chen et al. [28] present a fault-based testing approach to detect errors within NGAC policies, which hypothesizes about potential errors according to the fault model, generates the correct policy versions as mutants, and validates the hypothesis by executing tests.
3. Preliminaries
3.1. Administrative Obligations in NGAC
We refer to privilege configuration as a collection of assignment, association, and prohibition relations on the sets of basic policy elements. Thus, an NGAC policy comprises an initial configuration and a set of obligations . An obligation specifies the response to the access events that match an event pattern, represented by , where , and are sets of subjects (user or user attributes), access rights, and target policy elements (users, user attributes, objects, and object attributes). The response is triggered if an access event matches the event pattern, i.e., , , and , where s is a subject, ar is an access right, and t is a target policy element. The access event refers to the occurrence of a granted access request, i.e., request is permitted under the current privilege configuration.
3.1.1. Configuration and Access Adjudication
The decision to grant or deny an access request is adjudicated according to the current configuration. Formally, a configuration C is a 9-tuple (U, UA, O, OA, AR, PC, ASSIGN, ASSOCIATION, PROHIBITION), where ASSIGN, ASSOCIATION, and PROHIBITION are relations on the sets of users U, user attributes UA, objects O, object attributes OA, policy classes PC, and access rights AR. ASSIGN and ASSOCIATION specify what is permitted. The permissions can be overridden by PROHIBITION. The policy class is a mechanism for policy modularization; each user, user attribute, object, and object attribute should be contained within a policy class.
Assignments
The assignment relation is defined as a subset of the union of the Cartesian products of policy element sets as follows: .
A user can be assigned to a user attribute, a user attribute can be assigned to another user attribute or policy class, and an object attribute can be assigned to another object attribute or policy class.
Definition 1
(Containment). x is said to contain y, i.e., contains(x, y), defined as follows: (1) contains(x,y) if (y,x) ∈ ASSIGN; (2) contains(x, x) if x ∈ UA ∪ OA; (3) contains(x,z) if contains(x,y) and contains(y,z).
As a policy class is a container of certain users, user attributes, objects, and object attributes, its assignment relation can be represented as a directed acyclic graph, i.e., if and . It comprises a user/user attribute hierarchy and an object/object attribute hierarchy. For example, the user is contained by , i.e., , if the following holds: , i.e., there exists a hierarchical relation between and .
Associations
The association relation is defined as , where AR is the set of all access rights and is the set of user attributes and object attributes. Each association (ua, ars, at) specifies one or more access rights ars between a user attribute ua and an object (or user) attribute at.
Prohibitions
Prohibitions define the negation of associations to constrain access rights. They are specified by the conjunctive and disjunctive operators and the inclusion or exclusion complement operators on the assignment and association relations (i.e., the user/object attribute hierarchies and the permitted access rights). The prohibition syntax is , , …, , where s is a subject; is a set of access rights; is an operator, either or ; describes a prohibition container; is a complement operator, either inclusive or exclusive; and is a container (user attribute, object attribute, or policy class).We adopt the formalization of prohibitions provided in [9,10] in this work.
Below, we present the formal definition of access event adjudication that utilizes all the aforementioned relations.
Definition 2
(Access adjudication). Given a configuration C = (U, UA, O, OA, AR, PC, ASSIGN, ASSOCIATION, PROHIBITION) and access request (s, ar, pe), where s is a subject (user or user attribute), ar is an access right, and pe is a policy element (user, user attribute, object, or object attribute), the access decision is “permit”, if the following conditions hold; otherwise, it is “deny”:
- Request (s, ar, pe) is permitted by ASSIGN and ASSOCIATION. In other words, there exists (ua, ars, at) in each policy class pc containing pe such that (1) contains (ua, s), (2) ars, (3) contains(at, pe), and (4) contains (pc, at).
- No prohibition precludes request (s, ar, pe), i.e., there is no prohibition (u,ars,tps) ∈ PROHIBITION such that (1) s = u, (2) ars, and (3) tps, where tps is the prohibition set or policy elements that are targets of prohibition.
Figure 1 shows a portion of the EditingPolicyClass in the GPMS (Grant Proposal Management System) case study. GPMS, an open-source application developed alongside the NGAC standard’s reference implementation, aims at web-based automation of the grant proposal approval workflow at an academic institution. The workflow involves various users in the completion of a proposal data sheet. GPMS is the only open-source real-world NGAC application with complex authorization elements and 19 non-trivial obligations [29]. When a PI-eligible faculty user creates a proposal data sheet (PDS), EditingPolicyClass is instantiated for the new PDS as part of the initial configuration. The configuration also includes three other policy classes. It changes dynamically due to obligation-triggering access events. In Figure 1, there are several user attributes, i.e., UA = {PI,CoPI,SP}. For the object attributes, we use PDSWhole and PDSSections to reference the entire PDS object and the specific data sections of the PDS object, respectively. This is because access rights, such as submit and delete, apply to the entire PDS rather than a specific data section. PDSSections fall into two groups: PIEditable and CoPIEditable. There are several objects, i.e., O = {ProjectInfo, BudgetInfo, UnivCommitmentsInfo, ComplianceInfo, Collaboration Info}. This part of the assignment relation is {(PI, CoPI), (CoPI, SP), (SP, EditingPolicyClass), (ProjectInfo, PI Editable), (BudgetInfo, PIEditable), (PIEditable, PDSSections), (PDSSections, EditingPolicyClass), (PDSWhole, EditingPolicyClass), (UnivCommitmentsInfo, CoPIEditable), (ComplianceInfo, CoPIEditable), (CollaborationInfo, CoPIEditable), (CoPIEditable, PDSSections), (PDSSections, EditingPolicyClass)}. The association relation directly specifies the following privileges: {(PI, write, PIEditable), (PI, submit, PDSWhole), (CoPI, write, CoPIEditable), (PI, delete, PDSWhole), (SP, read, PDSSections), (PI, addCopi, CoPI), (PI, deleteCopi, CoPI), (CoPI, addSP, SP), (CoPI, deleteSP, SP)}. The user attribute hierarchy and object attribute hierarchy also imply the following privileges: {(CoPI, read, PDSSections), (SP, read, BudgetInfo)}, etc.
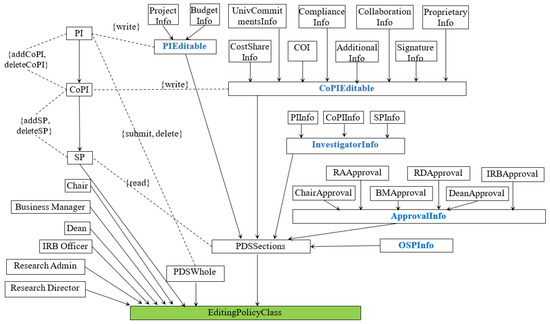
Figure 1.
Editing policy in GPMS.
3.1.2. Response
The response of an obligation is a sequence of one or more conditional actions:
. There are five types of actions: create, assign, grant, deny, and delete. A create action adds a new policy element. An assign action adds a new assignment (x, y) to the assignment relation, i.e., . A grant action adds a new association (ua, ars, at) to the association relation, i.e., ASSOCIATION’ = ASSOCIATION. A deny action adds a new prohibition, i.e., PROHIBITION’ = PROHIBITION . A delete action removes the specified policy elements. As such, the response of an obligation updates the current configuration’s assignment, association, and prohibition relations, thereby changing the access decisions.
The condition or action part in may reference built-in functions of the NGAC implementation and custom functions in the application code (e.g., in Java). For example, in an assign action that adds a new assignment (x,y) by assigning user x to user attribute y, x (or y) may be obtained from the invocation of a custom function rather than a predefined value.
In GPMS, there are 19 obligations. One of them, submit_proposal, is triggered when a PI user performs the operation submit on a PDSWhole. This obligation will remove all the permissions except read from PI, CoPI, and SP and grant the approval powers to Chair. The updated editing policy class is presented in Figure 2, and the obligation is described as follows:
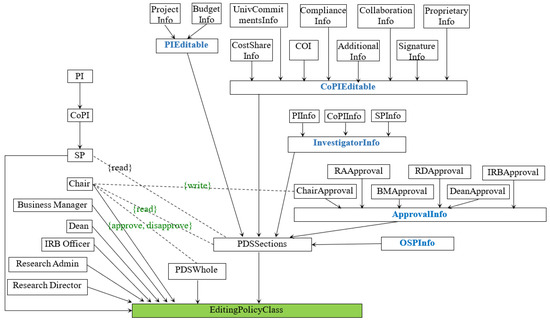
Figure 2.
Editing policy in GPMS after proposal submission.
- Event: A PI user performs submit on the PDSWhole editing policy class.
- Response:(1) Remove association (PI, {submit, delete}, PDSWhole);(2) Remove association (PI, {addCoPI, deleteCoPI}, CoPI);(3) Remove association (CoPI, {addSP, deleteSP}, SP);(4) Grant chair approval and disapproval access rights on PDSWhole;(5) Grant chair access rights on chair approval.
3.2. Satisfiability Modulo Theories
SMT builds upon a propositional satisfiability problem (SAT) that determines if the variables of a given Boolean formula can be assigned consistently to true or false values such that the formula evaluates to true. If such an assignment exists, the formula is satisfiable; otherwise, it is unsatisfiable. For example, is satisfiable because it evaluates to true when both a and b are true. is unsatisfiable because it is false for all possible assignments of a. Although SAT is the first problem proven to be NP-complete, heuristic algorithms in modern SAT solvers often handle hundreds of thousands of variables, sufficient for many practical problem instances. SMT extends SAT by using first-order logic (FOL), providing reasoning for objects and their relations as predicates and quantifiers and thus making the constraints more expressive. Specifically, SMT allows Boolean variables in SAT formulas to be replaced by predicates from various background theories, such as the theories of integers, real numbers, sets, and relations. A predicate is a Boolean variable with parameters representing an operation or relation. Suppose x is an integer and y is a set. The SMT formula , involving theories of integers and sets, is obtained from the SAT formula by replacing a and b with the predicates and , respectively.
Our work leverages the theory of finite sets with cardinality constraints [30]. This theory allows us to express policy elements and policy relations as sets and predicates, check for set membership (∈), and reason with union (∪), intersection (∩), set minus (∖), subset (⊂), and an empty set (∅). For example, adding an assignment can be expressively encoded using union as , where the new assignment is represented as a singleton of a tuple of size 2. Additionally, we use the theory of finite relations [31], which includes reasoning about relational structures. Its operators, such as join (⋈) and transpose , along with tuples of various sizes, allow for expressive encoding of and reasoning about complex NGAC relations. Notably, while cvc5 supports transitive closure, we found that using transitive closure significantly degrades performance in comparison with our current approach, which recalculates only the portion of the containment relation that has changed. A summary of symbols and notations is provided in Table 2.

Table 2.
List of symbols and notations.
4. Overview of the Verification Approach
Our approach aims to verify access control requirements that specify who (i.e., the subject–user or user attribute) can perform what actions (i.e., access rights) on what resources (i.e., objects or object attributes), and under what conditions. The focus is on tracking privilege changes that result from a sequence of obligation executions.
The verification is formalized as the following reachability problem [9]:
Definition 3
(Reachability problem). Given an NGAC policy and a goal property goalObligation(s,ar,t), , the reachability problem is to determine if there exists a sequence of obligation firings, , , …, , such that (1) () is a valid obligation firing, (2) and are satisfied by and , respectively, and (3) matches , including the access event if s, ar, or t is given.
In the goal property , is the goal obligation triggered by access event , describes the condition on the configuration that triggers the target obligation, and specifies the condition on the target configuration. While all three are optional, at least one of them must be given. When goalObligation(s,ar,t) is not specified, it refers to any obligation. When goalObligation(s,ar,t) is given, s, ar, and t are optional. If s is not specified, the event that fires the obligation may be performed by any subject (user or user attribute). This is similar when ar and t are not specified.
The general architecture of the verification approach is presented in Figure 3. It has three main components: reachability analyzer, configuration encoder, and obligation encoder. The reachability analyzer includes the verification algorithm and the logic to process the goal property, while the configuration and obligation encoders are responsible for transforming an NGAC policy into SMT formulas. Additionally, the obligation encoder can be extended by implementing custom functions via the custom function interface. The reachability analyzer uses the NGAC reference implementation to read the policy from JSON and YML files and cvc5 to run our encoding, verify the reachability of the goal, and report the result along the path of obligations and their access events back to the user.
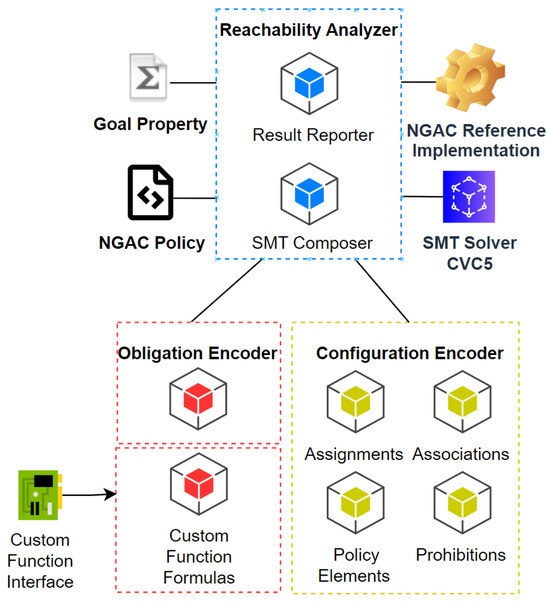
Figure 3.
Architecture of the reachability analyzer.
Our approach to solving the reachability problem aims to find a sequence of obligation firings that reaches the given goal from the initial configuration. To this end, we represent the policy elements and relations of each configuration as bound-tagged variables and access decisions as bound-tagged formulas in the form of (i.e., variable or formula v at bound k). Each obligation firing is translated into a formula that describes the transition of the configuration state from each bound to k according to the obligation’s event pattern and response. Let be the SMT encoding of expression e and represent the firing of obligation at bound k. , , , and are bound-tagged as , , , and , respectively. A solution at the given bound k exists if is satisfiable, where is the disjunction of the state transition formulas of all obligation firings from to k; otherwise, we continue with a new bound .
Algorithm 1 describes the verification procedure. Variable holds the SMT code of the configurations and obligations (to be discussed in subsequent sections). The outer loop iterates (lines 4–16) over the bounds until a solution is found. The solution includes the path of obligation firings and all user-defined variables in the property. If no solution exists at the bound k, the next bound reuses the encoding from all the previous iterations and only deals with the encoding for the new bound. The inner loop (lines 6–8) obtains the encoding of the state transitions of all obligation firings for the current bound. Their disjunction, i.e., , is asserted on line 10 using exactly one constraint, ensuring that only one obligation is fired at each bound. And lines 11–14 assert the goal based on the input, while line 15 sends the and to solver.
| Algorithm 1: SMT-based verification |
 |
While our approach bears similarity to SAT-/SMT-based planning [32,33] and bounded model checking [34], our SMT-based encoding is distinct. The configurations and obligations of NGAC policies are rather complex. As described in Section 3.1, access adjudication is determined by ASSIGN, ASSOCIATION, and PROHIBITION. The decision procedure involves reasoning about the user attribute hierarchies and object attribute hierarchies implied by , the transitive closure of ASSIGN. Thus, an SAT-/SMT-based approach must correctly encode the reasoning of hierarchies as a logical formula. There are two possible techniques: (a) applying transitive closure constraints to deal with the hierarchies directly and (b) flattening the hierarchies by calculating the transitive closure, i.e., enumerating every pair in . Solving constraints with transitive closure is generally an undecidable problem [31]. Our experiment has shown that the transitive closure implementation in cvc5 cannot solve the constraints in our case studies. In this paper, we calculate when encoding the assignment relation as an SMT formula. This requires recalculation of whenever an obligation firing changes ASSIGN. To deal with the complex structures of NGAC configurations, our approach builds upon SMT solvers for the Theory of Sets [30] and finite relations [31].
4.1. Configuration Encoding
Given the inherent support for set theory in the cvc5 SMT solver, we represent a set as a predicate, allowing the elements of the set to be determined by a predicate that can vary based on a bound. Previous work has largely encoded each element as a single proposition (true or false in logic). However, this approach is inefficient in the context of NGAC, where extensive operations on sets and evolving set membership are common. Given C=, , , , ASSIGN, ASSOCIATION, PROHIBITION), encoding of configuration C is defined as follows:
=
.
The encoding of set S depends on what a relation or set of policy elements S represents. For example, set U is encoded as a set of all users. And the relation ASSIGN is represented as a set of tuples (ancestor,descendant). Other policy elements and relations are encoded similarly.
We encode both ASSIGN and for reasoning about the explicit assignment, implicit assignment, and containment. The predicate permit(s,ar,pe) corresponds to the permission adjudication of subject s, access right , and policy element . Its SMT formula is defined as follows:
We utilize the operations of finite relations to derive the set of implicit prohibitions, PROHIBITION*, based on the PROHIBITION, , and sets:
, where is derived as follows:
and means whether the prohibition set is conjunctive or disjunctive. is the if–then–else structure in cvc5. If any prohibition set is marked as exclusive, each resulting set is subtracted from .
4.2. Event Encoding
As previously described, an obligation is fired if an event (i.e., permitted access request) matches the obligation’s event pattern EVENT(SS,SAR,ST). We encode the obligation firing implication for the event using access adjudication based on the configuration encoding of the previous bound :
Predicate represents a permitted access request. Its occurrence will trigger the obligation if (a) subject ?s is either included in the subject set SS or contained by a user attribute ua in SS; (b) target policy element ?t is either included in target set ST or indirectly included via containment by a user or object attribute at; and (c) ?ar is contained by the set of access rights SAR.
4.3. Response Encoding
The response consists of one or more conditional actions. The precondition specifies under which configuration the action applies, whereas the effect describes the action’s changes to the configuration. The relation between the action’s condition and effect is denoted as “if” or implies(⇒). We encode each action’s condition and action effect , where i is the index of the conditional action in the obligation :
The above formula demonstrates possible disabling causal interference by every preceding action on every consequent action . Such interference may disable consequent actions by falsifying their precondition. Additionally, the above formula includes enabling causal interference, , which enables action by satisfying the condition that was not satisfied prior to action execution.
We define causal interference below:
Definition 4
(Causal interference). Action has enabling causal interference on action if the effect of enables by satisfying its condition and disabling interference if the effect of disables by falsifying its condition . The causal interference is disabling if both and are augmentative or reductive and enabling if one is augmentative and the other is reductive.
The calculation of causal interference depends on the precise formalization of the precondition and effect of each individual action provided in Section 5. The interdependency analysis and encoding of conflicting actions will be shown in Section 6.
We categorize actions into two types: augmentative and reducing. Augmentative action expands ASSIGN and ASSOCIATE relations, while reductive actions shrink the relations.
Additionally, we need to encode the reason for a change to express why the NGAC configuration was changed based on which part of the configuration was affected by the actions of obligation . The reason for the change in ASSIGN, ASSOCIATION, and PROHIBITION is represented informally as follows: if there exists at least one obligation and one action , where the firing of entails , and if there is a change to the ASSIGN relation, then must be related to modifying assignments; if there is a change to the ASSOCIATION relation, then must be related to modifying associations; if there is a change to PROHIBITION, then must be related to modifying prohibitions. Formally, we represent this as follows:
4.4. Soundness and Completeness of SMT-Based Verification
The reachability problem in Definition 3 is undecidable, as shown in [9]. This result is consistent with the classical undecidability of the access matrix model [35] and highlights the additional complexity introduced by dynamic obligations. Nevertheless, the undecidability of the general problem does not preclude the development of practical verification techniques for real-world applications.
To enable formal reasoning in real-world scenarios, we introduce a terminal bound K and analyze reachability within this finite horizon. In this section, we formally prove the soundness and completeness of Algorithm 1 with respect to the bounded reachability formulation. We begin by defining symbolic encoding, model interpretation, and operational semantics.
Let C denote a configuration and let denote an access event. The transition semantics of NGAC are defined inductively by the relation
which holds if and only if
- 1.
- The access request is authorized in .
- 2.
- Any obligations triggered by are instantiated according to .
- 3.
- The execution of these obligations results in a state change to .
We say a configuration satisfies , written as follows:
if there exists a step such that
- 1.
- ;
- 2.
- is executed at step j;
- 3.
- The corresponding obligation , which is the same as the specified goal obligation , is triggered by ;
- 4.
- The obligation response actions are completed successfully in the trace;
- 5.
- The resulting configuration satisfies .
Let denote the SMT encoding of NGAC execution semantics and obligations over K steps. This encoding yields a formula such that any model M satisfying corresponds to a sequence of events that induce the following transitions:
We assume that is the correct abstraction of the NGAC semantics:
4.4.1. Soundness
Theorem 1
(Soundness). Let be the initial configuration, be the goal property, and K be a terminal time bound. If Algorithm 1 returns a at bound , then there exists a valid sequence of access events {}, such that starting from configuration , these events lead to configuration , where the goal property is satisfied:
Proof.
We prove the soundness of Algorithm 1 by induction on the length k of the access event trace, where and the SMT solver returns a satisfying model at bound k.
Let be an SMT formula encoding NGAC semantics and goal satisfaction over k steps. Suppose that the SMT solver finds a model . We aim to show that this model corresponds to a valid NGAC execution trace such that .
Base case (): The model M encodes a single access event such that
- 1.
- holds in ;
- 2.
- is executable in and triggers the obligation ;
- 3.
- The obligation executes fully within one step, resulting in configuration , where holds.
By the correctness of the transition relation, we conclude the following:
Inductive case (): Assume the inductive hypothesis holds for all . Any model corresponds to a valid execution trace such that satisfies the goal if the SMT encoding requires it.
Now suppose the SMT solver returns at bound , encoding the access events:
Through the construction of , the event is enabled in , which is a result of executing the prior n events. That is,
From the inductive hypothesis, we know the following:
and the semantic preconditions for hold in .
Furthermore, encodes the goal satisfaction condition as follows:
- holds in ;
- is triggered;
- The obligation has completed execution;
- .
Hence,
Conclusion: Through induction on k, any satisfying model of the SMT encoding corresponds to a valid NGAC execution trace of length k that satisfies the goal. Therefore, if Algorithm 1 returns SOLUTION, the goal is reachable within steps in the NGAC semantics. □
4.4.2. Completeness
Theorem 2
(Completeness). Let be the policy, the goal property, and K a terminal time bound. If there exists a valid access event sequence
such that, starting from configuration , the trace induces transitions
and with , then Algorithm 1 returns SOLUTION
at bound k; that is, the SMT encoding is satisfiable and a model exists.
Proof.
We prove the completeness of Algorithm 1 by construction. Assume there exists a valid execution trace
such that each transition
respects the NGAC operational semantics and satisfies the goal property
We aim to show that the SMT encoding produced by Algorithm 1 at bound k is satisfiable and that there exists a model .
Let be the sequence of access events in this valid trace and let be the corresponding sequence of configurations. Since all transitions are valid and respect NGAC semantics by assumption, we now define a model M such that
- 1.
- For each , the valuation of state variables in M at step i corresponds exactly to the configuration .
- 2.
- The event variables are assigned to represent the events executed at each step.
- 3.
- The valuation of any obligation-firing variables and state predicates (e.g., , ) matches the satisfaction conditions in the concrete trace.
Such a model M satisfies the transition constraints in because all transitions are valid according to the NGAC semantics. Furthermore,
- holds at ;
- is executed, triggering ;
- the obligation completes execution before step k;
- .
So the goal satisfaction constraints encoded in are also satisfied.
Therefore, we define model M over k steps such that:
- ;
- , and all other event variables at step i are false;
- if is fired at step j;
- and .
Therefore, this concrete execution trace induces an assignment to all symbolic variables that makes true. Hence, the SMT solver will find model , and Algorithm 1 will return SOLUTION at bound k.
Conclusion: If a valid execution trace satisfying the goal exists within bound K, then the SMT encoding is satisfiable and Algorithm 1 will find a solution. □
Remark: Since the encoding yields a quantifier-free formula in decidable SMT theories (e.g., sets, relations, integers, uninterpreted functions), satisfiability is decidable. Thus, soundness and completeness together imply that Algorithm 1 is a decision procedure for the bounded reachability problem.
5. Formalization of Individual Actions
To analyze the interdependencies of actions, we examine the preconditions and postconditions of each action. In this section, we provide specifications for the precondition p(a) and effect q(a) for each built-in action a in the NGAC standard, encoding these actions as SMT formulas.
5.1. Create Policy Element
The precondition for creating a policy element consists of three predicates: the policy element pe should not exist before its creation and the descendant d of the new policy element must exist and must be an object attribute for object attributes and objects, a user attribute for user attributes and users, or a policy class for attributes. Therefore, the precondition is formalized as follows:
The effect of creating a policy element must ensure that the policy element exists and the assignment to its descendant also exists.
Note that a policy class is unlikely to be created using obligations, but it is possible. In this case, there will be no need to check the descendant; the “policy class existence” check will be the only precondition required.
5.2. Delete Policy Element
The precondition for deleting a policy element should ensure that the policy element exists. If such a policy element is a descendant of any other policy element , such policy elements should have another descendant attribute . This ensures that we delete only one policy element.
The effect ensures that the policy element does not exist and the assignment to the last descendant d is deleted:
5.3. Add Assignment
The precondition for adding an assignment ensures that ancestor a and descendant d exist, that a is not a policy class, that d is an attribute, that the assignment does not exist, and that the assignment does not exist, as cycles are not allowed.
The effect ensures that the assignment has been created:
5.4. Delete Assignment
The precondition for removing an assignment ensures that assignment exists and that ancestor a has at least one other assignment to another attribute at. This ensures that we do not delete a policy element by deleting an assignment.
The effect ensures that the assignment (a,d) has been deleted:
5.5. Grant
The precondition for granting an access right or creating an association ensures that an association with the user attribute ua, access right ar, and attribute at does not exist and that the user attribute and the attribute of the association do exist and are of a correct policy element type.
The effect of the grant action ensures that the association has been created.
5.6. Delete Association
The precondition for removing an association ensures that the association exists, where is a user attribute of the association, is the access right, and is the attribute of the association.
The effect, meanwhile, ensures that the association has been deleted.
6. Action Interdependencies Analysis
To encode the obligation response correctly, we need to capture the exact sequence of the actions’ execution steps within an obligation, ensuring that they are executed in the correct order and that their interdependencies are accurately captured. For example, consider two sequential actions, and . These actions have respective preconditions and and effects and . The execution of the procedure is as follows: . In the absence of any conflict, the procedure can be encoded using the commutative logical operator ∧. As multiple state transitions can occur before the execution of the obligation, altering the ASSIGN and ASSOCIATION relations, conflicts may not be detectable until the obligation is executed.
Next, we define causal interference and present the interference rules and the SMT encoding of the interference within an obligation.
6.1. Interference Between Actions
While obligations are synchronized, no other obligation can change the configuration before the obligation completes its actions; an action’s effect within an obligation can affect the preconditions of subsequent actions. We separate actions into two groups: augmentative and reductive. An augmentative action adds either an assignment or association to a configuration relation, while a reductive action removes them from a configuration relation. For example, a reductive action like “delete policy element” will disable the augmentative action “assign” if the policy element is an ancestor or descendant of the former assignment. In this case, both actions are within the same relation, . Similarly, actions acting on two different relations can also interfere. The “delete policy element” action will also disable the “grant” action if the policy element is a user attribute or an attribute of the association being added.
To identify actions that cause interference with another action, we perform a static analysis of the actions before encoding. Consider Figure 4, where action has a disabling causal interference on action . Possible action executions are represented as a binary tree, with each path from event(s,ar,t) to the leaf representing a possible execution path for these two actions. If action is augmentative and action is disabling, we encode the precondition of as a conjunction of interference and the precondition of action 2, . If the precondition is satisfied, then the effect may interfere with the precondition action .
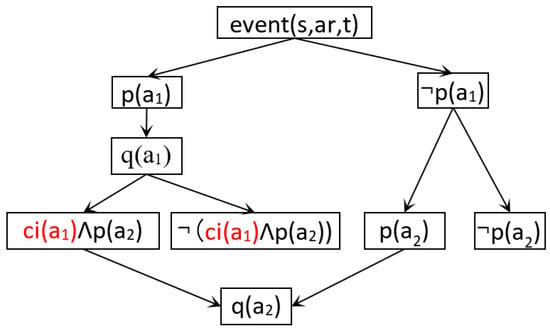
Figure 4.
Causal Interference of two actions.
Formally, without disabling conflict(e.g., no ), the actions are represented as follows:
Now, considering , the resulting encoding needs a disjunction of two traces: one trace represents the case where disabling causal interference does not prevent the effect of action . This encoding is presented below:
Of course, the above formula can be further simplified by extracting the independent action as follows:
Now let’s consider Figure 5, where three consecutive actions and action affects and , while action also affects . Each path from the root node event(s, ar, t) to a leaf node represents a possible execution trace conditioned on whether an action’s precondition holds or not. The branching corresponds to evaluating the truth values of preconditions , , and . If holds, then executes. However, this may invalidate the precondition of , expressed as the interference condition . If is not disabled, then may also interfere with through another interference condition .
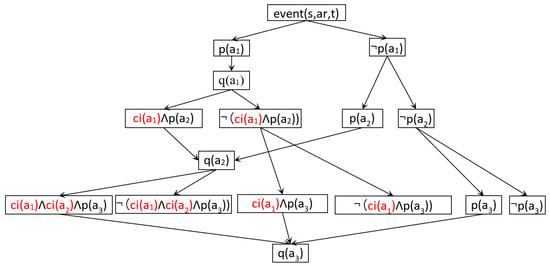
Figure 5.
Causal interference of three actions.
The tree structure explores all combinations of interference or non-interference:
- The leftmost leaf represents the case where and both interfere with , and holds. Hence, executes only if .
- The leaf represents the complementary case where at least one interfering condition fails, so ’s precondition can still hold.
- Other branches show intermediate scenarios, such as interfering but not interfering, or vice versa.
Thus, Figure 5 models all possible interference paths and highlights the cumulative effects of nested conflicts. This interference-aware encoding ensures that verification only considers sound execution traces during bounded reachability analysis.
In the absence of disabling conflicts, the actions are formulated as follows:
The formalization of the actions with conflicts is as follows:
The reason why encoding multiple traces is essential for accurately encoding NGAC obligations is due to the fluidity of the policy resulting from the obligation. It is unknown whether a conflict will occur before the obligation is triggered, and this depends on the configuration before the obligation is executed.
6.2. Interference Rules: Enabling Actions
In the previous subsection, we presented several examples of disabling causal interference between actions. This subsection describes every enabling causal interference using the configuration modification set defined below:
Definition 5
(configuration modification set). The configuration modification set (CMS) is a function of the action’s effect and the configuration relation changed by the action, which produces a subset of assignments or associations that are either added or removed by the effect, formally CMS(a, RELATION).
To find a correct interference, we utilize policy elements of the actions and the configuration modification set, which are extracted during the actions’ encoding phase and available for the analysis and encoding of the interference. For example, if there is an action “” followed by “”, the causal interference of action on action is as follows: , because CMS may contain the assignment , enabling a “remove assign” action as it requires an ancestor to have at least one other assignment. Such a condition of “at least one other assignment” is a guard (G). Therefore, we consider such interference enabling, as “assign” enables a “remove assign” action. The path condition for the enabling interference is , meaning that either the guard has to already be true before the former “assign” action execution or ci should be true, enabling the consequent “remove assign” action. Clearly, if the former action “assign” does not execute, the CMS will be empty, and therefore, ci will evaluate to false and the path condition will only rely on G. This approach avoids the need to build execution trees while conveniently utilizing CMS, which is calculated during the execution of actions. Below, we explain each enabling interference rule we use in our analysis.
6.2.1. Remove Assign Action Enables Assign Action
Given a remove assign action , “ ” followed by an assign action , “”, the causal interference affecting is represented as follows:
The left part of the disjunction represents removing an assignment that will be created; therefore, the precondition of must not be fulfilled before the execution of action . The right part fulfills the precondition that no circular implicit or explicit assignment is allowed; hence, is based on .
6.2.2. Create Policy Element Action Enables Remove Assign Action
Given a create policy element action , creating policy element contained by , followed by a remove assign action , removing the assignment , the causal interference affecting is as follows: .
The causal interference may enable because the ancestor of the deleted assignment, in this case, , must be contained by another policy element to remove the assignment, and may create such an assignment . While it may seem that is necessarily equal to , this may not always be true. NGAC obligations have standard and built-in functions that we also encode. These functions dynamically retrieve the user executing an event, triggering the obligation and the policy element on which the action was executed. Therefore, while may equal , there may be execution paths where they are not equal, and causal interference will not enable .
6.2.3. Create Policy Element Actions Enable Grant Action
Given a create policy element action , creating a policy element contained by , followed by a grant action , creating an association , the causal interference affecting is as follows:
This conflict represents an interesting case where a preceding action affects the action that changes a different relation (in this case, ). Therefore, our algorithm, presented in Section 6.4, analyzes both interfering actions of the same type and those where the type differs. Also, this is one of the cases where CMS is not utilized in calculating .
6.2.4. Delete Policy Element Actions Enable Create Policy Element Action
Given a delete policy element action , removing the policy element , and a create policy element action , creating policy element contained by , the causal interference affecting is represented as follows:
This interference represents perhaps the most straightforward conflict, where deleting a policy element enables the creation of a policy element, as the policy element is not a duplicate anymore.
6.2.5. Grant Action Enables Remove Grant Action
Given a grant action , creating an association , followed by a delete grant action , deleting an association , the causal interference affecting is as follows:
In the above formula, represents the predicate where creates an association with access rights and the consequent deletes either some access rights created by or the created association entirely.
6.2.6. Delete Grant Action Enables Grant Action
Given a delete grant action , deleting an association , followed by a grant action , creating an association , the causal interference affecting is as follows:
Similarly to the previous case, the conditional interference is based on the association of the previous action. may enable the association created by by deleting the previous action.
As all the above cases handle enabling causal interference, the complete precondition in each of the described cases of becomes , meaning that either the precondition (based on the RELATION of the previous step) is true or the enabling interference (based on changes in the previous action) is true.
6.3. Interference Rules: Disabling Actions
Similarly to enabling interference, a disabling interference calculation also relies on policy elements and CMS. For example, a “create policy element” action, which creates a policy element and assigns it to a specified descendant , may disable the consequent “” action, which may create a duplicate assignment, or it may lead to a cycle within the configuration. The G of the “assign” action is , meaning that there cannot be a conflicting assignment, and should not be contained by ; otherwise, the assignment will produce a cycle. Therefore, the causal interference is . Every action that produces disabling interference has the following execution path condition: . Note that, unlike in enabling interference, the execution path must contain the conjunction of the guard and the causal interference because both G and ci must be satisfied for an action to be executed, unlike with enabling action, where either G or ci must be true for an action to be eligible for execution.
6.3.1. Assign Action Disables Assign Action
Given an assign action , “”, followed by an assign action , “”, the causal interference affecting is represented as follows:
The left part of the conjunction checks for duplicate assignment; therefore, the precondition of must not be fulfilled before the action is executed. The right part fulfills the precondition that no circular implicit or explicit assignment is allowed; hence, is based on .
6.3.2. Remove Assign Action Disables Remove Assign Action
Given a remove assign action , “ ”, followed by a remove assign action , “”, the causal interference affecting is represented as follows:
The above condition represents a case where deletes a possible next-to-last remaining assignment of the ancestor . This case arises, and the descendants of both actions are different.
6.3.3. Delete Policy Element Action Disables Remove Assign Action
Now consider a delete policy element action , removing the policy element , followed by a remove assign action , removing the assignment , demonstrated as follows:
Like the previous conflict, may delete a possible next-to-last remaining assignment of the ancestor .
6.3.4. Delete Policy Element Action Disables Grant Action
Given a delete policy element action , removing the policy element , followed by grant actions and , creating an association , is a follows:
This interference occurs when a preceding action deletes a policy element of the association, preventing the grant action from being executed.
Notably, unlike other types of disabling interference, this conflict involves both an augmentative and a reductive action, which does not adhere to Definition 4 and is treated as an exception, where all disabling interference rules should involve actions of the same type. We treat this as a special case.
6.3.5. Grant Action Disables Grant Action
Given a grant action , creating an association , followed by grant action , creating an association , the causal interference disabling is as follows:
This causal interference represents the possible creation of a duplicate association by before the execution of .
6.3.6. Delete Grant Action Disables Delete Grant Action
Given a grant action , deleting an association , followed by a delete grant action , deleting an association , the causal interference disabling is as follows:
This causal interference describes the case where an association is removed before removing the association again, stopping the consequent action from being executed.
6.4. Interference Encoding
To encode the causal interference, we exploit the fact that the actions within obligations are sequential, and the sequence does not change. Therefore, our preprocessing algorithm is bounded by a time complexity of and space complexity of . In the algorithm, we process each action once and save the prerequisite, a collective term for CMS(a, relationType) and actionType, in a list of all prerequisites. During each iteration, the algorithm uses all prerequisites found so far and calculates the causal interference of the current action using rules described in the previous subsection. As there is a possibility that all prerequisites will impact the consecutive actions and the algorithm will have to find causal interference based on the prerequisites found so far (e.g., the series of prerequisites applied at each step is 1 + 2 + 3 + … + n), the time complexity will be bound by . Since one prerequisite is extracted per action, the space complexity is bound by , where n is the number of obligations. Note that the presented time complexity is only for the preprocessing of actions. The time complexity of reachability analysis will remain exponential, as previously described.
Algorithm 2 describes the procedure of encoding the causal interference. Prerequisites represent an ordered list of attributes that describe an action, such as the configuration modification set (a relation that the action modifies), the relation type, and the action type. The outer loop (lines 2–15) iterates over all the actions within an obligation, saving the action attributes. These attributes will be used to calculate causal interference within the inner loop (lines 5–12). The causal interference is calculated according to the rules described in the previous section based on each prerequisite extracted from the preceding actions. The first conditional (lines 6–8) describes enabling causal interference encoding, where the action type of the action and the action of the prerequisite differ, while the next conditional (lines 9–11) describes disabling causal interference encoding, where the action type is the same. The causal interference is amended to the precondition as a conjunction or disjunction based on the action type, as demonstrated. Finally, line 14 adds the prerequisite of the current action to the list of prerequisites to encode the subsequent actions. The prerequisite of the current action will not be used on itself.
| Algorithm 2: Conditional interference encoder |
 |
To encode possibly interfering actions, we first extract the configuration modification set (CMS) from the preceding action (1st action). The CMS describes the change in the configuration in terms of relations that are added or removed from the assignments or associations. Using the CMS, we find a causal interference that may occur in every subsequent action (second action). Such interference varies between actions and depends on the guard (or condition) of the subsequent action. There may be multiple types of guards. Additionally, if an action has a user-specified condition, that condition becomes part of the guard. After the causal interference is found and appended as a part of the actions’ precondition, we encode the obligation traces as a disjunction of all the obligation action traces. The encoding of obligation with actions and , where affects and both actions are of relation type ASSIGN with the same action type, “augmentative” (e.g., add assignment), is as follows:
Note the distinction between CMS(a, ASSIGN) and . The former is constant and represents the set being modified by the action. The latter is variable, can be empty if the action’s condition is not satisfied, and will be equal to CMS(a, ASSIGN) if the action is executed. Afterward, we combine the changes executed by and and the encoding of by either performing a union or set minus operation, depending on whether the action type is augmentative or reductive. In this case, both actions are augmentative:
Similarly, when there are three actions, affects and , and action is reductive, the response encoding is as follows:
Now, because is reductive, the encoding becomes as follows:
When the action ASSIGN is related, we must calculate the causal interference for the flattened version of the assign relation, . The encoding of is similar to the above; however, the configuration modification set, , is more complex as it captures the change in the ASSIGN relation and the changes that occur due to the containment relation within . For the above example, the encoding is as follows:
And the encoding is as follows:
Due to the changes in containment relations caused by assignment-related actions, the presence or absence of causal interference cannot be predicted before the obligation is executed. Therefore, the encoding of execution traces with and without interference is crucial. Importantly, we are not attempting to find the interference; we only aim to encode the actions correctly. The interference can then be found using the properties within our reachability analysis.
It is important to note that Algorithm 2 and the corresponding interference encoding do not constitute a decision procedure for detecting interference. Rather, the goal of the encoding is to conservatively capture all possible causal interference scenarios that may arise in the execution of obligations. The SMT constraints simply ensure that interfering paths are not prematurely excluded from the reachability formulation.
Because the interference encoding is structural and syntactic, based solely on the configuration modification sets and action attributes, it is not necessary to prove its soundness or completeness in a semantic sense. The correctness of the overall analysis is instead deferred to the reachability analysis itself, which operates over the fully encoded transition space. In this context, interference constraints serve as symbolic guards within SMT formulas and are not required to be semantically minimal. Thus, the correctness is subsumed under the soundness and completeness of the bounded reachability encoding presented in Section 4.4.
7. Case Studies
Our approach was based on the Java-based NGAC reference implementation [36] and the cvc5 solver. This section applies the approach to two NGAC policies, GPMS and LawFirm, from the recent literature [10,37].
7.1. The NGAC Applications
GPMS is the first fully fledged open-source NGAC application that utilizes obligations to address runtime privilege changes [37]. It automates an academic institution’s grant proposal approval workflow, involving various users such as faculty members (principal investigators/PIs; co-investigators/Co-PIs; and senior personnel/SP), department chairs, deans, business managers, IRB officers, and research administrators. Such workflows exist in many other domains, such as healthcare and finance.
GPMS has 30,249 lines of Java code. Its policy has four policy classes and 19 obligations. Each proposal data sheet (PDS) carries its own policy instance, where the configuration depends on the workflow status and the users involved. Consider a small portion of the workflow: a principal investigator (PI)-eligible faculty member initiates a PDS, works with CoPI and senior personnel (SP) users (added and deleted dynamically), edits the PDS, and submits it for approval by all PI and CoPI chairs (added and deleted dynamically).
LawFirm is an NGAC policy for case tracking at a law firm. Many law firms utilize case tracking systems to manage cases, billing, and file sharing. A law firm has attorneys of various ranks (lead attorneys and available attorneys), each with distinct access privileges. The dynamic changes are carried out via obligations. LawFirm has one policy class with two hierarchies of attributes. The user attribute hierarchy deals with the employees, and the object attribute hierarchy manages the cases. Unlike GPMS, LawFirm has no application code.
7.2. Conflict Identification in Verification of Access Control Requirements
For GPMS, we analyzed 197 requirements, and for LawFirm, we analyzed 92 requirements. As it is not hard to ensure the correctness of initial configurations, we focused on the obligation requirements. The primary goal was to verify the access control requirements arising from conflicting actions.
For example, consider the following example of a disabling action from a real-world faulty scenario:
- Event: A PI user performs deleteCoPI on the PDS’s CoPI data.
- Response:(1) Delete policy element copiuser;(2) Delete assignment (ChairFor(copiuser), Chair);(3) Delete assignment (BMFor(copiuser),BM);(4) Delete assignment (DeanFor(copiuser), Dean).
Let us break down the actions of the above scenario into preconditions (p) and effects (q).
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
In the above scenario, action (1) disables actions (2), (3), and (4) because by performing the delete policy element copiuser, it invalidates the common precondition of the action , as the copiuser must exist to find their chair, business manager, and dean. This is an example of a disabling action. This particular policy error could be fixed by making action (1) the last action. The following access control requirements can be used to detect this error:
The above property verifies that if , , and are still contained by the respective attributes, the chair, BM, and dean, after the obligation runs, this means that actions (2), (3), and (4) were disabled due to conflict with action (1).
An example of an enabling action is demonstrated below:
- Event: A PI user performs addSP on the PDS’s SP data.
- Response:(1) Create policy element in ;(2) Assign to SP if is eligible (i.e., is contained by ).
Similarly, the precondition and effect are demonstrated below:
- 1.
- ;
- 2.
- .
Here, action (1) is enabling as it enables the precondition of action (2) by creating a policy element contained by SPEligibleFaculty. In this case, the enabling interference does not represent an error and is intentional because in order to assign to attribute, this user needs to be eligible to be . To verify the correctness of this obligation, it is enough to simply check whether is contained by attribute after obligation addSP is triggered:
As discussed in Section 2, most prior methods rely on bounded model checking or specialized reachability analyses to verify administrative changes such as user–role assignments (URA), role–role assignments (RRA), permission–role assignments (PRA), inverse role reachability (iRR), and object permissions (O). These approaches typically assume a centralized administrator making predefined changes, without capturing real-time, user-triggered administrative events.
In contrast, the case studies in this section and the next section demonstrate that our SMT-based verification method supports policies in which relations similar to URA, RRA, PRA, and iRR emerge dynamically as part of user-driven obligations. Our approach verifies these changes not in isolation but as part of complex obligation chains triggered by real-world events. Both the GPMS and LawFirm workflows exhibit dynamic creation and deletion of users, hierarchical changes, and access grants, capturing the semantics of URA, RRA, and PRA, all controlled via obligations rather than static administrative actions.
Thus, our work not only statically verifies access control properties but also supports full verification of dynamic, user-initiated administrative workflows. This makes our contribution fundamentally more expressive and realistic for modern distributed systems. The ability to analyze obligations with conflicting actions further distinguishes our approach.
8. Scalability Analysis
To analyze the scalability of our approach, we created several GPMS test policies. These policies are described in Table 3 in terms of the number of assignments, flattened assignments, access rights, and obligations (we separate assignment- and association-related obligations as assign actions are significantly more complex due to hierarchical changes). Each obligation has up to five actions, with at least two conflicting actions.

Table 3.
GPMS synthetic policies.
For each policy, we conducted several experiments where we performed a reachability analysis and attempted to trigger a particular obligation within the provided number of steps (horizon). We recorded the cvc5 solver’s output, the time, and the lines of the generated SMT code. The experiments were conducted with 16GB of memory and six Intel Core i7 8th Gen 2.2GHz cores. In the policy with no hierarchical changes and changes only to the associations, , we reached a horizon of 15, meaning that 15 obligations were triggered consecutively. The changes to association relations are the most anticipated ones in any workflow (e.g., it is easier to grant or remove an access right without complex changes to the attribute hierarchy). While changes to assignment relations should be avoided, they may occur in certain workflows. Therefore, we also present , where three obligations change assignments and eleven change the association relation. With this policy, we achieved a horizon of 12 within the time allotted. The hardest policy, , had obligations that only changed the assignment relation. With this policy, we achieved a horizon of 5. However, several hierarchical changes within a workflow are highly unlikely in the production system. We also consider the number of facts inferred by cvc5 to measure the relative complexity of the task. Fact inference is a conclusion that the solver draws during its reasoning. For example, if the solver determines that a specific element must be a member of a particular set, that would be an inferred fact within set theory. We provide the lines of code (LOC) generated by our algorithm for reference. The complete results for each policy are presented in Table 4, Table 5 and Table 6.

Table 4.
.

Table 5.
.

Table 6.
.
9. Conclusions
We have presented an approach for analyzing the action interference of administrative obligations for an SMT-based verification. Unlike previous access control models, in NGAC, policies can be altered dynamically in response to access requests that match the obligation’s event. While obligations allow the policies to be more expressive and dynamic, they also introduce unique challenges. Our work presents a comprehensive analysis of the interdependencies among obligatory actions, where an action can both enable and disable other actions within an obligation. This requires careful encoding of the precondition and effect of each NGAC action, as well as analysis of their interactions within an obligation. Using the causal interference encoder algorithm and our proposed interference rules, we could encode and analyze these interdependencies as SMT formulas. The case studies demonstrate that the proposed approach can identify various errors in the event and response to obligations.
The presented approach is particularly relevant in systems where dynamic policy updates can introduce significant security risks, such as privilege escalation or denial-of-service. These risks arise in cloud environments, enterprise identity and access management platforms, and zero-trust architectures, where obligations or similar mechanisms are used to automate policy changes in response to specific events. Our approach enables precise analysis of such obligations to ensure that administrative actions do not inadvertently interfere with each other, helping to detect and prevent unsafe policy transitions before deployment.
Regarding future work, we aim to extend our methodology for encoding obligations to perform model checking of NGAC policies against intricate properties, such as those expressed in linear temporal logic. Additionally, we are interested in exploring the use of Large Language Models (LLMs) to generate NGAC policies and applying model checking techniques to identify potential hallucinations and errors within the generated policies. The increasing potential of smaller LLMs running on local servers makes it feasible to generate such policies without transferring access control requirements over the Internet. This approach aims to reduce the time administrators spend on policy design, allowing them to focus more on quality assurance.
Author Contributions
Conceptualization, V.D. and D.X.; methodology, V.D., L.C., and D.X.; writing—original draft preparation, V.D., L.C., and D.X.; supervision, D.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the US National Science Foundation (NSF) under grants 2152057 and 2318891.
Data Available Statement
Data is contained within the article. The software and data are available at https://github.com/dianxiangxu/POMA (accessed on 10 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| ABAC | Attribute-based Access Control |
| NGAC | Next Generation Access Control |
| FOL | First-Order Logic |
| SAT | Boolean Satisfiability Problem |
| SMT | Satisfiability modulo theories |
| POMA | POlicy Machine Analyzer |
| GPMS | Grant Proposal Management System |
References
- Irwin, K.; Yu, T.; Winsborough, W. On the Modeling and Analysis of Obligations. In Proceedings of the 13th ACM Conference on Computer and Communications Security (CCS’06), Alexandria, VA, USA, 30 October–3 November 2006; pp. 134–143. [Google Scholar]
- OASIS. eXtensible Access Control Markup Language (XACML), Version 3.0. 2013. Available online: https://www.oasis-open.org/committees/tc_home.php?wg_abbrev=xacml (accessed on 31 August 2025).
- Li, N.; Chen, H.; Bertino, E. On Practical Specification and Enforcement of Obligations. In Proceedings of the 2nd ACM Conference on Data and Application Security and Privacy (CODASPY’12), San Antonio, TX, USA, 8–10 February 2012; pp. 71–82. [Google Scholar]
- Sandhu, R.; Park, J. Usage Control: A Vision for Next Generation Access Control. In Computer Network Security; Gorodetsky, V., Popyack, L., Skormin, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 17–31. [Google Scholar]
- Jansen, W. Next Generation Access Control (NGAC), DPANS INCITS 565, Final, ANSI. 2020. [Google Scholar]
- Elrakaiby, Y.; Mouelhi, T.; Traon, Y.L. Testing Obligation Policy Enforcement Using Mutation Analysis. In Proceedings of the 7th International Workshop on Mutation Analysis, Montreal, QC, Canada, 17–21 April 2012; pp. 673–680. [Google Scholar]
- Khamaiseh, S.; Chapman, P.; Xu, D. Model-Based Testing of Obligatory ABAC Systems. In Proceedings of the 18th International Conference on Software Quality, Reliability and Security (QRS’18), Lisbon, Portugal, 16–20 July 2018; pp. 405–413. [Google Scholar]
- Park, J.; Sandhu, R. The UCON ABC Usage Control Model. ACM Trans. Inf. Syst. Secur. 2004, 7, 128–174. [Google Scholar] [CrossRef]
- Dubrovenski, V.; Chen, E.; Xu, D. SMT-Based Verification of NGAC Policies. In Proceedings of the 2023 IEEE 47th Annual Computers, Software, and Applications Conference (COMPSAC), Torino, Italy, 26–30 June 2023; pp. 860–869. [Google Scholar]
- Chen, E.; Dubrovenski, V.; Xu, D. Mutation Analysis of NGAC Policies. In Proceedings of the 26th ACM Symposium on Access Control Models and Technologies, Virtual, 16–18 June 2021; SACMAT’21. pp. 71–82. [Google Scholar]
- Barbosa, H.; Barrett, C.; Brain, M.; Kremer, G.; Lachnitt, H.; Mann, M.; Mohamed, A.; Mohamed, M.; Niemetz, A.; Nötzli, A.; et al. cvc5: A Versatile and Industrial-Strength SMT Solver. In Tools and Algorithms for the Construction and Analysis of Systems; Fisman, D., Rosu, G., Eds.; Springer: Cham, Switzerland, 2022; pp. 415–442. [Google Scholar]
- Margheri, A.; Masi, M.; Pugliese, R.; Tiezzi, F. A Rigorous Framework for Specification, Analysis and Enforcement of Access Control Policies. IEEE Trans. Softw. Eng. 2019, 45, 2–33. [Google Scholar] [CrossRef]
- Hariri, A.; Ibrahim, A.; Alangot, B.; Bandopadhyay, S.; La Marra, A.; Rosetti, A.; Joumaa, H.; Dimitrakos, T. UCON+: Comprehensive Model, Architecture and Implementation for Usage Control and Continuous Authorization. In Collaborative Approaches for Cyber Security in Cyber-Physical Systems; Springer: Cham, Switzerland, 2023; pp. 209–226. [Google Scholar]
- Schöpp, U.; Xu, C.; Ibrahim, A.; Faghih, F.; Dimitrakos, T. Specifying a Usage Control System. In Proceedings of the 28th ACM Symposium on Access Control Models and Technologies, Trento, Italy, 7–9 June 2023; SACMAT’23; Association for Computing Machinery: New York, NY, USA, 2023; pp. 193–200. [Google Scholar]
- Jha, S.; Sural, S.; Atluri, V.; Vaidysa, J. Specification and Verification of Separation of Duty Constraints in Attribute-Based Access Control. IEEE Trans. Inf. Forensics Secur. 2018, 13, 897–911. [Google Scholar] [CrossRef]
- Jha, S.; Sural, S.; Atluri, V.; Vaidya, J. An Administrative Model for Collaborative Management of ABAC Systems and Its Security Analysis. In Proceedings of the 2016 IEEE 2nd International Conference on Collaboration and Internet Computing (CIC), Pittsburgh, PA, USA, 1–3 November 2016; pp. 64–73. [Google Scholar]
- Jha, S.; Sural, S.; Atluri, V.; Vaidysa, J. Security Analysis of ABAC under an Administrative Model. IET Inf. Secur. 2019, 13, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, R.; Bhamidipati, V.; Munawer, Q. The ARBAC97 Model for Role-based Administration of Roles. ACM Trans. Inf. Syst. Secur. 1999, 2, 105–135. [Google Scholar] [CrossRef]
- Shahen, J.; Niu, J.; Tripunitara, M. Cree: A Performant Tool for Safety Analysis of Administrative Temporal Role-Based Access Control (ATRBAC) Policies. IEEE Trans. Dependable Secur. Comput. 2021, 18, 2349–2364. [Google Scholar] [CrossRef]
- Ferrara, A.; Madhusudan, P.; Nguyen, L.; Parlato, G. VAC—Verifier of Administrative Role-Based Access Control Policies. In Computer Aided Verification; Biere, A., Bloem, R., Eds.; Springer: Cham, Switzerland, 2014; pp. 184–191. [Google Scholar]
- Maanak, G.; Ravi, S.; Tanjila, M.; Benson, J. Reachability Analysis for Attributes in ABAC with Group Hierarchy. IEEE Trans. Dependable Secur. Comput. 2022, 20, 841–858. [Google Scholar] [CrossRef]
- Shahen, J. Automated Safety Analysis of Administrative Temporal Role-Based Access Control (ATRBAC) Policies using Mohawk+T. In Proceedings of the 20th ACM Symposium on Access Control Models and Technologies (SACMAT’15), Vienna, Austria, 1–3 June 2015. [Google Scholar]
- Truong, A.; That, D. Solving the User-Role Reachability Problem in ARBAC with Role Hierarchy. In Proceedings of the 2016 International Conference on Advanced Computing and Applications (ACOMP), Can Tho City, Vietnam, 23–25 June 2016; pp. 3–10. [Google Scholar]
- Arkoudas, K.; Chadha, R.; Chiang, J. Sophisticated Access Control via SMT and Logical Frameworks. ACM Trans. Inf. Syst. Secur. 2014, 16, 1–31. [Google Scholar] [CrossRef]
- Backes, J.; Bolignano, P.; Cook, B.; Dodge, C.; Gacek, A.; Luckow, K.; Rungta, N.; Tkachuk, O.; Varming, C. Semantic-based Automated Reasoning for AWS Access Policies using SMT. In Proceedings of the 2018 Formal Methods in Computer Aided Design (FMCAD), Austin, TX, USA, 30 October–2 November 2018; pp. 1–9. [Google Scholar]
- Xu, D.; Shrestha, R.; Shen, N. Automated Strong Mutation Testing of XACML Policies. In Proceedings of the 25th ACM Symposium on Access Control Models and Technologies (SACMAT’20), Barcelona, Spain, 10–12 June 2020; pp. 105–116. [Google Scholar]
- Xu, D.; Shrestha, R.; Shen, N. Automated Coverage-based Testing of XACML Policies. In Proceedings of the 23rd ACM Symposium on Access Control Models and Technologies (SACMAT’18), Indianapolis, IN, USA, 13–15 June 2018; pp. 3–14. [Google Scholar]
- Chen, E.; Dubrovenski, V.; Xu, D. Detecting Errors in NGAC Policies Via Fault-Based Testing. IEEE Trans. Dependable Secur. Comput. 2024, 22, 263–278. [Google Scholar] [CrossRef]
- Dubrovenski, V.; Karim, N.; Erzhuo, C.; Xu, D. Dynamic Access Control with Administrative Obligations: A Case Study. In Proceedings of the Workshop of 2023 IEEE 23nd International Conference on Software Quality, Reliability and Security (QRS), Chiang Mai, Thailand, 22–26 October 2023. [Google Scholar]
- Bansal, K.; Reynolds, A.; Barrett, C.; Tinelli, C. A New Decision Procedure for Finite Sets and Cardinality Constraints in SMT. In Automated Reasoning; Olivetti, N., Tiwari, A., Eds.; Springer: Cham, Switzerland, 2016; pp. 82–98. [Google Scholar]
- Meng, B.; Reynolds, A.; Tinelli, C.; Barrett, C. Relational Constraint Solving in SMT. In Automated Deduction—CADE 26; de Moura, L., Ed.; Springer: Cham, Switzerland, 2017; pp. 148–165. [Google Scholar]
- Arxer, J. Smt Techniques for Planning Problems. Ph.D. Thesis, University of Girona, Girona, Spain, 2018. [Google Scholar]
- Kautz, H.; Selman, B. Planning as Satisfiability. In Proceedings of the 10th European Conference on Artificial Intelligence (ECAI’92), Vienna, Austria, 3–7 August 1992; pp. 359–363. [Google Scholar]
- Biere, A.; Cimatti, A.; Clarke, E.; Zhu, Y. Symbolic Model Checking without BDDs. In Tools and Algorithms for the Construction and Analysis of Systems (TACAS’99); Springer: Berlin/Heidelberg, Germany, 1999; pp. 743–749. [Google Scholar]
- Harrison, M.; Ruzzo, W.; Ullman, J. Protection in operating systems. Commun. ACM 1976, 19, 461–471. [Google Scholar] [CrossRef]
- NGACTeam. NGAC Reference Implementation. Available online: https://github.com/usnistgov/policy-machine-core (accessed on 31 August 2025).
- Xu, D. Modern Software Engineering: Principles and Practices—Writing Clean, Dependable Code. 2021. Available online: https://www.amazon.co.jp/-/en/Modern-Software-Engineering-Principles-Dependable/dp/B08TY85J94 (accessed on 31 August 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).