Towards Analyzable Design Paradigms for Chaos-Based Cryptographic Primitives

Abstract

Although many chaos-based cryptosystems have been proposed over the past decade, they have yet to gain traction in real-world applications. A key reason for this is that most designs rely on security through obscurity, with unnecessarily complex structures that hinder cryptanalysis and formal evaluation. In this paper, we challenge this trend by showing that chaos-based ciphers can be constructed using conventional, well-understood cryptographic design paradigms without sacrificing performance. First, we present a minimalistic image encryption scheme based on the substitution–permutation network (SPN), demonstrating that it satisfies widely accepted criteria for evaluating chaos-based ciphers. We further show that simple, low-dimensional chaotic maps are sufficient to eliminate statistical biases and that variations in the underlying map have a negligible impact. Second, we propose a chaos-based Feistel block cipher (CFBC) grounded in the generalized Feistel network, enabling standard security evaluation through differential cryptanalysis. As a direct comparison with existing chaos-based image ciphers, we apply CFBC in cipher block chaining (CBC) mode to image encryption. Experimental results show that CFBC achieves a statistical performance comparable to that of state-of-the-art image ciphers. Our findings reinforce the idea that chaos-based cryptosystems need not rely on overly complex constructions and can instead adopt established principles to become more analyzable and robust.

1. Introduction

Chaotic systems are dynamic systems that exhibit chaotic behaviour. They have been extensively studied and have been used to solve real-world problems including numerical weather prediction [1] and market analysis [2]. Due to their properties such as ergodicity, sensitivity to initial conditions, and random-like behaviour, researchers have started looking into designing cryptosystems based on chaos. Parallels are often drawn between chaos and cryptography, whereby certain chaotic properties can be mapped directly to cryptographic requirements, as noted by Kocarev back in 2001 [3]. However, Kocarev also pointed out numerous problems with chaos-based cryptographic algorithms, noting that using real numbers makes practical realization and circuit implementation difficult. He also observed that chaos-based methods were not analysed using techniques developed within the field of cryptography and that many designs are ad hoc in nature.

Despite years of research, the fundamental issues in chaos-based encryption remain unresolved, as noted by multiple researchers [3,4,5,6]. Most existing work continues to focus predominantly on image encryption [7,8,9,10], with authors often claiming that conventional symmetric-key algorithms are unsuitable due to the high correlation between image pixels or due to their inefficiency in handling bulk data [11,12,13]. However, such claims are not only inconsistent with real-world practice—where block ciphers are routinely and effectively used to secure various types of media—but have also been directly challenged in prior studies [14]. This highlights a persistent misconception in the field and underscores the need for chaos-based encryption schemes that are grounded in sound cryptographic principles and that are rigorously evaluated.

Although chaos theory could, theoretically, be used to build practical cryptosystems, the current research direction still focuses on security through obscurity, whereby the cryptographic algorithms are very complex and rely on high-dimensional chaotic maps. Both design complexity and reliance on real numbers prevent the use of cryptanalytic tools to evaluate the security margin of these algorithms. We have reviewed recently proposed ciphers in Section 3 to verify that these problems are still prevalent. As a result, the majority of chaos-based algorithms are only of academic interest and see no real-world applications. Although some may question the need (or lack thereof) for chaos-based encryption algorithms, the study of chaos-based cryptosystems could lead to new findings that could supplement existing tools in conventional cryptography.

• Contributions: In this paper, we address this problem by taking a contrasting approach to that of current chaos-based cryptography research and answer the following question: How can we design a minimalistic chaos-based cryptosystem that still fulfils all the same requirements as the current ”state-of-the-art”? The main goal is to move away from security through obscurity and align the design of a chaos-based cryptosystem with the well-studied security notions in conventional cryptography. This will not only provide more confidence in the design but also facilitate third-party cryptanalysis efforts to provide accurate security bounds. As such, we study the use of well-known design paradigms such as the substitution–permutation network (SPN) and Feistel constructions in the context of image encryption. We begin by taking a look at some recently proposed chaos-based image ciphers to see if they have overcome at least some of the key problems highlighted in the past [6,15]. Then, we propose a simple chaos-based image cipher based on SPN and analyze the minimum number of rounds required to achieve a similar statistical security as the current state of the art in chaos-based cryptography. We also study the impact of changing its underlying chaotic map to other more complex ones.

Our extensive experiments show that the combination of a simple SPN configuration and a simple chaotic map is sufficient to provide similar performances to those demonstrated in existing work. These experiments are not intended to demonstrate superiority over existing schemes, but rather to show that a minimalistic and transparent design can meet widely accepted statistical security benchmarks, as used in prior chaos-based cryptography work. Next, we introduce a new chaos-based block cipher based on the Feistel construction. Note that the design goal of this block cipher is not acting as a replacement for mainstream block ciphers, such as AES, but to show that it is possible to use chaotic maps as a nonlinear component in a way that facilitates cryptanalytic efforts. We show that we can estimate the security margin of the proposed cipher against differential cryptanalysis using a standard approach of counting the number of active nonlinear components and obtaining the upper-bound differential probability of the chaotic map. For comparison with existing chaos-based ciphers (which are almost exclusively image ciphers), we used the proposed block cipher in the CBC mode of operation to encrypt images. Despite having a simpler design, the proposed cipher has equivalent statistical properties to the current state of the art. The main contributions of this paper are summarized below.

• An in-depth analysis of minimalistic SPN configurations for image encryption based on chaos-based cryptography.
• Empirical proof that changing the underlying chaotic map has minimal impact on statistical results, as long as the map is operating within its chaotic region.
• A new chaos-based block cipher based on the well-understood Feistel design paradigm with a provable upper bound security against differential cryptanalysis.
• Empirical proof that a simple block cipher design can have similar statistical properties as the current state of the art in chaos-based encryption.

The remainder of the paper is organized as follows: Section 2 provides preliminary information related to the proposed work, including the various chaotic maps used and metrics commonly used to evaluate chaos-based ciphers. Section 3 delves into the analysis of recent chaos-based image ciphers. Section 4 investigates minimalistic SPN configurations for image encryption, while Section 5 introduces the proposed chaos-based block cipher and its use in image encryption. The experimental results are described in Section 6; the paper is concluded in Section 7.

2. Preliminaries

2.1. Chaotic Maps

One-dimensional chaotic maps are commonly used in image encryption schemes due to their simple structure and simple implementation, which increases computational efficiency. Moreover, the chaotic sequence produced by the chaotic map is often used by image encryption systems to process plainimages. Thus, the output chaotic sequence’s overall complexity plays a significant role in determining the statistical properties of an image cipher. This section will review two commonly used one-dimensional chaotic maps. However, two-dimensional maps are also used in this paper.

2.1.1. Logistic Map

A logistic map is a unimodal map with a straightforward structure and low computational cost, making it one of the most popular chaotic maps used in the field of chaos-based cryptography. The logistic map fl is defined as follows:

$$F(x_n,r)=x_{n+1}=r{x}_n(1-x_n),$$

(1)

where $x_n$ is the initial state variable at iteration n, and r is the control parameter that ranges between [0, 4]. The logistic map operates on real numbers with a range of [0, 1]. By iterating Equation (1), the trajectory of state variables can be produced from the initial condition, $x_0, f_l(r,x_0), f_l^2(r,x_0)\dots f_l^N(r,x_0)$, where N is the total number of iterations. The chaotic map achieves full chaoticity at $r\ge 3.57$ as shown in Figure 1, where the Lyapunov exponent is nonzero (left figure) and the bifurcation diagram is within the shaded zone. The trajectory will only span the full phase space in the range of [0, 1] when $r\approx 4$. Commonly, the control parameter is set to $r=3.99$.

2.1.2. Tent Map

The tent map is a simple discrete one-dimensional chaotic map with one control parameter. It maps the interval of [0, 1] to itself. The mathematical representation of the tent map is defined as follows:

$$F(x_n,\lambda )=x_{n+1}=\left\{\begin{array}{cc}\lambda x_n/2,\hfill & \text{if} x_n<0.5\hfill \\ \lambda (1-x_n)/2,\hfill & \text{if} x_n\ge 0.5,\hfill \end{array}\right.$$

(2)

where $x_n\in [0,1]$ is the state variable; $\lambda$ is set to 1.99, which is the control parameter ranging from [0, 2]. The tent map demonstrates chaotic behavior as $\lambda$ approaches 2, as shown in its bifurcation diagram in Figure 2.

2.1.3. Piecewise Linear Map

The piecewise linear map is a higher-dimensional map, as described by the following equation:

$$F(x_n,p)=x_{n+1}=\left\{\begin{array}{cc}{x}_n/p,\hfill & 0<x_n<p\hfill \\ (x_n-p)/(0.5-p),\hfill & p<x_n<0.5\hfill \\ F(1-x_n,p),\hfill & 0.5<x_n<1,\hfill \end{array}\right.$$

(3)

where $x_n\in [0,1]$ is the initial condition, and $p\in [0,0.5]$. The piecewise linear map demonstrates chaotic behaviour when $p\in [0,0.5]$ [16].

2.1.4. Henon Map

The Henon map is a two-dimensional chaotic map [17]. The Henon map is described by the following quadratic nonlinear equation:

$$x_{i+1}=1-a{x}^2+y_n,y_{i+1}=b{x}_n,$$

(4)

where a and b are the control parameters; x and y are the initial conditions. The system is chaotic when its parameter values are a = 1.4 and b = 0.3 [18].

2.2. Image Encryption Evaluation Metrics

Unfortunately, nearly all chaos-based cryptosystems in the recent literature rely entirely on statistical tests for security evaluation. While conventional symmetric-key ciphers such as AES and SKINNY have been designed with analyzability in mind, chaos-based ciphers generally rely on security through obscurity. Their complex designs discourage the use of conventional cryptanalysis tools, such as differential cryptanalysis, to quantify their computational security. Therefore, chaos-based cryptographic researchers resort to relying entirely on statistical metrics. In this subsection, we introduce some of the statistical tests commonly used to evaluate the performance of chaos-based ciphers.

2.2.1. Histogram Analysis

A histogram is a graphical representation of how an image’s pixels are distributed. Based on the size of a digital image, it displays the frequency of each gray level as a number. A flat histogram will appear when a cipherimage’s frequency of gray levels is approximately equal [19]. This implies that there are no noticeable biases or patterns and that the image pixels are uniformly distributed, which improves security against statistical attacks. There are other histogram evaluations that are used to investigate the uniform distribution of cipherimages; these are maximum deviation (MD), irregular deviation (ID), and deviation from the uniform histogram (DUH). The difference between the gray level frequency histogram of the plainimage and the cipherimage is measured using the maximum deviation, which is calculated as follows:

$$M_D={\displaystyle \frac{D_0+D_{255}}{2}}+\sum _{i=1}^{255}{D}_i$$

(5)

where $D_i=\left|D_{C_i}-D_{P_i}\right|$ is the absolute difference of the gray values between the cipherimage and the plainimage at index i.

The irregular deviation evaluates how closely the histogram’s statistical distribution resembles a uniform distribution. Ideally, the irregular deviation should be close to a uniform distribution. The irregular deviation is calculated as follows. First, we compute the following:

$$D_i=\left|D_{C_i}-D_{P_i}\right|.$$

(6)

Then, we can obtain the histogram for D, as follows:

$$H=\mathrm{histogram}\left(D\right)$$

(7)

The average value of H can be found as follows:

$$M_H={\displaystyle \frac{1}{256}}\sum _{i=0}^{255}{H}_i,$$

(8)

where $H_i$ is the amplitude of histogram H at index i. Finally, the irregular deviation is calculated as follows:

$$I_D=\sum _{i=0}^{255}H{D}_i,$$

(9)

where

$$H{D}_i=\left|H_i-M_H\right|$$

(10)

Deviation from a uniform histogram (DUH) measures the difference between the histogram of a cipherimage and a uniform histogram. For any image size, the uniform histogram can be calculated as follows:

$$H_C=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{M\times N}{256}},& \hfill x\le i\le 255\\ \hfill 0,& \hfill \mathrm{elsewhere},\end{array}\right.$$

(11)

where M and N are the width and height of an image, respectively. Ideally, encrypted images should have minimal deviation from a uniform histogram for a suitable encryption scheme. The deviation from a uniform histogram is calculated as follows:

$$D_H={\displaystyle \frac{{\sum }_{C_i}^{255}\left|H_{C_i}-H_C\right|}{M\times N}},$$

(12)

where $H_{C_i}$ is the histogram of cipher text image. A lower value of $D_H$ shows a low deviation from the ideal histogram, which implies uniform distribution [19,20].

2.2.2. Correlation Analysis

The relationship between various variables is measured using the correlation coefficient (CC). When two images are nearly identical, the correlation coefficient is close to one (1). In this instance, the encrypted image is similar to the original image, indicating that the encryption method was ineffective in hiding the key features of the original image. If the correlation coefficient is equal to zero (0), the original image and its encryption are typically different from one another, meaning that the encrypted image has different properties and is completely independent of the original image. Normally, for this experiment, 1000 pairs of pixels associated with two adjacent (vertical, horizontal, and diagonal) directions are randomly selected from the image. The correlation coefficient is then calculated as follows:

$$C{C}_{XY}={\displaystyle \frac{COV(X,Y)}{\sqrt{D\left(X\right)}\times \sqrt{D\left(Y\right)}}},$$

(13)

$$\begin{array}{c}\hfill COV(X,Y)={\displaystyle \frac{1}{N}}\sum _{i=1}^N(X_i-E\left(X\right)(Y_i-E\left(Y\right)),\\ \hfill D\left(X\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(X_i-E\left(X\right))}^2,E\left(X\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}_i.\end{array}$$

(14)

X and Y are the values of adjacent pixels in the plainimage and the cipherimage [21].

2.2.3. Information Entropy

The most significant index to indicate the randomness and unpredictability of an information source is called information entropy $H\left(I\right)$. Theoretically, $H\left(I\right)$ for a 256-gray-level encrypted image is 8 when all gray levels appear with the same probability. Hence, the information entropy of the cipherimage should be close to 8 for a secure encryption system [22]. Shannon entropy can be calculated as follows:

$$H\left(I\right)=\sum _{j=0}^{L-1}p\left(I_j\right){log}_{2}p\left(I_j\right)$$

(15)

where I is the particular gray levels of a pixel and $p\left(I_j\right)$ is the probability that the pixel exists in the image. For an 8-bit gray image, $L=256$.

2.2.4. NPCR and UACI Analysis

When a new symmetric-key cipher (such as a block cipher) is proposed, it must be analysed for security against conventional attacks such as differential cryptanalysis [23]. This can be performed by modeling the differential properties of the nonlinear component of the cipher (such as S-boxes), as well as by modeling the search for differential trails using tools such as Mixed Integer Linear Programming (MILP) or Satisfiability Modulo Theory (SMT) solvers [24,25]. Applying these techniques to analyze chaos-based cryptosystems is difficult due to their complex designs. Therefore, their designers have to rely on yet another statistical test to evaluate security against differential attacks.

The ability to resist differential attack is measured by comparing differences between two cipherimages (i.e., when one pixel of the plainimage is changed, the cipherimage should be completely different). The number of pixels change rate (NPCR) and unified average changing intensity (UACI) can be used to quantitatively evaluate the aforementioned sensitivity. The NPCR refers to the rate at which one pixel in a cipherimage is changed while a pixel of the plainimage is changed. The UACI measures the average intensity of the differences between the plainimage and the cipherimage. First, two plainimages with a difference of one bit are encrypted to obtain two cipherimages—C1 and C2. Then, NPCR and UACI are calculated as follows:

$$NPCR(C1,C2)={\displaystyle \frac{{\sum }_{i,j}^{MN}D(i,j)}{MN}}\times 100\%$$

(16)

and

$$UACI(C1,C2)={\displaystyle \frac{1}{MN}}\sum _{i,j}^{MN}{\displaystyle \frac{\left|C1\right(i,j)-C2(i,j\left)\right|}{L}}\times 100\%$$

(17)

where $MN$ is the total number of pixels in plainimage, $L=255$ is the maximum gray level value for 8-bit pixels, $C1$ and $C2$ are encrypted images, and

$$D(i,j)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}C1(i,j)=C2(i,j)\hfill \\ 1,\hfill & \mathrm{if}C1(i,j)\ne C2(i,j)\hfill \end{array}\right.$$

(18)

3. Analysis of Recent Chaos-Based Image Ciphers

In this section, we focus on practical implementation issues of 14 recently proposed chaos-based cryptosystems that rely on digitized chaotic maps; some of these issues have already been discussed in Section 1. Specifically, our analysis is limited to newly proposed symmetric-key encryption algorithms that employ chaotic maps as their primary source of entropy, including image ciphers. We thoroughly investigated whether the 14 analyzed chaos-based cryptosystems have made progress in resolving the implementation problems listed below, some of which were previously identified in [6].

Table 1. Analysis of recent chaos-based cryptographic algorithms.

Ref.	JCR Tier	HD	CCM	HCC	DC	ROST
[26]	1	×		×	×	×
[27]	1	×	×	×	×	×
[28]	1	×	×	×	×	×
[29]	1	×		×		×
[30]	1	×		×		×
[8]	1	×	×	×	×	×
[7]	1	×		×	×	×
[31]	1	×		×	×	×
[32]	2	×	×	×		×
[33]	2	×		×	×	×
[12]	2	×	×	×	×	×
[11]	2	×	×	×	×	×
[34]	2	×		×	×	×
[35]	2	×	×	×		×
[36]	2	×	×	×		×
[37]	2	×	×	×	×	×
[38]	2	×	×	×		×
[9]	2	×		×		×
[10]	2			×	×	×

presents a comprehensive analysis of 14 recent chaos-based cryptographic algorithms, highlighting significant implementation challenges. Firstly, the use of high-dimensional (HD) maps poses a significant challenge due to their complexity and heavy resource demand. Using a combination of simpler chaotic maps (CCMs) rather than higher-dimensional maps has similar drawbacks. Higher computational cost (HCC) is related to the computational efficiency of the cryptographic algorithms themselves due to their inherent design. The design complexity (DC) of these algorithms also makes it difficult to perform third-party cryptanalysis in order to verify their security margins. As such, designers have no other option but to resort to statistical security testing. Reliance on statistical-based security tests (ROST) alone does not guarantee that a cipher is resistant to cryptanalytic attacks.

Unfortunately, it appears that most of these issues remain unaddressed, evidenced by the successful publication of new cryptosystems with these problems in reputable journals. Our findings are aligned with previous research highlighting the fundamental challenges of chaos-based cryptography that hinder its real-world applicability and reputation in the cryptographic community. New designs still seem to promote security through obscurity, as outlined in Section 1. Consequently, many of these algorithms remain only of academic interest rather than being used in real-world applications.

In our paper, we will address all of the aforementioned issues. We show that there is no need for high-dimensional or complex combinations of chaotic maps in cipher design by focusing just on simple, well-understood chaotic maps covered in Section 2.1. By using basic chaotic maps and well-studied yet simple design paradigms, we demonstrate that it is possible to design ciphers with strong security properties that can be analyzed using classical cryptanalysis techniques such as differential cryptanalysis.

4. Analysis of Optimal SPN Configurations for Image Encryption

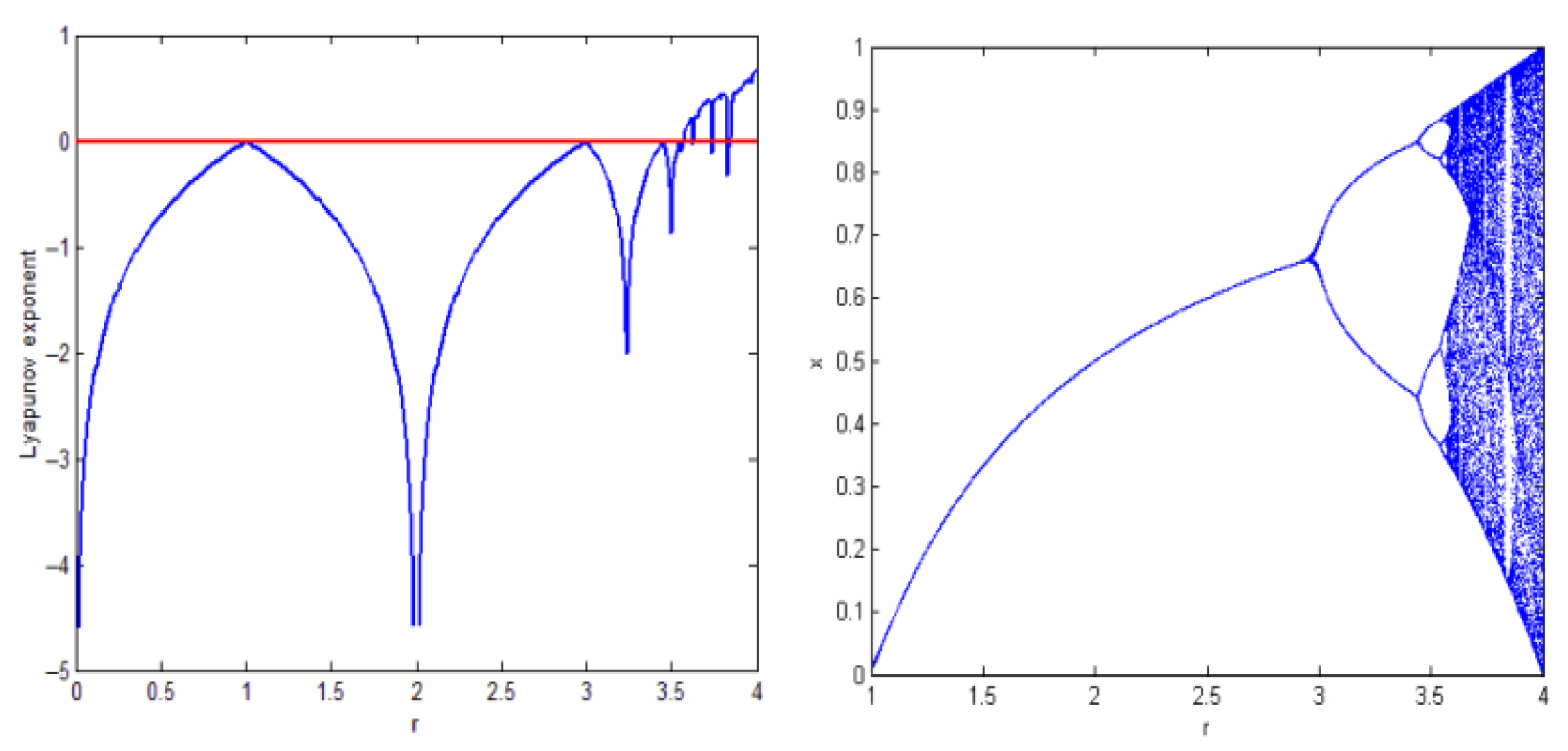
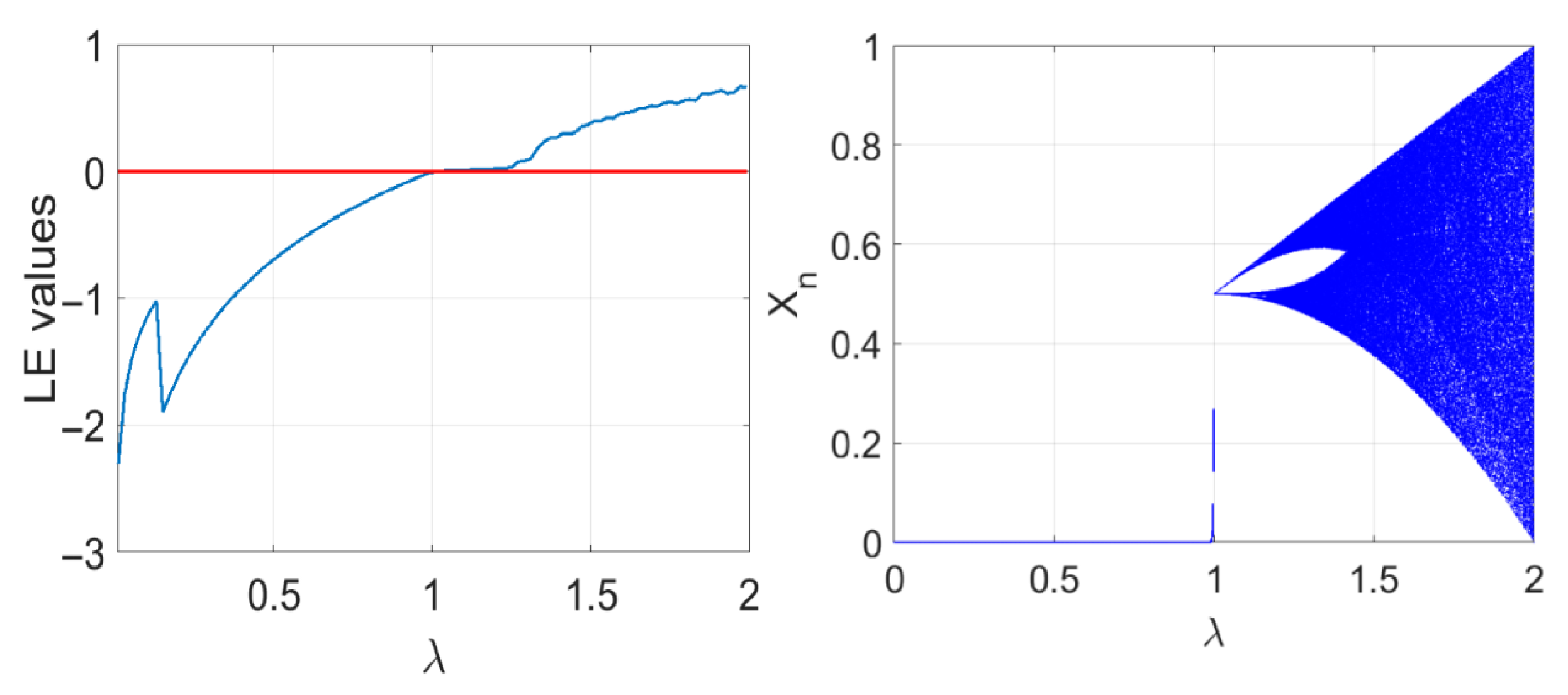
In this section, our goal is to identify a minimalistic configuration for image encryption based on the SPN. We want to show that to achieve the statistical properties that most chaos-based image ciphers are trying to attain, a complex design or the use of a high-dimensional chaotic map is not necessary. Therefore, all experiments were performed on simple one-dimensional maps. The parameters were chosen from standard values that are frequently used in the literature to ensure chaotic behaviour and to make the experiment reproducible and comparable with existing studies. Specifically, we used parameter $r=3.99$ for the logistic map, $r=1.99$ for the tent map, $a=1.4$, and $b=0.3$ for the Henon map, as well as $p=0.0256$ for the Piecewise linear map. These values were chosen to maintain high sensitivity to initial conditions while keeping the system simple and reproducible. To ensure consistency with the literature on chaos-based cryptography, we denote the substitution of each pixel as the modification of each pixel value based on a random sequence generated using a chaotic map and not the use of a substitution box. Permutation, on the other hand, refers to the shuffling of pixel positions to remove correlation between neighboring pixels.

4.1. SPN Cipher Design

The image encryption is designed based on the SPN, which operates on a plainimage with 256 × 256 pixels and also returns a cipherimage block of the same size. In this SPN, the encryption phase consists of three processes, which are pixel substitution, pixel permutation, and diffusion. Pixel substitution obscures the pixel values using a random sequence generated using a chaotic map to achieve confusion, pixel permutation shuffles pixel positions to remove correlation between the neighbouring pixels, and pixel diffusion modifies pixel values based on other pixel values in the plainimage. Thus, all pixels of the plainimage will be diffused throughout the resulting cipherimage. The following steps describe the encryption algorithm (decryption algorithm is just the inverse of the steps):

• Step 1: Read plainimage (original image); $P_{m\times n}$ is the size of the image P, where m = 256 and n = 256.
• Step 2: Input secret key $x_o$ and parameter r into the algorithm and iterate the chaotic map N times and obtain the key array; the size of the array is N.
• Step 3 (Substitution): Encrypt each element of the plainimage $P_{m\times n}$ using the key array generated by the chaotic map (i.e., modifying the original $P_{m\times n}$ pixels with the key array obtained from Step 2 using XOR operation).
• Step 4 (Substitution): Modify each pixel in the plainimage P using values from all other adjacent pixels in the horizontal and vertical directions. Modification is performed using the XOR operation; for pixels at the edge of the plainimage, we take pixels from the opposite edge as the adjacent pixel (pixel row and column numbers wrap around).
• Step 5 (Permutation): Shuffle the pixel positions based on the output of the logistic map. The chaotic map is used to determine row and column numbers within the plainimage. The current pixel at position $P_{(i,j)}$ will be swapped with a pixel $P_{(row,col)}$, where $row$ and $col$ are obtained by iterating the chaotic map. The $row$ and $col$ values are obtained from the chaotic map’s state, X, after each iteration by converting X into a number between 1 and the maximum number of rows or columns; in our case, this value is 256. This is calculated using a ceiling function and simple linear scaling, $row/col=\lceil X\times 256\rceil$.
• Step 6: The resulting image obtained from Step 5 is the cipherimage $C_{m\times n}$.

4.2. Ranking Method for SPN Configurations

In the ranking process, the performance of various substitution–permutation (SP) configurations is evaluated using widely accepted statistical security metrics. To quantify and compare the performance of each configuration, the results for each metric were linearly scaled between 0 and 100, where a score of 100 corresponds to the ideal outcome for that metric (e.g., maximum entropy, minimum correlation, and maximum NPCR and UACI values). These scaled scores were then aggregated to produce an overall security score for each configuration. This approach provides a transparent and reproducible approach for selecting optimal SPN configurations. The scaling for each of the metrics is described as follows:

• Irregular Deviation (ID) Score: For a 256 × 256 image, the worst-case scenario occurs when all the pixels have a value of zero (0), except for one instance where the value is 255. As the sum of (1:256) equals 65,536, it is possible to calculate the worst ID result as 255 × 256 + 65,280 = 130,560. On the other hand, the ideal result for ID is 0 (no difference between the cipher text distribution and a uniform distribution).

  $$\mathrm{ID}\mathrm{Score}=(130,560–\mathrm{Obtained}\mathrm{ID}\mathrm{results})/130,560\times 100.$$
• Maximum Deviation (MD) Score: The maximum value for a 256 × 256-pixel image is when the plain text has pixels with gray levels of 0 and the cipher text has pixels with gray levels of 255. Since the summation of (1:256) = 65,536, the highest MD is 65,536 × 3 = 196,608.

  $$\mathrm{MD}\mathrm{Score}=(\mathrm{Obtained}\mathrm{MD}\mathrm{results}/196,608)\times 100.$$
• Deviation from Uniform Histogram (DUH) Score: The cipherimage achieves the best histogram deviation when its pixels show a high probability of closely matching pixel values from a uniform histogram. The DUH values range between 0 and 1, where 0 implies perfect uniform distribution and 1 represents a complete departure from uniformity. Hence, the best scenario is when the value is not equal to 1.

  $$\mathrm{DUH}\mathrm{Score}=(1–\mathrm{Obtained}\mathrm{DUH}\mathrm{results})\times 100.$$
• Entropy Score: An 8-bit gray level image attains an optimal entropy value of 8 [39], signifying a well-balanced distribution of pixel values that reflects the information within the image.

  $$\mathrm{Entropy}\mathrm{Score}=(\mathrm{Obtained}\mathrm{entropy}\mathrm{results}/8)\times 100.$$
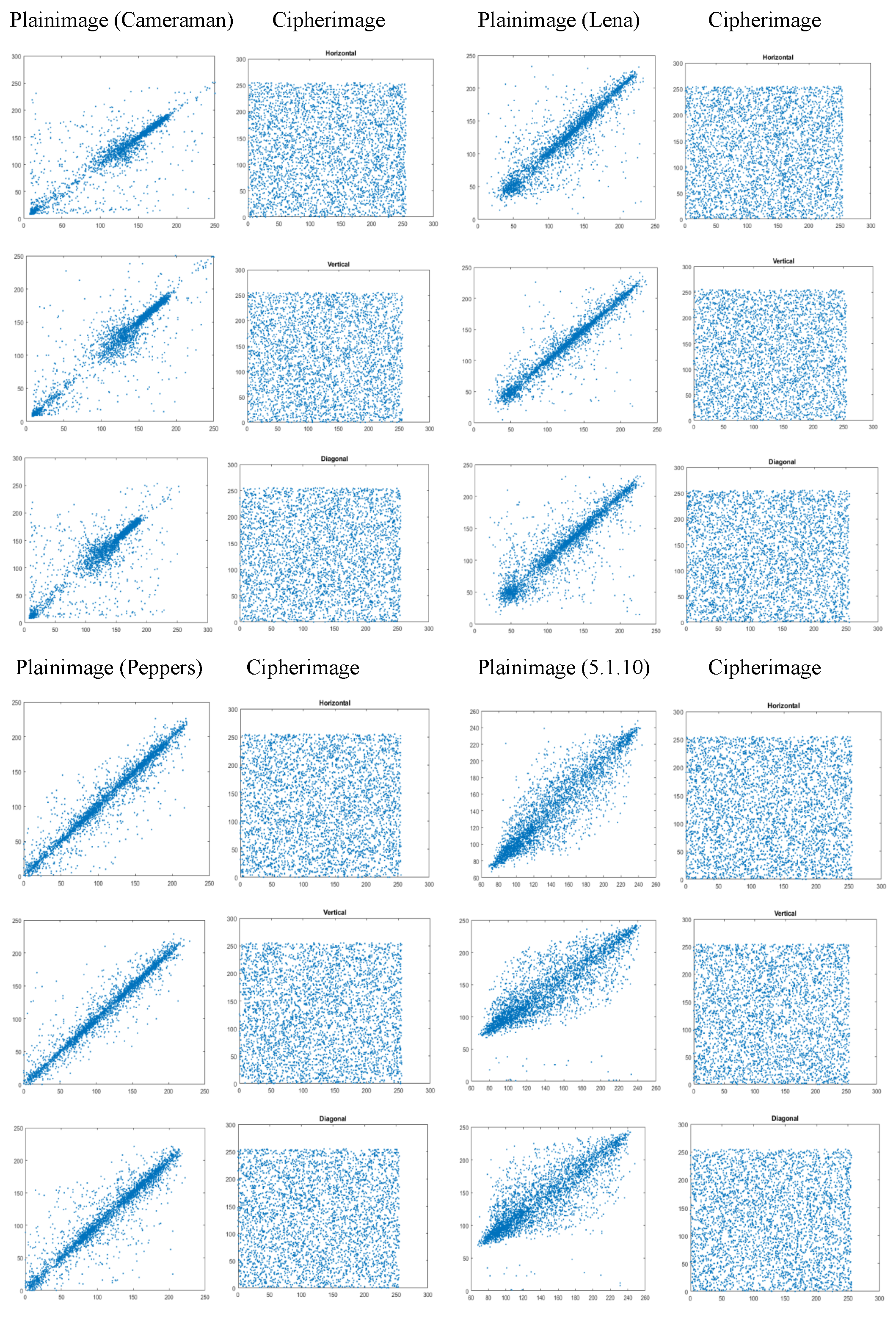
• Correlation Coefficient (CC) Score: When CC values approach 0, this indicates a minimal correlation between neighbouring pixels in an encrypted image, while CC values close to 1 or −1 signify a strong pixel correlation [19]. Since we consider three pixel directions (horizontal, vertical, and diagonal), it is possible to calculate the total CC score by summing the results from each direction, as follows:

  $$\begin{array}{c}\mathrm{Horizontal}\mathrm{results}=(1–\mathrm{ABS}\left(C{C}_H\right))\\ \mathrm{Vertical}\mathrm{results}=(1–\mathrm{ABS}\left(C{C}_V\right))\\ \mathrm{Diagonal}\mathrm{results}=(1–\mathrm{ABS}\left(C{C}_D\right)),\end{array}$$

  where, $C{C}_H$ represent correlation coefficient horizontal, $C{C}_V$ denotes correlation coefficient vertical, and $C{C}_D$ represents correlation coefficient diagonal.

  $$\begin{gathered} \mathrm{Total}\mathrm{CC}\mathrm{Score}=\left(\right(1–\mathrm{ABS}(\mathrm{Horizontal}\mathrm{results})+(1–\mathrm{ABS}(\mathrm{Vertical}\mathrm{results})+ \\ (1–\mathrm{ABS}(\mathrm{Diagonal}\mathrm{results})/3)\times 100. \end{gathered}$$
• Number of Pixel Change Rate (NPCR) Score: In the ideal scenario, the value of NPCR is considered optimal when it is greater than or equal to the average value (99.5693%) [40], indicating a high sensitivity to small changes in the plainimage.

  $$\mathrm{NPCR}\mathrm{Score}=(\mathrm{Obtained}\mathrm{NPCR}\mathrm{results}/\mathrm{Average}\mathrm{value})\times 100.$$
• Unified Average Change Intensity (UACI) Score: Ideally, the UACI value should be close to 33.46355% [40]. As such, a max score of 100 should be given for results close to the aforementioned value.

  $$\mathrm{UACI}\mathrm{Score}=(100–\left(\right(\mathrm{ABS}(34.6355–\mathrm{Obtained}\mathrm{UACI}\mathrm{results})/33.46355)\times 100).$$

4.3. Experimental Results Comparing SP Configurations

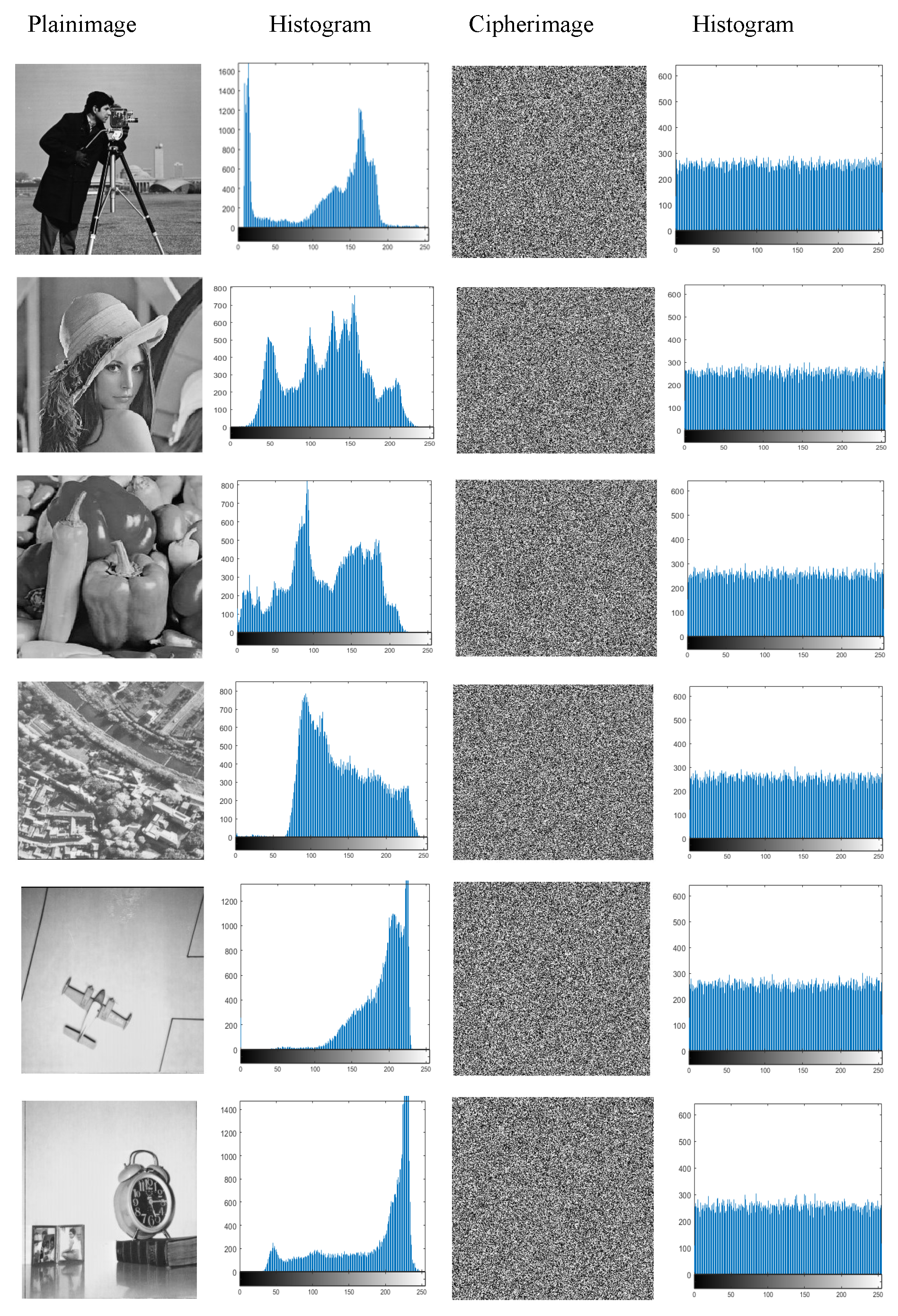
Experiments were performed using MATLAB 2021a on a PC with a 64-bit operating system, Intel Core i-5 CPU (2.60 GHz), and 8 GB memory. Standard test plainimages such as the Cameraman, Lena, and Pepper images of 256 × 256 pixels in size were used in our experiments as they are also commonly used in the field. The optimum configuration substitution–permutation (SP) combinations in this experiment are listed in

Table 2. Optimum configurations (S: substitution; P: permutation).

Combination of Operations

SP

PS

SPS

PSPS

SPSPS

, while the average results of three images using four different chaotic maps are presented in

Table 3. Average scores (%) of three images (Cameraman, Lena, and Peppers) using logistic map.

Cameraman
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	46.68	32.34	94.87	99.96	98.77	100	99.94
PS	46.87	31.17	84.67	99.72	98.24	99.98	99.71
SPS	47.20	31.33	84.89	99.72	98.92	99.97	99.57
PSPS	46.65	32.03	93.93	99.95	98.85	100	99.81
SPSPS	46.33	32.80	94.95	99.96	97.76	100	99.91
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Lena
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	48.18	20.34	94.6	99.96	99.02	100	99.88
PS	46.87	17.43	84.95	99.71	98.61	100	99.64
SPS	47.11	17.41	84.9	99.70	98.95	99.98	99.64
PSPS	48.00	20.63	94.23	99.95	98.41	100	99.95
SPSPS	48.43	21.25	94.77	99.96	98.08	100	99.84
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Peppers
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	45.15	17.50	93.51	99.94	97.87	100	99.87
PS	44.23	14.69	83.91	99.71	99.49	100	99.90
SPS	44.13	14.88	84.29	99.72	99.02	100	99.91
PSPS	45.00	17.64	94.03	99.94	99.07	100	99.69
SPSPS	45.09	18.16	94.94	99.96	98.31	100	99.63
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67

,

Table 4. Average scores (%) of the three images (Cameraman, Lena, and Peppers) using tent map.

Cameraman
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	46.16	32.93	94.96	99.96	98.70	99.98	99.71
PS	46.49	33.77	94.51	99.96	98.70	100	99.87
SPS	46.63	33.83	94.4	99.95	99.09	100	99.62
PSPS	46.20	32.85	94.17	99.95	99.06	100	99.89
SPSPS	46.26	33.12	94.75	99.96	99.47	100	99.67
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Lena
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	48.08	21.15	95.28	99.96	99.39	100	99.83
PS	48.32	22.32	94.72	99.95	98.52	100	99.96
SPS	48.72	22.02	94.55	99.95	99.55	100	99.93
PSPS	48.16	21.15	95.16	99.96	99.05	100	99.84
SPSPS	48.18	21.20	94.94	99.96	98.78	100	99.61
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Peppers
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	44.94	18.80	94.98	99.96	99.01	100	99.99
PS	45.19	19.66	94.52	99.95	97.74	100	99.84
SPS	45.52	19.59	94.63	99.95	97.78	100	99.93
PSPS	45.38	18.60	94.7	99.96	98.22	100	99.99
SPSPS	45.02	18.77	95.09	99.97	99.46	100	99.90
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67

,

Table 5. Average scores (%) of the three images (Cameraman, Lena, and Peppers) using piecewise linear map.

Cameraman
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	46.13	33.61	93.76	99.94	98.51	100	99.89
PS	46.35	33.04	94.85	99.96	97.41	100	99.99
SPS	46.51	33.00	94.9	99.96	98.07	100	99.98
PSPS	45.96	33.73	93.62	99.94	99.22	100	99.95
SPSPS	46.31	33.36	94.48	99.95	98.97	99.98	99.67
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Lena
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	48.25	20.65	91.39	99.90	98.00	100	99.90
PS	48.15	21.38	95.18	99.96	98.65	100	99.99
SPS	48.24	21.53	95.07	99.96	98.91	100	99.94
PSPS	48.20	20.64	91.27	99.90	98.79	100	99.83
SPSPS	49.94	21.50	94.72	99.95	99.18	100	99.55
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Peppers
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	45.52	19.60	94.05	99.95	98.76	100	99.98
PS	45.46	18.89	94.63	99.96	99.52	100	99.78
SPS	45.30	18.82	94.76	99.96	98.18	100	99.95
PSPS	45.46	19.60	94.21	99.95	99.34	100	99.92
SPSPS	45.06	19.30	94.82	99.96	98.51	100	99.76
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67

and

Table 6. Average score of the three images (Cameraman, Lena, and Peppers) using Henon map.

Cameraman
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	47.46	36.09	74.44	99.21	85.58	100	99.96
PS	44.25	35.66	86.05	99.72	88.07	99.71	99.47
SPS	44.09	35.69	85.82	99.72	88.67	99.73	99.91
PSPS	47.63	36.16	74.51	99.20	84.20	100	99.38
SPSPS	45.59	34.97	83.18	99.57	90.96	100	99.93
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Lena
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	47.69	19.65	87.3	99.78	87.41	100	99.96
PS	47.65	23.02	95.5	99.86	86.91	99.86	99.97
SPS	47.72	23.01	89.79	99.86	88.26	99.85	99.81
PSPS	48.05	19.62	86.89	99.78	85.35	100	99.49
SPSPS	48.07	24.09	85.15	99.75	91.44	100	99.94
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67
Peppers
Combination	ID Score	MD Score	DUH Score	Entropy Score	CC Score	NPCR Score	UACI Score
SP	43.27	16.45	87.22	99.78	86.10	100	99.96
PS	44.60	21.91	88.87	99.84	87.34	99.80	99.41
SPS	44.41	21.87	88.97	99.85	86.89	99.80	99.71
PSPS	43.57	16.45	86.67	99.77	84.83	100	99.94
SPSPS	44.69	23.84	83.45	99.70	90.95	100	99.91
[9]	N/A	N/A	N/A	99.98	99.78	100	90.83
[41]	N/A	N/A	N/A	99.98	99.89	100	95.87
[42]	N/A	N/A	N/A	99.99	99.79	100	90.62
[43]	N/A	N/A	N/A	99.98	99.82	100	90.67

.

4.4. Discussion

We have provided an extensive analysis of the performance of the substitution–permutation (SP) ciphers, using various statistical methods and comparing them with several recently proposed schemes, as shown in Table 3, Table 4, Table 5 and Table 6. One of the chosen examples in [9] relies on a hyperchaotic 4D Chen system to generate keys and construct six S-boxes, alongside the Mersenne Twister PRNG. Another scheme employs a 6D memristor hyperchaotic system together with multiple rounds of scrambling, diffusion, and S-box substitution [41]. In [42], the designers proposed a scheme that combines a 5D hyperchaotic system with elliptic curve operations and S-box transformations. Finally, in [43], their proposed cipher integrates three separate stages using cellular automata, an S-box built from modular inverses and permutations, and the Lorenz system.

In contrast, our experiments demonstrated that the use of simple constructions and chaotic maps is sufficient to eliminate statistical biases. Changing the underlying chaotic map also has minimal impact on the cipher’s performance. As shown in Table 3, Table 4, and Table 6, the proposed configurations either match or outperform the other chaos-based image ciphers with complex designs. This provides evidence that we do not need complex constructions or high-dimensional chaotic maps to improve security, as they complicate efforts to verify security claims using cryptanalytic methods.

Based on the performance metrics described in Section 2.2, where 100 implies that the cipher achieves the ideal results for a particular metric and 0 implies otherwise, the optimal configurations listed in Table 2 have better statistical properties compared to the chaos-based image ciphers used as benchmarks [9,41,42,43]. Since all of the proposed configurations perform similarly, SP or PS would provide the ideal trade-off between statistical performance and computational cost. Overall, the findings of this experiment show the advantage of adopting a minimalistic approach for encryption schemes, producing robust statistical results without excessive complexity, as well as that changing the underlying chaotic maps does not affect the results.

5. Chaotic Feistel Block Cipher (CFBC)

In this section, we investigate if a conventional block cipher can be designed using a chaotic map as a building block. Our design goal is for the cipher to have a simple, well-understood design that can facilitate third-party cryptanalysis efforts. We use the logistic map with its control parameter set to $r=3.99$. The decision to go with a simple one-dimensional map is to demonstrate that robust security can be attained without relying on complex chaotic systems. We propose a chaos-based block cipher based on the extended version of the original Feistel network, known as the generalized Feistel network (GFN) [44]. The GFN structure has been used in the design of ciphers such as WARP [45] and TWINE [46]. The aim of CFBC is not to propose a real-world-ready cipher, but to demonstrate how simple chaos-based substitutions can be embedded into a well-understood cryptographic structure while remaining analyzable using standard techniques.

The proposed block cipher has a block size of 128 bits, which is divided into eight sub-blocks $(k=8)$. The choice of $k=8$ branches (i.e., 16-bit sub-blocks) is motivated by the fixed-point implementation of the chaotic map, which uses 32-bit precision. The choice of 32-bit precision is a trade-off between sensitivity and computational overhead. Using 32 bits leaves a sufficiently large fractional state to extract 16 bits, while preserving high sensitivity to input differences. Then, half of these sub-blocks undergo mixing using the round function, followed by a permutation of the k sub-blocks.

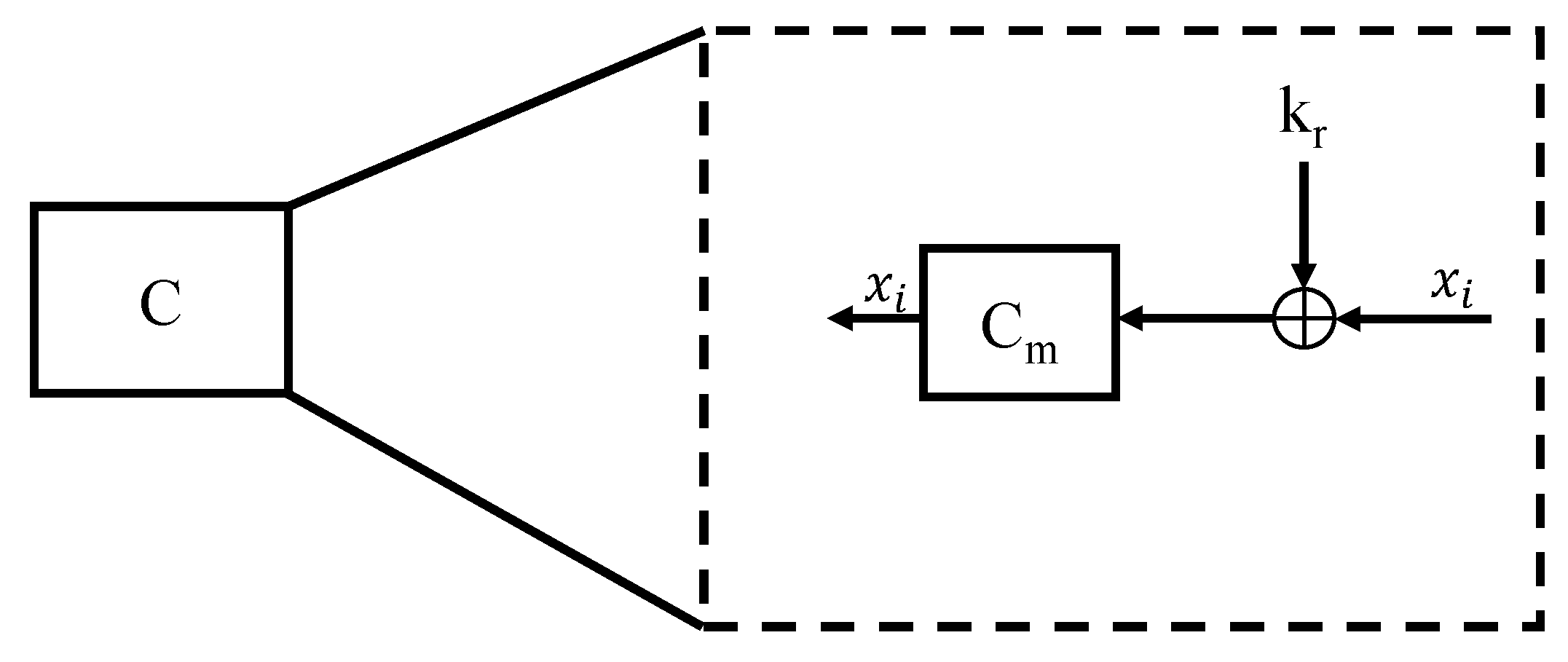
The use of the Feistel structure is motivated by several factors. Firstly, it allows for the use of the same code for both encryption and decryption processes, potentially reducing the implementation cost of decryption. The second factor is that the Feistel network allows the use of a one-way round function. Chaotic maps, which serve as the nonlinear component of the round function (which we refer to as the C-function), exhibit one-way behaviour. The architecture of the proposed CFBC is shown in Figure 3.

The C-Function provides nonlinearity to the cipher. The C-Function is defined as follows:

$$C(x_i,k_r)=C_m(x_i\oplus k_r),$$

(19)

where $C_m$ is the chaotic map, $x_i$ is a 16-bit sub-block of message bits, and $k_r$ is a 16-bit sub-block of the round key, as illustrated in Figure 4. The output of the C-function is calculated as follows:

• An XOR operation is performed between $x_i$ and $k_r$ to obtain $x_p$.
• The current state X of the chaotic map in 16-bit fixed-point representation is XOR-ed with $x_p$.
• The chaotic map (logistic map) is then iterated.
• The 16 least-significant bits of the chaotic map’s state, X, are extracted as the output of the C-function.

After applying the C-function to half of the plain text blocks, the output is XOR-ed with their corresponding halves, as shown in Figure 3, before undergoing a block-wise permutation or block shuffle. The permutation pattern employed in this cipher is illustrated in

Table 7. Block shuffle pattern.

x	0	1	2	3	4	5	6	7
$P\left(x\right)$	3	0	1	4	7	2	5	6

. This particular permutation pattern is known as the No.1 shuffle [44]. This pattern is chosen due to its ability to achieve complete diffusion in just six rounds, which is a fewer number of rounds compared to other types of block shuffles for $k=8$ branches. The minimum number of activated nonlinear functions evaluated for differential and linear cryptanalysis for No.1 shuffle is also superior [44]. The number of activated nonlinear functions serves as a basis for our analysis of the cipher’s security against differential cryptanalysis.

Both the block size and key size of the proposed block cipher are 128 bits. The block cipher requires a minimum of 6 rounds to ensure maximal diffusion but we recommend at least 20 rounds to be secure against attacks such as differential cryptanalysis (see Section 5.2). The initial values for the employed chaotic map ()the logistic map) are $X_0=0.5$ and $r=3.99$. These are public, fixed values that are not part of the secret key. To perform computations on real numbers, we use a 32-bit fixed-point representation where 2 of the most-significant bits represent integers and the 30 least-significant bits represent fractions. The use of fixed-point representation instead of floating point improves analyzability as it allows us to see how each bit in a real number is used in processing. The 128-bit secret key plays a crucial role in generating round keys. The key schedule of the proposed block cipher is as follows:

• The 128-bit secret key is divided into eight 16-bit registers.
• The logistic map is iterated once for each register.
• Bits from the logistic map’s state variable (represented as fixed-point numbers) are extracted after each iteration, where the least-significant bits are XOR-ed with the current value of each register.
• The round key is obtained from all eight updated registers.
• All steps are repeated to obtain round keys for other rounds.

5.1. Ciphertext Randomness Testing

Block ciphers are widely used cryptographic primitives that serve as fundamental building blocks for other cryptographic algorithms, including hash functions and pseudo-random number generators. At the very least, the ciphertexts generated from a block cipher must exhibit essential properties such as high complexity, non-period behaviour, and uniform distribution. To assess the statistical randomness of CFBC, we apply the NIST SP 800-22 test suite. To generate test samples, we create random cipher texts by randomly flipping a single bit of an arbitrary plain text. Each test is conducted with a fixed significance level $(\alpha =0.01)$, and the quality of the sequence is determined by its corresponding p value. If the p value is greater than 0.01, the generated sequence successfully passes the test; otherwise, it fails. A sample size of 100 binary sequences is utilized for each test, with a bit length of ${10}^6$ for each sequence.

The first test sample is obtained by encrypting a plain text consisting of interleaved bit values of 1 s and 0 s. Subsequent test samples are generated by randomly flipping a single bit in the plain text. The results presented in

Table 8. NIST SP 800-22 results.

Sub-Tests	p-Value	Proportion
Frequency	0.678686	98/100
Block Frequency	0.719747	98/100
Cumulative Sums	0.455937	99/100
Runs	0.401199	100/100
Longest Run	0.739918	97/100
Rank	0.096578	99/100
FFT	0.319084	100/100
Nonoverlapping Template	0.003996	100/100
Overlapping Template	0.678686	100/100
Universal	0.983453	98/100
Approximate Entropy	0.236810	100/100
Random Excursions	0.568055	59/60
Random Excursions Variant	0.002971	59/60
Serial	0.834308	100/100
Linear Complexity	0.213309	99/100
Success Counts	15/15

demonstrate that CFBC successfully passed all 15 sub-tests of the NIST test suite. This indicates that the outputs of the block cipher exhibit desirable characteristics of randomness, even distribution, and complexity.

The ENT test consist of five tests for randomness, and the results are presented in

Table 9. ENT test results.

Test Name	p-Value
Entropy	7.999990
Chi-square	218.94
Arithmetic mean	127.5063
Monte Carlo value of Pi	3.14698285
Serial correlation coefficient	−0.000229

. The entropy test measures the information density of the sequence, represented as the number of bits per byte, and quantifies the expected information contained in the generated sequence. CFBC exhibits a maximum level of entropy (ideal value 8), indicating a high degree of randomness. The chi-square test shows that the generated sequence is random and highly sensitive to errors in PRNG. The arithmetic mean for CFBC (calculated as the sum of all bytes in the generated file divided by the file length) is very close to random, falling within the mean range of 127 ± 0.01. Moreover, the Monte Carlo value converges to pi with an error of 0.01% for CFBC, further confirming the sequence’s proximity to randomness. Lastly, the serial correlation coefficient test demonstrates that there is no correlation between each byte and the previous byte in the sequence.

5.2. Security Against Differential Cryptanalysis

In this section, we show that it is indeed possible to analyze the security of a chaos-based cipher using conventional cryptanalysis methods. We use differential cryptanalysis as an example. Other attacks such as linear cryptanalysis can be trivially extended based on our findings. Note that we do not rely on statistical tests but instead perform analysis based on the differential property of the C-function and the number of active nonlinear functions. This approach is commonly used to estimate the security of S-box-based block ciphers against differential cryptanalysis, by counting the number of active S-boxes. We demonstrate a provable upper-bound of security against differential cryptanalysis for CFBC.

By using fixed-point representation to compute real numbers, we can compute the difference propagation through the logistic map. We use 32-bit fixed-point numbers where the two most-significant bits represent integers and the thirty least-significant bits represent the fraction. The choice of using a 32-bit fixed-point representation directly affects the precision of the logistic map’s internal state and hence its differential properties. Increasing the precision of the fixed-point representation expands the state space and leads to finer granularity in difference propagation. This enhanced sensitivity, especially in the least-significant bits, can result in lower differential probabilities and thus a higher security margin. This is analogous to using 8-bit S-boxes rather than 4-bit S-boxes in conventional block ciphers. Conversely, using fewer bits could lead to higher differential probabilities. Therefore, the bounds we present should be interpreted as specific to the 32-bit fixed-point configuration, with the potential for tighter bounds under higher precision.

Since the logistic map’s state variable is $X\in [0,1)$, only 30 fraction bits are active at any time. We can then compute the differential distribution table (DDT) by taking $X_i$ as the input to the logistic map, while $X_{i+1}$ is the output—similar to how the DDT is computed for any substitution box. However, computing the full DDT is computationally expensive since it would be equivalent to computing the differential distribution for a 30-bit S-box. As such, we first limit the search space to only the 18 most-significant fractional bits. This implies that the differential probability obtained is only an upper bound and that the actual probability would be much lower if all 30 bits were taken into consideration. After we identify the input-to-output difference propagation with the highest probability, we then consider all bits involved in the C-function and recompute the actual probability for the target differences.

Experimentally, the upper bound of the differential probability of the C-function is approximately ${\displaystyle \frac{2^{15.3}}{2^{30.0}}}=2^{-14.7}$, where the difference propagation is $0x00001000\to 0x00000002$. For 20 rounds of the cipher, the No.1 block shuffle would lead to 30 active nonlinear functions, which leads to an upper-bound differential probability of $2^{-14.7\times 30}=2^{-441}$. There is a significant security margin of $2^{441-128}=2^{313}$ or 313 bits against a differential attack.

As with different S-box choices in conventional ciphers, changing the chaotic map or the bit-precision configuration would lead to different differential profiles. Exploring such variants presents an interesting direction for future work. Note that we only focus on differential cryptanalysis as a baseline measure of security. Our goal is to demonstrate that chaotic components, when used within a well-understood design paradigm like GFN, can be meaningfully assessed using conventional cryptanalytic techniques. Future work may extend this to other forms of cryptanalysis (e.g., linear or boomerang attacks).

5.3. An Image Encryption Scheme Based on CFBC

Conventionally, block ciphers only need to provide proof of resistance against various attacks, such as differential cryptanalysis in the previous section, and do not need to be applied specifically to encrypt images. However, one of the common arguments in many papers for proposing new chaos-based image ciphers is that mainstream block ciphers are inadequate for image encryption. We want to, instead, show that our proposed block cipher can be applied to image encryption and attain similar statistical properties touted by past chaos-based image ciphers. The encryption phase comprises three main steps—reshaping the plainimage to obtain a one-dimensional array; CBC encryption; and, finally, reshaping the encrypted one-dimensional array to obtain the cipherimage. Each of these steps is elaborated below.

• Reshaping the image: The plainimage undergoes a reshaping process before encryption is applied. This process scales each pixel value in the plainimage to a 16-bit word. Each pixel value, which ranges between 0 and 255, is linearly scaled to fall between 0 and 65,535. For example, a pixel value of 189 ($0xBD$) will be expanded and stored as ${\displaystyle \frac{189}{255}}\times 65,535=48,573$ ($0xBDBD$). All pixels will be stored in a one-dimensional array of 65,536 16-bit words.
• CBC Encryption: The one-dimensional array is encrypted 8 words at a time (128-bit blocks) using CFBC in cipher block chaining (CBC) mode. In this process, an initialization vector (IV) based on the numbers of pi is chosen, which is an example of nothing up my sleeve numbers, which are commonly used in cryptography [47]. The encryption starts by XOR-ing the IV with the first image block, generating a chaining value for the first block. This chaining value is then encrypted using the block cipher (CFBC) algorithm, producing the first cipher text block. For subsequent blocks, the chaining value (the result of the previous block’s encryption) is XOR-ed with the plain text block. This operation ensures that each block’s encryption depends on the encryption of the previous block, providing the chaining effect. The resulting cipher text represents the encrypted array.
• Reshaping the array: The encrypted array is reshaped to form the cipherimage by reversing Step 1.

6. Experimental Results

This section presents an experimental evaluation of CFBC when used for image encryption, assessing its statistical properties and overall performance. The evaluation involves several metrics, including histogram analysis, correlation, NPCR, UACI, and entropy tests. The image samples used in the experiments were standard Lena, Cameraman, Peppers, and other samples obtained from the SC-SIPI ’Miscellaneous’ image dataset, sourced from the USC-SIPI Image Database.

6.1. Histogram Analysis

The histogram serves as a representation of the pixel value distribution in an image. Figure 5 displays histograms of the plainimages and their corresponding cipherimages. The histogram values are shown in

Table 10. Histogram results.

Image	MD	ID	DUH
Cameraman	70,194	64,201	0.0582
Lena	67,986	41,495	0.0508
Pepper	71,376	36,665	0.0534
5.1.10	59,308	48,348	0.0551
5.1.11	77,201	32,524	0.0537
5.1.12	62,261	35,938	0.0555

. The experimental results reveal that the histograms of the cipherimages exhibit a significantly uniform distribution and differ completely from the original images.

6.2. Correlation Coefficient

An effective encryption algorithm should significantly reduce the high correlation between adjacent pixels in the plainimage. To assess the proposed encryption algorithm’s impact on the correlation between adjacent pixels, we examine 4000 randomly chosen pairs of adjacent pixels from both the plainimage and the ciphered image along horizontal, vertical, and diagonal directions. The correlation of each pair is computed using Equation (13)). Figure 6 and

Table 11. Correlation coefficients.

Image	Plainimage			Cipherimage
	H	V	D	H	V	D
Camera	0.9348	0.9573	0.9049	0.0018	0.0138	−0.0077
Lena	0.9026	0.9452	0.8892	0.0031	−0.0021	0.0147
Pepper	0.9654	0.9721	0.9384	0.0082	0.0095	0.0011
5.1.10	0.9072	0.8620	0.8099	−0.0022	0.0046	−0.0185
5.1.11	0.9629	0.9368	0.8812	−0.0240	0.0087	0.0015
5.1.12	0.9580	0.9742	0.9351	0.0016	0.0340	0.0082

display the correlation coefficients of the plainimage and cipherimage. The plainimage exhibits a a strong correlation between adjacent pixels in each direction. However, the cipherimage shows a significant reduction in correlation coefficients, which are close to 0.

6.3. Information Entropy

Information entropy, as defined in Equation (15), serves as a measure of the distribution of information source states.

Table 12. Information entropy of images.

Image	Entropy
Cameraman	7.9962
Lena	7.9956
Pepper	7.9956
5.1.10	7.9952
5.1.11	7.9955
5.1.12	7.9951

presents the results for the ciphered images, which are close to the ideal value of 8.

6.4. NPCR and UACI

A robust cryptosystem should exhibit high sensitivity to both plainimages and secret keys. Even a slight change in a single pixel value of the plainimage should result in a completely different cipherimage. NPCR and UACI, as defined in Equations (16) and (17), respectively, provide quantitative measures to evaluate this sensitivity. The results for the NPCR and UACI values of the proposed scheme are presented in

Table 13. NPCR and UACI results of proposed scheme.

Image	NPCR	UACI
Cameraman	99.6536	31.1401
Lena	99.6185	28.6264
Pepper	99.6750	29.5561
5.1.10	99.5819	28.3981
5.1.11	99.6002	33.5047
5.1.12	99.6170	35.1788

.

6.5. Comparison

In this section, we compare the proposed cipher and other existing chaos-based ciphers. To ensure a fair comparison of the proposed cipher’s security characteristics, the experiments in this work were conducted using MATLAB on 256 × 256 plainimages, similar to other existing ciphers. The results in

Table 14. Comparison of proposed cipher against other existing image ciphers.

Algorithms	Entropy	Correlation Coefficient			NPCR	UACI
		Horizontal	Vertical	Diagonal
Proposed scheme	7.9962	0.0018	0.0138	−0.0077	99.6536	31.1401
[9]	7.99901	0.001750	0.002468	0.002143	99.6124	30.3951
[42]	7.9989	0.00112	0.00338	0.00166	99.6272	30.3258
[43]	7.99910	0.002289	−0.00160	−0.00132	99.6287	30.3432
[41]	7.9988	−0.00093	−0.00046	0.00175	99.6058	32.0826

show that the proposed block cipher has near-ideal statistical properties, similar to the current state of the art. Our results show that even with a simple block cipher design such as CFBC, it is possible to achieve the statistical results that chaos-based ciphers consider as secure.

We would like to note that chaos-based ciphers often use statistical testing to compare their performance. Marginally better statistical results are sometimes taken as improvements over the current state of the art. However, statistical testing is a stochastic process, meaning that the results of the test can vary depending on the random input data. This means that it is possible to obtain a marginally better statistical result simply by repeating the experiment multiple times. As a result, comparing chaos-based ciphers based on their statistical results can be misleading. It is also important to note that statistical testing is not a perfect measure of security. A cipher that passes all statistical tests may still be vulnerable to cryptanalysis. As such, having a simple design is important to facilitate cryptanalysis efforts, rather than a complex one that may hide some unintentional flaws. We have shown that it is possible to analyze a chaos-based cipher using classical cryptanalysis methods in Section 5.2.

7. Conclusions

In this paper, our goal was to address some of the problems in chaos-based cryptography, namely having complex designs based on security through obscurity that are difficult to analyze. It is important to note that this work focuses on the conceptual design and analysis of chaos-based ciphers rather than practical deployment or integration. In our work, we showed that it is possible to create minimalistic chaos-based encryption algorithms by adopting well-studied design paradigms such as SPN or the Feistel network. We proposed a chaos-based block cipher called CFBC. We show that the proposed cipher is secure against differential cryptanalysis using a standard approach of estimating the number of active nonlinear components. This was made possible due to the generalized Feistel-based design and a simple round function. To the best of our knowledge, this is the first time that the differential property of a logistic map has been analyzed using classical methods rather than just a statistical test. In addition, the ciphertexts produced by the proposed cipher do not have statistical biases, successfully passing the NIST statistical test suite. While passing such tests alone is not a strong indicator of cryptographic strength, it demonstrates that our design meets this baseline requirement in addition to offering provable bounds against differential cryptanalysis. We then used CFBC in CBC mode to encrypt images for comparison with other chaos-based image ciphers. Our evaluation shows that CFBC has the same statistical properties as any other chaos-based image cipher. These results reinforce our paper’s central claim—strong cryptographic properties can be achieved without resorting to unnecessarily complex or convoluted chaos-based designs. Future work will explore other cryptanalysis approaches, practical implementation considerations, performance optimization, and integration into existing cryptographic systems to assess real-world applicability.