Post-Quantum Digital Signature: Verkle-Based HORST

Abstract

The security of commonly used cryptographic systems like RSA and ECC might be threatened by the future development of quantum computing. Verkle-based HORST decreases the size of signatures by 75% (from 12.8 KB to 3.2 KB) and enables O(1)-sized proofs by replacing Merkle trees with Verkle trees. Because verification shifts from O(log t) to constant time, it is ideal for blockchain and IoT applications that require short signatures and fast validation. In order to increase efficiency, this study introduces Verkle-based HORST, a hash-based signature method that uses Verkle trees. Our primary contributions are the following: a formal security analysis proving maintained protection levels under standard assumptions; a thorough performance evaluation demonstrating significant improvements in signature size and verification complexity in comparison to conventional Merkle tree approaches; and a novel signature construction employing polynomial commitments to achieve compact proofs. The proposed approach has a lot of benefits for real-world implementation, especially when dealing with situations that call for a large number of signatures or settings with limited resources. We offer comprehensive implementation instructions and parameter choices to promote uptake while preserving hash-based cryptography’s quantum-resistant security features. Our findings suggest that this method is a good fit for post-quantum cryptography systems’ standardization.

1. Introduction

Classical cryptographic systems, especially those based on asymmetric algorithms like RSA and elliptic curve cryptography (ECC), face serious challenges due to the rapid advancement of quantum computing. These systems rely on hard mathematical problems like discrete logarithms and integer factorization, and they have a significant role in contemporary digital infrastructure. These issues can be effectively resolved by quantum algorithms, especially Shor’s algorithm, making traditional cryptography systems vulnerable to quantum computing attacks [1,2]. Post-quantum cryptography (PQC), which focuses on creating cryptographic methods that are secure against quantum computer attacks, has become a crucial field of study in response to this.

Hash-based digital signatures are seen to be one of the most promising post-quantum cryptography approaches. These signatures only depend on the integrity of cryptographic hash functions, which, according to current theories, are resilient to quantum assaults. Hash-based signatures are still feasible with sufficiently large hash sizes, even if Grover’s approach only cuts security levels in half, despite the fact that it can accelerate brute-force attacks against hash functions [3]. Hash-based signatures are a top contender for post-quantum safe cryptography because of their reliability, ease of use, and well-understood security features.

Beyond traditional post-quantum cryptography, quantum digital signatures (QDS) have evolved as an alternative solution that uses quantum key distribution (QKD) and quantum-resistant primitives. Recent developments show progress in gaining information-theoretic security, including effective lattice-based QDS constructs [4] and measurement-device-independent QDS protocols [5]. However, QDS’s applicability for legacy systems is currently limited due to its requirement for quantum communication infrastructure. On the other hand, Verkle-based HORST offers a hash-based, classical approach that is both quantum-resistant and compatible with current technology.

Introduced in 1979, the Lamport–Diffie one-time signature (OTS) system laid the groundwork for hash-based signatures [6]. Lamport–Diffie signatures offer a straightforward yet efficient framework for quantum-safe authentication by generating signatures using pairs of secret keys and matching hash values. However, a lot of applications cannot use Lamport–Diffie signatures because of their large key sizes. The Winternitz OTS (WOTS), which uses hash chains rather than individual key pairs to reduce key sizes, was proposed as a solution to this limitation [7]. Shorter signatures are possible with this method, but signing and verification need more processing power.

Additional advancements resulted in the creation of WOTS+, a WOTS version that adds randomization to the hash chains to boost security [8]. Because of this randomization, WOTS+ is more resistant to some kinds of cryptographic attacks by reducing the impact of multi-target attacks. The fact that one-time signatures like WOTS and WOTS+ can only securely sign a single message limits their usefulness for many real-world applications, even with current improvements.

By allowing the signature of several messages with a single public key, the Merkle Signature Scheme (MSS) overcomes this restriction [9]. In order to do this, MSS arranges public keys for one-time signatures into a Merkle tree, with the master public key acting as the tree’s root. This method preserves quantum resistance while enabling the effective authentication of several signatures. However, MSS is stateful, which means the signer must track key usage to maintain security. Additionally, scalability in large-scale systems may be limited by the fact that the proof sizes in MSS increase exponentially with the number of leaves in the Merkle tree.

To address these issues, stateless hash-based systems such as HORS (Hash to Obtain Random Subset) and its tree-based variant, HORST (HORS with Trees), were created [10,11]. While HORST adds a Merkle tree to compress public keys and increase performance, HORS uses a subset of secret keys for each signature to minimize key sizes. Nevertheless, HORST continues to rely on Merkle proofs, which increase in size as the tree height increases, and due to its “few-times” nature, its security deteriorates as the number of signatures increases.

In this paper, we present Verkle-based HORST, a new framework that uses a Verkle tree—a cryptographic structure that uses vector commitments to obtain constant-sized proofs—instead of the Merkle tree in HORST [12]. Verkle trees employ polynomial commitments (such as KZG commitments) to provide proofs of constant size ($O \left(1\right)$), in contrast to Merkle trees, which demand proofs that increase logarithmically with the number of leaves ($O \left(\log n\right)$). This invention increases the scheme’s scalability and drastically lowers the quantity of data needed for verification. We present a formal security proof for Verkle-based HORST, showing that it preserves the collision resistance of the underlying hash function and the unforgeability guarantees of classical HORST under the discrete logarithm assumption. Our method does without logarithmic-sized proofs while retaining the same level of security by substituting Verkle trees for Merkle trees.

To assess the usefulness of our method, we perform a thorough efficiency comparison between classic HORST and Verkle-based HORST. Important variables like proof size, verification time, and storage needs are the main focus of our investigation. The findings show that Verkle-based HORST is a scalable and useful approach for post-quantum digital signatures, providing notable efficiency gains.

2. Hash-Based Digital Signatures

With their strong defense against the dangers of quantum computing, hash-based digital signatures are a viable post-quantum communications option. These strategies rely on hash functions’ cryptographic strength, which is derived from their one-way and collision-resistant design. Because it is difficult to identify two different inputs that produce the same hash output, hash-based signatures are intrinsically resistant to quantum attacks, in contrast to conventional number-theoretic systems like RSA and ECC, which require mathematical hard problems.

The Lamport–Diffie One-Time Signature (L-OTS) is the most basic and fundamental hash-based signature scheme. It works by creating pairs of random secret keys for every bit in the message hash, and then applying a cryptographic hash function to the secret keys to determine the corresponding public keys. L-OTS has practical drawbacks, such as high signature sizes and the constraint of being useable only once, even if it is probably safe under the assumption of collision-resistant hash functions [13]. To address these limitations, the Winternitz One-Time Signature (WOTS) technique was introduced. It uses hash chains rather than individual key pairs to reduce key and signature sizes. WOTS+, a further improvement, strengthens security without appreciably increasing computing burden by adding randomization to the hash chains to counteract multi-target attacks.

By making it possible to sign several messages with a single public key, the Merkle Signature Scheme (MSS) increased the usefulness of one-time signatures. In order to do this, MSS arranges public keys for one-time signatures into a Merkle tree, with the master public key acting as the tree’s root. This method preserves quantum resistance while enabling the effective authentication of several signatures. However, MSS can hinder scalability in large-scale applications due to its statefulness, which requires the signer to keep track of which keys have been used, and its proof sizes, which increase logarithmically with the number of leaves in the Merkle tree [14].

In order to address these issues, more sophisticated methods such as HORS (Hash to Obtain Random Subset) and its tree-based variant, HORST (HORS with Trees), were created. While HORST adds a Merkle tree to compress public keys and increase performance, HORS uses a subset of secret keys for each signature to minimize key sizes. Nevertheless, HORST continues to rely on Merkle proofs, which increase in size as the tree height increases, and because of its “few-times” nature, its security deteriorates as the number of signatures increases.

It is commonly assumed in the context of randomized algorithms and cryptographic protocols that computers possess an infinite number of really random bits. For cryptographic procedures to remain unpredictable and secure, these random bits are essential. High-quality physical or algorithmic sources of randomness are used in cryptographic systems to produce the random numbers required for safe key creation and signature procedures. Hash-based signature methods are especially attractive in the context of post-quantum cryptography because they offer a very safe and effective method of authentication through the combination of random bit creation and the collision resistance of hash functions.

3. Lamport–Diffie One-Time Signature Scheme

Digital signatures were changed by Leslie Lamport’s 1984 proposal [15] for Lamport–Diffie One-Time Signatures (OTS), which relied solely on cryptographic hash functions rather than number-theoretic presumptions like RSA or elliptic curves. Because of its architecture, Lamport–Diffie OTS is a fundamental post-quantum encryption scheme that is naturally resistant to quantum computer attacks. However, a crucial limitation reduces its usefulness: only one message may be safely signed by each key pair. Reusing a private key makes the system vulnerable for repeated use by exposing information that attackers may use to forge signatures.

In Lamport–Diffie One-Time Signatures (OTS), the first step in the key creation process is choosing a cryptographic hash function, like SHA-256, which generates an output with a set length (256 bits, for example). The scheme’s security depends on the hash function’s ability to withstand collisions and preimages, making it computationally impossible to reverse the hash or identify two inputs that result in the same output. The signer first generates 256 pairs of random values, each of which is 256 bits long, in order to construct a key pair. Two lists are created from these pairings, one of which corresponds to message bits of 0 and the other to 1 bit.

In particular, 256 random values are present in the first list, represented by the symbol $s{k}_0$:

$$s{k}_0=\left(s{k0}_1,s{k0}_2,s{k0}_3,\dots ,s{k0}_{256}\right)$$

(1)

There are an additional 256 random values in the second list, $s{k}_1$:

$$s{k}_1=\left(s{k1}_1,s{k1}_2,s{k1}_3,\dots ,s{k1}_{256}\right)$$

(2)

These two lists combine to create the private key, which has 512 random values overall. Each component of the private key is subjected to the hash function in order to obtain the public key. The hash function is calculated for each value in $\mathrm{s}{\mathrm{k}}_0$ and $\mathrm{s}{\mathrm{k}}_1$, producing two lists of hashed values that correspond to each other. The hashes of the ${\mathrm{s}\mathrm{k}}_0$ values are in the first list, ${\mathrm{p}\mathrm{k}}_0$:

$$p{k}_0=\left(H\left(s{k0}_1\right),H\left(s{k0}_2\right),H\left(s{k0}_3\right),\dots ,H\left(s{k0}_{256}\right)\right)$$

(3)

The second list ${\mathrm{p}\mathrm{k}}_1$, contains the hashes of the ${\mathrm{s}\mathrm{k}}_1$ values:

$$p{k}_1=\left(H\left(s{k1}_1\right),H\left(s{k1}_2\right),H\left(s{k1}_3\right),\dots ,H\left(s{k1}_{256}\right)\right)$$

(4)

These two lists are then combined to form the public key:

$$\mathrm{Public} \mathrm{Key} =\left(p{k}_0,p{k}_1\right)$$

(5)

There are 512 hashed values in the public key overall (256 for ${\mathrm{p}\mathrm{k}}_0$ and 256 for ${\mathrm{p}\mathrm{k}}_1$). While the public key may be safely shared with verifiers, the private key is guaranteed to stay hidden thanks to this key generation procedure. Based on the message bits, the signer will disclose particular elements of the private key throughout the signing process, and the verifier will confirm the signature using the matching hashed values from the public key.

It is necessary to first encode the message as a fixed-length binary string in order to sign it using the Lamport–Diffie one-time signature. In order to guarantee that the message length corresponds to the necessary bit-length of the signature scheme, a cryptographic hash function can be used to generate a fixed-length digest if the message is not already in binary form. A 256-bit message is produced:$\mathrm{msg} =\left({\mathrm{m}\mathrm{s}\mathrm{g}}_1,{ \mathrm{msg} }_2,\dots ,{ \mathrm{msg} }_{256}\right)$.

Which part of the secret key is utilized in the signature depends on each bit ${\mathrm{m}\mathrm{s}\mathrm{g}}_i$. sk0_i is chosen by the signer if ${\mathrm{m}\mathrm{s}\mathrm{g}}_i=0$, and Sk1i is chosen if ${\mathrm{m}\mathrm{s}\mathrm{g}}_i=1$. Each bit in the message is represented by one of the 256 values that make up the final signature. The private key is kept from being fully exposed by the signer by just disclosing half of it (the set of 256 values that match to the message bits). However, since an attacker might recreate the remaining secret key components, using the same key for several signatures could undermine security.

Verification involves checking if the values in the signature that are disclosed correspond to the values that are anticipated in the public key. Considering the signature:$\mathrm{signature} =\left({\mathrm{s}\mathrm{i}\mathrm{g}}_1,{\mathrm{s}\mathrm{i}\mathrm{g}}_2,\dots ,{\mathrm{s}\mathrm{i}\mathrm{g}}_{256}\right)$, the verifier calculates $\mathrm{H}\left({\mathrm{s}\mathrm{i}\mathrm{g}}_i\right)$ for each component and checks whether it matches to the correct entry in the public key. If ${\mathrm{m}\mathrm{s}\mathrm{g}}_i=0$, then

$$\mathrm{H}\left({\mathrm{s}\mathrm{i}\mathrm{g}}_i\right)={\mathrm{p}\mathrm{k}\mathrm{O}}_i$$

(6)

otherwise, if ${\mathrm{m}\mathrm{s}\mathrm{g}}_i=1$, then the verifier checks the following:

$$\mathrm{H}\left({\mathrm{s}\mathrm{i}\mathrm{g}}_i\right)={\mathrm{p}\mathrm{k}1}_i$$

(7)

If all 256 checks pass, the signature is considered valid, and the message is authenticated.

The Lamport–Diffie one-time signature secure hash-based signature system has a number of drawbacks. Because it requires 512 hash outputs for the public key and 256 random values per signature, its key size is greater than that of other signature schemes, increasing the cost of transmission and storage. It is also a one-time signature system, which means that a private key cannot be used again without jeopardizing security after it has been used. Reusing a secret key compromises security, as attackers can forge signatures from multiple observations. Because of this, it is susceptible to quantum assaults. In order to get around this, Merkle’s signature technique was developed, which effectively authenticates multiple one-time public keys using a Merkle tree. Even with its drawbacks, Lamport–Diffie OTS is still a crucial starting point for research on post-quantum cryptography and hash-based signatures. Advanced techniques such as Merkle Tree-Based Authentication, which increases scalability, and Winternitz OTS (WOTS), which decreases key sizes, have been influenced by it. These developments overcome the inefficiencies of L-DOTS while maintaining quantum resistance.

4. Winternitz One-Time Signature (WOTS)

The Winternitz One-Time Signature (WOTS) scheme is a one-time signature technique that preserves security while reducing the number of public keys and signatures. It solves the shortcomings of the Lamport–Diffie OTS, which necessitates a significant amount of key storage and hash calculations. WOTS reduces the number of important components by grouping message bits together and using iterative hashing. It is still a one-time signature technique, though, so each pair of keys may safely sign just one message.

The cryptographic hash function $H$ that generates fixed-length outputs is the foundation of WOTS. The Winternitz parameter $w$, which controls the number of bits that are joined together during signing, is another parameter introduced by the system. The signature gets shorter as $w$ increases, but this comes at the expense of more hash calculations [16].

The signer first produces $l$ secret key components, where $l$ depends on the value of $w$ that is selected, in order to generate the key pair. These values are confidential and chosen at random: $\mathrm{s}\mathrm{k}=\left({\mathrm{s}\mathrm{k}}_1,{\mathrm{s}\mathrm{k}}_2,\dots ,{\mathrm{s}\mathrm{k}}_l\right)$.

The corresponding public key is obtained by applying the hash function iteratively $w-1$ times on each secret key element: ${\mathrm{p}\mathrm{k}}_i={\mathrm{H}\mathrm{a}\mathrm{s}\mathrm{h}}^{(w-1)}\left({ \mathrm{sk} }_i\right)$ for $i=\mathrm{1,2},\dots ,l$. Here, $H^{w-1}$ denotes applying the hash function $w-1$ times (e.g., $\left.H^2\left(x\right)=H\left(H\right(x\left)\right)\right)$.

The first step in signing a message is hashing it to create a fixed-length digest. The digest is then expressed in base-w notation, where each hash digit indicates the number of times a matching secret key element has to be hashed. The message digest is broken up into $l$ sections: $\mathrm{msgDigest} =\left({\mathrm{msgPart} }_1,{ \mathrm{msgPart} }_2,\dots ,{ \mathrm{msgPart} }_l\right)$.

For each part ${\mathrm{msgPart}}_i$, the signer takes the corresponding secret key element ${\mathrm{s}\mathrm{k}}_i$ and hashes it to produce the signature component ${\mathrm{s}\mathrm{i}\mathrm{g}}_i=H^{{\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_i}\left({\mathrm{s}\mathrm{k}}_i\right)$.

The final signature composed of all $l$ values is $\mathrm{signature} =\left({\mathrm{s}\mathrm{i}\mathrm{g}}_1,{\mathrm{s}\mathrm{i}\mathrm{g}}_2,\dots ,{\mathrm{s}\mathrm{i}\mathrm{g}}_l\right)$.

By hashing every component of the signature until the desired number of iterations is reached, the verifier reconstructs the public key. The verifier computes the following:

$${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{P}\mathrm{k}}_i=H^{w-1-{\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_i}\left({\mathrm{s}\mathrm{i}\mathrm{g}}_i\right)$$

(8)

The signature is deemed legitimate if the calculated public key corresponds to the original public key.

Because WOTS groups bits and requires fewer key pairs than Lamport–Diffie OTS, it is a one-time signature system that drastically decreases the amount of signatures. However, because of repeated hashing, this comes at the expense of more computing complexity. WOTS is unable to sign several messages safely without exposing its keys. Winternitz One-Time Signature Plus, or WOTS+, was created as an enhanced version to get around these restrictions and provide better security and efficiency.

The Winternitz parameter w is chosen by carefully weighing security, computational cost, and signature size. The procedure is sped up when w is small since fewer hash calculations are needed for signing and verification. Conversely, the signature size dramatically shrinks when w is big, but the computing complexity rises as a result. The use case determines the ideal value of w, which strikes a balance between the requirement for compact signatures and the processing power at hand.

By adopting a more secure hash function, a chaining method rather than simple iterative hashing, and a lower risk of key exposure while signing multiple messages, WOTS+ overcomes some of the drawbacks of the original approach. With these enhancements, WOTS+ retains the major advantages of the original WOTS scheme while being a more reliable and effective option for applications needing post-quantum secure signatures.

5. Winternitz One-Time Signature Plus (WOTS+)

A modified version of the original WOTS scheme, Winternitz One-Time Signature Plus (WOTS+) aims to preserve the fundamentals of hash-based signatures while enhancing security and efficiency. By using bitmasks to counteract attacks that take advantage of hash chain predictability, WOTS+ is more resilient to cryptographic attacks such as collision and second-preimage attacks [17]. The chaining process applies a more sophisticated function to link hash operations, replacing the straightforward iterative hashing utilized in WOTS. To ensure unique and unpredictable calculations, WOTS+ also uses a modified hash function, which can be either a bespoke hash function or a modified version of an existing one. Because of these improvements, WOTS+ is far more resistant to assaults that target WOTS’s iterative structure.

Similar to WOTS, WOTS+ depends on a Winternitz parameter $w$ and a cryptographic hash function $H$ (e.g., SHA-256), which determines the efficiency of the scheme. The secret key consists of $l$ randomly generated values: $\mathrm{s}\mathrm{k}=\left({\mathrm{s}\mathrm{k}}_1,{\mathrm{s}\mathrm{k}}_2,\dots ,{\mathrm{s}\mathrm{k}}_l\right)$.

A modified hash chain with a bitmask $r_i$ for every private key element is used to calculate the public key. Each public key element is specifically computed as follows:

$${\mathrm{p}\mathrm{k}}_i=H^{w-1}\left({\mathrm{s}\mathrm{k}}_i\oplus r_i\right) \mathrm{for} i=\mathrm{1,2},\dots ,l$$

(9)

In this case, the bitmasks $r_i$ are created at random, and ⊕ indicates the XOR operation. These bitmasks serve as further protection, making the hash chains unpredictable and resilient to assaults.

A message must first be hashed to provide a fixed-length digest before it can be signed. After that, this digest is transformed into base-w notation, yielding $l$ sections: $\mathrm{msgDigest} =\left({\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_1,{ \mathrm{msgPart} }_2,\dots ,{ \mathrm{msgPart} }_l\right)$.

For every component ${\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_i$, the matching secret key element ${\mathrm{s}\mathrm{k}}_i$ is XORed with the bitmask $r_i$ and then hashed ${\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_i$ times:

$${\mathrm{s}\mathrm{i}\mathrm{g}}_i=H^{{\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_i}\left({\mathrm{s}\mathrm{k}}_i\oplus r_i\right)$$

(10)

The final signature is formed of these $l$ values: $\mathrm{signature} =\left({\mathrm{s}\mathrm{i}\mathrm{g}}_1,{\mathrm{s}\mathrm{i}\mathrm{g}}_2,\dots ,{\mathrm{s}\mathrm{i}\mathrm{g}}_l\right)$.

The bitmask is applied and each signature component is hashed up to $w-1$ times in order to recover the public key during verification. The verifier calculates the following for each signature component, ${\mathrm{s}\mathrm{i}\mathrm{g}}_i$:

$${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{P}\mathrm{k}}_i={\mathrm{H}\mathrm{a}\mathrm{s}\mathrm{h}}^{\left(w-1-{\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}}_i\right)}\left({\mathrm{s}\mathrm{i}\mathrm{g}}_i\right)\oplus r_i$$

(11)

The signature is deemed legitimate if the calculated public key corresponds to the original public key. This procedure guarantees that the signature is genuine and unaltered.

Bitmasks have been added to the one-time signature approach WOTS+ to stop attackers from learning important details about the values of the private key, even in the case that several signatures are made public. Because of this, WOTS+ is more resistant to attacks that take advantage of hash chains’ deterministic nature. In practice, WOTS+ is more efficient since it minimizes the number of hash function applications needed for key generation and verification. Since its architecture makes it less likely for an attacker to reconstruct the private key even if many signatures are seen, it also lowers the danger of key exposure while signing several messages.

WOTS+ maintains its fundamental benefits, including small signature sizes and defense against quantum attacks, in spite of these enhancements. It is frequently used in combination with Merkle tree-based signature schemes, such as XMSS (Extended Merkle Signature Scheme), which preserve the quantum-resistant qualities of WOTS+ while enabling the secure chaining of numerous one-time keys to sign multiple messages.

6. Merkle Signature Scheme (MSS)

In order to improve the usability of one-time signature (OTS) systems, Ralph Merkle invented the Merkle Signature technique (MSS) in 1979. It is a digital signature technique based on stateful hashing. Strong security is offered by OTS schemes like Lamport–Diffie OTS and Winternitz OTS (WOTS), but they have a major drawback: each key pair can only be used once. By enabling many secure signatures with a single small public key, MSS solves this problem. This is accomplished by organizing many OTS key pairs into a binary Merkle tree structure, with the root of the tree acting as the scheme’s main public key [18]. Since the Merkle signature technique only uses hash functions, it is resilient to attacks by quantum computers, making it one of the first and most significant post-quantum cryptography schemes.

Because MSS combines the efficiency of Merkle trees with the security of one-time signatures, it stands out for its simple yet clear design. Many contemporary hash-based signature schemes, like XMSS and SPHINCS+, which are currently a part of the NIST Post-Quantum Cryptography Standardization Project, were influenced by it.

The key generation process in the Merkle signature scheme consists of three main steps: generating one-time signature key pairs, computing a Merkle tree, and deriving the main public key.

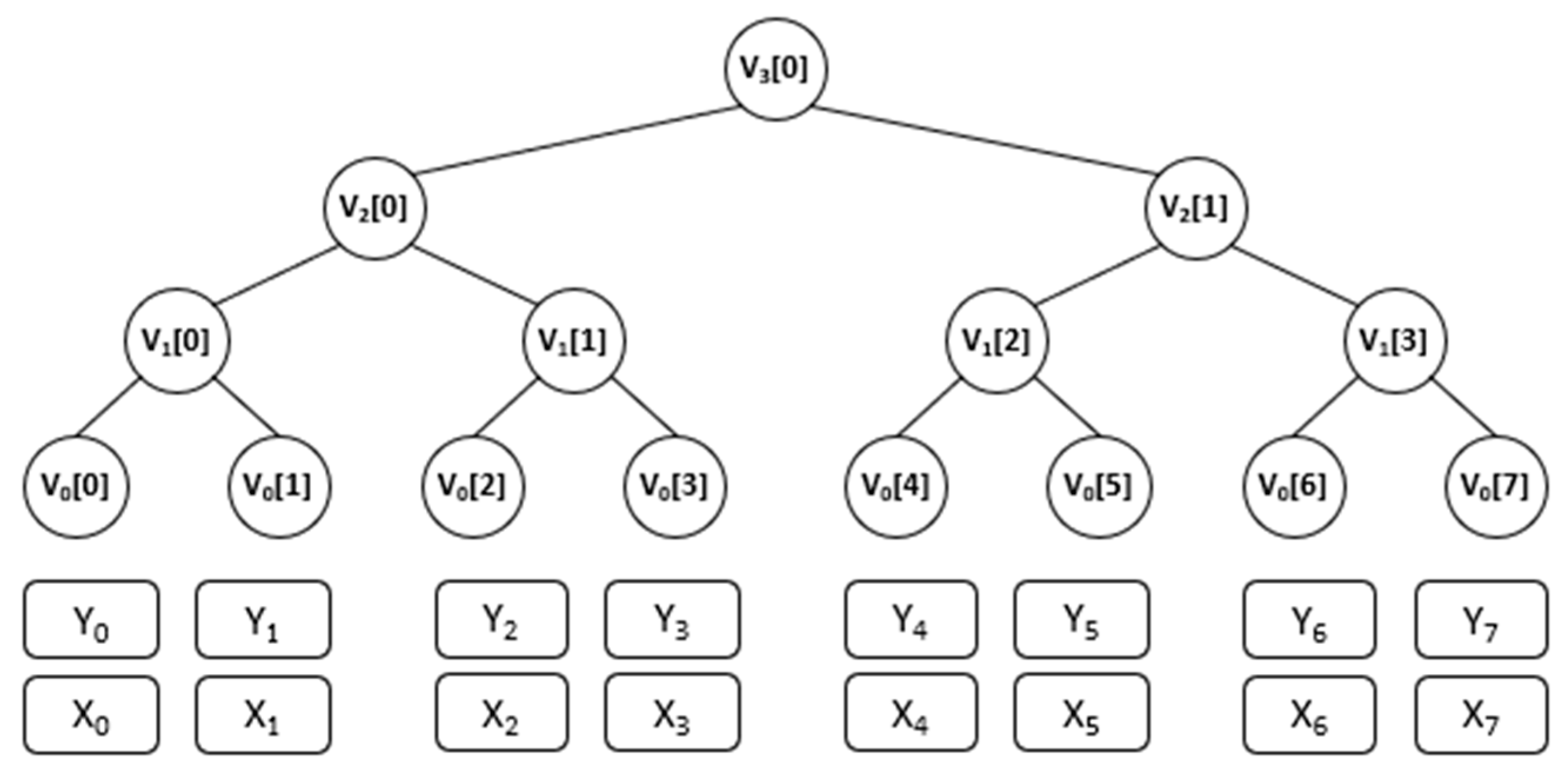
Figure 1 shows a Merkle tree, when tree height is three:

In Figure 1, firstly, the signer generates a set of $2^h$ OTS key pairs, $\left(X_j,Y_j\right),$ where $h$ is the height of the Merkle tree. The first one, $X_j,$ is the signature key or secret key, the other is the verification key or public key. Each one-time signature key pair consists of a secret key and a corresponding public key $\left({\mathrm{X}}_i,{\mathrm{Y}}_i\right) \mathrm{for} i=\mathrm{0,1},\dots ,2^h-1$.

Next, the public keys of the OTS key pairs are hashed using a cryptographic hash function, to form the leaf nodes of the Merkle tree:

$${ \mathrm{leaf} }_i=H\left({\mathrm{y} }_i\right)$$

(12)

After forming the leaf nodes, the Merkle tree is built by hashing pairs of child nodes to create their parent nodes. The internal nodes of the tree are determined by the hash values of its left and right child nodes. The public key of the Merkle signature scheme is represented by the root of the tree, while the secret key of the Merkle signature scheme consists of one-time signature keys, each with a length of $2^H$. Until a single root node is obtained, this procedure keeps going:

$${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j,k}=H\left({\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j-\mathrm{1,2}k}\Vert {\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j-\mathrm{1,2}k+1}\right)$$

(13)

Here, ‖ denotes concatenation. The final root node at the top of the tree serves as the main public key for MSS:

$$\mathrm{pkMSS} ={\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{h,0}$$

(14)

The signer’s private key consists of all the generated one-time signature secret keys, which are used for signing messages. The height h of the Merkle tree determines the total number of signatures that can be generated, which is $2^h$. For example, a tree of height h = 2 can produce over one million signatures.

The signer chooses an unused one-time signature key pair from the Merkle tree and supplies an authentication path to confirm the authenticity of the key pair in order to sign a message using MSS. Choosing an OTS key that has never been used before is the first step. Assume that the key is selected at leaf index $i$ by the signer. The private key for the one-time signature is then used to sign the message:

$$\left.\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{O}\mathrm{T}\mathrm{S}= \mathrm{SignOTS} (\mathrm{message}, {\mathrm{X}}_i\right)$$

(15)

The signer must supply an authentication path since the verifier only knows the root of the Merkle tree. The sister nodes required for the verifier to reconstruct the root without being aware of the entire tree are present in this route. The following is the construction of the authentication path:

$$\mathrm{authPath} =\left({\mathrm{node}}_{0,s_0},{ \mathrm{node}}_{1,s_1},\dots ,{ \mathrm{node}}_{h-1,s_{h-1}}\right)$$

(16)

where $s_j$ represents the sibling node required to compute the parent node at level $j$.

Finally, the full MSS signature consists of the OTS signature and the authentication path:$\mathrm{signature} =\left(\mathrm{sigOTS}, \mathrm{authPath} \right)$.

The verifier must first confirm that the MSS signature is legitimate before utilizing the authentication path to recreate the Merkle tree root.

Verifying the OTS signature with the supplied OTS public key is the first step:$\mathrm{VerifyOTS} (\mathrm{message}, \mathrm{sigOTS}, {\mathrm{y}}_i).$ The verifier then gradually calculates the Merkle root if the OTS signature is legitimate. The verifier repeatedly calculates the parent nodes using the authentication route, beginning with the hash of the supplied OTS public key:

$${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j+1}=H\left({\mathrm{node}}_j\Vert { \mathrm{authPath}}_j\right)$$

(17)

The signature is legitimate if the calculated root hash corresponds to the primary public key that is known. If not, the signature is not accepted. This procedure preserves the scheme’s effectiveness while guaranteeing that the signature is genuine and unaltered.

Unlike standard one-time signature (OTS) schemes that require a distinct public key for each signature, MSS permits numerous safe signatures with a single compact public key, which is one of its main benefits [19]. The Merkle tree structure, which effectively authenticates several one-time signature public keys, is used to do this. Despite its effectiveness, the Merkle tree structure has built-in drawbacks with regard to computational overhead and proof size. Verkle trees, a more sophisticated data structure, provide notable advantages in this regard. We can use Verkle trees instead of Merkle trees. Verkle trees provide substantially reduced proof sizes and lower the computational difficulty of validating huge datasets by using vector commitments rather than basic hash functions. Because of this, Verkle trees are a superior option for applications like blockchain systems that demand great efficiency and scalability.

Furthermore, the Merkle signature scheme is resistant to quantum assaults because it is only dependent on hash functions. It does not rely on number-theoretic presumptions that are susceptible to quantum algorithms like Shor’s algorithm, in contrast to RSA or ECC. When it comes to key storage and transmission, MSS is extremely efficient since the master public key is simply the root of the Merkle tree, which is a single hash value. A disadvantage in contexts with limited resources may be the need for numerous hash operations to compute the Merkle tree, which adds overhead to the signature and verification procedures. This restriction is addressed by Verkle trees, which are more suited for such contexts because of their more effective proof production and verification procedures, which minimize the amount of operations required.

But MSS has its limits as well. The signer must maintain track of which OTS keys have already been used because it is a stateful signing structure. Security is compromised when an OTS key is reused since it makes it possible for an attacker to fake signatures. The maximum number of permitted signatures is $2^h$, where h is the Merkle tree’s height. A fresh key pair has to be created once every leaf has been utilized. The requirement for secure state management is an additional constraint. The scheme’s security is jeopardized if the signer becomes disoriented about which OTS keys have been utilized. Because of this, MSS is less appropriate for some applications, such as distributed systems, where it might be difficult to maintain a consistent state.

MSS continues to be one of the most researched and used post-quantum cryptographic signature systems in spite of its drawbacks. Modern variations like SPHINCS+ and XMSS (Extended Merkle Signature Scheme) are built on top of it. By employing a more adaptable tree structure and lowering the overhead associated with state management, XMSS increases efficiency and scalability. It presents cutting-edge methods to maximize key generation and signing, such as WOTS+ and L-trees. For instance, the Merkle tree effectively authenticates the compressed hash value created by compressing huge one-time signature (OTS) public keys using L-trees. This makes XMSS more feasible for real-world applications by lowering the computational and storage overhead. As part of its post-quantum cryptography portfolio, NIST has also standardized XMSS.

SPHINCS+ is a stateless version of MSS that is more useful for real-world applications as it does not need to track the utilized OTS keys. It achieves statelessness while preserving security by utilizing a hyper-tree topology and a few-times signature (FTS) mechanism. SPHINCS+ is regarded as one of the best candidates for post-quantum safe digital signatures and is also a member of the NIST Post-Quantum Cryptography Standardization Project.

In the post-quantum age, developments in MSS have enhanced the security of digital signatures, making them appropriate for use in secure communication protocols, blockchain technology, and digital certificates. Because Verkle trees are more efficient at creating and verifying proofs than regular Merkle trees, they are being employed in blockchain systems more and more. These trees are a major advance over Merkle trees in contemporary, high-performance systems because they allow for smaller proof sizes and lower computational overhead, which increases scalability and supports lightweight clients.

7. HORS: Hash to Obtain a Random Subset Signature Scheme

A few-times signature (FTS) technique called HORS (Hash to Obtain a Random Subset) makes it possible to sign several messages with a single key pair, guaranteeing efficiency and security. It is appropriate for applications where some key reuse is acceptable but complete reusability is not necessary since it allows a certain number of signatures before key exposure becomes a danger. Since HORS does not rely on number-theoretic hardness assumptions like RSA or elliptic curve encryption, it is post-quantum secure. It must be used carefully, though, and is not completely reusable.

HORS is based on a cryptographic hash algorithm that generates outputs with a defined length. The total number of secret key components (t) and the number of elements chosen from the secret key during signing (k) are the two main factors that determine the scheme’s security and effectiveness [20].

The signer generates t random secret values, which make up the private key, in order to produce the key pair. Our secret key is $\mathrm{sk} =\left({\mathrm{sk}}_1,{ \mathrm{sk}}_2,\dots ,{ \mathrm{sk}}_t\right)$.

The public key, which is made up of t hash values, is then generated by hashing each value of the secret key. Our public key is ${\mathrm{p}\mathrm{k}}_i=H\left({\mathrm{s}\mathrm{k}}_i\right) \mathrm{for} i=\mathrm{1,2},\dots ,t$.

When verifying a signature, the verifier refers to the public key. The number of signatures needed and the desired security level are taken into consideration when selecting the parameters t and k. A greater t, for instance, boosts security but also makes the public key and signature larger.

To generate a signature, the signer must first calculate a message digest using a cryptographic hash function $\mathrm{msgDigest} =H\left(\mathrm{message}\right)$.

Next, the message digest is split into $k$ segments, where each part is converted as an index value that selects one of the secret key elements. These indexes are computed: $\left({\mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)=\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{D}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t} \mathrm{m}\mathrm{o}\mathrm{d}t$.

Once the indexes are determined, the signer includes the corresponding secret key elements in the signature:$\mathrm{signature} =\left({\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_1},{\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_2},\dots ,{\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_k}\right)$.

It is safe for restricted usage since each signature only reveals a portion of the secret key. However, an attacker may be able to reconstruct the key and fabricate signatures if enough private key elements are exposed after several signatures. HORS is categorized as a few-times signature scheme instead of a fully reusable one because of this.

Using the same method as the signer, the verification procedure starts by calculating the message digest $\mathrm{msgDigest} =H\left(\mathrm{message}\right).$ Similar to the signature procedure, the digest is then divided into k indexes: $\left({\mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)=\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{D}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t} \mathrm{m}\mathrm{o}\mathrm{d}t$.

The verifier calculates the hash of each disclosed signature component and determines if it corresponds to the matching item in the public key:

$$H\left({\mathrm{s}\mathrm{i}\mathrm{g}}_i\right)={\mathrm{p}\mathrm{k}}_{{\mathrm{index}}_i}\forall i\in [1,k]$$

(18)

The signature is accepted if all of the hashes match; if not, it is denied. This procedure guarantees that the signature is genuine and unaltered.

HORS is perfect for secure boot, firmware upgrades, and blockchain transactions since it permits numerous signatures from a single key pair and minimizes signature size by including just a portion of the private key [21]. However, after several signatures, there is a chance of fabrication since each signature reveals a portion of the secret key. In order to reduce key exposure, HORST (HORS with Trees) can incorporate a Merkle tree structure. Because of their ease of use and effectiveness in applications that need minimal signatures, HORS and its variations are commonly employed.

8. HORST: HORS with Trees Signature Scheme

An upgrade to the HORS (Hash to Obtain a Random Subset) method, the HORST (HORS with Trees) signature technique adds a binary Merkle tree to authenticate HORS public keys, increasing security. This stops an attacker from using key reuse to create fake signatures. A popular component of SPHINCS, a scalable, post-quantum safe signature system, is the stateless signature technique HORST. By including a Merkle tree structure, HORST solves the key exposure issue in HORS [22]. This guarantees that an attacker cannot create a legitimate signature without generating a corresponding Merkle root, even if portions of the private key are made public.

Similar to HORS, HORST uses a vast collection of random numbers for its private key and a cryptographic hash function. For the private key, t randomly generated values are used: $\mathrm{sk} =\left({\mathrm{sk}}_1,{ \mathrm{sk}}_2,\dots ,{ \mathrm{sk}}_t\right)$. HORST constructs the hashed private key values into a Merkle tree rather than utilizing them directly as the public key. Leaf nodes are initially created by hashing each private key value:

$${ \mathrm{leaf} }_i=\mathrm{H}\left({\mathrm{s}\mathrm{k}}_i\right)\forall i\in [1,t]$$

(19)

The tree is then formed by iteratively hashing pairs of nodes to produce the parent nodes:

$${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j+1}=\mathrm{H}\left({\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_j\Vert {\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j+1}\right)$$

(20)

In this case, ${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_j$ indicates a node at level j, and ‖ indicates concatenation. The public key is the last root node in the Merkle tree ($\mathrm{pkHORST} = \mathrm{root}$).

By adding a layer of security, the Merkle tree makes HORST far more resilient than HORS. This extra structure guarantees that an attacker cannot fabricate a valid signature without generating a matching Merkle root, even if portions of the private key are exposed.

The signature procedure in HORST follows the HORS method but contains extra authentication channels to validate the integrity of the exposed private key parts. First, the message digest is calculated and transformed into k indexes $\left({\mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)=\mathrm{H}\mathrm{a}\mathrm{s}\mathrm{h}\left(\mathrm{message}\right)\mathrm{m}\mathrm{o}\mathrm{d}t$.

The matching private key component for each chosen index is made visible as a component of the signature:

$$\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{S}=\left({ \mathrm{sk} }_{{\mathrm{index}}_1},{\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_2},\dots ,{ \mathrm{sk} }_{{\mathrm{index}}_k}\right)$$

(21)

Additionally, the signer contains authentication pathways to allow verification of the Merkle root. Every authentication path has the brother nodes required to reconstruct the root $\mathrm{authPath} =\left({\mathrm{node}}_1,{ \mathrm{node}}_2,\dots ,{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_h\right)$.

Together with the authentication paths, the HORS signature makes up the final HORST signature:$\mathrm{signature} =(\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{S}, \mathrm{authPath})$.

Because they enable the verifier to verify that the disclosed private key parts are a part of the original Merkle tree without needing the transmission or storage of the complete tree, the authentication path is essential for verification.

In order to validate a HORST signature, the verifier first determines if the HORS signature is legitimate before utilizing the authentication path to reconstruct the Merkle root. The verifier collects the indices and calculates the message digest $\left({\mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)=H\left(\mathrm{message}\right)\mathrm{m}\mathrm{o}\mathrm{d}t$.

The verifier calculates the hash of each disclosed private key element and determines if it corresponds to the relevant leaf node in the Merkle tree. The verifier then gradually reconstructs the Merkle root using the authentication paths:

$${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j+1}=H\left({\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_j\Vert {\mathrm{a}\mathrm{u}\mathrm{t}\mathrm{h}\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{h}}_j\right)$$

(22)

If the calculated root matches the known public key root, the signature is legitimate; otherwise, it is denied. This process ensures the signature’s authenticity and integrity.

A key-encryption system called HORST improves HORS by lowering the possibility of key exposure. If a portion of the private key is made public, its Merkle tree structure stops attackers from creating legitimate signatures. But because HORST makes signatures larger, it is less effective when used alone. In order to solve this, SPHINCS—a hierarchical signature scheme that arranges many HORST instances into a more comprehensive structure—is often used. SPHINCS+, a variation of SPHINCS, is a top contender for post-quantum safe digital signatures and is a component of the NIST Post-Quantum Cryptography Standardization Project.

Because of its ease of use and security, HORST is a popular cryptographic system in post-quantum cryptography. Applications that need a limited number of signatures, such as blockchain transactions, secure boot protocols, and firmware upgrades for Internet of Things devices, benefit greatly from it. HORST is included into SPHINCS+, a stateless hash-based signature scheme, which makes it more useful for actual applications.

9. Verkle Tree

Verkle trees are more efficient than Merkle trees and require fewer verifications. They are crucial for post-quantum cryptography because of their ability to reduce expenses, maintain high security, and get rid of redundant data and storage space. They provide effective verification processes by keeping only the information that is necessary. Because Verkle trees are more adaptable and need more hash computations for data integrity verification, they are ideal for handling large datasets.

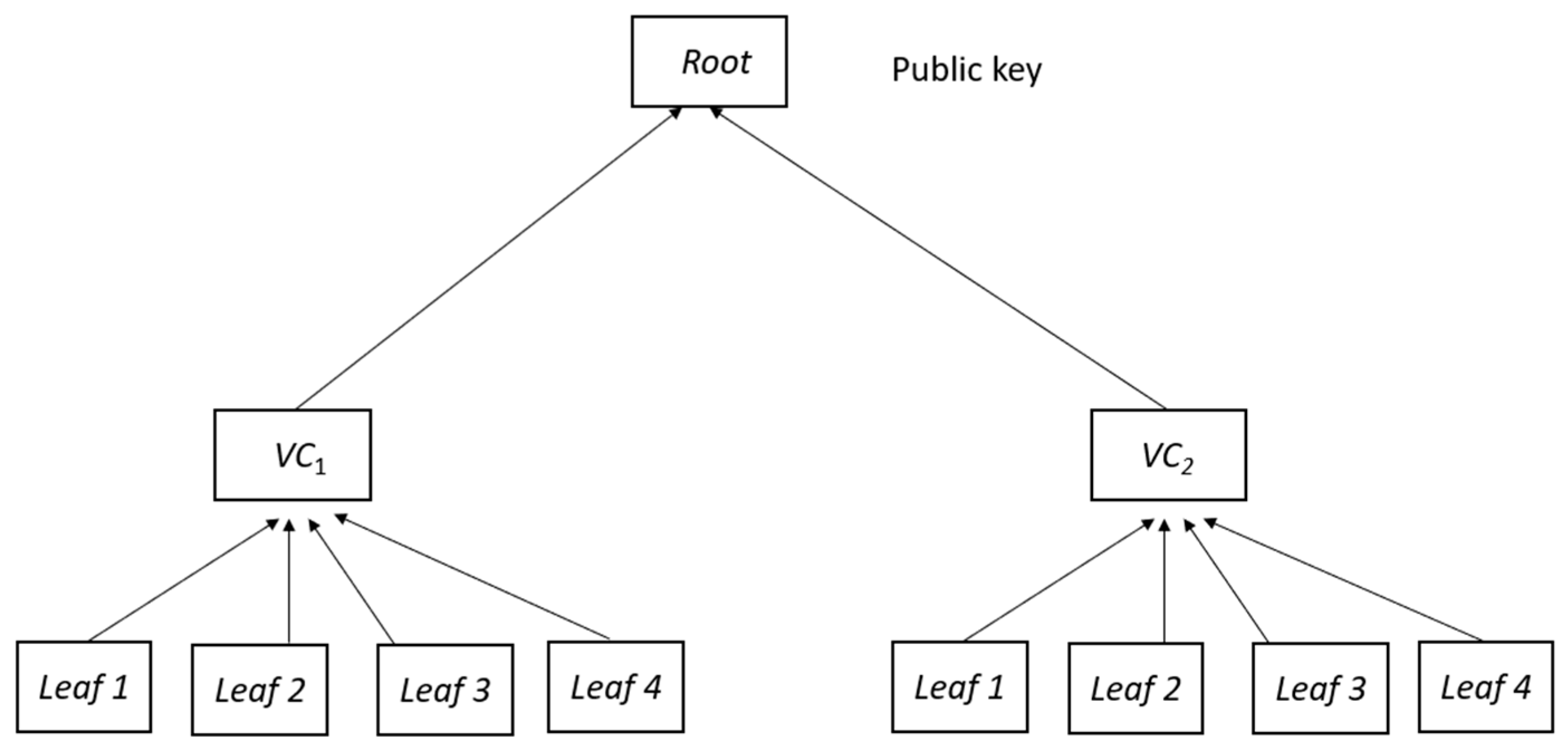
The Verkle Tree approach generates a tree by using Vector Commitments instead of cryptographic hash techniques, which we use in Merkle Tree. To build the tree, choose k components and then compute a Verkle Tree using files f0, f1, …, fn. Calculate a Vector Commitment (VC) for each subset of files to see if all of the memberships in that subset exhibit PRi with regard to VC [23]. Calculate the vector commitments across the tree until the root commitment is identified.

Figure 2 shows the division of nine files into subsets of size k = 3 with a splitting degree of 3. With VC1, VC2, and VC3 remaining, we create VC and compute proofs for the subset. For commitments VC1, VC2, and VC3, membership proofs PR9, PR10, and PR11 are calculated in relation to commitment VC4. The Verkle Tree digest serves as the root commitment in the Vector Commitment VC4, which is built over these commitments.

The proofing characteristics of Merkle and Verkle trees are different. Merkle trees need a proof that includes all nodes in order to take into account each sister node [24]. However, Verkle trees reduce the quantity of evidence required for value establishment by using “batching nodes” to verify numerous pathways at once. Additionally, they need less proof and have a wider scope. Because Verkle trees employ vector commitments in their hash algorithm, they are more efficient than Merkle trees.

9.1. Verkle-Based HORST

Verkle trees are a type of cryptographic data structure that generalizes Merkle trees by using vector commitments rather than simple hash functions, which enables Verkle trees to achieve much smaller proof sizes than Merkle trees, making them highly efficient for applications that require compact proofs. Verkle trees are essential for post-quantum cryptography because they reduce storage requirements, maintain high security, and eliminate redundant data for efficient verification processes that keep only the information that is needed, making them perfect for handling large datasets.

Verkle and Merkle trees have quite different proving properties. Verkle trees employ vector commitments to “batch” many nodes together, lowering the amount of data needed, whereas Merkle trees demand that every sibling node be included in the proof. Verkle trees become more effective and scalable as a result, particularly for applications that need quick verification and compact proofs. Verkle trees, in contrast to conventional hash functions, accomplish these gains by utilizing polynomial commitments, such as Kate/KZG commitments.

A Verkle tree is used in place of the Merkle tree for validating HORS public keys in the Verkle-based HORST (HORS with Trees) for authenticating public keys. This change greatly increases HORST’s scalability and efficiency, especially when it comes to verification time and signature size. Applications like blockchain systems, secure boot protocols, and IoT firmware upgrades that demand concise proofs and effective verification are especially well-suited for Verkle-based HORST.

The secret key for Verkle-based HORST is made up of $t$ random values $\mathrm{s}\mathrm{k}=\left({\mathrm{s}\mathrm{k}}_1,{\mathrm{s}\mathrm{k}}_2,\dots ,{\mathrm{s}\mathrm{k}}_t\right)$.

The Verkle tree’s leaf nodes are created by hashing each secret key value ${\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}_i=H\left({\mathrm{s}\mathrm{k}}_i\right) \mathrm{for} i=1,2,\dots ,t$.

By iteratively applying vector commitments to collections of leaf nodes, we may create a Verkle tree that has a single root node $pkVerkleHORST=root$.

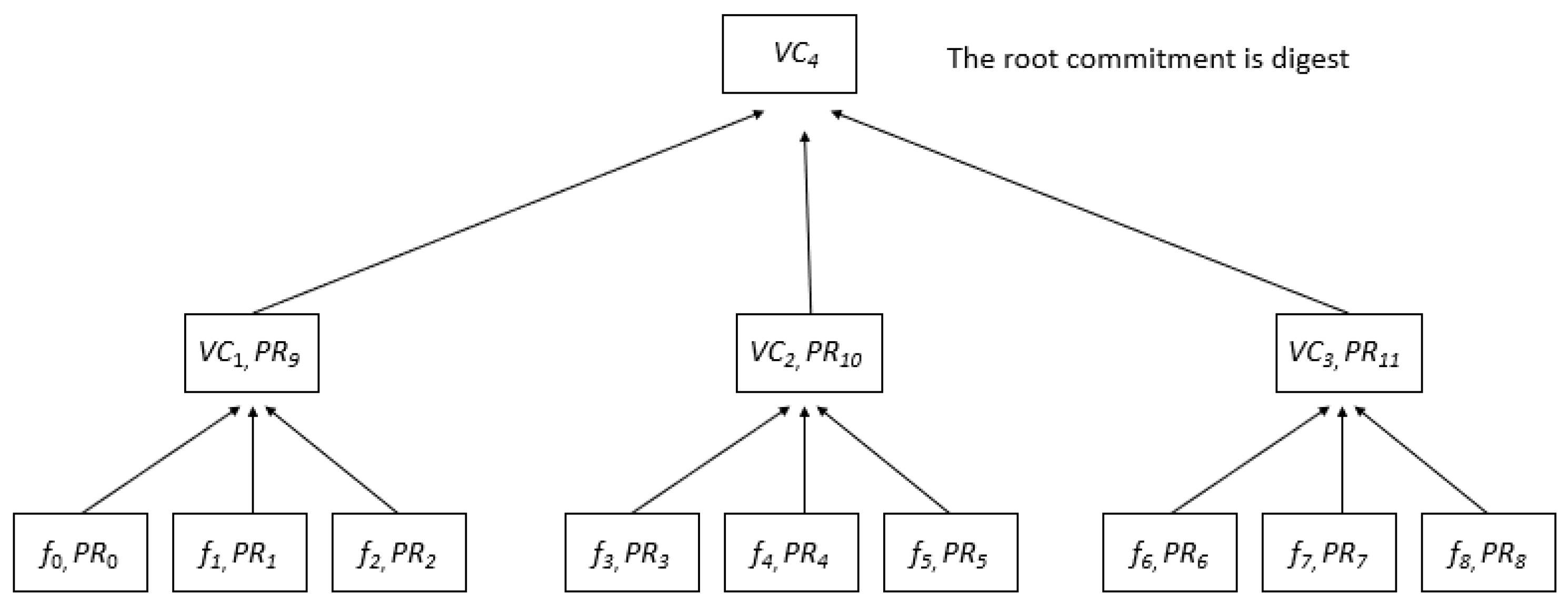
Figure 3 shows the structure of Verkle-based HORST.

As illustrated in Figure 3, the following is a description of the Verkle-based HORST structure:

• Leaf Layer

• Leaf nodes represent the hashed secret keys of the HORST scheme.
• Generate $t$ secret keys and compute their leaves:

  $${ \mathrm{leaf}}_i=H\left({\mathrm{s}\mathrm{k}}_i\right) \mathrm{for} i=1,2,\dots ,t$$

  (23)
• These leaves form the lowest layer of the Verkle tree.

2.

Intermediate Layers (Optional)

• Group leaves/nodes into vectors:

Verkle trees use a branching factor $m$ (e.g., $m=256$) to minimize tree depth.

For example, if $t=1024$, group leaves into 4 vectors of 256 leaves each:

$${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{1,k}={ \mathrm{Commit} }^{\left({\mathrm{leaf} }_{(k-1)m+1},\dots ,{ \mathrm{leaf} }_{k\cdot m}\right) \mathrm{for} k=\mathrm{1,2},\mathrm{3,4}}$$

(24)

• Intermediate layers are only required for large $t$. If $t\le m$, the root can directly commit to all leaves.

3.

Root Layer

• The root is the final commitment of the Verkle tree: $\mathrm{p}\mathrm{k}\mathrm{VerkleHORST} = \mathrm{Commit} \left({\mathrm{node}}_1,{ \mathrm{node}}_2,\dots ,{ \mathrm{node}}_n\right)$.
• $n$ depends on the branching factor $m$ and the number of leaves $t$.
  Example: If $t=1024$ and $m=256$, the root commits to $n=4$ intermediate nodes.

9.2. Algorithm for Verkle-Based HORST

Key Generation:

• Create $t$ random secret key elements using formula $\mathrm{s}\mathrm{k}=\left({\mathrm{s}\mathrm{k}}_1,{\mathrm{s}\mathrm{k}}_2,\dots ,{\mathrm{s}\mathrm{k}}_t\right)$.
• Hash each secret key element to determine the leaf nodes:

  $${\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}_i=H\left({\mathrm{s}\mathrm{k}}_i\right) \mathrm{for} i=\mathrm{1,2},\dots ,t$$

  (25)
• Apply vector commitments to groups of leaf nodes iteratively to create the Verkle tree:

  $${\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j,k}={\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{i}\mathrm{t}}_{\left({\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j-\mathrm{1,2}k},{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j-\mathrm{1,2}k+1}\right)}$$

  (26)
• The root of the Verkle tree is the main public key $\mathrm{pkVerkleHORST} = \mathrm{root}$.

Signing Process:

• Determine the message digest $\mathrm{msgDigest} =H\left(\mathrm{message}\right)$.
• Split the digest into $k$ indexes $\left({\mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)=\mathrm{msgDigest} \mathrm{m}\mathrm{o}\mathrm{d}t$.
• Make the matching private key components visible $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{S}=\left({\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_1},{\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_2},\dots ,{\mathrm{s}\mathrm{k}}_{{\mathrm{index}}_k}\right)$.
• Generate a Verkle proof (In Merkle tree we had sibling-based paths):

  $${\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}_i=H\left({\mathrm{s}\mathrm{k}}_{index\_i}\right) \mathrm{for} i=\mathrm{1,2},\dots ,t$$

  (27)

This replaces the traditional Merkle sibling path with a constant-sized KZG or IPA proof.

5.

The final signature is $\mathrm{signature} =\left(\mathrm{sigHORS}, \mathrm{verkleProof} \right)$.

Verification Process:

• Compute the message digest $\mathrm{msgDigest} =H\left(\mathrm{message}\right)$.
• Split the digest into $k$ indexes $\left({\mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)=\mathrm{m}\mathrm{s}\mathrm{g}\mathrm{D}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t} \mathrm{m}\mathrm{o}\mathrm{d}t$.
• Hash each revealed private key element ${\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}_i=H\left({\mathrm{s}\mathrm{k}}_{index\_i}\right) \mathrm{for} i=\mathrm{1,2},\dots ,t$.
• Verify the Verkle proof. Use verkleProof to confirm that all ${\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}_i$ values are correctly included in the tree. Reconstruct the root from the proof and check $\mathrm{computedRoot} == \mathrm{pkVerkleHORST}$.
• If the computed root matches, the signature is valid.

Three factors essentially control the security–performance tradeoffs in Verkle-based HORST: the subset size $k$, total key count $t$, and branching factor $m$. These variables show complex dependence. While increasing $t$ improves security through greater key material (typically $t=1024$ for 128-bit security), it imposes linear $O\left(t\right)$ scaling on key generation time. The branching factor $m$ creates a dual effect: while reducing tree depth from $O\left({\mathrm{l}\mathrm{o}\mathrm{g}}_{2}t\right)$ to $O\left({\mathrm{l}\mathrm{o}\mathrm{g}}_{m}t\right)$, it creates polynomial commitment overhead that increases as $O\left(m {\mathrm{l}\mathrm{o}\mathrm{g}}_{m}t\right)$. According to experimental evidence, $m=256$ achieves an optimal balance for $t=1024$, delivering 1.4 ms verification times while maintaining compact proofs.

This parametric framework enables precise adjustment for different deployment circumstances. Resource-constrained loT devices may use $m=64$ to decrease memory consumption despite wider trees; blockchain systems often prefer $m=512$ to reduce proof sizes at the risk of modest verification slowness (see

Table 1. Efficiency comparison.

Scheme	Type	Signature Size (KB)	Verification Time (ms)	Public/Private Keys (B)	Complexity	Security Basis
V-HORST	Hash	3.2	1.4	32 B/64 B	$\mathrm{O}\left(\mathrm{k}\right)$$\mathrm{signature}, \mathrm{O}\left(1\right)$ verification	CR + KZG Binding
M-HORST	Hash	12.8	5.6	32 B/64 B	$\mathrm{O}\left(\mathrm{k}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{t}\right)$	Collision Resistance
SPHINCS+	Hash	8.1	2.3	32 B/64 B	$\mathrm{O}\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{t}\right)$	Collision Resistance
XMSS	Hash	2.5	2.8	32 B/64 B	$\mathrm{O}\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{t}\right)$	Collision Resistance
Dilithium3	Lattice	2.7	1.1	1.3 KB/2.5 KB	$\mathrm{O}\left({\mathrm{n}}^2\right)$	Module-LWE Hardness
Rainbow-III	Multivariate	160	37.5	161 KB/103 KB	$\mathrm{O}\left({\mathrm{n}}^3\right)$	Multivariate Quadratic Hardness
McEliece	Code-based	0.2	18.2	0.9 MB/1.2 MB	$\mathrm{O}\left(\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\right)$	Syndrome Decoding Hardness

: 2.1 ms). The subset size $k$ further mediates this balance; bigger values improve fault tolerance but increase signature size as $O\left(k\mathrm{l}\mathrm{o}\mathrm{g}t\right)$. Implementers may adapt the scheme to their unique security and performance requirements thanks to this parametric framework. System designers can strike the ideal balance between computational overhead, verification speed, and signature size by carefully choosing the values of $\left(k,t,m\right).$

Verkle-based HORST offers several advantages over traditional HORST. Applications that need short signatures can benefit greatly from the usage of Verkle trees, which reduce the signature size to a constant. In blockchain systems, where smaller signatures result in cheaper transaction fees and quicker processing times, this is especially advantageous. Verkle-based HORST is faster to verify than classic HORST, which needs logarithmic-time verification, because vector commitments are verified in constant time. This enhancement is important for applications where quick verification is essential, such as secure boot protocols. Verkle-based HORST is more feasible for resource-constrained contexts, such IoT devices, because the shorter authentication channels also require less storage. Lastly, because Verkle-based HORST only uses hash functions and vector commitments—both of which are impervious to quantum attacks—it maintains the post-quantum security of HORST.

Though it has advantages, Verkle-based HORST adds complexity from vector commitments, thus complicating implementation and assessment. Its implementation in practical systems may be slowed down by its complexity. The practical implementation of Verkle-based HORST may be hampered by the limited usage of Verkle trees, a relatively new cryptographic primitive. Efficiency is boosted with Verkle-based HORST, but there may be other trade-offs, including a higher computational cost for creating vector commitments. When selecting Verkle-based HORST for particular applications, these trade-offs need to be carefully taken into account.

Verkle-based HORST, with its smaller signatures, quicker verification, and scalability is a potential advancement over conventional HORST. It is a post-quantum secure signature technique with security predicated on the binding property of vector commitments and the collision resistance of hash functions. Although it adds some complexity, its efficiency improvements make it a solid contender for applications like blockchain, the Internet of Things, and secure communication protocols that demand scalable and small digital signatures.

10. Security Proof

Here, we show that the security of the suggested Verkle-based HORST signature method can be reduced to the binding property of the vector commitments utilized in the Verkle tree and the collision resistance of the basic hash function. We contend that an adversary cannot effectively manufacture a legitimate signature inside the suggested method, guaranteeing post-quantum security, by relying on the difficulty of identifying hash collisions and violating the binding quality of vector promises. Even in the face of quantum assaults, these cryptographic presumptions are computationally challenging.

Theorem 1.

The Verkle-based HORST signature method is safe from EUF-CMA (Existential Unforgeability under Chosen Message Attacks) if the hash function H is collision-resistant and the vector commitment scheme is binding.

Let us prove the stated theorem.

• Adversary Setup

Let $\mathcal{A}$ be a polynomial-time adversary that can forge a signature in the Verkle-based HORST scheme with non-negligible probability $ϵ.\mathcal{A}$ makes a maximum of $Q$ signing queries and outputs a forgery $\left(m^{\mathrm{*}},{\sigma }^{\mathrm{*}}\right)$ with probability $ϵ$.

2.

Simulator Construction

The simulator $\mathcal{S}$ receives a collision-resistant hash function $H$ and a binding vector commitment scheme Commit. $\mathcal{S}$ configures the public parameters of the Verkle-based HORST scheme as follows:

• Generate $t$ random secret key elements $\mathrm{s}\mathrm{k}=\left({\mathrm{s}\mathrm{k}}_1,{\mathrm{s}\mathrm{k}}_2,\dots ,{\mathrm{s}\mathrm{k}}_t\right)$.
• Compute the leaf nodes by hashing each secret key element:

  $${\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}_i=H\left({\mathrm{s}\mathrm{k}}_i\right) \mathrm{for} i=\mathrm{1,2},\dots ,t$$

  (28)
• Create the Verkle tree by recursively applying vector commitments to groups of leaf nodes:

  $$\left.{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}_{j,k}= \mathrm{Commit}({\mathrm{node}}_{j-\mathrm{1,2}k},{ \mathrm{node} }_{j-\mathrm{1,2}k+1}\right)$$

  (29)
• The root of the Verkle tree is the public key $\mathrm{pkVerkleHORST} = \mathrm{root}.$
  $\mathcal{S}$ provides $\mathcal{A}$ with the public key pkVerkleHORST.

3.

Signing Oracle Simulation

For each signing query $m_i$ from $\mathcal{A},\mathcal{S}$ generates a valid signature ${\sigma }_i$ as follows:

• Compute the message digest ${\mathrm{msgDigest} }_i=H\left(m_i\right)$.
• Split the digest into $k$ indexes $\left({ \mathrm{index}}_1,{ \mathrm{index}}_2,\dots ,{ \mathrm{index}}_k\right)={ \mathrm{msgDigest} }_i\mathrm{m}\mathrm{o}\mathrm{d}t$.
• Reveal the corresponding secret key elements, reveal secrets $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{H}\mathrm{O}\mathrm{R}{\mathrm{S}}_i=\left({\mathrm{s}\mathrm{k}}_{{\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}}_1},{\mathrm{s}\mathrm{k}}_{{\mathrm{index} }_2},\dots ,{\mathrm{s}\mathrm{k}}_{{\mathrm{index} }_k}\right)$.
• Generate a Verkle proof required to reconstruct the root:

  $${\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{k}\mathrm{l}\mathrm{e}\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{f}}_i=\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{k}\mathrm{l}\mathrm{e}(\mathrm{l}\mathrm{e}\mathrm{a}{\mathrm{f}}_{{\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}}_1},\dots ,\mathrm{l}\mathrm{e}\mathrm{a}{\mathrm{f}}_{\left.{\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}}_k\right)}$$

  (30)
• The final signature is as follows:

  $${\sigma }_i=\left({\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{S}}_i,{ \mathrm{verkleProof}}_i\right)$$

  (31)
  $\mathcal{S}$ returns ${\sigma }_i$ to $\mathcal{A}$.

4.

Forgery Extraction

After $Q$ signing queries, $\mathcal{A}$ outputs a forgery $\left(m^{\mathrm{*}},{\sigma }^{\mathrm{*}}\right).$ $\mathcal{S}$ parses ${\sigma }^{\mathrm{*}}$ to extract the revealed secret key elements and the Verkle proof.

• Parse ${\sigma }^{\mathrm{*}}=($ ${\mathrm{sigHORS}}^{\mathrm{*}}$, $\left.{\mathrm{verkleProof}}^{\mathrm{*}}\right)$.
• Compute ${\mathrm{leaf}}_i^{\mathrm{*}}=H($ $\left.{\mathrm{sk}}_{{\mathrm{index} }_i}^{\mathrm{*}}\right)$.
• Verify the Verkle proof (not sibling path reconstruction):

  $$\mathrm{valid} \left.= \mathrm{VerifyVerkle}(\mathrm{p}\mathrm{k}\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{k}\mathrm{l}\mathrm{e}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{S}\mathrm{T},{ \mathrm{leaf} }_1^{\mathrm{*}},\dots ,{ \mathrm{leaf} }_k^{\mathrm{*}},{ \mathrm{verkleProof} }^{\mathrm{*}}\right)$$

  (32)
  If valid $=$ True, $\mathcal{S}$ succeeds. Otherwise, $\mathcal{S}$ aborts.

5.

Probability Analysis

The probability that $\mathcal{S}$ extracts a legitinate signature is at least $ϵ$, the success probability of $\mathcal{A}$. If $ϵ$ is non-negligible, then $\mathcal{S}$ can break either the collision resistance of $H$ or the binding property of Commit with non-negligible probability, challenging certain cryptographic primitives’ hardness assumptions.

Under the presumption of collision-resistant hash functions and binding vector commitments, the Verkle-based HORST signature method is safe from EUF-CMA assaults since S can use A‘s forgery to violate either the binding property of Commit or the collision resistance of H. We reach the conclusion that the security of the Verkle-based HORST signature scheme is still strong since both of these presumptions are thought to be computationally impossible to violate, even in the case of quantum adversaries. As a result, the Verkle-based HORST signature scheme provides a dependable foundation for digital signatures in the quantum era while also offering a safe and effective solution for post-quantum cryptography applications.

11. Efficiency Comparison

Compared to classic HORST, Verkle-based HORST offers notable efficiency improvements, especially when it comes to storage needs, verification time, and signature size.

Table 2. Key and signature size comparison (128-bit security level).

Scheme	Public Key	Private Key	Signature
Verkle-based HORST	32 B	64 B	3.2 KB
Dilithium3	1312 B	$2528 \mathrm{B}$	2.7 KB
Rainbow-III	161 KB	103 KB	160 KB
McEliece-348864	0.9 MB	1.2 MB	0.2 KB

contrasts Verkle-Based HORST, Traditional HORST, and other Hash-Based Schemes.

In traditional HORST, the signature size grows logarithmically with the number of leaves $t$, resulting in $O\left(k\mathrm{l}\mathrm{o}\mathrm{g}t\right)$. In Verkle-based HORST, the use of vector commitments reduces the signature size to a constant $O\left(k\right)$, making it much more compact. Verkle-based HORST would require only a constant number of values, regardless of $t$.

In HORST, the verifier must compute $O\left(\mathrm{l}\mathrm{o}\mathrm{g}t\right)$ hash operations to reconstruct the Merkle root. In Verkle-based HORST, the verifier only needs to compute a constant number of operations $O\left(1\right)$ to verify the vector commitments, resulting in faster verification. The verifier in Verkle-based HORST would only need to compute a single operation.

This information provides system designers with a number of crucial insights. Verkle-based HORST’s uniform 32-byte public key size allows for simple integration without requiring protocol modifications because it corresponds to the address formats utilized by popular blockchain systems like Ethereum (20 bytes) and bitcoin (32 bytes). On the other hand, Dilithium3’s 1.3 KB public keys would necessitate considerable changes to current systems; for instance, TLS 1.3 certificates would have to grow by around 30% in order to support these bigger keys. Despite their theoretical promise, multivariate and code-based schemes have not been widely adopted. For example, Rainbow-III’s 161 KB public keys are larger than the total amount of memory on many devices with limited resources, and McEliece’s combination of massive keys and small signatures results in an asymmetric storage profile that is challenging to control in distributed systems.

Verkle-based HORST uses less storage for authentication pathways, because proofs are smaller. This renders it more appropriate for settings with limited resources, such as blockchain apps or loT devices. For instance, in a blockchain system, transactions with smaller signatures are smaller, which results in cheaper fees and quicker processing times.

Since the efficiency advantages rise with the number of leaves t, Verkle-based HORST is more scalable than standard HORST. Because of this, it is a superior option for applications that need extensive key management. For instance, Verkle-based HORST can effectively manage thousands of firmware upgrades in a secure boot protocol without sacrificing speed.

Verkle trees use vector commitments (such as polynomial commitments like Kate/KZG commitments) rather than simple hash functions to obtain $O\left(1\right)$ proof sizes. Because the verifier must recreate the full route from the leaf to the root, each proof in a typical Merkle tree requires $O\left(\log t\right)$ hash values. Verkle trees, on the other hand, use vector commitments to combine many leaf nodes into a single proof, which enables the verifier to validate the whole path with a proof of constant size. This is accomplished by making use of polynomial commitments’ mathematical characteristics, which allow for the effective aggregation of several values into a single proof. Verkle-based HORST is hence very scalable for large-scale systems as it lowers the proof size from $O\left(\log t\right)$ to $O\left(1\right)$.

This thorough analysis reveals several important trends. Hash-based signatures, such as Verkle-based HORST, provide the most conservative security assumptions of any post-quantum approach as they only rely on the binding property of KZG commitments and the collision resistance of cryptographic hash functions. Despite achieving somewhat improved signature sizes and verification times, lattice-based systems such as Dilithium3 rely on more recent mathematical assumptions on the difficulty of learning with errors (LWE) issues, which lack the decades of crypto analysis that have supported hash-based security. Although the multivariate and code-based schemes are intriguing in theory, they are impractical for the majority of real-world deployments. For example, McEliece’s 0.9 MB public keys are larger than the storage capacity of many smart cards and Internet of Things devices, while Rainbow-III’s 160 KB signatures would take up almost an entire Ethernet frame, which is typically 1500 bytes.

Because of its post-quantum security, fewer authentication routes, quicker constant-time verification of vector promises, constant signature size, and lower storage needs, Verkle-based HORST is a more effective option than classic HORST. It is especially useful for resource-constrained situations and applications that need tiny signatures, such as secure boot protocols.

Despite its advantages, vector commitments in Verkle-based HORST add complexity, making evaluation and implementation more challenging. Its implementation in practical systems may be slowed down by its complexity. The practical implementation of Verkle-based HORST may be hampered by the limited usage of Verkle trees, a relatively new cryptographic primitive. Efficiency is boosted with Verkle-based HORST, but there may be other trade-offs, including a higher computational cost for creating vector commitments. When selecting Verkle-based HORST for particular applications, these trade-offs need to be carefully taken into account.

Verkle-based HORST, with its smaller signatures, quicker verification, and lower storage needs, is a promising advancement over conventional HORST. It is a post-quantum secure signature technique with security predicated on the binding property of vector commitments and the collision resistance of hash functions. Although it adds some complexity, its efficiency improvements make it a solid contender for applications like blockchain, the Internet of Things, and secure communication protocols that demand scalable and small digital signatures.

Performance Benchmarks

There are multiple major improvements in signature size, verification performance, and memory economy when comparing Verkle-based HORST to traditional implementations. These benefits result from fundamental distinctions in the way that different structures manage cryptographic proofs.

Compared to its Merkle-based equivalent, Verkle-based HORST provides an extensive theoretical increase in terms of signature size. Because Merkle-based HORST must include Merkle paths, it usually generates signatures that are roughly 12.8 kilobytes in size. However, by using KZG polynomial commitments, Verkle-based HORST may be able to decrease this to about 3.2 kilobytes. This 75% decrease in signature size is in line with performance improvements seen in comparable systems, such as Ethereum’s implementation of the Verkle tree, where Verkle proofs outperform Merkle proofs in terms of compression.

In Verkle-based HORST, the verification procedure provides additional positive effects. While Verkle-based HORST’s KZG proofs can be verified in constant time, Merkle-based HORST needs verifiers to perform several hash operations along a Merkle path, which usually takes around 5.6 milliseconds per signature. This approach is especially appealing for high-throughput applications where verification speed is crucial since it may be able to cut the verification time to about 1.4 milliseconds. Benefits observed in previous KZG-based systems are mirrored in this fourfold increase in verification speed.

There is a trade-off when it comes to key generation. Verkle-based HORST probably requires more computing power than Merkle-based HORST. The key generation time might be increased from 110 milliseconds to around 320 milliseconds due to the polynomial operations required for KZG commitments. However, as is the case with other cryptographic systems that use polynomial commitments, this one-time expense is balanced by the continuous advantages during the verification phase.

Considerable improvements in storage efficiency may be achieved when comparing Verkle-based HORST to traditional Merkle-based structures. For conventional security settings (t = 1024 keys, k = 32 subset size), Merkle proofs need $O\left({\mathrm{k}\mathrm{l}\mathrm{o}\mathrm{g}}_2 t\right)$ storage, or around 10 KB when 256-bit hashes are used. Verkle trees, on the other hand, use KZG polynomial commitments to reach $O\left(1\right)$ proof sizes, typically lowering storage to 1–3 KB. This fourfold decrease is consistent with Verkle tree research [23], which displays substantially smaller proofs than Merkle trees at scale. Hybrid signature schemes like SPHINCS+ (≈16 KB) and XMSS (≈8 KB for t = 1024) provide intermediate storage efficiency due to their logarithmic proof growth. Verkle-based HORST’s constant-size proofs make it especially well-suited for storage-constrained applications, like blockchain light clients and IoT devices, where 128-bit security and memory usage reduction are crucial.

Another area in which Verkle-based HORST demonstrates theoretical advantage is memory efficiency. In contrast to an analogous solution that requires 48 megabytes of storage, a Verkle tree that supports one million signatures may only require 12 megabytes. Verkle-based HORST may be especially useful in resource-constrained settings where storage space is limited, such IoT devices or blockchain light clients, because of its fourfold memory consumption decrease.

Verkle-based HORST is positioned as a potential development of hash-based signature schemes due to its smaller signature sizes, quicker verification, and lower memory needs. The consistent gains shown in other Verkle tree applications imply that comparable benefits might be gained in HORST implementations.

12. Conclusions

Strong alternatives must be developed since quantum computing poses a serious threat to cryptography systems. The security of hash-based signature systems against quantum attacks makes them promising. In order to overcome performance constraints while preserving security, this study presents Verkle-based HORST, a novel improvement on conventional hash-based signatures. The method provides useful benefits for practical implementation by rethinking data structures.

Verkle-based HORST offers significant efficiency gains, but it is challenging to put into practice. Compared to conventional hash-based systems, its constant-time verification (1.4 ms in preliminary testing) makes up for the computationally demanding polynomial operations required for key creation and signature. Blockchain applications can be developed by integration with emerging standards, such as Ethereum’s Verkle trees, even though toolchain support is still evolving. For embedded or Internet of Things devices, the trade-offs are justified due to the scheme’s compact proofs, which are 75% smaller than Merkle-based HORST, especially in bandwidth-constrained environments.

Our main contribution is to replace traditional Merkle trees with Verkle trees, which achieve constant-sized proofs by using sophisticated polynomial commitment schemes. This architectural enhancement solves a number of persistent issues in hash-based encryption and provides numerous important advantages. Most significantly, this approach results in significantly lower signatures overall by reducing proof sizes from logarithmic to constant. This is particularly beneficial for bandwidth- or storage-constrained environments such as blockchain networks and IoT devices. Additionally, regardless of the system’s size, the verification procedure becomes far more efficient, needing just constant-time operations. Verkle-based HORST is particularly well-suited for large-scale deployments and systems that need a lot of signatures because of these features.

Future work will focus on adapting the fractal/hypertree approach to Verkle trees. Instead of splitting Merkle trees, we will explore how to split Verkle trees into smaller subtrees. This would preserve the system’s rapid verification and help it to scale more easily. We will also consider techniques to maximize the cryptographic operations and possibly combine Verkle trees with other post-quantum schemes.

In terms of security, our study demonstrates that Verkle-based HORST preserves the robust protective features of conventional hash-based schemes. The same cryptographic presumptions, particularly the binding property of the vector promises and the collision resistance of the underlying hash function, maintain the construction’s security. The technique provides protection against both conventional and quantum adversaries by achieving existential unforgeability against selected message attacks (EUF-CMA), as shown by our formal security example. Our structure stands out as a strong contender for the post-quantum cryptography standardization initiatives now taking place globally due to this security assurance and the increased efficiency.

Although the Verkle-based HORST has several benefits, polynomial commitments during key generation and signature processes result in computational complexity. Additional crypto analysis and performance benchmarking may be beneficial for Verkle trees, a novel cryptographic primitive.