Password Similarity Using Probabilistic Data Structures
Abstract
:1. Introduction
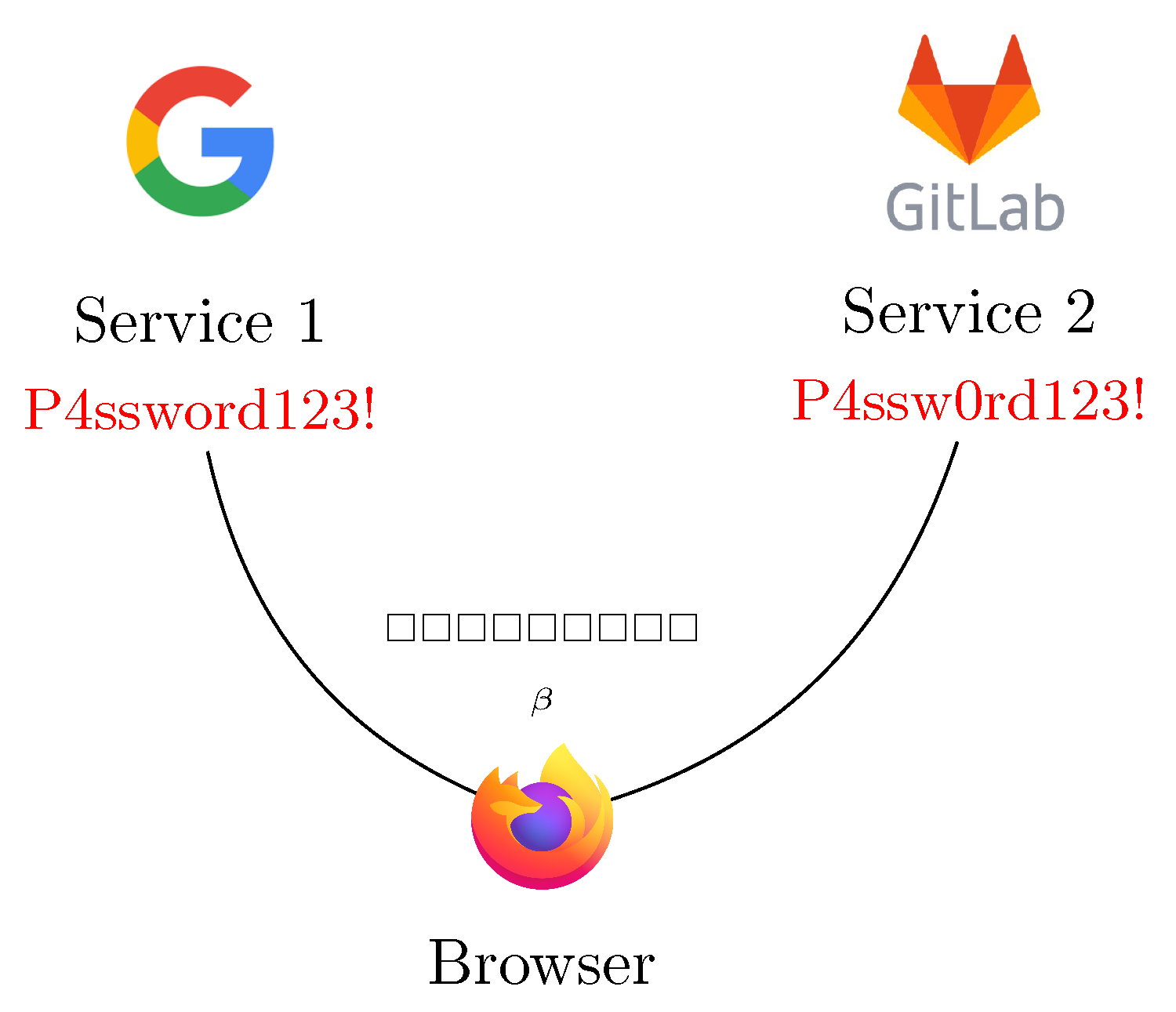
2. State of the Art
The No. 1 cause of harm on the internet.[12]
3. Password Similarity
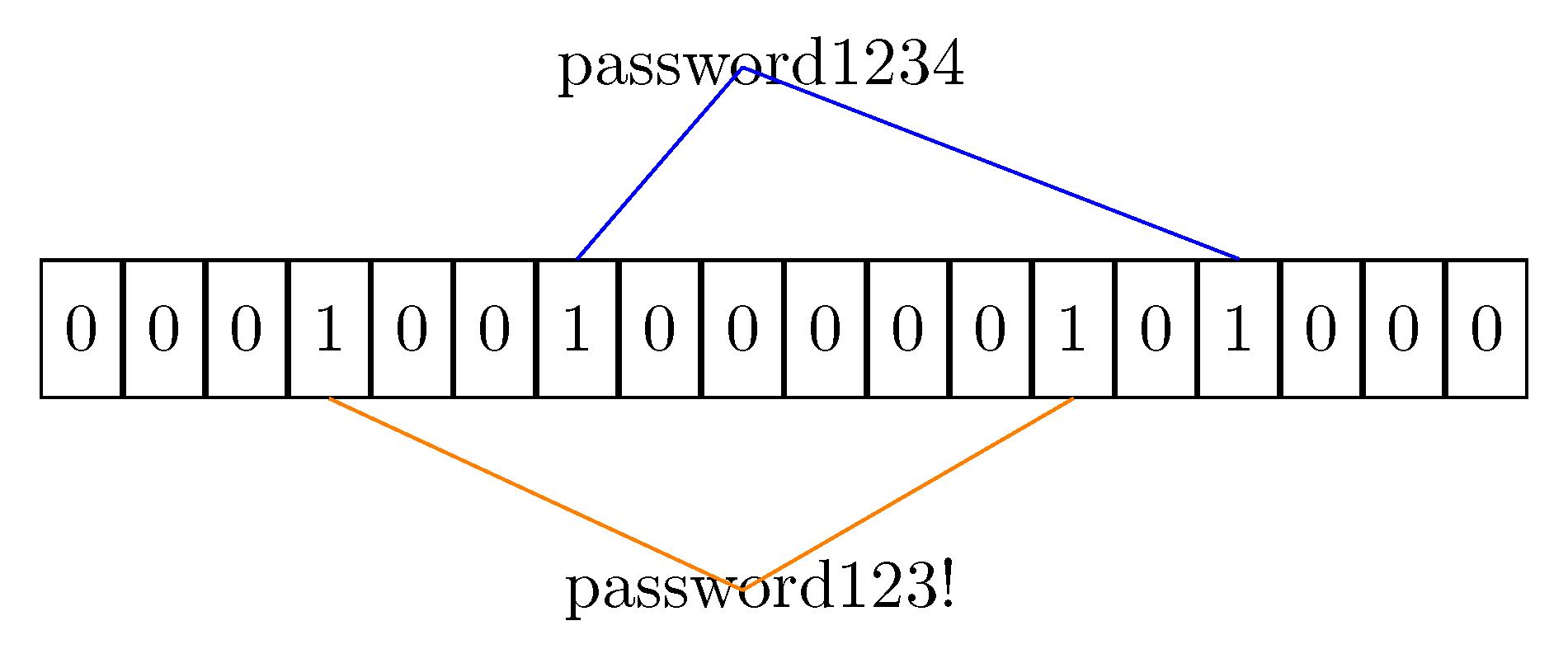
3.1. Bloom Filters for Text Similarity
- a bucket which can be an array of bits initially set to the false value (0), we reference to its size in the number of bits as ;
- , a set of hash functions which will be used to insert and check values.
- which generates a Bloom Filter using the hash functions present in the set with a bucket of size .
- which inserts the bit string s in the Bloom Filter.
- which checks if the value s is not present in the filter or if it collides with a value which is already there.
- that inserts the string s splitting it in -grams.
- that returns the distance between two Bloom Filters. To be comparable, two Bloom Filters must have the same bucket size , and need to use the same set of hash functions .
- the value that must be inserted into the bucket is hashed using the set of hash functions; The hash functions output must be re-mapped to provide indexes in the co-domain of cardinality .
- every bucket slot indexed by the keys got using the hash functions is set to the true value (1).
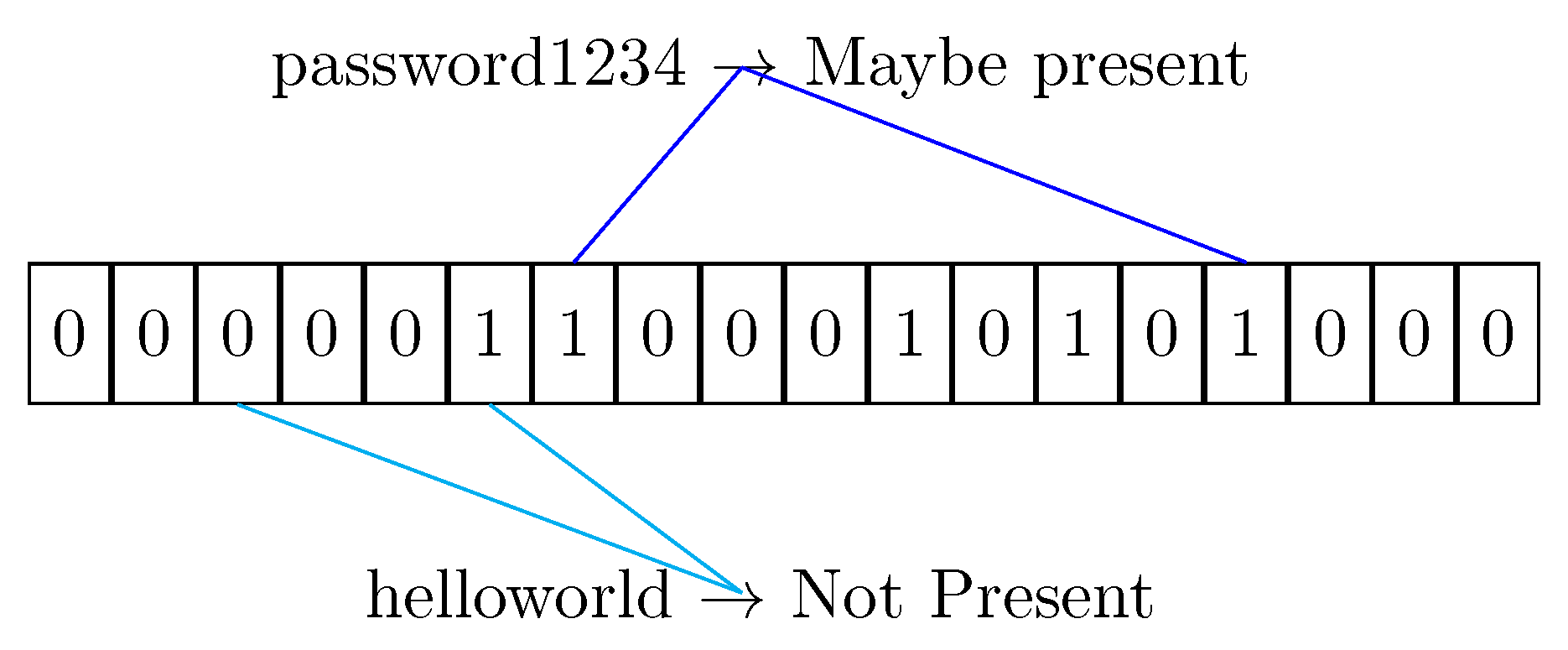
- The element s is hashed against all the functions to get a list of indexes;
- If any index points to a false value, then the element is not present in the filter for sure. The Bloom Filter never exhibits false negatives.
- Otherwise the value could be present in the filter, but due to the collision possibility of the hash functions, the result can be a false positive.
3.2. Privacy Guarantees
- m, the cardinality of the set on which the filter is built;
- k, the number of different hash functions that are used to hash values into the filter;
- n, the number of elements which will be inserted into the filter.
3.3. Analysis of the Hash Function Family
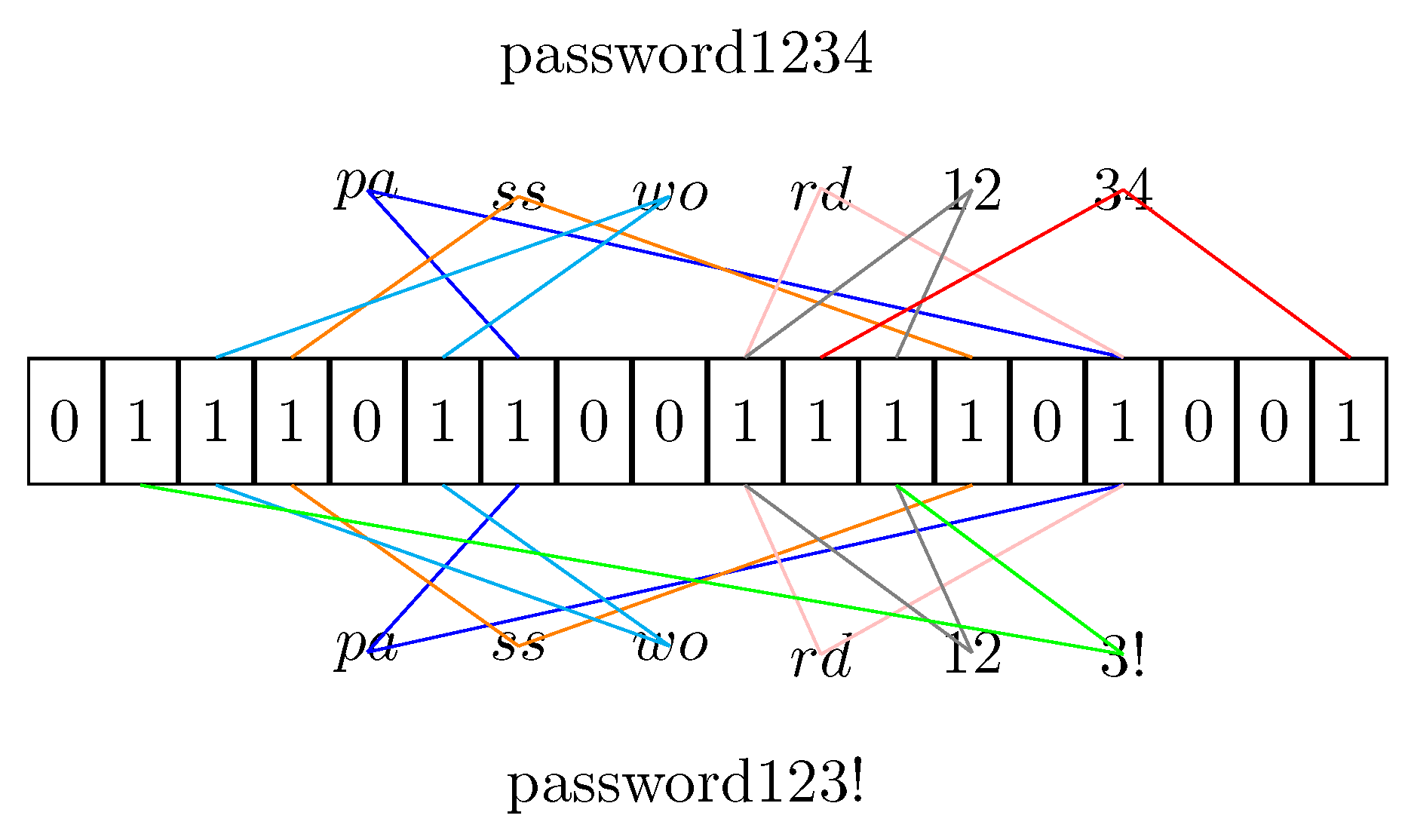
3.4. Anagram Attack
- Generate all the hashes for a specific n-gram;
- Hash the n-grams into a Bloom Filter;
- Analyze the Bloom Filter and get the position of bits set to the true value;
- Compose the various n-grams to create a password.
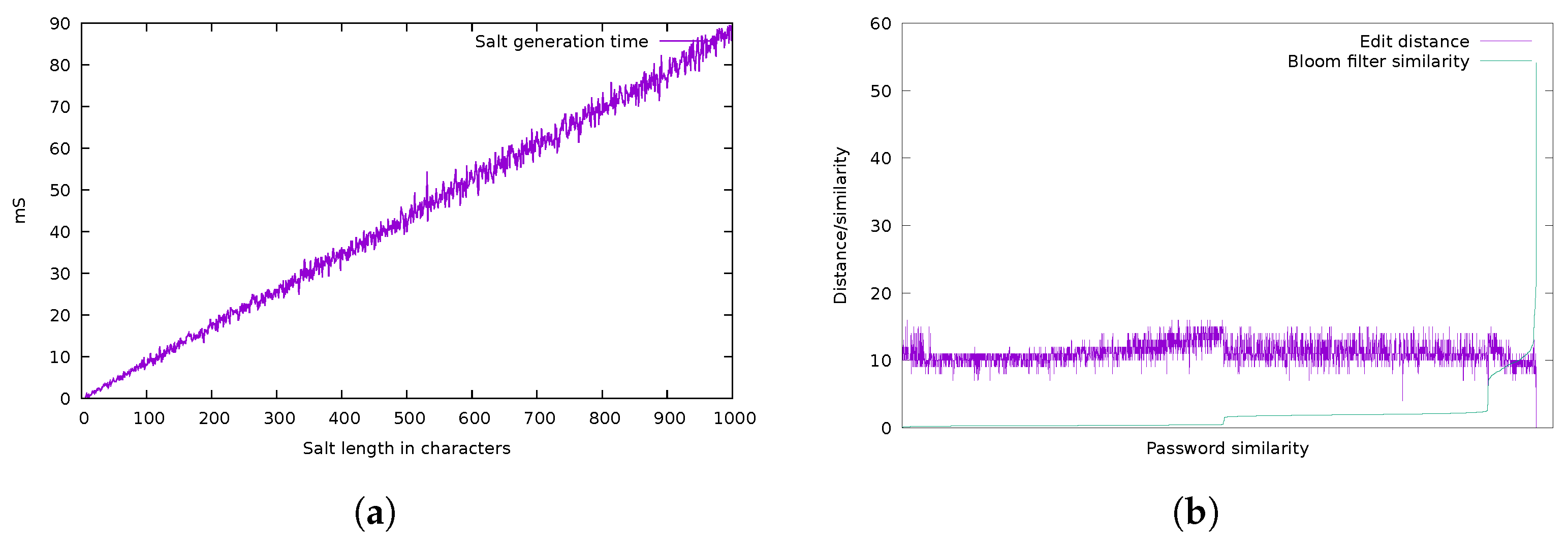
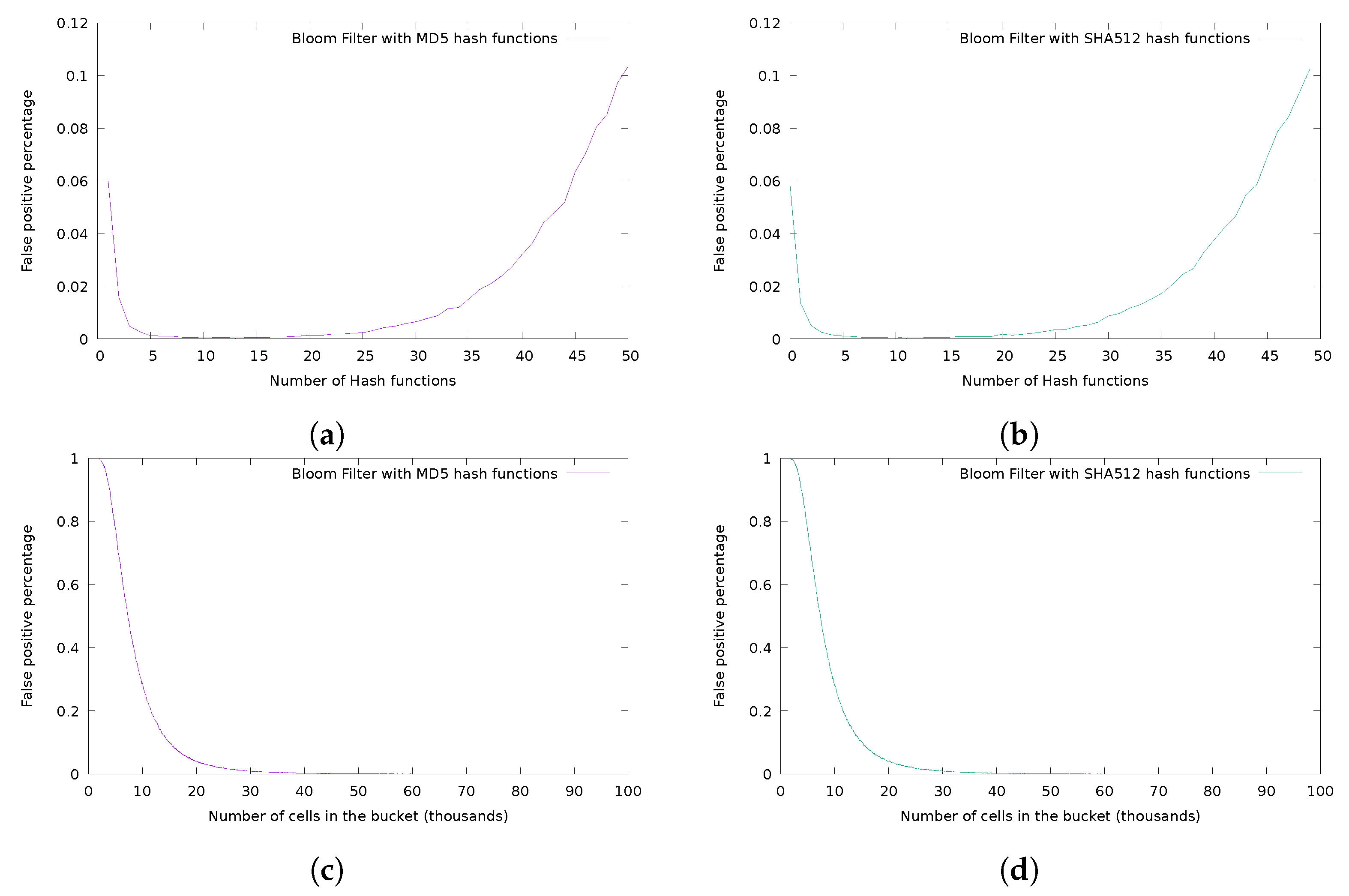
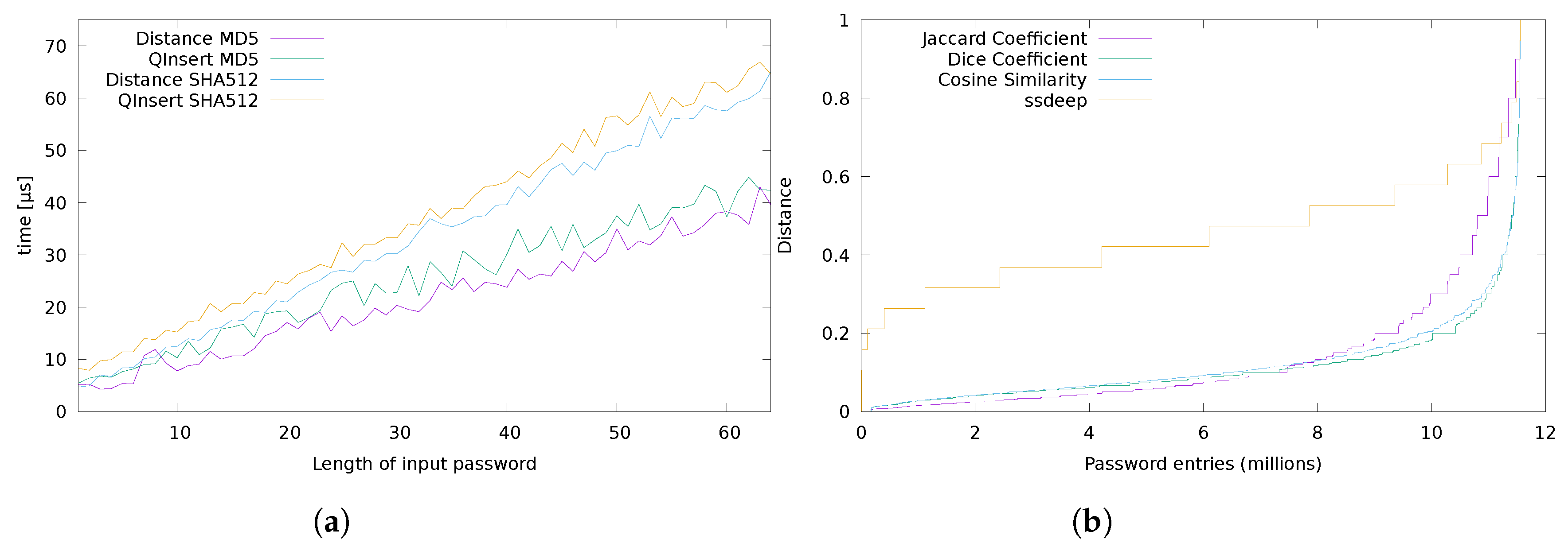
4. Experimental Analysis
5. Conclusions
Future Works
- As stated in the Section 3, the filter can be generated using encrypted salts in conjunction with a strong cryptographic hash function (for example SHA3). This approach can be employed to ensure that data inserted in the structure are analyzable only by the owner of the secret key. The crypto-analysis of the resultant system should be explored to create secure Bloom Filters like the one presented in this paper and similar works [29].
- A comparison with deep-learning based techniques can be introduced. This comparison should therefore include an analysis of the resistance against data-set reverse engineering. We argue that a neural network-based system needs a bigger data-set than our Bloom Filter-based one, and that the former approach can be difficult to analyze using black-box classifiers.
- The analysis of the crypto-system can be improved with a more in-depth comparison with privacy preserving techniques, such as -presence, k-anonymity or t-closeness as described in the surveys on the topic [45,46]. As stated in Section 5, these approaches can suffer from the same issues affecting the deep-learning based one, i.e., the user cannot provide a data-set big enough to make the analysis valuable.
- Analysis of homomorphic encryption could lead to devise an encryption scheme to compute distances between encrypted strings using algorithms present in literature [47].
Author Contributions
Funding
Conflicts of Interest
References
- Schneier, B. Two-factor authentication: Too little, too late. Commun. ACM 2005, 48, 136. [Google Scholar] [CrossRef]
- Scheidt, E.M.; Domanque, E.; Butler, R.; Tsang, W. Access System Utilizing Multiple Factor Identification and Authentication. U.S. Patent 7,178,025, 13 February 2007. [Google Scholar]
- Stobert, E.; Biddle, R. The password life cycle: User behaviour in managing passwords. In Proceedings of the 10th Symposium on Usable Privacy and Security, Menlo Park, CA, USA, 9–11 July 2014; pp. 243–255. [Google Scholar]
- Levenshtein, V.I. Binary codes capable of correcting deletions, insertions, and reversals. Sov. Phys. Dokl. 1966, 10, 707–710. [Google Scholar]
- Schnell, R.; Bachteler, T.; Reiher, J. Privacy-preserving record linkage using Bloom filters. BMC Med. Inform. Decis. Mak. 2009, 9, 41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alaggan, M.; Gambs, S.; Kermarrec, A.M. BLIP: Non-interactive differentially-private similarity computation on bloom filters. Stabilization, Safety, and Security of Distributed Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 202–216. [Google Scholar]
- Erlingsson, Ú.; Pihur, V.; Korolova, A. Rappor: Randomized aggregatable privacy-preserving ordinal response. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 1054–1067. [Google Scholar]
- Forman, S.; Samanthula, B.K. Secure Similar Document Detection: Optimized Computation Using the Jaccard Coefficient. In Proceedings of the 2018 IEEE 4th International Conference on Big Data Security on Cloud (BigDataSecurity), IEEE International Conference on High Performance and Smart Computing, (HPSC) and IEEE International Conference on Intelligent Data and Security (IDS), Omaha, NE, USA, 3–5 May 2018; pp. 1–4. [Google Scholar]
- Kornblum, J. Identifying almost identical files using context triggered piecewise hashing. Digit. Investig. 2006, 3, 91–97. [Google Scholar] [CrossRef]
- Li, Y.; Sundaramurthy, S.C.; Bardas, A.G.; Ou, X.; Caragea, D.; Hu, X.; Jang, J. Experimental study of fuzzy hashing in malware clustering analysis. In Proceedings of the 8th Workshop on Cyber Security Experimentation and Test (CSET’15), Washington, DC, USA, 10 August 2015. [Google Scholar]
- Grassi, P.A.; Garcia, M.E.; Fenton, J.L. DRAFT NIST Special Publication 800-63-3 Digital Identity Guidelines; National Institute of Standards and Technology: Los Altos, CA, USA, 2017.
- Facebook Buys Black Market Passwords to Keep Your Account Safe. Available online: https://www.cnet.com/news/facebook-chief-security-officer-alex-stamos-web-summit-lisbon-hackers/ (accessed on 15 December 2020).
- Ives, B.; Walsh, K.R.; Schneider, H. The domino effect of password reuse. Commun. ACM 2004, 47, 75–78. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, Z.; Yi, P.; Yao, Y.; Xie, T.; Wang, W.; Zhu, T. GENPass: A general deep learning model for password guessing with PCFG rules and adversarial generation. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Wood, C.C. Constructing difficult-to-guess passwords. Inf. Manag. Comput. Secur. 1996, 4, 43–44. [Google Scholar] [CrossRef]
- Bloom, B.H. Space/time trade-offs in hash coding with allowable errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Mitzenmacher, M. Compressed Bloom filters. IEEE/ACM Trans. Netw. 2002, 10, 604–612. [Google Scholar] [CrossRef]
- Gremillion, L.L. Designing a Bloom filter for differential file access. Commun. ACM 1982, 25, 600–604. [Google Scholar] [CrossRef]
- Aumüller, M.; Christiani, T.; Pagh, R.; Silvestri, F. Distance-sensitive hashing. In Proceedings of the 37th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, Houston, TX, USA, 10–15 June 2018; pp. 89–104. [Google Scholar]
- Kirsch, A.; Mitzenmacher, M. Distance-sensitive bloom filters. In Proceedings of the 2006 Eighth Workshop on Algorithm Engineering and Experiments (ALENEX), Miami, FL, USA, 21 January 2006; pp. 41–50. [Google Scholar]
- Indyk, P.; Motwani, R. Approximate nearest neighbors: Towards removing the curse of dimensionality. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 23–26 May 1998; pp. 604–613. [Google Scholar]
- Gionis, A.; Indyk, P.; Motwani, R. Similarity search in high dimensions via hashing. Vldb 1999, 99, 518–529. [Google Scholar]
- Brown, A.; Randall, S.; Boyd, J.; Ferrante, A. Evaluation of approximate comparison methods on Bloom filters for probabilistic linkage. Int. J. Popul. Data Sci. 2019, 4, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Jaccard, P. Le Coefficient Generique et le Coefficient de Communaute Dans la Flore Marocaine. Mémoires de la Société Vaudoise des Sciences Naturelles 1926, 14, 385–403. [Google Scholar]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Barkman, J.J. Phytosociology and Ecology of Cryptogamic Epiphytes (Including a Taxonomic Survey and Description of Their Vegetation Units in Europe); Barkman Van Gorcum & Company. N. V.: Assen, Netherlands, 1958. [Google Scholar]
- Niwattanakul, S.; Singthongchai, J.; Naenudorn, E.; Wanapu, S. Using of Jaccard coefficient for keywords similarity. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 13–15 March 2013; Volume 1, pp. 380–384. [Google Scholar]
- Vatsalan, D.; Sehili, Z.; Christen, P.; Rahm, E. Privacy-preserving record linkage for big data: Current approaches and research challenges. In Handbook of Big Data Technologies; Springer: Berlin/Heidelberg, Germany, 2017; pp. 851–895. [Google Scholar]
- Niedermeyer, F.; Steinmetzer, S.; Kroll, M.; Schnell, R. Cryptanalysis of Basic Bloom Filters Used for Privacy Preserving Record Linkage; Working Paper Series, No. WP-GRLC-2014-04; German Record Linkage Center: Nuremberg, Germany, 2014. [Google Scholar]
- Manalu, D.R.; Rajagukguk, E.; Siringoringo, R.; Siahaan, D.K.; Sihombing, P. The Development of Document Similarity Detector by Jaccard Formulation. In Proceedings of the 2019 International Conference of Computer Science and Information Technology (ICoSNIKOM), Jember, Indonesia, 16–17 October 2019; pp. 1–4. [Google Scholar]
- Ji, S.; Yang, S.; Das, A.; Hu, X.; Beyah, R. Password correlation: Quantification, evaluation and application. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Broder, A.; Mitzenmacher, M. Network applications of bloom filters: A survey. Internet Math. 2004, 1, 485–509. [Google Scholar] [CrossRef] [Green Version]
- Nergiz, M.E.; Atzori, M.; Clifton, C. Hiding the presence of individuals from shared databases. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, Beijing, China, 12–14 June 2007; pp. 665–676. [Google Scholar]
- Dwork, C. Differential privacy: A survey of results. International Conference on Theory and Applications of Models of Computation; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–19. [Google Scholar]
- Bianchi, G.; Bracciale, L.; Loreti, P. “Better Than Nothing” Privacy with Bloom Filters: To What Extent? International Conference on Privacy in Statistical Databases; Springer: Berlin/Heidelberg, Germany, 2012; pp. 348–363. [Google Scholar]
- Xue, W.; Vatsalan, D.; Hu, W.; Seneviratne, A. Sequence Data Matching and Beyond: New Privacy-Preserving Primitives Based on Bloom Filters. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2973–2987. [Google Scholar] [CrossRef]
- Appleby, A. Murmurhash 2.0. Open Source Software. 2008. Available online: https://sites.google.com/site/murmurhash/ (accessed on 30 December 2020).
- Gueron, S.; Johnson, S.; Walker, J. SHA-512/256. In Proceedings of the 2011 Eighth International Conference on Information Technology: New Generations, Las Vegas, Nevada, USA, 11–13 April 2011; pp. 354–358. [Google Scholar]
- Gilbert, H.; Handschuh, H. Security analysis of SHA-256 and sisters. International Workshop on Selected Areas in Cryptography; Springer: Berlin/Heidelberg, Germany, 2003; pp. 175–193. [Google Scholar]
- Kim, J.; Biryukov, A.; Preneel, B.; Hong, S. On the security of HMAC and NMAC based on HAVAL, MD4, MD5, SHA-0 and SHA-1. International Conference on Security and Cryptography for Networks; Springer: Berlin/Heidelberg, Germany, 2006; pp. 242–256. [Google Scholar]
- Álvarez-Sánchez, R.; Andrade-Bazurto, A.; Santos-González, I.; Zamora-Gómez, A. AES-CTR as a password-hashing function. In Proceedings of the International Joint Conference SOCO’17-CISIS’17- ICEUTE’17, León, Spain, 6–8 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 610–617. [Google Scholar]
- Gutterman, Z.; Pinkas, B.; Reinman, T. Analysis of the linux random number generator. In Proceedings of the 2006 IEEE Symposium on Security and Privacy (S&P’06), Oakland, CA, USA, 21–24 May 2006; p. 15. [Google Scholar]
- Gasser, M. A Random Word Generator for Pronounceable Passwords; Technical Report; Mitre Corp.: Bedford, MA, USA, 1975. [Google Scholar]
- Florencio, D.; Herley, C. A large-scale study of web password habits. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May 2007; pp. 657–666. [Google Scholar]
- Zigomitros, A.; Casino, F.; Solanas, A.; Patsakis, C. A Survey on Privacy Properties for Data Publishing of Relational Data. IEEE Access 2020, 8, 51071–51099. [Google Scholar] [CrossRef]
- Pannu, G.; Verma, S.; Arora, U.; Singh, A. Comparison of various Anonymization Technique. Int. J. Sci. Res. Netw. Secur. Commun. 2017, 5, 16–20. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, M.; Lauter, K. Homomorphic computation of edit distance. In International Conference on Financial Cryptography and Data Security; Springer: Berlin/Heidelberg, Germany, 2015; pp. 194–212. [Google Scholar]
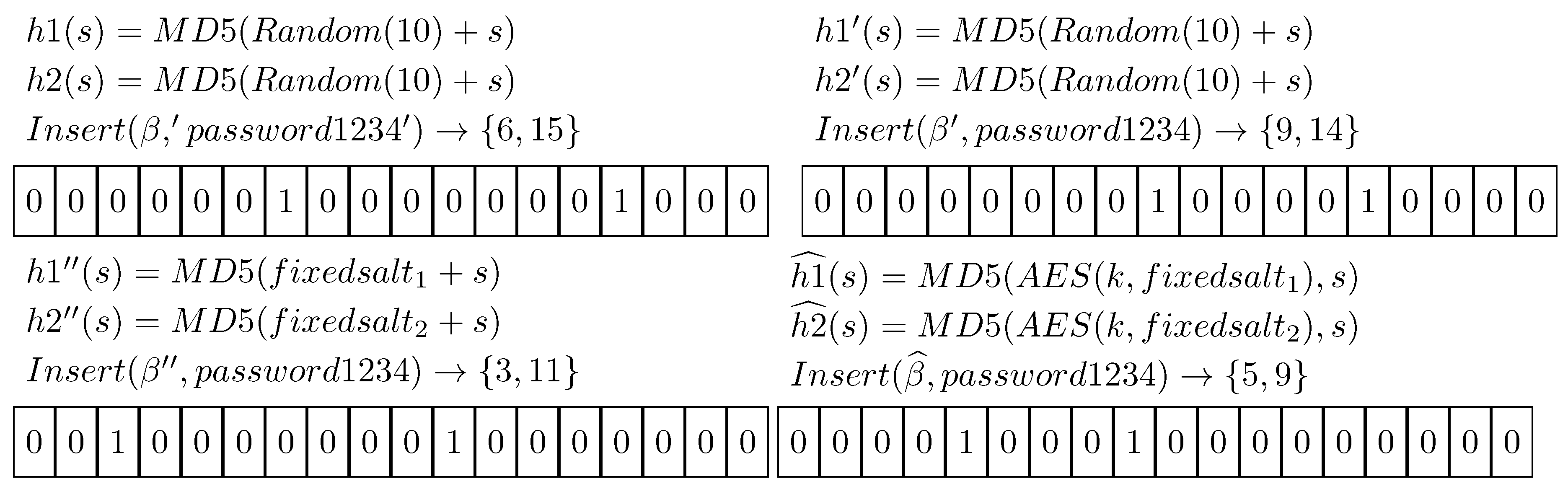
| Peculiarity | RAPPOR [7] | SSDD [8] | Schnell et al. [5] | CTPH [9] | Our Method |
|---|---|---|---|---|---|
| Detect exact matches | ● | ○ | ○ | ● | ○ |
| Detect similarities | ○ | ● | ● | ● | ● |
| Can be (natively) encrypted locally | ◖ | ◖ | ◖ | ○ | ● |
| Uses or can use secure hash function | ◖ | ◖ | ● | ◖ | ● |
| Main focus | Crowdsourcing | Documents | Medical Records | Malware analysis | Passwords |
| Main technology | BF (binary) | BF + HE | BF | PHF | BF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berardi, D.; Callegati, F.; Melis, A.; Prandini, M. Password Similarity Using Probabilistic Data Structures. J. Cybersecur. Priv. 2021, 1, 78-92. https://doi.org/10.3390/jcp1010005
Berardi D, Callegati F, Melis A, Prandini M. Password Similarity Using Probabilistic Data Structures. Journal of Cybersecurity and Privacy. 2021; 1(1):78-92. https://doi.org/10.3390/jcp1010005
Chicago/Turabian StyleBerardi, Davide, Franco Callegati, Andrea Melis, and Marco Prandini. 2021. "Password Similarity Using Probabilistic Data Structures" Journal of Cybersecurity and Privacy 1, no. 1: 78-92. https://doi.org/10.3390/jcp1010005
APA StyleBerardi, D., Callegati, F., Melis, A., & Prandini, M. (2021). Password Similarity Using Probabilistic Data Structures. Journal of Cybersecurity and Privacy, 1(1), 78-92. https://doi.org/10.3390/jcp1010005








