Earthquake History and Rupture Extents from Morphology of Fault Scarps Along the Valley Fault System (Philippines)
Abstract
1. Introduction
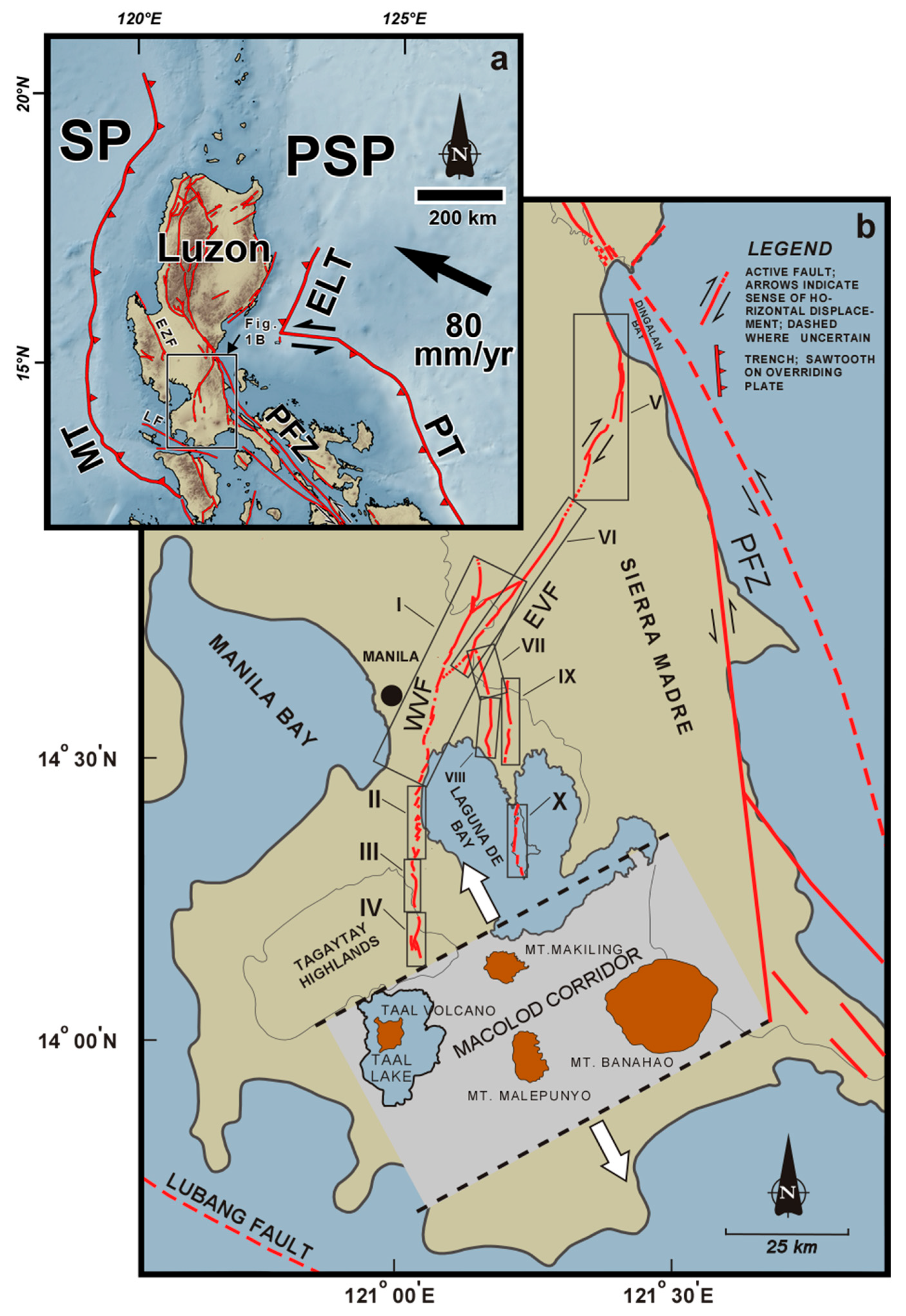
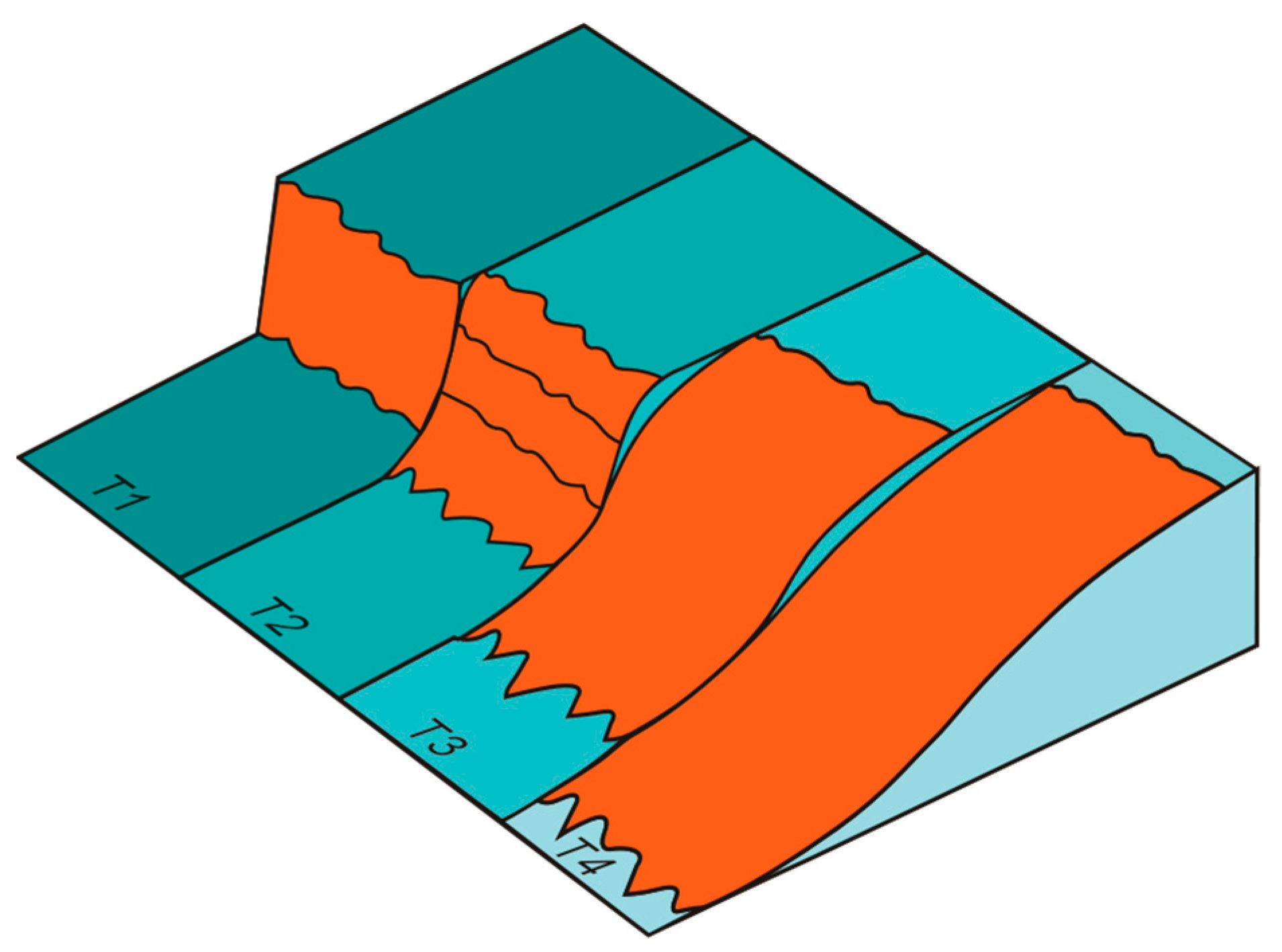
2. Materials and Methods
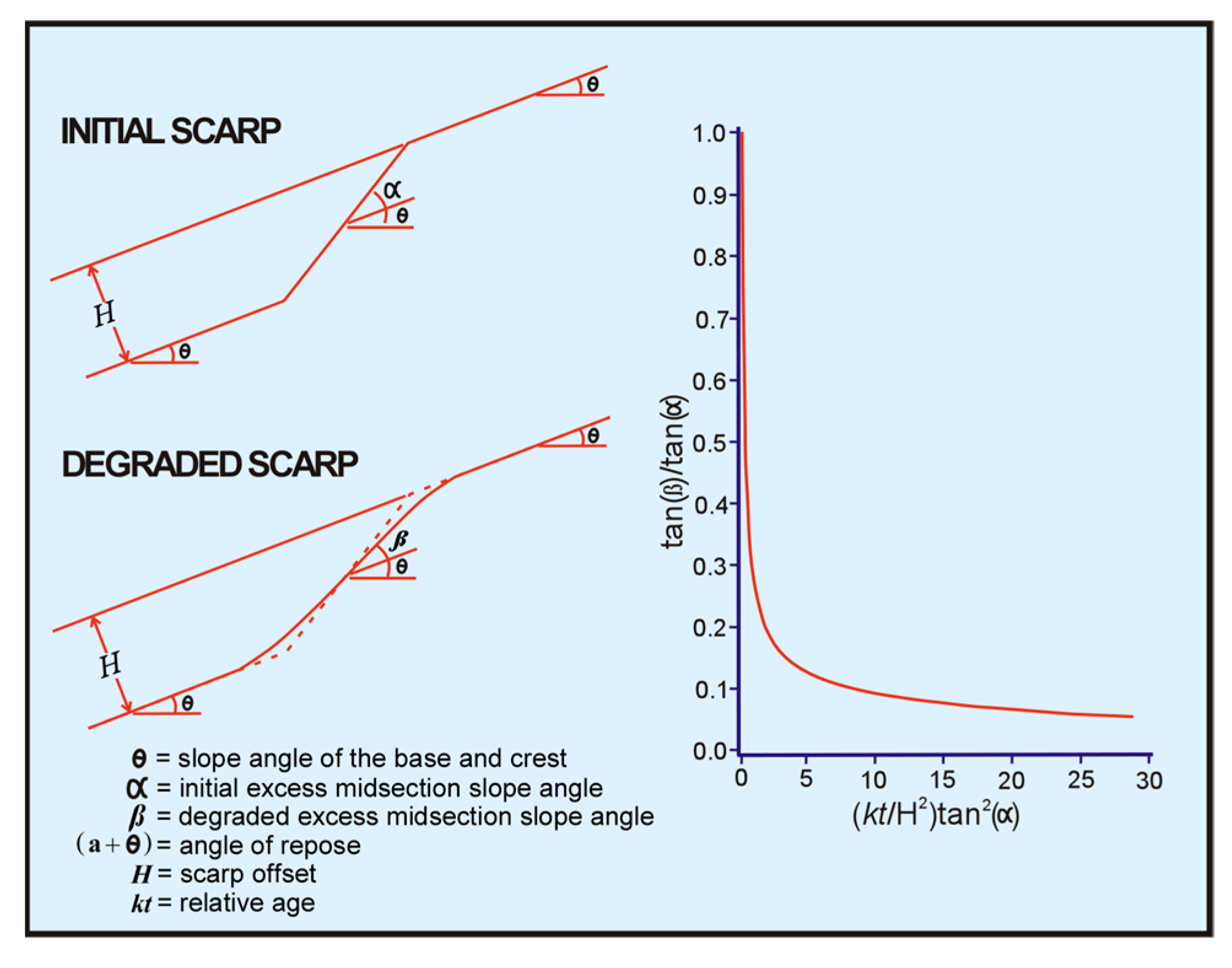
- Step 1: Determine H, β, and θ from a detailed profile of the scarp. (H = scarp offset; β = degraded excess midsection slope angle; θ = slope angle of the crest and base). See the left part of Figure 4 for these parameters.
- Step 2: Determine α, the initial excess midsection angle, either directly or indirectly, by measurement of the angle of internal friction, Φ (or angle of repose = α + θ), of the material underlying the scarp. α is equal to the difference between the angle of repose and slope of the crest and base (θ). The value of (α + θ) is equivalent to the angle of repose.
- Step 3: Calculate tan(β)/tan(α) and use it to determine the corresponding value of (kt/H2)tan2(α) from the curve (see right part of Figure 4) describing the relationship between the initial excess midsection slope angle, α; the degraded excess midsection slope angle, β; the scarp offset, H; the hillslope diffusivity, k; and the age of the hillslope, t.
- Step 4: Calculate relative age, kt, by multiplying (kt/H2)tan2(α), determined in step 3, by H2/tan2(α), calculated from the values of H and α found in Steps 1 and 2.
- Step 5: If t is known and k is to be calculated, determine k by dividing kt, found in Step 4, by t. If k is known and t is to be calculated, determine t by dividing kt, found in Step 4, by k.
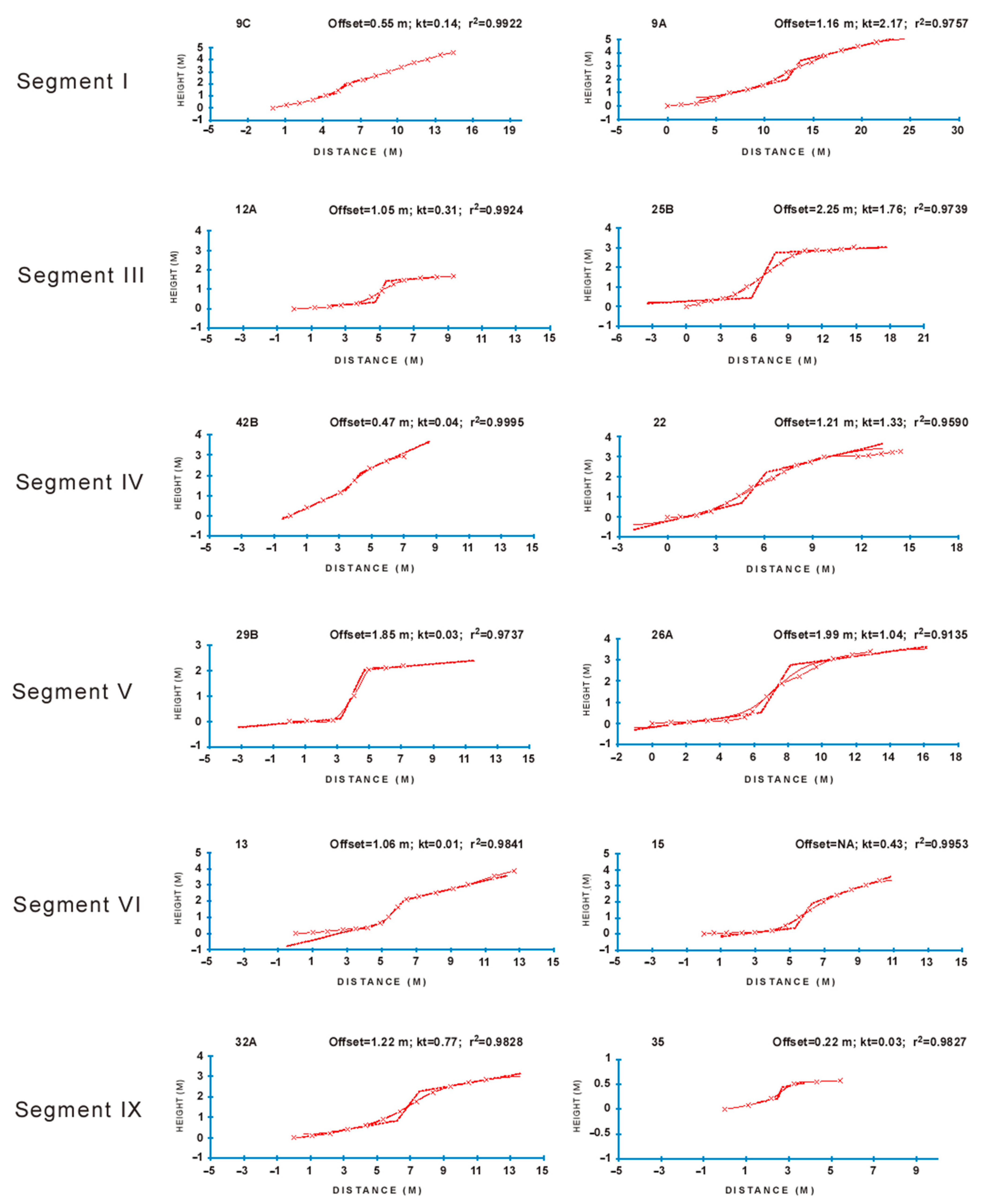
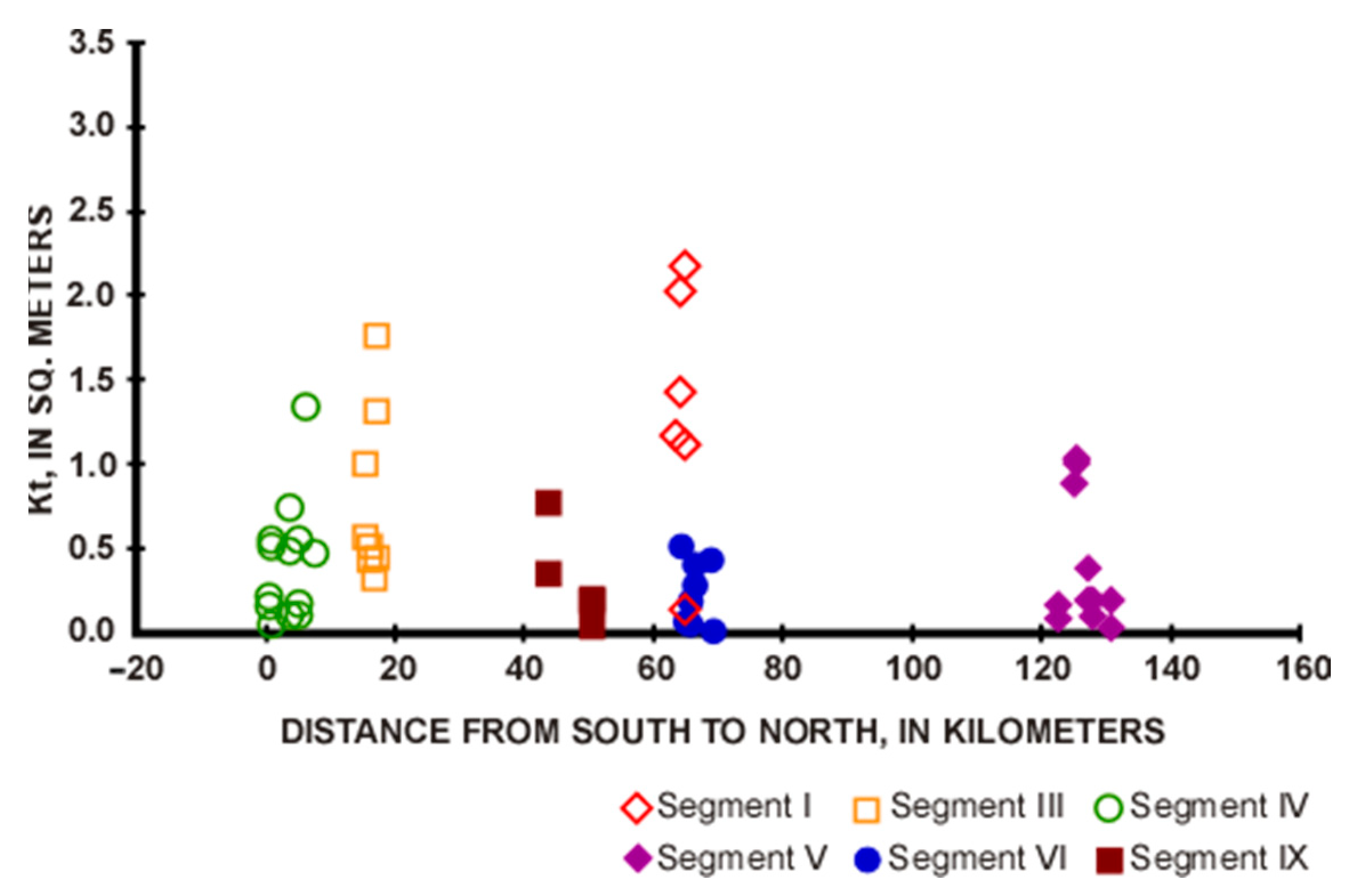
3. Results and Discussion
3.1. Relative Age Estimates
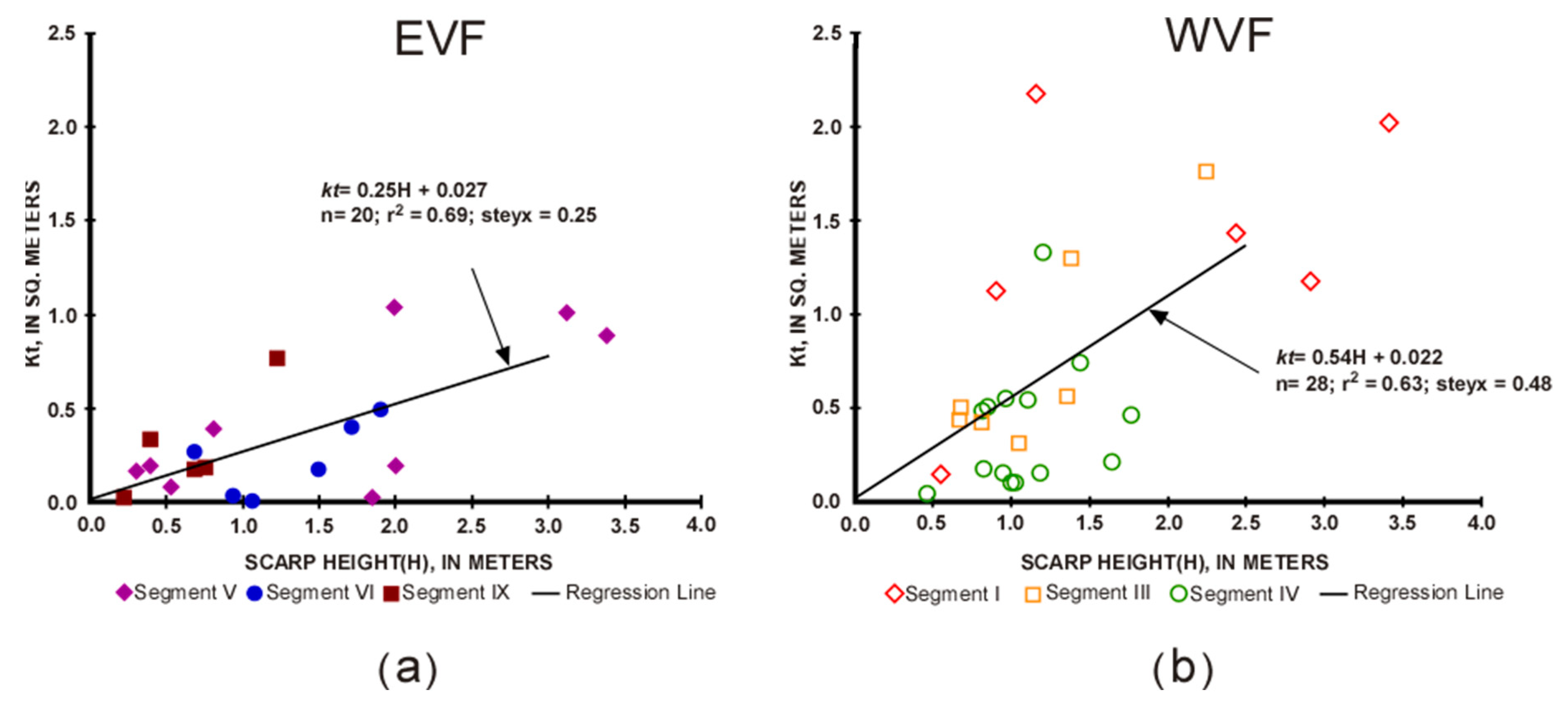
3.2. Diffusivity and Morphologic Ages
3.3. Aseismic Creep Scarps and Implications on Timing of Future Coseismic Events
3.3.1. Nature, Age, and Slip Rates
3.3.2. Possible Implications of Continued Creep: Induced Seismicity and Modulated Timing of Seismicity Along VFS Segments
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rimando, R.E. Neotectonic and Paleoseismic Study of the Marikina Valley Fault System, Philippines. Ph.D. Dissertation, State University of New York at Binghamton, Binghamton, NY, USA, 2002; 232p. [Google Scholar]
- Rimando, R.E.; Knuepfer, P.L. Neotectonics of the Marikina Valley fault system (MVFS) and tectonic framework of structures in northern and central Luzon, Philippines. Tectonophysics 2006, 415, 17–38. [Google Scholar] [CrossRef]
- Zanoria, E. The Depositional and Volcanological Origin of the Diliman Volcaniclastic Formation, Southwestern Luzon, Philippines. Master’s Thesis, University of Illinois, Chicago, IL, USA, 1988; p. 161. [Google Scholar]
- Arcilla, C.A.; Ruelo, H.B.; Umbal, J. The Angat ophiolite, Luzon, Philippines: Lithology, structure, and problems in age interpretation. Tectonophysics 1989, 168, 127–135. [Google Scholar] [CrossRef]
- Seno, T.; Stein, S.; Gripp, A.E. A model for the motion of the Philippine Sea Plate consistent with NUVEL-1 and geological data. J. Geophys. Res. 1993, 98, 17941–17948. [Google Scholar] [CrossRef]
- Schwartz, D.P.; Coppersmith, K.J. Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas fault zones. J. Geophys. Res. 1984, 89, 5681–5698. [Google Scholar] [CrossRef]
- Wheeler, R.L. Boundaries between segments of normal faults–criteria for recognition and interpretation. In Directions in Paleoseismology, Proceedings of the Conference XXXIX, Albuquerque, NM, USA, 21–23 April 1987; Crone, A.J., Omdahl, E.M., Eds.; United States Geological Survey: Denver, CO, USA, 1987. Available online: https://pubs.usgs.gov/of/1987/0673/report.pdf (accessed on 16 January 2025).
- Knuepfer, P.L.K. Implications for the nature of rupture segmentation from paleoseismic studies of normal faults, East-Central Idaho. In Proceedings of the Workshop on Paleoseismology, Marshall, CA, USA, 18–22 September 1994; U.S. Geological Survey: Menlo Park, CA, USA, 1994; pp. 97–99. [Google Scholar]
- Wheeler, R.L.; Krystinik, K.B. Persistent and nonpersistent segmentation of the Wasatch fault zone, Utah, Statistical analysis for evaluation of seismic hazard. In Assessment of Regional Earthquake Hazards and Risk Along the Wasatch Front, Utah—U.S. Geological Survey Professional Paper 1500; Gori, P.L., Hays, W.W., Eds.; USGS: Reston, VA, USA, 1992; pp. 1–47. [Google Scholar]
- Philippine Institute of Volcanology and Seismology (PHIVOLCS). Available online: https://earthquake.phivolcs.dost.gov.ph/EQLatest-Monthly/2014/2014Jan-Dec.html (accessed on 11 March 2025).
- Philippine Institute of Volcanology and Seismology (PHIVOLCS). Available online: https://earthquake.phivolcs.dost.gov.ph/EQLatest-Monthly/2021/2021_March.html (accessed on 11 March 2025).
- Hsu, Y.-J.; Yu, S.-B.; Loveless, J.P.; Bacolcol, T.; Solidum, R.; Luis, A.; Pelicano, A.; Woessner, J. Interseismic deformation and moment deficit along the Manila subduction zone and the Philippine Fault system. J. Geophys. Res. Solid Earth 2016, 121, 7639–7665. [Google Scholar] [CrossRef]
- Galgana, G.; Hamburger, M.; McCaffrey, R.; Corpuz, E.; Chen, Q.Z. Analysis of crustal deformation in Luzon, Philippines using geodetic observations and earthquake focal mechanisms. Tectonophysics 2007, 432, 63–87. [Google Scholar] [CrossRef]
- Bello, S.; Galli, P.; Perna, M.G.; Peronace, E.; Messina, P.; Rosatelli, G.; Andrenacci, C.; Lavecchia, G.; Pietrolungo, F.; Consalvo, A.; et al. Paleo-earthquake fingerprints and along strike slip variation of the silent Mt. Morrone normal fault (Central Italy): A structural-geochemical approach. Geochem. Geophys. Geosyst. 2025, 26, e2024GC011868. [Google Scholar] [CrossRef]
- Bello, S.; Perna, M.G.; Consalvo, A.; Brozzetti, F.; Galli, P.; Cirillo, D.; Andrenacci, C.; Tangari, A.C.; Carducci, A.; Menichetti, M.; et al. Coupling rare earth element analyses and high-resolution topography along fault scarps to investigate past earthquakes: A case study from the Southern Apennines (Italy). Geosphere 2023, 19, 1348–1371. [Google Scholar] [CrossRef]
- Mouslopoulou, V.; Moraetis, D.; Fassoulas, C. Identifying past earthquakes on carbonate faults: Advances and limitations of the ‘Rare Earth Element’ method based on analysis of the Spili Fault, Crete, Greece. Earth Planet. Sci. Lett. 2011, 309, 45–55. [Google Scholar] [CrossRef]
- Carcaillet, J.; Manighetti, I.; Chauvel, C.; Schlagenhauf, A.; Nicole, J.-M. Identifying past earthquakes on an active normal fault (Magnolia, Italy) from the chemical analysis of its exhumed carbonate fault plane. Earth Planet. Sci. Lett. 2008, 271, 145–158. [Google Scholar] [CrossRef]
- Nelson, A.R.; Personius, S.F.; Rimando, R.E.; Punongbayan, R.S.; Tuñgol, N.M.; Mirabueno, H.M.; Rasdas, A.S. Multiple large earthquakes in the past 1500 years on a fault in metropolitan Manila, the Philippines. Bull. Seismol. Soc. Am. 2000, 90, 73–85. [Google Scholar] [CrossRef]
- Wallace, R.E. Profiles and ages of young fault scarps, north-central Nevada. Geol. Soc. Am. Bull. 1977, 88, 1267–1281. [Google Scholar] [CrossRef]
- Hanks, T.C.; Bucknam, R.C.; Lajoie, K.R.; Wallace, R.E. Modification of wave-cut and fault-controlled landforms. J. Geophys. Res. 1984, 89, 5771–5790. [Google Scholar] [CrossRef]
- Hanks, T.C.; Schwartz, D.P. Morphologic dating of the pre-1983 fault scarp on the Lost River fault at Doublepring Pass Road, Custer County, Idaho. Bull. Seismol. Soc. Am. 1987, 77, 837–846. [Google Scholar]
- Tapponnier, P.; Meyer, B.; Avouac, J.P.; Peltzer, G.; Gaudemer, Y.; Guo, S.; Xiang, H.; Yin, K.; Chen, Z.; Cai, S.; et al. Active thrusting and folding in the Qilian Shan and decoupling between upper crust and mantle in northeastern Tibet. Earth Planet. Sci. Lett. 1990, 97, 382–403. [Google Scholar] [CrossRef]
- Enzel, Y.; Amit, R.; Bruce, J.; Harrison, J.; Porat, N. Morphologic dating of fault scarps and terrace risers in the southern Arava, Israel: Comparison to other age-dating techniques and implications for paleoseismicity. Isr. J. Earth Sci. 1994, 43, 91–103. [Google Scholar]
- Enzel, Y.; Amit, R.; Porat, N.; Zilberman, E.; Harrison, J.B.J. Estimating the ages of fault scarps in the Arava, Israel. Tectonophysics 1995, 253, 305–317. [Google Scholar] [CrossRef]
- Arrowsmith, J.R. Coupled Tectonic Deformation and Geomorphic Degradation Along the San Andreas Fault System. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1995; 356p. [Google Scholar]
- Kokkalas, S.; Koukouvelas, I.K. Fault-scarp degradation modeling in central Greece: Te Kaparelli and Eliki faults (Gulf of Corinth) as a case study. J. Geodyn. 2005, 40, 200–215. [Google Scholar] [CrossRef]
- Padmalal, A.; Khonde, N.; Maurya, D.M.; Shaikh, M.; Kumar, A.; Vanik, N.; Chamyal, L.S. Geomorphic Characteristics and Morphologic Dating of the Allah Bund Fault Scarp, Great Rann of Kachchh, Western India. In Tectonics and Structural Geology: Indian Context; Mukherjee, S., Ed.; Springer: Cham, Switzerland, 2018; p. 455. [Google Scholar] [CrossRef]
- Peltzer, G.; Nathan, D.; Brown, N.D.; Meriaux, A.-S.D.; van der Woerd, J.; Rhodes, E.J.; Finkel, R.C.; Ryerson, F.J.; Hollingsworth, J. Stable rate of slip along the Karakax section of the Altyn Tagh Fault from observation of interglacial and postglacial offset morphology and surface dating. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018893. [Google Scholar] [CrossRef]
- Turko, J.M.; Knuepfer, P.L.K. Late Quaternary fault segmentation from analysis of scarp morphology. Geology 1991, 19, 718–721. [Google Scholar] [CrossRef]
- Crone, A.J.; Haller, K.M. Segmentation and the coseismic behavior of Basin-and-Range normal faults; examples from east-central Idaho and southwestern Montana. J. Struct. Geol. 1991, 13, 151–164. [Google Scholar] [CrossRef]
- DuRoss, C.B.; Bunds, M.P.; Gold, R.D.; Briggs, R.W.; Reitman, N.G.; Personius, S.F.; Toké, N.A. Variable normal-fault rupture behavior, northern Lost River fault zone, Idaho, USA. Geosphere 2019, 15, 1869–1892. [Google Scholar] [CrossRef]
- Bello, S.; Andrenacci, C.; Cirillo, D.; Scott, C.P.; Brozzetti, F.; Arrowsmith, J.R.; Lavecchia, G. High-Detail Fault Segmentation: Deep Insight into the Anatomy of the 1983 Borah Peak Earthquake Rupture Zone (Mw 6.9, Idaho, USA). Lithosphere 2022, 2022, 8100224. [Google Scholar] [CrossRef]
- Bello, S.; Scott, C.P.; Ferrarini, F.; Brozzetti, F.; Scott, T.; Cirillo, D.; de Nardis, R.; Arrowsmith, J.R.; Lavecchia, G. High-resolution surface faulting from the 1983 Idaho Lost River Fault Mw 6.9 earthquake and previous events. Sci. Data 2021, 8, 68. [Google Scholar] [CrossRef]
- Andrews, D.J.; Bucknam, R.C. Fitting degradation of shoreline scarps by a nonlinear diffusion model. J. Geophys. Res. 1987, 92, 12857–12867. [Google Scholar] [CrossRef]
- Nash, D.B. Morphologic dating of degraded normal fault scarps. J. Geol. 1980, 88, 353–360. [Google Scholar] [CrossRef]
- Stewart, I.S.; Hancock, P.L. Normal fault zone evolution and fault scarp degradation in the Aegean region. Basin Res. 1988, 1, 139–153. [Google Scholar] [CrossRef]
- McCalpin, J.P.; Nelson, A.R. Introduction to paleoseismology. In Paleoseismology; McCalpin, J.P., Ed.; Academic Press: Orlando, FL, USA, 1996; pp. 1–32. [Google Scholar]
- Bucknam, R.C.; Anderson, R.E. Estimation of fault-scarp ages from a scarp-height-slope-angle relationship. Geology 1979, 7, 11–14. [Google Scholar] [CrossRef]
- Pierce, K.L.; Colman, S.M. Effect of height and orientation (microclimate) on geomorphic degradation rates and processes, late-glacial terrace scarps in central Idaho. Geol. Soc. Am. Bull. 1986, 97, 869–885. [Google Scholar] [CrossRef]
- Pierce, K.L.; Colman, S.M. Effect of height and orientation (microclimate) on degradation rates of Idaho terrace scarps. In Directions in Paleoseismology, Proceedings of the Conference XXXIX, Albuquerque, NM, USA, 21–23 April 1987; Crone, A.J., Omdahl, E.M., Eds.; United States Geological Survey: Denver, CO, USA, 1987. Available online: https://pubs.usgs.gov/of/1987/0673/report.pdf (accessed on 16 January 2025).
- Culling, W.E.H. Analytical theory of erosion. J. Geol. 1960, 68, 336–344. [Google Scholar] [CrossRef]
- Nash, D.B. Morphologic dating of fluvial terrace scarps and fault scarps near West Yellowstone, Montana. Geol. Soc. Am. Bull. 1984, 95, 1413–1424. [Google Scholar] [CrossRef]
- Nash, D.B. Morphologic Dating of Fault Scarps: Final Technical Report; US Geological Survey: Reston, VA, USA, 1986; p. 83. ISBN 14-08-0001-21960. [Google Scholar]
- Wallace, R.E. Ground-Squirrel Mounds and Related Patterned Ground Along the San Andreas Fault in Central California. Open-File Report 91-149; US Geological Survey: Menlo Park, CA, USA, 1991; pp. 1–21. [Google Scholar] [CrossRef]
- Arrowsmith, J.R.; Rhodes, D.D.; Pollard, D.D. Morphologic dating of scarps formed by repeated slip events along the San Andreas fault, Carrizo Plain, California. J. Geophys. Res. 1998, 103, 10,141–10,160. [Google Scholar] [CrossRef]
- Carson, M.A.; Kirkby, M.J. Hillslope Form and Process; Cambridge University Press: London, UK, 1972; p. 475. [Google Scholar]
- Nash, D.B. Reevaluation of the linear diffusion model for morphologic dating of scarps. In Directions in Paleoseismology, Proceedings of Conference XXXIX, Albuquerque, NM, USA, 21–23 April 1987; Crone, A.J., Omdahl, E.M., Eds.; United States Geological Survey: Denver, CO, USA, 1987. Available online: https://pubs.usgs.gov/of/1987/0673/report.pdf (accessed on 16 January 2025).
- Wallace, R.E. Degradation of the Hebgen Lake fault scarps of 1959. Geology 1980, 8, 225–229. [Google Scholar] [CrossRef]
- Crone, A.J.; Machette, M.N. Surface faulting accompanying the Borah Peak earthquake, central Idaho. Geology 1984, 12, 664–667. [Google Scholar] [CrossRef]
- Colman, S.M. Limits and constraints of the diffusion equation in modeling geological processes of scarp degradation. In Directions in Paleoseismology, Proceedings of Conference XXXIX, Albuquerque, NM, USA, 21–23 April 1987; Crone, A.J., Omdahl, E.M., Eds.; United States Geological Survey: Denver, CO, USA, 1987. Available online: https://pubs.usgs.gov/of/1987/0673/report.pdf (accessed on 16 January 2025).
- Dodge, R.L.; Grose, L.T. Tectonics and geomorphic evolution of the Black Rock Fault, northwestern Nevada. In Proceedings of the Conference X: Earthquake Hazards Along the Wasatch and Sierra-Nevada Frontal Fault Zones; Alta, UT, USA, 29 July–1 August 1979, United States Geological Survey: Denver, CO, USA, 1980. Available online: https://pubs.usgs.gov/of/1980/0801/report.pdf (accessed on 27 February 2025).
- Colman, S.M.; Watson, K. Ages estimated from a diffusion equation model for scarp degradation. Science 1983, 221, 263–265. [Google Scholar] [CrossRef]
- Hanks, T.C. The age of scarp-like landforms from diffusion equation analysis. In Quaternary Geochronology: Methods and Applications; Noller, J.S., Sowers, J.M., Lettis, W.R., Eds.; Wiley: New York, NY, USA, 2000; Volume 4, pp. 313–338. [Google Scholar] [CrossRef]
- Morisawa, M. Geomorphology Laboratory Manual (With Report Forms); John Wiley and Sons: New York, NY, USA, 1976; 253p. [Google Scholar]
- Andrews, D.J.; Hanks, T.C. Scarp degraded by linear diffusion: Inverse solution for age. J. Geophys. Res. 1985, 90, 10,193–10,208. [Google Scholar] [CrossRef]
- Repetti, W.C. Catalog of Philippine earthquakes. Bull. Seismol. Soc. Am. 1946, 36, 133–322. [Google Scholar] [CrossRef]
- Garcia, L.C.; Valenzuela, R.G.; Macalingcag, T.G. Catalog of Philippine earthquakes, Parts A to D 1589-1983. In Southeast Asia Association of Seismology and Earthquake Engineering, Series on Seismology: Philippines; Arnold, E.P., Ed.; Southeast Asia Association of Seismology and Earthquake Engineering: Quezon City, Philippines, 1985; Volume 4, pp. 1–547. [Google Scholar]
- Bautista, M.L.P. Estimation of the Magnitudes and Epicenters of Historical Earthquakes of the Philippines. Master’s Thesis, Kyoto University, Kyoto, Japan, 1996; 201p. [Google Scholar]
- Valenzuela, R.G.; Garcia, L.C.; Ambubuyog, G.M. Assessment of seismic intensity of Philippine historical earthquakes, Part F. In Southeast Asia Association of Seismology and Earthquake Engineering, Series on Seismology: Philippines; Arnold, E.P., Ed.; Southeast Asia Association of Seismology and Earthquake Engineering: Quezon City, Philippines, 1985; Volume 4, pp. 743–792. [Google Scholar]
- Bautista, M.L.P.; Oike, K. Estimation of the magnitude and epicenters of Philippine historical earthquakes. Tectonophysics 2000, 317, 137–169. [Google Scholar] [CrossRef]
- Rimando, R.E.; Knuepfer, P.L.K. Tectonic Control of Aseismic Creep and Potential for Induced Seismicity Along the West Valley Fault in Southeastern Metro Manila, Philippines. GeoHazards 2024, 5, 1172–1189. [Google Scholar] [CrossRef]
- Holzer, T.L. Ground failure induced by ground-water withdrawal from unconsolidated sediment. In Man-Induced Land Subsidence; Holzer, T., Ed.; Geological Society of America: Boulder, CO, USA, 1984; Volume 6, pp. 67–105. [Google Scholar]
- Hernández-Madrigal, V.M.; Muñiz-Jáuregui, J.A.; Garduño-Monroy, V.H.; Flores-Lázaro, N.; Figueroa-Miranda, S. Depreciation factor equation to evaluate the economic losses from ground failure due to subsidence related to groundwater withdrawal. Nat. Sci. 2014, 6, 108–113. [Google Scholar] [CrossRef]
- Rimando, R.E.; Kurita, K.; Kinugasa, Y. Spatial and temporal variation of aseismic creep along the dilational jog of the West Valley Fault, Philippines: Hazard implications. Front. Earth Sci. 2022, 10, 935161. [Google Scholar] [CrossRef]
- Ambraseys, N.N. Some characteristic features of the Anatolian fault zone. Tectonophysics 1970, 9, 143–165. [Google Scholar] [CrossRef]
- Savage, J.C.; Prescott, W.H.; Lisowski, M.; King, N. Geodolite measurements of deformation near Hollister, California, 1971–1978. J. Geophys. Res. 1979, 84, 7599–7615. [Google Scholar] [CrossRef]
- Burford, R.O.; Harsh, P.W. Slip on the San Andreas fault in central California from alinement array surveys. Bull. Seismol. Soc. Am. 1980, 70, 1233–1261. [Google Scholar]
- Yu, S.B.; Liu, C.C. Fault creep on the central segment of the Longitudinal Valley fault, eastern Taiwan. Proc. Geol. Soc. China 1989, 32, 209–231. [Google Scholar]
- Lienkaemper, J.J.; Borchardt, G.; Lisowski, M. Historic creep rate and potential for seismic slip along the Hayward fault. Calif. J. Geophys. Res. 1991, 96, 18261–18283. [Google Scholar] [CrossRef]
- Kelson, K.I.; Simpson, G.D.; Lettis, W.R.; Haraden, C.C. Holocene slip rate and earthquake recurrence of the northern Calaveras fault at Leyden Creek, northern California. J. Geophys. Res. 1996, 101, 5961–5975. [Google Scholar] [CrossRef]
- Stenner, H.D.; Ueta, K. Looking for evidence of large surface rupturing events on the rapidly creeping Southern Calaveras fault, California. In Proceedings of the Hokudan International Symposium and School on Active Faulting, Hokudan-cho, Awaji Island, Japan, 13–17 January 2000; pp. 479–486. [Google Scholar]
- Gonzalez, P.J.; Tiampo, K.F.; Palano, M.; Cannavo, F.; Fernandez, J. The 2011 Lorca earthquake slip distribution controlled by groundwater crustal unloading. Nat. Geosci. 2012, 5, 821–825. [Google Scholar] [CrossRef]
- Amos, C.B.; Audet, P.; Hammond, W.C.; Bürgmann, R.; Johanson, I.A.; Blewitt, G. Uplift and seismicity driven by groundwater depletion in central California. Nature 2014, 509, 483–486. [Google Scholar] [CrossRef]
- Kundu, B.; Vissa, N.K.; Gahalaut, V.K. Influence of anthropogenic groundwater unloading in Indo-Gangetic plains on the 25 April 2015 Mw 7.8 Gorkha, Nepal earthquake. Geophys. Res. Lett. 2015, 42, 10607–10613. [Google Scholar] [CrossRef]
- Kundu, B.; Vissa, N.K.; Gahalaut, K.; Gahalaut, V.K.; Panda, D.; Malik, K. Influence of anthropogenic groundwater pumping on the 2017 November 12 M7.3 Iran-Iraq border earthquake. Geophys. J. Int. 2019, 218, 833–839. [Google Scholar] [CrossRef]
- Foulger, G.R.; Wilson, M.P.; Gluyas, J.G.; Julian, B.R.; Davies, R.J. Global review of human-induced earthquakes. Earth Sci. Rev. 2018, 178, 438–514. [Google Scholar] [CrossRef]
- Wu, W. A review of unloading-induced fault instability. Undergr. Space 2021, 6, 528–538. [Google Scholar] [CrossRef]
- Ellsworth, W.L. Injection-induced earthquakes. Science 2013, 341, 142–147. [Google Scholar] [CrossRef]
- Tiwari, D.K.; Jha, B.; Kundu, B.; Gahalaut, V.K.; Vissa, N.K. Groundwater extraction-induced seismicity around Delhi region. India Sci. Rep. 2021, 11, 10097. [Google Scholar] [CrossRef] [PubMed]
- Pennington, W.D.; Davis, S.D.; Carlson, S.M.; Dupree, J.; Ewing, T.E. The evolution of seismic barriers and asperities caused by the depressuring of fault planes in oil and gas fields of South Texas. Bull. Seismol. Soc. Am. 1986, 76, 939–948. [Google Scholar]
- Holzer, T.L.; Davis, S.N.; Lofgren, B.E. Faulting caused by groundwater extraction in southcentral Arizona. J. Geophys. Res. 1979, 84, 603–612. [Google Scholar] [CrossRef]
- Segall, P. Earthquakes triggered by fluid extraction. Geology 1989, 17, 942–946. [Google Scholar] [CrossRef]
- Segall, P. Stress and subsidence resulting from subsurface fluid withdrawal in the epicentral region of the 1983 Coalinga earthquake. J. Geophys. Res. 1985, 90, 6801–6816. [Google Scholar] [CrossRef]
- Segall, P. Induced stresses due to fluid extraction from axisymmetric reservoirs. Pure Appl. Geophys. 1992, 139, 535–560. [Google Scholar] [CrossRef]
- Guglielmi, Y.; Cappa, F.; Avouac, J.P.; Henry, P.; Elsworth, D. Seismicity triggered by fluid injection-induced aseismic slip. Science 2015, 348, 1224–1226. [Google Scholar] [CrossRef] [PubMed]
- Scholz, C.; Engelder, J.T. The role of asperity indentation and ploughing in rock friction. I. Asperity creep and stick slip. Int. J. Rock Mech. Min. Sci. 1976, 13, 149–154. [Google Scholar] [CrossRef]
- Aki, K. Characterization of barriers on an earthquake fault. J. Geophys. Res. 1979, 84, 6140–6148. [Google Scholar] [CrossRef]
- Lay, T.; Kanamori, H.; Ruff, L. The asperity model and the nature of large subduction zone earthquakes. Earthq. Predict. Res. 1982, 1, 3–71. [Google Scholar]
- Sibson, R.N. Effects of fault heterogeneity on rupture propagation. In Directions in Paleoseismology, Proceedings of Conference XXXIX, Albuquerque, NM, USA, 21–23 April 1987; Crone, A., Omdahl, E., Eds.; United States Geological Survey: Denver, CO, USA, 1987. [Google Scholar]
- Bakun, W.H.; Stewart, R.M.; Bufe, C.G.; Marks, S.M. Implication of seismicity for failure of a section of the San Andreas fault. Bull. Seismol. Soc. Am. 1980, 70, 185–201. [Google Scholar] [CrossRef]
- King, G.; Nábělek, J. Role of fault bends in the initiation and termination of earthquake rupture. Science 1985, 228, 984–987. [Google Scholar] [CrossRef]
- King, G.C.P. Speculations on the geometry of the initiation and termination processes of earthquake rupture and its relation to morphology and geological structure. Pure Appl. Geophys. 1986, 124, 567–585. [Google Scholar] [CrossRef]

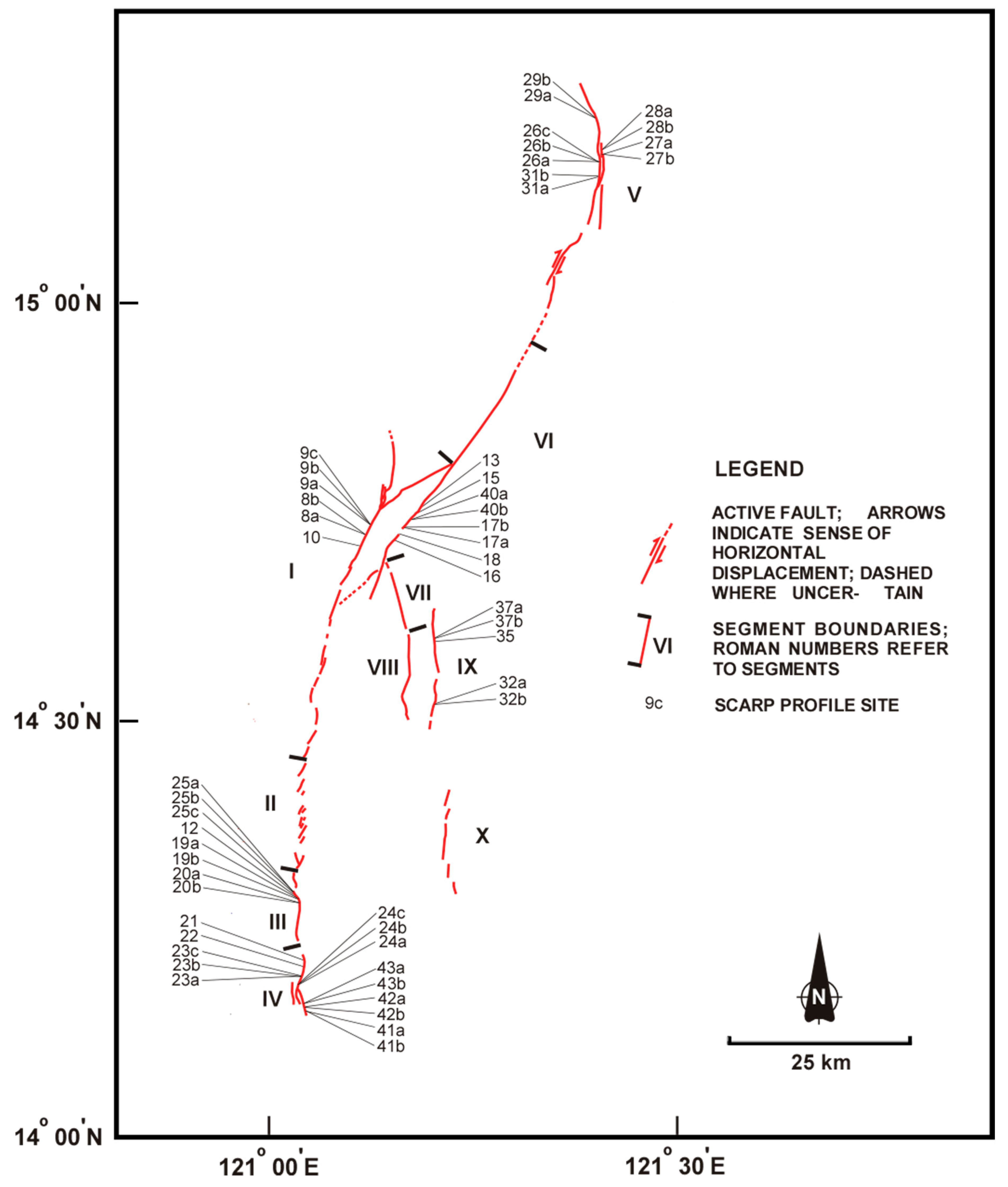



| Sample | Mean | Standard Deviation | Site Mean |
|---|---|---|---|
| 8A | 44.2 | 1.8 | 44.8 |
| 8B | 45.3 | 3.4 | 44.8 |
| 9A | 43.3 | 1.8 | 44.0 |
| 9B | 45.4 | 1.4 | 44.0 |
| 9C | 43.2 | 1.7 | 44.0 |
| 10 | 50.4 | 2.9 | 50.4 |
| 12 | 61.3 | 2.2 | 61.3 |
| 13 | 47.5 | 2.1 | 47.5 |
| 15 | 56.3 | 4.3 | 56.3 |
| 16 | 47.4 | 2.1 | 47.4 |
| 17A | 60.6 | 2.1 | 59.8 |
| 17B | 59.0 | 2.7 | 59.8 |
| 18 | 49.4 | 1.9 | 49.4 |
| 19A | 47.2 | 2.8 | 45.7 |
| 19B | 44.2 | 2.0 | 45.7 |
| 20A | 50.6 | 2.9 | 50.0 |
| 20B | 49.4 | 1.9 | 50.0 |
| 21 | 47.2 | 2.2 | 47.2 |
| 22 | 45.7 | 3.0 | 45.7 |
| 23A | 44.8 | 2.0 | 46.0 |
| 23B | 47.3 | 2.7 | 46.0 |
| 23C | N.D. | N.D. | N.D. |
| 24A | 44.2 | 2.4 | 47.6 |
| 24B | 50.9 | 1.5 | 47.6 |
| 24C | N.D. | N.D. | N.D. |
| 25A | 44.8 | 1.1 | 46.9 |
| 25B | 41.7 | 1.5 | 46.9 |
| 25C | 54.3 | 2.7 | 46.9 |
| 26A | 54.3 | 3.2 | 53.3 |
| 26B | 50.8 | 2.8 | 53.3 |
| 26C | 54.7 | 3.0 | 53.3 |
| 27A | 56.6 | 4.3 | 56.1 |
| 27B | 55.6 | 3.7 | 56.1 |
| 28A | 52.9 | 3.7 | 54.8 |
| 28B | 56.6 | 3.6 | 54.8 |
| 29A | 49.2 | 3.6 | 53.2 |
| 29B | 57.3 | 2.4 | 53.2 |
| 31A | 58.7 | 2.3 | 56.0 |
| 31B | 53.3 | 3.8 | 56.0 |
| 32A | 49.8 | 4.1 | 48.5 |
| 32B | 47.3 | 2.6 | 48.5 |
| 35 | 47.4 | 1.9 | 48.6 |
| 37A | 50.3 | 3.0 | 50.1 |
| 37B | 49.9 | 2.1 | 50.1 |
| 40A | 56.4 | 4.3 | 52.2 |
| 40B | 48.1 | 3.4 | 52.2 |
| 41A | 49.2 | 3.5 | 49.2 |
| 41B | 49.2 | 3.5 | 49.2 |
| 42A | 42.2 | 1.6 | 43.0 |
| 42B | 43.8 | 2.2 | 43.0 |
| 43A | 44.8 | 2.0 | 46.1 |
| 43B | 47.4 | 2.7 | 46.1 |
| Segment | Site | Dist. | Offset | kt * | r2 † | Andrews Hanks |
|---|---|---|---|---|---|---|
| (km) | (m) | (m2) | (tk) § | |||
| I | 8A | 64.1 | 2.44 | 1.43 | 0.9626 | 1.54 |
| 8B | 64.1 | 3.42 | 2.02 | 0.9898 | 1.87 | |
| 9A | 64.8 | 1.16 | 2.17 | 0.9757 | 2.02 | |
| 9B | 64.8 | 0.91 | 1.12 | 0.9296 | 2.90 | |
| 9C | 64.8 | 0.55 | 0.14 | 0.9922 | 0.38 | |
| 10 | 63.6 | 2.92 | 1.17 | 0.9945 | 1.22 | |
| III | 20A | 15.5 | 1.36 | 0.56 | 0.9595 | 0.49 |
| 20B | 15.5 | 0.90 | 0.99 | 0.8863 | 0.96 | |
| 19A | 16.1 | 0.81 | 0.42 | 0.9866 | 0.42 | |
| 19B | 16.1 | 0.68 | 0.50 | 0.9849 | 0.69 | |
| 12 | 16.8 | 1.05 | 0.31 | 0.9924 | 0.36 | |
| 25A | 17.3 | 1.38 | 1.30 | 0.9770 | 1.24 | |
| 25B | 17.3 | 2.25 | 1.76 | 0.9739 | 1.58 | |
| 25C | 17.3 | 0.67 | 0.44 | 0.9761 | 0.57 | |
| IV | 41A | 0.7 | 1.65 | 0.21 | 0.9914 | 0.27 |
| 41B | 0.7 | 1.19 | 0.15 | 0.9926 | 0.21 | |
| 42A | 0.9 | 0.95 | 0.15 | 0.9961 | 0.22 | |
| 42B | 0.9 | 0.47 | 0.04 | 0.9995 | 0.14 | |
| 43A | 1.0 | 0.85 | 0.50 | 0.9935 | 0.59 | |
| 43B | 1.0 | 0.97 | 0.55 | 0.9924 | 0.59 | |
| 24A | 3.9 | 0.82 | 0.48 | 0.9927 | 0.42 | |
| 24B | 3.9 | 1.03 | 0.10 | 0.9963 | 0.10 | |
| 24C | 3.9 | 1.44 | 0.74 | 0.9868 | 0.67 | |
| 23A | 5.3 | 0.83 | 0.17 | 0.9842 | 0.17 | |
| 23B | 5.3 | 1.00 | 0.10 | 0.9799 | 0.11 | |
| 23C | 5.3 | 1.11 | 0.54 | 0.9907 | 0.57 | |
| 22 | 6.5 | 1.21 | 1.33 | 0.9590 | 1.15 | |
| 21 | 7.7 | 1.77 | 0.46 | 0.9804 | 0.46 | |
| V | 31A | 122.5 | 0.53 | 0.08 | 0.9867 | 0.24 |
| 31B | 122.5 | 0.30 | 0.17 | 0.9957 | 0.51 | |
| 26A | 125.3 | 1.99 | 1.04 | 0.9135 | 1.02 | |
| 26B | 125.3 | 3.38 | 0.89 | 0.9766 | 0.87 | |
| 26C | 125.3 | 3.12 | 1.01 | 0.9443 | 0.88 | |
| 27A | 127.3 | 0.81 | 0.39 | 0.9950 | 0.58 | |
| 27B | 127.3 | 0.39 | 0.20 | 0.9990 | 0.50 | |
| 28A | 127.8 | N.A. | 0.10 | 0.9989 | N.A. | |
| 28B | 127.8 | N.A. | 0.19 | 0.9964 | N.A. | |
| 29A | 130.8 | 2.00 | 0.20 | 0.9821 | 0.33 | |
| 29B | 130.8 | 1.85 | 0.03 | 0.9737 | 0.19 | |
| VI | 16 | 64.5 | 1.90 | 0.50 | 0.9424 | 0.48 |
| 18 | 65.2 | N.A. | 0.06 | 0.9805 | N.A. | |
| 17A | 65.8 | 1.49 | 0.18 | 0.9732 | 0.16 | |
| 17B | 65.8 | 0.93 | 0.04 | 0.9970 | 0.05 | |
| 40A | 66.7 | 1.71 | 0.40 | 0.9783 | 0.39 | |
| 40B | 66.7 | 0.68 | 0.27 | 0.9931 | 0.32 | |
| 15 | 69.1 | N.A. | 0.43 | 0.9953 | N.A. | |
| 13 | 69.5 | 1.06 | 0.01 | 0.9841 | 0.03 | |
| IX | 32A | 43.8 | 1.22 | 0.77 | 0.9828 | 0.88 |
| 32B | 43.8 | 0.39 | 0.34 | 0.9637 | 0.69 | |
| 35 | 50.5 | 0.22 | 0.03 | 0.9825 | 0.13 | |
| 37A | 50.6 | 0.75 | 0.19 | 0.9950 | 0.32 | |
| 37B | 50.6 | 0.68 | 0.18 | 0.9796 | 0.26 |
| Segments | Distance | Mean kt | Stdev. | Sample | t Score | t Range | |
|---|---|---|---|---|---|---|---|
| Size | 0.01 Level | 0.05 Level | |||||
| I and III | |||||||
| I | 63.6 to 64.8 | 1.34 | 0.73 | 6 | |||
| III | 15.5 to 17.3 | 0.79 | 0.52 | 8 | |||
| −1.54 | −3.06 to 3.06 | −2.18 to 2.18 | |||||
| III and IV | |||||||
| III | 15.5 to 17.3 | 0.79 | 0.52 | 8 | |||
| IV | 0.7 to 7.7 | 0.39 | 0.35 | 14 | |||
| −2.02 | −2.84 to 2.84 | −2.09 to 2.09 | |||||
| I and IV | |||||||
| I | 63.6 to 64.8 | 1.34 | 0.73 | 6 | |||
| IV | 0.7 to 7.7 | 0.39 | 0.35 | 14 | |||
| 3.72 | −2.88 to 2.88 | −2.10 to 2.10 | |||||
| I and VI | |||||||
| I | 63.6 to 64.8 | 1.34 | 0.73 | 6 | |||
| VI | 64.5 to 69.5 | 0.24 | 0.19 | 8 | |||
| 3.79 | −3.06 to 3.06 | −2.18 to 2.18 | |||||
| V and VI | |||||||
| V | 122.5 to 130.8 | 0.39 | 0.39 | 11 | |||
| VI | 64.5 to 69.5 | 0.24 | 0.19 | 8 | |||
| −0.98 | −2.9 to 2.9 | −2.11 to 2.11 | |||||
| I and V | |||||||
| I | 63.6 to 64.8 | 1.34 | 0.73 | 6 | |||
| V | 122.5 to 130.8 | 0.39 | 0.39 | 11 | |||
| 3.28 | −2.95 to 2.95 | −2.13 to 2.13 | |||||
| I + III + IV and VI | |||||||
| I + III + IV | 0.7 to 64.8 | 0.71 | 0.61 | 28 | |||
| VI | 64.5 to 69.5 | 0.24 | 0.19 | 8 | |||
| −2.11 | −2.73 to 2.73 | −2.03 to 2.03 | |||||
| VI and IX | |||||||
| VI | 64.5 to 69.5 | 0.24 | 0.19 | 8 | |||
| IX | 43.8 to 50.6 | 0.30 | 0.28 | 5 | |||
| −0.46 | −3.11 to 3.11 | −2.2 to 2.2 | |||||
| V and IX | |||||||
| V | 122.5 130.8 | 0.39 | 0.39 | 11 | |||
| IX | 43.8 to 50.6 | 0.30 | 0.28 | 5 | |||
| 0.43 | −2.98 to 2.98 | −2.14 to 2.14 | |||||
| I + III + IV and V + VI + IX | |||||||
| I + III + IV | 0.7 to 64.8 | 0.71 | 0.61 | 28 | |||
| V + VI + IX | 64.5 to 130.8 | 0.32 | 0.31 | 24 | |||
| 2.78 | −2.68 to 2.68 | −2.01 to 2.01 | |||||
| Segment | Mean kt | Stdev. | Age | k | Stdev. | Age | Stdev. | ktnor § (m2) | knor † (m2/kyr) |
|---|---|---|---|---|---|---|---|---|---|
| (m2) | (m2) | (Years) | (m2/kyr) | (m2/kyr) | (Years) | (Years) | to 2 m | to 2 m | |
| EVF | |||||||||
| VI | 0.30 | 0.28 | - | ND | ND | ND | ND | - | - |
| IX | 0.24 | 0.19 | - | ND | ND | ND | ND | - | - |
| X | 0.39 | 0.39 | - | ND | ND | ND | ND | - | - |
| X + IX + VI | 0.32 | 0.31 | ~130 * | 2.47 | 2.39 | - | - | 0.53 ± 0.25 | 4.07 ± 1.92 |
| WVF | |||||||||
| I | 1.34 | 0.73 | - | 2.47 | 2.39 | 544 | 604 | - | - |
| III | 0.79 | 0.52 | - | ND | ND | ND | ND | - | - |
| IV | 0.39 | 0.35 | - | 2.47 | 2.39 | 160 | 209 | - | - |
| I + III + IV | 0.71 | 0.61 | - | 2.47 | 2.39 | ND | ND | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rimando, R.E.; Knuepfer, P.L.K. Earthquake History and Rupture Extents from Morphology of Fault Scarps Along the Valley Fault System (Philippines). GeoHazards 2025, 6, 23. https://doi.org/10.3390/geohazards6020023
Rimando RE, Knuepfer PLK. Earthquake History and Rupture Extents from Morphology of Fault Scarps Along the Valley Fault System (Philippines). GeoHazards. 2025; 6(2):23. https://doi.org/10.3390/geohazards6020023
Chicago/Turabian StyleRimando, Rolly E., and Peter L. K. Knuepfer. 2025. "Earthquake History and Rupture Extents from Morphology of Fault Scarps Along the Valley Fault System (Philippines)" GeoHazards 6, no. 2: 23. https://doi.org/10.3390/geohazards6020023
APA StyleRimando, R. E., & Knuepfer, P. L. K. (2025). Earthquake History and Rupture Extents from Morphology of Fault Scarps Along the Valley Fault System (Philippines). GeoHazards, 6(2), 23. https://doi.org/10.3390/geohazards6020023





