Examining the Relationship between Rainfall, Runoff, and Turbidity during the Rainy Season in Western Japan
Abstract
1. Introduction
2. Study Area and Records
2.1. Study Area
2.2. Hydrological Records
3. Methods
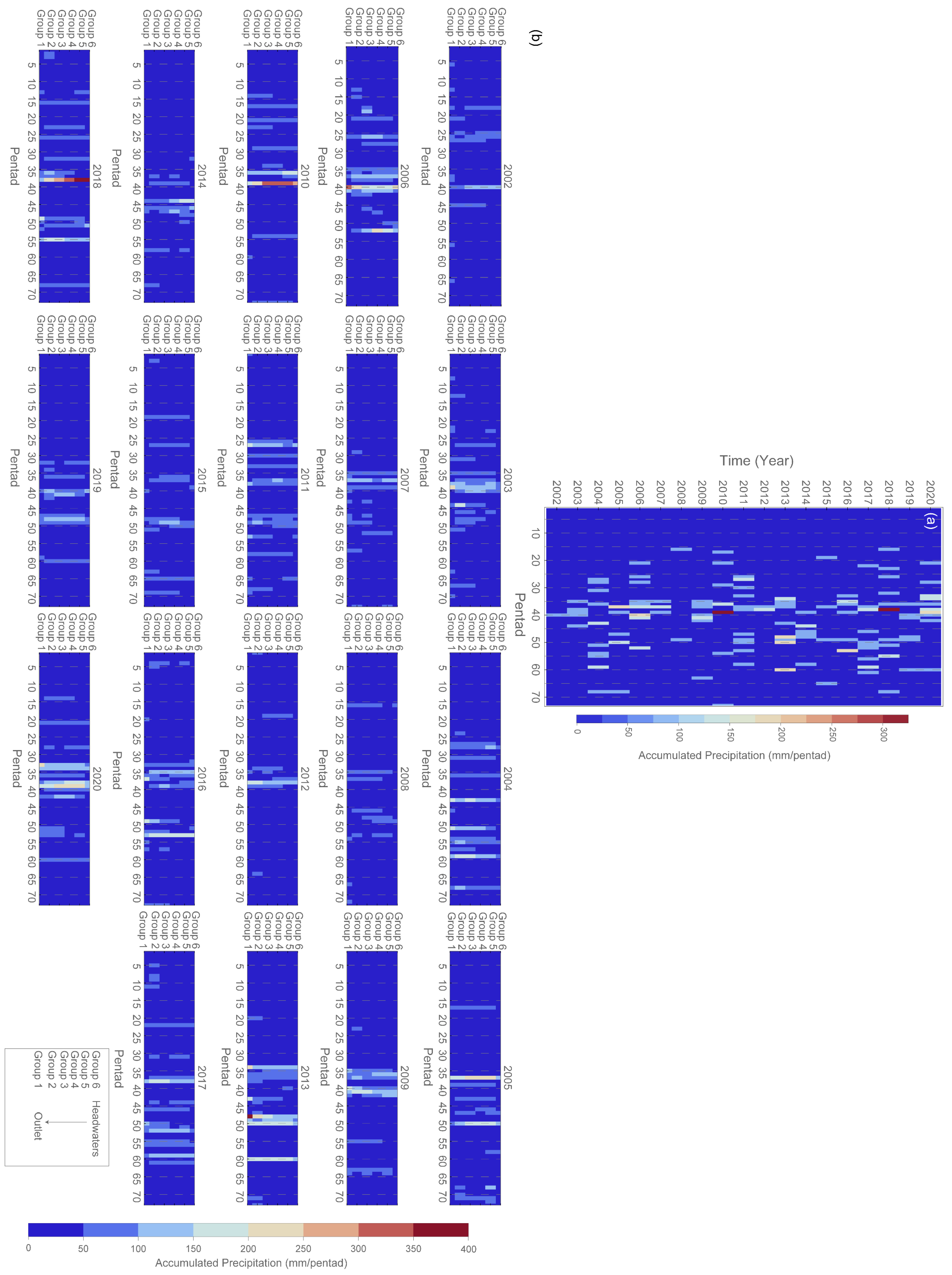
3.1. Pentad Precipitation Analysis
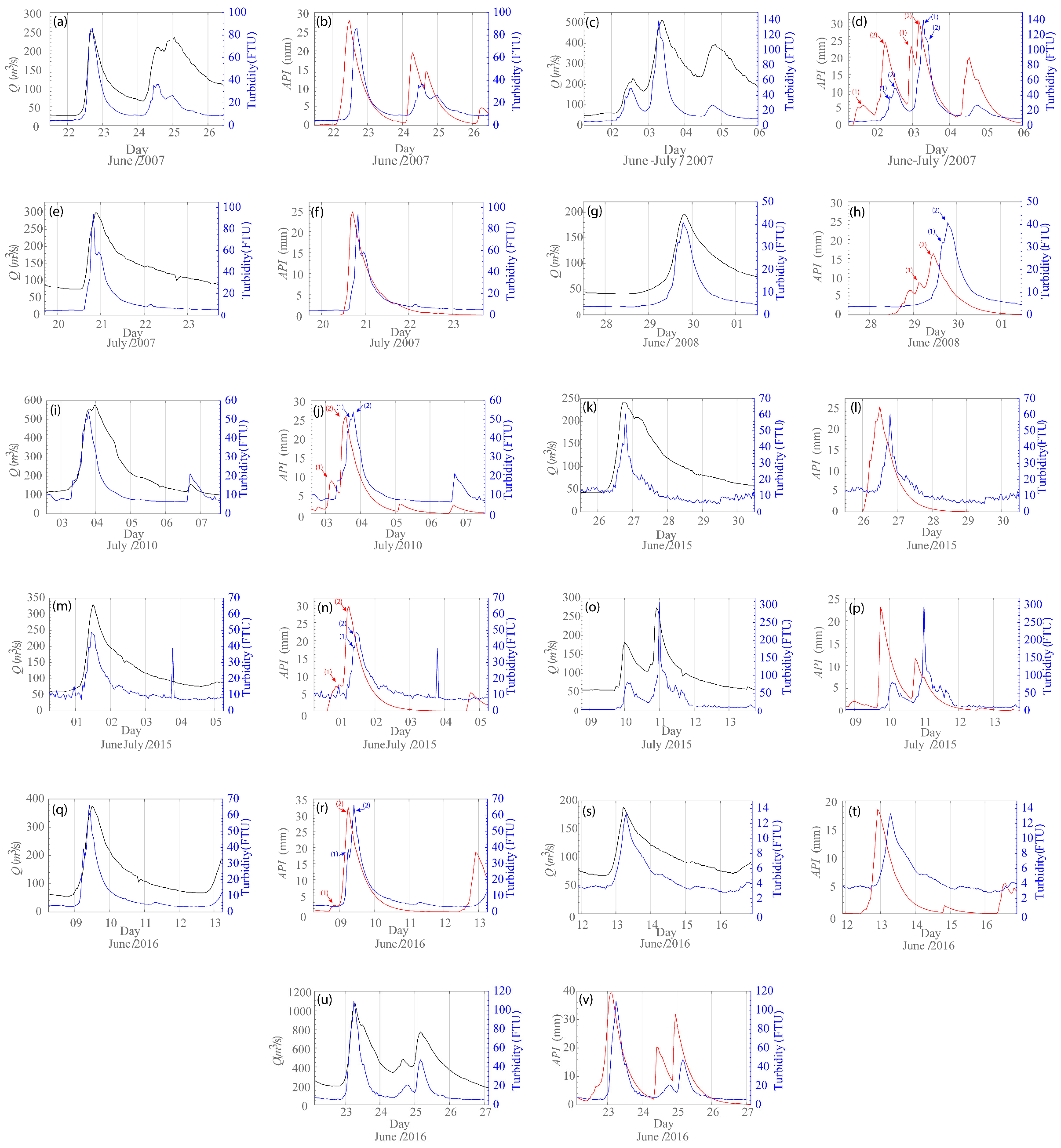
3.2. Rainfall–Runoff Response Analysis
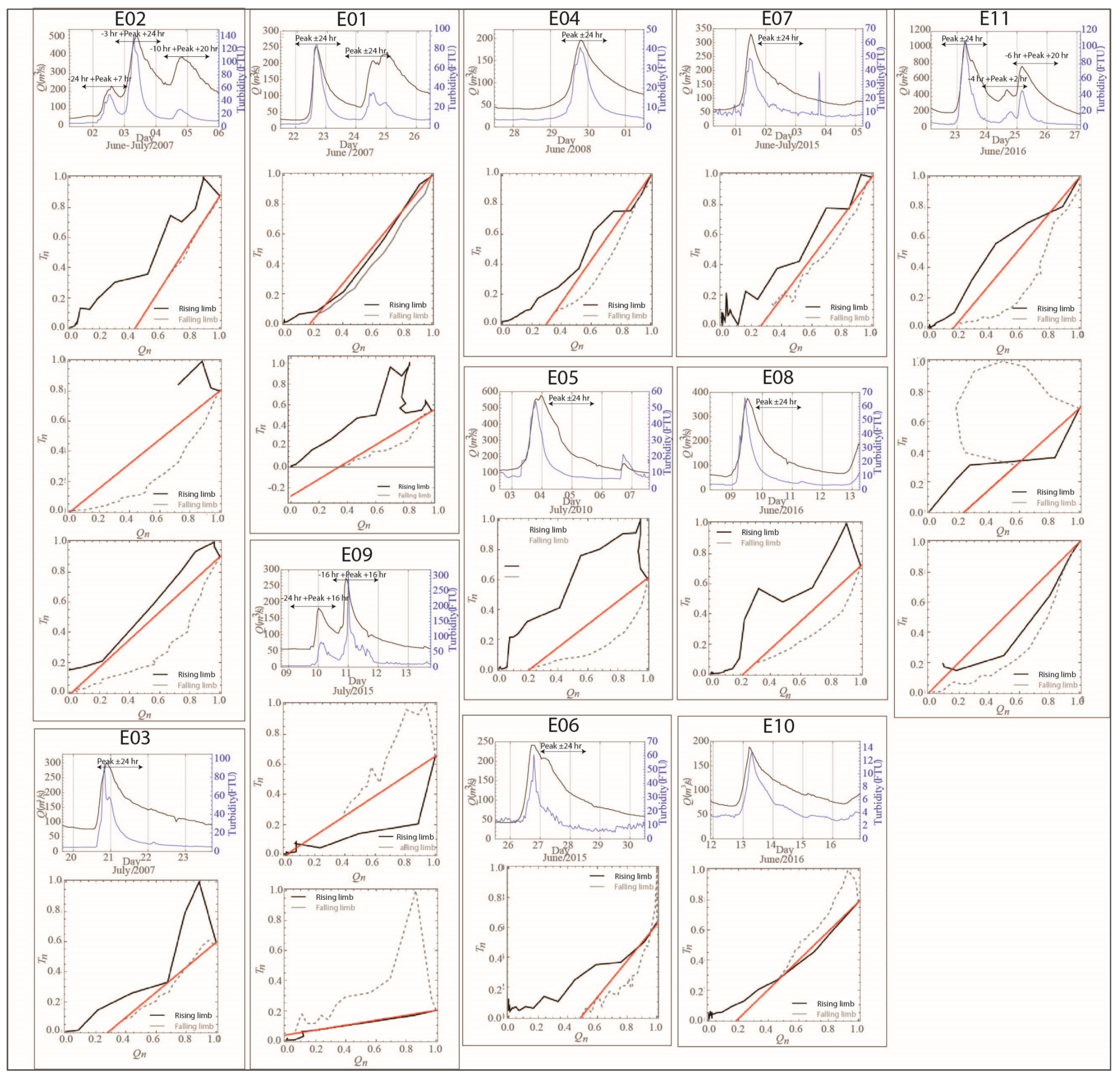
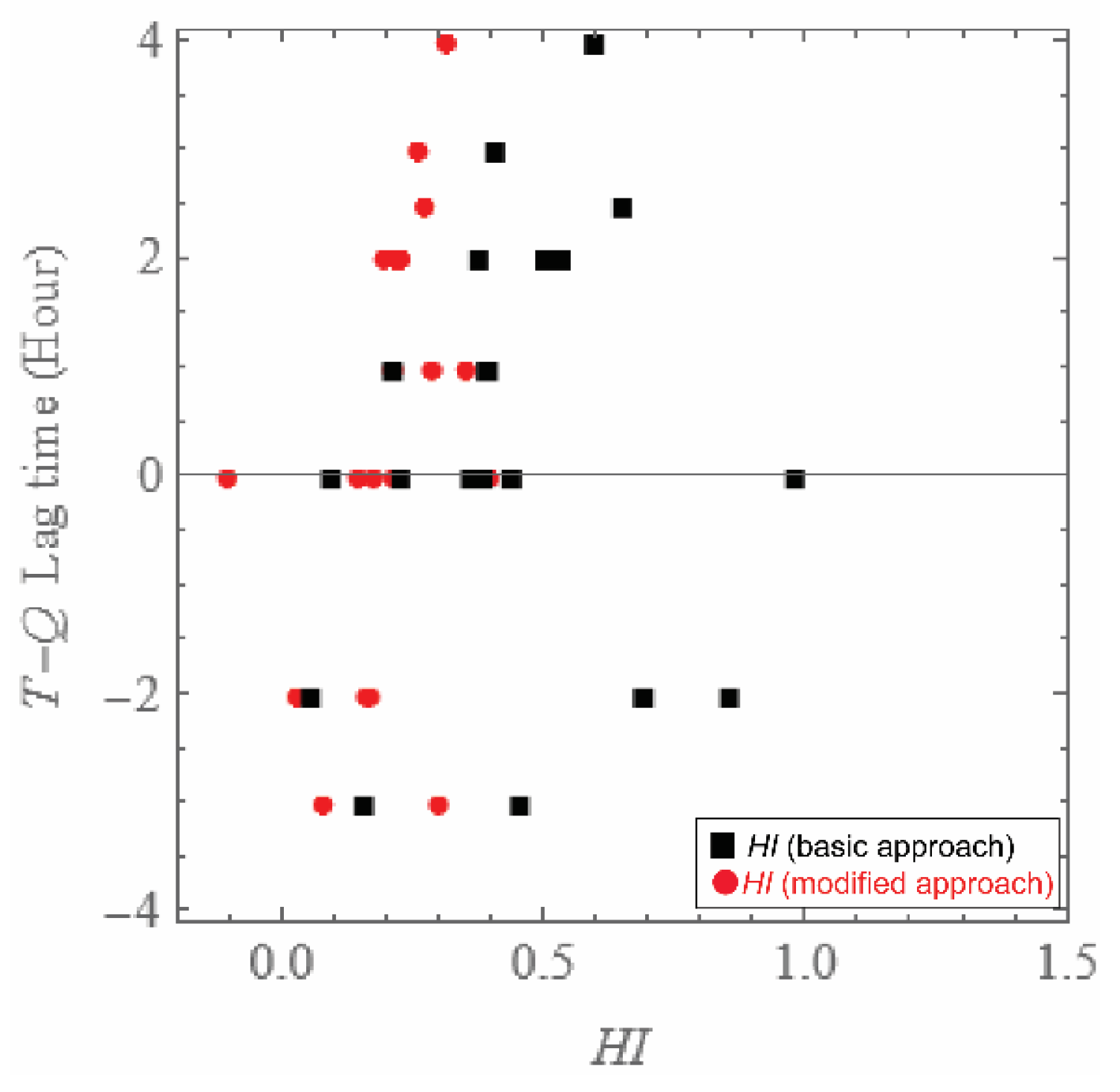
3.3. Quantification of Discharge Turbidity Hysteresis Patterns
4. Results and Discussion
4.1. Pentad Precipitation Plots
4.2. Storage–Turbidity and Flow–Turbidity Events
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Das, S.; Kamruzzaman, M.; Islam, A.R.M.T. Assessment of characteristic changes of regional estimation of extreme rainfall under climate change: A case study in a tropical monsoon region with the climate projections from CMIP6 model. J. Hydrol. 2022, 610, 128002. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a changing climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Uchimura, T.; Towhata, I.; Wang, L.; Nishie, S.; Yamaguchi, H.; Seko, I.; Qiao, J. Precaution and early warning of surface failure of slopes using tilt sensors. Soils Found. 2015, 55, 1086–1099. [Google Scholar] [CrossRef]
- Yamamoto, M. Effects of sea surface temperature anomalies on heavy rainfall in Tsushima Strait in late July 2020. Atmos. Res. 2022, 278, 106336. [Google Scholar] [CrossRef]
- Robinson, J.D.; Vahedifard, F.; Aghakouchak, A. Rainfall-triggered slope instabilities under a changing climate: Comparative study using historical and projected precipitation extremes. Can. Geotech. J. 2017, 54, 117–127. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ahmed, K.; Ismail, T.; Ziarh, G.F.; Chung, E.S.; Wang, X. Evaluation of CMIP6 GCM rainfall in mainland Southeast Asia. Atmos. Res. 2021, 254, 105525. [Google Scholar] [CrossRef]
- Al Sawaf, M.B.; Kawanisi, K.; Xiao, C. Characterizing annual flood patterns variation using information and complexity indices. Sci. Total Environ. 2021, 806, 151382. [Google Scholar] [CrossRef]
- Xu, Y.; Su, C.; Huang, Z.; Yang, C.; Yang, Y. Research on the protection of expansive soil slopes under heavy rainfall by anchor-reinforced vegetation systems. Geotext. Geomembr. 2022, 50, 1147–1158. [Google Scholar] [CrossRef]
- Sato, Y.; Kojiri, T.; Michihiro, Y.; Suzuki, Y.; Nakakita, E. Estimates of Climate Change Impact on River Discharge in Japan Based on a Super-High-Resolution Climate Model. Terr. Atmos. Ocean. Sci. 2012, 23, 527. [Google Scholar] [CrossRef][Green Version]
- Higashino, M.; Stefan, H.G. Variability and change of precipitation and flood discharge in a Japanese river basin. J. Hydrol. Reg. Stud. 2019, 21, 68–79. [Google Scholar] [CrossRef]
- Ohba, M.; Kadokura, S.; Yoshida, Y.; Nohara, D.; Toyoda, Y. Anomalous Weather Patterns in Relation to Heavy Precipitation Events in Japan during the Baiu Season. J. Hydrometeorol. 2015, 16, 688–701. [Google Scholar] [CrossRef]
- Om, K.-C.; Ren, G.; Li, S.; Kang-Chol, O. Climatological characteristics and long-term variation of rainy season and torrential rain over DPR Korea. Weather Clim. Extrem. 2018, 22, 48–58. [Google Scholar] [CrossRef]
- Ram, A.R.; Terry, J.P. Stream turbidity responses to storm events in a pristine rainforest watershed on the Coral Coast of southern Fiji. Int. J. Sediment Res. 2016, 31, 279–290. [Google Scholar] [CrossRef]
- Al Sawaf, M.B.; Kawanisi, K. Assessment of mountain river streamflow patterns and flood events using information and complexity measures. J. Hydrol. 2020, 590, 125508. [Google Scholar] [CrossRef]
- Hashimoto, R.; Tsuchida, T.; Moriwaki, T.; Kano, S. Hiroshima Prefecture geo-disasters due to Western Japan Torrential rainfall in July 2018. Soils Found. 2020, 60, 283–299. [Google Scholar] [CrossRef]
- Tsuchida, T.; Kano, S.; Nakagawa, S.; Kaibori, M.; Nakai, S.; Kitayama, N. Landslide and mudflow disaster in disposal site of surplus soil at Higashi-Hiroshima due to heavy rainfall in 2009. Soils Found. 2014, 54, 621–638. [Google Scholar] [CrossRef][Green Version]
- Michalek, A.; Zarnaghsh, A.; Husic, A. Modeling linkages between erosion and connectivity in an urbanizing landscape. Sci. Total Environ. 2021, 764, 144255. [Google Scholar] [CrossRef]
- Heckmann, T.; Cavalli, M.; Cerdan, O.; Foerster, S.; Javaux, M.; Lode, E.; Smetanová, A.; Vericat, D.; Brardinoni, F. Indices of sediment connectivity: Opportunities, challenges and limitations. Earth-Sci. Rev. 2018, 187, 77–108. [Google Scholar] [CrossRef]
- de Vente, J.; Poesen, J. Predicting soil erosion and sediment yield at the basin scale: Scale issues and semi-quantitative models. Earth-Sci. Rev. 2005, 71, 95–125. [Google Scholar] [CrossRef]
- Das, A.; Remesan, R.; Chakraborty, S.; Kumar Gupta, A. Investigation of human-induced land use dynamics in a representative catchment on the Chota Nagpur Plateau, India: A spatiotemporal application of soil erosion modeling with connectivity index studies. Catena 2022, 217, 106524. [Google Scholar] [CrossRef]
- Wu, J.; Nunes, J.P.; Baartman, J.E.M.; Faúndez Urbina, C.A. Testing the impacts of wildfire on hydrological and sediment response using the OpenLISEM model. Part 1: Calibration and evaluation for a burned Mediterranean forest catchment. Catena 2021, 207, 105658. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: Distributed River Basin Flow and Transport Modeling System. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef]
- de Vente, J.; Poesen, J.; Verstraeten, G.; Govers, G.; Vanmaercke, M.; Van Rompaey, A.; Arabkhedri, M.; Boix-Fayos, C. Predicting soil erosion and sediment yield at regional scales: Where do we stand? Earth-Sci. Rev. 2013, 127, 16–29. [Google Scholar] [CrossRef]
- Williams, G.P. Sediment concentration versus water discharge during single hydrologic events in rivers. J. Hydrol. 1989, 111, 89–106. [Google Scholar] [CrossRef]
- Hudson, P.F. Event sequence and sediment exhaustion in the lower Panuco Basin, Mexico. Catena 2003, 52, 57–76. [Google Scholar] [CrossRef]
- Al Sawaf, M.B.; Kawanisi, K. Novel high-frequency acoustic monitoring of streamflow-turbidity dynamics in a gravel-bed river during artificial dam flush. Catena 2019, 172, 738–752. [Google Scholar] [CrossRef]
- Göransson, G.; Larson, M.; Bendz, D. Variation in turbidity with precipitation and flow in a regulated river system–river Göta Älv, SW Sweden. Hydrol. Earth Syst. Sci. 2013, 17, 2529–2542. [Google Scholar] [CrossRef]
- Andrade, V.S.; Gutierrez, M.F.; Regaldo, L.; Paira, A.R.; Repetti, M.R.; Gagneten, A.M. Influence of rainfall and seasonal crop practices on nutrient and pesticide runoff from soybean dominated agricultural areas in Pampean streams, Argentina. Sci. Total Environ. 2021, 788, 147676. [Google Scholar] [CrossRef] [PubMed]
- Ochiai, S.; Kashiwaya, K. Measurement of suspended sediment for model experiments using general-purpose optical sensors. Catena 2010, 83, 1–6. [Google Scholar] [CrossRef]
- Slaets, J.I.F.; Schmitter, P.; Hilger, T.; Lamers, M.; Piepho, H.-P.; Vien, T.D.; Cadisch, G. A turbidity-based method to continuously monitor sediment, carbon and nitrogen flows in mountainous watersheds. J. Hydrol. 2014, 513, 45–57. [Google Scholar] [CrossRef]
- Solano-Rivera, V.; Geris, J.; Granados-Bolaños, S.; Brenes-Cambronero, L.; Artavia-Rodríguez, G.; Sánchez-Murillo, R.; Birkel, C. Exploring extreme rainfall impacts on flow and turbidity dynamics in a steep, pristine and tropical volcanic catchment. Catena 2019, 182, 104118. [Google Scholar] [CrossRef]
- Aich, V.; Zimmermann, A.; Elsenbeer, H. Quantification and interpretation of suspended-sediment discharge hysteresis patterns: How much data do we need? Catena 2014, 122, 120–129. [Google Scholar]
- Smith, H.G.; Dragovich, D. Interpreting sediment delivery processes using suspended sediment-discharge hysteresis patterns from nested upland catchments, south-eastern Australia. Hydrol. Process. 2009, 23, 2415–2426. [Google Scholar] [CrossRef]
- MLIT 2007 Gono River System and Its Watershed. (In Japanese). Available online: https://www.mlit.go.jp/river/shinngikai_blog/shaseishin/kasenbunkakai/shouiinkai/kihonhoushin/070810/pdf/ref1-1.pdf (accessed on 1 December 2023).
- Gramzow, R.H.; Henry, W.K. The Rainy Pentads of Central America. J. Appl. Meteorol. 1972, 11, 637–642. [Google Scholar] [CrossRef]
- Nishiyama, K.; Endo, S.; Jinno, K.; Bertacchi Uvo, C.; Olsson, J.; Berndtsson, R. Identification of typical synoptic patterns causing heavy rainfall in the rainy season in Japan by a Self-Organizing Map. Atmos. Res. 2007, 83, 185–200. [Google Scholar] [CrossRef]
- Malutta, S.; Kobiyama, M.; Chaffe, P.L.B.; Bonumá, N.B. Hysteresis analysis to quantify and qualify the sediment dynamics: State of the art. Water Sci. Technol. 2020, 81, 2471–2487. [Google Scholar] [CrossRef] [PubMed]
- Asselman, N.E.M. Suspended sediment dynamics in a large drainage basin: The River Rhine. Hydrol. Process. 1999, 13, 1437–1450. [Google Scholar] [CrossRef]
- Lawler, D.M.; Petts, G.E.; Foster, I.D.L.; Harper, S. Turbidity dynamics during spring storm events in an urban headwater river system: The Upper Tame, West Midlands, UK. Sci. Total Environ. 2006, 360, 109–126. [Google Scholar] [CrossRef] [PubMed]
- Langlois, J.L.; Johnson, D.W.; Mehuys, G.R. Suspended sediment dynamics associated with snowmelt runoff in a small mountain stream of Lake Tahoe (Nevada). Hydrol. Process. 2005, 19, 3569–3580. [Google Scholar] [CrossRef]
- Hamshaw, S.D.; Dewoolkar, M.M.; Schroth, A.W.; Wemple, B.C.; Rizzo, D.M. A New Machine-Learning Approach for Classifying Hysteresis in Suspended-Sediment Discharge Relationships Using High-Frequency Monitoring Data. Water Resour. Res. 2018, 54, 4040–4058. [Google Scholar] [CrossRef]
- Zuecco, G.; Penna, D.; Borga, M.; van Meerveld, H.J. A versatile index to characterize hysteresis between hydrological variables at the runoff event timescale. Hydrol. Process. 2016, 30, 1449–1466. [Google Scholar] [CrossRef]
- Geawhari, M.; Huff, L.; Mhammdi, N.; Trakadas, A.; Ammar, A. Spatial-temporal distribution of salinity and temperature in the Oued Loukkos estuary, Morocco: Using vertical salinity gradient for estuary classification. Springerplus 2014, 3, 643. [Google Scholar] [CrossRef]


| Dataset | Station Name(s) | Available Period | Dataset Source |
|---|---|---|---|
| Hourly rainfall (mm/h) | Shijihara, Ōasa, Kurome, Kōbo, Hiwa, Saijō, Tsuna, Tōhara, Nishino, Kamiryōke, Honji, Midori, Otsuki, Izuha, Itaki, Kamiyasuda, Sōryō, Haizuka, Haji, Shōbara, Funo, Kisa, Takamiya, Yoshida, Ida, Asuna, Miyoshi, Otsu, Kawamoto, Gōtsu | 2002~2020 | MLIT observatory station |
| Hourly discharge (m3/s) | Ozekiyama | 2002~2020 | MLIT observatory station |
| Hourly turbidity (FTU) | Ozekiyama | 2007, 2008, and 2010 | MLIT observatory station, |
| 2015/06~2015/07 and 2016/06~2016/07 | Hiroshima University |
| Event Code | Event | Peak Order | APIMax | TMax | QMax | TMax–APIMax* | QMax–APIMax** | QMax–TMax*** | Drise | Dfall | HI | Drise | Dfall | HI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T-Q (Basic Index) | T-Q (Modified Index) | |||||||||||||
| E01 | 2007/06/21~2007/06/26 | 1st peak | 06/22/12:00 | 06/22/17:00 | 06/22/17:00 | 5 | 5 | 0 | 0.14 | 0.09 | 0.23 | 0.1 | 0.04 | 0.15 |
| 2nd peak | 06/24/07:00 | 06/24/11:00 | 06/24/13:30 | 4 | 6.5 | 2.5 | 0.53 | 0.12 | 0.65 | 0.22 | 0.05 | 0.27 | ||
| E02 | 2007/07/01~2007/07/06 | 1st peak | 07/02/06:00 | 07/02/13:00 | 07/02/14:00 | 7 | 8 | 1 | 0.38 | 0.02 | 0.39 | 0.28 | 0.01 | 0.29 |
| 2nd peak | 07/02/23:00 | 07/03/07:00 | 07/03/09:00 | 8 | 10 | 2 | 0.24 | 0.3 | 0.53 | 0.12 | 0.11 | 0.23 | ||
| 3rd peak | 07/04/13:00 | 07/04/18:00 | 07/04/20:00 | 5 | 7 | 2 | 0.14 | 0.24 | 0.38 | 0.08 | 0.12 | 0.2 | ||
| E03 | 2007/07/20~2007/07/23 | Single | 07/20/17:00 | 07/20/21:00 | 07/20/21:00 | 4 | 4 | 0 | 0.38 | 0.06 | 0.44 | 0.16 | 0.01 | 0.18 |
| E04 | 2008/06/26~2008/06/30 | Single | 06/29/11:00 | 06/29/19:00 | 06/29/19:00 | 8 | 8 | 0 | 0.25 | 0.11 | 0.36 | 0.16 | 0.06 | 0.21 |
| E05 | 2010/07/02~2010/07/07 | Single | 07/03/14:00 | 07/03/19:00 | 07/03/23:00 | 5 | 9 | 4 | 0.441 | 0.19 | 0.6 | 0.2 | 0.11 | 0.31 |
| E06 | 2015/06/25~2015/06/30 | Single | 06/26/12:00 | 06/26/18:00 | 06/26/19:00 | 6 | 7 | 1 | 0.45 | −0.24 | 0.21 | 0.31 | 0.04 | 0.35 |
| E07 | 2015/06/30~2015/07/05 | Single | 07/01/06:00 | 07/01/11:00 | 07/01/12:00 | 5 | 6 | 1 | 0.1 | 0.08 | 0.39 | 0.18 | 0.03 | 0.21 |
| E08 | 2015/07/09~2015/07/13 | Single | 07/09/18:00 | 07/10/02:00 | 07/10/00:00 | 8 | 6 | −2 | 0.31 | 0.38 | 0.69 | 0.02 | 0.14 | 0.16 |
| E09 | 2015/07/08~2015/07/13 | 1st peak | 07/10/18:00 | 07/11/00:00 | 07/10/22:00 | 6 | 4 | −2 | 0.03 | 0.82 | 0.86 | 0.02 | 0.15 | 0.17 |
| 2nd peak | 06/09/06:00 | 06/09/10:00 | 06/09/12:00 | 4 | 6 | 2 | 0.36 | 0.14 | 0.5 | 0.15 | 0.07 | 0.22 | ||
| E10 | 2016/06/08~2016/06/13 | Single | 06/12/22:00 | 06/13/07:00 | 06/13/05:00 | 9 | 7 | −2 | −0.15 | 0.2 | 0.06 | −0.07 | 0.1 | 0.03 |
| E11 | 2016/06/22~2016/06/27 | 1st peak | 06/23/03:00 | 06/23/06:00 | 06/23/06:00 | 3 | 3 | 0 | 0.15 | 0.24 | 0.38 | 0.1 | 0.12 | 0.22 |
| 2nd peak | 06/24/11:00 | 06/24/19:00 | 06/24/16:00 | 8 | 5 | −3 | −0.2 | 0.66 | 0.46 | −0.09 | 0.39 | 0.3 | ||
| 3rd peak | 06/24/23:00 | 06/25/04:00 | 06/25/04:00 | 5 | 5 | 0 | −0.17 | 0.27 | 0.09 | 0.03 | −0.14 | −0.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Sawaf, M.B.; Kawanisi, K.; Bahreinimotlagh, M. Examining the Relationship between Rainfall, Runoff, and Turbidity during the Rainy Season in Western Japan. GeoHazards 2024, 5, 176-191. https://doi.org/10.3390/geohazards5010009
Al Sawaf MB, Kawanisi K, Bahreinimotlagh M. Examining the Relationship between Rainfall, Runoff, and Turbidity during the Rainy Season in Western Japan. GeoHazards. 2024; 5(1):176-191. https://doi.org/10.3390/geohazards5010009
Chicago/Turabian StyleAl Sawaf, Mohamad Basel, Kiyosi Kawanisi, and Masoud Bahreinimotlagh. 2024. "Examining the Relationship between Rainfall, Runoff, and Turbidity during the Rainy Season in Western Japan" GeoHazards 5, no. 1: 176-191. https://doi.org/10.3390/geohazards5010009
APA StyleAl Sawaf, M. B., Kawanisi, K., & Bahreinimotlagh, M. (2024). Examining the Relationship between Rainfall, Runoff, and Turbidity during the Rainy Season in Western Japan. GeoHazards, 5(1), 176-191. https://doi.org/10.3390/geohazards5010009







