Probabilistic Tsunami Hazard Analysis for Vancouver Island Coast Using Stochastic Rupture Models for the Cascadia Subduction Earthquakes
Abstract
1. Introduction
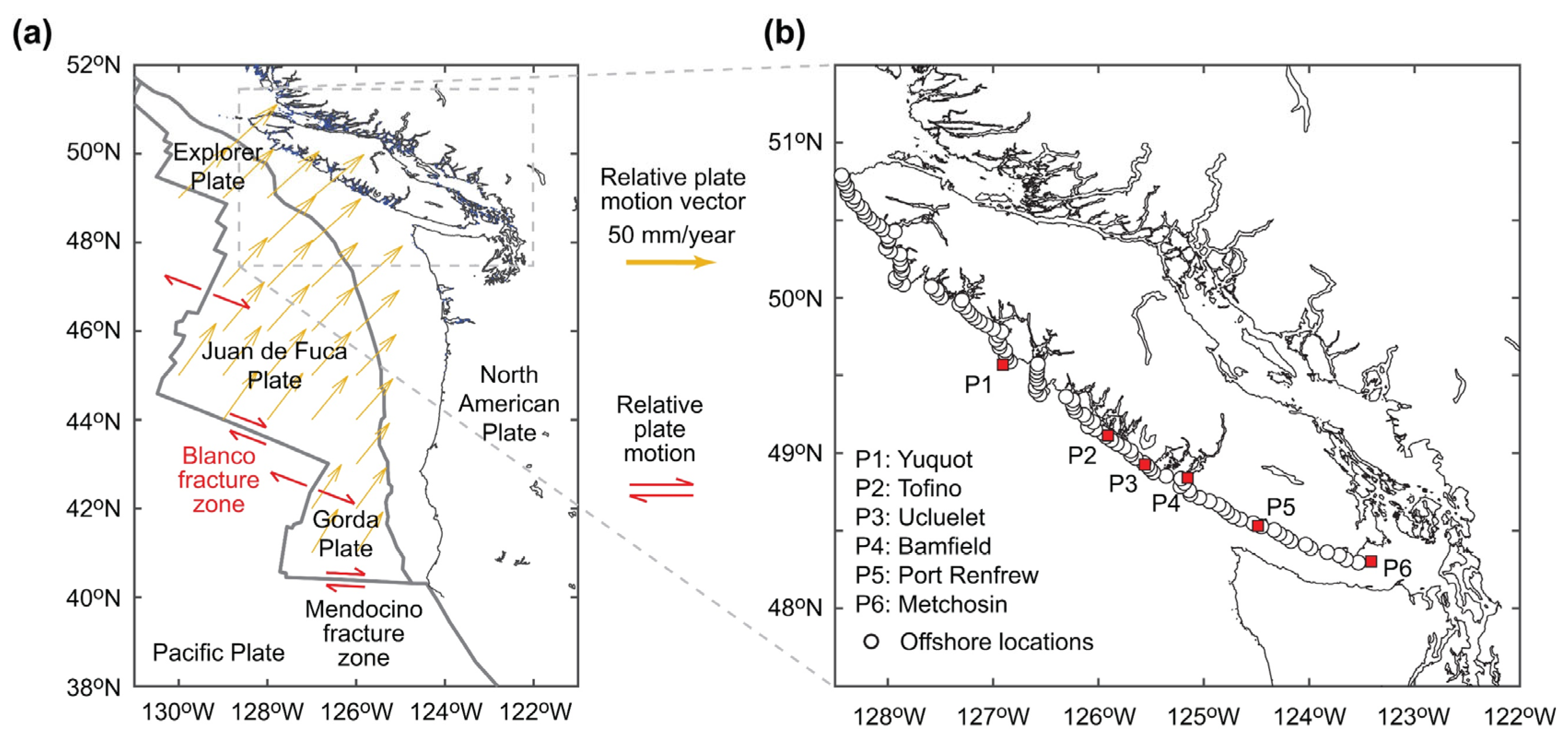
2. Cascadia Subduction Zone
2.1. Tectonic Characteristics
2.2. Earthquake History Data Based on Offshore Turbidite Records
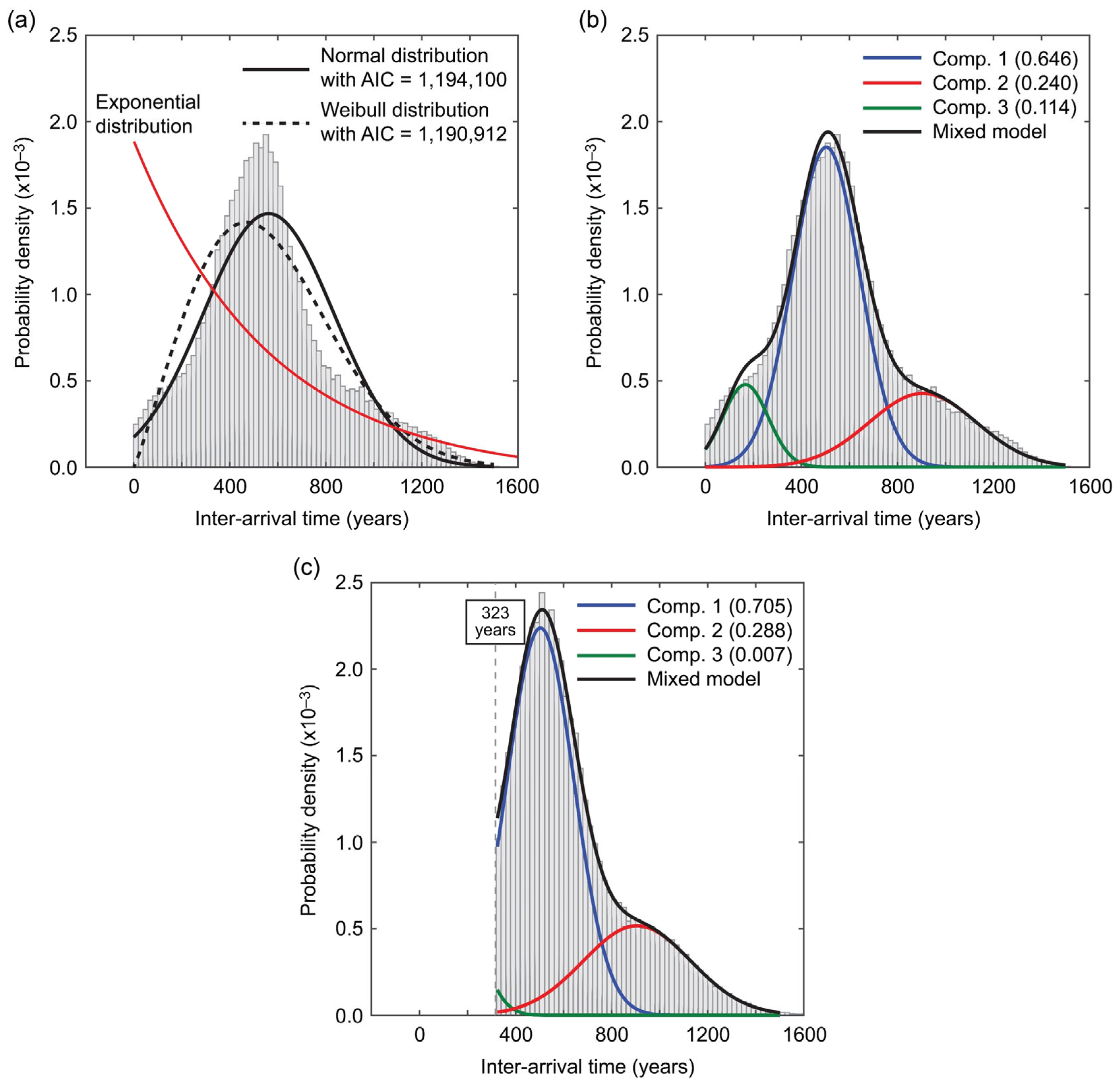
2.3. Resampled Turbidite-Based Earthquake History Data
- Set the number of Monte Carlo resampling.
- For each turbidite event, choose one of the pieces of data randomly with equal chance (i.e., all listed data in [21] are regarded as equally reliable).
- Sample the age of the turbidite data chosen in Step 2 from the triangle distribution, which is determined by the best and +/− 2 sigma bounds.
- Repeat Steps 2 and 3 for all turbidite data (i.e., T1 to T18). The inter-arrival time data can be obtained for each catalog.
- Repeat Steps 2 to 4 for the resampling number specified in Step 1.
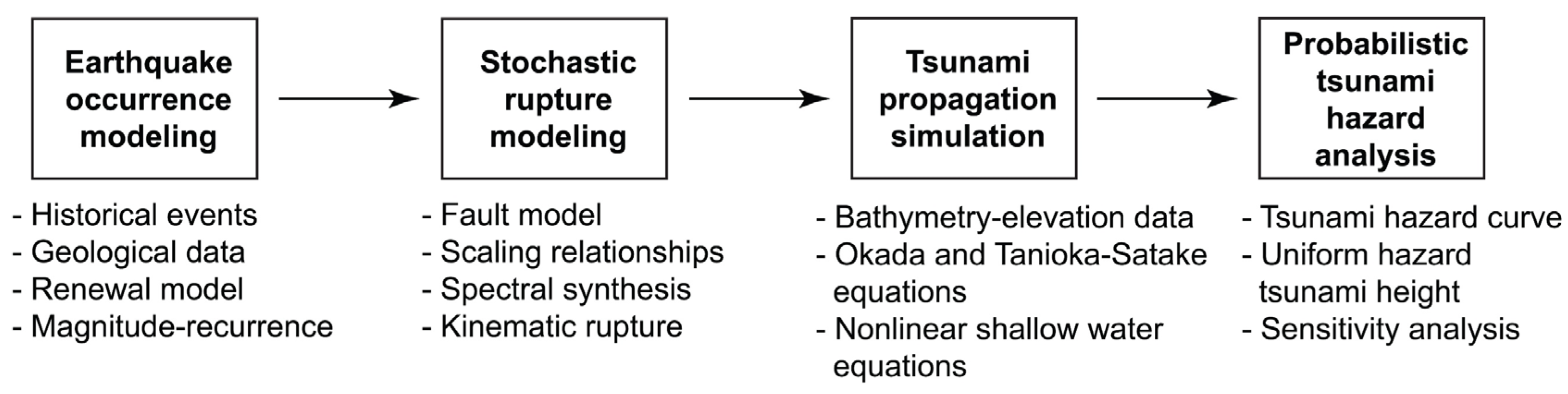
3. Probabilistic Tsunami Hazard Model for the Cascadia Subduction Earthquakes
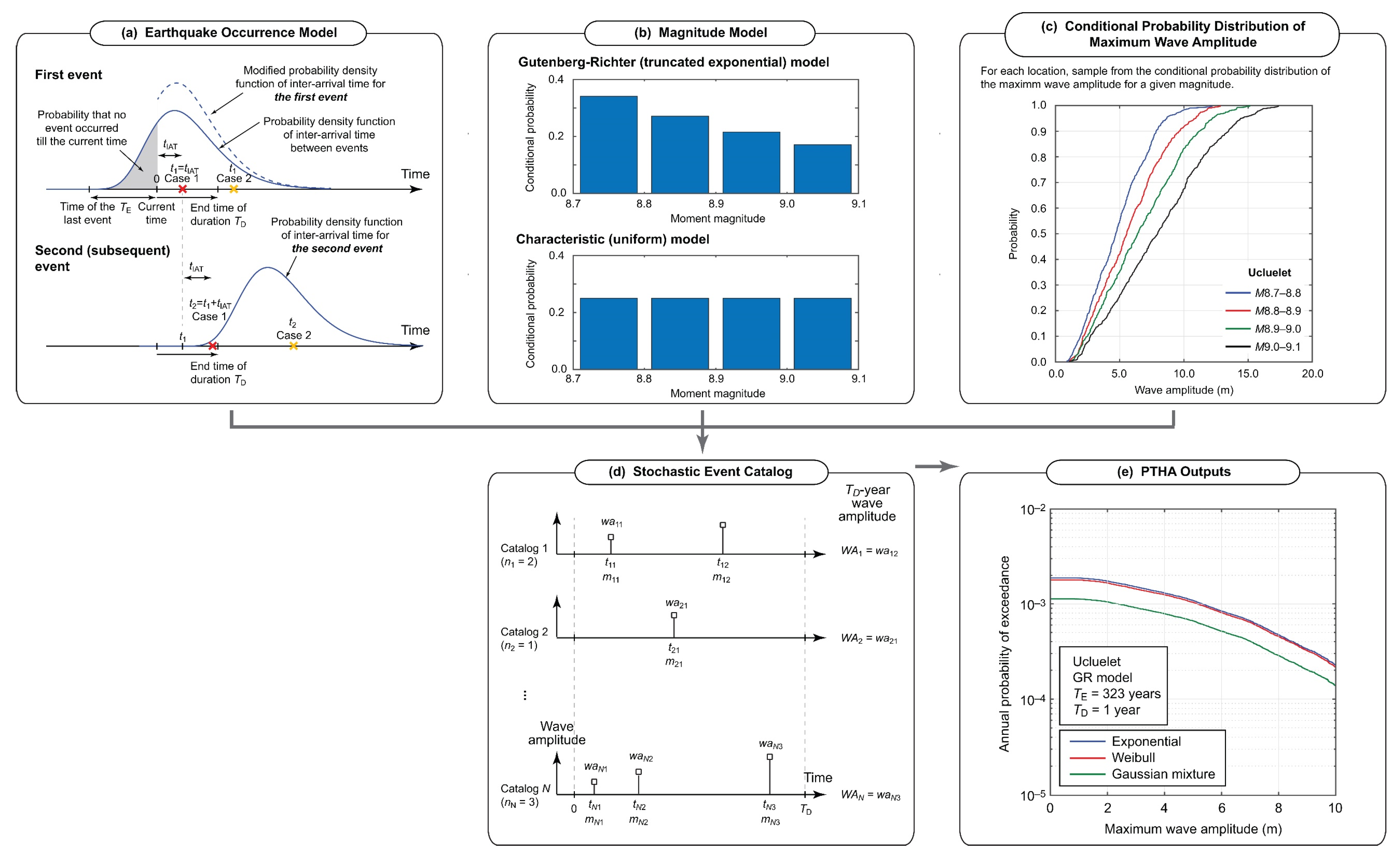
3.1. Earthquake Occurrence Model
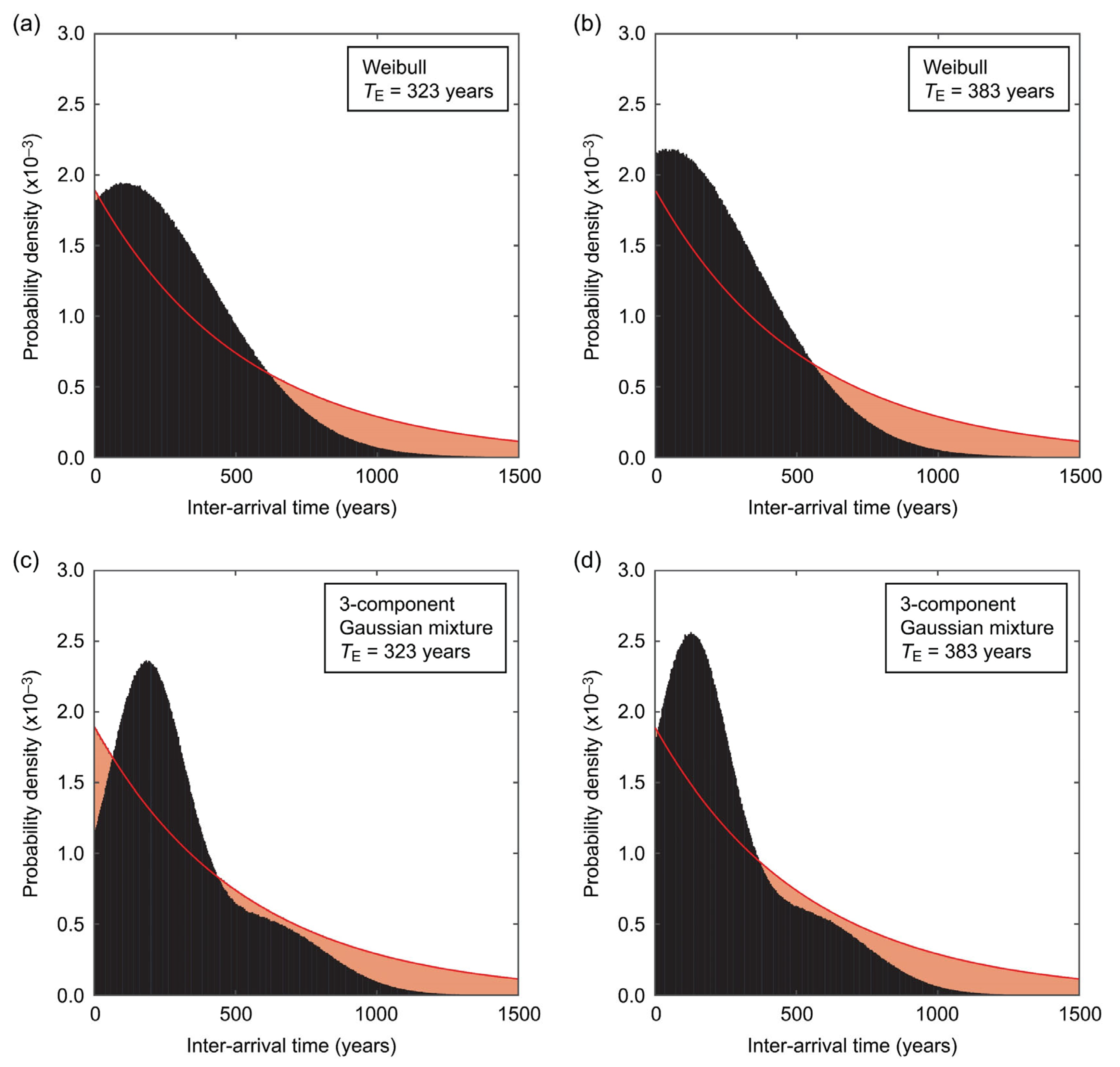
3.1.1. One-Component Renewal Model
3.1.2. Gaussian Mixture Model
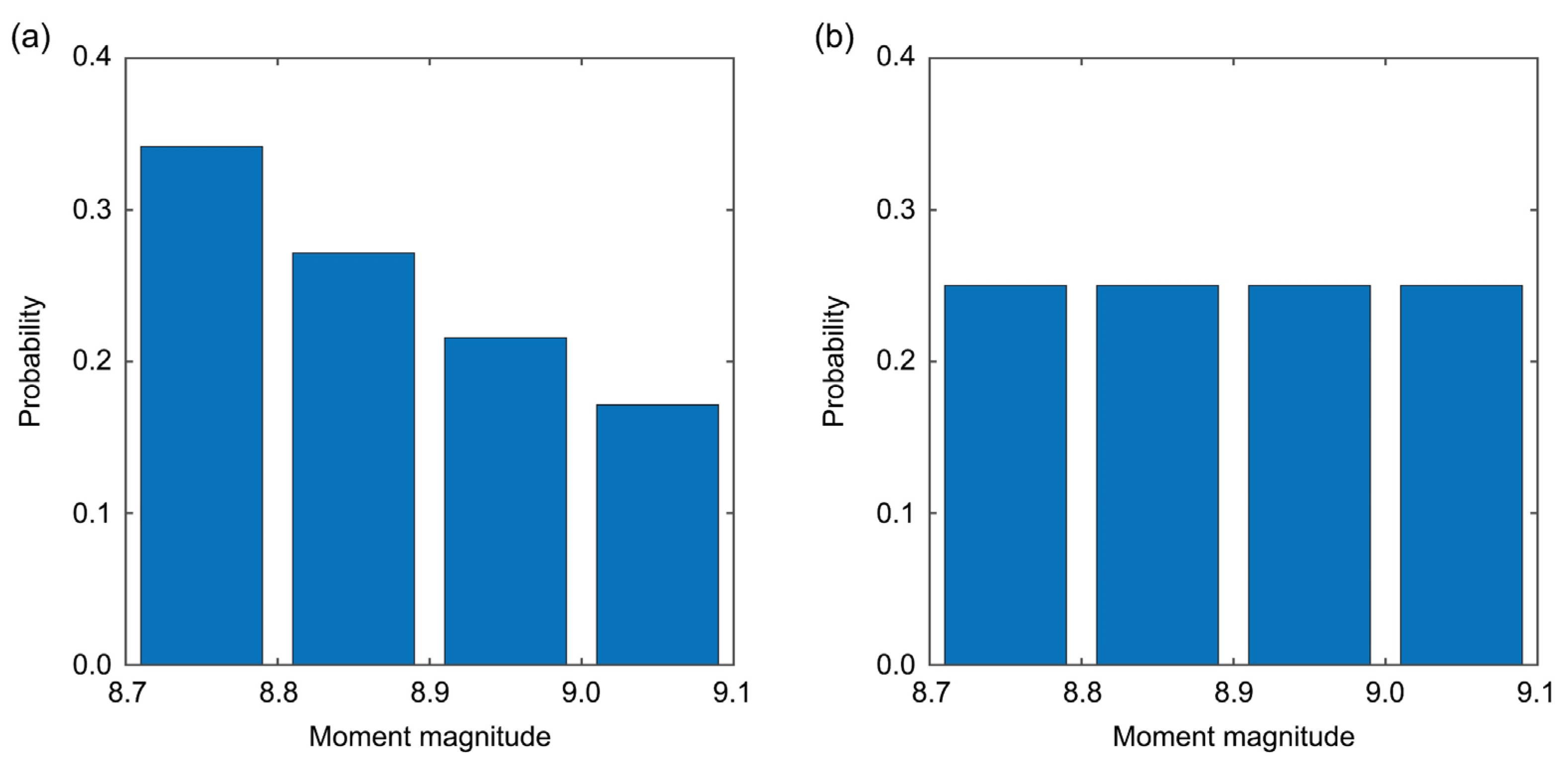
3.2. Earthquake Magnitude Model
3.3. Stochastic Tsunami Simulations
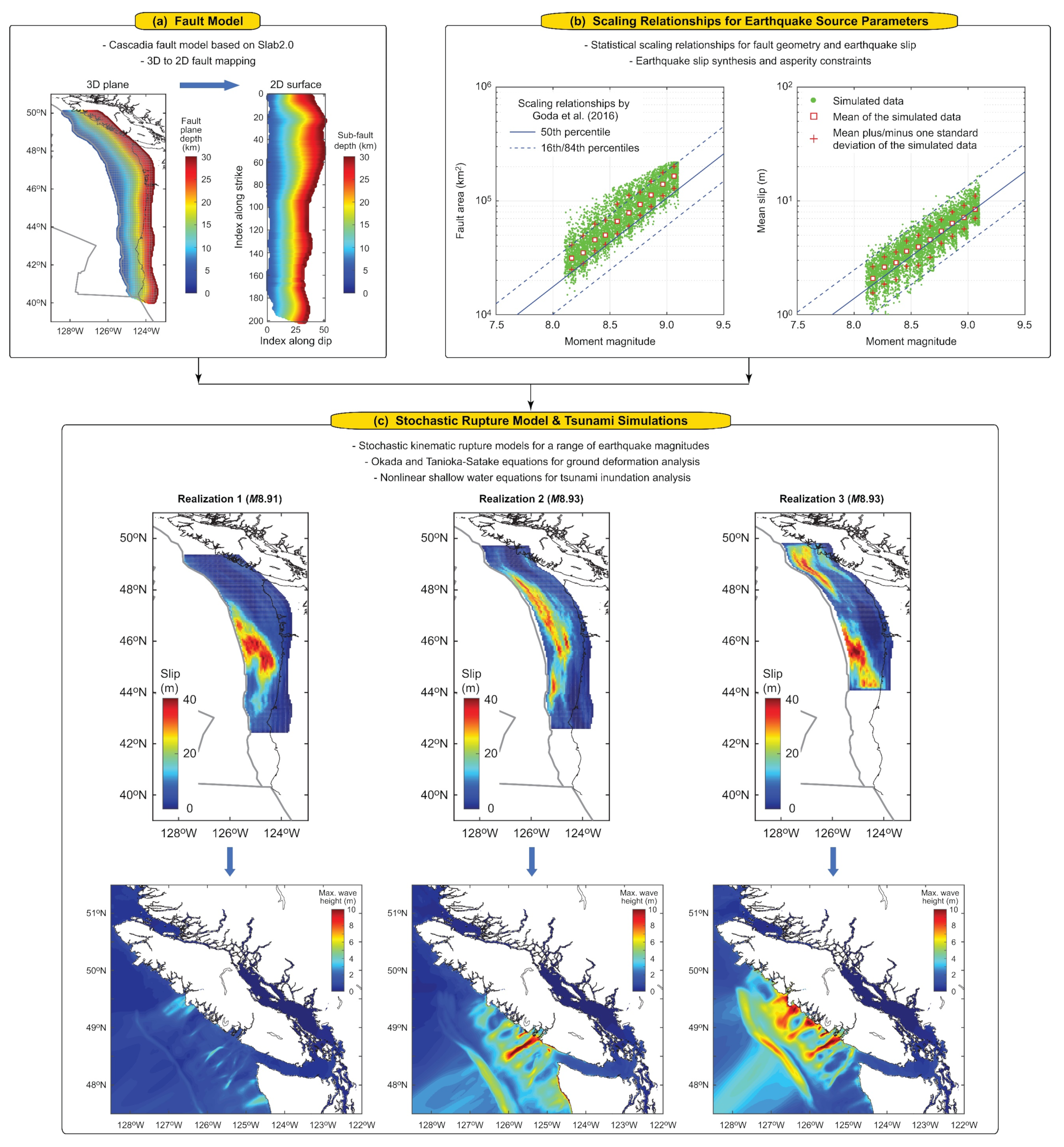
3.3.1. Stochastic Source Models
3.3.2. Tsunami Propagation Simulation
3.4. Computational Procedure
4. Regional Tsunami Hazard Assessment for Vancouver Island Due to the Cascadia Subduction Earthquakes
4.1. Analysis Set-Up
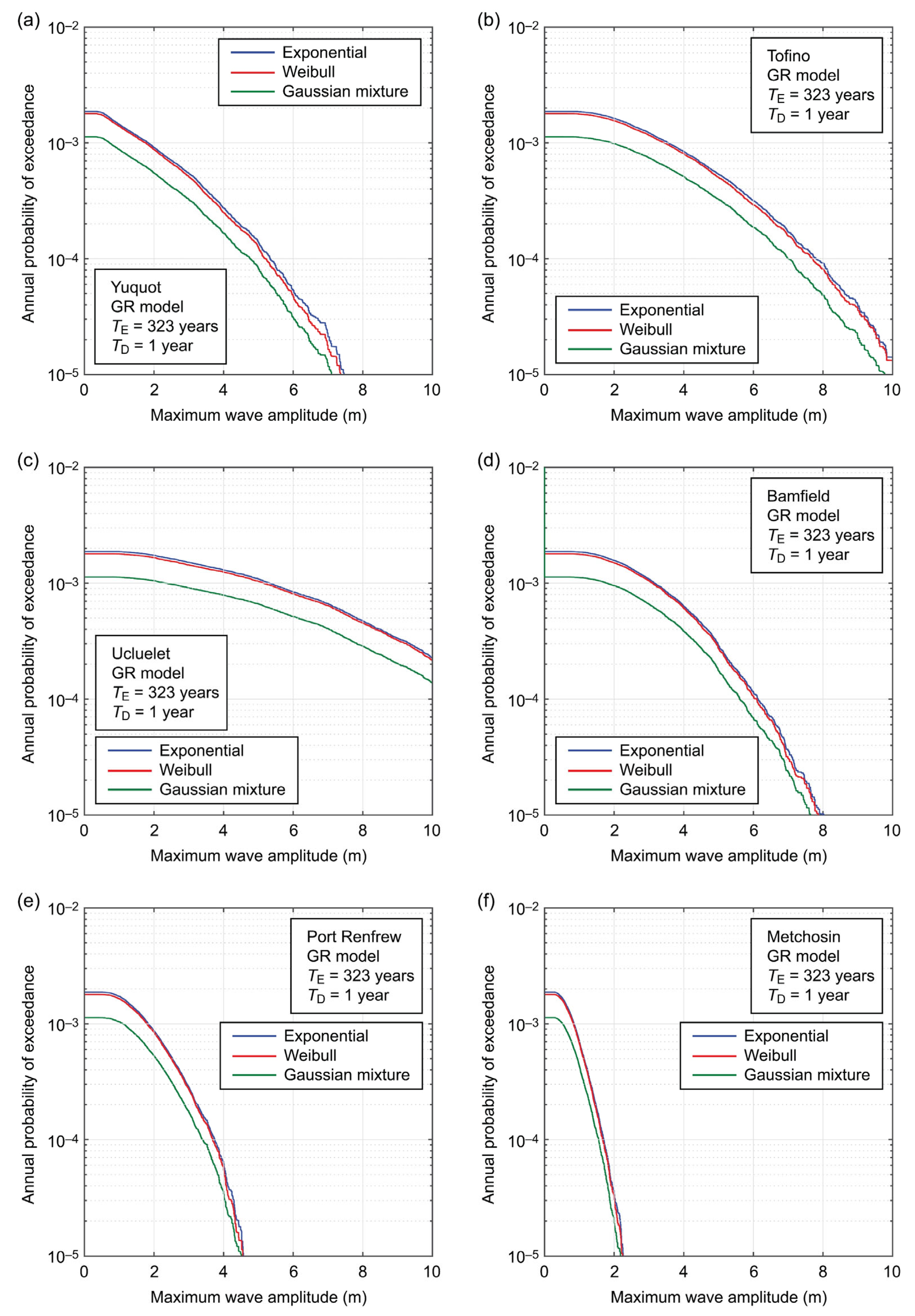
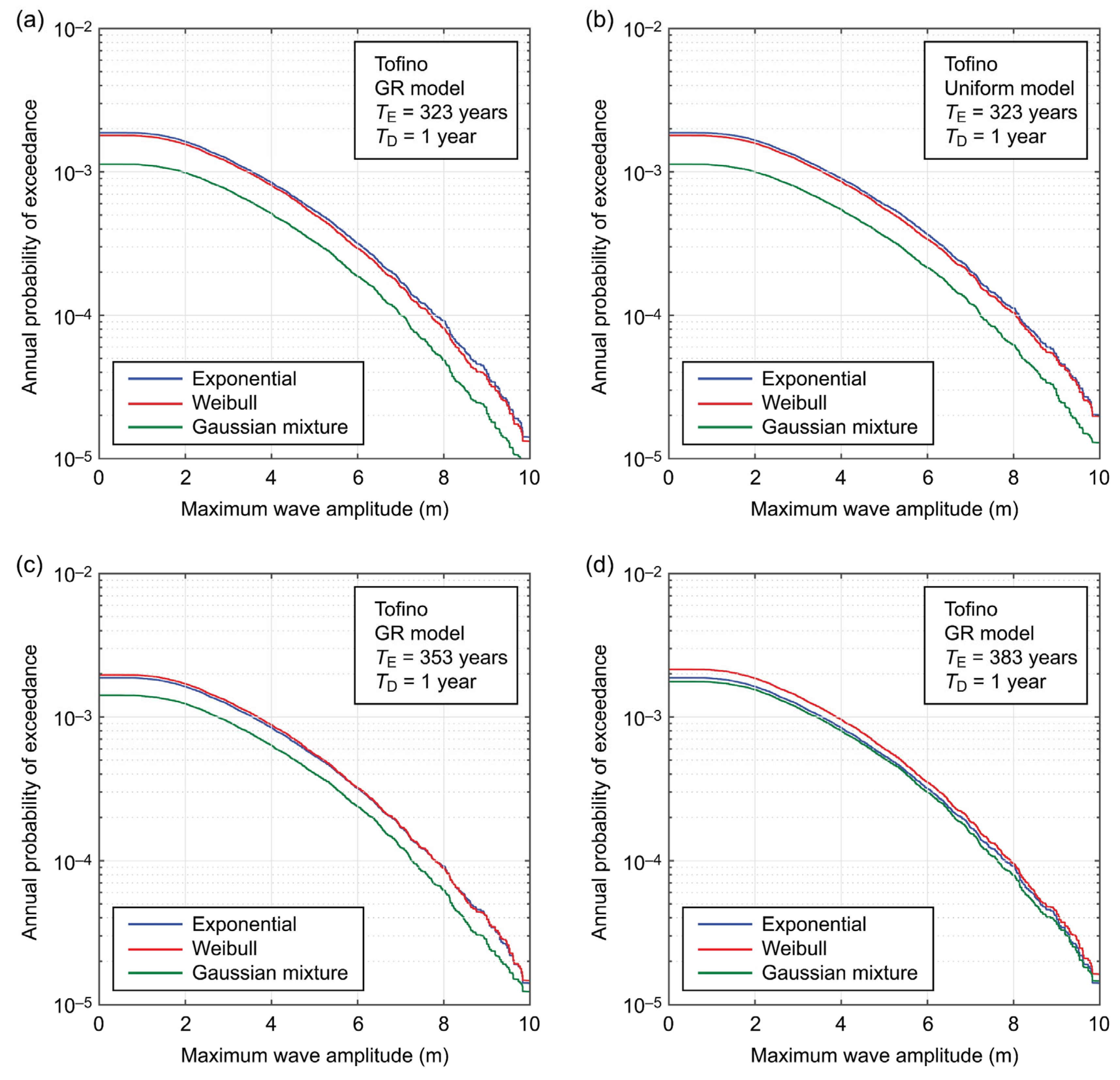
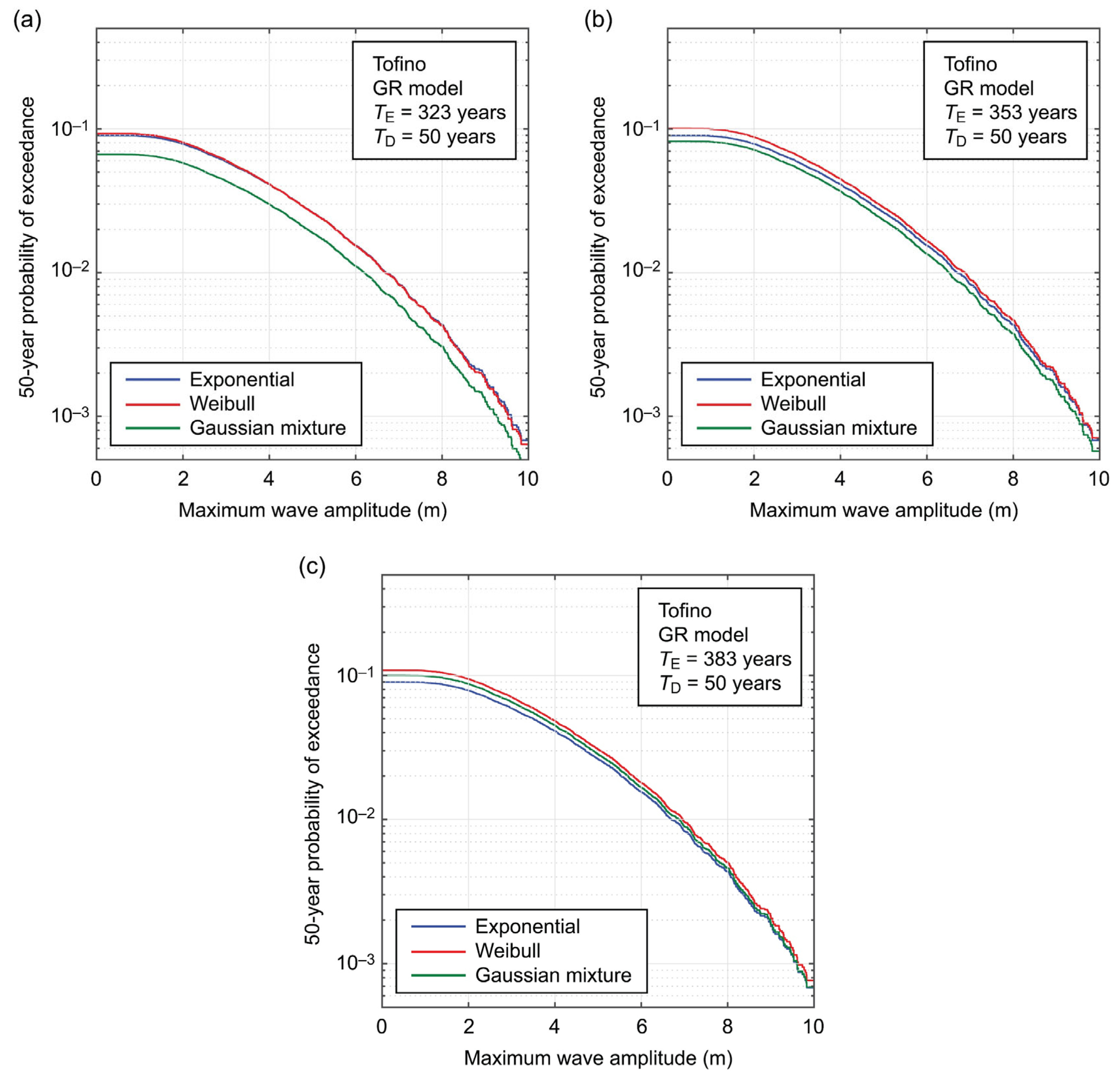
4.2. Site-Specific Tsunami Hazard Curves
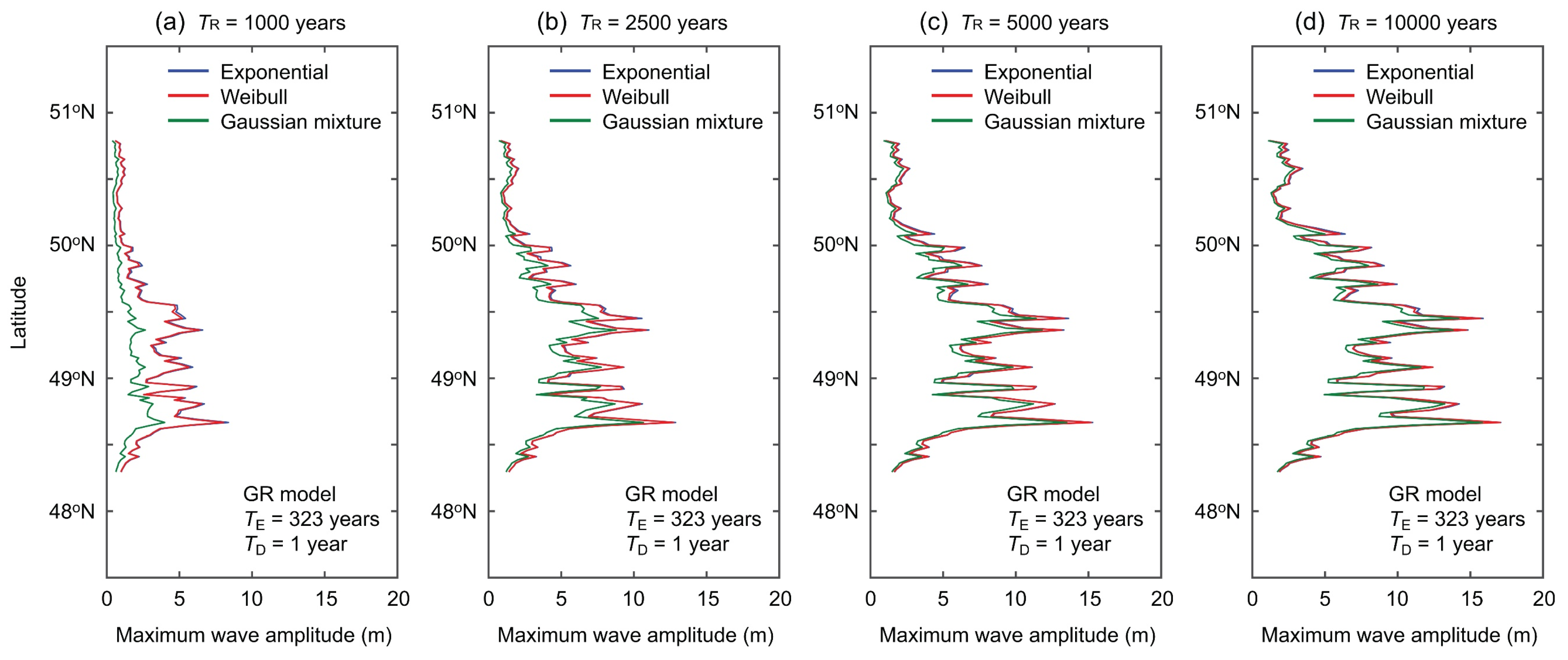
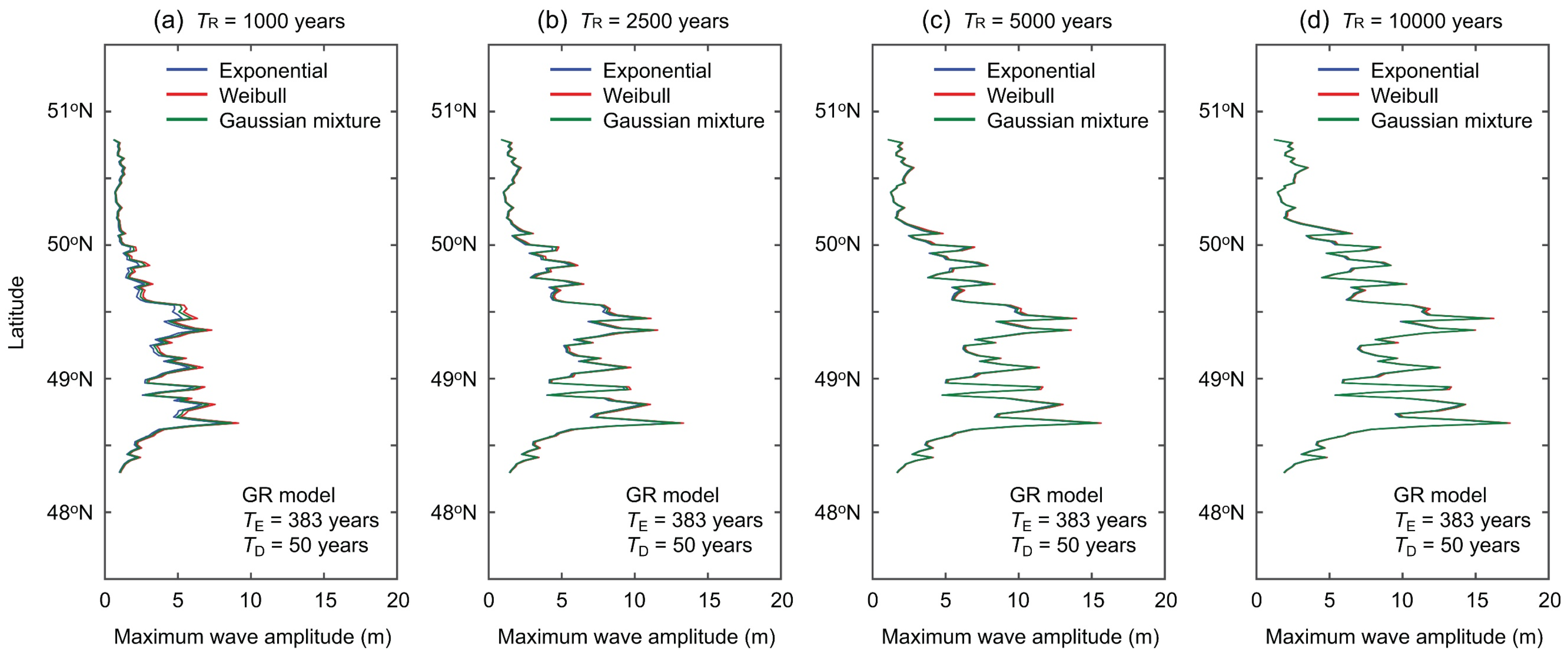
4.3. Regional Uniform Tsunami Hazard Curves
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Walton, M.; Staisch, L.; Dura, T.; Pearl, J.; Sherrod, B.; Gomberg, J.; Engelhart, S.; Tréhu, A.; Watt, J.; Perkins, J.; et al. Toward an integrative geological and geophysical view of Cascadia Subduction Zone earthquakes. Annu. Rev. Earth Planet. Sci. 2021, 49, 367–398. [Google Scholar] [CrossRef]
- Satake, K.; Shimazaki, K.; Tsuji, Y.; Ueda, K. Time and size of a giant earthquake in Cascadia inferred from Japanese tsunami records of January 1700. Nature 1996, 378, 246–249. [Google Scholar] [CrossRef]
- Atwater, B.; Hemphill-Haley, E. Recurrence Intervals for Great Earthquakes of the Past 3500 Years at Northeastern Willapa Bay, Washington; Professional Paper 1576; United States Geological Survey: Denver, CO, USA, 1997. Available online: https://pubs.er.usgs.gov/publication/pp1576 (accessed on 1 April 2023).
- Wang, K.; Wells, R.; Mazzotti, S.; Hyndman, R.D.; Sagiya, T. A revised dislocation model of interseismic deformation of the Cascadia subduction zone. J. Geophys. Res. Solid Earth 2003, 108, B1. [Google Scholar] [CrossRef]
- McCrory, P.A.; Blair, J.L.; Waldhauser, F.; Oppenheimer, D.H. Juan de Fuca slab geometry and its relation to Wadati-Benioff zone seismicity. J. Geophys. Res. Solid Earth 2012, 117, B09306. [Google Scholar] [CrossRef]
- Goldfinger, C.; Nelson, C.H.; Morey, A.E.; Johnson, J.E.; Patton, J.; Karabanov, E.; Gutierrez-Pastor, J.; Eriksson, A.T.; Gracia, E.; Dunhill, G.; et al. Turbidite Event History: Methods and Implications for Holocene Paleoseismicity of the Cascadia Subduction Zone; Professional Paper 1661–F; United States Geological Survey: Reston, VA, USA, 2012. Available online: https://pubs.er.usgs.gov/publication/pp1661F (accessed on 1 April 2023).
- Goda, K.; De Risi, R. Future perspectives of earthquake-tsunami catastrophe modelling: From single-hazards to cascading and compounding multi-hazards. Front. Built Environ. 2023, 8, 1022736. [Google Scholar] [CrossRef]
- Cherniawsky, J.Y.; Titov, V.V.; Wang, K.; Li, J.Y. Numerical simulations of tsunami waves and currents for southern Vancouver Island from a Cascadia megathrust earthquake. Pure Appl. Geophys. 2007, 164, 465–492. [Google Scholar] [CrossRef]
- Clague, J.J.; Munro, A.; Murty, T. Tsunami hazard and risk in Canada. Nat. Hazards 2003, 28, 435–461. [Google Scholar] [CrossRef]
- Stephenson, F.E.; Rabinovich, A.B. Tsunamis on the Pacific coast of Canada recorded in 1994–2007. Pure Appl. Geophys. 2009, 166, 177–210. [Google Scholar] [CrossRef]
- AECOM Modeling of Potential Tsunami Inundation Limits and Run-Up. Report for the Capital Region District. 2013. Available online: https://www.crd.bc.ca/docs/default-source/news-pdf/2013/modelling-of-potential-tsunami-inundation-limits-and-run-up-report-.pdf (accessed on 1 April 2023).
- Gao, D.; Wang, K.; Insua, T.L.; Sypus, M.; Riedel, M.; Sun, T. Defining megathrust tsunami source scenarios for northernmost Cascadia. Nat. Hazards 2018, 94, 445–469. [Google Scholar] [CrossRef]
- Wiebe, D.M.; Cox, D.T. Application of fragility curves to estimate building damage and economic loss at a community scale: A case study of Seaside, Oregon. Nat. Hazards 2014, 71, 2043–2061. [Google Scholar] [CrossRef]
- Takabatake, T.; St-Germain, P.; Nistor, I.; Stolle, J.; Shibayama, T. Numerical modelling of coastal inundation from Cascadia subduction zone tsunamis and implications for coastal communities on Western Vancouver Island, Canada. Nat. Hazards 2019, 98, 267–291. [Google Scholar] [CrossRef]
- Goda, K. Stochastic source modeling and tsunami simulations of Cascadia subduction earthquakes for Canadian Pacific coast. Coast. Eng. J. 2022, 64, 575–596. [Google Scholar] [CrossRef]
- Mori, N.; Goda, K.; Cox, D. Recent progress in probabilistic tsunami hazard analysis (PTHA) for mega thrust subduction earthquakes. In The 2011 Japan Earthquake and Tsunami: Reconstruction and Restoration: Insights and Assessment after 5 Years; Santiago-Fandiño, V., Sato, S., Maki, N., Iuchi, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 469–485. [Google Scholar] [CrossRef]
- Behrens, J.; Løvholt, F.; Jalayer, F.; Lorito, S.; Salgado-Gálvez, M.A.; Sørensen, M.; Abadie, S.; Aguirre-Ayerbe, I.; Aniel-Quiroga, I.; Babeyko, A.; et al. Probabilistic tsunami hazard and risk analysis: A review of research gaps. Front. Earth Sci. 2021, 9, 628772. [Google Scholar] [CrossRef]
- Matthews, M.V.; Ellsworth, W.L.; Reasenberg, P.A. A Brownian model for recurrent earthquakes. Bull. Seismol. Soc. Am. 2002, 92, 2233–2250. [Google Scholar] [CrossRef]
- Abaimov, S.G.; Turcotte, D.L.; Shcherbakov, R.; Rundle, J.B.; Yakovlev, G.; Goltz, C.; Newman, W.I. Earthquakes: Recurrence and interoccurrence times. Pure Appl. Geophys. 2008, 165, 777–795. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Van Dissen, R.J.; Dowrick, D.J. On the handling of uncertainties in estimating the hazard of rupture on a fault segment. J. Geophys. Res. Solid Earth 1994, 99, 13701–13712. [Google Scholar] [CrossRef]
- Kulkarni, R.; Wong, I.; Zachariasen, J.; Goldfinger, C.; Lawrence, M. Statistical analyses of great earthquake recurrence along the Cascadia subduction zone. Bull. Seismol. Soc. Am. 2013, 103, 3205–3221. [Google Scholar] [CrossRef]
- Goda, K. Time-dependent probabilistic tsunami hazard analysis using stochastic source models. Stoch. Environ. Res. Risk Assess. 2019, 33, 341–358. [Google Scholar] [CrossRef]
- DeMets, C.; Gordon, R.G.; Argus, D.F. Geologically current plate motions. Geophys. J. Int. 2010, 181, 1–80. [Google Scholar] [CrossRef]
- Leonard, L.J.; Currie, C.A.; Mazzotti, S.; Hyndman, R.D. Rupture and displacement of past Cascadia Great earthquakes from coastal coseismic subsidence. GSA Bull. 2010, 122, 1951–1968. [Google Scholar] [CrossRef]
- Kagan, Y.; Jackson, D.D. Tohoku earthquake: A surprise? Bull. Seismol. Soc. Am. 2013, 103, 1181–1194. [Google Scholar] [CrossRef]
- Thio, H.K.; Somerville, P.; Ichinose, G. Probabilistic analysis of strong ground motion and tsunami hazards in Southeast Asia. J. Earthq. Tsunami 2007, 1, 119–137. [Google Scholar] [CrossRef]
- Fukutani, Y.; Suppasri, A.; Imamura, F. Stochastic analysis and uncertainty assessment of tsunami wave height using a random source parameter model that targets a Tohoku-type earthquake fault. Stoch. Environ. Res. Risk Assess. 2015, 29, 1763–1779. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Tanioka, Y.; Satake, K. Tsunami generation by horizontal displacement of ocean bottom. Geophys. Res. Lett. 1996, 23, 861–864. [Google Scholar] [CrossRef]
- Goto, C.; Ogawa, Y.; Shuto, N.; Imamura, F. Numerical Method of Tsunami Simulation with the Leap-Frog Scheme; IOC Manual 35; UNESCO: Paris, France, 1997. [Google Scholar]
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; 427p. [Google Scholar]
- Hayes, G.P.; Moore, G.L.; Portner, D.E.; Hearne, M.; Flamme, H.; Furtney, M.; Smoczyk, G.M. Slab2, a comprehensive subduction zone geometry model. Science 2018, 362, 58–61. [Google Scholar] [CrossRef]
- Goda, K.; Yasuda, T.; Mori, N.; Maruyama, T. New scaling relationships of earthquake source parameters for stochastic tsunami simulation. Coast. Eng. J. 2016, 58, 1650010. [Google Scholar] [CrossRef]
- Mai, P.M.; Beroza, G.C. A spatial random field model to characterize complexity in earthquake slip. J. Geophys. Res. Solid Earth 2002, 107, 2308. [Google Scholar] [CrossRef]
- Melgar, D.; Hayes, G.P. Systematic observations of the slip pulse properties of large earthquake ruptures. Geophys. Res. Lett. 2017, 44, 9691–9698. [Google Scholar] [CrossRef]
- Japan Society of Civil Engineers (JSCE). Tsunami Assessment Method for Nuclear Power Plants in Japan. 2002. Available online: https://www.jsce.or.jp/committee/ceofnp/Tsunami/eng/JSCE_Tsunami_060519.pdf (accessed on 1 April 2023).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goda, K. Probabilistic Tsunami Hazard Analysis for Vancouver Island Coast Using Stochastic Rupture Models for the Cascadia Subduction Earthquakes. GeoHazards 2023, 4, 217-238. https://doi.org/10.3390/geohazards4030013
Goda K. Probabilistic Tsunami Hazard Analysis for Vancouver Island Coast Using Stochastic Rupture Models for the Cascadia Subduction Earthquakes. GeoHazards. 2023; 4(3):217-238. https://doi.org/10.3390/geohazards4030013
Chicago/Turabian StyleGoda, Katsuichiro. 2023. "Probabilistic Tsunami Hazard Analysis for Vancouver Island Coast Using Stochastic Rupture Models for the Cascadia Subduction Earthquakes" GeoHazards 4, no. 3: 217-238. https://doi.org/10.3390/geohazards4030013
APA StyleGoda, K. (2023). Probabilistic Tsunami Hazard Analysis for Vancouver Island Coast Using Stochastic Rupture Models for the Cascadia Subduction Earthquakes. GeoHazards, 4(3), 217-238. https://doi.org/10.3390/geohazards4030013





