Abstract
In the mapping and assessment of mountain hazard susceptibility using machine learning models, the selection of model parameters plays a critical role in the accuracy of predicting models. In this study, we present a novel approach for developing a prediction model based on random forest (RF) by incorporating ensembles of hyperparameter optimization. The performance of the RF model is enhanced by employing a Bayesian optimization (Bayes) method and a genetic algorithm (GA) and verified in the Wudu section of the Bailong River basin, China, which is a typical hazard-prone, mountainous area. We identified fourteen influential factors based on field measurements to describe the “avalanche–landslide–debris flow” hazard chains in the study area. We constructed training (80%) and validation (20%) datasets for 378 hazard sites. The performance of the models was assessed using standard statistical metrics, including recall, confusion matrix, accuracy, F1, precision, and area under the operating characteristic curve (AUC), based on a multicollinearity analysis and Relief-F two-step evaluation. The results indicate that all three models, i.e., RF, GA-RF, and Bayes-RF, achieved good performance (AUC: 0.89~0.92). The Bayes-RF model outperformed the other two models (AUC = 0.92). Therefore, this model is highly accurate and robust for mountain hazard susceptibility assessment and is useful for the study area as well as other regions. Additionally, stakeholders can use the susceptibility map produced to guide mountain hazard prevention and control measures in the region.
1. Introduction
The accelerated growth and proliferation of urban areas have led to a marked escalation in the vulnerability of mountainous regions to an array of geological hazards, encompassing landslides, avalanches, and debris flows [1]. Landslides and avalanches provide a solid material supply for debris flows and always develop directly into debris flows in the routing processes (Figure 1). In other words, those cascading processes ultimately convert to fatal disaster chains under certain conditions (i.e., triggered by precipitation, earthquakes, and human activities), which we define herein as mountain hazards accounting for catastrophic loss to the world’s economy and the production and security of people’s lives and property [2,3]. According to China’s 2019 National Geological Disaster Bulletin, among the 6181 geological disasters that have occurred in the country, 95.5 were triggered by natural factors, while only 4.5% were triggered by human factors. The direct economic loss of these disasters is USD 434 million. Mainly due to the unforeseen stochastic characteristics of the conditioning factors as well as the chain and cascading features of the disaster processes, the developing processes of mountain hazards always have significant and complicated multivariate nonlinear characteristics. Therefore, assessing the susceptibility to mountain hazards while scientifically, accurately and rapidly seeking effective solutions for disaster risk mitigation is not only a key academic issue but is also urgently needed to allow the government and stakeholders to make land use and risk management strategy decisions [4,5].
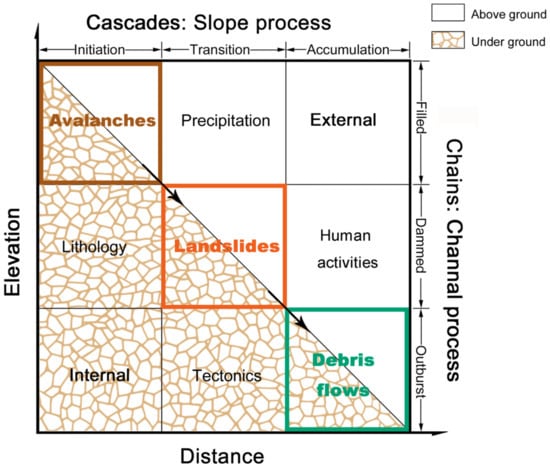
Figure 1.
Schematic diagram of cascading hazard chains.
Conventional geological hazard susceptibility assessments are mainly classified into two distinct groups: qualitative and quantitative. Qualitative evaluations mainly rely on the experience and knowledge of experts in field investigations and the attributes of disaster susceptibility. Judgments are made based on the literature, and the disaster susceptibility is evaluated by the empirical method with strong subjectivity. Quantitative evaluations, in contrast, emphasize the use of mathematical models as the basis and predict the occurrence of disasters based on the calculation results of mathematical models, presenting them in a quantitative form, which is more objective than qualitative evaluation methods.
Over the last three decades, although many models and methodologies for disaster risk evaluation have been applied, few models have proven to be preferable for providing effective evaluation modeling solutions [6,7]. In the past 10 years, with the technological progress of GIS, remote sensing, and GPS, conventional mathematical and statistical models and machine learning models, such as the weight of evidence, frequency ratio [8,9], even and parallel models [10], and other methods for constructing weighted index systems [11], have been widely used for disaster susceptibility assessments. Studies have shown that conventional mathematical and statistical models, such as the informative model, are affected by the size and grading of raster image elements and do not reflect the nonlinear relationship between disasters and their underlying environmental factors, while machine learning models can accurately detect the data structure and efficiently predict the occurrence of disasters. According to the literature, there are many frequently used machine learning models, including logistic regression [12,13], decision trees [14,15], random forests (RFs) [16,17], support vector machines (SVMs) [18,19,20], Bayesian algorithms (Bayes) [21,22], genetic algorithms (GAs) [23], and artificial neural networks (ANNs) [24,25]. However, there is no consensus on which machine learning model is most suitable for susceptibility modeling due to the different predisposing factors of geological hazards, the quality of databases, and the selection of machine learning models. Sameen [26] presented a deep learning-based approach for landslide susceptibility assessment, using 1D-CNN and Bayesian optimization. The method shows high accuracy and outperforms ANN and SVM models in complex situations. Sun [27] used a Bayesian algorithm to establish an optimized logistic regression model and a random forest model for the landslide susceptibility evaluation with hyperparameter optimization and concluded that the AUC value of the test dataset in the optimized model increased by 10% in the random forest model, and the AUC value of the test dataset in the logistic regression model increased by 4%. The random forest model had better stability and predictive power than the two cases that required hyperparameter optimization. All of the related research demonstrated that machine-learning-based models perform well in susceptibility assessments. However, it appears that these models have only been used for single hazard types rather than the cascading hazard chains mentioned above. Consequently, it is necessary for the susceptibility of mountain hazard chains to be studied under changing environmental conditions.
China has experienced some of the most serious geological disasters in the world. As China is located at the intersection of the mid-latitude global natural disaster belt and the Pacific Rim disaster belt in the northern hemisphere and has a mountainous landscape and strong crustal movement, diverse and serious natural disasters occur widely. This has gradually become an obvious obstacle to the construction of ecological security and high-quality economic development in recent years. In this study, based on a sufficient field survey and data collection on the developing features of mountain hazard chains in the Longnan mountainous area in China, while taking the Wudu section of the Bailong River basin (i.e., Wudu District) where mountain hazards are particularly common as an example, 14 influencing factors—elevation, slope, aspect, plane curvature, profile curvature, distance to a road, distance to a river, distance to a fault, roughness, lithology, normalized difference vegetation index (NDVI), terrain moisture index (TWI), ground cover type, and precipitation—were selected for the integrated datasets. Two novel model frameworks were developed with the Bayesian algorithm and genetic algorithm embedded into the RF model, and a performance analysis of the three different machine learning models was then conducted. Finally, mountain hazard susceptibility mapping was conducted, and the model performance and robustness as well as the accuracy were evaluated. The hybrid RF–Bayes machine learning model and the ensemble modeling approaches established are expected to provide effective theoretical guidance for the predictive modeling of vulnerability in other geographically similar areas while putting insight into the application of data-driven models on earth science systems.
2. Study Area and Data
2.1. Study Area
The Wudu District is located in the southeast of Longnan City, Gansu Province within the Yangtze River basin between latitudes 32°47′ and 33°42′ N and longitudes 104°34′ and 105°38′ E. The whole region covers an area of 4683 km2 with a north–south longest span of 100.8 km and an east–west widest span of 76.2 km. It is composed of 36 townships, 643 villages, and a total population of about 546,600. The main stream of the Bailong River flows in from the northwest and out from the southwest, and most of the G212 highway is arranged along the Bailong River (Figure 2). As the study area is in the north subtropical semihumid climate zone, the climate is characterized by frequent rainfall from May to September (accounting for 75–85% of the total annual precipitation of 400–900 mm), which is also the season of the high rates of avalanches, landslides, and debris flow disasters. The high and middle mountain erosion structures in the study area are mainly distributed in the north–central and southern parts and the southern mountainous area of the Bailong River, consisting of metamorphic sandstone, sand slate, and tuff, with an elevation of 1000–3600 m and a relative elevation difference of 1000–1500 m. Landslides and avalanches occur frequently in this area, especially in the steep mountains with deep gullies and valleys. The mountains in the north–central area are mainly composed of phyllite rock, metamorphic sandstone, chalk, and tertiary sandstones dated from the Devonian period, together with sandstone, shale and mudstones from the Cretaceous and Tertiary periods. They are prone to landslides, avalanches, and debris flows due to the weak and loose geotechnical bodies, sparse vegetation, and fragmentation. In recent years, climate-warming-induced extreme rainfall events, population growth, urbanization, and other human activities have led to an increasing number of mountain disasters, having serious impacts on the sustainable development of the mountain ecosystem. The Bailong River basin located in the Longnan mountainous area, to which the Wudu District belongs, is an earthquake-prone area, so its internal geological dynamics can provide data on the occurrence of disasters, while data on precipitation, weathering, and human engineering activities provide external geological dynamics. Thus, in this work, based on the historical data of 378 typical mountain hazards in the study area, we conducted a prediction analysis of a mountain hazard susceptibility assessment based on GIS and machine learning models.
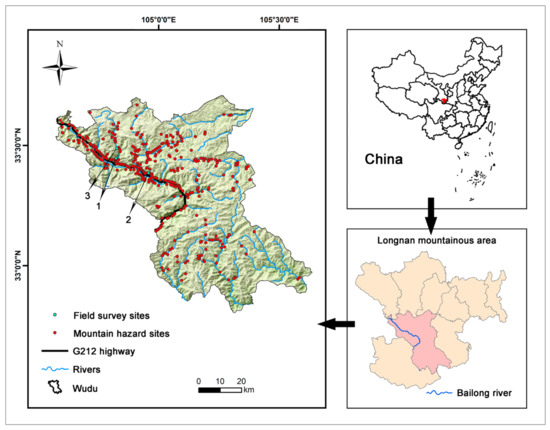
Figure 2.
Geographical location and distribution of historical mountain hazard sites (i.e., hazard inventory) in the study area.
2.2. Data Preparation
2.2.1. Mountain Hazard Inventory
A hazard inventory records the location and time of occurrence of a geological hazard body as well as the hazard types that leave identifiable traces in an area [28]. The data on the mountain hazard sites covered in this paper were obtained from historical geohazard literature published up to 2015 [29,30], field surveys, and the government’s open resource website (www.ngac.cn, accessed on 1 February 2023). A total of 378 geohazards of various types were recorded, including 110 landslides, 260 debris flows, and 8 avalanches. Field observations indicated that landslides and avalanches are generally associated with cascading processes in the study area, and avalanches and landslides also transform gradually into debris flows in the routing processes or are entrained by heavy-rainfall-induced flooding after channel fill and ultimately develop into debris flows and even disasters. During the formation of these hazard chains, landslides often act as a link between the other two processes (Figure 1). According to the implementation rules of the Basic Requirements for Geological Hazard Investigation and Zoning in Counties (Cities), huge landslides in the Wudu District account for 27% of all landslides, large landslides account for 47%, medium landslides account for 6%, and small landslides account for 20%, with the huge and large landslides being dominant and the medium and small landslides being sporadically distributed. According to their formation eras, the old landslides (early Holocene) and the ancient landslides (early Late Pleistocene) account for 69% of all landslides, and the new landslides (or modern landslides) account for 31% of all landslides [31]. In this study, the 378 hazard sites were used as positive samples (PS), and 378 non-geological hazard sites were randomly generated as negative samples (NSs) outside the 500 m buffer zone of the hazard sites. Ultimately, 605 sample points (80%) were used as the training dataset, and 151 sample points (20%) were used as the validation dataset. The collected historical hazard data revealed that the geological hazards showed the characteristics of being large in number and having a high distribution density, with landslides occurring in all 43 townships in the region, making it the center of hazards in the Longnan mountain area [32]. In addition, statistics along the G212 highway showed an average of one landslide every 2 km on the roadside, with one landslide developing every 1 km in the serious sections.
In order to ensure the accuracy of the statistics of historical disaster sites where possible and to provide accurate and reliable data for the subsequent attributes analysis, impact factor selection, dataset classification testing, model validation, algorithm optimization, and even the disaster susceptibility assessment based on the hazard inventory, we carried out field surveys on three of the representative historical disaster sites that have been active for long periods of time. This was conducted through funding for “Research on the prevention and control techniques of landslides and debris flows from Longnan section of the G212 highway (Lanzhou–Chongqing)” (supported by the western transportation construction science and technology project of Ministry of Transport, China).
As shown in Table 1, the Xiaoshui gully is representative of typical gully debris flows where flash floods in the gully channel entrain the accumulated avalanches. The new tectonic movement in this region is characterized by differential vertical movement with fragmented and easily movable rocks and crevice water development as well as intense human engineering activities. Under the direct influence of the Wenchuan earthquake in May 2008, an avalanche occurred. According to onsite measurements, the avalanche volume was 680,000 m3, resulting in an economic loss of RMB 2 million and representing the largest typical avalanche event in recent years. The Dujia gully is a typical historical landslide hazard site, and the landslide body is located on the left bank of the Bailong River, with the free face positioned directly toward the Bailong River. A field investigation in August 2015 demonstrated that the exposed bedrock of the landslide body is strongly and fully weathered with severe extrusion and deformation due to long-term tectonic movement. The loose cover of the landslide is mainly composed of loess-like clay and fully weathered phyllite rock rubble soil with a soil stone ratio of 3:7. The surface of the landslide body is seriously disintegrated and the foot of the slope is scoured, forming a 20–40 m high scrape with an obvious shear outlet from a large landslide. The Taoshu gully is a typical, valley-type, dilute debris flow channel with steep terrain on both sides and an average longitudinal slope of 21.3%. It is a mid-mountain area characterized by a large topographic relief with a relative elevation difference of 673 m, providing sufficient potential energy for the initiation of debris flows. The intense rainfall events in this region are mainly characterized by high intensity, short-duration storms, which can provide sufficient hydrodynamic conditions for the formation of debris flows. Additionally, the wide distribution of loose solid materials in the channel provides an abundant natural supply for the formation of debris flows. Following a landslide disaster in August 2017, a serious debris flow disaster occurred in August 2020. The site investigation revealed that the event led to serious channel damming and the destruction and avalanches of part of the drainage guide dike, posing greater threats to the lives and property of 57 households and 236 people located downstream.

Table 1.
Attributes of the surveyed hazard sites in the Wudu section of the Bailong River basin.
The fieldwork not only further demonstrates the chain and cascading nature of mountain hazards in the study area but also indicates some of the main influencing factors.
2.2.2. Mountain Hazard Influencing Factors
As hazard susceptibility assessment involves a wide range of factors, the reliability of field data collection is crucial. To accurately evaluate the background of the study area, a systematic and scientific index system needs to be established through an analysis of the historical occurrence of geological hazards as well as the regional natural conditions, geo-environmental conditions, and human activities [33,34]. Therefore, in this work, 14 influencing factors, including elevation, slope, aspect, plan curvature, profile curvature, distance to a road, distance to a river, distance to a fault, roughness, lithology, NDVI, TWI, ground cover, and precipitation, were selected to study three perspectives (i.e., topography and tectonics, external dynamic geological environment, and engineering geological rock group) in a susceptibility assessment. The analysis of Ning [35] on the conditioning factors of debris flows and the analysis of Qi [30] on the integration of indicators for geological hazard assessments in the study area further confirm that the above-mentioned influencing factors significantly influence the development of landslides, debris flows, and avalanches in the Wudu district.
In accordance with the results of the field survey and the analysis of the underlying geological conditions in the study area, seven factors were identified in terms of topography and tectonics (Figure 3a–g): elevation, slope, aspect, plan curvature, profile curvature, distance to a fault, and roughness. Firstly, the topographic factors of elevation, slope, and aspect influence the balance of gravitational forces and the surface movement of soil and rock materials. Specifically, the steeper the slope is, the greater the gravitational force is, which consequently increases the potential for landslides. The Wudu mountainous area, which is controlled by regional tectonics, extends in the east–west direction, with the highest elevation being 3600 m in the northwest and the lowest being 660 m in the southeast. The overall topography is characterized by strong gully-dissected, steep mountains, a large topographic relief, and steep slopes. In this study, a 30 m × 30 m digital elevation model (DEM) of the study area was derived from ALOS multispectral remote sensing image data (www.usgs.gov, accessed on 1 February 2023). An analysis of the dataset using ArcGIS 10.8 software revealed that the majority of mountain hazards occurred between 918 and 1214 m with a distribution rate of 34% (Figure 3a). Most hazards are situated within the slope range of 20°–30° with nearly no occurrence recorded on slopes exceeding 50° (Figure 3b). Although the study area encompasses various hills with different slope aspects, the distribution of hazards is generally even and demonstrates no significant differences (Figure 3c). Few hazards occur in flat areas. The curvature factors of the plan and profile pertain to the topography of the land surface, where concave forms are more susceptible to the accumulation of water, rocks, and debris and are thus more prone to landslides. The plan curvature is the curvature of a curve projected onto a plane, typically the horizontal plane. It is defined as the reciprocal of the radius of the circle that best fits the curve on the plane. Given the first and second partial derivatives of a surface, the formula for plan curvature is
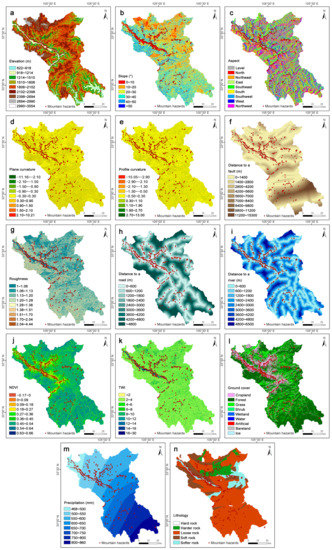
Figure 3.
Factors influencing the mountain hazard susceptibility: (a) elevation, (b) slope, (c) aspect, (d) plan curvature, (e) profile curvature, (f) distance to a fault, (g) roughness, (h) distance to a road, (i) distance to a river, (j) NDVI, (k) TWI, (l) ground cover, (m) precipitation, (n) lithology.
The profile curvature is the curvature of the curve that is normal to the contour lines of the surface. It is an important factor when modeling the flow of water over a surface. Given the slope (S) and the second partial derivatives of the surface, the formula for the profile curvature can be given as
In terms of the plan curvature and profile curvature, the majority of the hazard sites are located in areas where the curvature of the ground contours is relatively gentle (Figure 3d,e).
The distance between the hazard and fault is another critical influencing factor for mountain hazards, where the shorter the distance between the hazard and the fault is, the higher the probability of triggering dynamic events, such as earthquakes or fault rupture, resulting in debris flows or landslides. The geotechnical fragmentation, complex structural deformation, and poor stability in the vicinity of the fault and fracture zones are obvious, and the number of hazard sites decreases as the distance from the fracture increases (Figure 3f).
Finally, roughness, based on the terrain surface complexity, influences the transportation and accumulation of debris, thereby increasing the potential for debris flows. The units of measurement for roughness are typically meters (m), representing the degree of deviation from a perfectly flat surface. Roughness, often denoted as Ra, is a measure of the texture of a surface. It is quantified by the vertical deviations of a real surface from its ideal form. One way to calculate roughness is by using the arithmetic average (mean) of the absolute values of the surface height deviations from the mean line within a sampling length. The formula for roughness (Ra) can be expressed as follows:
Previous results indicated that landslides, avalanches, and debris flows mainly develop in locations with high levels of slope roughness, as such conditions are not conducive to the diversion of precipitation, thus accelerating the alteration of the physical and mechanical characteristics of the rock by groundwater which, in turn, leads to landslides, debris flows, and avalanches [36]. On the other hand, the occurrence of mountain hazards in the study area decreases significantly as the slope roughness increases (Figure 3g, also see Appendix A for detail).
The development of landslides, avalanches, and debris flows is controlled by the internal dynamics of the environment and is also influenced by the external dynamics. External dynamic factors are often the direct cause of the above-mentioned mountain hazards. In this study, six factors were selected as the external dynamic geoenvironmental factors (Figure 3h–m): distance to road, distance to river, NDVI, TWI, ground cover, and precipitation. Since the Holocene, human activities have gradually become the main trigger for geological hazards. The distance to a road and river factors affect the distribution of water and the stability of slopes. Roads and rivers can trigger landslides and other hazards through the excavation or diversion of water. Their proximity can also impact debris flow transportation and accumulation, increasing the likelihood of a disaster. We applied ArcGIS 10.8 to extract the Euclidean distances of roads and rivers based on the road and river data already collected in the study area (www.tianditu.gov.cn, accessed on 1 February 2023) and concluded that 62.43% of the hazards occurred within 600 m of the roads, and 46.3% of the hazards occurred within 600 m of the rivers (Figure 3h,i).
The Normalized Difference Vegetation Index (NDVI) is a measure of the vegetation coverage and productivity. It plays a crucial role in terrain stability, erosion control, and regulation of the water cycle. Vegetation prevents erosion, increases soil cohesion, and regulates infiltration rates. The higher the NDVI, the greater the vegetation coverage, and it lowers the likelihood of the occurrence of landslides and other hazards. The vegetation cover within the study area was calculated according to the NDVI proposed by Xu [37]. If there is good vegetation cover on the ground, the rate of erosion is very slow due to the shading of plants and the consolidation of roots, and most geological hazards occur in areas with sparse vegetation cover (Figure 3j). The Topographical Wetness Index (TWI) [38] provides comprehensive information on the hydrological characteristics of the terrain, which are essential for the management of mountainous areas. Surface runoff and soil moisture are key factors that influence the slope stability and the occurrence of landslides. The equations provided by Obled [39] and Tarboton [40] were used to calculate the TWI and to assess the development of geohazards in the context of the spatial distribution characteristics of soil moisture (Figure 3k). The ground cover fraction denotes the surface area covered by different types of ground cover, such as rock, soil, vegetation, and water. The characterized slope stability, erosion control, rainfall infiltration, and runoff gathering capacity are all relevant factors for mountain hazard assessments. Ground cover data provided by Globeland 30 (www.globallandcover.com, accessed on 1 February 2023) were used to count nine different land use types in the study area, with 15.24% of the land being used for human activities and representing 46.83% of all hazard occurrences. Compared to the 84.06% vegetation cover and the corresponding 49.74% hazard occurrence, it is clear that human activities have a significant impact on hazard occurrence (Figure 3l). Finally, precipitation plays an essential role in hazardous mountain processes. The precipitation intensity and duration can influence the soil saturation, pore pressure, and slope stability, increasing the potential for landslides and other hazards to occur. We produced rainfall contour maps for the study area based on the annual average rainfall data recorded at 19 stations at the National Meteorological Science Data in China (data.cma.cn, accessed on 1 February 2023) (Figure 3m).
Lithology and engineering geological rock formations are closely linked to the development and formation of mountain hazards, and lithology influences and even determines the characteristics of mountain hazards. Lithology (Figure 3n) was selected to assess the geology of the region based on statistical data and hazard susceptibility assessments conducted by Ning [41]. In order to rapidly and accurately recognize the lithological factor grouping on the basis of the 1:500,000 geological maps in the study area and with reference to the Engineering Rock Classification Standard (2014.GB/T 50218-2014.), the Code for the Design of Building Foundations (2011.GB 50007-2011.), and the Code for Geotechnical Investigation (2002.GB 50021-2001.), the rock groups in the study area were divided into four categories according to their levels of softness and hardness: hard rocks, harder rocks, softer rocks, soft rocks, and loose rocks.
A dataset was created for the study area of Wudou District, Longnan City, China, and each subset of influencing factors was treated as a point attribute in the model. We used 5,164,435 grids, 30 m × 30 m in size, which were selected based on data resolution, computational requirements, analysis precision, and consistency with prior research. The grid size is supported by previous studies in hazard-prone areas [42] and aligns with the ALOS DEM dataset resolution. This choice balances computational efficiency and processing time, making it suitable for our study. The grids were raster aligned using ‘Alignment Points’ in the projection tool. The raster data were processed to obtain the attributes of all points from a raster map of the study area, and all data were normalized before the model was implemented. Finally, the dataset was analyzed and evaluated using ArcGIS 10.8 software (see Table A1 for the frequency ratio of the influencing factors).
3. Methodology
In this study, we used a hyperparametric optimized machine learning model with 5 main steps for mountain hazard susceptibility mapping (Figure 4). The steps were as follows: (1) generation of a list of mountain hazards and mountain hazard influencing factors; (2) influencing factor evaluation and dataset classification; (3) benchmark RF model construction; (4) optimization of the RF model using Bayesian and genetic algorithms and susceptibility mapping; and (5) a mountain hazard susceptibility assessment involving model validation and comparison.
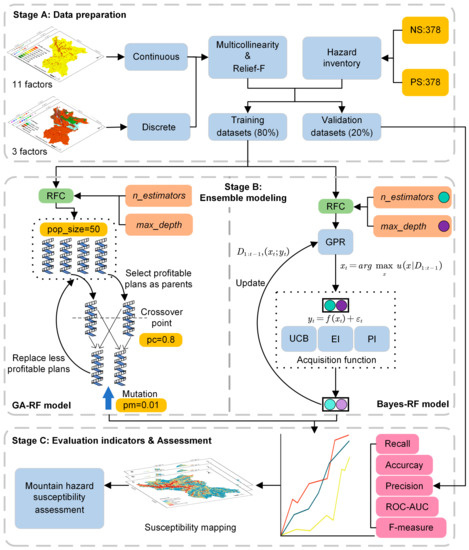
Figure 4.
Flowchart of the framework used for ensemble modeling (RFC: Random Forest Classifier, GPR: Gaussian Process Regression).
3.1. Evaluation of Influencing Factors
The occurrence of disasters is controlled by a variety of influencing factors, and there are differences in the impacts of individual factors on the occurrence of disasters [43]. Therefore, it is necessary to study the importance and mechanism of each influencing factor to guide the stability and accuracy of prediction models and aid in disaster prediction and prevention. As mentioned above, although we initially selected 14 possible gestation factors related to mountain hazards in the study area through literature research and field surveys, it was still necessary to identify the sequence of the most significant influencing factors for modeling purposes. Given the complex nonlinear characteristics of the development of hazard chains, such as avalanches, landslides, and debris flows, we used a multicollinearity analysis and relief-F two-step analysis to quantitatively assess and measure the predictive ability of the 14 influencing factors in order to establish a targeted and highly accurate evaluation and prediction model to assess the vulnerability of chain and cascading mountain hazards in the study area.
3.1.1. Multicollinearity Analysis
When performing a linear regression model analysis, the independent variables are prone to correlation with each other, and when serious co-linearity problems occur, unstable model prediction results can be obtained. In this case, it is necessary to eliminate the independent variables with significant co-linearity to eliminate the effects of multiple co-linearity. [44]. The Pearson correlation coefficient method [45] is usually used to quantify multicollinearity. The values produced range from −1 to 1, where −1 indicates that the two variables are perfectly negatively correlated, 1 indicates that the two variables are perfectly positively correlated, and 0 indicates that they are not correlated. In this study, Pearson’s correlation coefficient was used to detect the correlations between two factors influencing mountain hazards. A value greater than 0.5 indicates a high correlation. Meanwhile, the discriminant variance inflation factor (VIF) and tolerance level (TOL) were introduced in this study. It is generally considered that when VIF > 10, TOL < 0.1, a serious covariance problem occurs in the model, and the two indicators have logical correspondence. Either one of them can be chosen. In this study, multiple co-integration tests were conducted for the 14 disaster impact factors using SPSS 26 software.
3.1.2. Relief-F
Relief-F is an effective quantitative analysis method that is used to evaluate the importance of factors [46]. It measures the importance of each feature by the correlation statistic and assigns different weight values. Negative importance is eliminated as a redundancy factor. In this study, by using Relief-F on the MATLAB 2016b platform, we randomly took one sample R from the training sample set at a time, found k nearest-neighbor samples of R from the R sample set, and then found k nearest-neighbor samples from each sample set of different classes of R. Then, we updated the weight of each feature as shown in (4):
where diff(A, R1, R2) denotes the difference between samples R1 and R2 on feature A, and MJ(C) denotes the j nearest neighbor sample in C class(R). As shown in (5),
3.2. Random Forest (RF)
RF is a “Leatherman” in the field of machine learning, not only having the best accuracy of any current algorithm but also being able to run large datasets efficiently. RF is an integration of the decision tree, which extracts multiple training sets from the original sample set by the Bagging method and performs decision tree modeling for each training set separately. During the growth of the decision tree, random sampling of the feature set is performed every time the internal nodes split, and the optimal selection is made from the extracted feature sets. Finally, the final result is obtained by averaging or voting using the results of all decision tree calculations [47]. The method of classification prediction using the RF model is as follows [48,49,50,51,52,53].
- A training set is formed by sampling N times from N original samples in the form of sample bagging. The unsampled samples are called Out-Of-Bag (OOB) data and can be used to evaluate the model’s performance; this is known as OOB estimation.
- For each training set, a decision tree is generated. Assuming that the sample has M features and the number of features F ≤ M is specified, F features are randomly selected from the M features as the split feature set at each internal node of the decision tree, and the node is split by the best split in the split feature set. The value of F is generally kept constant and is usually taken as F = M/3 for the regression and as shown in (6) for the classification.
- 3.
- Decision trees are generated using classification and regression tree algorithms with each tree growing freely without pruning.
- 4.
- The above steps are repeated k times to obtain a total of k training sets, forming k decision trees, where each tree corresponding to the unselected sample set forms a total of k out-of-bag data points.
- 5.
- The generated k decision trees form an RF, and a regression analysis or classification prediction is performed on the new data. When used for regression, the final result is the mean of the computed results of each tree. When used for classification, the final result is generated by voting on the results of each tree.
In this study, Python 3.5 was used to build an RF model using the Scikit-learn module. The basic parameters of the running device used were as follows: 11th Gen IntelI CoITM) i7-11800H @ 2.30 GHz, and a running memory of 16 GB.
3.3. Optimization Algorithm
3.3.1. Bayesian Hyperparameter Optimization
In machine learning, hyperparameters are parameters that need to be set in advance during the learning process of a machine learning model, and algorithms are rarely hyperparameter free. For all algorithms, some hyperparameters significantly impact the predictive power, and some hyperparameters significantly impact the predictive accuracy or the accuracy of the model. Therefore, the rational adjustment of these hyperparameters, i.e., hyperparameter optimization, is particularly important. However, hyperparameter optimization is a combinatorial optimization problem. It is not optimized by gradient descent like normal parameters. The computation used to evaluate a set of hyperparameter configurations is very difficult, because adjusting individual hyperparameters requires retraining to evaluate their effects.
Nowadays, more and more hyperparameter optimization processes are performed using automated methods that aim to find the best hyperparameters in shorter time periods using a policy-based, informed search. Moreover, no initial setup or additional manual operations are required other than the manual operations conducted during the process. Bayesian optimization is the primary choice for optimizing the objective function [54,55,56]. For most optimization algorithms, it is necessary to assume that the objective function is known in order to solve the derivative, and the function must be convex, but for some problems, the objective function position is a nonconvex function in the process of parameter tuning, which leads to a huge amount of computation and an insignificant solution effect. To solve such problems, Bayesian optimization algorithms were developed. In such algorithms, the posterior distribution of the unknown objective function is approximated by using prior knowledge, and then the next combination of hyperparameters for sampling is selected according to the optimal partial objective function. To get as close as possible to the true objective function, the Bayesian algorithm uses an agent model. Moreover, the Bayesian optimization algorithm is now widely used in hyperparameter tuning for machine learning.
3.3.2. Genetic Algorithm (GA) Hyperparameter Optimization
As a classical algorithm, the GA uses a stochastic global search algorithm to simulate the physical process of natural biological evolution. The basic principle lies in simulating a population of potential solutions, whereby the initial individuals in this population are randomly generated. Then, the GA algorithm performs selection, crossover, and mutation operations on each individual to search for the optimal solution, corresponding to the principles of survival of the fittest, the recombination of genetic material, and random mutations observed in nature, respectively. By iterating these three operations, the GA can continuously regenerate solutions that approximate the true value until a certain number of new generations of individuals are generated, and then, the objective function is recalculated for all individuals of the new generation. The best performing individuals in the new generation are retained in the next generation according to their fitness levels. Thus, as each generation reproduces, the fitness function of the entire population decreases. The process is repeated until the results can no longer be improved.
In this study, the idea of genetic function was used to optimize the parameters, and the process of parameter optimization can be defined as a multiobjective optimization problem, i.e., using (7):
where V − min denotes vector minimization, i.e., each subobjective function in the vector objective f(x) is minimized as much as possible.
The parameter optimization of the genetic function needs firstly to be encoded, and the encoding is carried out in binary form. The length of the chromosome is selected according to the types of model parameters, and the number of decimal numbers corresponding to binary is calculated (Mo et al. 2001) using (8):
The initial population is thus generated, and its fitness level is calculated, i.e., the value of the evaluation criterion for measuring cross-validation. The population enters the reproduction iteration loop, and reproduction replication is performed according to different cross-validation and variation ratios. If the set number of iterations is reached, the reproduction will be terminated; otherwise, the reproduction will be continued, and the optimal solution will be found in the final population.
3.4. Model Validation and Comparison
3.4.1. Model Performance Evaluation Metrics
In this paper, five commonly used statistical metrics were used to validate the performance of the prediction model: Accuracy (ACC), Recall, Precision, F1, and ROC-AUC. The first four are statistically-based metrics. ACC is the ratio of the number of samples correctly classified by the model to the total number of samples. Recall is the ratio of the number of positive samples classified by the model into positive classes to the number correctly classified by the model. Precision is the ratio of the number of positive samples predicted as positive classes by the classification model to the sum of samples predicted as positive classes, and F1 is a composite measure of the recall and precision of the model. ROC and AUC are metrics used for evaluating classifiers. ROC is the abbreviation for the subject operating characteristic curve, which is also known as the perceptivity curve. The points on the curve respond in the same way, and they are all responses to the same signal stimulus. This differs from results obtained with several judgment criteria. AUC is the abbreviation for the area under the ROC curve. Usually, the larger the AUC is, the higher the diagnostic accuracy is. These parameters are commonly used and representative indicators.
3.4.2. Mountain Hazard Susceptibility Mapping
The spatial prediction of geological hazards is a binary classification process [57]. Equal numbers of positive samples (hazard points) and negative samples (nonhazard points) need to be prepared before model training [58]. In this study, the negative sample data were randomly generated by ArcGIS 10.8 software outside the 500 m range of positive samples, after which the positive and negative data were divided into training and test sets in a ratio of 8:2. The established hazard evaluation model was used to calculate a unique probability value for each raster cell in the whole study area, which was expressed as the hazard susceptibility index of the area. The geometric interval classification method was used to classify the hazard susceptibility index into five susceptibility classes: very low, low, medium, high, and very high. This is an effective classification method for classifying hazard susceptibility values [59,60].
4. Results
4.1. Importance of Influencing Factors
According to the results of the multicollinearity analysis of the influencing factors (Table 2), the maximum VIF and the minimum TOL values were 5.914 and 0.169, respectively. Therefore, there was no multicollinearity in the factors used in this study.

Table 2.
Multicollinearity diagnosis statistics for the 14 conditioning factors.
The Pearson correlation coefficient method was used to correlate the 14 factors in the study area according to the two-step analysis of the multiple covariance and Relief-F significance analysis, and the results are shown in Figure 5.
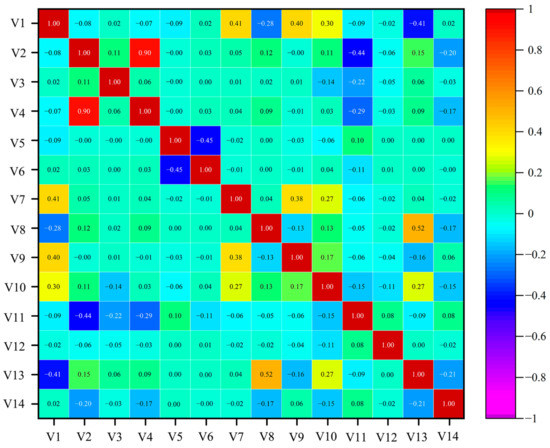
Figure 5.
Results of Pearson correlation coefficient analysis (V1 elevation; V2 slope; V3 aspect; V4 roughness; V5 profile curvature; V6 plan curvature; V7 distance to a road; V8 distance to a fault; V9 distance to a river; V10 NDVI; V11 TWI; V12 ground cover; V13 precipitation; V14 lithology).
As shown in Figure 5, the correlation coefficient between the slope and roughness is 0.90. As this is greater than 0.50, it indicates a high correlation. Therefore, in this study, the roughness factor was excluded from the mountain disaster susceptibility modeling process, and the remaining 13 factors were used for the hazard susceptibility assessment.
Based on the Relief-F model, the contributions of the 13 influencing factors to the occurrence of disasters in the study area were obtained. As shown in Figure 6, lithology, precipitation, and NDVI contribute more to the occurrence of hazards than the other influencing factors, which is consistent with common perceptions about the causes of geological hazards [61,62] and is also highly consistent with the results of field survey investigations in this paper (Table 1). The statistical values of the importance of plane curvature and profile curvature factors were negative, so these aspects are considered to be redundant factors that should be eliminated. This result is similar to the results of the previous reference [63]. Therefore, 11 assessment factors—elevation, slope, aspect, distance to a road, distance to a river, distance to a fault, lithology, NDVI, TWI, ground cover, and precipitation—were used for the subsequent model construction.
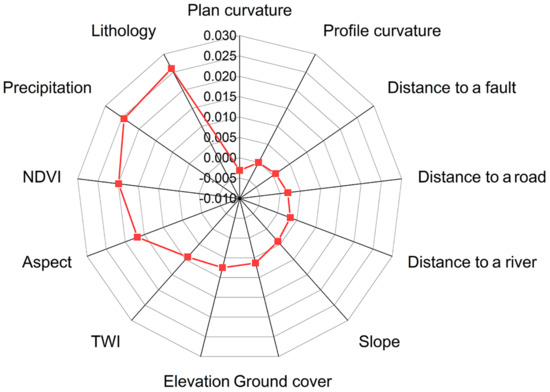
Figure 6.
Importance of mountain hazard factors based on the Relief-F model.
4.2. Hyperparametric Optimized RF Model
The RF model contains six hyperparameters: n_estimators, max_features, max_depths, min_samples_split, min_samples_leaf, and bootstrap. Among these, n_estimators represents the number of trees in the random forest, max_features is the number of features at each split, max_depths is the maximum number of splits each tree can have, min_samples_split is the minimum number of observations required before a node in the tree splits, min_samples_leaf is the minimum number of observations required at the end of each tree’s leaf nodes at the end of each tree, and bootstrap indicates whether bootstrapping was used to provide the data for each tree in the random forest (bootstrapping is random sampling with replacements from the dataset). In this study, n_estimators and max_depths, which had the large impacts on the results, were selected for hyperparameter optimization. The samples were selected using repeated sampling with replacement sampling, so the bootstrap value was true.
The Bayesian algorithm was used to optimize the hyperparameters of n_estimators and max_depths and to obtain the hyperparameter values for each iteration. In the hyperparameter optimization process, the accuracy was chosen as a measure of the accuracy of the model. In this study, through hyperparameter optimization training, the optimal parameters of the model appeared before the 20th iteration, and the accuracy of the model could not be improved after 30 iterations. Therefore, for hyperparameter optimization, the number of iterations was chosen to be 50, and the accuracy of the 10th iteration was 0.942. The optimal hyperparameters were (n_estimators:96.76385895424721, max_depths: 32).
The Genetic Algorithm (GA) model was optimized with hyperparameters and executed for 50 iterations, having an accuracy level of 0.915. The accuracy reached its maximal value at the 41st iteration, at which point the model exhibited an optimal performance. The hyperparameters were (n_estimators: 42, max_depths: 27).
In this study, optimization of the hyperparameters of the GA-RF model was carried out, and 80% of the dataset was used as the training sample for modeling and training. The selected 11 pregnancy disaster factors were input into the RF model and the GA-RF model, respectively, and the susceptibility zoning map was drawn (Figure 7a,b). The susceptibility index of geological hazards in the study area ranged from 0 to 1. The GA-RF model-drawn geological hazard susceptibility zoning map of the Wudu District was divided into five levels using the natural breakpoint method, extremely low (0–0.14), low (0.15–0.33), medium (0.33–0.52), high (0.52–0.74), and extremely high (0.74–1), with probability distributions of 30.35%, 31.64%, 17.35%, 12.54%, and 8.12%, respectively. Among them, the distribution results of the extremely high and high susceptibility zones were consistent with the results of the RF model-drawn geological hazard susceptibility zoning map and the historical distribution pattern of geological hazards.
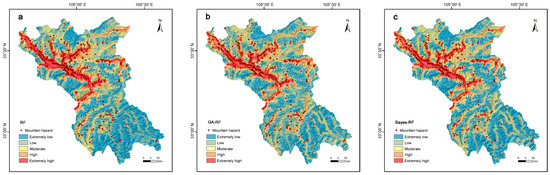
Figure 7.
Mountain hazard susceptibility maps: (a) RF model; (b) GA-RF model; (c) Bayes-RF model.
In this study, optimization of the hyperparameters of the Bayes-RF model was carried out, and 80% of the dataset was used as the training sample for modeling and training. The selected 11 pregnancy disaster factors were input into the model, and the susceptibility index of geological hazards in Wudu District was divided into five levels: extremely low (0–0.19), low (0.19–0.36), medium (0.36–0.55), high (0.55–0.75) and extremely high (0.75–1), with probability distributions of 34.27%, 29.13%, 17.19%, 11.37%, and 8.03%, respectively. The results of the geological hazard susceptibility zoning map drawn by the Bayes-RF model (Figure 7c) showed that the extremely high and high hazard susceptibility zones are mainly distributed along the rivers and valleys, where human activities are frequent and soil erosion is severe. The low susceptibility zones are mainly distributed in areas where human activities are less frequent, the elevation is higher, and the rock is harder, which is consistent with the historical distribution of geological hazards.
4.3. Model Validation and Comparison
To measure the overall performance of the models, we utilized the ROC-AUC metric to validate the training success and prediction ability of two optimization models (GA-RF and Bayes-RF). The AUC value of the training dataset indicates the success of the model, while the AUC of the validation dataset represents the predictive ability of the model.
As shown in Figure 8, the AUC values for the training dataset of the GA-RF and Bayes-RF models were 0.99 and 0.99, respectively. The AUC values for the validation dataset were 0.91 and 0.92, while the AUC values for the training and validation datasets of the unoptimized RF model were 0.97 and 0.89, respectively. The difference in the AUC values of the training dataset indicates that the GA-RF and Bayes-RF models exhibited good fits (success capability) and outperformed the unoptimized RF model in terms of the overall performance. However, the Bayes-RF model had a higher success capability for the training data. Similarly, both optimized models had higher prediction abilities, while the Bayes-RF model predicted with greater accuracy. To evaluate the merit of the training dataset, four metrics (i.e., ACC, recall, precision and F1) calculated from the confusion matrix were applied in the training phase of this study. The results are shown in Table 3.
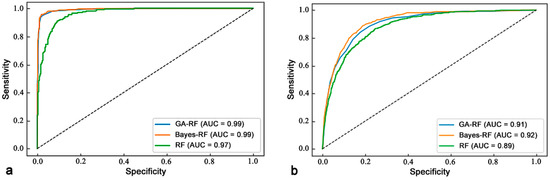
Figure 8.
ROC curves for the RF, GA-RF, and Bayes-RF models: (a) training data; (b) validation data.

Table 3.
Confusion matrix for RF, GA-RF and Bayes-RF models.
As demonstrated from the metric assignments, the Bayes-RF model and the GA-RF model exhibited better fits and higher prediction accuracy levels than the RF model. However, overall, the training and prediction results of the Bayes-RF model were better than those of the GA-RF model. Therefore, in the model application presented in this study, the Bayes-RF model has higher predictive power than the GA-RF model.
Based on the predicted mountain hazard susceptibility map of the study area and historical mountain hazard occurrences, the model of this study was quantitatively analyzed and compared in terms of frequency ratios. When the frequency ratio is greater than 1, mountain hazards are likely to occur, and the larger the frequency ratio, the higher the likelihood of mountain hazards. The results presented in Table 4 show that there are 251 hazard points in the very high susceptibility area of the Bayes-RF model, accounting for 66.40% of all hazards, and there are 254 hazard points in the very high susceptibility area of the GA-RF model, accounting for 67.20% of all hazards. There are one and two hazard points in the very low susceptibility areas of the Bayes-RF and GA-RF models, accounting for 0.26% and 0.53% of all hazards, respectively. However, the very low susceptibility area of the Bayes-RF model (0.26%) is smaller than that of the GA-RF model (0.53%). The frequency ratio (FR) results presented in Table 4 show that the high susceptibility (1.977) and low susceptibility (0.136) regions of the Bayes-RF model are larger than the high susceptibility (1.519) and low susceptibility (0.117) regions of the GA-RF model. The very high susceptibility (8.266) and very low susceptibility (0.008) regions of the Bayes-RF model are smaller than the very high susceptibility region of the GA-RF model (8.273) and the very low susceptibility region (0.017) of the GA-RF model. The above statistical results together indicate that the susceptibility assessment results and the mountain hazard distribution pattern of the Bayes-RF model are more reasonable than those of the GA-RF model.

Table 4.
Statistical results of frequency ratios of the RF, GA-RF, and Bayes-RF models.
5. Discussion
This study combined machine learning models (data-driven) with field survey (knowledge-driven) research to explore human–machine complementarity to improve disaster prediction accuracy in the future. Based on the physical mechanism of mutual transformation and cascading of various types of geological hazards in the study area, a multifactor dataset was established from the perspective of avalanche, landslide and debris flow hazard chains. The mountain hazard susceptibility assessment results were found to be generally consistent with the results of historical geological hazard surveys. The team’s long-term, continuous analysis of the causes of mountain hazards showed that human activities are increasingly becoming the primary driver of disaster occurrence. Therefore, in this section, we discuss the model performance further through an in-depth analysis based on an exploration of how the results of the data analysis in this paper reflect the impacts of human activities. Then, we present the future research objectives of the team, which are aimed at improving the prediction accuracy of the model.
5.1. Susceptibility Responses to Human Activities
The Relief-F model further revealed that elevation and NDVI are important factors that characterize the association between disaster occurrence and human activities in the study area. For this purpose, the frequency ratios of disaster distribution at different elevations and NDVI values are plotted as shown in Figure 9.
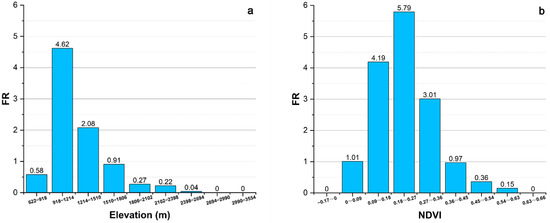
Figure 9.
Frequency ratio plot of elevation and NDVI (a) Elevation; (b) NDVI.
As shown in Figure 9a, the frequency ratio at elevations of 918–1214 m is the highest, reaching 4.62, and this value gradually decreases as the elevation rises. Additionally, as shown in Appendix A, 65.35% of the hazards occurred in the low elevation area of 918–1510 m. Frequent human activities in low elevation areas, such as large areas of reclamation, are associated with low vegetation cover which, in turn, has serious impacts on the slope stability and frequently causes hazard development. Relatively speaking, human activities are less common in high elevation areas, and fewer hazards occur in the mountains. The results presented in Figure 9b show that 84 hazards occurred in the vegetation cover range of 0.18–0.27 with a frequency ratio as high as 5.79. The frequency ratio decreases as the vegetation cover increases. Meanwhile, 81.2% of the hazards occurred in the low vegetation cover range (Appendix A), indicating that the human-activity-triggered destruction of vegetation is positively related to the hazard frequency.
5.2. Model Optimization and Performance Improvement
Hyperparameters of machine learning algorithms can affect the model prediction accuracy [64,65], and previous studies have typically used trial-and-error and grid search methods to determine hyperparameters [66]. However, such methods may miss the best parameters and can be time consuming, which greatly reduces the accuracy and stability of the model prediction. Therefore, the Bayesian optimization algorithm was created to find the best hyperparameters rapidly. The algorithm fits the posterior distribution of the objective function by increasing the data volume of the samples and input and output data, and it finally achieves hyperparameter optimization of the model, obtaining the best parameters while ensuring the accuracy and stability of the model are maintained. The GA is the most popular evolutionary algorithm, highlighting the properties of the biological evolutionary process. Most previously developed algorithms are heuristic models that were built based on different ideal assumptions and cannot guarantee the basic local optimum. However, the GA basically has no prerequisite assumptions and only needs to design the value of the objective function, which is much less reliant on the nature of the optimization problem itself and does not depend on a large set of conditions. From the results of the RF model before and after optimization shown in Figure 7, it can be seen that after using both optimization algorithms, the model has a good fit for the training data, and the accuracy has been improved. In comparison, the Bayesian algorithm hyperparametric optimization model is more capable of preventing the overfitting problem. Therefore, the accuracy of fitting and prediction can be improved to a certain extent, and the results of the hazard susceptibility assessment are more robust and reliable.
In addition to the parameters of the model itself, which can affect the final accuracy, the strategy of collecting disaster samples is equally important. There are numerous sampling methods for hazard data, such as the seed cell, point, scarp, and fuzzy C-means clustering [67,68]. A comparison of the effects of the scarp, seed cell, and point sampling strategies on landslide susceptibility partition maps concluded that the scarp sampling strategy provides better results than the point sampling strategy, while the scarp and seed cell methods have similar results. Dou [69] derived the order of predictive power by comparing landslide slope surface samples, slope centroids, landslide body samples, and landslide body centroids as follows: landslide surface > landslide body > slope centroids > body centroids. This further demonstrated that the disaster sampling strategy also has a large impact on the prediction ability of the model. Therefore, in future research, the influence of the model parameters as well as the hazard sampling strategy need to be taken into consideration. In addition, the hazard sample number also affects the prediction accuracy of the model. Having adequate disaster samples can make the trained model more stable and the prediction results more accurate. The mountain hazard sample data used in this study were obtained from field geological hazard surveys, the geological hazard data collection library, and remote sensing image verification. However, individual hazard samples may be missed in the collection process, resulting in incomplete hazard lists. Therefore, the interferometric synthetic aperture radar (InSAR) technique can be considered in future studies to identify hazards [70] to compensate for the missing hazard data and make the evaluation results more reliable.
5.3. Assessment of Susceptibility Mapping Accuracy
In disaster susceptibility studies, the performance of different models is generally compared by AUC values, but the differences in susceptibility maps cannot be identified distinctly through visualization. Therefore, the susceptibility maps were compared before and after optimization according to the research method presented by Xiao [71]. The optimized susceptibility maps (GA-RF and Bayes-RF) were used to subtract the susceptibility map without optimization (benchmark RF), and the results are shown in Figure 10.
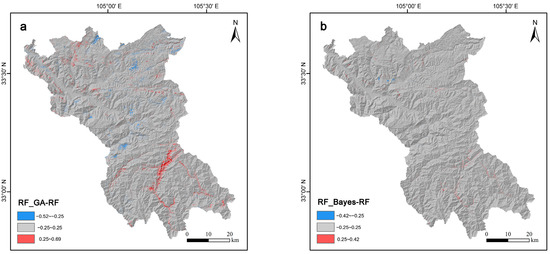
Figure 10.
Spatial locations showing the underlying underestimations and overestimations in the two compared models: (a) RF_GA-RF model (b) RF_Bayes-RF model.
The values of RF_GA-RF are within the range of −0.52 to 0.69 (Figure 10a), and the values of RF_Bayes-RF are within the range of −0.42 to 0.42 (Figure 10b). The comparison indicated that the overall difference of RF_Bayes-RF is small and shows no obvious distribution law, while the difference of RF_GA-RF is obvious. The high values of RF_GA-RF (0.25–0.69) are mainly distributed in river valleys (elevation: 1214–1806 m), and the low values (−0.52 to 0.25) are distributed in mountain ridges (elevation: 1806–2649 m) and areas of high human activity. In this paper, we argue that there are two reasons for the large discrepancy in RF_GA-RF. On the one hand, it may be due to the overfitting of the unoptimized RF model that occurred during the training process, making the error of the model-predicted susceptibility map larger. Another reason may be that factors such as elevation, human activities, and distance to a river are associated with extremely high and low values of hazard susceptibility, implying the importance of geomorphological meaning and other underlying patterns in susceptibility assessments. Accordingly, we further revealed that the Bayes-RF model is quite robust, while the GA-RF seems to still have significant room for optimization, so when conducting susceptibility prediction studies, it is suggested that different state-of-the-art models and metrics besides the AUC are selected for comparison as much as possible to further guarantee the reliability of the susceptibility mapping.
6. Conclusions
This study was based on GIS technology and machine learning methods for mountain hazard susceptibility predictions and assessments. Two integrated machine learning models, the GA-RF model and the Bayes-RF model, were developed and the RF model was used as the benchmark classifier. The results show that the Bayes-RF model (AUC = 0.92) provides significantly better results than the GA-RF model (AUC = 0.91) and the RF model (AUC = 0.89) when used for hazard susceptibility predictions and mapping. The Bayes-RF machine-learning-based ensemble modeling method operates robustly and performs well, so it can be adopted as a model for the spatial prediction of mountain hazard susceptibility in the study area. The susceptibility mapping results indicate that the densely populated areas along the Bailong River and the G212 highway in the northwest part of the study area should be the focus for disaster prevention and mitigation planning.
Based on the physical mechanism of mountain hazards characterized mainly as cascading landslides, avalanches and debris flow chains and the complex nonlinear characteristics of hazard occurrence, this study established a more reliable dataset by selecting 14 hazard impact factors with the aid of a field survey analysis. Consequently, we enhanced the accuracy of the Bayes-RF model through a multicollinearity analysis and Relief-F two-step evaluation. The data preparation method, the corresponding hazard susceptibility assessment, and the prediction method can be extended and applied to other mountainous areas that are susceptible to hazards. Moreover, this study proposes the future objective of exploring the establishment of a hybrid model that integrates a physical mechanism model and a data-driven model in order to further expand the applications of machine learning and even deep learning technologies in multiple fields of scientific assessment and prediction of earth systems.
Author Contributions
Conceptualization, Z.W. and Z.C.; methodology, Z.W.; software, Z.C.; validation, Z.C. and K.M.; formal analysis, Z.C.; investigation, K.M.; resources, Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.W.; writing—review and editing, Z.W.; visualization, Z.C.; supervision, Z.W.; project administration, Z.W.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Grant Nos. 42167043 and 51269009), Gansu Province Key Research and Development Program (Grant No. 20YF8ND141) and the Western Transportation Construction Science and Technology Project of the Ministry of Transport, China (Grant No. 2002 318 000 36).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We appreciate the valuable feedback and guidance provided by the two anonymous reviewers and editors which enhanced the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Frequency ratios (FRs) of the influencing factors.
Table A1.
Frequency ratios (FRs) of the influencing factors.
| Class | Value | Type | Pixels in Domain | Pixel (%) | Hazard Points | Hazard (%) | FR |
|---|---|---|---|---|---|---|---|
| Geomorphology and structure | |||||||
| Elevation (m) | 622–918 | Continuous | 46,842 | 0.91 | 2 | 0.53 | 0.58 |
| 918–1214 | 381,802 | 7.39 | 129 | 34.13 | 4.62 | ||
| 1214–1510 | 773,992 | 14.99 | 118 | 31.22 | 2.08 | ||
| 1510–1806 | 1,292,308 | 25.02 | 86 | 22.75 | 0.91 | ||
| 1806–2102 | 1,548,613 | 29.99 | 31 | 8.20 | 0.27 | ||
| 2102–2398 | 671,677 | 13.01 | 11 | 2.91 | 0.22 | ||
| 2398–2694 | 349,662 | 6.77 | 1 | 0.26 | 0.04 | ||
| 2694–2990 | 90,410 | 1.75 | 0 | 0.00 | 0.00 | ||
| 2990–3554 | 9129 | 0.18 | 0 | 0.00 | 0.00 | ||
| Slope (°) | 0°–10° | Continuous | 510,164 | 9.91 | 39 | 10.32 | 1.04 |
| 10°–20° | 897,118 | 17.42 | 77 | 20.37 | 1.17 | ||
| 20°–30° | 1,664,789 | 32.33 | 135 | 35.71 | 1.10 | ||
| 30°–40° | 1,494,180 | 29.02 | 103 | 27.25 | 0.94 | ||
| 40°–50° | 509,507 | 9.89 | 22 | 5.82 | 0.59 | ||
| >50° | 73,906 | 1.44 | 2 | 0.53 | 0.37 | ||
| Aspect | Level | Discrete | 144,270 | 2.80 | 10 | 2.65 | 0.94 |
| North | 613,964 | 11.92 | 32 | 8.47 | 0.71 | ||
| Northeast | 648,775 | 12.60 | 56 | 14.81 | 1.18 | ||
| East | 621,581 | 12.07 | 55 | 14.55 | 1.21 | ||
| Southeast | 683,261 | 13.27 | 56 | 14.81 | 1.12 | ||
| South | 603,608 | 11.72 | 63 | 16.67 | 1.42 | ||
| Southwest | 666,433 | 12.94 | 41 | 10.85 | 0.84 | ||
| West | 570,245 | 11.07 | 27 | 7.14 | 0.65 | ||
| Northwest | 597,527 | 11.60 | 38 | 10.05 | 0.87 | ||
| Plan curvature | −11.16 to −2.10 | Continuous | 15,881 | 0.31 | 0 | 0.00 | 0.00 |
| −2.10 to −1.50 | 53,862 | 1.04 | 1 | 0.26 | 0.25 | ||
| −1.50 to −0.90 | 251,392 | 4.87 | 13 | 3.44 | 0.71 | ||
| −0.90 to −0.30 | 997,039 | 19.31 | 63 | 16.67 | 0.86 | ||
| −0.30 to 0.30 | 2,463,614 | 47.71 | 206 | 54.50 | 1.14 | ||
| 0.30–0.90 | 1,028,772 | 19.92 | 73 | 19.31 | 0.97 | ||
| 0.90–1.50 | 275,196 | 5.33 | 16 | 4.23 | 0.79 | ||
| 1.50–2.10 | 60,030 | 1.16 | 5 | 1.32 | 1.14 | ||
| 2.10–10.21 | 18,475 | 0.36 | 1 | 0.26 | 0.74 | ||
| Profile curvature | −15.05 to −2.90 | Continuous | 12,555 | 0.24 | 0 | 0.00 | 0.00 |
| −2.90 to −2.10 | 33,546 | 0.65 | 0 | 0.00 | 0.00 | ||
| −2.10 to −1.30 | 142,997 | 2.77 | 13,500 | 3.97 | 1.43 | ||
| −1.30 to −0.50 | 612,532 | 11.86 | 27,900 | 8.20 | 0.69 | ||
| −0.50 to 0.30 | 3,107,184 | 60.17 | 206,100 | 60.58 | 1.01 | ||
| 0.30–1.10 | 971,309 | 18.81 | 71,100 | 20.90 | 1.11 | ||
| 1.10–1.90 | 212,169 | 4.11 | 19,800 | 5.82 | 1.42 | ||
| 1.90–2.70 | 52,221 | 1.01 | 1800 | 0.53 | 0.52 | ||
| 2.70–13.00 | 19,748 | 0.38 | 0 | 0.00 | 0.00 | ||
| Distance to a fault (m) | 0–1400 | Continuous | 2,061,661 | 39.92 | 167 | 44.18 | 1.11 |
| 1400–2800 | 1,206,521 | 23.36 | 103 | 27.25 | 1.17 | ||
| 2800–4200 | 713,656 | 13.82 | 67 | 17.72 | 1.28 | ||
| 4200–5600 | 389,221 | 7.54 | 18 | 4.76 | 0.63 | ||
| 5600–7000 | 247,265 | 4.79 | 12 | 3.17 | 0.66 | ||
| 7000–8400 | 174,649 | 3.38 | 6 | 1.59 | 0.47 | ||
| 8400–9800 | 152,306 | 2.95 | 3 | 0.79 | 0.27 | ||
| 9800–11,200 | 133,363 | 2.58 | 2 | 0.53 | 0.20 | ||
| 11,200–15,300 | 85,687 | 1.66 | 0 | 0.00 | 0.00 | ||
| Roughness | 1–1.06 | Continuous | 1,206,403 | 23.42 | 108 | 28.57 | 1.22 |
| 1.06–1.13 | 1,227,880 | 23.84 | 103 | 27.25 | 1.14 | ||
| 1.13–1.20 | 956,001 | 18.56 | 79 | 20.90 | 1.13 | ||
| 1.20–1.28 | 731,988 | 14.21 | 43 | 11.38 | 0.80 | ||
| 1.28–1.38 | 516,868 | 10.04 | 23 | 6.08 | 0.61 | ||
| 1.38–1.51 | 301,528 | 5.85 | 11 | 2.91 | 0.50 | ||
| 1.51–1.70 | 146,928 | 2.85 | 10 | 2.65 | 0.93 | ||
| 1.70–2.04 | 52,998 | 1.03 | 1 | 0.26 | 0.26 | ||
| 2.04–4.44 | 10,056 | 0.20 | 0 | 0.00 | 0.00 | ||
| External dynamic geological environment | |||||||
| Distance to a road (m) | 0–600 | Continuous | 1,063,274 | 20.59 | 236 | 62.43 | 3.03 |
| 600–1200 | 764,896 | 14.81 | 75 | 19.84 | 1.34 | ||
| 1200–1800 | 665,424 | 12.88 | 23 | 6.08 | 0.47 | ||
| 1800–2400 | 576,527 | 11.16 | 14 | 3.70 | 0.33 | ||
| 2400–3000 | 491,529 | 9.52 | 12 | 3.17 | 0.33 | ||
| 3000–3600 | 418,827 | 8.11 | 7 | 1.85 | 0.23 | ||
| 3600–4200 | 329,689 | 6.38 | 3 | 0.79 | 0.12 | ||
| 4800–5400 | 254,513 | 4.93 | 5 | 1.32 | 0.27 | ||
| >5400 | 599,710 | 11.61 | 3 | 0.79 | 0.07 | ||
| Distance to river (m) | 0–600 | Continuous | 1,044,339 | 20.22 | 175 | 46.30 | 2.29 |
| 600–1200 | 974,622 | 18.87 | 112 | 29.63 | 1.57 | ||
| 1200–1800 | 887,629 | 17.19 | 33 | 8.73 | 0.51 | ||
| 1800–2400 | 755,208 | 14.62 | 15 | 3.97 | 0.27 | ||
| 2400–3000 | 588,124 | 11.39 | 19 | 5.03 | 0.44 | ||
| 3000–3600 | 411,297 | 7.96 | 15 | 3.97 | 0.50 | ||
| 3600–4200 | 254,621 | 4.93 | 6 | 1.59 | 0.32 | ||
| 4200–4800 | 140,460 | 2.72 | 2 | 0.53 | 0.19 | ||
| 4800–6500 | 108,065 | 2.09 | 1 | 0.26 | 0.13 | ||
| NDVI | −0.17 to 0 | Continuous | 5922 | 0.11 | 0 | 0.00 | 0.00 |
| 0–0.09 | 13,499 | 0.26 | 1 | 0.26 | 1.01 | ||
| 0.09–0.18 | 52,154 | 1.01 | 16 | 4.23 | 4.19 | ||
| 0.18–0.27 | 198,057 | 3.84 | 84 | 22.22 | 5.79 | ||
| 0.27–0.36 | 522,153 | 10.11 | 115 | 30.42 | 3.01 | ||
| 0.36–0.45 | 1,280,418 | 24.79 | 91 | 24.07 | 0.97 | ||
| 0.45–0.54 | 2,374,744 | 45.98 | 63 | 16.67 | 0.36 | ||
| 0.54–0.63 | 716,918 | 13.88 | 8 | 2.12 | 0.15 | ||
| 0.63–0.66 | 345 | 0.01 | 0 | 0.00 | 0.00 | ||
| TWI | <2 | Continuous | 1,407,116 | 27.32 | 86 | 22.75 | 0.83 |
| 2–4 | 1,029,832 | 20.00 | 95 | 25.13 | 1.26 | ||
| 4–6 | 1,566,516 | 30.42 | 94 | 24.87 | 0.82 | ||
| 6–8 | 649,138 | 12.61 | 52 | 13.76 | 1.09 | ||
| 8–10 | 225,259 | 4.37 | 24 | 6.35 | 1.45 | ||
| 10–12 | 100,898 | 1.96 | 12 | 3.17 | 1.62 | ||
| 12–14 | 36,637 | 0.71 | 4 | 1.06 | 1.49 | ||
| 14–16 | 64,978 | 1.26 | 5 | 1.32 | 1.05 | ||
| 16–30 | 69,240 | 1.34 | 6 | 1.59 | 1.18 | ||
| Ground cover | Cropland | Discrete | 727,981 | 14.10 | 158 | 41.80 | 2.97 |
| Forest | 3,133,568 | 60.68 | 118 | 31.22 | 0.51 | ||
| Grass | 1,197,002 | 23.18 | 70 | 18.52 | 0.80 | ||
| Shrub | 10,382 | 0.20 | 0 | 0.00 | 0.00 | ||
| Wetland | 800 | 0.02 | 0 | 0.00 | 0.00 | ||
| Water | 6002 | 0.12 | 0 | 0.00 | 0.00 | ||
| Artificial | 58,798 | 1.14 | 19 | 5.03 | 4.41 | ||
| Bareland | 29,843 | 0.58 | 13 | 3.44 | 5.95 | ||
| Ice | 27 | 0.00 | 0 | 0.00 | 0.00 | ||
| Precipitation (mm) | 468–500 | Continuous | 301,757 | 5.84 | 39 | 10.32 | 1.77 |
| 500–550 | 815,298 | 15.79 | 97 | 25.66 | 1.63 | ||
| 550–600 | 1,084,602 | 21.01 | 107 | 28.31 | 1.35 | ||
| 600–650 | 701,797 | 13.59 | 73 | 19.31 | 1.42 | ||
| 650–700 | 678,150 | 13.13 | 24 | 6.35 | 0.48 | ||
| 700–750 | 573,149 | 11.10 | 28 | 7.41 | 0.67 | ||
| 750–800 | 644,650 | 12.48 | 8 | 2.12 | 0.17 | ||
| 800–860 | 364,114 | 7.05 | 2 | 0.53 | 0.08 | ||
| Engineering geological petrofabric | |||||||
| Lithology | Loose rock | Discrete | 3,419,409 | 66.21 | 172 | 45.50 | 0.69 |
| Softer rock | 745,401 | 14.43 | 45 | 11.90 | 0.82 | ||
| Soft rock | 460,951 | 8.93 | 102 | 26.98 | 3.02 | ||
| Harder rock | 399,788 | 7.74 | 55 | 14.55 | 1.88 | ||
| Hard rock | 138,832 | 2.69 | 4 | 1.06 | 0.39 | ||
References
- Aksha, S.K.; Resler, L.M.; Juran, L.; Carstensen, L.W., Jr. A geospatial analysis of multi-hazard risk in Dharan, Nepal. Geomat. Nat. Hazards Risk 2020, 11, 88–111. [Google Scholar] [CrossRef]
- Shi, P.; Ye, T.; Wang, Y.; Zhou, T.; Xu, W.; Du, J.; Wang, J.; Li, N.; Huang, C.; Liu, L.; et al. Disaster Risk Science: A Geographical Perspective and a Research Framework. Int. J. Disaster Risk Sci. 2020, 11, 426–440. [Google Scholar] [CrossRef]
- Du, W.; Sheng, Q.; Fu, X.; Chen, J.; Zhou, Y. A TPDP-MPM-based approach to understanding the evolution mechanism of landslide-induced disaster chain. J. Rock Mech. Geotech. Eng. 2022, 14, 1200–1209. [Google Scholar] [CrossRef]
- Yong, C.; Jinlong, D.; Fei, G.; Bin, T.; Tao, Z.; Hao, F.; Li, W.; Qinghua, Z. Review of landslide susceptibility assessment based on knowledge mapping. Stoch. Environ. Res. Risk Assess. 2022, 36, 2399–2417. [Google Scholar] [CrossRef]
- Shao, X.; Xu, C. Earthquake-induced landslides susceptibility assessment: A review of the state-of-the-art. Nat. Hazards Res. 2022, 2, 172–182. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Karaman, M.O.; Çabuk, S.N.; Pekkan, E. Utilization of frequency ratio method for the production of landslide susceptibility maps: Karaburun Peninsula case, Turkey. Environ. Sci. Pollut. Res. 2022, 29, 91285–91305. [Google Scholar] [CrossRef]
- Zare, N.; Hosseini, S.A.O.; Hafizi, M.K.; Najafi, A.; Majnounian, B.; Geertsema, M. A Comparison of an adaptive neuro-fuzzy and frequency ratio model to landslide-susceptibility mapping along forest road networks. Forests 2021, 12, 1087. [Google Scholar] [CrossRef]
- Zuo, X.Z.; Zhang, Z.; Su, Y.-H.; Liu, Y.; Ge, Q.; Tian, J.-F. Extraction Algorithm of NDVI Based on GPU Multi-stream Parallel Model. Comput. Sci. 2020, 47, 25–29. [Google Scholar]
- Liu, J.; Xu, Z.; Chen, F.; Chen, F.; Zhang, L. Flood hazard mapping and assessment on the Angkor world heritage site, Cambodia. Remote Sens. 2019, 11, 98. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Arabameri, A.; Pal, S.C.; Rezaie, F.; Chakrabortty, R.; Saha, A.; Blaschke, T.; Di Napoli, M.; Ghorbanzadeh, O.; Ngo, P.T.T. Decision tree based ensemble machine learning approaches for landslide susceptibility mapping. Geocarto Int. 2021, 37, 4594–4627. [Google Scholar] [CrossRef]
- Pham, B.T.; Phong, T.V.; Nguyen-Thoi, T.; Parial, K.; Singh, S.K.; Ly, H.B.; Prakash, I. Ensemble modeling of landslide susceptibility using random subspace learner and different decision tree classifiers. Geocarto Int. 2020, 37, 735–757. [Google Scholar] [CrossRef]
- Yu, C.; Chen, J. Application of a GIS-based slope unit method for landslide susceptibility mapping in Helong City: Comparative assessment of ICM, AHP, and RF model. Symmetry 2020, 12, 1848. [Google Scholar] [CrossRef]
- Park, S.; Kim, J. Landslide susceptibility mapping based on random forest and boosted regression tree models, and a comparison of their performance. Appl. Sci. 2019, 9, 942. [Google Scholar] [CrossRef]
- Kamran, K.V.; Feizizadeh, B.; Khorrami, B.; Ebadi, Y. A comparative approach of support vector machine kernel functions for GIS-based landslide susceptibility mapping. Appl. Geomat. 2021, 13, 837–851. [Google Scholar] [CrossRef]
- Sheng, M.; Liu, Z.; Zhang, X.; Hu, S.; Guo, Z.; Huang, F. Landslide susceptibility prediction based on frequency ratio analysis and support vector machine. Sci. Technol. Eng. 2021, 21, 10620–10628. [Google Scholar]
- Wang, Z.; Brenning, A. Active-learning approaches for landslide mapping using support vector machines. Remote Sens. 2021, 13, 2588. [Google Scholar] [CrossRef]
- Sun, D.; Xu, J.; Wen, H.; Wang, D. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization: A comparison between logistic regression and random forest. Eng. Geol. 2021, 281, 105972. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S. GIS-based comparative study of Bayes network, Hoeffding tree and logistic model tree for landslide susceptibility modeling. Catena 2021, 203, 105344. [Google Scholar] [CrossRef]
- Mabdeh, A.N.; Al-Fugara, A.; Ahmadlou, M.; Al-Adamat, R.; Al-Shabeeb, A.R. GIS-based landslide susceptibility assessment and mapping in Ajloun and Jerash governorates in Jordan using genetic algorithm-based ensemble models. Acta Geophys. 2022, 70, 1253–1267. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C. Comparison and evaluation of landslide susceptibility maps obtained from weight of evidence, logistic regression, and artificial neural network models. Nat. Hazards 2018, 93, 249–274. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Pašek, J. Inventaire Des Glissements de Terrain. Bull. Int. Assoc. Eng. Geol. Bull. Lassociation Int. Géologie Lingénieur 1975, 12, 73–74. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, Z.; Liu, G. Rsearch on Engineering Geology of Gansu Section of Lanzhou-Haikou Expressway; Lanzhou Univ. Press: Lanzhou, China, 2006. [Google Scholar]
- Qi, S.; Liu, D.; Ma, J.; Tian, L. An assessment index system for landslide risk in Bailong river basin. J. Lanzhou Univ. Nat. Sci. 2014, 50, 356–362. [Google Scholar]
- Li, S. Discussion on landslide activities in Bailong River Basin of Wudu. Bull. Soil Water Conserv. 1997, 17, 28–32. [Google Scholar]
- Li, S. Preliminary study of the landslides in middle reaches of Bailong River. Hydrogeol. Eng. Geol. 1995, 22, 13–15. [Google Scholar]
- Ma, Z.; Mei, G. Deep learning for geological hazards analysis: Data, models, applications, and opportunities. Earth-Sci. Rev. 2022, 223, 103858. [Google Scholar] [CrossRef]
- Liu, Y. Risk analysis and zoning of geological hazards (chiefly landslide, rock fall and debris flow) in China. Chin. J. Geol. Hazard Control 2003, 14, 95–99. [Google Scholar]
- Ning, N.; Tian, L.; Zhang, P.; Qi, S.; Ma, J. The hazards assessment of debris flow in wudu of southern Gansu, China. Mt. Res. 2013, 31, 601–609. [Google Scholar]
- Santacana, N.; Baeza, B.; Corominas, J.; De Paz, A.; Marturiá, J. A GIS-based multivariate statistical analysis for shallow landslide susceptibility mapping in La Pobla de Lillet area (Eastern Pyrenees, Spain). Nat. Hazards 2003, 30, 281. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Y.; Chen, X.; Liu, Y. Bibliometric Analysis of Global NDVI Research Trends from 1985 to 2021. Remote Sens. 2022, 14, 3967. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Obled, C.; Wendling, J.; Beven, K. The sensitivity of hydrological models to spatial rainfall patterns: An evaluation using observed data. J. Hydrol. 1994, 159, 305–333. [Google Scholar] [CrossRef]
- Tarboton, D.G. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef]
- Ning, N.M.; Ma, J.; Zhang, P.; Qi, S.; Tian, L. Debris Flow Hazard Assessment for the Bailongjiang River, Southern Gansu. Resour. Sci. 2013, 35, 892–899. [Google Scholar]
- Liao, M.; Wen, H.; Yang, L. Identifying the essential conditioning factors of landslide susceptibility models under different grid resolutions using hybrid machine learning: A case of Wushan and Wuxi counties, China. Catena 2022, 217, 106428. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Alimohammadlou, Y.; Najafi, A.; Gokceoglu, C. Estimation of rainfall-induced landslides using ANN and fuzzy clustering methods: A case study in Saeen Slope, Azerbaijan province, Iran. Catena 2014, 120, 149–162. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Chen, W.; Clague, J.J.; Geertsema, M.; Jaafari, A.; Avand, M.; Miraki, S.; Asl, D.T.; et al. Shallow landslide susceptibility mapping by random forest base classifier and its ensembles in a semi-arid region of Iran. Forests 2020, 11, 421. [Google Scholar] [CrossRef]
- Chuanhua, Z.; Shouwen, Z. GIS Based Analysis of Accessibility Impact of BRT and Metro Line in Hefei China. Geogr. Geo Inf. Sci. 2014, 30, 21–24. [Google Scholar]
- Schonlau, M.; Zou, R.Y. The random forest algorithm for statistical learning. Stata J. 2020, 20, 3–29. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land cover classification using Google Earth Engine and random forest classifier—The role of image composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Zhang, C.-c.; Cui, L.; Yang, G. Comparative Study for Ensemble Learning Algorithms. J. Hebei Univ. Nat. Sci. Ed. 2007, 27, 551. [Google Scholar]
- Xiao, C.; Tian, Y.; Shi, W.; Guo, Q.; Wu, L. A new method of pseudo absence data generation in landslide susceptibility mapping with a case study of Shenzhen. Sci. China Technol. Sci. 2010, 53, 75–84. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural. Inf. Process. Syst 2012, 25, 2951–2959. [Google Scholar]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef]
- Shano, L.; Raghuvanshi, T.K.; Meten, M. Landslide susceptibility evaluation and hazard zonation techniques–A review. Geoenvironmental Disasters 2020, 7, 18. [Google Scholar] [CrossRef]
- Bennett, G.L.; Miller, S.R.; Roering, J.J.; Schmidt, D.A. Landslides, threshold slopes, and the survival of relict terrain in the wake of the Mendocino Triple Junction. Geology 2016, 44, 363–366. [Google Scholar] [CrossRef]
- Kornejady, A.; Ownegh, M.; Bahremand, A. Landslide susceptibility assessment using maximum entropy model with two different data sampling methods. Catena 2017, 152, 144–162. [Google Scholar] [CrossRef]
- Hong, H.; Jaafari, A.; Zenner, E.K. Predicting spatial patterns of wildfire susceptibility in the Huichang County, China: An integrated model to analysis of landscape indicators. Ecol. Indic. 2019, 101, 878–891. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Lin, J.; Chen, W.; Qi, X.; Hou, H. Risk assessment and its influencing factors analysis of geological hazards in typical mountain environment. J. Clean. Prod. 2021, 309, 127077. [Google Scholar] [CrossRef]
- Feifan, R.; Wenwu, C.; Wenfeng, H. Study on reason and spatial-temporal distribution characteristics of debris flow in Longnan area along G212. Chin. J. Rock Mech. Eng. 2008, 27, 3237–3243. [Google Scholar]
- Namous, M.; Hssaisoune, M.; Pradhan, B.; Lee, C.-W.; Alamri, A.; Elaloui, A.; Edahbi, M.; Krimissa, S.; Eloudi, H.; Ouayah, M.; et al. Spatial Prediction of Groundwater Potentiality in Large Semi-Arid and Karstic Mountainous Region Using Machine Learning Models. Water 2021, 13, 2273. [Google Scholar] [CrossRef]
- Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall induced landslide susceptibility mapping based on Bayesian optimized random forest and gradient boosting decision tree models—A case study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol 2019, 17, 26–40. [Google Scholar]
- Meena, S.R.; Puliero, S.; Bhuyan, K.; Floris, M.; Catani, F. Assessing the importance of conditioning factor selection in landslide susceptibility for the province of Belluno (region of Veneto, northeastern Italy). Nat. Hazards Earth Syst. Sci. 2022, 22, 1395–1417. [Google Scholar] [CrossRef]
- Yilmaz, I. The effect of the sampling strategies on the landslide susceptibility mapping by conditional probability and artificial neural networks. Environ. Earth Sci. 2010, 60, 505–519. [Google Scholar] [CrossRef]
- Mersha, T.; Meten, M. GIS-based landslide susceptibility mapping and assessment using bivariate statistical methods in Simada area, northwestern Ethiopia. Catena 2020, 7, 20. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Merghadi, A.; Shirzadi, A.; Nguyen, H.; Hussain, Y.; Avtar, R.; Chen, Y.; Pham, B.T.; Yamagishi, H. Different sampling strategies for predicting landslide susceptibilities are deemed less consequential with deep learning. Sci. Total Environ. 2020, 720, 137320. [Google Scholar] [CrossRef]
- Zhao, F.; Meng, X.; Zhang, Y.; Chen, G.; Su, X.; Yue, D. Landslide susceptibility mapping of karakorum highway combined with the application of SBAS-InSAR technology. Sensors 2019, 19, 2685. [Google Scholar] [CrossRef]
- Xiao, T.; Segoni, S.; Chen, L.; Yin, K.; Casagli, N. A step beyond landslide susceptibility maps: A simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 2020, 17, 627–640. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).