Abstract
The application of simulation software has proven to be a crucial tool for tsunami hazard assessment studies. Understanding the potentially devastating effects of tsunamis leads to the development of safety and resilience measures, such as the design of evacuation plans or the planning of the economic investment necessary to quickly mitigate their consequences. This article introduces a pseudo-probabilistic seismic-triggered tsunami simulation approach to investigate the potential impact of tsunamis in the southwestern coast of Spain, in the provinces of Huelva and Cádiz. Selected faults, probabilistic distributions and sampling methods are presented as well as some results for the nearly 900 Atlantic-origin tsunamis computed along the 250 km-long coast.
1. Introduction
As natural hazards, tsunamis are considered amongst the most potentially devastating phenomena [1]. From the mid-nineteenth century to today, advances in technology have expanded the possibilities for the development of preventive safety measures, laying the groundwork for warning operations known as tsunami early warning systems (TEWS). TEWS provide real-time information on the occurrence and characteristics of a seismic event and enable the launching of corresponding action and/or evacuation plans if the alert level so indicates. These systems are composed of quite different elements, from physical seismic and tsunami sensors to empirical relationships derived from historical records and communication and actuation organisations.
An important aspect of the warning process is the estimation of arrival times, wave height and run-up, which have recently been enhanced through tsunami-wave simulation codes [2,3]. The events in Sumatra (2004) and Japan (2011) have prompted the need to deepen our knowledge of the phenomenom of tsunamis in order to design adequate preventive measures. For example, some measures for tsunami risk reduction have focused on the construction of artificial or natural structures near to the shore [4,5]. However, the high economic impact of the construction of physical barriers, in addition to its doubtful reliability when facing large events [4], has made them controversial. In this example and many others, numerical simulations appear to be an essential tool for tsunami impact studies [6]. In recent years, tsunami modeling tools have been significantly enhanced; the precision of the numerical methods have increased, whilst computing times have drastically decreased [7]. TEWS is a tsunami hazard management tool that focuses on the most relevant element to protect, that of human life. However, TEWS cannot prevent property damage, nor do they help to mitigate the aftermath of the tsunami. Therefore, it is a concern, and a challenge, to provide stakeholders with the best possible tools to understand and quantify the damage caused by tsunamis. One of these stakeholders is the insurance sector and in this paper we present numerical modeling and simulation as a tool to quantify the impact of tsunamis. The final objective of the long-term project with the insurance sector in Spain is to estimate the maximum economic cost of a natural hazard of this type that can affect any Spanish coastal area.
In the literature, many authors have employed numerical models to simulate seismic-triggered tsunamis with the aim of gaining knowledge for distinct purposes. Mas et al. [8] designed vulnerability functions for structures using data from the 2004 Sumatra event, launching a single simulation of a six-segment fault. Fragility functions were also developed in the context of aquaculture rafts and eelgrass for the Japan 2011 event [9], involving the running of three different simulations. With respect to economic impact, research for developing loss functions related to marine vessels was also carried out in [10], where one simulation was computed for the 2011 Japan event as well. Pakoksung et al. [11] launched six simulations to estimate the maximum potential damage loss for a hypothetical non-historical event in Okinawa Island. Goda et al. [12] discussed the tsunami risk potential of the strike-slip fault 2018 Sulawesi event, grounding their work in four simulations. Chenthamil et al. [13] predicted the potential run-up and inundation that might occur in a worst-case scenario on the Koodankulam coast, making use of five tsunamigenic events. Their article also contained a preliminary review concerning epicenter sensibility analysis with 28 simulations computed. Probabilistic-oriented studies, termed probabilistic tsunami hazard analysis (PTHA), use several hundreds of computed simulations to provide results with diverse purposes. In [14], structural losses were evaluated by simulating 242 tsunami events with a mesh resolution of 500 m. In [15], a rigorous computational framework was presented to visualize tsunami hazard and risk assessment uncertainty, where 726 simulations were launched for the 2011 Japan event. A more recent study [16] presents a novel PTHA methodology based on the generation of synthetic seismic catalogues and the incorporation of sea-level variation in a Monte Carlo simulation. Its results were derived from 619 simulations, constructed from five faults surrounding the past event in Cádiz, 1755.
To our knowledge, few PTHA studies have been developed in the northeast Atlantic area. In [17], the authors suggest their study is the first PTHA for the NE Atlantic region for earthquake-generated tsunamis. The methodology followed combined probabilistic seismic hazard assessment, tsunami numerical modeling, and statistical approaches. A set of 150 tsunamigenic scenarios were generated and simulated using a linear shallow water approximation and a 30 arc-seconds (≈90 m) resolution GEBCO bathymetry grid without nesting. In [18], the authors performed a preliminary assessment of probabilistic tsunami inundation in the NE Atlantic region. Their approach consisted of an event-tree method that gathered probability models for seismic sources, tsunami numerical modeling, and statistical methods which were then applied to the coastal test-site of Sines, located on the NE Atlantic coast of Portugal. A total of 94 scenarios were simulated using the non-linear SW equations and a nested grid system at 10 m pixel resolution in a single test-site. An innovative and ambitious initiative within this research field was presented as the North-Eastern Atlantic and Mediterranean (NEAM) Tsunami Hazard Model 2018 [19], which aims to provide a probabilistic hazard model focusing on earthquake-generated tsunamis in the entire NEAM region. The hazard assessment was performed in four steps: probabilistic earthquake model, tsunami generation and modeling in deep water (performed with the Tsunami-HySEA code), shoaling and inundation, inclusion of a local amplification factor and Green’s law, and hazard aggregation in conjunction with uncertainty treatment. The authors of this study stated that, although NEAMTHM18 represents a first action, it cannot be a substitute for detailed hazard and risk assessments at a local scale.
Most of the novel techniques in the field of PTHA are based on the notion of reducing the number of required computational runs with the aid of Gaussian process emulators, which are capable of maintaining good output accuracy and uncertainty quantification. The investigations of Gopinathan et al. [20] and Salmanidou et al. [21] are good examples of this approach, where the former delivered millions of output predictions based on 300 numerically simulated earthquake-tsunami scenarios, and the latter produced 2000 output predictions at each prescribed location, examining 60 full-fledged simulations.
This article takes advantage of the most advanced tsunami computational technology to shed light on seismic-triggered tsunamis and their impact on Spanish coasts. The results presented here are intended to generate information in relation to the estimation of the potential economic impact that tsunamis can cause in Spanish territory.
This research project arises from an arrangement between two public entities: the Spanish Geological Survey (CNIGME-CSIC; hereafter IGME) and the Insurance Compensation Consortium of Spain (CCS). The IGME is a National Centre dedicated to research within the Spanish National Research Council (CSIC, Ministry of Science and Innovation), whilst CCS is a Spanish public business entity related to the insurance sector (Ministry of Economic Affairs and Digital Transformation) which takes responsibility for compensation for damages after certain natural events (such as tsunamis), among other areas of activity. Expertise in the numerical simulation of tsunamis and HPC was provided by the University of Málaga.
Bearing in mind the final objective of the simulations considered in this study, these require to be carried out using high-resolution topographic and bathymetric data, since it is of primary importance to be able to discern particular buildings or areas affected by water waves. A five-meter grid resolution is the best nation-wide, readily available, dataset as provided by the National Geographic Institute (IGN) and was considered suitable for the inundation simulations.
The present work presents results of the 896 inundation simulations computed in the Andalusian Atlantic coast, located in the south-west of the Iberian Peninsula. The “Materials and Methods” section begins by explaining the selection of the simulated faults, together with providing some insights on how to generate the Okada parameters that describe each fault. Subsequently, the resolution and source of the different topobathymetric data used for the simulations are detailed. A pseudo-probabilistic approach to the simulations is then presented, explaining how probabilistic distribution for the uncertainty parameters considered has been determined, along with the sampling procedure. The tsunami-simulation numerical model used, as well as the characteristics of the computational cluster, are described to conclude this section. The “Results” section details the outputs obtained for each previously described subsection. It includes a detailed list of the Okada parameters adopted for the simulations, the probabilistic distributions associated with each random variable accounting for every fault, samples obtained by the chosen sampling technique and inundation maps generated from the numerical results. Finally, the discussion section provides an assessment of the possibilities that the generated data create for future research.
2. Materials and Methods
The general methodology followed to achieve the results presented in this study is summarized in Figure 1.
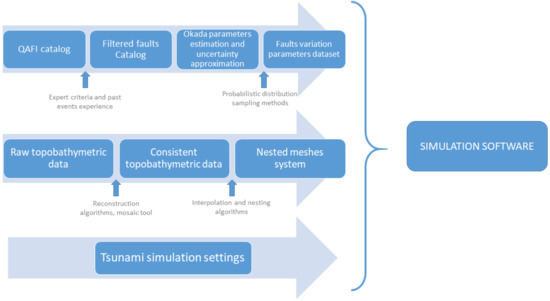
Figure 1.
Methodology scheme for this work.
2.1. Tsunami-Triggering Faults
Potential fault sources capable of producing seafloor deformation in SW offshore Iberia were retrieved from the latest version of the QAFI database [22]. The QAFI database compiles information on Quaternary-active faults in the Iberia region both onshore and offshore [23,24]. The database provides basic geometric parameters (e.g., length, strike, dip), as well as a summary of the available evidence of Quaternary activity for each fault. The information compiled in the QAFI database comes chiefly from published sources such as [25,26,27,28], among others. A total of 12 faults were selected to be used in this study (Figure 2) after careful review and update of available published information and considering the opinion of a number of experts gathered in a workshop devoted to this task held in 2017 [29]. All the faults considered have published evidence of Quaternary activity, although this activity is very likely but has not yet been definitely demonstrated in the case of the Gorringe Bank (AT001), Guadalquivir Bank (AT002) and Portimao Bank (AT013) faults. Importantly, the so-called Cádiz Wegde Thrust, which some authors assume still involves an ongoing subduction process, was discarded here as there is evidence of inactivity since upper Miocene times [30]. Finally, two additional fault-sources were included to consider potential ruptures comprising two main faults, the Horseshoe and San Vicente (AT005 + AT012) and the Guadalquivir and Portimao (AT002 + AT013) (see Section 3.1).
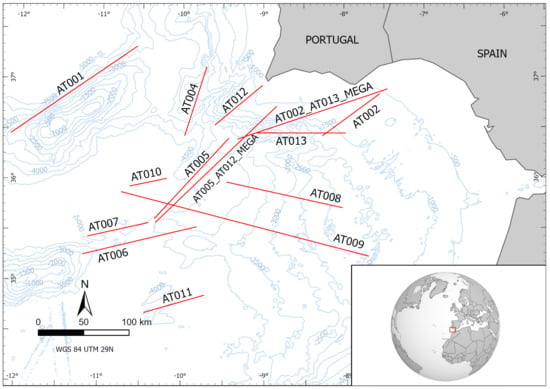
Figure 2.
Vector lines corresponding to the tsunamigenic faults considered in this study [22]. The code naming each line corresponds to that used in the QAFI database for cataloguing the faults (Table 1). The suffix ‘mega’ refers to sources combining two faults.
2.2. Topobathymetric Data Description
The elevation data used for the simulations in the studied area have different resolutions and origins. Concerning emerged terrain elevation data at 5 m pixel resolution, two options were readily available for the project. One option was the data published by the National Geographic Institute (IGN), covering the whole Spanish territory. It can be downloaded from the website [31]. This data was obtained with LIDAR technology and was processed by IGN to derive diverse types of elevation model. The second option was the national Spanish elevation model generated by IGME using IGN’s original data, including LIDAR and other IGN archives (such as stereocorrelation photograms at 25 to 50 cm pixels). This elevation model was processed, in particular, to aid in the construction of the National Continuous Geological Map (GEODE), bearing in mind other geological needs. Both models excel in their quality and extent, and may be the best suited for different purposes. Some comparison work carried out between both elevation models indicated that the IGME processing results better represented the geometry of the topographical surface suitable for tsunami simulations since it further cleaned the data of different objects (such as greenhouses, buildings, trees or bridges). This is a critical feature when computing inundation since it prevents most (yet certainly not all) unreal barriers an inundation may face. It is important to note that the IGME model does not include the most up-to-date data from the IGN, as post-processing the entire country at 5 m pixel resolution using the most recent data takes quite a long time and much effort. Therefore, the IGME elevation model at 5 m pixel resolution derived from the IGN data was used, with a granted maximum error 90% lower than 1 m. It should also be noted that the IGME model may present some lower quality results in shadowed slopes than the IGN model because some of the input sources are stereo-imaging in nature—even so, it is more suitable for the purposes of this study but may not be adequate for other approaches or studies.
Regarding submerged topography information (bathymetry), the readily available data comes from different providers at different resolutions and have been obtained by different methods. On the one hand, shallow bathymetry used for the Huelva coast has 20 m pixel resolution, as provided by the Andalusian Environmental Information Network (REDIAM). On the other hand, bathymetric data selected for simulations in the Cádiz region is at 5 m pixel resolution, as provided by the former Ministry of Agriculture, Fisheries and Food (MAPAMA), now the Ministry for Ecological Transition and Demographic Challenge (MITECO). Taking into account that these high-resolution data do not cover the entire region of interest of the project, other sources of information have been used to account for open sea areas and, therefore, to simulate wave propagation. For those regions without high-resolution data, models from the European Marine Observation and Data Network (EMODnet) and The General Bathymetric Chart of the Oceans (GEBCO) at 1/16 arc-minutes (≈115 m) and 15 arc-seconds (≈450 m) pixel resolution, respectively, were used. Both databases are freely available at their respective websites [32,33].
2.3. Pseudo-Probabilistic Approach. Random Variables Distribution and Sobol Sampling Method
Models to simulate tsunamis triggered by seismic events require, in the first instance, to reproduce the initial displacement of the water-free surface produced by the transfer of energy from the movement of the seafloor as a consequence of the fault rupture. As mentioned previously, most commonly accepted and used solutions for co-seismic seabed displacement follow Okada’s work [34], which is presented in a relatively simple and analytic form. Then, the static seafloor deformation is directly transmitted to the free surface as an initial condition [35]. Due to the uncertainty related to the determination of the Okada parameters, the simulation of the 14 faults that have been considered for the present study, may be insufficient if the goal is to understand the economic impact that any potential seismic tsunamigenic source of a given probability could produce. Accounting for a given probability is a requirement derived from the EU regulations on insurance after the Solvency II Directive 2009/138/EC. Hence a deterministic approach to unraveling a random problem in nature may not be the best approach to take. An alternative is to account for uncertainty in some of the parameters involved in the seafloor deformation. This idea is the basis of a pseudo-probabilistic study of economic impact. An artificial seismic register is generated by means of the uncertainty associated with some Okada parameters, then each artificial event is simulated and used for the economic impact assessment.
The best case scenario for a pseudo-probabilistic approach would be to consider uncertainty for all the Okada parameters, to the extent that many more different scenarios would be taken into account. However, appropriately exploring a 10-dimensional continuous parameter space for each fault, and consequently simulating every crafted event would implicate a computing power that is currently unattainable or unreasonable costly. If all ten Okada parameters were to be sampled only three times, for both extremes and the average, the amount of combinations to produce an adequate coverage of the input parameter space would increase to , which in turn would boost the simulation needs beyond combinations. Moreover, sampling only the extreme values and the average may not appropriately describe the spectrum of damage, considering the highly non-linear issues involved that play a major role. These include wave propagation, wave interaction with the coast and the bathymetry, the elevation data, inundation, and, last but not least, the distribution of elements subject to damage.
As the fault-source modeling employed for this investigation assumes geometric values for which maximum seismic rupture is plausible, parameters, such as dip angle, fault length and width, remain fixed as they illustrate maximum potential values. Furthermore, all faults are assumed to be composed by a single segment. Although variations in segmentation number can have a major impact on inundation results, their assessment would imply adding an Okada parameters list for each segment, thus exponentially increasing the number of possibilities to be combined for a single fault. With respect to the remaining parameters, some tests have been carried out to assess which of them may be described as the driving factors. It is clear that some parameters involve more uncertainty than others, such as strike, rake and slip. For example, although the strike parameter is fairly well-known, it measures fault orientation with respect to the north; thus, minor variations of this orientation could lead to situations where completely different areas become flooded. On the other hand, the rake parameter is chosen to vary to reflect its natural variation along the fault depending on the deflections of the strike with respect to the stress field. Therefore, slip as a random variable is assumed to follow a Gaussian distribution, whilst strike- and rake-associated random variables, due to their circular nature, are considered to follow a Von-Mises distribution.
To reduce the number of scenarios to be simulated, and considering that the resulting economic damage distribution is unknown, such distributions require to be sampled.
In relation to random variable sampling methods, there are several sampling techniques [36], including random-sampling, stratified sampling, Latin hypercube sampling (LHS) and quasi-random sampling with low-discrepancy sequences. Random sampling means that every case of the population has an equal probability of inclusion in the sample. It is a very straightforward method; however, it can lead to a set of gaps or clustering, meaning that there would be some sampled areas overemphasised and some non-sampled areas. Stratified sampling tackles the problem of dividing the input space into strata (or subgroups) and a random sample is taken from each subgroup. This has the advantage of obtaining representation from all the space, although some gaps may still appear. LHS is a type of stratified sampling where each parameter is individually stratified over levels, such that each level contains the same number of points ([36], p. 76). It can have the advantage of requiring less samples to adequately describe the input space, but this depends on the function to be sampled [37]. Quasi-random sampling sequences are designed to generate samples as uniformly as possible over the unit hypercube. Unlike random numbers, quasi-random points know about the position of previously sampled points, avoiding the appearance of gaps and clusters. One of the best known quasi-random sequences is the Sobol sequences.
The main sampling techniques have been tested in the context of building simulation by MacDonald and Burhenne et al. [37,38], which indicated that the Sobol sequences were superior to LHS, stratified sampling and random sampling in terms of mean convergence speed. In addition, the Sobol sequences method reduced the variability in the cumulative density function, which meant that it was the most robust method among those considered. Burhenne’s conclusions were that the Sobol sampling method should be used for building simulation, as the high computational cost requirements for the model make it impossible to run a large number of fully fledged simulations in a reasonable time. It is worth mentioning that the Sobol sequences have already been used successfully in the context of uncertainty quantification of landslide-generated waves [39].
Bearing in mind that the work presented in this paper requires huge computational effort, and in light of the literature reviewed, the Sobol sequences were used as the sampling method to explore the input parametric space considered.
2.4. Simulation Software Tsunami-Hysea and Hpc Resources
The equations most widely accepted by the scientific community to model tsunami wave propagation in the open sea are the nonlinear shallow water equations (NLSWE) [40]. This system of equations comes from a simplification of the Navier–Stokes equations for incompressible and homogeneous fluids, where vertical dynamics can be neglected in comparison to horizontal dynamics, and are set in the framework of a system of hyperbolic partial differential equations.
Nonetheless, NLSWE presents a downside when it comes to model inundation dynamics, since a tsunami wave arriving onshore generates a turbulent regime. Interaction with structures and sediments from the sea deposited on land makes 3D models a necessary tool to accurately simulate these turbulent flow dynamics [41]. In spite of the availability of numerous effective 3D models, they are computationally expensive, rendering it impossible to run complex simulations in a reasonable time or at reasonable cost. Efforts focused on calculating acceleration have included techniques such as adaptative mesh refinement (AMR) [42,43] or multicore parallel computing [44,45]. However, in the last decade, a great paradigm shift occurred in terms of calculation units, with numerical methods traditionally implemented in CPU beginning to be implemented in a graphics processing unit (GPU) environment [46,47,48], obtaining numerical simulations up to 60 times faster for real events [49].
In this study, the required tsunami simulations were performed using the Tsunami-HySEA code. Tsunami-HySEA is a numerical propagation and inundation model focused on tsunamis that was developed by the EDANYA group at Málaga University in Spain. It implements most advanced finite volume methods, combining robustness, reliability and precision on a single model based on GPU structure, allowing simulation faster than real time. Tsunami-HySEA has been widely tested [50,51,52,53,54] and has also been validated and verified following the standards of the National Tsunami Hazard and Mitigation Program (NTHMP) of the US [55,56,57]. One key feature implemented in this numerical model is the possibility of using two-way nested meshing for high-resolution simulations. The nested mesh system approach allows computing of open ocean and offshore wave propagation using meshes of lower pixel resolution since the wave length is so long that the minimum number of points needed to adequately capture its form can extend to several kilometres. Near the coast, however, the wavelength is sufficiently small that higher pixel resolution meshes are used, both to reproduce its shape and to capture complex inundation features.
The simulation setup is described as follows. First, the Okada parameters are provided for every scenario. An open boundary condition is assumed on water boundaries, the Manning coefficient is set to 0.03, which is considered a good average value for natural bed roughness, the simulation time is set to 4 h, and the output variables are maximum water height, maximum velocity and maximum mass flow. Each simulation consist of a four-level nested mesh configuration that will be detailed in the next section.
To launch all the simulations, large computational resources are required. Today, high-performance computing (HPC) centers exist all over the world and provide HPC resources for scientific applications, which can be requested and accessed by researchers. These simulations were launched in the Barcelona Supercomputing Center (BSC) cluster, located in Barcelona (Spain). The specifications of this cluster are as follows:
- Linux Operating System and an Infiniband interconnection network.
- 2 login node and 52 compute nodes, each of them:
- -
- 2 × IBM Power9 8335-GTH @ 2.4 GHz (3.0 GHz on turbo, 20 cores and 4 threads/core, total 160 threads per node)
- -
- 512 GB of main memory distributed in 16 dimms × 32 GB @ 2666 MHz
- -
- 2 × SSD 1.9 TB as local storage
- -
- 2 × 3.2 TB NVME
- -
- 4 × GPU NVIDIA V100 (Volta) with 16 GB HBM2
- -
- Single Port Mellanox EDR
- -
- GPFS via one fiber link 10 GBit
Each simulation was computed on a single GPU.
3. Results
In this section, a description of the numerical results obtained in the present study is provided. First, the complete set of the seismic sources used for the simulations is given. Then, the nested mesh configuration used for the numerical simulations is described. Later, the assignment of probabilistic distributions and the Sobol sampling process are described. Finally, this section concludes with a description of the numerical results that have been obtained.
3.1. Faults List
Figure 2 shows the distribution of the tsunamigenic fault-sources considered in this study and described in Section 2.1. They correspond to complex faults compiled in the QAFI database but are modeled here as rectangular shapes from their basic geometric parameters: length, width, dip and strike (Table 1). The slip was determined from the seismic moment equation [58] considering the rupture area of the fault from the length and width, and a shear modulus that varies between 30, 40 and 60 GPa for faults in the continental crust, oceanic crust or exhumed mantle, respectively. The seismic moment was previously calculated from its relation with the moment magnitude according to Hanks and Kanamori [59]. The moment magnitude was estimated from the empirical relationships recommended in Stirling et al. [60].

Table 1.
Okada parameters for each of the faults identified as tsunamigenic sources in the southwest of Iberia. The fault code naming corresponds to that used in the QAFI database. The coordinates correspond to the rupture centre of the fault considered as a rectangular shape. All faults are assumed to be composed of one single segment.
3.2. Nested Meshes Spatial Configuration and Resolutions
A set of four levels of nested meshes was considered to carry out the present inundation study at very high resolution along the Andalusian Atlantic coast. The computational domain is covered by the ambient mesh with a numerical resolution of 640 m per pixel, spanning from 34.28° N to 37.49° N and from 12.05° W to 5.5° W. Next, three levels of grids were nested, considering 3 meshes of 160 m pixel resolution, 10 meshes of 40 m pixel resolution and 43 meshes of 5 m pixel resolution that finally shaped the coverage of all areas of interest at high resolution. Figure 3 and Figure 4 show spatial configuration of the meshes. The areas not covered by the highest resolution meshes did not contain sufficient elements of interest for the purposes of this study, but should be included in future revisions if further urbanisation were to be undertaken.
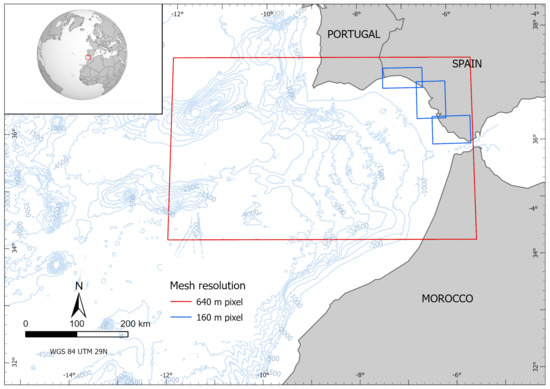
Figure 3.
Boundaries of meshes at 640 m and 160 m pixel resolution. The red rectangle delimits the simulation domain boundary, coinciding with the 640 m pixel resolution mesh. Blue rectangles indicate the extension of the three meshes at 160 m pixel resolution.
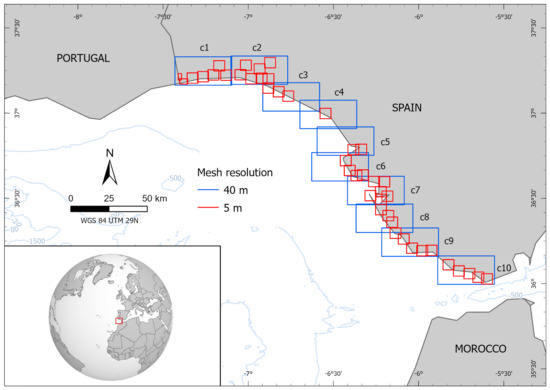
Figure 4.
Boundaries of meshes at 40 m and 5 m pixel resolution. Blue rectangles (termed as c1, …, c10, from top left to bottom right) indicate the extension of the ten meshes at 40 m pixel resolution. Red rectangles indicate the extension of the 43 meshes at 5 m pixel resolution.
Each 5 m pixel resolution mesh covers an area of 37 km, and each 40 m pixel resolution mesh covers an area of 515 km. The number of control volumes are the following:
- Each 5 m pixel resolution mesh: 1,381,952 volumes.
- Each 40 m pixel resolution mesh: 304,192 volumes.
- Upper 160 m pixel resolution mesh: 104,448 volumes.
- Middle 160 m pixel resolution mesh: 142,848 volumes.
- Bottom 160 m pixel resolution mesh: 138,592 volumes.
- 640 m pixel resolution mesh: 470,400 volumes.
The total size of the computational problem to be solved for every single simulation, if they were performed as a single simulation, is quite large, composed of 63,322,144 volumes.
3.3. Assigning Probabilistic Distributions and the Sobol Sampling Process
As previously mentioned, the strike and rake parameters are assumed to follow a Von-Mises distribution, while the slip parameter follows a normal distribution. Given the fact that the available processed data that provide information on the uncertainty of these three parameters is only related to the mean () and the standard deviation (), some intermediate work is necessary to adequately describe each fault’s Von-Mises parameters. The process is represented as follows.
Recall that the Von-Mises (VM) distribution of the mean and the dispersion , denoted as , has similar properties to the linear normal distribution. To estimate the Von-Mise distribution parameters of a circular random variable using mean and standard deviation sample values, conversion to radian units is first necessary. On the one hand, the mean value of the sample is used for the VM distribution straightforwardly. On the other hand, the standard deviation requires a different treatment, since it has to be adapted to the VM dispersion parameter, . Under certain conditions, the parameter can be considered as the inverse of the variance, [61]. The way to relate with has to do with the first trigonometric moment of the VM distribution [62]. First define the quantity (related to dispersion of circular random variable) and then solve
where is the modified Bessel function of the first kind and p the order evaluated in . The Equation (1) can be approximated using the maximum likelihood estimate of , which yields a piecewise function of (see [63], pp.85–86) defined as
This procedure allows establishing of the well-defined Von-Mises probabilistic distribution for the strike and rake parameters. Table 2 shows the different probabilistic distributions assigned by applying the described procedure.

Table 2.
For each of the faults considered in this study, probabilistic distributions associated with the parameter uncertainty is included. In the strike and rake distributions, the first parameter represents the mean in radian units.
Once the probabilistic distributions have been constructed, the procedure used to sample the three-dimensional input space of each fault using the Sobol sequence technique is described below.
- 1.
- Select a fixed number of samples N. The number of samples should be a power of 2 due to properties of the Sobol sequences, i.e., , . We choose .
- 2.
- Generate a Sobol sequence of size N in three-dimensional unit cube. This will return a three-dimensional sequence with coordinates , each one inside the interval .
- 3.
- Each coordinate is used to sample the corresponding parameter, i.e., for strike, for rake and for slip. The way to obtain the sample is through the use of the inverse transform sampling method (see [64], p. 28).
- 4.
- Now that each coordinate is associated with its corresponding sample , the tuple (, , ) is chosen for the simulation.
The Appendix A includes five tables detailing the sampled values using this procedure according to the probabilistic distributions specified in Table 2. Extracting 64 samples expresses that each fault has 64 associated variations, adding a total of synthetically generated events.
3.4. Numerical Simulations
A total of 896 simulations were launched in the BSC cluster. The simulation runtime was around 4 h for each simulation. As mentioned before, the simulation outputs were maximum water height, maximum velocity and maximum mass flow at each 5 m resolution pixel, producing a 30 MB NetCDF file each. A total amount of 1.1 TB data was generated. Among the data contained in the entire constructed database, some results have been processed and represented to demonstrate how uncertainty in the fault-source parameters affects flood distribution. The illustrations depicted come from simulations of faults AT002 and AT013, as their epicenter locations are closer to the western coast of Andalusian. In order to exemplify the uncertainty in flood distribution, considering the uncertainty associated with the 64 variants of these faults, maximum water height data were prepared for two of the 40 m sub-grids, namely, c1 and c7. The inspection consists of counting how many times each land-located pixel of the 5 m grids contained within the 40 m grids has been wet, in consideration of the 64 fault variants. Each pixel counting is then transformed into relative flood uncertainty levels by application of the Weibull-like function
where i accounts for the number of times the pixel has been wet and n is the number of fault variants (). Figure 5 and Figure 6 show the results obtained. Figure 5 displays the relative flood uncertainty behaviour with respect to the 64 variants of fault AT013 inside the 40 m grid termed as c1. It is remarkable how the areas surrounding the diverse rivers are prone to be flooded, with flood uncertainty increasing as we move away from the river courses, in contrast to the poor penetration found through Playa de Bruno and Playa Punta del Moral, which display high levels of uncertainty. Although that is not the case for the beach on the far right side region.
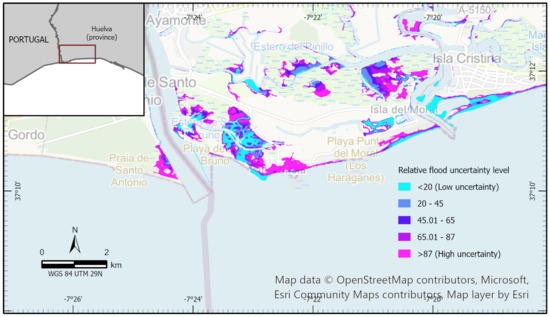
Figure 5.
Relative flood uncertainty levels inside the 40 m-grid c1 for the 64 variants of fault AT013.
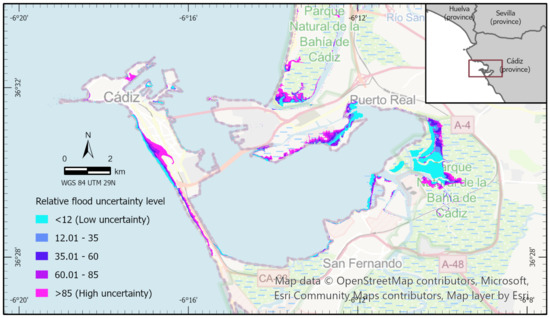
Figure 6.
Relative flood uncertainty levels inside the 40 m-grid c7 for the 64 variants of fault AT002.
Moving on to the other area, Figure 6 shows the relative behavior of the flood uncertainty with respect to the 64 variants of the AT002 fault within the 40 m grid termed as c7. It is still remarkable how flooding affects the river course’s surroundings, with low levels of uncertainty mainly found at the eastern rivers in Parque Natural de la Bahía de Cádiz. However, greater flood penetration can be seen along the coast, particularly along the western side of the city of Cádiz and in the bay coast adjacent to Puerto Real, where higher flood uncertainty is expected across some sections. In particular, the high-uncertainty area along the western coast of the city of Cádiz and the isthmus is mainly driven by variant 62, as is shown in Appendix B. Both figures illustrate regions with low and high relative flood uncertainty. Low-uncertainty regions (blue) can be interpreted as being more independent of the uncertainty in the fault-source parameters, whereas high-uncertainty regions (violet) only get flooded under a very specific configuration in the source or by concrete sources.
In addition to the flood-uncertainty figures, some results concerning the maximum water depth, maximum current velocity and maximum mass flow are presented. These results were compiled to fully harness the computational resources reserved for the project at the BSC cluster, and keeping in mind their usefulness for future research. Nonetheless, the data regarding the maximum current velocity and maximum mass flow are not of particular interest for the purpose of the final product, since the estimate of the economic damage will be performed using the data of the maximum water height. Furthermore, isolated results such as these do not contain enough useful information to derive any compelling conclusion; it is necessary to look at all the simulation results to fully understand the underlying phenomena.
Next, the same faults and regions as before are considered, i.e., faults AT002 and AT013, but now we focus on the results concerning variant 37. Variant 37 was chosen because it presents the maximum slip value sampled for both faults. Figure 7 shows three maps including the aforementioned output variables in the 5 m sub-grids placed inside the c1 grid. Figure 8 displays similar data describing the results for the 5 m sub-grids placed inside the c7 grid. Both sets of figures show a slight land inundation. This is an excellent example of why the moment magnitude (related to the slip-rate value) is not the only active factor in terms of a widening in the flooded area, since, for example, variant 62 has a lower slip value but the inundated area is larger (see Appendix B). Although the results presented in this section only account for data collected on some of the 5 m grids, they provide some insight into how uncertainty in the fault-source parameters affects wave propagation. This examination has been undertaken and pointed out in Appendix B.
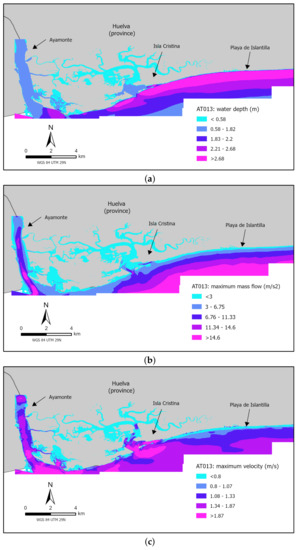
Figure 7.
Spatial representation of results obtained for the 5m sub-grids inside the 40 m-grid c1 due to variant 37 of fault AT013 for maximum water depth (a) maximum velocity (b) and maximum mass flow (c).
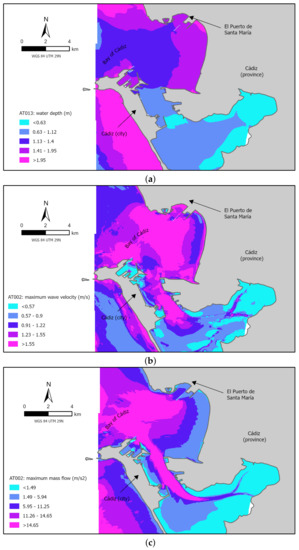
Figure 8.
Spatial representation of results obtained for the 5 m sub-grids inside the 40 m-grid c7 due to variant 37 of fault AT002 for maximum water depth (a), maximum velocity (b) and maximum mass flow (c).
4. Discussion
The most recent advances in the field of tsunami hazard assessment research have been progressively oriented towards two main areas of study: scenario-based tsunami hazard analysis (STHA) and probabilistic tsunami hazard analysis (PTHA). One technique or the other is used depending on whether the objective of a project is to design evacuation plans, including evacuation routes, or to analyze various consequences related to damage. Regarding this topic, most of the literature is populated by STHA methods, which take advantage of few simulations to address the consequences of what is generally called “the worst case scenario”—namely, a theoretical unlikely devastating event. The focal point of some of these studies is reproducing past events from historical records for which inundation maps are generated based on intensity measures, such as water heights or run-up [11,13,65,66,67]. In contrast to STHA, PTHA is a relatively new area of tsunami hazard research. Its foundations were formally established in 2006 with the pioneering work of Geist and Parsons [68], which was grounded in a probabilistic seismic hazard analysis approach. The need to consider the uncertainties involved in seismic-triggered tsunami events, together with the enhancement in computing power, has steadily led to establishing PTHA as the standard viewpoint in this matter [14,15,16,17,18,19,68,69,70]. This novel vision in dealing with problems of this nature is founded on the motivation to account for part of the inherent uncertainty in the entire generation-propagation-inundation process of a tsunami event. The key idea in the procedure is to avoid the limitations derived from considering a small set of potential catastrophes, and to produce a catalogue of varied events with the intention of reaching some conclusions in light of all the possible scenarios. The primary results deriving from these investigations are generally directed at risks, commonly related to insurance, or stochastic inundations maps. Moreover, by virtue of assigning fixed return periods to the phenomena (normally seismic ones), probability exceedance maps can be derived, in which the water height or current velocities information delivered is linked to the occurrence probabilities. In this study, we provide a major insight into why the deterministic reference frameworks mentioned above may fail to adequately identify the worst case scenario, since the non-linearity of all elements may lead to the worst consequences far from the largest seismic occurrence. A probabilistic view is difficult, but it is attainable today, and should be the way forward. The methodology followed throughout our work could be placed intermediately between STHA and PTHA. We have shown how to design a synthetic inventory of tsunamigenic events without explicitly prescribing return periods to them. Although we have not produced results comparable with other PTHA studies, what is comparable is the process of building the synthetic inventory. A common way to reconstruct this database consists of fixing some of the Okada parameters and using any sampling strategy to obtain the remaining parameters. Another methodology commonly found in the literature considers randomly distributed heterogeneous slip models [15,70], where several variants of an archetypal slip model are linked to a single fault in a process where the fault is divided into multiple subfaults and a random-generated slip is designated to each one of them. Then, the co-seismic seafloor deformation is calculated empirically from the slip and spatial distribution of the constructed subfaults, providing the initial water elevation by a simple one-on-one translation. This alternative practice for generating the database is a powerful tool when the activity is focused on the underlying uncertainties across complex fault rupture mechanisms. In the context of the previous way of building the database just described, some authors (such as González et al. [16] and Zamora et al. [69]) have designed probable seismic ruptures aiming to cover a wide variety of moment magnitude values. In [16], parameters such as strike, rake and dip remain fixed, while the main effort is concentrated on sampling a seismic moment cumulative density function and thereafter generating slip and fault area size values using some empirical relations. In [69], the authors adopt Gutenberg–Richter’s law to estimate b-values, annual earthquake rate and maximum moment magnitude with the purpose of sampling events that incorporate a significant range of seismic moments with respect to predetermined exceedance probabilities. Additionally, they use uniform and normal distributions, as well as empirical relationships to estimate the rest of the geometric parameters. In [71], the artificially crafted register is undertaken via a movement along the fault trace of what the authors termed a typical fault, which is a fault with pre-established Okada parameters in a determined source zone. The González et al., and Zamora et al., approximations have the advantage of generating events that cover a wide spectrum of seismic magnitude, thus indirectly taking into account a large limit of slip values (according to the seismic moment scalar equation [58]). We are aware that either increasing seismic moment or slip values can lead to amplification in the run-up, thus widening the flooded section. Our perspective adds uncertainty directly to the slip variable, without examining the seismic moment directly. Furthermore, we also acknowledge that the moment magnitude or slip rate are not the only variables that play an important role in understanding flood distribution, in as much as the fault segmentation number or the fault-plane dimensions may strongly contribute to it. As mentioned in Section 2.3, this work is based on fault models with the number of segments set to 1, while the fault-plane dimensions and dip angle remain fixed as well. Therefore, in order to capture differences in fault orientation and strike deviations from the stress field, we have emphasized the variability in strike and rake parameters.
In addition to the treatment of uncertainty already mentioned, it is also worth noting the high-resolution simulations that have been carried out and on which this work is based, together with the large extension of the coast that has been covered. The final objective of this project is to examine all the Spanish coasts. In the literature, authors state that, depending on the territory of study and on the local authorities, the available elevation data may or may not be adequate for the final objectives of the project. In [69], the authors use a single 1 arc-min resolution bathymetry to compute the propagation, and then, using some techniques such as Green’s Law, they project wave height at some offshore locations towards the coastline. They state that formulas such as Green’s Law are needed today because accurate modeling of the tsunami propagation and coastal impact over high-resolution nearshore bathymetry is not yet feasible for regional-scale PTHA, due to high computing resource requirements when targeting hundreds of thousands of seismic scenarios. Their concerns are justified as their inundation modeling is over 4000 km-long, making accurate data acquisition a major issue. Our study, however, is intended to grasp knowledge about inundation in a country-scale scenario and is committed to high-resolution grids in a pseudo-probabilistic scope, meaning that tens of thousands of simulations are being undertaken, covering a 2000 km-long coast. The numerical results presented here represent only a small part of the full picture we are elaborating. The aforementioned statement about infeasibility could derive from factors of limited time, limited computational resources, or even limited high-resolution elevation data collected; however, in general, we believe that, if suitable data are already available, in combination with sufficient HPC resources, the most recent tsunami codes are able to reproduce high-resolution inundation for country-scale dimensions in a matter of months. Even so, it is common knowledge that expensive computational resources for an accurate PTHA study are the main downside. Recent work aimed at circumventing this problem makes use of stochastic approximations, called emulators, built upon a pre-computed training set [20,21,39]. An emulator can be seen as an interpolating operator of the map that assigns to each input parametric array its corresponding desired output through a fully fledged simulation. The emulator encompasses the whole generation, propagation and inundation process without explicitly computing, thus allowing output predictions and uncertainty quantification at fairly low computational cost. The effectiveness of an emulator approach is closely related to the construction of the training set, which is its core. In [20], the epicenter location and moment magnitude were sampled using the LHS method to simulate 300 scenarios and retrieve the maximum water height and maximum current velocity at several locations, which in turn constitute the basis for building the training set. In [21], the authors sampled a seven-dimensional input space using a sequential design MICE algorithm to generate a training set of 60 simulated scenarios. Their sampling technique outperforms the LHS method in the sense that one-shot random sampling for the training set lacks the information acquisition achieved by the sequential design. One-shot methods, such as LHS, can overemphasize unnecessary regions and consequently waste computational resources. On the other hand, the sequential design takes into account the previously computed quantities to select the next input parameters for the next simulation batch.
Finally, recalling the grid resolution, other studies found in the literature reach highest resolution grid pixel sizes of 5 m, 10 m, 50 m, 52 m, 90 m, 93 m [8,9,10,11,12,13,15,16,17,18]. Probabilistic-oriented studies, such as [14,15], run many simulations, but either use a relatively coarse mesh (50 m and 500 m, resp.) or the affected area is relatively small, such as the studies centered only on Tohoku Island. An exception to these studies is the aforementioned emulator-oriented approach [20,21], where the highest resolution grid pixel sizes are 10 m and 30 m, respectively.
5. Conclusions
The methodology adopted in this study follows the general first-step framework in a PTHA environment, where a synthetic seismic catalogue is required to proceed with the subsequent examination. Furthermore, this study could be fully encompassed in the PTHA field if return periods and a logic-tree were added. Even without the probabilistic treatment arising from a potential attachment of return periods, the numerically computed database derived in this study regarding wave height, maximum velocity and maximum mass flow provides an excellent starting point to assess different tsunami-hazard-related issues, such as designing vulnerability functions, developing loss functions or evaluating structural losses (e.g., [8,9,10,14]).
In particular, our objectives are aimed at drawing conclusions about the economic-related damage distribution caused by a theoretical but plausible tsunamigenic event. In practice, we will determine economic damage due to a specific variation of a single fault in a specific region by overlaying the maximum water height data with the building-scale data in the insurance field. Based on the maximum height of the water column recorded on a single pixel containing any type of construction, an economic value will be associated with it due to a preselected vulnerability function. Adding together the pixel-scale damage estimates for all covered locations will deliver a mapping that links every fault variation to a singular value representing its potential economic damage. By repeating the indicated procedure for the variations of each fault, a probabilistic distribution of the economic damage will be naturally generated, which will be further analyzed. The damage distribution function may have little to do with the largest triggered magnitudes, or the damage may even not be concentrated around the largest flood-likely areas. Direct damage is only possible with the coalescence of any sort of valuable elements (such as people, property, services) with the consequent impact of the phenomena. Such direct damage may then be responsible for further indirect losses (due to the topological and dependent construction of human societies). Considering that neither valuable items nor the value itself are uniformly distributed, in addition to the fact that what is insured, and up to how much, is also unevenly allocated, a probabilistic approach makes more sense to better understand the final damage curve distribution. The most likely damage estimation in terms of monetary loss for the insurance sector cannot be evaluated without considering the full extent of uncertainties in the source and their effects in flooding valuable assets. The results of this work show that some areas are less influenced by the uncertainty in the triggering mechanisms, whereas other areas will only get flooded under a very specific set of triggering conditions. If we only account for one of those sets (a scenario-based approach), it is unclear whether the resulting damage belongs to the most likely output of the many uncertain initial conditions or is actually a representative event of the outcome considering variations in the initial conditions. This method contributes to a better understanding of the damage function, providing crucial and non-pre-existing information for the insurance sector to make better-informed decisions.
Concerning other applications, water height data can also be exploited to understand nearshore and onshore flood distribution from an arbitrary tsunami of Atlantic origin, facilitating the production of stochastic inundations maps and evacuation routes for people living near the coast. Additional information regarding maximum velocity and maximum mass flow can undoubtedly be useful in approaching the evaluation of particular structural damage.
We would like to highlight the importance of the results of this article concerning the numerous computed numerical simulations in conjunction with their high-resolution discretization, where each simulation has produced relevant information for the outstanding population nucleus placed alongside the Atlantic Andalusian coast in building-scale detail.
Future research with reference to this topic should aim to exploit the generated database in search of building-related information of interest in the field of PTHA. The extra work required to achieve these objectives would undeniably be worth the immense enhancement in people’s safety and tsunami risk management by regional and local authorities.
Author Contributions
Conceptualization, M.L.; methodology, A.G., J.M., C.S.-L., J.G.-M. and C.P.; literature review, A.G., J.M. and J.G.-M.; supervision, M.L., J.M. and C.S.-L.; visualization, M.F. and M.L.; resources, A.G., J.M., C.S.-L. and J.G.-M.; funding, M.L., J.M.; data curation, A.G. and C.S.-L. All authors have read and agreed to the published version of the manuscript.
Funding
This work has being carried out under a project funded by a public mutual agreement of understanding between the CN-IGME (CSIC) and the CCS (Law reference: BOE 103, 30/04/2019). This project is supported by an agreement of understanding between CN-IGME and UMA, creating a cooperative entity INGEA (Law reference: BOE 332, 22/12/2020). The numerical results presented in this work have been performed with the computational resources allocated by the Spanish Network for Supercomputing (RES) grants AECT-2020-3-0023 and AECT-2021-2-0018. Further support has also been received from the Spanish Government research project MEGAFLOW (RTI2018-096064-B-C21) and ChEESE project (EU Horizon 2020, grant agreement No. 823844, https://cheese-coe.eu/) due to the synergies found between the projects.
Acknowledgments
This work has been carried out with the cooperation of many institutions backing up and helping us in the discussions. Amongst them: IGN, IEO, Civil Protection Authorities (national and regional), ICM-CSIC, IHC, IHM, State Ports, and CEDEX, and several universities, including UA, UGRA, UPM School of Civil Engineering, UCM School of Mining and Energy Engineering, UCM, and UMA.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PTHA | Probabilistic Tsunami Hazard Analysis |
| STHA | Scenario-based Tsunami Hazard Analysis |
| PSHA | Probabilistic Seismic Hazard Analysis |
| VM | Von-Mises |
| QAFI | Quaternary Active Fault of Iberia |
| TEWS | Tsunami Early Warning Systems |
| CCS | Insurance Compensation Consortium of Spain |
| CSIC | Spanish National Research Council |
| IGME | Spanish Geological Survey |
| IGN | National Geographic Institute |
| GEODE | National Continuous Geological Map |
| LIDAR | Light Detection And Ranging |
| REDIAM | Andalusian Environmental Information Network |
| MITECO | Ecological Transition and Demographic Challenge |
| EMODnet | European Marine Observation and Data Network |
| GEBCO | General Bathymetric Chart of the Oceans |
| LHS | Latin Hypercube Sampling |
| NLSWE | Non-linear Shallow Water Equations |
| AMR | Adaptative Mesh Refinement |
| NTHMP | National Tsunami Hazard and Mitigation Program |
| HPC | High-Performance Computing |
| BSC | Barcelona Supercomputing Center |
| EDANYA | Differential Equations, Mathematical Analysis and Applications |
Appendix A. Sobol Sampling Method Results
Results of the sampling technique described in Section 3.3 are presented within this appendix. Table A1, Table A2, Table A3, Table A4 and Table A5 encapsulate all sampled values used for the subsequent simulations.

Table A1.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
Table A1.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
| AT002 | AT005 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT001 | AT002 | AT004 | AT005 | AT006 | AT007 | AT008 | AT009 | AT010 | AT011 | AT012 | AT013 | + | + | |
| AT013 | AT012 | |||||||||||||
| 0 | 60.0 90.0 3.684 | 240.0 90.0 3.022 | 21.0 90.0 3.015 | 48.0 90.0 3.978 | 78.0 90.0 5.365 | 79.0 90.0 2.789 | 100.0 180.0 1.212 | 102.0 180.0 1.748 | 80.0 180.0 0.694 | 76.0 90.0 2.746 | 56.0 90.0 3.027 | 270.0 90.0 4.229 | 255.0 90.0 7.367 | 52.0 90.0 6.345 |
| 1 | 61.686 76.69 4.712 | 243.37 76.69 3.865 | 22.686 83.277 3.858 | 49.686 83.277 5.091 | 79.686 83.277 6.866 | 80.686 83.277 3.568 | 100.674 173.277 1.549 | 103.012 173.277 2.237 | 80.674 173.277 0.89 | 82.723 83.277 3.515 | 57.686 83.277 3.873 | 273.37 76.69 5.413 | 258.37 76.69 9.431 | 53.686 83.277 8.092 |
| 2 | 58.314 103.31 2.655 | 236.63 103.31 2.179 | 19.314 96.723 2.172 | 46.314 96.723 2.866 | 76.314 96.723 3.865 | 77.314 96.723 2.01 | 99.326 −173 0.875 | 100.988 −173 1.259 | 79.326 −173 0.499 | 69.277 96.723 1.977 | 54.314 96.723 2.181 | 266.63 103.31 3.046 | 251.63 103.31 5.303 | 50.314 96.723 4.598 |
| 3 | 59.204 83.724 4.169 | 238.408 83.724 3.42 | 20.204 86.825 3.413 | 47.204 86.825 4.504 | 77.204 86.825 6.074 | 78.204 86.825 3.157 | 99.681 176.825 1.371 | 101.522 176.825 1.979 | 79.681 176.825 0.787 | 72.825 86.825 3.109 | 55.204 86.825 3.427 | 268.408 83.724 4.789 | 253.408 83.724 8.342 | 51.204 86.825 7.17 |
| 4 | 62.875 112.804 1.929 | 245.749 112.804 1.584 | 23.875 101.479 1.577 | 50.875 101.479 2.08 | 80.875 101.479 2.806 | 81.875 101.479 1.46 | 101.15 −168 0.637 | 103.725 −168 0.914 | 81.15 −168 0.361 | 87.479 101.479 1.435 | 58.875 101.479 1.583 | 275.749 112.804 2.21 | 260.749 112.804 3.847 | 54.875 101.479 3.366 |
| 5 | 60.796 67.196 3.198 | 241.592 67.196 2.624 | 21.796 78.521 2.617 | 48.796 78.521 3.453 | 78.796 78.521 4.656 | 79.796 78.521 2.421 | 100.319 168.521 1.053 | 102.478 168.521 1.517 | 80.319 168.521 0.602 | 79.175 78.521 2.383 | 56.796 78.521 2.627 | 271.592 67.196 3.67 | 256.592 67.196 6.392 | 52.796 78.521 5.52 |
| 6 | 57.125 96.276 5.438 | 234.251 96.276 4.46 | 18.125 93.175 4.453 | 45.125 93.175 5.877 | 75.125 93.175 7.925 | 76.125 93.175 4.117 | 98.85 −176 1.787 | 100.275 −176 2.582 | 78.85 −176 1.028 | 64.521 93.175 4.057 | 53.125 93.175 4.471 | 264.251 96.276 6.248 | 249.251 96.276 10.887 | 49.125 93.175 9.325 |
| 7 | 57.783 80.366 2.938 | 235.567 80.366 2.411 | 18.783 85.13 2.404 | 45.783 85.13 3.172 | 75.783 85.13 4.278 | 76.783 85.13 2.224 | 99.113 175.13 0.968 | 100.669 175.13 1.394 | 79.113 175.13 0.552 | 67.154 85.13 2.189 | 53.783 85.13 2.414 | 265.567 80.366 3.372 | 250.567 80.366 5.871 | 49.783 85.13 5.079 |
| 8 | 61.222 107.537 5.036 | 242.442 107.537 4.131 | 22.222 98.846 4.124 | 49.222 98.846 5.442 | 79.222 98.846 7.339 | 80.222 98.846 3.813 | 100.489 −171 1.656 | 102.733 −171 2.391 | 80.489 −171 0.951 | 80.87 98.846 3.757 | 57.222 98.846 4.14 | 272.442 107.537 5.786 | 257.442 107.537 10.082 | 53.222 98.846 8.643 |
| 9 | 63.835 59.418 3.923 | 247.669 59.418 3.219 | 24.835 74.671 3.212 | 51.835 74.671 4.238 | 81.835 74.671 5.715 | 82.835 74.671 2.97 | 101.534 164.671 1.291 | 104.301 164.671 1.862 | 81.534 164.671 0.74 | 91.329 74.671 2.925 | 59.835 74.671 3.224 | 277.669 59.418 4.505 | 262.669 59.418 7.848 | 55.835 74.671 6.753 |
| 10 | 59.607 93.097 1.344 | 239.214 93.097 1.104 | 20.607 91.567 1.097 | 47.607 91.567 1.447 | 77.607 91.567 1.952 | 78.607 91.567 1.017 | 99.843 −178 0.445 | 101.764 −178 0.636 | 79.843 −178 0.249 | 74.433 91.567 0.997 | 55.607 91.567 1.102 | 269.214 93.097 1.537 | 254.214 93.097 2.673 | 51.607 91.567 2.372 |
| 11 | 58.778 72.463 6.023 | 237.558 72.463 4.94 | 19.778 81.154 4.933 | 46.778 81.154 6.51 | 76.778 81.154 8.779 | 77.778 81.154 4.56 | 99.511 171.154 1.979 | 101.267 171.154 2.861 | 79.511 171.154 1.139 | 71.13 81.154 4.495 | 54.778 81.154 4.952 | 267.558 72.463 6.922 | 252.558 72.463 12.062 | 50.778 81.154 10.319 |
| 12 | 62.217 99.634 3.444 | 244.433 99.634 2.825 | 23.217 94.87 2.818 | 50.217 94.87 3.719 | 80.217 94.87 5.015 | 81.217 94.87 2.607 | 100.887 −175 1.133 | 103.331 −175 1.634 | 80.887 −175 0.648 | 84.846 94.87 2.567 | 58.217 94.87 2.83 | 274.433 99.634 3.953 | 259.433 99.634 6.886 | 54.217 94.87 5.938 |
| 13 | 60.393 86.903 2.331 | 240.786 86.903 1.913 | 21.393 88.433 1.906 | 48.393 88.433 2.515 | 78.393 88.433 3.391 | 79.393 88.433 1.764 | 100.157 178.433 0.769 | 102.236 178.433 1.105 | 80.157 178.433 0.437 | 77.567 88.433 1.735 | 56.393 88.433 1.914 | 270.786 86.903 2.672 | 255.786 86.903 4.652 | 52.393 88.433 4.047 |

Table A2.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
Table A2.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
| AT002 | AT005 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT001 | AT002 | AT004 | AT005 | AT006 | AT007 | AT008 | AT009 | AT010 | AT011 | AT012 | AT013 | + | + | |
| AT013 | AT012 | |||||||||||||
| 14 | 56.165 120.582 4.429 | 232.331 120.582 3.633 | 17.165 105.329 3.626 | 44.165 105.329 4.785 | 74.165 105.329 6.453 | 75.165 105.329 3.353 | 98.466 −164 1.457 | 99.699 −164 2.103 | 78.466 −164 0.836 | 60.671 105.329 3.303 | 52.165 105.329 3.64 | 262.331 120.582 5.087 | 247.331 120.582 8.863 | 48.165 105.329 7.611 |
| 15 | 56.705 88.456 5.224 | 233.413 88.456 4.284 | 17.705 89.219 4.277 | 44.705 89.219 5.645 | 74.705 89.219 7.612 | 75.705 89.219 3.955 | 98.682 179.219 1.717 | 100.023 179.219 2.481 | 78.682 179.219 0.987 | 62.841 89.219 3.897 | 52.705 89.219 4.295 | 263.413 88.456 6.002 | 248.413 88.456 10.458 | 48.705 89.219 8.961 |
| 16 | 60.593 127.363 3.07 | 241.185 127.363 2.519 | 21.593 108.639 2.512 | 48.593 108.639 3.315 | 78.593 108.639 4.47 | 79.593 108.639 2.324 | 100.237 −161 1.011 | 102.356 −161 1.457 | 80.237 −161 0.577 | 78.363 108.639 2.287 | 56.593 108.639 2.522 | 271.185 127.363 3.523 | 256.185 127.363 6.136 | 52.593 108.639 5.303 |
| 17 | 62.525 74.667 1.674 | 245.047 74.667 1.374 | 23.525 82.26 1.367 | 50.525 82.26 1.804 | 80.525 82.26 2.433 | 81.525 82.26 1.266 | 101.01 172.26 0.553 | 103.515 172.26 0.793 | 81.01 172.26 0.312 | 86.074 82.26 1.243 | 58.525 82.26 1.373 | 275.047 74.667 1.916 | 260.047 74.667 3.334 | 54.525 82.26 2.931 |
| 18 | 58.995 101.421 4.045 | 237.991 101.421 3.318 | 19.995 95.772 3.311 | 46.995 95.772 4.37 | 76.995 95.772 5.893 | 77.995 95.772 3.063 | 99.598 −174 1.331 | 101.397 −174 1.92 | 79.598 −174 0.763 | 71.992 95.772 3.016 | 54.995 95.772 3.325 | 267.991 101.421 4.646 | 252.991 101.421 8.093 | 50.995 95.772 6.959 |
| 19 | 59.804 63.814 3.564 | 239.608 63.814 2.924 | 20.804 76.841 2.917 | 47.804 76.841 3.849 | 77.804 76.841 5.191 | 78.804 76.841 2.698 | 99.922 166.841 1.173 | 101.882 166.841 1.691 | 79.922 166.841 0.671 | 75.219 76.841 2.657 | 55.804 76.841 2.929 | 269.608 63.814 4.092 | 254.608 63.814 7.127 | 51.804 76.841 6.142 |
| 20 | 64.657 94.671 6.524 | 249.315 94.671 5.35 | 25.657 92.363 5.343 | 52.657 92.363 7.052 | 82.657 92.363 9.51 | 83.657 92.363 4.94 | 101.863 −177 2.143 | 104.794 −177 3.099 | 81.863 −177 1.234 | 94.639 92.363 4.869 | 60.657 92.363 5.365 | 279.315 94.671 7.498 | 264.315 94.671 13.067 | 56.657 92.363 11.17 |
| 21 | 61.448 82.074 4.567 | 242.893 82.074 3.746 | 22.448 85.992 3.739 | 49.448 85.992 4.934 | 79.448 85.992 6.654 | 80.448 85.992 3.457 | 100.579 175.992 1.502 | 102.869 175.992 2.168 | 80.579 175.992 0.862 | 81.772 85.992 3.406 | 57.448 85.992 3.754 | 272.893 82.074 5.246 | 257.893 82.074 9.139 | 53.448 85.992 7.845 |
| 22 | 58.059 109.989 2.5 | 236.121 109.989 2.051 | 19.059 100.074 2.044 | 46.059 100.074 2.697 | 76.059 100.074 3.638 | 77.059 100.074 1.892 | 99.224 −169 0.824 | 100.835 −169 1.185 | 79.224 −169 0.469 | 68.26 100.074 1.861 | 54.059 100.074 2.053 | 266.121 109.989 2.867 | 251.121 109.989 4.991 | 50.059 100.074 4.334 |
| 23 | 57.475 70.011 3.803 | 234.953 70.011 3.12 | 18.475 79.926 3.113 | 45.475 79.926 4.108 | 75.475 79.926 5.54 | 76.475 79.926 2.879 | 98.99 169.926 1.251 | 100.485 169.926 1.805 | 78.99 169.926 0.717 | 65.926 79.926 2.835 | 53.475 79.926 3.125 | 264.953 70.011 4.367 | 249.953 70.011 7.607 | 49.475 79.926 6.548 |
| 24 | 61.005 97.926 0.843 | 242.009 97.926 0.693 | 22.005 94.008 0.687 | 49.005 94.008 0.905 | 79.005 94.008 1.221 | 80.005 94.008 0.637 | 100.402 −175 0.281 | 102.603 −175 0.398 | 80.402 −175 0.154 | 80.008 94.008 0.622 | 57.005 94.008 0.689 | 272.009 97.926 0.96 | 257.009 97.926 1.667 | 53.005 94.008 1.521 |
| 25 | 63.295 85.329 2.8 | 246.587 85.329 2.298 | 24.295 87.637 2.291 | 51.295 87.637 3.023 | 81.295 87.637 4.077 | 82.295 87.637 2.12 | 101.318 177.637 0.923 | 103.977 177.637 1.328 | 81.318 177.637 0.526 | 89.159 87.637 2.086 | 59.295 87.637 2.3 | 276.587 85.329 3.213 | 261.587 85.329 5.595 | 55.295 87.637 4.845 |
| 26 | 59.407 116.186 4.868 | 238.815 116.186 3.992 | 20.407 103.159 3.985 | 47.407 103.159 5.26 | 77.407 103.159 7.093 | 78.407 103.159 3.685 | 99.763 −166 1.6 | 101.644 −166 2.311 | 79.763 −166 0.919 | 73.637 103.159 3.631 | 55.407 103.159 4.001 | 268.815 116.186 5.592 | 253.815 116.186 9.743 | 51.407 103.159 8.356 |
| 27 | 58.552 78.579 2.143 | 237.107 78.579 1.759 | 19.552 84.228 1.752 | 46.552 84.228 2.312 | 76.552 84.228 3.118 | 77.552 84.228 1.622 | 99.421 174.228 0.707 | 101.131 174.228 1.016 | 79.421 174.228 0.401 | 70.228 84.228 1.595 | 54.552 84.228 1.759 | 267.107 78.579 2.457 | 252.107 78.579 4.277 | 50.552 84.228 3.729 |

Table A3.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
Table A3.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
| AT002 | AT005 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT001 | AT002 | AT004 | AT005 | AT006 | AT007 | AT008 | AT009 | AT010 | AT011 | AT012 | AT013 | + | + | |
| AT013 | AT012 | |||||||||||||
| 28 | 61.941 105.333 4.297 | 243.879 105.333 3.525 | 22.941 97.74 3.518 | 49.941 97.74 4.642 | 79.941 97.74 6.26 | 80.941 97.74 3.253 | 100.776 −172 1.413 | 103.165 −172 2.04 | 80.776 −172 0.811 | 83.74 97.74 3.205 | 57.941 97.74 3.532 | 273.879 105.333 4.935 | 258.879 105.333 8.598 | 53.941 97.74 7.387 |
| 29 | 60.196 52.637 5.694 | 240.392 52.637 4.669 | 21.196 71.361 4.662 | 48.196 71.361 6.153 | 78.196 71.361 8.298 | 79.196 71.361 4.311 | 100.078 161.361 1.871 | 102.118 161.361 2.704 | 80.078 161.361 1.076 | 76.781 71.361 4.249 | 56.196 71.361 4.681 | 270.392 52.637 6.542 | 255.392 52.637 11.4 | 52.196 71.361 9.759 |
| 30 | 55.343 91.544 3.322 | 230.685 91.544 2.725 | 16.343 90.781 2.718 | 43.343 90.781 3.587 | 73.343 90.781 4.837 | 74.343 90.781 2.515 | 98.137 −179 1.094 | 99.206 −179 1.576 | 78.137 −179 0.625 | 57.361 90.781 2.476 | 51.343 90.781 2.729 | 260.685 91.544 3.813 | 245.685 91.544 6.641 | 47.343 90.781 5.731 |
| 31 | 55.81 77.649 4.107 | 231.621 77.649 3.369 | 16.81 83.76 3.362 | 43.81 83.76 4.437 | 73.81 83.76 5.983 | 74.81 83.76 3.109 | 98.324 173.76 1.351 | 99.486 173.76 1.95 | 78.324 173.76 0.775 | 59.245 83.76 3.063 | 51.81 83.76 3.376 | 261.621 77.649 4.717 | 246.621 77.649 8.217 | 47.81 83.76 7.064 |
| 32 | 60.294 104.302 1.808 | 240.588 104.302 1.485 | 21.294 97.222 1.478 | 48.294 97.222 1.949 | 78.294 97.222 2.629 | 79.294 97.222 1.368 | 100.118 −172 0.597 | 102.177 −172 0.857 | 80.118 −172 0.337 | 77.173 97.222 1.344 | 56.294 97.222 1.484 | 270.588 104.302 2.071 | 255.588 104.302 3.604 | 52.294 97.222 3.16 |
| 33 | 62.076 46.507 3.134 | 244.15 46.507 2.572 | 23.076 68.415 2.565 | 50.076 68.415 3.384 | 80.076 68.415 4.564 | 81.076 68.415 2.373 | 100.83 158.415 1.032 | 103.246 158.415 1.487 | 80.83 158.415 0.59 | 84.281 68.415 2.335 | 58.076 68.415 2.575 | 274.15 46.507 3.597 | 259.15 46.507 6.265 | 54.076 68.415 5.412 |
| 34 | 58.667 90.771 5.327 | 237.335 90.771 4.369 | 19.667 90.39 4.362 | 46.667 90.39 5.756 | 76.667 90.39 7.763 | 77.667 90.39 4.033 | 99.467 −179 1.751 | 101.2 −179 2.53 | 79.467 −179 1.007 | 70.684 90.39 3.974 | 54.667 90.39 4.379 | 267.335 90.771 6.12 | 252.335 90.771 10.664 | 50.667 90.39 9.136 |
| 35 | 59.507 68.658 2.579 | 239.015 68.658 2.116 | 20.507 79.25 2.109 | 47.507 79.25 2.783 | 77.507 79.25 3.753 | 78.507 79.25 1.952 | 99.803 169.25 0.85 | 101.704 169.25 1.223 | 79.803 169.25 0.484 | 74.036 79.25 1.92 | 55.507 79.25 2.118 | 269.015 68.658 2.958 | 254.015 68.658 5.15 | 51.507 79.25 4.469 |
| 36 | 63.544 97.094 4.638 | 247.087 97.094 3.804 | 24.544 93.588 3.798 | 51.544 93.588 5.012 | 81.544 93.588 6.758 | 82.544 93.588 3.512 | 101.418 −176 1.525 | 104.127 −176 2.202 | 81.418 −176 0.876 | 90.16 93.588 3.46 | 59.544 93.588 3.813 | 277.087 97.094 5.328 | 262.087 97.094 9.283 | 55.544 93.588 7.967 |
| 37 | 61.112 84.531 6.968 | 242.223 84.531 5.714 | 22.112 87.233 5.707 | 49.112 87.233 7.532 | 79.112 87.233 10.158 | 80.112 87.233 5.276 | 100.445 177.233 2.289 | 102.668 177.233 3.31 | 80.445 177.233 1.319 | 80.435 87.233 5.201 | 57.112 87.233 5.73 | 272.223 84.531 8.009 | 257.223 84.531 13.958 | 53.112 87.233 11.924 |
| 38 | 57.633 114.405 3.624 | 235.269 114.405 2.973 | 18.633 102.275 2.966 | 45.633 102.275 3.914 | 75.633 102.275 5.278 | 76.633 102.275 2.743 | 99.053 −167 1.193 | 100.58 −167 1.72 | 79.053 −167 0.683 | 66.558 102.275 2.701 | 53.633 102.275 2.978 | 265.269 114.405 4.161 | 250.269 114.405 7.247 | 49.633 102.275 6.244 |
| 39 | 58.189 61.79 4.95 | 236.38 61.79 4.06 | 19.189 75.84 4.053 | 46.189 75.84 5.349 | 76.189 75.84 7.213 | 77.189 75.84 3.748 | 99.276 165.84 1.627 | 100.913 165.84 2.35 | 79.276 165.84 0.935 | 68.778 75.84 3.693 | 54.189 75.84 4.069 | 266.38 61.79 5.687 | 251.38 61.79 9.908 | 50.189 75.84 8.496 |
| 40 | 61.565 93.881 2.87 | 243.128 93.881 2.355 | 22.565 91.964 2.348 | 49.565 91.964 3.098 | 79.565 91.964 4.178 | 80.565 91.964 2.172 | 100.626 −178 0.945 | 102.939 −178 1.362 | 80.626 −178 0.539 | 82.24 91.964 2.138 | 57.565 91.964 2.358 | 273.128 93.881 3.293 | 258.128 93.881 5.735 | 53.565 91.964 4.964 |
| 41 | 65.385 81.229 1.128 | 250.775 81.229 0.927 | 26.385 85.565 0.92 | 53.385 85.565 1.213 | 83.385 85.565 1.636 | 84.385 85.565 0.853 | 102.154 175.565 0.374 | 105.231 175.565 0.533 | 82.154 175.565 0.208 | 97.585 85.565 0.835 | 61.385 85.565 0.924 | 280.775 81.229 1.288 | 265.775 81.229 2.239 | 57.385 85.565 2.004 |

Table A4.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
Table A4.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
| AT002 | AT005 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT001 | AT002 | AT004 | AT005 | AT006 | AT007 | AT008 | AT009 | AT010 | AT011 | AT012 | AT013 | + | + | |
| AT013 | AT012 | |||||||||||||
| 42 | 59.902 108.726 3.863 | 239.804 108.726 3.169 | 20.902 99.442 3.162 | 47.902 99.442 4.173 | 77.902 99.442 5.627 | 78.902 99.442 2.925 | 99.961 −170 1.271 | 101.941 −170 1.834 | 79.961 −170 0.728 | 75.61 99.442 2.88 | 55.902 99.442 3.175 | 269.804 108.726 4.436 | 254.804 108.726 7.727 | 51.902 99.442 6.65 |
| 43 | 59.1 87.681 3.383 | 238.201 87.681 2.776 | 20.1 88.827 2.769 | 47.1 88.827 3.653 | 77.1 88.827 4.927 | 78.1 88.827 2.561 | 99.64 178.827 1.114 | 101.46 178.827 1.605 | 79.64 178.827 0.637 | 72.412 88.827 2.521 | 55.1 88.827 2.78 | 268.201 87.681 3.883 | 253.201 87.681 6.764 | 51.1 88.827 5.835 |
| 44 | 62.693 123.492 5.846 | 245.384 123.492 4.794 | 23.693 106.755 4.787 | 50.693 106.755 6.318 | 80.693 106.755 8.52 | 81.693 106.755 4.426 | 101.077 −163 1.921 | 103.616 −163 2.776 | 81.077 −163 1.105 | 86.75 106.755 4.362 | 58.693 106.755 4.806 | 275.384 123.492 6.718 | 260.384 123.492 11.706 | 54.693 106.755 10.017 |
| 45 | 60.694 73.591 4.362 | 241.387 73.591 3.578 | 21.694 81.719 3.571 | 48.694 81.719 4.713 | 78.694 81.719 6.356 | 79.694 81.719 3.303 | 100.278 171.719 1.435 | 102.417 171.719 2.071 | 80.278 171.719 0.823 | 78.767 81.719 3.253 | 56.694 81.719 3.586 | 271.387 73.591 5.01 | 256.387 73.591 8.729 | 52.694 81.719 7.498 |
| 46 | 56.926 100.516 2.24 | 233.854 100.516 1.838 | 17.926 95.316 1.831 | 44.926 95.316 2.416 | 74.926 95.316 3.259 | 75.926 95.316 1.695 | 98.77 −174 0.739 | 100.155 −174 1.062 | 78.77 −174 0.42 | 63.725 95.316 1.667 | 52.926 95.316 1.839 | 263.854 100.516 2.568 | 248.854 100.516 4.47 | 48.926 95.316 3.893 |
| 47 | 56.456 75.698 2.729 | 232.913 75.698 2.239 | 17.456 82.778 2.232 | 44.456 82.778 2.945 | 74.456 82.778 3.972 | 75.456 82.778 2.065 | 98.582 172.778 0.899 | 99.873 172.778 1.294 | 78.582 172.778 0.513 | 61.84 82.778 2.032 | 52.456 82.778 2.241 | 262.913 75.698 3.131 | 247.913 75.698 5.451 | 48.456 82.778 4.724 |
| 48 | 60.493 102.351 4.788 | 240.985 102.351 3.928 | 21.493 96.24 3.921 | 48.493 96.24 5.174 | 78.493 96.24 6.977 | 79.493 96.24 3.625 | 100.197 −173 1.574 | 102.296 −173 2.274 | 80.197 −173 0.904 | 77.964 96.24 3.572 | 56.493 96.24 3.936 | 270.985 102.351 5.501 | 255.985 102.351 9.584 | 52.493 96.24 8.222 |
| 49 | 62.367 89.229 3.743 | 244.731 89.229 3.071 | 23.367 89.61 3.064 | 50.367 89.61 4.043 | 80.367 89.61 5.452 | 81.367 89.61 2.834 | 100.947 179.61 1.232 | 103.42 179.61 1.777 | 80.947 179.61 0.705 | 85.442 89.61 2.791 | 58.367 89.61 3.076 | 274.731 89.229 4.298 | 259.731 89.229 7.487 | 54.367 89.61 6.447 |
| 50 | 58.888 133.493 0.399 | 237.777 133.493 0.33 | 19.888 111.585 0.323 | 46.888 111.585 0.425 | 76.888 111.585 0.573 | 77.888 111.585 0.301 | 99.555 −158 0.135 | 101.332 −158 0.187 | 79.555 −158 0.069 | 71.565 111.585 0.291 | 54.888 111.585 0.324 | 267.777 133.493 0.449 | 252.777 133.493 0.776 | 50.888 111.585 0.767 |
| 51 | 59.706 82.906 5.559 | 239.412 82.906 4.559 | 20.706 86.412 4.552 | 47.706 86.412 6.008 | 77.706 86.412 8.102 | 78.706 86.412 4.209 | 99.882 176.412 1.827 | 101.823 176.412 2.64 | 79.882 176.412 1.051 | 74.827 86.412 4.148 | 55.706 86.412 4.57 | 269.412 82.906 6.388 | 254.412 82.906 11.13 | 51.706 86.412 9.53 |
| 52 | 64.19 111.342 3.26 | 248.379 111.342 2.675 | 25.19 100.75 2.668 | 52.19 100.75 3.52 | 82.19 100.75 4.747 | 83.19 100.75 2.468 | 101.676 −169 1.073 | 104.514 −169 1.547 | 81.676 −169 0.614 | 92.755 100.75 2.429 | 60.19 100.75 2.679 | 278.379 111.342 3.742 | 263.379 111.342 6.517 | 56.19 100.75 5.626 |
| 53 | 61.333 65.595 2.04 | 242.665 65.595 1.675 | 22.333 77.725 1.668 | 49.333 77.725 2.201 | 79.333 77.725 2.968 | 80.333 77.725 1.544 | 100.533 167.725 0.673 | 102.8 167.725 0.967 | 80.533 167.725 0.382 | 81.316 77.725 1.518 | 57.333 77.725 1.675 | 272.665 65.595 2.338 | 257.665 65.595 4.07 | 53.333 77.725 3.554 |
| 54 | 57.924 95.469 4.233 | 235.85 95.469 3.472 | 18.924 92.767 3.465 | 45.924 92.767 4.573 | 75.924 92.767 6.167 | 76.924 92.767 3.205 | 99.17 −177 1.392 | 100.754 −177 2.009 | 79.17 −177 0.799 | 67.719 92.767 3.157 | 53.924 92.767 3.479 | 265.85 95.469 4.861 | 250.85 95.469 8.469 | 49.924 92.767 7.278 |
| 55 | 57.307 86.119 1.521 | 234.616 86.119 1.25 | 18.307 88.036 1.243 | 45.307 88.036 1.639 | 75.307 88.036 2.211 | 76.307 88.036 1.151 | 98.923 178.036 0.503 | 100.384 178.036 0.72 | 78.923 178.036 0.283 | 65.25 88.036 1.13 | 53.307 88.036 1.248 | 264.616 86.119 1.741 | 249.616 86.119 3.029 | 49.307 88.036 2.673 |

Table A5.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
Table A5.
Sobol sampling results. Each cell numbers are, from top to bottom, strike, rake and slip. Strike and rake units are decimal degrees.
| AT002 | AT005 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT001 | AT002 | AT004 | AT005 | AT006 | AT007 | AT008 | AT009 | AT010 | AT011 | AT012 | AT013 | + | + | |
| AT013 | AT012 | |||||||||||||
| 56 | 60.9 118.21 3.984 | 241.799 118.21 3.268 | 21.9 104.16 3.261 | 48.9 104.16 4.304 | 78.9 104.16 5.804 | 79.9 104.16 3.016 | 100.36 −165 1.311 | 102.54 −165 1.891 | 80.36 −165 0.751 | 79.588 104.16 2.971 | 56.9 104.16 3.274 | 271.799 118.21 4.575 | 256.799 118.21 7.97 | 52.9 104.16 6.856 |
| 57 | 63.074 71.274 5.127 | 246.146 71.274 4.205 | 24.074 80.558 4.198 | 51.074 80.558 5.541 | 81.074 80.558 7.472 | 82.074 80.558 3.882 | 101.23 170.558 1.686 | 103.845 170.558 2.435 | 81.23 170.558 0.969 | 88.275 80.558 3.825 | 59.074 80.558 4.215 | 276.146 71.274 5.891 | 261.146 71.274 10.264 | 55.074 80.558 8.797 |
| 58 | 59.306 98.771 3.005 | 238.613 98.771 2.466 | 20.306 94.435 2.459 | 47.306 94.435 3.244 | 77.306 94.435 4.375 | 78.306 94.435 2.274 | 99.722 −175 0.99 | 101.583 −175 1.426 | 79.722 −175 0.565 | 73.233 94.435 2.239 | 55.306 94.435 2.468 | 268.613 98.771 3.448 | 253.613 98.771 6.005 | 51.306 94.435 5.192 |
| 59 | 58.435 56.508 4.497 | 236.872 56.508 3.689 | 19.435 73.245 3.682 | 46.435 73.245 4.859 | 76.435 73.245 6.552 | 77.435 73.245 3.405 | 99.374 163.245 1.479 | 101.061 163.245 2.135 | 79.374 163.245 0.849 | 69.76 73.245 3.354 | 54.435 73.245 3.696 | 266.872 56.508 5.165 | 251.872 56.508 8.999 | 50.435 73.245 7.727 |
| 60 | 61.811 92.319 2.417 | 243.62 92.319 1.984 | 22.811 91.173 1.977 | 49.811 91.173 2.608 | 79.811 91.173 3.517 | 80.811 91.173 1.829 | 100.724 −178 0.797 | 103.087 −178 1.146 | 80.724 −178 0.453 | 83.222 91.173 1.799 | 57.811 91.173 1.985 | 273.62 92.319 2.772 | 258.62 92.319 4.826 | 53.811 91.173 4.194 |
| 61 | 60.098 79.484 3.504 | 240.196 79.484 2.875 | 21.098 84.684 2.868 | 48.098 84.684 3.784 | 78.098 84.684 5.103 | 79.098 84.684 2.653 | 100.039 174.684 1.153 | 102.059 174.684 1.663 | 80.039 174.684 0.66 | 76.39 84.684 2.612 | 56.098 84.684 2.879 | 270.196 79.484 4.023 | 255.196 79.484 7.007 | 52.098 84.684 6.04 |
| 62 | 54.615 106.409 6.239 | 229.225 106.409 5.117 | 15.615 98.281 5.11 | 42.615 98.281 6.744 | 72.615 98.281 9.094 | 73.615 98.281 4.724 | 97.846 −171 2.05 | 98.769 −171 2.963 | 77.846 −171 1.18 | 54.415 98.281 4.657 | 50.615 98.281 5.13 | 259.225 106.409 7.171 | 244.225 106.409 12.495 | 46.615 98.281 10.686 |
| 63 | 55.031 84.931 3.474 | 230.06 84.931 2.85 | 16.031 87.436 2.843 | 43.031 87.436 3.752 | 73.031 87.436 5.059 | 74.031 87.436 2.63 | 98.013 177.436 1.143 | 99.019 177.436 1.649 | 78.013 177.436 0.654 | 56.101 87.436 2.589 | 51.031 87.436 2.854 | 260.06 84.931 3.988 | 245.06 84.931 6.946 | 47.031 87.436 5.989 |
Appendix B. Uncertainty Visualization in Wave Propagation and Building-Scale Inundation for a Particular Fault-Source Configuration
This appendix is devoted to portraying how the alterations in fault-source parameters considered throughout the article affect wave propagation at several locations in the open sea. In order to proceed with the examination, three virtual buoys have been allocated in the open sea, and one more has been placed closer to the shoreline. Figure A1 shows the studied area as well as the position of the buoys. All buoys belong to a line with latitude of 36.5 N and are numbered from 1 to 4, buoy number 1 being the farthest from the coast and buoy number 4 the closest one. Wave propagation due to rupture of all 64 variants of fault AT002 has been simulated, and a time series regarding the wave amplitude values produced by every fault variant has been constructed with respect to each buoy. Fault AT002 has been chosen because of its proximity to the Cádiz’s coast. The simulation time is set to 4 h for every variant; the time series temporal resolution is 1min.
Figure A2 shows wave height variations in all four locations. At first glance, it can be noted how all variants follow a similar trend as to what time peaks are recorded, though peak values may present important discrepancies among variants. Variants 50 and 62 are highlighted in all cases, as they represent extreme behaviours. The fact that these two specific variations display the mentioned behaviour is something to be expected—they come from retrieving extreme slip values in the sampling methods described in Section 3.3. Variant 50 has a slip value of 0.33, whilst variant 62 has a slip value of 5.117 (Table A4 and Table A5). Looking at the four graphs, from buoy 1 (furthest) to 4 (closest), it is possible to observe how waves are being propagated, as well as an increase in maximum wave amplitude due to the progressive decrease in water depth.
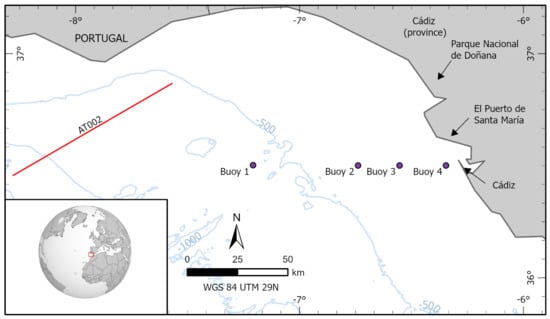
Figure A1.
Location of the four virtual buoys together with the simulated fault.
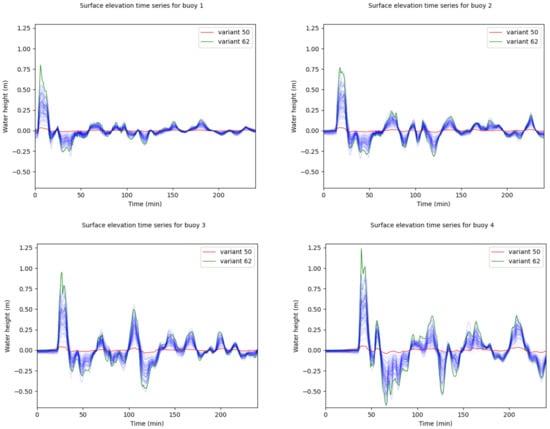
Figure A2.
Water elevation time series for each variant of fault AT002 for the four selected fictional buoys. Variants 50 (red) and 62 (green) are highlighted as they display extreme behaviours as to wave amplitude ranges.
To conclude this appendix, a particular result of the water depth is depicted in order to demonstrate how important is the use of high-resolution grids when a study of economic damage is to be undertaken. Variant 62 of fault AT002 is chosen because its particular fault-source parameter configuration provokes a more extensive flood area than other variants in the city of Cádiz. The water depth simulated results are superposed to the street’s path. Figure A3 provides a direct visualization of the flooded zones. It can be seen how water penetrates through the western coast, wetting some streets and building with maximum height below 1m. Water depth below 1m is also reached through the northern port. High-resolution inundation, in conjunction with building-scale data, permits the identification of economic damage with relatively high accuracy.
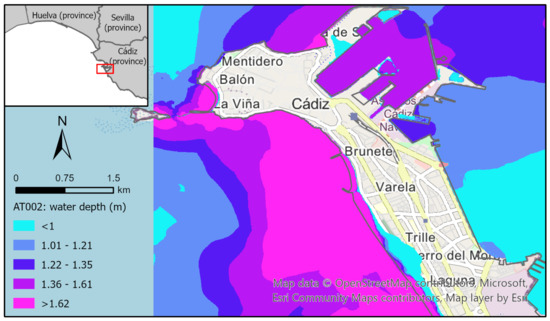
Figure A3.
Water depth values obtained by variant 62 of fault AT002 in Cádiz city. Streets have been added to the map in order to visualize how they might be potentially wet by the tsunami wave.
References
- United Nations Office for Disaster Risk Reduction Documents and Publications Page. Available online: https://www.preventionweb.net/files/64454_unisdrannualreport2018eversionlight.pdf (accessed on 18 February 2022).
- Liu, P.; Wang, X.; Salisbury, A. Tsunami hazard and early warning system in South China Sea. J. Asian Earth Sci. 2009, 36, 2–12. [Google Scholar] [CrossRef]
- Rudloff, A.; Lauterjung, J.; Münch, U.; Tinti, S. Preface “The GITEWS Project (German-Indonesian Tsunami Early Warning System)”. Nat. Hazards Earth Syst. Sci. 2009, 9, 1381–1382. [Google Scholar] [CrossRef]
- Ishiwatari, M.; Sagara, J. World Bank. Available online: http://hdl.handle.net/10986/16160 (accessed on 18 February 2022).
- Lunghino, B.; Tate, A.F.S.; Mazereeuw, M.; Muhari, A.; Giraldo, F.X.; Marras, S.; Suckale, J. The protective benefits of tsunami mitigation parks and ramifications for their strategic design. Proc. Natl. Acad. Sci. USA 2020, 117, 10740–10745. [Google Scholar] [CrossRef] [PubMed]
- Behrens, J.; Dias, F. New computational methods in tsunami science. Philos. Trans. R. Soc. A 2015, 373, 20140382. [Google Scholar] [CrossRef]
- Marras, S.; Mandli, K.T. Modeling and Simulation of Tsunami Impact: A Short Review of Recent Advances and Future Challenges. Geosciences 2021, 11, 5. [Google Scholar] [CrossRef]
- Mas, E.; Koshimura, S.; Suppasri, A.; Matsuoka, M.; Matsuyama, M.; Yoshii, T.; Jimenez, C.; Yamazaki, F.; Imamura, F. Developing Tsunami fragility curves using remote sensing and survey data of the 2010 Chilean Tsunami in Dichato. Nat. Hazards Earth Syst. Sci. 2012, 8, 2689–2697. [Google Scholar] [CrossRef]
- Suppasri, A.; Fukui, K.; Yamashita, K.; Leelawat, N.; Ohira, H.; Imamura, F. Developing fragility functions for aquaculture rafts and eelgrass in the case of the 2011 Great East Japan tsunami. Nat. Hazards Earth Syst. Sci. 2018, 18, 145–155. [Google Scholar] [CrossRef]
- Muhari, A.; Charvet, I.; Tsuyoshi, F.; Suppasri, A.; Imamura, F. Assessment of tsunami hazards in ports and their impact on marine vessels derived from tsunami models and the observed damage data. Nat. Hazards 2015, 78, 1309–1328. [Google Scholar] [CrossRef][Green Version]
- Pakoksung, K.; Suppasri, A.; Matsubae, K.; Imamura, F. Estimating tsunami economic losses of Okinawa island with multi-regional-input-output modeling. Geosciences 2019, 9, 349. [Google Scholar] [CrossRef]
- Goda, K.; Mori, N.; Yasuda, T.; Prasetyo, A.; Muhammad, A.; Tsujio, D. Cascading Geological Hazards and Risks of the 2018 Sulawesi Indonesia Earthquake and Sensitivity Analysis of Tsunami Inundation Simulations. Front. Earth Sci. 2019, 7, 261. [Google Scholar] [CrossRef]
- Selvan, S.C.; Kankara, R.S. Tsunami model simulation for 26 December 2004 and its effect on Koodankulam region of Tamil Nadu Coast. Int. J. Ocean Clim. Syst. 2016, 7, 62–69. [Google Scholar] [CrossRef]
- Jaimes, M.; Reinoso, E.; Ordaz, M.; Huerta, B.; Silva, R.; Mendoza, E.; Rodriguez, J. A new approach to probabilistic earthquake-induced tsunami risk assessment. Ocean Coast Manag. 2016, 119, 68–75. [Google Scholar] [CrossRef]
- Goda, K.; Song, J. Uncertainty modeling and visualization for tsunami hazard and risk mapping: A case study for the 2011 Tohoku earthquake. Stoch. Environ. Res. Risk Assess. 2015, 30, 2271–2285. [Google Scholar] [CrossRef]
- González, M.; Álvarez-Gómez, J.A.; Aniel-Quiroga, Í.; Otero, L.; Olabarrieta, M.; Omira, R.; Luceño, A.; Jelinek, R.; Krausmann, E.; Birkman, J.; et al. Probabilistic Tsunami Hazard Assessment in Meso and Macro Tidal Areas. Application to the Cádiz Bay, Spain. Front. Earth Sci. 2021, 9, 591383. [Google Scholar] [CrossRef]
- Omira, R.; Baptista, M.A.; Matias, L. Probabilistic Tsunami Hazard in the Northeast Atlantic from Near-and Far-Field Tectonic Sources. Pure Appl. Geophys. 2015, 172, 901–920. [Google Scholar] [CrossRef]
- Omira, R.; Matias, L.; Baptista, M.A. Developing an event-tree probabilistic tsunami inundation model for NE Atlantic coasts: Application to a case study. Pure Appl. Geophys. 2016, 173, 3775–3794. [Google Scholar] [CrossRef]
- Basili, R.; Brizuela, B.; Herrero, A.; Iqbal, S.; Lorito, S.; Maesano, F.E.; Murphy, S.; Perfetti, P.; Romano, F.; Scala, A.; et al. The Making of the NEAM Tsunami Hazard Model 2018 (NEAMTHM18). Front. Earth Sci. 2021, 8, 616594. [Google Scholar] [CrossRef]
- Gopinathan, D.; Heidarzadeh, M.; Guillas, S. Probabilistic quantification of tsunami current hazard using statistical emulation. Proc. R. Soc. A 2021, 477, 20210180. [Google Scholar] [CrossRef]
- Salmanidou, D.M.; Beck, J.; Pazak, P.; Guillas, S. Probabilistic, high-resolution tsunami predictions in northern Cascadia by exploiting sequential design for efficient emulation. Nat. Hazards Earth Syst. Sci. 2021, 21, 3789–3807. [Google Scholar] [CrossRef]
- Instituto Geológico y Minero de España QAFI, v.4: Quaternary-Active Faults Database of Iberia (2022). Version 3. Available online: http://info.igme.es/qafi (accessed on 20 April 2022).
- García-Mayordomo, J.; Insua-Arévalo, J.M.; Martínez-Díaz, J.J.; Jiménez-Díaz, A.; Martín-Banda, R.; Martín-Alfageme, S.; Álvarez-Gómez, J.A.; Rodríguez-Peces, M.; Pérez-López, R.; Rodríguez-Pascua, M.A.; et al. The Quaternary Faults Database of Iberia (QAFI v.2.0). J. Iber. Geol. 2012, 38, 285–302. [Google Scholar] [CrossRef]
- García-Mayordomo, J.; Martín-Banda, R.; Insua-Arévalo, J.M.; Álvarez-Gómez, J.A.; Martínez-Díaz, J.J.; Cabral, J. Active fault databases: Building a bridge between earthquake geologists and seismic hazard practitioners, the case of the QAFI v.3 database. Nat. Hazards Earth Sci. Syst. 2017, 17, 1447–1459. [Google Scholar] [CrossRef]
- Martínez-Loriente, S.; Gràcia, E.; Bartolome, R.; Sallarés, V.; Connors, C.; Perea, H.; Lo Iacono, C.; Klaeschen, D.; Terrinha, P.; Dañobeitia, J.J.; et al. Active deformation in old oceanic lithosphere and significance for earthquake hazard: Seismic imaging of the Coral Patch Ridge area and neighboring abyssal plains (SW Iberian Margin). Geochem. Geophys. Geosyst. 2013, 14, 2206–2231. [Google Scholar] [CrossRef]
- Martínez-Loriente, S.; Gràcia, E.; Bartolome, R.; Perea, H.; Klaeschen, D.; Dañobeitia, J.J.; Zitellini, N.; Wynn, R.B.; Masson, D.G. Morphostructure, tectono-sedimentary evolution and seismic potential of the Horseshoe Fault, SW Iberian Margin. Basin Res. 2018, 30, 382–400. [Google Scholar] [CrossRef]
- Ramos, A.; Fernández, O.; Terrinha, P.; Muñoz, J.A. Neogene to recent contraction and basin inversion along the Nubia-Iberia boundary in SW Iberia. Tectonics 2017, 36, 257–286. [Google Scholar] [CrossRef]
- Serra, C.S.; Martínez-Loriente, S.; Gràcia, E.; Urgeles, R.; Vizcaino, A.; Perea, H.; Bartolome, R.; Pallàs, R.; Lo Iacono, C.; Diez, S.; et al. Tectonic evolution, geomorphology and influence of bottom currents along a large submarine canyon system: The São Vicente Canyon (SW Iberian margin). Mar. Geol. 2020, 426, 106219. [Google Scholar] [CrossRef]
- Proceedings of the IGME and UMA Expert Meeting on Tsunamigenic Sources with Potential Impact in the Iberian Coast, Balearic and Canary Islands, Málaga, Spain, 6–7 November 2017. Available online: https://eventos.uma.es/event_detail/9535/detail/expert-meeting-on-tsunamigenic-sources-with-potential-impact-in-the-iberian-coast-balearic-and-cana.html (accessed on 1 March 2022).
- Pedrera, A.; Ruiz Constán, A.; Galindo Zaldívar, J.; Chalouan, A.; Sanz de Galdeano, C.; Marín Lechado, C.; Ruano, P.; Benmakhlouf, M.; Akil, M.; López Garrido, A.C.; et al. Is there an active subduction beneath the Gibraltar orogenic arc? Constraints from Pliocene to present-day stress field. J. Geodyn. 2011, 52, 83–96. [Google Scholar] [CrossRef]
- Instituto Geográfico Nacional Centro de Descargas. Available online: https://centrodedescargas.cnig.es/CentroDescargas/index.jsp (accessed on 1 March 2022).
- European Marine Observation and Data Network Bathymetry Page. Available online: https://www.emodnet-bathymetry.eu/data-products (accessed on 1 March 2022).
- General Bathymetric Chart of the Oceans Gridded Bathymetry Data Page. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 1 March 2022).
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Kajiura, K. The leading wave of tsunami. Bull. Earthq. Res. Inst. Tokyo Univ. 1963, 41, 535–571. [Google Scholar] [CrossRef][Green Version]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons Ltd.: West Sussex, UK, 2008; ISBN 978-0470059975. [Google Scholar]
- Macdonald, I.A. Comparison of sampling techniques on the performance of Monte-Carlo based sensitivity analysis. In Proceedings of the 11th International IBPSA Building Simulator, Glasgow, Scotland, 27–30 July 2009. [Google Scholar]
- Burhenne, S.; Dirk, J.; Gregor, P.H. Sampling based on Sobol’ sequences for Monte Carlo techniques applied to building simulations. In Proceedings of the 12th IBPSA Building Simulator, Sydney, Australia, 14–16 January 2011. [Google Scholar]
- Snelling, B.; Neethling, S.; Horsburgh, K.; Collins, G.; Piggott, M. Uncertainty Quantification of Landslide Generated Waves Using Gaussian Process Emulation and Variance-Based Sensitivity Analysis. Water 2020, 12, 416. [Google Scholar] [CrossRef]
- George, D.L.; LeVeque, R.L. Finite volume methods and adaptive refinement for global tsunami propagation and local inundation. Sci. Tsunami Hazards 2006, 24, 319–328. [Google Scholar]
- Qin, X.; Motley, M.; LeVeque, R.; Gonzalez, F.; Mueller, K. A comparison of a two-dimensional depth-averaged flow model and a three-dimensional RANS model for predicting tsunami inundation and fluid forces. Nat. Hazards Earth Syst. Sci. 2018, 18, 2489–2506. [Google Scholar] [CrossRef]
- Berger, M.J.; LeVeque, R.J. Adaptive mesh refinement using wave-propagation algorithms for hyperbolic systems. SIAM J. Numer. Anal. 1998, 35, 2298–2316. [Google Scholar] [CrossRef]
- LeVeque, R.J.; George, D.L.; Berger, M.J. Tsunami modelling with adaptively refined finite volume methods. Acta Numer. 2011, 20, 211–289. [Google Scholar] [CrossRef]
- Delis, A.I.; Mathioudakis, E.N. A finite volume method parallelization for the simulation of free surface shallow water flows. Math. Comput. Simul. 2009, 79, 3339–3359. [Google Scholar] [CrossRef]
- Pophet, N.; Kaewbanjak, N.; Asavanant, J.; Ioualalen, M. High grid resolution and parallelized tsunami simulation with fully nonlinear Boussinesq equations. Comput. Fluids 2011, 40, 258–268. [Google Scholar] [CrossRef]
- Brodtkorb, A.; Hagen, T.; Lie, K.; Natvig, J. Simulation and visualization of the Saint-Venant system using GPUs. Comput. Vis. Sci. 2010, 13, 341–353. [Google Scholar] [CrossRef][Green Version]
- Asunción, M.; Mantas, J.; Castro, M. Programming CUDA-Based GPUs to Simulate Two-Layer Shallow Water Flows. In Proceedings of the 16th International Euro-Par Conference, Ischia, Italy, 31 August–3 September 2010; pp. 353–364. [Google Scholar]
- Amouzgar, R.; Liang, Q.; Smith, L. A GPU-accelerated shallow flow model for tsunami simulations. Proc. Inst. Civ. Eng. Eng. Comput. Mech. 2014, 167, 117–125. [Google Scholar] [CrossRef]
- Amouzgar, R.; Liang, Q.; Clarke, P.; Yasuda, T.; Mase, H. Computationally Efficient Tsunami Modelling on Graphics Processing Units (GPU). Int. J. Offshore Polar Eng. 2017, 26, 154–160. [Google Scholar] [CrossRef][Green Version]
- Castro, M.J.; Ferreiro, A.; García, J.A.; González, J.M.; Macías, J.; Parés, C.; Vázquez, M.E. On the numerical treatment of wet/dryfronts in shallow flows: Applications to one-layer and two-layer systems. Math. Comp. Model 2005, 42, 419–439. [Google Scholar] [CrossRef]
- Castro, M.J.; González, J.M.; Parés, C. Numerical treatment of wet/dry fronts in shallow flows with a modified Roe scheme. Math. Mod. Meth. App. Sci. 2006, 16, 897–931. [Google Scholar] [CrossRef]
- Castro, M.J.; Chacón, T.; Fernández-Nieto, E.D.; González-Vida, J.M.; Parés, C. Well-balanced finite volume schemes for 2D non-homogeneous hyperbolic systems. Applications to the dam break of Aznalcóllar. Comp. Meth. Appl. Mech. Eng. 2008, 197, 3932–3950. [Google Scholar] [CrossRef][Green Version]
- Asunción, M.; Castro, M.J.; Fernández-Nieto, E.D.; Mantas, J.M.; Ortega, S.; González-Vida, J.M. Efficient GPU implementation of a two waves TVD-WAF method for the two-dimensional one layer shallow water system on structured meshes. J. Comput. Fluids 2013, 80, 441–452. [Google Scholar] [CrossRef]
- Gallardo, J.M.; Parés, C.; Castro, M. On a well-balanced high-order finite volume scheme for shallow water equations with topography and dry areas. J. Comp. Phys. 2007, 227, 574–601. [Google Scholar] [CrossRef]
- Macías, J.; Castro, M.J.; Escalante, C. Performance assessment of Tsunami-HySEA model for NTHMP tsunami currents benchmarking. Laboratory data. Coast. Eng. 2020, 158, 103667. [Google Scholar] [CrossRef]
- Macías, J.; Castro, M.J.; Ortega, S.; González-Vida, J.M. Performance assessment of Tsunami-HySEA model for NTHMP tsunami currents benchmarking. Field cases. Ocean Model. 2020, 152, 101645. [Google Scholar] [CrossRef]
- Macías, J.; Castro, M.J.; Ortega, S.; Escalante, C.; González-Vida, J.M. Performance benchmarking of Tsunami-HySEA model for NTHMP’s inundation mapping activities. Pure Appl. Geophys. 2017, 174, 3147–3183. [Google Scholar] [CrossRef]
- Aki, K. Generation and propagation of G waves from Niigata earthquake of June 16, 1964. Part 2. Estimation of earthquake moment, released energy, and stress-strain drop from the G wave spectrum. Bull. Earthq. Res. Inst. 1966, 44, 73–88. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Stirling, M.; Goded, T.; Berryman, K.; Litchfield, N. Selection of earthquake scaling relationships for seismic-hazard analysis. Bull. Seismol. Soc. Am. 2013, 103, 2993–3011. [Google Scholar] [CrossRef]
- Fisher, N.I.; Lewis, T.; Embleton, B.J. Statistical Analysis of Spherical Data; Cambridge University Press: Cambridge, UK, 1993; ISBN 9780521456999. [Google Scholar]
- Jammalamadaka, S.R.; Sengupta, A. Topics in Circular Statistics; World Scientific: Singapore, 2001; Volume 5, ISBN 9789810237783. [Google Scholar]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley & Sons: Chichester, UK, 2009; Volume 494, ISBN 9780471953333. [Google Scholar]
- Devroye, L. Non-Uniform Random Variate Generation; Springer: New York, NY, USA, 1986; ISBN 978-1-4613-8645-2. [Google Scholar]
- Schneider, B.; Hoffmann, G.; Reicherter, K. Scenario-based tsunami risk assessment using a static flooding approach and high-resolution digital elevation data: An example from Muscat in Oman. Glob. Planet. Change 2016, 139, 183–194. [Google Scholar] [CrossRef]
- Okumura, N.; Jonkman, S.N.; Esteban, M.; Hofland, B.; Shibayama, T. A method for tsunami risk assessment: A case study for Kamakura, Japan. Nat. Hazards 2017, 88, 1451–1472. [Google Scholar] [CrossRef]
- Rose, A.; Sue Wing, I.; Wei, D.; Wein, A. Economic impacts of a California tsunami. Nat. Hazards Rev. 2016, 17, 04016002. [Google Scholar] [CrossRef]
- Geist, E.; Parsons, T. Probabilistic analysis of tsunami hazards. Nat. Hazards 2006, 37, 277–314. [Google Scholar] [CrossRef]
- Zamora, N.; Babeyko, A.Y. Probabilistic tsunami hazard assessment for local and regional seismic sources along the Pacific coast of Central America with emphasis on the role of selected uncertainties. Pure Appl. Geophys. 2020, 177, 1471–1495. [Google Scholar] [CrossRef]
- Griffin, J.; Pranantyo, I.R.; Kongko, W.; Haunan, A.; Robiana, R.; Miller, V.; Davies, G.; Horspool, N.; Maemunah, I.; Widjaja, W.B.; et al. Assessing tsunami hazard using heterogeneous slip models in the Mentawai Islands, Indonesia. Geol. Soc. Spec. 2016, 441, 47–70. [Google Scholar] [CrossRef]
- El-Hussain, I.; Omira, R.; Deif, A.; Al-Habsi, Z.; Al-Rawas, G.; Mohamad, A.; Al-Jabri, K.; Baptista, M.A. Probabilistic tsunami hazard assessment along Oman coast from submarine earthquakes in the Makran subduction zone. Arab. J. Geosci. 2016, 9, 668. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).