Adsorption-Based Hydrogen Storage in Activated Carbons and Model Carbon Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Microporous Carbon Adsorbents
2.1.1. Activated Carbons
2.1.2. Model Porous Carbon Structures
2.2. Hydrogen
2.3. Measurement of Hydrogen Adsorption
3. Results and Discussion
3.1. Structural and Energy Characteristics of the Model and Real Carbon Adsorbents
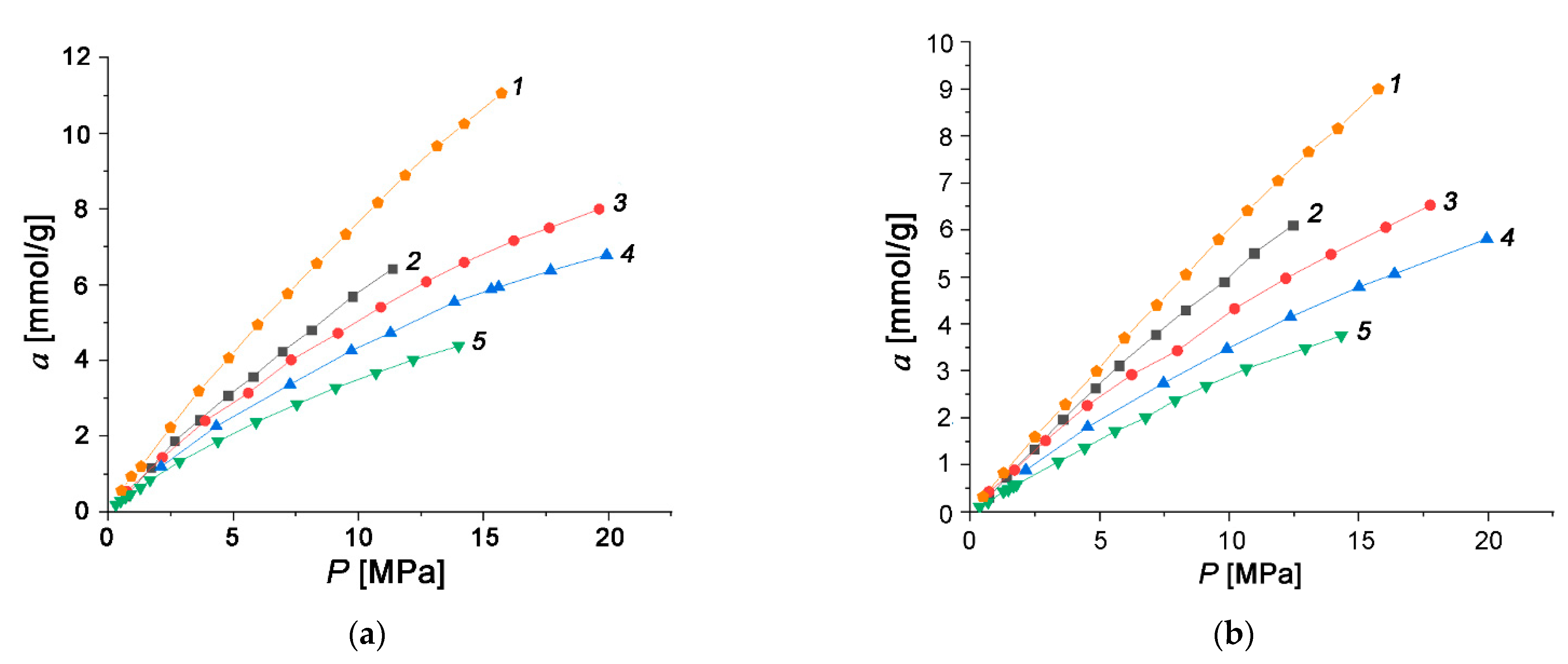
3.2. Hydrogen Adsorption
3.2.1. Hydrogen Adsorption in the Model Carbon Adsorbents
- The differential molar work of adsorption was calculated as A = RTln(fs/f) using reference data for hydrogen. Here, R is the universal gas constant, fs is the volatility of saturation vapor of hydrogen, and f is the volatility of an equilibrium phase.
- For the temperatures T within a range from the boiling point Tb to the triple point temperature TTP on the saturation line, we assumed that the density of an adsorbate (ρad) was equal to the density of the liquid, ρl. Therefore, the limiting value of hydrogen adsorption was calculated as follows: a0(T) = W0·ρl.
3.2.2. Hydrogen Adsorption in the Activated Carbons
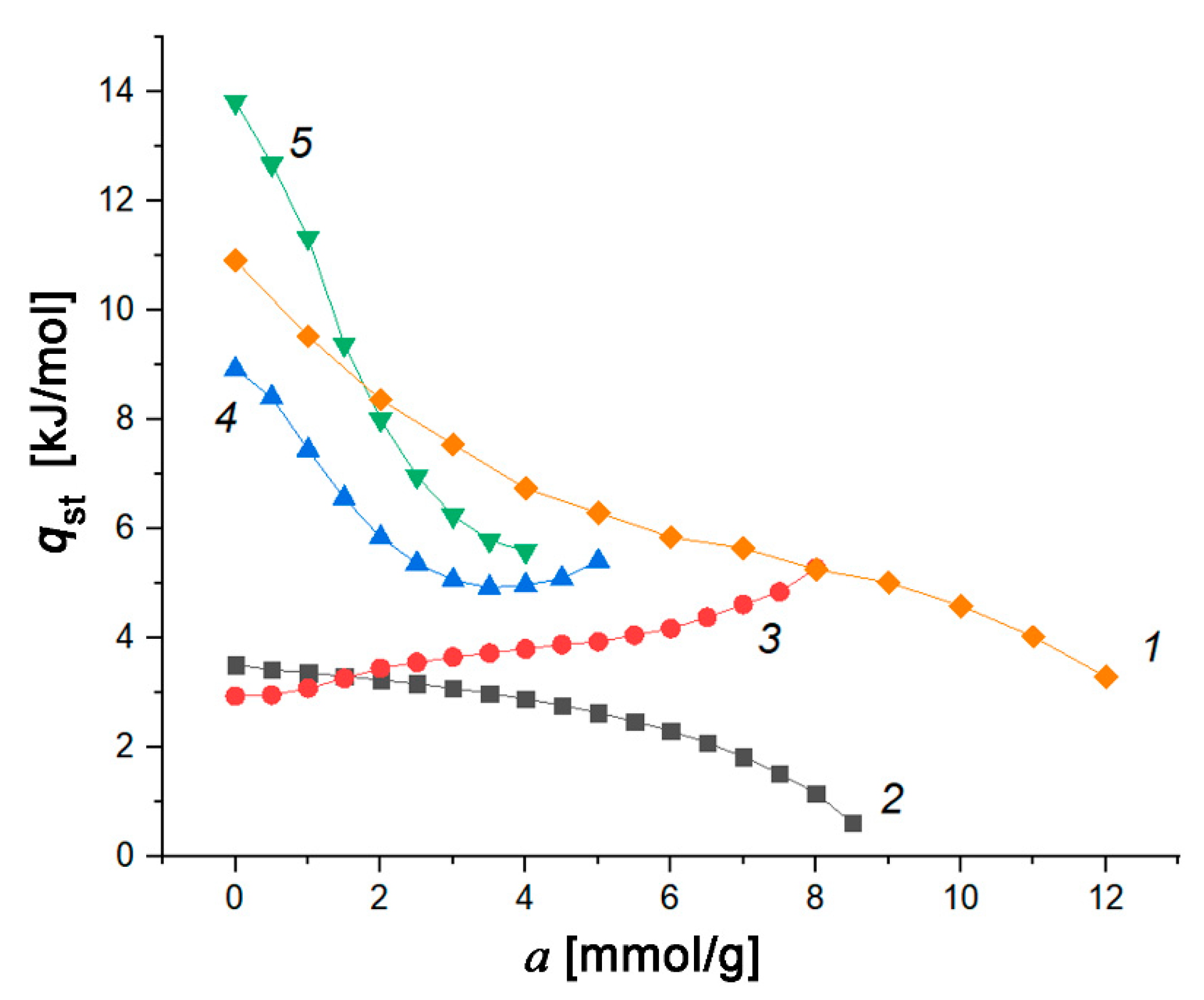
3.3. Thermodynamics of Hydrogen Adsorption in the Carbon Adsorbents
4. Conclusions
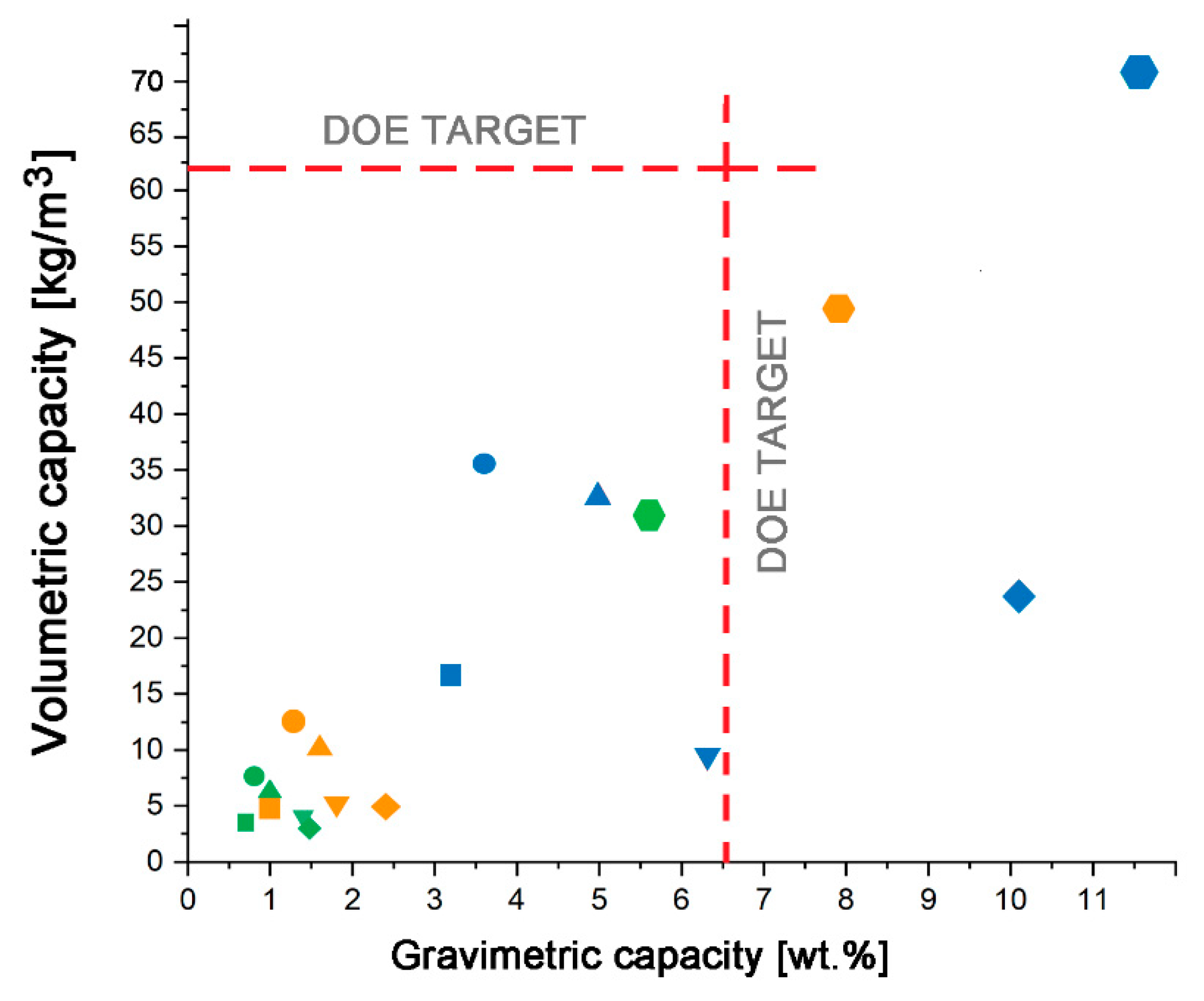
- Both at ambient and low temperatures, the highest gravimetric hydrogen density found for the ACS adsorbent at high pressures could be attributed to the largest micropore volume, bimodal pore size distribution, and specific BET surface among the rest samples.
- Under the same conditions, the highest values of AC density combined with the high energy of adsorption provided the advantage in the volumetric capacity of the AUK adsorbent, although it demonstrated the lower gravimetric capacity compared to ACS.
- A decrease in temperature led to an expected increase in the amount of adsorbed hydrogen on the studied carbon adsorbents. At the P,T-conditions corresponding to the hydrogen boiling point, the gravimetric hydrogen capacity of ACS (which was calculated by the TVFM) exceeded the DOE target.
- The highest differential molar isosteric heats of hydrogen adsorption on ACS, PAC-700, and AUK were determined by the significant amounts of high-energy adsorption sites, which were determined by a precursor and synthesis procedure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melnikov, Y.; Mitrova, T.; Chugunov, D. The Hydrogen Economy: A Path towards Low Carbon Development, SKOLKOVO Energy Centre, Moscow School of Management SKOLKOVO. June 2019. Available online: https://energy.skolkovo.ru/downloads/documents/SEneC/Research/SKOLKOVO_EneC_Hydrogen-economy_Eng.pdf (accessed on 13 December 2020).
- Gamburg, D.Y.; Semenov, V.P.; Dubovkin, N.F.; Smirnova, L.N. Hydrogen; Khimiya: Moscow, Russia, 1989; p. 672. [Google Scholar]
- Aksyutin, O.; Ishkov, A.; Romanov, K. Hydrogen, methane, carbon: New markets, new opportunities. Oil Gas Vert. 2021, 1–2, 40–47. [Google Scholar]
- Niaz, S.; Manzoor, T.; Pandith, A.H. Hydrogen storage: Materials, methods and perspectives. Renew. Sustain. Energy Rev. 2015, 50, 457–469. [Google Scholar] [CrossRef]
- Graetz, J. Metastable Metal Hydrides for Hydrogen Storage. ISRN Mater. Sci. 2012, 2012, 863025. [Google Scholar] [CrossRef]
- Zaluska, A.; Zaluski, L.; Strom-Olsen, J.O. Sodium alanates for reversible hydrogen storage. J. Alloys Compd. 2000, 298, 125–134. [Google Scholar] [CrossRef]
- Zhu, Q.-L.; Xu, Q. Liquid organic and inorganic chemical hydrides for high-capacity hydrogen storage. Energy Environ. Sci. 2015, 8, 478–512. [Google Scholar] [CrossRef]
- Klerke, A.; Christensen, C.H.; Nørskov, J.K.; Vegge, T. Ammonia for hydrogen storage: Challenges and opportunities. J. Mater. Chem. 2008, 18, 2304–2310. [Google Scholar] [CrossRef]
- Klyamkin, S.N. Metal-hybrid compositions based on magnesium as materials for hydrogen batteries. Russ. Chem. J. 2006, L(6), 49–55. [Google Scholar]
- Zaluska, A.; Zaluski, L.; Strom-Olsen, J.O. Nanocrystalline magnesium for hydrogen storage. J. Alloys Compd. 2000, 288, 217–225. [Google Scholar] [CrossRef]
- Rodrigo Leiva, D.R.; de Almeida Costa, H.C.; Huot, J.; Pinheiro, T.S.; Jorge, A.M., Jr.; Ishikawa, T.T.; Botta, W.J. Magnesium-Nickel Alloy for Hydrogen Storage Produced by Melt Spinning Followed by Cold Rolling. Mater. Res. 2012, 15, 813–817. [Google Scholar] [CrossRef][Green Version]
- Liang, G.; Huot, J.; Schulz, R. Hydrogen storage properties of the mechanically alloyed LaNi5-based materials. J. Alloys Compd. 2001, 320, 133–139. [Google Scholar] [CrossRef]
- Alexandrou, S.; Joseph, P.; Cook, J.P. Silicon Fuel: A hydrogen storage material. Int. J. Hydrogen Energy 2021, 46, 1627–1633. [Google Scholar] [CrossRef]
- DOE. Fuel Cell Technologies Office Multi-Year Research, Development, and Demonstration Plan. 2013. Available online: http://energy.gov/eere/fuelcells/downloads/fuel-cell-technologies-office-multi-year-research-development-and-22 (accessed on 9 March 2019).
- Bradley, T.H.; Moffitt, B.A.; Mavris, D.N.; Parekh, D.E. Development and experimental characterization of a fuel cell powered aircraft. J. Power Sources 2007, 171, 793–801. [Google Scholar] [CrossRef]
- Stroman, R.O.; Schuette, M.W.; Swider-Lyons, K.; Rodgers, J.A.; Edwards, D.J. Liquid hydrogen fuel system design and demonstration in a small long endurance air vehicle. Int. J. Hydrogen Energy 2014, 39, 11279–11290. [Google Scholar] [CrossRef]
- Dubinin, M.M. Physical Adsorption of Gases and Vapors in Micropores. Prog. Surf. Membr. Sci. 1975, 9, 1–70. [Google Scholar]
- Vlasov, A.I.; Bakaev, V.A.; Dubinin, M.M.; Serpinskii, V.V. Monte Carlo modeling of argon adsorption on active carbons. Dokl. Akad Nauk SSSR 1981, 260, 904–906. [Google Scholar]
- Meconi, G.M.; Zangi, R. Adsorption-induced clustering of CO2 on graphene. Phys. Chem. Chem. Phys. 2020, 22, 21031–21041. [Google Scholar] [CrossRef] [PubMed]
- Shkolin, A.V.; Fomkin, A.A.; Tsivadze, A.Y.; Anuchin, K.M.; Men’shchikov, I.E.; Pulin, A.L. Experimental study and numerical modeling: Methane adsorption in microporous carbon adsorbent over the subcritical and supercritical temperature regions. Protect. Metals Phys. Chem. Surf. 2016, 52, 955–963. [Google Scholar] [CrossRef]
- Kel’tsev, N.V. Foundations of Adsorption Technique; Khimiya: Moscow, Russia, 1976. [Google Scholar]
- Breck, D.W. Zeolite Molecular Sieves; Wiley-Interscience: New York, NY, USA, 1974. [Google Scholar]
- Langmi, H.W.; Walton, A.; Al-Mamouri, M.M.; Johnson, S.R.; Book, D.; Speight, J.D.; Edwards, P.P.; Gameson, I.; Anderson, P.A.; Harris, I.R. Hydrogen adsorption in zeolites A, X, Y and RHO. J. Alloys Compd. 2003, 356–357, 710–715. [Google Scholar] [CrossRef]
- Isaeva, V.I.; Kustov, L.M. Metal-organic frameworks—New materials for hydrogen storage. Russ. J. Gen. Chem. 2007, 77, 721–739. [Google Scholar] [CrossRef]
- Rostami, S.; Pour, A.N.; Salimi, A.; Abolghasempour, A. Hydrogen adsorption in metal-organic frameworks (MOFs): Effects of adsorbent architecture. Int. J. Hydrogen Energy 2018, 43, 7072–7080. [Google Scholar] [CrossRef]
- Li, Y.; Yang, R.T. Hydrogen storage in metal-organic and covalent-organic frameworks by spillover. AlChE 2008, 54, 269–279. [Google Scholar] [CrossRef]
- Ahmed, A.; Seth, S.; Purewal, J.; Wong-Foy, A.G.; Veenstra, M.; Matzger, A.J.; Siegel, D.J. Exceptional hydrogen storage achieved by screening nearly half a million metal-organic frameworks. Nat. Comm. 2019, 10, 1568. [Google Scholar] [CrossRef]
- Srtobel, R.; Jorissen, L.; Schiermann, T.; Trapp, V.; Schutz, W.; Bohmhammel, K.; Wolf, G.; Garche, J. Hydrogen adsorption on carbon materials. J. Power Sources 1999, 84, 221–224. [Google Scholar]
- Shindo, K.; Kondo, T.; Arakowa, M.; Sakurai, Y.J. Hydrogen adsorption/desorption properties of mechanically milled activated carbon. J. Alloys Comp. 2003, 359, 267–271. [Google Scholar] [CrossRef]
- Sevilla, M.; Mokaya, R. Energy storage applications of activated carbons: Supercapacitors and hydrogen storage. Energy Environ. Sci. 2014, 7, 1250–1280. [Google Scholar] [CrossRef]
- Sethia, G.; Sayari, A. Activated carbon with optimum pore size distribution for hydrogen storage. Carbon 2016, 99, 289–294. [Google Scholar] [CrossRef]
- Kostoglou, N.; Koczwara, C.; Prehal, C.; Terziyska, V. Nanoporous activated carbon cloth as a versatile material for hydrogen adsorption, selective gas separation and electrochemical energy storage. Nano Energy 2017, 40, 49–64. [Google Scholar] [CrossRef]
- Darkrim, F.L.; Malbrunot, P.; Tartaglia, G.P. Review of hydrogen storage by adsorption in carbon nanotubes. Int. J. Hydrogen Energy 2002, 27, 193–202. [Google Scholar] [CrossRef]
- Tibbetts, G.G.; Meisher, G.P.; Olk, C.H. Hydrogen storage capacity of carbon nanotubes, filaments, and vapor-grown fibers. Carbon 2001, 39, 2291–2301. [Google Scholar] [CrossRef]
- Jimenez, V.; Ramirez-Lucas, A.; Sanchez, P.; Valverde, J.L.; Romero, A. Hydrogen storage in different carbon materials: Influence of the porosity development by chemical activation. Appl. Surf. Sci. 2012, 258, 2498–2509. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A. Supramolecular microporous structures based on carbon nanotubes and coordinating cumene (C9H12) molecules. Colloid. J. 2017, 79, 701–706. [Google Scholar] [CrossRef]
- Park, C.; Anderson, P.E.; Tan, C.D.; Hidalgo, R.; Rodrigez, N.M. Further Studies of the Interaction of Hydrogen with Graphite Nanofibers. J. Phys. Chem. B 1999, 103, 10572–10581. [Google Scholar] [CrossRef]
- Ivanovskaya, V.; Zobelli, A.; Teillet-Billy, D.; Rougeau, N.; Sidis, V.; Briddon, P.R. Hydrogen adsorption on graphene: A first principles study. Eur. Phys. J. B 2010, 76, 481–486. [Google Scholar] [CrossRef]
- Tozzini, V.; Pellegrini, V. Prospects for hydrogen storage in graphene. Phys. Chem. Chem. Phys. 2013, 15, 80–89. [Google Scholar] [CrossRef]
- Alekseeva, O.K.; Pushkareva, I.V.; Pushkarev, A.S.; Fateev, V.N. Graphene and Graphene-Like Materials for Hydrogen Energy. Nanotechnol. Russ. 2020, 15, 273–300. [Google Scholar] [CrossRef] [PubMed]
- Zacharia, R.; Rather, S. Review of Solid State Hydrogen Storage Methods Adopting Different Kinds of Novel Materials. J. Nanomater. 2015, 2015, 914845. [Google Scholar] [CrossRef]
- Gordon, R. Composite Pressure Vessels for Gaseous Hydrogen-Powered Vehicles in Hydrogen Energy Progress; Veziroglu, T.N., Taylor, J.B., Eds.; Pergamon: New York, NY, USA, 1984; pp. 1225–1236. [Google Scholar]
- Dillon, A.C.; Heben, M.J. Hydrogen storage using carbon adsorbents: Past, present and future. Appl. Phys. A 2001, 72, 133–142. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Sinitsyn, V.A.; Gur’yanov, V.V. Hydrogen adsorption on nanoporous carbon adsorbents prepared from furaldehyde by thermochemical synthesis. Colloid J. 2008, 70, 372–376. [Google Scholar] [CrossRef]
- Mohan, M.; Sharma, V.K.; Kumar, E.A.; Gayathri, V. Hydrogen storage in carbon materials—A review. Energy Starage 2019, 1, e35. [Google Scholar] [CrossRef]
- Xu, W.C.; Takahashi, K.; Matsuo, Y.; Hattori, Y.; Kumagai, M.; Ishiyama, S.; Kaneko, K.; Iijima, S. Investigation of hydrogen storage capacity of various carbon materials. Int. J. Hydrogen Energy 2007, 32, 2504–2512. [Google Scholar] [CrossRef]
- Masika, E.; Robert Mokaya, R. Exceptional gravimetric and volumetric hydrogen storage for densified zeolite templated carbons with high mechanical stability. Energy Environ. Sci. 2014, 7, 427–434. [Google Scholar] [CrossRef]
- Romanos, J.; Barakat, F.; Abou Dargham, S. Nanoporous Graphene Monolith for Hydrogen Storage. Mater. Today Proc. 2018, 5, 17478–17483. [Google Scholar] [CrossRef]
- Ania, C.O.; Raymundo-Piñero, E. Nanoporous Carbons with Tuned Porosity. Chapter 5. In Nanoporous Materials for Gas Storage, 1st ed.; Rodríguez-Reinoso, F., Kaneko, K., Eds.; Springer Nature Singapore Pte Ltd.: Singapore, 2019; pp. 91–135. [Google Scholar]
- Fenelonov, V.B. Poristyi Uglerod (Porous Carbon); Izd. IK RAN: Novosibirsk, Russia, 1995; p. 518. (In Russian) [Google Scholar]
- Mukhin, V.M.; Tarasov, A.V.; Klushin, V.N. Aktivnie ugli Rossii (Active Carbons of Russia); Metallurgiya: Moscow, Russia, 2000; p. 352. [Google Scholar]
- Men’shchikov, I.E.; Shiryaev, A.A.; Shkolin, A.V.; Vysotskii, V.V.; Khozina, E.V.; Fomkin, A.A. Carbon adsorbents for methane storage: Genesis, synthesis, porosity, adsorption. Korean J. Chem. Eng. 2021, 38, 276–291. [Google Scholar] [CrossRef]
- Dubinin, M.M. Fundamentals of the theory of adsorption in micropores of carbon adsorbents: Characteristics of their adsorption properties and microporous structures. Carbon 1989, 27, 457–467. [Google Scholar] [CrossRef]
- Men´shchikov, I.E.; Fomkin, A.A.; Shkolin, A.V.; Yakovlev, V.Y.; Khozina, E.V. Optimization of structural and energy characteristics of adsorbents for methane storage. Russ. Chem. Bull. 2018, 67, 1814–1822. [Google Scholar] [CrossRef]
- Ivakhnyuk, G.K.; Sevryugov, L.B.; Plachenov, T.G. Preparation, Structure, and Properties of Adsorbents; Izd. LTI im. Lensoveta: Leningrad, Russia, 1977; p. 19. [Google Scholar]
- Fedorov, N.F.; Ivakhnyuk, G.K.; Gavrilov, D.N.; Tetenev, V.V.; Smetanin, G.N.; Samonin, V.V.; Babkin, O.E.; Zaitsev, Y.A. Carbon Adsorbents and Their Application in Industry; Nauka: Moscow, Russia, 1983; p. 20. [Google Scholar]
- Guryanov, V.V.; Mukhin, V.M.; Kurilkin, A.A. Development of high-strength ash-free spherical carbon catalyst supports. Catal. Ind. 2012, 2, 41–48. (In Russian) [Google Scholar]
- Tkachev, A.G.; Melezhik, A.V.; Solomakho, G.V. Method of Obtaining Mesoporous Carbon. Patent for Invention RU2630404C1, 25 May 2017. [Google Scholar]
- Anuchin, K.M.; Fomkin, A.A.; Korotych, A.P.; Tolmachev, A.M. Adsorption concentration of methane. Dependence of adsorbate density on the width of slit-shaped micropores in activated carbons. Prot. Met. Phys. Chem. Surf. 2014, 50, 173–177. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry; Cornell University Press: Ithaca, NY, USA, 1939; 429p. [Google Scholar]
- Vainshtein, B.; Fridkin, V.; Indenbom, V. Structure of Crystals, 2nd ed.; Modern Crystallography, Springer: Berlin/Heidelberg, Germany, 1995; p. 82. [Google Scholar]
- Pribylov, A.A.; Serpinskii, V.V.; Kalashnikov, S.M. Adsorption of Gases by Microporous Adsorbents under Pressures up to Hundreds of Megapascals. Zeolites 1991, 11, 846–849. [Google Scholar] [CrossRef]
- Men’shchikov, I.E.; Shkolin, A.V.; Khozina, E.V.; Fomkin, A.A. Thermodynamics of Adsorbed Methane Storage Systems Based on Peat-Derived Activated Carbons. Nanomaterials 2020, 10, 1379. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Seliverstova, I.I.; Serpinskii, V.V. Determination of the parameters of the microprobe structure of solid adsorbents. Communication 1. Method of determination of the specific volume of totally microporous adsorbents. Russ. Chem. Bull. 1986, 35, 256–259. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- GOST R 55959-2014. Activated Carbon. Standard Test Method for Bulk Density. Available online: http://docs.cntd.ru/document/1200109447?section=text (accessed on 25 June 2021).
- Sugden, S. The Parachor and Valency; George Routledge&Sons: London, UK, 1930; 224p. [Google Scholar]
- Nikolaev, K.M.; Dubinin, M.M. Concerning adsorptional properties of carbon adsorbents 3. A study of adsorption isotherms of gases and vapors on active carbons over a wide interval of temperatures, including the critical region. Russ. Chem. Bull. 1958, 7, 1124–1133. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Sinitsyn, V.A. Hydrogen adsorption on a carbon adsorbent with slitlike micropores below and above the critical temperature. Colloid. J. 2008, 70, 112–117. [Google Scholar] [CrossRef]
- Men’shchikov, I.E.; Fomkin, A.A.; Tsivadze, A.Y.; Shkolin, A.V.; Strizhenov, E.M.; Khozina, E.V. Adsorption accumulation of natural gas based on microporous carbon adsorbents of different origin. Adsorpt. J. 2017, 23, 327–339. [Google Scholar] [CrossRef]
- Hill, T.L. Theory of Physical Adsorption. In Advances in Catalysis and Related Subjects; Frankerburg, Y.I., Ed.; Academic Press: New York, NY, USA, 1952; Volume 4, pp. 211–258. [Google Scholar]
- Bakaev, V.A. One possible formulation of the thermodynamics of sorption equilibrium. Bull. Acad. Sci. USSR Div. Chem. Sci. 1971, 20, 2516–2520. [Google Scholar] [CrossRef]
- Fomkin, A.A. Adsorption of gases, vapors and liquids by microporous adsorbents. Adsorption 2005, 11, 425–436. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A. Deformation of AUK microporous carbon adsorbent induced by methane adsorption. Colloid J. 2009, 71, 119–124. [Google Scholar] [CrossRef]
- Potapov, S.V.; Shkolin, A.V.; Fomkin, A.A. Deformation of AUK microporous carbon adsorbent induced by krypton adsorption. Colloid J. 2014, 76, 351–357. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Potapov, S.V.; Fomkin, A.A. Deformation of AUK microporous carbon adsorbent induced by xenon adsorption. Colloid J. 2015, 77, 812–820. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A.; Yakovlev, V.Y. Analysis of adsorption isosteres of gas and vapor on microporous adsorbents. Russ. Chem. Bull. 2007, 56, 393–396. [Google Scholar] [CrossRef]
- Bering, B.P.; Zhukovskaya, E.G.; Rakhmukov, B.K.; Serpinskii, V.V. Adsorption in micropores. Communication 2. Experimental isosteres of adsorption. Izv. Akad. Nauk SSSR. Ser. Khim. 1967, 16, 1662–1669. [Google Scholar]
- Barrer, R.M.; Papadopoulos, R. The sorption of krypton and xenon in zeolites at high pressures and temperatures I. Chabazite. Proc. Roy. Soc. Lond. Ser. A Math Phys. Sci. 1972, 326, 315–330. [Google Scholar]
- Fomkin, A.A.; Serpinskii, V.V.; Fidler, K. State of an adsorbed substance in the micropores of zeolites at high degrees of filling. Bull. Acad. Sci. USSR Div. Chem. Sci. 1982, 31, 1071–1077. [Google Scholar] [CrossRef]
- Bülow, M.; Shen, D.; Jale, S. Measurement of sorption equilibria under isosteric conditions: The principles, advantages and limitations. Appl. Surf. Sci. 2002, 196, 157–172. [Google Scholar] [CrossRef]
- Dubinin, M.M. Carbon Adsorbents and Their Use in Industry; Nauka: Moscow, Russia, 1983; p. 100. [Google Scholar]
- Tarkovskaya, I.A. Oxidized Carbon; Naukova Dumka: Kiev, Ukrain, 1981; p. 198. [Google Scholar]





| Adsorbent | W0 [cm3/g] | E0 [kJ/mol] | 2x0 [nm] | SBET [m2/g] | ρ [kg/m3] |
|---|---|---|---|---|---|
| PAC-700 | 0.46 | 29.3 | 0.80 | 1021 | 500 |
| AUK | 0.51 | 29.0 | 0.82 | 1340 | 950 |
| FAC-3 | 0.71 | 18.0 | 1.34 | 1830 | 620 |
| FAC-2008 | 0.96 | 14.0 | 1.70 | 2015 | 285 |
| ACS | 2.00 | E01 = 16.94 E02 = 3.95 | 2x01 = 1.42 2x02 = 3.8 | 2760 | 200 |
| Single-Layer Carbon Pore Wall | |||||||
| SEC | AC 1:3 | AC 2:4 | AC 3:5 | AC 4:6 | AC 5:7 | AC 6:8 | AC 7:9 |
| X0 = 2x0 [nm] | 0.53 | 0.87 | 1.20 | 1.54 | 1.87 | 2.21 | 2.54 |
| W0 [cm3/g] | 0.70 | 1.14 | 1.58 | 2.02 | 2.46 | 2.90 | 3.34 |
| E0 [kJ/mol] | 45.3 | 27.7 | 20.0 | 15.6 | 12.8 | 10.9 | 9.4 |
| ρads [g/cm3] | 1.137 | 0.758 | 0.568 | 0.455 | 0.379 | 0.325 | 0.284 |
| EH2 [kJ/mol] | 7.5 | 4.6 | 3.3 | 2.6 | 2.1 | 1.8 | 1.6 |
| Double-Layer Carbon Pore Wall | |||||||
| SEC | AC 1:5 | AC 2:6 | AC 3:7 | AC 4:8 | AC 5:9 | AC 6:10 | AC 7:11 |
| X0 = 2x0 [nm] | 0.53 | 0.87 | 1.20 | 1.54 | 1.87 | 2.21 | 2.54 |
| W0 [cm3/g] | 0.35 | 0.57 | 0.79 | 1.01 | 1.23 | 1.45 | 1.67 |
| E0 [kJ/mol] | 45.3 | 27.8 | 20.0 | 15.6 | 12.8 | 10.9 | 9.4 |
| ρads [g/cm3] | 1.515 | 1.137 | 0.909 | 0.758 | 0.649 | 0.568 | 0.505 |
| EH2 [kJ/mol] | 7.5 | 4.6 | 3.3 | 2.6 | 2.1 | 1.8 | 1.6 |
| Parameters of Hydrogen Adsorption | Single-Layer Carbon Pore Wall | ||||||
|---|---|---|---|---|---|---|---|
| AC 1:3 | AC 2:4 | AC 3:5 | AC 4:6 | AC 5:7 | AC 6:8 | AC 7:9 | |
| Limiting amount of adsorbed hydrogen, a0 [mmol/g] | 24.5 | 40.1 | 55.6 | 71.1 | 86.6 | 102.1 | 117.6 |
| Gravimetric density of adsorbed hydrogen, GH2 [wt.%] | 4.9 | 8.1 | 11.2 | 14.3 | 17.5 | 20.6 | 23.7 |
| Volumetric density of adsorbed hydrogen, VH2 [m3(H2, NTP)/m3] | 671 | 730 | 760 | 777 | 789 | 798 | 804 |
| Amount of Adsorbed Hydrogen, GH2 [wt.%] | Adsorbent | |||||
|---|---|---|---|---|---|---|
| PAC-700 | AUK | FAC-3 | FAC-2008 | ACS | AC 3:5 | |
| GH2 (101 kPa; 20.38 K) | 3.2 | 3.6 | 5.0 | 6.3 | 10.08 | 11.3 |
| GH2 (10 MPa; 303 K) | 0.7 | 0.8 | 1.0 | 1.4 | 1.48 | 5.3 |
| GH2 (20 MPa; 303 K) | 1.0 | 1.3 | 1.6 | 1.8 | 2.4 1 | 7.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fomkin, A.; Pribylov, A.; Men’shchikov, I.; Shkolin, A.; Aksyutin, O.; Ishkov, A.; Romanov, K.; Khozina, E. Adsorption-Based Hydrogen Storage in Activated Carbons and Model Carbon Structures. Reactions 2021, 2, 209-226. https://doi.org/10.3390/reactions2030014
Fomkin A, Pribylov A, Men’shchikov I, Shkolin A, Aksyutin O, Ishkov A, Romanov K, Khozina E. Adsorption-Based Hydrogen Storage in Activated Carbons and Model Carbon Structures. Reactions. 2021; 2(3):209-226. https://doi.org/10.3390/reactions2030014
Chicago/Turabian StyleFomkin, Anatoly, Anatoly Pribylov, Ilya Men’shchikov, Andrey Shkolin, Oleg Aksyutin, Alexander Ishkov, Konstantin Romanov, and Elena Khozina. 2021. "Adsorption-Based Hydrogen Storage in Activated Carbons and Model Carbon Structures" Reactions 2, no. 3: 209-226. https://doi.org/10.3390/reactions2030014
APA StyleFomkin, A., Pribylov, A., Men’shchikov, I., Shkolin, A., Aksyutin, O., Ishkov, A., Romanov, K., & Khozina, E. (2021). Adsorption-Based Hydrogen Storage in Activated Carbons and Model Carbon Structures. Reactions, 2(3), 209-226. https://doi.org/10.3390/reactions2030014






