A Multi-Objective Genetic Algorithm for Retrieving the Parameters of Sweet Pepper (Capsicum annuum) from the Diffuse Spectral Response
Abstract
1. Introduction
2. Materials and Methods
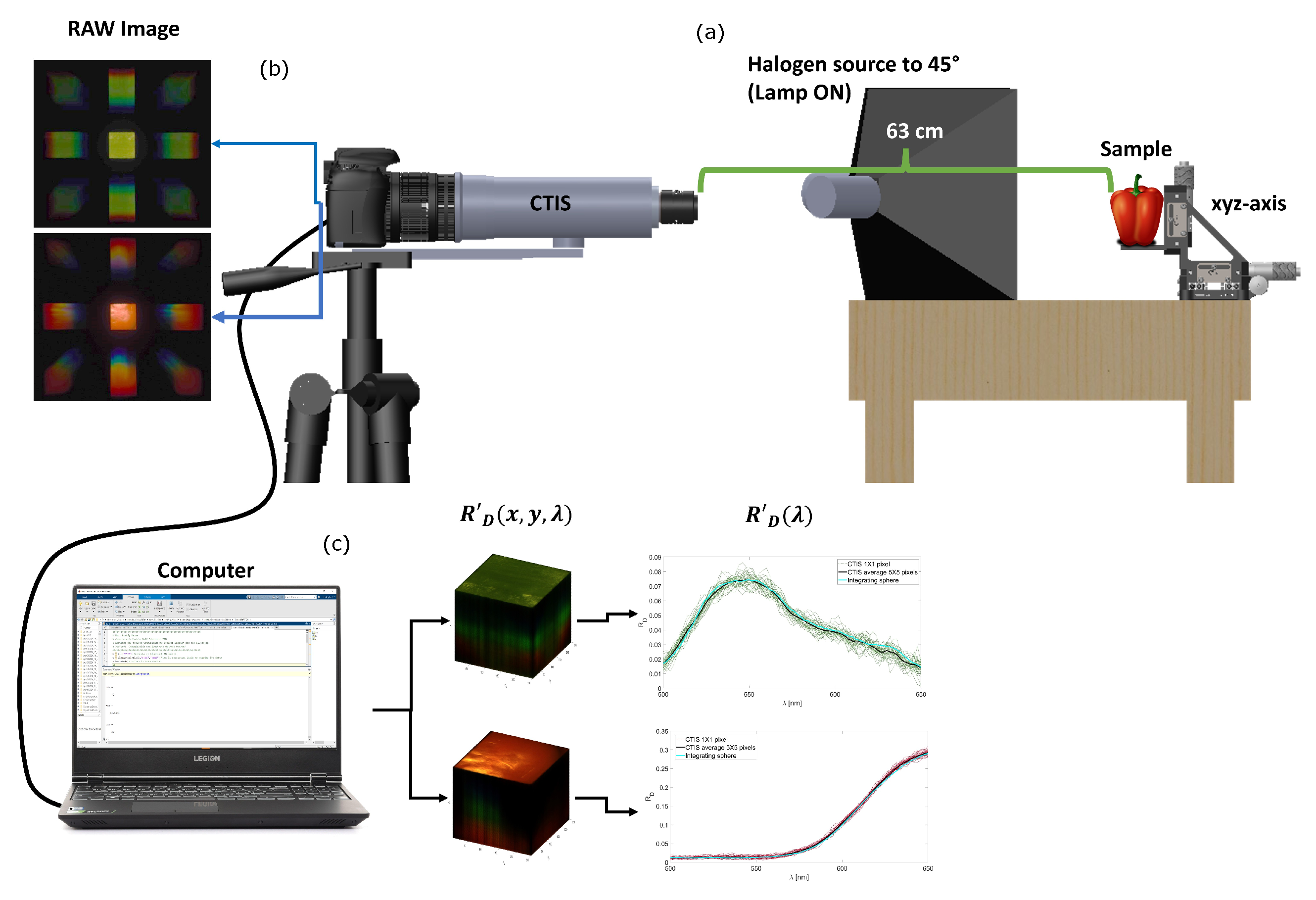
2.1. Data Acquisition
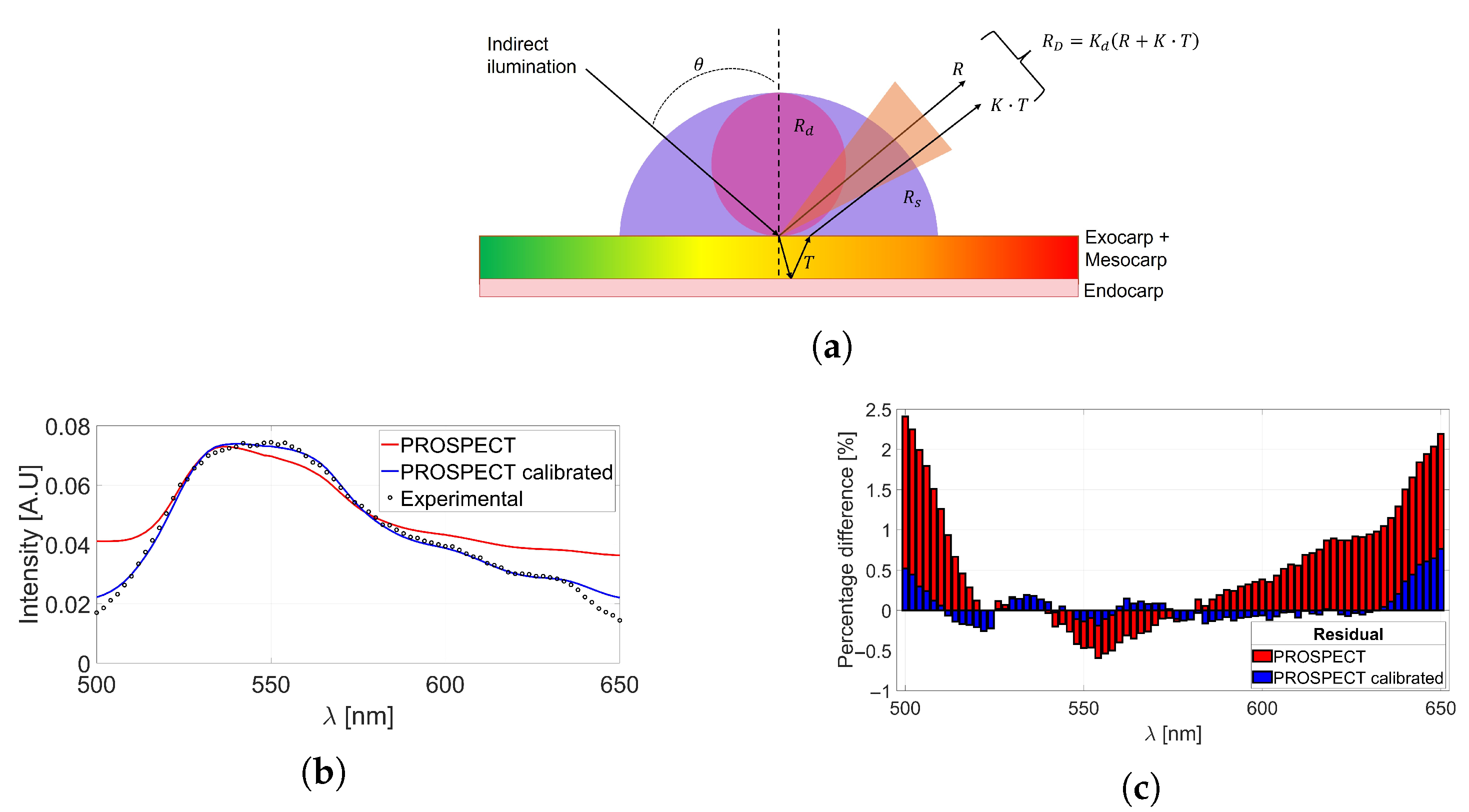
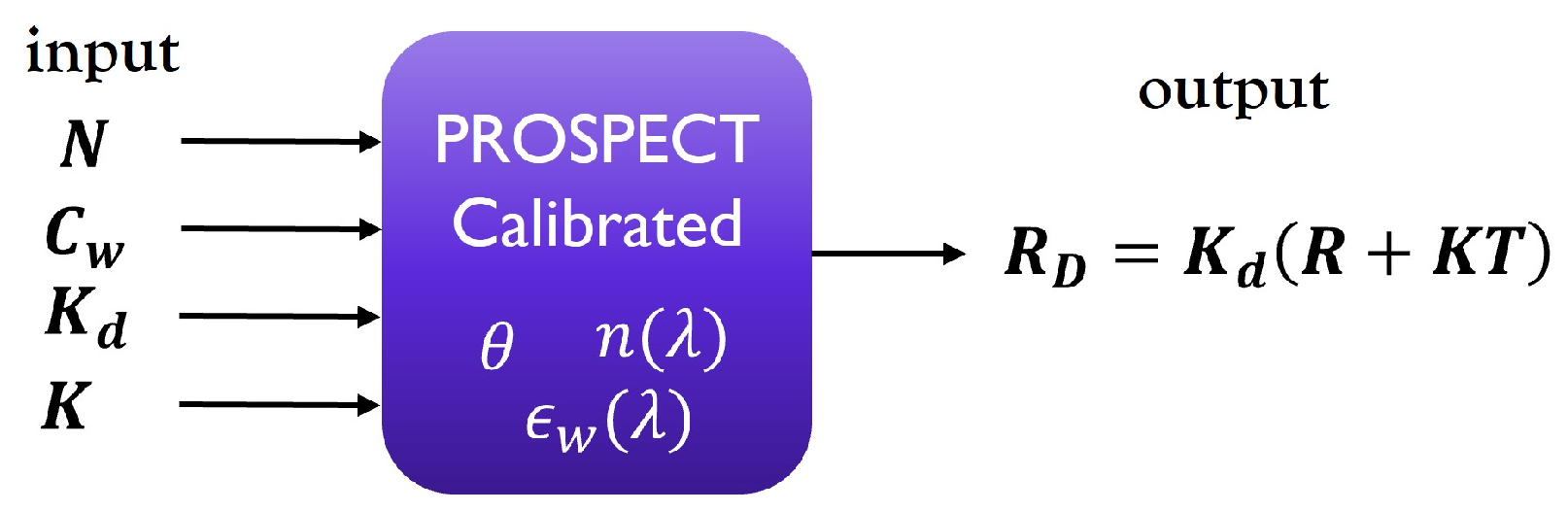
2.2. PROSPECT Radiative Transfer Model
2.3. Genetic Algorithms
| Algorithm 1: Genetic Algorithm (GA) |
 |
Proposed Stochastic Optimization Numerical Method
3. Results
3.1. Evaluation of the GA Investment Algorithm
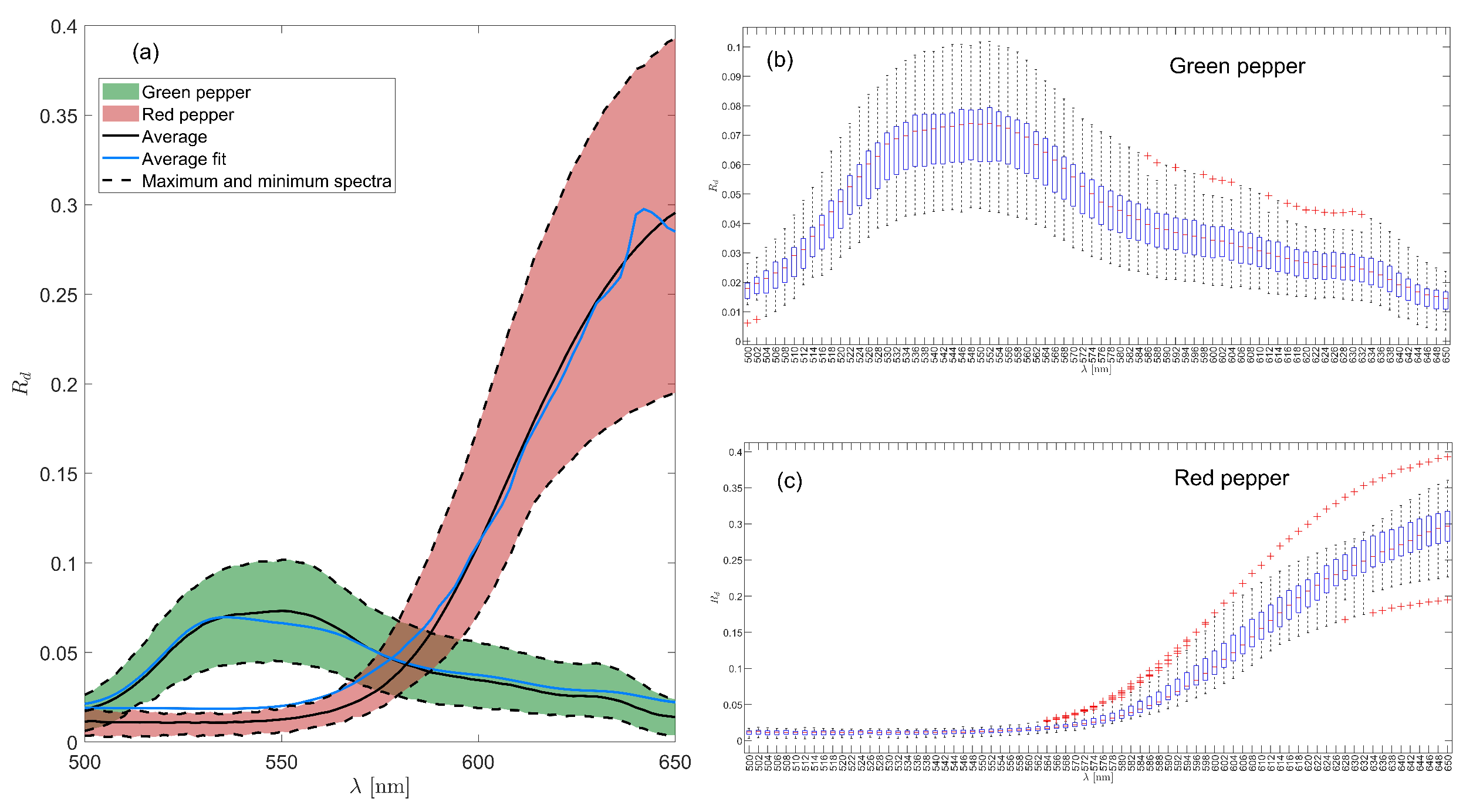
3.2. Spectral Information of the Samples
3.3. Retrieving of Pigment Concentrations
3.4. Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SESD | Experimental Spectral Data |
| CTIS | Computed Tomography Imaging Spectrometer |
| GA | Genetic Algorithm |
| HPLC | High-Performance Liquid Chromatography |
| FFFS | Front-Facing Fluorescence Spectroscopy |
| SI | Spectral Images |
| ME | Maximization–Expectation |
| DHR | Directional Hemispherical Reflectance |
| DHT | Directional Hemispherical Transmittance |
| GPU | Graphics Processing Unit |
| ED | Euclidean Distance |
| STD | Standard Deviation |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
References
- Sancho, J.; Navarro, F. Pimientos y Pimentón. Estudio Químico-Físico; Instituto de Orientación: Murcia, Spain, 1962. [Google Scholar]
- Monsurat, M.R.; Suraj, A.S.; Olumide, A.O. Physicochemical Properties and Mineral Composition of Capsicum annum and Capsicum frutescens Oils. IOSR-JAC 2014, 7, 112–116. [Google Scholar] [CrossRef]
- Batiha, G.E.-S.; Alqahtani, A.; Ojo, O.A.; Shaheen, H.M.; Wasef, L.; Elzeiny, M.; Ismail, M.; Shalaby, M.; Murata, T.; Zaragoza-Bastida, A.; et al. Biological Properties, Bioactive Constituents, and Pharmacokinetics of Some Capsicum spp. and Capsaicinoids. Int. J. Mol. Sci. 2020, 21, 5179. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). FAOSTAT; FAO: Rome, Italy, 2021; Available online: https://www.fao.org/faostat/ (accessed on 21 March 2025).
- Paredes, A.; Peche, J.; León, N. Index of Carotenoids of Bell Pepper (Capsicum annuum) Based on Color Measurement, Using Hyperspectral and Digital Images. Sci. Agropecu. 2019, 10, 531–539. [Google Scholar] [CrossRef]
- Kim, J.-S.; An, C.G.; Park, J.-S.; Lim, Y.P.; Kim, S. Carotenoid Profiling from 27 Types of Paprika (Capsicum annuum L.) with Different Colors, Shapes, and Cultivation Methods. Food Chem. 2016, 201, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Deli, J.; Molnár, P.; Matus, Z.; Tóth, G. Carotenoid Composition in the Fruits of Red Paprika (Capsicum annuum Var. Lycopersiciforme Rubrum) During Ripening; Biosynthesis of Carotenoids in Red Paprika. J. Agric. Food Chem. 2001, 49, 1517–1523. [Google Scholar] [CrossRef] [PubMed]
- Mohd Hassan, N.; Yusof, N.A.; Yahaya, A.F.; Mohd Rozali, N.N.; Othman, R. Carotenoids of Capsicum Fruits: Pigment Profile and Health-Promoting Functional Attributes. Antioxidants 2019, 8, 469. [Google Scholar] [CrossRef] [PubMed]
- Villa-Rivera, M.G.; Ochoa-Alejo, N. Chili Pepper Carotenoids: Nutraceutical Properties and Mechanisms of Action. Molecules 2020, 25, 5573. [Google Scholar] [CrossRef]
- Shim, Y.-S.; Kim, K.-J.; Seo, D.; Ito, M.; Nakagawa, H.; Arai, S.; Ha, J. Simultaneous Determination of Free Capsorubin and Capsanthin in Red Pepper Powder Using U-HPLC. J. AOAC Int. 2013, 96, 341–345. [Google Scholar] [CrossRef]
- Kim, J.-S.; Park, J.-T.; Ahn, J.; Ha, T.-Y.; Kim, S. Optimization of Accelerated Solvent Extraction of Capsanthin from Red Paprika (Capsicum annuum L.) Using Response Surface Methodology. Food Sci. Technol. Res. 2019, 25, 519–528. [Google Scholar] [CrossRef]
- Patsilinakos, A.; Ragno, R.; Carradori, S.; Petralito, S.; Cesa, S. Carotenoid Content of Goji Berries: CIELAB, HPLC-DAD Analyses and Quantitative Correlation. Food Chem. 2018, 268, 49–56. [Google Scholar] [CrossRef]
- Lozada, D.N.; Coon, D.L.; Guzmán, I.; Bosland, P.W. Heat Profiles of ‘Superhot’ and New Mexican Type Chile Peppers (Capsicum Spp.). Sci. Hortic. 2021, 283, 110088. [Google Scholar] [CrossRef]
- Guevara, L.; Domínguez-Anaya, M.Á.; Ortigosa, A.; González-Gordo, S.; Díaz, C.; Vicente, F.; Corpas, F.J.; Pérez del Palacio, J.; Palma, J.M. Identification of Compounds with Potential Therapeutic Uses from Sweet Pepper (Capsicum annuum L.) Fruits and Their Modulation by Nitric Oxide (NO). Int. J. Mol. Sci. 2021, 22, 4476. [Google Scholar] [CrossRef] [PubMed]
- Campmajó, G.; Rodríguez-Javier, L.R.; Saurina, J.; Núñez, O. Assessment of Paprika Geographical Origin Fraud by High-Performance Liquid Chromatography with Fluorescence Detection (HPLC-FLD) Fingerprinting. Food Chem. 2021, 352, 129397. [Google Scholar] [CrossRef]
- Tan, J.; Li, M.-F.; Li, R.; Jiang, Z.-T.; Tang, S.-H.; Wang, Y. Front-Face Synchronous Fluorescence Spectroscopy for Rapid and Non-Destructive Determination of Free Capsanthin, the Predominant Carotenoid in Chili (Capsicum annuum L.) Powders Based on Aggregation-Induced Emission. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 255, 119696. [Google Scholar] [CrossRef] [PubMed]
- Logan, R.D.; Scherrer, B.J.; Senecal, J.; Walton, N.S.; Peerlinck, A.; Sheppard, J.W.; Shaw, J.A. Hyperspectral Imaging and Machine Learning for Monitoring Produce Ripeness. In Sensing for Agriculture and Food Quality and Safety XII; Kim, M.S., Cho, B.-K., Chin, B.A., Eds.; SPIE: Bellingham, WA, USA, 2020; p. 25. [Google Scholar] [CrossRef]
- Schmilovitch, Z.; Ignat, T.; Alchanatis, V.; Gatker, J.; Ostrovsky, V.; Felföldi, J. Hyperspectral Imaging of Intact Bell Peppers. Biosyst. Eng. 2014, 117, 83–93. [Google Scholar] [CrossRef]
- Althaus, B.; Blanke, M. Non-Destructive, Opto-Electronic Determination of the Freshness and Shrivel of Bell Pepper Fruits. J. Imaging 2020, 6, 122. [Google Scholar] [CrossRef]
- Okamoto, T.; Takahashi, A.; Yamaguchi, I. Simultaneous Acquisition of Spectral and Spatial Intensity Distribution. Appl. Spectrosc. 1993, 47, 1198–1202. [Google Scholar] [CrossRef]
- Descour, M.R.; Dereniak, E.L.; Dubey, A.C. Mine Detection Using Instantaneous Spectral Imaging. In Detection Technologies for Mines and Minelike Targets; Dubey, A.C., Cindrich, I., Ralston, J.M., Rigano, K.A., Eds.; SPIE: Bellingham, WA, USA, 1995; Volume 2496, pp. 286–304. [Google Scholar] [CrossRef]
- Descour, M.R.; Volin, C.E.; Dereniak, E.L.; Thome, K.J.; Schumacher, A.B.; Wilson, D.W.; Maker, P.D. Demonstration of a High-Speed Nonscanning Imaging Spectrometer. Opt. Lett. 1997, 22, 1271. [Google Scholar] [CrossRef]
- Johnson, W.R.; Wilson, D.W.; Fink, W.; Humayun, M.; Bearman, G. Snapshot Hyperspectral Imaging in Ophthalmology. J. Biomed. Opt. 2007, 12, 014036. [Google Scholar] [CrossRef]
- Habel, R.; Kudenov, M.; Wimmer, M. Practical Spectral Photography. Comput. Graph. Forum 2012, 31, 449–458. [Google Scholar] [CrossRef]
- Lu, R.; Van Beers, R.; Saeys, W.; Li, C.; Cen, H. Measurement of Optical Properties of Fruits and Vegetables: A Review. Postharvest Biol. Technol. 2020, 159, 111003. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A Model of Leaf Optical Properties Spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Solovchenko, A.E.; Pogosyan, S.I. Application of Reflectance Spectroscopy for Analysis of Higher Plant Pigments. Russ. J. Plant Physiol. 2003, 50, 704–710. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Solovchenko, A.E.; Gitelson, A.A. Reflectance Spectral Features and Non-Destructive Estimation of Chlorophyll, Carotenoid and Anthocyanin Content in Apple Fruit. Postharvest Biol. Technol. 2003, 27, 197–211. [Google Scholar] [CrossRef]
- Sonobe, R.; Yamashita, H.; Mihara, H.; Morita, A.; Ikka, T. Estimation of Leaf Chlorophyll a, b and Carotenoid Contents and Their Ratios Using Hyperspectral Reflectance. Remote Sens. 2020, 12, 3265. [Google Scholar] [CrossRef]
- Morales Cruzado, B.; y Montiel, S.V.; Atencio, J.A.D. Genetic Algorithms and MCML Program for Recovery of Optical Properties of Homogeneous Turbid Media. Biomed. Opt. Express 2013, 4, 433. [Google Scholar] [CrossRef]
- Mridha, N.; Sahoo, R.N.; Kumar, D.N.; Sehgal, V.K.; Pradhan, S.; Gupta, V.K. Genetic Algorithm Based Inversion Modelling of PROSAIL for Retrieval of Wheat Biophysical Parameters from Bi-Directional Reflectance Data. J. Agric. Phys. 2014, 14, 10. [Google Scholar]
- Jiang, J.; Comar, A.; Burger, P.; Bancal, P.; Weiss, M.; Baret, F. Estimation of Leaf Traits from Reflectance Measurements: Comparison between Methods Based on Vegetation Indices and Several Versions of the PROSPECT Model. Plant Methods 2018, 14, 23. [Google Scholar] [CrossRef]
- Berger, K.; Verrelst, J.; Féret, J.-B.; Hank, T.; Wocher, M.; Mauser, W.; Camps-Valls, G. Retrieval of Aboveground Crop Nitrogen Content with a Hybrid Machine Learning Method. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102174. [Google Scholar] [CrossRef]
- Narea-Jiménez, F.; Castro-Ramos, J.; Sánchez-Escobar, J.J.; Muñoz-Morales, A. Assessment of a Computed Tomography Imaging Spectrometer Using an Optimized Expectation-Maximization Algorithm. Appl. Opt. 2022, 61, 6076–6085. [Google Scholar] [CrossRef]
- Boren, E.J.; Boschetti, L.; Johnson, D.M. Characterizing the Variability of the Structure Parameter in the PROSPECT Leaf Optical Properties Model. Remote Sens. 2019, 11, 1236. [Google Scholar] [CrossRef]
- Allen, W.A.; Gausman, H.W.; Richardson, A.J.; Thomas, J.R. Interaction of Isotropic Light with a Compact Plant Leaf. J. Opt. Soc. Am. 1969, 59, 1376. [Google Scholar] [CrossRef]
- Kumar, L.; Schmidt, K.; Dury, S.; Skidmore, A. Imaging Spectrometry and Vegetation Science. In Imaging Spectrometry: Basic Principles and Prospective Applications; van der Meer, F.D., de Jong, S.M., Eds.; Remote sensing and digital image processing; Springer: Dordrecht, The Netherlands, 2010; pp. 111–155. [Google Scholar]
- Clementson, L.A.; Wojtasiewicz, B. Dataset on the Absorption Characteristics of Extracted Phytoplankton Pigments. Data Brief 2019, 24, 103875. [Google Scholar] [CrossRef]
- Weryszko-Chmielewska, E.; Michałojć, Z. Anatomical Traits of Sweet Pepper (Capsicum annuum L.) Fruit. Acta Agrobot. 2012, 64, 181–188. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S.L.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating Leaf Biochemistry Using the PROSPECT Leaf Optical Properties Model. Remote Sens. Environ. 1996, 56, 194–202. [Google Scholar] [CrossRef]
- Govender, M.; Chetty, K.; Bulcock, H. A Review of Hyperspectral Remote Sensing and Its Application in Vegetation and Water Resource Studies. Water SA 2009, 33, 145–151. [Google Scholar] [CrossRef]
- Jurise, M.; Udal, A.; Kaugerand, J.; Sell, R. Easy to Use Empirical Model for Green Vegetation Reflection Spectrum in VIS-NIR Range. In Eighth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2020); Themistocleous, K., Michaelides, S., Ambrosia, V., Hadjimitsis, D.G., Papadavid, G., Eds.; SPIE: Paphos, Cyprus, 2020; p. 36. [Google Scholar] [CrossRef]
- Féret, J.-B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards Modeling Leaf Optical Properties through a Complete Lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Merzlyak, M.N. Modeling Pigment Contributions to Spectral Reflection of Apple Fruit. Photochem. Photobiol. Sci. 2006, 5, 748. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; Wiley Series in Engineering Design and Automation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Sánchez Escobar, J.J.; Barbosa Santillán, L.I.; Ramos, J.C.; Barbosa Santillán, L.F. Reconstruyendo La Diferencia de Camino Óptico de Un Interferogram Real Degradado Por Ruido Mediante La Solución de Diferentes Problemas de Optimización. Rev. Mex. Fis. E 2021, 18, 020207. [Google Scholar] [CrossRef]
- Vázquez-Montiel, S.; Sánchez-Escobar, J.J.; Fuentes, O. Obtaining the Phase of an Interferogram by Use of an Evolution Strategy: Part I. Appl. Opt. 2002, 41, 3448–3452. [Google Scholar] [CrossRef]
- Sanchez-Escobar, J.J.; Magaña, P.A.; Vazquez-Montiel, S. Obtaining the Wavefront Aberrations of a Real Interferogram by Use of a Hybrid Genetic Algorithm. Opt. Eng. 2006, 45, 105605. [Google Scholar] [CrossRef]
- Sánchez-Escobar, J.J.; Santillán, L.I.B. Reconstruction of the Wavefront Aberration from Real Interferometric Data Using a Hybrid Evolutionary Optimization Algorithm with Zernike Polynomials. Opt. Eng. 2015, 54, 094102. [Google Scholar] [CrossRef]
- LLiu, X.; Li, Y. Optimal Design of DFG-Based Wavelength Conversion Based on Hybrid Genetic Algorithm. Opt. Express 2003, 11, 1677–1688. [Google Scholar] [CrossRef]
- Lara, A.; Sanchez, G.; Coello, C.A.C.; Schutze, O. HCS: A New Local Search Strategy for Memetic Multiobjective Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2010, 14, 112–132. [Google Scholar] [CrossRef]
- Sindhya, K.; Miettinen, K.; Deb, K. A Hybrid Framework for Evolutionary Multi-Objective Optimization. IEEE Trans. Evol. Comput. 2013, 17, 495–511. [Google Scholar] [CrossRef]
- MathWorks. Global Optimization Toolbox; The MathWorks, Inc.: Carlsbad, CA, USA, 2019; Available online: https://www.mathworks.com/products/global-optimization.html (accessed on 21 March 2025).
- Ackora-Prah, J.; Gyamerah, S.A.; Andam, P.S. A Heuristic Crossover for Portfolio Selection. Appl. Math. Sci. 2014, 8, 3215–3227. [Google Scholar] [CrossRef]
- Marsili Libelli, S.; Alba, P. Adaptive Mutation in Genetic Algorithms. Soft Comput. 2000, 4, 76–80. [Google Scholar] [CrossRef]
- Luning, P.A.; de Rijk, T.; Wichers, H.J.; Roozen, J.P. Gas Chromatography, Mass Spectrometry, and Sniffing Port Analyses of Volatile Compounds of Fresh Bell Peppers (Capsicum annuum) at Different Ripening Stages. J. Agric. Food Chem. 1994, 42, 977–983. [Google Scholar] [CrossRef]
- Guzman, I.; Hamby, S.; Romero, J.; Bosland, P.W.; O’Connell, M.A. Variability of Carotenoid Biosynthesis in Orange Colored Capsicum Spp. Plant Sci. 2010, 179, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.J. Chemometrics in Analytical Spectroscopy, 2nd ed.; RSC analytical spectroscopy monographs; Royal Society of Chemistry: Cambridge, UK, 2004. [Google Scholar]
- Räty, J.; Peiponen, K.-E.; Asakura, T. UV-Visible Reflection Spectroscopy of Liquids; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Mark, H.; Workman, J.L. Chemometrics in Spectroscopy; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mishra, P.; Karami, A.; Nordon, A.; Rutledge, D.N.; Roger, J.-M. Automatic De-Noising of Close-Range Hyperspectral Images with a Wavelength-Specific Shearlet-Based Image Noise Reduction Method. Sens. Actuators B Chem. 2019, 281, 1034–1044. [Google Scholar] [CrossRef]
- Garcia, J.P.; Dereniak, E.L. Mixed-Expectation Image-Reconstruction Technique. Appl. Opt. 1999, 38, 3745–3748. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics Corner: A Guide to Appropriate Use of Correlation Coefficient in Medical Research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar] [PubMed]
- Wang, W.; Lu, Y. Analysis of the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) in Assessing Rounding Model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 324, 012049. [Google Scholar] [CrossRef]
- Khan, S.S.; Madden, M.G. New Similarity Metrics for Raman Spectroscopy. Chemom. Intell. Lab. Syst. 2012, 114, 99–108. [Google Scholar] [CrossRef]
- Har-Peled, S.; Raichel, B. The Fréchet Distance Revisited and Extended. ACM Trans. Algorithms 2014, 10, 1–22. [Google Scholar] [CrossRef]
- Volin, C.E.; Descour, M.R.; Dereniak, E.L. Signal-to-Noise Ratio Analysis of the Computed Tomography Imaging Spectrometer. In Proceedings of the SPIE, San Diego, CA, USA, 16 October 1998; Volume 3438, pp. 68–77. [Google Scholar] [CrossRef]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research, 9th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2010. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer series in operations research; Springer: New York, NY, USA, 2006. [Google Scholar]
- Schittkowski, K. An Active Set Strategy for Solving Optimization Problems with up to 200,000,000 Nonlinear Constraints. Appl. Numer. Math. 2009, 59, 2999–3007. [Google Scholar] [CrossRef]
- Fowler, M.E.; Mikota, S.K. Appendix 4: Toxicology Terms, Abbreviations, and Equivalents. In Biology, Medicine, and Surgery of Elephants; Wiley: Hoboken, NJ, USA, 2006; pp. 497–498. [Google Scholar] [CrossRef]
- Yi, Q.; Jiapaer, G.; Chen, J.; Bao, A.; Wang, F. Different Units of Measurement of Carotenoids Estimation in Cotton Using Hyperspectral Indices and Partial Least Square Regression. ISPRS J. Photogramm. Remote Sens. 2014, 91, 72–84. [Google Scholar] [CrossRef]
- Tyner, T.; Francis, J. Useful Equations and Conversions; ACS Reagent Chemicals; American Chemical Society: Washington, DC, USA, 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Zur, Y.; Chivkunova, O.B.; Merzlyak, M.N. Assessing Carotenoid Content in Plant Leaves with Reflectance Spectroscopy. Photochem. Photobiol. 2002, 75, 272. [Google Scholar] [CrossRef]
- Moser, D.; Matile, P. Chlorophyll Breakdown in Ripening Fruits of Capsicum annuum. J. Plant Physiol. 1997, 150, 759–761. [Google Scholar] [CrossRef]
- Féret, J.-B.; Berger, K.; de Boissieu, F.; Malenovský, Z. PROSPECT-PRO for Estimating Content of Nitrogen-Containing Leaf Proteins and Other Carbon-Based Constituents. Remote Sens. Environ. 2021, 252, 112173. [Google Scholar] [CrossRef]
- Ignat, T.; Schmilovitch, Z.; Feföldi, J.; Bernstein, N.; Steiner, B.; Egozi, H.; Hoffman, A. Nonlinear Methods for Estimation of Maturity Stage, Total Chlorophyll, and Carotenoid Content in Intact Bell Peppers. Biosyst. Eng. 2013, 114, 414–425. [Google Scholar] [CrossRef]


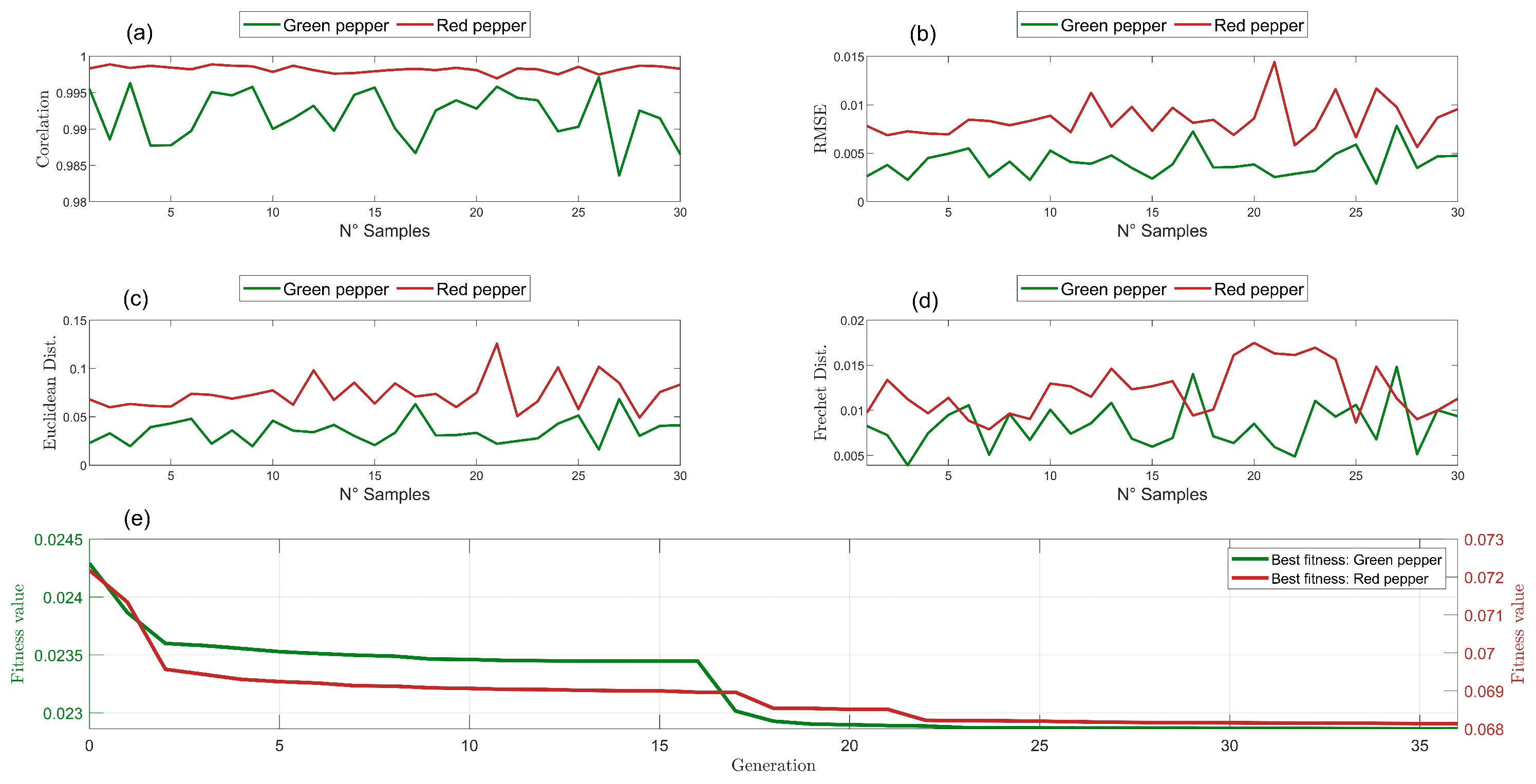
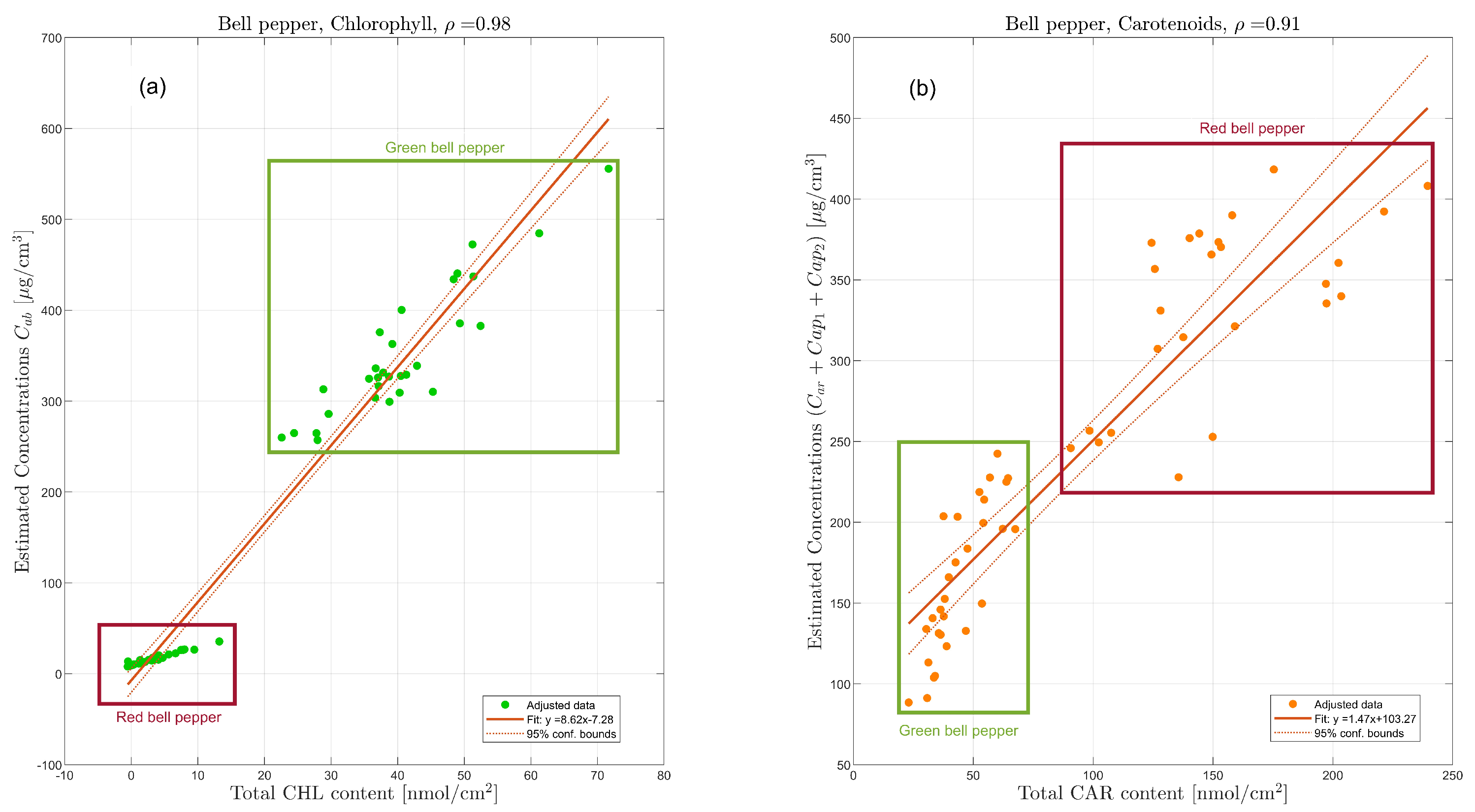
| Methods | Green Pepper | Red Pepper | ||
|---|---|---|---|---|
| Noise 7% | Noise 20% | Noise 7% | Noise 20% | |
| GA | 3.89 | 8.46 | 3.14 | 5.38 |
| Interior-Point | 21.94 | 34.42 | 3.97 | 9.57 |
| SQP | 59.76 | 55.92 | 12.16 | 34.93 |
| Active-Set | 22.13 | 33.84 | 8.35 | 9.44 |
| Green Pepper | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [%] | RMSE | ||||||||
| Average | 4.31 | 385.57 | 67.53 | 183.11 | 32.07 | 0.18 | 0.03 | 2.13 | 0.37 | 0.48 | 0.88 | |
| Typical error | 0.04 | 17.96 | 1.01 | 8.94 | 1.03 | 0.04 | 0.01 | 0.12 | 0.02 | 0.01 | 0.02 | |
| Reference | - | 416.60 | 68.72 | 186.79 | 30.81 | 0.47 | 0.08 | 2.33 | 0.38 | - | - | - |
| - | 31.03 | 1.19 | 3.68 | 1.26 | 0.29 | 0.05 | 0.20 | 0.01 | - | - | - | |
| Red pepper | ||||||||||||
| N | [%] | [%] | [%] | [%] | K | RMSE | ||||||
| Average | 4.13 | 26.42 | 6.69 | 89.87 | 22.78 | 251.40 | 63.71 | 26.91 | 6.82 | 0.47 | 0.96 | |
| Typical error | 0.03 | 1.76 | 0.47 | 2.50 | 0.73 | 7.11 | 1.20 | 2.03 | 0.49 | 0.00 | 0.01 | |
| Reference | - | 20.00 | 4.98 | 99.94 | 24.89 | 251.43 | 62.62 | 30.16 | 7.51 | - | - | - |
| - | 6.42 | 1.71 | 10.07 | 2.11 | 0.03 | 1.09 | 3.25 | 0.69 | - | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narea-Jiménez, F.; Castro-Ramos, J.; Sánchez-Escobar, J.J. A Multi-Objective Genetic Algorithm for Retrieving the Parameters of Sweet Pepper (Capsicum annuum) from the Diffuse Spectral Response. AgriEngineering 2025, 7, 284. https://doi.org/10.3390/agriengineering7090284
Narea-Jiménez F, Castro-Ramos J, Sánchez-Escobar JJ. A Multi-Objective Genetic Algorithm for Retrieving the Parameters of Sweet Pepper (Capsicum annuum) from the Diffuse Spectral Response. AgriEngineering. 2025; 7(9):284. https://doi.org/10.3390/agriengineering7090284
Chicago/Turabian StyleNarea-Jiménez, Freddy, Jorge Castro-Ramos, and Juan Jaime Sánchez-Escobar. 2025. "A Multi-Objective Genetic Algorithm for Retrieving the Parameters of Sweet Pepper (Capsicum annuum) from the Diffuse Spectral Response" AgriEngineering 7, no. 9: 284. https://doi.org/10.3390/agriengineering7090284
APA StyleNarea-Jiménez, F., Castro-Ramos, J., & Sánchez-Escobar, J. J. (2025). A Multi-Objective Genetic Algorithm for Retrieving the Parameters of Sweet Pepper (Capsicum annuum) from the Diffuse Spectral Response. AgriEngineering, 7(9), 284. https://doi.org/10.3390/agriengineering7090284









