Study on the Influence of Hole Shape and Grain Orientation on the Adsorption Characteristics of Maize Seeds and CFD Analysis
Abstract
1. Introduction
2. Analysis Methods and Research Principles
2.1. Theoretical Model and Analysis
2.2. Maize Kernel Classification
- Dent-like kernels: Wadell sphericity ranges from 0.78 to 0.82. These kernels feature two relatively flat lateral surfaces and prominent edges.
- Conical-like kernels: Sphericity ranges from 0.86 to 0.92. They possess smooth top surfaces and lateral faces with similar curvature and area.
- Spherical-like kernels: Sphericity ranges from 0.95 to 0.99. Except for the tip, their overall shape exhibits high symmetry across multiple surfaces.
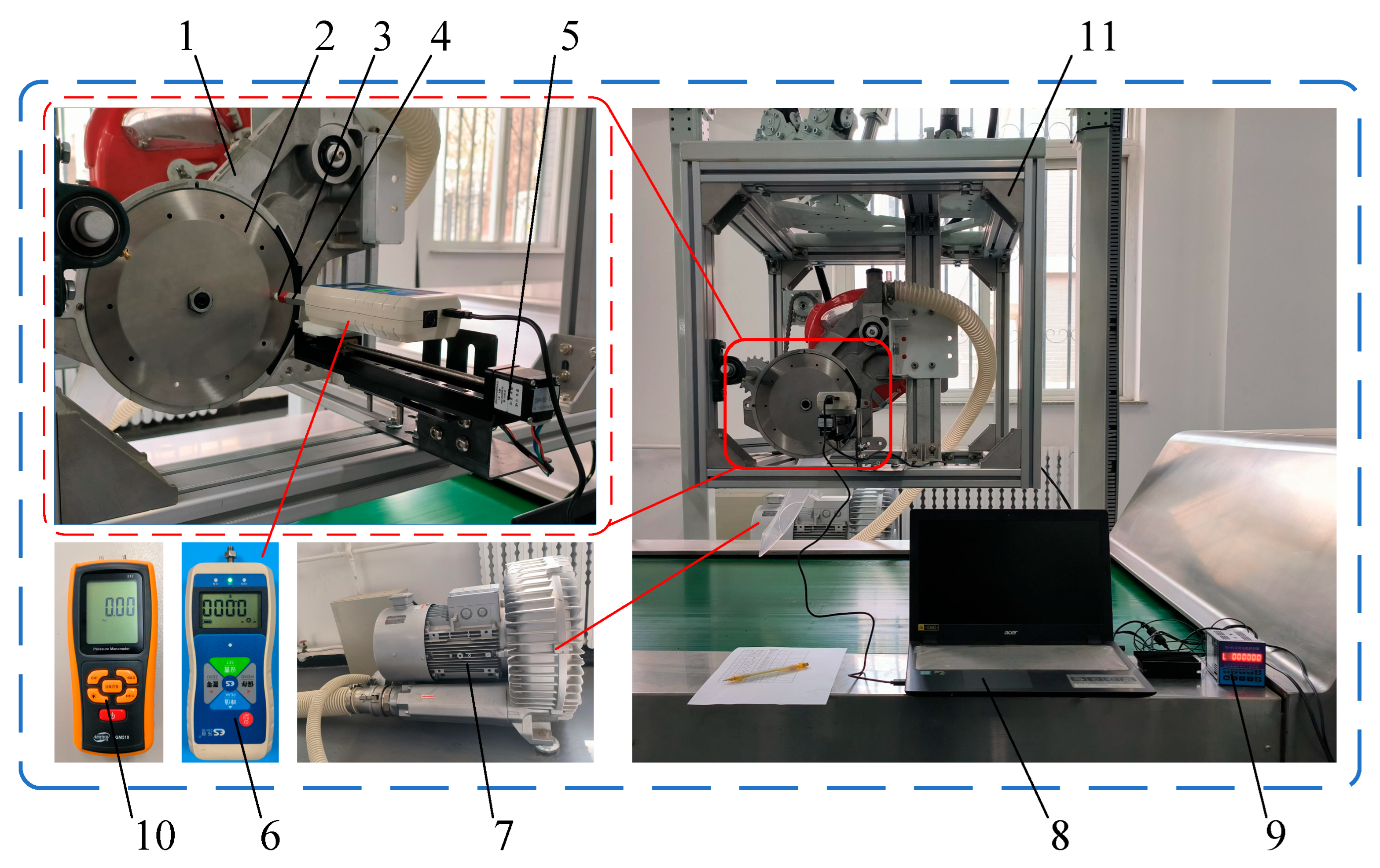
2.3. Experimental Setup
3. Experimental Design
3.1. Standard Particle Experiment Plan
3.1.1. Study of the Effect of Suction Hole Shape
3.1.2. Study of the Effect of Equivalent Suction Area
3.1.3. Study of the Effect of Particle Diameter
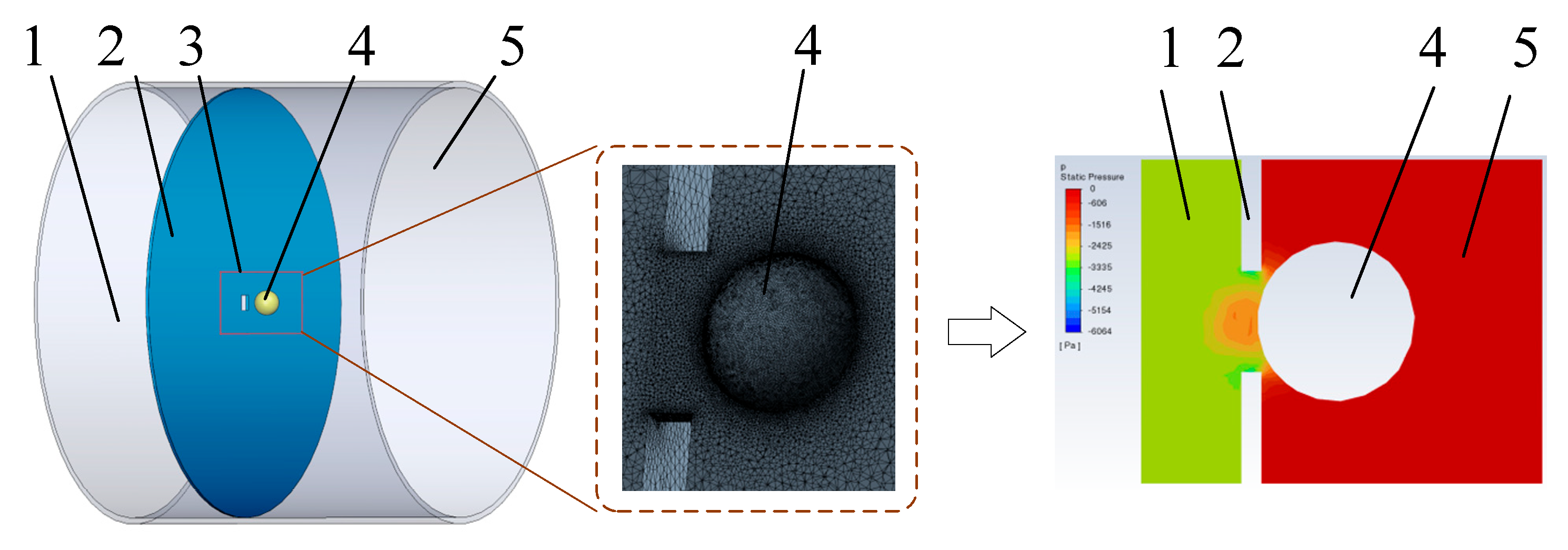
3.2. CFD Simulation Experiment Design
3.3. Maize Kernel Suction Force Measurement Plan
4. Results
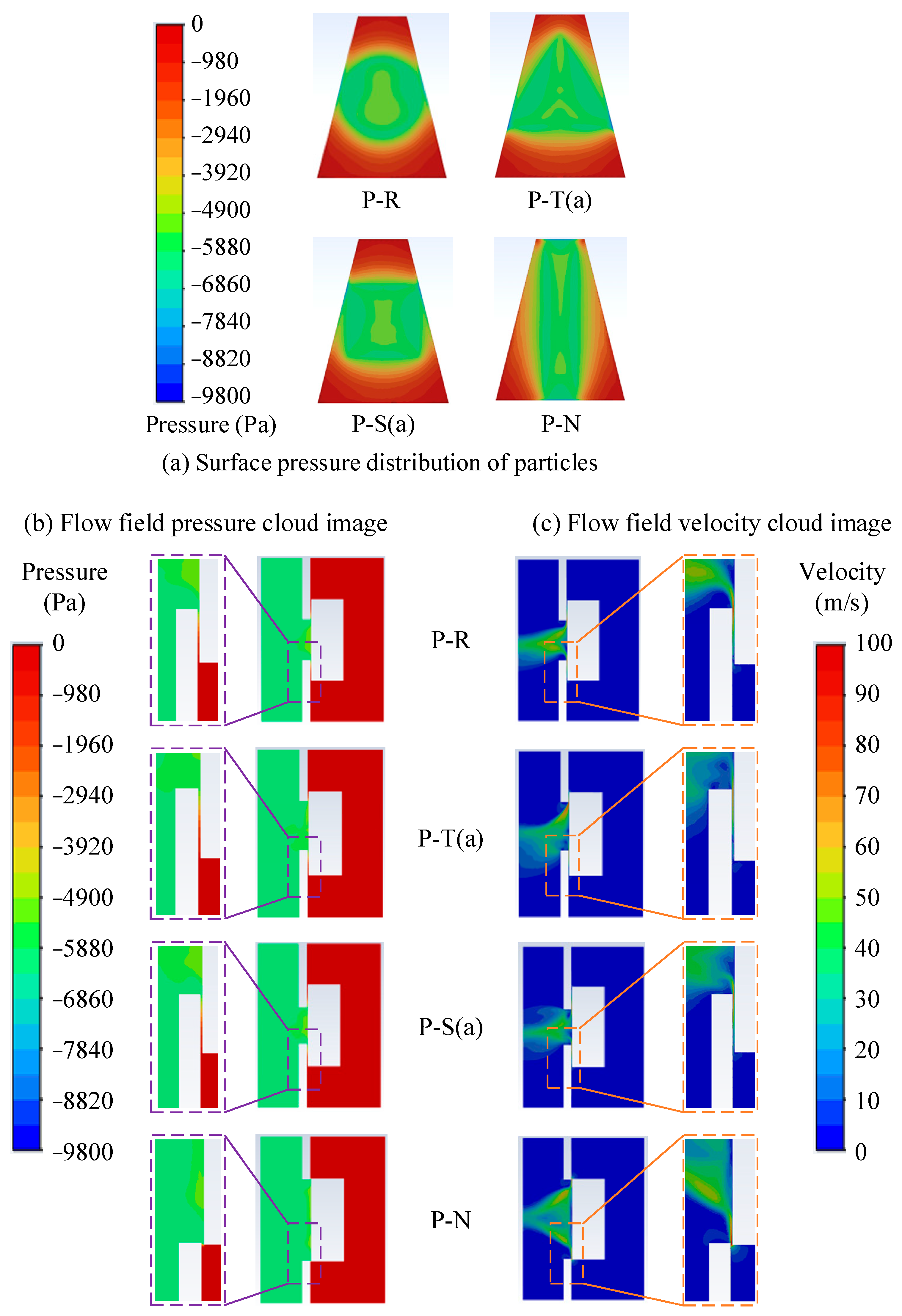
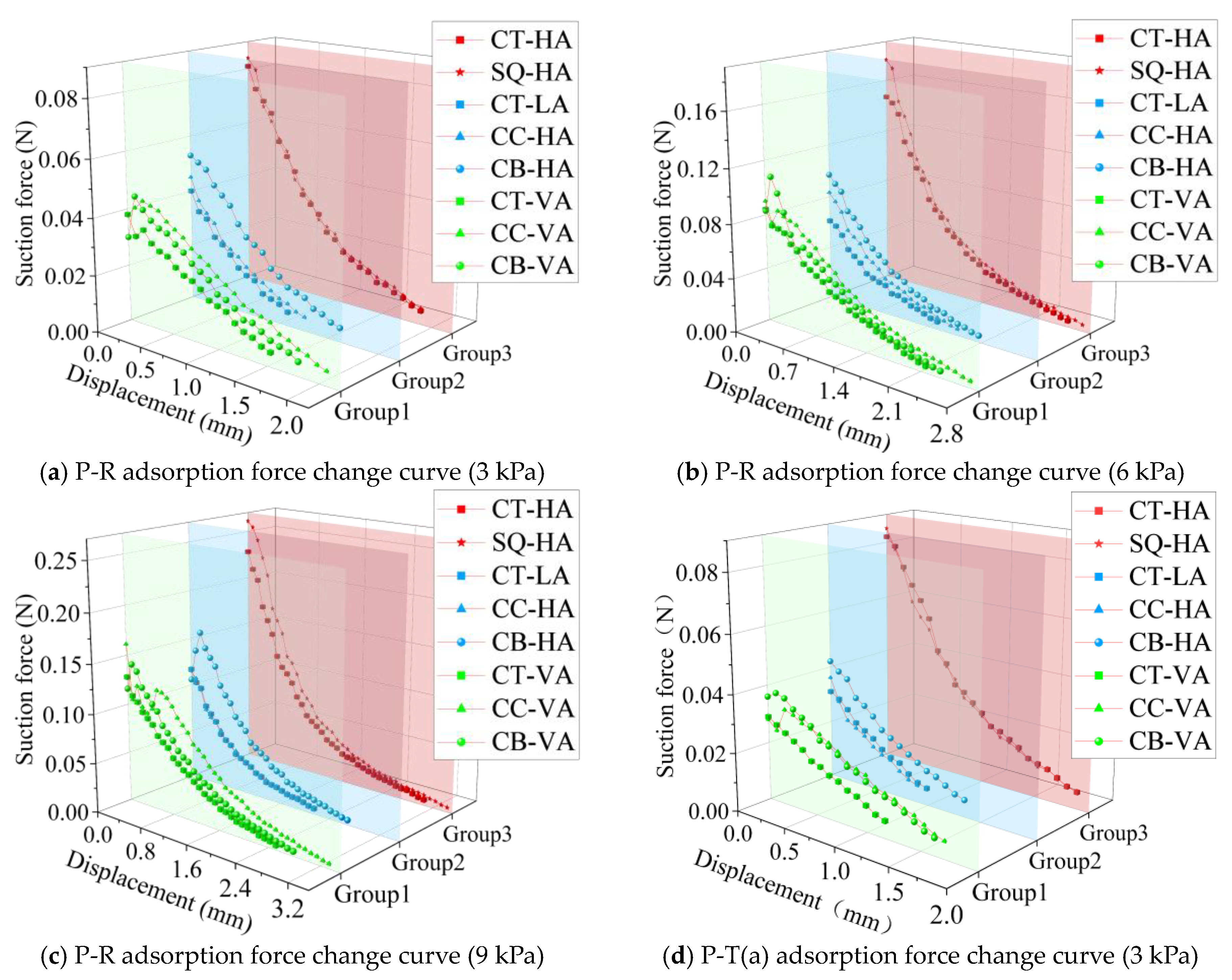
4.1. Impact of Suction Hole Shape on Adsorption Performance
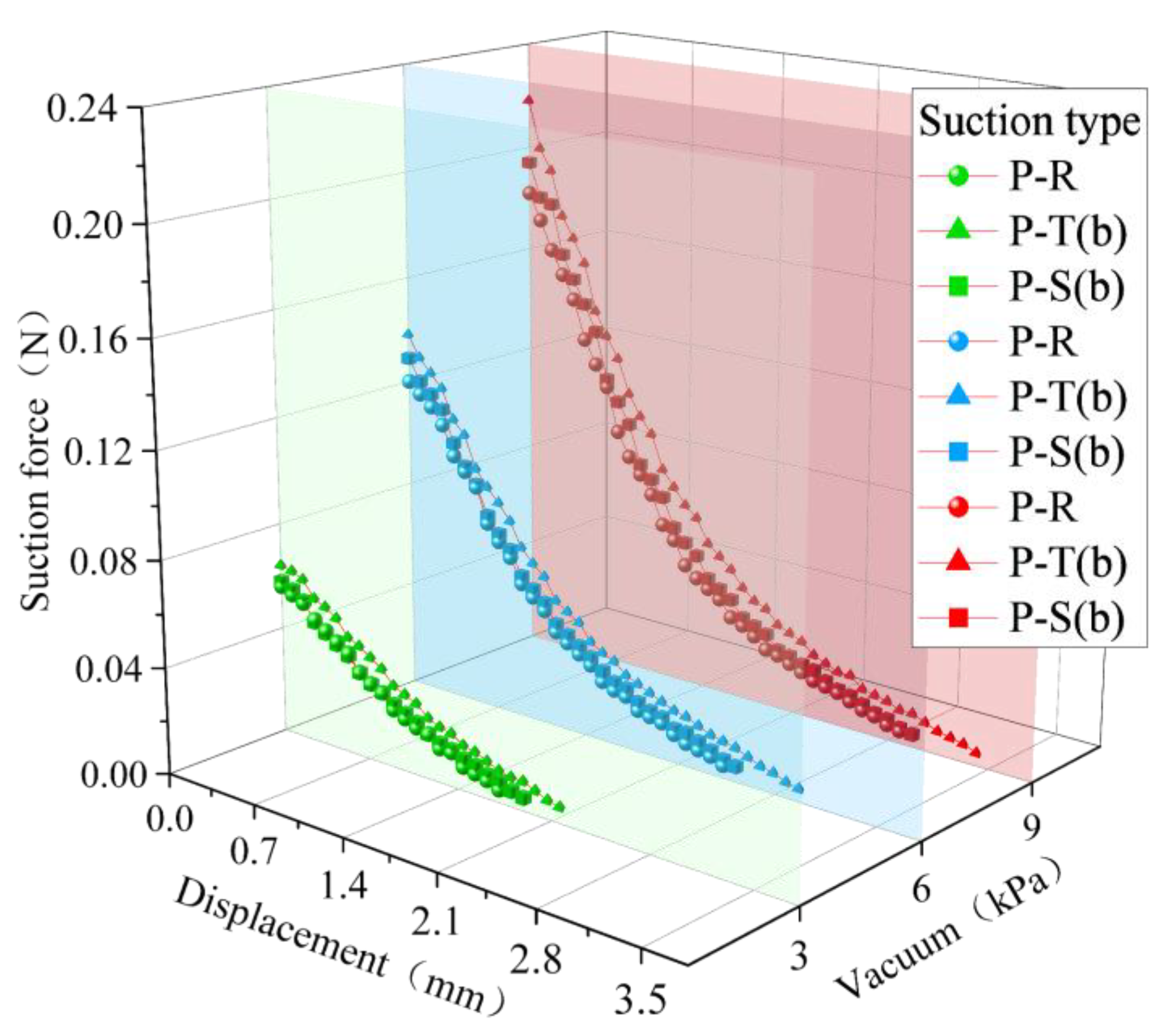
4.2. Impact of Effective Adsorption Area on Adsorption Performance
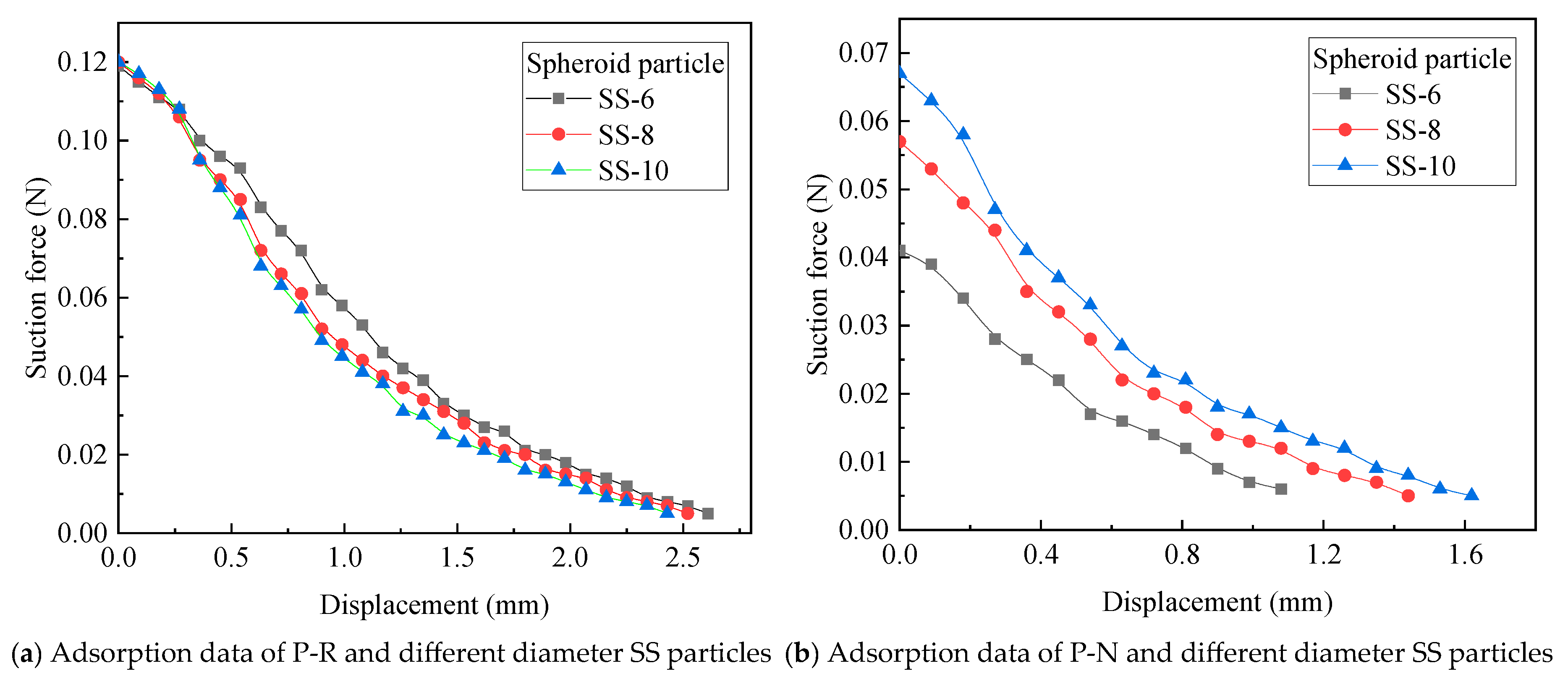
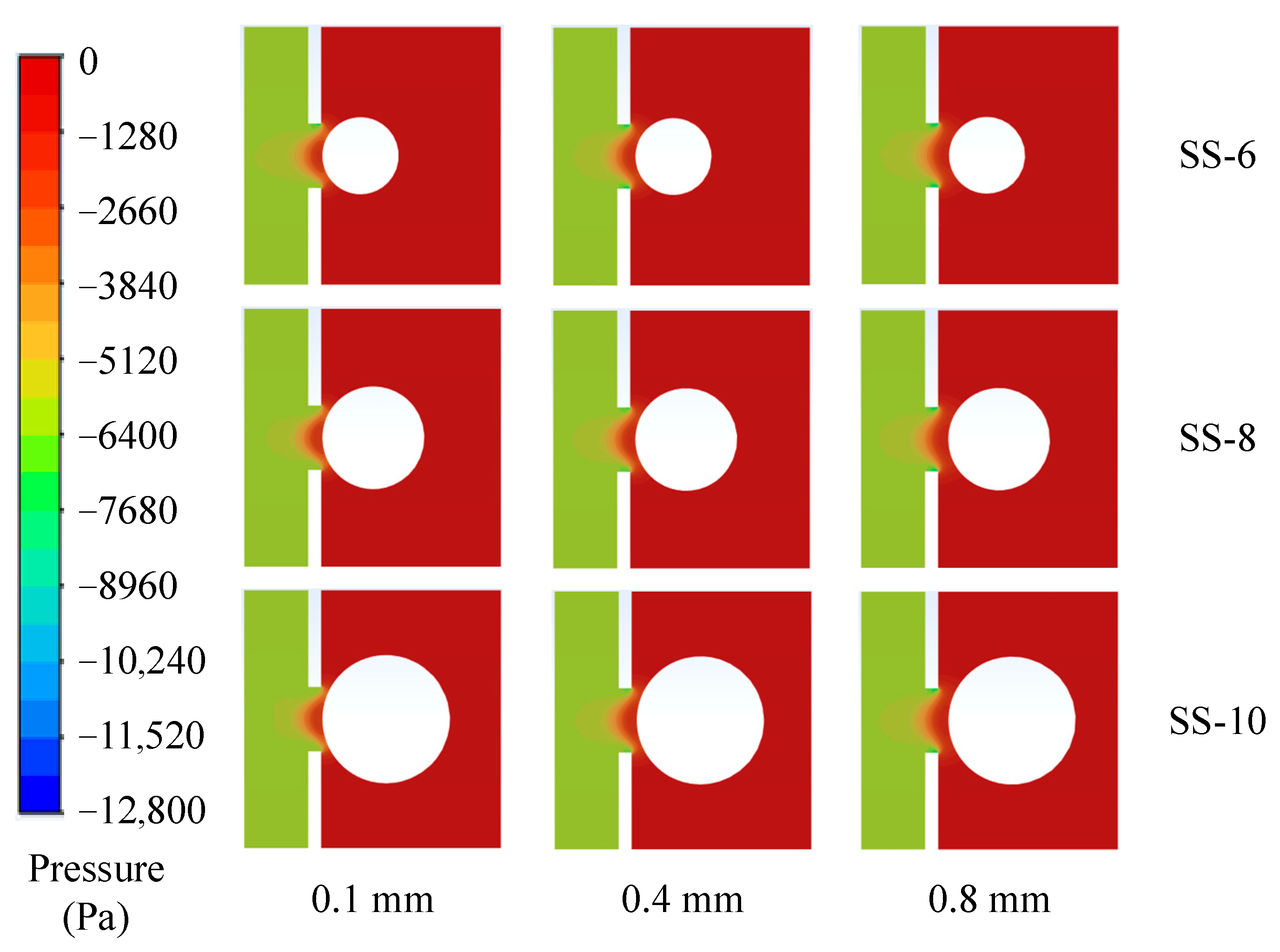
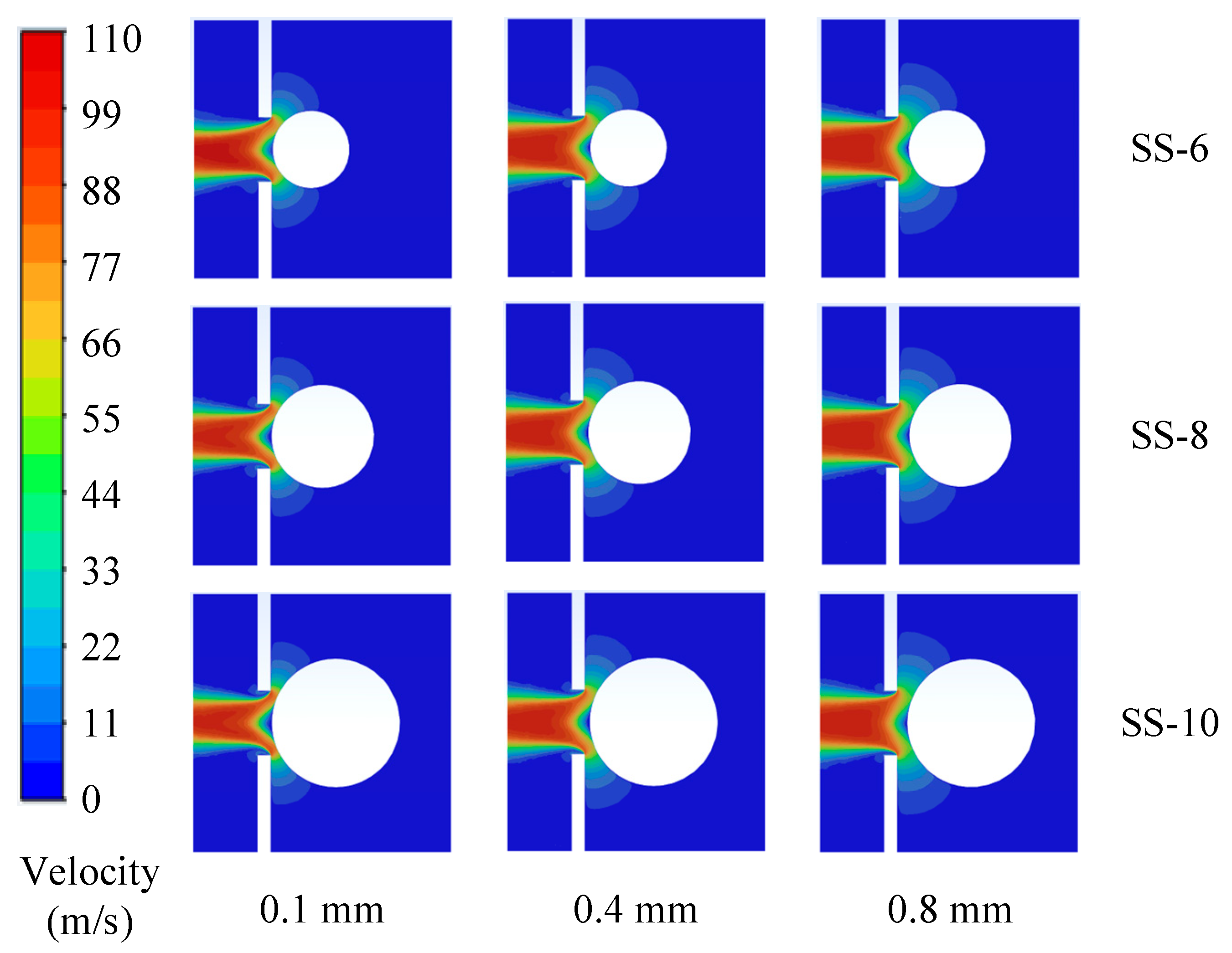
4.3. Effect of Particle Diameter on Adsorption Efficiency
4.4. Maize Seed Adsorption Test Results
5. Discussion
- Based on the force analysis, maize seeds experience the effects of gravity, suction force from the seeding hole, and support from the seed plate during the adsorption process. The closer the seed’s center of mass is to the seed plate, the more stable the adsorption. When the seed is positioned flat against the seeding hole, it covers a larger area, resulting in greater suction force. In this orientation, the seed’s center of mass is also closest to the seed plate, making it the most stable posture for adsorption. When the seed is adsorbed by its edge or side, it will rotate due to gravity to adjust its center of mass, ultimately achieving a balanced and stable state with the support force.
- When the seeding hole area is the same, under the same vacuum pressure and when the seeding hole is fully covered, the shape of the hole does not significantly affect the adsorption performance of the SQ particle. During the initial phase of detachment from the seeding hole, the hole transitions from being blocked to connecting with the external environment. Air near the particle begins to flow from the high-pressure zone outside to the low-pressure zone inside the hole, with the shape of the hole affecting the distribution of pressure on the particle surface (i.e., the flow field distribution). However, there was no significant difference in the forces acting on the particle. The high-speed airflow in the gap between the particle and the seed plate creates a pressure difference (pressure gradient force) that prevents the particle from detaching from the hole, and this force is influenced by the airflow pattern and speed. This observed regularity aligns with the conclusion drawn by Wang et al. [9] from their experimental analysis of ellipsoidal seed adsorption.
- When studying the effect of airflow around the particles, the adsorption position of the material was controlled (keeping the relative position between SS-8 material and the seeding hole constant). As the unblocked area increased, the airflow speed in the gap between the particle and the hole increased, causing a slight increase in suction force. However, the rate of increase in suction force was much smaller than the increase in the unblocked area. This is because the airflow through the hole acts on the particle in the same position, and when the particle is 0.1 mm from the hole, a small increase in the seeding hole area has little effect on the vacuum pressure difference around the particle. The symmetry of the flow field and spherical particle causes the components of the forces generated by the increased airflow angle to cancel each other out. Therefore, increasing the unblocked area of the seeding hole has a minimal effect on the suction force acting on a particle in the same position.
- The adsorption results of spherical materials with different diameters on the P-R seeding hole under constant pressure show that, since the particles exhibit the same hole-blocking effect during adsorption, the three spherical particles had similar maximum adsorption forces at 6 kPa. As the particles moved further from the hole, the pressure gradient force decreased, and the differences in airflow around the particle surface became more pronounced. The SS-6 particle, having a larger curvature, exhibited a greater airflow wrap-around angle, causing a slower reduction in suction force, while the SS-10 particle experienced a faster reduction in suction force. However, smaller diameter particles are more likely to be captured by the same suction force, which could lead to re-adsorption of smaller particles. The P-N seeding hole’s adsorption results under constant pressure showed that the short edge of the hole limited the particle overlap distance (tx) with the seeding hole, resulting in the suction force being positively correlated with the overlap length along the long edge of the hole. This indicates that the P-N hole has advantages when used for materials with mass-to-characteristic-length ratios. The above analysis indirectly confirms the discovery of Barut et al. [34] that rectangular suction holes are more conducive to the adsorption of corn seeds [35].
- The actual adsorption tests with maize kernels show that the shape of the seeding hole significantly impacts the adsorption effect on the maize kernels. The seeding hole tends to perform better with seed shapes that match its contours. Research findings by Tang et al. [13] indicate that designing suction holes with irregular shapes can enhance seeding performance. Due to the irregular shape and large individual variation of maize kernels, the suction force depends on kernel morphology, the effective blocking area of the kernel and hole, and the kernel’s posture, making it difficult to precisely categorize kernels and obtain accurate adsorption forces. Because of the geometric characteristics and flow field symmetry of the material, kernels with similar adsorption surfaces exhibit similar adsorption effects. Classifying kernels based on equivalent adsorption characteristics is an effective means of standardizing the adsorption features of irregular materials, but further research is needed to better understand the characteristics and effects of the airflow field from the seeding holes. (Although the data are representative of typical results from multiple repeated tests, the variability still reflects some randomness, and the differences between maize kernel types mean that each data set only represents random outcomes for specific kernel shapes in a particular posture.) Additionally, this experiment did not account for factors such as field vibrations and humidity under complex operating conditions, which may influence seed adsorption efficacy. Therefore, it is of great significance to quantify the movement patterns of individual seeds under suction holes in complex field conditions in future research.
- Traditional pressure calculation models and airflow drag calculation models have limitations when applied to calculate the suction force of seeding holes. Similarly, Li et al. [7] highlighted the unreliability of traditional suction models in their adsorption studies on highly spherical seeds. According to gas–solid two-phase flow theory, particles should be influenced by FD, FP, and Fsa forces during the adsorption process. However, due to variations in flow fields, theoretical calculations should be adjusted based on the flow field characteristics and the specific particles being adsorbed. This paper proposes a hypothetical suction force calculation model (Equation (4)) for further research and discussion. The vacuum pressure, hole area, particle size, curvature of the particle’s suction surface, and distance between the particle and the hole all affect the magnitude of the suction force. The establishment of a suction model can provide theoretical support for the design and development of seed metering devices, facilitating the advancement of precise and quantitative seeding technology.
6. Conclusions
- The study demonstrated that commonly used methods for calculating the suction force of seeding holes (pressure calculations and airflow drag calculations) have limitations in their application. In experiments evaluating the effect of equivalent adsorption area, the relative error between the suction force estimated by the traditional pressure-based method for triangular holes and the actual measured force reached 40.82%. Similarly, the relative error between the force estimated by the airflow drag method for square suction holes and the actual measured force under the same conditions was 17.14%.
- Adsorption tests with standard particles showed that vacuum pressure, hole-blocking area, particle diameter, suction surface curvature, particle distance from the seeding hole, and the effective action area of the seeding hole all influence suction force. When fully blocked, the shape of the seeding hole has little effect on flat suction surfaces (the standard deviation of the maximum suction force for the four tested orifice geometries was less than 0.005 N under vacuum levels of 3, 6, and 9 kPa). When the particle adsorption position is the same, differences in the unblocked area of the hole have minimal impact on suction force (the variation in unblocked area among the orifices reached 139%, while the maximum adsorption force difference among the four orifice geometries remained below 0.036 N across all three vacuum levels). The overlap depth between the particle boundary and the hole affects the forces on the particle during the initial phase of detachment.
- Actual maize kernel adsorption tests showed significant differences in the suction force and suction distance depending on the posture of the seed under the same seeding hole type. Different seeding hole types have specific suitability and guidance effects on seed adsorption. Dent-like maize seeds in a horizontal adsorption posture had the highest stability and maximum suction force, while conical seeds in a vertical posture exhibited significant variations in suction force due to their higher overlap with the seeding hole.
- This study experimentally measured the adsorption force and effective suction range of tooth-like, cone-like, and spherical maize kernels under various postures and vacuum levels (3, 6, 9 kPa), using four suction hole shapes with equal area: circular, equilateral triangular, square, and narrow elongated. The results provide valuable data to support the design and development of air-suction maize seed metering devices.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, X. Design and Performance Test of Sunflower Seed Directional Adsorption Seed-Metering Device. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2023. [Google Scholar] [CrossRef]
- Wang, G.D.; Xu, S.C.; Feng, N.N.; Wang, X.Q.; Zhang, Y. Design of sucker arrangement for vacuum sucker plate grabbing device. Manuf. Autom. 2021, 43, 14–16+31. [Google Scholar] [CrossRef]
- Deng, X.L.; Luo, Z.Y.; Pang, J.Q.; Zhang, Y.M.; Yang, C.J.; Li, R.Q. Design and experiment of bionic nondestructive handheld suction apple picker. J. China Agric. Univ. 2019, 24, 100–108. [Google Scholar] [CrossRef]
- Liu, H.B.; Li, X.R.; Liu, L.D. Research progress of automatic grabbing and transfer methods for garment fabrics. J. Text. Res. 2021, 42, 190–196. [Google Scholar] [CrossRef]
- Schulz, A.K.; Ning, W.J.; Ha, S.Y.S.; Kom, G.; Slade, S.B.; Rivera, S.; Reidenberg, J.S.; Hu, D.L. Suction feeding by elephants. J. R. Soc. Interface 2021, 18, 20210215. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, W.; Wang, Y. Design and test of the automatic loading and unloading vacuum adsorption device for glue-laminated timber. J. For. Eng. 2021, 6, 126–132. [Google Scholar] [CrossRef]
- Li, J.H.; Lai, Q.H.; Zhang, H.; Zhang, Z.G.; Zhao, J.W.; Wang, T.T. Suction force on high-sphericity seeds in an air-suction seed-metering device. Biosyst. Eng. 2021, 211, 125–140. [Google Scholar] [CrossRef]
- Li, J.H.; Lai, Q.H.; Su, W.; Xie, Y.R.; Zhang, Z.G. Research on the influence of the suction force on spherical particles in suction flow. Powder Technol. 2021, 393, 824–836. [Google Scholar] [CrossRef]
- Wang, Y.J.; Su, W.; Lin, Y.H.; Lai, Q.H.; Li, J.H. Measurement and modeling the suction force on ellipsoidal particles. Vacuum 2024, 219, 112743. [Google Scholar] [CrossRef]
- Pareek, C.M.; Tewari, V.K.; Machavaram, R. Multi-objective optimization of seeding performance of a pneumatic precision seed metering device using integrated ANN-MOPSO approach. Eng. Appl. Artif. Intel. 2023, 117, 105559. [Google Scholar] [CrossRef]
- Yousry, S.; Youseef, S.; Hossam, E.; Solaf, A.E. Design of a vacuum seed plate based on physical and mechanical properties of maize seeds. Int. J. Adv. Res. 2020, 8, 114–123. [Google Scholar] [CrossRef]
- Hussain, S.; Chen, Y.; Yu, X.; Farid, M.U.; Ghafoor, A.; Alshamali, S.J.; Munir, T.; Hu, J. Design Optimization and Aerodynamic Investigations of Air Suction Seed Metering Systems through CFD-DEM Approach. Smart Agric. Technol. 2025, 12, 101082. [Google Scholar] [CrossRef]
- Tang, H.; Guan, T.Y.; Xu, F.D.; Xu, C.S.; Wang, J.W. Test on adsorption posture and seeding performance of the high-speed precision dual-chamber maize metering device based on the seed characteristics. Comput. Electron. Agr. 2024, 216, 108471. [Google Scholar] [CrossRef]
- Sun, S.C. Simulation Analysis of Working Process of Air Suction Corn Precision Seed-Metering Device Based on DEM-CFD Coupling Method. Master’s Thesis, Jilin University, Changchun, China, 2016. Available online: https://kns.cnki.net/kcms2/article/abstract?v=-Y4qPNLDuvbMD7ab05z_43mQWW9eb8U7Ce3W_hHhjwbU6V7ciWI4Wlh1nKXrTceCMngF840VktCRAHiN05a_1WYsFsqDHb-vUUaX6IwR5IRy8hwUGPn4OJFwrlOOV4CDwxEFnCVraaEtDWDuDfIDC8Cvh14k1qWvIZc25GpdPGQ=&uniplatform=NZKPT (accessed on 28 June 2025).
- Zhao, X.G.; Xu, L.M.; Wang, Y.B.; Li, C. Directional adsorption characteristics of corn seed based on fluent and high-speed photography. Trans. Chin. Soc. Agric. Mach. 2014, 45, 103–109+28. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Zhang, D.X.; Cui, T.; Zhang, K.L.; Zhong, X.J. Effect of seed adsorption posture of corn air-suction metering device on seed feeding performance. Trans. Chin. Soc. Agric. Mach. 2021, 52, 40–50. [Google Scholar] [CrossRef]
- Sial, F.S.; Persson, S.P. Vacuum nozzle design for seed metering. Trans. ASAE 1984, 27, 688–696. [Google Scholar] [CrossRef]
- Fan, L.S.; Zhu, C. Principles of Gas-Solid Flows, 2nd ed.; Cambridge University Press: Cambridge, Britain, 1998. [Google Scholar]
- Zhao, Z.; Li, Y.M.; Chen, J.; Zhou, H. Dynamic analysis on seeds pick-up process for vacuum-cylinder seeder. Trans. CSAE 2011, 27, 112–116. [Google Scholar] [CrossRef]
- Deng, F.H. Experimental Research on the Drag Coefficient of Non-Spherical Particles. Master’s Thesis, China University of Petroleum, Beijing, China, 2018. [Google Scholar] [CrossRef]
- Dai, J.G. Study on discrete element parameters of maize kernel based on PFC(3D). Agric. Technol. 2021, 41, 22–26. [Google Scholar]
- Zhou, L. DEM-Based Modelling of Maize Seeds and the Simulation Analysis and Experimental Study of the Seed-Sowing. Ph.D. Thesis, Jilin University, Changchun, China, 2021. [Google Scholar] [CrossRef]
- Wang, J.W.; Tang, H.; Wang, Q.; Zhou, W.Q.; Yang, W.P.; Shen, H.G. Numerical simulation and experiment on seeding performance of pickup finger precision seed-metering device based on EDEM. Trans. CSAE 2015, 31, 43–50. [Google Scholar] [CrossRef]
- Shi, S. Design and Experimental Research of the Pneumatic Maize Precision Seed-Metering Device with Combined Holes. Ph.D. Thesis, China Agricultural University, Beijing, China, 2015. Available online: https://kns.cnki.net/kcms2/article/abstract?v=-Y4qPNLDuvaQNqtCE40L1FJWry6d9th3SB18M9LO-ULzr8pA8bIP6NLtNlIc2CydEcVcbe7-gWJn8EUWF5ie6iYgBTZPc4_W-P7HOe9pXNv2z6oWRjzGWDhHkIEsdQ69oBcz6T2pEKgveLgEmLwlT4nE6cmq7n0aqeIkRbHEHFejgQvTMxaajEGVIpZJrLTg&uniplatform=NZKPT&language=CHS (accessed on 28 June 2025).
- Yang, Q.; Yue, L.J.; Chen, Y.; Li, Z.; Liu, Y.H. Effects of maize seed morphology on seeding performance of precise seed metering device of socket-roller. Southwest China J. Agric. Sci. 2021, 34, 1847–1852. [Google Scholar]
- Chinese Academy of Agricultural Mechanization Sciences (CAAMS). Agricultural Machinery Design Manual, 2nd ed.; China Agricultural Science and Technology Press: Beijing, China, 2007. [Google Scholar]
- Abdolahzare, Z.; Mehdizadeh, S.A. Real time laboratory and field monitoring of the effect of the operational parameters on seed falling speed and trajectory of pneumatic planter. Comput. Electron. Agr. 2018, 145, 187–198. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Wu, D.Y.; Zhang, D.X.; Liu, S.R. Simulation and experiment of corn air suction seed metering device based on DEM-CFD coupling method. Trans. Chin. Soc. Agric. Mach. 2018, 49, 48. [Google Scholar] [CrossRef]
- Chen, Y.L.; Liu, Z.Q.; Han, J.; Zhao, L.Q.; Sui, X.H.; Zhang, J.W.; Lan, Y.B. Design and experiments of the flat seed-adsorbing posture adjustment mechanism for the air-suction metering device. Trans. Chin. Soc. Agric. Eng. 2022, 38, 1–11. [Google Scholar] [CrossRef]
- Djojodihardjo, H. Overview on the influence of coanda blanket curvature on coanda device performance. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Wang, J.; Li, Y.D.; Song, Z.H.; Tian, F.Y.; Yan, Y.F.; Sun, X.Z. Simulation study on key components of combined air suction seed metering device based on fluent. Agric. Eng. 2023, 13, 90–96. [Google Scholar] [CrossRef]
- Dai, W.L. Structural Design and Experimental Study of a New Type of Air-Suction Precision Seed-Metering Device for Maize. Master’s Thesis, Jilin Agricultural University, Changchun, China, 2019. [Google Scholar] [CrossRef]
- Shi, L.R.; Sun, B.G.; Zhao, W.Y.; Yang, X.P.; Xin, S.L.; Wang, J.X.; Ackermann, K. Optimization and test of performance parameters of elastic air suction type corn roller seed-metering device. Trans. Chin. Soc. Agric. Mach. 2019, 50, 88–95+207. [Google Scholar]
- Barut, Z.B.; Özmerzi, A. Effect of different operating parameters on seed holding in the single seed metering unit of a pneumatic planter. Turk. J. Agric. For. 2004, 28, 435–441. [Google Scholar]
- Bao, G.C.; Zhang, Z.D.; Liu, L.J.; Li, J.D.; Tao, C.S.; Yang, W. Study on the Adsorption Mechanism of Spherical Particles near the Seed Metering Disk Surface by Narrow Elongated Suction Holes. Agriculture 2025, 15, 657. [Google Scholar] [CrossRef]






| Test Object | Picture | Feature Size | Value/mm | Designation |
|---|---|---|---|---|
| Dent-like kernel |  | h × w × t | 12.61 × 8.68 × 3.84 | CT |
| Conical-like kernel |  | h × w × t | 11.63 × 6.74 × 5.61 | CC |
| Spherical-like kernel |  | h × w × t | 9.98 × 8.45 × 8.39 | CB |
| Tetragonal prism particles |  | wa × wb × h × t | 3 × 8 × 10 × 4 | SQ |
| Spherical particles |  | R | 6/8/10 | SS |
| Graphical |  |  |  |
| Features | Circular suction | Positive trilateral suction(a) | Square suction(a) |
| Designation | P-R | P-T(a) | P-S(a) |
| Graphical |  |  |  |
| Features | Long narrow suction | Positive trilateral suction(b) | Square suction(b) |
| Designation | P-N | P-T(b) | P-S(b) |
| Test Number | Test Object | Suction Shape | Vacuum/kPa |
|---|---|---|---|
| Experiment 1 | SQ | P-R, P-T(a), P-S(a), P-N | 3, 6, 9 |
| Experiment 2 | SS-8 | P-R, P-T(b), P-S(b) | 3, 6, 9 |
| Experiment 3 | SS-6, SS-8, SS-10 | P-R, P-N | 6 |
| Test Number | Test Object | Suction Shape | Vacuum/kPa | Distance/mm |
|---|---|---|---|---|
| Simulation 1 | SQ | P-R, P-T(a), P-S(a), P-N | 6 | 0.1 |
| Simulation 2 | SS-8 | P-R, P-T(b), P-S(b) | 6 | 0.1 |
| Simulation 3 | SS-6, SS-8, SS-10 | P-R, P-N | 6 | 0.1, 0.4, 0.8 |
| Object | Parameters |
|---|---|
| Fluid density ρg (kg/m3) | 1.225 |
| Dynamic viscosity μg (kg/m/s) | 1.789 × 10−5 |
| Atmospheric pressure P0 (Pa) | 101.325 |
| Pressure inlet (Pa) | −6000 |
| Pressure outlet (Pa) | 0 |
| Factors | Suction Hole Shape | Particle Shape—Adsorption Posture | Vacuum | |
|---|---|---|---|---|
| Level | ||||
| 1 | P-R | CT-HA | 3 kPa | |
| 2 | P-T(a) | CT-LA | 6 kPa | |
| 3 | P-S(a) | CT-VA | 9 kPa | |
| 4 | P-N | CC-HA | / | |
| 5 | / | CC-VA | / | |
| 6 | / | CB-HA | / | |
| 7 | / | CB-VA | / | |
| Suction Hole Shape | P-R | P-T(b) | P-S(b) | Standard Deviation | |
|---|---|---|---|---|---|
| Force | |||||
| Maximum suction force /N | 0.1202 | 0.1384 | 0.1295 | 0.0091 | |
| FS (N) | 0.1178 | 0.1949 | 0.15 | 0.0387 | |
| The relative error of FS /% | 2 | 40.82 | 15.83 | / | |
| FD (N) | 0.1002 | 0.1223 | 0.1073 | 0.0113 | |
| The relative error of FD /% | 16.64 | 11.63 | 17.14 | / | |
| Particle Type | SS-6 | SS-8 | SS-10 | |
|---|---|---|---|---|
| Force | ||||
| FS (N) | 0.1178 | 0.1178 | 0.1178 | |
| FD (N) | 0.0493 | 0.1002 | 0.1714 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, G.; Zhang, Z.; Liu, L.; Yang, W.; Li, J.; Lv, Z.; Chen, X. Study on the Influence of Hole Shape and Grain Orientation on the Adsorption Characteristics of Maize Seeds and CFD Analysis. AgriEngineering 2025, 7, 218. https://doi.org/10.3390/agriengineering7070218
Bao G, Zhang Z, Liu L, Yang W, Li J, Lv Z, Chen X. Study on the Influence of Hole Shape and Grain Orientation on the Adsorption Characteristics of Maize Seeds and CFD Analysis. AgriEngineering. 2025; 7(7):218. https://doi.org/10.3390/agriengineering7070218
Chicago/Turabian StyleBao, Guocheng, Zhendong Zhang, Lijing Liu, Wei Yang, Jiandong Li, Zhouyi Lv, and Xinxin Chen. 2025. "Study on the Influence of Hole Shape and Grain Orientation on the Adsorption Characteristics of Maize Seeds and CFD Analysis" AgriEngineering 7, no. 7: 218. https://doi.org/10.3390/agriengineering7070218
APA StyleBao, G., Zhang, Z., Liu, L., Yang, W., Li, J., Lv, Z., & Chen, X. (2025). Study on the Influence of Hole Shape and Grain Orientation on the Adsorption Characteristics of Maize Seeds and CFD Analysis. AgriEngineering, 7(7), 218. https://doi.org/10.3390/agriengineering7070218






