Methodological Advancements in Testing Agricultural Nozzles and Handling of Drop Size Distribution Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Investigated Nozzles
2.2. Nozzle Characterisation by PDIA
2.3. Toward ISO-Compliance: Optimisation of Instrumental Protocol
- Which distance between nozzle orifice and PDIA instrument ensures the sampling of the fully developed flow?
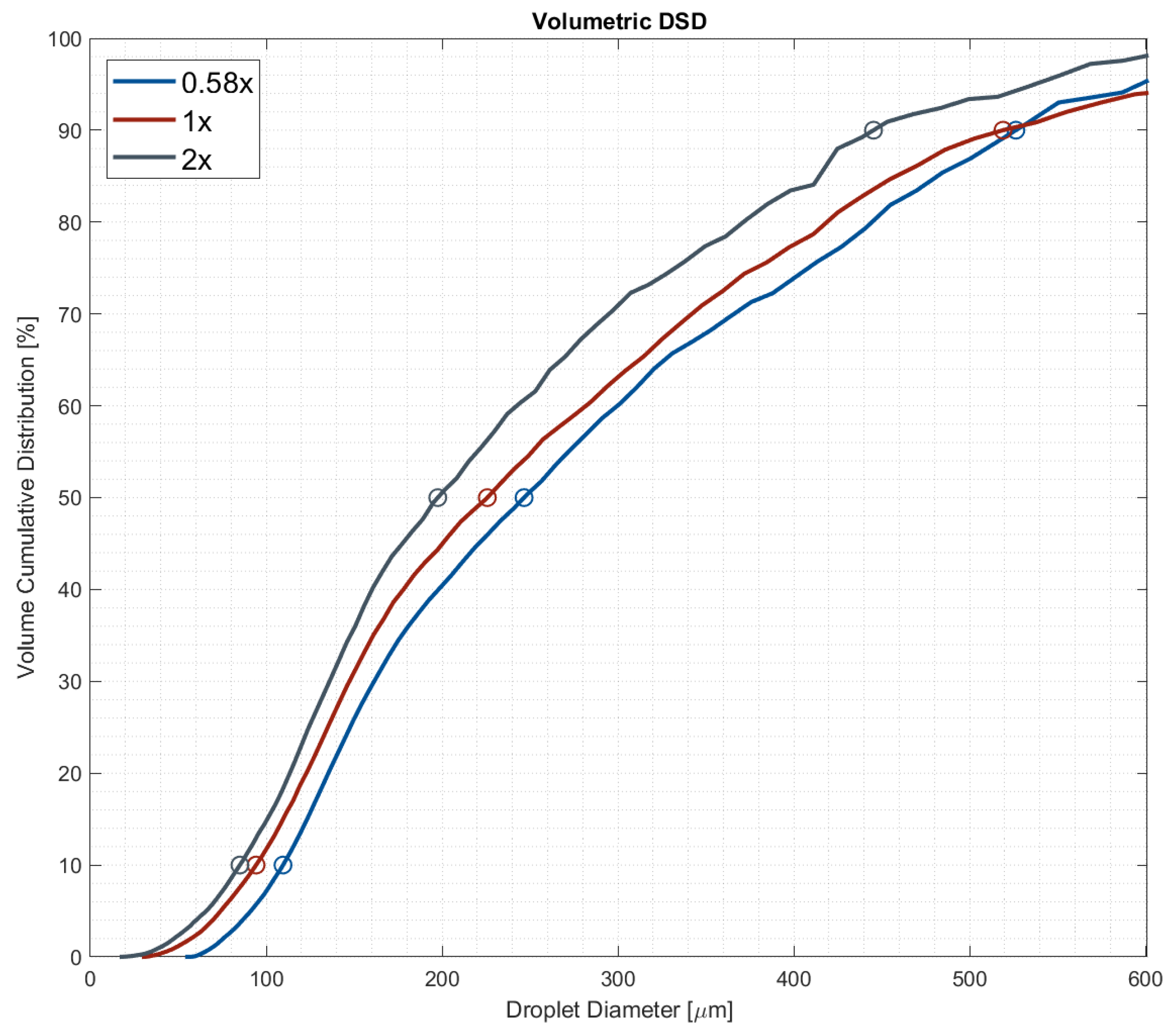
- Which zoom level of the adjustable lens ensures proper sampling of the drop size distributions?
2.4. Notes on the Logistic Curve
2.5. Data Fitting
3. Results and Discussion
3.1. Validation of New Methodology
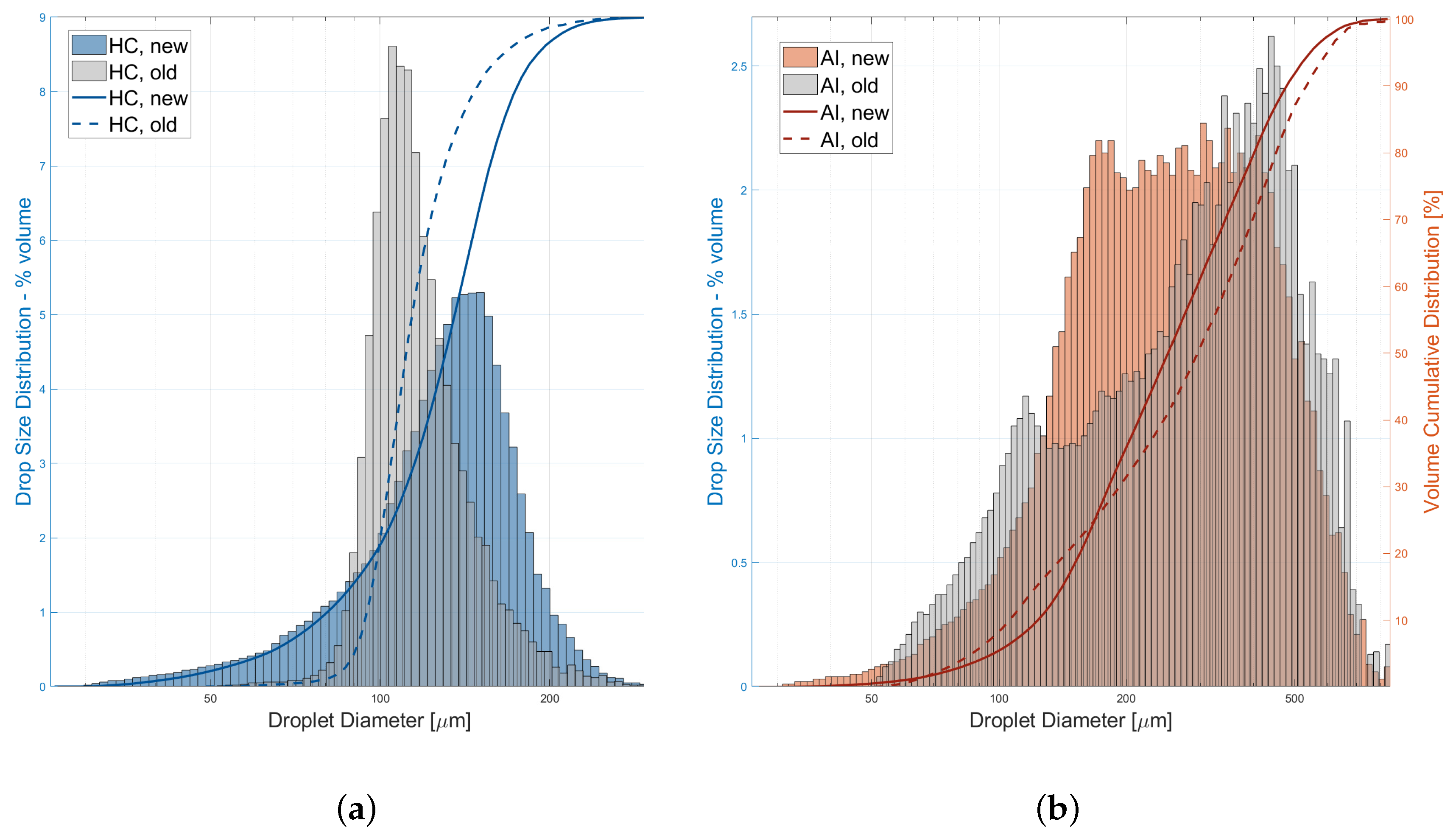
3.2. Data from New Methodology: Comparison with Old
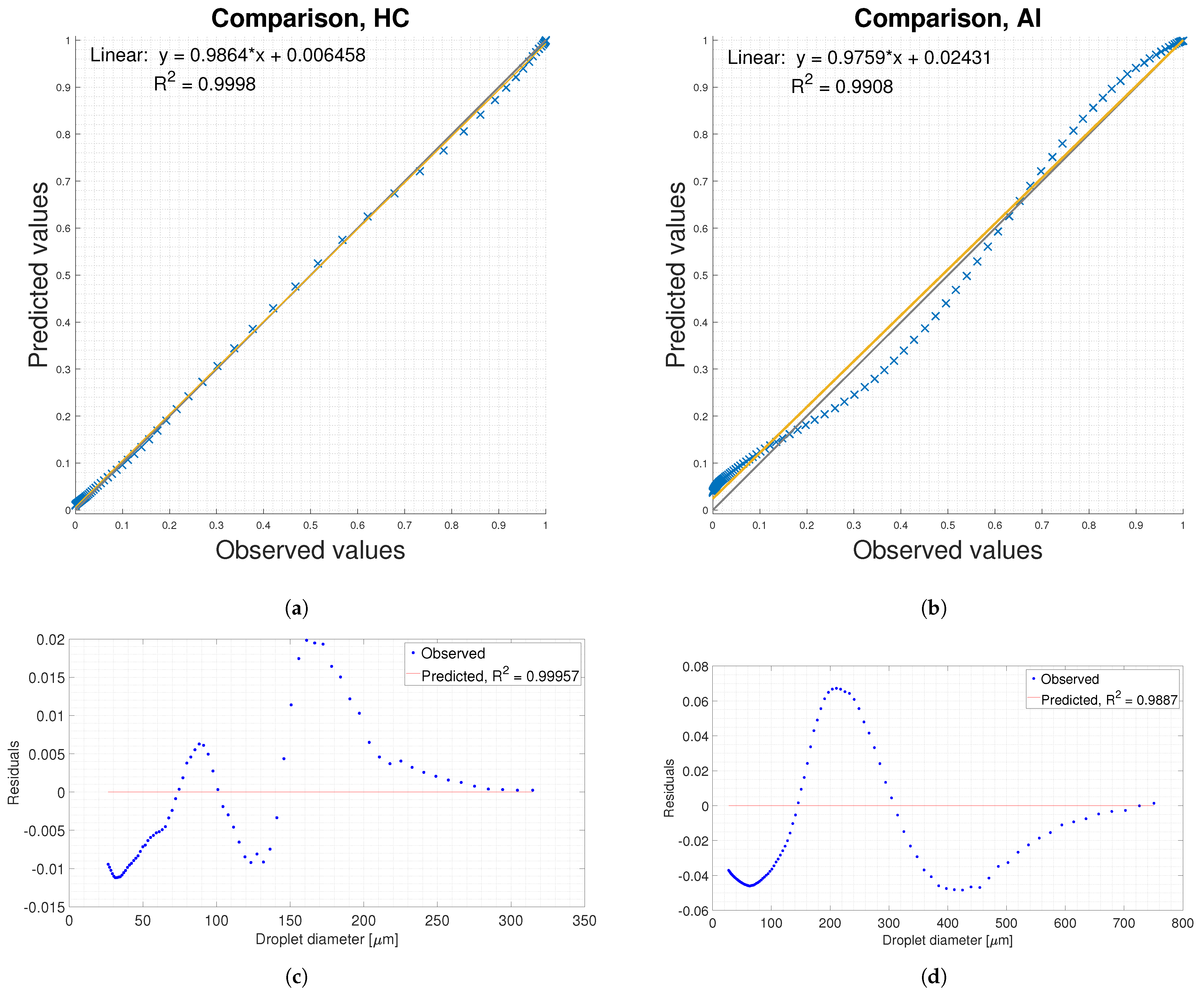
3.3. Data Fitting with Logistic Curve
4. Conclusions & Future Perspectives
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSD | Cumulative Size Distribution |
| DSD | Droplet Size Distribution |
| GoF | Goodness of Fit |
| PDIA | Particle/droplet image analysis |
| PPP | Plant Protection Product |
| RMSE | Root Mean Square Error |
References
- Hilz, E.; Vermeer, A.W. Spray Drift Review: The Extent to Which a Formulation Can Contribute to Spray Drift Reduction. Crop Prot. 2013, 44, 75–83. [Google Scholar] [CrossRef]
- Torrent, X.; Gregorio, E.; Douzals, J.P.; Tinet, C.; Rosell-Polo, J.R.; Planas, S. Assessment of Spray Drift Potential Reduction for Hollow-Cone Nozzles: Part 1. Classification Using Indirect Methods. Sci. Total Environ. 2019, 692, 1322–1333. [Google Scholar] [CrossRef] [PubMed]
- Tudi, M.; Daniel Ruan, H.; Wang, L.; Lyu, J.; Sadler, R.; Connell, D.; Chu, C.; Phung, D.T. Agriculture Development, Pesticide Application and Its Impact on the Environment. Int. J. Environ. Res. Public Health 2021, 18, 1112. [Google Scholar] [CrossRef] [PubMed]
- Perine, J.; Anderson, J.; Kruger, G.; Abi-Akar, F.; Overmyer, J. Effect of Nozzle Selection on Deposition of Thiamethoxam in Actara® Spray Drift and Implications for Off-Field Risk Assessment. Sci. Total Environ. 2021, 772, 144808. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, J.C.; O’Donnell, C.C.; Chauhan, B.S.; Adkins, S.W.; Kruger, G.R.; Wang, R.; Urach Ferreira, P.H.; Hewitt, A.J. Determining the Uniformity and Consistency of Droplet Size across Spray Drift Reducing Nozzles in a Wind Tunnel. Crop Prot. 2015, 76, 1–6. [Google Scholar] [CrossRef]
- Becce, L.; Mazzi, G.; Ali, A.; Bortolini, M.; Gregoris, E.; Feltracco, M.; Barbaro, E.; Contini, D.; Mazzetto, F.; Gambaro, A. Wind Tunnel Evaluation of Plant Protection Products Drift Using an Integrated Chemical–Physical Approach. Atmosphere 2024, 15, 656. [Google Scholar] [CrossRef]
- Cunha, J.P.A.R.D.; Lopes, L.D.L.; Alves, C.O.R.; Alvarenga, C.B.D. Spray Deposition and Losses to Soil from a Remotely Piloted Aircraft and Airblast Sprayer on Coffee. AgriEngineering 2024, 6, 2385–2394. [Google Scholar] [CrossRef]
- Palma, R.P.; Cunha, J.P.A.R.D. Multivariate Analysis Applied to the Ground Application of Pesticides in the Corn Crop. AgriEngineering 2023, 5, 829–839. [Google Scholar] [CrossRef]
- Nuyttens, D.; Zwertvaegher, I.K.; Dekeyser, D. Spray Drift Assessment of Different Application Techniques Using a Drift Test Bench and Comparison with Other Assessment Methods. Biosyst. Eng. 2017, 154, 14–24. [Google Scholar] [CrossRef]
- Jomantas, T.; Lekavičienė, K.; Steponavičius, D.; Andriušis, A.; Zaleckas, E.; Zinkevičius, R.; Popescu, C.V.; Salceanu, C.; Ignatavičius, J.; Kemzūraitė, A. The Influence of Newly Developed Spray Drift Reduction Agents on Drift Mitigation by Means of Wind Tunnel and Field Evaluation Methods. Agriculture 2023, 13, 349. [Google Scholar] [CrossRef]
- Wang, G.; Han, Y.; Li, X.; Andaloro, J.; Chen, P.; Hoffmann, W.C.; Han, X.; Chen, S.; Lan, Y. Field Evaluation of Spray Drift and Environmental Impact Using an Agricultural Unmanned Aerial Vehicle (UAV) Sprayer. Sci. Total Environ. 2020, 737, 139793. [Google Scholar] [CrossRef] [PubMed]
- Bourodimos, G.; Koutsiaras, M.; Psiroukis, V.; Balafoutis, A.; Fountas, S. Development and Field Evaluation of a Spray Drift Risk Assessment Tool for Vineyard Spraying Application. Agriculture 2019, 9, 181. [Google Scholar] [CrossRef]
- Sapkota, M.; Virk, S.; Rains, G. Spray Deposition and Quality Assessment at Varying Ground Speeds for an Agricultural Sprayer with and without a Rate Controller. AgriEngineering 2023, 5, 506–519. [Google Scholar] [CrossRef]
- Butler Ellis, M.; Alanis, R.; Lane, A.; Tuck, C.; Nuyttens, D.; Van De Zande, J. Wind Tunnel Measurements and Model Predictions for Estimating Spray Drift Reduction under Field Conditions. Biosyst. Eng. 2017, 154, 25–34. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, S.; Wang, G.; Lan, Y. Drift Evaluation of a Quadrotor Unmanned Aerial Vehicle (UAV) Sprayer: Effect of Liquid Pressure and Wind Speed on Drift Potential Based on Wind Tunnel Test. Appl. Sci. 2021, 11, 7258. [Google Scholar] [CrossRef]
- Nuyttens, D.; Taylor, W.; De Schampheleire, M.; Verboven, P.; Dekeyser, D. Influence of Nozzle Type and Size on Drift Potential by Means of Different Wind Tunnel Evaluation Methods. Biosyst. Eng. 2009, 103, 271–280. [Google Scholar] [CrossRef]
- Becce, L.; Mazzi, G.; Ali, A.; Bortolini, M.; Gambaro, A.; Mazzetto, F. Nozzle Characterisation to Support Aerosol Spray Drift Measurement in a Semi-Controlled Environment. In Proceedings of the 2023 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Pisa, Italy, 6–8 November 2023; pp. 646–651. [Google Scholar] [CrossRef]
- Sijs, R.; Kooij, S.; Holterman, H.J.; Van De Zande, J.; Bonn, D. Drop Size Measurement Techniques for Sprays: Comparison of Image Analysis, Phase Doppler Particle Analysis, and Laser Diffraction. AIP Adv. 2021, 11, 015315. [Google Scholar] [CrossRef]
- Gil, E.; Balsari, P.; Gallart, M.; Llorens, J.; Marucco, P.; Andersen, P.G.; Fàbregas, X.; Llop, J. Determination of Drift Potential of Different Flat Fan Nozzles on a Boom Sprayer Using a Test Bench. Crop Prot. 2014, 56, 58–68. [Google Scholar] [CrossRef]
- Grella, M.; Marucco, P.; Balsari, P. Toward a New Method to Classify the Airblast Sprayers According to Their Potential Drift Reduction: Comparison of Direct and New Indirect Measurement Methods. Pest Manag. Sci. 2019, 75, 2219–2235. [Google Scholar] [CrossRef]
- Grella, M.; Gil, E.; Balsari, P.; Marucco, P.; Gallart, M. Advances in Developing a New Test Method to Assess Spray Drift Potential from Air Blast Sprayers. Span. J. Agric. Res. 2017, 15, e0207. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, H.; Guler, H. Quantitative Analysis and Correction of Temperature Effects on Fluorescent Tracer Concentration Measurement. Sustainability 2020, 12, 4501. [Google Scholar] [CrossRef]
- ISO 25358:2018; Crop Protection Equipment—Droplet-Size Spectra from Atomizers—Measurement and Classification. ISO: Geneva, Switzerland, 2018.
- Krishnan, G.; Cryer, S.A.; Turner, J.E.; Sasi Rajan, N. Spray Atomisation in Multiphase Flows with Reference to Tank Mixes of Agricultural Products. Biosyst. Eng. 2022, 223, 232–248. [Google Scholar] [CrossRef]
- Cooper, J.; Smith, D.; Dobson, H. An Evaluation of Two Field Samplers for Monitoring Spray Drift. Crop Prot. 1996, 15, 249–257. [Google Scholar] [CrossRef]
- Coscollà, C.; Muñoz, A.; Borrás, E.; Vera, T.; Ródenas, M.; Yusà, V. Particle Size Distributions of Currently Used Pesticides in Ambient Air of an Agricultural Mediterranean Area. Atmos. Environ. 2014, 95, 29–35. [Google Scholar] [CrossRef]
- Radoman, N.; Christiansen, S.; Johansson, J.H.; Hawkes, J.A.; Bilde, M.; Cousins, I.T.; Salter, M.E. Probing the Impact of a Phytoplankton Bloom on the Chemistry of Nascent Sea Spray Aerosol Using High-Resolution Mass Spectrometry. Environ. Sci. Atmos. 2022, 2, 1152–1169. [Google Scholar] [CrossRef]
- Becce, L.; Amin, S.; Carabin, G.; Mazzetto, F. Preliminary Spray Nozzle Characterization Activities through Shadowgraphy at the AgroForestry Innovation Lab (AFI-Lab). In Proceedings of the 2022 IEEE Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Perugia, Italy, 3–5 November 2022; pp. 136–140. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Milton Park, UK, 2017. [Google Scholar]
- Gil, Y.; Sinfort, C. Emission of Pesticides to the Air during Sprayer Application: A Bibliographic Review. Atmos. Environ. 2005, 39, 5183–5193. [Google Scholar] [CrossRef]
- Arvidsson, T.; Bergström, L.; Kreuger, J. Spray Drift as Influenced by Meteorological and Technical Factors. Pest Manag. Sci. 2011, 67, 586–598. [Google Scholar] [CrossRef]
- Grella, M.; Marucco, P.; Manzone, M.; Gallo, R.; Mazzetto, F.; Balsari, P. Indoor Test Bench Measurements of Potential Spray Drift Generated by Multi-Row Sprayers. In Proceedings of the 2021 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento-Bolzano, Italy, 3–5 November 2021; pp. 356–361. [Google Scholar] [CrossRef]
- Garnier, J.; Quetelet, A. Correspondance Mathématique et Physique; Number v. 10; M.Hayez, Imprimeur: Lognes, France, 1838. [Google Scholar]
- Cerruto, E.; Ramírez-Cuesta, J.M.; Privitera, S.; Pascuzzi, S.; Manetto, G. Use of the Logistic Function to Model Cumulative Volumes of Spray Nozzles. In Proceedings of the 2023 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Pisa, Italy, 6–8 November 2023; pp. 635–639. [Google Scholar] [CrossRef]




| Lens Magnification Options | |||
|---|---|---|---|
| 0.58× | 1× | 2× | |
| Minimum diam. [ | 41.15 | 19.26 | 10.73 |
| Maximum diam. [ | 3543 | 2081 | 1003 |
| Field of view [ × | 18,662 × 10,631 | 10,965 × 6246 | 5280 × 3008 |
| -to-pixel factor | 9.561 | 5.617 | 2.705 |
| Average particles/frame [n] | 33.3 | 11.3 | 1.3 |
| Mag. | Distance [mm] | dV10 | dV50 | dV90 | V100 | V200 |
|---|---|---|---|---|---|---|
| 0.58× | 300 | 109.8 | 311.0 | 584.0 | 7.1 | 31.1 |
| 0.58× | 400 | 117.2 | 256.2 | 527.1 | 5.9 | 38.6 |
| 1× | 300 | 95.2 | 278.8 | 567.8 | 11.6 | 36.7 |
| 1× | 400 | 96.4 | 243.6 | 546.4 | 11.1 | 42.5 |
| 2× | 300 | 93.8 | 227.7 | 476.5 | 12.1 | 44.0 |
| 2× | 400 | 95.1 | 212.9 | 462.6 | 11.8 | 47.1 |
| HC, Old | HC, New | AI, Old | AI, New | |
|---|---|---|---|---|
| In-focus count | 45,293 | 180,313 | 45,056 | 130,982 |
| Min. diameter | 48.2 | 26.9 | 48.5 | 25.7 |
| Max. diameter | 297.4 | 353.3 | 932.5 | 818.8 |
| dV10 | 94.1 | 78.0 | 106.0 | 123.6 |
| dV50 (VMD) | 111.4 | 130.9 | 295.0 | 251.2 |
| dV90 | 149.8 | 176.1 | 533.5 | 479.1 |
| RS | 0.50 | 0.75 | 1.45 | 1.42 |
| V50 | <0.01 | 2.3 | N/A | 0.5 |
| V100 | 21.9 | 21.1 | 8.3 | 5.5 |
| V150 | 90.1 | 71.4 | 21.2 | 18.1 |
| V200 | 98.5 | 96.3 | 31.5 | 35.8 |
| HC | AI | |
|---|---|---|
| R2, training | 0.9995 | 0.9863 |
| RMSE, training | 0.0091 | 0.0437 |
| k | 0.0451 | 0.0136 |
| 129.65 | 266.65 | |
| R2, validation | 0.9996 | 0.9887 |
| RMSE, validation | 0.0086 | 0.0396 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzi, G.; Becce, L.; Ali, A.; Bortolini, M.; Gregoris, E.; Feltracco, M.; Barbaro, E.; Gronauer, A.; Gambaro, A.; Mazzetto, F. Methodological Advancements in Testing Agricultural Nozzles and Handling of Drop Size Distribution Data. AgriEngineering 2025, 7, 139. https://doi.org/10.3390/agriengineering7050139
Mazzi G, Becce L, Ali A, Bortolini M, Gregoris E, Feltracco M, Barbaro E, Gronauer A, Gambaro A, Mazzetto F. Methodological Advancements in Testing Agricultural Nozzles and Handling of Drop Size Distribution Data. AgriEngineering. 2025; 7(5):139. https://doi.org/10.3390/agriengineering7050139
Chicago/Turabian StyleMazzi, Giovanna, Lorenzo Becce, Ayesha Ali, Mara Bortolini, Elena Gregoris, Matteo Feltracco, Elena Barbaro, Andreas Gronauer, Andrea Gambaro, and Fabrizio Mazzetto. 2025. "Methodological Advancements in Testing Agricultural Nozzles and Handling of Drop Size Distribution Data" AgriEngineering 7, no. 5: 139. https://doi.org/10.3390/agriengineering7050139
APA StyleMazzi, G., Becce, L., Ali, A., Bortolini, M., Gregoris, E., Feltracco, M., Barbaro, E., Gronauer, A., Gambaro, A., & Mazzetto, F. (2025). Methodological Advancements in Testing Agricultural Nozzles and Handling of Drop Size Distribution Data. AgriEngineering, 7(5), 139. https://doi.org/10.3390/agriengineering7050139







