Crop Water Productivity: Within-Field Spatial Variation in Irrigated Alfalfa (Medicago sativa L.)
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Study Site
2.2. Measurement of Soil Water Content
2.3. Crop Evapotranspiration
2.4. Alfalfa Biomass Yield
2.5. Crop Water Productivity
2.6. Spatial Statistical Analysis
3. Results
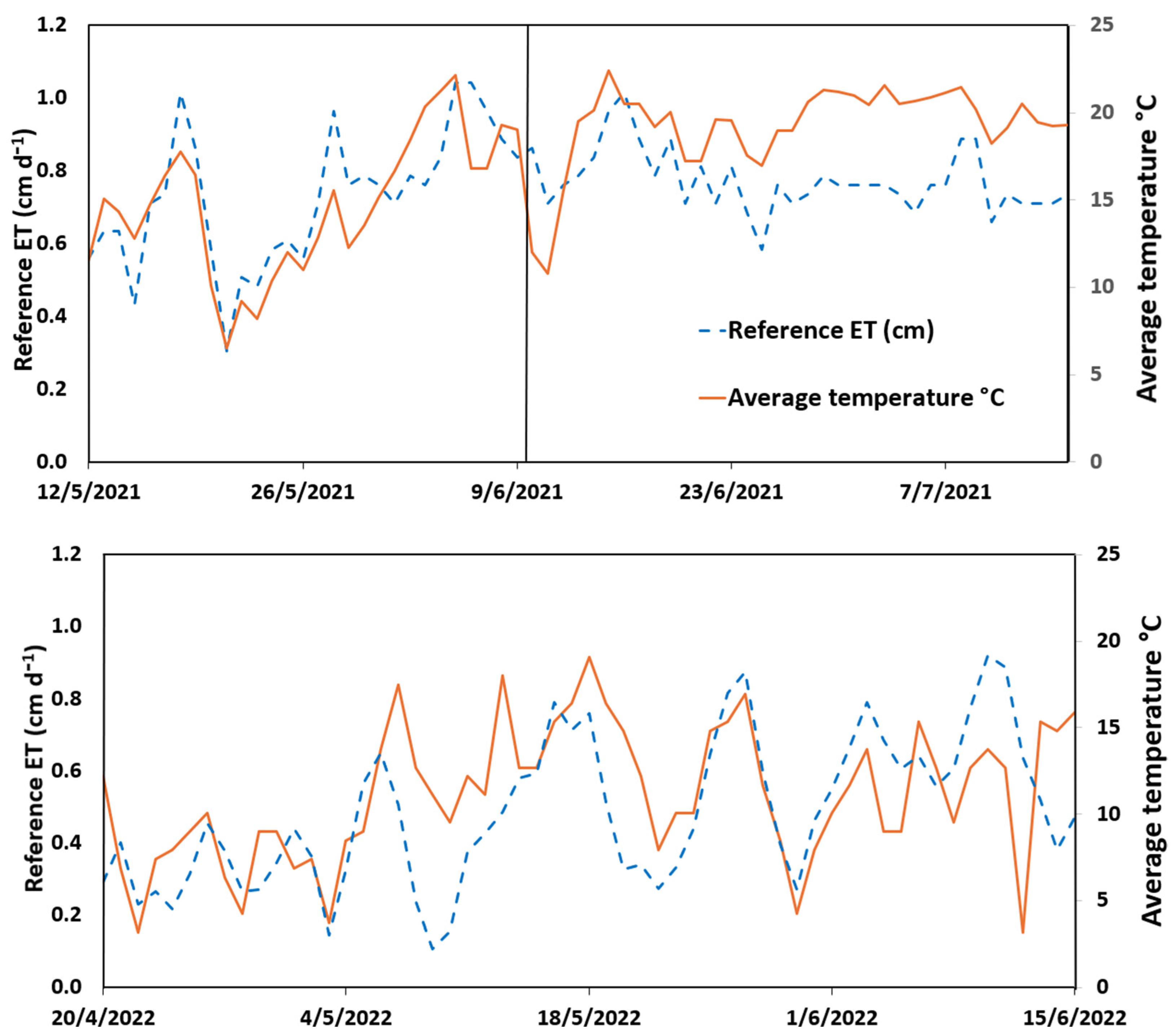
3.1. Daily Evapotranspiration and Mean Temperature
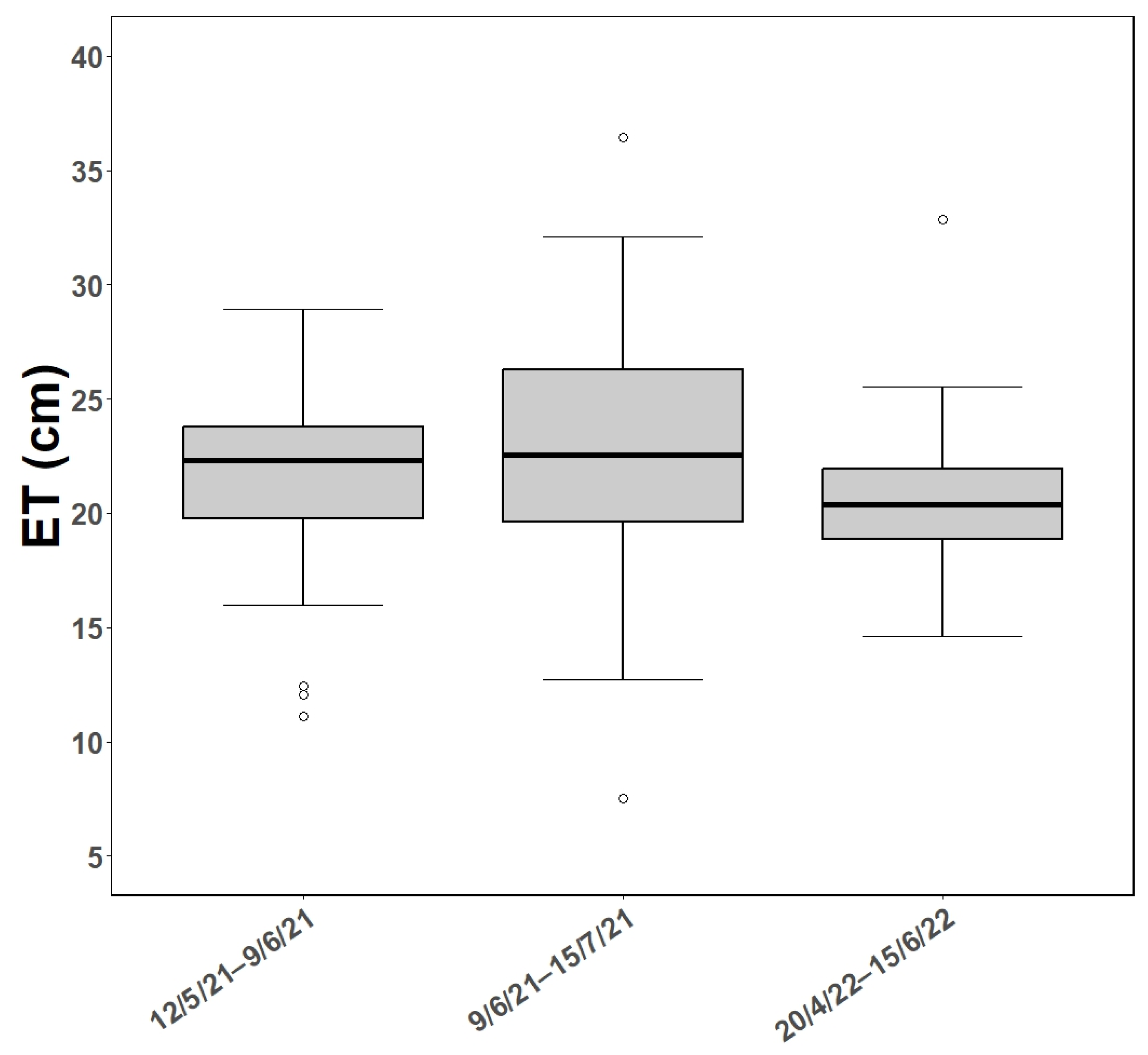
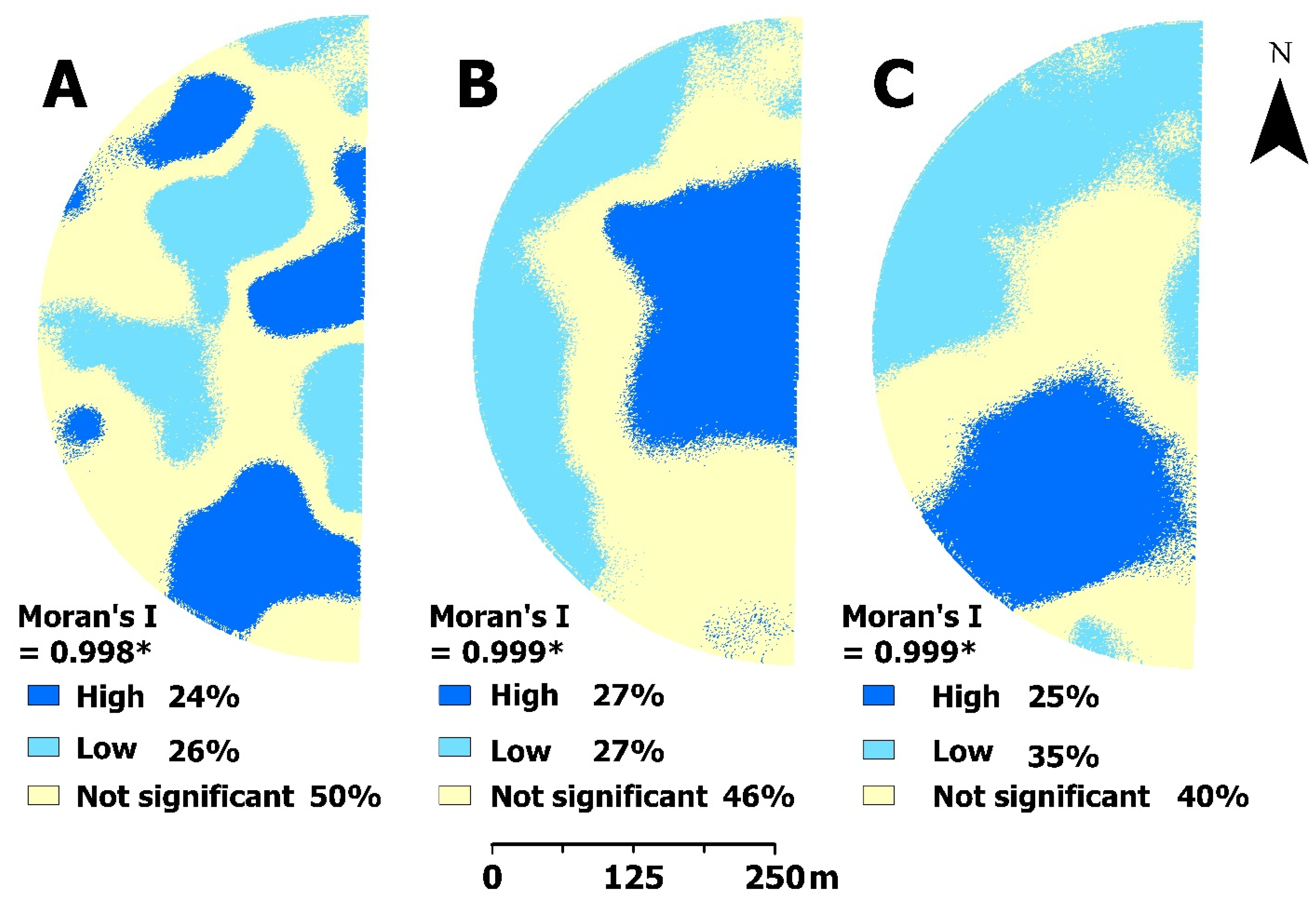
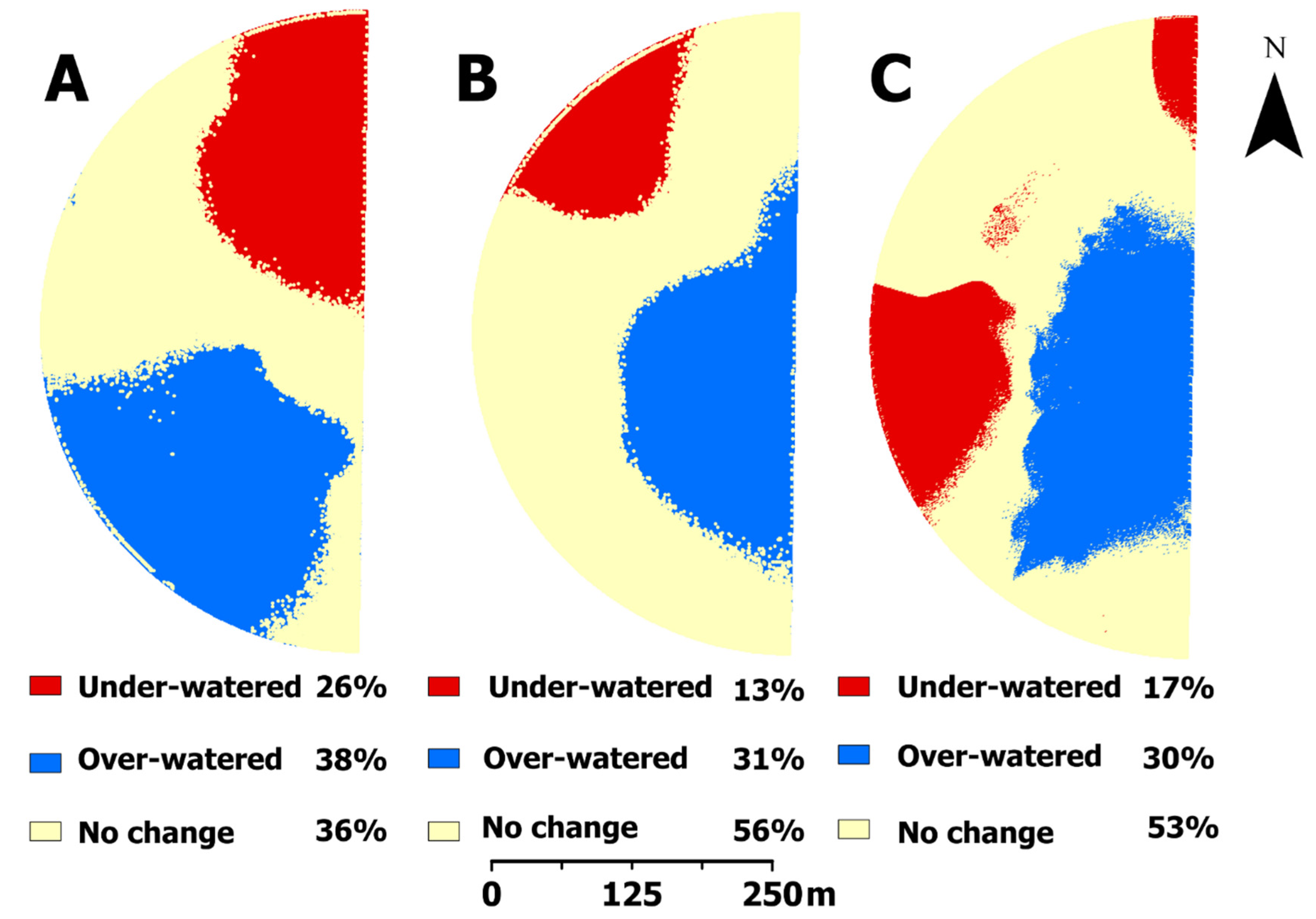
3.2. Spatial Variation in Crop Evapotranspiration
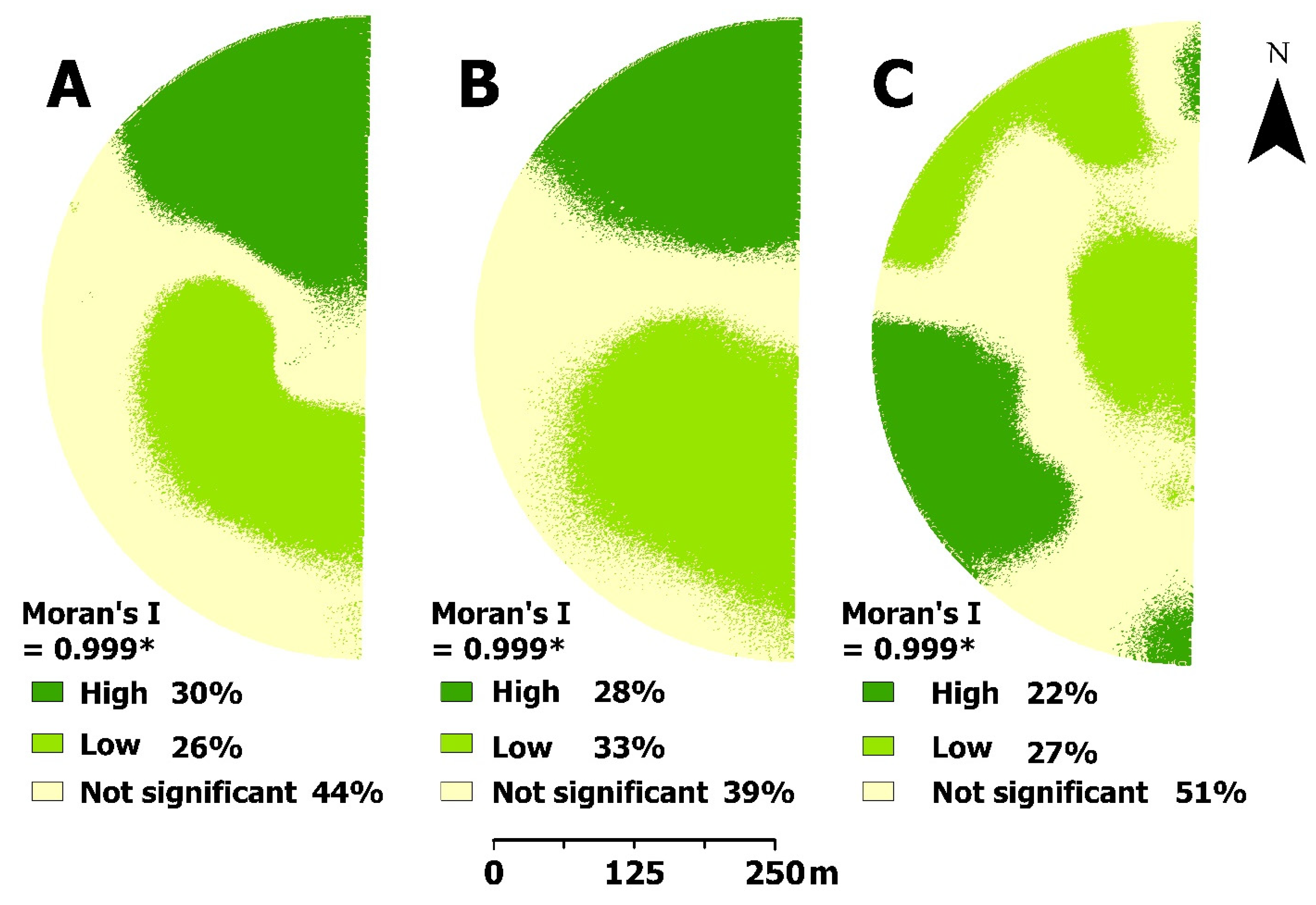
3.3. Spatial Variation in Biomass Yield
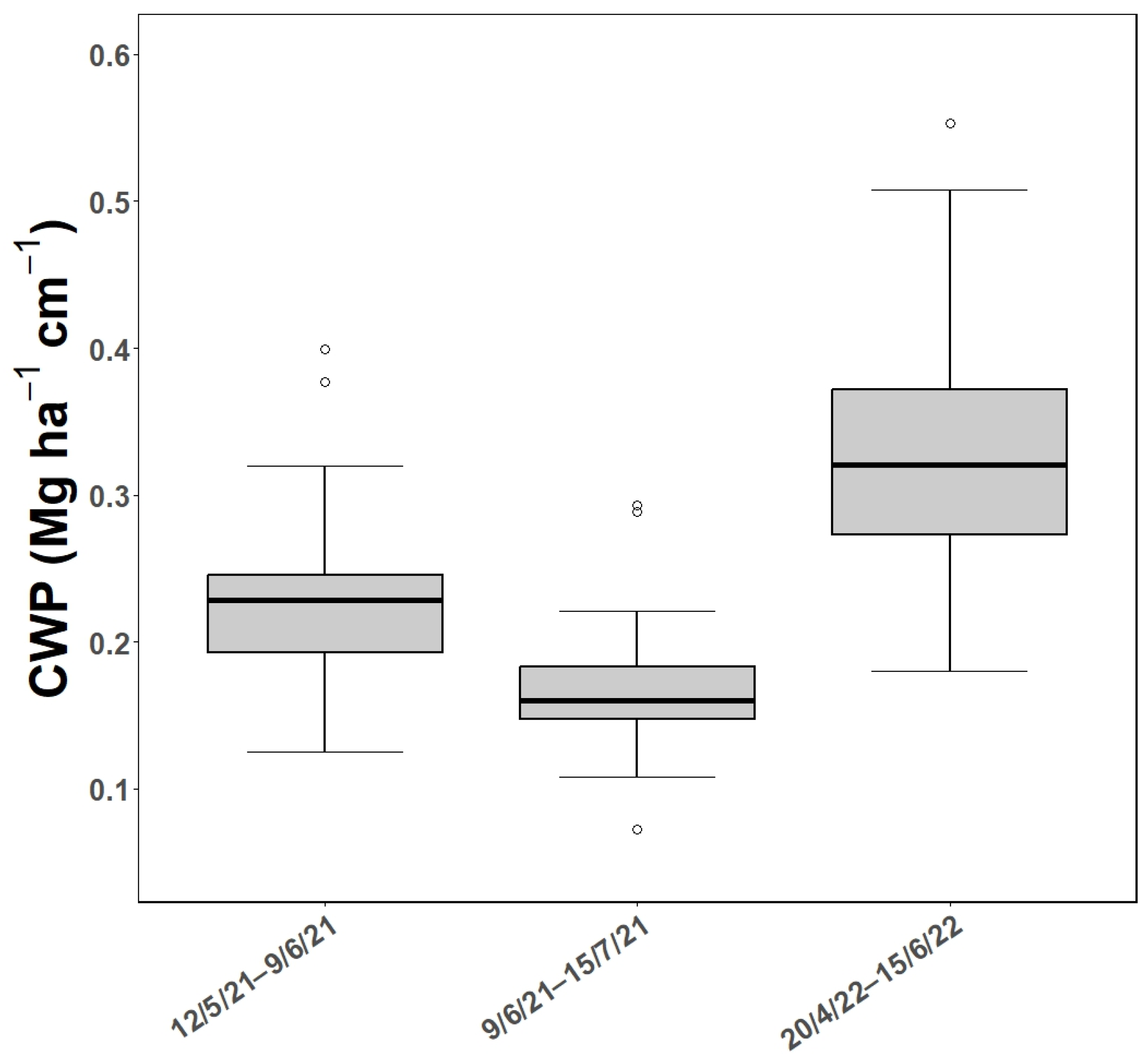
3.4. Spatial Variability of Crop Water Productivity
4. Discussion
4.1. Within-Field Variation in Crop Evapotranspiration
4.2. Spatial Variability of Biomass Yield
4.3. Spatiotemporal Variability of Crop Water Productivity
4.4. Water Conservation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BD | bulk density |
| CWP | crop water productivity |
| D | drainage |
| ET | evapotranspiration |
| GWC | gravimetric water content |
| HI | harvest interval |
| I | irrigation |
| METRIC | Mapping EvapoTranspiration at High Resolution with Internalized Calibration |
| NDVI | Normalized Difference Vegetation Index |
| P | precipitation |
| R | runoff |
| SSEBop | Simplified Surface Energy Balance approach |
| UAS | Unmanned Aircraft System |
| VRI | variable rate irrigation |
| VWC | volumetric water content |
| ∆Θ | change in soil water |
References
- Ghorbanpour, A.K.; Kisekka, I.; Afshar, A.; Hessels, T.; Taraghi, M.; Hessari, B.; Tourian, M.J.; Duan, Z. Crop Water Productivity Mapping and Benchmarking Using Remote Sensing and Google Earth Engine Cloud Computing. Remote Sens. 2022, 14, 4934. [Google Scholar] [CrossRef]
- Li, Y.; Su, D. Alfalfa Water Use and Yield under Different Sprinkler Irrigation Regimes in North Arid Regions of China. Sustainability 2017, 9, 1380. [Google Scholar] [CrossRef]
- Poudel, U.; Stephen, H.; Ahmad, S. Evaluating Irrigation Performance and Water Productivity Using EEFlux ET and NDVI. Sustainability 2021, 13, 7967. [Google Scholar] [CrossRef]
- Bodner, G.; Nakhforoosh, A.; Kaul, H.-P. Management of Crop Water under Drought: A Review. Agron. Sustain. Dev. 2015, 35, 401–442. [Google Scholar] [CrossRef]
- Djaman, K.; Smeal, D.; Koudahe, K.; Allen, S. Hay Yield and Water Use Efficiency of Alfalfa under Different Irrigation and Fungicide Regimes in a Semiarid Climate. Water 2020, 12, 1721. [Google Scholar] [CrossRef]
- Kang, J.; Hao, X.; Zhou, H.; Ding, R. An Integrated Strategy for Improving Water Use Efficiency by Understanding Physiological Mechanisms of Crops Responding to Water Deficit: Present and Prospect. Agric. Water Manag. 2021, 255, 107008. [Google Scholar] [CrossRef]
- Kaivosoja, J.; Hautsalo, J.; Heikkinen, J.; Hiltunen, L.; Ruuttunen, P.; Näsi, R.; Niemeläinen, O.; Lemsalu, M.; Honkavaara, E.; Salonen, J. Reference Measurements in Developing UAV Systems for Detecting Pests, Weeds, and Diseases. Remote Sens. 2021, 13, 1238. [Google Scholar] [CrossRef]
- Lacerda, L.; Snider, J.; Cohen, Y.; Liakos, V.; Levi, M.; Vellidis, G. Correlation of UAV and Satellite-Derived Vegetation Indices with Cotton Physiological Parameters and Their Use as a Tool for Scheduling Variable Rate Irrigation in Cotton. Precis. Agric. 2022, 23, 2089–2114. [Google Scholar] [CrossRef]
- Flint, E.A.; Hopkins, B.G.; Svedin, J.D.; Kerry, R.; Heaton, M.J.; Jensen, R.R.; Campbell, C.S.; Yost, M.A.; Hansen, N.C. Irrigation Zone Delineation and Management with a Field-Scale Variable Rate Irrigation System in Winter Wheat. Agronomy 2023, 13, 1125. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Guo, H.; Ding, F.; Yan, H. Evaluation of Variable Rate Irrigation Management in Forage Crops: Saving Water and Increasing Water Productivity. Agric. Water Manag. 2023, 275, 108020. [Google Scholar] [CrossRef]
- Madugundu, R.; Al-Gaadi, K.A.; Tola, E.; Zeyada, A.M.; Alameen, A.A.; Edrris, M.K.; Edrees, H.F.; Mahjoop, O. Impact of Field Topography and Soil Characteristics on the Productivity of Alfalfa and Rhodes Grass: RTK-GPS Survey and GIS Approach. Agronomy 2022, 12, 2918. [Google Scholar] [CrossRef]
- Patil, V.C.; Al-Gaadi, K.A.; Madugundu, R.; Tola, E.H.; Marey, S.; Aldosari, A.; Biradar, C.M.; Gowda, P.H. Assessing Agricultural Water Productivity in Desert Farming System of Saudi Arabia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 284–297. [Google Scholar] [CrossRef]
- Svedin, J.D. Characterizing the Spatial Variation of Crop Water Productivity for Variable-Rate Irrigation Management. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2018. [Google Scholar]
- Hansen, N.; Flint, E.; Hopkins, A.; Larsen, I.; Kerry, R.; Hopkins, B.; Jensen, R.; Heaton, M. On-Farm Evaluation of Variable Rate Irrigation for Winter Wheat in Semi-Arid Western USA. In Precision Agriculture’23; Wageningen Academic Publishers: Wageningen, The Netherlands, 2023; pp. 269–276. [Google Scholar]
- O’Shaughnessy, S.; Evett, S.; Colaizzi, P. Dynamic Prescription Maps for Site-Specific Variable Rate Irrigation of Cotton. Agric. Water Manag. 2015, 159, 123–138. [Google Scholar] [CrossRef]
- Sui, R.; Fisher, D.K.; Reddy, K.N. Yield Response to Variable Rate Irrigation in Corn. J. Agric. Sci. 2015, 7, 11. [Google Scholar] [CrossRef]
- Sui, R.; Yan, H. Field Study of Variable Rate Irrigation Management in Humid Climates: Field Study of Variable Rate Irrigation Management. Irrig. Drain. 2017, 66, 327–339. [Google Scholar] [CrossRef]
- Crosby, T.W.; Wang, Y. Effects of Different Irrigation Management Practices on Potato (Solanum tuberosum L.). Sustainability 2021, 13, 10187. [Google Scholar] [CrossRef]
- Hedley, C.; Yule, I.; Tuohy, M.; Vogeler, I. Key Performance Indicators for Simulated Variable-Rate Irrigation of Variable Soils in Humid Regions. Trans. ASABE 2009, 52, 1575–1584. [Google Scholar] [CrossRef]
- Grimes, D.W.; Wiley, P.L.; Sheesley, W.R. Alfalfa Yield and Plant Water Relations with Variable Irrigation. Crop Sci. 1992, 32, 1381–1387. [Google Scholar] [CrossRef]
- Wang, L.; Xie, J.; Luo, Z.; Niu, Y.; Coulter, J.A.; Zhang, R.; Lingling, L. Forage Yield, Water Use Efficiency, and Soil Fertility Response to Alfalfa Growing Age in the Semiarid Loess Plateau of China. Agric. Water Manag. 2021, 243, 106415. [Google Scholar] [CrossRef]
- Al-Gaadi, K.A.; Patil, V.C.; Tola, E.H.; Madugundu, R.; Marey, S.A.; Al-Omran, A.; Al-Dosari, A. Variable Rate Application Technology for Optimizing Alfalfa Production in Arid Climate. Int. J. Agric. Biol. 2015, 17, 71–79. [Google Scholar]
- Shewmaker, G.E.; Allen, R.G.; Neibling, W.H. Alfalfa Irrigation and Drought; University of Idaho, College of Agricultural and Life Sciences: Moscow, ID, USA, 2011. [Google Scholar]
- Hill, R.; Barker, J.; Lewis, C. Updated Consumptive Use Estimates at EWS Sites. In Crop and Wetland Consumptive Use and Open Water Surface Evaporation for Utah, 1st ed.; Utah State University: Logan, UT, USA, 2011; Appendix J; pp. 6–101. [Google Scholar]
- Zhang, Q.; Liu, X.; Zhang, Z.; Liu, N.; Li, D.; Hu, L. Melatonin Improved Waterlogging Tolerance in Alfalfa (Medicago Sativa) by Reprogramming Polyamine and Ethylene Metabolism. Front. Plant Sci. 2019, 10, 44. [Google Scholar] [CrossRef] [PubMed]
- Fink, K.P.; Grassini, P.; Rocateli, A.; Bastos, L.M.; Kastens, J.; Ryan, L.P.; Lin, X.; Patrignani, A.; Lollato, R.P. Alfalfa Water Productivity and Yield Gaps in the US Central Great Plains. Field Crops Res. 2022, 289, 108728. [Google Scholar] [CrossRef]
- Lindenmayer, R.B.; Hansen, N.C.; Brummer, J.; Pritchett, J.G. Deficit Irrigation of Alfalfa for Water-savings in the Great Plains and Intermountain West: A Review and Analysis of the Literature. Agron. J. 2011, 103, 45–50. [Google Scholar] [CrossRef]
- NRCS Web Soil Survey. Available online: https://websoilsurvey.sc.egov.usda.gov/app/ (accessed on 1 June 2021).
- Hammond, K. Spatiotemporal Variation of Alfalfa Leaf Area Index and Crop Water Productivity in an Irrigated Alfalfa Field. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2023. [Google Scholar]
- Kerry, R.; Oliver, M.A. Variograms of Ancillary Data to Aid Sampling for Soil Surveys. Precis. Agric. 2003, 4, 261–278. [Google Scholar] [CrossRef]
- Svedin, J.D.; Kerry, R.; Hansen, N.C.; Hopkins, B.G. Identifying Within-Field Spatial and Temporal Crop Water Stress to Conserve Irrigation Resources with Variable-Rate Irrigation. Agronomy 2021, 11, 1377. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; p. D05109. [Google Scholar]
- Bureau of Reclamation AgriMet Columbia-Pacific Northwest Region. Available online: https://www.usbr.gov/pn/agrimet/webarcread.html (accessed on 7 April 2023).
- Abdul-Jabbar, A.; Sammis, T.; Lugg, D. Effect of Moisture Level on the Root Pattern of Alfalfa. Irrig. Sci. 1982, 3, 197–207. [Google Scholar] [CrossRef]
- Kohl, R.A.; Kolar, J.J. Soil Water Uptake by Alfalfa 1. Agron. J. 1976, 68, 536–538. [Google Scholar] [CrossRef]
- Hojilla-Evangelista, M.P.; Selling, G.W.; Hatfield, R.; Digman, M. Extraction, Composition, and Functional Properties of Dried Alfalfa (Medicago sativa L.) Leaf Protein. J. Sci. Food Agric. 2017, 97, 882–888. [Google Scholar] [CrossRef]
- Turner, I.; Kerry, R.; Jensen, R.R.; Flint, E.A.; Svedin, J.; Hansen, N.C.; Hopkins, B.; Hammond, K. Automated Analysis of Snowmelt from Sentinel-2 Imagery to Determine Variable Rate Irrigation Zones in the American Mountain West. Geocarto Int. 2023, 38, 2230939. [Google Scholar] [CrossRef]
- Smith, R.; Oyler, L.; Campbell, C.; Woolley, E.A.; Hopkins, B.G.; Kerry, R.; Hansen, N.C. A New Approach for Estimating and Delineating Within-Field Crop Water Stress Zones with Satellite Imagery. Int. J. Remote Sens. 2021, 42, 6003–6022. [Google Scholar] [CrossRef]
- French, A.N.; Sanchez, C.A.; Wirth, T.; Scott, A.; Shields, J.W.; Bautista, E.; Saber, M.N.; Wisniewski, E.; Gohardoust, M.R. Remote Sensing of Evapotranspiration for Irrigated Crops at Yuma, Arizona, USA. Agric. Water Manag. 2023, 290, 108582. [Google Scholar] [CrossRef]
- Sabiston, L.; Sabie, R.; Buenemann, M.; Stringam, B.; Fernald, A. Comparing Field-Scale Eddy Covariance Measurements and Crop Coefficient Estimates of Alfalfa Evapotranspiration to OpenET Model Estimates and Exploring Water Budget Implications in a Dryland Environment. Irrig. Sci. 2024, 1–18. [Google Scholar] [CrossRef]
- Tawalbeh, Z.M.; Bawazir, A.S.; Fernald, A.; Sabie, R. Spatiotemporal Variabilities in Evapotranspiration of Alfalfa: A Case Study Using Remote Sensing METRIC and SSEBop Models and Eddy Covariance. Remote Sens. 2024, 16, 2290. [Google Scholar] [CrossRef]
- Kayad, A.G.; Al-Gaadi, K.A.; Tola, E.; Madugundu, R.; Zeyada, A.M.; Kalaitzidis, C. Assessing the Spatial Variability of Alfalfa Yield Using Satellite Imagery and Ground-Based Data. PLoS ONE 2016, 11, e0157166. [Google Scholar] [CrossRef]
- Canevari, M.; Vargas, R.; Orloff, S. Weed Management in Alfalfa; University of California Division of Agriculture and Natural Resources: Davis, CA, USA, 2007; pp. 1–14. [Google Scholar]
- Fontanet, M.; Scudiero, E.; Skaggs, T.H.; Fernàndez-Garcia, D.; Ferrer, F.; Rodrigo, G.; Bellvert, J. Dynamic Management Zones for Irrigation Scheduling. Agric. Water Manag. 2020, 238, 106207. [Google Scholar] [CrossRef]
- O’Shaughnessy, S.A.; Evett, S.R.; Colaizzi, P.D.; Andrade, M.A.; Marek, T.H.; Heeren, D.M.; Lamm, F.R.; LaRue, J.L. Identifying Advantages and Disadvantages of Variable Rate Irrigation: An Updated Review. Appl. Eng. Agric. 2019, 35, 837–852. [Google Scholar] [CrossRef]
- Al-Gaadi, K.; Madugundu, R.; Tola, E. Temporal Dynamics of Alfalfa Water Use Efficiency under Hyper Arid Conditions of Saudi Arabia. Adv. Anim. Biosci. 2017, 8, 540–545. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa Yield Prediction Using UAV-Based Hyperspectral Imagery and Ensemble Learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, J.; Xu, B.; Huang, J.; Memon, M.S.; Yin, G.; Zeng, Y.; Zhao, J.; Liu, K. Evaluation of Global Decametric-Resolution LAI, FAPAR and FVC Estimates Derived from Sentinel-2 Imagery. Remote Sens. 2020, 12, 912. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Imhoff, M.; Lawrence, W.; Easterling, D.; Peterson, T.; Karl, T. A Closer Look at United States and Global Surface Temperature Change. J. Geophys. Res. Atmos. 2001, 106, 23947–23963. [Google Scholar] [CrossRef]



| VWC (cm) | |||||
|---|---|---|---|---|---|
| Date (d/m/yr) | Harvest Interval-# | Days Prior to Harvest | Min. | Max. | Mean |
| 12/5/2021 | Start of HI-1 | 27 | 9.9 | 25 | 16 |
| 9/6/2021 | End HI-1 | 1 | 6.2 | 20 | 12 |
| 9/6/2021 | Start of HI-2 | 36 | 6.2 | 20 | 12 |
| 15/7/2021 | End HI-2 | 1 | 0.13 | 12 | 3.3 |
| 20/4/2022 | Start HI-3 | 56 | 10 | 22 | 14 |
| 15/6/2022 | End HI-3 | 1 | 7.2 | 21 | 12 |
| Harvest Interval Dates (d/m/yr) | Irrigation Events | Irrigation Rate (cm) | Total Irrigation (cm) | Precipitation (cm) | (cm) |
|---|---|---|---|---|---|
| 12/5/2021–9/6/2021 | 8 | 1.5 | 12 | 3.6 | 6.1 |
| 9/6/2021–15/7/2021 | 8 | 1.5 | 12 | 0.2 | 10 |
| 20/4/2022–15/6/2022 | 7 | 1.8 | 12 | 6.5 | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammond, K.; Kerry, R.; Spackman, R.; Hulet, A.; Hopkins, B.G.; Yost, M.A.; Hansen, N.C. Crop Water Productivity: Within-Field Spatial Variation in Irrigated Alfalfa (Medicago sativa L.). AgriEngineering 2025, 7, 115. https://doi.org/10.3390/agriengineering7040115
Hammond K, Kerry R, Spackman R, Hulet A, Hopkins BG, Yost MA, Hansen NC. Crop Water Productivity: Within-Field Spatial Variation in Irrigated Alfalfa (Medicago sativa L.). AgriEngineering. 2025; 7(4):115. https://doi.org/10.3390/agriengineering7040115
Chicago/Turabian StyleHammond, Keegan, Ruth Kerry, Ross Spackman, April Hulet, Bryan G. Hopkins, Matt A. Yost, and Neil C. Hansen. 2025. "Crop Water Productivity: Within-Field Spatial Variation in Irrigated Alfalfa (Medicago sativa L.)" AgriEngineering 7, no. 4: 115. https://doi.org/10.3390/agriengineering7040115
APA StyleHammond, K., Kerry, R., Spackman, R., Hulet, A., Hopkins, B. G., Yost, M. A., & Hansen, N. C. (2025). Crop Water Productivity: Within-Field Spatial Variation in Irrigated Alfalfa (Medicago sativa L.). AgriEngineering, 7(4), 115. https://doi.org/10.3390/agriengineering7040115






