Abstract
Sugarcane (Saccharum spp.) is a crop of significant industrial and nutritional value, essential for producing various products. Due to its importance, genetic improvement programs involve a rigorous selection process. In this study, growth curve models were used to analyze the maturity curves of 33 hybrids (currently in the adaptability testing phase) and 6 control varieties (MEX 69-290, ITV 92-1424, CP 72-2086, COLMEX 94-8, COLMEX 95-27, RB 85-5113) during both plant and ratoon periods at the Melchor Ocampo Sugar Mill fields in Jalisco, México. With the use of clustering techniques, the materials were classified into four maturity groups: early, early–intermediate, intermediate–late, and late. Hybrids with a larger intercept and smaller slope were classified as having early and early–intermediate maturity. Conversely, hybrids with a smaller intercept and larger slope were classified as having intermediate–late and late maturity. According to the Connectivity and Dunn indexes, the DBSCAN algorithm provides the best clustering structure for materials in the plant cycle, while for the ratoon cycle, the k-means algorithm offers the best clustering structure. This highlights the versatility of each algorithm in the context of hybrid and varietal maturity analysis. These results are crucial for optimizing the productivity and sustainability of the crop, with significant implications for the sugar industry.
1. Introduction
The development of new sugarcane varieties provides a solution to the genetic deterioration experienced by commercial varieties. This deterioration manifests as a decrease in field performance, which impacts its industrial use. The lack of new genotypes to replace the deteriorated varieties is the main factor limiting yield [1,2].
To develop new sugarcane varieties, materials adapted to environmental conditions and the needs of the agro-industry are sought, with resistance to pests, diseases, and drought, good adaptation to different soil types, low post-harvest deterioration, lower production costs, and high sucrose concentration [3,4]. The development of an outstanding commercial variety for a specific region requires approximately ten to twelve years of constant evaluation in the field and in an industrial environment. The main stages that new materials must go through include the selection of strains, trials in furrows, multiplication I, II, and III, plot establishment, adaptability, agro-industrial evaluation, and semi-commercial trials [5].
During the adaptability phase, new hybrids are evaluated in different soils and climates using agronomic variables (germination, height, density, and health) and industrial variables (sucrose percentage (PS), Brix degrees, purity, fiber, and reducing sugars). Destructive sampling is performed to analyze the maturity curve, which constitutes a key criterion for selecting the most promising materials [6].
In the agro-industrial phase, variables such as polarization (PP), Brix degrees, purity, fiber, juiciness, and stem hardness are studied. PP is a key maturity indicator, as it equates to apparent sucrose [7,8]. While biological maturity is reached when the sucrose content is optimal, this is identified through the maturity curve, which is crucial for the selection of genotypes in the sugar industry [9,10].
Since data related to the maturity curve exhibit temporal autocorrelation, it is necessary to apply appropriate statistical methodologies for analysis. In this regard, growth curve models, a class of linear mixed models (LMMs), capture variability between and within genotypes over time [11,12].
Smith’s work [13] highlights the use of LMMs in multi-environment trials to evaluate varietal performance in different geographical locations, being particularly useful for handling incomplete data, as they improve precision when modeling error variation. In plant breeding, LMMs are commonly used in multi-environment trials to select lines adapted to the climate, resistant to pests, and with higher yield and quality [12,14,15,16].
In sugarcane, commercial and new hybrids have been compared using repeated measurements of Brix degrees, PP, and PS. Quadratic regression has been applied to model sucrose accumulation, determine the optimal harvest time, and maximize yield [17]. Additionally, genotypes have been evaluated using analysis of variance and linear regression, identifying the best agro-industrial response and classifying cultivars as having early, intermediate, and late maturity [7].
Another study in Tucumán, Argentina, analyzed sucrose accumulation curves and clustering techniques to classify sugarcane genotypes using segmented polynomials. To group the materials, the estimated accumulation curve and two clustering techniques, UPGMA and k-means, were used, facilitating the selection of the most promising genotypes [10]. According to [10], clustering algorithms can be used in agriculture to classify crops. In this regard, Seta [18] applied k-means to classify sugarcane-producing regions, while Mbukwa [19] used k-means and k-medoids to identify high-yield districts for maize and bean in Tanzania.
This study used growth curve models to analyze sucrose accumulation in 33 sugarcane hybrids under adaptability trials, along with six commercial control varieties. The 39 materials were grouped using k-means, k-medoids, and DBSCAN to identify their maturity type and select the most promising for the next selection phase.
2. Materials and Methods
A total of 39 materials from the experimental fields of the National Institute of Forestry, Agricultural and Livestock Research (INIFAP) were studied. They form two groups: the control materials and the new materials. The control group corresponds to six commercial varieties, and the new materials correspond to 33 varieties of Mexican and foreign origin (Table 1). The new materials are in the adaptability phase, and all the materials were evaluated in plant and ratoon crop cycles under irrigation conditions in both seasons.

Table 1.
Materials evaluated during the plant and ratoon crop cycles, Las Pilas experimental field.
The experiment was established on 10 March 2011, at Las Pilas experimental field (19°46′48.85″ N, 104°13′57.65″ W) and the Melchor Ocampo Sugar Mill (19°47′18.0″ N, 104°14′24.3″ W), which is located in the Zacapala area of Autlán de Navarro, Jalisco, México [6]. The experimental field had loam soil, pH , and organic matter of with an accumulated annual precipitation of 998 mm, an altitude of 860 m above sea level, and an average annual temperature of 22.3 °C.
Regarding agronomic management, the local technological package was used, which consists of fertilization per hectare of 200-100-200 units of N-P-K, respectively, divided into two applications, plus the application of sugarcane compost (1.5 t ha 1) in one application. Irrigation was carried out every two months during the rainfed period from October to June. For pest control, quarterly releases of Trichogramma sp. were used against the sugarcane borer (Diatraea saccharalis and Eoreuma loftini). For rodent control, poisoned baits were used in two applications per year. There was no disease control, and mechanical weeding was used to combat weeds during the first three months after planting or sprouting.
The experimental unit consisted of four rows, with each row measuring m in length and m in width. The useful plot area consisted of the two central rows, with 2 m removed from the ends.
The SP of the materials was measured through destructive sampling on four dates (Table 2), with 30 to 34 days between the measurement dates. Seven months elapsed from planting to the first measurement date in the plant cycle, and six months from harvesting to the first measurement date in the ratoon cycle.

Table 2.
Sucrose percentage evaluation dates (month-day-year) of the 39 materials studied, Las Pilas.
Accordingly, by measuring the sucrose percentage in the materials at four different times (Table 2), we have what is known as repeated measurements, which are not independent. Therefore, the variation recorded in repeated measurements will reflect the variation in the response of the material over time, hence the relevance of using growth curve models to model repeated measurements. In this case, the PS is the variable of study.
Depending on environmental, geographical, and soil conditions, commercial varieties show a specific type of maturity: early, early–intermediate, intermediate–late, or late. According to [20], Mex 69-290 and CP 72-2086 exhibit late–intermediate and early maturity, respectively. ITV 92-1424 and COLMEX 95-27 exhibit early maturity; on the other hand, COLMEX 94-8 exhibits early–intermediate maturity [21], these varieties develop in clayey (AR), loam, silty crumb, and clayey crumb (FAR), and clay–loam (ARL) soils [22] under the conditions of temperature and altitude described in Table 3. Finally, RB 85-5113 has early–intermediate maturity and grows in medium-textured soils (loam = F, FAR, silt loam = FLI) [23].

Table 3.
Biological maturity of the six commercial materials.
2.1. Growth Curve Model
Growth curve models are useful for studying variability between and within subjects over time, as their covariance structure accounts for the correlation between observations from the same subject and the independence between different subjects. This type of data, known as repeated measures or longitudinal data, is characterized by observations ordered over time. The main advantage of these models is that, with up to four measurements per experimental unit, it is possible to analyze the temporal response and the variation in trends between experimental units.
The matrix form of the growth curve model is given by
where is the response vector; and are design matrices of dimensions and , respectively; is the fixed-effect parameter vector of dimensions ; is the random-effects vector of dimensions ; and is the error vector of dimensions . In Model (1), is the fixed component, and is the random component. It is assumed that and are independent, that is, , and that they each have a multivariate normal distribution:
where and are the covariance matrices of the random-effects vector and the error vector, respectively; both positive definite matrices. denotes the variance and covariance matrix of the random effects, and can be decomposed as , where is a covariance matrix and is a correlation matrix. From these assumptions, we have that the response variable has the following distribution:
where . Both components allow for modeling the correlation and heteroscedasticity in subject measurements. In using the Henderson equations [24] to estimate the Model (1) parameters, the best unbiased linear estimator for and the best unbiased linear predictor for are obtained:
In the growth curve models, is the j-th observation of the i-th material, denote the number of measurements, and denote the number of materials; the growth curve model is given by
where indicates the time at which the data were observed, and is the error associated with that observation. and are unknown parameters representing the intercept and slope of the model, respectively; is the random effect associated with the intercept; and is the random effect associated with the slope of the model (Appendix A.1). The fixed component of Model (2) is , and the random component is . According to this model and considering four measurement dates (Table 2), the design matrices for each material i are of dimensions and are given by
The fixed-effects parameter vector, the random-effects vectors, and the error vectors are given by
Then, the model of growth curves for the i-th material is given by
Random effects , are assumed to be independent and identically distributed, that is, , with
There are several covariance structures for that provide a more accurate representation of the variability and correlation between observations within a group or subject [25] that enables more flexible and appropriate model fitting to longitudinal data.
The error vectors , are also assumed to be independent and identically distributed, that is, , with
This matrix can be decomposed in the form
where is a diagonal matrix with nonnegative diagonal elements for the i-th material, with , , representing functions of variance [25]; is a correlation matrix for the i-th material. This way, the presence of heteroscedasticity in the elements of the vector is explained by , and explains the correlation between the observations of the i-th material. Some structures for include autoregressive processes of order 1 and autoregressive structures [26].
For the plant and ratoon crop cycles, Model (3) was used. For the plant cycle, the specification of assumes that , and the elements of are given by (varPower variance function), where is a constant; this variance function indicates that the magnitude of the variance error changes nonlinearly over time (Appendix A.2.1). Then, for the plant cycle
and
For the plant cycle, the intraclass correlation coefficient was calculated; it indicates the degree of correlation that exists between the observations of the same group. It is calculated using the following equation:
where is the covariance between the random effects of the intercept and slope, and and are the standard deviations of the random intercept and the random slope, respectively.
For the ratoon cycle, , . For the specification of , was assumed, and the dependence of the elements of in time are given by (varIdent variance function); this variance function is suitable when the data exhibit less variation within a group (Appendix A.2.2). We set ∀ i and j; then, for the ratoon cycle,
If the growth curve model correctly explains the variability of the materials, then the assumptions of normality, homogeneity of variances, and independence in the residuals should be satisfactorily met. The Kolmogorov–Smirnov (normality), Bartlett (homogeneity of variances), and Box–Pierce (independence) statistical tests were used to verify the fulfillment of these assumptions.
The normality hypothesis was tested with the ks.test function, the independence hypothesis was tested with the Box.test function, and the homogeneity of variances was tested with the bartlett.test function; all three functions are available in the stats package [27].
The modeling of the growth curves was performed with the lme function of the nlme package [28].
2.2. Grouping Techniques
After performing the statistical modeling, an estimated growth curve was obtained for each of the 39 materials, capturing both the variability among materials and within each material over time. This estimated curve consists of an intercept value and a slope value. These two values represent the newly available information for each of the 39 materials and will be used for the clustering analysis. The maturity type of the 33 new materials is determined by observing the biological maturity of the commercial varieties present in each of the formed groups.
The clustering techniques of k-means, k-medoids, and DBSCAN were employed to classify genotypes with similar sucrose accumulation patterns. k-means was chosen for its efficiency in data partitioning [29], k-medoids for its robustness against noise and outliers [30], and DBSCAN for its ability to identify non-spherical clusters and detect outliers [31].
k-means and k-medoids are partition-based algorithms [32], whereas DBSCAN is a density-based method that is robust to outliers [33].
2.2.1. k-means
The k-means algorithm is a non-hierarchical clustering method used to analyze numerical data, with the goal of partitioning a data set into K groups, each represented by a centroid. The value of K must be defined in advance. The algorithm iteratively adjusts the position of the centroids in the object space, seeking the best grouping of similar individuals. To calculate the distance between objects and determine their similarity, several distance functions can be used, with Euclidean distance being one of the most commonly used, as it measures the shortest distance between two points [34,35,36].
For this research, the value of K was set to four, as four maturity types were considered for the 33 materials in the study. Additionally, an inflection point was identified using the elbow method. This analysis revealed that the optimal number of clusters was four, aligning with the expectation based on the four previously defined maturity types: early, early–intermediate, intermediate–late, and late. The metric used in k-means was Euclidean distance.
2.2.2. k-medoids
The k-medoids algorithm uses a partitioning method to group a set of n objects into K clusters. The process starts by setting the number of clusters and randomly selecting the initial centroids. Then, the distance of each object to the centroid of each cluster is calculated. Subsequently, an iteration is performed to adjust the centroids according to the assignment of the data [37]. For this method, the value of K was also equal to four to consider four degrees of maturity in the 33 new materials. The metric used was the Euclidean distance.
2.2.3. DBSCAN
DBSCAN is a density-based clustering algorithm that identifies clusters as dense regions separated by lower-density areas. It performs well with nonlinear data and distinguishes between high- and low-density clusters. The process starts by selecting an unvisited point; if its neighborhood contains enough points, a cluster is formed; otherwise, it is classified as noise. The key parameters are (maximum distance between neighbors) and (minimum number of points to form a dense region) [38]. In this study, was determined using the kNN function from the dbscan package [39], and several values of were tested.
2.3. Validation Indices
The evaluation of the clusters identified was carried out using the Silhouette index, the Dunn index, and the Connectivity index.
The Silhouette index measures the confidence with which an observation is assigned to a cluster, providing information about the cohesion and separation of the clusters. This index varies in the range from to 1, where a value close to 1 indicates that the point has been correctly assigned to the cluster and is well separated from other clusters [40]. Values from to 1 indicate a strong cluster structure has been found; from to , a reasonable structure; from to , the structure is weak; and less than or equal to , no substantial structure [41]. Negative values have a similar interpretation and indicate that the object may be incorrectly assigned and is closer to points from another cluster [42]. The Silhouette index is given by
where n is the total number of objects in the dataset, K is the number of clusters, is the set of objects in cluster k, is the average distance between object i and all other objects in the same cluster, is the average distance between object i and all objects in the nearest cluster, and is the maximum value of and .
The Dunn index is a measure of the quality of a partition in terms of the ratio between the minimum distance between cluster centroids and the maximum distance between points and their respective centroids [43]. This index is given by
where K is the number of clusters, is the minimum of the distances between the centroids of each cluster and the global center , and is the maximum distance between each point in the dataset and its respective centroid in its corresponding cluster. The minimum distance is a measure of the internal coherence of the clusters, and the maximum distance is a measure of the separation between clusters.
The Connectivity index is calculated by constructing a neighbor matrix. Define as the j-th nearest neighbor of observation i, and let be zero if i and are in the same cluster and otherwise. The Connectivity index has a value between 0 and ∞ and should be minimized [44]. This index is given by
where n is the total number of objects in the dataset, and L is a parameter that determines the number of neighbors that contribute to the connectivity measure.
The quality of the clustering was determined with the Silhouette (Silhouette function of the package [45]), Dunn (Dunn function of the package [44]) and Connectivity (Connectivity function of the package [44]) indices.
3. Results
3.1. Plant Cycle
To effectively model the heteroscedasticity observed in the data, the varPower function was implemented, setting the parameter to , which allowed for a better fit of the model to the variability of the data. After that, the fitted model for the plant cycle satisfies the assumptions of normality (Kolmogorov–Smirnov, p-value ), homogeneity of variance (Bartlett, p-value ), and independence (Box–Pierce, p-value ).
Table 4 presents the parameter estimates of the fitted model (Model (3)), along with their respective 95% confidence interval (CI), showing both fixed and random effects. The fixed effects include the estimated parameters and , both significant, which represent the intercept and slope, respectively. The estimated intercept, , reflects that all materials have an average SP value of when time is zero. The slope indicates the change in SP for each unit change in time; thus, a value of signifies that, on average, SP increases by units for each additional unit of time, which according to Table 2, on average, is 31 days.

Table 4.
Estimated parameters of fixed and random effects of Model (3) for the plant cycle.
The intraclass correlation coefficient, (Table 4), indicates the degree of correlation that exists between the observations of the same group.
Since both random effects were statistically significant, specific estimated intercepts and slopes were obtained for each of the 39 materials from Las Pilas (Table 5). The variety COLMEX 94-8, which is known to have an early maturity, has an estimated intercept of and an estimated slope of ; similar values are observed for the variety RB 85-5113, which has an estimated intercept of and an estimated slope of . The variety MEX 69-290, which is known to have an intermediate–late maturity, has an estimated intercept of and an estimated slope of . From the estimations of all materials, it can be deduced that materials with an early maturity tend to have a higher intercept. Since both the intercept and the slope are random, their values vary depending on the specific sugarcane material being evaluated. Thus, materials that have a late maturity tend to have a smaller intercept and a larger slope.

Table 5.
Estimated parameters of Model (3) for the 39 materials for the plant cycle.
Figure 1 presents the estimates of the intercept and slope for each material, where a high intercept indicates an early accumulation of sucrose (typical of early materials), and a steep slope reflects a higher accumulation rate over time (characteristic of late materials). The red color in the intercept indicates materials with a higher intercept value, while the blue color represents those with a lower intercept. Similarly, color coding is applied to the slope: blue highlights materials with a steeper slope, while red indicates materials with a gentler slope. This color scheme provides a clear way to identify which materials are positioned above or below others based on these parameters. Together, this explains the behavior of the materials according to their respective fitted models. This is the graphical representation of Table 5.
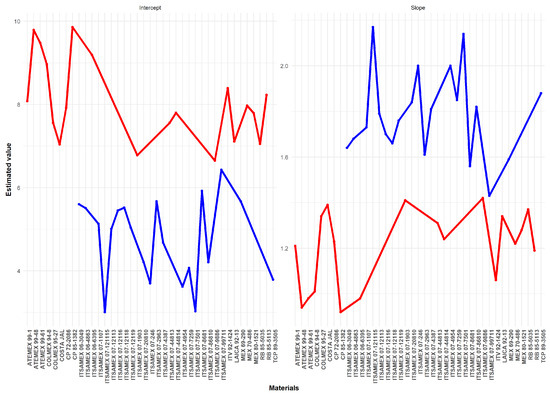
Figure 1.
Estimated curves for materials based on intercept and slope for the plant cycle.
Clustering Materials in the Plant Cycle
Clustering was performed using the intercept and slope estimates of the estimated maturity curve (Table 5). Since sugarcane materials can express any of the four types of maturity in the sugar industry, early, early–intermediate, intermediate–late, and late, the number of groups was set at 4.
The clustering of the materials using the k-means algorithm with is shown in Figure 2a and Table 6. The early-maturity group has four early-maturing commercial varieties—ITV 92-1424, RB 85-5113, CP 72-2086, and COLMEX 95-27—and ten new materials. The early–intermediate-maturity group contains four new materials and variety COLMEX 94-8. The group designated with intermediate–late maturity comprises variety MEX 69-290, which is known to exhibit intermediate–late maturity and 11 new materials. The l-te maturity group has eight new materials.
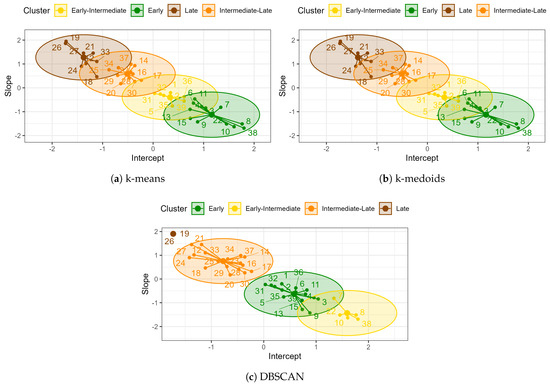
Figure 2.
Clustering of Las Pilas materials in the plant cycle.

Table 6.
Comparison of the clustering results for the plant cycle, Las Pilas.
The validation indices for clustering the materials with k-means are , , and . The value of indicates that the grouping of materials shows moderately good cohesion and appropriate separation between the clusters. The value of indicates relatively low separation between clusters and a potential for improvement in cohesion within the clusters. Meanwhile, the value of indicates good separation between clusters and appropriate compactness within the clusters. Therefore, two out of three indexes indicate that the k-means clustering is good.
The clustering of the materials using the k-medoids algorithm with is shown in Figure 2b and Table 6. The early-maturity group has 12 materials, including commercial varieties ITV 92-1424, RB 85-5113, CP 72-2086, and COLMEX 94-8, all of which are reported to have an early maturity. The early–intermediate-maturity group has seven new materials. The intermediate–late-maturity group has 11 as it incorporates variety MEX 69-290, which has intermediate–late maturity. The late-maturity group contains eight new materials.
The validation indices for clustering the materials with k-medoids clustering are , , and . The value of indicates that the clustering exhibits moderate cohesion and appropriate separation among the groups, but there is still room for improvement in terms of group separation. The value of indicates relatively low separation between clusters and a potential for improvement in cohesion within the clusters. The value of indicates good separation between the groups and appropriate compactness within the clusters.
For the DBSCAN clustering algorithm with and a , we have groups with 15, 5, 17, and 2 materials, as shown in Figure 2c and Table 6. The early group consists of 11 new materials and 4 commercial varieties: ITV 92-1434, RB 85-5113, CP 72-2086, and COLMEX 95-27. The early–intermediate group includes four materials and commercial variety COLMEX 94-8. The intermediate–late group comprises 16 new materials, along with commercial variety MEX 69-290. Lastly, the late group consists of two new materials, ITSAMEX 07-7501 and ITSAMEX 07-121115.
The validation indices for clustering the materials with DBSCAN are , , and . The values of and indicate that the clustering exhibits moderately good cohesion and adequate separation between the groups. The value of suggests reasonable connectivity between the groups, implying that there is internal connectedness within each group and good relationships between observations in each group. Thus, it can be concluded that the clustering performed with DBSCAN has achieved satisfactory separation and cohesion among the groups, along with suitable connectivity.
The k-means and DBSCAN algorithms are more similar to each other than to k-medoids, as they coincide in the maturity type assignment for 32 materials, while k-means and k-medoids coincide for 26, and k-medoids and DBSCAN for 20. According to the index values (Table 7), DBSCAN is the most suitable method for characterizing the 33 materials by maturity, and its use should be considered in the adaptation phase of the plant cycle. Thus, given the grouping by DBSCAN, it is up to the researcher to choose the materials that will pass to the next phase, given the type of maturity they present.

Table 7.
Validation indices for the plant cycle.
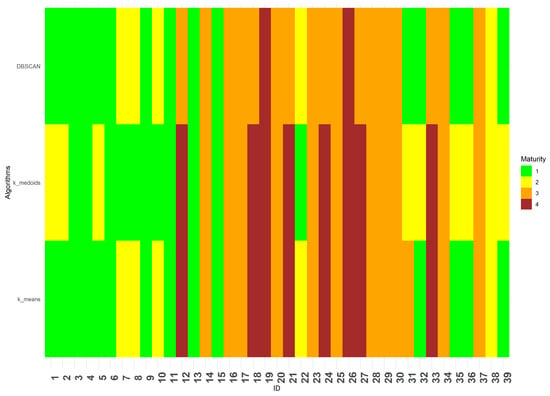
Figure 3.
Heatmap of material maturity based on clustering algorithms for the plant cycle.
The heatmap displays the classification of the 39 sugarcane materials according to three clustering algorithms, based on the four defined maturity types (early (1), early–intermediate (2), intermediate–late (3), late (4)). The color distribution allows for visualizing the correspondence between the methods used, highlighting a general consistency in the assignment of materials to the different maturity groups. This coherence between the algorithms suggests the stability and robustness of the classification patterns obtained, as shown in Figure 2.
3.2. Ratoon Cycle
The model satisfies the assumptions of normality (Kolmogorov–Smirnov, p-value = 0.85), homogeneity of variances (Bartlett, p-value = 0.34), and independence (Box–Pierce, p-value = 0.23).
For this cycle, incorporating only the random intercept was sufficient to improve the model fit (Model 3), which allowed for capturing the variation in the intercept, indicating notable differences in the initial SP among the different genotypes. Table 8 shows that both the intercept and the slope of the fitted model for the ratoon cycle are significant, with narrow confidence intervals, indicating high precision in the estimates. The significant variability among the subject intercepts () and the moderate residual variability () suggest that the model adequately captures the variation present in the data.

Table 8.
Estimated parameters of fixed and random effects of Model (3) for the ratoon cycle.
Since only the intercept has a statistically significant random effect, specific estimated intercepts were obtained for each of the 39 materials from Las Pilas (Table 9). Similarly to in the plant cycle, a higher intercept is observed in varieties known to have an early maturity: ITV 92-1424 had an intercept of , CP 72-2086 had an intercept of , and COLMEX 95-27 had an intercept of . Higher intercepts were also observed for the early–intermediate-maturity variety: COLMEX 94-8 had an intercept of . A lower intercept was observed in the MEX 69-290 variety, which had an intercept of .

Table 9.
Estimated parameters for the 39 materials in the ratoon cycle, Las Pilas.
The estimates of the models for the plant and ratoon cycles show some differences in terms of the estimated intercept. For the early-maturing varieties, the following results are obtained: the ITV 92-1434 variety had an SP of in the plant cycle and an SP of in the ratoon cycle, a difference of units; the CP 72-2086 variety had an SP of in the plant cycle and an SP of in the ratoon cycle, a difference of units; and the COLMEX 95-27 variety had an SP of in the plant cycle and an SP of in the ratoon cycle, a difference of units. This indicates that the three early-maturing varieties showed higher sucrose percentage yields in the ratoon cycle. The early–intermediate-maturity varieties showed the following results; the COLMEX 94-8 variety had an SP of in the plant cycle and an SP of in the ratoon cycle, a difference of units, and the RB 85-5113 variety had an SP of in the plant cycle and an SP of in the ratoon cycle, a difference of units. Finally, the late–intermediate-maturity variety, MEX 69-290, presented an SP of in the plant cycle and an SP of in the ratoon cycle, a difference of units. This variety also showed higher yields in sucrose percentage in the ratoon cycle.
An illustration of the behavior of the materials from Table 9, based on their estimated parameters, is shown in Figure 4. It can be observed that the slope remains constant for all 39 materials, while the intercept varies from one material to another. Furthermore, it is clearly noticeable that some materials exhibit a significant difference in their initial value (intercept). The red color indicates materials with a higher intercept, reflecting a greater initial accumulation. In contrast, the blue color highlights materials with a lower intercept, indicating a lower initial accumulation. This color coding facilitates the interpretation of material behavior based on the estimated parameter.
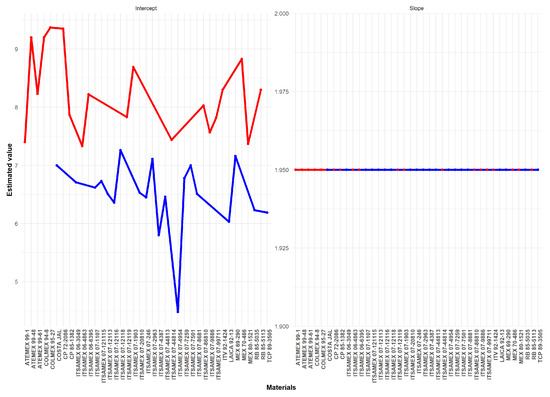
Figure 4.
Estimated curves for materials based on intercept and slope for the ratoon cycle.
Clustering Materials in the Ratoon Cycle
The clustering of materials using the k-means algorithm is shown in Figure 5a and Table 10. The early group consists of five new materials and five commercial varieties: ITV 92-1424, RB 85-5113, CP 72-2086, COLMEX 95-27 and COLMEX 94-8. The early–intermediate group is composed of 14 materials, including the MEX 69-290 variety. Despite being identified as intermediate–late in the plant cycle, the MEX 69-290 variety was assigned to the early–intermediate cluster in this cycle due to its higher SP in the ratoon cycle. Regarding the absence of the COLMEX 94-8 variety in the early–intermediate-maturity group, its maturity is determined based on the average SP value that the hybrids in this group have (). We have a group of 14 materials that are of intermediate–late maturity. Their maturity is inferred from the average value () of sucrose that the hybrids exhibit. Finally, the late group contains only ITSAMEX 07-4954 material.
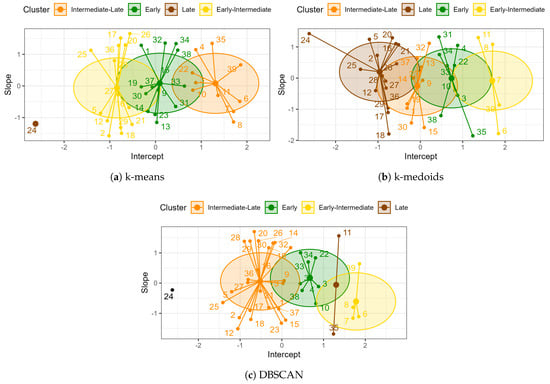
Figure 5.
Clustering of materials in the ratoon cycle, Las Pilas.

Table 10.
Comparison of the algorithms for the ratoon cycle.
According to the Silhouette index (), the clustering performed with the k-means algorithm indicates moderate cohesion and satisfactory separation between the clusters. However, it is observed that the separation between groups could be improved, as the Dunn index was low (). Finally, according to the Connectivity index (), the groups are well defined and internally connected.
The clustering of materials using the k-medoids algorithm is shown in Figure 5b and Table 10. The early group is composed of eight materials, including commercial varieties ITV 92-1434 and RB 85-5113. The early–intermediate group contains three new hybrids and commercial varieties CP 72-2086, COLMEX 94-8, and COLMEX 95-27. Similarly, the intermediate–late group consists of commercial variety Mex 69-290 and ten new hybrids, while the late group contains 14 hybrids.
These groups had clustering validation indices with the following values: , , and . The results indicate that the clustering carried out through the k-medoids algorithm forms groups in which there are similar characteristics among the materials within the same group in terms of and . The groups show good cohesion and appropriate separation.
For this cycle, the DBSCAN algorithm with and identified four groups with 24, 8, 4, and 2 materials. In this cycle, one material was left out of the four groups. In Figure 5c and Table 10, some groups are more compact, with a low point density (early–intermediate and late groups), while others are more dispersed, with a high point density (intermediate–late and early groups). Thus, the early-maturity group consists of commercial varieties ITV 92-1434 and RB 85-5113 and six new materials. The early–intermediate-maturity group contains commercial varieties CP 72-2086, COLMEX 94-8, and COLMEX 95-27 and one new hybrid. The intermediate–late-maturity group includes 23 new materials and the Mex 69-290 variety. Lastly, the late group contains two new materials. Finally, the DBSCAN algorithm did not assign hybrid ITSAMEX 07-4954 to any group. That is, according to the algorithm, this material presents a maturity type different from the four established in the analysis. For this clustering, the validation indices were , , and . These values indicate good cohesion and appropriate separation between the groups. The separation between the groups is reflected in the high value of the Dunn index. These results suggest that the formed groups represent different maturity types of sugarcane and exhibit distinctive characteristics in terms of their density.
Table 10 presents a comparison of the clustering algorithms for the ratoon cycle. It can be observed that the k-medoids and DBSCAN algorithms have more coincidences in the assigned maturity type (23 materials); k-means and k-medoids share five assignments, and k-means and DBSCAN have 17 shared assignments. The intermediate–late and early–intermediate groups have more materials according to the k-means algorithm, while according to the k-medoids algorithm, the late and intermediate–late groups have more assigned materials. Finally, the intermediate–late and early groups have more assigned materials according to the DBSCAN algorithm.
Similarly to the previous graph, Figure 6 is a graphical representation of Table 10, complemented by Figure 5. In both cases, the material that was not classified into any group can be observed. Furthermore, the color distribution, which intuitively indicates the maturity type of each material, is clearly depicted.

Figure 6.
Heatmap of material maturity based on clustering algorithms for the ratoon cycle.
The k-means algorithm achieved the best values for the (highest) and (lowest) indices, while DBSCAN obtained the best value for the index (Table 11). Therefore, k-means is the most suitable method for clustering materials in the ratoon cycle, allowing for the selection of materials that will advance to the next evaluation phase.

Table 11.
Validation indices for the ratoon cycle.
4. Discussion
Improving sugarcane varieties with high yield and higher sucrose content is essential for the sugar industry. Previous studies, such as [46,47], have emphasized the importance of these goals. The present research analyzes how sucrose accumulation varies among different hybrids and varieties, and how this variability is observable in both the plant cycle and the ratoon cycle.
Variations in sucrose accumulation depend on genetic, soil, climatic, and management factors [48,49]. Ref. [50] observed higher sucrose yields in the plant cycle, with decreases in the ratoon and second ratoon cycles, highlighting the importance of agronomic management and soil conditions.
The selection of adapted varieties and agronomic management are key to optimizing sucrose production [51]. The development of new varieties is complex and requires multiple evaluations before commercialization. Growth curve models can model maturity in the adaptability phase with at least four measurements per material, explaining their variability over time.
The Silhouette index exceeded 0.5 for all three algorithms evaluated, surpassing the 0.34 reported in [10] with k-means. However, the Connectivity and Dunn indices indicated that DBSCAN was the best method for the plant cycle, while k-means was the most appropriate for the ratoon cycle, aligning with its recognition in clustering [52].
DBSCAN correctly identified the maturity of the commercial varieties in the plant cycle, validating the estimation of their maturity curve and the methodology for characterizing the 33 hybrids. In the ratoon cycle, k-means also correctly identified maturity, ensuring proper characterization.
Some materials changed classification between cycles due to variations in sucrose caused by environmental factors, agronomic management, and algorithm differences. This underscores the importance of management and harvest timing to maximize sucrose content [53], demonstrating the usefulness of these methods in characterizing materials based on maturity.
Different maturity types impact crop yield and performance by influencing sucrose accumulation, the optimal harvest time, and industrial processing efficiency [54,55]. Early-maturing varieties allow for an earlier harvest and resource optimization, while intermediate- and late-maturing varieties can achieve higher yields over time, benefiting logistical planning and preventing processing plant overload. Thus, maturity classification not only enhances the understanding of the behavior of the evaluated materials but also has practical implications for agricultural and industrial management.
These results are crucial for identifying genetically adapted materials and developing varieties with high sucrose content [56].
This study opens up various opportunities to extend the application of statistical models to future research. In addition to sugarcane, mixed models that incorporate the interaction between genotype and environment could be applied to a wide range of agricultural crops, such as sugar beet, sweet sorghum, forage maize, rice, soybeans, and oilseed crops like sunflower and canola. These models can be useful not only for studying variations in sugar production but also other variables such as grain yield, water use efficiency, disease resistance, and crop quality, all of which are influenced by environmental conditions.
Furthermore, applying these models in different geographical regions with varying climatic conditions and soil types can provide a more precise understanding of how environmental factors impact crop performance and quality. For instance, in tropical or subtropical areas, the models could offer insights into how crops respond to consistent temperature and humidity conditions, while in more arid or temperate zones, they could analyze how seasonal fluctuations, water availability, or droughts affect performance. The ability of mixed models to capture the spatial and temporal variability of data would be particularly useful in tailoring agricultural practices to local environments, enabling farmers to make more informed decisions to optimize resource use.
In conjunction with the inclusion of additional variables, such as fertilizer use, pest control, crop rotation, and soil management practices, these models could provide a more comprehensive view of the factors affecting agricultural productivity. This multifaceted approach could improve sustainability, efficiency, and profitability in the production of a wide variety of crops, contributing to agriculture that is better adapted to local conditions and more resilient to climate change.
5. Conclusions
The sucrose accumulation curves of 33 new sugarcane hybrids were analyzed using growth curve models, enabling the modeling of their variability over time and sucrose yield across two cycles. Based on the estimated intercept and slope, the materials were characterized and grouped according to their maturity type (early, early–intermediate, intermediate–late, and late), facilitating the selection of the most promising hybrids for the next evaluation stage.
This characterization in the adaptability testing phase is valuable for plant breeders and geneticists in the search for new commercial sugarcane varieties. The methodology employed can serve as a reference for studying and selecting genotypes in advanced selection stages, optimizing agricultural management and harvest planning.
Growth curve models, combined with k-means, k-medoids, and DBSCAN clustering algorithms, allowed for the classification of genotypes based on their agronomic and industrial performance, contributing to the selection of more productive varieties. In the agro-industrial phase, these materials can be further evaluated to confirm their stability under different environmental conditions.
Author Contributions
Conceptualization, M.G.M. and C.D.C.M.; methodology, M.G.M., C.D.C.M. and F.G.-J.; software, C.D.C.M., M.G.M. and F.G.-J.; validation, M.G.M., C.D.C.M., J.C.G.-P., E.P.A. and R.R.C.; formal analysis, M.G.M., C.D.C.M. and J.C.G.-P.; investigation, J.C.G.-P.; resources, J.C.G.-P.; data curation, C.D.C.M., J.T.S. and J.C.G.-P.; writing—original draft preparation, C.D.C.M., M.G.M. and F.G.-J.; writing—review and editing, M.G.M., C.D.C.M., F.G.-J., J.C.G.-P., J.T.S. and R.R.C.; visualization, C.D.C.M., M.G.M., E.P.A. and F.G.-J.; supervision, M.G.M., J.C.G.-P., J.T.S. and F.G.-J.; project administration, J.C.G.-P.; funding acquisition, J.C.G.-P. All authors have read and agreed to the published version of the manuscript.
Funding
The project entitled “Agro-industrial selection and transfer of new sugarcane varieties for the state of Jalisco”, led by García Preciado José Concepción, was carried out from 30 March 2010, to 31 March 2013. It was funded by Fundación Produce de Jalisco, while land availability and technical monitoring of the research were supported by the Sugarcane Production and Quality Committees of the Melchor Ocampo Sugar Mill and INIFAP. The project was conducted at the Tecomán Experimental Station, within the agricultural subsector and at the state level, and was classified as applied research. Currently, the project is listed as inactive.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found at https://github.com/arimagm/New-Sugarcane-Hybrids (accessed on 2 September 2024).
Acknowledgments
The authors express their thanks to the technical field department of Ingenio Melchor Ocampo S.A. de C.V., to the engineer Filemón Zavalza Garcia, and to the sugarcane production and quality committee of the mentioned mill, as well as special thanks to Gabriel Ricardo Blackaller Ayala and Jesús Zúniga Mendoza.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Growth Curve Model
The model analyzes how the observations of a set of materials vary over time, considering not only the effect of time but also differences among materials (genotypes). We use a random-effects structure to account for individual differences between genotypes and how these affect both the initial value (, i.e., the starting point of each genotype), and the rate at which observations change over time (, the variation in the slope of each genotype).
In this model, represents the average response value at for the entire population, while captures the specific deviation in each genotype from this value. Similarly, represents the average rate of change over time, whereas describes how this rate varies among genotypes. Thus, the combination defines the actual intercept for each genotype, and determines its specific slope. This approach captures both the general trend of observations over time and the individual variations in each genotype, providing a more precise evaluation of how time and genotype influence crop measurements.
Appendix A.2. Variance Structure
In this study, two variance structures were used to model how errors vary across time for each hybrid. These structures help us understand how errors in the measurements may be correlated between each other and over time.
Appendix A.2.1. Power Variance Model (varPower)
The structure varPower is used to model a nonlinear relationship between errors and time. The variance structure is given by
- : This is the common variance of the errors.
- : This represents the time at which the measurement is taken for hybrid i.
- : This is the parameter controlling the relationship between the errors and time. If is 0.5, the relationship is a square root in time, while if it is 1, the relationship is linear. With , the errors increase with time, but more gradually compared to higher values of .
This model allows for errors to either increase or decrease over time, depending on the value of . For example, if , the errors still increase with time, but at a slower rate compared to when or .
This model allows for errors to either increase or decrease over time, depending on the value of .
Appendix A.2.2. Identity Variance Model (varIdent)
The structure varIdent is simpler and assumes that the errors have the same variance over time. The variance structure for this model is
- : As in the previous model, this is the common variance of the errors.
- 1: This indicates that the variance of the errors is constant across all time points.
References
- Alejandre Rosas, J.A.; Galindo Tovar, M.E.; Lee Espinosa, H.E.; Alvarado Gómez, O.G. Variabilidad genética en 22 variedades híbridas de caña de azúcar (Saccharum spp. Híbrido). Phyton (Buenos Aires) 2010, 79, 87–94. Available online: https://revistaphyton.fund-romuloraggio.org.ar/vol79/Alejandre-Rosas.pdf (accessed on 23 May 2024).
- Arntzen, C.J.; Ritter, E.M. Encyclopedia of Agricultural Science Volume 2: EL, 1st ed.; Academic Press: San Diego, CA, USA, 1994; Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/19951403738 (accessed on 4 January 2023).
- CONADESUCA. Nota Informativa Sobre Innovaciones en Materia de Productividad del sector. Nuevas Variedades de Caña de Azúcar; Sagarpa: Ciudad de México, México, 2016; Available online: https://www.gob.mx/cms/uploads/attachment/file/136406/NotaNuevasVariedadesd_Cana_deAzucar.compressed.pdf (accessed on 22 February 2023).
- Que, Y.; Wu, Q.; Zhang, H.; Luo, J.; Zhang, Y. Developing new sugarcane varieties suitable for mechanized production in China: Principles, strategies and prospects. Front. Plant Sci. 2024, 14, 1337144. [Google Scholar] [CrossRef] [PubMed]
- Sentíes-Herrera, H.E.; Valdez-Balero, A.; Loyo-Joachin, R.; Gómez-Merino, F.C. Fases experimentales en el mejoramiento genético de la caña de azúcar (Saccharum spp.) En México. AgroProductividad 2017, 10, 93–99. Available online: https://go.gale.com/ps/i.do?p=IFME&u=anon~3406d702&id=GALE|A530914354&v=2.1&it=r&sid=googleScholar&asid=76e56977 (accessed on 15 January 2024).
- García-Preciado, J.C. Evaluación de variables de calidad en híbridos de Saccharum Spp. En Difer. Ambient. Agroecol. De Jalisco, México. AgroProductividad 2017, 10. Available online: https://www.revista-agroproductividad.org/index.php/agroproductividad/article/view/55 (accessed on 16 April 2023).
- Rodríguez Gross, R.; Puchades Izaguirre, Y.; Abiche Maceo, W.; Rill Martínez, S.; Suarez, H.J.; Salmón Cuspineda, Y.; Gálvez, G. Estudio del rendimiento y modelación del período de madurez en nuevos cultivares de caña de azúcar. Cultiv. Trop. 2015, 36, 134–143. Available online: http://scielo.sld.cu/scielo.php?pid=S0258-59362015000400019&script=sci_arttext (accessed on 25 August 2023).
- Hernández, O.L.; García, S.S.; Nataren, E.H.; Espinoza, L.C.L.; Oliva, A.C.; Sanchez, S.C.; Romero, E.R.; Zossi, S. La espectroscopía de infrarrojo cercano (NIRS) en el seguimiento de la madurez del cultivo de la caña de azúcar (Saccharum spp.). Agro Product. 2019, 12, 107–113. [Google Scholar] [CrossRef]
- Larrahondo, J.E.; Cassalett, C.; Torres, J.; Issacs, C. El cultivo de la caña de azúcar en la zona azucarera de Colombia. In Centro de Investigación de la Caña de Azúcar de Colombia (Cenicaña); 1995; pp. 337–354. Available online: https://www.cenicana.org/pdf_privado/documentos_no_seriados/libro_el_cultivo_cana/libro_p3-394.pdf (accessed on 19 June 2023).
- Ostengo, S.; Rueda Calderón, M.A.; Bruno, C.; Cuenya, M.I.; Balzarini, M. A protocol for identifying characteristic sucrose accumulation curves of sugarcane genotypes (Saccharum spp.). Sugar Tech 2021, 23, 519–523. [Google Scholar] [CrossRef]
- Palmito dos Santos, D.; Nascimento, M.; Ferreira, D.F.; Verardi, C.K. Optimal Designs in Plant Breeding Experiments: A Simulation Study Comparing Grid-Plot and Partially Replicated (p-Rep) Design. Sugar Tech 2024, 26, 387–395. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Jarquin, D.; Cuevas, J.; Montesinos-López, O. Genome and Environment Based Prediction Models and Methods of Complex Traits Incorporating Genotype × Environment Interaction. In Genomic Prediction of Complex Traits; Ahmadi, N., Bartholomé, J., Eds.; Methods and Protocols; Humana: New York, NY, USA, 2022; pp. 245–283. [Google Scholar] [CrossRef]
- Smith, A.B.; Cullis, B.R.; Thompson, R. The analysis of crop cultivar breeding and evaluation trials: An overview of current mixed model approaches. J. Agric. Sci. 2005, 143, 449–462. [Google Scholar] [CrossRef]
- Jarquin, D.; Crossa, J.; Lacaze, X.; Cheyron, P.; Pérez-Rodríguez, P. A Reaction Norm Model for Genomic Selection Using High-Dimensional Genomic and Environmental Data. Theor. Appl. Genet. 2014, 127, 595–607. [Google Scholar] [CrossRef]
- Cuevas, J.; Crossa, J.; Montesinos-López, O.; Burgueño, J.; Pérez-Rodríguez, P.; de los Campos, G. Bayesian Genomic Prediction with Genotype × Environment Interaction Kernel Models. G3 Genes Genomes Genet. 2017, 7, 41–53. [Google Scholar] [CrossRef] [PubMed]
- Burgueño, J.; Crossa, J.; Cotes, J.M.; Vicente, F.S.; Dasgupta, S. Genomic Prediction of Breeding Values When Modeling Genotype × Environment Interaction Using Pedigree and Dense Molecular Markers. Crop Sci. 2012, 52, 707–719. [Google Scholar] [CrossRef]
- Gilbert, R.A.; Shine, J.M., Jr.; Miller, J.D.; Rice, R.W. Sucrose accumulation and harvest schedule recommendations for CP sugarcane cultivars. Crop Manag. 2004, 3, 1–7. [Google Scholar] [CrossRef]
- Seta, P.T.; Hartomo, K.D. Mapping land suitability for sugar cane production using k-means algorithm with leaflets library to support food sovereignty in central java. Khazanah Inform. J. Ilmu Komput. Dan Inform. 2020, 6, 15–25. [Google Scholar] [CrossRef]
- Mbukwa, J.N.; Anjaneyulu, G.V.S.R. Application of K-Means and Partitioning Around Mediods (PAM) clustering techniques on Maize and Beans yield in Tanzania. KY Publ. 2016, pp. 146–158. Available online: http://bomsr.com/4.4.16/146-158%20JUSTINE%20NKUNDWE%20MBUKWA.pdf (accessed on 9 June 2024).
- Cervantes-Preciado, J.F.; Milanés-Ramos, N.; Castillo, M.A. Evaluation of 11 hybrids of sugar cane (Saccharum spp.) in the Central region of Veracruz, México. Agroproductividad 2019, 12, 69–73. Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/20203314828 (accessed on 25 August 2023). [CrossRef]
- Moreno Torres, V.M. Nuevas Variedades de Caña de Azúcar; Deschamps, L., Ed.; Deschamps & Escamilla: Colima, México, 2010; Fundación Produce Colima A.C., Instituto Interamericano de Cooperación para la Agricultura (IICA); pp. 1–59. [Google Scholar] [CrossRef]
- Villa Godoy, S.; De Teresa y Polignac, F. Manual Azucarero Mexicano, Edición 2024; Cía. Editora del Manual Azucarero, S.A. de C.V.: Ciudad de México, México, 2024; pp. 1–500. Available online: https://www.manualazucarero.com/_files/ugd/fc2095_b4e9661cd898438aadc336a83992d281.pdf (accessed on 12 November 2023).
- Fernandes, A.M.; de Queiroz, A.C.; Pereira, J.C.; Lana, R.d.P.; Barbosa, M.H.P.; da Fonseca, D.M.; Detmann, E.; Cabral, L.d.S.; Pereira, E.S.; Vittori, A. Composição químico-bromatológica de variedades de cana-de-açúcar (Saccharum spp L.) com diferentes ciclos de produção (precoce e intermediário) em três idades de corte. Rev. Bras. De Zootec. 2003, 32, 977–985. [Google Scholar] [CrossRef]
- McCulloch, C.E.; Searle, S.R. Generalized, Linear, and Mixed Models, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Gałecki, A.; Burzykowski, T. Linear Mixed-Effects Models Using R, 1st ed.; Springer: New York, NY, USA, 2013; pp. 245–273. [Google Scholar] [CrossRef]
- Aguirre-Calderón, O.A. ¿Cómo corregir la heterocedasticidad y autocorrelación de residuales en modelos de ahusamiento y crecimiento en altura? Rev. Mex. De Cienc. For. 2018, 9, 28–59. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 18 July 2024).
- Pinheiro, J.; Bates, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models, R package version 3; R Foundation for Statistical Computing: Viena, Austria, 2023; pp. 1–163. Available online: https://CRAN.R-project.org/package=nlme (accessed on 3 February 2024).
- Zhang, L.; Lu, F.; Liu, A.; Guo, P.; Liu, C. Application of K-means clustering algorithm for classification of NBA guards. Int. J. Sci. Eng. Appl. 2016, 5, 1–6. Available online: https://ijsea.com/archive/volume5/volume5issue1.pdf (accessed on 13 October 2024). [CrossRef]
- Kaur, N.K.; Kaur, U.; Singh, D. K-Medoid clustering algorithm—A review. Int. J. Comput. Appl. Technol. 2014, 1, 42–45. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. Available online: https://cdn.aaai.org/KDD/1996/KDD96-037.pdf?source=post_page (accessed on 30 November 2024).
- Zhang, C.; Huang, W.; Niu, T.; Liu, Z.; Li, G.; Cao, D. Review of Clustering Technology and Its Application in Coordinating Vehicle Subsystems. Automot. Innov. 2023, 6, 89–115. [Google Scholar] [CrossRef]
- Khan, M.M.R.; Siddique, M.A.B.; Arif, R.B.; Oishe, M.R. ADBSCAN: Adaptive density-based spatial clustering of applications with noise for identifying clusters with varying densities. In Proceedings of the 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT), Dhaka, Bangladesh, 13–15 September 2018; pp. 107–111. [Google Scholar] [CrossRef]
- Franco-Árcega, A.; Sobrevilla-Sólis, V.I.; Gutiérrez-Sánchez, M.J.; García-Islas, L.H.; Suárez-Navarrete, A.; Rueda-Soriano, E. Sistema de enseñanza para la técnica de agrupamiento k-means. Pädi Boletín Científico De Cienc. Básicas E Ing. Del ICBI 2021, 9, 53–58. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Q.; Xu, L.; Xu, X.; Liang, Z. Wheat Lodging Direction Detection for Combine Harvesters Based on Improved K-Means and Bag of Visual Words. Agronomy 2023, 13, 2227. [Google Scholar] [CrossRef]
- Gupta, M.K.; Chandra, P. Effects of similarity/distance metrics on k-means algorithm with respect to its applications in IoT and multimedia: A review. Multimed. Tools Appl. 2022, 81, 37007–37032. [Google Scholar] [CrossRef]
- Juliantho, D.A.; Hendrik, B. Komparasi Algoritma K-Means Dan K-Medoids Dalam Clustering Penyebaran Kasus Covid 19. J. Inf. Syst. Educ. Dev. 2023, 1, 30–32. Available online: https://journal.mwsfoundation.or.id/index.php/jised/article/view/12 (accessed on 7 December 2024).
- Ansari, Z. Discovery of web user session clusters using DBSCAN and leader clustering techniques. Int. J. Res. Appl. Sci. Eng. Technol. (iJRASET) 2014, 2, 209–217. [Google Scholar]
- Hahsler, M.; Piekenbrock, M. dbscan: Density-Based Spatial Clustering of Applications with Noise (DBSCAN) and Related Algorithms, R package version 1.2-0; R Foundation for Statistical Computing: Vienna, Austria, 2024. Available online: https://CRAN.R-project.org/package=dbscan (accessed on 30 October 2023).
- Ben Ncir, C.-E.; Hamza, A.; Bouaguel, W. Parallel and scalable Dunn Index for the validation of big data clusters. Parallel Comput. 2021, 102, 102751. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; illustrated, revised, reprint ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; Available online: https://books.google.es/books?hl=es&lr=&id=YeFQHiikNo0C&oi=fnd&pg=PR11&dq=Finding+groups+in+data:+an+introduction+to+cluster+analysis&ots=5CofD1KFAE&sig=CaZq_JCe5uV8RB_ymUHSuad8bKQ#v=onepage&q=Finding%20groups%20in%20data:%20an%20introduction%20to%20cluster%20analysis&f=false (accessed on 10 November 2024).
- Videla, M.E.; Bruno, C. Validación de agrupamientos para representar estructura genética poblacional. Agriscientia 2022, 39, 1–10. [Google Scholar] [CrossRef]
- Luna-Romera, J.M.; del Mar Martinez-Ballesteros, M.; Garcia-Gutierrez, J.; Riquelme-Santos, J.C. An approach to silhouette and dunn clustering indices applied to big data in spark. In Advances in Artificial Intelligence: 17th Conference of the Spanish Association for Artificial Intelligence, CAEPIA 2016, Salamanca, Spain, 14–16 September 2016; Proceedings 17; Springer: Cham, Switzerland, 2016; pp. 160–169. [Google Scholar] [CrossRef]
- Brock, G.; Pihur, V.; Datta, S.; Datta, S. clValid: An R Package for Cluster Validation. J. Stat. Softw. 2008, 25, 1–22. Available online: https://www.jstatsoft.org/v25/i04/. (accessed on 12 November 2024). [CrossRef]
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K. cluster: Cluster Analysis Basics and Extensions; R package version 2.1.4; 2022. Available online: https://CRAN.R-project.org/package=cluster (accessed on 8 November 2024).
- Zhao, Y.; Liu, J.; Huang, H.; Zan, F.; Zhao, P.; Zhao, J.; Deng, J.; Wu, C. Genetic improvement of sugarcane (Saccharum spp.) contributed to high sucrose content in China based on an analysis of newly developed varieties. Agriculture 2022, 12, 1789. [Google Scholar] [CrossRef]
- Cheavegatti-Gianotto, A.; De Abreu, H.M.C.; Arruda, P.; Bespalhok Filho, J.C.; Burnquist, W.L.; Creste, S.; di Ciero, L.; Ferro, J.A.; de Oliveira Figueira, A.V.; de Sousa Filgueiras, T.; et al. Sugarcane (Saccharum X officinarum): A reference study for the regulation of genetically modified cultivars in Brazil. Trop. Plant Biol. 2011, 4, 62–89. [Google Scholar] [CrossRef]
- Marcano, M.; Manrique, U.; Garcia, M.; Salcedo, F. Prueba de ocho variedades de caña de azúcar (Saccharum sp.) bajo condiciones de secano en un suelo de sabana del estado Monagas, Venezuela. Rev. Científica UDO Agrícola 2005, 5, 54–61. Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=2221593 (accessed on 14 September 2023).
- Vasantha, S.; Kumar, R.A.; Tayade, A.S.; Krishnapriya, V.; Ram, B.; Solomon, S. Physiology of sucrose productivity and implications of ripeners in sugarcane. Sugar Tech 2022, 24, 715–731. [Google Scholar] [CrossRef]
- García, S.S.; Escobar, R.N.; Alanis, L.B. Determinación de la dosis óptima económica de fertilización en caña de azúcar. Terra Latinoam. 2003, 21, 267–272. Available online: http://www.redalyc.org/articulo.oa?id=57315595012 (accessed on 6 April 2023).
- Gómez-Merino, F.C. Manual para la identificación varietal de caña de azúcar, 1st ed.; Colegio de Postgraduados: Texcoco, México, 2015; pp. 5–7. Available online: https://www.researchgate.net/profile/Fernando-Gomez-Merino/publication/271647569_Manual_para_la_Identificacion_Varietal_de_Cana_de_Azucar/links/54f483720cf2eed5d734bf55/Manual-para-la-Identificacion-Varietal-de-Cana-de-Azucar.pdf (accessed on 6 April 2023).
- Mei, H.; Mao, L.; Zhang, Y.; Chen, M. BDT-ADBSCAN: Adaptive Density-Based Spatial Clustering of Applications with Noise Based on Bayesian Decision Theory for Identifying Clusters with Multi-Densities. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; pp. 1510–1516. [Google Scholar] [CrossRef]
- Jackson, P.A. Breeding for improved sugar content in sugarcane. Field Crops Res. 2005, 92, 277–290. [Google Scholar] [CrossRef]
- Delgado Mora, I.; Jorge Suarez, H.; Vera, A.; Cornide Hernández, M.T.; Díaz Mujica, F.R.; Gómez Pérez, J.R.; Suárez Sanchez, O.; Puchades Isaguirre, Y. Influencia de la edad y cultivar de caña de azúcar en el momento de la cosecha. Cent. Agrícola 2016, 43, 59–65. Available online: http://scielo.sld.cu/scielo.php?pid=S0253-57852016000200008&script=sci_arttext (accessed on 3 July 2024).
- Espinoza, J.G. Maduración de la caña de azúcar y floración de la caña de azúcar y su manejo. Cengicaña. 2012, pp. 262–281. Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=5149559 (accessed on 3 July 2024).
- Mendoza Batista, Y.; Cruz Sarmiento, R.; Vaillant Cáceres, Y.; Luis Martínez, O.; Céspedes Argota, M. Comportamiento de los cultivares de caña de azúcar C97-445 y C95-416 en localidades de la provincia Holguín. Cent. Agrícola 2019, 46, 49–53. Available online: http://scielo.sld.cu/scielo.php?pid=S0253-57852019000100049&script=sci_arttext&tlng=en (accessed on 6 July 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).