What Is the Optimal Sampling Time of Environmental Parameters? Fourier Analysis and Energy Harvesting to Reduce Sensors Consumption in Smart Greenhouses

Abstract

Smart greenhouses offer crucial solutions for reducing our atmospheric impact and resource waste. However, two fundamental challenges persist in their implementation, massive energy consumption and a high level of human intervention, particularly for sensor battery replacement or recharging. Unfortunately, sensors are indispensable in greenhouses and agriculture, such as for monitoring environmental parameters for air quality assessment. Therefore, while sensors cannot be eliminated, it is essential to optimize their energy consumption. This work introduces an energy-efficient monitoring system for smart greenhouses, aiming to reduce the energy consumption of individual sensors and enhance system sustainability. This study focuses on optimizing the sampling intervals of commonly monitored environmental parameters to minimize sensor energy usage while maintaining data acquisition accuracy adequate for the intended purpose. Additionally, to further reduce battery energy draw, an energy harvesting system using solar panels was implemented. In conclusion, adopting an optimal sampling strategy for each parameter significantly reduces energy consumption compared to fixed, inefficient sampling intervals commonly used in commercial weather stations. Furthermore, by employing an energy harvesting system for each sensor, leveraging the light emitted by greenhouse lamps and external sources ensures the autonomy of sensors within the greenhouse, thereby minimizing the need for human intervention for battery replacement and recharging.

1. Introduction

The pressing issue of our time is climate change and its impact on people’s lives, marked by increasingly frequent extreme events such as torrential rainstorms and prolonged droughts. One particularly affected sector is agriculture, where climate change has a significant impact, sometimes forcing farmers to switch crop types in the same area as the environment becomes unsuitable for previously cultivated species, leading to a migration of crops.

The adoption of smart greenhouses could be a viable solution to mitigate the effects of climate change and rising temperatures on populations. Smart greenhouses, equipped with intelligent monitoring systems, can reduce the environmental impact and resource waste, eliminating the need for crop migration and even reducing reliance on food imports from other countries. This is achieved by adapting and controlling the greenhouse’s internal microclimate to suit the specific needs of the crops being cultivated.

However, two major challenges arise with these implementations—excessive energy consumption and the high frequency of human intervention—particularly for recharging or replacing batteries in devices installed inside and outside the system. Monitoring both internal [1] and external [2] parameters is essential for air quality assessment [3], including factors such as temperature, humidity, CO₂, SO₂, and PM₁₀ [4]. This monitoring is also crucial for resource management, particularly water usage [5]. These parameters are monitored at varying sampling frequencies, ranging from seconds [6] to hours [7], depending on the monitoring system used and, less frequently, on the parameters being measured. As observed in the agricultural market, companies offering environmental monitoring systems provide products with highly variable sampling intervals, as summarized in

Table 1. Common monitoring system’s sampling interval.

	2.5 s	16 s	16.5 s	5 min	10 min	15 min
[8,9,10]	✓
[11]		✓
[12]			✓
[13,14]				✓
[15,16]					✓
[17]						✓

, often without a specific criterion.

Regarding the energy efficiency of devices installed in greenhouses, the studies in the literature propose various methodologies. One approach involves adapting the data rate based on the distance between the end-node and the gateway to minimize energy consumption [18]. Another method adjusts the transmission power by considering the signal-to-noise ratio [19]. Additionally, transmission frequency adaptation is explored as a strategy [20]. For instance, the work [21] plans and optimizes the placement of cluster heads to balance data traffic using priority queuing with fuzzy logic. This demonstrates that it is possible to minimize and distribute energy consumption across the network. Another approach focuses on managing the sleep and active periods of both end-nodes and gateways to reduce the overall energy consumption [22].

Today, any well-equipped greenhouse integrates artificial lighting alongside natural sunlight. Therefore, a system capable of harvesting luminous flux and converting it into electrical power to supply the underlying devices via solar panels can significantly enhance the greenhouse’s efficiency by potentially reusing wasted energy [23]. Another example of reusing energy emitted by lamps is employing two different communication methods for downlink and uplink. The study [24] leverages and optimizes light emissions from lamps using Light Fidelity (Li-Fi) technology to send commands to the end-nodes. For data transmission, it employs Chirp Spread Spectrum (CSS) modulation, thereby optimizing energy usage for both illumination and command reception.

This paper investigates and analyzes the optimal sampling times for monitoring environmental parameters critical to plant growth. Additionally, it seeks to better understand how this sampling interval varies across parameters and seasons. To achieve this, the analysis employs frequency-domain techniques for time series data, a commonly used approach in telecommunications and signal processing, which is equally valuable in agriculture. The second part of this study focuses on outlining the key steps for designing and implementing an energy harvesting system, emphasizing the reuse of energy emitted by lamps and sunlight. The last goal is to extend the sensor’s lifespan, making it independent of battery life and significantly reducing the need for human intervention in battery management.

This paper is organized as follows: Section 2 outlines the proposed methodology, divided into two main areas: the analysis of time series for environmental parameters, and the design of an energy harvesting system to improve the energy efficiency of the smart greenhouse. Section 3 presents and discusses the results obtained, and Section 4 concludes the work.

2. Methods and Materials

The following section describes and presents the steps to achieve the results, which are subsequently discussed in Section 3. As previously mentioned, this study is divided into two main parts:

• Section 2.1: Analysis of environmental parameters to determine the optimal sampling interval and its variations, aiming to reduce energy consumption by managing the sleep and active phases of individual sensors.
• Section 2.2: Design and implementation of an energy harvesting system to utilize energy from solar radiation and, more importantly, reuse the artificial light emitted by lamps. This approach seeks to improve the energy efficiency and reduce the sensor’s reliance on battery power.

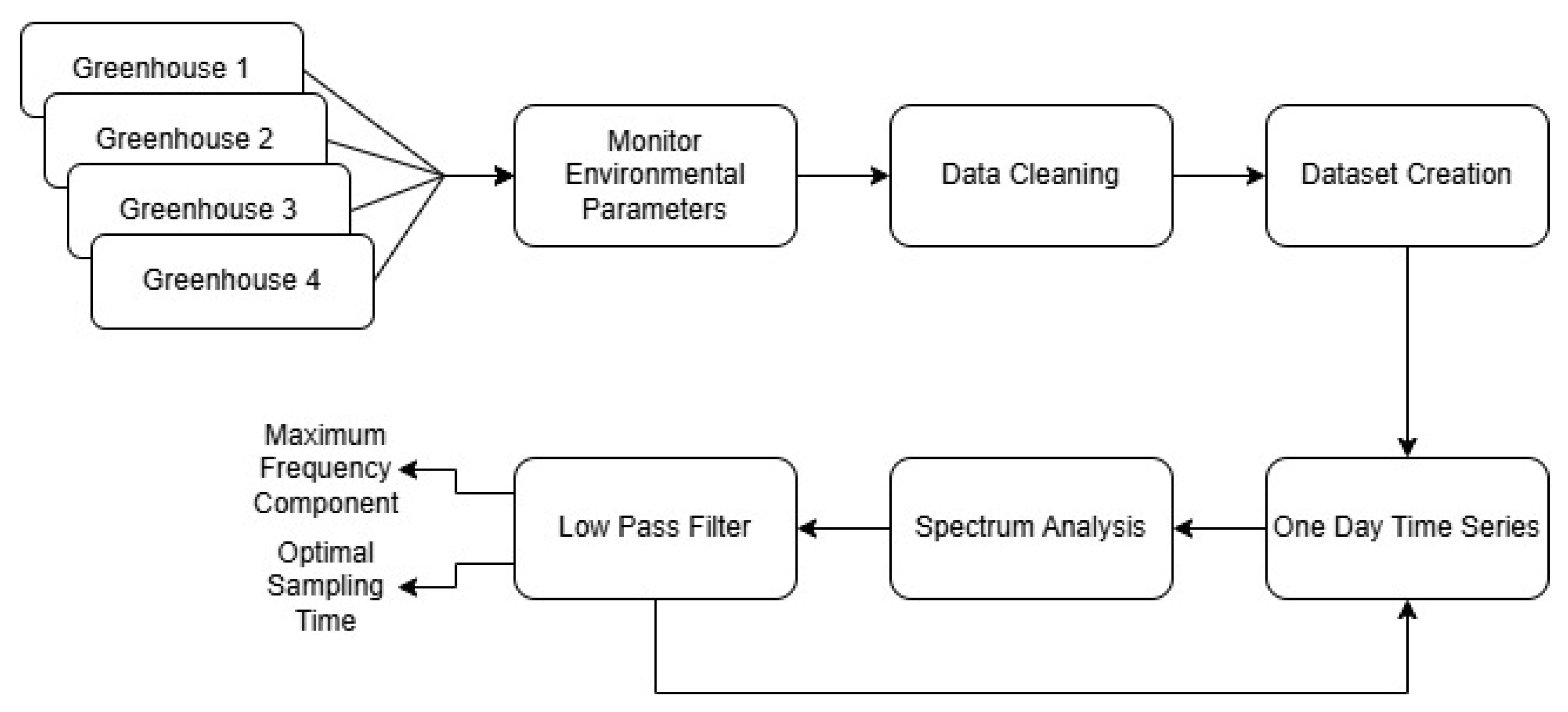
2.1. Optimizing Sampling Intervals for Energy-Efficient Sensor Operation

To optimize the energy consumption of sensors installed in greenhouses, we firstly determine the optimal sampling time for the environmental parameters that we aim to monitor. In this study, we have analyzed and monitored temperature and humidity, both external and internal, across four different greenhouses located in the same area. Figure 1 illustrates the workflow followed for the sampling time analysis.

In general, the workflow for determining the optimal sampling time of the monitored parameter can be applied to any time series values and is independent of the specific scenario in which it is implemented, such as the type of greenhouse or sensor used. The parameter for which the optimal sampling interval was determined was first monitored by collecting and storing samples in a database. Once the dataset is created, it undergoes analysis by dividing it into daily segments. For each day, the signal spectrum is computed using transformations such as the Discrete Fourier Transform (DFT), Fast Fourier Transform (FFT), Short-Time Fourier Transform (STFT), Wavelet Transform, or Hilbert Transform. These methods differ in terms of resolution, computational speed, and time–frequency analysis capabilities. In this study, as detailed later, the DFT is employed due to its simplicity and the fact that the signal under analysis is discrete in time. The variation in climate, depending on the location and region, affects the spectrum of the sampled signal. If the parameter exhibits greater fluctuations within the analysis window, the frequency spectrum will be broader, and vice versa. The frequency spectrum is then filtered to remove irrelevant signal frequencies. Finally, to determine the specific sampling interval for the selected time window, the well-known Nyquist theorem is applied.

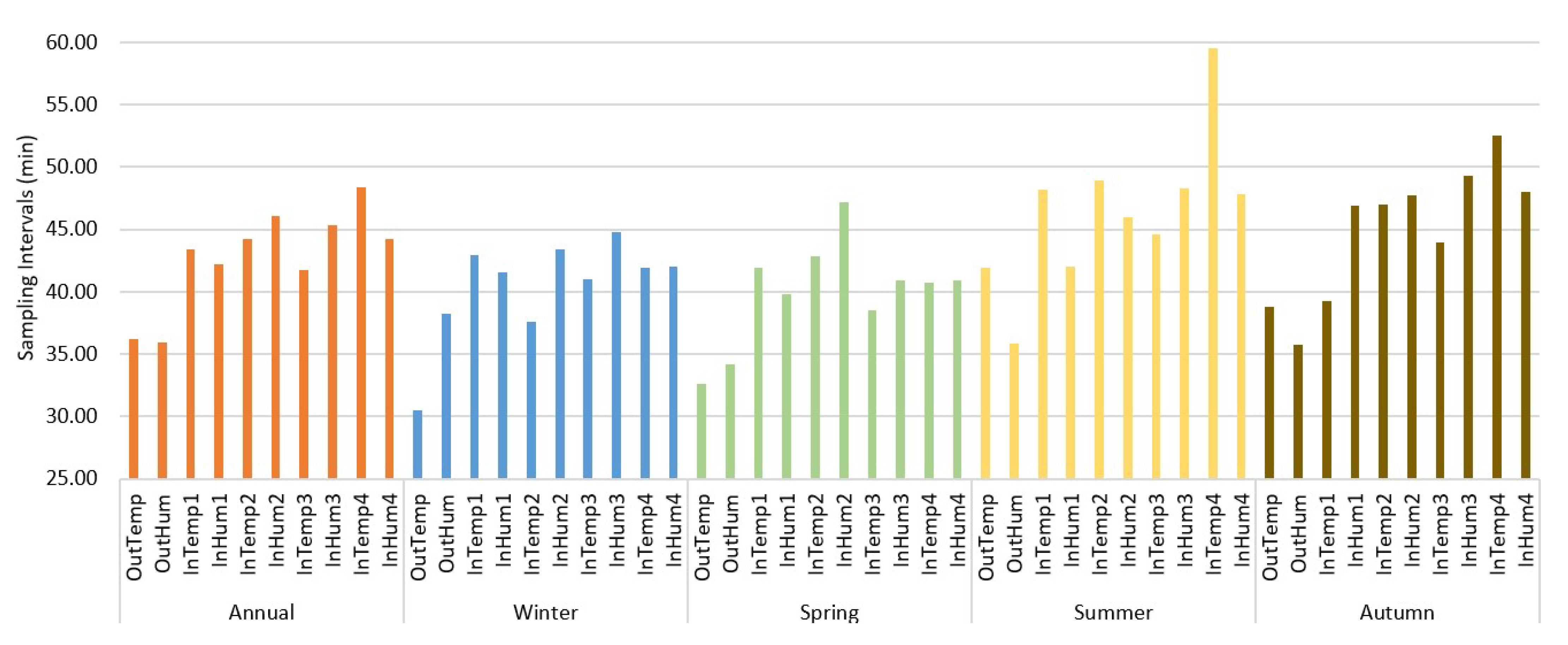
More specifically, we began by monitoring and collecting temperature and humidity data provided by the greenhouse sensors with a sampling interval of 5 min (as explained in detail in Section 3.1), which we assume to be significantly smaller than the optimal sampling interval since the average variation between consecutive samples is very low, as demonstrated in Section 3.1, providing minimal additional information. After collecting the data, we cleaned any errors or missing entries encountered during transmission, creating a dataset that serves as the reference for this study.

During the data analysis process, we first divided the data into daily subsets and then processed them by applying the Discrete Fourier Transform (DFT), as described in Equation (1). The DFT is the most important discrete transform used for Fourier analysis in many practical applications. In digital signal processing, a function represents any quantity or signal that varies over time (e.g., the pressure of a sound wave, a radio signal, or daily temperature readings) sampled over a finite time interval. The DFT transforms a sequence of N complex numbers $x_n$ into another sequence of complex numbers $X_k$.

$$X_k=\sum _{n=0}^{N-1}{x}_n·e^{-i2\pi kn/N}$$

(1)

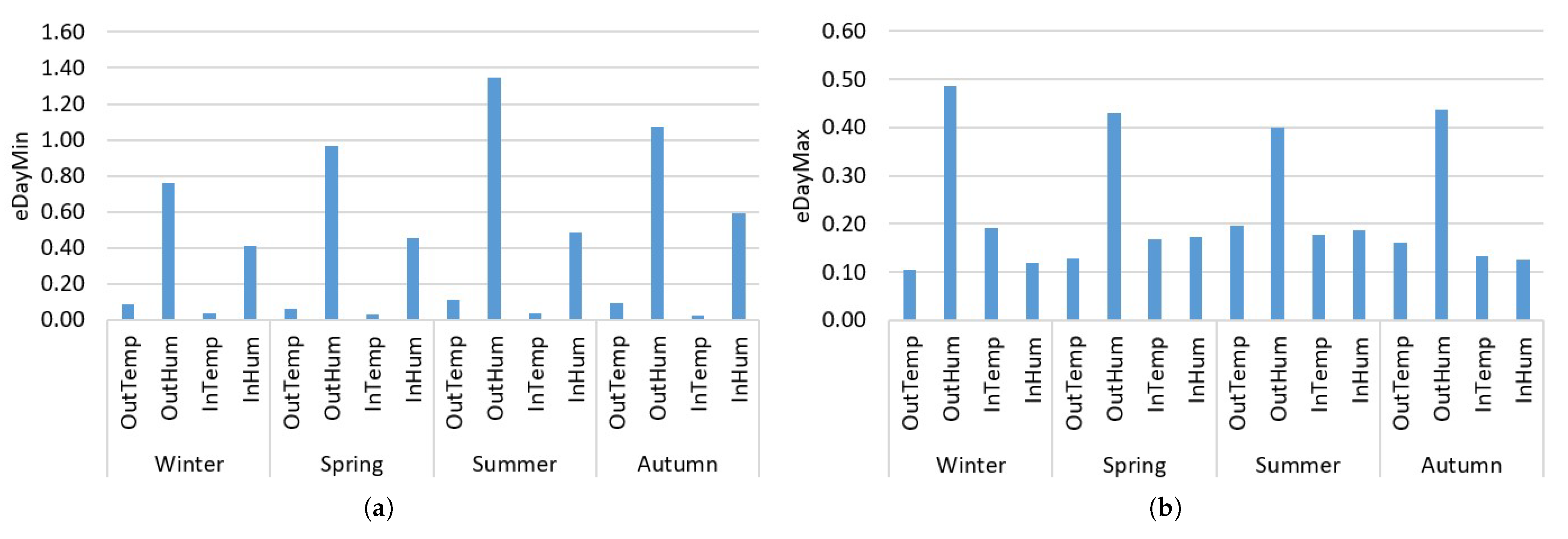
where $X_k$ is the signal represented in the frequency domain. After computing the signal spectrum, it is passed through a low-pass filter, retaining only the portion of the spectrum where the majority of the signal’s energy resides. At this stage, the maximum spectral frequency ($f_{max}$) and the optimal sampling time ($T_{opt}$) for the day can be extracted using Equation (2), considering the Nyquist theorem. The theorem states that the sampling frequency must be at least twice the maximum frequency component of the signal being sampled to accurately reconstruct the original signal.

$$T_{opt}={\displaystyle \frac{1}{f_{SamplingOpt}}}={\displaystyle \frac{1}{2\times f_{max}}}$$

(2)

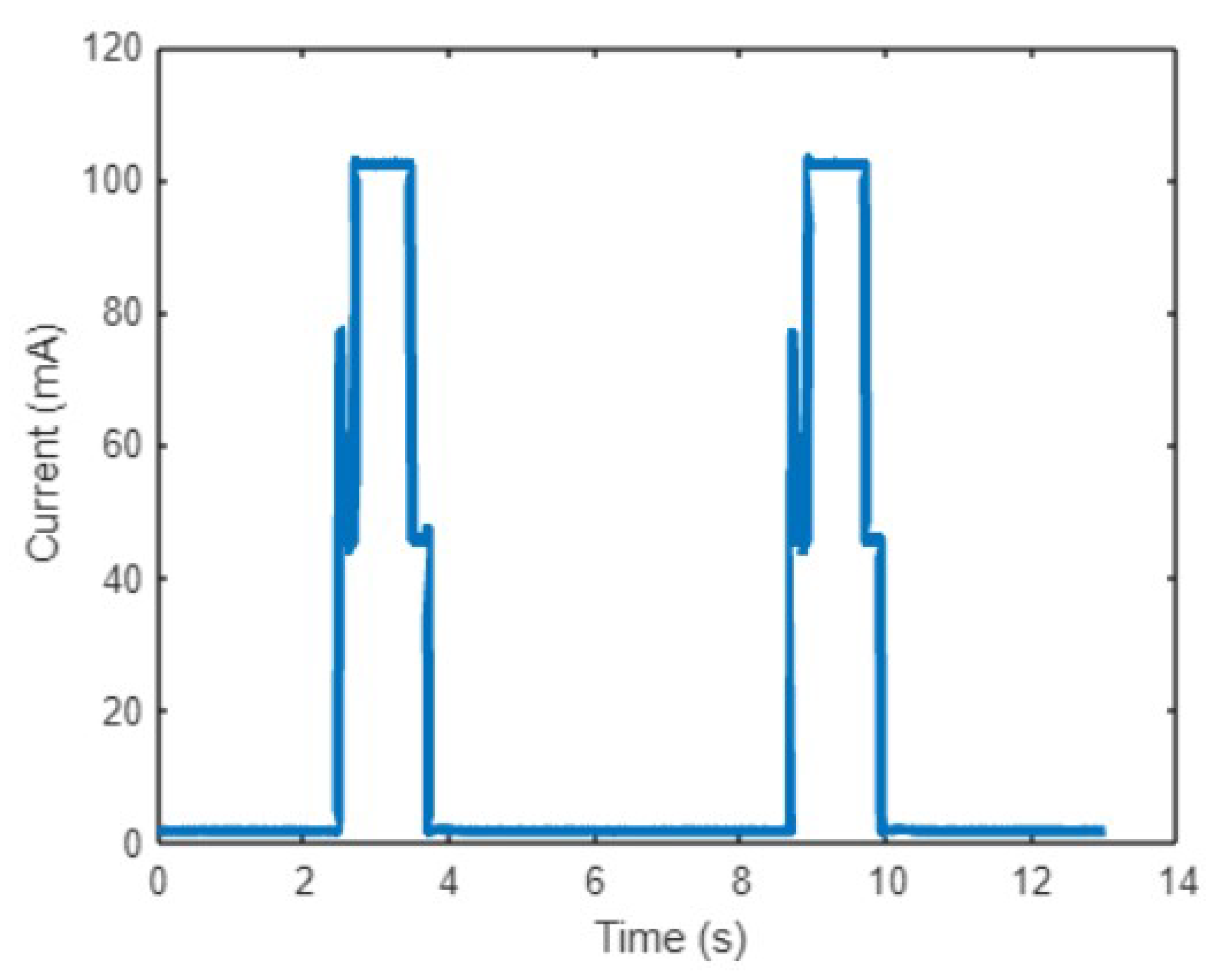
Once $T_{opt}$ is calculated on a day-by-day basis, the next step involves performing an energy analysis of the individual Micro-Controller Unit (MCU) board to which the sensor is connected, in order to optimize its energy consumption. The steps followed for this analysis are outlined in Figure 2.

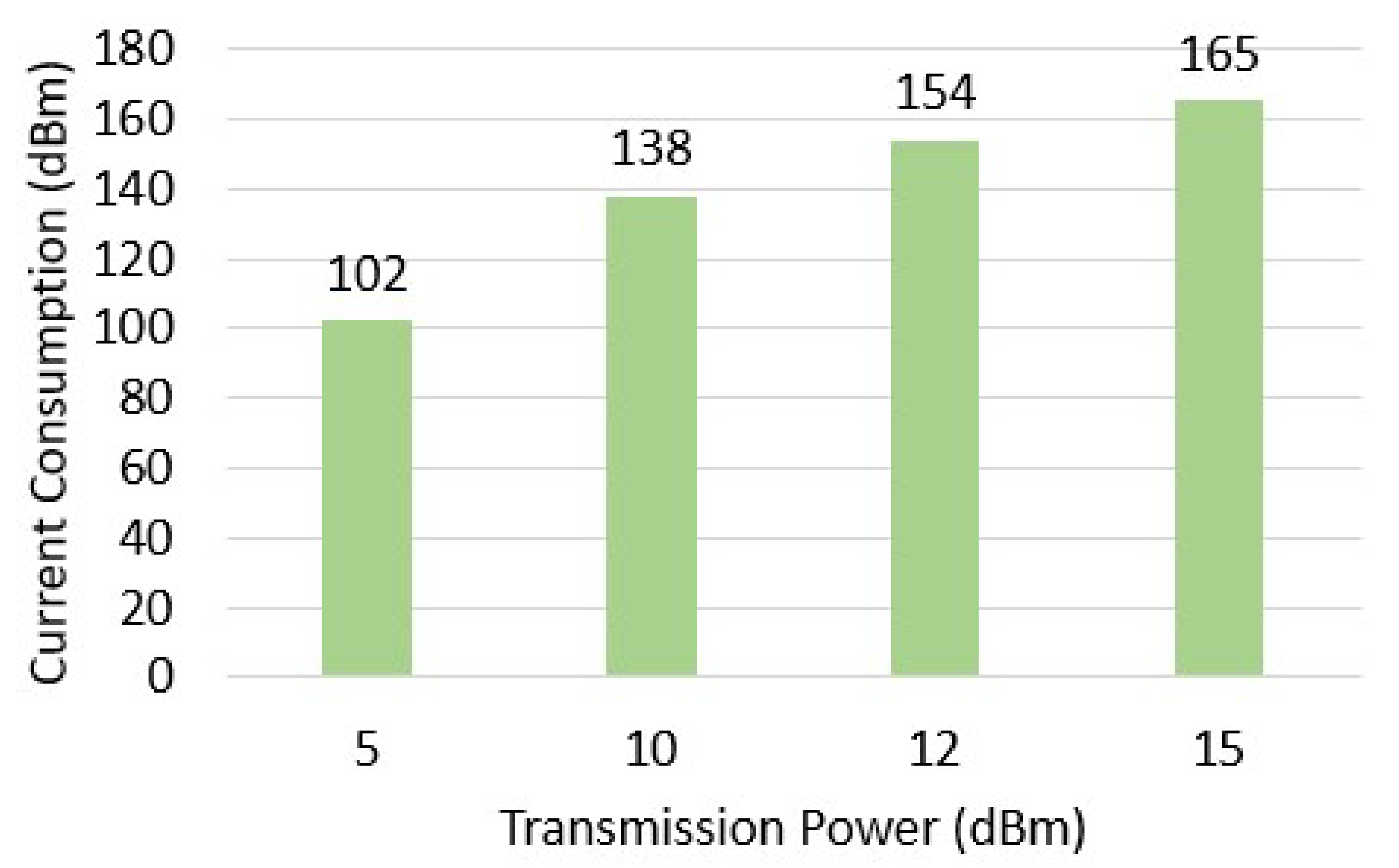
Upon completing the energy consumption analysis, the average current consumption (ACC) can be calculated by measuring the current consumption of the MCU board in its various states and then applying Equation (3).

$$ACC={\displaystyle \frac{T_{TX}\times I_{TX}+\left(T_{Opt}-T_{TX}\right)\times I_{DS}}{T_{Opt}}}$$

(3)

Here, $I_{TX}$ represents the current consumed in transmission mode, $I_{RX}$ in receiver mode, and $I_{DS}$ in deep sleep mode. Meanwhile, $T_{TX}$ is the time taken to transmit the message, and $T_{opt}$ is the sampling period of the environmental parameter.

At the end, based on the duration of sunlight ($h_{sunlight}$) and night-time ($h_{night}$) hours in the greenhouse, Equation (4) can be used to calculate the minimum battery capacity ($B{C}_{min}$) required to provide sufficient energy for the MCU board to operate throughout the night, assuming that sufficient energy is harvested during the day to power the board, as is the case in our work.

$$\begin{array}{cc}\hfill & B{C}_{min}=ACC\times h_{night}=\hfill \\ \hfill & ={\displaystyle \frac{T_{TX}\times I_{TX}+\left(T_{Opt}-T_{TX}\right)\times I_{DS}}{T_{Opt}}}\times h_{night}=\hfill \\ \hfill & =2\times \left(T_{TX}\times I_{TX}+\left({\displaystyle \frac{1-2\times f_{max}\times T_{TX}}{2\times f_{max}}}\right)\times I_{DS}\right)\times f_{max}\times h_{night}\hfill \end{array}$$

(4)

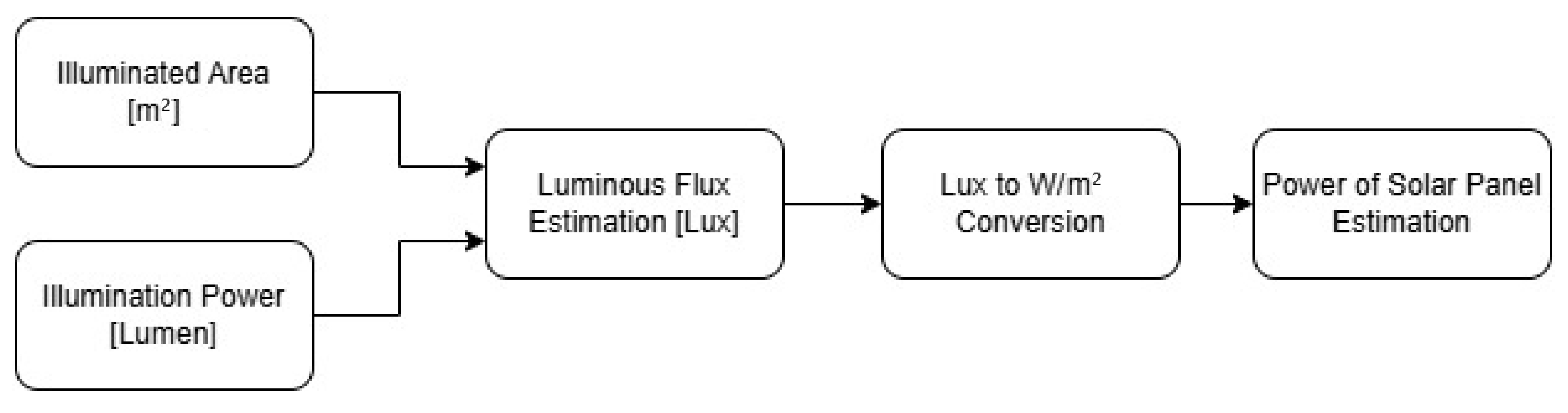
2.2. Design of the Energy Harvesting System

We assumed the presence of high-power LEDs in a smart greenhouse to provide artificial illumination even when sunlight is low or absent [25]. To make the duration of the MCU board independent from battery life, we have proposed the workflow, as shown in Figure 3. The goal is to convert and reuse the energy emitted by the lamps and external sources, such as sunlight, using small solar panels directly attached to the individual MCU boards. The aim is to fully power the boards during the day and recharge the mini battery to supply energy during the night, when both lamps and sunlight are absent.

Given the size of the area to be illuminated (A[m²]) and the optimal lighting power ($P_{Lighting}$[lumen]) required for plant growth (provided by both sunlight and artificial lamps), the estimated luminous flux ($ELF$[lux]) can be calculated using Equation (5).

$$ELF={\displaystyle \frac{P_{Lighting}}{A}}$$

(5)

Then, we convert them from lux to W/m² ($Lumen2W{m}^2$) using Equation (6).

$$Lumen2W{m}^2={\displaystyle \frac{ELF}{685}}$$

(6)

To estimate the current provided by the solar panel ($I_{SP}$[A]) with a certain area ($A_{SP}$[m²]), efficiency ($\eta$), and provided voltage ($V_{SP}$[V]), Equation (7) is used.

$$I_{SP}={\displaystyle \frac{Lumen2W{m}^2\times A_{SP}\times \eta }{V_{SP}}}={\displaystyle \frac{P_{Lighting}\times A_{SP}\times \eta }{685\times A\times V_{SP}}}$$

(7)

2.3. Materials

To collect environmental data both inside and outside the greenhouses, we utilized a central weather station, the Davis Vantage Pro 2 [26]. This weather station is capable of measuring wind direction and speed, air temperature with an accuracy of ±0.3 °C, air humidity with an accuracy of ±2%, atmospheric pressure, and rainfall. The data collection system consists of the central station, from which we collect external temperature and humidity data, and four distributed units, each located within a greenhouse, with the same measurement accuracy. The four greenhouses are located in the same area in Pisa, Italy. The data collected from the five stations constitute the dataset under study in this work.

Assuming the same network architecture as in our previous work [25], the test MCU board used was the Heltec WiFi LoRa v3 [27], which supports communication via both Wi-Fi and long-range technology (LoRa) at 868 MHz. The studies in the literature demonstrate that LoRa modulation is more energy-efficient compared to Wi-Fi; therefore, in this study, the boards communicate using LoRa modulation. The sensor used to collect air temperature and humidity data were the DHT11 [28]. The Heltec board was powered by a polycrystalline solar panel from Star Solar, model CNC85x115-18 [29], with dimensions of 85 mm × 115 mm. The panel delivers a maximum power of 1.5 W, a maximum voltage of 18 V, and a maximum current of 83 mA before being connected to the energy harvesting module EH302 [30]. To power the board during the night, a Li-Po battery [31] with a nominal voltage of 3.7 V and a capacity of 1350 mAh was used.

Finally, to analyze the power consumption of the Heltec board, the Qoitech Otii Arc PRO device [32] was used. This device serves as a two-quadrant source measure unit with constant voltage or constant current sourcing and sinking capabilities. It also features a high-precision multichannel multimeter and a linear power supply (0.5–5 V). The Otii Arc PRO functions as a power analyzer or profiler, enabling real-time recording and display of currents, voltages, and/or UART logs. It provides current measurements with nanoampere resolution and supports a sampling rate of up to 4 ksps.

3. Results

In this section, we present the results obtained from determining the optimal sampling times using frequency domain analysis (see Section 3.1). Subsequently, we analyze the energy consumption of the MCU board under test for implementing an optimized energy harvesting system aimed at reducing the board’s reliance on battery power (see Section 3.2).

3.1. Determination of the Optimal Sampling Times

To determine the optimal sampling time, it is first necessary to analyze historical data. In our case, we monitored and saved temperature and humidity values, both external and internal, from four different greenhouses located in the same area in Pisa, Italy. The data were collected every 5 min, used as the reference time ($T_{Ref}$), throughout the entire year 2023. The decision to use a reference sampling interval of 5 min is based on the fact that numerous studies in the literature define the sensor sampling interval as 5 min [33]. Moreover, many weather stations have a sampling interval set to a value lower than or equal to our reference interval $T_{Ref}$[8,9,10,11,12,13,14]. Therefore, our approach aims to ensure comparability with existing research by adopting this reference interval. To calculate the optimal sampling time ($T_{Opt}$), we performed frequency domain analysis on a day-by-day basis using the Discrete Fourier Transform (DFT) implemented in MATLAB R2023b [34], as described in Section 2.1. To better understand the error introduced in reconstructing the trend sampled with $T_{Opt}$ compared to $T_{Ref}$, we employed various interpolation methods to reconstruct the missing samples resulting from the less frequent optimal sampling. Several interpolation methods were tested, including linear, polynomial, rational, and spline interpolation. Among these, the linear interpolation method was selected as it produced a reconstructed signal with lower Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE) in our case. The MSE quantifies how much the interpolated signal ($\hat{s}$) deviates from the real signal (s) on average, emphasizing larger errors due to squaring, as in Equation (8).

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(s_i-{\hat{s}}_i)}^2,$$

(8)

where n is the total number of observation and i is the punctual observation.

The RMSE is the square root of the MSE. It provides an interpretable error metric in the same unit as the original data. The Equation is

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(s_i-{\hat{s}}_i)}^2}.$$

(9)

The MAPE evaluates the average percentage error between the real and interpolated signals, offering a normalized measure of accuracy, as depicted in Equation (10).

$$\mathrm{MAPE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{s_i-{\hat{s}}_i}{s_i}}\right|\times 100.$$

(10)

Additionally, the average variation between adjacent samples ($AVA{S}_{Ref}$ and $AVA{S}_{Opt}$ in Equation (11)) is

$$AVAS={\displaystyle \frac{1}{N-1}}\sum _{i=1}^{N-1}|x_{i+1}-x_i|,$$

(11)

where $x_i$ represents the value of the i-th sample and N is the total number of samples; the average error of the daily minimum ($e_{DayMin}$ in Equation (12)) is

$$e_{DayMin}={\displaystyle \frac{1}{D}}\sum _{j=1}^D|min\left({\mathit{x}}_{j,Ref}\right)-min\left({\mathit{x}}_{j,Opt}\right)|,$$

(12)

and the average error of the daily maximum ($e_{DayMax}$ in Equation (13)) is

$$e_{DayMax}={\displaystyle \frac{1}{D}}\sum _{j=1}^D|max\left({\mathit{x}}_{j,Ref}\right)-max\left({\mathit{x}}_{j,Opt}\right)|,$$

(13)

where ${\mathit{x}}_{j,Ref}$ is the set of daily reference samples for day j, ${\mathit{x}}_{j,Opt}$ is the set of optimal daily samples for day j, and D is the total number of days, which were calculated for the entire year as well as across the four seasons: winter (1 January 2023–19 March 2023, and 22 December 2023–31 December 2023), spring (20 March 2023–20 June 2023), summer (21 June 2023–22 September 2023), and autumn (23 September 2023–21 December 2023). This analysis was conducted to assess whether the potential errors introduced are negligible for our purposes.

Table 2. Annual average indices.

	${\mathit{T}}_{\mathit{Opt}}$ [min]	MSE	RMSE	MAPE	${\mathit{AVAS}}_{\mathit{Ref}}$	${\mathit{AVAS}}_{\mathit{Opt}}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
OutTemp	36.17	0.03	0.14	0.71	0.10	0.48	0.09	0.15
OutHum	35.94	0.91	0.87	0.83	0.61	2.06	1.05	0.44
InTemp1	43.44	0.14	0.23	0.46	0.54	1.07	0.04	0.23
InHum1	42.24	0.76	0.55	0.58	1.39	2.63	0.40	0.13
InTemp2	44.19	0.09	0.21	0.53	0.48	1.00	0.04	0.15
InHum2	46.06	1.02	0.64	0.72	1.42	2.85	0.52	0.16
InTemp3	41.75	0.05	0.15	0.32	0.47	0.89	0.03	0.10
InHum3	45.31	0.67	0.57	0.64	1.29	2.56	0.34	0.17
InTemp4	48.42	0.09	0.18	0.44	0.44	0.95	0.03	0.21
InHum4	44.25	1.32	0.79	0.65	1.58	2.65	0.64	0.16

presents all the aforementioned indices computed as annual averages, while

Table 3. Winter average indices.

	${\mathit{T}}_{\mathit{Opt}}$ [min]	MSE	RMSE	MAPE	${\mathit{AVAS}}_{\mathit{Ref}}$	${\mathit{AVAS}}_{\mathit{Opt}}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
OutTemp	30.53	0.02	0.12	1.25	0.10	0.37	0.09	0.11
OutHum	38.27	0.73	0.79	0.77	0.56	1.85	0.76	0.49
InTemp1	42.96	0.21	0.20	0.67	0.47	0.86	0.05	0.25
InHum1	41.57	0.81	0.51	0.45	1.23	2.18	0.47	0.12
InTemp2	37.62	0.05	0.14	0.76	0.35	0.55	0.04	0.18
InHum2	43.35	0.67	0.56	0.38	1.30	2.16	0.51	0.12
InTemp3	41.01	0.03	0.12	0.36	0.36	0.68	0.04	0.10
InHum3	44.77	0.23	0.35	0.39	0.82	1.55	0.28	0.15
InTemp4	41.96	0.14	0.15	0.60	0.51	0.90	0.02	0.24
InHum4	41.98	0.57	0.40	0.33	1.27	2.19	0.39	0.08

,

Table 4. Spring average indices.

	${\mathit{T}}_{\mathit{Opt}}$ [min]	MSE	RMSE	MAPE	${\mathit{AVAS}}_{\mathit{Ref}}$	${\mathit{AVAS}}_{\mathit{Opt}}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
OutTemp	32.59	0.03	0.13	0.62	0.10	0.41	0.06	0.13
OutHum	34.22	0.98	0.89	0.88	0.65	2.06	0.97	0.43
InTemp1	41.96	0.16	0.28	0.47	0.65	1.21	0.02	0.22
InHum1	39.77	0.93	0.54	0.67	1.61	2.87	0.22	0.13
InTemp2	42.80	0.12	0.23	0.49	0.58	1.09	0.04	0.14
InHum2	47.19	1.88	0.84	1.11	1.70	3.45	0.63	0.21
InTemp3	38.51	0.08	0.18	0.35	0.59	1.01	0.05	0.12
InHum3	40.92	0.92	0.66	0.79	1.58	2.88	0.31	0.16
InTemp4	40.71	0.07	0.18	0.32	0.52	0.94	0.02	0.20
InHum4	40.89	2.00	0.96	0.82	1.99	3.00	0.65	0.19

,

Table 5. Summer average indices.

	${\mathit{T}}_{\mathit{Opt}}$ [min]	MSE	RMSE	MAPE	${\mathit{AVAS}}_{\mathit{Ref}}$	${\mathit{AVAS}}_{\mathit{Opt}}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
OutTemp	41.95	0.04	0.17	0.46	0.11	0.59	0.11	0.20
OutHum	35.88	1.12	0.99	0.96	0.67	2.30	1.35	0.40
InTemp1	48.16	0.14	0.29	0.42	0.61	1.34	0.04	0.23
InHum1	41.97	0.81	0.61	0.70	1.52	2.89	0.42	0.14
InTemp2	48.89	0.13	0.27	0.40	0.57	1.33	0.04	0.17
InHum2	45.96	0.89	0.61	0.81	1.47	3.12	0.37	0.21
InTemp3	44.56	0.05	0.16	0.26	0.48	0.99	0.02	0.10
InHum3	48.30	0.86	0.66	0.75	1.42	3.09	0.30	0.20
InTemp4	59.51	0.07	0.22	0.42	0.36	1.06	0.04	0.21
InHum4	47.83	1.56	0.99	0.83	1.62	2.84	0.85	0.20

and

Table 6. Autumn average indices.

	${\mathit{T}}_{\mathit{Opt}}$ [min]	MSE	RMSE	MAPE	${\mathit{AVAS}}_{\mathit{Ref}}$	${\mathit{AVAS}}_{\mathit{Opt}}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
OutTemp	38.82	0.03	0.15	0.48	0.09	0.52	0.10	0.16
OutHum	35.79	0.74	0.80	0.70	0.53	1.97	1.08	0.44
InTemp1	39.27	0.03	0.12	0.23	0.38	0.73	0.03	0.21
InHum1	46.90	0.39	0.50	0.41	1.11	2.43	0.54	0.15
InTemp2	47.02	0.05	0.16	0.33	0.38	0.90	0.02	0.10
InHum2	47.73	0.43	0.50	0.43	1.12	2.44	0.62	0.05
InTemp3	43.92	0.03	0.13	0.29	0.38	0.79	0.02	0.10
InHum3	49.26	0.54	0.61	0.49	1.24	2.50	0.59	0.19
InTemp4	52.53	0.11	0.17	0.47	0.31	0.78	0.03	0.13
InHum4	48.01	0.62	0.63	0.45	1.08	2.28	0.61	0.12

display the seasonal averages for winter, spring, summer, and autumn, respectively, for external temperature (OutTemp), external humidity (OutHum), and internal temperature and humidity (InTemp and InHum) for each greenhouse, from 1 to 4.

In Table 2, Table 3, Table 4, Table 5 and Table 6, it can be observed that the optimal sampling time is significantly longer than the reference time of 5 min, both across seasons and for the parameters monitored inside and outside the greenhouses. In Figure 4, it is also possible to observe the trends in sampling intervals across different seasons.

As expected, less frequent sampling introduces reconstruction errors in the signal, which can be considered negligible. Typically, the primary indicators used in weather stations or environmental parameter trends are the daily minimum and maximum values. Figure 5 shows the minimum (a) and maximum (b) daily error across seasons, as well as the error for external and internal temperature and humidity in the greenhouses, with the latter being averaged across the greenhouses.

The annual and seasonal average errors for internal and external parameters are reported in the tables and figures. It can be seen that the committed error for the daily minimum ranges from 0.0159 °C to 0.1126 °C for temperature and from 0.2243% to 1.3474% for humidity. For the daily maximum, the error ranges from 0.0955 °C to 0.2452 °C for temperature and from 0.0511% to 0.4868% for humidity. It is important to note that in our case, the sensitivity of the sensors used is ±0.3 °C and ±2%. Thus, the errors in detecting the daily minimum and maximum for both temperature and humidity always remain below the sensitivity threshold, making them negligible. With this conclusion, it is possible to adopt the new sampling times ($T_{Opt}$) to optimize the power consumption of the MCU boards.

3.2. Energy Consumption Reduction

To better understand the benefits of determining the optimal sampling time, following the frequency domain analysis, we analyzed the current consumption of the MCU used in our system through the Otii Arc PRO device to compute $ACC$ and $B{C}_{min}$, as described in Section 2.1. Since our MCU transmits messages using LoRa modulation at 868 MHz, we measured the current consumption in three different operational modes: transmission mode, receiver mode, and deep sleep mode.

Figure 6 illustrates the current consumed in transmission mode ($I_{TX}$) as a function of transmission power.

In receiver mode, the current consumption ($I_{RX}$) is 58 mA, while in deep sleep mode ($I_{DS}$), it is 1.75 mA. To calculate $AC{C}_{Opt}$, it is necessary to understand the time required by the MCU to send a typical LoRa message ($T_{TX}$).

Table 7. LoRa message transmission time in seconds.

	$\mathit{SF}7$	$\mathit{SF}8$	$\mathit{SF}9$	$\mathit{SF}10$	$\mathit{SF}11$	$\mathit{SF}12$
$t_{125}$	0.429	0.686	1.170	2.257	4.714	8.286
$t_{250}$	0.221	0.354	0.603	1.163	2.430	4.271
$t_{500}$	0.101	0.161	0.275	0.530	1.107	1.945

displays the time required to transmit a 200 bytes LoRa message assumed to be the typical size for IoT sensor messages at different bandwidths of 125, 250, and 500 kHz ($t_{125}$, $t_{250}$, and $t_{500}$, respectively). The transmission times are also shown relative to the LoRa spreading factors ($SF7$ to $SF12$) that can be employed.

As an illustrative example and to demonstrate that the current consumption can be modeled as constant across different MCU operational modes, Figure 7 shows the current consumption over time when the MCU is in transmission mode and deep sleep mode during two distinct periods.

To calculate $AC{C}_{Opt}$ using $T_{Opt}$, $B{C}_{min-Opt}$ (as described in Section 2.1), and $I_{SP-Opt}$ (as detailed in Section 2.2), we considered the worst-case scenario, where the MCU operates in transmission mode at 15 dBm, with a bandwidth of 125 kHz and SF12. Using the annual average values of $T_{Opt}$ presented in Table 2,

Table 8. Percentual energy reduction.

	${\mathit{ACC}}_{\mathit{Opt}}$	${\mathit{BC}}_{\mathit{min}-\mathit{Opt}}$	${\mathit{I}}_{\mathit{SP}-\mathit{Opt}}$	$\mathit{PER}$
	$\left[\mathbf{mA}\right]$	$\left[\mathbf{mAh}\right]$	$\left[\mathbf{mA}\right]$	$[\%]$
OutTemp	2.3709	14.2256	3.1613	61.3714
OutHum	2.3749	14.2492	3.1665	61.3072
InTemp1	2.2674	13.6041	3.0231	63.059
InHum1	2.2819	13.6917	3.0426	62.8212
InTemp2	2.2586	13.5513	3.0114	63.2025
InHum2	2.238	13.4282	2.984	63.5367
InTemp3	2.2882	13.7293	3.051	62.7191
InHum3	2.246	13.4763	2.9947	63.4062
InTemp4	2.2143	13.2859	2.9524	63.923
InHum4	2.2579	13.5476	3.0106	63.2126

provides the average current consumption, minimum battery capacity, current provided by the solar panel, and the percentual energy reduction ($PER$).

The $PER$ is defined as the percentage reduction in current consumption when using $T_{Opt}$ as the sampling time compared to $T_{Ref}$. It is important to note that the reference sampling time ($T_{Ref}$) is 5 min, from which $AC{C}_{Ref}$, $B{C}_{min-Ref}$, and $I_{SP-Ref}$ are derived. These values are 6.1378 mA, 36.8266 mAh, and 8.1837 mA, respectively, considering $h_{night}$ as six hours.

As shown in Table 8, when using $T_{Opt}$ instead of $T_{Ref}$, the PER ranges from 61.3072% to 63.923%, indicating a significant reduction in current consumption. Considering the worst-case scenario to determine the current that the solar panel must supply to the MCU ($I_{SP-Opt}$) as 3.1665 mA, it is possible to calculate the amount of ELF required in the greenhouse backward, as described in Section 2.2, to ensure that the solar panel provides a sufficient current value to make the MCU’s operation independent of the battery.

In this scenario, we consider a solar panel, described in Section 2.3, with an efficiency ($\eta$) of 0.12 and dimensions of 9.775 $\times {10}^{-3}$ m², which must supply 3.7 V to the MCU. Using the theoretical formula from Section 2.2, the required ELF was calculated to be 6842 lux to keep the system active. Typically, in greenhouses, as shown in one of our previous studies [25], the ELF was approximately 50,000 lux, which is significantly higher than the calculated minimum ELF. Based on this observation, we can conclude that the solar panel considered, when installed in the described environment, is capable of supplying a current greater than the minimum required, adequately powering the MCU board daily.

3.3. Considerations

In the previously described results, we demonstrate how an optimal sampling time can reduce the energy consumption of individual sensors installed in the greenhouse. To further reduce the energy consumption of individual sensors, machine learning or predictive algorithms can be employed to optimize the sampling frequency in real-world scenarios. By predicting future time windows, the deep sleep mode of the sensor’s MCU can be extended. Although this approach is feasible, it introduces a limitation: the methodology would no longer be immediately applicable to different scenarios, climates, and crop types. This is because the neural network model requires training and must learn the temporal patterns of the parameter within a specific environment, which typically varies from one greenhouse to another.

For the calculation of the current consumption and the design of the energy harvesting system, we considered the annually averaged $T_{Opt}$ derived from the mean of the seasonal $T_{Opt}$ values. Overall, the annual current consumption remains unchanged when considering the four seasonal $T_{Opt}$ values separately.

Table 9. Outdoor air temperature: annual vs. seasonal sampling times.

$\mathit{OutTemp}$	$\mathit{MSE}$	$\mathit{RMSE}$	$\mathit{MAPE}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
$T_{Opt}$ Annual	0.02870	0.14280	0.70890	0.08920	0.14970
$T_{Opt}$ Seasonal	0.02845	0.14170	0.70318	0.08912	0.14785
Percentual Reduction	0.87108	0.77031	0.80759	0.08969	1.23580

,

Table 10. Outdoor air humidity: annual vs. seasonal sampling times.

$\mathit{OutHum}$	$\mathit{MSE}$	$\mathit{RMSE}$	$\mathit{MAPE}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
$T_{Opt}$ Annual	0.90670	0.87440	0.83390	1.05230	0.43600
$T_{Opt}$ Seasonal	0.89165	0.86723	0.82558	1.03833	0.43580
Percentual Reduction	1.65987	0.82056	0.99832	1.32804	0.04587

,

Table 11. Indoor air temperature: annual vs. seasonal sampling times.

$\mathit{InTemp}$	$\mathit{MSE}$	$\mathit{RMSE}$	$\mathit{MAPE}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
$T_{Opt}$ Annual	0.09418	0.19328	0.43670	0.03375	0.17118
$T_{Opt}$ Seasonal	0.09191	0.18726	0.42751	0.03314	0.16770
Percentual Reduction	2.40908	3.11085	2.10385	1.79630	2.03009

and

Table 12. Indoor air humidity: annual vs. seasonal sampling times.

$\mathit{InHum}$	$\mathit{MSE}$	$\mathit{RMSE}$	$\mathit{MAPE}$	${\mathit{e}}_{\mathit{DayMin}}$	${\mathit{e}}_{\mathit{DayMax}}$
$T_{Opt}$ Annual	0.94530	0.63698	0.64580	0.47533	0.15600
$T_{Opt}$ Seasonal	0.88167	0.62096	0.61270	0.47511	0.15158
Percentual Reduction	6.73133	2.51383	5.12543	0.04481	2.83654

illustrate how the reconstruction of parameter trends and the identification of daily minima and maxima vary for the four parameters under consideration: outdoor air temperature, outdoor air humidity, greenhouse air temperature, and greenhouse air humidity. The latter two parameters are averaged across the four greenhouses under study.

From the resulting values, it is evident that adopting a dynamic sampling time that varies with the seasons reduces the error in identifying the daily minimum and maximum of each parameter. It can be observed that, although the total energy consumption over a year remains unchanged, dynamically adjusting the sampling time reduces the error in signal reconstruction and in the identification of daily minimum and maximum values. Specifically, for an external temperature, the reduction is 0.08969% in identifying the minimum and 1.2358% in identifying the maximum. A similar reduction is observed for the other parameters: external humidity of 1.32804% and 0.04587%, internal greenhouse temperature of 1.7963% and 2.03009%, and internal greenhouse humidity of 0.04481% and 2.83654%.

4. Conclusions

In conclusion, this work aims to address two major challenges associated with the implementation of smart greenhouses—excessive energy consumption and the high frequency of human intervention—particularly for recharging or replacing batteries in devices installed both inside and outside the system. Specifically, this study employed a frequency domain approach to determine the optimal sampling time for commonly monitored parameters, such as indoor and outdoor air temperature and humidity, in the context of greenhouses. Sampling intervals commonly used in these systems and weather stations range between 5 and 15 min. However, as demonstrated in this study, these intervals are inefficient and energy-intensive. We propose adapting the sampling time based on the parameter being measured (e.g., temperature sampling time: 41.75–48.42 min; humidity sampling time: 42.24–46.06 min) and potentially adjusting it dynamically according to seasonal changes. This approach reconstructs temporal trends with lower errors in terms of the MSE, RMSE, and MAPE. Additionally, by optimizing the sampling time and thereby reducing the energy consumption of individual sensors, and with the aid of greenhouse lamps providing a consistent light flux, an energy harvesting system was designed and tested using a solar panel. This system enables the use of sensors with smaller battery capacities, making their operation independent of battery life. Consequently, human intervention for battery replacement and recharging is significantly reduced, and the greenhouse’s energy efficiency is enhanced by reusing the light flux from lamps or external sources.