Assessing Whole-Body Vibrations in an Agricultural Tractor Based on Selected Operational Parameters: A Machine Learning-Based Approach
Abstract
1. Introduction
1.1. Whole-Body Vibrations (WBVs) in Agricultural Tractors: Health Risks and Regulatory Context
1.2. Limitations of Existing Research on WBV and Operational Parameters
1.3. The Untapped Potential of Operational Parameters in WBV Analysis
1.4. Advancing WBV Prediction Through Machine Learning
2. Materials and Methods
2.1. Exploitation Research
2.2. Machine Learning Prediction of Whole-Body Vibrations
2.2.1. Dataset Analysis
2.2.2. Dataset Preprocessing
- The agrotechnical surface in the original dataset was encoded as numbers from 1 to 6 (1 being smooth track, 2 being rough track, etc.). This numerical representation was converted into one-hot encoded vectors using the one-hot encoder provided by scikit-learn [36]. This was necessary so that the machine learning models would not mistakenly think that there was some numerical relationship between the values of the agrotechnical surface feature.
- The air pressure in the tires was mapped to its actual value (i.e., 1 was mapped to 1.9 bar, 2 was mapped to 2.4 bar, etc.).
- The dataset was divided into two separate subsets—a training and validation subset and a testing subset. The dataset contains 6 data samples related to a single measurement. In other words, 6 data samples with the same input feature values and the same (or slightly different) target variable values are used. In order to prevent data leakage (i.e., 4 out of 6 data samples related to the same measurement are in the training and validation subset, while 2 out of 6 data samples are in the testing subset), all samples from a single measurement were completely in the training and validation subset or the testing subset. A stratified split on the agrotechnical surface feature was also performed, which means that an attempt was made to ensure that the same distribution of the agrotechnical surface feature was present in both the training and validation subset and the testing subset. We used 80% of our total data for training and validation, and we used 20% of our total data for testing the model.
2.2.3. Hyperparameter Tuning, Training, and Evaluation
2.2.4. Feature Importance Analysis
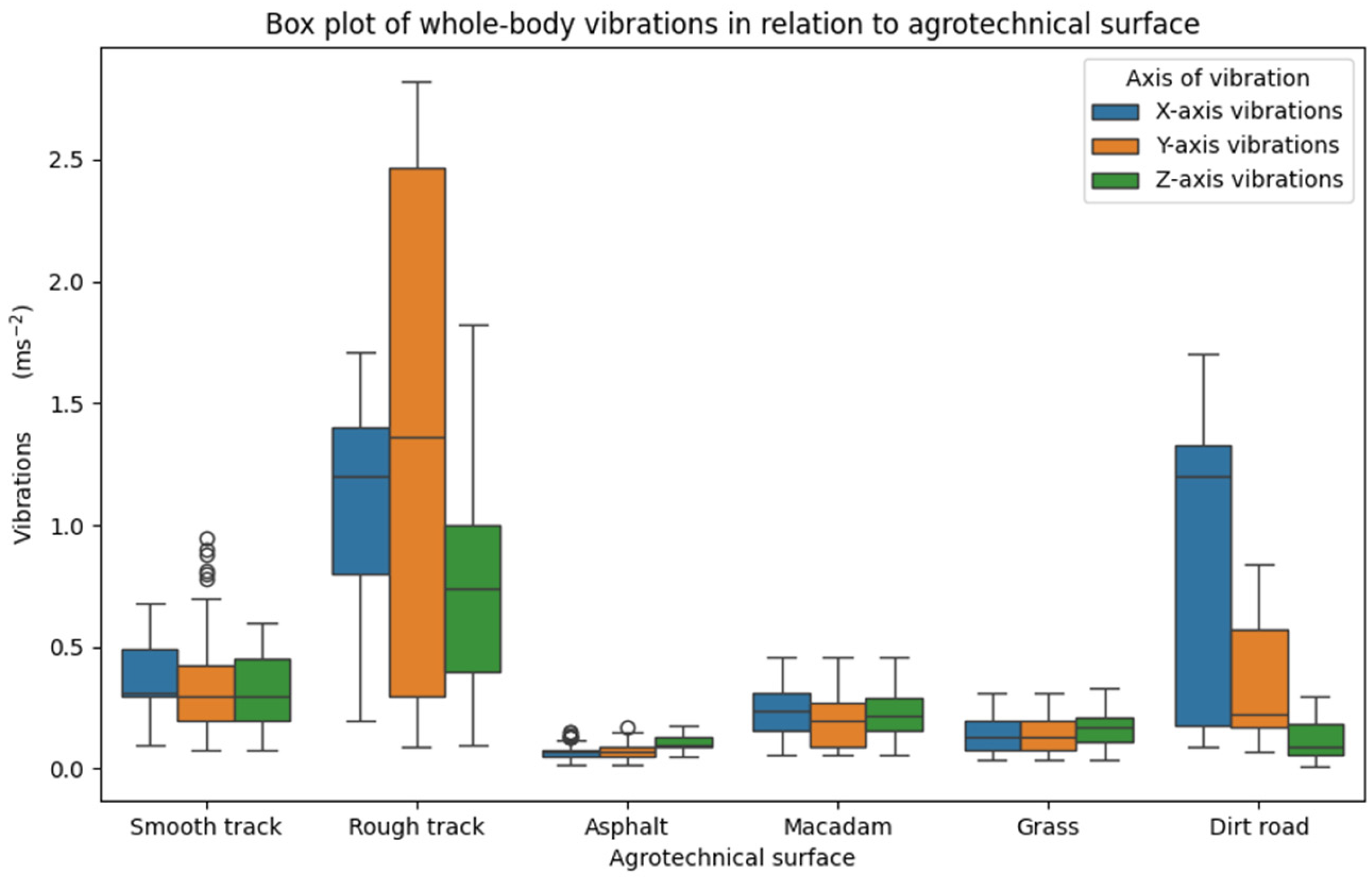
3. Results and Discussion
4. Conclusions
- Whole-body vibrations were most prominent on the rough track;
- In almost all instances, the machine learning models were better than the baseline (linear regression);
- For the x-axis and the y-axis, the model of choice would be the gradient boosting regressor, while for the z-axis, the model of choice would be the SVM regressor (which beat gradient boosting slightly);
- The most important input features for predicting whole-body vibrations across all three axes are, in order, agrotechnical surface, the speed of movement, and air pressure in the tires.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bovenzi, M.; Hulshof, C.T. An Updated Review of Epidemiologic Studies on the Relationship between Exposure to Whole-Body Vibration and Low Back Pain (1986–1997). Int. Arch. Occup. Env. Health 1999, 72, 351–365. [Google Scholar] [CrossRef] [PubMed]
- Griffin, M.J. (Ed.) 14—Vascular Disorders Associated with Hand-Transmitted Vibration. In Handbook of Human Vibration; Academic Press: London, UK, 1990; pp. 553–593. ISBN 978-0-12-303040-5. [Google Scholar]
- de la Hoz-Torres, M.L.; Aguilar, A.J.; Martínez-Aires, M.D.; Ruiz, D.P. A Methodology for Assessment of Long-Term Exposure to Whole-Body Vibrations in Vehicle Drivers to Propose Preventive Safety Measures. J. Saf. Res. 2021, 78, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Wikström, B.-O.; Kjellberg, A.; Landström, U. Health Effects of Long-Term Occupational Exposure to Whole-Body Vibration: A Review. Int. J. Ind. Ergon. 1994, 14, 273–292. [Google Scholar] [CrossRef]
- Krajnak, K. Health Effects Associated with Occupational Exposure to Hand-Arm or Whole Body Vibration. J. Toxicol. Env. Health B Crit. Rev. 2018, 21, 320–334. [Google Scholar] [CrossRef]
- Bovenzi, M. A Longitudinal Study of Low Back Pain and Daily Vibration Exposure in Professional Drivers. Ind. Health 2010, 48, 584–595. [Google Scholar] [CrossRef]
- Blood, R.P.; Yost, M.G.; Camp, J.E.; Ching, R.P. Whole-Body Vibration Exposure Intervention among Professional Bus and Truck Drivers: A Laboratory Evaluation of Seat-Suspension Designs. J. Occup. Env. Hyg. 2015, 12, 351–362. [Google Scholar] [CrossRef]
- Directive—2002/44—EN—EUR-Lex. Available online: https://eur-lex.europa.eu/eli/dir/2002/44/oj/eng (accessed on 24 February 2025).
- Singh, A.; Samuel, S.; Singh, H.; Kumar, Y.; Prakash, C. Evaluation and Analysis of Whole-Body Vibration Exposure during Soil Tillage Operation. Safety 2021, 7, 61. [Google Scholar] [CrossRef]
- Cazani, A.C.; Miyajima, R.H.; Simões, D.; dos Santos, J.E.G. Operator Exposure to Whole-Body Vibration in Timber Extraction with Grapple Skidder. J. Vib. Eng. Technol. 2021, 9, 177–182. [Google Scholar] [CrossRef]
- Scarlett, A.J.; Price, J.S.; Stayner, R.M. Whole-Body Vibration: Evaluation of Emission and Exposure Levels Arising from Agricultural Tractors. J. Terramech. 2007, 44, 65–73. [Google Scholar] [CrossRef]
- Barač, Ž.; Radočaj, D.; Plaščak, I.; Jurišić, M.; Marković, M. Prediction of Noise Levels According to Some Exploitation Parameters of an Agricultural Tractor: A Machine Learning Approach. AgriEngineering 2024, 6, 995–1007. [Google Scholar] [CrossRef]
- de la Hoz-Torres, M.L.; Aguilar, A.J.; Ruiz, D.P.; Martínez-Aires, M.D. Whole Body Vibration Exposure Transmitted to Drivers of Heavy Equipment Vehicles: A Comparative Case According to the Short- and Long-Term Exposure Assessment Methodologies Defined in ISO 2631-1 and ISO 2631-5. Int. J. Environ. Res. Public Health 2022, 19, 5206. [Google Scholar] [CrossRef]
- Du, X.; Sun, C.; Zheng, Y.; Feng, X.; Li, N. Evaluation of Vehicle Vibration Comfort Using Deep Learning. Measurement 2021, 173, 108634. [Google Scholar] [CrossRef]
- Al-Mafrachi, A.A.H. Measuring Vibration at Tractor Platform, Steering Wheel and Seat Effective Amplitude Transmissibility Factor During Operation Tillage. Iraqi J. Agric. Sci. 2016, 47, 365–378. [Google Scholar] [CrossRef][Green Version]
- Hoz-Torres, M.L.; López-Alonso, M.; Ruíz, D.P.; Martínez-Aires, M.D. Analysis of Whole-Body Vibrations Transmitted by Earth Moving Machinery. In Proceedings of the Occupational Safety and Hygiene V, Guimarães, Portugal, 10 April 2017; pp. 453–456. [Google Scholar]
- Singh, A.; Samuel, S.; Singh, H.; Singh, J.; Prakash, C.; Dhabi, Y.K. Whole Body Vibration Exposure among the Tractor Operator during Soil Tillage Operation: An Evaluation Using ISO 2631-5 Standard. Shock Vib. 2022, 2022, 6412120. [Google Scholar] [CrossRef]
- Anifantis, A.S.; Cutini, M.; Bietresato, M. An Experimental–Numerical Approach for Modelling the Mechanical Behaviour of a Pneumatic Tyre for Agricultural Machines. Appl. Sci. 2020, 10, 3481. [Google Scholar] [CrossRef]
- Halmai, B.; Holsgrove, T.P.; Vine, S.J.; Harris, D.J.; Williams, G.K.R. The After-Effects of Occupational Whole-Body Vibration on Human Cognitive, Visual, and Motor Function: A Systematic Review. Appl. Ergon. 2024, 118, 104264. [Google Scholar] [CrossRef]
- Deboli, R.; Calvo, A.; Preti, C. Whole-Body Vibration: Measurement of Horizontal and Vertical Transmissibility of an Agricultural Tractor Seat. Int. J. Ind. Ergon. 2017, 58, 69–78. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine Learning: Trends, Perspectives, and Prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Son, H.; Lim, J.W.; Park, S.; Park, B.; Han, J.; Kim, H.B.; Lee, M.C.; Jang, K.-J.; Kim, G.; Chung, J.H. A Machine Learning Approach for the Classification of Falls and Activities of Daily Living in Agricultural Workers. IEEE Access 2022, 10, 77418–77431. [Google Scholar] [CrossRef]
- Nath, N.D.; Chaspari, T.; Behzadan, A.H. Automated Ergonomic Risk Monitoring Using Body-Mounted Sensors and Machine Learning. Adv. Eng. Inform. 2018, 38, 514–526. [Google Scholar] [CrossRef]
- Aguilar, A.J.; de la Hoz-Torres, M.L.; Martínez-Aires, M.D.; Ruiz, D.P.; Arezes, P.; Costa, N. Artificial Neural Network-Based Model for Assessing the Whole-Body Vibration of Vehicle Drivers. Buildings 2024, 14, 1713. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep Learning in Agriculture: A Survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Machine Learning in Agriculture: A Review. Available online: https://www.mdpi.com/1424-8220/18/8/2674 (accessed on 25 February 2025).
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- HRN4You Mechanical Vibration and Shock—Assessment of Human Exposure to Whole-Body Vibration—Part 1: General Requirements (HRN ISO 2631-1:1997). Available online: https://repozitorij.hzn.hr/norm/HRN+ISO+2631-1%3A1999 (accessed on 30 January 2025).
- HRN4You Agricultural Wheeled Tractors and Field Machinery—Measurement of Whole-Body Vibration of the Operator (ISO 5008:2002+Cor 1:2005). Available online: https://repozitorij.hzn.hr/norm/HRN+ISO+5008%3A2015 (accessed on 25 June 2024).
- What Is Power Steering and How Does Tractor Power Steering Work? Available online: https://www.tractorjunction.com/blog/what-is-power-steering/ (accessed on 13 February 2025).
- TractorData.Com Landini Powerfarm 100 Tractor Information. Available online: https://www.tractordata.com/farm-tractors/008/6/2/8627-landini-powerfarm-100.html (accessed on 13 February 2025).
- HRN4You Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 4: Guidelines for the Evaluation of the Effects of Vibration and Rotational Motion on Passenger and Crew Comfort in Fixed-Guideway Transport Systems (HRN ISO 2631-4:2001/Amd 1:2010). Available online: https://repozitorij.hzn.hr/norm/HRN+ISO+2631-4%3A2010%2FA1%3A2018 (accessed on 30 January 2025).
- Metra Meß- und Frequenztechnik Home Page. Available online: https://www.mmf.de/wp-content/uploads/2023/08/vm30-wmane.pdf (accessed on 30 January 2025).
- OneHotEncoder. Available online: https://scikit-learn/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html (accessed on 30 January 2025).
- Linear Regression in Machine Learning. Available online: https://www.geeksforgeeks.org/ml-linear-regression/ (accessed on 30 January 2025).
- Gradient Boosting Trees, vs. Random Forests|Baeldung on Computer Science. Available online: https://www.baeldung.com/cs/gradient-boosting-trees-vs-random-forests (accessed on 30 January 2025).
- GradientBoostingRegressor. Available online: https://scikit-learn/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html (accessed on 30 January 2025).
- SVR. Available online: https://scikit-learn/stable/modules/generated/sklearn.svm.SVR.html (accessed on 30 January 2025).
- MLPRegressor. Available online: https://scikit-learn/stable/modules/generated/sklearn.neural_network.MLPRegressor.html (accessed on 30 January 2025).
- GridSearchCV. Available online: https://scikit-learn/stable/modules/generated/sklearn.model_selection.GridSearchCV.html (accessed on 30 January 2025).
- Permutation_Importance. Available online: https://scikit-learn/stable/modules/generated/sklearn.inspection.permutation_importance.html (accessed on 30 January 2025).
- Zeng, X.; Kociolek, A.M.; Khan, M.I.; Milosavljevic, S.; Bath, B.; Trask, C.M. Predicting Whole-Body Vibration Exposure in Canadian Prairie Farmers. Ann. Work. Expo. Health 2017, 61, 554–565. [Google Scholar] [CrossRef]
- Tian, H.; Ji, A. Real-Time Adaptive Tractor Ride Comfort Adjustment System Based on Machine Learning Method. IEEE Access 2025, 13, 3274–3283. [Google Scholar] [CrossRef]
- Ali, D.; Frimpong, S. DeepImpact: A Deep Learning Model for Whole Body Vibration Control Using Impact Force Monitoring. Neural Comput. Applic. 2021, 33, 3521–3544. [Google Scholar] [CrossRef]
- Waleed, M.; Um, T.-W.; Kamal, T.; Usman, S.M. Classification of Agriculture Farm Machinery Using Machine Learning and Internet of Things. Symmetry 2021, 13, 403. [Google Scholar] [CrossRef]
- Ramar, K.; Kumaraswamidhas, L.A.; Balaji, P.S.; Agasthian, A. Whole Body Vibration Impact Assessment on Dumper Operator Using Computational Learning Technique. Int. J. Precis. Eng. Manuf. 2023, 24, 219–238. [Google Scholar] [CrossRef]
- Hota, S.; Tewari, V.K.; Chandel, A.K. Workload Assessment of Tractor Operations with Ergonomic Transducers and Machine Learning Techniques. Sensors 2023, 23, 1408. [Google Scholar] [CrossRef] [PubMed]





| Specifications | Units |
|---|---|
| Maximum engine power | 68/92.5 (kW/hp) |
| Maximum torque | 363 (Nm) |
| Number of cylinders/displacement | 4/4400 (Num./cm3) |
| Gearbox speeds | 12 forward + 12 backward |
| Lifting capacity | 260 (kg) |
| Tank volume | 102 (l) |
| Weight (without weights and cabin) | 3330 (kg) |
| Cabin weight | 150 (kg) |
| Tires | 18.4-R30 |
| Tractor length | 4136 mm |
| Tractor width | 2063 mm |
| Distance between tractor axles | 2341 mm |
| Height with tractor cab | 2550 mm |
| Tractor clearance | 453 mm |
| Parameter | Details |
|---|---|
| Measurement range of sensor (1 mV/ms−2) | Whole-body vibration = 0.10–12.00/1.0–120.0/10–1200/1000/6000 ms−2peak; acceleration = 0.10–12.00/1.0–120.0/10–1200/1000/6000 ms−2peak; speed = 0.001–0.120/0.010–1200/0.10–0.12/1.00/60.00 ms−1peak; shift = 0.001–0.120/0.010–1200/0.10–0.12/1.00/60.00 mmpeak. |
| Accuracy specifications | Linearity deviation: ±3% and ±2 digits; measurement discrepancies remain below 5% across all operational ranges. |
| Display parameters | Real-time RMS (1-s interval); maximum transient vibration value (MTVV); interval RMS (up to 10 h); estimated vibration dose value (eVDV); total vibration exposure (Ahv); peak instantaneous value (1-s sampling); crest factor and maximum peak detection |
| Frequency weighting filters | ISO-compliant filters: Wb, Wc, Wd, We, Wg, Wh, Wj, Wk, and Wm |
| Interface and hardware | Display: graphical LCD (32 × 120 pixels) with LED illumination, showing triaxial values, units, and operational status; sensor interface: triaxial IEPE-compatible inputs via Binder 711 series connector (4-pin female); IEPE power: 3 regulated current sources (2 A per channel, 20 V total supply) |
| Compatible transducers | Primary sensor: KB103SV-100 (calibrated for whole-body vibrational analysis, 1 mV/ms−2 sensitivity) |
| Data storage | Integrated flash storage: 1000–3000 datasets (capacity varies by recording mode) |
| Recording modes | Manual capture: triggered via dedicated button; automated logging: programmable intervals (1 s to 10 h) |
| Environmental tolerance | Operational temperature: −20 °C to +40 °C |
| Physical dimensions | Device size: 165 mm × 92 mm × 31 mm (compact form factor) |
| Machine Learning Model | Hyperparameter Search Space |
|---|---|
| Gradient boosting regressor | n_estimators: [50, 100, 150] learning_rate: [0.01, 0.1, 0.2] max_depth: [3, 5, 7] |
| SVM regressor | C: [0.1, 1, 10] epsilon: [0.01, 0.1, 0.2] kernel: [“linear”, “rbf”, “poly”] |
| Multi-layer perceptron regressor | hidden_layer_sizers: [(50,), (100,), (50, 50)] activation: [“relu”, “tanh”] alpha: [0.0001, 0.001, 0.01] |
| Machine Learning Model | Axis | Best Hyperparameters |
|---|---|---|
| Gradient boosting regressor | x | learning_rate: 0.2 max_depth: 3 n_estimators: 50 |
| y | learning_rate: 0.2 max_depth: 3 n_estimators: 50 | |
| z | learning_rate: 0.1 max_depth: 3 n_estimators: 150 | |
| SVM regressor | x | C: 1 epsilon: 0.01 kernel: “poly” |
| y | C: 0.1 epsilon: 0.01 kernel: “poly” | |
| z | C: 1 epsilon: 0.01 kernel: “poly” | |
| Multi-layer perceptron regressor | x | activation: “tanh” alpha: 0.001 hidden_layer_sizes: (50, 50) |
| y | activation: “relu” alpha: 0.0001 hidden_layer_sizes: (50, 50) | |
| z | activation: “relu” alpha: 0.01 hidden_layer_sizes: (100, ) |
| Axis | Mean | SEM | SD | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|---|
| x-axis | 0.48 | 0.02 | 0.51 | 0.02 | 0.11 | 0.24 | 0.71 | 1.71 |
| y-axis | 0.42 | 0.02 | 0.62 | 0.02 | 0.09 | 0.2 | 0.37 | 2.82 |
| z-axis | 0.28 | 0.01 | 0.31 | 0.01 | 0.1 | 0.18 | 0.3 | 1.82 |
| Model | Data Subset | RMSE (ms−2) | NRMSE | MAE (ms−2) | |
|---|---|---|---|---|---|
| Linear regression | Training and validation | 0.64 | 0.31 | 0.18 | 0.2 |
| Test | 0.83 | 0.21 | 0.13 | 0.14 | |
| SVM regressor | Training and validation | 0.83 | 0.21 | 0.12 | 0.11 |
| Test | 0.77 | 0.25 | 0.15 | 0.15 | |
| Gradient boosting regressor | Training and validation | 0.99 | 0.06 | 0.03 | 0.04 |
| Test | 0.98 | 0.08 | 0.05 | 0.05 | |
| MLP | Training and validation | 0.95 | 0.12 | 0.07 | 0.08 |
| Test | 0.94 | 0.12 | 0.08 | 0.08 |
| Model | Data Subset | RMSE (ms−2) | NRMSE | MAE (ms−2) | |
|---|---|---|---|---|---|
| Linear regression | Training and validation | 0.64 | 0.38 | 0.14 | 0.27 |
| Test | 0.76 | 0.29 | 0.11 | 0.21 | |
| SVM regressor | Training and validation | 0.93 | 0.17 | 0.06 | 0.1 |
| Test | 0.96 | 0.12 | 0.04 | 0.07 | |
| Gradient boosting regressor | Training and validation | 0.99 | 0.07 | 0.03 | 0.05 |
| Test | 0.98 | 0.09 | 0.03 | 0.05 | |
| MLP | Training and validation | 0.98 | 0.1 | 0.04 | 0.07 |
| Test | 0.97 | 0.1 | 0.04 | 0.08 |
| Model | Data Subset | RMSE (ms−2) | NRMSE | MAE (ms−2) | |
|---|---|---|---|---|---|
| Linear regression | Training and validation | 0.68 | 0.18 | 0.10 | 0.12 |
| Test | 0.73 | 0.16 | 0.11 | 0.11 | |
| SVM regressor | Training and validation | 0.95 | 0.07 | 0.04 | 0.05 |
| Test | 0.95 | 0.07 | 0.05 | 0.05 | |
| Gradient boosting regressor | Training and validation | 0.98 | 0.04 | 0.02 | 0.03 |
| Test | 0.94 | 0.08 | 0.05 | 0.05 | |
| MLP | Training and validation | 0.94 | 0.08 | 0.04 | 0.05 |
| Test | 0.92 | 0.09 | 0.06 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barač, Ž.; Jurić, M.; Plaščak, I.; Jurić, T.; Marković, M. Assessing Whole-Body Vibrations in an Agricultural Tractor Based on Selected Operational Parameters: A Machine Learning-Based Approach. AgriEngineering 2025, 7, 72. https://doi.org/10.3390/agriengineering7030072
Barač Ž, Jurić M, Plaščak I, Jurić T, Marković M. Assessing Whole-Body Vibrations in an Agricultural Tractor Based on Selected Operational Parameters: A Machine Learning-Based Approach. AgriEngineering. 2025; 7(3):72. https://doi.org/10.3390/agriengineering7030072
Chicago/Turabian StyleBarač, Željko, Mislav Jurić, Ivan Plaščak, Tomislav Jurić, and Monika Marković. 2025. "Assessing Whole-Body Vibrations in an Agricultural Tractor Based on Selected Operational Parameters: A Machine Learning-Based Approach" AgriEngineering 7, no. 3: 72. https://doi.org/10.3390/agriengineering7030072
APA StyleBarač, Ž., Jurić, M., Plaščak, I., Jurić, T., & Marković, M. (2025). Assessing Whole-Body Vibrations in an Agricultural Tractor Based on Selected Operational Parameters: A Machine Learning-Based Approach. AgriEngineering, 7(3), 72. https://doi.org/10.3390/agriengineering7030072









