Control of Magnetic-Navigation Pigeon Farm-Cleaning Robot Based on Fuzzy PID and Kalman Filter
Abstract
1. Introduction
2. Working Principle and Control System Design
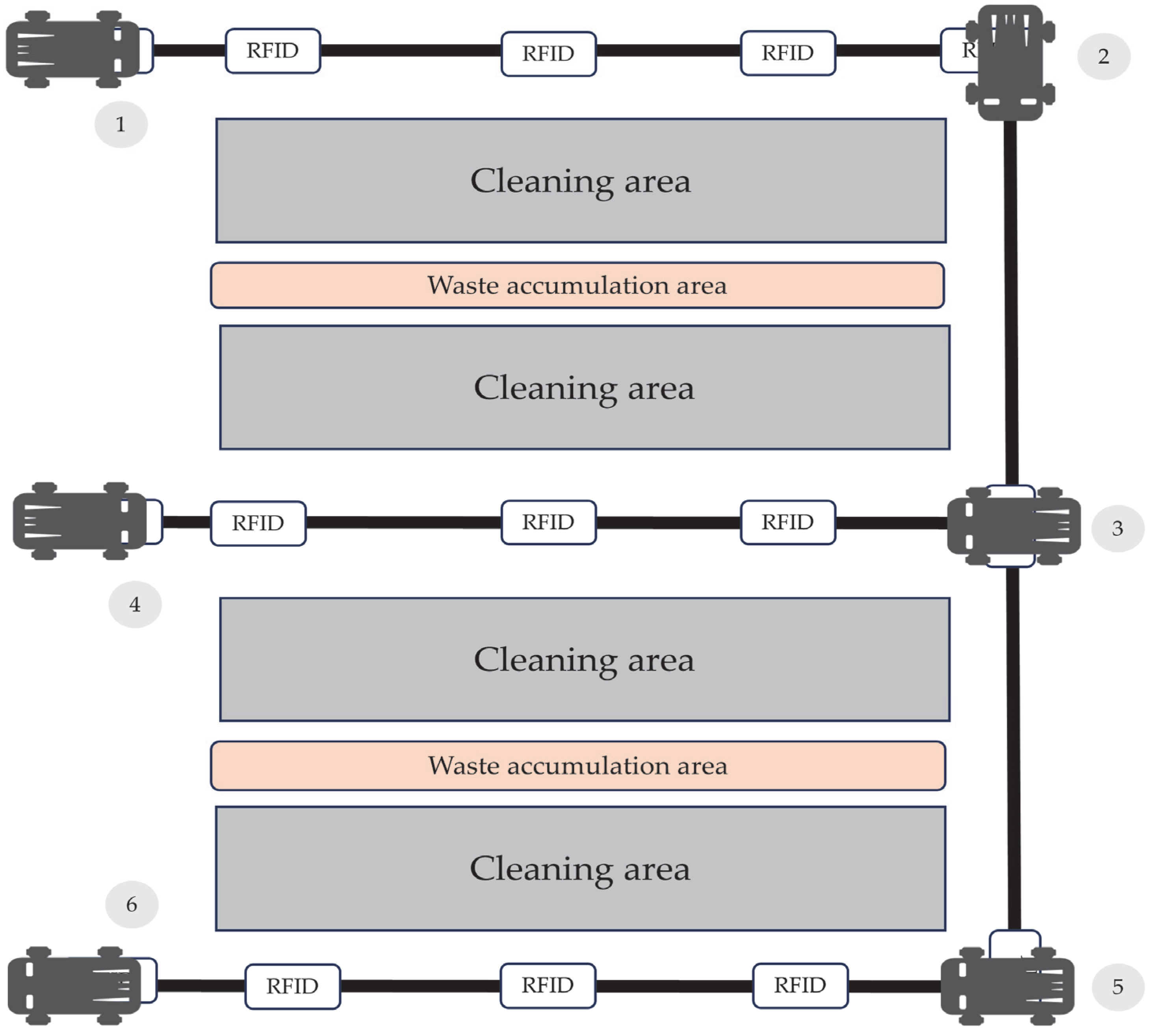
2.1. Introduction to the Work Environment
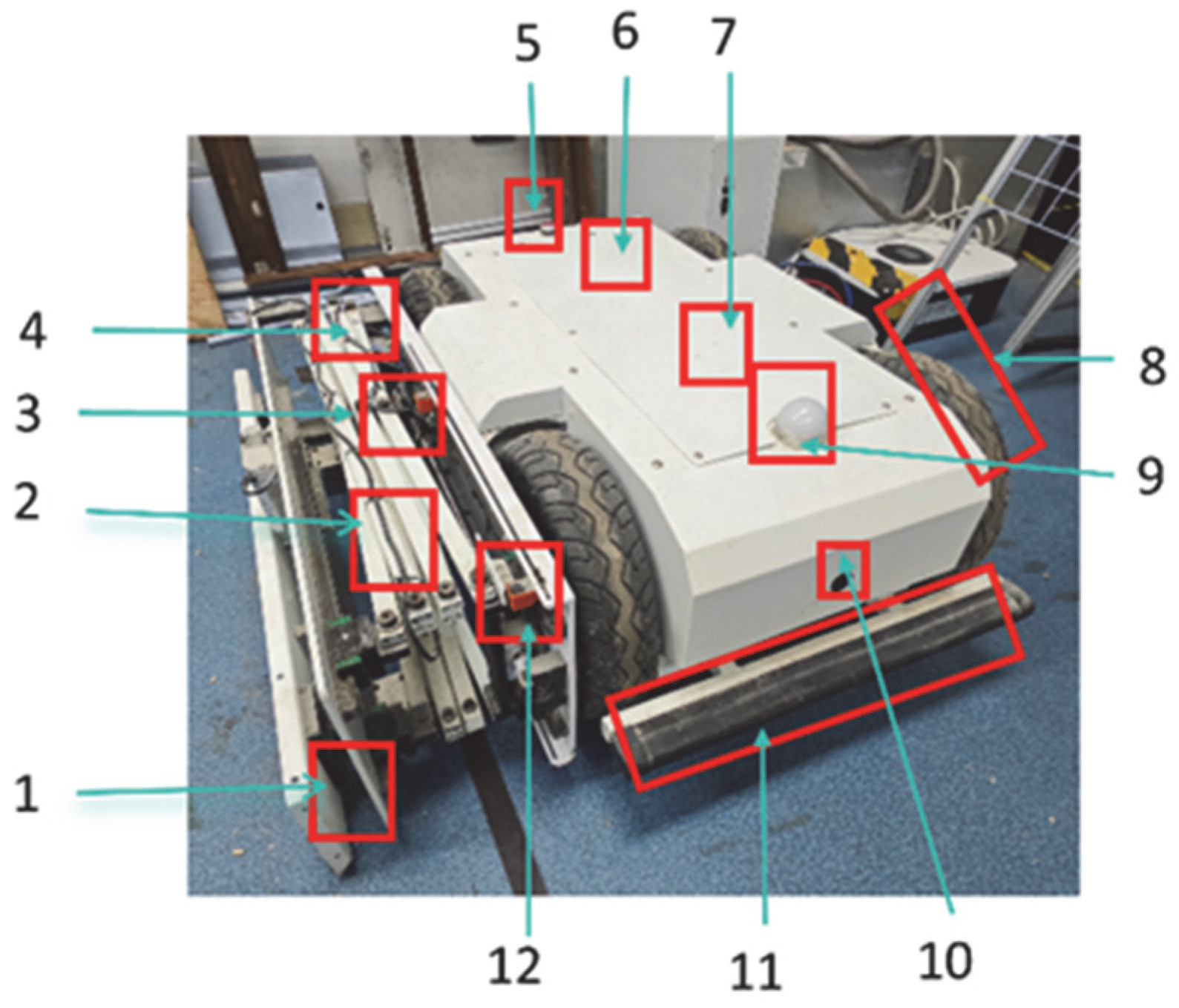
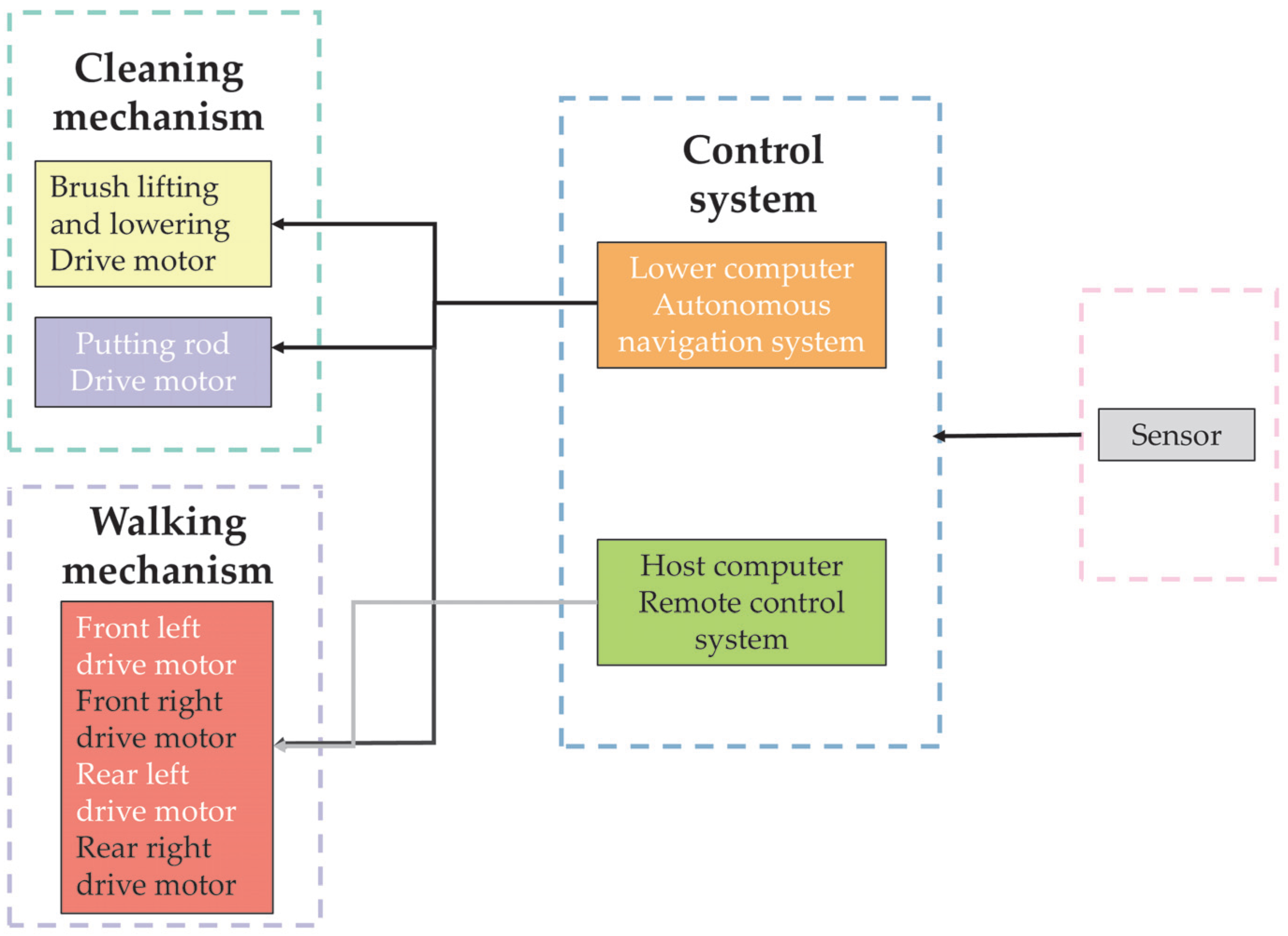
2.2. Overall Structure of the Robot
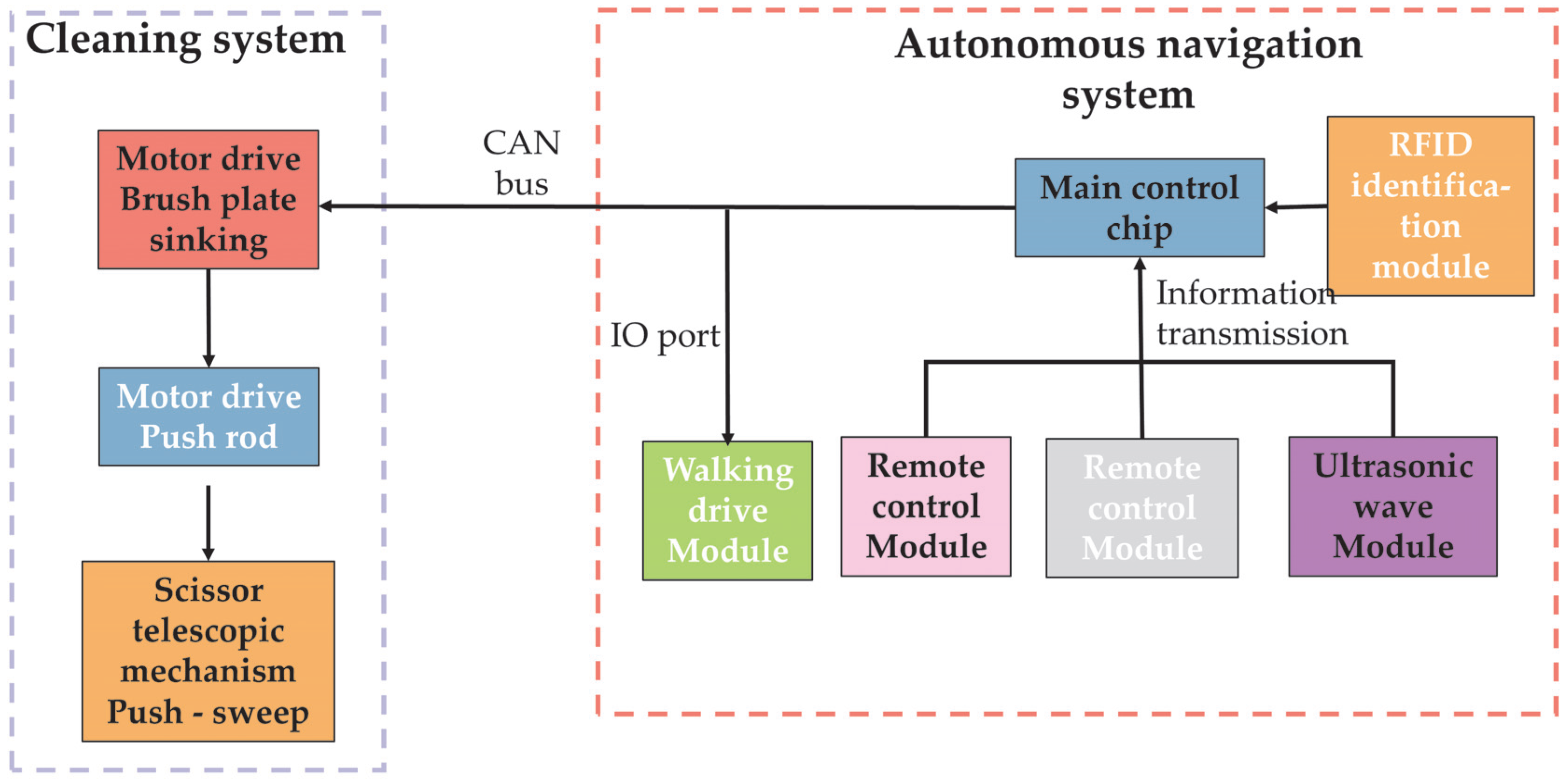
2.3. Working Principle
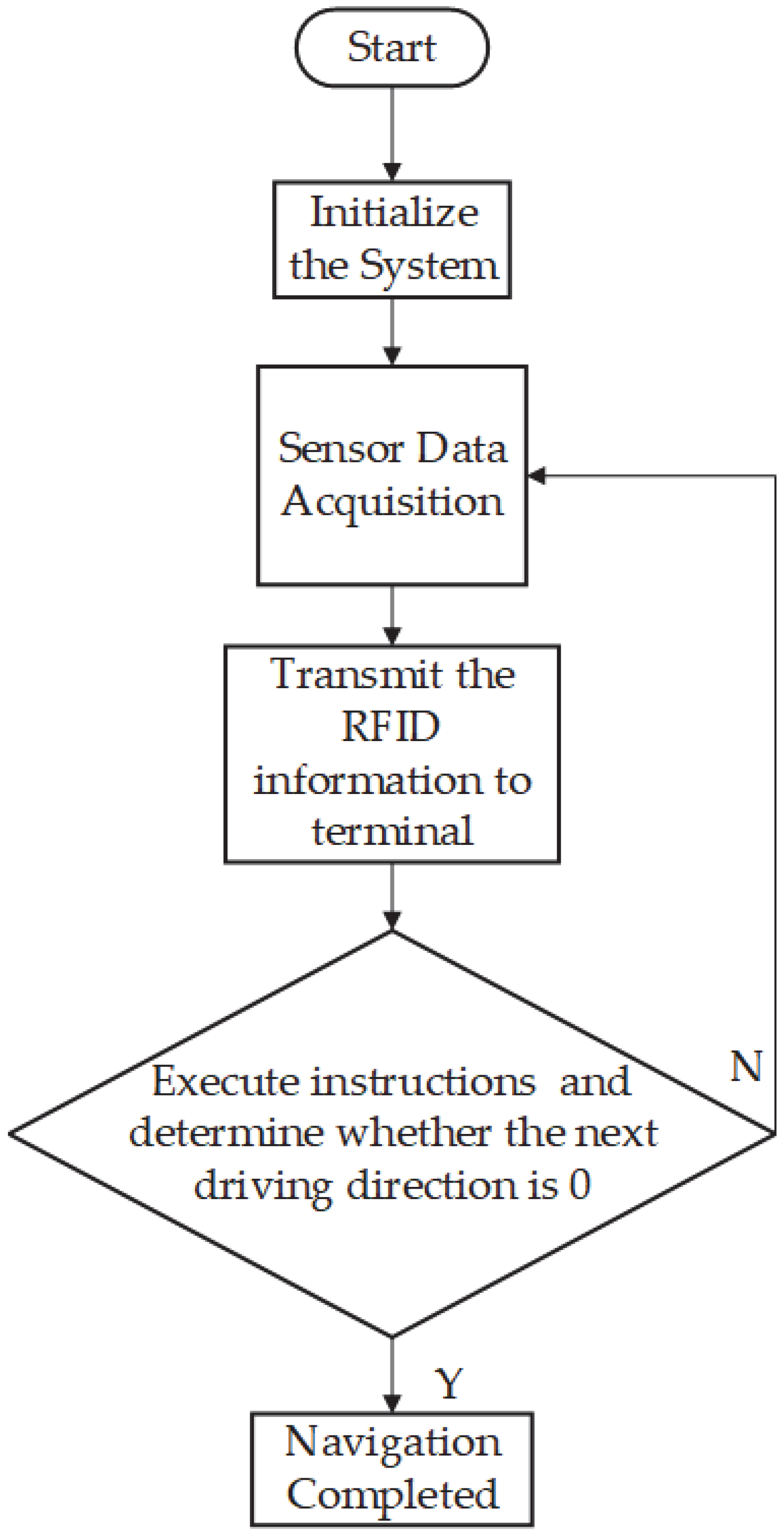
2.4. Software Design
2.5. Cleaning Path Setting
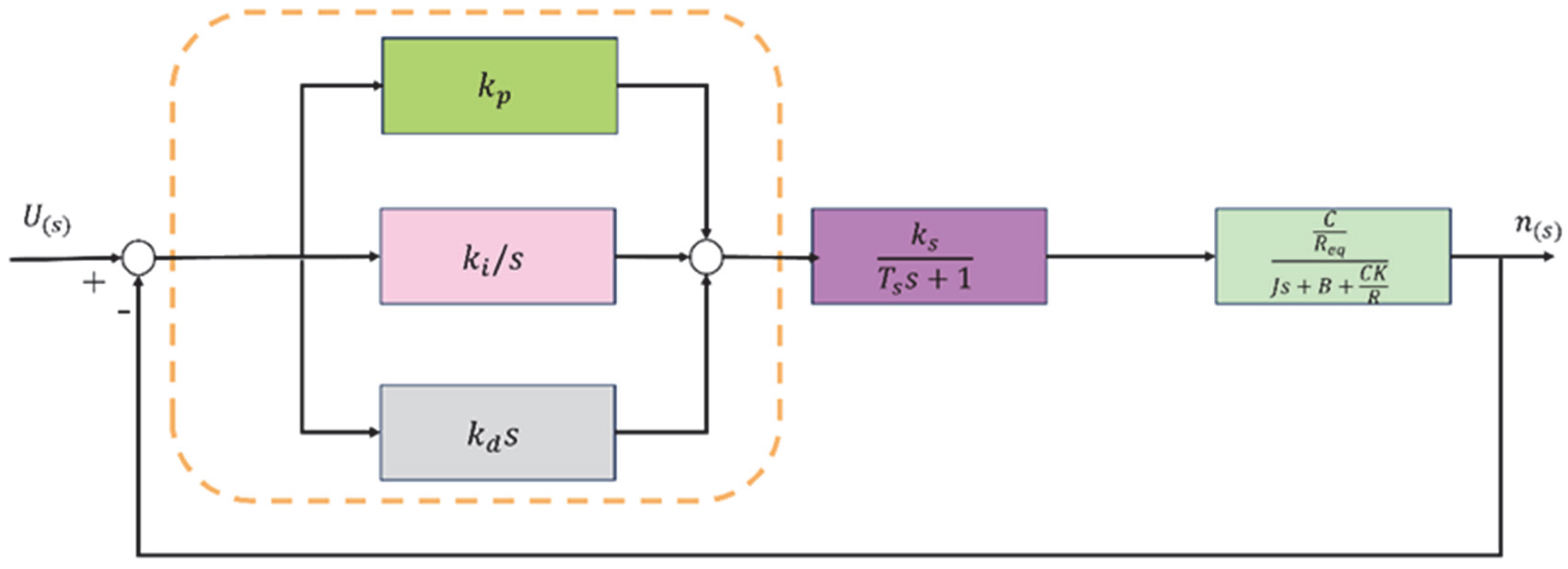
3. Design of the Robotic Magnetic-Navigation Control Model
4. Design of Magnetic-Strip Autonomous Navigation Control Algorithm
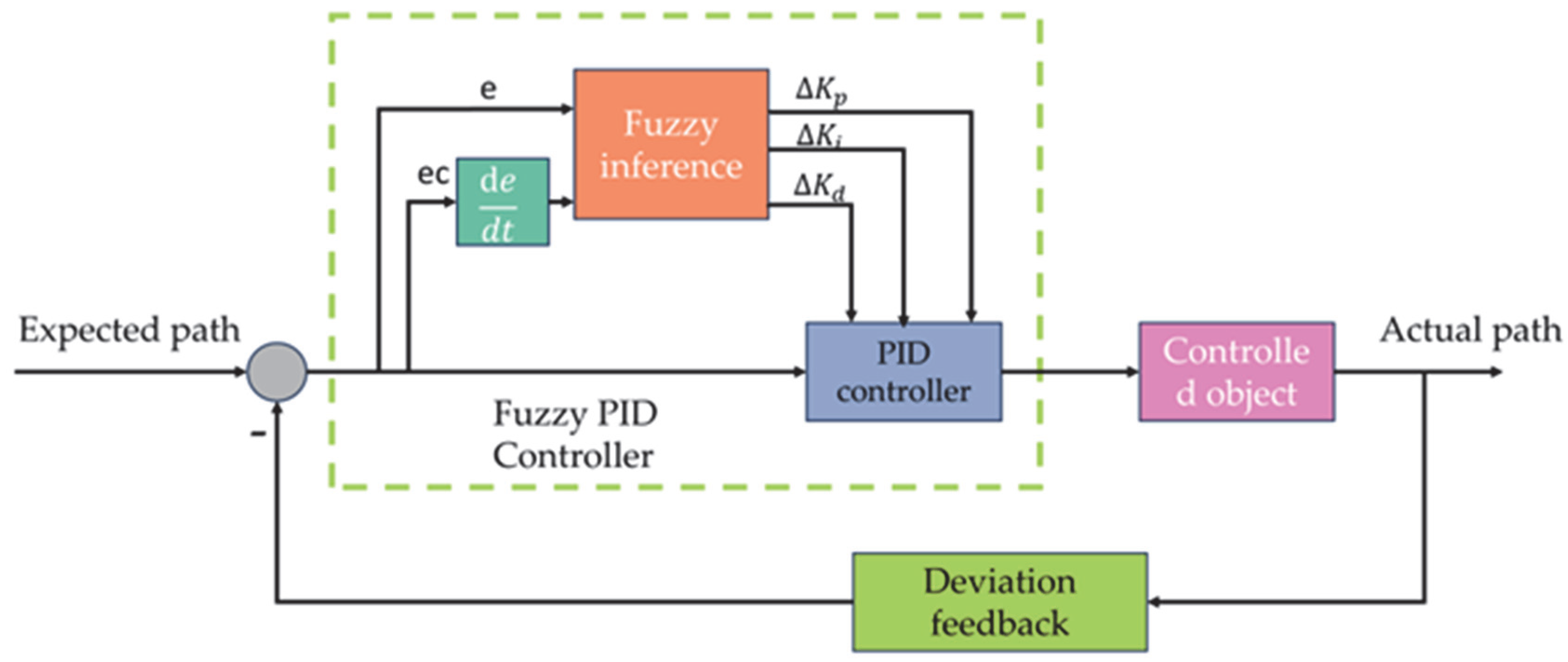
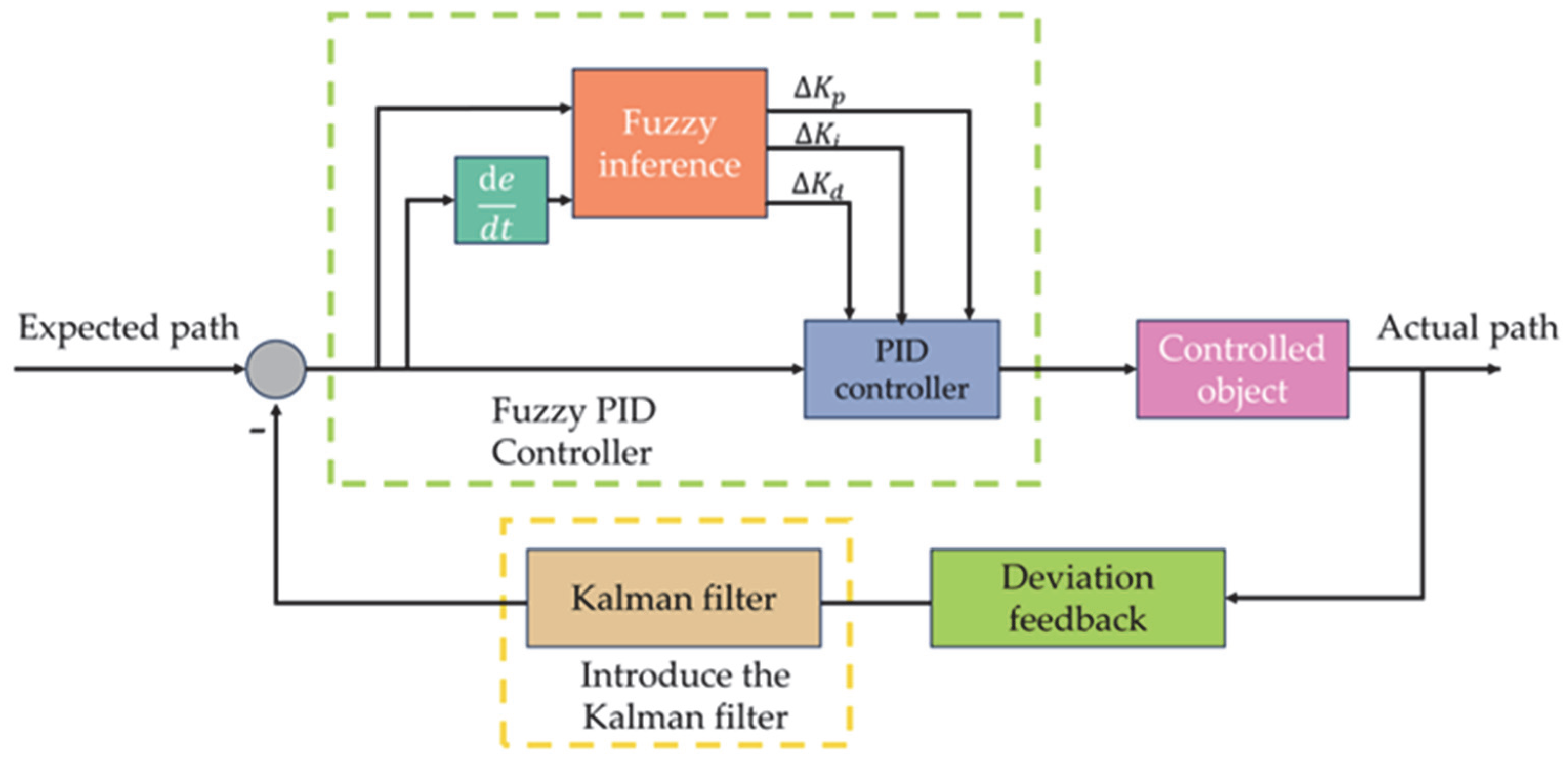
4.1. Fuzzy PID Control-System Model
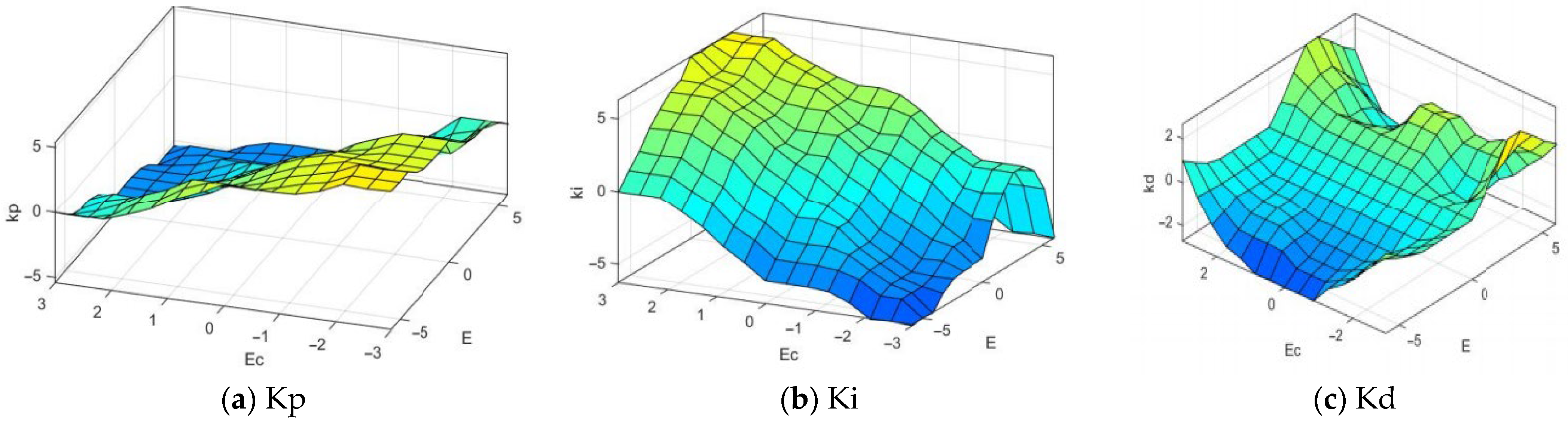
4.2. Fuzzy Controller Rule Design
4.3. Kalman Filter Model Establishment
5. Simulation Analysis and Experimental Testing
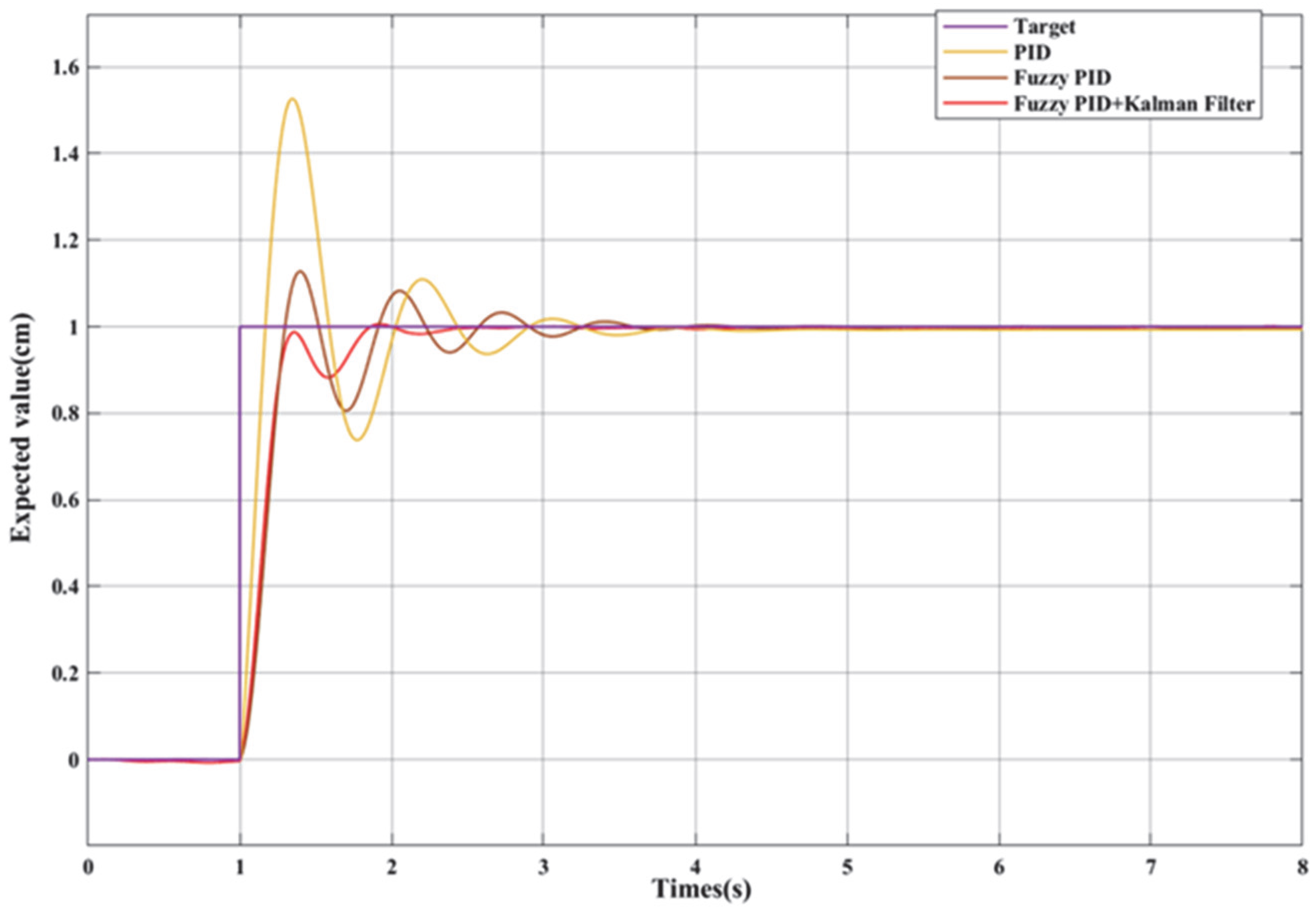
5.1. Simulation Analysis
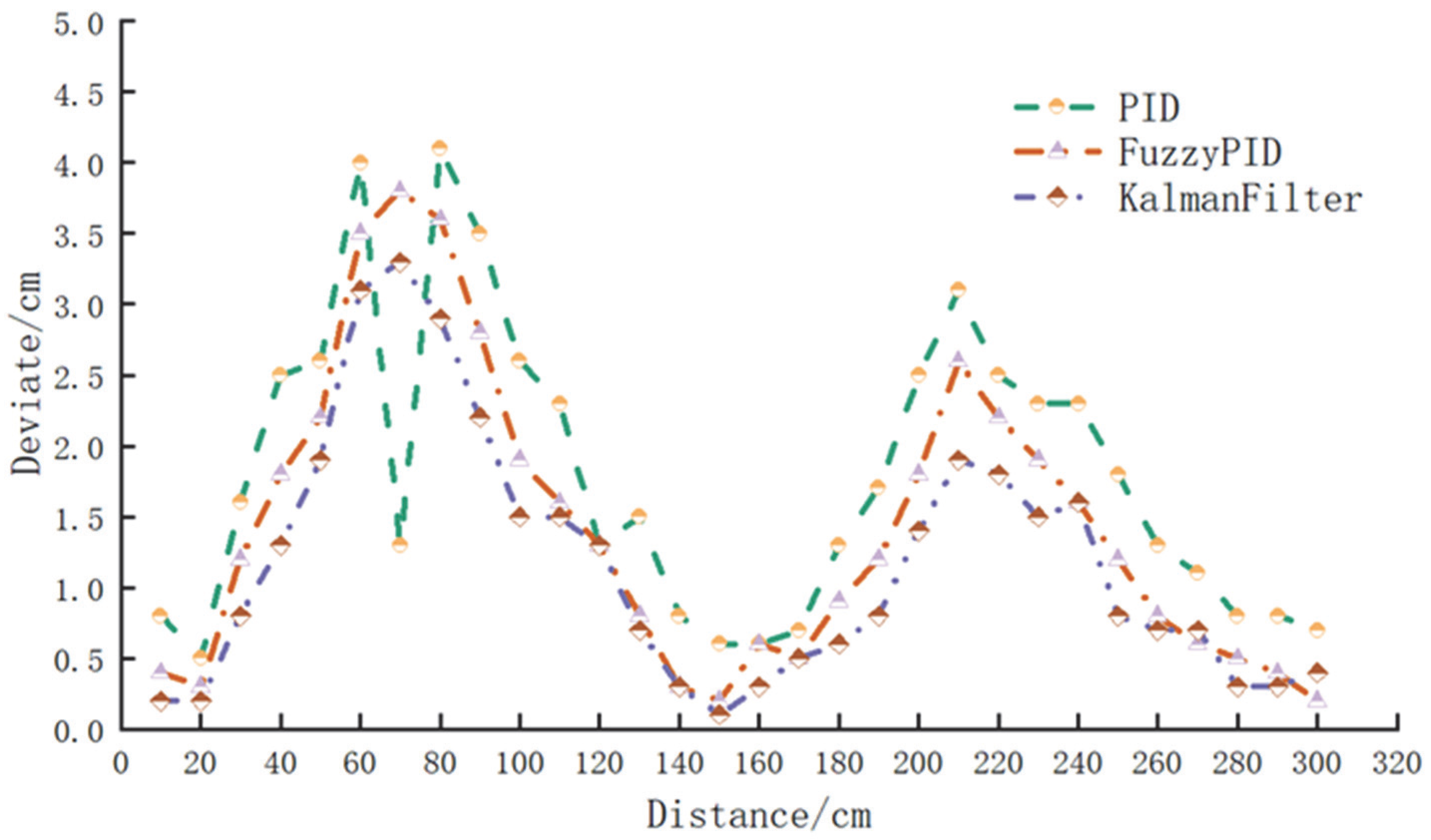
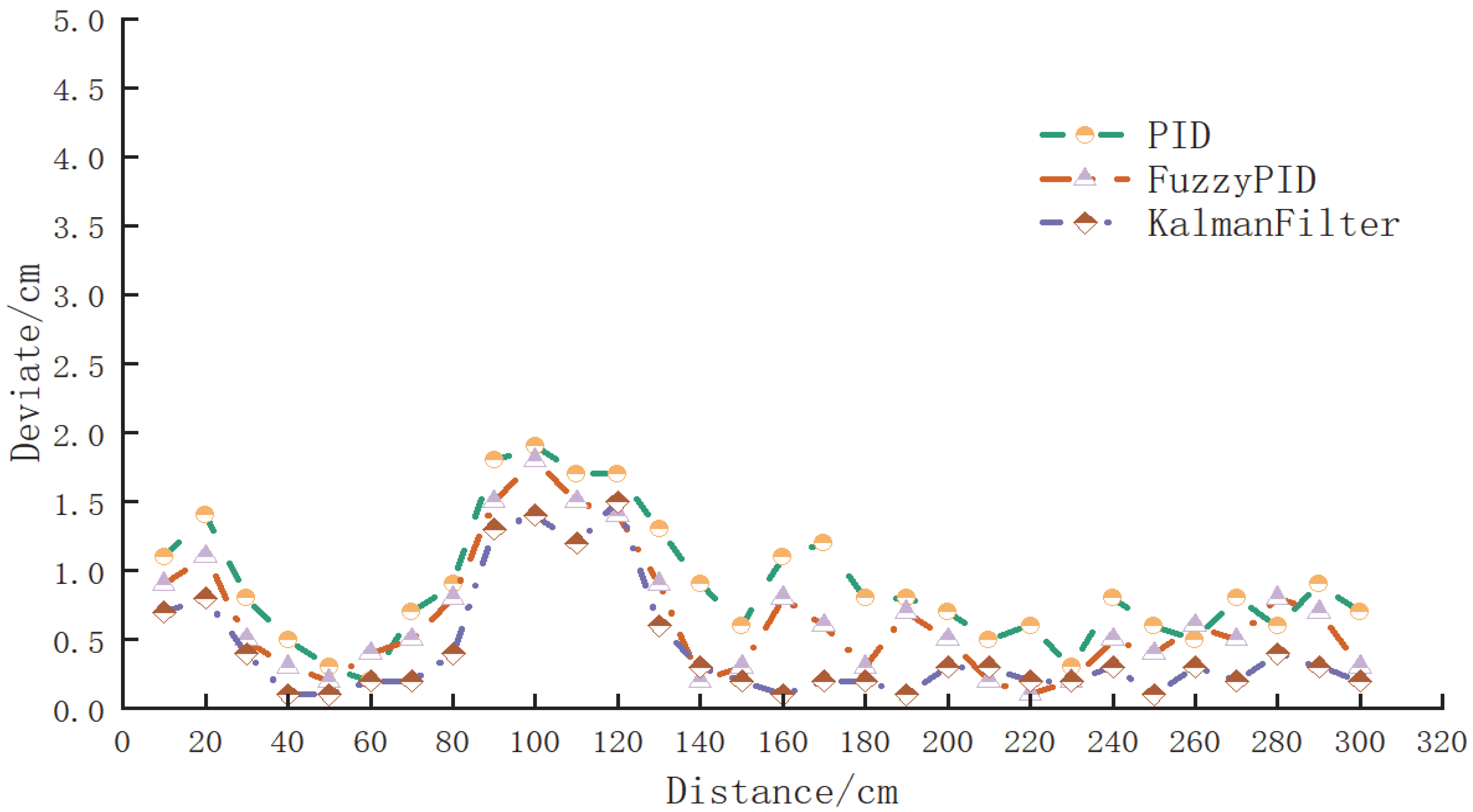
5.2. Experimental Test
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hou, C.; Meng, J.; Bian, B. Research, Analysis, and Countermeasure Suggestions on the Development Status of the Pigeon Industry in Nanjing Area. China Anim. Husb. Poult. Breed. 2023, 19, 198–202. [Google Scholar]
- Song, Z.; Yang, J.; Gao, X. Large-scale pigeon breeding technology in southern Xinjiang region. Xinjiang Farml. Reclam. Sci. Technol. 2023, 46, 30–34. [Google Scholar]
- Zhou, B.; Xie, D.; Chen, S.; Mo, H.; Li, C.; Li, Q. Comparative analysis of SLAM algorithms for mechanical LiDAR and solid-state LiDAR. IEEE Sens. J. 2023, 23, 5325–5338. [Google Scholar] [CrossRef]
- Zhou, J.; Geng, S.; Qiu, Q.; Shao, Y.; Zhang, M. A deep-learning extraction method for orchard visual navigation lines. Agriculture 2022, 12, 1650. [Google Scholar] [CrossRef]
- Radočaj, D.; Plaščak, I.; Jurišić, M. Global navigation satellite systems as state-of-the-art solutions in precision agriculture: A review of studies indexed in the web of science. Agriculture 2023, 13, 1417. [Google Scholar] [CrossRef]
- Huang, Y.; Fu, J.; Xu, S.; Han, T.; Liu, Y. Research on integrated navigation system of agricultural machinery based on RTK-BDS/INS. Agriculture 2022, 12, 1169. [Google Scholar] [CrossRef]
- Miao, J.; Niu, P. Design of Path Tracking Control System for Magnetic Navigation AGV. Modul. Mach. Tool Autom. Manuf. Tech. 2021, 09, 107–110+116. [Google Scholar]
- Lim, S.; Yook, Y.; Heo, J.P.; Im, C.G.; Ryu, K.H.; Sung, S.W. A new PID controller design using differential operator for the integrating process. Comput. Chem. Eng. 2022, 170, 108105. [Google Scholar] [CrossRef]
- Siddique, A.A.; Kim, W.-S.; Kim, Y.-S.; Kim, T.-J.; Choi, C.-H.; Lee, H.-J.; Chung, S.-O.; Kim, Y.-J. Effects of temperatures and viscosity of the hydraulic oils on the proportional valve for a rice transplanter based on PID control algorithm. Agriculture 2020, 10, 73. [Google Scholar] [CrossRef]
- Yu, S.; Hao, G. On a Vision-based manipulator simulator. Actuators 2023, 12, 78. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, L. PID controller design for second order nonlinear uncertain systems. Sci. China Inf. Sci. 2017, 60, 022201. [Google Scholar] [CrossRef]
- Xia, T.; Zhang, Z.; Hong, Z.; Huang, S. Design of fractional order PID controller based on minimum variance control and application of dynamic data reconciliation for improving control performance. ISA Trans. 2022, 133, 91–101. [Google Scholar] [CrossRef]
- Yin, M.; Feng, C. Underwater robot motion control based on fuzzy technology. Microcomput. Appl. 2015, 34, 75–77. [Google Scholar]
- Li, Y.; Fu, C.; Yang, H.; Li, H.; Zhang, R.; Zhang, Y.; Wang, Z. Design of a closed piggery environmental monitoring and control system based on a track inspection robot. Agriculture 2023, 13, 1501. [Google Scholar] [CrossRef]
- Li, S.Y. Fuzzy Control, Neural Control and Intelligent Cybernetics, 2nd ed.; Harbin Institute of Technology Press: Harbin, China, 1998. [Google Scholar]
- Yu, Q.; Zhang, X.; Cao, G.; Gong, Y.; Chen, X. Design and Experiment of Electric Control System for Self-Propelled Chinese Herbal Medicine Materials Transplanter. Agriculture 2025, 15, 621. [Google Scholar] [CrossRef]
- Zhu, J.; Feng, T.; Kang, S.; Chen, D.; Ni, X.; Wang, L. Design and Simulation of Steering Control Strategy for Four-Wheel Steering Hillside Tractor. Agriculture 2024, 14, 2238. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, Y.; Dian, S.; Guo, R.; Li, S. General type-2 fuzzy gain scheduling PID controller with application to power-line inspection robots. Int. J. Fuzzy Syst. 2019, 22, 181–200. [Google Scholar] [CrossRef]
- Kodagoda, K.R.S.; Wijesoma, W.S.; Teoh, E.K. Fuzzy speed and steering control of an AGV. IEEE Trans. Control Syst. Technol. 2002, 10, 112–120. [Google Scholar] [CrossRef]
- Men, L. Simulation Analysis of Vehicle Four-Wheel Steering Control. Int. J. Sci. Adv. 2023, 4, 259–264. [Google Scholar] [CrossRef]
- Liu, K.; Bai, M.; Ni, Y. Two-wheel self-balanced car based on Kalman filtering and PID algorithm. In Proceedings of the 2011 IEEE 18th International Conference on Industrial Engineering and Engineering Management, Changchun, China, 3–5 September 2011; pp. 281–285. [Google Scholar]
- Wang, S.; Yang, Y. Quadrotor aircraft attitude estimation and control based on kalman filter. In Proceedings of the 31st Chinese Control Conference, Nanchang, China, 3–5 June 2012; pp. 5634–5639. [Google Scholar]
- Filho, L.C.Q.; Filho, J.F.R.; da Silva, N.B.F.; Branco, K.C. Attitude estimation of a simulated flight and GPS positioning with Kalman filter. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 742–750. [Google Scholar]
- Wu, T.; Bai, R.; Zhu, L.; Qian, Z. Design of a navigation posture reference system based on Kalman filtering. J. Sens. Technol. 2016, 29, 531–535. [Google Scholar]






| ΔKp/ΔKi/ ΔKd | Ec | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| e | NB | PB/NB/PS | PB/NB/NS | PM/NM/NB | PM/NS/NM | PS/NS/NM | ZO/ZO/NM | ZO/ZO/PS |
| NM | PB/NB/ZO | PB/NM/NS | PM/NS/NM | PS/NS/NM | PS/NO/ZS | ZO/PS/NS | NS/PS/ZO | |
| NS | PM/NM/ZO | PM/NM/NS | PM/NS/NS | PS/ZO/NS | ZO/PS/NS | NS/PM/NS | NS/PM/ZO | |
| ZO | PM/NM/ZO | PM/NS/ZO | PS/ZO/ZO | ZO/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO | |
| PS | PS/ZO/PB | PS/ZO/NS | ZO/PS/PS | NS/PS/PS | NS/PM/PS | NM/PB/PS | NM/PB/PB | |
| PM | PS/ZO/PB | ZO/ZO/PM | NS/PS/PM | NM/PM/PM | NM/PM/PS | NM/PB/PS | NB/PB/PB | |
| PB | ZO/NB/PS | ZO/NB/NS | NM/NM/NB | NM/NM/NB | NM/NS/NB | NB/ZO/NM | NB/ZO/PS | |
| Measurement Point | PID Deviation | Fuzzy PID Deviation | Kalman Filter Deviation | Measurement Point | PID Deviation | Fuzzy PID Deviation | Kalman Filter Deviation |
|---|---|---|---|---|---|---|---|
| 1 | 1.1 | 0.9 | 0.7 | 16 | 1.1 | 0.8 | 0.1 |
| 2 | 1.4 | 1.1 | 0.8 | 17 | 1.2 | 0.6 | 0.2 |
| 3 | 0.8 | 0.5 | 0.4 | 18 | 0.8 | 0.3 | 0.2 |
| 4 | 0.5 | 0.3 | 0.1 | 19 | 0.8 | 0.7 | 0.1 |
| 5 | 0.3 | 0.2 | 0.1 | 20 | 0.7 | 0.5 | 0.3 |
| 6 | 0.2 | 0.4 | 0.2 | 21 | 0.5 | 0.2 | 0.3 |
| 7 | 0.7 | 0.5 | 0.2 | 22 | 0.6 | 0.1 | 0.2 |
| 8 | 0.9 | 0.8 | 0.4 | 23 | 0.3 | 0.2 | 0.2 |
| 9 | 1.8 | 1.5 | 1.3 | 24 | 0.8 | 0.5 | 0.3 |
| 10 | 1.9 | 1.8 | 1.4 | 25 | 0.6 | 0.4 | 0.1 |
| 11 | 1.7 | 1.5 | 1.2 | 26 | 0.5 | 0.6 | 0.3 |
| 12 | 1.7 | 1.4 | 1.5 | 27 | 0.8 | 0.5 | 0.2 |
| 13 | 1.3 | 0.9 | 0.6 | 28 | 0.6 | 0.8 | 0.4 |
| 14 | 0.9 | 0.2 | 0.3 | 29 | 0.9 | 0.7 | 0.3 |
| 15 | 0.6 | 0.3 | 0.2 | 30 | 0.7 | 0.3 | 0.2 |
| Measurement Point | PID Deviation | Fuzzy PID Deviation | Kalman Filter Deviation | Measurement Point | PID Deviation | Fuzzy PID Deviation | Kalman Filter Deviation |
|---|---|---|---|---|---|---|---|
| 1 | 0.8 | 0.4 | 0.2 | 16 | 0.6 | 0.6 | 0.3 |
| 2 | 0.5 | 0.3 | 0.2 | 17 | 0.7 | 0.5 | 0.5 |
| 3 | 1.6 | 1.2 | 0.8 | 18 | 1.3 | 0.9 | 0.6 |
| 4 | 2.5 | 1.8 | 1.3 | 19 | 1.7 | 1.2 | 0.8 |
| 5 | 2.6 | 2.2 | 1.9 | 20 | 2.5 | 1.8 | 1.4 |
| 6 | 4.0 | 3.5 | 3.1 | 21 | 3.1 | 2.6 | 1.9 |
| 7 | 1.3 | 3.8 | 3.3 | 22 | 2.5 | 2.2 | 1.8 |
| 8 | 4.1 | 3.6 | 2.9 | 23 | 2.3 | 1.9 | 1.5 |
| 9 | 3.5 | 2.8 | 2.2 | 24 | 2.3 | 1.6 | 1.6 |
| 10 | 2.6 | 1.9 | 1.5 | 25 | 1.8 | 1.2 | 0.8 |
| 11 | 2.3 | 1.6 | 1.5 | 26 | 1.3 | 0.8 | 0.7 |
| 12 | 1.3 | 1.3 | 1.3 | 27 | 1.1 | 0.6 | 0.7 |
| 13 | 1.5 | 0.8 | 0.7 | 28 | 0.8 | 0.5 | 0.3 |
| 14 | 0.8 | 0.3 | 0.3 | 29 | 0.8 | 0.4 | 0.3 |
| 15 | 0.6 | 0.2 | 0.1 | 30 | 0.7 | 0.2 | 0.4 |
| Measurement Point | PID Deviation | Fuzzy PID Deviation | Kalman Filter Deviation | Measurement Point | PID Deviation | Fuzzy PID Deviation | Kalman Filter Deviation |
|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.5 | 0.2 | 16 | 1.5 | 0.9 | 0.6 |
| 2 | 0.8 | 0.6 | 0.2 | 17 | 2.9 | 2.2 | 1.8 |
| 3 | 0.8 | 0.5 | 0.3 | 18 | 3.7 | 3.1 | 2.5 |
| 4 | 0.7 | 0.3 | 0.4 | 19 | 3.3 | 2.8 | 2.3 |
| 5 | 1.3 | 0.9 | 0.6 | 20 | 2.5 | 1.6 | 0.8 |
| 6 | 1.5 | 1.1 | 0.7 | 21 | 1.6 | 1.2 | 0.8 |
| 7 | 1.3 | 1.3 | 0.9 | 22 | 1.5 | 0.9 | 0.7 |
| 8 | 1.6 | 1.2 | 0.8 | 23 | 1.3 | 0.8 | 0.8 |
| 9 | 1.3 | 0.9 | 0.8 | 24 | 0.9 | 0.6 | 0.5 |
| 10 | 1.4 | 0.8 | 0.5 | 25 | 0.8 | 0.3 | 0.2 |
| 11 | 0.5 | 0.2 | 0.3 | 26 | 0.6 | 0.5 | 0.3 |
| 12 | 2.6 | 3.0 | 2.8 | 27 | 0.5 | 0.7 | 0.4 |
| 13 | 3.7 | 2.8 | 2.7 | 28 | 0.3 | 0.5 | 0.2 |
| 14 | 2.3 | 1.5 | 1.6 | 29 | 0.8 | 0.6 | 0.2 |
| 15 | 1.3 | 0.5 | 0.3 | 30 | 0.9 | 0.8 | 0.3 |
| Algorithm | Sample Size | Mean | Standard Deviation |
|---|---|---|---|
| PID | 30 | 0.89 | 0.082 |
| Fuzzy PID | 30 | 0.65 | 0.080 |
| Kalman | 30 | 0.43 | 0.074 |
| Algorithm | Sample Size | Mean | Standard Deviation |
|---|---|---|---|
| PID | 30 | 1.50 | 0.173 |
| Fuzzy PID | 30 | 1.12 | 0.152 |
| Kalman | 30 | 0.85 | 0.143 |
| Algorithm | Sample Size | Mean | Standard Deviation |
|---|---|---|---|
| PID | 30 | 1.78 | 0.188 |
| Fuzzy PID | 30 | 1.42 | 0.191 |
| Kalman | 30 | 1.16 | 0.162 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Hu, H.; Cao, G.; Zhan, Q.; Zhu, L.; Wen, X.; Lin, H.; Zhang, S. Control of Magnetic-Navigation Pigeon Farm-Cleaning Robot Based on Fuzzy PID and Kalman Filter. AgriEngineering 2025, 7, 351. https://doi.org/10.3390/agriengineering7100351
Huang S, Hu H, Cao G, Zhan Q, Zhu L, Wen X, Lin H, Zhang S. Control of Magnetic-Navigation Pigeon Farm-Cleaning Robot Based on Fuzzy PID and Kalman Filter. AgriEngineering. 2025; 7(10):351. https://doi.org/10.3390/agriengineering7100351
Chicago/Turabian StyleHuang, Shinian, Hongnan Hu, Gaofeng Cao, Qingyu Zhan, Lixue Zhu, Xiangyu Wen, Hai Lin, and Shiang Zhang. 2025. "Control of Magnetic-Navigation Pigeon Farm-Cleaning Robot Based on Fuzzy PID and Kalman Filter" AgriEngineering 7, no. 10: 351. https://doi.org/10.3390/agriengineering7100351
APA StyleHuang, S., Hu, H., Cao, G., Zhan, Q., Zhu, L., Wen, X., Lin, H., & Zhang, S. (2025). Control of Magnetic-Navigation Pigeon Farm-Cleaning Robot Based on Fuzzy PID and Kalman Filter. AgriEngineering, 7(10), 351. https://doi.org/10.3390/agriengineering7100351







