Impact of Wetting-Drying Cycles on Soil Intra-Aggregate Pore Architecture Under Different Management Systems
Abstract
1. Introduction
2. Materials and Methods
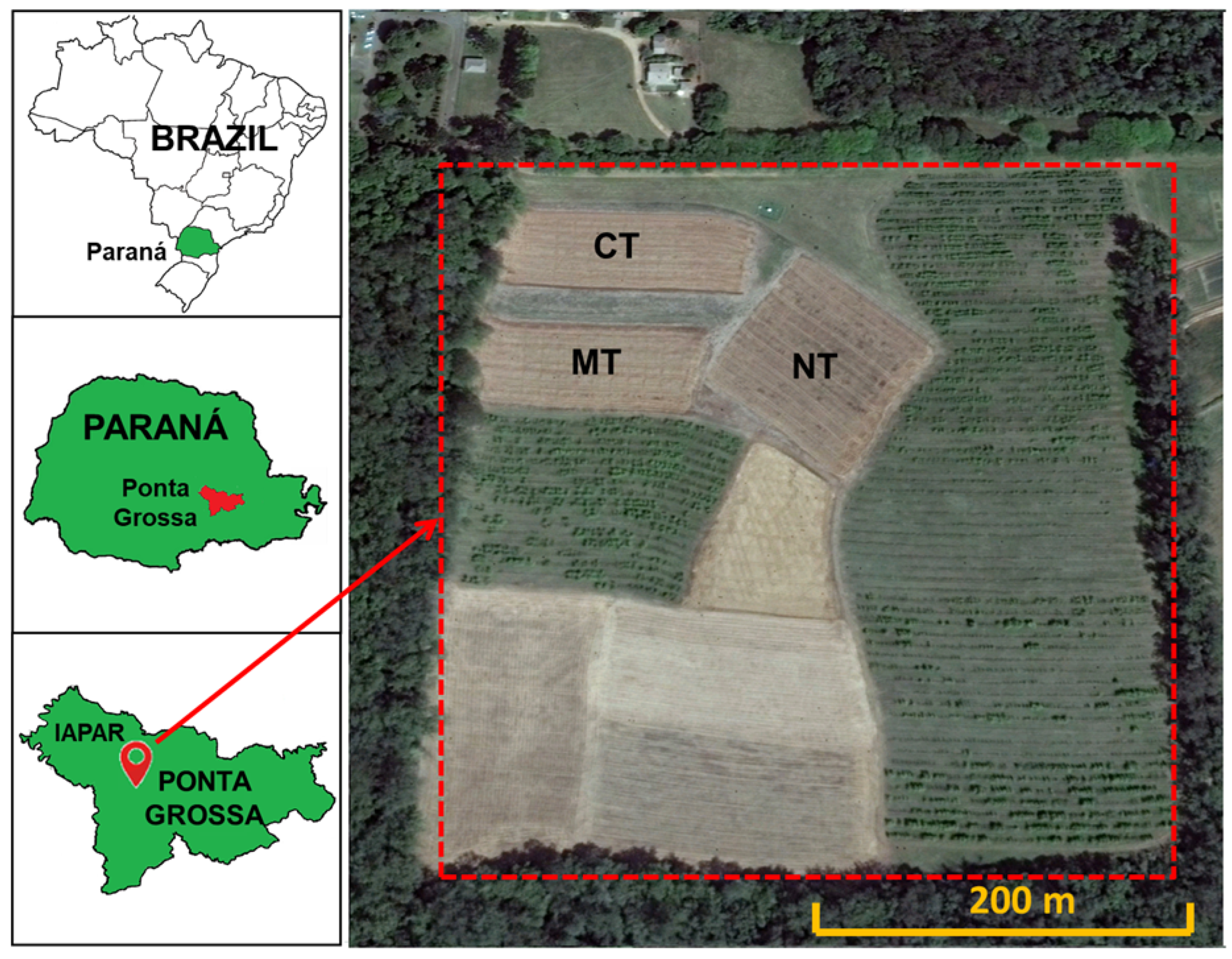
2.1. Experimental Area and Soil Sampling
2.2. Wetting and Drying (W-D) Cycles
2.3. X-ray Micro-Computed Tomography (X-CT)
2.4. Quantification of Physical and Morphometric Properties Analyzed Using 3D Imaging
3. Results
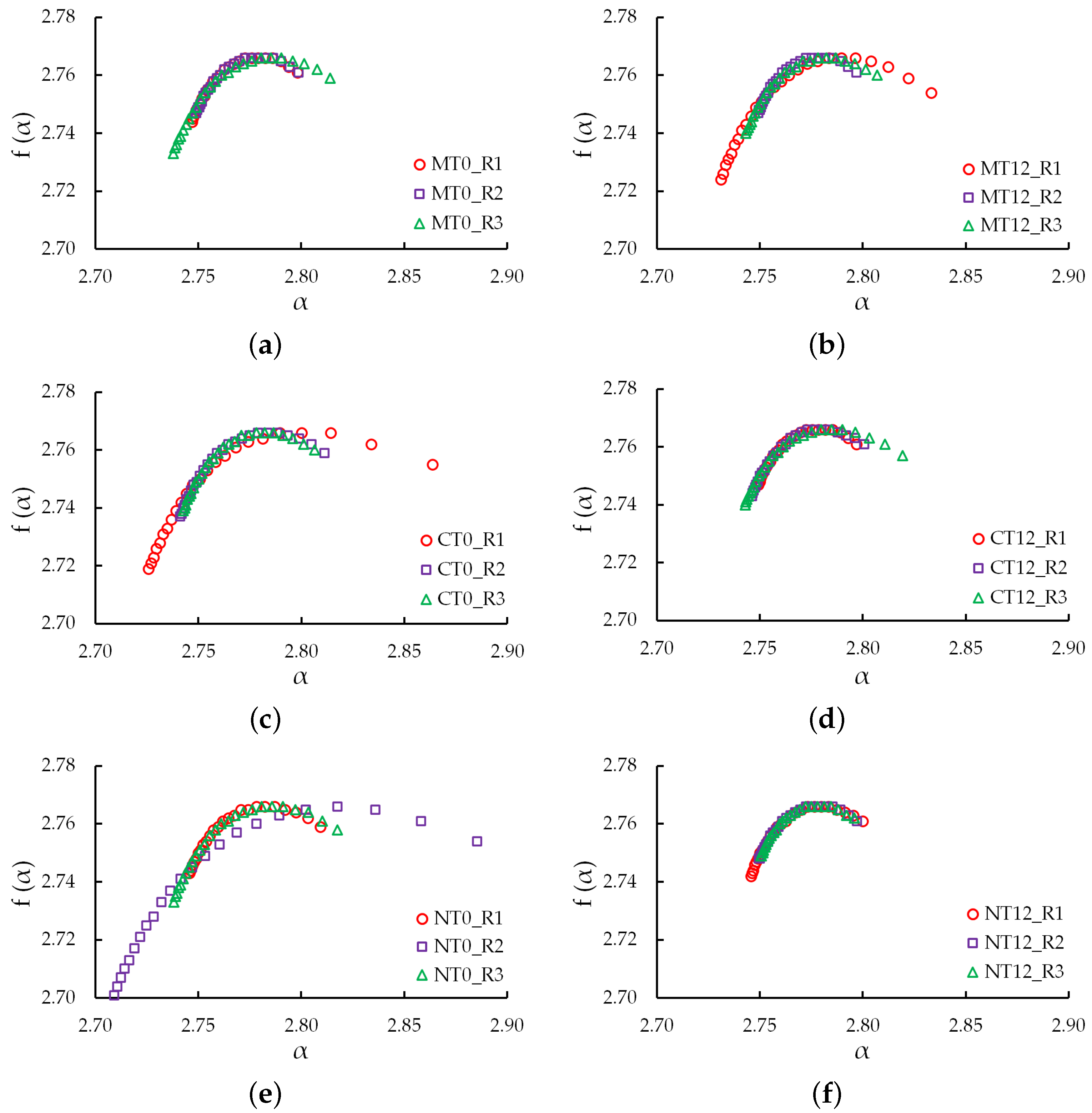
3.1. Image Analysis
3.2. Three-Dimensional Lacunarity, Normalized Shannon Entropy, Three-Dimensional Multifractal Spectra, and Generalized Fractal Dimensions
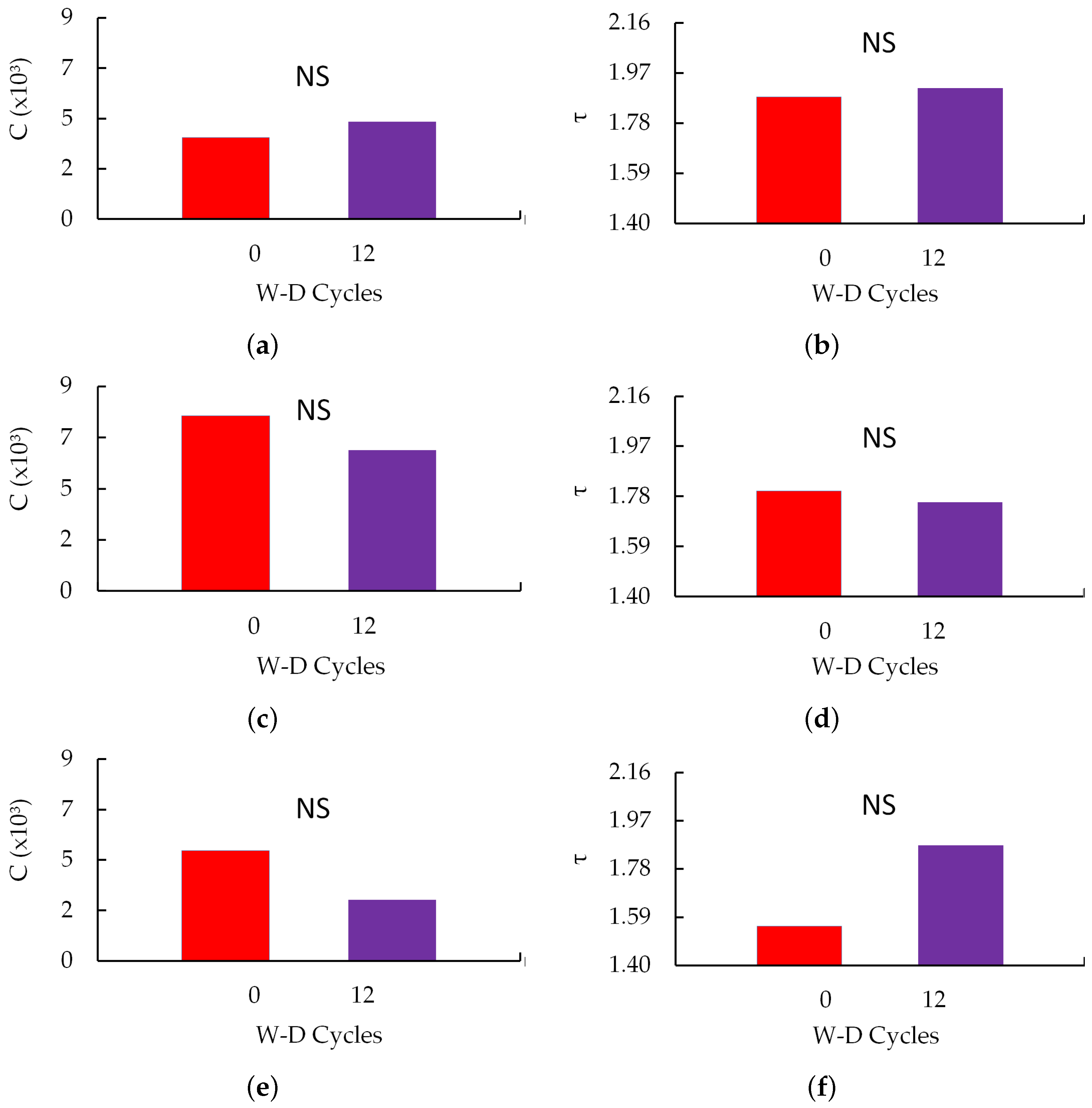
3.3. Physical Properties: Porosity, Degree of Anisotropy and Number of Pores
3.4. Morphometric Properties: Connectivity of Pores, Tortuosity, Volume and Number of Pores by Shape
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| W-D | wetting–drying |
| NT | no tillage |
| MT | minimum tillage |
| CT | conventional tillage |
| X-CT | X-ray micro-computed tomography |
| IAPAR | Instituto de Desenvolvimento Rural do Paraná |
| 3D | three-dimensional |
| TIFF | tag image file format |
| NASS | non-linear analysis scaling system |
Appendix A

| Management | Cycles | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Replicates | A | f() | |||||||
| CT | 0 | R1 | 0.26 | 0.40 | 2.77 | 2.99 | 2.77 | 2.75 | 2.73 |
| R2 | 0.07 | 1.51 | 2.77 | 2.81 | 2.77 | 2.75 | 2.75 | ||
| R3 | 0.06 | 1.64 | 2.77 | 2.81 | 2.77 | 2.75 | 2.74 | ||
| 12 | R1 | 0.05 | 1.59 | 2.77 | 2.80 | 2.77 | 2.76 | 2.75 | |
| R2 | 0.05 | 1.64 | 2.77 | 2.82 | 2.77 | 2.75 | 2.75 | ||
| R3 | 0.08 | 1.21 | 2.77 | 2.82 | 2.77 | 2.75 | 2.75 | ||
| MT | 0 | R1 | 0.05 | 1.69 | 2.77 | 2.80 | 2.77 | 2.76 | 2.75 |
| R2 | 0.05 | 1.54 | 2.77 | 2.81 | 2.77 | 2.75 | 2.75 | ||
| R3 | 0.08 | 1.64 | 2.77 | 2.81 | 2.77 | 2.75 | 2.74 | ||
| 12 | R1 | 0.10 | 1.34 | 2.77 | 2.79 | 2.77 | 2.75 | 2.74 | |
| R2 | 0.05 | 1.57 | 2.77 | 2.80 | 2.77 | 2.75 | 2.75 | ||
| R3 | 0.06 | 1.59 | 2.77 | 2.81 | 2.77 | 2.75 | 2.75 | ||
| NT | 0 | R1 | 0.06 | 1.38 | 2.77 | 2.81 | 2.77 | 2.75 | 2.74 |
| R2 | 0.25 | 0.77 | 2.77 | 2.96 | 2.77 | 2.75 | 2.74 | ||
| R3 | 0.08 | 1.50 | 2.77 | 2.82 | 2.77 | 2.75 | 2.74 | ||
| 12 | R1 | 0.05 | 1.52 | 2.77 | 2.80 | 2.77 | 2.76 | 2.75 | |
| R2 | 0.05 | 1.55 | 2.77 | 2.80 | 2.77 | 2.75 | 2.75 | ||
| R3 | 0.05 | 1.52 | 2.77 | 2.80 | 2.77 | 2.76 | 2.75 | ||
References
- Bronick, C.; Lal, R. Soil structure and management: A review. Geoderma 2005, 124, 3–22. [Google Scholar] [CrossRef]
- Alaoui, A.; Lipiec, J.; Gerke, H. A review of the changes in the soil pore system due to soil deformation: A hydrodynamic perspective. Soil Tillage Res. 2011, 115–116, 1–15. [Google Scholar] [CrossRef]
- Schlüter, S.; Sammartino, S.; Koestel, J. Exploring the relationship between soil structure and soil functions via pore-scale imaging. Geoderma 2020, 370, 114370. [Google Scholar] [CrossRef]
- Weidhuner, A.; Hanauer, A.; Krausz, R.; Crittenden, S.J.; Gage, K.; Sadeghpour, A. Tillage impacts on soil aggregation and aggregate-associated carbon and nitrogen after 49 years. Soil Tillage Res. 2021, 208, 104878. [Google Scholar] [CrossRef]
- Aziz, I.; Mahmood, T.; Islam, K.R. Effect of long term no-till and conventional tillage practices on soil quality. Soil Tillage Res. 2013, 131, 28–35. [Google Scholar] [CrossRef]
- Diel, J.; Vogel, H.J.; Schlüter, S. Impact of wetting and drying cycles on soil structure dynamics. Geoderma 2019, 345, 63–71. [Google Scholar] [CrossRef]
- Hochman, D.; Dor, M.; Mishael, Y. Diverse effects of wetting and drying cycles on soil aggregation: Implications on pesticide leaching. Chemosphere 2021, 263, 127910. [Google Scholar] [CrossRef]
- Leij, F.J.; Ghezzehei, T.A.; Or, D. Modeling the dynamics of the soil pore-size distribution. Soil Tillage Res. 2002, 64, 61–78. [Google Scholar] [CrossRef]
- Ma, R.; Cai, C.; Li, Z.; Wang, J.; Xiao, T.; Peng, G.; Yang, W. Evaluation of soil aggregate microstructure and stability under wetting and drying cycles in two Ultisols using synchrotron-based X-ray micro-computed tomography. Soil Tillage Res. 2015, 149, 1–11. [Google Scholar] [CrossRef]
- Yudina, A.; Klyueva, V.; Romanenko, K.; Fomin, D. Micro- within macro: How micro-aggregation shapes the soil pore space and water-stability. Geoderma 2022, 415, 115771. [Google Scholar] [CrossRef]
- Wang, W.; Kravchenko, A.N.; Smucker, A.J.M.; Liang, W.; Rivers, M.L. Intra-aggregate Pore Characteristics: X-ray Computed Microtomography Analysis. Soil Sci. Soc. Am. J. 2012, 76, 1159–1171. [Google Scholar] [CrossRef]
- Singh, N.; Kumar, S.; Udawatta, R.P.; Anderson, S.H.; de Jonge, L.W.; Katuwal, S. X-ray micro-computed tomography characterized soil pore network as influenced by long-term application of manure and fertilizer. Geoderma 2021, 385, 114872. [Google Scholar] [CrossRef]
- Meira Cássaro, F.A.; Posadas Durand, A.N.; Gimenez, D.; Pedro Vaz, C.M. Pore-Size Distributions of Soils Derived using a Geometrical Approach and Multiple Resolution MicroCT Images. Soil Sci. Soc. Am. J. 2017, 81, 468–476. [Google Scholar] [CrossRef]
- Ngom, N.F.; Garnier, P.; Monga, O.; Peth, S. Extraction of three-dimensional soil pore space from microtomography images using a geometrical approach. Geoderma 2011, 163, 127–134. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Wang, F.; Zhang, X. Comparison of soil tortuosity calculated by different methods. Geoderma 2021, 402, 115358. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Crawford, J. Fractal analysis of soils. In Encyclopedia of Soils in the Environment; Academic Press Inc.: Cambridge, MA, USA, 2004; pp. 85–97. [Google Scholar]
- Posadas, A.N.D.; Giménez, D.; Quiroz, R.; Protz, R. Multifractal Characterization of Soil Pore Systems. Soil Sci. Soc. Am. J. 2003, 67, 1361–1369. [Google Scholar] [CrossRef]
- Chun, H.C.; Giménez, D.; Yoon, S.W. Morphology, lacunarity and entropy of intra-aggregate pores: Aggregate size and soil management effects. Geoderma 2008, 146, 83–93. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, X.; Li, X. Analysis of the intra-aggregate pore structures in three soil types using X-ray computed tomography. Catena 2020, 193, 104622. [Google Scholar] [CrossRef]
- Gao, Y.; Liang, A.; Fan, R.; Guo, Y.; Zhang, Y.; McLaughlin, N.; Chen, X.; Zheng, H.; Wu, D. Quantifying influence of tillage practices on soil aggregate microstructure using synchrotron-based micro-computed tomography. Soil Use Manag. 2022, 38, 850–860. [Google Scholar] [CrossRef]
- Kravchenko, A.; Wang, A.N.W.; Smucker, A.J.M.; Rivers, M.L. Long-term Differences in Tillage and Land Use Affect Intra-aggregate Pore Heterogeneity. Soil Sci. Soc. Am. J. 2011, 75, 1658–1666. [Google Scholar] [CrossRef]
- Peth, S.; Horn, R.; Beckmann, F.; Donath, T.; Fischer, J.; Smucker, A.J.M. Three-Dimensional Quantification of Intra-Aggregate Pore-Space Features using Synchrotron-Radiation-Based Microtomography. Soil Sci. Soc. Am. J. 2008, 72, 897–907. [Google Scholar] [CrossRef]
- Menon, M.; Mawodza, T.; Rabbani, A.; Blaud, A.; Lair, G.J.; Babaei, M.; Kercheva, M.; Rousseva, S.; Banwart, S. Pore system characteristics of soil aggregates and their relevance to aggregate stability. Geoderma 2020, 366, 114259. [Google Scholar] [CrossRef]
- MINEROPAR. Serviço Geológico do Paraná. 2013. Available online: http://www.mineropar.pr.gov.br/modules/conteudo/conteudo.php?conteudo=154 (accessed on 11 September 2024).
- de Moraes Sá, J.C.; Séguy, L.; Tivet, F.; Lal, R.; Bouzinac, S.; Borszowskei, P.R.; Briedis, C.; dos Santos, J.B.; da Cruz Hartman, D.; Bertoloni, C.G.; et al. Carbon Depletion by Plowing and its Restoration by No-Till Cropping Systems in Oxisols of Subtropical and Tropical Agro-Ecoregions in Brazil. Land Degrad. Dev. 2015, 26, 531–543. [Google Scholar] [CrossRef]
- Nitsche, P.; Caramori, P.; Ricce, W.; Pinto, L. Atlás Climático do Estado do Paraná; IAPAR: Londrina, Brazil, 2019. [Google Scholar]
- The University of Nottingham. Our Facilities: Nanotom microCT Scanner. Available online: https://www.nottingham.ac.uk/microct/facilities/nanotom.aspx (accessed on 16 October 2024).
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- The MathWorks, I. MATLAB, Version R2018a; Mathworks: Natick, MA, USA, 2018; Available online: https://www.mathworks.com (accessed on 16 October 2024).
- Dong, P. Lacunarity analysis of raster datasets and 1D, 2D, and 3D point patterns. Comput. Geosci. 2009, 35, 2100–2110. [Google Scholar] [CrossRef]
- Monreal, J.C.; Martínez, F.S.J.; Martí, J.I.; Pérez-Gómez, R. Lacunarity of the Spatial Distributions of Soil Types in Europe. Vadose Zone J. 2013, 12, 1–9. [Google Scholar] [CrossRef]
- Posadas, A.N.D.; Lourenço, A.L.F. NASS: Non-Linear Analysis Scaling System, Version 2; Software developed with the support of the Department of Environmental Science; Rutgers, The State University of New Jersey: New Brunswick, NJ, USA, 2023. [Google Scholar]
- Andraud, C.; Beghdadi, A.; Haslund, E.; Hilfer, R.; Lafait, J.; Virgin, B. Local entropy characterization of correlated random microstructures. Phys. A Stat. Mech. Its Appl. 1997, 235, 307–318. [Google Scholar] [CrossRef]
- Bullock, P.; Fedoroff, N.; Jongerius, A.; Stoops, G.; Tursina, T. Handbook for Soil Thin Section Description; Waine Research: Albrighton, UK, 1985; pp. 147–150. [Google Scholar]
- Dhaliwal, J.K.; Kumar, S. 3D-visualization and quantification of soil porous structure using X-ray micro-tomography scanning under native pasture and crop-livestock systems. Soil Tillage Res. 2022, 218, 105305. [Google Scholar] [CrossRef]
- Odgaard, A.; Gundersen, H. Quantification of connectivity in cancellous bone, with special emphasis on 3-D reconstructions. Bone 1993, 14, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Roque, W.L.; Costa, R.R. A plugin for computing the pore/grain network tortuosity of a porous medium from 2D/3D MicroCT image. Appl. Comput. Geosci. 2020, 5, 100019. [Google Scholar] [CrossRef]
- Hammer, Ø.; Harper, D.A.; Ryan, P.D. PAST: Paleontological statistics software package for education and data analysis. Palaeontol. Electron. 2001, 4, 9. [Google Scholar]
- Cheik, S.; Jouquet, P.; Maeght, J.; Capowiez, Y.; Tran, T.; Bottinelli, N. X-ray tomography analysis of soil biopores structure under wetting and drying cycles. Eur. J. Soil Sci. 2021, 72, 2128–2132. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Vanapalli, S.K.; Mehmood, M. Soil-water characteristic curve of expansive soils considering cumulative damage effects of wetting and drying cycles. Eng. Geol. 2024, 339, 107642. [Google Scholar] [CrossRef]
- Hussein, J.; Adey, M. Changes of structure and tilth mellowing in a Vertisol due to wet/dry cycles in the liquid and vapour phases. Eur. J. Soil Sci. 1995, 46, 357–368. [Google Scholar] [CrossRef]
- Hussein, J.; Adey, M. Changes in microstructure, voids and b-fabric of surface samples of a Vertisol caused by wet/dry cycles. Geoderma 1998, 85, 63–82. [Google Scholar] [CrossRef]
- de Oliveira, J.A.T.; Cássaro, F.A.M.; Posadas, A.N.D.; Pires, L.F. Soil Pore Network Complexity Changes Induced by Wetting and Drying Cycles—A Study Using X-ray Microtomography and 3D Multifractal Analyses. Int. J. Environ. Res. Public Health 2022, 19, 10582. [Google Scholar] [CrossRef]
- Tang, C.S.; Shi, B. Swelling and shrinkage behaviour of expansive soil during wetting-drying cycles. Chin. J. Geotech. Eng. 2011, 33, 1376–1384. [Google Scholar]
- Fomin, D.S.; Yudina, A.V.; Romanenko, K.A.; Abrosimov, K.N.; Karsanina, M.V.; Gerke, K.M. Soil pore structure dynamics under steady-state wetting-drying cycle. Geoderma 2023, 432, 116401. [Google Scholar] [CrossRef]
- Kravchenko, S. X-ray Computed Tomography Imaging & Soil Biology. In X-ray Imaging of the Soil Porous Architecture; Jon Mooney, S., Young, I.M., Heck, R.J., Peth, S., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 159–182. [Google Scholar] [CrossRef]
- Tang, C.S.; Wang, D.Y.; Shi, B.; Li, J. Effect of wetting–drying cycles on profile mechanical behavior of soils with different initial conditions. Catena 2016, 139, 105–116. [Google Scholar] [CrossRef]
- Caniego, F.; Martí, M.; San José, F. Rényi dimensions of soil pore size distribution. Geoderma 2003, 112, 205–216. [Google Scholar] [CrossRef]
- Vázquez, E.V.; Ferreiro, J.P.; Miranda, J.G.V.; González, A.P. Multifractal Analysis of Pore Size Distributions as Affected by Simulated Rainfall. Vadose Zone J. 2008, 7, 500–511. [Google Scholar] [CrossRef]
- Soto-Gómez, D.; Pérez-Rodríguez, P.; Vázquez Juíz, L.; Paradelo, M.; López-Periago, J.E. 3D multifractal characterization of computed tomography images of soils under different tillage management: Linking multifractal parameters to physical properties. Geoderma 2020, 363, 114129. [Google Scholar] [CrossRef]
- Sartori, G.; Ferrari, G.; Pagliai, M. Changes in soil porosity and surface shrinkage in a remolded, saline clay soil treated with compost. Soil Sci. 1985, 139, 523. [Google Scholar] [CrossRef]
- Zemenu, G.; Martine, A.; Roger, C. Analyse du comportement d’un sol argileux sous sollicitations hydriques cycliques. Bull. Eng. Geol. Environ. 2009, 68, 421–436. [Google Scholar] [CrossRef]
- Pires, L.F.; Auler, A.C.; Roque, W.L.; Mooney, S.J. X-ray microtomography analysis of soil pore structure dynamics under wetting and drying cycles. Geoderma 2020, 362, 114103. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.M.; Guo, N.; Liu, L. Effects of Wetting-Drying Cycles on the CT-Measured Macropore Characteristics under Farmland in Northern China. Eurasian Soil Sci. 2023, 56, 747–755. [Google Scholar] [CrossRef]
- Bodner, G.; Scholl, P.; Kaul, H.P. Field quantification of wetting–drying cycles to predict temporal changes of soil pore size distribution. Soil Tillage Res. 2013, 133, 1–9. [Google Scholar] [CrossRef]
- Wen, T.; Chen, X.; Shao, L. Effect of multiple wetting and drying cycles on the macropore structure of granite residual soil. J. Hydrol. 2022, 614, 128583. [Google Scholar] [CrossRef]
- Pires, L.F.; Villanueva, F.C.; Dias, N.M.; Bacchi, O.O.S.; Reichardt, K. Chemical migration during soil water retention curve evaluation. An. Acad. Bras. Ciências 2011, 83, 1097–1108. [Google Scholar] [CrossRef] [PubMed]
- An, R.; Kong, L.; Zhang, X.; Li, C. Effects of dry-wet cycles on three-dimensional pore structure and permeability characteristics of granite residual soil using X-ray micro computed tomography. J. Rock Mech. Geotech. Eng. 2022, 14, 851–860. [Google Scholar] [CrossRef]
- Tang, C.S.; Cheng, Q.; Gong, X.; Shi, B.; Inyang, H.I. Investigation on microstructure evolution of clayey soils: A review focusing on wetting/drying process. J. Rock Mech. Geotech. Eng. 2023, 15, 269–284. [Google Scholar] [CrossRef]
- Ye, W.m.; Qi, Z.y.; Chen, B.; Xie, J.; Huang, Y.; Lu, Y.r.; Cui, Y.J. Mechanism of cultivation soil degradation in rocky desertification areas under dry/wet cycles. Environ. Earth Sci. 2010, 64, 269–276. [Google Scholar] [CrossRef]
- Chakraborty, P.; Singh, N.; Bansal, S.; Sekaran, U.; Sexton, P.; Bly, A.; Anderson, S.H.; Kumar, S. Does the duration of no-till implementation influence depth distribution of soil organic carbon, hydro-physical properties, and computed tomography-derived macropore characteristics? Soil Tillage Res. 2022, 222, 105426. [Google Scholar] [CrossRef]
- Pagliai, M.; Vignozzi, N.; Pellegrini, S. Soil structure and the effect of management practices. Soil Tillage Res. 2004, 79, 131–143. [Google Scholar] [CrossRef]
- Mady, A.Y.; Shein, E.V. Assessment of pore space changes during drying and wetting cycles in hysteresis of soil water retention curve in Russia using X-ray computed tomography. Geoderma Reg. 2020, 21, e00259. [Google Scholar] [CrossRef]
- Hillel, D. Introduction to Environmental Soil Physics; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Ambus, J.V.; Awe, G.O.; Faccio Carvalho, P.C.d.; Reichert, J.M. Integrated crop-livestock systems in lowlands with rice cultivation improve root environment and maintain soil structure and functioning. Soil Tillage Res. 2023, 227, 105592. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pires, L.F.; Oliveira, J.A.T.d.; Gaspareto, J.V.; Posadas, A.N.D.; Lourenço, A.L.F. Impact of Wetting-Drying Cycles on Soil Intra-Aggregate Pore Architecture Under Different Management Systems. AgriEngineering 2025, 7, 9. https://doi.org/10.3390/agriengineering7010009
Pires LF, Oliveira JATd, Gaspareto JV, Posadas AND, Lourenço ALF. Impact of Wetting-Drying Cycles on Soil Intra-Aggregate Pore Architecture Under Different Management Systems. AgriEngineering. 2025; 7(1):9. https://doi.org/10.3390/agriengineering7010009
Chicago/Turabian StylePires, Luiz F., Jocenei A. T. de Oliveira, José V. Gaspareto, Adolfo N. D. Posadas, and André L. F. Lourenço. 2025. "Impact of Wetting-Drying Cycles on Soil Intra-Aggregate Pore Architecture Under Different Management Systems" AgriEngineering 7, no. 1: 9. https://doi.org/10.3390/agriengineering7010009
APA StylePires, L. F., Oliveira, J. A. T. d., Gaspareto, J. V., Posadas, A. N. D., & Lourenço, A. L. F. (2025). Impact of Wetting-Drying Cycles on Soil Intra-Aggregate Pore Architecture Under Different Management Systems. AgriEngineering, 7(1), 9. https://doi.org/10.3390/agriengineering7010009








