Abstract
This article presents a nonlinear control strategy designed to address parametric uncertainties in an agricultural tractor system coupled to a towed implement. The controller ensures accurate tracking of lateral and yaw velocities relative to desired reference trajectories, even under the presence of parametric variations and external disturbances. The reference trajectories are derived from an “ideal” tractor model, excluding the effects of the towed implement. A High-Order Sliding Mode (HOSM) estimator is employed to provide an estimation of disturbances, which are subsequently mitigated by the controller to maintain system stability and precision. The effectiveness of the proposed control strategy is validated through Matlab-Simulink simulations, which include a double-step steer maneuver. This maneuver tests the system’s ability to handle abrupt steering changes, providing insight into the controller’s robustness and its capacity to ensure accurate trajectory tracking in demanding conditions.
1. Introduction
Meeting global food demands necessitates improvements in agricultural productivity, and automation of agricultural machinery plays a vital role in this endeavor. By streamlining essential tasks such as plowing, seeding, fertilizing, and harvesting, automation significantly enhances both efficiency and productivity. Moreover, by reducing the time, energy, and resources needed for these operations, it offers a compelling solution for lowering production costs and improving overall farming practices [1,2].
The integration of automated systems in farm tractors offers significant potential to improve the accuracy and precision of field operations, reducing crop damage and minimizing the negative impacts associated with the excessive use of chemical pesticides when performing agrotechnical operation of crop protection. In recent years, significant research and development efforts have been made to advance automation technologies in farm tractors. For example, Ref. [3] explored the use of vision-based techniques to create position-based guidance systems, a field that has greatly benefited from the advent of GPS (Global Positioning System) technology, now widely incorporated into farm tractor guidance systems [4,5,6,7,8,9].
These advances have enabled the development of new controls systems designed to improve steering in agricultural tractors, Refs. [10,11,12,13]. However, it is essential to enhance the performance of automatic guidance systems, especially for tractors connected to implements, as these are responsible for the actual agrotechnical operations in the field [14,15]. Several researchers have developed steering control systems that can manage these implements. For example, Refs. [4,5] developed a computer–controlled steering mechanism based on a mathematical kinematic model of a farmer tractor with a specific towed implement. Similarly, Ref. [6] used a kinetic model of the tractor-implement system to construct a Model Predictive controller (MPC). Finally, Ref. [16] proposed a non-linear controller using basic electronics to ensure the tractor follows a predefined trajectory, which is given by the farmer while driving a tractor.
Although the discussed control strategies focus primarily on steering, their effectiveness is limited when it comes to ensuring precise trajectory tracking in demanding agricultural operations. To overcome this, it is crucial to integrate advanced systems such as Active Front Steering (AFS) and Rear Torque Vectoring (RTV). While these technologies are widely used in the automotive industry, incorporating them into modern agricultural tractors is critical for enhancing control precision and operational efficiency. The capacity to regulate the attitude of a tractor-mounted agricultural system plays a vital role in increasing productivity by preventing operational overlaps and ensuring optimal use of agrochemicals. This requires controllers that not only manage steering but also ensure stability and maneuverability. By replacing traditional mechanical and hydraulic systems with mechatronics, such as AFS and RTV, better control flexibility is achieved. AFS compensates for external disturbances by adjusting the steering angle in response to the driver’s input, while RTV improves tractor stability by utilizing braking subsystems and active differentials to generate a specific yaw moment. Together, these systems eliminate the direct connection between the steering wheel and the wheel assembly, enabling precise trajectory tracking and robust control even under challenging field conditions [17].
This article presents a novel method for robustly controlling an agricultural tractor equipped with a towed implement system, addressing both parametric uncertainties and environmental disturbances. The focus is on managing the lateral and yaw dynamics of the tractor using advanced technologies like AFS and RTV, which are critical for ensuring accurate trajectory tracking. The proposed controller, designed with HOSM estimators, swiftly estimates and compensates for perturbations. This approach is novel, as no prior work has addressed agricultural tractor tracking when subject to unmodeled dynamics and parametric variations. The HOSM estimators guarantee that estimation errors converge to zero in finite time, even under semi-global conditions. Such real-time compensation significantly enhances the system’s robustness, improving both tracking accuracy and operational safety. External factors, like sudden shifts in road conditions or unaccounted dynamics (e.g., rolling, pitching during rapid turns or braking), can alter a tractor’s trajectory, making this control strategy vital for maintaining stability and precise control in challenging environments.
The implementation of controllers such as AFS and RTV has been made possible by the development of so-called “by-wire subsystems”, such as steer-by-wire, brake-by-wire, which replace the existing mechanical and hydraulic subsystems with mechatronics, offering greater flexibility for control design [18,19,20,21]. However, while control strategies like NMPC [22] and adaptive sliding mode controls [23], have been proposed to manage uncertainties, they often require sophisticated estimation techniques to handle real-time parameter variations and unmodeled dynamics. Approaches like the finite time trajectory tracking with nonsingular fast terminal sliding mode [24] or the combination of Moving Horizon Estimation (MHE) and NMPC [25] show promise, but may lack the robustness needed for dynamically varying environments. In contrast, the proposed HOSM-based control strategy integrates advanced compensation mechanisms for both internal parametric uncertainties and external disturbances, enabling precise trajectory tracking under challenging agricultural conditions.
The structure of the paper is as follows: Section 2 outlines the mathematical model of the agricultural tractor equipped with a towed implement system and formulates the control problem. In Section 3, the Control based on nonlinear estimators of parametric uncertainties applied to an agricultural tractor equipped with a towed implement system is presented. Section 4 presents the simulation results, which evaluate the controller’s performance, and demonstrate its robustness and accuracy in handling abrupt steering changes. This section also includes a discussion of these results. The paper culminates with final conclusions that highlight the practical significance of the proposed approach.
2. Mathematical Model of the Tractor–Implement System
The agricultural tractor considered in this section is a rigid body connected to the ground by pneumatic tires, with a towed implement attached at the hitch point, as depicted in Figure 1. This figure illustrates the key velocities and angles in the system, simplifying it into a single-track or "bicycle" model where the front and rear axles are represented as single points. The tractor’s motion is primarily influenced by lateral forces from both the tires and the implement, while the yaw rate is affected by forces acting on both components. The model assumes that longitudinal velocity remains constant, while lateral velocity and yaw dynamics are critical for steering and stability.
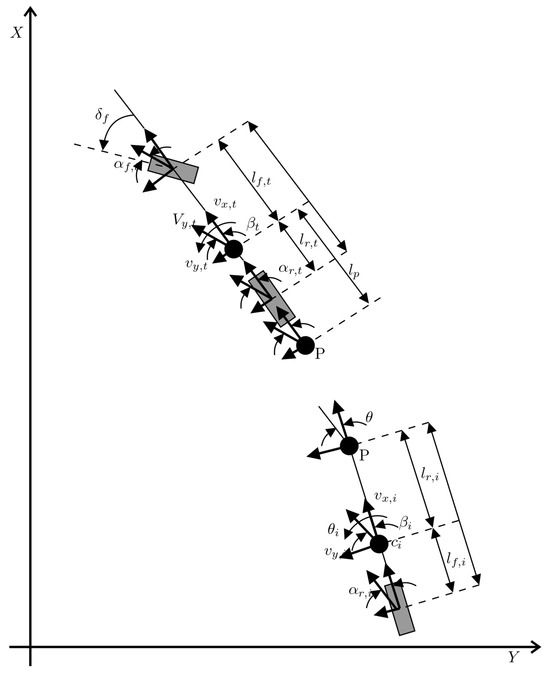
Figure 1.
Dynamic model of the Tractor-Implement system.
The attitude dynamics of the tractor-implement system are characterized by the longitudinal and lateral velocities, along with the yaw rate. The longitudinal velocity can be presented as a constant value or with small variations, so in this case the longitudinal traction forces and rolling resistance are neglected.
In this article, a novel technology is proposed for the application to agricultural tractors. As mentioned in [26,27,28,29], the new tractors can be equipped with “by–wire” technology, i.e., AFS and RTV control systems. The AFS system exerts control through the front tires, which increases the driver’s angle, while the RTV mechanism applies negative lateral force, thus providing an additional yaw moment. It should be noted that these two control actions are decoupled, avoiding interference.
Using the Figure 1 and assuming that the longitudinal velocity of the tractor remains constant, the lateral and yaw velocities can be analyzed in the following mathematical model
where , , represent the tractor’s mass, and the tractor’s moment of inertia around the z-axis. The terms , , and represent the different lengths and distances within the tractor–implement system, where is the length from the front axle to the tractor’s center of gravity, is the length from the rear axle to the tractor’s center of gravity, and denotes the distance between the hitch point and the tractor’s center of gravity. The steering angle is represented by . Additionally, and are the longitudinal and lateral velocities at the tractor’s center of mass, and is the tractor’s yaw rate. The longitudinal force acting on the tractor is , the front and rear lateral forces are and respectively, and is the lateral force applied to the tractor through the implement.
Assumption 1.
The tractor’s steering angle, denoted , is assumed to be small.
Under Assumption 1, the tractor–implement system (1) becomes
To analyze the dynamics of the implement, we can assume that the velocity at the tractor’s center of gravity (CG) is transmitted to the implement’s CG via the hitch point, enabling the subsequent analysis:
In this context, , denote the implement’s longitudinal and lateral velocities, respectively. The yaw rate of the implement is represented by . denotes the front-end length of the implement, and , , where the angle indicates the direction difference between the agricultural tractor and the towed implement.
Considering that the agricultural tractor’s longitudinal velocity closely matches that of the implement (), one may consider the dynamics of the implement’s lateral velocity () to be as follows
However, based on Assumption 1, the angle is expected to remain small.
Assumption 2.
The angle θ that indicates the direction difference between the tractor and the implements is considered small.
Given Assumptions 1 and 2, the dynamics of the implement’s lateral velocity (3) can be expressed as
where
Conversely, the implement’s yaw dynamics is
where the variable represents the rear length of the implement, while the variable represents the implement’s moment of inertia. The lateral force acting on the rear of the implement system, denoted by the variable , and the forces exerted on the implement, represented by the variable .
Therefore, using the system of Equations (2) and (6), it is possible to establish the mathematical model of the agricultural tractor equipped with a towed implement system as:
The Traction Force
In this subsection, we focus on the forces that influence the tractor-implement system. Figure 2 illustrates the key forces affecting the motion of both the tractor and the implement. These include lateral forces on the tires, which are calculated using a nonlinear tire model (Pacejka’s formula), as well as forces transmitted from the implement to the tractor. The lateral tire forces are a function of slip angles, which describe the difference between the direction of the tires and the actual path taken by the vehicle. These forces significantly impact both the tractor’s lateral stability and its yaw moment.
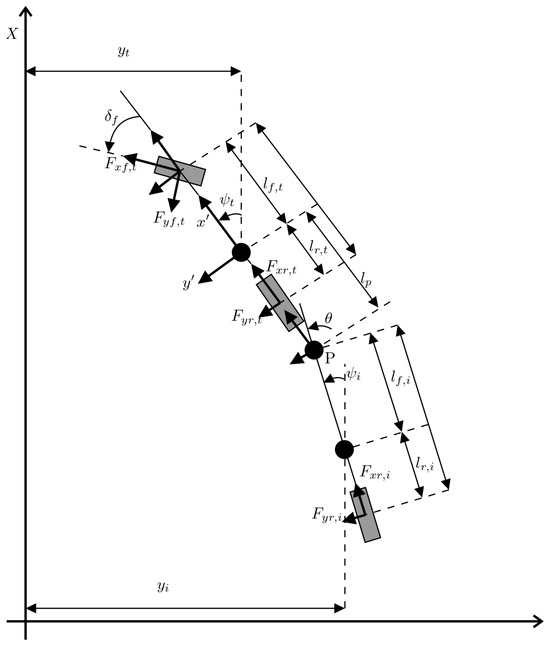
Figure 2.
Forces applied to Tractor-Implement system.
According to the Figure 2, the bicycle model is considered a non-linear system due of the influence of the forces and . The mathematical model of the tire used in this paper is known as the simplified Pacejka formula
where , , , with , and , are parameters determined experimentally [30].
The lateral forces exerted by the front/rear tires on the agricultural tractor, designated as and , respectively, are found to be nonlinearly dependent on the slip angles of the front and rear tires (see Figure 1)
where represents the steering angle of the agricultural tractor, with as the driver’s steering angle and the AFS angle as . In this article it is assumed that the angle is continuously differentiable in time.
The tire slip angle has certain properties, such as a defined minimum and maximum value, . It is also considered an invertible function with respect to , where .
The front tire lateral force, , is assumed to be an invertible function with respect to the AFS control input . Therefore, for a specified value , the equation has a unique solution, given by
The lateral force is treated as an invertible function, allowing the following control input to be considered [31].
The mathematical model of the farmer tractor–implement system, as described in (7), can be rewritten by substituting the controller for the lateral velocity and the controller for the yaw rate as follows
Similarly, the lateral force of the implement system can be obtained in a manner analogous to that described by (2), i.e.,
where depends on the slip angles of the rear tyres . Also, it is possible to solve for the term , such as
and under the following Assumptions 1 and 2, one gets
3. Nonlinear Robust Control
The control objective is to design a nonlinear estimator-based controller that ensures the agricultural tractor’s lateral velocity closely follows the desired reference and that the yaw rate converges to the target , even in the presence of disturbances and parameter uncertainties To achieve this, the error variables and are introduced, with the control problem focusing on designing a controller such that and . A HOSM estimator is used to estimate and cancel disturbances and parametric uncertainties through the controller. It is assumed in this study that the longitudinal velocity remains constant and measurable during the operation of the nonlinear controller. The measurable variables for the farm tractor include the lateral velocity and yaw rate , while the implement provides measurements of the lateral velocity and yaw rate .
Therefore, taking into account the tracking error variables
where and are taken from the Equation (18), we derive the subsequent error dynamical system.
Should one propose a control input of the following form:
with
The resultant system (23) is the closed–loop of the dynamical tracking error (21) and the controller proposed (22). Furthermore, the closed–loop system (23) is asymptotically stable with suitable gains [32].
To guarantee the stability of the closed-loop system against uncertainties in parameters and neglected dynamics, it is essential to express these dynamics using the nominal parameters in the system (21). This approach will highlight the unknown terms, which can then be estimated using a HOSM differentiator. Therefore, denoting
where
with
and
where and represent the nominal masses of the agricultural tractor and towed implement, respectively, and and denote the nominal moments of inertia of the tractor and implement around the z-axis. In addition, the nominal front/rear lateral forces acting on the agricultural tractor are . refers to the nominal rear lateral force on the implement.
The control problem with estimation of variations in external disturbances is solved by the following statement, where , .
Theorem 1.
Under Assumptions 1 and 2, and provided that has bounded derivative , the nonlinear estimator-based control
ensures that the tracking errors , asymptotically converge to zero. Additionally, the estimation errors and converge to zero within finite time. Furthermore, , are bounded such as , for , and
with appropriate bounds.
Proof.
The closed–loop dynamics of , , , can be rewritten as follows
These represent two decoupled subsystems. Focusing on the subsystem formed by the first two Equation (30), i.e.,
one considers the Lyapunov candidate [33]
by performing the derivative with respect to time of , one works out
by grouping previous terms (32)
Hence,
where
Considering that Assumptions 1 and 2 hold, and since the forces in (7) are considered bounded, it can be seen that is bounded. Furthermore, the control inputs and are also bounded. From the Definition (25), the term , and its derivative are also assumed to be bounded, i.e., remains bounded over any finite–time period. Taking into account , the derivative of the Lyapunov function is rewrite as
with , if (29) holds and proposing . It can therefore be concluded that the signals in question are bounded for any finite time interval, and that , ensure that one gets the finite–time convergence of to the origin.
In a manner similar to (31), the following subsystem can be analyzed using the Lyapunov function provided below. i.e.,
can be studied in a similar way, using the Lyapunov candidate
with the bound for for any finite time interval.
□
4. Simulation Results and Discussion
4.1. Simulation Results
This section demonstrates the performance of the robust control for an agricultural tractor equipped with a towed implement system under disturbances and uncertainty estimation as developed in (28). The nominal coefficients for the system adapted by the tractor implement (18) , , , , , , , , . The nominal coefficients of the tire are , , , and , , . Furthermore, the gains of the controller designed in this article (28) are , , . To assess the system’s robustness, the real values of the parameters were varied by to , allowing the nominal values mentioned earlier to be derived.
The simulation results are obtained using Matlab–Simulink. A double-step steer of is proposed as a test maneuver. This maneuver comprises a rapid turn to the left after one second, with an angle of , followed by a rapid turn to the right after 12.5 s, with an angle of . Finally, at 25 s, the steering wheel is set to zero. For a visual representation of this, please refer to Figure 3. A rate limiter is employed to constrain the rate of change of the steering wheel angle throughout the course of this maneuver. This specific maneuver was used because rapid changes in steering angle test the lateral and yaw dynamics of any ground vehicle, including farm tractors. Therefore, this maneuver helps evaluate the control system’s ability to handle abrupt steering changes. This highlights both the controller’s accuracy in maintaining trajectory and its robustness to parametric uncertainties, which is crucial to ensure stability and safety under demanding operating conditions.
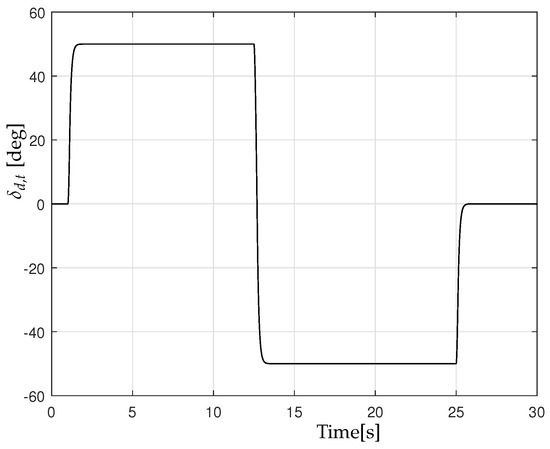
Figure 3.
Steering angle .
The following analysis demonstrates the performance of the tractor-implement system described in (1) when controlled by (22). Figure 3 illustrates the double-step steer maneuver applied to the steering angle.
Remark 1.
The double-step steer maneuver is widely used in the field of ground vehicles. However, in this paper, it is used to demonstrate that any maneuver imposed by the farmer through allows the controller to solve the control problem given in (20).
The variables and represent the behavior of an idealized agricultural tractor model. This model mirrors the mathematical representation of tractor dynamics (1), but with input controls set to zero (i.e., and ) and with decoupled longitudinal and roll dynamics. It is also assumed that the dynamic performance of this reference model aligns with that of the actual tractor. For this purpose, some assumptions are made, such as , and .
with
The reference generator’s lateral force can then be expressed as
where and are selected to emulate the ideal tire characteristics of the farmer tractor. These characteristics help prevent undesirable behaviors in the reference system and remain bounded, which is crucial because the controller might otherwise impose unwanted dynamics on the farm tractor-implement system. To characterize the mathematical model of the reference (33), the following values are proposed , , , , , .
The initial conditions selected to evaluate the controller’s performance, as described in (22), are km/h, km/h, rad/s, km/h, and rad/s.
Remark 2.
The velocity km/h was determined by conducting a survey with several producers in the Ciénega region, Ocotlán, Jalisco, México.
Figure 4 and Figure 5 illustrate and along with their reference values and , as well as the tracking errors and . In Figure 4a and Figure 5a, the controller’s performance is clearly effective despite parameter uncertainties.
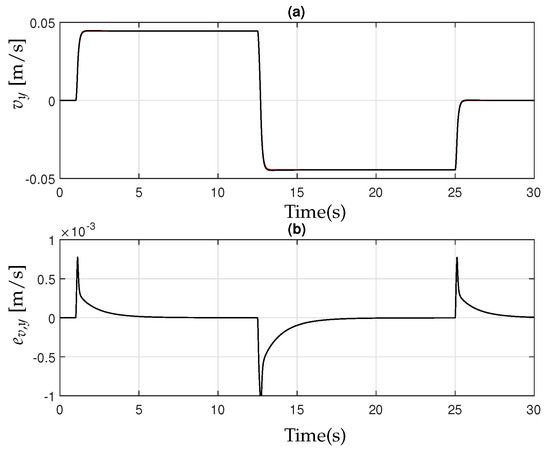
Figure 4.
(a) Tractor lateral velocity (black) and reference (red); (b) Tracking error .
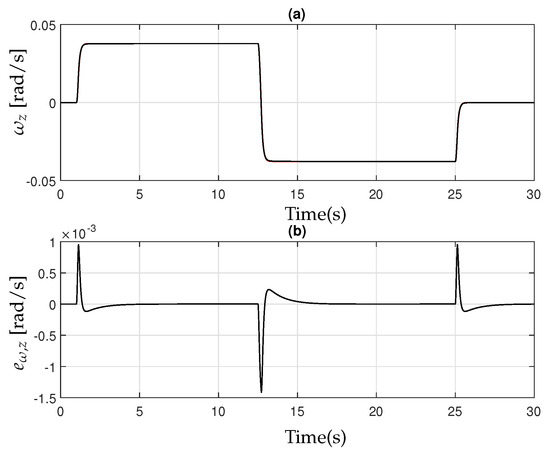
Figure 5.
(a) Tractor Yaw rate (black) and reference (red); (b) Tracking error .
The active control inputs from AFS and from RTV, calculated in (28), are depicted in Figure 6. Figure 7 further illustrates the yaw rate of the implement .
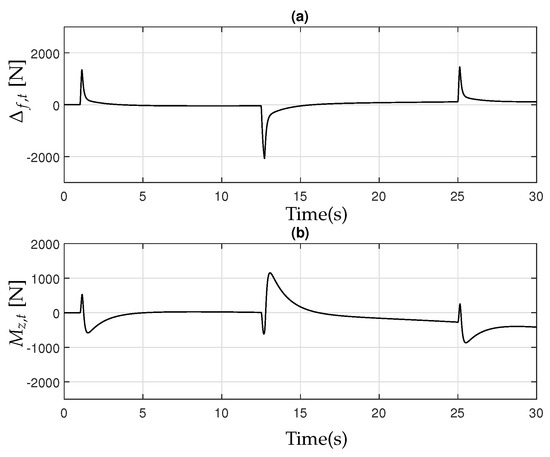
Figure 6.
(a) AFS ; (b) RTV .
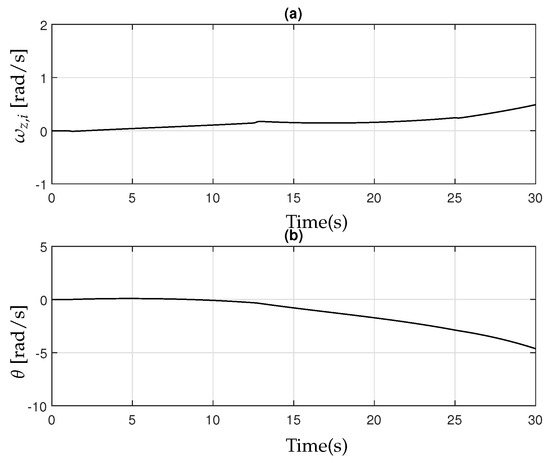
Figure 7.
(a) Yaw rate of the implement ; (b) Difference between .
The controller in (28) utilizes robust differentiators to ensure the closed-loop system remains resilient external disturbances, and unmodeled dynamics. Figure 8a,b present the outputs of the differentiators, and , compared with the tracking errors and . Additionally, Figure 8c,d show the errors and . Similarly, Figure 9a,b display the outputs of the differentiators, and , compared with the tracking errors and . Figure 9c,d show the errors and . The results presented herein demonstrate that the controller referenced in (28) exhibits high performance with practical control actions.
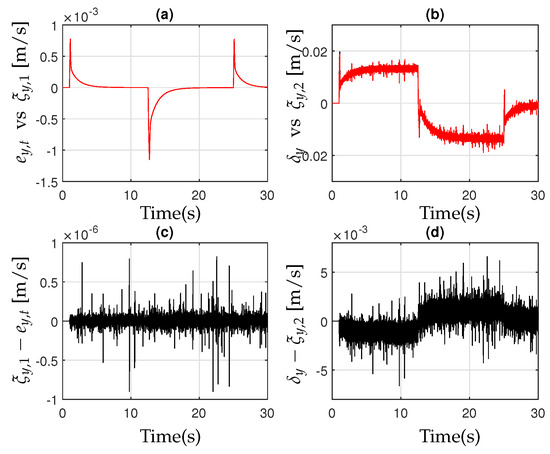
Figure 8.
(a) Tracking error (black) and estimation (red); (b) Parameter estimation (black) and estimation (cyan); (c) Error ; (d) Error .
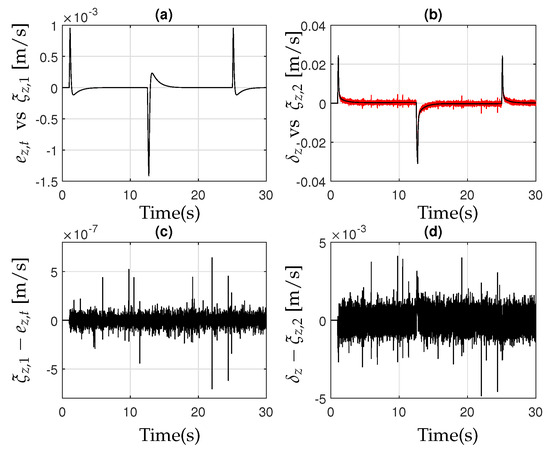
Figure 9.
(a) Tracking error (black) and estimation (red); (b) Parameter estimation (black) and estimation (cyan); (c) Error ; (d) Error .
4.2. Discussion
The proposed control strategy demonstrates notable improvements in adaptability and robustness compared to existing control methods such as Model Predictive Control (MPC) [6] and adaptive controls [34]. While these traditional methods are effective, they often rely on frequent parameter adjustments or approximations that may limit their adaptability under dynamically varying conditions. In contrast, Nonlinear Model Predictive Control (NMPC) [22] and adaptive sliding mode controls [23], offer advanced handling but require sophisticated estimation techniques for real-time applications. The HOSM-based controller developed in this study addresses these challenges more efficiently, providing precise tracking performance and stability by managing both internal parametric uncertainties and external disturbances effectively. This advantage is critical for real-world agricultural applications, where varying terrains and environmental conditions demand robust and adaptable control systems.
5. Conclusions
This study introduces a robust control strategy for agricultural tractors equipped with towed implement systems, designed to compensate for parametric variations, including those arising from tire-road interactions. Nonlinear tire behavior was modeled using Pacejka’s formula to capture the dynamics accurately, and the control strategy was validated through comprehensive Simulink simulations. The control framework integrates a PI-like controller for precise trajectory tracking in the presence of model uncertainties, and employs a High-Order Sliding-Mode (HOSM) estimator to estimate external disturbances in finite time. While simulation results demonstrate that the controller maintains high tracking accuracy and robust performance across varying conditions, future work will focus on implementing the control strategy on real-time digital platforms. This will validate its practical performance under real-world field conditions, providing opportunities for further optimization. Future research will also explore controller optimization for diverse terrains and agricultural implement configurations and integrating advanced sensing technologies, such as cameras or LIDAR, to improve feedback accuracy and dynamic adaptation to environmental changes. Furthermore, this study offers a promising approach that could be recommended to tractor manufacturers to enhance the performance of their control systems by providing a robust solution that compensates for parametric variations and external disturbances, suggesting significant potential for optimizing tractor operation in various field conditions.
Author Contributions
Conceptualization, C.A.L.; methodology, C.A.L. and C.V.V.V.; software, C.A.L.; investigation, C.A.L., J.H.-D. and C.C.V.G.; resources, C.A.L., C.V.V.V., J.H.-D. and C.C.V.G.; writing—original draft preparation, C.A.L.; writing—review and editing, C.V.V.V., J.H.-D. and C.C.V.G.; project administration, C.A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Acknowledgments
Vera Vaca C. V. gratefully acknowledges the scholarship number 827938 provided by CONHACYT to carry out her postgraduate studies from which this research was derived.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Trimble. Available online: https://agriculture.trimble.com/product/ez-guide-250/ (accessed on 28 September 2021).
- Deere, J. Future of Farming. Available online: https://www.deere.co.uk/en/agriculture/future-of-farming/ (accessed on 28 September 2021).
- Reid, J.; Searcy, S. Vision–based guidance of an agriculture tractor. IEEE Control Syst. Mag. 1987, 7, 39–43. [Google Scholar] [CrossRef]
- O’Connor, M.L.; Bell, T.; Elkaim, G.; Parkinson, B. Automatic Steering of Farm Vehicles Using GPS. In Proceedings of the Third International Conference on Precision Agriculture, Madison, WI, USA, 23–26 June 1996; pp. 767–777. [Google Scholar]
- O’Connor, M.L. Carrier–Phase Differential GPS for Automatic Control of Land Vehicles. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1997. [Google Scholar]
- Bell, T. Precision Robotic Control of Agricultural Vehicles on Realistic Farm Trajectories. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1999. [Google Scholar]
- Bell, T. Automatic tractor guidance using carrier–phase differential GPS. Comput. Electron. Agric. 2000, 25, 53–66. [Google Scholar] [CrossRef]
- Erickson, B.; Widmar, D.A. Precision Agricultural Services Dealership Survey Results; Purdue University: West Lafayette, IN, USA, 2015. [Google Scholar]
- Poteko, J.; Eder, D.; Noack, P.O. Identifying operation modes of agricultural vehicles based on GNSS measurements. Comput. Electron. Agric. 2021, 185, 106105. [Google Scholar] [CrossRef]
- Stombaugh, T.S.; Benson, E.R.; Hummel, J.W. Guidance control of agricultural vehicles at high field speeds. Trans. ASAE 1999, 42, 537. [Google Scholar] [CrossRef]
- Yin, C.; Wang, S.; Gao, J.; Zhao, L.; Miao, H. Steering Tracking Control Based on Assisted Motor for Agricultural Tractors. Int. J. Control Autom. Syst. 2019, 17, 2556–2564. [Google Scholar] [CrossRef]
- Karkee, M.; Steward, B.L. Study of the open and closed loop characteristics of a tractor and a single axle towed implement system. J. Terramech. 2010, 47, 379–393. [Google Scholar] [CrossRef]
- Bevly, D.M.; Gerdes, J.C.; Parkinson, B.W. A new yaw dynamic model for improved high speed control of a farm tractor. J. Dyn. Syst. Meas. Control 2002, 124, 659–667. [Google Scholar] [CrossRef]
- Bevly, D.M. High Speed, Dead Reckoning, and Towed Implement Control for Automatically Steered Farm Tractors Using GPS. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2001. [Google Scholar]
- Pota, H.; Katupitiya, J.; Eaton, R. Simulation of a tractor-implement model under the influence of lateral disturbances. In Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 596–601. [Google Scholar]
- Sandoval-Pérez, S.; González-López, J.M.; Jimenez-Betancourt, R.O.; Villalvazo-Laureano, E.; Molinar-Solís, E.; Sánchez-Cervantes, M.G.; Ochoa-Guzmán, V.J. A Low-Cost Platform for Modeling and Controlling the Yaw Dynamics of an Agricultural Tractor to Gain Autonomy. Electronics 2020, 9, 1826. [Google Scholar] [CrossRef]
- Burgio, G.; Castillo-Toledo, B.; Di Gennaro, S. Nonlinear adaptive tracking for ground vehicles. In Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai, China, 15–18 December 2009; pp. 7645–7650. [Google Scholar]
- Ley-Rosas, J.J.; González-Jiménez, L.; Loukianov, A.G.; Ruiz-Duarte, J.E. Observer based sliding mode controller for vehicles with roll dynamics. J. Frankl. Inst. 2019, 356, 2559–2581. [Google Scholar] [CrossRef]
- Etienne, L.; Acosta Lúa, C.; Di Gennaro, S.; Barbot, J.-P. A Super–Twisting Controller for Active Control of Ground Vehicles with Lateral Tire–Road Friction Estimation and CarSim Validation. Int. J. Control Autom. Syst. 2020, 18, 1177–1189. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Wang, Z. Chassis Coordinated Control for Full X-by-Wire Vehicles—A Review. Chin. J. Mech. Eng. 2021, 34, 42. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, C. Nonlinear Stability Control of Steer-by-Wire System. In Nonlinear Control Technology of Vehicle Chassis-by-Wire System; Recent Advancements in Connected Autonomous Vehicle Technologies; Springer: Singapore, 2022; Volume 2. [Google Scholar]
- Backman, J.; Oksanen, T.; Visala, A. Nonlinear Model Predictive Trajectory Control in Tractor-Trailer System for Parallel Guidance in Agricultural Field Operations. IFAC Proc. Vol. 2010, 43, 133–138. [Google Scholar] [CrossRef]
- Yin, C.; Wang, S.; Li, X.; Yuan, G.; Jiang, C. Trajectory Tracking Based on Adaptive Sliding Mode Control for Agricultural Tractor. IEEE Access 2020, 8, 113021–113029. [Google Scholar] [CrossRef]
- Zhang, T.; Jiao, X.; Lin, Z. Finite Time Trajectory Tracking Control of Autonomous Agricultural Tractor Integrated Nonsingular Fast Terminal Sliding Mode and Disturbance Observer. Biosyst. Eng. 2022, 219, 53–164. [Google Scholar] [CrossRef]
- Kraus, T.; Ferreau, H.J.; Kayacan, E.; Ramon, H.; De Baerdemaeker, J.; Diehl, M.; Saeys, W. Moving Horizon Estimation and Nonlinear Model Predictive Control for Autonomous Agricultural Vehicles. Comput. Electron. Agric. 2013, 98, 25–33. [Google Scholar] [CrossRef]
- Eglington, M.; O’Connor, M.; Leckie, L.; Sapilewski, G. System and Method for Guiding an Agricultural Vehicle through a Recorded Template of Guide Paths. U.S. Patent 20060178820A1, 4 February 2005. [Google Scholar]
- Blackwell, R.; Schildroth, R.; Myers, M.J.; Rolffs, M.J.; Becker, D. Autonomous Systems, Methods, and Apparatus for Ag Based Operations. U.S. Patent 20150105963A1, 10 October 2014. [Google Scholar]
- Basset, D.; Arthur, R.J. Modular Autonomous Farm Vehicle. U.S. Patent 20170164548A1, 11 April 2017. [Google Scholar]
- Shah, J. Pull-Drift-Compensation Mittels AFS. U.S. Patent 20150105965A1, 3 August 2018. [Google Scholar]
- Pacejka, H. Tyre and Vehicle Dynamics; Elsevier Butterworth—Heinemann: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Acosta Lua, C.; Bianchi, D.; Di Gennaro, S. Nonlinear Observer–Based Adaptive Control of Ground Vehicles with Uncertainty Estimation. J. Frankl. Inst. 2023, 360, 14175–14189. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice–Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Kayacan, E.; Kayacan, E.; Ramon, H.; Saeys, W. Nonlinear modeling and identification of an autonomous tractor–trailer system. Comput. Electron. Agric. 2014, 106, 1–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).