Integrating Actuator Fault-Tolerant Control and Deep-Learning-Based NDVI Estimation for Precision Agriculture with a Hexacopter UAV
Abstract
1. Introduction
- 1.
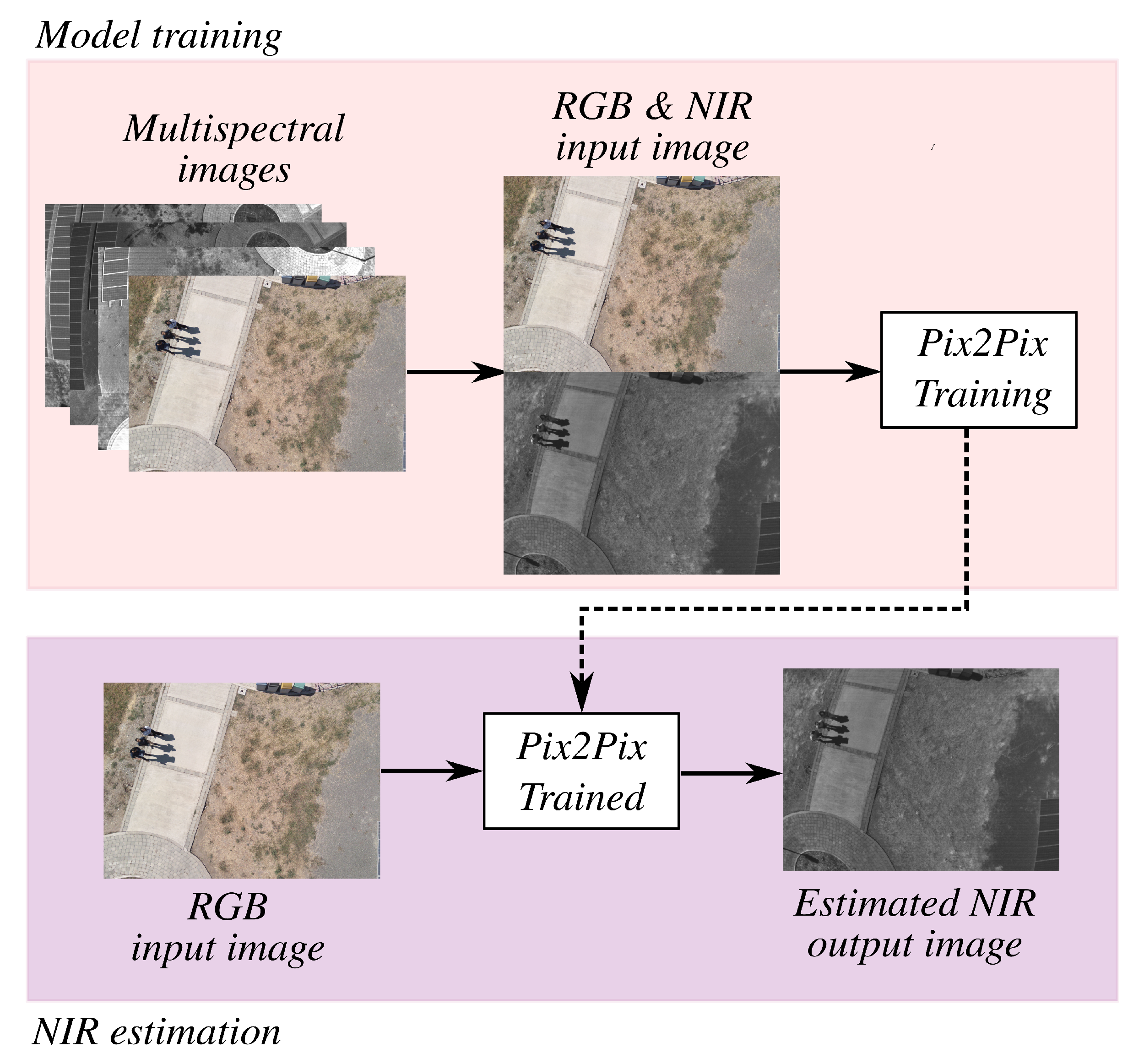
- The development of an actuator fault-tolerant control strategy specifically designed for a hexacopter UAV in precision agriculture applications. The proposed approach integrates advanced sensing techniques, such as the estimation of NIR reflectance from RGB imagery using the Pix2Pix deep learning network based on conditional Generative Adversarial Networks (cGANs) to enable the calculation of the NDVI for crop health assessment. In this work, the NDVI is presented for a sugarcane crop using the estimated NIR to assess the crop’s condition during its tillering stage.
- 2.
- The design of a trajectory planning that ensures efficient coverage of the targeted agricultural area while considering the vehicle’s dynamics and fault-tolerant capabilities, even in the presence of total actuator failures.
- 3.
- The validation of the proposed FTC system through extensive simulations using MATLAB. The effectiveness of the system is demonstrated in a simulation by considering agriculture flight planning.
- 4.
- The successful integration of advanced sensing techniques, FTC strategies, and trajectory planning to create a comprehensive solution for reliable and accurate data collection in precision agriculture applications using hexacopter UAVs, even in the presence of actuator failures.
2. Materials and Methods
2.1. Aircraft Description
2.2. Hexacopter UAV Dynamics Model
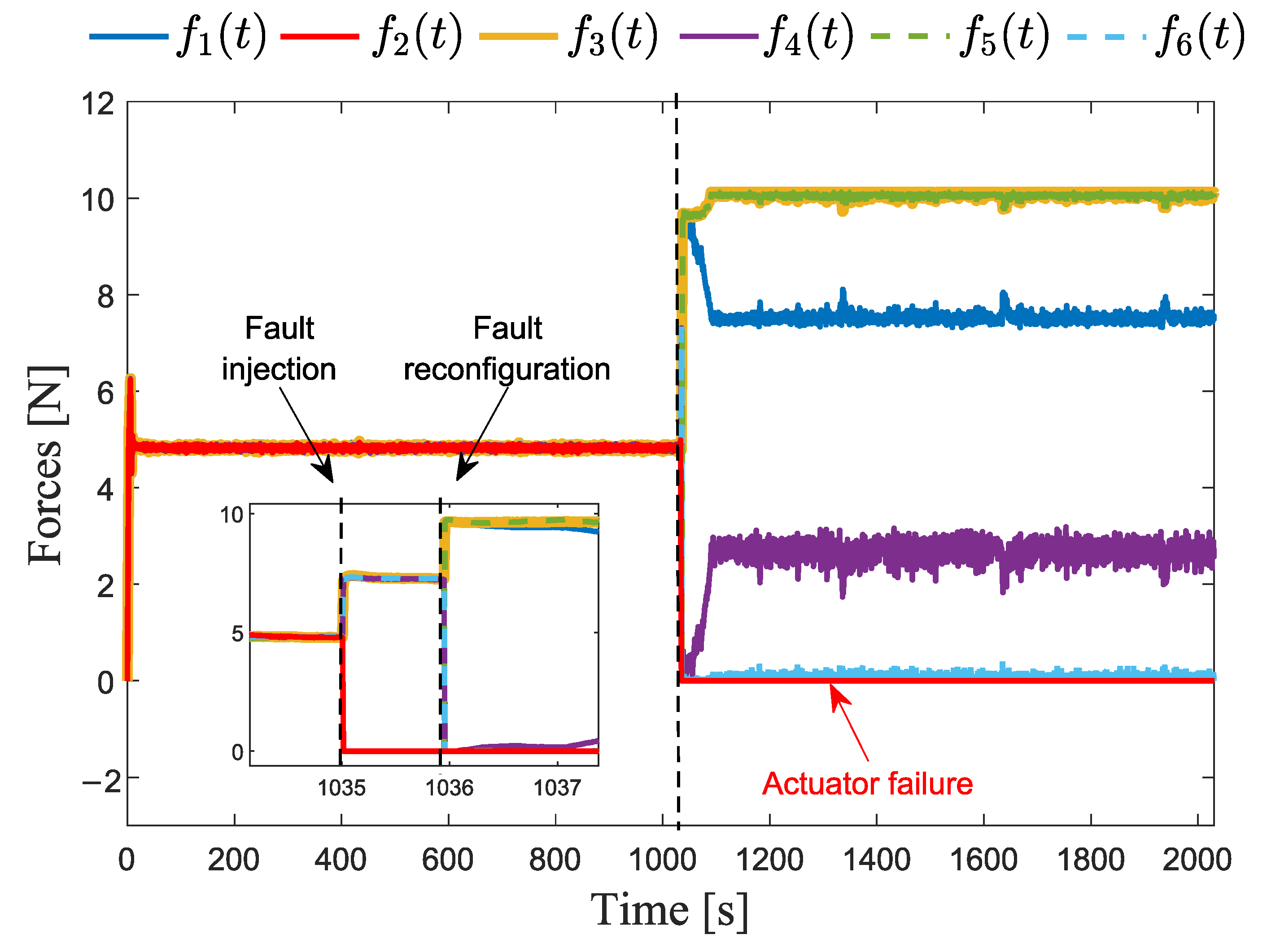
2.3. Fault-Tolerant Control System
2.3.1. Attitude and Altitude Controller
2.3.2. Translational Controller
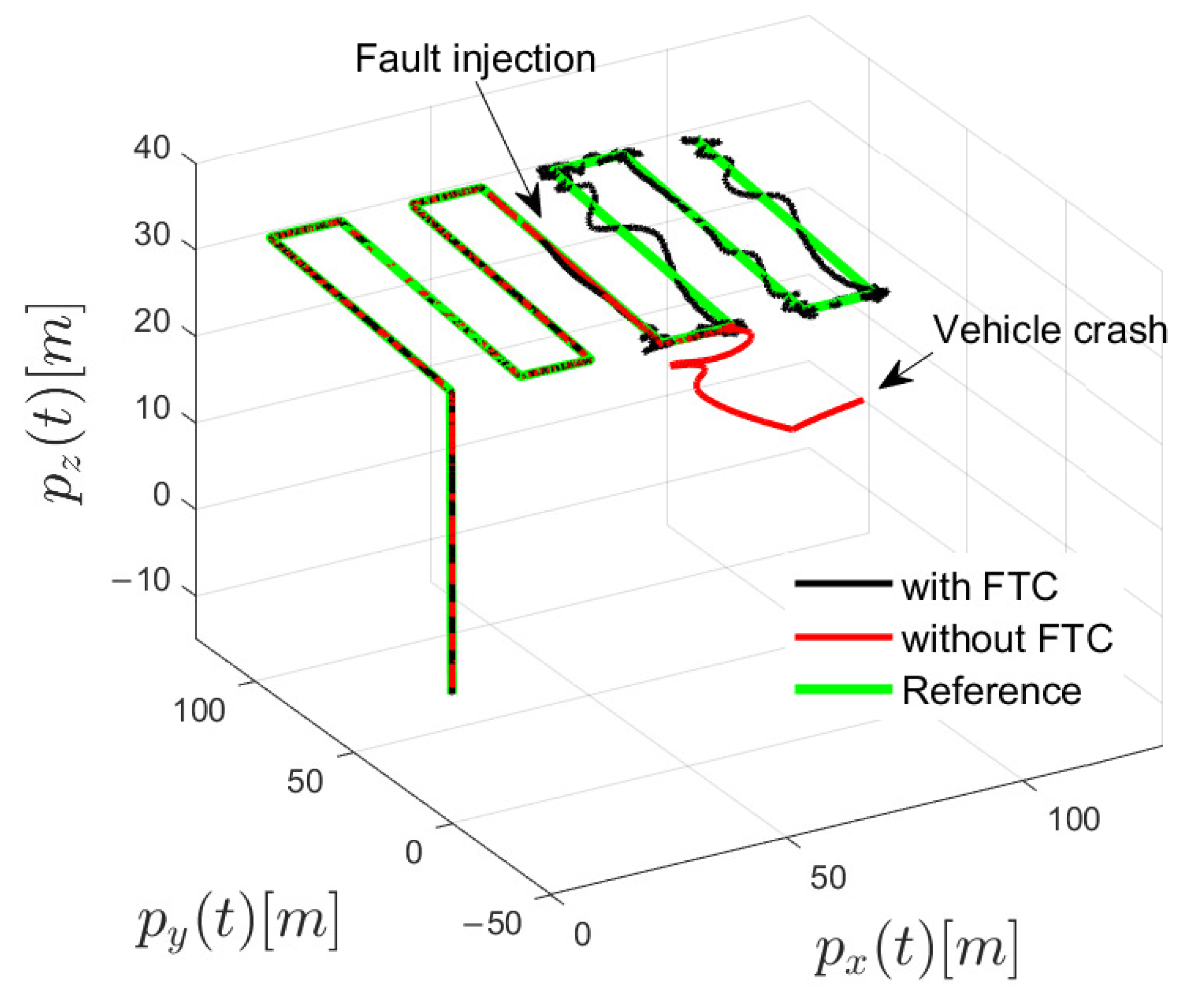
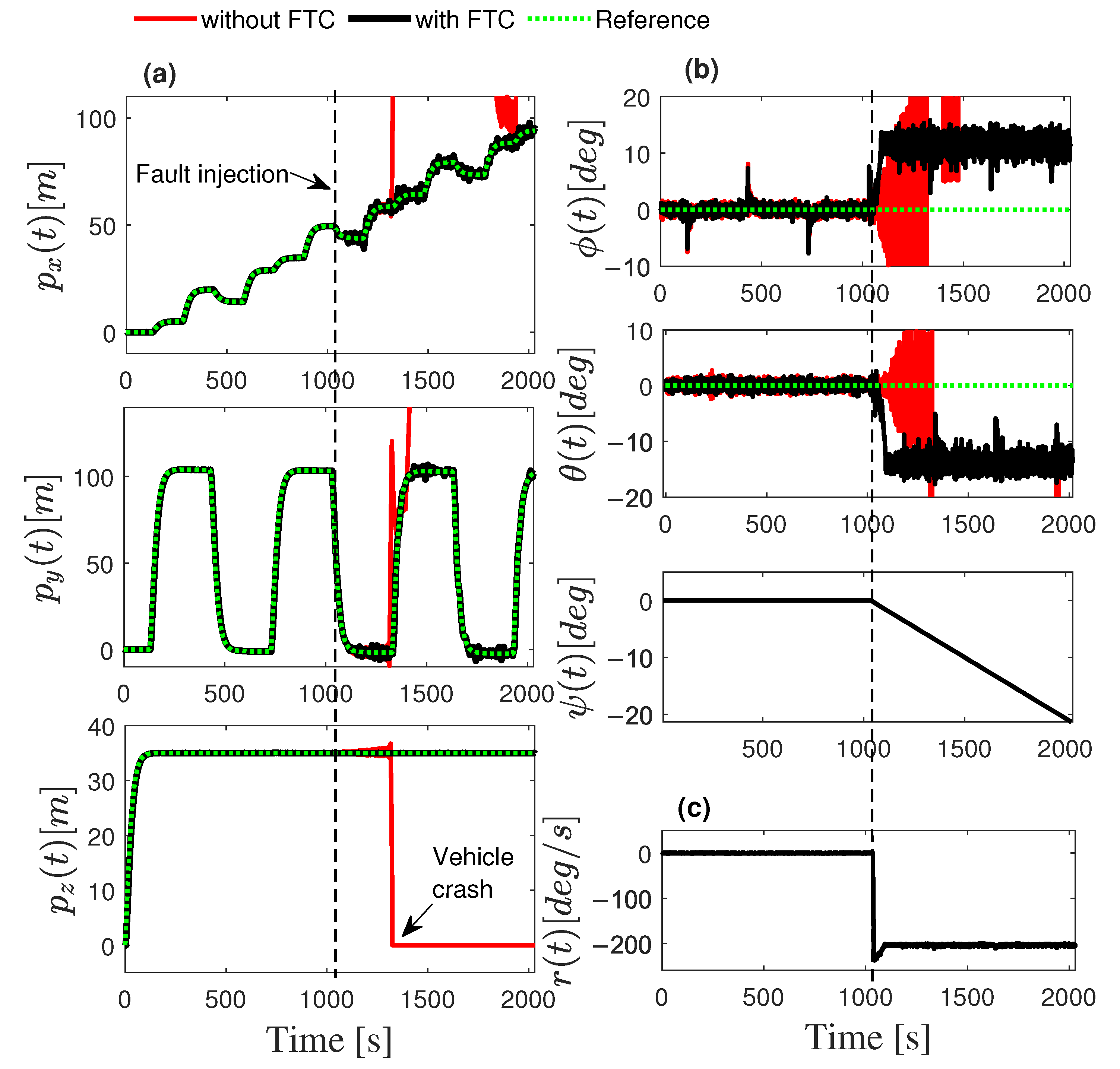
2.4. Validation of the Fault-Tolerant Control Scheme
2.5. In-Flight Image Acquisition
2.5.1. Digital Camera
2.5.2. Multispectral Camera
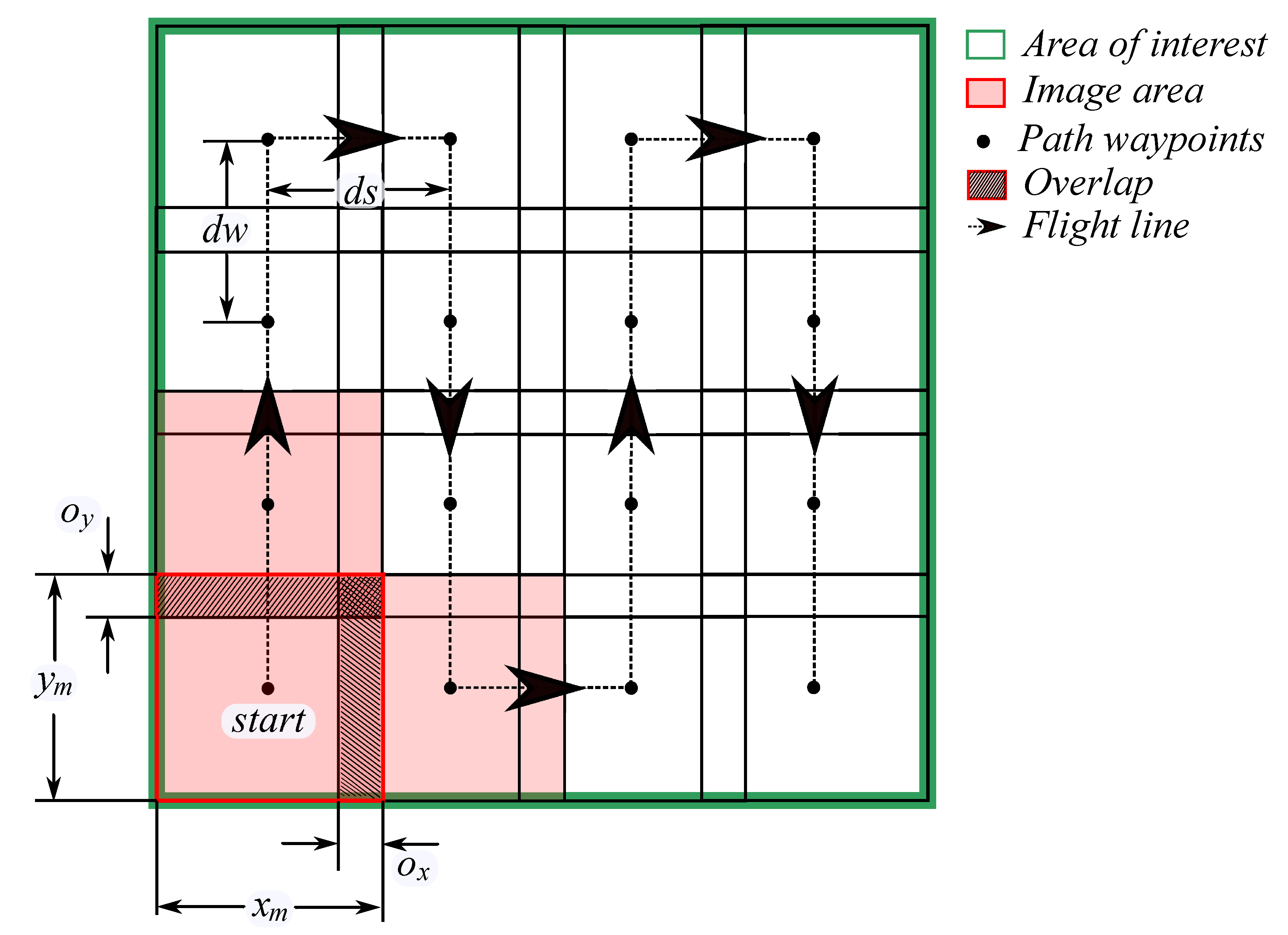
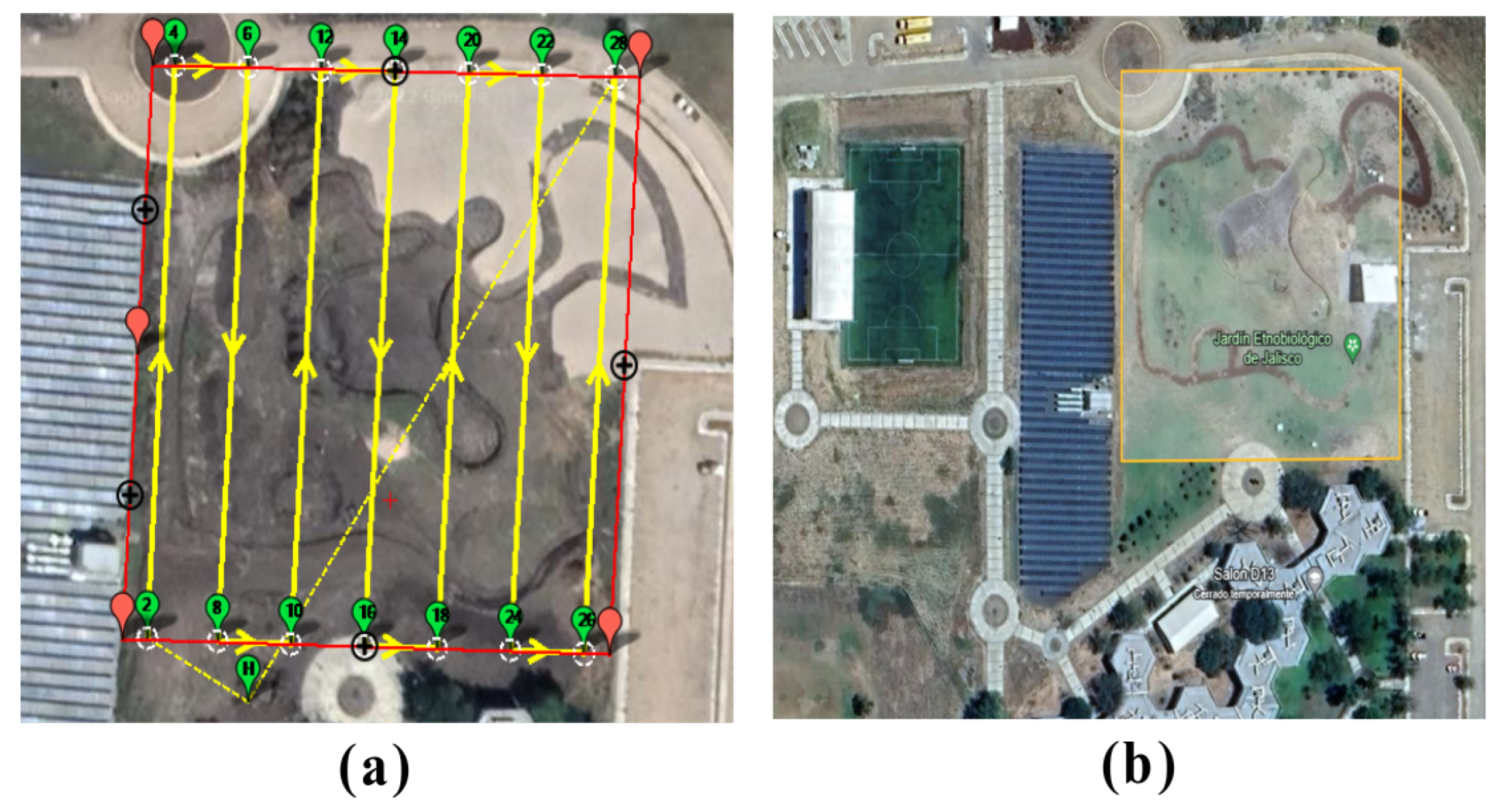
2.6. Data Collection and Flight Planning
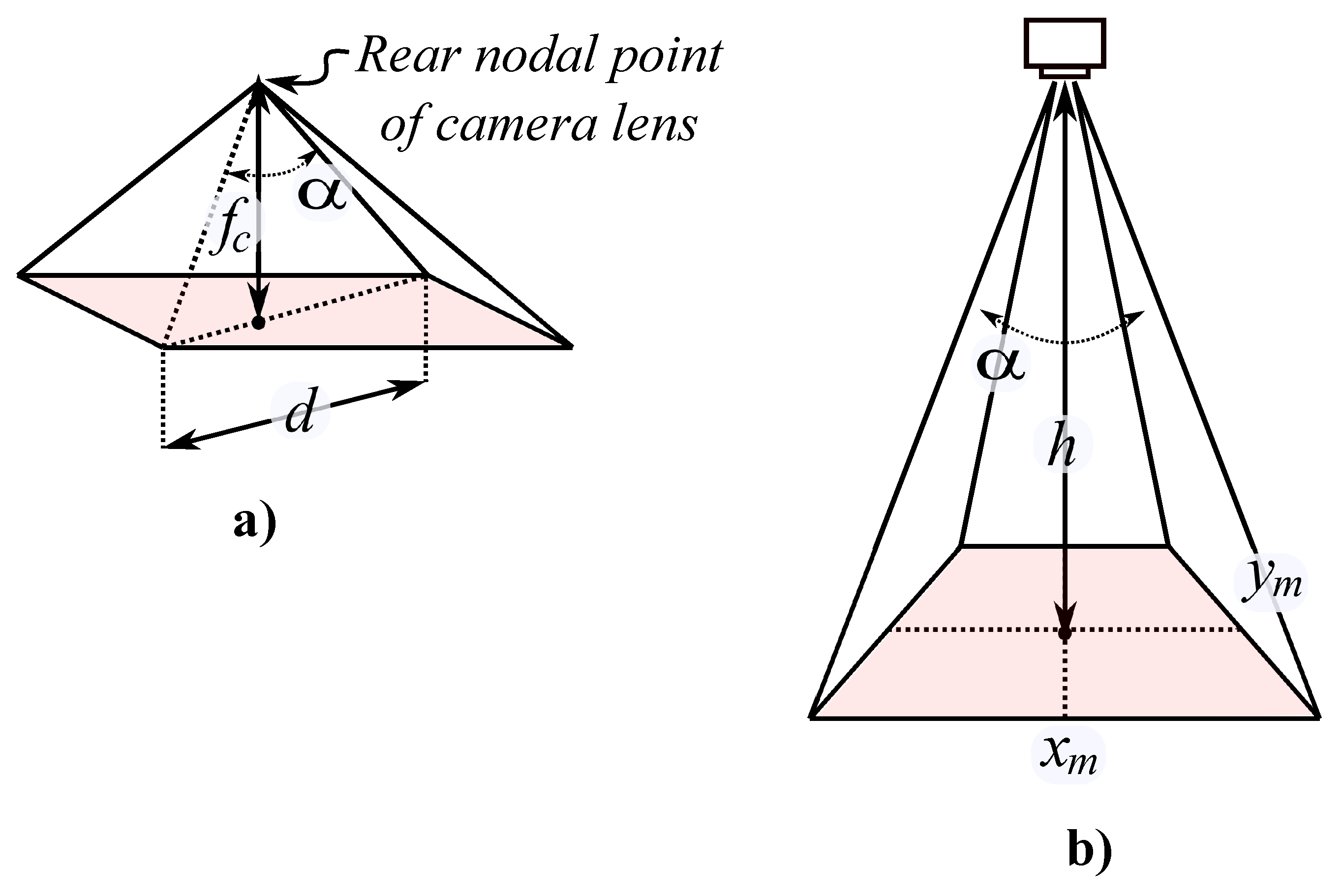
2.6.1. Camera Model
2.6.2. Estimation of Agricultural Near-Infrared Images from RGB Data
3. Results
3.1. Scenario 1—Experimental Flight Planning and Data Collection
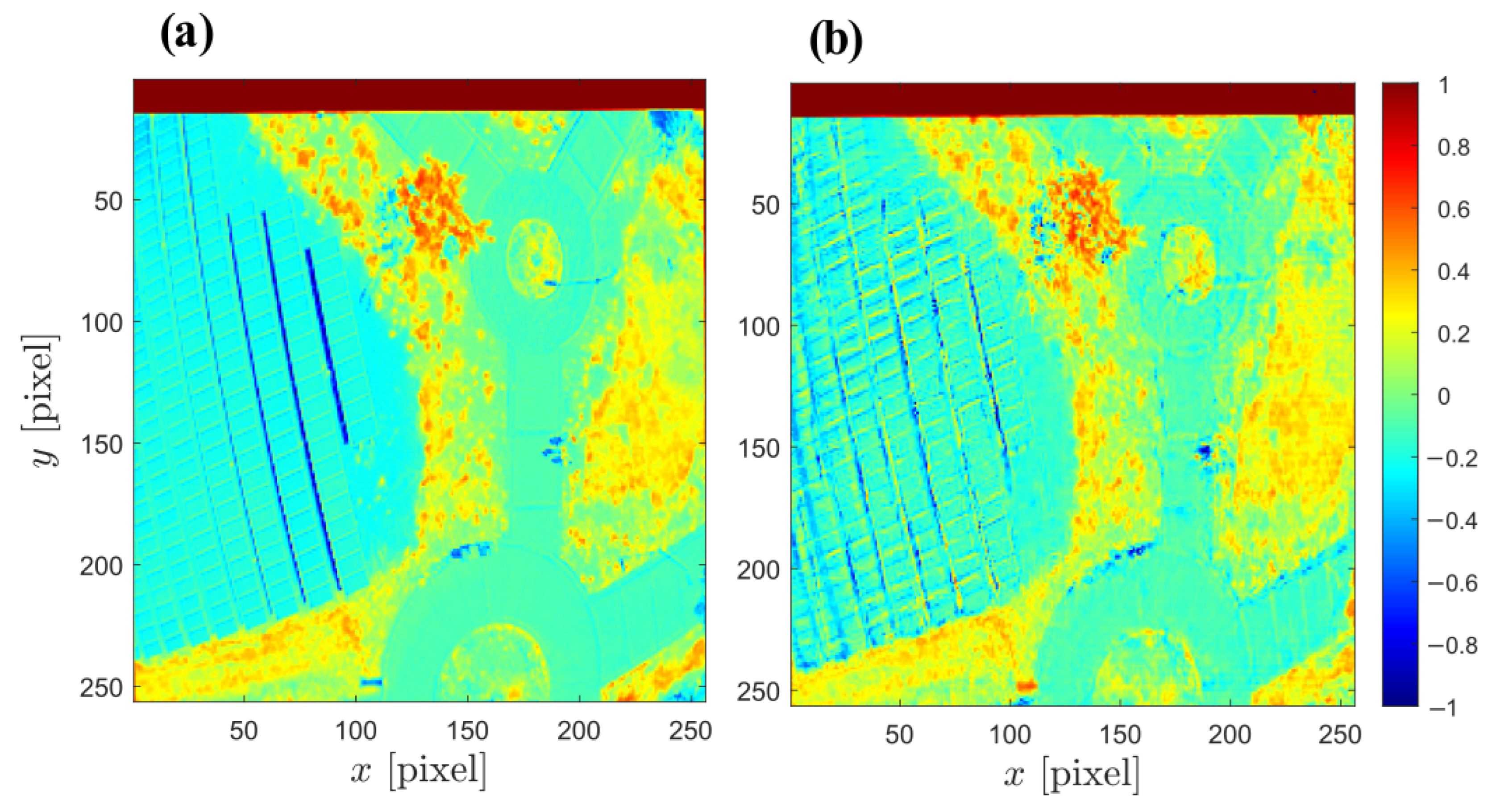
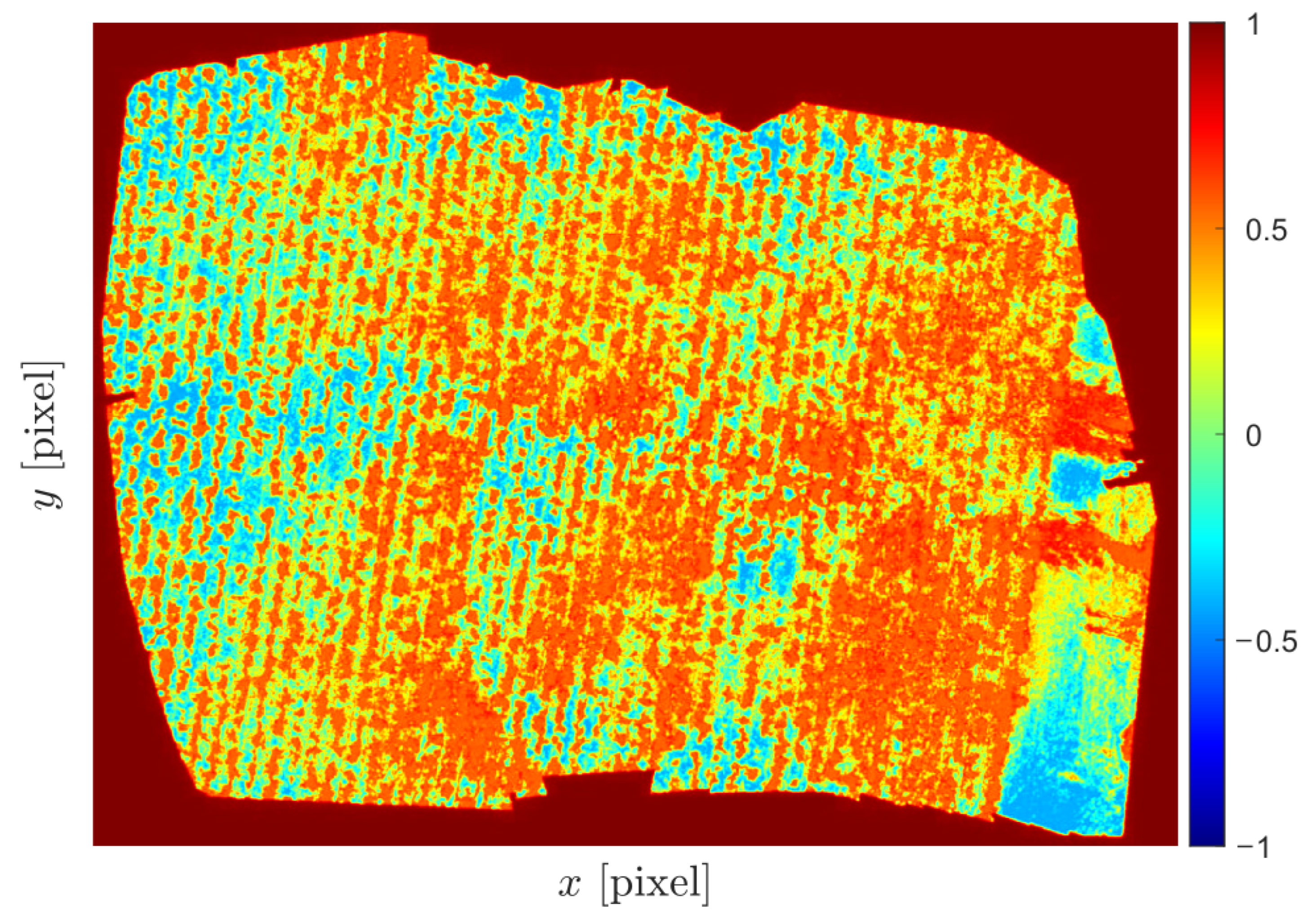
3.2. Scenario 2—Experimental Estimation of Agricultural NIR Band
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alzahrani, B.; Oubbati, O.S.; Barnawi, A.; Atiquzzaman, M.; Alghazzawi, D. UAV assistance paradigm: State-of-the-art in applications and challenges. J. Netw. Comput. Appl. 2020, 166, 102706. [Google Scholar] [CrossRef]
- Sadeghzadeh, I.; Zhang, Y. A review on fault-tolerant control for unmanned aerial vehicles (UAVs). In Proceedings of the Infotech@ Aerospace 2011, St. Louis, MO, USA, 29–31 March 2011; p. 1472. [Google Scholar]
- Fourlas, G.K.; Karras, G.C. A survey on fault diagnosis and fault-tolerant control methods for unmanned aerial vehicles. Machines 2021, 9, 197. [Google Scholar] [CrossRef]
- Saied, M.; Shraim, H.; Francis, C. A Review on Recent Development of Multirotor UAV Fault-Tolerant Control Systems. IEEE Aerosp. Electron. Syst. Mag. 2023, 1, 1–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Saussie, D.; Saydy, L. Design and experimental validation of robust self-scheduled fault-tolerant control laws for a multicopter UAV. IEEE/ASME Trans. Mechatronics 2020, 26, 2548–2557. [Google Scholar] [CrossRef]
- Saied, M.; Lussier, B.; Fantoni, I.; Shraim, H.; Francis, C. Active versus passive fault-tolerant control of a redundant multirotor UAV. Aeronaut. J. 2020, 124, 385–408. [Google Scholar] [CrossRef]
- Asadi, D.; Ahmadi, K.; Nabavi, S.Y. Fault-tolerant trajectory tracking control of a quadcopter in presence of a motor fault. Int. J. Aeronaut. Space Sci. 2022, 23, 129–142. [Google Scholar] [CrossRef]
- Dutta, A.; Niemiec, R.; Kopsaftopoulos, F.; Gandhi, F. Machine-Learning Based Rotor Fault Diagnosis in a Multicopter with Strain Data. AIAA J. 2023, 61, 4182–4194. [Google Scholar] [CrossRef]
- Rot, A.G.; Hasan, A.; Manoonpong, P. Robust actuator fault diagnosis algorithm for autonomous hexacopter UAVs. IFAC-PapersOnLine 2020, 53, 682–687. [Google Scholar] [CrossRef]
- Emran, B.J.; Najjaran, H. A review of quadrotor: An underactuated mechanical system. Annu. Rev. Control 2018, 46, 165–180. [Google Scholar] [CrossRef]
- Kim, M.; Lee, H.; Kim, J.; Kim, S.H.; Kim, Y. Hierarchical fault tolerant control of a hexacopter UAV against actuator failure. In Proceedings of the International Conference on Robot Intelligence Technology and Applications; Springer: Cham, Switzerland, 2021; pp. 79–90. [Google Scholar]
- Pose, C.D.; Giribet, J.I.; Mas, I. Fault tolerance analysis for a class of reconfigurable aerial hexarotor vehicles. IEEE/ASME Trans. Mechatronics 2020, 25, 1851–1858. [Google Scholar] [CrossRef]
- Colombo, L.J.; Giribet, J.I. Learning-Based Fault-Tolerant Control for an Hexarotor With Model Uncertainty. IEEE Trans. Control. Syst. Technol. 2023, 32, 672–679. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A review on UAV-based applications for precision agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Gandhi, G.M.; Parthiban, S.; Thummalu, N.; Christy, A. Ndvi: Vegetation Change Detection Using Remote Sensing and Gis—A Case Study of Vellore District. Procedia Comput. Sci. 2015, 57, 1199–1210. [Google Scholar] [CrossRef]
- Rabatel, G.; Labbé, S. Registration of visible and near infrared unmanned aerial vehicle images based on Fourier-Mellin transform. Precis. Agric. 2016, 17, 564–587. [Google Scholar] [CrossRef]
- Zheng, H.; Li, W.; Jiang, J.; Liu, Y.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; Zhang, Y.; Yao, X. A comparative assessment of different modeling algorithms for estimating leaf nitrogen content in winter wheat using multispectral images from an unmanned aerial vehicle. Remote Sens. 2018, 10, 2026. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Brisolara, L.B.; Ferreira, P.R., Jr. Survey on coverage path planning with unmanned aerial vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Vivaldini, K.C.; Martinelli, T.H.; Guizilini, V.C.; Souza, J.R.; Oliveira, M.D.; Ramos, F.T.; Wolf, D.F. UAV route planning for active disease classification. Auton. Robot. 2019, 43, 1137–1153. [Google Scholar] [CrossRef]
- Basiri, A.; Mariani, V.; Silano, G.; Aatif, M.; Iannelli, L.; Glielmo, L. A survey on the application of path-planning algorithms for multi-rotor UAVs in precision agriculture. J. Navig. 2022, 75, 364–383. [Google Scholar] [CrossRef]
- Vazquez-Carmona, E.V.; Vasquez-Gomez, J.I.; Herrera-Lozada, J.C.; Antonio-Cruz, M. Coverage path planning for spraying drones. Comput. Ind. Eng. 2022, 168, 108125. [Google Scholar] [CrossRef]
- Zhao, Z.; Jin, X. Adaptive neural network-based sliding mode tracking control for agricultural quadrotor with variable payload. Comput. Electr. Eng. 2022, 103, 108336. [Google Scholar] [CrossRef]
- Mogili, U.R.; Deepak, B. Review on application of drone systems in precision agriculture. Procedia Comput. Sci. 2018, 133, 502–509. [Google Scholar] [CrossRef]
- Puri, V.; Nayyar, A.; Raja, L. Agriculture drones: A modern breakthrough in precision agriculture. J. Stat. Manag. Syst. 2017, 20, 507–518. [Google Scholar] [CrossRef]
- Hafeez, A.; Husain, M.A.; Singh, S.; Chauhan, A.; Khan, M.T.; Kumar, N.; Chauhan, A.; Soni, S. Implementation of drone technology for farm monitoring & pesticide spraying: A review. Inf. Process. Agric. 2022, 10, 192–203. [Google Scholar]
- Ortiz-Torres, G.; Castillo, P.; Sorcia-Vázquez, F.D.; Rumbo-Morales, J.Y.; Brizuela-Mendoza, J.A.; De La Cruz-Soto, J.; Martínez-García, M. Fault estimation and fault tolerant control strategies applied to VTOL aerial vehicles with soft and aggressive actuator faults. IEEE Access 2020, 8, 10649–10661. [Google Scholar] [CrossRef]
- Morales, J.Y.R.; Mendoza, J.A.B.; Torres, G.O.; Vázquez, F.d.J.S.; Rojas, A.C.; Vidal, A.F.P. Fault-tolerant control implemented to Hammerstein–Wiener model: Application to bio-ethanol dehydration. Fuel 2022, 308, 121836. [Google Scholar] [CrossRef]
- Du, G.X.; Quan, Q.; Yang, B.; Cai, K.Y. Controllability analysis for multirotor helicopter rotor degradation and failure. J. Guid. Control. Dyn. 2015, 38, 978–985. [Google Scholar] [CrossRef]
- Freddi, A.; Lanzon, A.; Longhi, S. A feedback linearization approach to fault tolerance in quadrotor vehicles. IFAC Proc. Vol. 2011, 44, 5413–5418. [Google Scholar] [CrossRef]
- Delavarpour, N.; Koparan, C.; Nowatzki, J.; Bajwa, S.; Sun, X. A technical study on UAV characteristics for precision agriculture applications and associated practical challenges. Remote Sens. 2021, 13, 1204. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A.; Wilkinson, B.E. Elements of Photogrammetry with Applications in GIS; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Di Franco, C.; Buttazzo, G. Coverage path planning for UAVs photogrammetry with energy and resolution constraints. J. Intell. Robot. Syst. 2016, 83, 445–462. [Google Scholar] [CrossRef]
- Wang, L.; Duan, Y.; Zhang, L.; Rehman, T.U.; Ma, D.; Jin, J. Precise estimation of NDVI with a simple NIR sensitive RGB camera and machine learning methods for corn plants. Sensors 2020, 20, 3208. [Google Scholar] [CrossRef] [PubMed]
- Damian, J.M.; de Castro Pias, O.H.; Cherubin, M.R.; da Fonseca, A.Z.; Fornari, E.Z.; Santi, A.L. Applying the NDVI from satellite images in delimiting management zones for annual crops. Sci. Agric. 2019, 77, e20180055. [Google Scholar] [CrossRef]
- de Lima, D.C.; Saqui, D.; Mpinda, S.A.T.; Saito, J.H. Pix2pix network to estimate agricultural near infrared images from rgb data. Can. J. Remote Sens. 2022, 48, 299–315. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Li, C.; Wand, M. Precomputed real-time texture synthesis with markovian generative adversarial networks. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part III 14. Springer: Cham, Switzerland, 2016; pp. 702–716. [Google Scholar]
- Dong, W.; Zhang, C.N.; Yu, Q.; Li, H. Image quality assessment using rough fuzzy integrals. In Proceedings of the 27th International Conference on Distributed Computing Systems Workshops-Supplements (ICDCSW’07), Toronto, ON, Canada, 22–29 June 2007; pp. 1–5. [Google Scholar]
- Horé, A.; Ziou, D. Is there a relationship between peak-signal-to-noise ratio and structural similarity index measure? IET Image Process. 2013, 7, 12–24. [Google Scholar] [CrossRef]
- Zheng, Y.; dos Santos Luciano, A.C.; Dong, J.; Yuan, W. High-resolution map of sugarcane cultivation in Brazil using a phenology-based method. Earth Syst. Sci. Data Discuss. 2021, 2021, 2065–2080. [Google Scholar] [CrossRef]

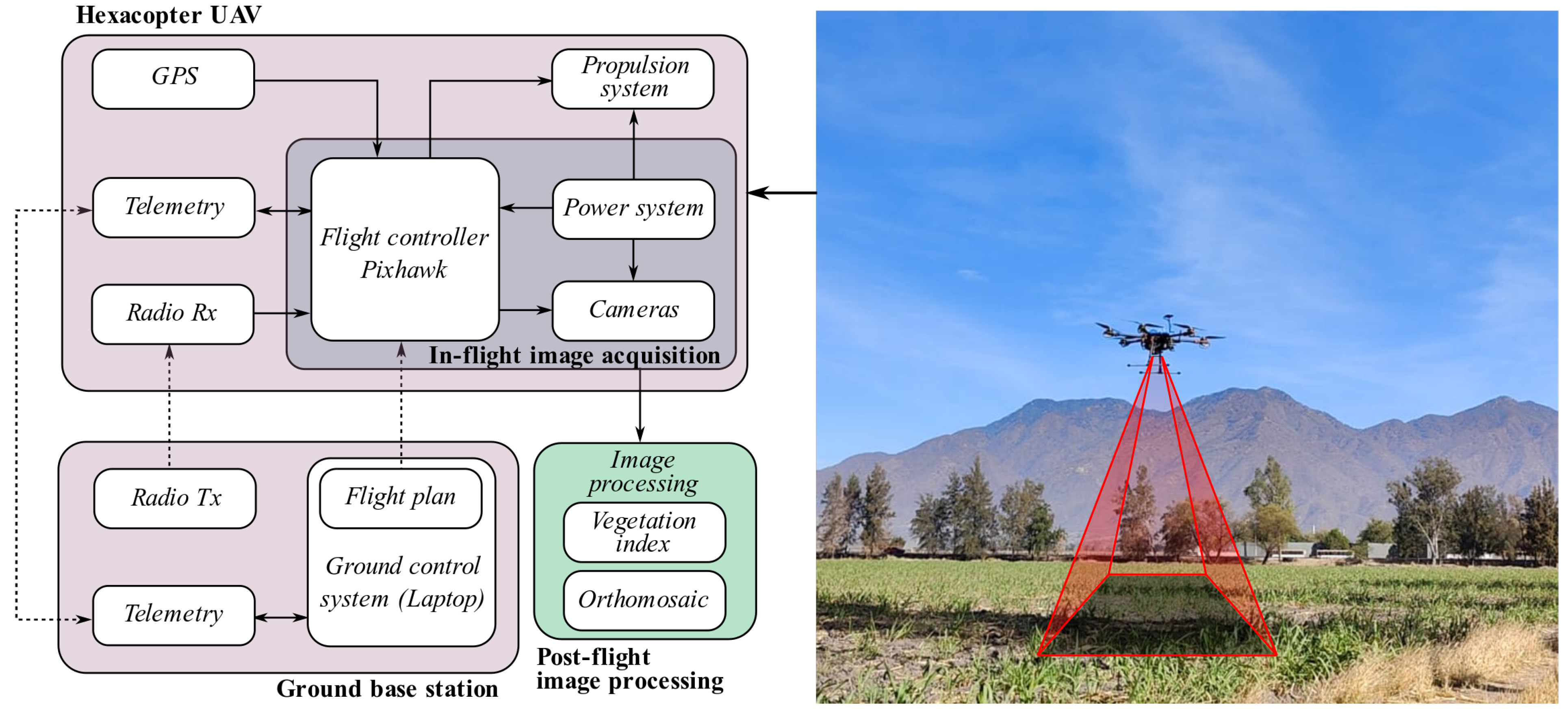
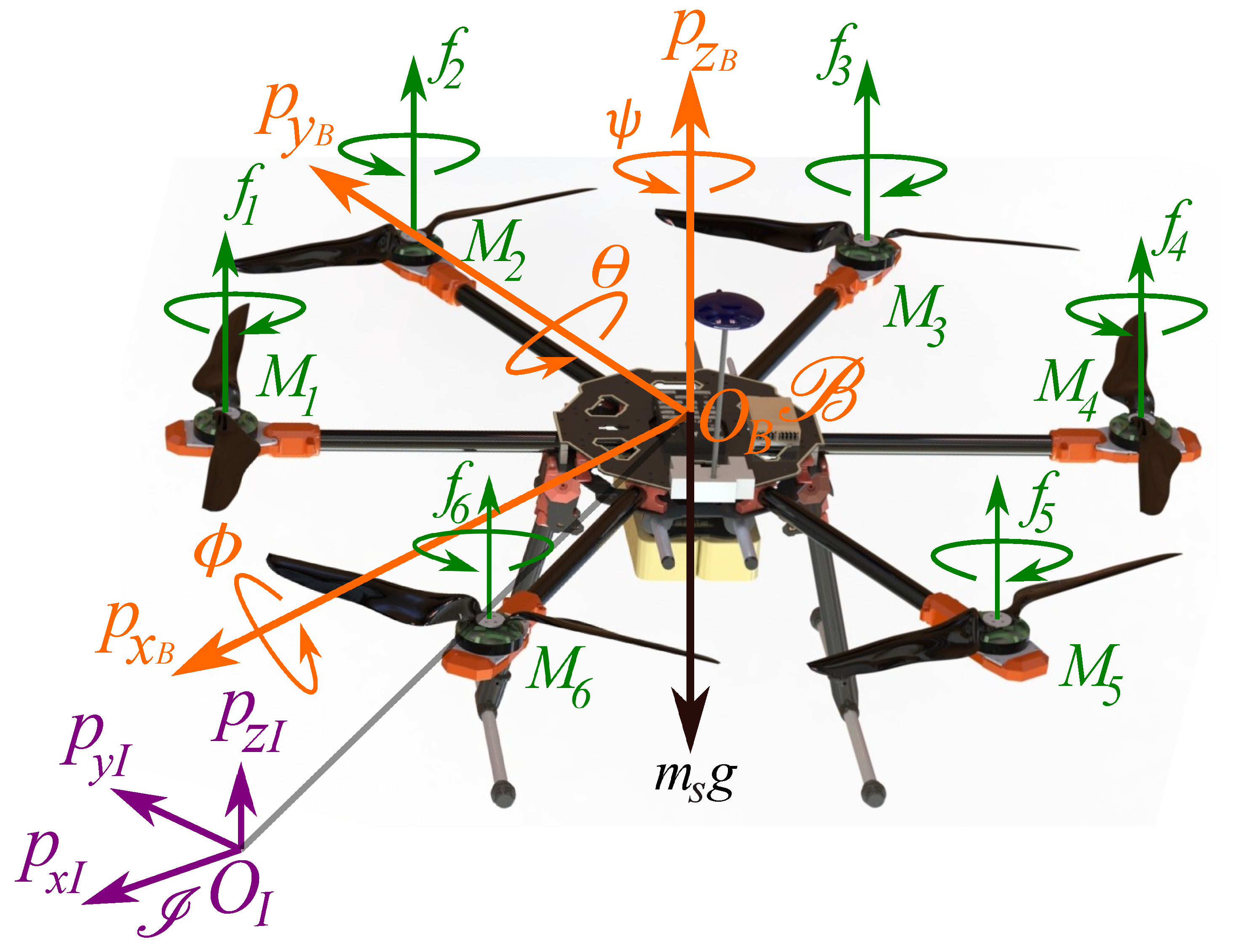
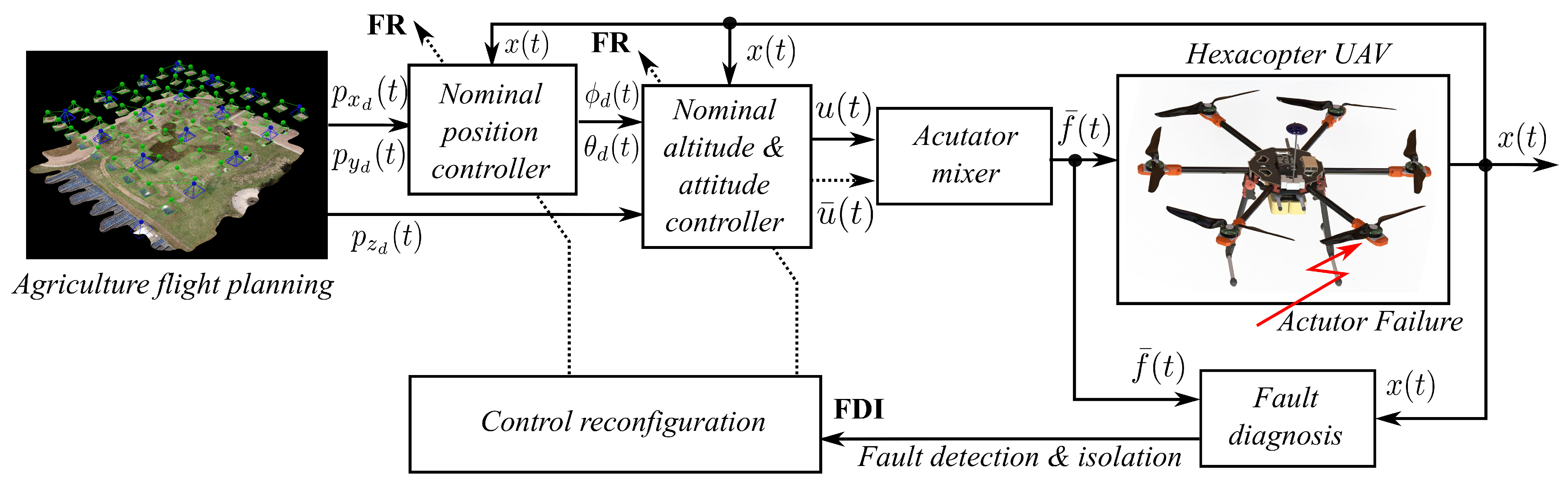





| Component | Specification | Value |
|---|---|---|
| Motor | Turnigy multistar | 600 kv (×6) |
| Propeller | Carbon fiber | 13 × 4 in (×6) |
| ESC controller | Afro ESC | 30 A (×6) |
| Power bank | Portable charger | 10 Ah |
| Battery | Li-Po | 10 Ah 3 s 25 c |
| Radio control | Turnigy 9X | 2.4 GHz |
| Telemetry | 3DR | 915 MHz |
| Frame | Tarot 680 pro | – |
| Flight controller | Pixhawk 2.4.8 | – |
| GPS | Ublox Neo-M8N | – |
| RGB camera | SJ9000 | – |
| Multispectral camera | Parrot Sequoia | – |
| Parameter | Value | Unit |
|---|---|---|
| Mass of the vehicle, | Kg | |
| Acceleration due to gravity, g | m/s2 | |
| Drag force coefficient, | Ns | |
| Drag torque coefficient, | Nms | |
| Moment of inertia about x, | Kgm2 | |
| Moment of inertia about y, | Kgm2 | |
| Moment of inertia about z, | Kgm2 | |
| Ratio between torque and lift, | − | |
| Motor’s maximum thrust force, | N | |
| Motor’s constant, | 39 | – |
| Fault | 1 | 0 | |||||||||
| ACAI * | 0 | ||||||||||
| CY * | CN * | CN | CN | CN | CN | CN | CN | CN | CN | CN | UCN * |
| ACAI-WY * | – | – | – | – | – | – | – | – | – | – | |
| Type | Parameter |
|---|---|
| Independent | UAV flight altitude |
| Independent | Sensor type |
| Independent | Actuator fault scenarios |
| Dependent | NDVI values |
| Dependent | UAV stability |
| Dependent | Data accuracy |
| Crop | Sugarcane |
| Other | Tillering stage |
| Data | SSIM | PSNR |
|---|---|---|
| Image 1 | dB | |
| Image 2 | dB |
| Type of Objects | NDVI Value |
|---|---|
| High, dense vegetation | 0.1–0.7 |
| Sparse vegetation | 0.5–0.2 |
| Open soil | 0.2–0.025 |
| Clouds | 0 |
| Snow, ice, dust, rocks | 0.1–−0.1 |
| Water | −0.33–−0.42 |
| Artificial materials | −0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortiz-Torres, G.; Zurita-Gil, M.A.; Rumbo-Morales, J.Y.; Sorcia-Vázquez, F.D.J.; Gascon Avalos, J.J.; Pérez-Vidal, A.F.; Ramos-Martinez, M.B.; Martínez Pascual, E.; Juárez, M.A. Integrating Actuator Fault-Tolerant Control and Deep-Learning-Based NDVI Estimation for Precision Agriculture with a Hexacopter UAV. AgriEngineering 2024, 6, 2768-2794. https://doi.org/10.3390/agriengineering6030161
Ortiz-Torres G, Zurita-Gil MA, Rumbo-Morales JY, Sorcia-Vázquez FDJ, Gascon Avalos JJ, Pérez-Vidal AF, Ramos-Martinez MB, Martínez Pascual E, Juárez MA. Integrating Actuator Fault-Tolerant Control and Deep-Learning-Based NDVI Estimation for Precision Agriculture with a Hexacopter UAV. AgriEngineering. 2024; 6(3):2768-2794. https://doi.org/10.3390/agriengineering6030161
Chicago/Turabian StyleOrtiz-Torres, Gerardo, Manuel A. Zurita-Gil, Jesse Y. Rumbo-Morales, Felipe D. J. Sorcia-Vázquez, José J. Gascon Avalos, Alan F. Pérez-Vidal, Moises B. Ramos-Martinez, Eric Martínez Pascual, and Mario A. Juárez. 2024. "Integrating Actuator Fault-Tolerant Control and Deep-Learning-Based NDVI Estimation for Precision Agriculture with a Hexacopter UAV" AgriEngineering 6, no. 3: 2768-2794. https://doi.org/10.3390/agriengineering6030161
APA StyleOrtiz-Torres, G., Zurita-Gil, M. A., Rumbo-Morales, J. Y., Sorcia-Vázquez, F. D. J., Gascon Avalos, J. J., Pérez-Vidal, A. F., Ramos-Martinez, M. B., Martínez Pascual, E., & Juárez, M. A. (2024). Integrating Actuator Fault-Tolerant Control and Deep-Learning-Based NDVI Estimation for Precision Agriculture with a Hexacopter UAV. AgriEngineering, 6(3), 2768-2794. https://doi.org/10.3390/agriengineering6030161










