Traction Force, Sowing Quality, and Deformation Characteristics of the Coulter of a Grain–Fertilizer–Grass Seeder
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Study of the Traction Force
2.2. Traction Force Determination under Laboratory Conditions
2.3. Design of Experiment Using the Box–Behnken Method
- The levels of factors variation should be selected.
- Encode the factors values −1, 0, and +1.
- Use a planning matrix.
- Calculate the regression coefficient.
- Perform statistical analysis of the obtained model.
2.4. Traction Force Determinations in the Field
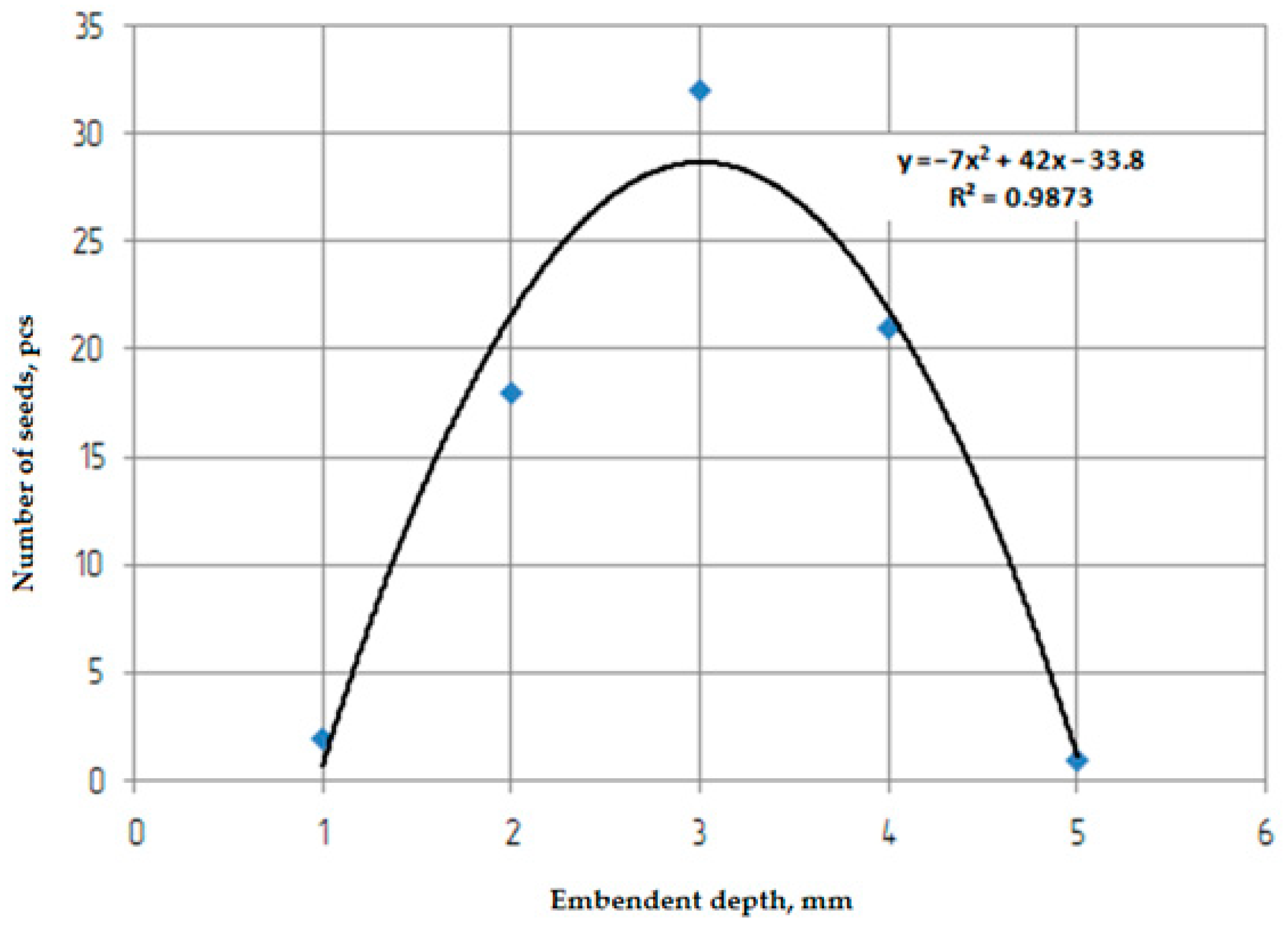
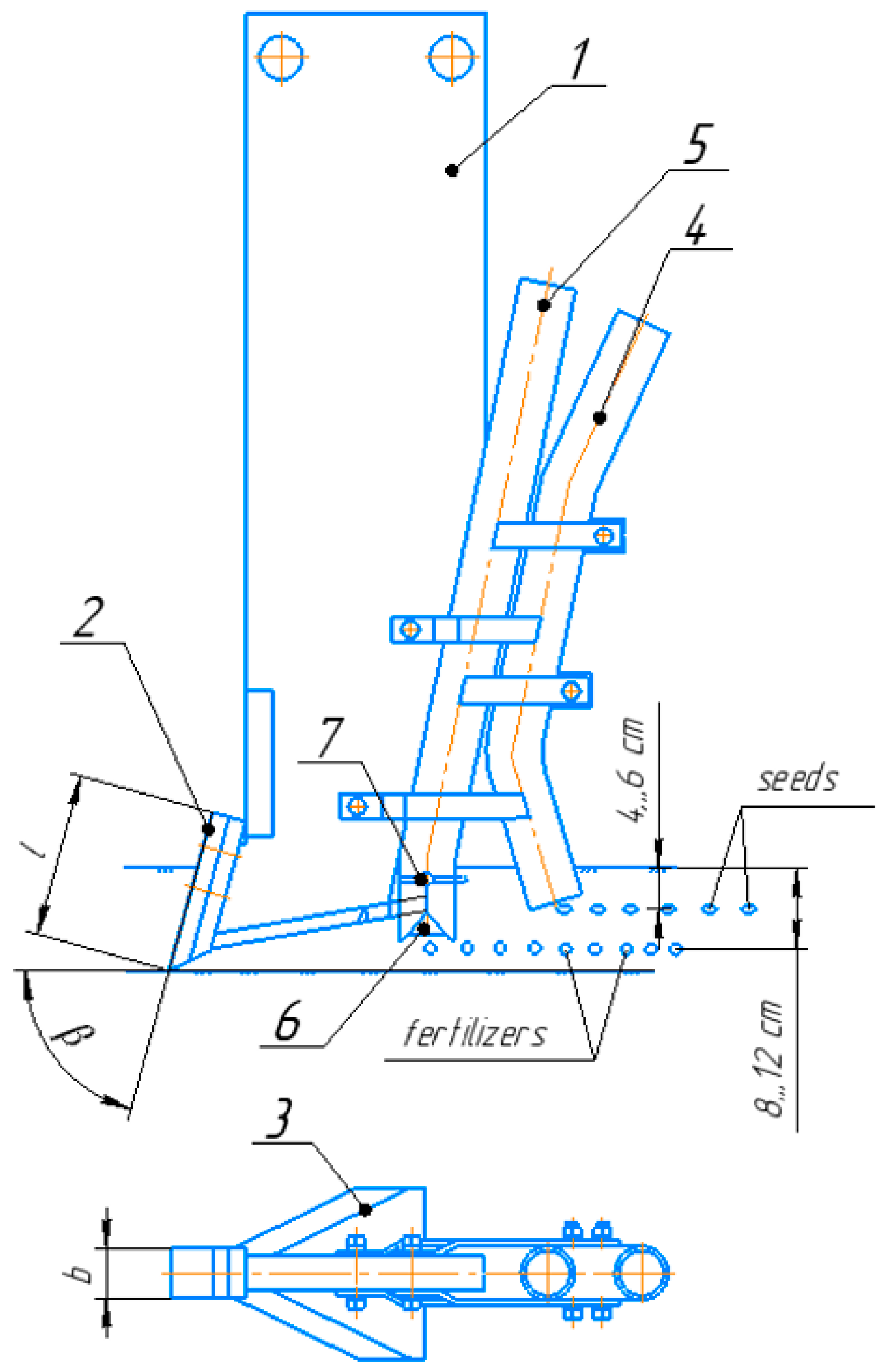
2.5. Determination of the Unevenness of Seed Embedment Depths
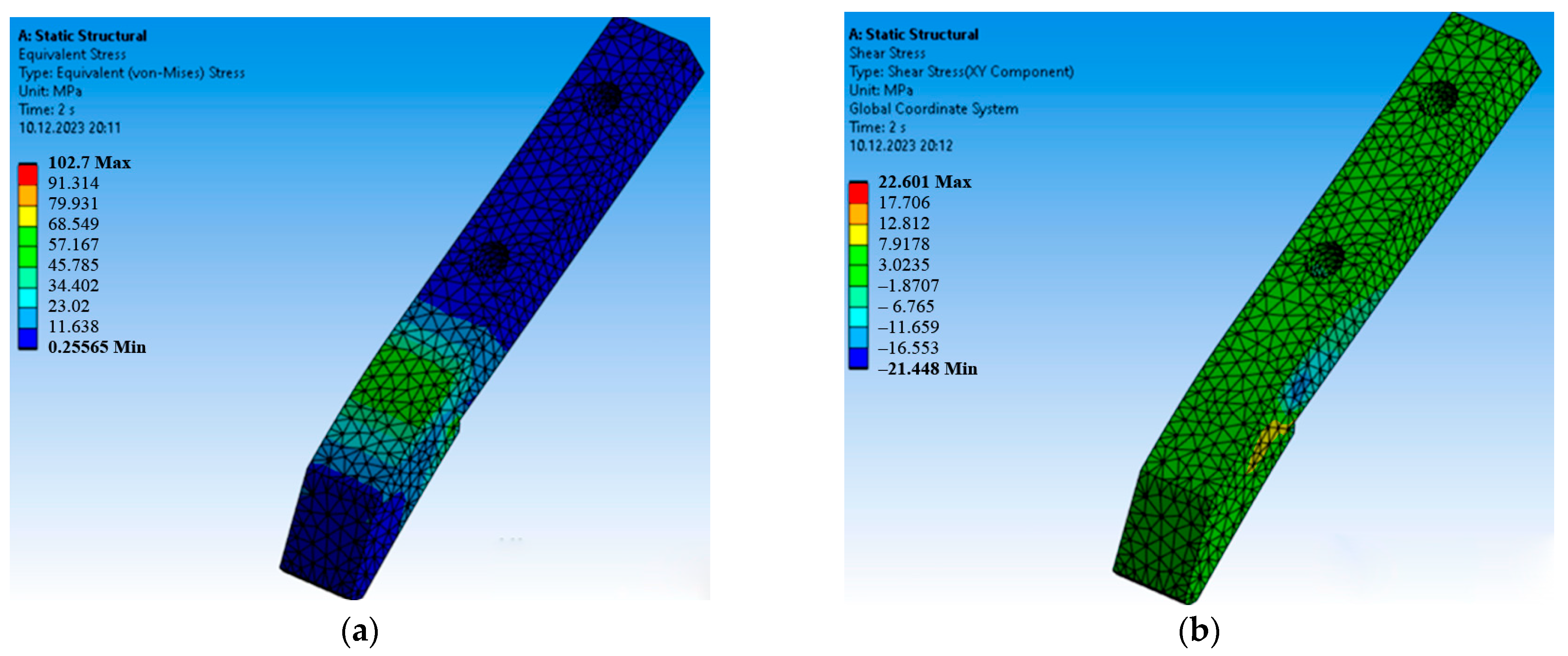
2.6. Modeling of Chisel Parameters Using the Finite Element and SPH Methods
3. Results
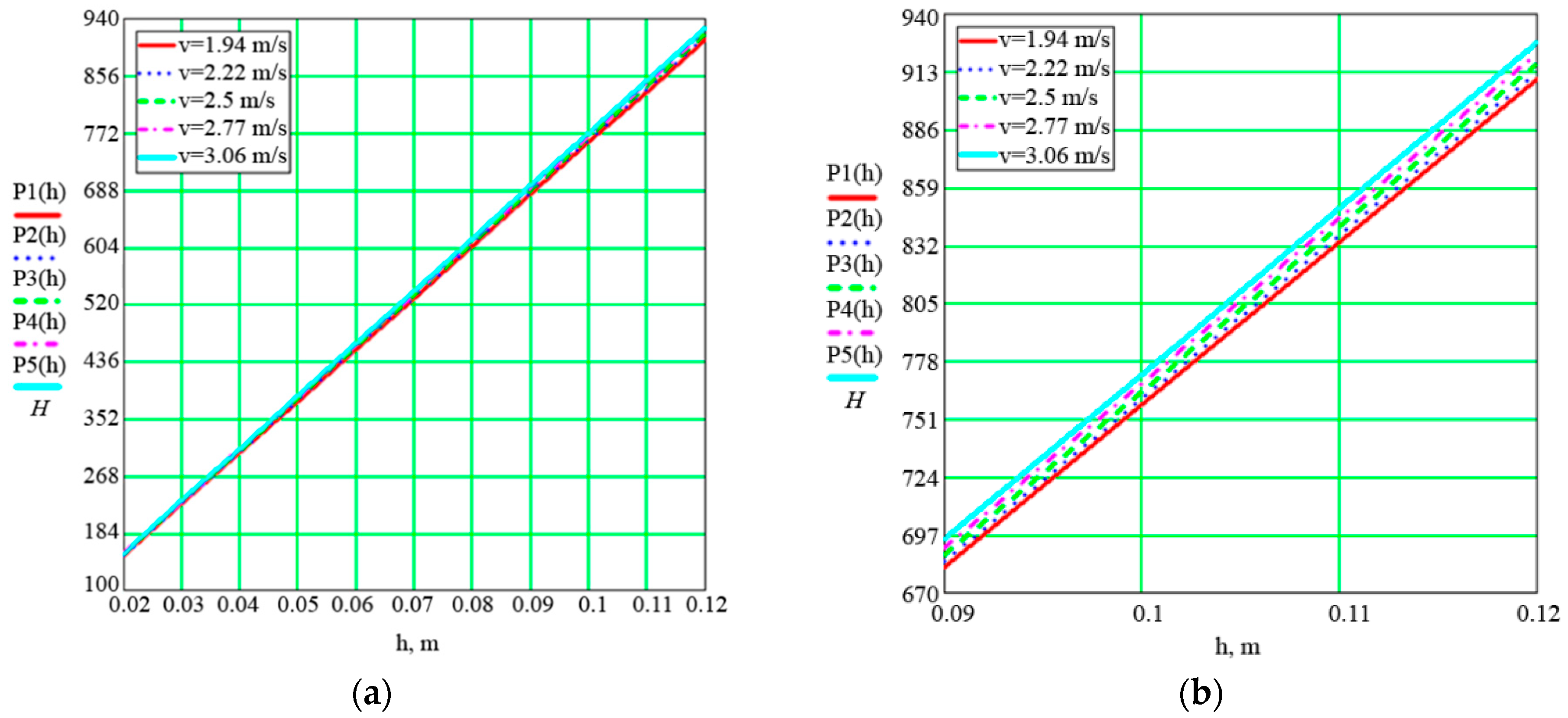
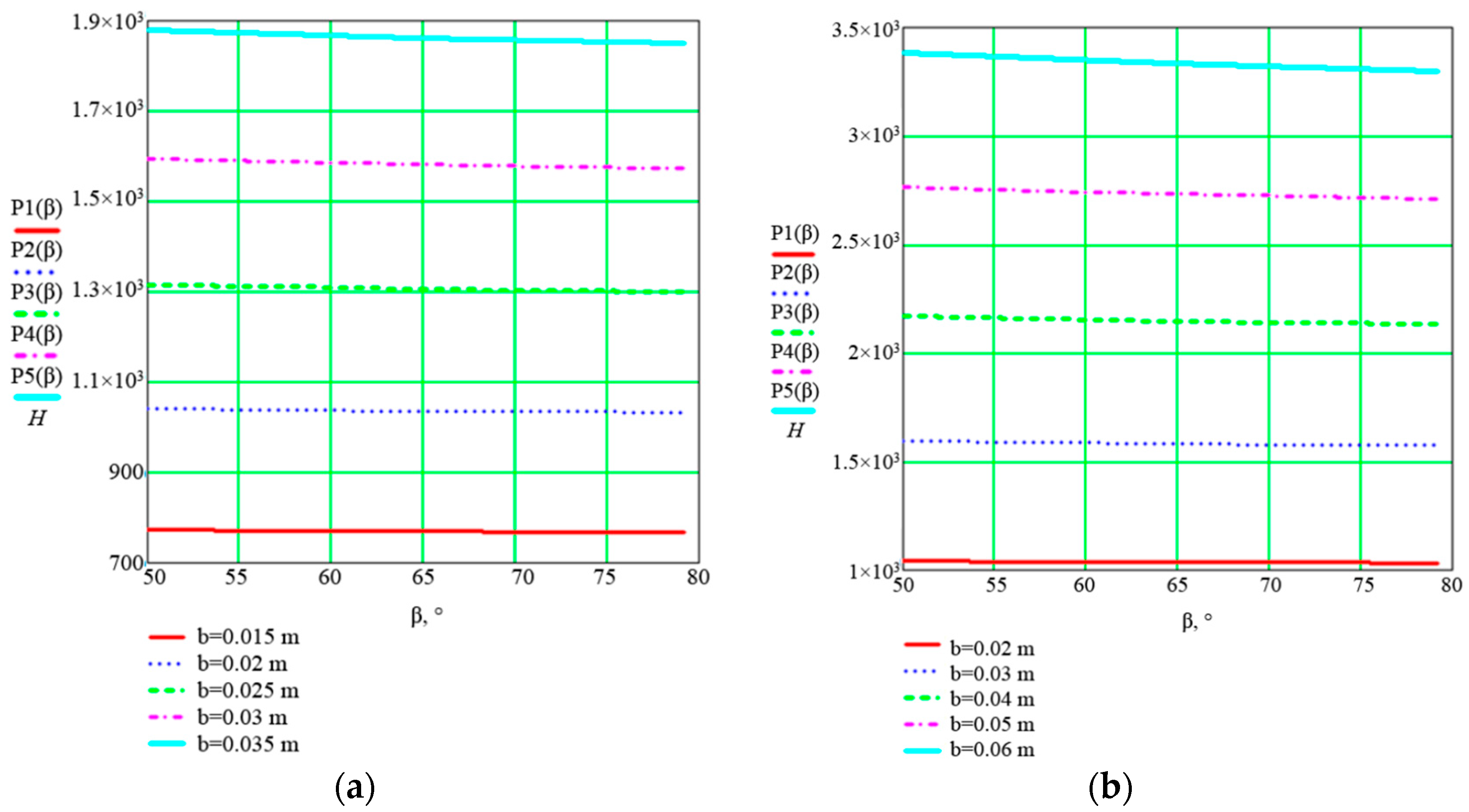
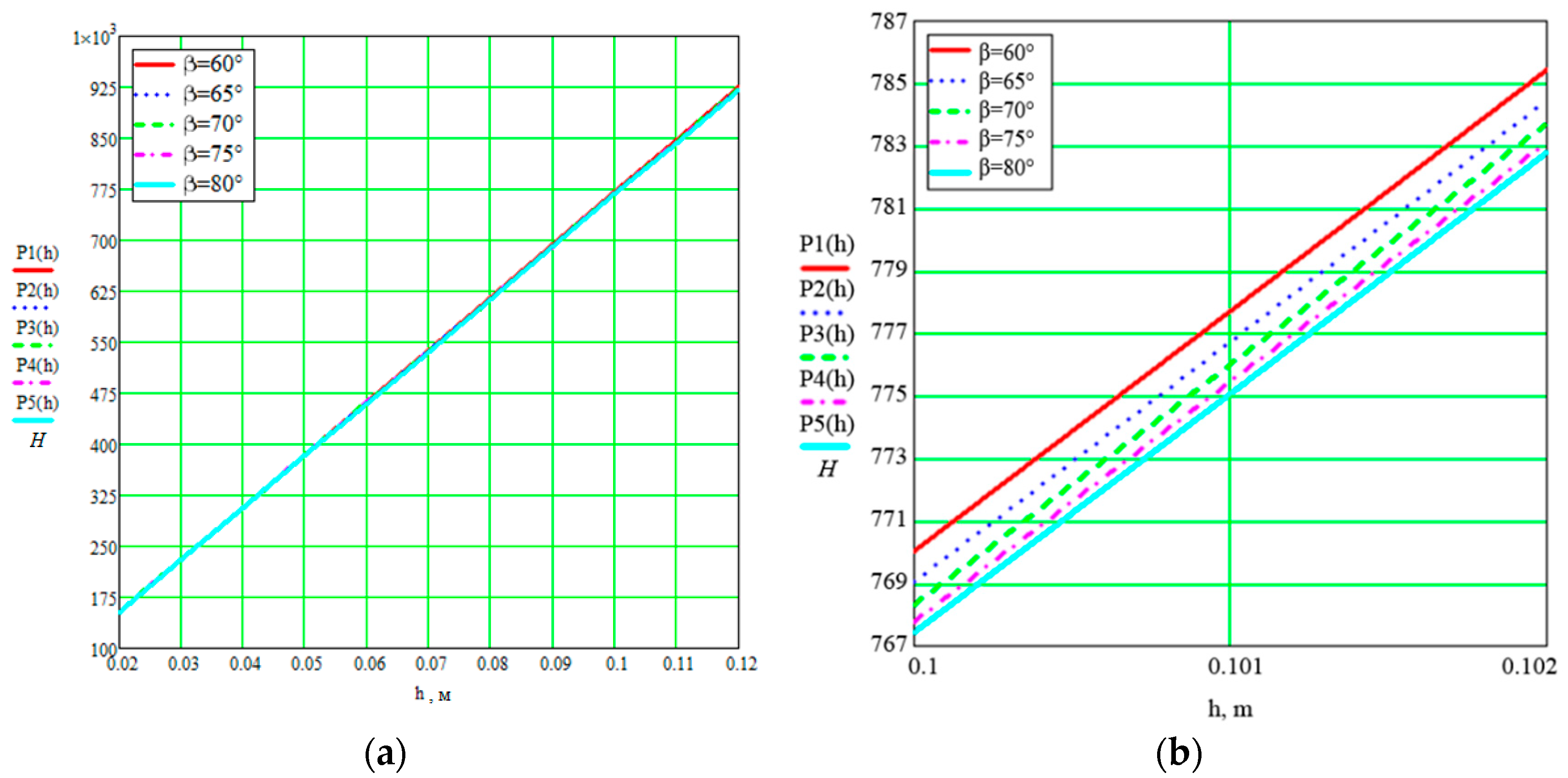
3.1. Theoretical Study of the Dependence of Coulter Traction Force on Structural and Technological Parameters
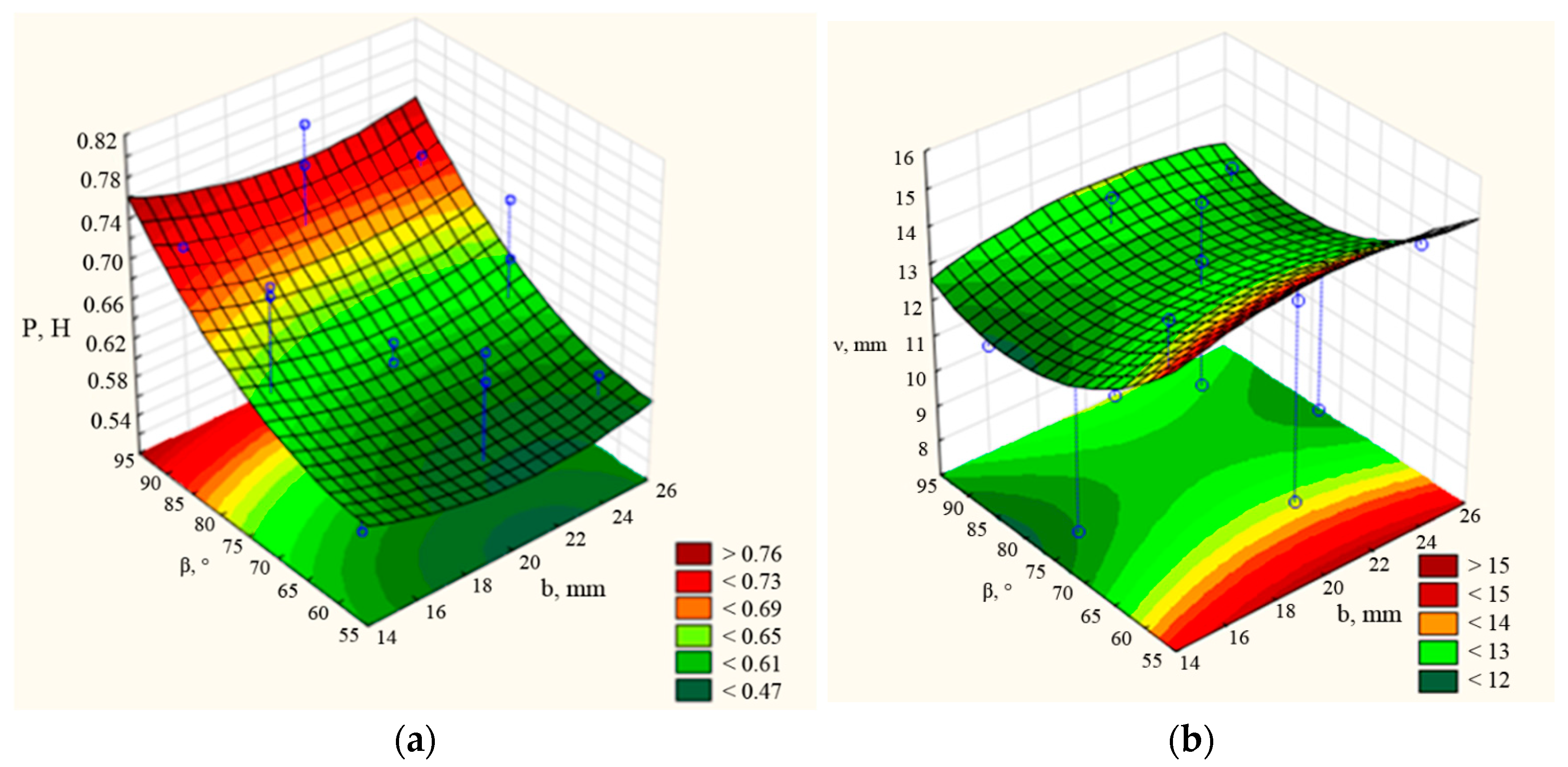
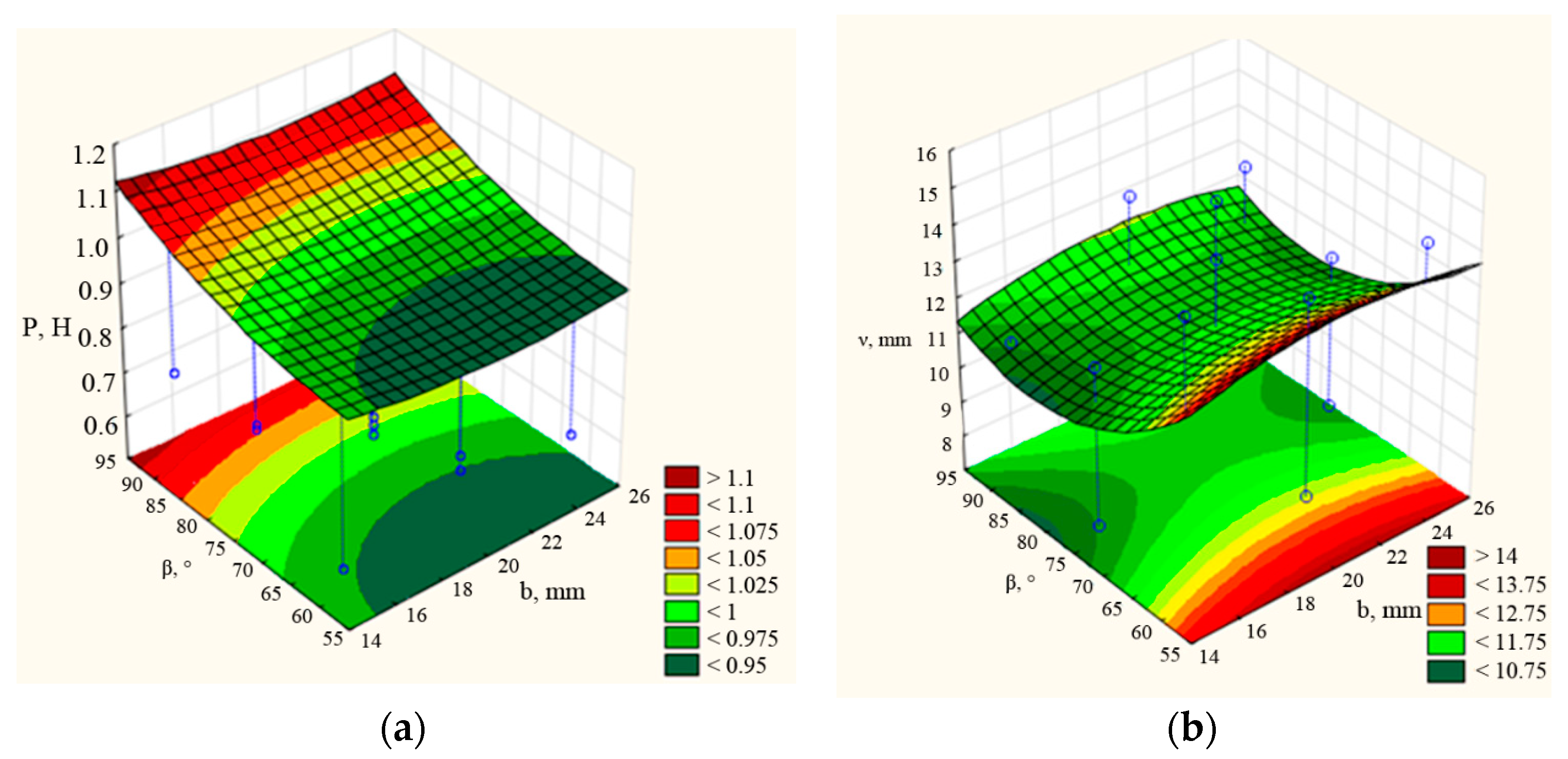
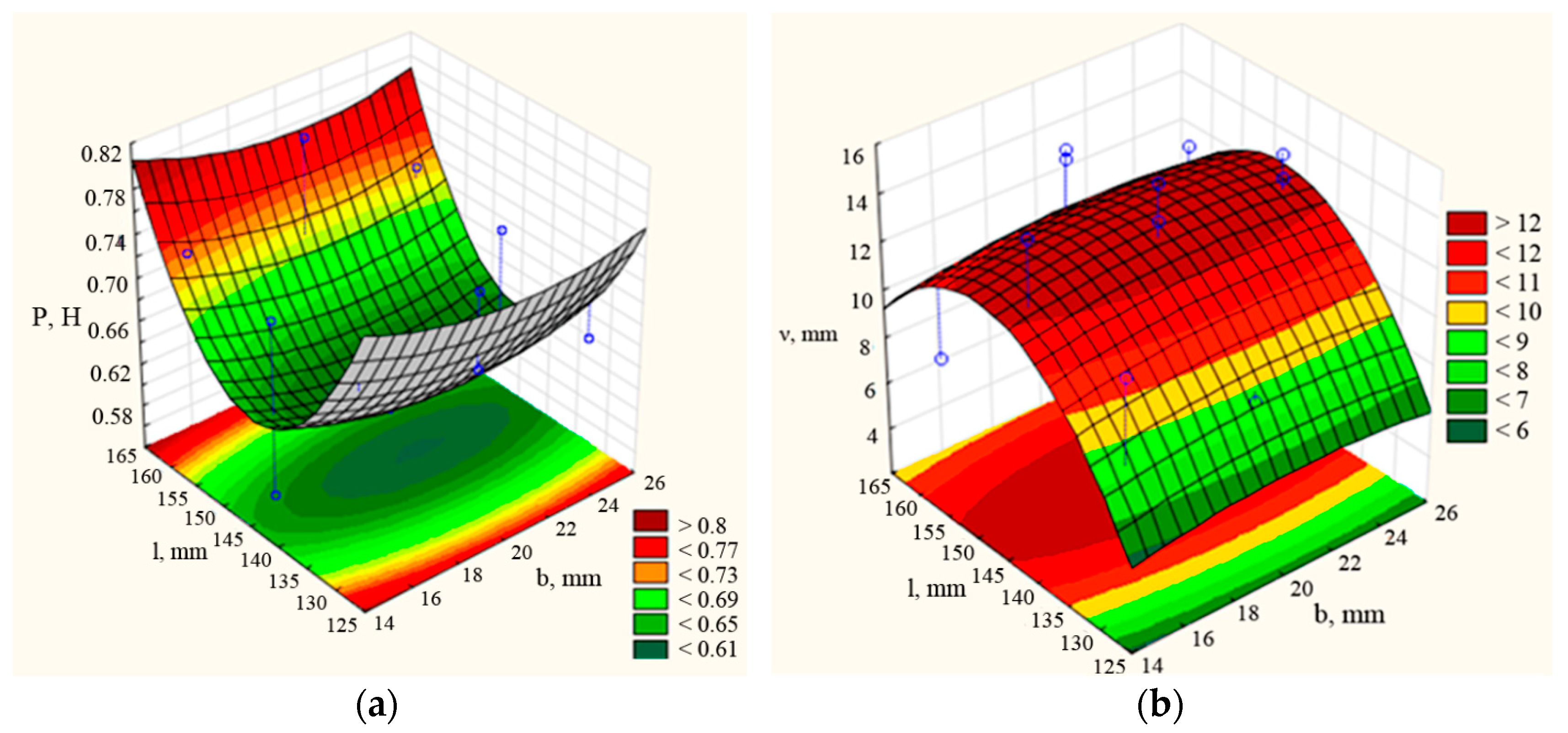
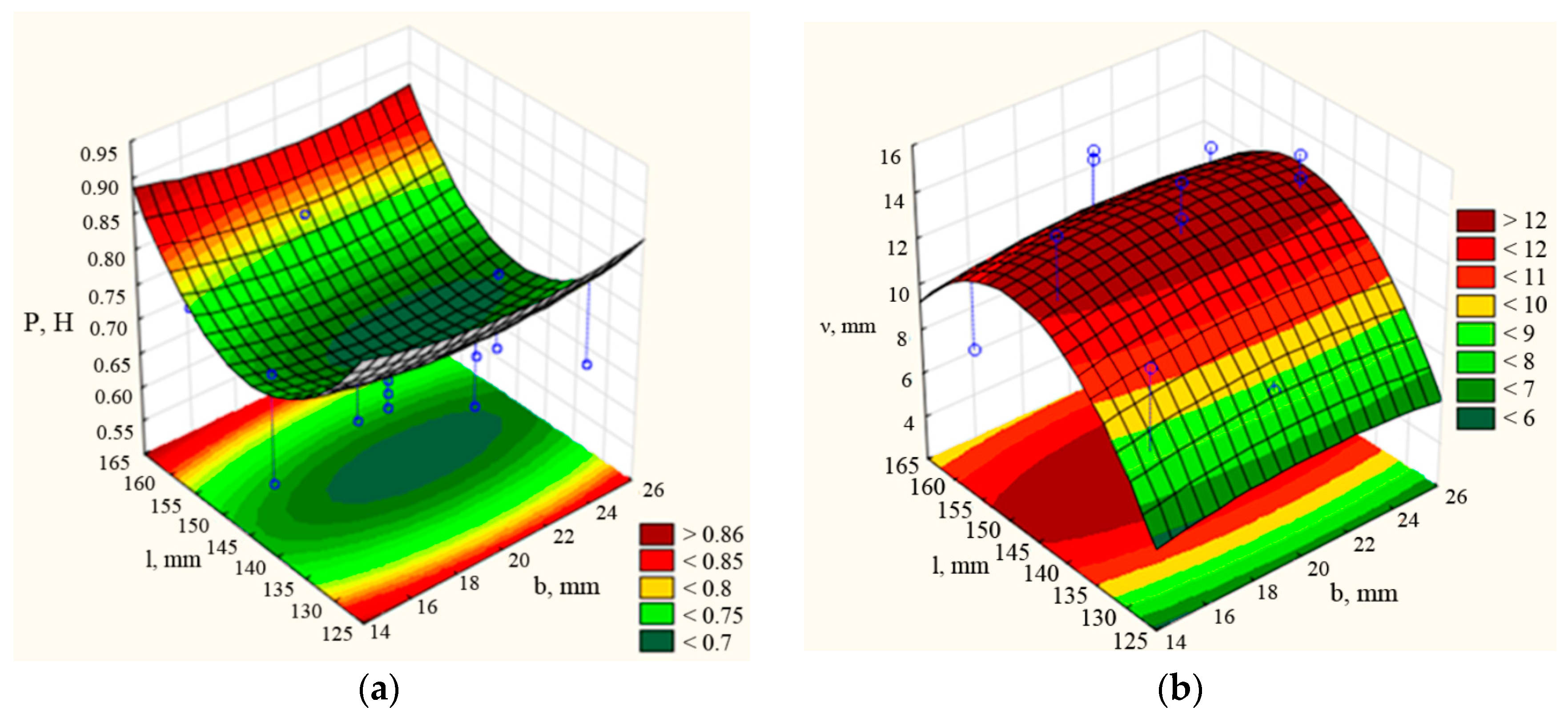
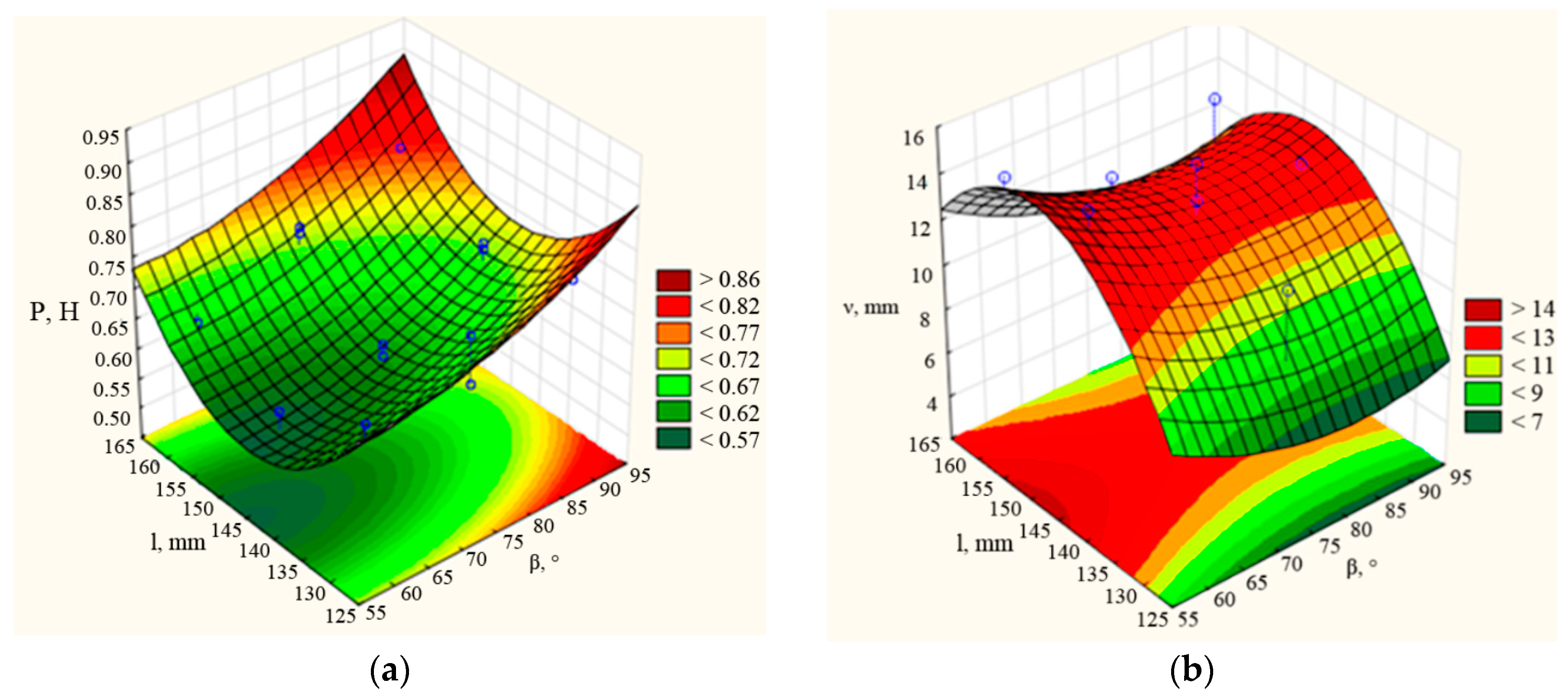
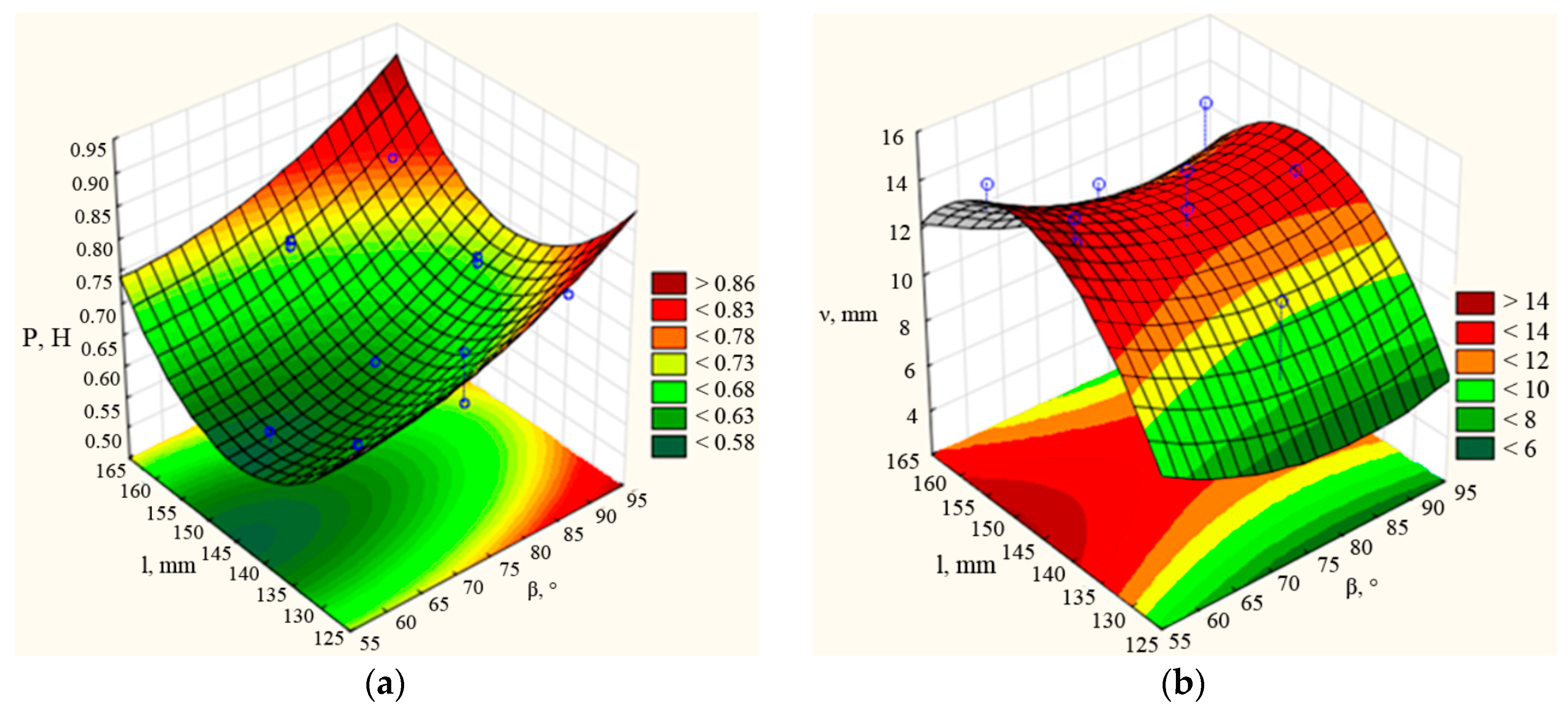
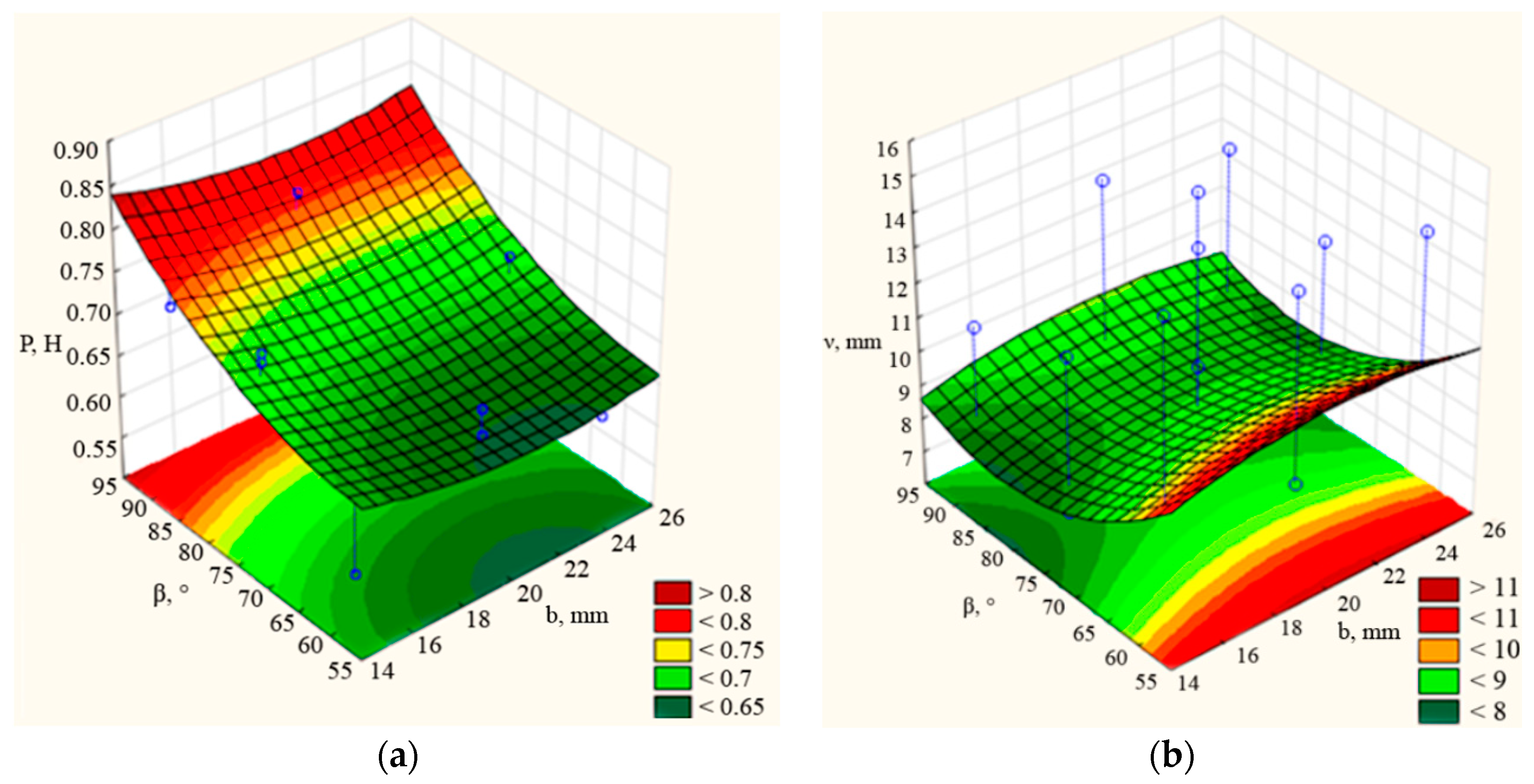
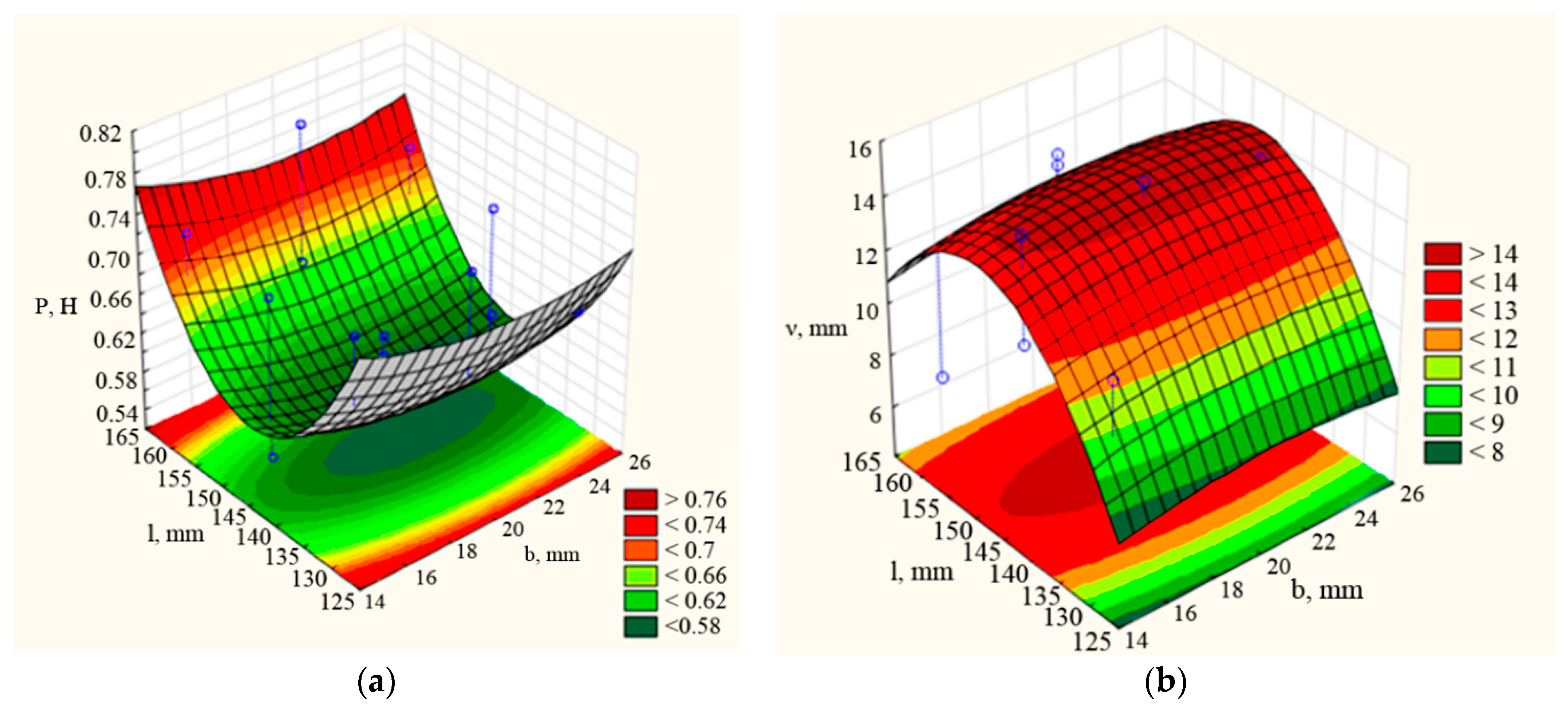
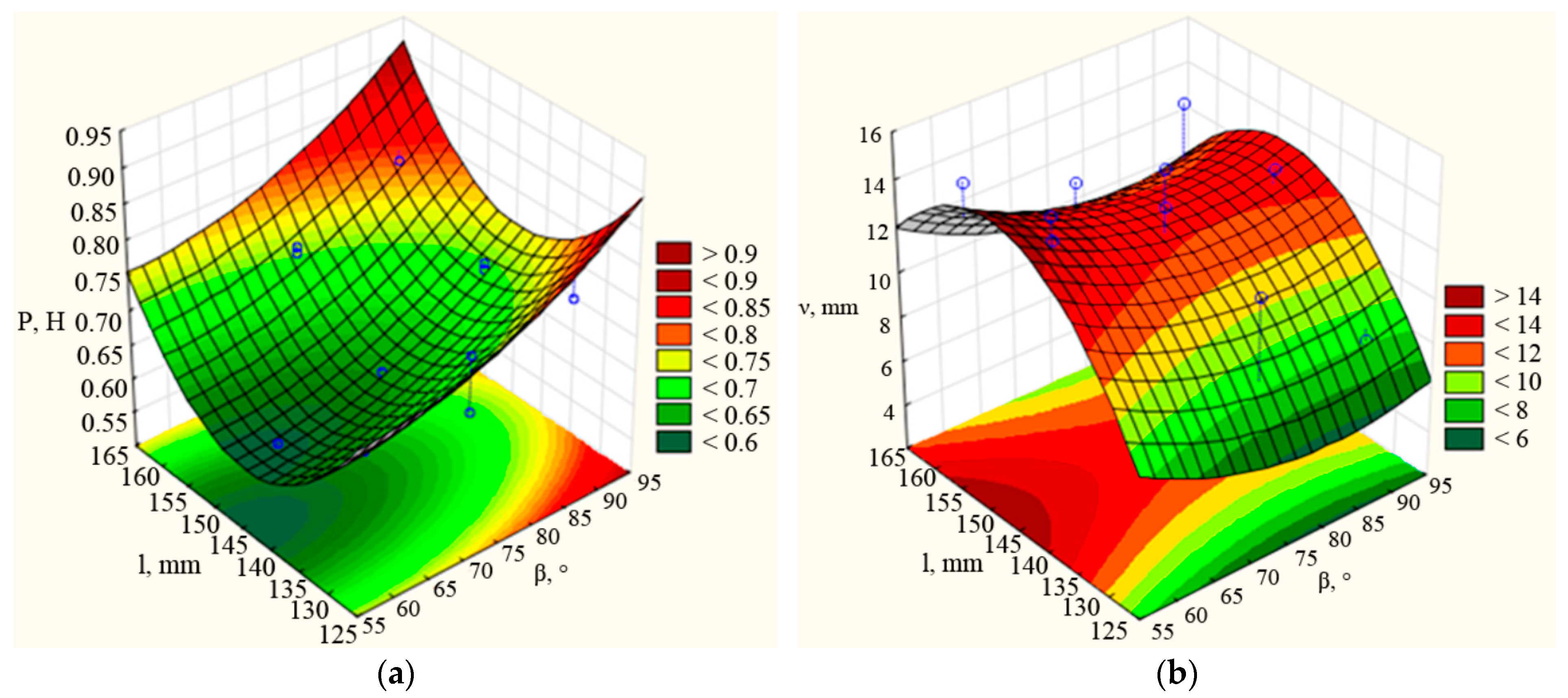
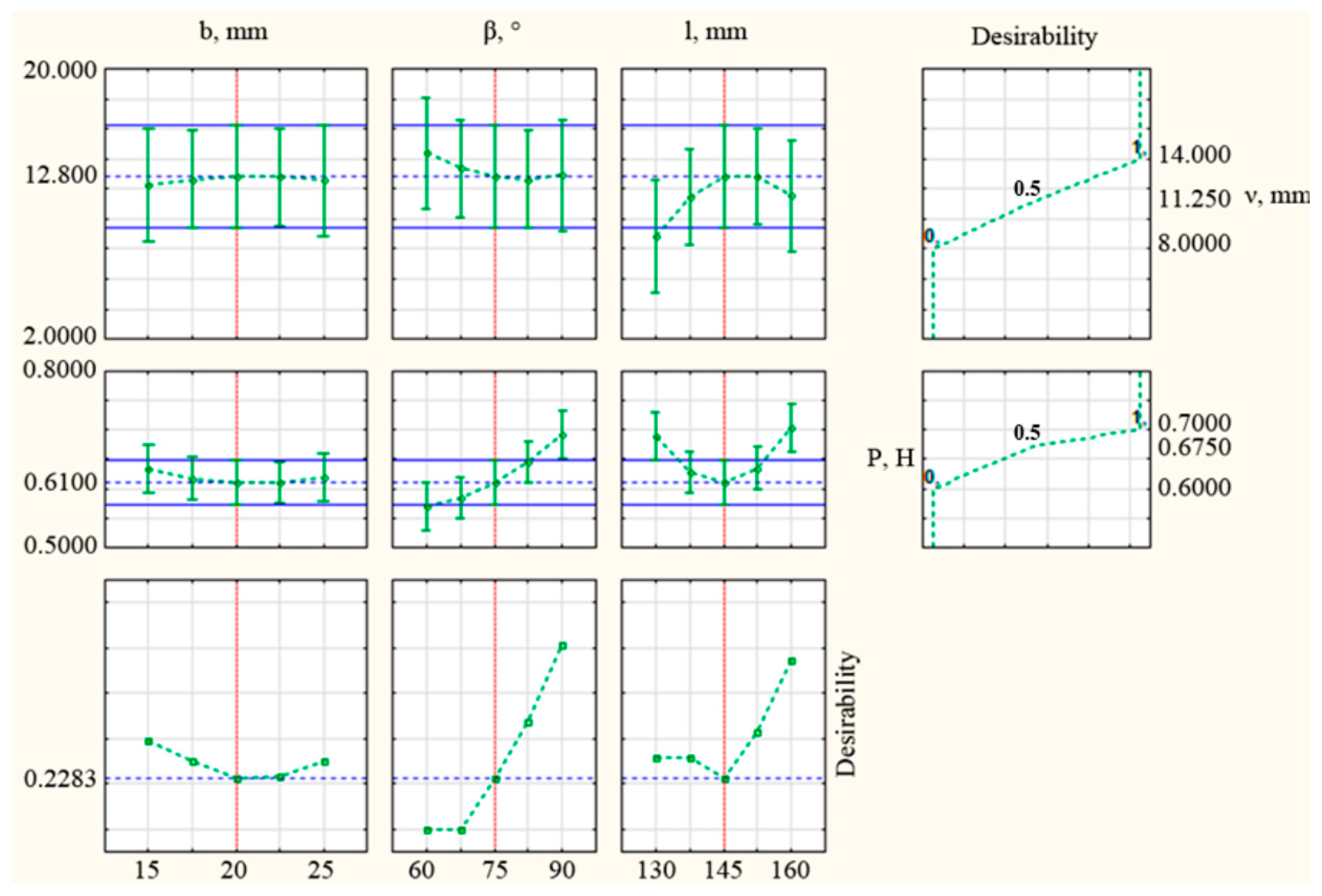
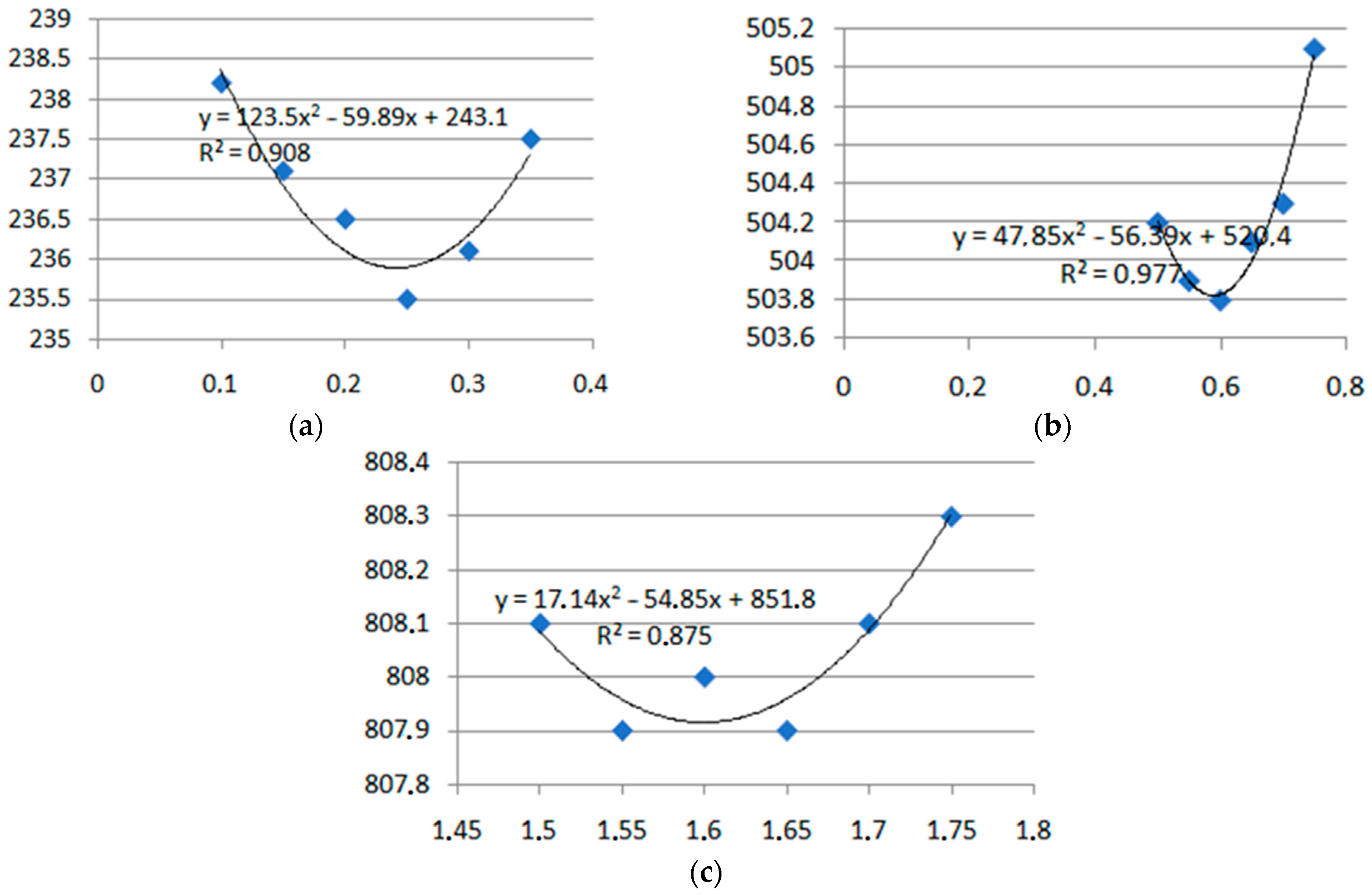
3.2. Selection of Optimal Structural and Technological Parameters of the Coulter
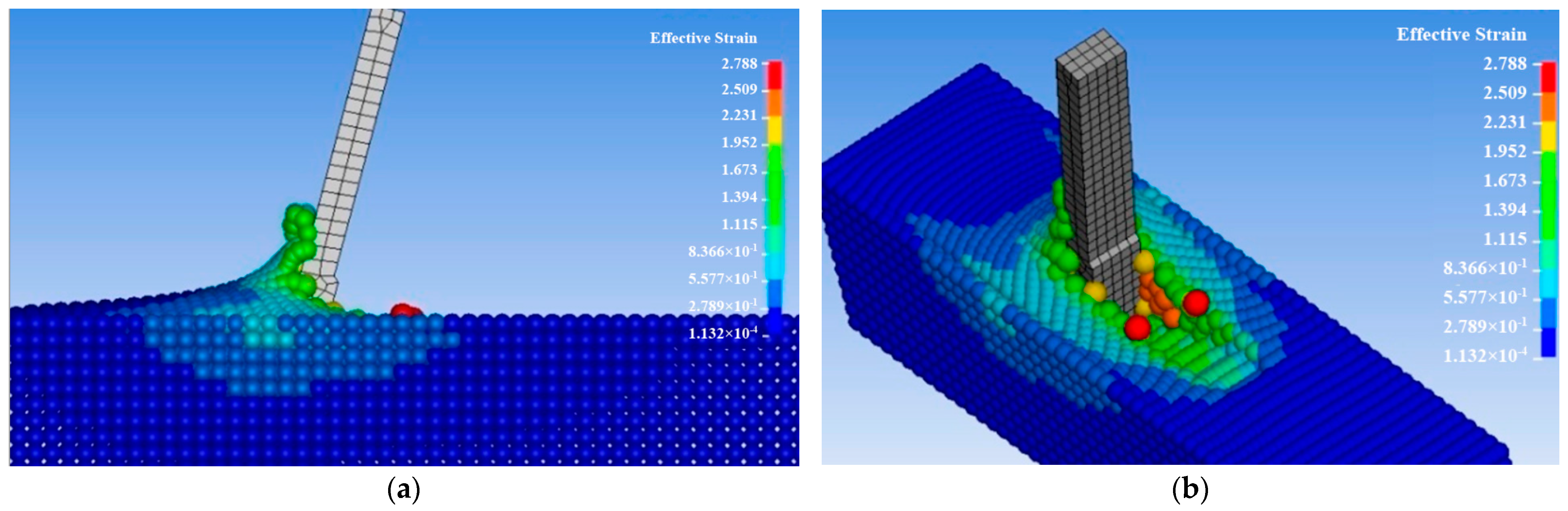
3.3. Modeling of Chisel Parameters Using the Finite Element and SPH Methods
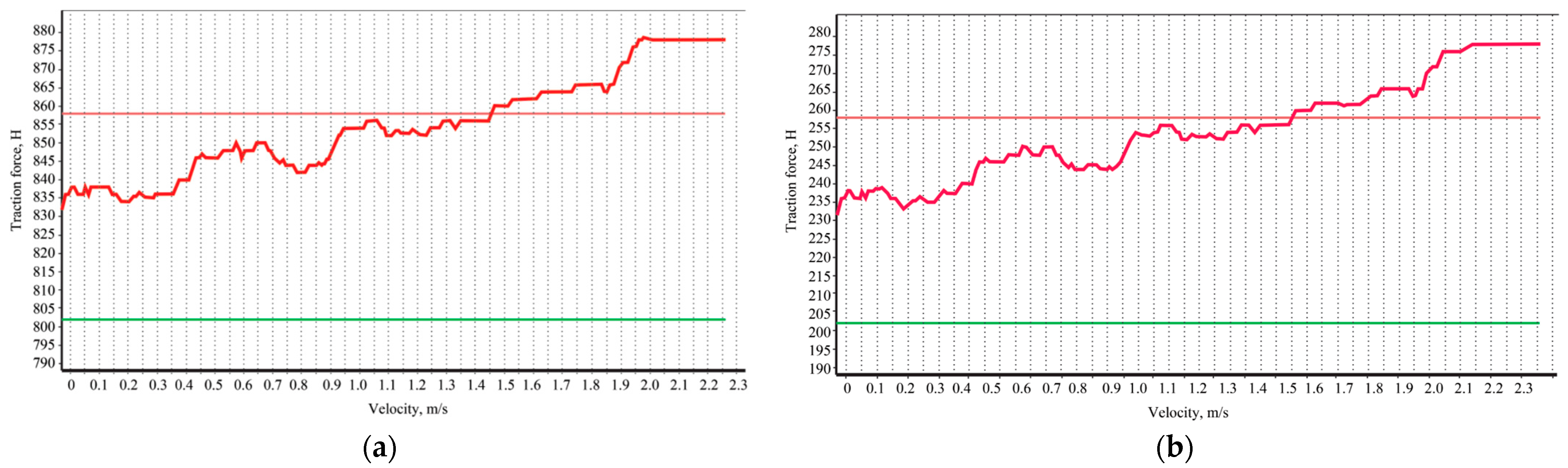
3.4. Traction Force of the Working Body in the Soil Bin
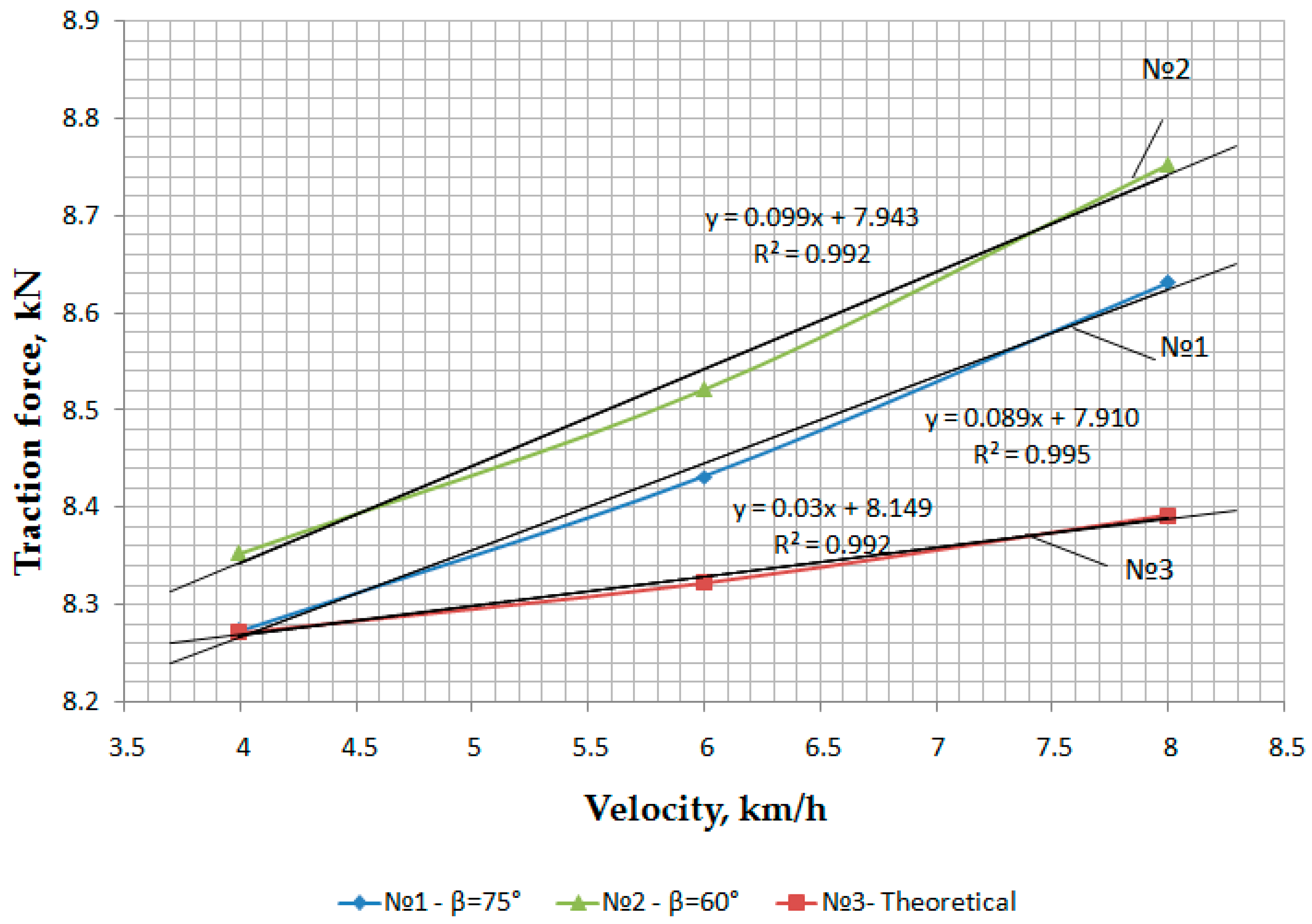
3.5. Seeder Traction Force in Field Conditions
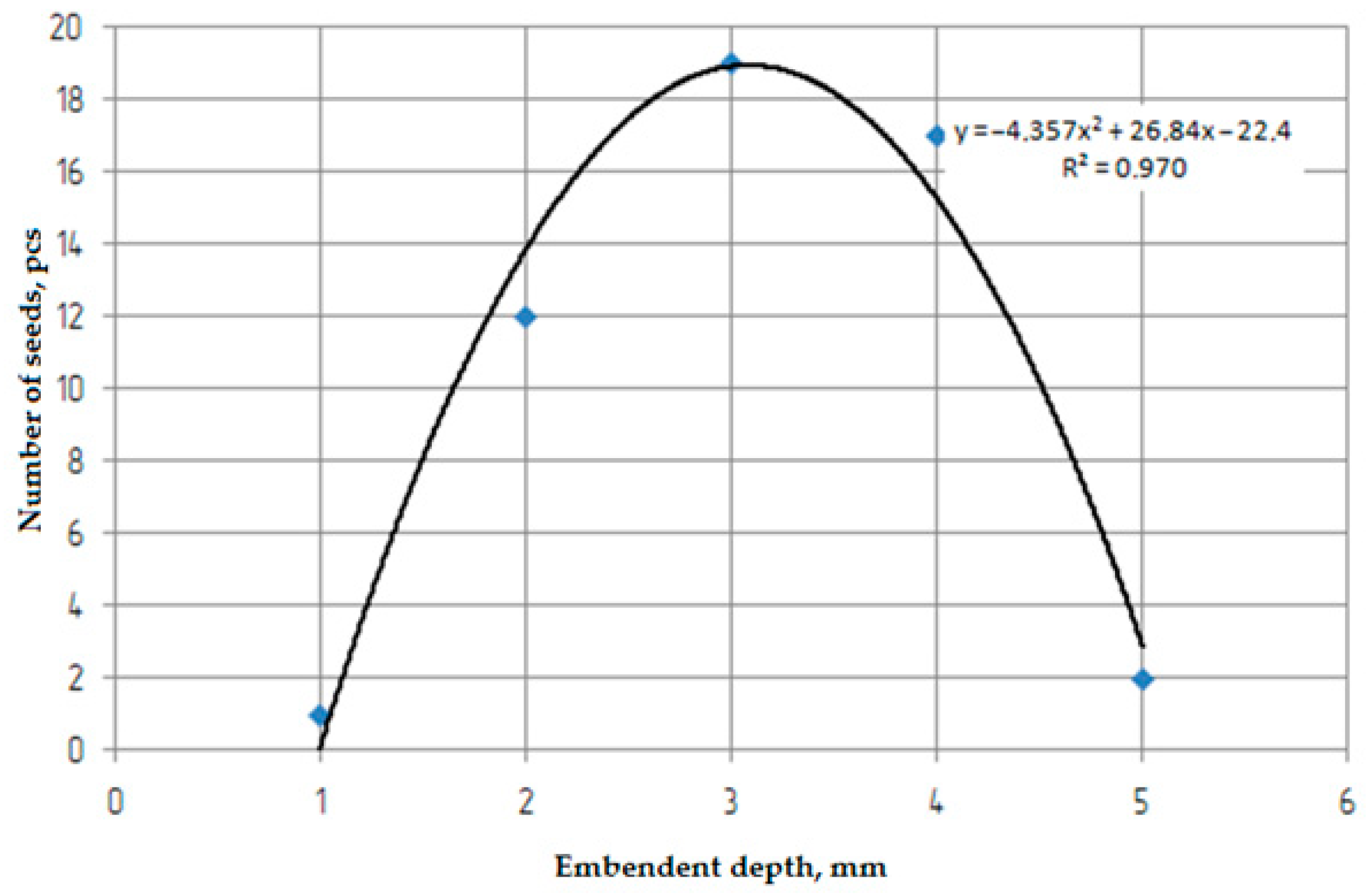
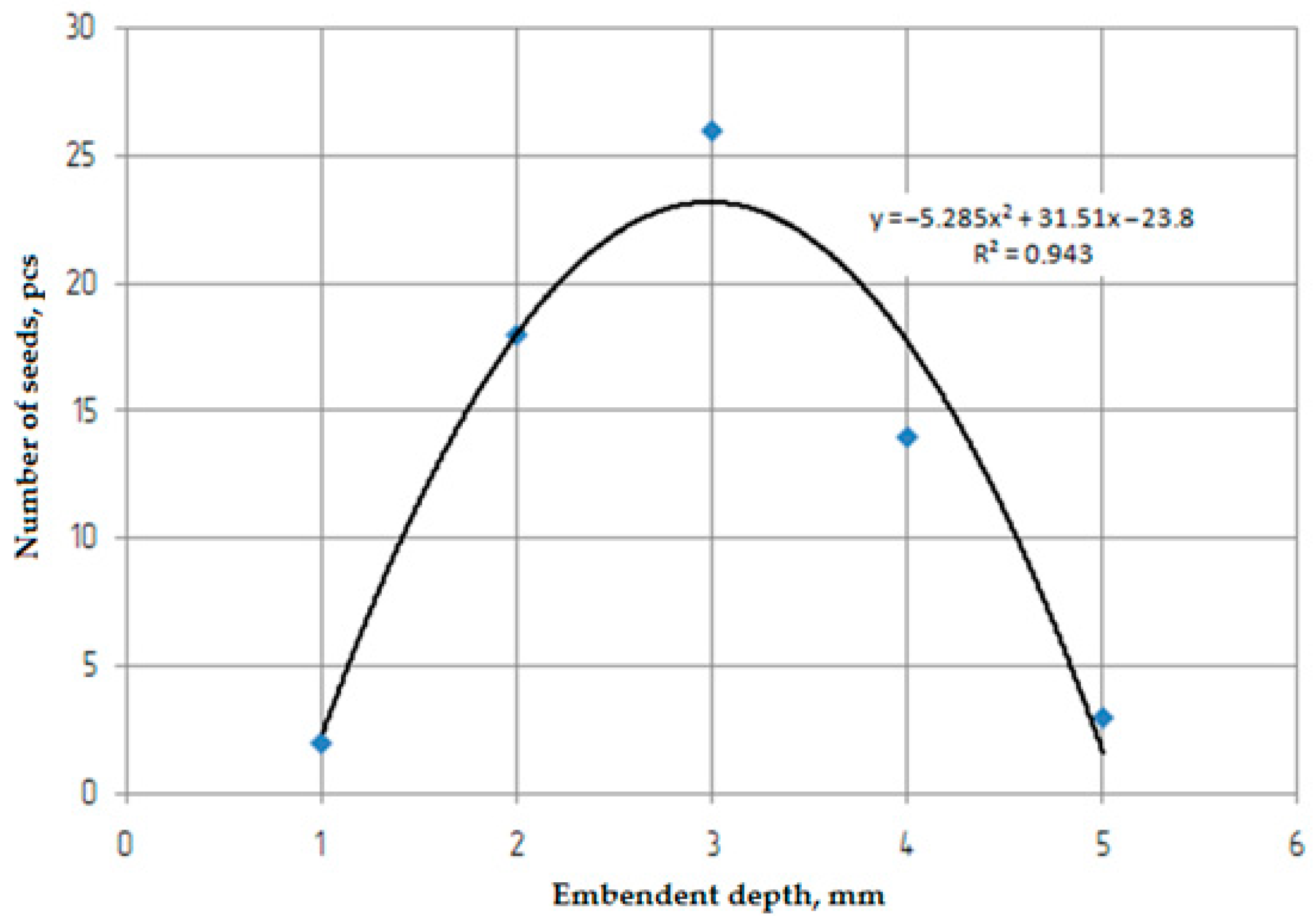
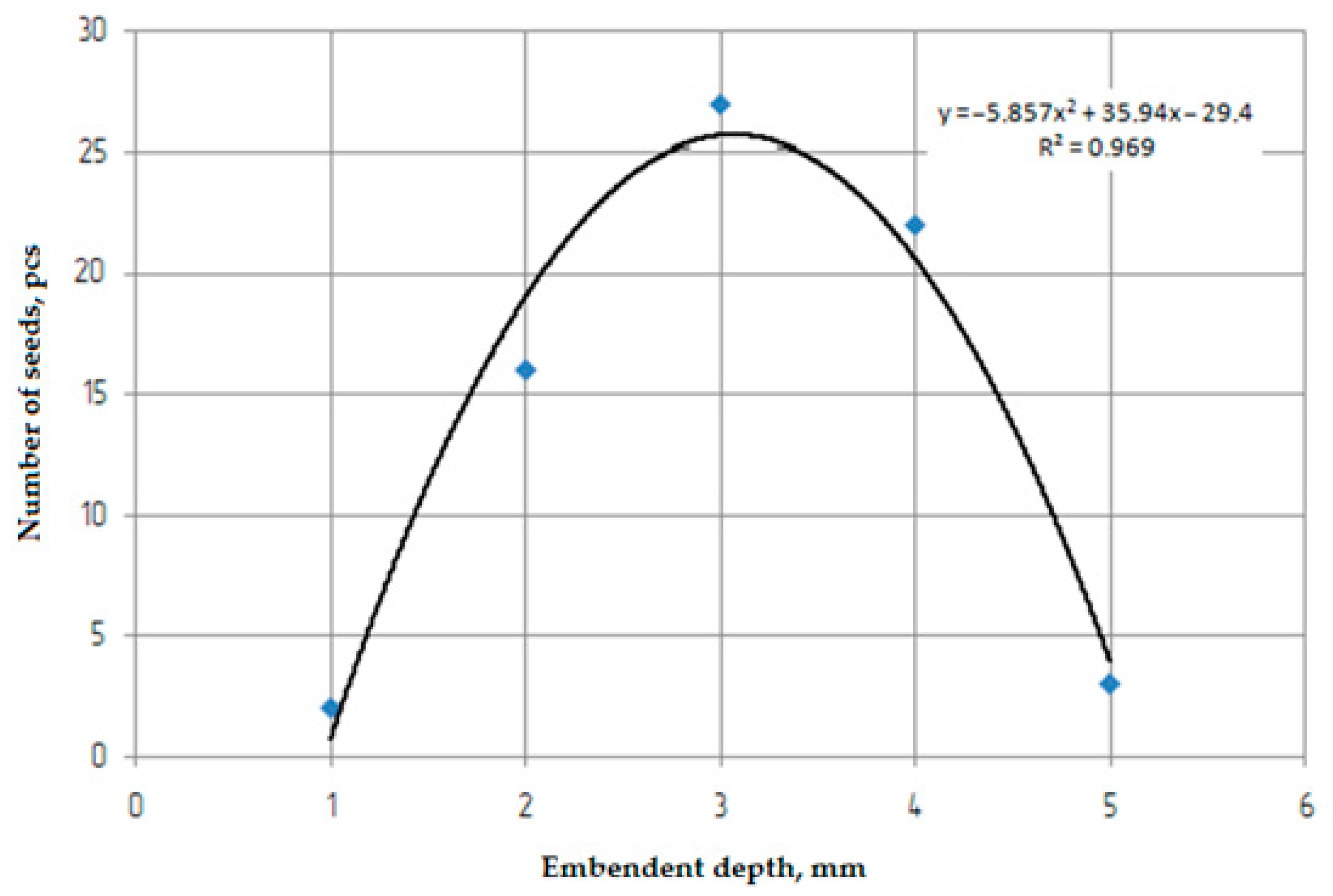
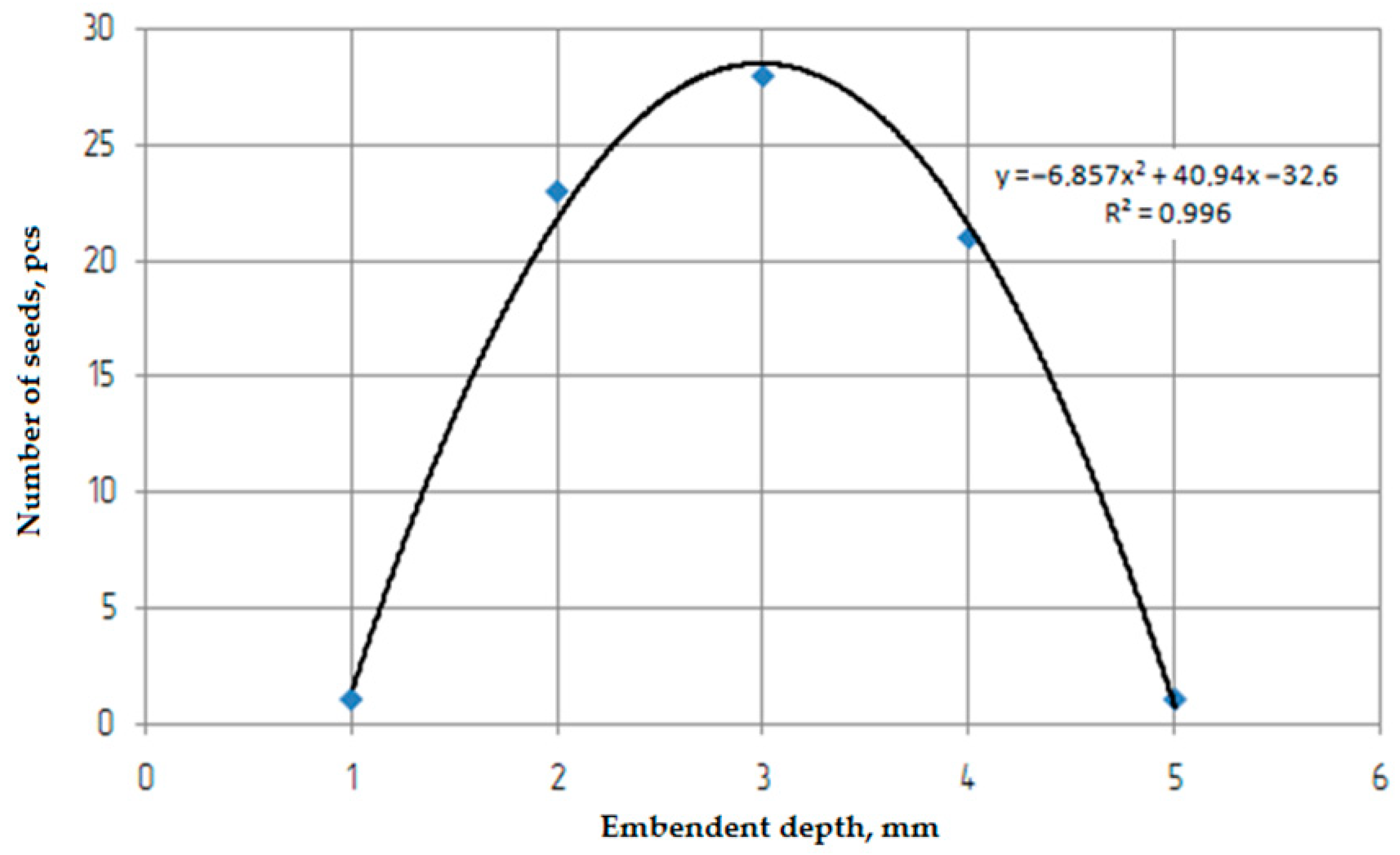
3.6. Unevenness of Seeder Depth in Field Conditions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Factors | Unit | Code Designation | Variation Intervals | Natural Factor Levels Corresponding to Coded | ||||
|---|---|---|---|---|---|---|---|---|
| −1.682 | −1 | 0 | +1 | +1.682 | ||||
| b—the coulter chisel width | mm | x1 | 5 | 10 | 15 | 20 | 25 | 30 |
| β—the mounting angle | degree | x2 | 15 | 45 | 60 | 75 | 90 | 105 |
| l—the coulter chisel length | mm | x3 | 15 | 115 | 130 | 145 | 160 | 175 |
| Experiment Number | P | νd | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.56 | 15 |
| 2 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 0.6 | 14 |
| 3 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | 1 | 1 | 0.72 | 11 |
| 4 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 1 | 0.71 | 13 |
| 5 | 1 | −1 | 1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | 0.74 | 12 |
| 6 | 1 | −1 | 1 | −1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 0.66 | 7.7 |
| 7 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 | 0.73 | 7.5 |
| 8 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | −1 | 1 | 1 | 1 | 0.72 | 12 |
| 9 | 1 | 1.682 | 0 | 0 | 0 | 0 | 0 | 0 | 2.829 | 0 | 0 | 0.68 | 8.5 |
| 10 | 1 | −1.682 | 0 | 0 | 0 | 0 | 0 | 0 | 2.829 | 0 | 0 | 0.75 | 8 |
| 11 | 1 | 0 | 1.682 | 0 | 0 | 0 | 0 | 0 | 0 | 2.829 | 0 | 0.65 | 14 |
| 12 | 1 | 0 | −1.682 | 0 | 0 | 0 | 0 | 0 | 0 | 2.829 | 0 | 0.79 | 13.6 |
| 13 | 1 | 0 | 0 | 1.682 | 0 | 0 | 0 | 0 | 0 | 0 | 2.829 | 0.61 | 15 |
| 14 | 1 | 0 | 0 | −1.682 | 0 | 0 | 0 | 0 | 0 | 0 | 2.829 | 0.59 | 13.4 |
| 15 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.63 | 10 |
| 16 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 8.9 |
| 17 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.66 | 11.5 |
| 18 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.65 | 12 |
| 19 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.6 | 10 |
| 20 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.62 | 13 |
| sum | 20 | 0 | 0 | 0 | 0 | 0 | 2 | −2 | 13.658 | 13.658 | 13.658 | 13.37 | 230.1 |
Appendix B
References
- Nukeshev, S.; Eskhozhin, K.; Karaivanov, D.; Sankibaev, T.; Kakabayev, N. Theoretical and Experimental Substantiation of the Design of an Opener for Intrasoil Broadcast Sowing of Grain Crops. Bulg. J. Agric. Sci. 2016, 22, 862–868. [Google Scholar]
- He, S.; Qian, C.; Jiang, Y.; Qin, W.; Huang, Z.; Huang, D.; Wang, Z.; Zang, Y. Design and Optimization of the Seed Feeding Device with DEM-CFD Coupling Approach for Rice and Wheat. Comput. Electron. Agric. 2024, 219, 108814. [Google Scholar] [CrossRef]
- Hou, S.; Zhu, Y.; Zhu, X.; Wang, Y.; Ji, W.; Chen, H. Design and Experiment of a Straw Clearing Mulching No-Tillage Planter. Biosyst. Eng. 2022, 221, 69–80. [Google Scholar] [CrossRef]
- Romanyuk, N.; Ednach, V.; Nukeshev, S.; Troyanovskaya, I.; Voinash, S.; Kalimullin, M.; Sokolova, V. Improvement of the Design of the Plow-Subsoiler-Fertilizer to Increase Soil Fertility. J. Terramechanics 2023, 106, 89–93. [Google Scholar] [CrossRef]
- Malikov, V.; Ishkov, A.; Shevtsova, L.; Katasonov, A.; Tihonskii, N.; Kozlova, V. The Stress-Strain State of the 3D Models Lancet Paw. Transp. Res. Procedia 2022, 63, 2781–2788. [Google Scholar] [CrossRef]
- Eskhozhin, K.; Hukeshev, S.; Eskhojin, D. Karaivanov, Dimitar Stress Distribution in Soil under Action of Paraplow Ripper. Life Sci. J. 2014, 11, 20–24. [Google Scholar]
- Battiato, A.; Diserens, E. Tractor Traction Performance Simulation on Differently Textured Soils and Validation: A Basic Study to Make Traction and Energy Requirements Accessible to the Practice. Soil Tillage Res. 2017, 166, 18–32. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, X.; Dong, J.; Wang, X.; Zhao, H.; Chen, X.; Zhang, Z.; Huang, Y.; Shi, J. Optimization of Operating Angles of Disc Coulters for Maize Residue Management Using Discrete Element Method. Comput. Electron. Agric. 2024, 218, 108691. [Google Scholar] [CrossRef]
- Nukeshev, S.; Slavov, V.; Kakabayev, N.; Amantayev, M. Mathematical Modelling in 3D of Opener with Scatterer of the Grain-Fertilizer Seeder. Mechanika 2019, 24, 840–844. [Google Scholar] [CrossRef]
- Conte, O.; Levien, R.; Trein, C.R.; Mazurana, M.; Debiasi, H. Resistência Mecânica Do Solo e Força de Tração Em Hastes Sulcadoras de Semeadoras-Adubadoras Em Sistema de Integração Lavoura-Pecuária. Eng. Agríc. 2008, 28, 730–739. [Google Scholar] [CrossRef][Green Version]
- Damanauskas, V.; Janulevičius, A. Differences in Tractor Performance Parameters between Single-Wheel 4WD and Dual-Wheel 2WD Driving Systems. J. Terramechanics 2015, 60, 63–73. [Google Scholar] [CrossRef]
- Barbosa, L.A.P.; Magalhães, P.S.G. Tire Tread Pattern Design Trigger on the Stress Distribution over Rigid Surfaces and Soil Compaction. J. Terramechanics 2015, 58, 27–38. [Google Scholar] [CrossRef]
- Moitzi, G.; Haas, M.; Wagentristl, H.; Boxberger, J.; Gronauer, A. Energy Consumption in Cultivating and Ploughing with Traction Improvement System and Consideration of the Rear Furrow Wheel-Load in Ploughing. Soil Tillage Res. 2013, 134, 56–60. [Google Scholar] [CrossRef]
- Silva, P.R.A. Mecanismos Sulcadores de Semeadora-Adubadoracultura do Milho (Zea mays L.) no Sistema de Plantio Direto. Master’s Thesis, Universida de Estadual Paulista “Júlio de Mesquita Filho”, Botucatu, Brazil, 2003. [Google Scholar]
- Levien, R.; Furlani, C.E.A.; Gamero, C.A.; Conte, O.; Cavichioli, F.A. Semeadura Direta de Milho Com Dois Tipos de Sulcadores de Adubo, Em Nível e No Sentido Do Declive Do Terreno. Cienc. Rural 2011, 41, 1003–1010. [Google Scholar] [CrossRef]
- Seki, A.S.; Benez, S.H.; Arbex Da Silva, P.R. Desempenho Operacional de Semeadora e Produtividade Do Milho em Plantio Direto e Cultivo Mínimo. EnergAgric 2012, 27, 1. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, R.; Huang, Y. Discrete Element Simulations and Experiments of Soil Disturbance Behaviours as Affected by the Upward Angle of Subsoiler’s Wing. In Proceedings of the 2019 ASABE Annual International Meeting, St. Joseph, MI, USA, 7–10 July 2019; p. 1900390. [Google Scholar]
- Wang, X.; Gao, P.; Yue, B.; Shen, H.; Fu, Z.; Zheng, Z.; Zhu, R.; Huang, Y. Optimisation of Installation Parameters of Subsoiler’ Wing Using the Discrete Element Method. Comput. Electron. Agric. 2019, 162, 523–530. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Chen, J. Comparison of Two Subsoiler Designs Using the Discrete Element Method (DEM). Trans. ASABE 2018, 61, 1529–1537. [Google Scholar] [CrossRef]
- Wang, X.; Fu, Z.; Zhang, Q.; Huang, Y. Short-Term Subsoiling Effects with Different Wing Mounting Heights before Winter Wheat on Soil Properties and Wheat Growth in Northwest China. Soil Tillage Res. 2021, 213, 105151. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, H.; Ji, J. Effect of Mounting Angle on Bending Subsoiling Tool–Soil Interactions Using DEM Simulations. Agriculture 2022, 12, 1830. [Google Scholar] [CrossRef]
- AAskari, M.; Shahgholi, G.; Abbaspour-Gilandeh, Y.; Tash-Shamsabadi, H. The Effect of New Wings on Subsoiler Performance. Appl. Eng. Agric 2016, 32, 353–362. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. 3D DEM Tillage Simulation: Validation of a Hysteretic Spring (Plastic) Contact Model for a Sweep Tool Operating in a Cohesionless Soil. Soil Tillage Res. 2014, 144, 220–227. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Pan, H.; Zheng, Z.; Huang, Y.; Zhu, R. Effect of Soil Particle Size on Soil-Subsoiler Interactions Using the Discrete Element Method Simulations. Biosyst. Eng. 2019, 182, 138–150. [Google Scholar] [CrossRef]
- Barr, J.B.; Desbiolles, J.M.A.; Fielke, J.M. Minimising Soil Disturbance and Reaction Forces for High Speed Sowing Using Bentleg Furrow Openers. Biosyst. Eng. 2016, 151, 53–64. [Google Scholar] [CrossRef]
- Barr, J.B.; Ucgul, M.; Desbiolles, J.M.A.; Fielke, J.M. Simulating the Effect of Rake Angle on Narrow Opener Performance with the Discrete Element Method. Biosyst. Eng. 2018, 171, 1–15. [Google Scholar] [CrossRef]
- Barr, J.; Desbiolles, J.; Ucgul, M.; Fielke, J.M. Bentleg Furrow Opener Performance Analysis Using the Discrete Element Method. Biosyst. Eng. 2020, 189, 99–115. [Google Scholar] [CrossRef]
- Solhjou, A.; Fielke, J.M.; Desbiolles, J.M.A. Soil Translocation by Narrow Openers with Various Rake Angles. Biosyst. Eng. 2012, 112, 65–73. [Google Scholar] [CrossRef]
- Ucgul, M.; Saunders, C.; Fielke, J.M. Comparison of the Discrete Element and Finite Element Methods to Model the Interaction of Soil and Tool Cutting Edge. Biosyst. Eng. 2018, 169, 199–208. [Google Scholar] [CrossRef]
- Saunders, C.; Ucgul, M.; Godwin, R.J. Discrete Element Method (DEM) Simulation to Improve Performance of a Mouldboard Skimmer. Soil Tillage Res. 2021, 205, 104764. [Google Scholar] [CrossRef]
- Ucgul, M.; Saunders, C.; Fielke, J.M. Discrete Element Modelling of Top Soil Burial Using a Full Scale Mouldboard Plough under Field Conditions. Biosyst. Eng. 2017, 160, 140–153. [Google Scholar] [CrossRef]
- Barr, J.B.; Desbiolles, J.M.A.; Fielke, J.M.; Ucgul, M. Development and Field Evaluation of a High-Speed No–till Seeding System. Soil Tillage Res. 2019, 194, 104337. [Google Scholar] [CrossRef]
- Solhjou, A.; Desbiolles, J.M.A.; Fielke, J.M. Soil Translocation by Narrow Openers with Various Blade Face Geometries. Biosyst. Eng. 2013, 114, 259–266. [Google Scholar] [CrossRef]
- Nukeshev, S.; Yeskhozhin, K.; Akhmetov, Y.; Kossatbekova, D.; Tleumbetov, K.; Tanbayev, K. Traction Force Investigation of The New Working Body of The Sod Seeder. IJTech 2023, 14, 536. [Google Scholar] [CrossRef]
- Nukeshev, S.; Eskhozhin, K.; Akhmetov, Y.; Kossatbekova, D.; Tleumbetov, K.; Tanbayev, K. Grain-fertilizer-grass anti-erosion seeder: Eurasian Patent EA038584B1; S.Seifullin Kazakh Agrotechnical University, Astana, Kazakhstan, 2021, 1. Available online: https://patents.google.com/patent/EA038584B1/ru (accessed on 15 July 2024).
- Sagitov, A.; Sherov, K.; Mardonov, B.; Akhmetov, Y.; Ramazanova, Z.; Ainabekova, S.; Tattimbek, G.; Tussupbekova, G.; Esirkepov, A. Experimental Study of Improving the Durability of a Cup Cutter by Pre-Processing. JMMP 2023, 7, 146. [Google Scholar] [CrossRef]
- Ferreira, S.L.C.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandão, G.C.; Da Silva, E.G.P.; Portugal, L.A.; Dos Reis, P.S.; Souza, A.S.; et al. Box-Behnken Design: An Alternative for the Optimization of Analytical Methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.; Lewicki, P.; Lewicki, P. Statistics: Methods and Applications: A Comprehensive Reference for Science, Industry, and Data Mining; StatSoft, Inc.: Tulsa, OK, USA, 2006; ISBN 1-884233-59-7. [Google Scholar]
- Brujaka, V.A.; Fokin, V.G.; Kuraeva, Y.V. Engineering Analysis in Ansys Workbench: A Textbook; Samara State Technical University: Samara, Russia, 2013. [Google Scholar]
- Spiridonov, A.A. Experiment Planning in the Study of Technological Processes; Engineering: Moscow, Russia, 1981. [Google Scholar]





| Characteristics | Unit | Value |
|---|---|---|
| Soil bin dimensions: Length | m | 3.93 |
| Height | 0.63 | |
| Width | 0.85 | |
| Type of soil | Chernozem, heavy loamy (dark chestnut soils) | |
| Moisture | % | 19 ÷ 23 |
| Hardness | MPa | 1.9 ÷ 3.2 |
| Density | kg/m3 | 1850 |
| Indicators | Value of Indicators |
|---|---|
| Soil type and name by mechanical composition | Southern carbonate chernozem, heavy loamy |
| Soil moisture, %, in layers, cm: 0–5 | 17.8 |
| 5–10 | 21.56 |
| 10–15 | 22.86 |
| 15–20 | 19.14 |
| 20–25 | 20.65 |
| Soil hardness, MPa, in layers cm: 0–5 | 1.9 |
| 5–10 | 3.5 |
| 10–15 | 3.1 |
| 15–20 | 3.3 |
| 20–25 | 4.3 |
| Item | Input Parameters of Materials | Unit | Numerical Value |
|---|---|---|---|
| Soil | Density | kg/m3 | 1850 |
| Shear modulus | Pa | 1 × 106 | |
| Poisson’s ratio | Dimensionless | 0.38 | |
| Bulk modulus for unloading | Dimensionless | 30,000 | |
| Soil–soil restitution coefficient | Dimensionless | 0.66 | |
| Soil–steel restitution coefficient | Dimensionless | 0.51 | |
| Soil–soil static friction | Dimensionless | 0.83 | |
| Soil–steel static friction | Dimensionless | 0.5 | |
| Soil–soil rolling friction | Dimensionless | 0.5 | |
| Soil–steel rolling friction | Dimensionless | 0.05 |
| Item | Input Parameters of Materials | Unit | Numerical Value |
|---|---|---|---|
| Tool (chisel) | Density of steel 65 Mn | kg/m3 | 7850 |
| Shear modulus | Pa | 8.23 × 1010 | |
| Poisson’s ratio | Dimensionless | 0.3 | |
| Young’s modulus | Pa | 2 × 1011 | |
| Center of mass constraint option | Dimensionless | 1 | |
| Global translational constraint | Dimensionless | 3 | |
| Global rotational constraint | Dimensionless | 7 |
| Factor | Critical Values; Variable νd (3 Factor Box–Behnken Plan); Predicted Value: 12.8298 | ||
|---|---|---|---|
| Observed Minimum | Critical Value | Observed Maximum | |
| b | 15.0000 | 20.9677 | 25.0000 |
| β | 60.0000 | 81.6045 | 90.0000 |
| l | 130.000 | 148.9115 | 160.0000 |
| Factor | Critical Values; Variable P (3 Factor Box–Behnken Plan); Predicted Value: 0.5666 | ||
|---|---|---|---|
| Observed Minimum | Critical Value | Observed Maximum | |
| b | 15.0000 | 21.1538 | 25.0000 |
| β | 60.0000 | 53.8235 | 90.0000 |
| l | 130.000 | 144.3478 | 160.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nukeshev, S.; Kossatbekova, D.; Ramaniuk, M.; Sagitov, A.; Akhmetov, Y.; Mamyrbayeva, I.; Tanbayev, K.; Tleumbetov, K. Traction Force, Sowing Quality, and Deformation Characteristics of the Coulter of a Grain–Fertilizer–Grass Seeder. AgriEngineering 2024, 6, 2326-2351. https://doi.org/10.3390/agriengineering6030136
Nukeshev S, Kossatbekova D, Ramaniuk M, Sagitov A, Akhmetov Y, Mamyrbayeva I, Tanbayev K, Tleumbetov K. Traction Force, Sowing Quality, and Deformation Characteristics of the Coulter of a Grain–Fertilizer–Grass Seeder. AgriEngineering. 2024; 6(3):2326-2351. https://doi.org/10.3390/agriengineering6030136
Chicago/Turabian StyleNukeshev, Sayakhat, Dinara Kossatbekova, Mikalai Ramaniuk, Almat Sagitov, Yerzhan Akhmetov, Indira Mamyrbayeva, Khozhakeldi Tanbayev, and Kaldybek Tleumbetov. 2024. "Traction Force, Sowing Quality, and Deformation Characteristics of the Coulter of a Grain–Fertilizer–Grass Seeder" AgriEngineering 6, no. 3: 2326-2351. https://doi.org/10.3390/agriengineering6030136
APA StyleNukeshev, S., Kossatbekova, D., Ramaniuk, M., Sagitov, A., Akhmetov, Y., Mamyrbayeva, I., Tanbayev, K., & Tleumbetov, K. (2024). Traction Force, Sowing Quality, and Deformation Characteristics of the Coulter of a Grain–Fertilizer–Grass Seeder. AgriEngineering, 6(3), 2326-2351. https://doi.org/10.3390/agriengineering6030136









