Leaf Area Index Estimation of Fully and Deficit Irrigated Alfalfa through Canopy Cover and Canopy Height
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Experiment
2.2. Imagery Acquisition
2.3. Canopy Cover (CC) and Canopy Height (CH)
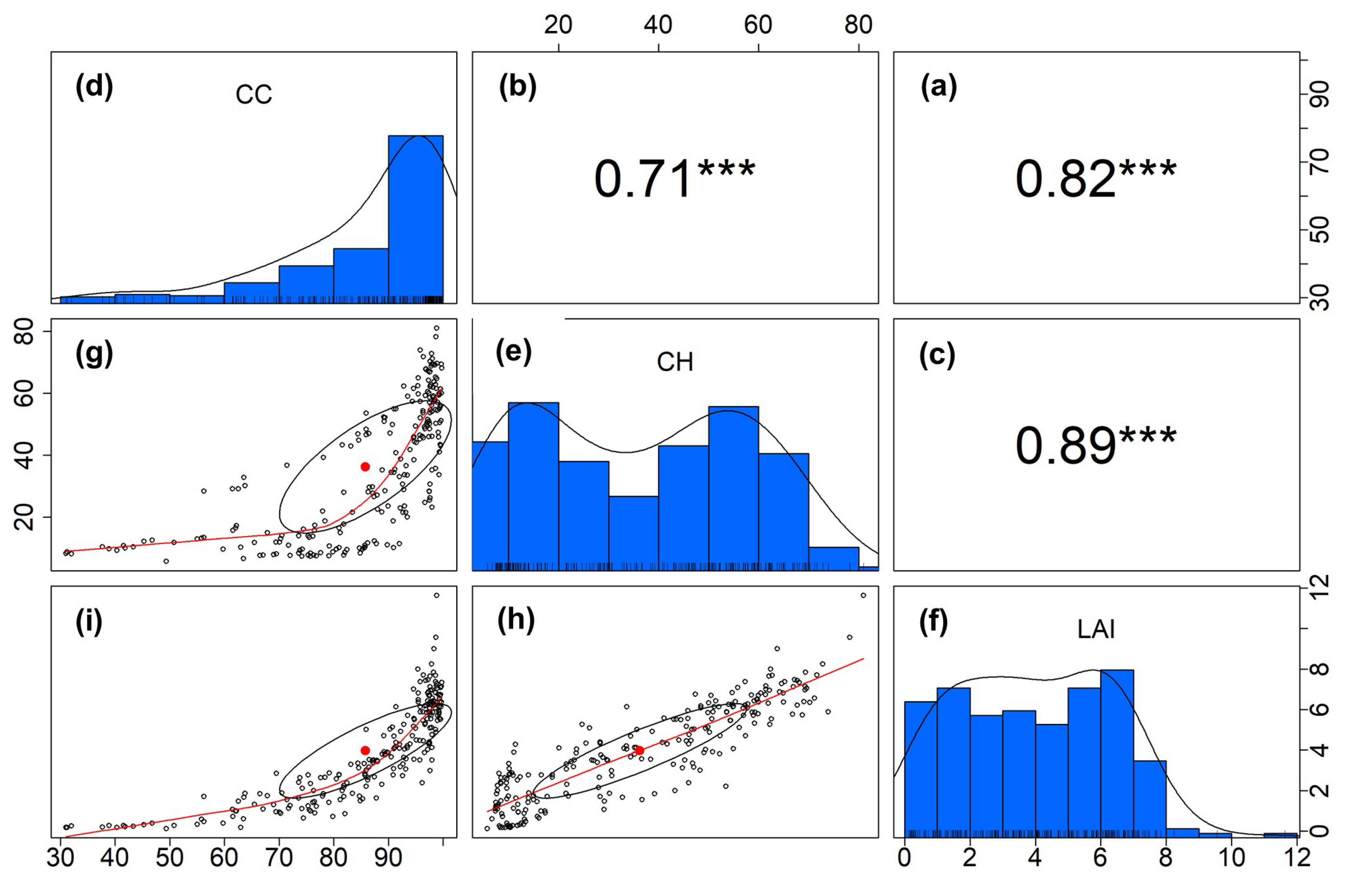
2.4. Leaf Area Index (LAI) Data Collection
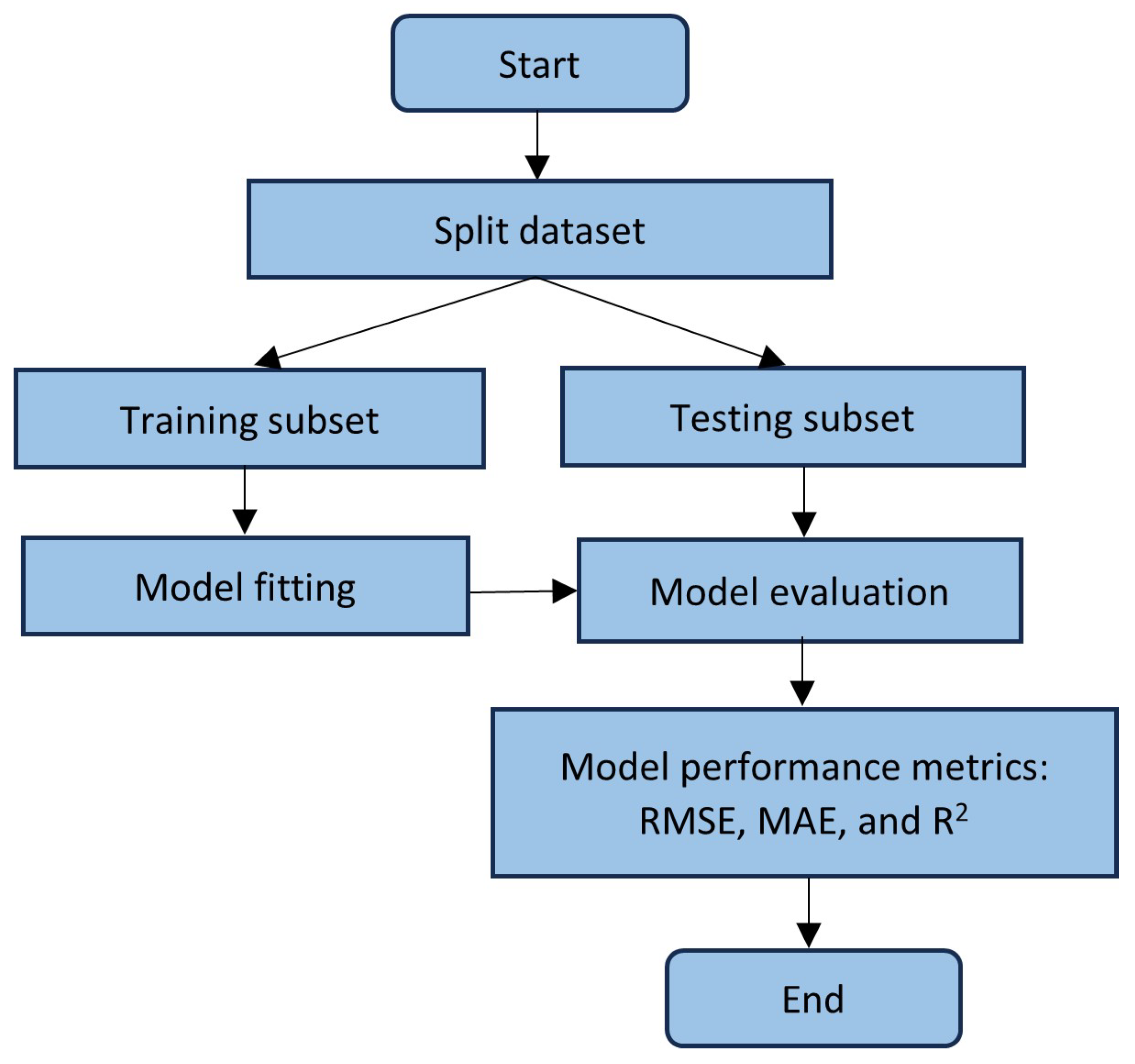
2.5. Model Fitting and Evaluation
2.6. Analysis of Variance
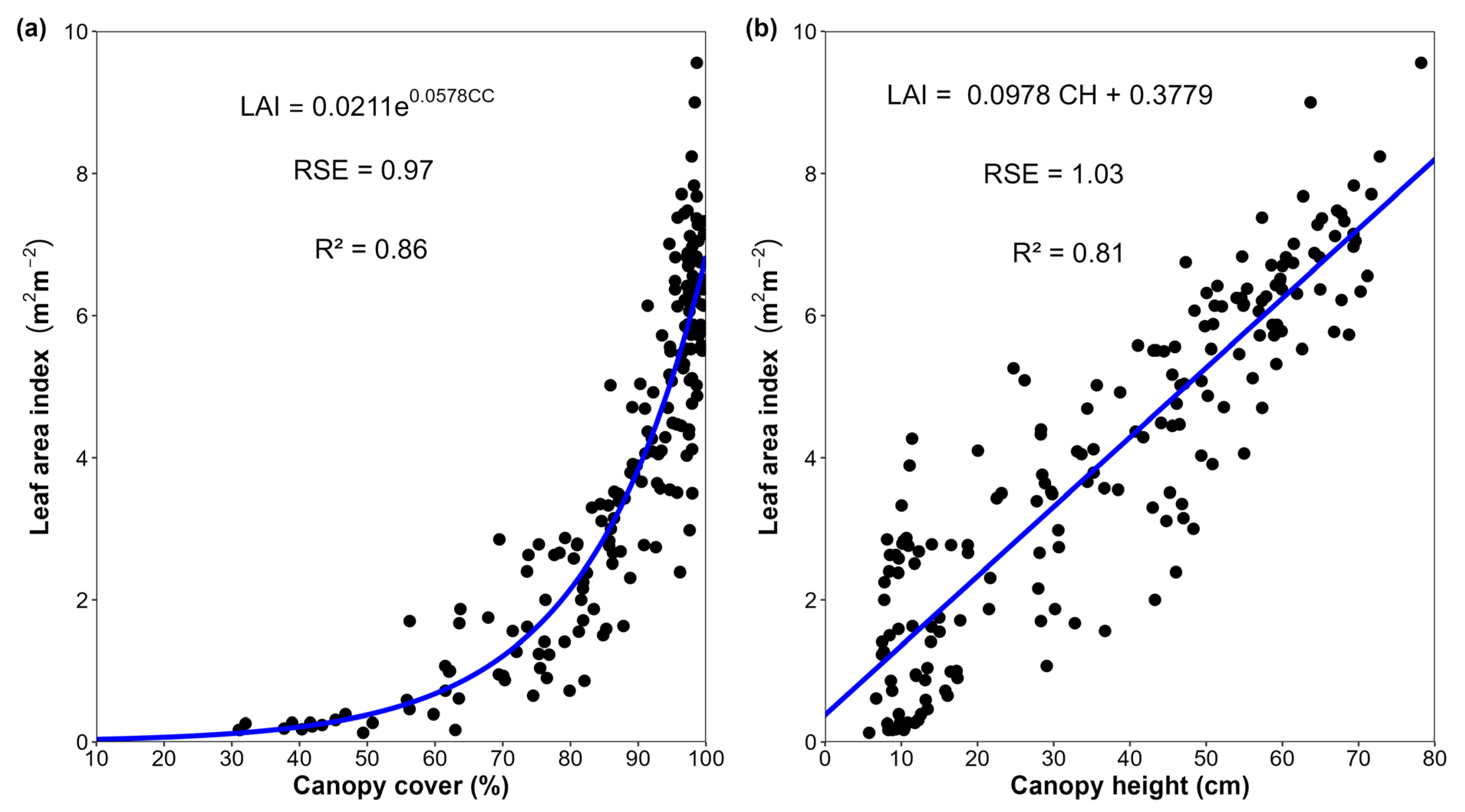
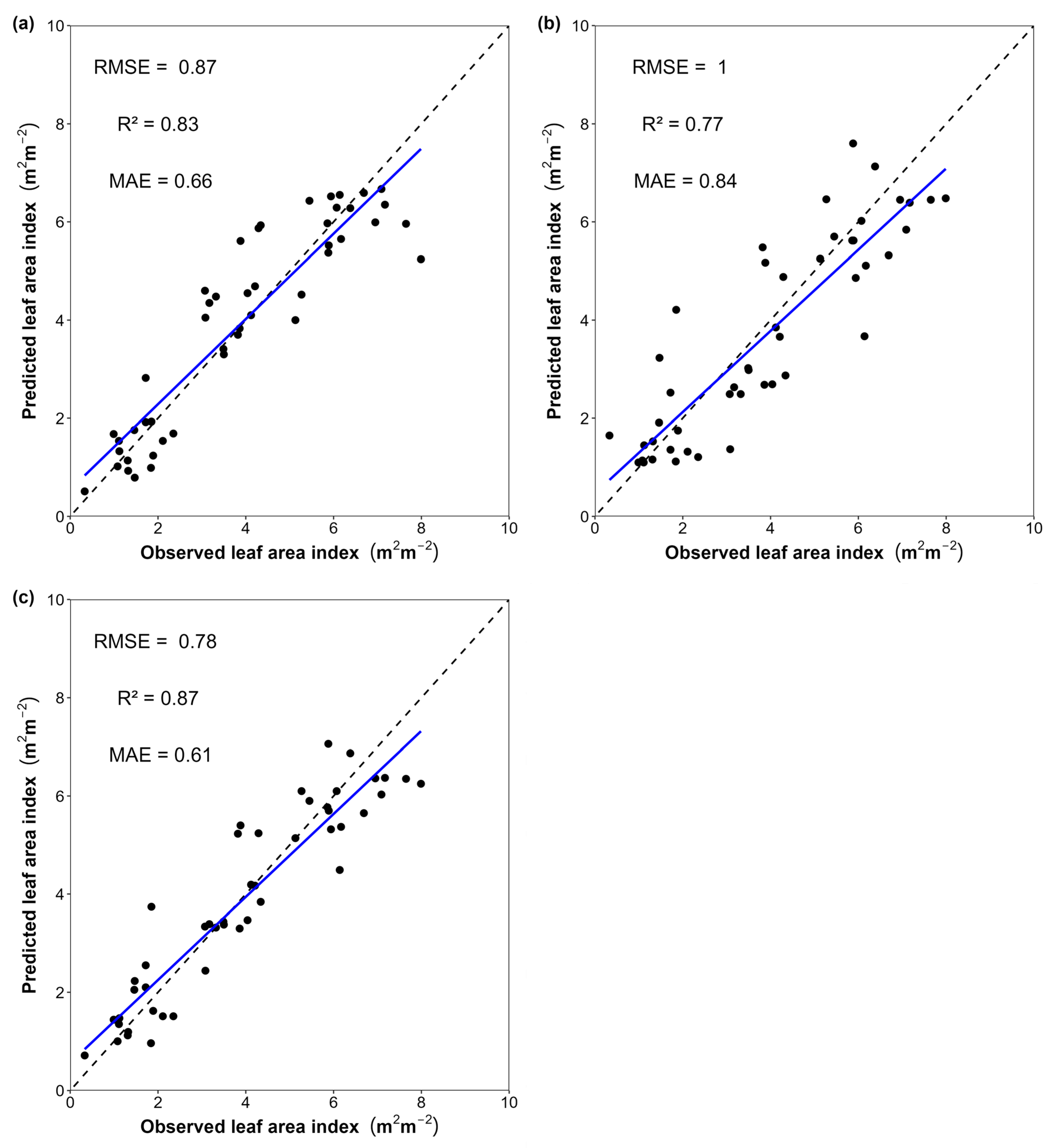
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-Flat Leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Dobrenz, A.K.; Back, M. Changing the Leaf Area on Alfalfa; Forage and Grain: A college of Agriculture Report; College of Agriculture, University of Arizona: Tucson, AZ, USA, 1984; pp. 6–7. Available online: https://repository.arizona.edu/handle/10150/200452 (accessed on 1 October 2021).
- Liu, M.; Mu, L.; Lu, Y.; Yang, H. Forage Accumulation and Radiation Use of Alfalfa under Deficit Irrigation. Crop Sci. 2021, 61, 2190–2202. [Google Scholar] [CrossRef]
- Nelson, C.J.; Smith, D. Growth of Birdsfoot and Alfalfa. III Changes in Carbohydrates Reserves and Growth Analysis Under Field Conditions1. Crop Sci. 1968, 8, 25–28. [Google Scholar] [CrossRef]
- Bolger, T.P.; Matches, A.G. Water-Use Efficiency and Yield of Sainfoin and Alfalfa. Crop Sci. 1990, 30, 143–148. [Google Scholar] [CrossRef]
- Greub, L.J.; Wedin, W.F. Leaf Area, Dry-Matter Accumulation, and Carbohydrate Reserves of Alfalfa and Birdsfoot Trefoil Under a Three-Cut Management1. Crop Sci. 1971, 11, 341–344. [Google Scholar] [CrossRef]
- Afsharmanesh, G. Study of Some Morphological Traits and Selection of Drought-Resistant Alfalfa Cultivars (Medicago sativa L.) in Jiroft, Iran. Plant Ecophysiol. 2009, 3, 109–118. [Google Scholar]
- Rimi, F.; Macolino, S.; Leinauer, B.; Lauriault, L.M.; Ziliotto, U. Alfalfa Yield and Morphology of Three Fall-Dormancy Categories Harvested at Two Phenological Stages in a Subtropical Climate. Agron. J. 2010, 102, 1578–1585. [Google Scholar] [CrossRef]
- Patrignani, A.; Ochsner, T.E. Canopeo: A Powerful New Tool for Measuring Fractional Green Canopy Cover. Agron. J. 2015, 107, 2312–2320. [Google Scholar] [CrossRef]
- Trout, T.J.; Johnson, L.F.; Gartung, J. Remote Sensing of Canopy Cover in Horticultural Crops. HortScience 2008, 43, 333–337. [Google Scholar] [CrossRef]
- Xiong, Y.; West, C.P.; Brown, C.P.; Green, P.E. Digital Image Analysis of Old World Bluestem Cover to Estimate Canopy Development. Agron. J. 2019, 111, 1247–1253. [Google Scholar] [CrossRef]
- Baxter, L.L.; West, C.P.; Brown, C.P.; Green, P.E. Comparing Nondestructive Sampling Techniques for Predicting Forage Mass in Alfalfa–Tall Wheatgrass Pasture. Agron. J. 2017, 109, 2097–2106. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT Cropping System Model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, Z.; et al. An Overview of APSIM, a Model Designed for Farming Systems Simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Geerts, S.; Raes, D.; Garcia, M. Using AquaCrop to Derive Deficit Irrigation Schedules. Agric. Water Manag. 2010, 98, 213–216. [Google Scholar] [CrossRef]
- Holman, J.; Min, D.; Klocke, N.; Kisekka, I.; Currie, R. Effects of Irrigation Amount and Timing on Alfalfa Nutritive Value. Trans. ASABE 2016, 59, 849–860. [Google Scholar] [CrossRef]
- Linker, R.; Kisekka, I. Model-Based Deficit Irrigation of Maize in Kansas. Trans. ASABE 2017, 60, 2011–2022. [Google Scholar] [CrossRef]
- Linker, R.; Ioslovich, I.; Sylaios, G.; Plauborg, F.; Battilani, A. Optimal Model-Based Deficit Irrigation Scheduling Using AquaCrop: A Simulation Study with Cotton, Potato and Tomato. Agric. Water Manag. 2016, 163, 236–243. [Google Scholar] [CrossRef]
- Thorp, K.; Hunsaker, D.; Bronson, K.; Andrade-Sanchez, P.; Barnes, E. Cotton Irrigation Scheduling Using a Crop Growth Model and FAO-56 Methods Field and Simulation Studies. Trans. ASABE 2017, 60, 2023–2039. [Google Scholar] [CrossRef]
- Linker, R.; Kisekka, I. Concurrent Data Assimilation and Model-Based Optimization of Irrigation Scheduling. Agric. Water Manag. 2022, 274, 107924. [Google Scholar] [CrossRef]
- Nielsen, D.C.; Miceli-Garcia, J.J.; Lyon, D.J. Canopy Cover and Leaf Area Index Relationships for Wheat, Triticale, and Corn. Agron. J. 2012, 104, 1569–1573. [Google Scholar] [CrossRef]
- Córcoles, J.I.; Ortega, J.F.; Hernández, D.; Moreno, M.A. Estimation of Leaf Area Index in Onion (Allium cepa L.) Using an Unmanned Aerial Vehicle. Biosyst. Eng. 2013, 115, 31–42. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E. Retrieval of Leaf Area Index from Top-of-Canopy Digital Photography over Agricultural Crops. Agric. For. Meteorol. 2010, 150, 1485–1490. [Google Scholar] [CrossRef]
- Labbafi, M.; Khalaj, H.; Allahdadi, I.; Nadjafi, F.; Akbari, G.A. Using Models for Estimation of Leaf Area Index in Cucurbita pepo L. J. Saudi Soc. Agric. Sci. 2019, 18, 55–60. [Google Scholar] [CrossRef]
- Logsdon, S.D.; Cambardella, C.A. An Approach for Indirect Determination of Leaf Area Index. Trans. ASABE 2019, 62, 655–659. [Google Scholar] [CrossRef]
- Hammond, K.; Kerry, R.; Jensen, R.R.; Spackman, R.; Hulet, A.; Hopkins, B.G.; Yost, M.A.; Hopkins, A.P.; Hansen, N.C. Assessing Within-Field Variation in Alfalfa Leaf Area Index Using UAV Visible Vegetation Indices. Agronomy 2023, 13, 1289. [Google Scholar] [CrossRef]
- WRCC. Station Daily Time Series. Available online: https://wrcc.dri.edu/cgi-bin/rawMAIN2.pl?nvunrc (accessed on 1 October 2021).
- Soil Survey Staff; NRCS; USDA. Web Soil Survey. Available online: https://websoilsurvey.sc.egov.usda.gov/App/HomePage.htm (accessed on 15 March 2022).
- R Core Team. The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 3 December 2021).
- Tuszynski, J. CaTools: Tools: Moving Window Statistics, GIF, Base64, ROC, AUC, Etc. 2021. R package version 1.18.2. Available online: https://CRAN.R-project.org/package=caTools (accessed on 1 October 2021).
- Hanson, A.A.; Barnes, D.K.; Hill, R.J. Alfalfa and Alfalfa Improvement; American Society of Agronomy, Crop Science Society of America, Soil Science Society of America: Madison, WI, USA, 1988. [Google Scholar]
- Brown, P.W.; Tanner, C.B. Alfalfa Stem and Leaf Growth During Water Stress. Agron. J. 1983, 75, 799–805. [Google Scholar] [CrossRef]
- Mouradi, M.; Bouizgaren, A.; Farissi, M.; Ghoulam, C. Assessment of Deficit Irrigation Responses of Moroccan Alfalfa (Medicago sativa L.) Landraces Grown Under Field Conditions. Irrig. Drain. Irrig. Drain 2018, 67, 179–190. [Google Scholar] [CrossRef]
- Saeed, I.A.M.; El-Nadi, A.H. Irrigation Effects on Growth, Yield, and Water Use Efficiency of Alfalfa. Irrig. Sci. 1997, 17, 63–68. [Google Scholar] [CrossRef]
- Liu, F.; Stützel, H. Leaf Expansion, Stomatal Conductance, and Transpiration of Vegetable Amaranth (Amaranthus sp.) in Response to Soil Drying. J. Am. Soc. Hortic. Sci. 2002, 127, 878–883. [Google Scholar] [CrossRef]
- Hanson, B.; Putnam, D.; Snyder, R. Deficit Irrigation of Alfalfa as a Strategy for Providing Water for Water-Short Areas. Agric. Water Manag. 2007, 93, 73–80. [Google Scholar] [CrossRef]
- Cholula, U.; Quintero, D.; Andrade, M.A.; Solomon, J. Effects of Deficit Irrigation on Yield and Water Productivity of Alfalfa in Northern Nevada. In 2022 ASABE Annual International Meeting; American Society of Agricultural and Biological Engineers: Houston, TX, USA, 2022. [Google Scholar]
- Raj, R.; Walker, J.P.; Pingale, R.; Nandan, R.; Naik, B.; Jagarlapudi, A. Leaf Area Index Estimation Using Top-of-Canopy Airborne RGB Images. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102282. [Google Scholar] [CrossRef]
- Peters, R.T.; Evett, S.R. Spatial and Temporal Analysis of Crop Conditions Using Multiple Canopy Temperature Maps Created with Center-Pivot-Mounted Infrared Thermometers. Trans. ASABE 2007, 50, 919–927. [Google Scholar] [CrossRef]
- O’Shaughnessy, S.A.; Andrade, M.A.; Evett, S.R. Using an Integrated Crop Water Stress Index for Irrigation Scheduling of Two Corn Hybrids in a Semi-Arid Region. Irrig. Sci. 2017, 35, 451–467. [Google Scholar] [CrossRef]




| Month | Growing Season 2021 | Growing Season 2022 | ||||
|---|---|---|---|---|---|---|
| Ave. Air Temp. (°C) | Solar Radiation (MJ m−2 month−1) | Precipitation (mm) | Ave. Air Temp. (°C) | Solar Radiation (MJ m−2 month−1) | Precipitation (mm) | |
| January | 2.7 | 271.2 | 29.5 | 2.2 | 321.3 | 0.0 |
| February | 3.8 | 370.4 | 2.3 | 2.8 | 399.1 | 2.5 |
| March | 5.9 | 573.6 | 1.5 | 8.5 | 565.3 | 0.8 |
| April | 12.1 | 749.1 | 0.3 | 10.1 | 754.1 | 7.6 |
| May | 16.1 | 897.7 | 3.8 | 14.2 | 833.4 | 0.0 |
| June | 24.1 | 919.1 | 4.3 | 20.4 | 767.8 | 0.3 |
| July | 27.2 | 840.4 | 3.1 | 25.8 | 902.1 | 0.0 |
| August | 23.9 | 744.3 | 0.0 | 24.9 | 770.9 | 21.3 |
| September | 19.7 | 638.1 | 1.0 | 20.4 | 576.9 | 7.4 |
| October | 10.8 | 419.7 | 87.1 | 13.2 | 523.8 | 0.0 |
| November | 7.8 | 318.3 | 2.3 | 2.2 | 320.5 | 10.7 |
| December | 1.7 | 227.9 | 76.7 | 1.4 | 226.2 | 89.7 |
| Sensor and Lens Parameters | Specification |
|---|---|
| Sensor dimensions | 6.55 × 4.92 mm |
| Image resolution | 2048 × 1536 pixels (3.2 Megapixels) |
| Pixel size | 3.2 µ |
| Camera lens focal length | 8.0 mm |
| Field of view | 1.51 m |
| Spatial resolution | 0.98 mm |
| Spectral resolution | 0.52–0.92 µm (Green, Red, NIR) |
| Image storage format | RAW 10 (10 bits) |
| Processed image format | 8-bit JPEG (256 bits) |
| Date | Canopy Cover (%) | Canopy Height (cm) | Leaf Area Index (m2 m−2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD * | Min † | Max ‡ | Mean | SD | Min | Max | Mean | SD | Min | Max | |
| 1 June 2021 | 93.64 | 3.83 | 85.90 | 98.35 | 59.00 | 7.26 | 46.63 | 71.68 | 6.23 | 1.69 | 2.20 | 9.00 |
| 15 June 2021 | End of first harvest period in 2021 | |||||||||||
| 9 July 2021 | 78.90 | 12.35 | 56.26 | 94.60 | 43.36 | 10.81 | 28.32 | 62.22 | 3.00 | 1.56 | 1.07 | 7.01 |
| 15 July 2021 | End of second harvest period in 2021 | |||||||||||
| 23 July 2021 | 46.32 | 10.57 | 31.04 | 62.21 | 11.77 | 2.73 | 8.17 | 17.25 | 0.39 | 0.27 | 0.17 | 1.00 |
| 16 August 2021 | End of third harvest period in 2021 | |||||||||||
| 22 September 2021 | 98.92 | 0.77 | 97.48 | 99.66 | 44.01 | 10.57 | 25.50 | 59.95 | 5.66 | 1.11 | 2.98 | 7.09 |
| 23 September 2021 | End of fourth harvest period in 2021 | |||||||||||
| 8 April 2022 | 71.86 | 7.67 | 49.39 | 81.87 | 13.40 | 2.74 | 5.78 | 17.73 | 1.34 | 0.72 | 0.13 | 2.78 |
| 23 April 2022 | 88.21 | 9.79 | 59.78 | 97.98 | 21.55 | 3.97 | 9.67 | 28.33 | 3.10 | 1.32 | 0.39 | 5.26 |
| 7 June 2022 | 98.02 | 0.81 | 95.82 | 98.88 | 68.49 | 5.91 | 56.10 | 80.94 | 7.10 | 1.53 | 5.12 | 11.63 |
| 8 June 2022 | End of first harvest period in 2022 | |||||||||||
| 23 June 2022 | 82.60 | 5.27 | 74.18 | 92.01 | 9.06 | 1.32 | 7.38 | 11.41 | 2.05 | 1.07 | 0.72 | 4.27 |
| 7 July 2022 | 97.81 | 1.69 | 94.67 | 99.77 | 52.75 | 8.76 | 38.44 | 69.33 | 5.04 | 1.37 | 2.39 | 7.33 |
| 8 July 2022 | End of second harvest period in 2022 | |||||||||||
| 21 July 2022 | 75.91 | 7.48 | 63.52 | 87.82 | 9.18 | 1.66 | 6.70 | 12.30 | 2.13 | 0.69 | 0.61 | 2.87 |
| 3 August 2022 | 96.32 | 2.23 | 91.40 | 98.57 | 53.33 | 9.29 | 38.71 | 69.37 | 5.99 | 0.92 | 4.29 | 7.83 |
| 4 August 2022 | End of third harvest period in 2022 | |||||||||||
| 19 August 2022 | 89.56 | 3.18 | 81.84 | 93.46 | 31.20 | 3.32 | 26.66 | 36.64 | 3.59 | 0.60 | 2.16 | 4.69 |
| 30 August 2022 | 97.13 | 0.83 | 94.94 | 98.13 | 54.12 | 4.51 | 46.51 | 62.59 | 5.88 | 0.58 | 4.47 | 6.82 |
| 31 August 2022 | End of fourth harvest period in 2022 | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cholula, U.; Andrade, M.A.; Solomon, J.K.Q. Leaf Area Index Estimation of Fully and Deficit Irrigated Alfalfa through Canopy Cover and Canopy Height. AgriEngineering 2024, 6, 2101-2114. https://doi.org/10.3390/agriengineering6030123
Cholula U, Andrade MA, Solomon JKQ. Leaf Area Index Estimation of Fully and Deficit Irrigated Alfalfa through Canopy Cover and Canopy Height. AgriEngineering. 2024; 6(3):2101-2114. https://doi.org/10.3390/agriengineering6030123
Chicago/Turabian StyleCholula, Uriel, Manuel A. Andrade, and Juan K. Q. Solomon. 2024. "Leaf Area Index Estimation of Fully and Deficit Irrigated Alfalfa through Canopy Cover and Canopy Height" AgriEngineering 6, no. 3: 2101-2114. https://doi.org/10.3390/agriengineering6030123
APA StyleCholula, U., Andrade, M. A., & Solomon, J. K. Q. (2024). Leaf Area Index Estimation of Fully and Deficit Irrigated Alfalfa through Canopy Cover and Canopy Height. AgriEngineering, 6(3), 2101-2114. https://doi.org/10.3390/agriengineering6030123






