A CFD Methodology for the Modelling of Animal Thermal Welfare in Hybrid Ventilated Livestock Buildings

Abstract

Computational fluid dynamics (CFD) may aid the design of barn ventilation systems by simulating indoor cattle thermal welfare. In the literature, CFD models of mechanically and naturally ventilated barns are proposed separately. Hybrid ventilation relies on cross effects between air change mechanisms that cannot be studied using existing models. The objective of this study was to develop a CFD methodology for modelling animal thermal comfort in hybrid ventilated barns. To check the capability of CFD as a design evaluation tool, a real case study (with exhaust blowers) and an alternative roof layout (with ridge gaps) were simulated in summer and winter weather. Typical phenomena of natural and mechanical ventilation were considered: buoyancy, solar radiation, and wind together with high-speed fans and exhaust blowers. Cattle thermal load was determined from a daily animal energy balance, and the assessment of thermal welfare was performed using thermohygrometric indexes. Results highlight that the current ventilation layout ensures adequate thermal welfare on average, despite large nonuniformity between stalls. The predicted intensity of heat stress was successfully compared with experimental measurements of heavy breathing duration. Results show strong interactions between natural and mechanical ventilation, underlining the need for an integrated simulation methodology.

1. Introduction

In modern precision farming, special attention is paid to animal productivity and welfare. In order to maintain homeostasis, animals must keep an equilibrium between metabolic heat and heat transfer to the environment. Metabolic heat is dissipated through different mechanisms such as respiration, sweating, convection, and radiation. High external temperature and humidity hinder animal heat transfer with the ambient, and the metabolic heat is likely to become physiologically harmful [1]. This unbalanced condition is called heat stress, and its onset is related to several biological issues such as increased body temperature, worse reproductive performances [2] and behavioural changes [3]. In addition, animals reduce their dry matter intake in the strive to decrease their metabolic heat. Animals tend to enhance heat dissipation by activating additional transfer mechanisms, for instance, panting or sweating [4]. Heat stress is remarkably critical for dairy cows as it correlates directly to a loss of milk yield [5,6] and relevant economical losses [7,8]. Since heat stress stems from the inability to dissipate an excess of metabolic heat, the productivity level of dairy cows is directly influenced by thermohygrometric conditions inside livestock buildings. Therefore, the design of barn ventilation systems has a strong influence on cows’ thermal comfort and milk production. To delay the onset of heat stress, dairy barns are equipped with several heat-stress abatement devices. Intake and exhaust fans may be used to enhance air change and control internal air conditions. Box and basket fans are commonly employed to drive high-speed airflows to animals and enhance convective heat transfer on their skin [9]. The rise in skin convection can also be obtained with horizontally mounted high-volume low-speed fans. In spite of their lower velocities, the inflow depth of the airflow is reported to be higher, and their energy efficiency is higher than box or basket fans [10]. Generally, recirculation fans only improve internal mixing and animal heat transfer; however, in some cases, they could also be exploited to enhance the air change rate by inducing air entrainment. Heat-stress abatement can also be obtained with evaporative systems such as fogging or direct wetting. Despite being very effective, their usage involves a large amount of water, and they are sometimes connected with an increase in infections and mastitis [11]. Therefore, their usage should be limited to critical conditions, for instance, when animals gather in the holding pen before milking [12].

2. Motivation, Objective and Analysed Case Study

The optimal barn configuration must provide high levels of animal thermal comfort and productivity, together with minimum water and energy usage. In the design process, a predictive model is required for the sizing of ventilation systems and heat-stress abatement devices. Hybrid ventilation systems are especially critical, as recirculation fans need to be positioned to have effective air entrainment. The definition of a correct fan layout is not straightforward, as it involves complex fluid dynamics phenomena. State-of-the-art methodologies for barn thermal simulation are based on lumped thermal models solved from mass and energy balances on the entire building [13]. This approach is widely adopted for the modelling of civil and industrial buildings, though it may not be suitable for large livestock constructions. These models are based on the implicit assumption of uniform indoor air conditions that may not be satisfied for large animal buildings. Therefore, these models cannot provide information on the internal non-uniformity of temperature and humidity. Furthermore, as the analysis is performed on a control volume corresponding to the perimeter boundary of the barn, these models are not able to predict internal phenomena. Lumped mass thermal models are not suitable for hybrid ventilation systems, as air entrainment is generated by internal recirculation fans that cannot be easily predicted. In order to overcome the limitations of these models, a different strategy must be adopted: in the literature, several authors have applied computational fluid dynamics (CFD) to the thermal simulation of livestock buildings. CFD allows the complete and detailed physical description of air behaviour inside the barn. The design of mechanically ventilated livestock buildings has been extensively analysed through CFD in the literature [14]. Zhou et al. [15] performed CFD simulations to assess the optimal baffle location in a cross-ventilated building. Similarly, Pakari and Ghani [16] analysed different mechanical ventilation systems for very hot climates. Cheng et al. [17] compared different design solutions for a laying-hen house through CFD in order to assess the optimal configuration. CFD may also be used to improve the positioning of ventilation components such as a precision air supplier, as reported by Wang et al. [18]. Similarly, the geometry of a naturally ventilated barn was previously investigated in the literature as it influences wind and stack effects. Complex models such as computational fluid dynamics can also be employed to calibrate simpler models for wind inflow [19,20]. Wu et al. [21] created a numerical fluid dynamic model to assess with high accuracy the air change rate in a naturally ventilated building and check the accuracy of experimental measurements obtained with different techniques. De Masi et al. [13] employed CFD to validate a lumped mass thermal model for a dairy barn in a Mediterranean climate. Even though the capabilities of CFD codes for the design of naturally and mechanically ventilated barns have been largely investigated in the literature, very few studies focus on a complete model for hybrid systems.

The objective of this study is to provide a general CFD methodology for the analysis of hybrid ventilated livestock buildings. With mechanical ventilation, some natural effects such as wind or buoyancy can be neglected. Indeed, in closed barns, the simulation of the external domain is not required.

The modelling of naturally ventilated barns mainly focuses on the wind effect, and the presence of a recirculation fan is often neglected as it is considered a local phenomenon. Hybrid systems require an integrated simulation methodology, as the cross effect between ventilation mechanisms is essential to provide a correct description of air entrainment. In the modelling of a hybrid barn, the effects of both natural and mechanical ventilation must be included. Since the building has large perimeter openings, wind-induced ventilation and buoyancy are relevant. Moreover, high-speed airflows are present due to box and basket fans. Previous research works mainly focus on summer weather as it is highly demanding for cooling systems. CFD analysis of winter conditions is often neglected, as cows are less likely to suffer from excessive low temperature and humidity. Nevertheless, the behaviour of the barn in cold weather must be verified, as minimum hourly ventilation rates of 4–10 ${\mathrm{h}}^{-1}$ must be always provided to control indoor air quality. Summer simulations include solar radiation, wind-induced ventilation and fans that run at maximum speed. In winter simulations, fans are inactive except for blowers, and the air change rate is determined by buoyancy-driven flows.

This study could have a positive impact on livestock farming only if the proposed modelling strategy is able to provide useful guidelines for barn design. Therefore, the developed model was applied in the simulation of a real building. The experimental barn of “Centro di Ricerche per la Zootecnia e l’Ambiente” (CerZoo) was simulated as a relevant case study. CerZoo is a hybrid ventilated barn located in an agricultural area near Piacenza (Italy). The analysed barn is designed to house around 100 cows in four separated stall lines. The main body of the building includes stalls and prepartum and postpartum paddocks with a central feeding alley. A milking parlour and other facilities are located in an auxiliary lateral building. The ventilation system consists of 19 basket fans over the feeding alley, 12 box fans over stalls and 2 high-volume low-speed fans over the prepartum and postpartum paddocks. All high-speed fans are oriented south-to-north in order to generate a macroscopic airflow parallel to cubicle lines by air entrainment. This cooling strategy is widespread in hybrid ventilated livestock buildings, and it is referred as “tunnel ventilation”. A schematic representation of fan positions is illustrated in Figure 1.

The CerZoo barn has an unusual roof geometry with a close apex and five fan-actuated blowers on top. This configuration is uncommon in large-scale applications, as an open roof with single or double openings is preferred. In order to assess whether the developed CFD model is able to provide useful guidelines, the existing closed-roof configuration is compared with a more traditional open roof with a ridge gap. Figure 2 illustrates the existing closed-roof configuration, while Figure 3 shows the open-roof geometry. Since the design process considers both cold and hot weather, the two configurations are simulated in both winter and summer weather. The presented work was carried out using the open-source CFD code OpenFOAM in order to have freedom in the implementation of new solutions and models. This CFD simulation code has already been employed and validated for the simulation of a livestock building [22,23], even if all applications reported in the literature refer to naturally or mechanically ventilated barns.

3. Materials and Methods

3.1. Animal Thermal Modelling

The main challenge in the simulation of livestock buildings is animal thermal modelling. Cattle are the main thermal load, and water evaporation by sweating and respiration is a relevant source of humidity. In the literature, two different approaches have been proposed and tested. A possible solution is to represent the cows’ surface in the mesh, and sensible and latent thermal loads might be modelled through the phenomenological relations of each mechanism. For detailed modelling, it is possible to adopt a custom boundary condition coupled with a lumped mass animal thermal model [24]. Several authors have developed correlations for the estimation of skin/fur thermal conductivity [25,26], surface convection [27,28] and respiration tidal volume [29]. These correlations can be used to develop a lumped mass thermal model for dairy cows [30,31]; however, the adoption of such models in CFD has not been validated yet. In addition, a large uncertainty is connected to the phenomenological relations of skin conduction, respiration and sweating [32,33,34]. On the one hand, this approach allows a detailed resolution of fluid dynamic conditions, but on the other, it requires one to describes the animal surface in the mesh, with a relevant increase in cell number. Due to its high computational cost, this approach can only be applied if the geometry can be simplified using symmetry planes, for instance, in the case of cross-mechanical ventilation [15].

In order to overcome these limitations, a different approach was adopted. Animal shape was not depicted in the simulation, but thermal load was considered as uniformly distributed energy and water sources. This approach was already used in the literature by Iqbal et al. [35] and validated against the surface description approach. The animal thermal load was computed starting from a daily-averaged energy balance. The Large Ruminant Nutrition System (LRNS) provides an accurate description of dairy cow metabolism [36]. The intake energy can be estimated starting from the daily dry matter intake, while the amount of solid and liquid residues can be estimated from the fraction of digestible compound in dry matter intake. The energy content in milk was evaluated starting from the daily yield and the specific milk energy. The energy content and amount of dry matter intake were set according to the diet plan of the considered animals. The animal daily energy balance was similar to the one reported for highly fed animals [37]. The energy converted in mechanical work was neglected, as the movement of animals is limited during the day.

It was possible to compute the metabolic energy as a solution of the daily energy balance, and afterwards, the metabolic heat was evaluated considering the constant generation during the day. The obtained value of 1938 $\mathrm{W}$ for lactating cows is in good agreement with the evaluation of 1855 $\mathrm{W}$ by Gebremedhin et al. [38]. It is important to notice that the LRNS model requires external temperature, humidity and wind speed that are outputs of the CFD simulation. To avoid an implicit coupling between models, external noncritical conditions were considered. This is a conservative estimation: metabolic heat is expected to decrease if animals reach heat stress as their dry matter intake reduces. Heat transfer by long-wave radiation was neglected in this study. Elting and Brody’s [39] correlation can be used to estimate skin surface (S), assuming a body weight ($BW$) of 600 $\mathrm{kg}$ as reported in Equation (1).

$$S=0.147B{W}^{0.56}=5.285\left[{\mathrm{m}}^2\right]$$

(1)

External skin temperature $T_{Skin}$ and emissivity $ϵ$ can be considered equal to 34.7 °C and 0.98 as measured by Khakimov et al. [40] through thermographic imaging. A safe estimate of the fraction of metabolic heat ($Q_{Met}$) transferred by long-wave radiation ($Q_{Rad}$) can be evaluated from Equation (2) [41].

$$\frac{{\dot{Q}}_{Rad}}{{\dot{Q}}_{Met}}=\frac{\sigma ϵS\left(T_{Skin}^4-T_{Amb}^4\right)}{{\dot{Q}}_{Met}}=8.5[\%]$$

(2)

$\sigma$ is the Stefan– Boltzmann constant, while external temperature $T_{Amb}$ was considered at 30 °C, representing an average radiating temperature between sky and ground. In a real case, fur external temperature is expected to be lower. Moreover the mean radiative temperature is likely to be higher, as a relevant fraction of the solid view angle will be occupied by other animals at the same temperature. The proposed modelling strategy is not suitable for the application of detailed radiation models such as P1 or view factor since animal surface is not characterised in the simulation.

A relevant fraction of thermal load is dissipated through evaporation. Therefore, an equivalent distributed water source was considered in animal-occupied zones. The fraction of heat removed by evaporation was considered following the results obtained by Li et al. [42] using a validated lumped mass thermal model of a dairy cow. Li et al. [42] computed the fraction of heat transferred through evaporation as ranging between 45.7% and 57.0% during the day, depending on external temperature and humidity. Based on these considerations, the metabolic heat was considered equally dissipated through sensible and latent heat transfer. The corresponding evaporated mass can be computed through the latent heat load and the latent evaporation energy of water. The location of the energy and water source terms followed the usual barn management strategy. Fregonesi et al. [43,44] report that dairy cows in standard conditions tend to spend between 16 and 17 h/day in the stall. The time spent by animals in the two regions was arbitrarily split as follows: 70% in stalls and 30% in feeding lines. The number of cows in feeding lines and stalls can be then determined by knowing the total number of animals in the barn. A more detailed report on the number and position of dairy cows is presented in

Table 1. Cattle position according to usual barn management strategy and corresponding energy and water source terms.

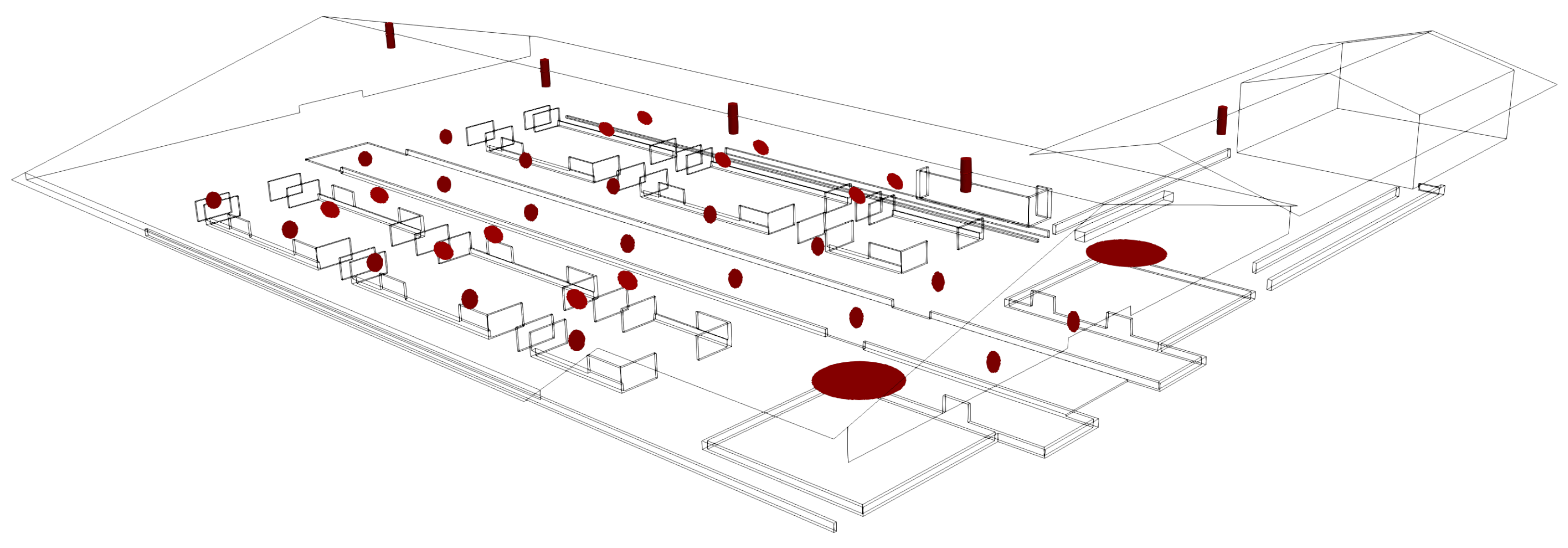
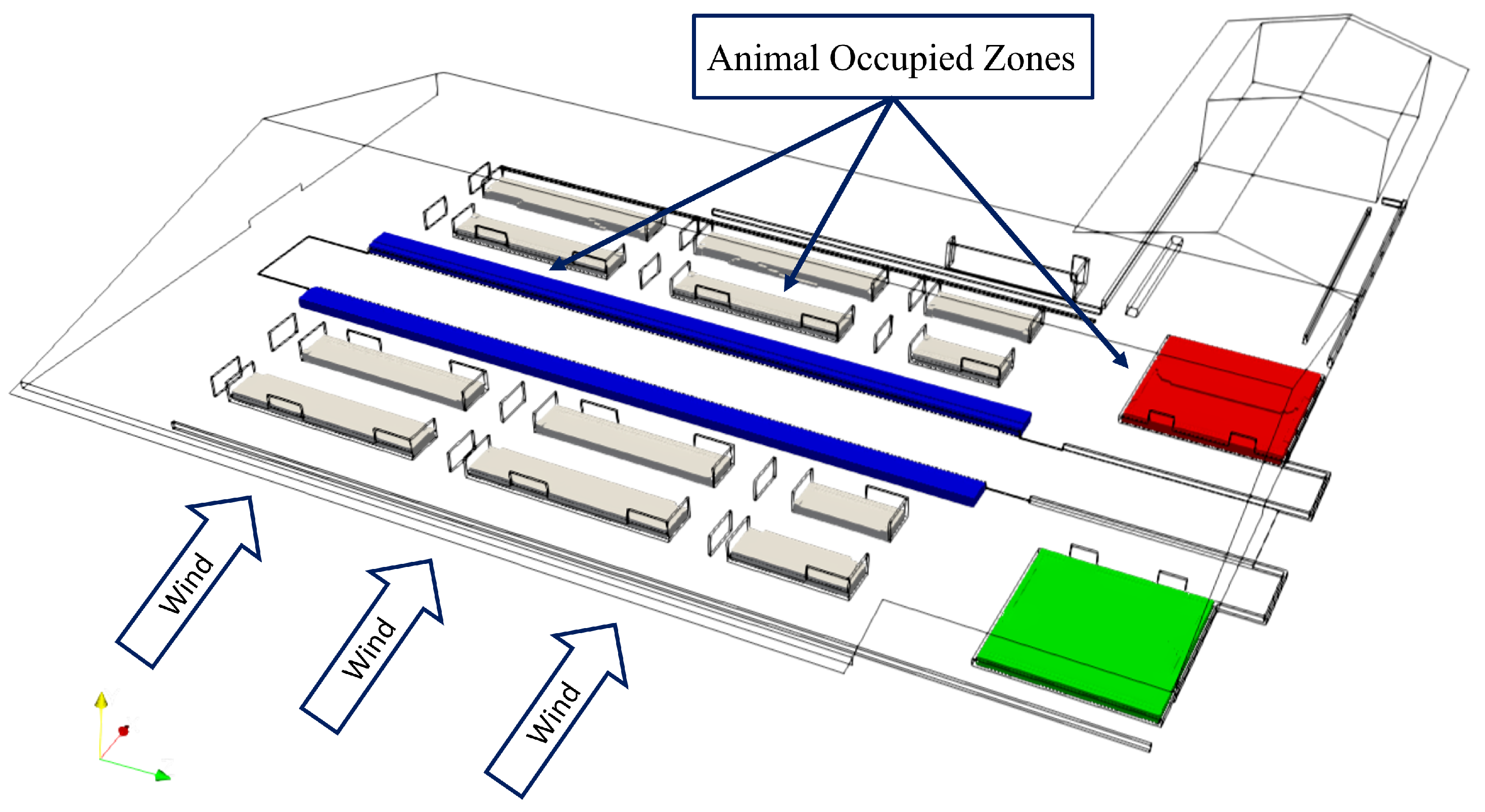
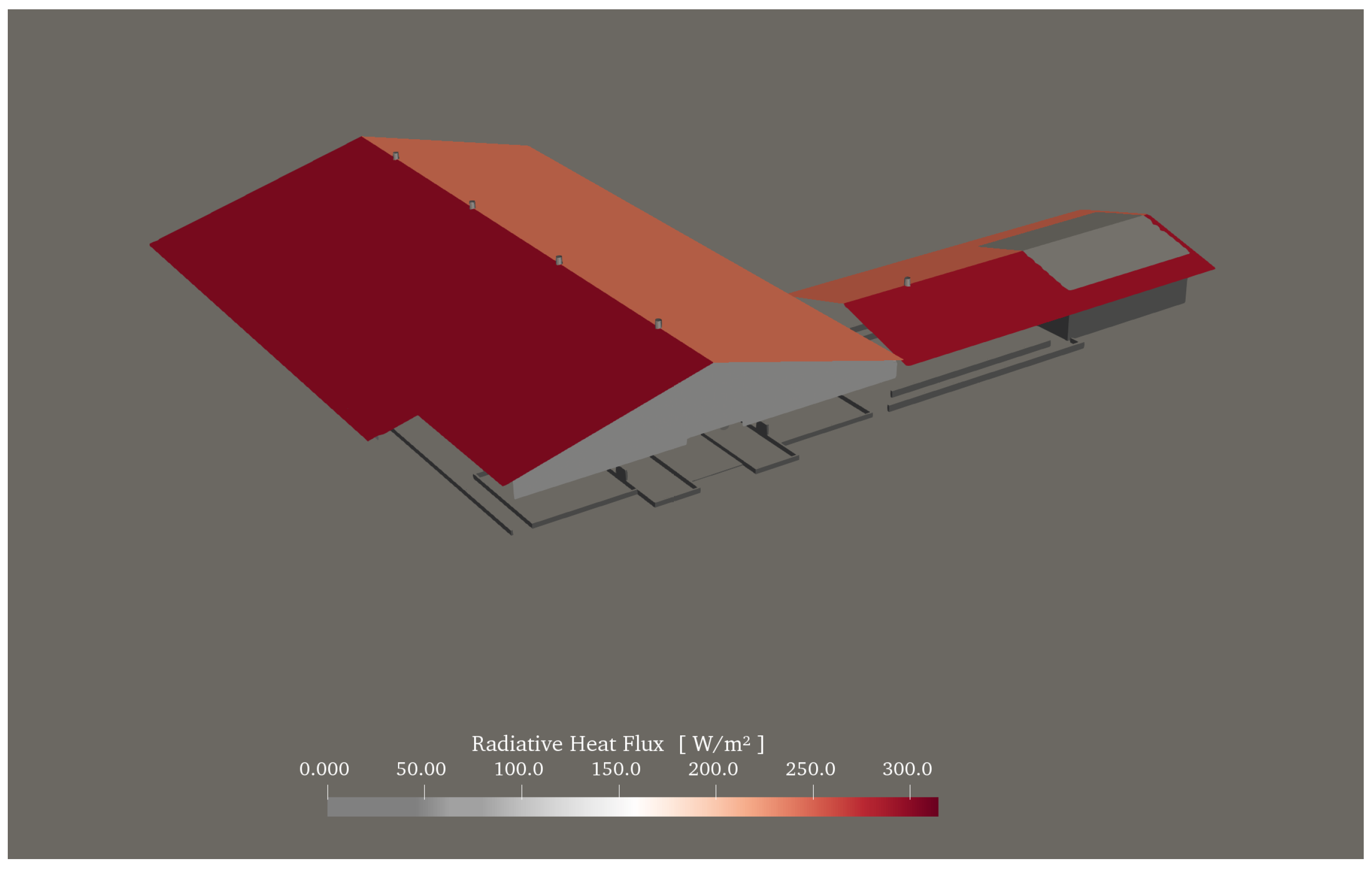
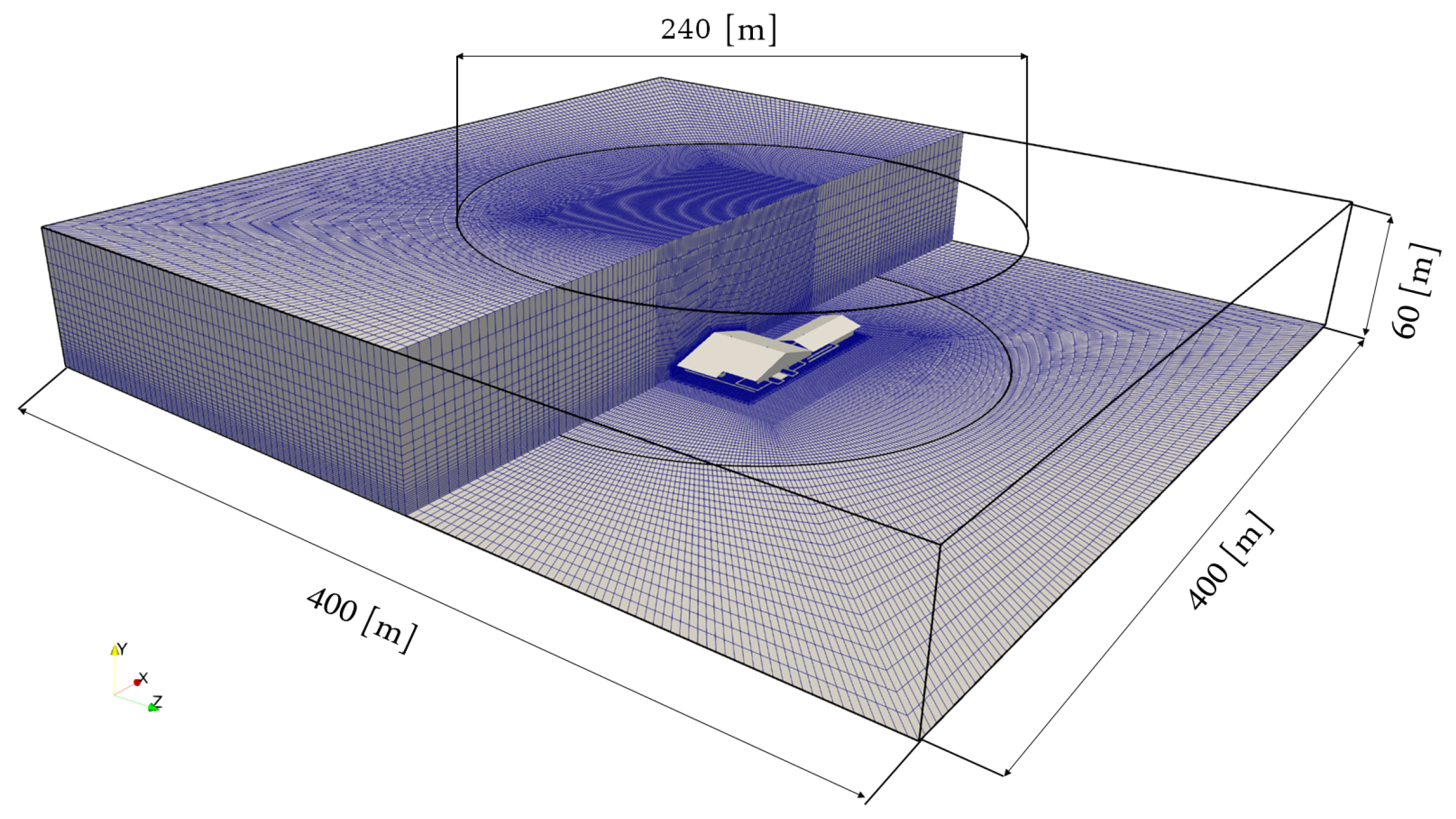
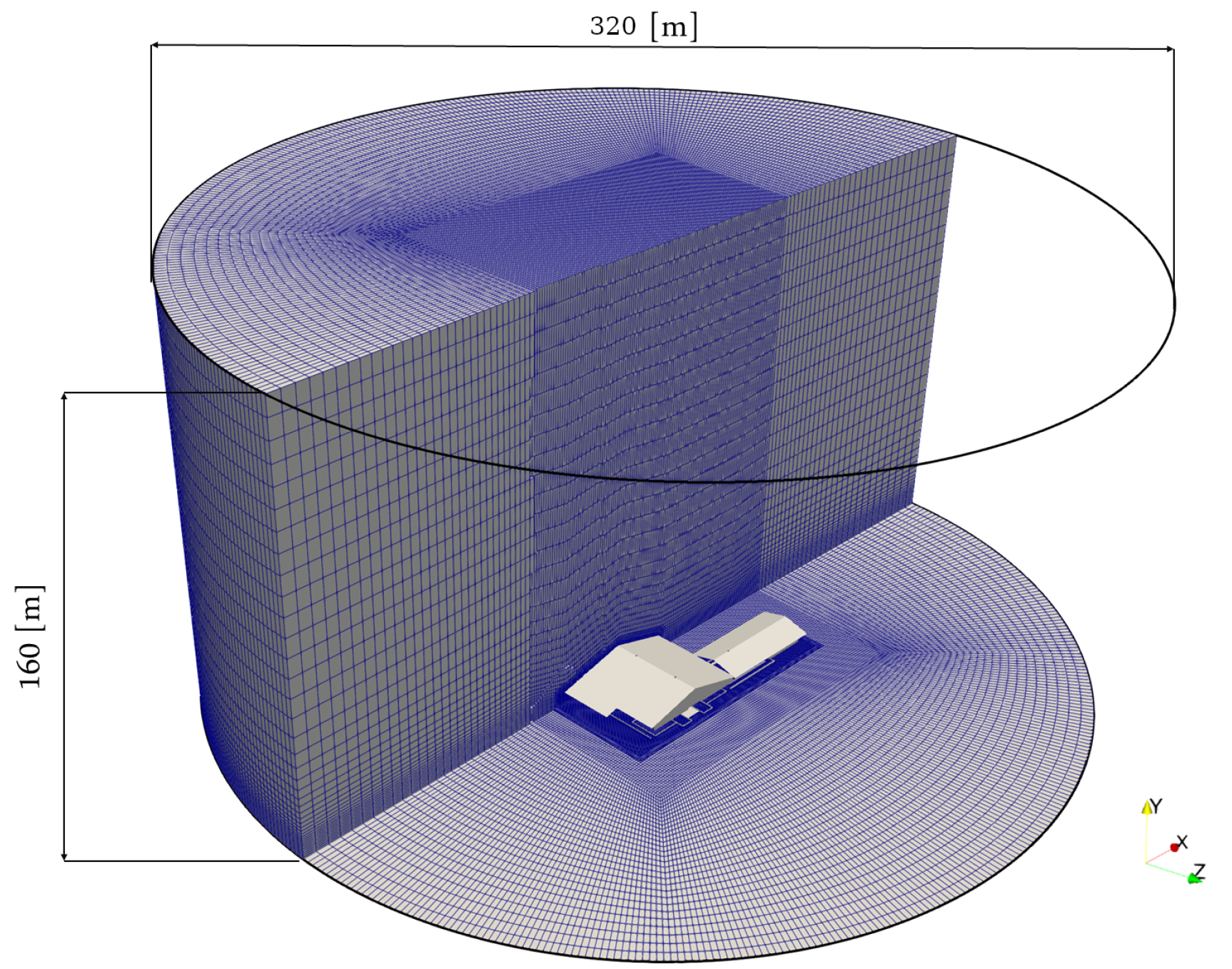
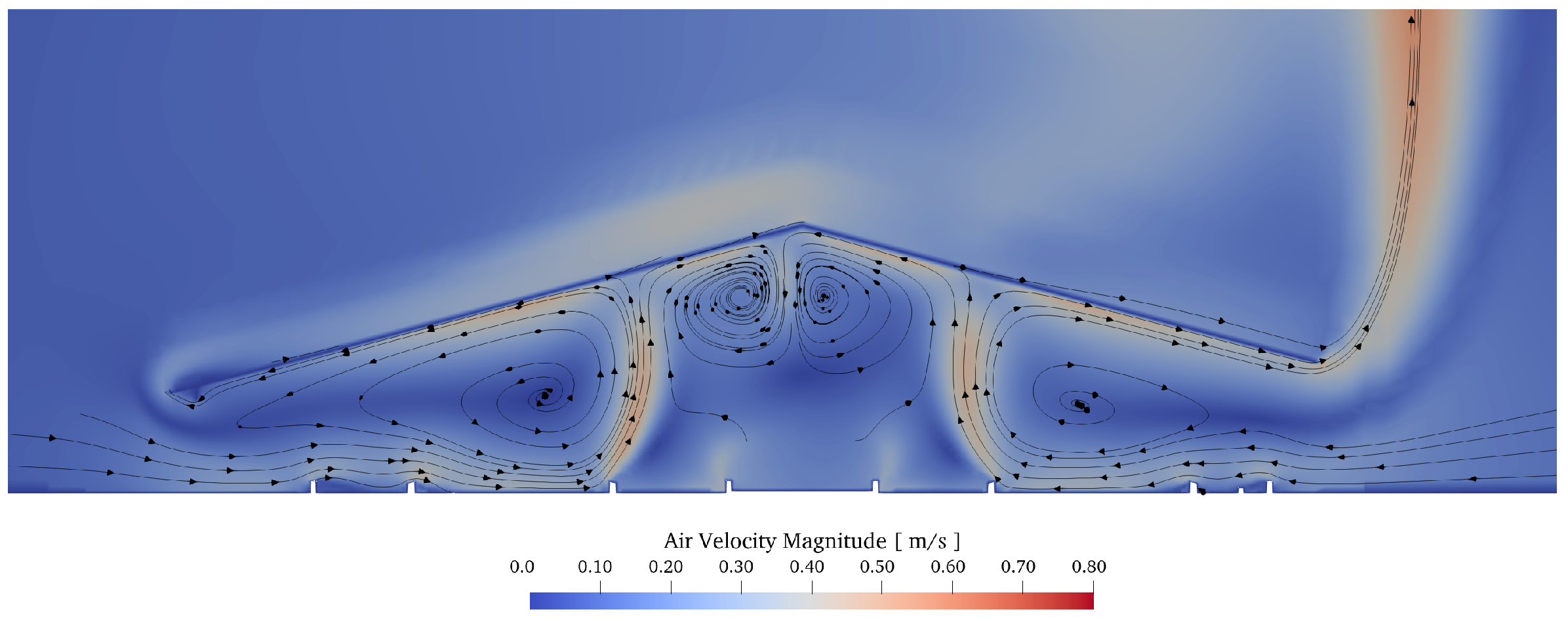
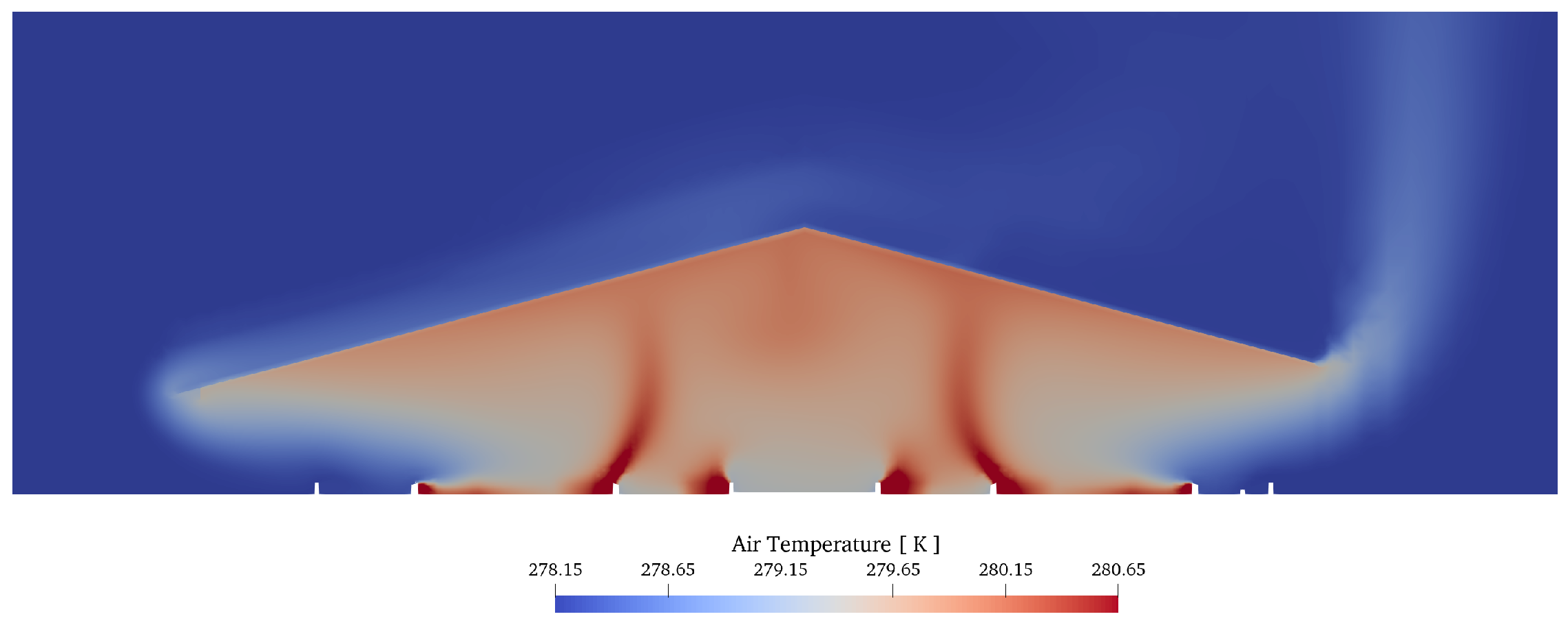
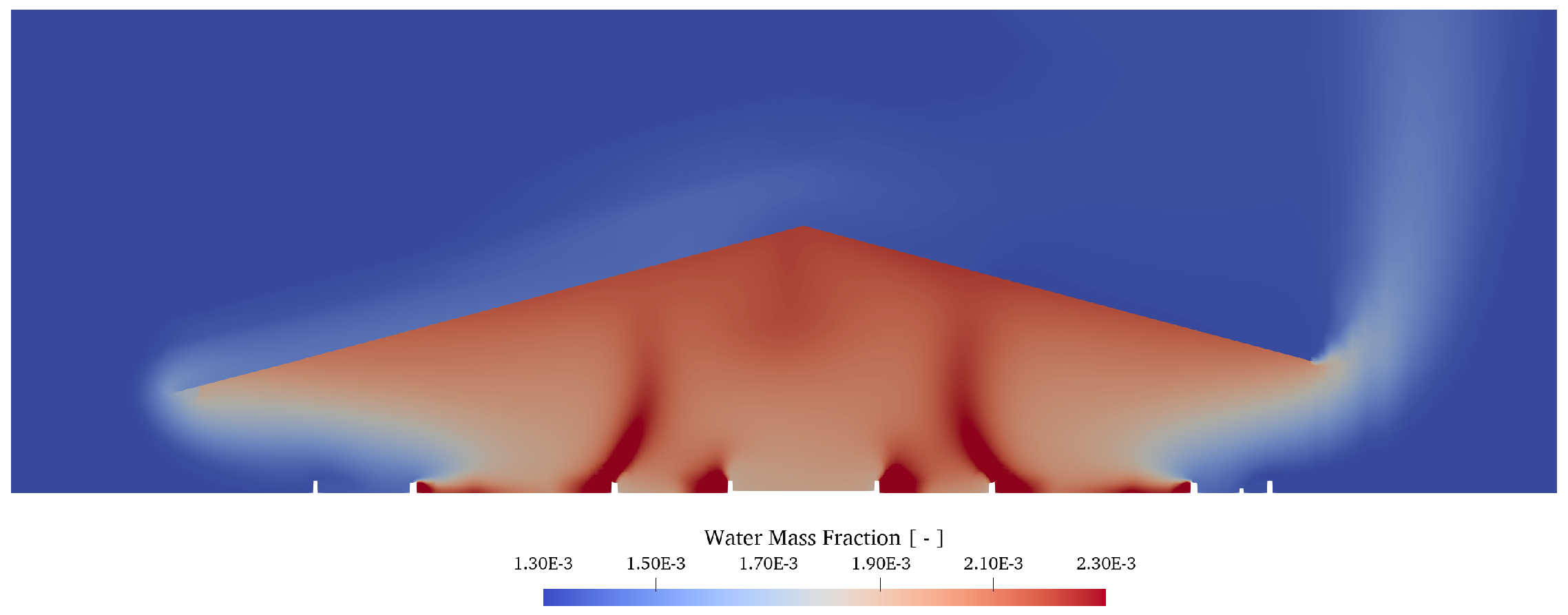
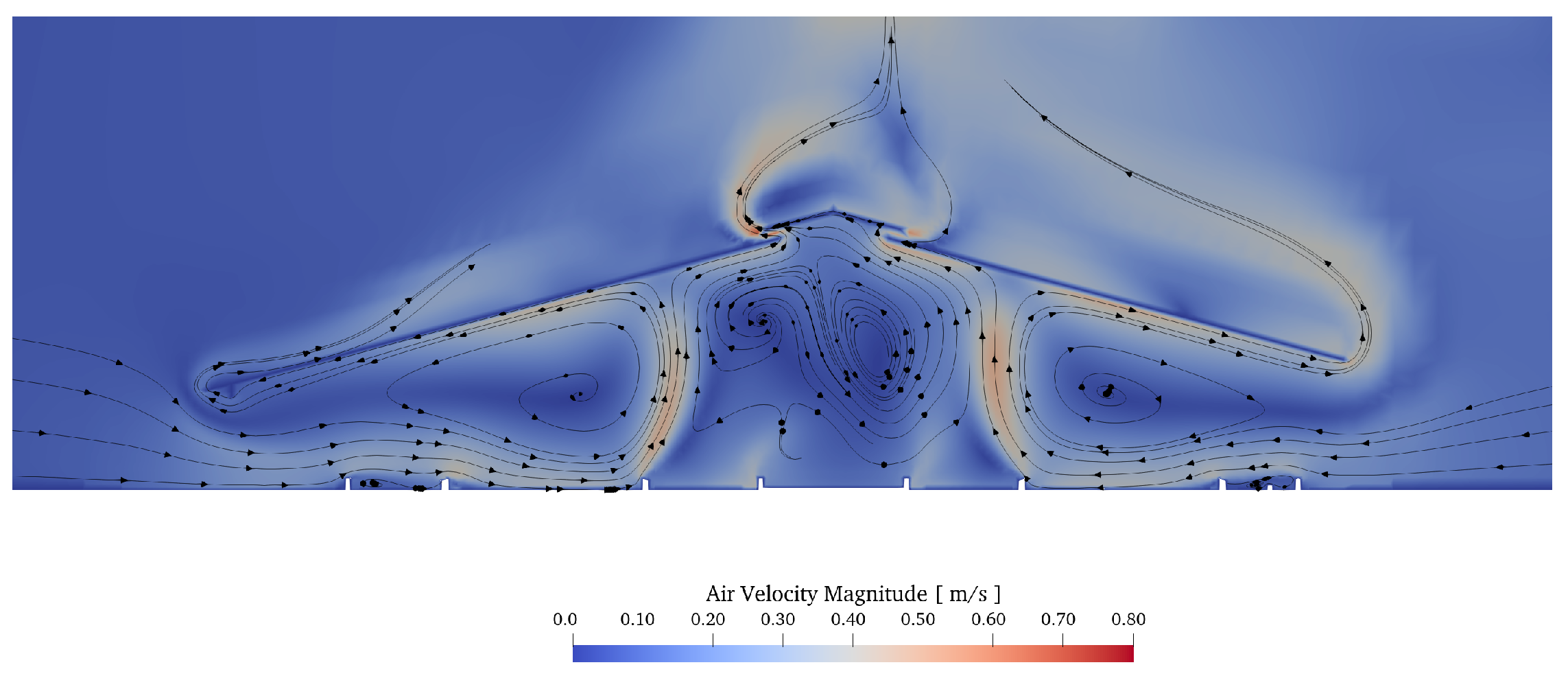
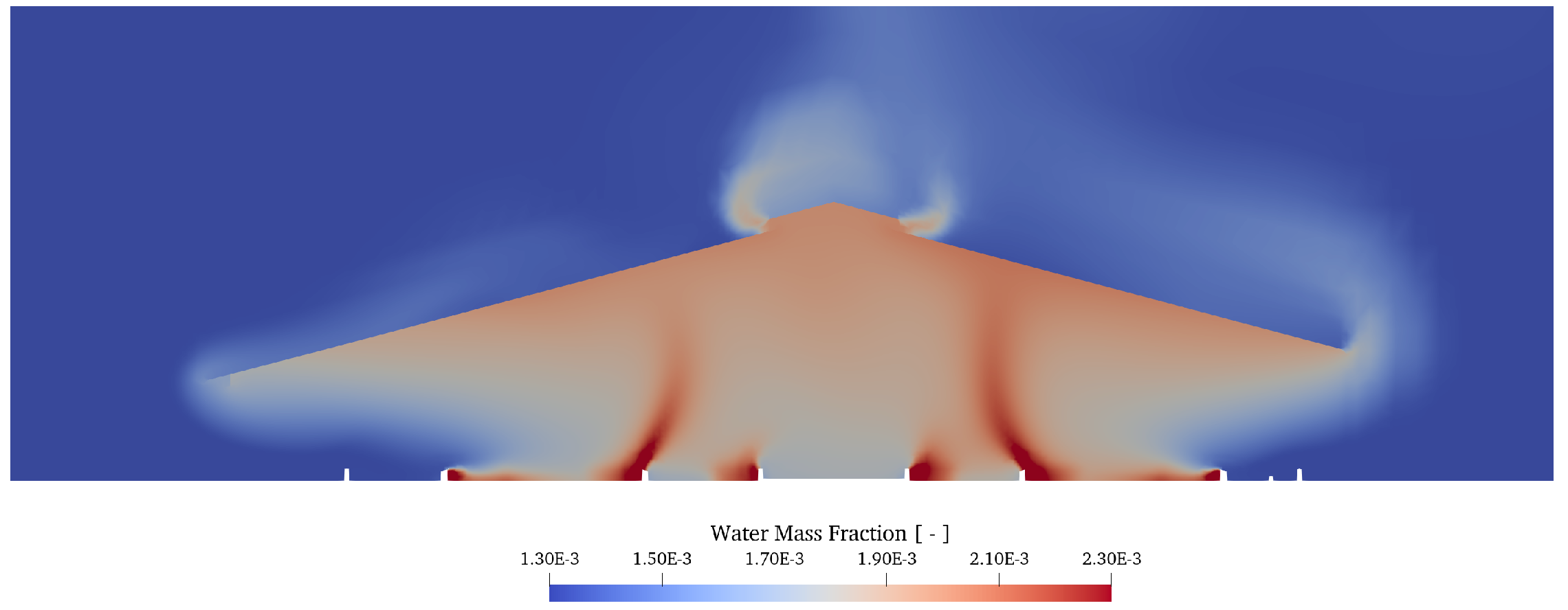
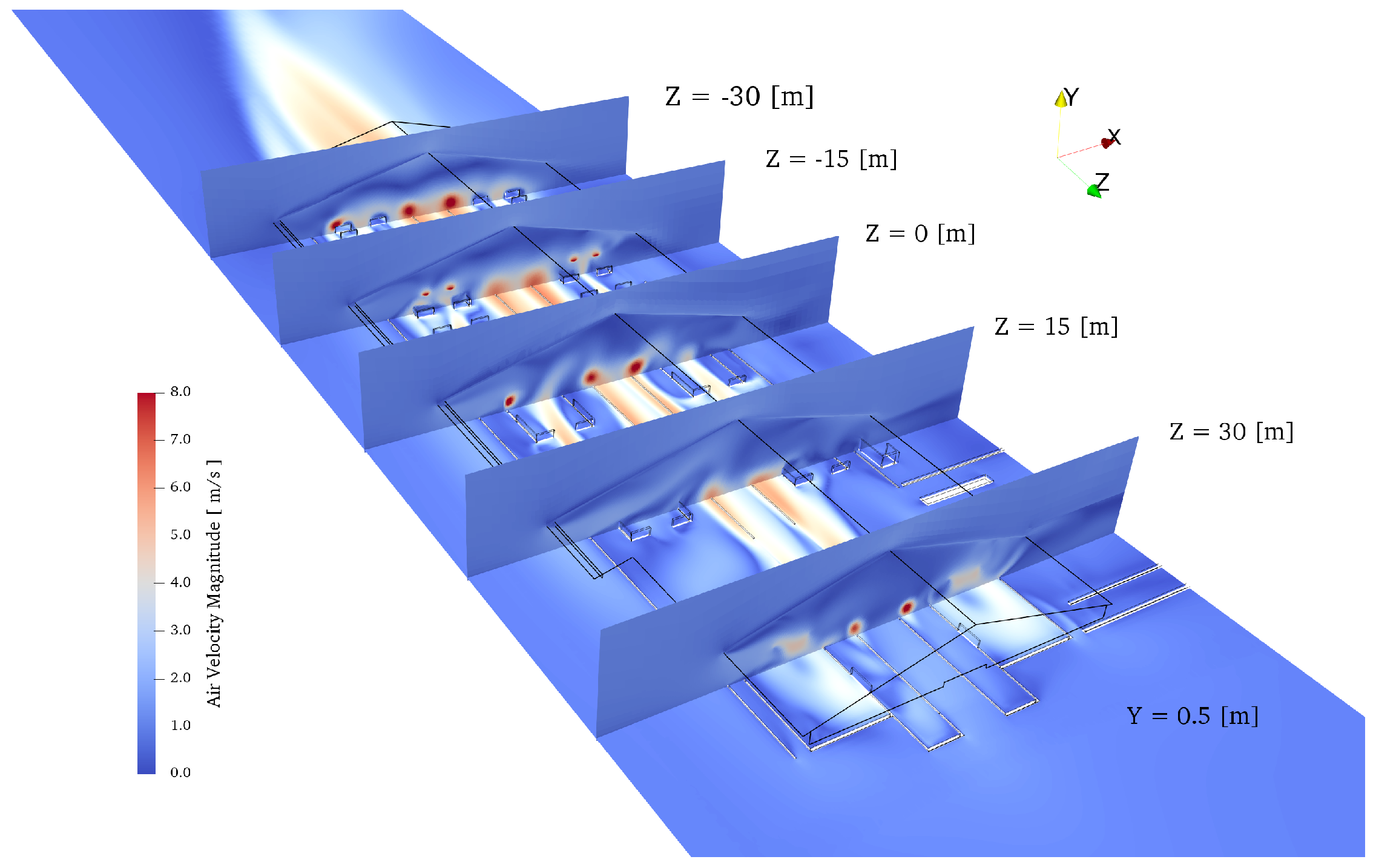
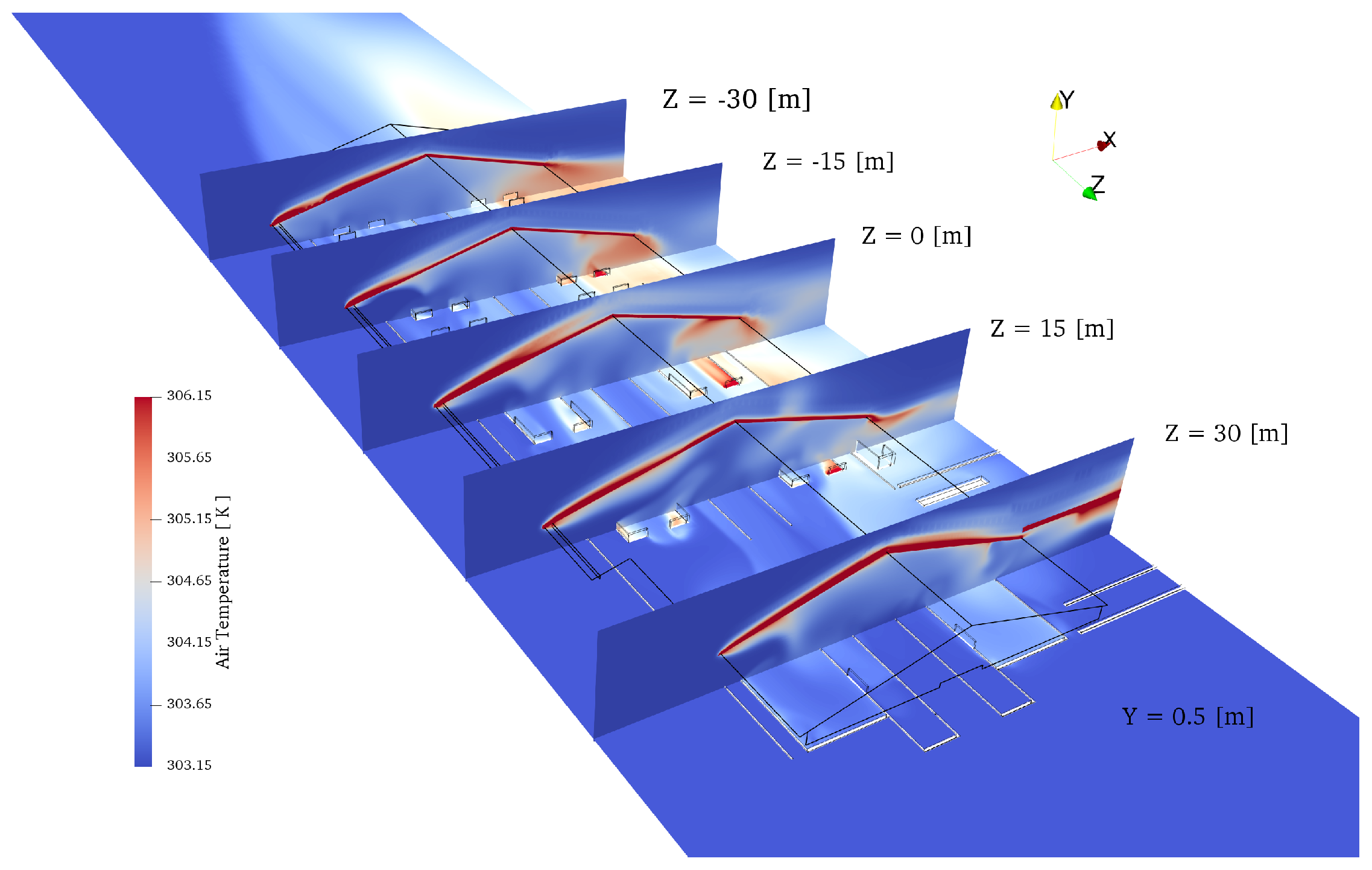
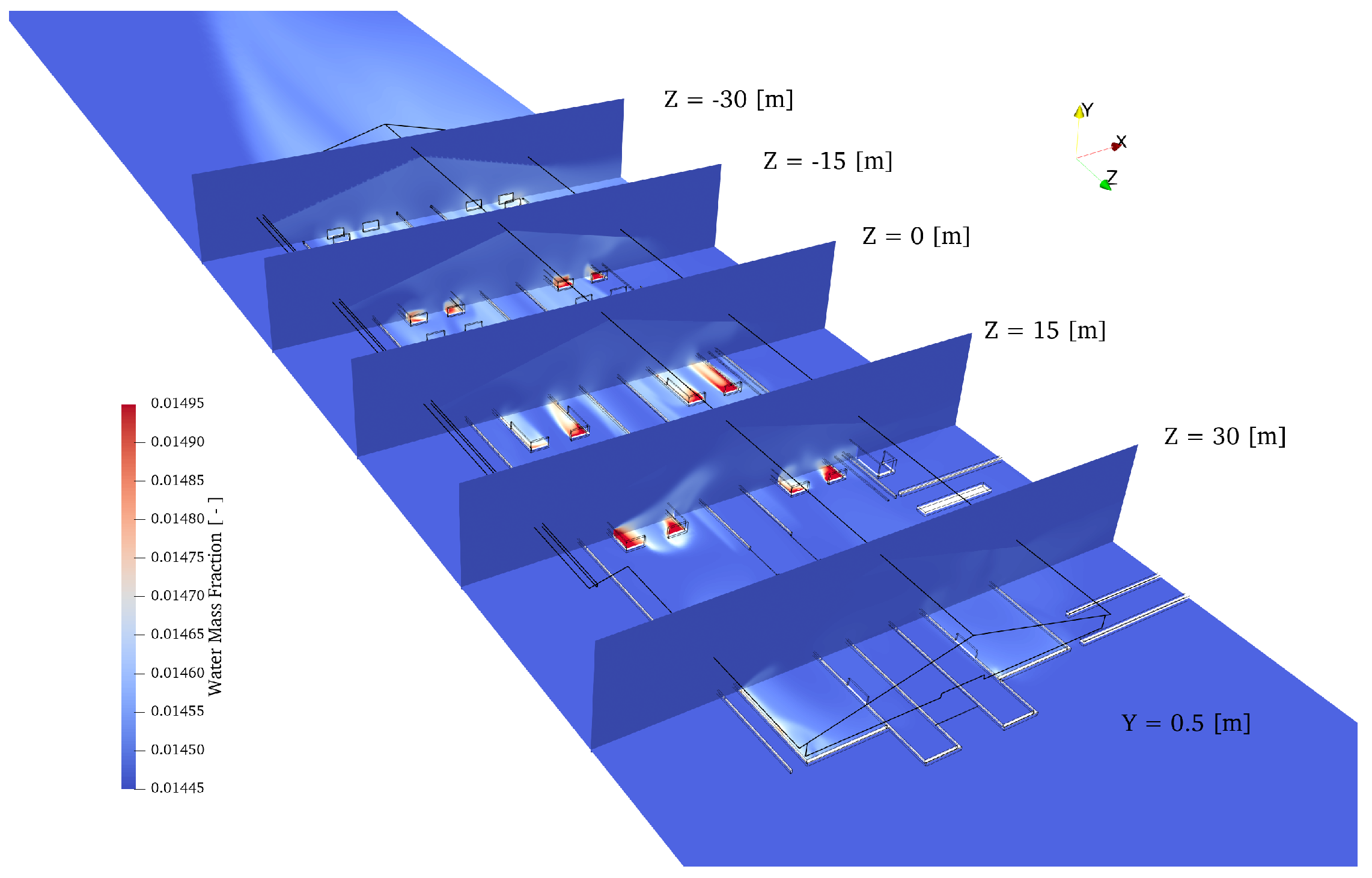
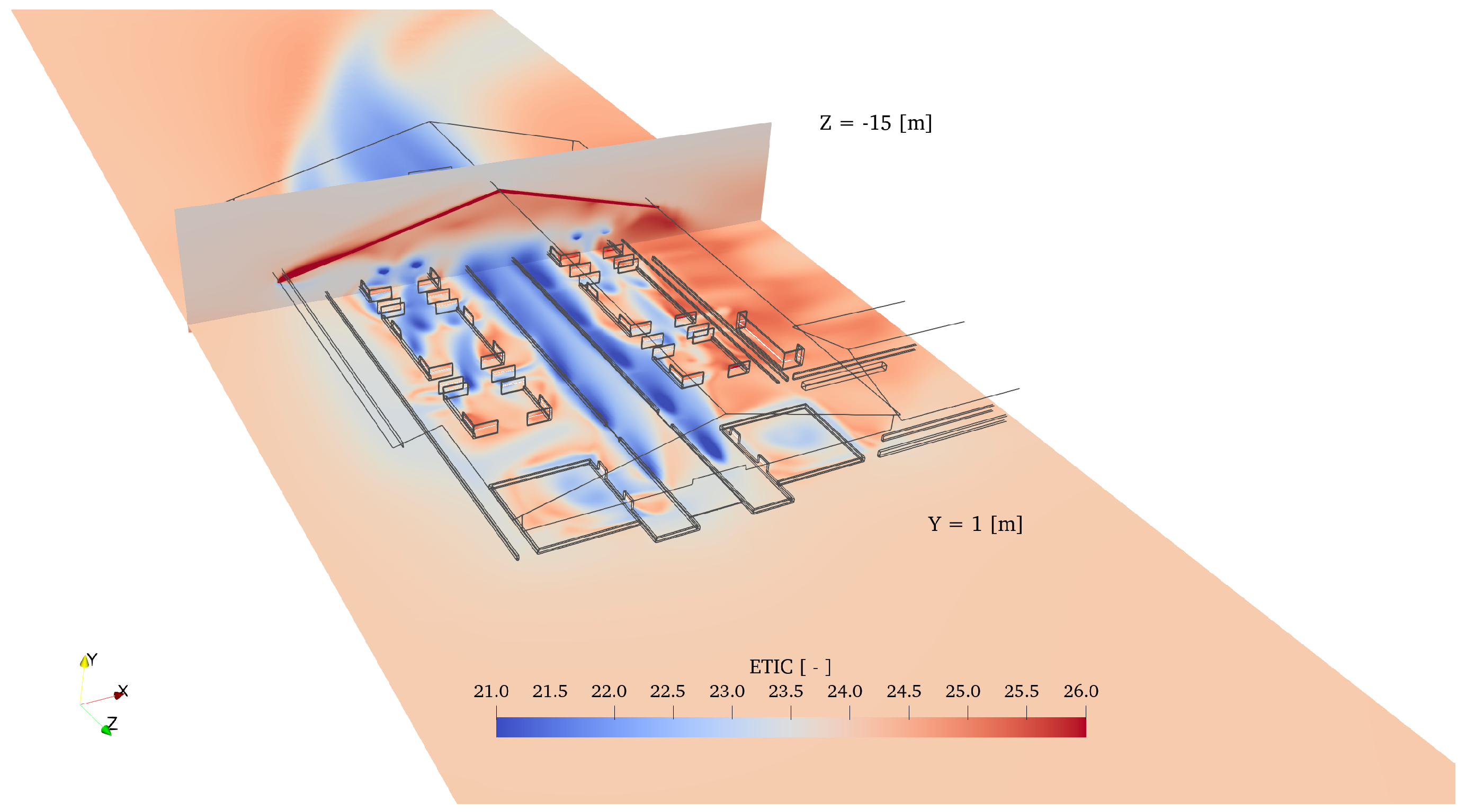
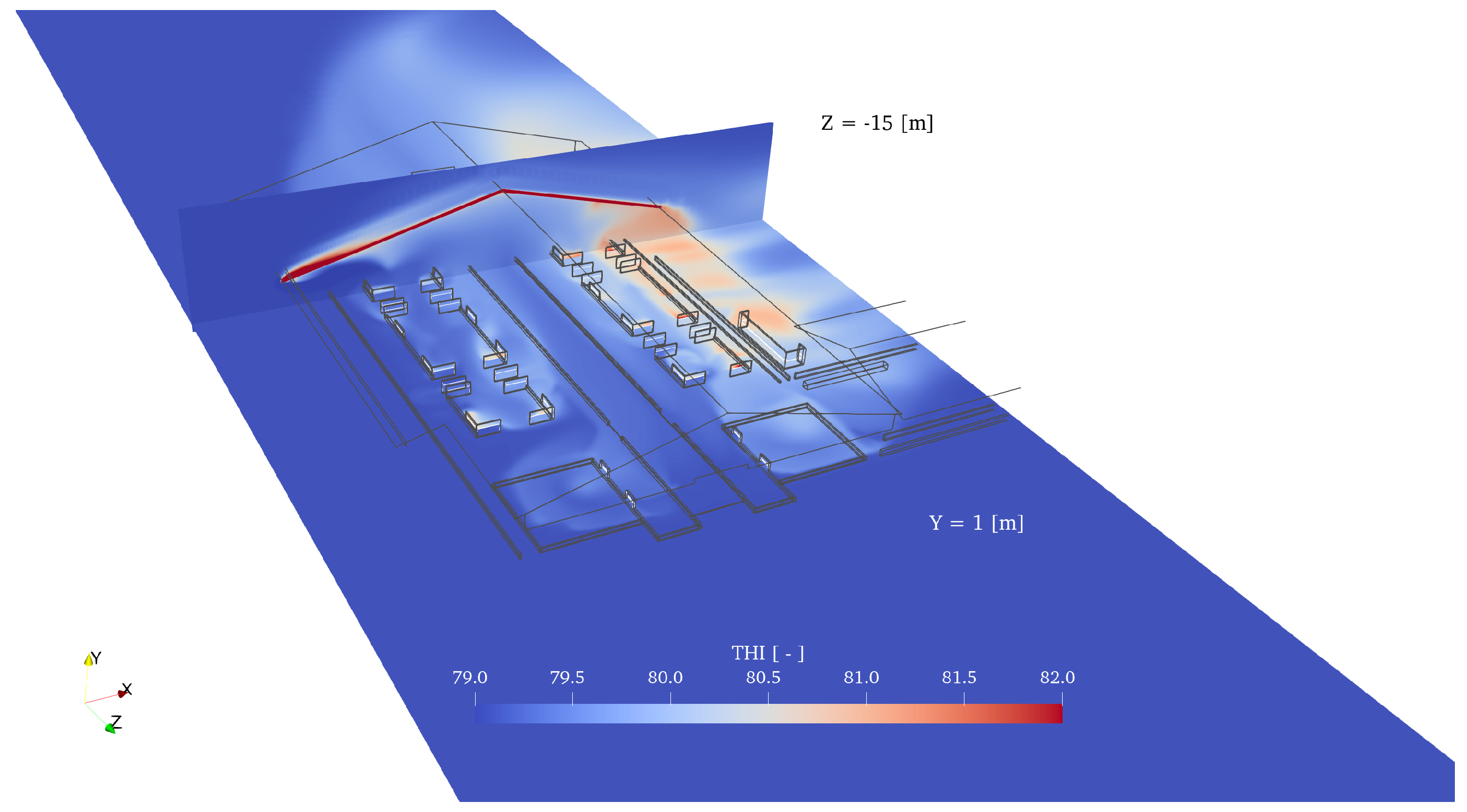
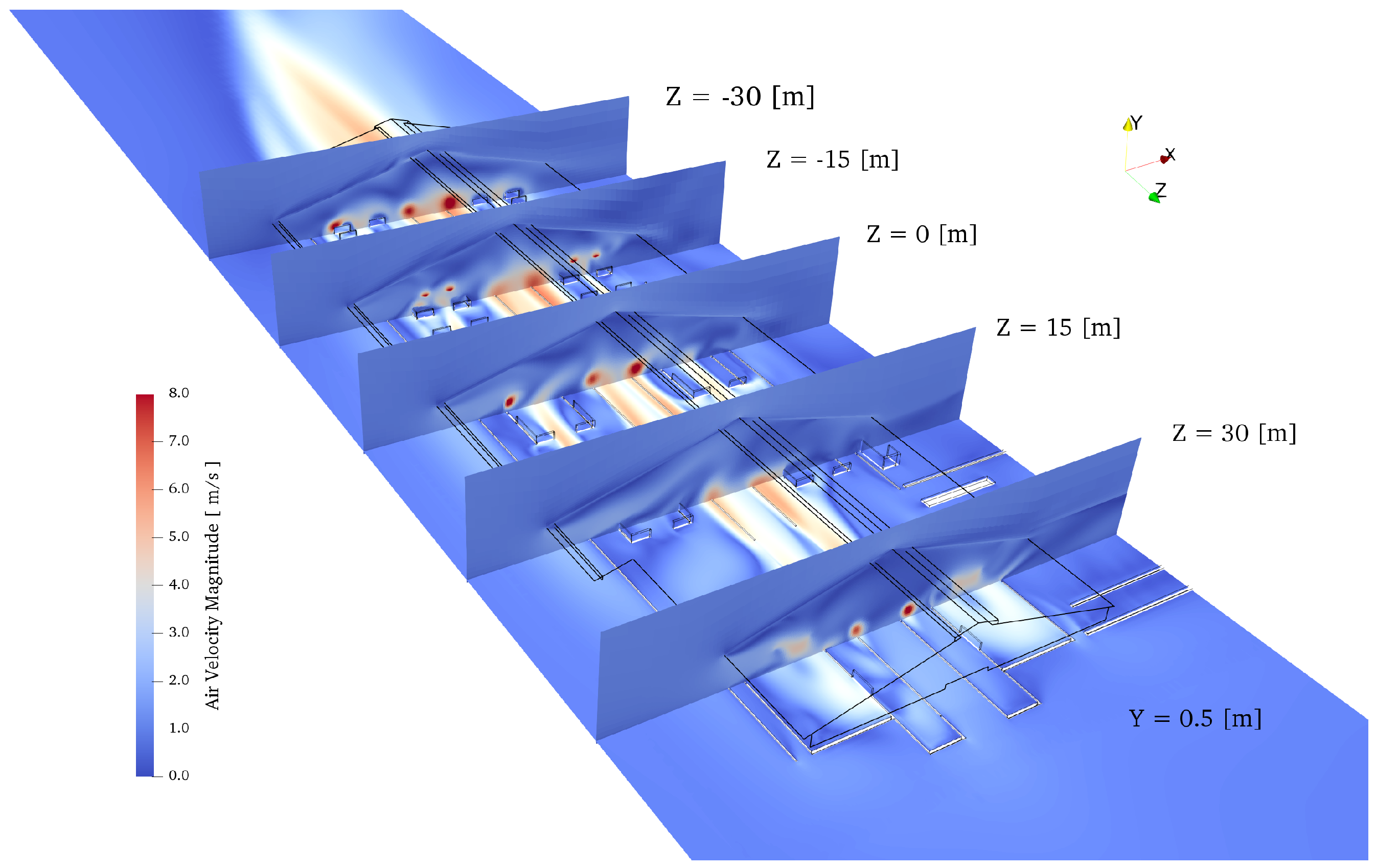
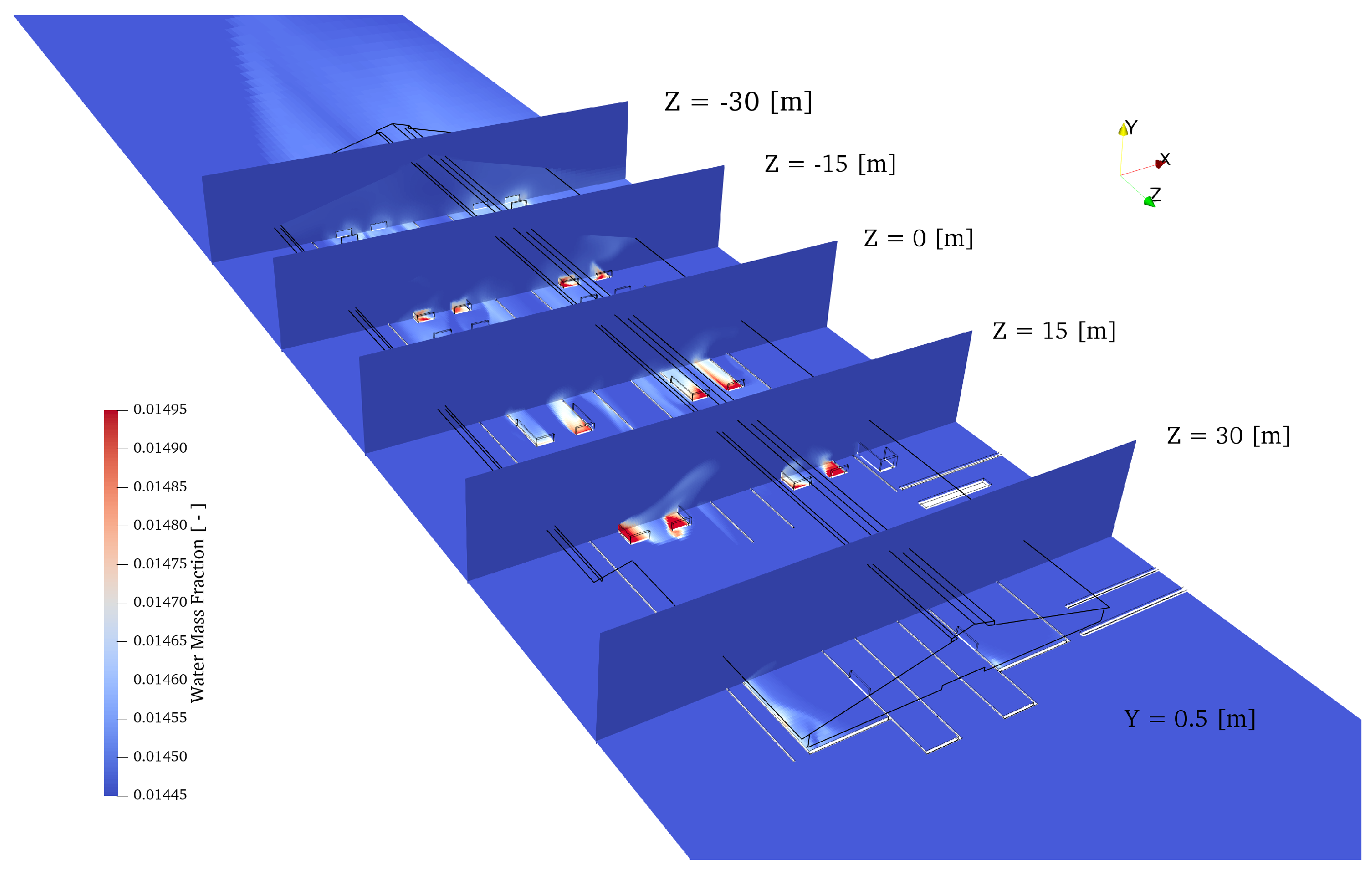
Region	Number	State	Metabolic Heat	Total Energy Source	Total Water Source
[-]	[-]	[-]	[W]	[kW]	[g/s]
Stalls	70	Lactation	1938	67.83	27.92
Feeding line	30	Lactation	1938	29.07	11.96
Prepartum box	6	Dry	1197	3.59	1.48
Postpartum box	6	Early lactation	1357	4.07	1.68

.

3.2. Wind-Induced Ventilation and Turbulence Modelling

Wind is likely to be relevant, and it may strongly influence the air change rate since the analysed building has large perimeter openings [45]. Nearby buildings and obstacles must be included in the simulation as they are likely to influence the surrounding wind airflow. For this reason, the side building was simulated together with the main body of the barn. A logarithmic inlet velocity profile was adopted together with a slip condition on lateral boundaries. The inlet velocity obeys standard atmospheric boundary layer (ABL) theory with a constant shear stress in free flow. As suggested by Hargreaves et al. [46], a uniform velocity gradient computed from the shear stress was applied to the upper boundary. Wind speed was considered at 2 m/s at 25 $\mathrm{m}$ with an east–west direction in accordance with average meteorological data for the city of Piacenza in the considered time interval. Wind direction in the computational domain can be seen in Figure 4.

The relative angle between building and wind can be adjusted by performing a rotation of the geometry of the barn instead of changing boundaries. In simulations with an active ventilation system, high-speed regions with an elevated Reynolds number are expected. In these simulations, the $k-ϵ$ turbulence model was used, but characteristic model constants were adjusted to correctly describe the atmospheric boundary layer [46]. The turbulent kinetic energy and dissipation rate on the wind inlet surface were modelled using nonuniform profiles according to ABL theory (atmBoundaryLayerInletK and atmBoundaryLayerInletEpsilon [47]). A $k-ϵ$ turbulence model with additional buoyancy generation/dissipation terms (buoyantKEpsilon) has been used if natural convection is expected to be the main fluid motion in the domain. Even though a large fraction of the domain is likely to be in a laminar condition, airspeed may generate turbulence, and a dedicated model is needed. In both winter and summer weather, high Reynolds wall treatment was used owing to the high cell size. At the end of the simulations, it was verified that $y^{+}$ values were above the critical value of 30 on all surfaces with the exception of some limited stagnation points.

3.3. Assessment of Animal Welfare

At the end of the CFD simulation, temperature and humidity distributions were known with high spatial detail. The assessment of animal thermal welfare can be performed through the analysis of the temperature humidity index (THI). This index is widely used, and it has been largely correlated with such relevant physiological parameters of cows as respiration rate, heartbeat frequency, rectal temperature and milk yield. Even though the THI has been largely used in the literature for the assessment of cows’ thermal comfort, it has important weaknesses [48]. Recirculation fans enhance heat transfer on an animal by increasing airspeed on cows’ coat surface. Even though air velocity is a relevant factor for the thermal comfort of dairy cows, it does not influence the THI. In addition, the temperature humidity index was originally defined starting from outdoor data which are not descriptive of air conditions near animals, resulting in a biased estimation of animal welfare. THI is computed using NRC’s [36] definition and threshold values for the onset of moderate and severe heat stress are 72 and 80.

$$THI=(1.8T_{DB}+32)-0.0055(100-RH)(1.8T_{DB}-26)$$

(3)

$T_{DB}$ is the dry-bulb temperature in °C, and $RH$ is the percentage relative humidity.

In order to overcome the limitations of the THI, Wang et al. [49] developed the equivalent temperature index for cattle (ETIC). This index was obtained using results from both a climate chamber and outdoor measurements of temperature, humidity, wind speed and radiation in dairy facilities with lactating Holstein-Friesian cows. Wang et al. [49] identified ETIC thresholds of 26 for moderate heat stress and 31 for severe heat stress.

$$ETIC=T_{DB}-0.0038T_{DB}(100-RH)-0.1173u^{0.707}(39.20-T_{DB})+1.86{10}^{-4}{T}_{DB}{q}_{Sun}$$

(4)

$RH$ is the air relative humidity, and $q_{Sun}$ is the local radiative solar heat flux. It must be pointed out that the effect of wind may be different from the effect of recirculation fans even at the same air speed, as the airflow structure and turbulent intensity may be different. Nevertheless, it is an important step forward from the usage of an animal welfare index that does not consider air velocity as the THI. In Section 3.10 and Section 4.3, both indexes are used to predict the percentage of cows in a thermoneutral state or experiencing mild, moderate, severe, and critical heat stress. Heat-stress intensity computed from the THI and ETIC is compared with an experimental estimation evaluated from the respiration rate.

3.4. Solar Radiation

In summer conditions, the thermal load related to solar radiation is expected to be relevant. No direct irradiation is present on animals, since stalls are located in shaded areas. Nevertheless, solar irradiation is likely to increase air temperature locally, and hot air may flow inside a building from perimeter openings or roof gaps. An additional effect of solar radiation is related to the thermal conduction through the barn roof. The roof was modelled as a conductive baffle with a thermal coupling between internal and external surface temperatures. The thermal resistance of all exposed surfaces was considered equal to 4.17 W/${\mathrm{m}}^2$K as specified by the manufacturer of the panels. Internal and external surface temperatures were computed from local energy balances, taking into account the thermal conduction in the panels. The considered sun position corresponded to 1 August, at 14:00 with a direct normal irradiation equal to 500 W/${\mathrm{m}}^2$ and a sky cloud cover fraction equal to 0.1. The sun’s position was computed according to the real geographical position of the barn with a latitude of 45.00° and a longitude of 9.70°. The simulation of the solar thermal load was performed using a dedicated radiation model (solarLoad) [47]. The radiative heat flux was modelled as a source term on exposed faces considering a correction for the view angle between the surface normal and ray direction. Due to the presence of planes at different slopes, the radiative source term took unique values on surfaces, as depicted in Figure 5. The intensity of the solar heat flux was uniform, as all roof surfaces were flat. Even though cows were not exposed to direct solar irradiation, reflected radiation might be relevant for animal heat transfer. This side consequence of solar radiation cannot be evaluated since animals were modelled without describing their heat transfer surface.

3.5. Air Change Rate and Wind-Induced Ventilation

A relevant factor in the evaluation of the effectiveness of ventilation systems is the hourly air change rate (ACR).

$$ACR=\frac{\dot{V}}{V}\left[\frac{1}{h}\right]$$

(5)

$\dot{V}$ is the hourly inlet flow rate in m³/h, and V is the barn indoor volume in ${\mathrm{m}}^3$. The ACR is a key factor for simplified models based on the mass and energy balance of the whole building. In addition, design guidelines for ventilation systems often provide minimum and maximum values of ACR to have adequate air quality and limited emission of pollutants [50]. In CFD simulations, the air flow is described in high detail, and the calculation of ACR is not straightforward. The calculation of inlet flow may be performed using Equation (6) since at the same time, inlet and outlet flows can be present.

$$ACR=\frac{1}{7200V}{\int }_A\left|\overrightarrow{u}·\overrightarrow{n}\right|d{A}^{\prime }\left[\frac{1}{h}\right]$$

(6)

V is the barn indoor volume in ${\mathrm{m}}^3$, A is the perimeter surface in ${\mathrm{m}}^2$, $\overrightarrow{u}$ is the fluid velocity in m/s and $\overrightarrow{n}$ is the surface normal.

3.6. Weather Conditions and Analysed Configurations

To have a complete description of building thermal behaviour, two different meteorological conditions were simulated. First, hypothetical winter conditions were analysed, then more realistic summer weather was studied. For winter conditions, the external temperature was set equal to 5 °C with a relative humidity of 40%. In these simulations, wind-induced ventilation and solar radiation were considered. The ventilation system is expected to be switched off as external conditions are not critical for dairy cows. Winter conditions may occur, but they are unlikely as solar radiation or wind is often present. Nevertheless, these simulations have an important engineering relevance as ventilation is only given by buoyancy-driven flows. Therefore, the air change rate took the minimum possible value, providing an important baseline for the assessment of the impact of the ventilation system. The minimum air change rate might also be relevant for consideration regarding the evaluation of air quality in the barn [51]. The only ventilation devices that were considered active in winter conditions were chimneys, as they run all the time independent of external conditions. In the summer simulation, all modelled effects were included: the ventilation system ran at maximum speed and wind was present, as well as solar radiation. Buoyancy was considered also in summer conditions even though it was unlikely to be relevant. External temperature was considered at 30 °C with a relative humidity equal to 55%. Note that these external conditions are critical, and dairy cows outside the barn are likely to suffer from heat stress.

This study could have a beneficial impact on the farming sector if CFD enables a barn manufacturer to design more effective and efficient ventilation systems. In order to assess the capabilities of the developed model to give useful guidelines, an exemplificative design choice was analysed. The CerZoo barn is equipped with 5 electric blowers that substitute for the traditional open ridge of the rooftop. This innovative solution was compared with the traditional configuration to assess which solution is more effective in improving animal thermal welfare. All other influencing phenomena such as thermal loads, wind and recirculation fans were kept unchanged in this analysis.

3.7. Heat-Stress Abatement Devices

For the correct prediction of animal thermal welfare, the effect of heat-stress abatement must be considered. Therefore, fans, chimneys and other ventilation devices must be modelled and included in the simulation. The CerZoo barn has 12 high-speed box fans, 19 high-speed basket fans, 2 low-speed high-volume fans and 5 exhaust chimneys. Fans were modelled as disk-shaped cyclic patches, while blowers were considered as cylinders with lateral walls and cyclic patches on both ends. Fans were simulated using the fan boundary condition of OpenFOAM, while chimneys were modelled using uniformJumpAMI [47]. Cyclic patches were adopted for fan patches as they are bidimensional surfaces with shared faces, and a perfect matching between points was present.

Chimneys Chimneys have been modelled using AMI patches since inlet and outlet are detached surfaces not perfectly aligned. For both fans and blowers, a constant pressure difference between coupled faces was applied in order to simulate the presence of the machine. The manufacturer did not provide the performance curve for recirculation fans; however, the pressure difference can be evaluated from the thrust in normal operating conditions (i.e., with open boundaries). The pressure differences for basket and box fans were equal to 112.76 and 107.39 m²/s², while they were 14.35 and 86.77 m²/s² for HVLS fans and exhaust blowers. Momentum, flow rate, temperature, humidity and turbulent properties were conserved through fan surfaces. The fan control system allowed us to partialise the fan rotational speed and plan active and inactive time intervals. The developed CFD model has the capability to simulate all possible situations, but simulations were performed for the most severe conditions, with machines working continuously at maximum speed.

3.8. Meshing Strategy

Mesh size and quality are fairly influential on computational cost and results accuracy; therefore, particular attention was given to the finite-volume discretization. Depending on weather conditions, two different meshing strategies were adopted. In all cases, unstructured hex-dominant meshes were used. In summer simulations, the domain was square to model the atmospheric boundary layer with defined inlet and outlet sections. Since the CerZoo barn has large perimeter windows, it was necessary to include a large open area around the building. The main body of the building is 10.3 $\mathrm{m}$ tall, and it extends for around 70 and 45 $\mathrm{m}$ in horizontal directions. Tominaga et al. [52] provide guidelines for the application of CFD to wind flow around buildings. Tominaga et al. recommend the adoption of a vertical space above the roof equal to 5 times the building’s height. According to these guidelines, the horizontal distance between an obstacle and boundaries should be the maximum value between 2.3 times the building’s width or 5 times its height. In addition, a free space equal to 15 times the height is advised for the outflow direction. Following these guidelines, the barn was placed in the centre of an extended domain that measured 400 $\mathrm{m}$ in horizontal directions and 60 $\mathrm{m}$ in height. Boundary dimensions computed using these guidelines were rounded to have a square domain and to match the desired cell size of the background mesh. In order to model the different angles between the barn and wind, the barn was placed at the centre of a cylindrical AMI surface with a radius of 120 $\mathrm{m}$. If a different wind direction was required, it was sufficient to perform a rotation of the central surface without repeating the entire meshing process. This solution is especially suitable if the average wind direction is unknown and a sensitivity analysis is needed. In winter conditions, the airflow was given by buoyancy-driven flows that have an upward primary direction. In this configuration, the mesh was cylindrical with a radius of 160 $\mathrm{m}$, and the top boundary was raised up to 160 $\mathrm{m}$. As the outflow was expected to be on the top boundary, a free space of 15 times the building height was left above the roof. A variable cell size was used to decrease the computational cost of the simulation and have the maximum definition indoors. Far from the barn, the average cell size was 5 $\mathrm{m}$, while inside the barn, it was equal to 0.25 $\mathrm{m}$ (0.125 $\mathrm{m}$ near walls and fans). The independence of results from the mesh size was not investigated, but simulations were performed with the lowest possible cell size within acceptable computational time and memory occupation. In addition, Hong et al. [23] already performed an extensive mesh sensitivity analysis for the simulation of naturally ventilated barns with OpenFOAM code. Hong et al. concluded that the optimal mesh size ranges between 0.5 and 0.25 $\mathrm{m}$ depending on near-wall turbulence treatment. The background mesh was defined following the main geometries of the barn. This helps to decrease the cell number and computational effort; furthermore, it helps in achieving higher mesh quality. All four meshes were created following strict quality criteria to achieve accurate results and have a stable numerical behaviour. The same meshing strategy was used for both closed- and open-roof configurations, and only roof geometries differ. Depending on geometry and weather, each mesh had between 5 and 5.5 million cells. The meshes and computational domains for the closed-roof configuration in summer and winter weather are depicted in Figure 6 and Figure 7.

3.9. Solution Strategy

Simulations were performed with a custom solver based on incompressible fluid assumption. Compressibility is expected to be limited, as the maximum Mach number will take very low values. Even though variations are limited, the description of buoyancy-driven flow requires a variable density to model the change in the gravitational force between regions at different temperatures. The developed solver models the presence of differentiated gravitational force through a variable mass force that is not dependent on density but directly on local temperature. The dependence of buoyancy forces on pressure was neglected as minimum variations are expected in the domain. This solution strategy is based on the Boussinesq approximation, and it is largely used for heat transfer problems. The solver includes the effect of humidity transport since it is a relevant factor for the assessment of animal welfare. The modelling of species transport within an incompressible solver is not straightforward; nevertheless, in the studied case, two simplifications can be assumed. The values of water mass fraction are likely to be limited with a minimum effect on air thermophysical properties; moreover, a binary mixture of water–air can be considered. Based on these assumptions, humidity was modelled as a transported field that is superimposed after the solution of momentum and temperature equations. The influence of water mass fraction on the variation of fluid properties was neglected; nevertheless, adopted constant values correspond to external humid air and not to dry air. The computed water mass fraction was bounded below the physical limit for condensation, but this phenomenon is not expected to occur in simulations.

$$\frac{\partial Y_{H_{2}O}}{\partial t}+\nabla ·\left(u{Y}_{H_{2}O}\right)-\nabla ·\left(\frac{{\alpha }_{Eff}}{Le}\nabla Y_{H_{2}O}\right)=S_T$$

(7)

$Y_{H_{2}O}$ is the water mass fraction, u is the air velocity in m/s, ${\alpha }_{Eff}$ is the effective thermal diffusivity, Le is the water steam–air Lewis number and $S_T$ is a local volume-specific source term that is exploited for the modelling of the animal latent load following the methodology described previously. The considered Lewis number was assumed to be 0.809 in winter weather, while it was considered equal to 0.814 in the summer simulation [53]. All simulations were performed using a second-order numerical scheme, except for time, which was discretised using a first-order Euler scheme [47]. The adoption of a first-order scheme for time is not influential on final results, since the simulation will reach a steady state at convergence. As variations in temperature, pressure and humidity are limited, the change in thermophysical properties may be considered negligible. Constant values were used for all thermophysical properties; however, different values for winter and summer weather were used. The isobaric expansion coefficient used in the Boussinesq approximation for buoyancy was computed analytically from a perfect gas equation of state. A summary of the thermophysical properties used can be found in

Table 2. Fluid thermophysical properties.

Thermophysical Property	Unit of Measure	Winter Weather	Summer Weather
Density	kg/m3	Not needed	1.1641
Specific heat capacity	J/kgK	Not needed	1007
Kinematic viscosity	m2/s	1.382 × 10−5	1.608 × 10−5
Expansion coefficient	1/K	−4.562 × 10−3	−3.841 × 10−3
Reference temperature	K	278.15	303.15
Prandtl number	−	0.735	0.728
Lewis number	−	0.809	0.814

.

The barn was simulated as a transient system with constant boundary conditions until a steady-state solution was reached. In each solution iteration, pressure was solved using a geometric–algebraic multigrid (GAMG) solver with an absolute tolerance of 1 × 10⁻⁷, while all other transport equations were solved using a preconditioned biconjugate gradient (PBiCGStab) with an absolute tolerance of 1 × 10⁻⁸. The convergence of each timestep was checked through an absolute residual control of 1 × 10⁻⁵ on pressure, temperature and velocity. Maximum temperature in animal-occupied zones and area-averaged pressure on the east patch were monitored to check whether a steady-state condition was reached. In winter conditions, also, the area-averaged flow rate exiting from the top boundary was checked. For these variables, a relative tolerance of 1 × 10⁻³ was used as the convergence criterion. It was observed that the model seemed to reach a steady solution within 15 $\min$ of simulation time in summer conditions and 1 $\mathrm{h}$ in winter ones. This difference is due to the different air change rate that strongly shortens the characteristic thermal time between the two configurations. In winter conditions, the timestep was equal to 1 $\mathrm{s}$, but in summer weather, it was necessary to decrease the timestep down to 0.1 $\mathrm{s}$ due to the presence of high-speed flows generated by fans. As a transient-to-steady approach was adopted, the size of the timestep was not influential on simulation results at a steady state. The timestep was progressively lowered until a good compromise between numerical stability and simulation cost was reached.

3.10. Experimental and Simulated Heat-Stress Intensity

CFD predicts the distributions of indoor air temperature, humidity and velocity; then, through thermohygrometric indexes, it is possible to predict the intensity of heat stress. In order to understand whether the developed model was able to correctly predict the intensity of heat stress, simulation results were compared with experimental measurements. Dairy cows in CerZoo barn wear sensor-based collars (Allflex HR-LDn manufactured by SCR Engineers Ltd., Netanya, Israel) that measure behavioural parameters such as heavy breathing, laying and ruminating time. The detection of heavy breathing is performed using an accelerometer that estimates the instantaneous respiration rate. An animal is considered in a state of heavy breathing whenever the respiration rate exceeds the threshold of 80 $\mathrm{bpm}$ [54], which corresponds to the transition between mild and moderate heat stress [55]. The data acquisition system provides, on a daily basis, the total number of minutes on average in which cows are in heavy breathing. This parameter is expressed in min/day and it is averaged over the total number of animals (112 cows). This index is referred to as heavy breathing duration (HBD), and it is already extensively used to analyse the daily intensity of heat stress [54,56]. In the CerZoo barn, the data history of HBD is available from the beginning of 2022 until the end of 2023. Starting from HBD measurements, it is possible to compute the total percentage of cows in moderate, severe and critical heat stress. This percentage was compared with the prediction from CFD in summer weather with a close-roof layout.

At first, days with external weather similar to simulations must be selected. Meteorological data were extracted from the open database of ARPAE (Regional Agency for Environmental Protection) [57]. HBD provides a cumulative value over 24 h including periods in which heat stress is not critical. Therefore, a reference time interval is needed to compute the fraction of animals in heavy breathing. It was assumed that each event of heat stress had a duration of 8 consecutive hours. Air temperature was averaged over the hottest 8 consecutive hours (${\overline{T}}_{Air,Max8h}$) for any day between 2022 and 2023. Average relative humidity (${\overline{RH}}_{Air,Max8h}$) and direct normal irradiation (${\overline{DNI}}_{Air,Max8h}$) were computed for the same time intervals starting from the ARPAE dataset. Since weather conditions must be as close as possible to simulation boundaries, three different criteria were adopted to select days: ${\overline{T}}_{Air,Max8h}$ between 29 and 31 °C, ${\overline{RH}}_{Air,Max8h}$ higher than 50% and ${\overline{DNI}}_{Air,Max8h}$ higher than 350 W/m². It should be noted that wind velocity was not used as a criterion since the ARPAE dataset does not include this information. Then, HBD values were gathered for selected days. The cumulative percentage of cows in moderate, severe and critical heat stress ($X_{Moderate,Severe,Critical}$) in the reference 8 h period was computed with Equation (8).

$$X_{Moderate,Severe,Critical}=\frac{HBD}{8\times 60}\times 100\left[\%\right]$$

(8)

The remaining fraction of cows were in thermoneutral conditions or in mild heat stress. Through the analysis of the simulated THI and ETIC, it is possible to predict the fraction of cows in each class of heat stress intensity. This analysis is straightforward as Wang et al. [48] defined ranges of the THI and ETIC for each class. Since animals were not meshed in the simulation, these fractions were evaluated basing on cell volumes weighted by the number of animals in each region. The fraction of cows belonging to each class was computed using Equation (9).

$$X_{Class}=\sum _{i=0}^{N_{AOZ}}\sum _{j=1}^{N_{Cell}}\frac{V_j}{V_i}\frac{n_i}{n_{Tot}}{c}_{j}100\left[\%\right]c_j=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{I}_{Max,Class}<I_j<I_{Min,Class}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.\forall \mathrm{Class}$$

(9)

$X_{Class}$ is the fraction of animals in the considered class of heat stress intensity (thermoneutral, mild, moderate, severe or critical), $N_{AOZ}$ is the number of animal-occupied zones as defined in Table 1 and $N_{Cell}$ is the number of cells in each animal-occupied zone. $V_j$ is the single-cell volume, while $V_i$ is the total volume of each animal-occupied zone. $I_{Max,Class}$ and $I_{Min,Class}$ are class range boundaries for thermohygrometric indexes as defined by Wang et al. [48], while $I_j$ is the single-cell index value. $c_j$ is a binary variable to determine whether the selected cell is in the considered range.

4. Results and Discussion

4.1. Simulations in Winter Weather

The simulated fluid dynamic behaviour of the CerZoo barn in winter weather was analysed for both geometries. The simulated velocity field on the vertical cross section at the midplane (at z = 0 $\mathrm{m}$) of the barn for the closed-roof geometry is presented in Figure 8, while temperature and water mass fraction fields can be seen in Figure 9 and Figure 10. The same analysis is proposed in Figure 11, Figure 12 and Figure 13 for the open-roof configuration. In Figure 8, it can be noticed that hot air coming from an animal-occupied zone flows up due to buoyancy toward the roof ridge. The hot stream from stalls creates an upward flow in the centre of the barn that drives fresh air from outside. This phenomenon might be harmful in very cold environments; however, in the geographical region of Piacenza, the chances are that cold stress will not occur. Therefore, the adoption of perimeter curtains may be beneficial, especially in more rigid climates. The computed hourly air change rate for the closed-roof geometry is 10.81 1/h. This value is in good agreement with the measurements of 4.3–14.5 1/h performed by Snell et al. [51], even though the barn geometry was different and minimum wind velocity was present. In the closed-roof configuration, hot and humid air tends to accumulate under the roof, creating a large stagnation region. The model predicts the creation of outflows in the upper portions of lateral openings; however, a prevalent discharge is present in the right-hand side. In addition, buoyancy-driven flows are not exactly symmetrical to the axis of the barn. This effect is due to the geometry of the barn roof: the opening on he east side is 1 $\mathrm{m}$ taller than the west one, resulting in an asymmetrical velocity field. During winter, roof blowers are active continuously, but their rate is not enough to eject all flows due to buoyancy, and an important outflow from perimeter windows is still present.

In Figure 9 and Figure 10, it can be noticed that the presence of buoyancy induces a vertical stratification of air temperature and water mass fraction. A similar effect was seen by Chen et al. [58] in an office building. The same analysis can be repeated with the open-roof configuration. Like the closed geometry, buoyancy-driven flows are present in the central region of the barn, and hot air accumulates under the roof. The presence of ridge gaps creates an outflow from the rooftop due to higher air temperatures; nevertheless, a limited flow rate runs through these openings. Even though exhaust blowers accelerate air at high speed, the ridge-gap flow area is much larger, and the volumetric inlet flow rate is similar. With this configuration, the computed hourly air change rate is 11.08 1/h: the open-roof configuration provides a higher inlet flow rate, but the increase is minimal in comparison with the reference case. In both cases, the major source of air change rate is the outflow on the right-hand side, and the rooftop ventilation solution is bound to be marginally influential.

The solution with blowers might be beneficial in colder climates since it allows one to partialise air flow rates and increase internal temperatures to avoid cold stress. As suggested by Snell et al. [51] and by Teye et al. [59], with lower flow rates, air quality may become relevant, and a dedicated model could be included in the simulation. Since the computed air change rate is higher than recommendations for air quality, an analysis of pollutants such as methane or ammonia was not included in the present study, and the onset of heat stress is the strictest criterion for ventilation. Pollutant transport may be overlooked as the hourly ventilation provided only by natural ventilation is twice as high as the minimum recommendation for air quality [59].

4.2. Simulations in Summer Weather

The simulated fluid dynamic behaviour of the ventilation system was examined for both solutions. Simulation results are presented on five vertical surfaces 15 $\mathrm{m}$ apart from each other and on a horizontal surface 0.5 $\mathrm{m}$ from the ground. Figure 14 shows the velocity field for the closed-roof configuration, whereas Figure 15 and Figure 16 illustrate temperatures and water mass fractions. The position of recirculation can be identified by means of spots at very high air speed. It can be noticed that high-speed airflows are present above the feeding line and in animal-occupied zones. Flow behaviour induced by fans is similar to that described by Pakari and Ghani [16] in a mechanically ventilated barn. By placing all fans facing the same direction, it is possible to induce the air entrainment typical of hybrid ventilation systems. A macroscopic unidirectional flow can be clearly seen in Figure 14; therefore, the studied fan layout appears to be very effective. In Figure 17, the velocity field on a horizontal surface at a height of 2 $\mathrm{m}$ is reported, and the outflow induced by fans can be clearly seen. The computed hourly air change rate is equal to 80.70 1/h, that is eight times as high as the winter one. From the analysis of the temperature field, it is clear that a strong nonuniformity is present in animal-occupied zones. Internal walls generate stagnation regions with very low velocities and a limited local air change rate. The contemporaneous presence of minimal local air change and cows’ load implies the creation of spots with elevated temperature and humidity. In other words, the ventilation system manages to keep temperatures limited on average, but hotspots are present. The creation of stagnation zones due to internal walls is visible in simulation results by Zhou et al. [15], while hotspots due to animal thermal load were previously reported by Iqbal et al. [35]. In summer conditions, wind is also present, and it induces a relevant drifting effect on upwind lines of fans. This may be problematic as fan airflows deviate from the desired path and provide no more high-speed air to upwind lines of stalls. A similar phenomenon was seen by Pakari and Ghani [16]; indeed, in their mechanically ventilated barn, the fan flow deviates from the desired path due to the inflow from perimeter openings. The presence of the animal sensible load causes a growth in temperatures in stalls, feeding lines and boxes. In summer conditions, solar radiation is considered, hence a strong increase in air temperature can be noticed near the barn roof. A fair increase in temperatures can be observed in the right side of the barn as air entrainment attracts hot air from the rooftop. The creation of a recirculation zone on the downwind side of the barn was previously reported by Wu et al. [21] and by Janke et al. [22]. Differently from naturally ventilated barns reported in the literature, the stagnation zone is driven inside the barn by ventilation devices. Fan drifting and hot air inflow due to fans are two important cross effects that can be present in hybrid ventilated buildings. These phenomena can be modelled and predicted only through an integrated simulation methodology that includes the complexities of both natural and mechanical ventilation.

The assessment of animal thermal comfort can be performed using both the equivalent temperature index for cattle (ETIC) and the temperature humidity index (THI). Predicted distributions of ETIC and THI indoor for close roof configuration in summer weather can be seen in Figure 18 and Figure 19. THI predicts the onset of moderate or severe heat stress for all animals in the barn as indoor computed values everywhere are above the threshold of 72. In contrast, ETIC predicts a condition with no, mild and moderate heat stress as values in animal-occupied zones range between 21 and 26. This difference is due to the effect of air velocity, which is strongly beneficial for cows but is neglected by the THI. According to ETIC, cows are likely to suffer from severe heat stress behind internal walls due to high temperatures and humidity as well as low velocities. In a nutshell, the THI predicts the onset of heat stress in all stalls, while the ETIC predicts that only animals in hotspots are likely to suffer from heat stress. In addition, through the analysis of the ETIC, it is possible to see that a high level of animal welfare is present in feeding lines and boxes. This analysis is in good agreement with the results of Zhou et al. [15], in which higher animal welfare is present in high-speed regions.

Animal density is limited, as cows spend only 30% of their time in this zone; in addition, a large number of fans are present in the feeding line. The chances are that the analysed fan configuration is providing an excessive air change to the central line with unnecessary electrical consumption. Solar radiation has an important indirect effect: air heats up notably after flowing on the roof, and then it is driven indoors from the east side due to air entrainment. As a consequence, stalls on the east side are swept by very hot air coming from the roof. All things considered, the improvement in animal welfare and air change rate is mainly caused by recirculation fans. Wind slightly enhances the air change rate, but it is likely to be harmful for both upwind and downwind stall lines. The adoption of curtains during the summer may be beneficial to reduce the negative influence of wind. A growth of the water mass fraction can be noticed in animal-occupied zones; however, the variation in cows’ comfort is limited.

The same analysis can be performed on the open-roof configuration, whose results are presented in Figure 20, Figure 21 and Figure 22. Velocity and humidity fields are remarkably similar to the closed configuration, and roof geometry seems to scarcely influence the internal conditions. Nevertheless, the ridge gap induces a different flow behaviour on the top of the roof, and consequently, the downwind hot region is more notable. Since temperature, humidity and velocity fields in animal-occupied zones are identical to the close-roof layout, the analysis of the THI and ETIC gives the same results and is not reported.

The hourly air change rate is equal to 83.46 1/h with a moderate increase in comparison with the closed-roof configuration. A comparison of hourly air change rate in real and modified layouts for both winter and summer weather can be seen in Figure 23.

4.3. Comparison of Experimental and Simulated Heat-Stress Intensity

In this section, the heat-stress intensity predicted by CFD is compared with the estimation from experimental heavy breathing duration.

Table 3. Weather conditions, measured HBD and experimental percentage of cows’ heat-stress intensity level as observed in CerZoo barn during summer.

Date	Time Interval	${\overline{\mathit{T}}}_{\mathit{Air},\mathit{Max}8\mathit{h}}$	${\overline{\mathit{RH}}}_{\mathit{Air},\mathit{Max}8\mathit{h}}$	${\overline{\mathit{DNI}}}_{\mathit{Air},\mathit{Max}8\mathit{h}}$	Heavy Breathing Duration	${\mathit{X}}_{\begin{array}{c}\mathbf{Thermoneutral},\\ \mathbf{Mild}\end{array}}$	${\mathit{X}}_{\begin{array}{c}\mathbf{Moderate},\\ \mathbf{Severe}, \mathbf{Critical}\end{array}}$
[–]	[h]	[°C]	[%]	[W/${\mathrm{m}}^2$]	[min/day]	[%]	[%]
23 June 2022	8	29.8	52.0	437	60	87.5	12.5
28 August 2022	8	29.1	50.3	370	23	95.2	4.8
2 July 2023	8	30.2	50.5	612	17	96.5	3.5
13 July 2023	8	29.2	51.2	475	57	88.1	11.9
29 July 2023	8	30.2	51.2	540	24	95.0	5.0
1 August 2023	8	29.4	53.5	576	36	92.5	7.5
Average	8	29.6	51.4	502	36	92.5	7.5
Simulation	Steady State	30.0	55.0	500	See Table 4

provides a summary of weather conditions on selected days and reports the estimated percentage of cows with a heat-stress intensity of moderate or worse. Six days were found to match CFD boundary conditions in the period between 2022 and 2023. Thanks to strict criteria adopted for day selection, differences between simulated and real conditions are limited. Average ${\overline{T}}_{Air,Max8h}$ is 0.4 °C lower than simulations, and ${\overline{RH}}_{Air,Max8h}$ is only 3.6% greater. Despite a large variability, average ${\overline{DNI}}_{Air,Max8h}$ matches almost exactly the value adopted in CFD. The experimental values of HBD range between 17 and 60 min/day. The estimated average percentage of cows with a heat-stress intensity that is moderate or worse lies in the interval between 3.5 and 12.5% with a mean value of 7.5%. Consequently, the percentage of cattle that are thermoneutral or in mild heat stress varies from 87.5 and 96.5%, with an average of 92.5%.

The percentage of animals in each heat-stress class, as predicted by CFD, is reported in

Table 4. Percentage of cows at heat-stress intensity levels as predicted by CFD in summer weather.

	THI		ETIC
Heat Stress Intensity	Class Range	${\mathit{X}}_{\mathbf{Class}}$	Class Range	${\mathit{X}}_{\mathbf{Class}}$
	[-]	[%]	[-]	[%]
Thermoneutral	THI < 68	0.0	ETIC < 23	25.3
Mild	$68⩽\mathrm{THI}<72$	0.0	$23⩽\mathrm{ETIC}<26$	70.5
Moderate	$72⩽\mathrm{THI}<80$	25.0	$26⩽\mathrm{ETIC}<31$	4.2
Severe	$80⩽\mathrm{THI}<90$	75.0	$31⩽\mathrm{ETIC}<37$	0.0
Critical	$\mathrm{THI}⩾90$	0.0	$\mathrm{ETIC}⩾37$	0.0

. The estimation of heat-stress intensity was performed using both the THI and ETIC. The THI predicts the onset of heat stress for all cows in the CerZoo barn: 75.0 and 25.0% are expected to be, respectively, in severe and moderate heat stress. The ETIC gives a fairly different estimation: 25.3% of cows are expected to be thermoneutral, while 70.5% and 4.2% are predicted to be in mild and moderate heat stress. The cumulative percentage of animals in moderate, severe and critical heat stress predicted by the ETIC lies inside the range of experimental data, while it is strongly overestimated by the THI. The marked difference between the ETIC and THI is due to the presence of mechanical fans. The THI only considers temperature and relative humidity, while the ETIC also considers the effect of air velocity. The discrepancy between the ETIC and THI is an additional proof of the effectiveness of the ventilation strategy used in CerZoo barn. In a nutshell, the proposed CFD model appears to be able to successfully predict heat-stress intensity only through the ETIC. The difference between ETIC prediction and experimental measurements may be due to animal variability and long-term environmental conditions. Lactation state and body weight influences the intensity of heat stress [60], yet neither the THI nor ETIC consider animal conditions. Furthermore, both the ETIC and THI predicts the onset of heat stress in a given state: the repetition of several days with critical conditions may increase the gravity of each heat-stress event.

This analysis should not be considered a complete validation, as the comparison with measurements was performed in specific conditions. Firstly, the analysis was performed only in summer weather. In winter conditions, due to low temperature and humidity, all animals are expected to be in thermoneutral conditions, and HBD is bound to be zero. In addition, the detailed behaviour of the model cannot be validated as the comparison was performed only on comprehensive indexes.

5. Conclusions and Future Works

The developed model seems to be able to correctly describe the cross effects between natural and mechanical ventilation. In addition, the increase in air change rate between summer and winter weather suggests that the typical air entrainment effects of hybrid ventilated barns were successfully modelled. The presented methodology provides a detailed description of both internal and external airflows; moreover, it highlights all the criticalities of the studied geometries. The presence of internal walls seems to be harmful due to the creation of stagnation zones and hotspots in animal-occupied zones. Therefore, the presence of obstacles near animals must be limited as much as possible. The ventilation system seems to be correctly sized and designed, as it creates a tunnel ventilation effect and provides high air change.

Simulation results in summer weather with the existing layout were compared with experimental data from the real barn. The measured percentage of animals in each class of heat-stress intensity appears to be in good agreement with the estimation by the ETIC in CFD results. In contrast, the THI strongly overestimates the intensity of heat stress in cattle. The analysis of the temperature humidity index provides no useful information on the ventilation system, as air speed has a limited effect on temperature and humidity. Therefore, it is advised to adopt the ETIC instead of the THI for the assessment of heat stress in hybrid ventilated barns.

CFD predicts a slightly different air change rate for open- and closed-roof layouts in both summer and winter weather. Therefore, the chances are that the CFD model can be used to evaluate design solutions. Nevertheless, temperature, humidity and air speed are very similar in animal-occupied zones. For the analysed hybrid ventilated barn, the effect of roof geometry on thermal conditions in animal-occupied zones appears to be limited. In comparison with the layout with blowers, the solution with ridge gaps is likely to provide slightly higher air change with lower costs and electricity consumption. A similar analysis could be performed on the number of fans inside the barn to identify the best trade-off between energy consumption and ventilation.

In future works, a fluid dynamic validation will be performed through a comparison with measurements of temperature, humidity and air speed in selected locations of the barn. This additional validation will provide more information on the detailed behaviour of the fluid dynamics model. The validation should also be repeated to extend the validity of the CFD model. Additional simulations will be performed in different weather conditions, and the methodology will be applied to other hybrid ventilated livestock buildings. The presented study focuses exclusively on thermal management, and it is the starting point for the CFD simulation of barn air quality and pollutant emissions. The predicted air change rate for the CerZoo barn is sufficiently high that air quality is unlikely to be critical [51]. However, air quality may be relevant for other test cases, especially in winter weather [61]. In addition, the prediction of ammonia emission also has environmental relevance, as the zootechnical sector is reported to be the main emitter of this pollutant [62].