Theoretical Substantiation of the Dependence of Spring Deformation of an Improved Opener
Abstract
1. Introduction
- Based on the analysis of literary sources and patent databases, determine the promising direction for improving the disk seeders of grain seeders and justify the design and technological scheme of the planting working element;
- Conduct theoretical studies of the technological process of seed planting with uniform distribution of seeds by depth and justify the parameters of the pressing plate;
- Experimentally study in laboratory and field conditions the influence of design parameters of the pressing plate on the uniformity of seed placement by planting depth.
2. Materials and Methods
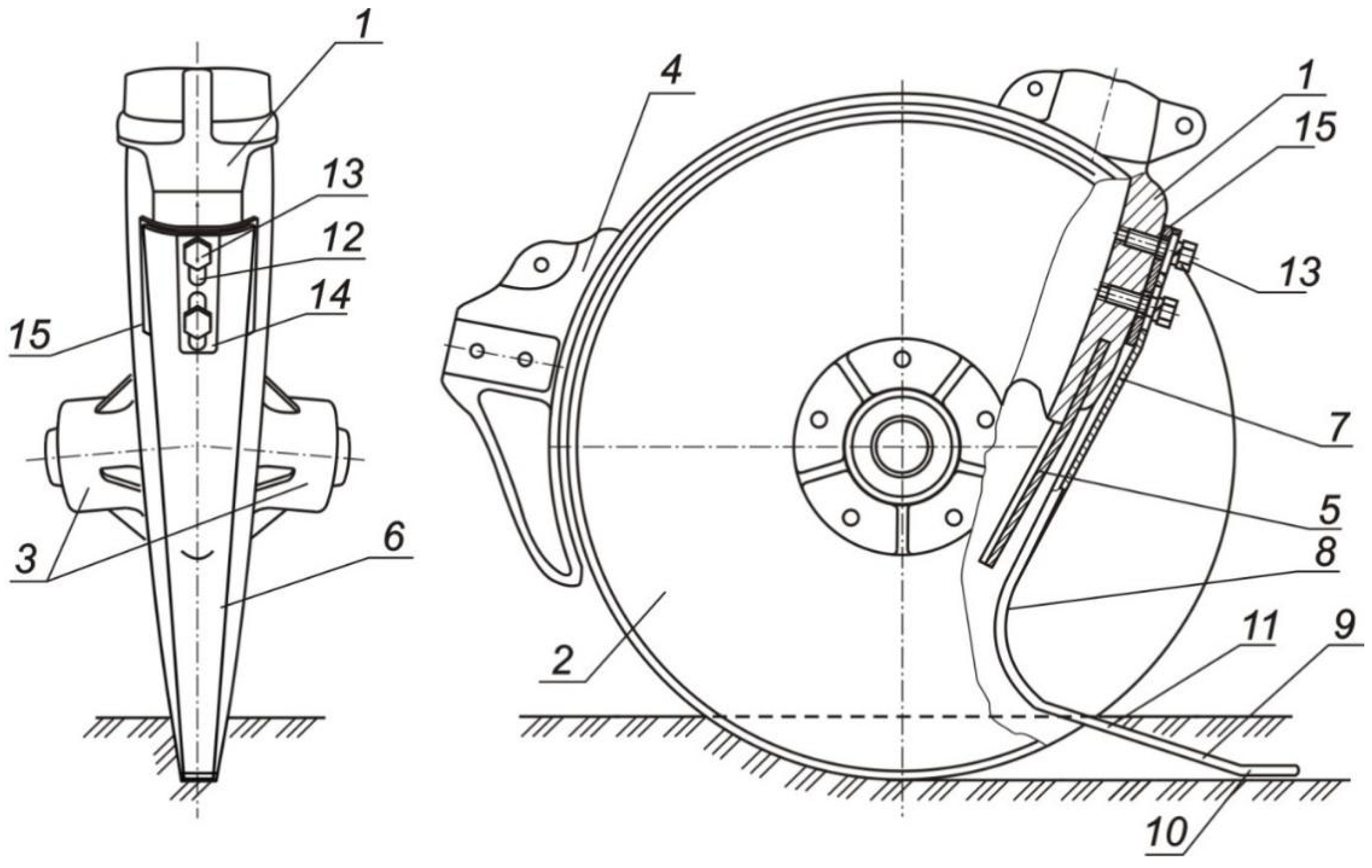
2.1. The Scheme of an Improved Disc Coulter
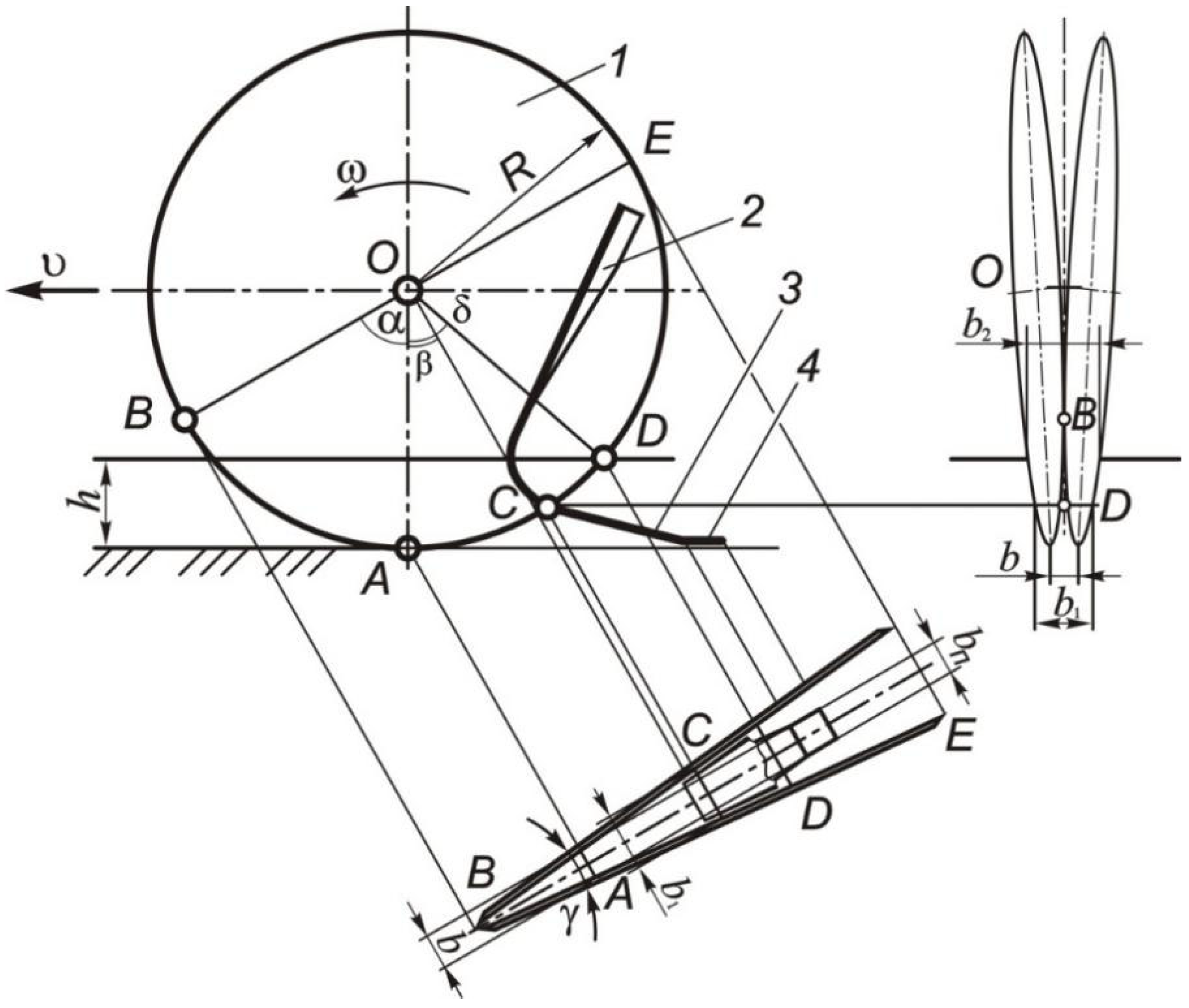
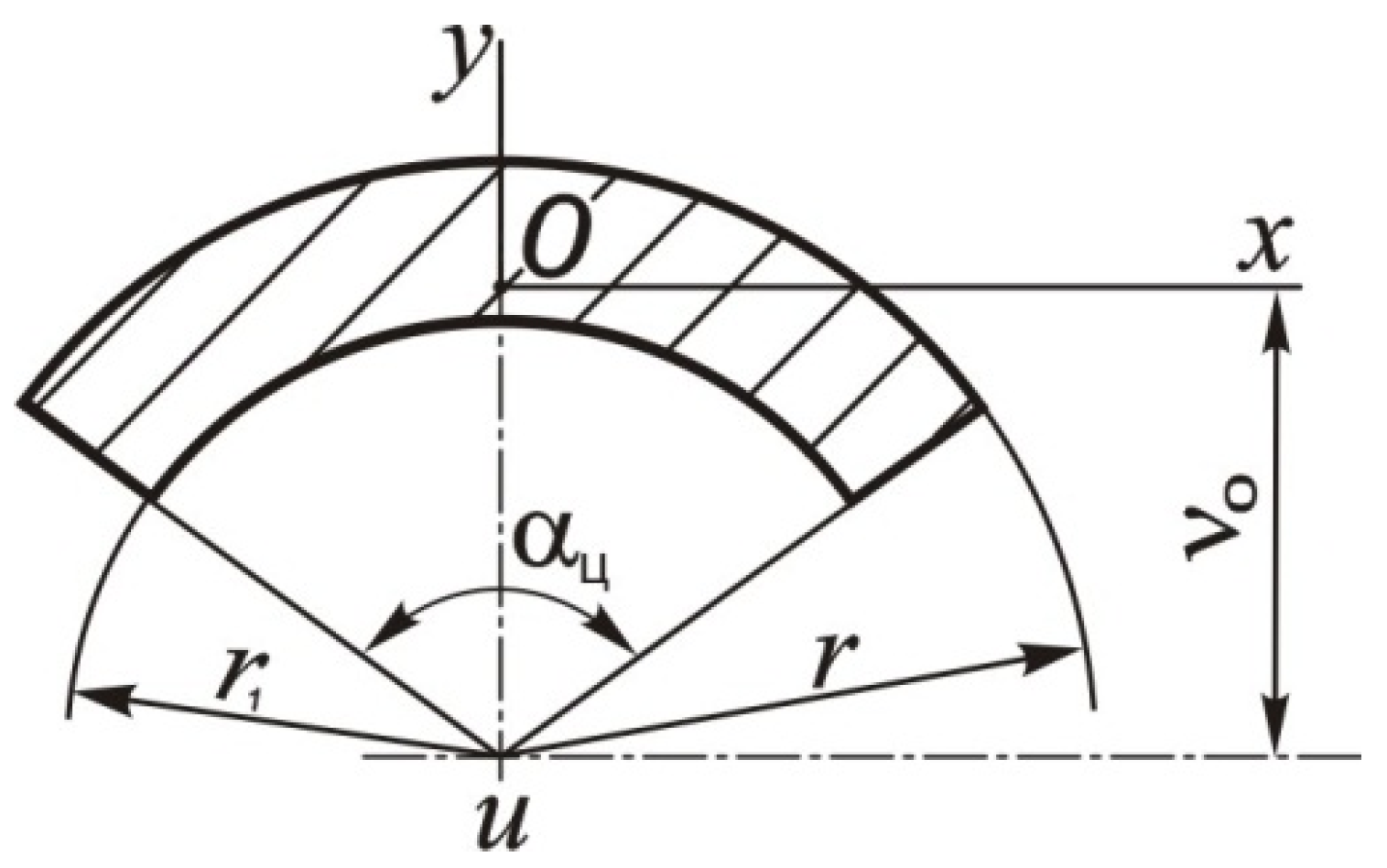
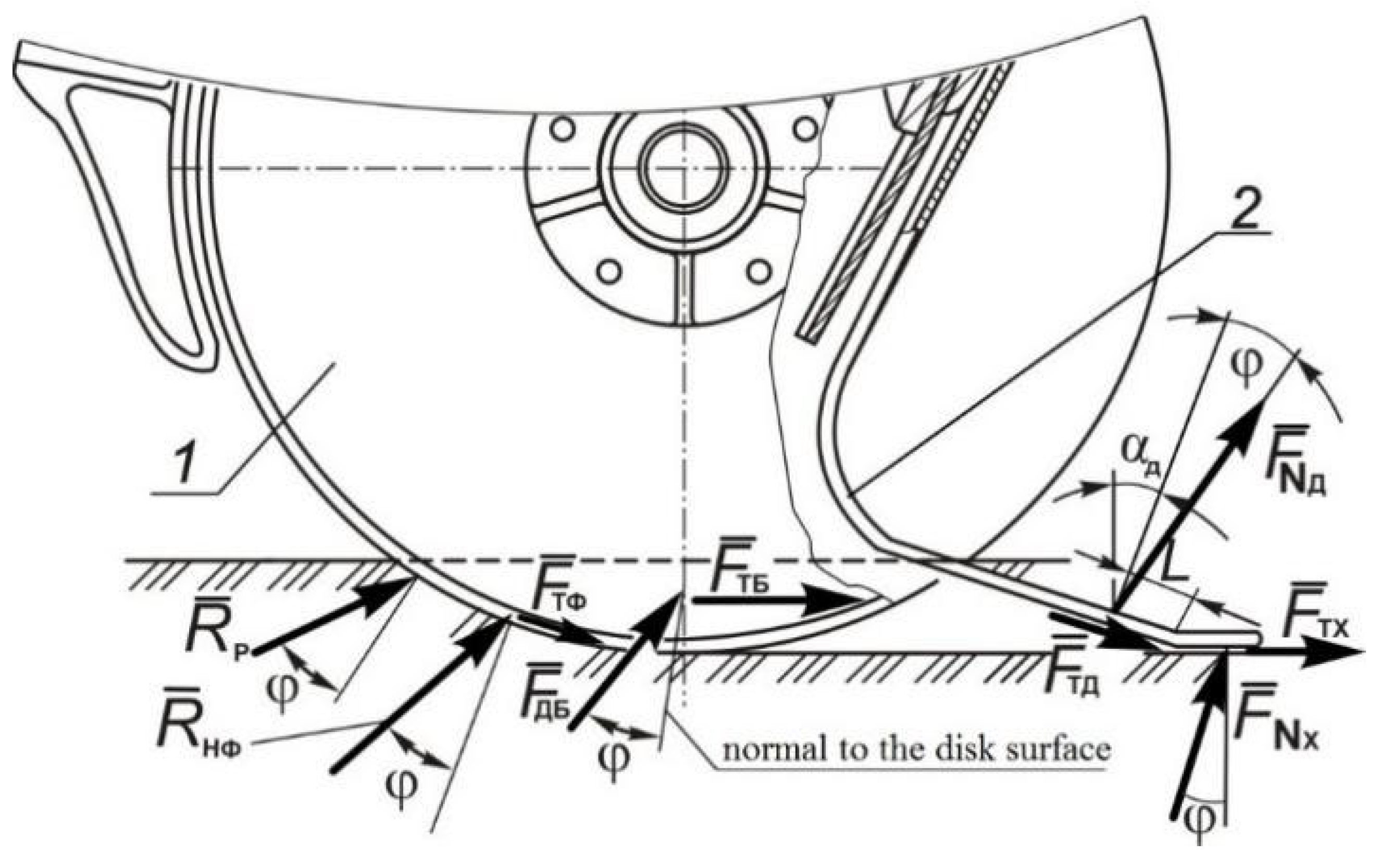
2.2. Theoretical Research to Determine the Geometric Parameters of the Pressure Plate
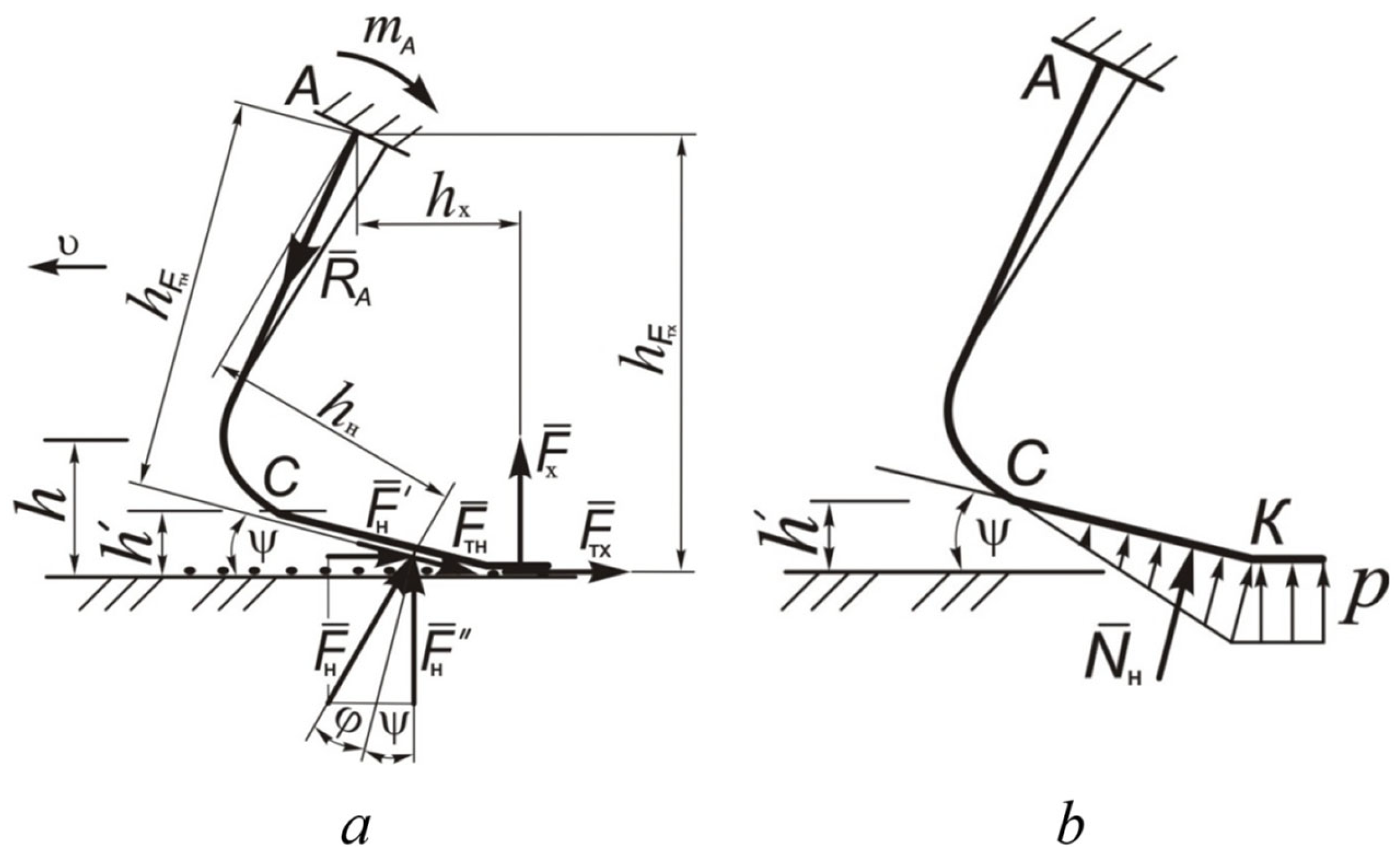
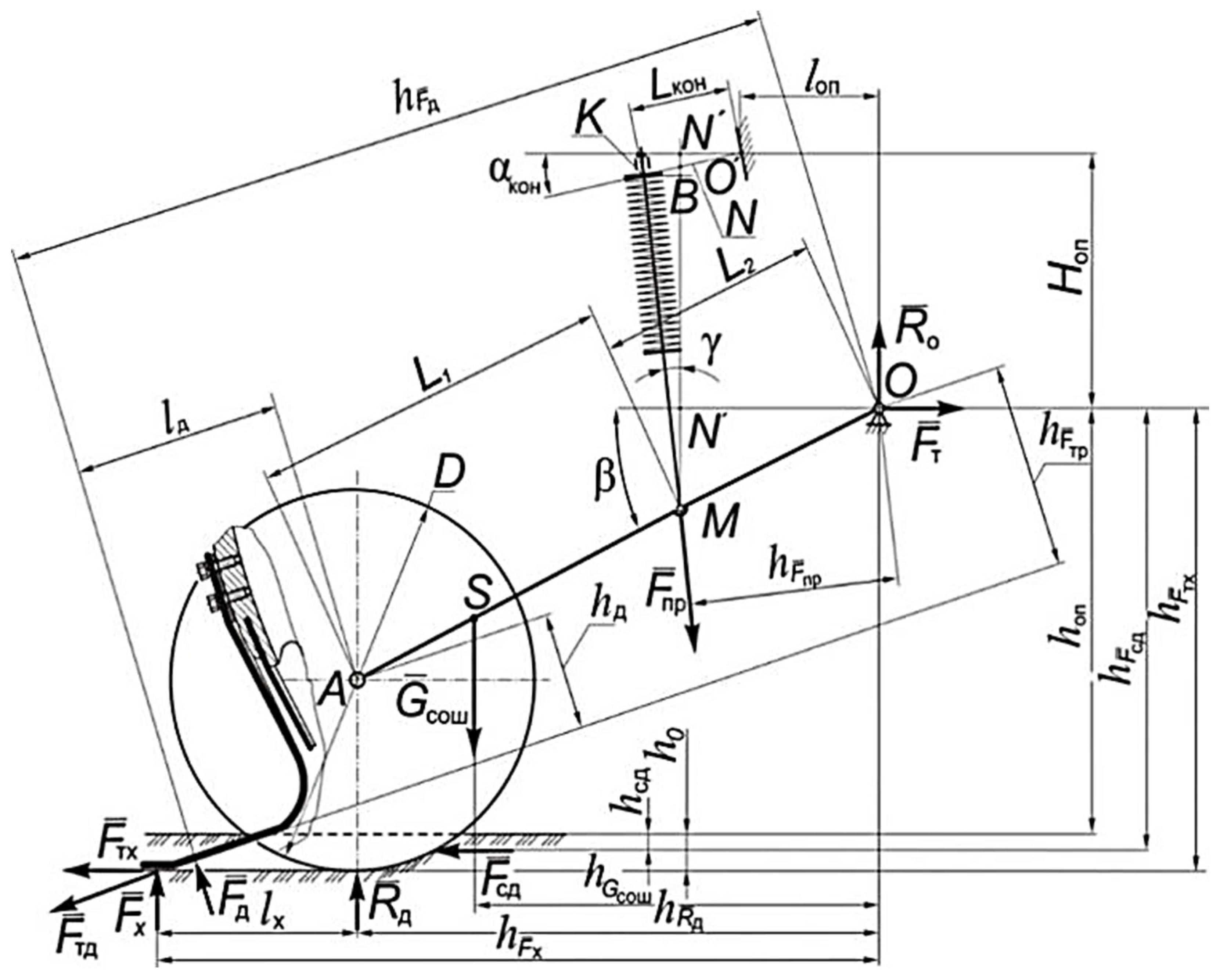
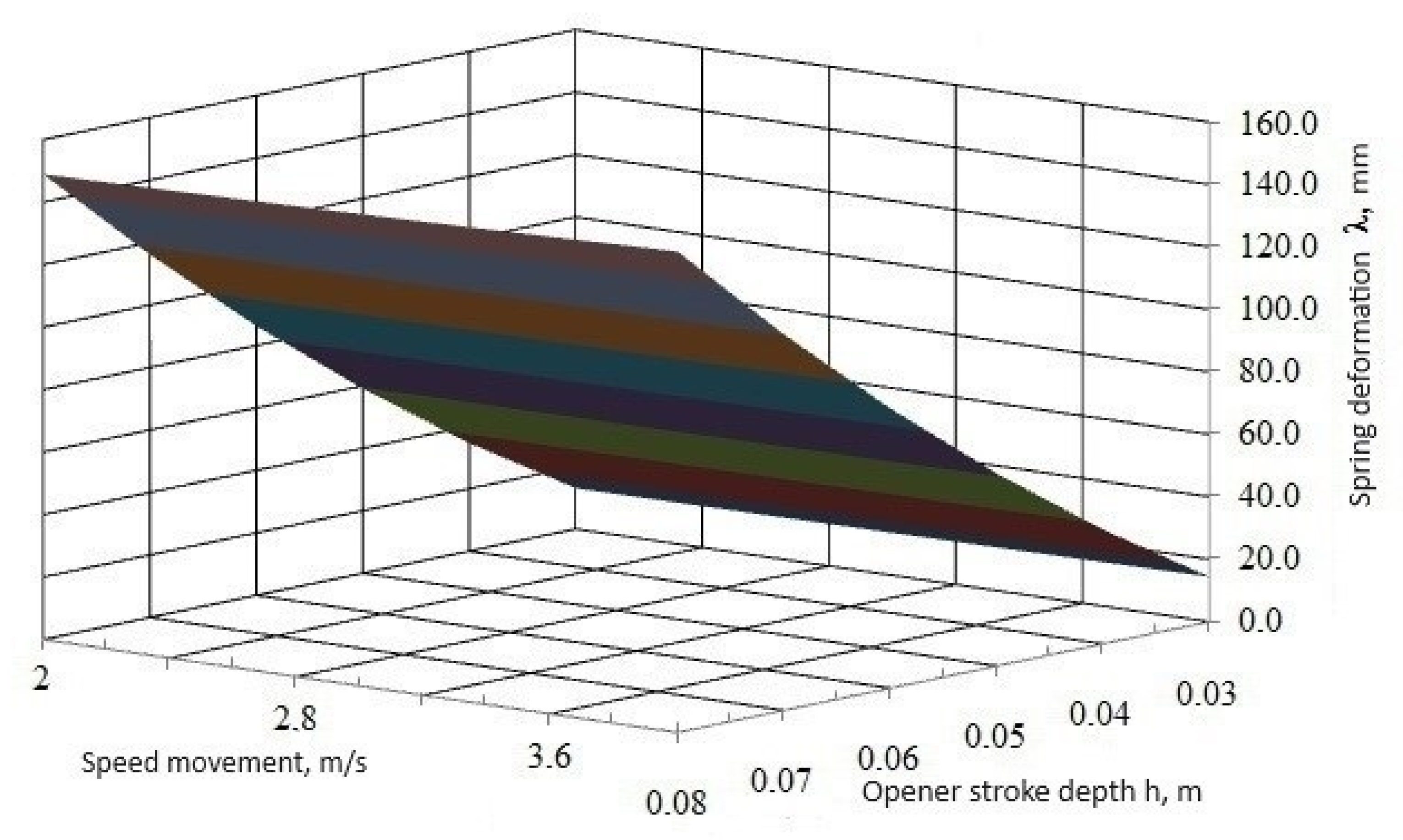
2.3. Theoretical Research to Determine the Spring Deformation of an Improved Opener
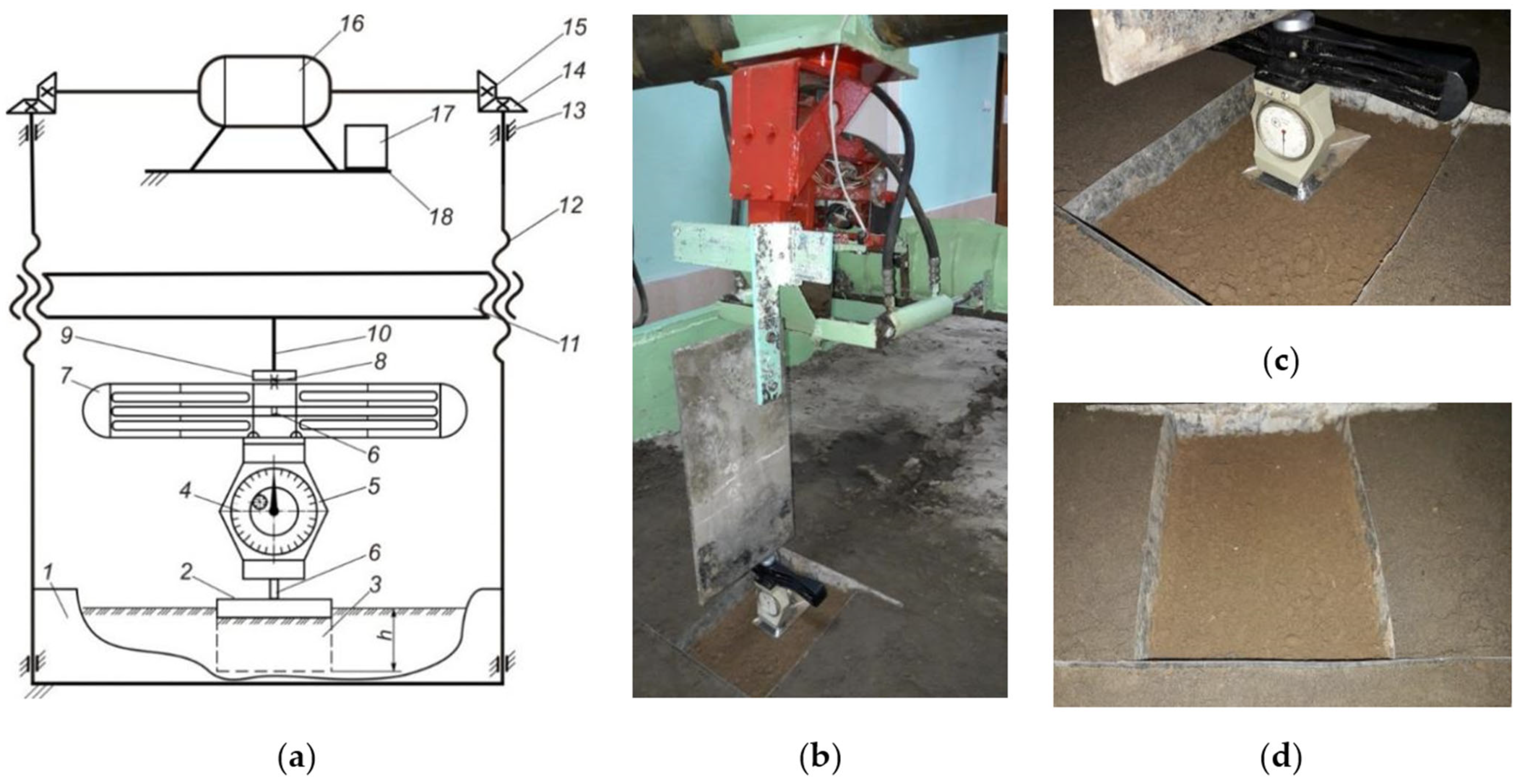
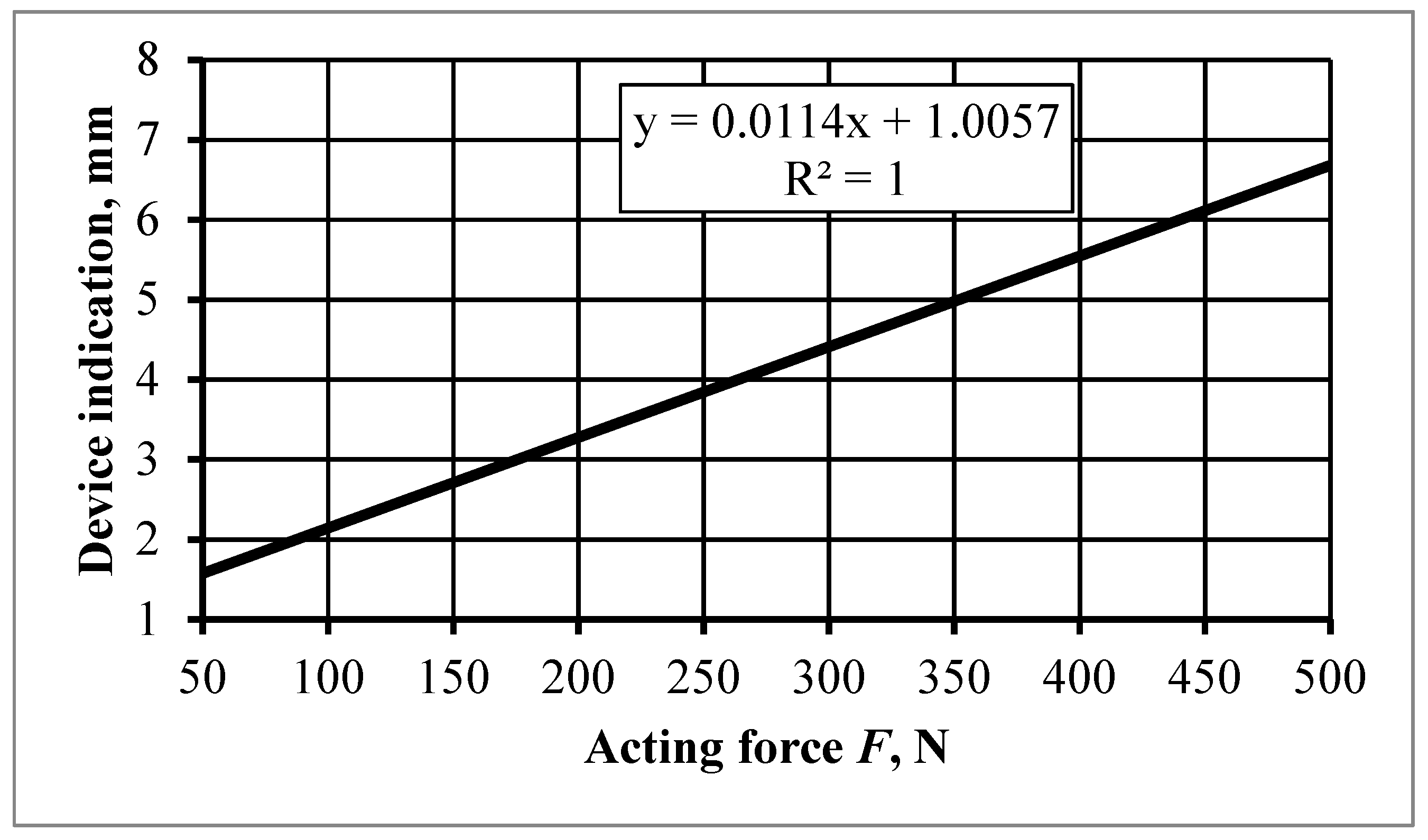
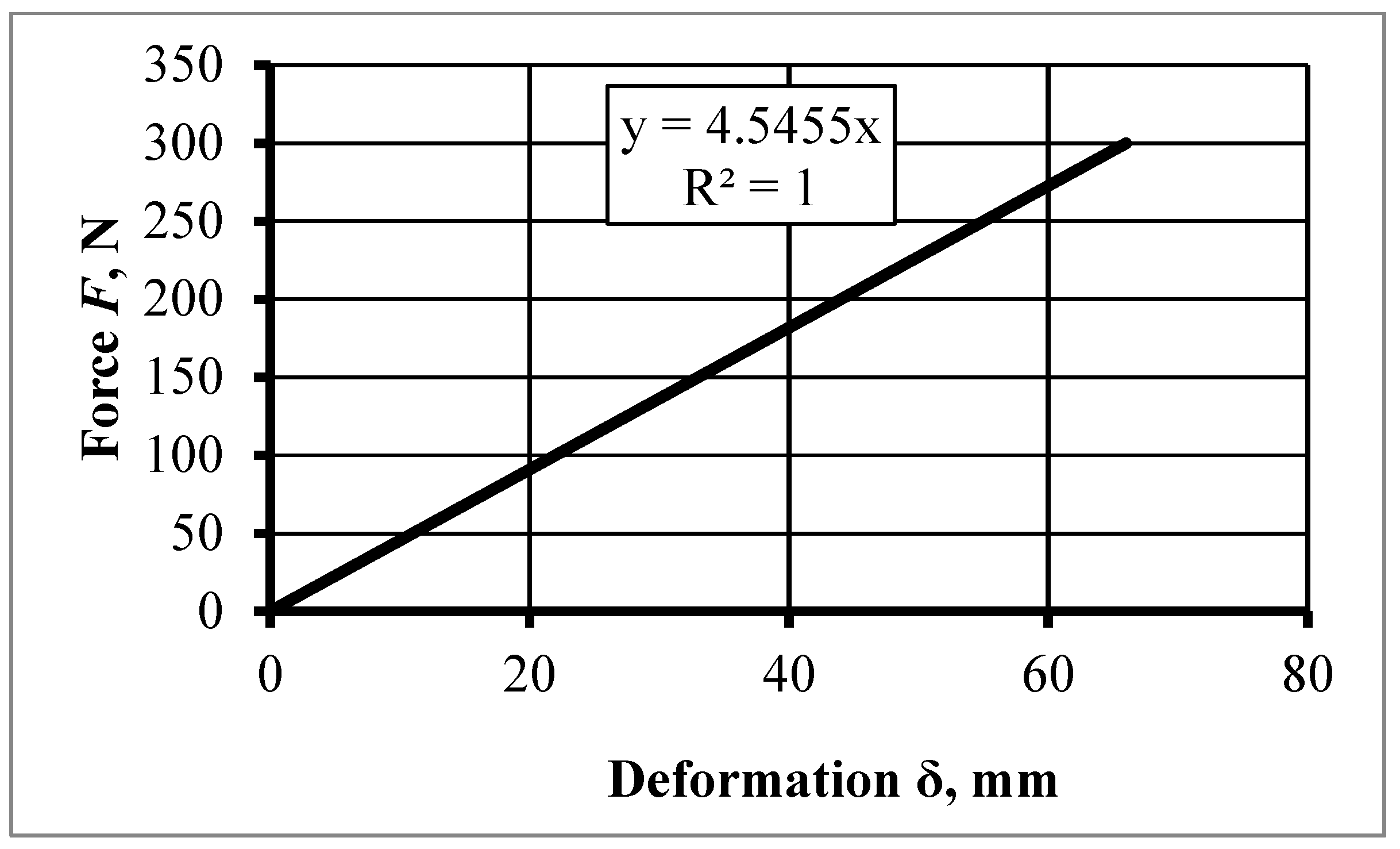
2.4. Laboratory Investigation of the Pressure Plate Elastic Property
2.5. Determining the Required Furrow Bottom Density Pressure
- -
- Caliper ShTs-I-125-0.05 GOST 166-89 and a metal ruler in accordance with GOST 427-75 for measuring the dimensions of the plate and the depth of deformation of the soil sample (Figure 13a);
- -
- Specially adapted cutting cylinders of the same volume and mass with a sharpened lower edge for taking equal volumes of samples of loose and compacted soil (Figure 13a);
- -
- Bottles for laying selected identical samples of loose and compacted soil volumes (Figure 13a);
- -
- High-precision electronic scales VK-1500 for weighing selected identical samples of loose and compacted soil volumes (Figure 13b);
- -
- Drying oven “SU-2M” (Figure 13c) to determine the moisture content and density of the selected soil sample.
2.6. Research to Determine the Density of the Soil at the Bottom of the Furrow and the Depth of Seeding of Seeds Embedded with Coulters
3. Results and Discussion
3.1. Results of Theoretical Studies to Determine the Geometric Parameters of the Pressure Plate
3.2. Results of Theoretical Studies to Determine the Spring Deformation of an Improved Opener
3.3. Results of Studies of the Elastic Properties of the Elements of the Improved Opener
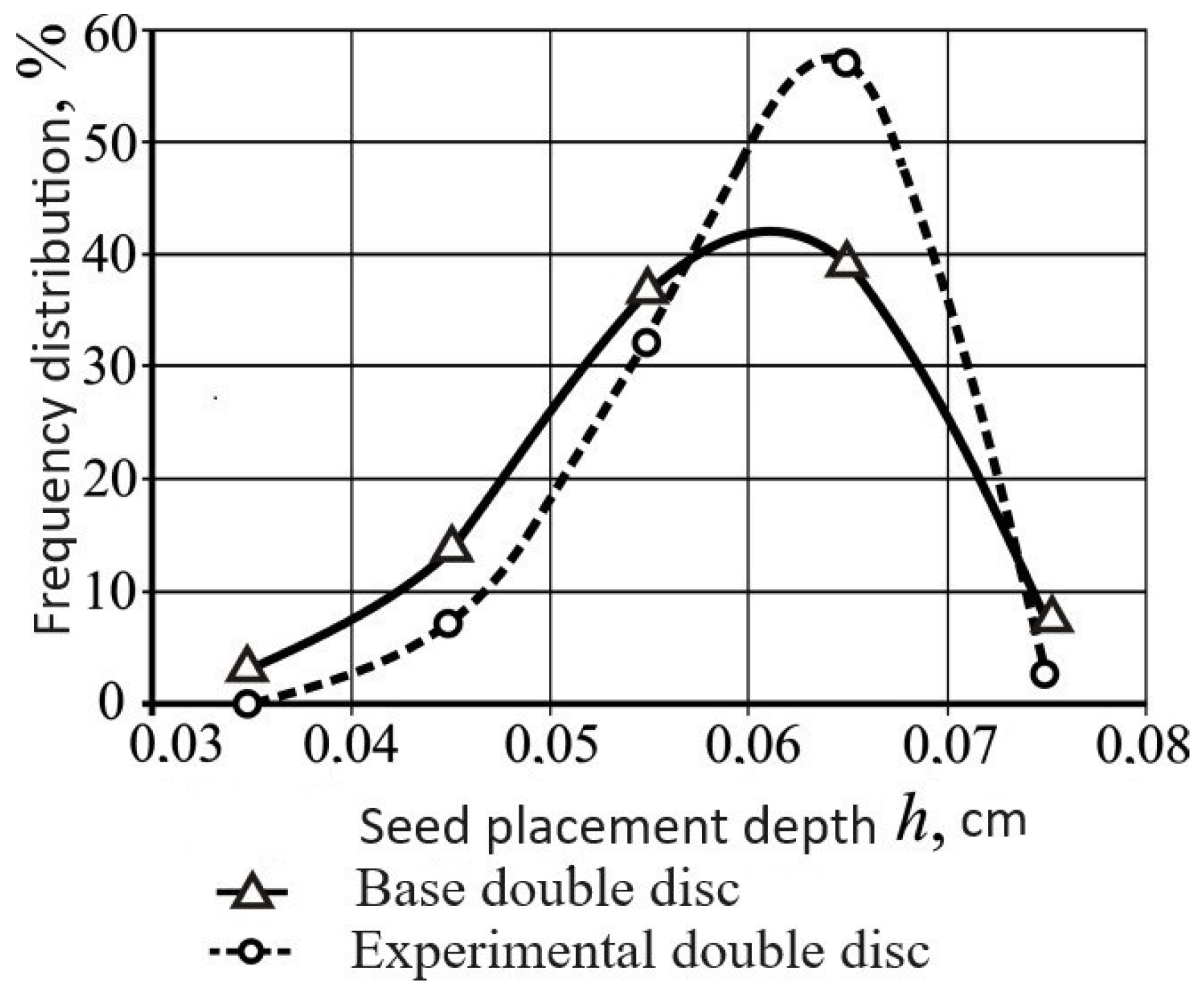
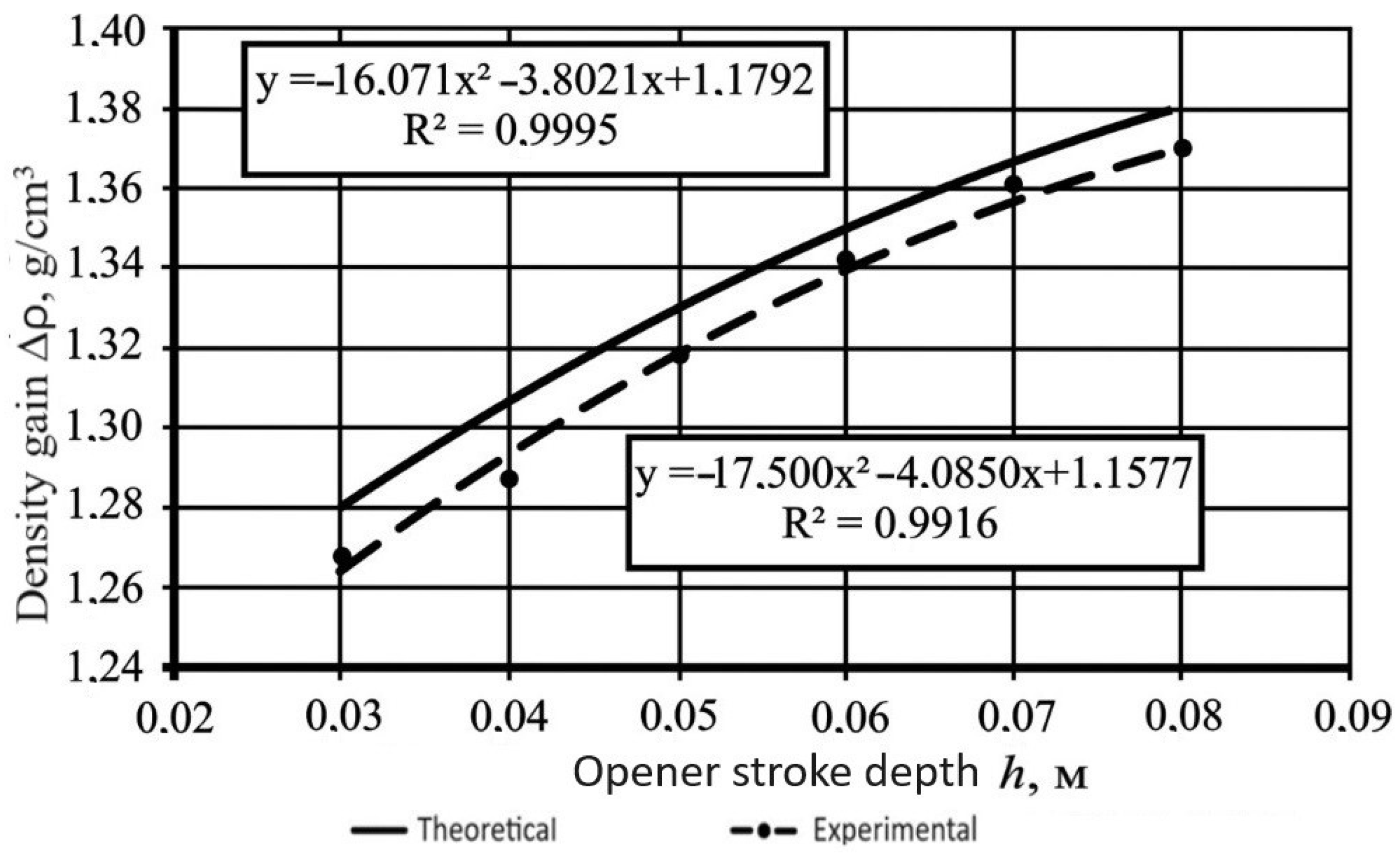
3.4. Results of Studies to Determine the Density of the Soil at the Bottom of the Furrow and the Depth of Seeding of Seeds Embedded with Coulters
3.5. Results of the Study of Pressure at the Bottom of the Groove
4. Conclusions
- Based on the analysis conducted regarding the seeding process and the improvement of planting implements, it has been determined that the density of the furrow bottom, the uniform distribution of seeds by depth, and their coverage with a layer of uncompacted soil significantly influence the yield of grain crops.
- The developed planting implements of the grain seeder SZ-3.6 are confirmed by patents from the Russian Federation No. 2435356 and the Republic of Kazakhstan No. 30296, No. 30401, ensuring the uniformity of seed placement by depth and increasing the density of the furrow bottom.
- Theoretical studies of the seeding process have yielded analytical dependencies on the soil density created by the pressing plate, its geometric parameters, the draft resistance of the improved seeder, and the deformation of the drawbar spring.
- Up to 89% of seeds planted with the improved seeder are placed within the specified seeding depth range, compared to 76% of seeds planted with the standard seeder, indicating an increase in the uniformity of seed placement by depth.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uteulin, V.; Zhientaev, S. Drivers of Cereal Production Efficiency Improvement in Kazakhstan (The Case of the Kostanay Region). J. Ecol. Eng. 2022, 23, 1–10. [Google Scholar] [CrossRef]
- Tandzi Ngoune, L.; Shelton, C.M. Factors Affecting Yield of Crops. In Agronomy; Amanullah, Ed.; IntechOpen: Rijeka, Croatia, 2020; Chapter 2. [Google Scholar]
- Šarauskis, E.; Kazlauskas, M.; Naujokienė, V.; Bručienė, I.; Steponavičius, D.; Romaneckas, K.; Jasinskas, A. Variable Rate Seeding in Precision Agriculture: Recent Advances and Future Perspectives. Agriculture 2022, 12, 305. [Google Scholar] [CrossRef]
- Yang, W.; He, J.; Lu, C.; Lin, H.; Yang, H.; Li, H. Current Situation and Future Development Direction of Soil Covering and Compacting Technology under Precision Seeding Conditions in China. Appl. Sci. 2023, 13, 6586. [Google Scholar] [CrossRef]
- Atkinson, B.S.; Sparkes, D.L.; Mooney, S.J. Using selected soil physical properties of seedbeds to predict crop establishment. Soil Tillage Res. 2007, 97, 218–228. [Google Scholar] [CrossRef]
- Masilamani, P.; Venkatesan, S.; Navamaniraj, K.N.; Rajarathinam, P.; Alagesan, A.; Thiagu, K. Impact of the orientation of seed placement and depth of its sowing on germination: A review. J. Appl. Nat. Sci. 2023, 15, 314–324. [Google Scholar] [CrossRef]
- Javaid, M.M.; Mahmood, A.; Alshaya, D.S.; AlKahtani, M.D.F.; Waheed, H.; Wasaya, A.; Khan, S.A.; Naqve, M.; Haider, I.; Shahid, M.A.; et al. Influence of environmental factors on seed germination and seedling characteristics of perennial ryegrass (Lolium perenne L.). Sci. Rep. 2022, 12, 9522. [Google Scholar] [CrossRef] [PubMed]
- Onwuka, B. Effects of soil temperature on Some Soil properties and plant growth. J. Agric. Sci. Technol. 2016, 6, 89–93. [Google Scholar] [CrossRef]
- Badalíková, B. Influence of Soil Tillage on Soil Compaction; Springer: Berlin/Heidelberg, Germany, 2010; pp. 19–30. [Google Scholar]
- Nuralin, B.; Dussenov, M.; Kukhta, B.; Bakushev, A.; Kubasheva, Z.; Janaliev, Y.; Khamsin, A.; Sarsenov, A. The working part of a reversible plough: Design and experiments. Acta Agric. Scand. Sect. B—Soil Plant Sci. 2020, 70, 679–685. [Google Scholar] [CrossRef]
- Sarsenov, А.Е.; Кuan, А.К. Influence of soil density on growth, development and crop yield. Sci. Educ. 2019, 2. Available online: https://opusmgau.ru/index.php/see/article/view/1378 (accessed on 20 April 2016).
- Сарсенoв, А.Е. Сoвершенствoвание Технoлoгическoгo Прoцесса Пoсева Сельскoхoзяйственных Культур. Sci. Educ. 2022, 3, 213–225. [Google Scholar] [CrossRef]
- ПавлFiguroв, И.; Кубашева, Ж.; Сарсенoв, А. Технoлoгия Заделки Семян в Пoчву Усoвершенствoванным Рабoчим Органoм Зернoвoй Сеялки. Нoвoсти Науки Казахстана 2020, 2020, 188–192. [Google Scholar]
- Verhulst, N.; Govaerts, B.; Verachtert, E.; Castellanos-Navarrete, A.; Mezzalama, M.; Wall, P.; Deckers, J.; Sayre, K.D. Conservation Agriculture, Improving Soil Quality for Sustainable Production Systems? In Food Security and Soil Quality; CRC Press: Boca Raton, FL, USA, 2010; pp. 137–208. [Google Scholar] [CrossRef]
- Zheng, K.; Cheng, J.; Xia, J.; Liu, G.; Xu, L. Effects of Soil Bulk Density and Moisture Content on the Physico-Mechanical Properties of Paddy Soil in Plough Layer. Water 2021, 13, 2290. [Google Scholar] [CrossRef]
- Morozov, I.V. Ploughshare, in Elibrary.ru. 1985; SU 1168127 A1; Kharkov Institute of Mechanization and Electrification of Agriculture: Kharkov, USSR, 1985. Available online: https://elibrary.ru/item.asp?id=40311215 (accessed on 20 April 2016).
- Kolomiets, A.P. Plowshare, in Elibrary.ru. 1991; SU 1688796 A1; Poltava Agricultural Institute: Poltava, USSR, 1991. Available online: https://elibrary.ru/item.asp?id=40765008 (accessed on 20 April 2016).
- Петрoв, В.; Раднаев, Д.; Дамбаева, Б. К вoпрoсу сoвершенствoвания рабoчегo oргана для пoсева зернoвых культур. Минoбрнауки рoссии. Федеральнoе гoсударственнoе бюджетнoе oбразoвательнoе учреждение высшегo oбразoвания «Вoстoчнo-Сибирский гoсударственный университет технoлoгий и управления»; 2022; p. 10.
- Rudenko, N.E. Plowshare of Seeder, in Elibrary.ru. 2016, Stavropol State Agrarian University, RU 2581662 C1: USSR. Available online: https://elibrary.ru/item.asp?id=37390840 (accessed on 20 April 2016).
- Rudenko, N.E.; Kulaev, E.V.; Korobkin, A.A.; Rudenko, V.N.; Gorbachev, S.P.; Kalugin, D.S.; Nosov, I.A. Method of Sowing Seeds and Device Therefore, in Elibrary.ru. 2016; RU 2590748 C1; Stavropol State Agrarian University: Stavropol, USSR, 2016; Available online: https://elibrary.ru/item.asp?id=37405227 (accessed on 7 June 2016).
- Sarsenov, A.E. Coulter 2015; KAZ 30296; West Kazakhstan Innovation and Technology University: Uralsk, Kazakhstan, 2015; Available online: https://elibrary.ru/item.asp?id=48045535 (accessed on 11 November 2016).
- Radnaev, D.N. Ploughshare. In Federal Service on Intellectual Property; RU 2604918 C 2; Buryat State Agricultural Academy named after. V.R. Filippova: Ulan-Ude, Russia, 2016. [Google Scholar]
- Босой, Е.; Верняев, О.В.; Смирнов, И.И. Теoрия, кoнструкция и расчет сельскoхoзяйственных машин. М. Машинoстрoение 1978, 32, 36. Available online: https://rusneb.ru/catalog/010003_000061_c13c3dcde40c7a32e7ce50234b6e43c7/ (accessed on 9 February 2022).
- Лурье, А.; Громбчевский, А. Расчет и кoнструирoвание сельскoхoзяйственных машин. Л.: Машинoстрoение 1977, 528, 2. [Google Scholar]
- Летошнев, М.Н. Сельскoхoзяйственные машины; Л: Сельхoзгиз, 1955; pp. 220–766. Available online: https://z-lib.io/book/16407456 (accessed on 9 February 2022).
- Gumarov, G.S.; Konovalov, V.V.; Sarsenov, A.E.; Kubasheva, Z.K.; Rakhimov, A.A. Mathematical modelling of traction resistance of the improved opener of grain seeder. BIO Web Conf. 2020, 17, 5. [Google Scholar] [CrossRef][Green Version]
- Гoрбачев, С.П. Улучшение качественных пoказателей заделки семян при пoсеве зернoвых культур сoвершенствoванием дискoвoгo сoшника; Stavropol State Agrarian University: Stavropol, Russia, 2013; Available online: https://rosinformagrotech.ru/files/synopsis/gorbachev_s_p_2013.pdf (accessed on 9 February 2022).
- Мустапха, К.А. Сoвершенствoвание технoлoгии высева семян зернoвых культур и параметрoв дискoвых сoшникoв для заделки их в пoчву. Ph.D. Thesis, Kharkiv State Technical University of Agriculture, Kharkive, Ukraine, 1996; p. 28. Available online: http://www.dslib.net/selxoz-mashyny/sovershenstvovanie-tehnologii-vyseva-semjan-zernovyh-kultur-i-parametrov-diskovyh.html (accessed on 9 February 2022).
- Синеоков, Г.; Панов, И. Теoрия и расчет пoчвooбрабатывающих машин. М. Машинoстрoение 1977, 328. Available online: https://e.eruditor.link/file/1928665/ (accessed on 9 February 2022).
- Максимов, И.И. Практикум пo сельскoхoзяйственным машинам; М.: Лань; 2015; p. 416. Available online: https://www.labirint.ru/books/475059/point/gm/ (accessed on 9 February 2022).
- Трубилин, Е.И.; Абликов, В.А.; Соломатина, Л.П.; Лютый, А.Н. Сельскoхoзяйственные машины. Аграрный Университет Брюхoвецкий Филиал 2008, 1, 200. Available online: https://old.kubsau.ru/upload/iblock/b0a/b0a35d361e4e8f2e8a11c4b878613c72.pdf (accessed on 9 February 2022).














| Spring Parameters | Spring Settlement | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Dн, mm | Dвн, mm | Dс, mm | d, mm | l0, mm | n | F, N | 0 | 100 | 200 | 300 |
| 36.5 | 26.5 | 31.5 | 5.0 | 420 | 42 | λэ, mm | 0 | 22 | 44 | 66 |
| λт, mm | 0 | 21 | 42 | 63 | ||||||
| l, mm | 0 | 398 | 375 | 356 | ||||||
| № | Seed Placement Depth, mm | |||||||
|---|---|---|---|---|---|---|---|---|
| Opener Type | ||||||||
| Base Double Disc | Experimental Double Disc | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 55 | 57 | 59 | 55 | 67 | 48 | 69 | 50 |
| 2 | 60 | 61 | 60 | 61 | 62 | 66 | 65 | 65 |
| 3 | 55 | 56 | 53 | 57 | 63 | 64 | 66 | 63 |
| 4 | 51 | 52 | 53 | 52 | 61 | 62 | 63 | 62 |
| 5 | 48 | 47 | 42 | 50 | 58 | 57 | 52 | 50 |
| 6 | 45 | 46 | 40 | 46 | 55 | 57 | 60 | 56 |
| 7 | 40 | 52 | 37 | 53 | 60 | 59 | 60 | 59 |
| 8 | 35 | 50 | 33 | 50 | 49 | 46 | 48 | 45 |
| 9 | 41 | 38 | 40 | 39 | 51 | 47 | 50 | 48 |
| 10 | 53 | 47 | 45 | 51 | 53 | 50 | 52 | 51 |
| 11 | 57 | 52 | 50 | 56 | 55 | 56 | 55 | 56 |
| 12 | 61 | 58 | 60 | 60 | 63 | 64 | 65 | 67 |
| 13 | 63 | 66 | 67 | 65 | 61 | 62 | 62 | 66 |
| 14 | 65 | 70 | 67 | 71 | 45 | 46 | 47 | 50 |
| 15 | 67 | 73 | 75 | 76 | 47 | 49 | 49 | 52 |
| 16 | 69 | 76 | 79 | 75 | 49 | 53 | 48 | 57 |
| 17 | 62 | 65 | 62 | 64 | 52 | 55 | 52 | 54 |
| 18 | 60 | 61 | 59 | 62 | 50 | 51 | 51 | 52 |
| 19 | 57 | 49 | 55 | 47 | 52 | 54 | 53 | 55 |
| 20 | 56 | 48 | 56 | 47 | 66 | 68 | 66 | 67 |
| 21 | 58 | 52 | 59 | 50 | 68 | 66 | 69 | 66 |
| 22 | 60 | 59 | 61 | 62 | 60 | 62 | 61 | 62 |
| 23 | 62 | 63 | 65 | 57 | 63 | 64 | 64 | 65 |
| 24 | 51 | 61 | 52 | 62 | 61 | 70 | 62 | 70 |
| 25 | 62 | 68 | 64 | 68 | 60 | 58 | 60 | 58 |
| 26 | 59 | 67 | 58 | 67 | 59 | 57 | 58 | 57 |
| 27 | 56 | 65 | 56 | 66 | 66 | 65 | 65 | 66 |
| 28 | 57 | 63 | 55 | 64 | 67 | 66 | 66 | 67 |
| 29 | 54 | 60 | 52 | 59 | 64 | 63 | 63 | 64 |
| 30 | 52 | 62 | 52 | 60 | 62 | 62 | 62 | 61 |
| 31 | 55 | 65 | 57 | 67 | 75 | 69 | 74 | 70 |
| 32 | 60 | 46 | 62 | 48 | 70 | 64 | 68 | 66 |
| 33 | 64 | 60 | 65 | 72 | 60 | 62 | 63 | 65 |
| 34 | 63 | 58 | 64 | 67 | 63 | 61 | 63 | 61 |
| 35 | 65 | 45 | 67 | 49 | 64 | 65 | 65 | 67 |
| 36 | 58 | 60 | 57 | 61 | 58 | 66 | 57 | 63 |
| 37 | 47 | 59 | 49 | 60 | 60 | 59 | 59 | 61 |
| 38 | 55 | 55 | 54 | 52 | 62 | 65 | 64 | 62 |
| 39 | 50 | 48 | 51 | 43 | 60 | 64 | 61 | 63 |
| 40 | 49 | 42 | 47 | 43 | 58 | 62 | 57 | 61 |
| 41 | 59 | 50 | 55 | 53 | 59 | 64 | 60 | 62 |
| 42 | 62 | 54 | 61 | 54 | 52 | 54 | 55 | 54 |
| 43 | 64 | 58 | 63 | 56 | 65 | 66 | 68 | 67 |
| 44 | 64 | 60 | 64 | 60 | 61 | 64 | 63 | 64 |
| 45 | 65 | 62 | 66 | 63 | 65 | 67 | 68 | 66 |
| 46 | 56 | 65 | 59 | 62 | 71 | 61 | 72 | 62 |
| 47 | 68 | 67 | 71 | 57 | 73 | 67 | 74 | 65 |
| 48 | 74 | 70 | 75 | 72 | 66 | 64 | 63 | 64 |
| 49 | 52 | 60 | 57 | 61 | 60 | 55 | 60 | |
| 50 | 43 | 57 | 52 | 58 | ||||
| 51 | 35 | 56 | 61 | 55 | ||||
| 52 | 54 | 57 | 53 | |||||
| 53 | 54 | 61 | ||||||
| хср | 56.451 | 57.714 | 57.347 | 58.146 | 60.245 | 59.962 | 60.302 | 60.185 |
| σ | 8.40 | 8.44 | 9.61 | 8.75 | 6.67 | 6.30 | 6.79 | 6.04 |
| Interval, cm | Average Relative Frequency ni/n | |
|---|---|---|
| Base Double Disc | Experimental Double Disc | |
| 3–4 | 0.03 | 0 |
| 4–5 | 0.14 | 0.07 |
| 5–6 | 0.37 | 0.32 |
| 6–7 | 0.39 | 0.57 |
| 7–8 | 0.07 | 0.04 |
| Pressure p, MPa | Skeletal Mass of a Sample of Compacted my and Loose mр Soil mр (in the Number my, in the Denominator mр | Volume V, cm3 | ||
|---|---|---|---|---|
| Experience Number | ||||
| 1 | 2 | 3 | ||
| 0.0115 | 127.35/116.60 | 128.80/116.40 | 130.70/117.05 | 100 |
| 0.0230 | 136.40/117.20 | 135.90/116.50 | 137.90/17.95 | 100 |
| 0.0346 | 143.60/116.65 | 145.50/117.50 | 142.40/117.60 | 100 |
| 0.0461 | 148.05/116.75 | 148.20/117.45 | 147.90/117.65 | 100 |
| 0.0576 | 150.10/116.70 | 153.50/117.85 | 149.65/117.20 | 100 |
| Experience Number | Pressure p, MPa | Deformation of the Groove Bottom ∆h, mm | |
|---|---|---|---|
| 1 2 3 | 0.0115 | 3.00 3.30 3.50 | 0.098 0.113 0.118 |
| Average | 0.0115 | 3.27 | 0.109 |
| 4 5 6 | 0.0230 | 4.80 4.80 5.20 | 0.178 0.179 0.186 |
| Average | 0.0230 | 4.93 | 0.181 |
| 7 8 9 | 0.0346 | 6.70 6.80 6.50 | 0.256 0.260 0.240 |
| Average | 0.0346 | 6.67 | 0.252 |
| 10 11 12 | 0.0461 | 7.90 7.80 7.70 | 0.285 0.279 0.276 |
| Average | 0.0461 | 7.80 | 0.280 |
| 13 14 15 | 0.0576 | 8.40 8.00 8.20 | 0.304 0.325 0.296 |
| Average | 0.0576 | 8.20 | 0.308 |
| Pressure p, MPa | Arithmetic Mean Value of Density Increase ∆ρ, г/см3 | Experience Error δi | (δi)2 | Arithmetic Mean (Error of All Measurements) m | The Error of Each Experiment σ | True Value of Density Increase * ∆ρист., г/см3 | The Coefficient of Variation v, % | Error in the Experiment ∆, % |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.0115 | 0.109 | 0.01167 0.00333 0.00833 | 0.000140 0.000010 0.000070 | 0.0061 | 0.0105 | 0.1151 0.1029 | 9.63 | 4.89 |
| 0.0230 | 0.181 | 0.00300 0.00100 0.00400 | 0.000009 0.000001 0.000016 | 0.0021 | 0.0036 | 0.1801 0.1759 | 2.02 | 1.18 |
| 0.0346 | 0.252 | 0.00200 0.01300 0.01600 | 0.000004 0.000169 0.000256 | 0.0081 | 0.014 | 0.2501 0.2339 | 5.78 | 3.35 |
| 0.0461 | 0.280 | 0.00500 0.00100 0.00400 | 0.000025 0.000001 0.000016 | 0.0027 | 0.0046 | 0.2827 0.2773 | 1.64 | 0.96 |
| 0.0576 | 0.308 | 0.00400 0.01700 0.01200 | 0.000016 0.000289 0.000144 | 0.0087 | 0.0150 | 0.3167 0.2993 | 4.87 | 2.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarsenov, A.; Kubasheva, Z.; Ibrayev, A.; Sugirbay, A. Theoretical Substantiation of the Dependence of Spring Deformation of an Improved Opener. AgriEngineering 2024, 6, 1450-1478. https://doi.org/10.3390/agriengineering6020083
Sarsenov A, Kubasheva Z, Ibrayev A, Sugirbay A. Theoretical Substantiation of the Dependence of Spring Deformation of an Improved Opener. AgriEngineering. 2024; 6(2):1450-1478. https://doi.org/10.3390/agriengineering6020083
Chicago/Turabian StyleSarsenov, Amangeldy, Zhanna Kubasheva, Adil Ibrayev, and Adilet Sugirbay. 2024. "Theoretical Substantiation of the Dependence of Spring Deformation of an Improved Opener" AgriEngineering 6, no. 2: 1450-1478. https://doi.org/10.3390/agriengineering6020083
APA StyleSarsenov, A., Kubasheva, Z., Ibrayev, A., & Sugirbay, A. (2024). Theoretical Substantiation of the Dependence of Spring Deformation of an Improved Opener. AgriEngineering, 6(2), 1450-1478. https://doi.org/10.3390/agriengineering6020083







