Abstract
Including the correct combination of factors for the application technology of pesticides can improve their distribution on their targets. The aim of this work was to use multivariate analysis to study the effect size and the order of influence of three factors that interfere with pesticide application technology in corn crops. A 2 × 2 × 3 factorial experiment was conducted with two droplet size classes (fine and coarse), two application rates (80 and 150 L ha−1), and the presence of adjuvants (mineral oil one and two, and no adjuvant). A knapsack boom sprayer was used for the applications. Droplet deposition on the corn leaves was evaluated by detecting a tracer added to the spray via spectrophotometry and the droplet spectrum by analyzing water-sensitive papers. Univariate and multivariate statistical analyses were performed to integrate the variables analyzed. Droplet size has proven to be the most important factor in spraying planning, and the second factor is the application rate. With the association between fine droplets and higher application rates, a better performance was obtained in coverage, droplet density, and droplet deposition.
1. Introduction
Among application technologies for crop protection products, the use of adjuvants, the correct selection of droplet size, and consequently operating pressure and nozzle type, as well as the definition of the application rate, can impact the deposition of the spray liquid on the target and thus optimize the control of pests and diseases. In general, depending on the spraying conditions and crops, application rates vary from very high (>1000 L ha−1) to ultra-low (<50 L ha−1) volume [1]. Within this range, studies have shown increased spray deposition with increased [2] or decreased [3] application rates for perennial plants. In annual plants, different results in deposition and control efficacy have also been reported at different application rates and droplet sizes [4,5,6].
The use of adjuvants can help improve the quality of application through preparing and maintaining the physical stability of the spray liquid over time and improving the performance of treatments [7]. However, the incorrect use of adjuvants can be detrimental to the deposition of the active ingredient on plants because they can alter the physical-chemical properties of the solution. Furthermore, with the addition of adjuvants to the tank mixture, care must be taken with the application rate, because if these two factors are not perfectly combined, the spray retention on the leaves can be decreased, and consequently, increase runoff to the soil [8].
Currently, the required deposition of the pesticide throughout the plant profile is related to the combination of several factors, such as plant architecture, planting density, droplet size produced by different types of spray tips, application rate, working speed, working pressure, wind speed, and type of equipment [9,10,11,12,13], with the relationship between the application rate, spray tip type, and solution quality being key factors [14]. However, due to numerous results in the different crops, it has been challenging to define a priority among these factors for the proper planning of the application of crop protection products.
The product used is often considered more important than other factors [15]. However, even when applying a highly effective molecule, the application technology is a limiting factor for pest control to be adequate without detriment to efficiency.
Many studies have highlighted the importance of droplet size, application rate, and adjuvant use but did not weigh them at the time of planning through multivariate analysis. Thus, this work aims to study the effect size and the order of influence of the droplet size class, the application rate, and the adjuvant use on the quality of the ground application of pesticides on the corn crop.
2. Materials and Methods
The corn crop trials were conducted on the Eldorado farm (Municipality of Uberlândia, Minas Gerais, Brazil). The corn field was planted with hybrid DKB 335 Vt Pro 3, with a density of 64,000 plants ha−1 and rows spaced at 0.5 m with 3.2 plants per meter.
To study the most influential factors on the spray deposition on targets, this study followed the methodology used by Palma et al. [16], using a completely randomized design with four replications in a 2 × 2 × 3 factorial model, with two droplet classes (fine and coarse), two application rates (80 and 150 L ha−1), and three mixture compositions (two treatments with different adjuvant and one without). To facilitate the identification of the treatments in the graphs, each replication was associated with the letters a, b, c, and d (Table 1). The adjuvants used in the trials were two mineral oils: aliphatic hydrocarbon adjuvant 428 g L−1—Nimbus® (Syngenta, São Paulo, Brazil), and aliphatic hydrocarbon adjuvant 756 g L−1—Assist® (Basf, São Paulo, Brazil). The concentrations/doses of the adjuvants recommended in the label of 0.5 mL per 100 L of water for Nimbus® and 1 L ha−1 for Assist® were adopted. The use of these adjuvants is intended to improve the spray coverage and droplet adhesion to the leaves.

Table 1.
Description of treatments employed.
The applications were made in the vegetative phenological stage (stage 16 on the BBCH code) [17], 38 days after sowing (DAS), using a CO2 pressurized knapsack sprayer with a 2 m boom and 4 tips (Figure 1). Teejet’s XR11002 and AIXR 11002 air-induction flat spray tips (Glendale Heights, IL, USA) were used to generate the fine (volume median diameter between 106 and 235 µm) and coarse (volume median diameter between 341 and 403 µm) droplet class, according to the ASABE S572.3 standard [18]. The working pressure was 200 kPa and the work speed was adjusted according to the required droplet size and application rate (1.4 m s−1 for 150 L ha−1 and 2.8 m s−1 for 80 L ha−1). The nozzle height above the spray target was 0.5 m.

Figure 1.
Pressurized knapsack sprayer used for treatment applications.
The study used 48 plots. Each repetition used a 3 × 4 m plot, totaling 576 m2 of experimental area. The central area of 2 × 3 m of each plot was used for sampling.
The weather conditions were monitored using a thermo-hygrometer anemometer (model 4000, Kestrel, Boothwyn, PA, USA), keeping within the parameters recommended for applications of plant protection products: a temperature below 30 °C, relative humidity above 55%, and wind speed between 0.8 and 2.8 m s−1.
After application, two leaves were collected as a sample from each third of the plant profile (upper, middle, and lower) to study the spray deposition on the different positions of the corn crop (Figure 2).
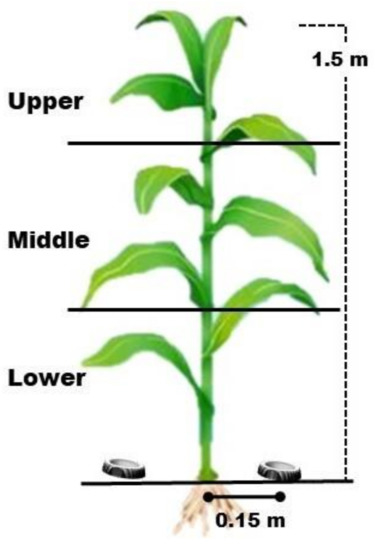
Figure 2.
Sampling scheme on corn crop.
Two Petri dishes were placed below the foliage area approximately 15 cm from the stem to evaluate the runoff to the soil. The samples were placed in a thermally insulating box for transport to the laboratory to avoid sun exposure and prevent tracer degradation.
The tracer “Brilliant Blue (internationally listed by the “Food, Drug & Cosmetic” as FD&C Blue n.1) was added to the spray mixture at a dose of 400 g ha−1” [16]. A spectrophotometer (model SP-22, Biospectro, Curitiba, Brazil) was set to a wavelength of 630 nm to detect the tracer by absorbance. We employed the methodology of Gitirana Neto et al. [10] for tracer extraction in leaf and Petri dish samples. Mechanical shaking of the samples was achieved using a pendular shaking table (model TE240/I, Tecnal, Piracicaba, Brazil) at 21 rad s−1 for 2 min for each sample. The leaf areas were measured with a leaf area meter (L1-3100, Li-Cor, Lincoln, NE, USA).
The droplet spectrum was analyzed and the volume median diameter (VMD), percentage of covered surface, relative span factor (RA), and droplet density were evaluated. For this purpose, one water-sensitive paper (76 × 26 mm) (Syngenta, Basel, Switzerland) was stapled to the leaves’ adaxial part at the leaf sampling heights in each third (upper, middle, and lower) of the plant canopy prior to application (Figure 1). After application, the papers were collected, digitized at 2500 dpi, and analyzed using DropScope v 2015 software (2016.1124.1). This software is specific to water-sensitive paper analysis [19] and takes into account the spreading factor of the paper used. It has an automated routine to calculate the droplet spectrum.
The relative span factor is a parameter calculated as (Dv0.9 − Dv0.1)/Dv0.5 with Dv0.9, Dv0.5 (or VMD) and Dv0.1 being the droplet diameter such that 90%, 50% and 10%, respectively, of the volume of the sprayed liquid is constituted of droplets of a smaller size.
Once the deposition and droplet spectrum data were obtained, statistical analyses were performed using univariate and multivariate statistical techniques to integrate all the variables analyzed [20]. We started by determining the existence of discrepant data with the Mahalanobis distance calculation method (D2). Next, the degree to which the variables are associated with each other was assessed using Pearson’s linear correlation matrix [21,22]. Multivariate normality was also tested for skewness and kurtosis using Mardia’s test. Next, Bartlett’s assumptions of sphericity and the Kaiser-Meyer-Olkin (KMO) measure of sample adequacy were tested.
Univariate analysis of variance (ANOVA) was performed to determine the effects of the factors (droplet size, application rate and mixture composition) on each variable. To determine the magnitude of the effect, the eta square index (η2) was calculated, including whenever it is significant for factorial experiments [23].
Effect size is defined as the estimate of the difference between means as a function of a null hypothesis [24,25]. It is employed to determine whether the effects of specific treatments have an important magnitude, and shows statistical differences [26,27,28]. Therefore, its estimation and interpretation could be more important than determining the desired variability [29]. Furthermore, effect size is considered more suitable than the p-value because it does not depend on the sample size [24].
Furthermore, based on the ANOVA results, response variables with no significant effect were determined to be of minimal or no importance, and were removed from the following analyses.
Next, the similarities between the experimental units were determined using the Euclidean distance method, and Ward’s method was used for hierarchical clustering [16]. The statistical difference between groups was verified by subjecting the clusters to the F-test and then to the Tukey mean-difference test when the number of groups was greater than two. After that, the main characteristics in the cluster were analyzed and the factor that predominates in the cluster (droplet size, application rate or mixture composition) was considered the factor with the most significant influence on the spray deposition.
Next, the association between the groups formed and the variables were studied using principal component analysis (PCA). The components were chosen following the criteria proposed by Kaiser [30], in which “the number of components chosen is the one whose eigenvalue is greater than one and which explains up to 70% of the accumulated variance of the data”.
The relationships of the variables and the groups were displayed on biplot graphs, where each treatment/cluster is placed on the x and y axes corresponding to the variables with which they have the most significant influence. Each group formed was considered a new population, and to determine the second most influential factor, the analyses were repeated within each cluster. All statistical analyses were performed using R v 4.0.2 software [31] with a significant level of p ≤ 0.05 when necessary.
3. Results and Discussion
3.1. Discrepant Data Analysis and Multivariate Analysis Assumptions
All plots were used in the analyses because no discrepant values were detected with the Mahalanobis distance test (D2). Multivariate normality was also determined (p-value asymmetry = 0.0662; kurtosis = 0.0550).
Correlation between studied variables was proven (X2 = 500.07; p-value < 0.001). The sample adequacy measure was determined to be adequate, with a KMO coefficient of 0.62.
3.2. Univariate Analysis of Variance and Effect Size (η2)
A comparative scale with the results of other studies using effect size estimates can be used when there is no accepted scale [32]. However, no studies were found that referred to any scale regarding research in the area of application technology for crop protection products.
Although there is no scale for the valuation of the eta-squared (η2), Cohen’s scale is used as a reference [33], which proposes a small or low effect for a value of η2 = 0.0099, a medium effect for η2 = 0.0588, and a large effect for η2 = 0.1379.
Even effect size can be analyzed on response variables with no statistical difference [34]. Since variables in this condition do not contribute to determining the priority of factors over response variables, they could be eliminated from the analyses [16]. In this study, variables that showed these conditions were deposition in the upper and middle part of the plants, and relative span factor in the middle and lower part of the plants (Table 2).

Table 2.
Effect size (eta square—η2) of the factors droplet class, application rate, and use of adjuvants on the variables of droplet deposition and droplet spectrum in the three-thirds of the corn plants.
Only the droplet density variable showed dependence (p < 0.05) between droplet class and application rate in the middle and lower third, with an η2 estimate of 0.05 for both cases, which is considered low (Table 2). Plots with high application rate and fine droplet class reached a higher quantity of droplets per cm2,130 at the middle and 96 at the lower third of the corn plants (Tables S2 and S3).
All remaining variables showed a difference between means only for factors as main effects. The VMD showed a high effect size estimate, which was expected since it aimed to contrast two droplet classes. The difference between the measured VMD values and the values from the droplet class (ASABE standard [18]) is probably due to the difference from the used methods. In this paper, an indirect method was used (water-sensitive paper), which differs from the direct methods (e.g., laser diffraction).
Density was a direct function of droplet size in the upper (0.36), middle (0.31), and lower (0.27) thirds. This observation can be attributed to the ease with which the fine droplets can penetrate the lower parts of the plant canopy. The droplet density for the fine and coarse classes differed by 3.9 times (115 and 29 drops cm−2, in average respectively).
Coverage was a function of application rate with high effect size estimates in the upper (0.33), middle (0.40), and lower (0.20) thirds (Table 2). Variation in coverage due to application rate has also been reported by Ferguson et al. [35] in evaluations in oats. For coverage and droplet density, differences were observed in the plots to the treatments applied with fine droplets at the upper (7.86%), middle (4.91%), and lower (4.0%) thirds of the plants (Table S1, Table S2, Table S3, respectively), but not to a specific treatment. This behavior may be due to the effect size estimates for the evaluated factors being between medium and high.
Spray deposition, depending on the combination of the other parameters involved in the application technology, varied with the application rate or the tip used [4]. In this study, no factor influenced the deposition in the upper and middle third, so the estimation of these effects was not analyzed. In the lower third, deposition varied as a function of droplet class with a medium effect size (0.10). With coarse droplets, greater deposition was achieved in the lower third (0.16 µg cm−2); however, runoff to the soil was also droplet class dependent, but with a low effect size (0.1). Runoff to the soil can also be higher with a higher application rate (4.08 µg cm−2) when compared to the lower application rate (2.89 µg cm−2) (Table S4). The Petri dishes collected part of the direct spray plus the runoff (part of the droplets that were deposited on the leaves went to the soil).
In the upper third, the relative span factor differed as a function of the application rate with a high effect size (0.14). A higher application rate could result in a less technical application, characterized by a higher relative span factor (0.68) when compared to the lower application rate (0.55) (Table S1). However, these results cannot be considered as a determinant because droplet size uniformity (relative span factor) is more related to the different droplet sizes generated by the same spray tip [36]. The use of adjuvants had no effect.
In corn applications, there was a decreasing gradient in deposition between the thirds going up the plants, regardless of the significance of the treatments. A similar effect was reported by Machado and Reynaldo [36] when evaluating the differences between aerial and ground applications. This difference can be mitigated depending on the equipment and technology used [37].
3.3. Cluster Analysis
The dendrogram analysis (Figure 3) is the simplest way to present the complex relationships between the elements. The groupings by droplet class agreed with the results obtained in the previous analyses, where this factor had the largest effect size when it was significant. “A very important prerequisite for a good plant protection is optimally adjusted technical spraying factors, with an optimal droplet size distribution, which is the most important” [38].
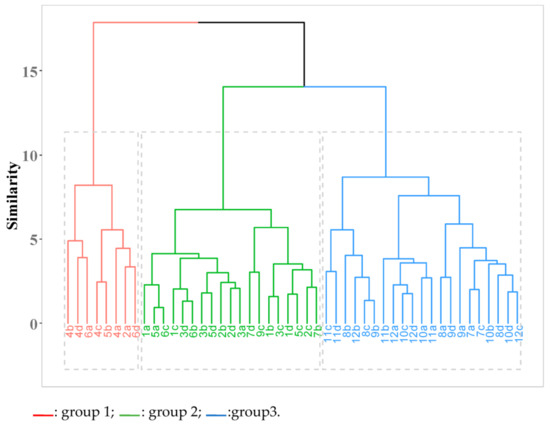
Figure 3.
Dendrogram of the cluster analysis of the plots as a function of droplet class for spray application on corn crop.
Despite the plots being separated into three groups, groups 1 and 2 corresponded to the plots applied with mainly fine-class droplets. The separate plots (group 1) mostly correspond to the treatments with adjuvant use; however, since the adjuvant factor did not present statistical significance in the previous analysis, only the fine and coarse droplet groups are considered.
3.4. Principal Component Analysis (PCA)
This analysis allowed us to relate the plots, treatments, and variables in an exploratory way [39,40]. The droplet characterization variables were clustered in component one and the deposition and runoff to the soil variables were clustered in the other components. Four components were required to achieve the given criteria (explains at least 70% of the data variance) due to the smaller number of variables within each analysis (Figure 4).
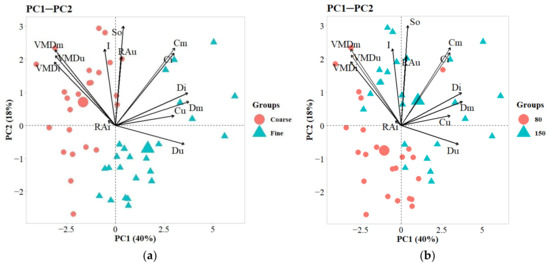
Figure 4.
Biplot graph containing principal components one and two, and the distribution of treatments and variables in the plane grouped by droplet class (a) and application rate (b). So: solution runoff to the soil. VMD: volume median diameter; RA: relative span factor; C: coverage area; D: droplet density in the thirds u: upper; m: middle i: lower.
In the biplot graphs (Figure 4), the variables and treatments had similar behavior, being polarized for component one (horizontal axis), and were more dispersed for component two (vertical axis).
When analyzing the components and treatments grouped according to application rate, patterns could be observed (Figure 4b). The fine droplet application had better coverage, and better droplet density variables. “Coverage of treated area is the main goal of whole plant protection process, and the main task of technical spraying factors is to increase this property” [41].
Variables were discriminated and arranged into components according to the correlation between them. In turn, the group of variables that contributed the most to each component was determined. Low or non-significant correlations were observed between deposition variables and percent coverage, density, relative span factor, and VMD, and these were thus arranged into separate components (Table S5). All variables presented high contributions and high and significant correlations with at least one component, indicating that each was important for explaining the variance and characterizing the quality of the application of pesticides.
Separately analyzing the plots applied with fine drops and those applied with thick drops, it was found that the higher application rate provided greater coverage and droplet density (Figure 5). The 90° angles between the upper third and the middle and lower thirds in coverage and droplet density demonstrates the non-correlation between each group. Therefore, the results for each group must be inferred in isolation.
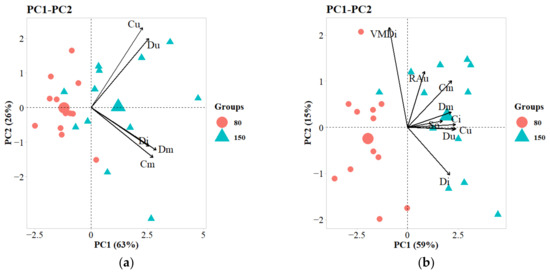
Figure 5.
Biplot graph of principal components one and two with separate plots according to application rate on the corn crop. (a): Fine droplet class. (b): Coarse droplet class. VMD: volume median diameter; RA: relative span factor; C: coverage area; D: droplet density in the thirds u: upper; m: middle i: lower.
The limitation of this study is that in practical pesticide applications, farmers use sprayers different from the knapsack sprayer used in this research. Although the spray nozzles and the application rate may be the same as those used in the study, other characteristics may be different, such as travel speed and boom stability. Regardless, the results in the field are not expected to be very different from those found in this work.
4. Conclusions
The droplet class used for application, and consequently the nozzle type, was the most important factor in planning a spray application. The second factor is the application rate.
Effect size of droplet class was higher in deposition, the volume median diameter, and droplet density. The effect for application rate was more predominate in coverage area and runoff to the soil.
Using adjuvants such as mineral oils, linked with a fine droplet class, resulted in greater droplet loss to the soil. However, for application with coarse droplets, adding adjuvants to the spray helped in the deposition and adhesion of droplets on the leaves. With the association of fine droplets and higher application rates (150 L ha−1), better results were obtained for the percentage of covered surface area, droplet density, and overall droplet deposition.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agriengineering5020051/s1, Table S1: Means of volume median diameter, relative span factor, coverage area and droplet density at the upper third of corn plants; Table S2: Means of volume median diameter, relative span factor, coverage area and droplet density at the middle third of corn plants; Table S3: Means of volume median diameter, relative span factor, coverage area and droplet density at the lower third of corn plants; Table S4: Means of runoff to the soil; Table S5: Correlation coefficients and statistical significance in correlations between variables.
Author Contributions
Conceptualization, R.P.P. and J.P.A.R.d.C.; methodology, R.P.P.; formal analysis, R.P.P. and J.P.A.R.d.C.; investigation, R.P.P. and J.P.A.R.d.C.; resources, J.P.A.R.d.C.; data curation, R.P.P.; writing—original draft preparation, R.P.P.; writing—review and editing, J.P.A.R.d.C.; visualization, R.P.P. and J.P.A.R.d.C.; supervision, J.P.A.R.d.C.; project administration, J.P.A.R.d.C.; funding acquisition, J.P.A.R.d.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded partially by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001, and Conselho Nacional de Desenvolvimento Científico e Tecnológico—Brasil (CNPq)—Finance Code 311371/2021-3.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Minguela, J.V.; Cunha, J.P.A.R. Manual de Aplicação de Produtos Fitossanitários, 1st ed.; Aprenda Fácil: Viçosa, MG, Brasil, 2017. [Google Scholar]
- Souza Júnior, J.M.; Ruas, R.A.A.; Duarte, L.O.; Faria, V.R.; Carvalho Filho, A.; Santos Júnior, C.R. Influência da densidade foliar na distribuição de calda no dossel do cafeeiro (Coffea arabica L.). Coffee Sci. 2017, 12, 216–222. [Google Scholar] [CrossRef]
- Alves, T.C.; Cunha, J.A.R.; Alves, G.S.; Silva, S.M.; Lemes, E.M. Canopy volume and application rate interaction on spray deposition for different phenological stages of coffee crop. Coffee Sci. 2020, 15, e151777. [Google Scholar] [CrossRef]
- Baio, F.H.R.; Silva, E.E.; Vrech, M.A.; Souza, F.H.Q.; Zanin, A.R.; Teodoro, P.E. Vegetation indices to estimate spray application rates of crop protection products in corn. Agron. J. 2018, 110, 1254–1259. [Google Scholar] [CrossRef]
- Souza, F.H.Q.; Martins, P.H.A.; Dresch Martins, T.H.; Teodoro, P.E.; Baio, F.H.R. The use of vegetation index via remote sensing allows estimation of soybean application rate. Remote Sens. Appl. Soc. Environ. 2020, 17, 100279. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Song, X.P.; Liang, Y.J.; Qin, Z.Q.; Zhang, B.Q.; Wei, J.J.; Li, Y.R.; Wu, J.M. Effects of spray parameters of drone on the droplet deposition in sugarcane canopy. Sugar Tech. 2020, 22, 583–588. [Google Scholar] [CrossRef]
- Castro, M.J.L.; Ojeda, C.; Cirelli, A.F. Advances in surfactants for agrochemicals. Environ. Chem. Lett. 2014, 12, 85–95. [Google Scholar] [CrossRef]
- Ferreira, M.C.; Alandia, R.A.; Carvalho, G.F.G.; Baggio, M.V. Determinação de área foliar e retenção de líquido por folhas de café em pulverização a alto volume. Nucleus 2010, 7, 277–283. [Google Scholar] [CrossRef]
- Petrovic, D.; Banaj, Đ.; Banaj, A.; Željko, B.; Vidaković, I.; Tadić, V. The Impact of conventional and sensor spraying on drift and deposit in cherry orchard. Teh. Vjesn. 2019, 26, 1211–1217. [Google Scholar] [CrossRef]
- Gitirana Neto, J.; Cunha, J.P.A.R.; Marques, R.S.; Lasmar, O.; Borges, E.B. Deposição de calda promovida por pulverizadores empregados na cafeicultura de montanha. Coffee Sci. 2016, 11, 267–275. [Google Scholar]
- Tang, Y.; Hou, C.J.; Luo, S.M.; Lin, J.T.; Yang, Z.; Huang, W.F. Effects of operation height and tree shape on droplet deposition in citrus trees using an unmanned aerial vehicle. Comput. Electron. Agric. 2018, 148, 1–7. [Google Scholar] [CrossRef]
- Martins, P.H.A.; Baio, F.H.R.; Martins, T.H.D.; Fontoura, J.V.P.F.; Teodoro, L.P.R.; Silva Junior, C.A.; Teodoro, P.E. Estimating spray application rates in cotton using multispectral vegetation indices obtained using an unmanned aerial vehicle. Crop Prot. 2021, 140, 105407. [Google Scholar] [CrossRef]
- Penney, A.J.; Kandel, Y.R.; Viggers, J.N.; Robertson, A.E.; Mueller, D.S. Comparison of aerial and ground sprayer fungicide application technologies on canopy coverage, disease severity, lodging, and yield of corn. Crop Prot. 2021, 139, 105393. [Google Scholar] [CrossRef]
- Cunha, J.P.A.R.; França, J.A.L.; Alvarenga, C.B.; Alves, G.S.; Antuniassi, U.R. Performance of air induction spray nozzle models under different operating conditions. Eng. Agrí. 2020, 40, 711–718. [Google Scholar] [CrossRef]
- Cunha, J.P.A.R.; Peres, T.C.M. Influência de pontas de pulverização e adjuvante no controle químico da ferrugem asiática da soja. Acta Sci. Agron. 2010, 32, 597–602. [Google Scholar] [CrossRef]
- Palma, R.P.; Cunha, J.P.A.R.D.; Guimarães, E.C.; De Santana, D.G.; de Assunção, H.H.T. Multivariate analysis applied to spray deposition in ground application of phytosanitary products in coffee plants. Eng. Agríc. 2021, 41, 458–467. [Google Scholar] [CrossRef]
- Meier, U.; Bleiholder, H.; Buhr, L.; Feller, C.; Hack, H.; Heß, M.; Lancashire, P.D.; Schnock, U.; Stauß, R.; Van Den Boom, T.; et al. The BBCH system to coding the phenological growth stages of plants—History and publications. J. Cultiv. Plants 2009, 61, 41–52. [Google Scholar]
- American Society of Agricultural and Biological Engineers (ASABE). Spray Nozzle Classification by Droplet Spectra–ASABE S572.3; ASABE: St. Joseph, MI, USA, 2020. [Google Scholar]
- Nascimento, V.P.; Vitória, E.L. Spraying quality using unmanned aerial vehicle in citrus. R. Eng. Agric. 2022, 30, 214–221. [Google Scholar] [CrossRef]
- Paredes, J.A.; Cazón, L.I.; Oddino, C.; Monguillot, J.H.; Rago, A.M.; Molina, J.P.E. Efficacy of fungicides against peanut smut in Argentina. Crop Prot. 2021, 140, 105403. [Google Scholar] [CrossRef]
- Araújo, A.O.; Mendonça, L.A.R.; Lima, M.G.S.; Feitosa, J.V.; Silva, F.J.A.; Ness, R.L.L.; Frischkorn, H.; Simplício, A.A.F.; Kerntopf, M.R. Modificações nas propriedades dos solos de uma área de manejo florestal na Chapada do Araripe. R. Bras. Ciên. Solo 2013, 37, 754–762. [Google Scholar] [CrossRef]
- Oliveira Júnior, A.I.; Mendonça, L.A.R.; Fontenele, S.B.; Araújo, A.O.; de Sousa Lima Brito, M.G. Statistical multivariate analysis applied to environmental characterization of soil in semiarid region. R. Caatinga 2019, 32, 200–210. [Google Scholar] [CrossRef]
- Fritz, C.O.; Morris, P.E.; Richler, J.J. Effect size estimates: Current use, calculations, and interpretation. J. Exp. Psychol. General 2012, 141, 2–18. [Google Scholar] [CrossRef] [PubMed]
- Espirito Santo, H.; Daniel, F.B. Calcular e apresentar tamanhos do efeito em trabalhos científicos (1): As limitações do p < 0,05 na análise de diferenças de médias de dois grupos. R. Portug. Investig. Compor. Social 2015, 1, 3–16. [Google Scholar] [CrossRef]
- Sheppard, C.R.C. How large should my sample be? Some quick guides to sample size and the Power of Tests. Ma. Pollut. Bull. 1999, 38, 439–447. [Google Scholar] [CrossRef]
- Levine, T.R.; Hullett, C.R. Eta squared, partial eta squared, and misreporting of effect size in communication research. Hum. Commun. Res. 2002, 28, 612–625. [Google Scholar] [CrossRef]
- Richardson, J.T.E. Eta squared and partial eta squared as measures of effect size in educational research. Educ. Res. Rev. 2011, 6, 135–147. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Y.; Sun, J.; Shao, H. Negative interactive effects between biochar and phosphorus fertilization on phosphorus availability and plant yield in saline sodic soil. Sci. Total Environ. 2016, 568, 910–915. [Google Scholar] [CrossRef]
- Ortiz, M. Optimum sample size to detect perturbation effects: The importance of statistical power analysis—A critique. Mar. Ecol. 2002, 23, 1–9. [Google Scholar] [CrossRef]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing: Reference Index. Vienna: R Foundation for Statistical Computing, 2010. Available online: https://www.r-project.org (accessed on 30 October 2020).
- Espirito Santo, H.M.A.; Daniel, F. Calcular e apresentar tamanhos do efeito em trabalhos científicos (3): Guia para reportar os tamanhos do efeito para análises de regressão e ANOVAs. R. Portug. Investig. Compor. Social 2018, 4, 43–60. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Erlbaum Associates: Hillsdale, NJ, USA, 1988; p. 567. [Google Scholar]
- Trigo Sánchez, M.E.; Martínez Cervantes, R.J. Generalized eta squared for multiple comparisons on between-groups designs. Psicothema 2016, 28, 340–345. [Google Scholar] [CrossRef]
- Ferguson, J.C.; Chechetto, R.G.; Hewitt, A.J.; Chauhan, B.S.; Adkins, S.W.; Kruger, G.R.; O’donnell, C.C. Assessing the deposition and canopy penetration of nozzles with different spray qualities in an oat (Avena sativa L.) canopy. Crop Prot. 2016, 81, 14–19. [Google Scholar] [CrossRef]
- Machado, T.; Reynaldo, É.R. Comparação do uso de aplicação aérea e terrestre na qualidade de deposição de produto na cultura da soja. Encic. Biosfera 2019, 16, 504–514. [Google Scholar] [CrossRef]
- Hoffmann, L.L.; Roehrig, R.; Boller, W.; Forcelini, C.A. Deposition and coverage of soybean leaf surfaces by sprays applied using different assisted boom sprayer systems. Eng. Agríc. 2019, 39, 198–207. [Google Scholar] [CrossRef]
- Tomantschger, K.; Petrović, D.V.; Radojević, R.L.; Tadić, V. Mathematical method for droplet size distribution of agricultural nozzles. Teh. Vjesn. 2021, 28, 1749–1754. [Google Scholar] [CrossRef]
- Araújo, R.S.; Bernardes, R.C.; Martins, G.F. A mixture containing the herbicides Mesotrione and Atrazine imposes toxicological risks on workers of Partamona helleri. Sci. Total Environ. 2020, 763, 142980. [Google Scholar] [CrossRef]
- Castilla, N.P.; Stuart, A.M.; Makara, O.; Sathya, K.; Somany, S.; Kumar, V.; Ratna Hadi, B.A. Characterization of cropping practices, pest constraints, and yield variation in irrigated lowland rice of Cambodia. Crop Prot 2020, 135, 104906. [Google Scholar] [CrossRef]
- Tadic, V.; Marković, M.; Plaščak, I.; Stošić, M.; Lukinac-Čačić, J.; Vujcic, B. Impact of technical spraying factors on leaf area coverage in an apple orchard. Teh. Vjesn. 2014, 21, 1117–1124. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).