Next Article in Journal
Research on Biomechanical Properties of Laver (Porphyra yezoensis Ueda) for Mechanical Harvesting and Postharvest Transportation
Previous Article in Journal
Performance Assessment of Farm Machinery for Persimmon Fruit Cultivation in a Japanese Mountainous Area
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
AgriEngineering
Volume 4
Issue 1
10.3390/agriengineering4010003
agriengineering-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Automatic Classification of the Ripeness Stage of Mango Fruit Using a Machine Learning Approach

by
Denchai Worasawate
1,
Panarit Sakunasinha
2 and
Surasak Chiangga
2,*
1
Department of Electrical Engineering, Faculty of Engineering, Kasetsart University, Bangkok 10900, Thailand
2
Department of Physics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand
*
Author to whom correspondence should be addressed.
AgriEngineering 2022, 4(1), 32-47; https://doi.org/10.3390/agriengineering4010003
Submission received: 13 December 2021 / Revised: 6 January 2022 / Accepted: 6 January 2022 / Published: 13 January 2022
Browse Figures
Review Reports Versions Notes

Abstract

:
Most mango farms classify the maturity stage manually by trained workers using external indicators such as size, shape, and skin color, which can lead to human error or inconsistencies. We developed four common machine learning (ML) classifiers, the k-mean, naïve Bayes, support vector machine, and feed-forward artificial neural network (FANN), all of which were aimed at classifying the ripeness stage of mangoes at harvest. The ML classifiers were trained on biochemical data and then tested on physical and electrical data.The performance of the ML models was compared using fourfold cross validation. The FANN classifier performed the best, with a mean accuracy of 89.6% for unripe, ripe, and overripe classes, when compared to the other classifiers.

1. Introduction

The classification of mango fruit according to ripeness stage is important for successful marketing because variability in ripeness affects eating quality as well as postharvest shelf life and selling strategies [1,2,3]. Ripe mangoes have a pleasant flavor and aroma. However, they allow the development of numerous diseases [4]. Overripe mango fruit has lower or even no retail value, resulting in severe profit loss and resource waste. During ripening, the mango fruit undergoes several changes, including the conversion of starch to sugars, an increase in pH, the degradation of the cell wall, the biosynthesis of carotenoids, and the formation of fragrances [5,6,7]. In theory, any of these changes can be used as an indicator of fruit ripening. However, climate, horticultural practices, and cultivars all influence the indicator for fruit ripeness, resulting in variations in the indicator [8,9]. Some mango cultivars, such as the “Nam Dok Mai Si Tong” cultivar, lack an obvious indicator, making classification difficult.
The mango cultivar “Nam Dok Mai Si Tong” is grown widely in Thailand and is popular for consumption and is exported to Japan, Korea, Vietnam, China, and Malaysia. This cultivar has a golden yellow skin, like that of a ripe mango, even when it is still on the plant, and the flesh is fragrant, sweet, aromatic, and juicy with no fibrous tissue when ripe [10]. Most “Nam Dok Mai Si Tong” mango farms manually classify the ripeness stage using external indicators such as size, shape, and skin color as assessed by trained, experienced individuals. This may lead to inaccuracies or inconsistencies [11,12]. Studies have shown that the external indicators of mango fruit are often unreliable [13,14]. Although fruit internal indicators, such as total soluble solids (TSS) and titratable acidity (TA), are more accurate classifications than measurements of the external characteristics, measurements of these parameters are time-consuming and require the destruction of the fruit sample [15].
In recent decades, several technologies used for nondestructive assessment of the internal quality features of fruit have been developed and evaluated. These technologies include NIR spectroscopy, magnetic resonance imaging (MRI), hyperspectral imaging (HSI), and acoustic sensors [12,14,16,17,18]. However, there are some limitations to these technologies. MRI technologies are integrated with expensive equipment. HSI requires high-performance computing systems because of the vast amount of data used for image processing tasks. With acoustic techniques, it is hard to match the impedance between the sensors and the fruit sample. Compared to other technologies, handheld and portable NIR spectrometers are the most advanced in many aspects, such as miniaturization, software enhancement, and expanding the operating wavelengths into the visible range. A commercial Vis/NIR spectrometer with wavelengths ranging from 310 nm to 1100 nm was recently used to assess the soluble solid concentration, dry matter, and flesh firmness in stone fruits at harvest [19]. In general, NIR spectral data are analyzed and correlated with fruit traits using multiple linear regression (MLR) and partial least squares regression (PLS). To predict the mango maturity index, the PLS model obtained from portable NIR spectroscopy at wavelengths ranging from 1200 to 2200 nm was found superior to the MLR model [20]. Updates to NIR spectrometers and the machine learning models used for maturity prediction of various fruits have recently been reviewed [17].
Recently, there has been an interest in utilizing machine learning (ML) methods to construct models for predicting mango ripeness [21,22,23]. The ML techniques are classified into two types: unsupervised and supervised. Unsupervised ML is typically used for data visualization and clustering within the input data, whereas supervised ML is typically used for predicting a known output from a set of inputs. The k-means algorithm is an unsupervised learning approach for clustering and visualizing nonlinear relationships of data without requiring explicit knowledge of the underlying correlations between the variables [24]. Various supervised ML classifiers often used for autonomous decision making include support vector machines (SVM) [25,26], random forests (RF) [27], k-nearest neighbors (KNN) [28], and artificial neural networks [28], each of which has varied levels of model complexity.
The accuracy of supervised ML classifiers is affected by unbalanced amounts of labeled data for learning, because a lack of data for minority classes may produce biased learning classification in ML classifiers. The class imbalance is typical of many real-world data classifications [29,30,31]. Several methods have been developed to overcome these negative effects, including the synthetic minority oversampling technique (SMOTE) [32]. The SMOTE approach creates artificial minority samples by interpolating between existing minority samples and their closest minority neighbors. To improve the SMOTE method, the technique employs the Tomek links [33] method to remove noisy data.
The changes in skin color of ripe mangoes were used as the input to SVM, KNN, Gaussian naïve Bayes (GNB), and back-propagation neural network classifiers to classify mangoes according to their ripening stages with a mean accuracy of greater than 80% [34,35,36,37,38]. The changes in skin color of the cultivar used in their experiments were easily noticed by human eyes.
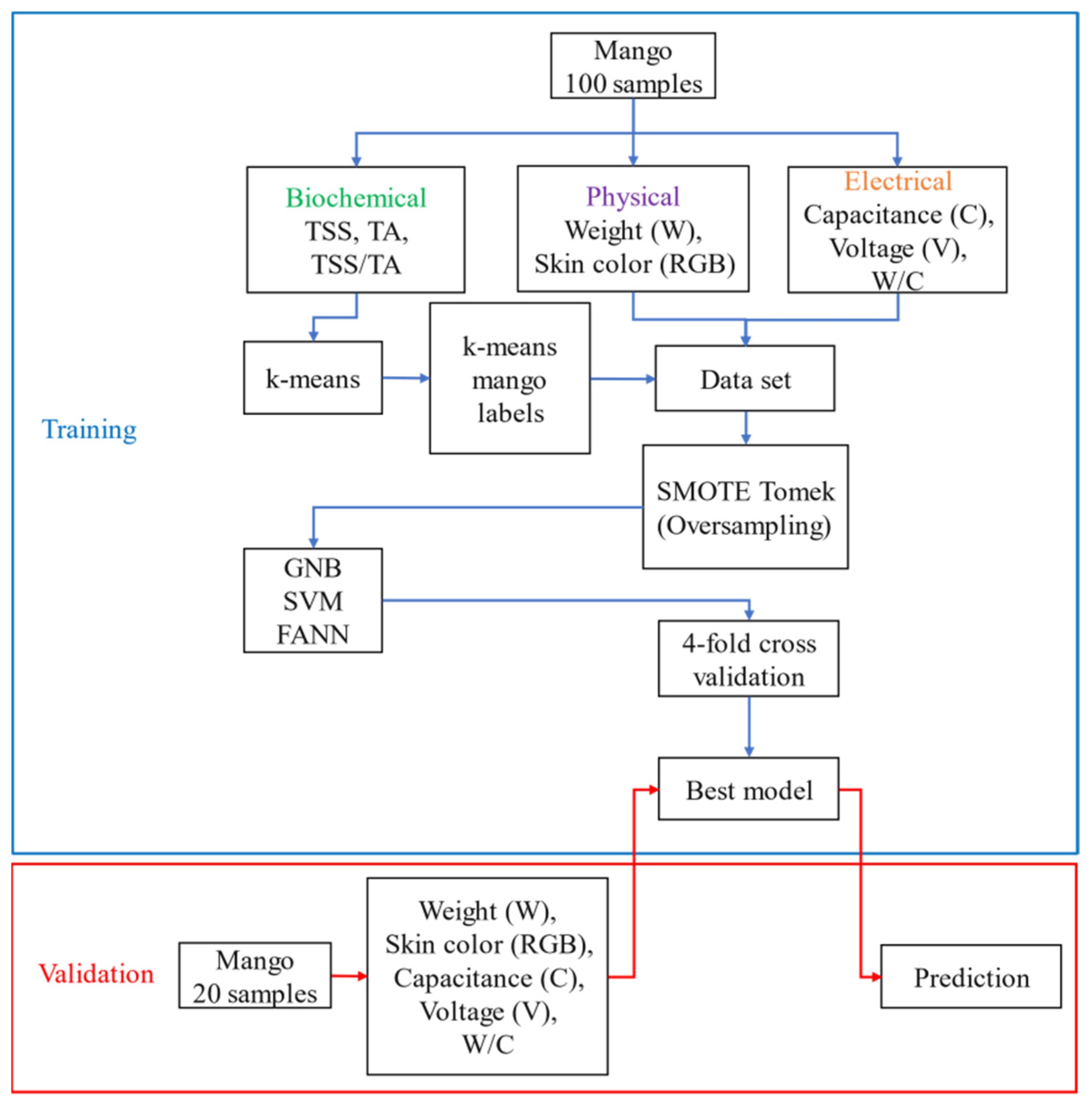
This study presents an approach to assess the ripeness stage of “Nam Dok Mai Si Tong” mango with unsupervised and supervised ML techniques. The skin color of this cultivar is yellow in all ripeness stages (unripe, ripe, and overripe stages). The objective of this study was to develop models for predicting the ripeness stage of mangoes at harvest based on chemical as well as physical (weight, skin color) and electrical (capacitance, voltage) qualities. We used well-known machine learning classifiers to predict the maturity and ripeness of fruits.

2. Materials and Methods

2.1. Mango Samples

Mangoes of the variety “Nam Dok Mai Si Tong”, at a commercial orchard in Nakorn Ratchasima province, Thailand, were tagged in November 2018, when they were approximately 5 mm in diameter. The commercial maturation stage for “Nam Dok Mai Si Tong” for export has been determined to be 85–95 days after fruit set (DAFS) [10]. From January to February 2019, the mangoes were harvested four times, at 80, 90, 100, and 110 DAFS. Mango samples were brought to a laboratory at Kasetsart University in Bangkok on the same day they were harvested. At each harvesting, we divided mango samples into two groups: one that contained twenty-five samples for evaluation of biochemical, physical, and electrical properties; and one that contained five samples for measurement of only physical and electrical qualities. The mango samples in both groups were measured on days 1, 3, 5, 7, and 9 after harvest. The biochemical examination of mango samples in one group was not carried out so that the same mangoes were tested for 9 days. A total of 120 mango fruits were used in this research.

2.2. Measurement of Properties of Mango

2.2.1. Physical Properties

The mangoes were weighed individually with an electronic balance (DH-2000, Dongguan, Guangdong, China) accurate to 0.01 g.
The CIELab color space has been proven to be better related to maturity in several fruit crops than other color spaces [39,40]. The a* value corresponds to the degree of red or green color; the –a* value is green, and the a* value is red. Specifically, a* and hue angle are two good indicators of fruit maturity in peach [41], nectarine [42], and most fruits that turn from green to red. CIELab color parameters can be derived from RGB by image processing. The skin colors at the top (near stem), center, and bottom of each fruit on both sides of the mangoes were measured in RGB color space using ColorMax sensors (EMX Industries, CM1000-7-25, Johnston Parkway Cleveland, OH, USA), and the average of RGB color values was calculated.

2.2.2. Biochemical Properties

For biochemical measurements, we selected 5 of 25 mango fruits on day 1 and 5 of 20 mango fruits on day 3 (from those that were left from the previous two days). The process was repeated, and all mangoes were completely measured on day 9.Total soluble solids (TSS) and titratable acidity (TA) were determined from the extracted mango juice using a digital refractometer (ATAGO, PAL-1, Shiba-koen, Minato-ku, Japan) and a pHmeter (HANNA, HI98127, Woonsocket, RI, USA). The extracted mango juice was manually titrated to pH 8.1 with 0.1 mol/L NaOH for TA.

2.2.3. Electrical Properties

The capacitance of each mango and the voltage across the plates of the parallel-plate capacitor sensor were measured using methods as described in previous works [43,44,45] with a handheld LCR Meter (Keysight, U1733C, Santa Rosa, CA, USA) set to a frequency of 100 kHz (Figure 1). The parallel-plate capacitor sensor was constructed to measure the capacitance of mangoes. It had two rectangular copper plates, each approximately 0.15 m long, 0.1 m wide, and 0.005 m thick, mounted on the linear guide rails to adjust the spacing between the plates.

2.3. Data

The data measured from mango attributes included 10 variables: weight, red color, green color, blue color, TSS, TA, TSS–TA ratio, capacitance, voltage, and the ratio of capacitance and weight. The biochemical data were used for the k-means method. Since the results of the k-means method revealed class imbalances, the SMOTETomek was applied to generate synthetic data for balancing and cleaning the data of classes. The balanced classes of ripeness stages and physical and electrical data were utilized to train the GNB, SVM, and FANN classifiers; the balanced classes of ripeness stages were employed as the target variables. The data from 100 mango fruits were input to the GNB, SVM, and FANN algorithms for training and for fourfold cross validation. After comparing the performance of GNB, SVM, and FANN algorithms, the best performing ML model was selected and further tested with the data from 20 mangoes.

2.4. Machine Learning Methods

2.4.1. k-Means

k-means is an unsupervised learning algorithm for clustering data objects based on their similarity. The k-means algorithm starts by choosing a number of clusters. Each cluster is identified with its centroid, which is the average of all data points in the cluster. Each data object is then assigned to its nearest centroid while minimizing the distance between objects. The centroid of each cluster is then recomputed. The distance between clusters is calculated, aiming at a minimum total sum of square errors. This procedure is repeated until no data points change the centroids.

2.4.2. Gaussian Naïve Bayes (GNB)

GNB is a probabilistic classifier that employs Bayes’ theorem for computing the conditional probability of the class that the attribute values belong to. The GNB classifier assumes independence, and the Gaussian distribution of attributes. The GNB algorithm starts by calculating the prior probability for given class labels. The likelihood probability for each attribute is then computed for each class. The posterior probability is calculated by inserting the prior and likelihood probability values into the Bayes formula. Finally, the input attribute is determined to the class with the greater probability. To avoid zero probability, we used Laplace’s rule with a smoothing parameter of 0.01.

2.4.3. Support Vector Machine (SVM)

SVM is a binary classifier that finds linear hyperplanes that maximize class separation [46]. SVM simulates decision boundaries between classes by mapping the data to a higher-dimensional space to find a separable hyperplane between classes. Because SVM is a binary classifier, several classifiers must be built and aggregated to be used for multiclass classifications. We employed the LIBSVM library [47] in Python. The polynomial kernel was used with the hyperparameters given in Table 1.

2.4.4. Feed-Forward Artificial Neural Network (FANN)

The final classification technique studied in this paper was the feed-forward artificial neural network (FANN). We implemented the FANN algorithms in Python script using the Keras package [48]. The architecture of our FANN model was one input layer, two hidden layers, and one output layer (Figure 2). The input layer had 7 variables, which were the same as those used in the GNB and SVM analysis. The first and the second hidden layers had 64 and 128 neurons, respectively. In the activation layers, the rectified linear unit (ReLU) activation function was utilized. The output layer had either two or three outputs, according to stages obtained from the k-means technique. The FANN model was trained using a back-propagation algorithm with the hyperparameters given in Table 2.

2.5. Summary of Overall Procedure

According to published literature, taste and skin color are key parameters that influence consumer acceptability and preference [49]. The total soluble solids (TSS) and titratable acidity (TA) of “Nam Dok Mai Si Tong” mangoes are strongly correlated with the ripeness stage at harvest of mangoes [10,50]. This mango has an inherent skin color that attracts consumers. As a result, we decided to classify mangoes into groups using biochemical properties (namely, TSS and TA) and to employ machine learning techniques to transform the correlation between the physical and electrical properties and the biochemical properties into a predictive model. The procedures for predicting the ripeness stage of mangoes are shown in Figure 3. The process began by separating mangoes into two groups: one for measuring physical, electrical, and biochemical properties of mangoes and one for measuring only physical and electrical properties. The k-means unsupervised learning algorithm was chosen to visualize the data distributions of the biochemical data of mangoes (TSS and TA) and to find outliers.The biochemical data were fed into the k-means algorithm, which was used to label stages for each mango. Fortunately, the k-means algorithm reported no outliers in our biochemical data. However, it disclosed a class imbalance in the number of mango samples, which is common in practice data classifications. Thus, the SMOTETomek technique was used for data oversampling. Three supervised ML techniques, namely GNB, SVM, and FANN, have already been used in literature for classification of the ripeness stage in several fruit crops. We wanted to find the most suitable ML algorithm for predicting the ripeness stage of mangoes. For this reason, we compared the performances of the GNB, SVM, and FANN classifiers using fourfold cross validation on both the unbalanced and balanced datasets of classes by considering the percent of corrected predictions. The results showed that the FANN classifier outperformed the others. We employed datasets of biochemical, physical, and electrical variables (100 data) from 100 mangoes to test the GNB, SVM, and FANN, while datasets of physical and electrical variables (100 data) from 20 mangoes were used as external datasets to validate the FANN model. The ML algorithms were implemented in Python using the scikit-learn and Keras packages.

2.6. The Optimal Number of Clusters

The elbow and silhouette methods were employed to evaluate the optimal number of clusters of ripeness stage of mango fruits [51].

2.6.1. Elbow Method

The elbow method calculates the total of squared errors of data points in a cluster and the centroids of clusters, which is known as the distortion score. The number of squared errors decreases, indicating an improvement in clustering quality. When the total of squared errors is plotted against the number of clusters, the optimal number of clusters is revealed as a significant change in slope, which is known as an elbow.

2.6.2. Silhouette Method

The silhouette method determines the proper number of clusters in a dataset by measuring cluster separation distance. The silhouette coefficient (SC) lies between −1 and 1, with negative and positive values indicating that the samples are in the wrong and correct cluster, respectively. Higher SC values indicate better quality of clustering.

2.7. Evaluation of Classifier Performance

The performance of ML classifiers was evaluated using k-fold cross validation. The process starts by choosing a number, k, and partitioning the data into k subsets: k-folds. Next, the data of one of k − 1 folds israndomly chosen for training, while that of another is used to test the classifier. The error rate of the test is then computed. This process was repeated with a different randomly selected training and testing dataset. In this study, the process was repeated 4 times, and an average error rate was computed for these 4 runs, i.e., fourfold cross validation was performed. The accuracy of the ML classifier was computed as the ratio between the sum of the true results and the sum of the true and false results, while the precision was calculated as the ratio of true outcomes to the sum of true and false outcomes.

3. Results

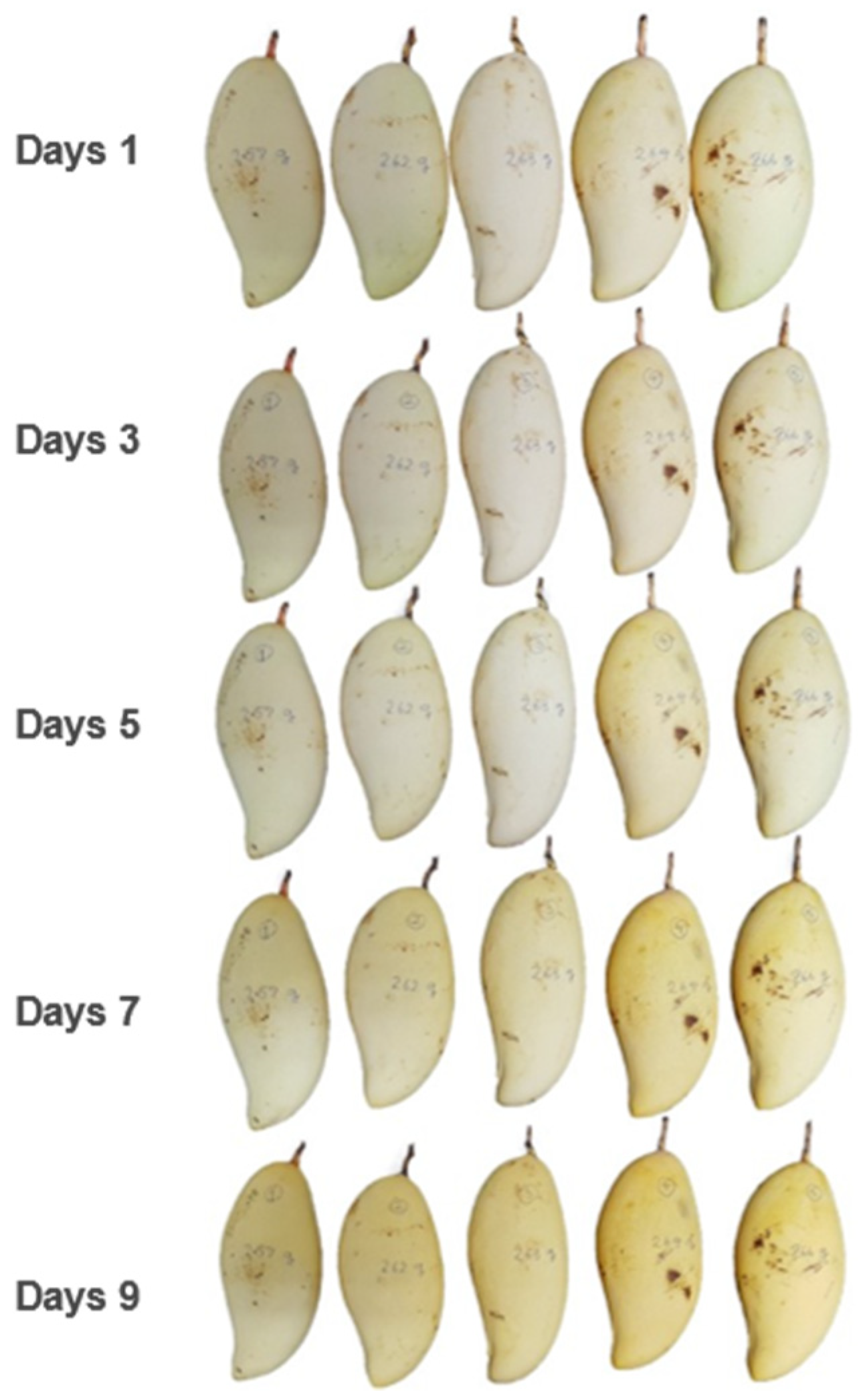
The images of the example mangoes at 80 days old are shown in Figure 4. Notice that the skin color of these mangoes was similar from day 1 to day 9 after harvest. Therefore, the color attributes used in this study (RGB) were not good indicators for classifying ripeness. We used the pandas library in Python to calculate the data collected as described in the Section 2. Table 3 shows the average and standard deviation for the original data of the titratable acidity (TA), total soluble solids (TSS), TSS/TA ratio, weight, voltage, capacitance, weight/capacitance ratio, and red (R), green (G), and blue (B) skin colors of 100 mango samples.

3.1. k-Means Clustering Results

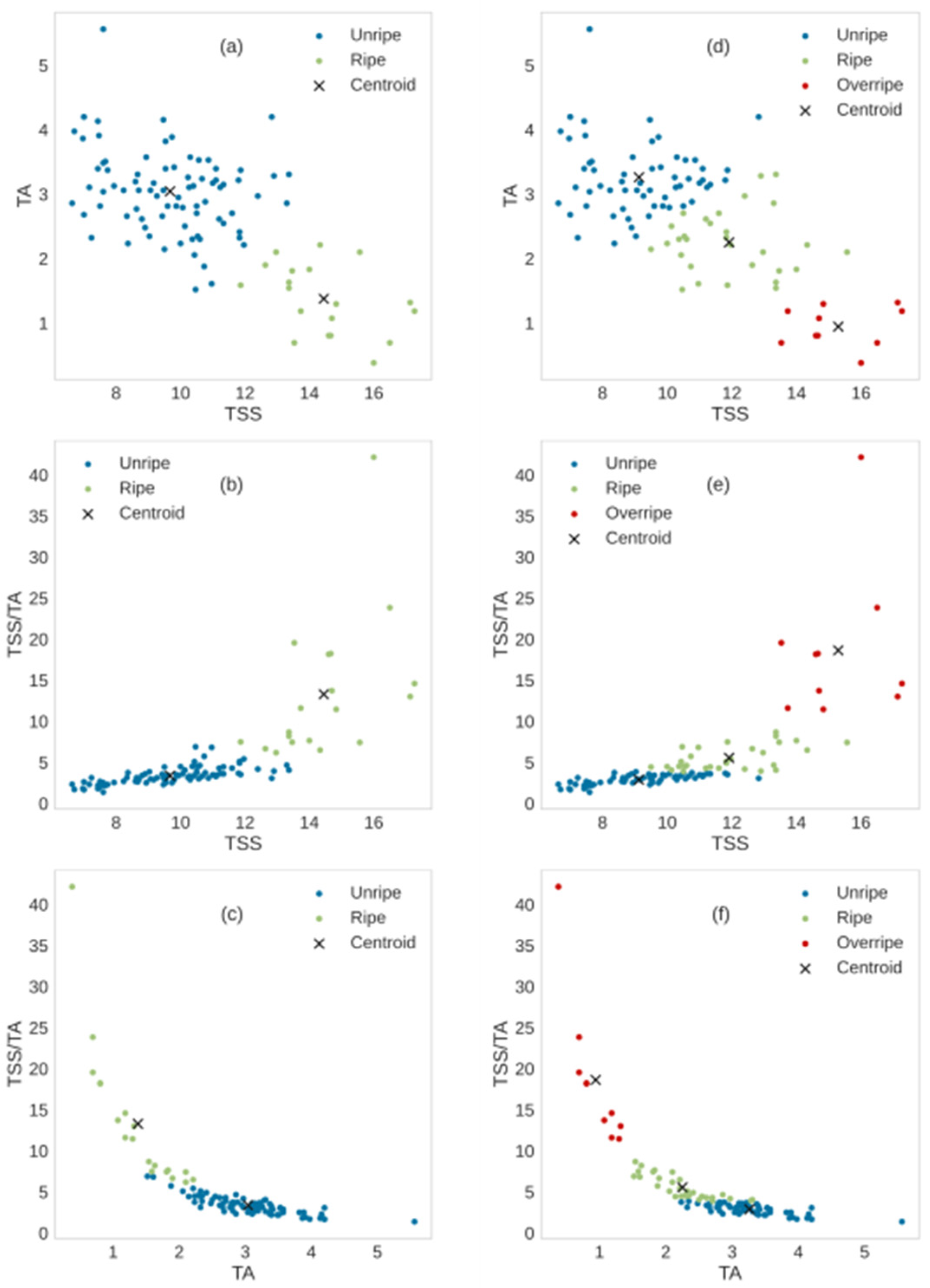
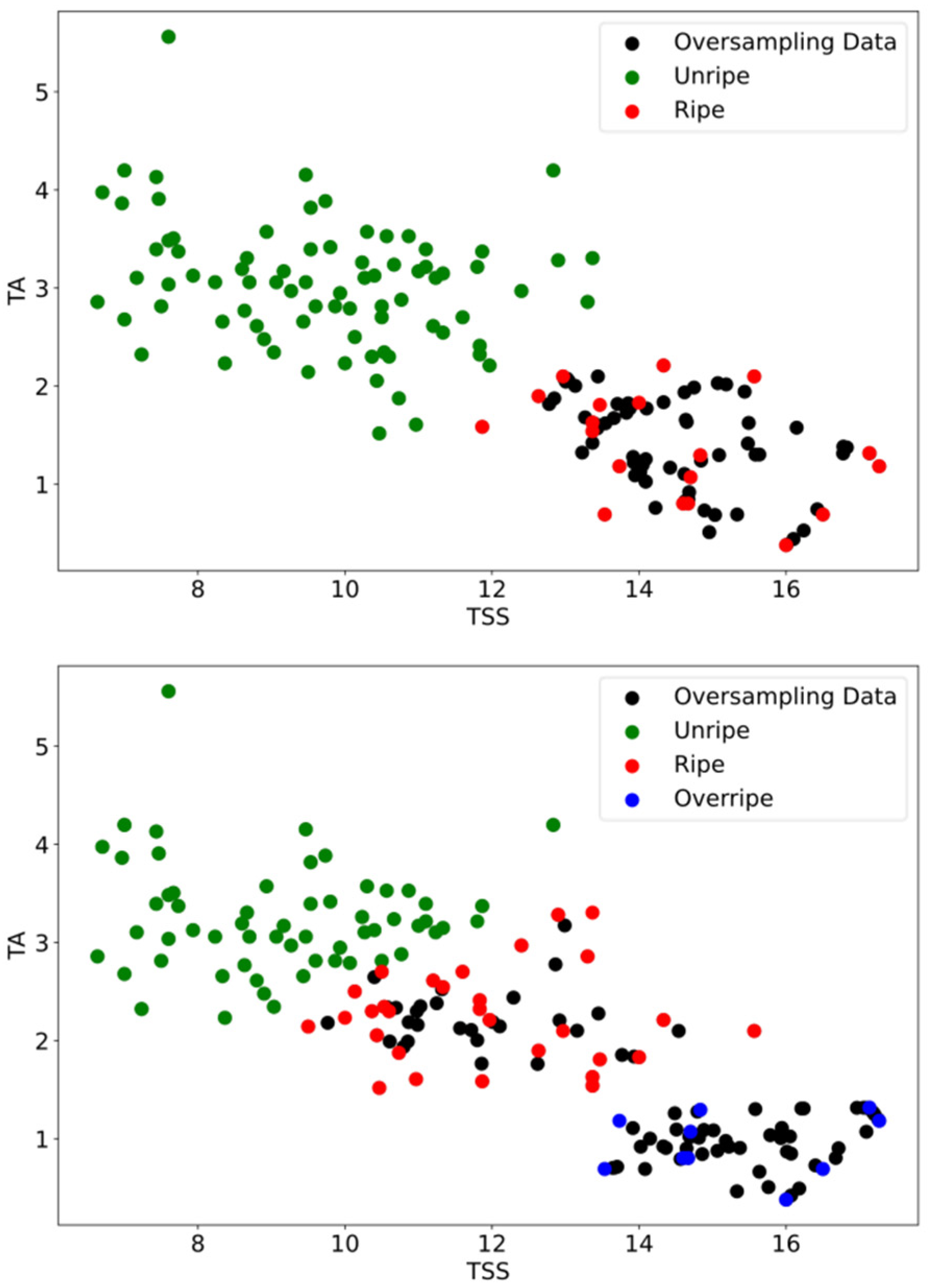
Figure 5 shows scatter plots of biochemical data of 100 mangoes using the k-means clustering with k = 2 clusters (Figure 5a–c) and k = 3 clusters (Figure 5d–f). The results from the k-means algorithm showed clear boundaries between clusters, which suggested that the k-means method using TSS, TA, and TSS/TA was adequate to separate the ripening stages of mangoes. For two-ripenessclass clustering, the distribution of data in the unripe cluster was denser than that in the ripe cluster. The numbers of mangoes in the unripe and ripe stages were 81 and 19, respectively (Table 4). For three-ripeness class clustering, the distribution of data in the unripe cluster was denser than those in the ripe and overripe clusters. The numbers of mangoes in the unripe, ripe, and overripe stages were 60, 30, and 10, respectively (Table 4). There was some overlap between mango samples within their own clusters. This indicated the similarity of the TSS and TA of mangoes. A negative relation between TSS and TA during the ripening of mangoes was shown, which is consistent with previous studies [50,52]. Mangoes in the overripe cluster showed the highest TSS, indicating more ripeness, and were sweeter than mangoes in the unripe and ripe stages.

3.2. The Optimal Number of Clusters

3.2.1. Elbow Method

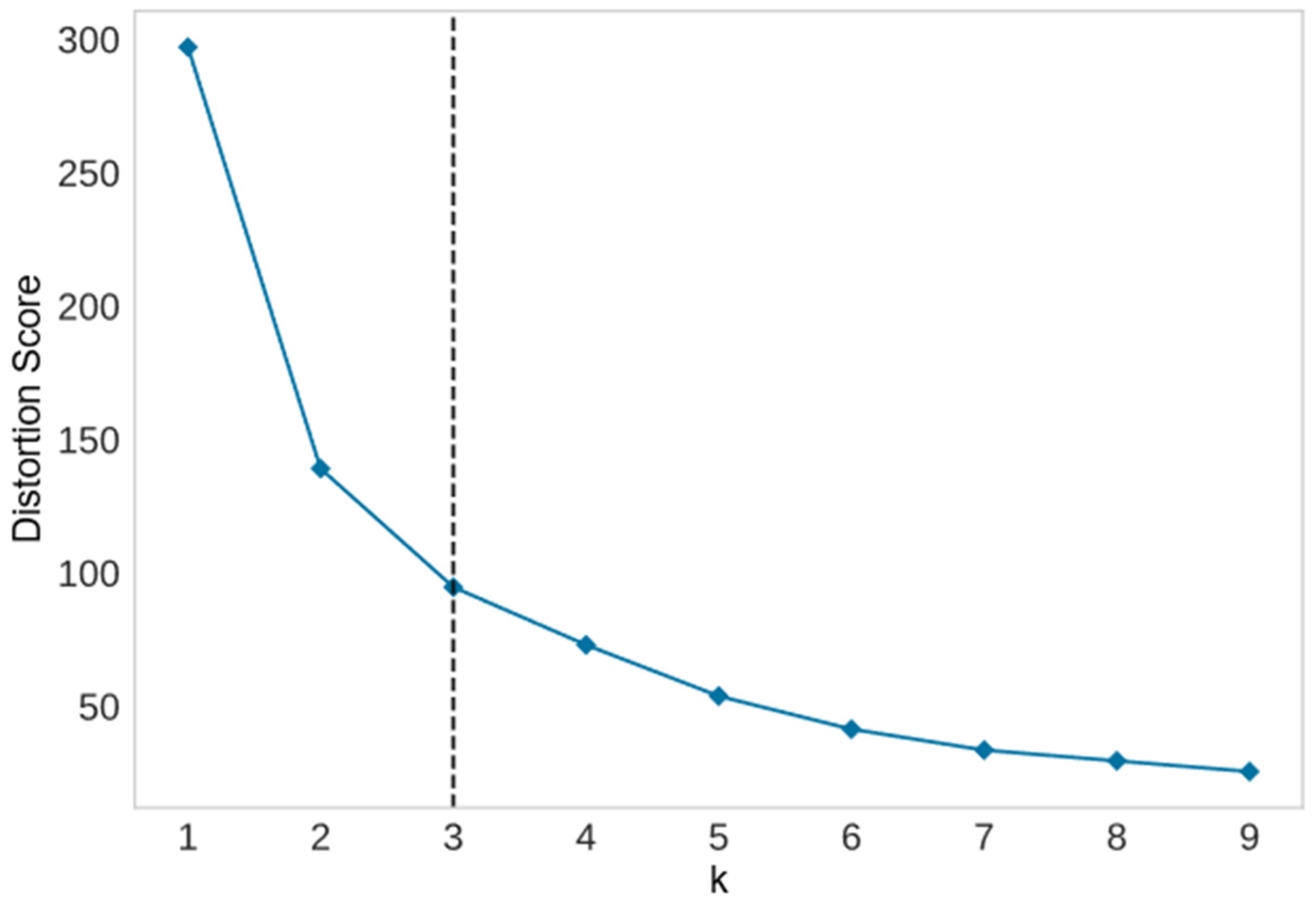
Figure 6 shows the elbow results versus the number of clusters for the same biochemical data. The elbow method indicated that the optimal number of clusters was three.

3.2.2. Silhouette Method

Figure 7 depicts a plot of the SC value versus the number of clusters for biochemical data of 100 mangoes. The silhouette method showed that the optimal number of clusters was two.
Unfortunately, the results from the silhouette and elbow methods were inconsistent. Even though two clusters was previously thought to match the natural number of ripeness stages, we investigated the performance of three supervised machinelearning classifiers in predicting mango ripeness stages for two and three classes.

3.3. Results of Oversampling Data

Results from the k-means clustering described in Section 2.5 showed an unequal number of mango samples for both two and three ripeness classes. For two ripeness classifications, the unripe class was the majority mango class, and the ripe class was the minority class. For three ripeness classifications, the unripe class was the majority mango class, and the overripe class was the minority class. We employed the SMOTETomek oversampling algorithm to generate additional training samples to balance the data distribution in minority classes. Table 4 displays the number of mango samples prior to and following the SMOTETomek technique. The numbers of mangoes in the unripe and ripe classes after oversampling data were 79 and 79, respectively. The numbers of mangoes in the unripe, ripe, and overripe classes after oversampling data were 58, 57, and 59, respectively. The distribution of the amount of data after oversampling with the SMOTETomek algorithm is depicted in Figure 8.
Table 5 displays that the averages and standard deviations of the oversampling data of 10 variables, the same as those given in Table 4, from 100 mango samples, were not much different from the statistics regarding the original data. Regarding the two classes (ripe and unripe) and three classes (ripe, unripe, and overripe), Table 6 shows that no significant difference was found between the averages and standard deviations of the original data and oversampling data for the 10 variables listed in Table 4 from 100 mango samples.

3.4. Comparison of Machine Learning Models

We classified mango ripeness using GNB, SVM, and FANN classifiers. The data for training the ML classifiers were mango weight, skin color, capacitance, and voltage across parallel-plate sensors. The performance of the classifier models was evaluated using fourfold cross validation. Table 7 shows the results of the ML models for two-class classification without any data sampling. The GNB, and SVM, and FANN models had average accuracies of 73.0%, 75.0%, and 85.0%, respectively. Table 8 manifests the results of the ML models for three-class classification using original data. For three-class classification, the average accuracies of the GNB, SVM, and FANN classifiers were 57.0%, 55.0%, and 79.0%, respectively.
The performance data of the three ML models with balanced data that were generated through the SMOTETomek algorithm for two-class and three-class classifications are shown in Table 9 and Table 10, respectively.
In the comparison between the results from Table 7 and Table 9, and also between the results from Table 8 and Table 10, we found that the machine learning models with oversampling data performed significantly better than those without it. Specifically, the performance of the FANN classifier was improved by approximately 8.3% and 10.6% for two-class and three-class classification, respectively, using the SMOTETomek algorithm. According to the findings, the FANN classifier performed better than the GNB and SVM classifiers. We noted that classification accuracy and precision were sufficient for supervised ML classifiers in the categorization classification of mango ripeness into both two and three stages.

3.5. Model Validation and Discussion

In Section 3.4, we performed fourfold cross validation of the GNB, SVM, and FANN models and compared their accuracies. The results dictated that the FANN model outperformed the others (Table 7, Table 8, Table 9 and Table 10).
To make certain that our FANN model was an effective model for ripeness stage classifying, we used the external unseen physical and electrical data from 20 mangoes for further validation. The results are shown in Table 11. “Nam Dok Mai Si Tong” mangoes are generally picked for export on days 85–95 after fruit set. In this work, mangoes were harvested at 80, 90, 100, and 110 days after fruit set (DAFS).
On day 1 following harvest, the FANN model identified mangoes that were 80 DAFS as unripe mangoes and those that were 100 and 110 DAFS as ripe mangoes. These results were as we expected. The 80 DAFS mangoes labeled 1 were predicted by the FANN model as overripe on day 7 after harvest.
The 90 DAFS mangoes labeled 1 and 5 were predicted as ripe on day 1 after harvest; however, they were predicted as unripe from days 2 to 7 after harvest. We thought that these two samples had a total soluble solid (TSS) overlap between unripe and ripe levels. This is naturally possible because there is no clear-cut boundary between unripe and ripe mangoes using biochemical properties as indicators. The 90 DAFS mangoes were indicated by the FANN model as ripe and overripe on day 9 after harvest.
Most of the mangoes at 100 DAFS and 110 DAFS were predicted to be in the ripening stage, as expected, since they were harvested after the commercial export practice. The 100 DAF mangoes labeled 1 and 4 could have been incorrectly predicted by the machine learning model, since they were forecasted as unripe from day 1 to day 9 after harvest. The FANN model wrongly predicted the 110 DAFS mangoes labeled 3, 4, and 5 on day 7 after picking, because these mangoes should have been classified into either the ripe or overripe stage. The predicted ripeness stage of each batch of mangoes altered from day 1 to day 9 after harvest, as expected.

4. Conclusions

The goal of this study was to develop machine learning models for predicting the ripeness stage of mangoes at harvest. The procedures for the development of machine learning classifiers were described. The k-means algorithm was able to distinguish mango ripening stages either into unripe and ripe or into unripe, ripe, and overripe using biochemical properties. We demonstrated that oversampling data with the SMOTETomek algorithm improved both the average precision and accuracy of prediction of machine learning classifiers compared to using only the data without oversampling. The feed-forward artificial neural network was able to classify the data with a significantly higher accuracy than the Gaussian naïve Bayes and support vector machine algorithms. The Gaussian naïve Bayes classifier was the worst classifier among the three used. The findings led to the conclusion that the combination of supervised and unsupervised machine learning techniques presented in this work was successful in classifying the ripeness stage of mangoes, which is important for the fruit industry. The original measurement data in this research is publicly available [53]. Further research may involve more samples and cultivars to test the reliability of our approach.

Author Contributions

Conceptualization, D.W. and S.C.; investigation, P.S.; software, D.W.; analysis, D.W., P.S. and S.C.; writing—original draft preparation, review and editing, S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original measurement data supporting the reported results are available at http://doi.org/10.34740/kaggle/dsv/2998552 (accessed on 20 December 2021).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kader, A.A. Fruit maturity, ripening, and quality relationships. Acta Hortic. 1999, 485, 203–208. [Google Scholar] [CrossRef]
  2. Reid, M.S. Maturation and maturity indices. In Postharvest Technology of Horticultural Crops; Kader, A.A., Ed.; University of California: Oakland, CA, USA, 2002; pp. 55–62. [Google Scholar]
  3. Brecht, J.K.; Yahia, E.M. Postharvest physiology. In The Mango: Botany, Production and Uses; Litz, R.E., Ed.; CABI: Wallingford, UK, 2009; pp. 484–528. [Google Scholar]
  4. Ploetz, R.C. The major diseases of mango: Strategies and potential for sustainable management. Acta Hortic. 2004, 645, 137–150. [Google Scholar] [CrossRef]
  5. Lizada, C. Mango. In Biochemistry of Fruit Ripening; Seymour, G.B., Taylor, J.E., Tucker, G.A., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 255–271. [Google Scholar]
  6. Evans, E.A.; Ballen, F.H.; Siddiq, M. Mango production, global trade, consumption trends, and postharvest processing and nutrition. In Handbook of Mango Fruit; John Wiley & Sons, Ltd.: Chichester, UK, 2017; pp. 1–16. [Google Scholar]
  7. Wanitchang, P.; Terdwongworakul, A.; Wanitchang, J.; Nakawajana, N. Non-destructive maturity classification of mango based on physical, mechanical and optical properties. J. Food Eng. 2011, 105, 477–484. [Google Scholar] [CrossRef]
  8. Coates, L.; Johnson, G.; Dale, M. Postharvest diseases of fruit and vegetables. In Plant Pathogens and Plant Diseases; Brown, J.F., Ogle, H.J., Eds.; Rockvale Publications: Armidale, Australia, 1997; pp. 533–548. [Google Scholar]
  9. Brecht, J.K.; Yahia, E.M. Harvesting and postharvest technology of mango. In Handbook of Mango Fruit; John Wiley & Sons, Ltd.: Chichester, UK, 2017; pp. 105–129. [Google Scholar]
  10. Penchaiya, P.; Tijskens, L.M.M.; Uthairatanakij, A.; Srilaong, V.; Tansakul, A.; Kanlayanarat, S. Modelling quality and maturity of ‘NamdokmaiSithong’ mango and their variation during storage. Postharvest Biol. Technol. 2020, 159, 111000. [Google Scholar] [CrossRef]
  11. Vásquez-Caicedo, A.L.; Neidhart, S.; Carle, R. Postharvest ripening behavior of nine Thai mango cultivars and their suitability for industrial applications. Acta Hortic. 2004, 645, 617–625. [Google Scholar] [CrossRef]
  12. Jha, S.N.; Narsaiah, K.; Sharma, A.D.; Singh, M.; Bansal, S.; Kumar, R. Quality parameters of mango and potential of non-destructive techniques for their measurement—A review. J. Food Sci. Technol. 2010, 47, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Kienzle, S.; Sruamsiri, P.; Carle, R.; Sirisakulwat, S.; Spreer, W.; Neidhart, S. Harvest maturity detection for ‘Nam Dokmai #4’ mango fruit (Mangifera indica L.) in consideration of long supply chains. Postharvest Biol. Technol. 2012, 72, 64–75. [Google Scholar]
  14. Slaughter, D.C. NondestructiveMaturity Assessment MethodsforMango; University of California: Oakland, CA, USA, 2009; pp. 1–18. [Google Scholar]
  15. Li, B.; Lecourt, J.; Bishop, G. Advances in non-destructive early assessment of fruit ripeness towards defining optimal time of harvest and yield prediction—A review. Plants 2018, 7, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Zakaria, A.; Shakaff, A.Y.M.; Masnan, M.J.; Saad, F.S.A.; Adom, A.H.; Ahmad, M.N.; Jaafar, M.N.; Abdullah, A.H.; Kamarudin, L.M. Improved maturity and ripeness classifications of Magnifera Indica cv. Harumanis mangoes through sensor fusion of an electronic nose and acoustic sensor. Sensors 2012, 12, 6023–6048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Shah, S.S.A.; Zeb, A.; Qureshi, W.S.; Arslan, M.; Ullah Malik, A.; Alasmary, W.; Alanazi, E. Towards fruit maturity estimation using NIR spectroscopy. Infrared Phys. Technol. 2020, 111, 103479. [Google Scholar] [CrossRef]
  18. Magwaza, L.S.; Opara, U.L. Analytical methods for determination of sugars and sweetness of horticultural products—A review. Sci. Hortic. 2015, 184, 179–192. [Google Scholar] [CrossRef]
  19. Scalisi, A.; O’Connell, M.G. Application of visible/NIR spectroscopy for the estimation of soluble solids, dry matter and flesh firmness in stone fruits. J. Sci. Food Agric. 2020, 101, 2100–2107. [Google Scholar] [CrossRef]
  20. Jha, S.N.; Narsaiah, K.; Jaiswal, P.; Bhardwaj, R.; Gupta, M.; Kumar, R.; Sharma, R. Nondestructive prediction of maturity of mango using near infrared spectroscopy. J. Food Eng. 2014, 124, 152–157. [Google Scholar] [CrossRef]
  21. Gabriëls, S.H.E.J.; Mishra, P.; Mensink, M.G.J.; Spoelstra, P.; Woltering, E.J. Non-destructive measurement of internal browning in mangoes using visible and near-infrared spectroscopy supported by artificial neural network analysis. Postharvest Biol. Technol. 2020, 166, 111206. [Google Scholar] [CrossRef]
  22. Nguyen, C.-N.; Phan, Q.-T.; Tran, N.-T.; Fukuzawa, M.; Nguyen, P.-L.; Nguyen, C.-N. Precise sweetness grading of mangoes (Mangifera indica L.) based on random forest technique with low-cost multispectral sensors. IEEE Access 2020, 8, 212371–212382. [Google Scholar] [CrossRef]
  23. Sun, J.; Li, S.; Yao, X. A novel method for multi-feature grading of mango using machine vision. J. Comput. 2020, 31, 65–77. [Google Scholar]
  24. Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100. [Google Scholar] [CrossRef]
  25. Vapnik, V.N. Statistical Learning Theory; John Wiley & Sons: Nashville, TN, USA, 1998; ISBN 9780471030034. [Google Scholar]
  26. Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
  27. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  28. Hand, D.J.; Mannila, H.; Smyth, P. Principles of Data Mining; Bradford Books: Cambridge, MA, USA, 2001. [Google Scholar]
  29. Chan, P.K.; Stolfo, S.J. Learning with Non-Uniform Class and Cost Distributions: Effects and a Distributed Multi-Classifier Approach. in Workshop Notes KDD-98 Workshop on Distributed Data Mining. 1998. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.35.3392 (accessed on 27 November 2020).
  30. Kubat, M.; Holte, R.C.; Matwin, S. Machine learning for the detection of oil spills in satellite radar images. Mach. Learn. 1998, 2, 195–215. [Google Scholar] [CrossRef] [Green Version]
  31. Bauder, R.A.; Khoshgoftaar, T.M. The effects of varying class distribution on learner behavior for medicare fraud detection with imbalanced big data. Health Inf. Sci. Syst. 2018, 6, 9. [Google Scholar] [CrossRef]
  32. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
  33. Tomek, I. Two modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, 6, 769–772. [Google Scholar]
  34. Minsky, M. Steps toward artificial intelligence. Proc. IRE 1961, 49, 8–30. [Google Scholar] [CrossRef]
  35. Raghavendra, A.; Guru, D.; Rao, M.K.; Sumithra, R. Hierarchical approach for ripeness grading of mangoes. Artif. Intell. Agric. 2020, 4, 243–252. [Google Scholar] [CrossRef]
  36. Mavi, M.F.; Husin, Z.; Ahmad, B.; Yacob, Y.M.; Farook, R.S.M.; Tan, W.K. Mango ripeness classification system using hybrid technique. Indones. J. Electr. Eng. Comput. Sci. 2019, 14, 859. [Google Scholar] [CrossRef]
  37. Mim, F.S.; Galib, S.M.; Hasan, M.F.; Jerin, S.A. Automatic detection of mango ripening stages—An application of information technology to botany. Sci. Hortic. 2018, 237, 156–163. [Google Scholar] [CrossRef]
  38. Janardhana, K.; Jesi, V.E.; Vijayaragavan, M.; Kumar, R.B.D.A.N. Non-destructive classification of fruits based on color by using machine learning techniques. Int. J. Mod. Agric. 2021, 10, 1057–1069. [Google Scholar]
  39. Robertson, J.A.; Meredith, F.I.; Horvat, R.J.; Senter, S.D. Effect of cold storage and maturity on the physical and chemical characteristics and volatile constituents of peaches (cv. Cresthaven). J. Agric. Food Chem. 1990, 38, 620–624. [Google Scholar] [CrossRef]
  40. Ferrer, A.; Remón, S.; Negueruela, A.I.; Oria, R. Changes during the ripening of the very late season Spanish peach cultivar Calanda. Sci. Hortic. 2005, 105, 435–446. [Google Scholar] [CrossRef]
  41. Scalisi, A.; Pelliccia, D.; O’Connell, M.G. Maturity prediction in yellow peach (Prunus persica L.) cultivars using a fluorescence spectrometer. Sensors 2020, 20, 6555. [Google Scholar] [CrossRef]
  42. Scalisi, A.; O’Connell, M.G.; Pelliccia, D.; Plozza, T.; Frisina, C.; Chandra, S.; Goodwin, I. Reliability of a handheld bluetoothcolourimeter and its application to measuring the effects of time from harvest, row orientation and training system on nectarine skin colour. Horticulturae 2021, 7, 255. [Google Scholar] [CrossRef]
  43. Juansah, J.; Budiastra, I.W.; Dahlan, K.; Seminar, K.B. Electrical properties of garut citrus fruits at low alternating current signal and its correlation with physicochemical properties during maturation. Int. J. Food Prop. 2014, 17, 1498–1517. [Google Scholar] [CrossRef] [Green Version]
  44. Teerachaichayut, S.; Terdwongworakul, A.; Keawsumnuk, K.; Rangsi, M.; Seangkeaw, K. A feasibility study for the nondestructive detection of granulation in tangerine fruit using a capacitance based technique. In Proceedings of the Post Harvest, Food and Process Engineering, International Conference of Agricultural Engineering-CIGR-AgEng 2012: Agriculture and Engineering for a Healthier Life, Valencia, Spain, 8–12 July 2012. [Google Scholar]
  45. Wells, B.; Baker, E.; Farwell, A.; Foster, H.; Gao, X.; Gruber, B.; Jones, E.; Vu, D.; Xu, S.; Ye, J. An adjustable parallel-plate capacitor instrument—Test of the theoretical capacitance formula. Am. J. Phys. 2016, 84, 723–726. [Google Scholar] [CrossRef]
  46. Bishop, C.M. Pattern Recognition and Machine Learning; Elsevier: Amsterdam, The Netherlands, 2006; Volume 128, pp. 338–356. [Google Scholar]
  47. Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
  48. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  49. Sivakumar, D.; Jiang, Y.; Yahia, E.M. Maintaining mango (Mangifera indica L.) fruit quality during the export chain. Food Res. Int. 2011, 44, 1254–1263. [Google Scholar] [CrossRef]
  50. Rungpichayapichet, P.; Nagle, M.; Yuwanbun, P.; Khuwijitjaru, P.; Mahayothee, B.; Müller, J. Prediction mapping of physicochemical properties in mango by hyperspectral imaging. Biosyst. Eng. 2017, 159, 109–120. [Google Scholar] [CrossRef]
  51. Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
  52. Lebrun, M.; Plotto, A.; Goodner, K.; Ducamp, M.-N.; Baldwin, E. Discrimination of mango fruit maturity by volatiles using the electronic nose and gas chromatography. Postharvest Biol. Technol. 2008, 48, 122–131. [Google Scholar] [CrossRef]
  53. Worasawate, D.; Sakunasinha, P.; Chiangga, S. Classification of Ripeness Stage of Mango Fruit; Kaggle: San Francisco, CA, USA, 2022. [Google Scholar] [CrossRef]
Agriengineering 04 00003 g001 550
Figure 1. The parallel-plate capacitor sensor.
Figure 1. The parallel-plate capacitor sensor.
Agriengineering 04 00003 g001
Agriengineering 04 00003 g002 550
Figure 2. The feed-forward artificial neural network structure.
Figure 2. The feed-forward artificial neural network structure.
Agriengineering 04 00003 g002
Agriengineering 04 00003 g003 550
Figure 3. The procedures for predicting the ripeness stage of mangoes.
Figure 3. The procedures for predicting the ripeness stage of mangoes.
Agriengineering 04 00003 g003
Agriengineering 04 00003 g004 550
Figure 4. Images of samples of 80 days after fruit set mangoes from day 1 to day 9 after harvest.
Figure 4. Images of samples of 80 days after fruit set mangoes from day 1 to day 9 after harvest.
Agriengineering 04 00003 g004
Agriengineering 04 00003 g005 550
Figure 5. The results from the k-means algorithm on biochemical data of 100 mangoes with k = 2 (a–c) and k = 3 (d–f): (a,d) TSS versus TA; (b,e) TSS versus TSS/TA ratio; (c,f) TA versus TSS/TA ratio. The symbol colors represent different clusters: unripe = blue, ripe = green, and overripe = red. The mean value (centroid) for each cluster is shown as cross.
Figure 5. The results from the k-means algorithm on biochemical data of 100 mangoes with k = 2 (a–c) and k = 3 (d–f): (a,d) TSS versus TA; (b,e) TSS versus TSS/TA ratio; (c,f) TA versus TSS/TA ratio. The symbol colors represent different clusters: unripe = blue, ripe = green, and overripe = red. The mean value (centroid) for each cluster is shown as cross.
Agriengineering 04 00003 g005
Agriengineering 04 00003 g006 550
Figure 6. Theoptimal numbers of clusters calculated with the elbow method.
Figure 6. Theoptimal numbers of clusters calculated with the elbow method.
Agriengineering 04 00003 g006
Agriengineering 04 00003 g007 550
Figure 7. The optimal numbers of clusters calculated with the silhouette method for the same data as used in Figure 6.
Figure 7. The optimal numbers of clusters calculated with the silhouette method for the same data as used in Figure 6.
Agriengineering 04 00003 g007
Agriengineering 04 00003 g008 550
Figure 8. The distribution of oversampling data based on the SMOTETomek algorithm for two (Top) and three classes (Bottom).
Figure 8. The distribution of oversampling data based on the SMOTETomek algorithm for two (Top) and three classes (Bottom).
Agriengineering 04 00003 g008
Table
Table 1. Hyperparameters for support vector machines.
Table 1. Hyperparameters for support vector machines.
Hyper-ParameterOriginalOversampling
Number of ClustersNumber of Clusters
2323
C1.261.542.961.32
coef0000.50.1
gamma0.10.111
d3333
Table
Table 2. Hyperparameters for the feed-forward artificial neural network.
Table 2. Hyperparameters for the feed-forward artificial neural network.
HyperparameterNumber of Clusters
23
Number of hidden layers22
Epoch600600
Learning Rate0.010.01
Hidden layer 16464
Dropout 10.10.1
Activation function 1relurelu
Hidden layer 2128128
Activation function 2relurelu
Output Layer23
Table
Table 3. The average and standard deviation for biochemical, physical, and electrical properties of 100 mango samples.
Table 3. The average and standard deviation for biochemical, physical, and electrical properties of 100 mango samples.
VariablesAverageStandard Deviation
TA (g/L)2.70.9
TSS (°Brix)10.62.5
TSS/TA5.35.5
Weight (g)344.549.0
Voltage (mV)646.818.5
Capacitance (pF)2.220.20
Weight/Capacitance154.314.2
R (%)44.01.0
G (%)40.90.8
B (%)15.31.3
Table
Table 4. Comparison of the original data and oversampling data for training ML classifiers.
Table 4. Comparison of the original data and oversampling data for training ML classifiers.
ModelNumber of ClustersImbalance ClassOversampling Data
(Original Data)(SMOTETomek Data)
UnripeRipeOverripeUnripeRipeOverripe
GNB28119None7979none
SVM
FANN
GNB3603010585759
SVM
FANN
Table
Table 5. The average and standard deviation of the oversampling data of 10 variables, the same as those given in Table 4, from 100 mango samples.
Table 5. The average and standard deviation of the oversampling data of 10 variables, the same as those given in Table 4, from 100 mango samples.
Variables2-Class SMOTETomek Data 3-Class SMOTETomek Data
AverageStandard DeviationAverageStandard Deviation
TA (g/L)2.21.02.11.0
TSS (°Brix)12.12.812.22.9
TSS/TA8.07.28.97.9
Weight (g)353.545.6351.144.9
Voltage (mV)650.318.4649.617.5
Capacitance (pF)2.260.202.260.19
Weight/Capacitance156.113.7155.413.6
R (%)44.21.044.31.1
G (%)40.80.740.80.6
B (%)15.11.214.91.2
Table
Table 6. The average and standard deviation of the original data and over sampling data of 10 variables, as in Table 4, from 100 mango samples.
Table 6. The average and standard deviation of the original data and over sampling data of 10 variables, as in Table 4, from 100 mango samples.
VariablesImbalance ClassOversampling Data
(Original Data)(SMOTETomek Data)
2 Classes 3 Classes2 Classes3 Classes
UnripeRipeUnripeRipeOverripeUnripeRipeUnripeRipeOverripe
TA (g/L)3.0 (0.7)1.4 (0.5)3.3 (0.6)2.3 (0.5)0.9 (0.3)3.1 (0.7)1.4 (0.5)3.3 (0.6)2.2 (0.4)0.9 (0.3)
TSS (°Brix)9.6 (1.7)14.4 (1.5)9.1 (1.5)11.9 (1.5)15.3 (1.3)9.7 (1.7)14.5 (1.2)9.1 (1.5)11.9 (1.3)15.4 (1.1)
TSS/TA3.4 (1.1)13.3 (8.3)2.9 (0.6)5.5 (1.5)18.6 (9.2)3.3 (1.1)12.7 (7.6)2.9 (0.6)5.5 (1.2)18.0 (7.1)
Weight (g)338.6 (48.5)369.3 (43.7)334.5 (48.2)357.3 (45.6)366 (52.1)337.1 (48.1)369.8 (36.6)334.9 (48.2)359.0 (40.0)359.4 (42.2)
Voltage (mV)644.1 (17.4)658.1 (19.4)640.6 (14.9)656.9 (19.0)653.6 (23.3)643.1 (16.4)657.6 (17.5)640.3 (14.4)657.5 (16.0)651.1 (17.7)
Capacitance (pF)2.20 (0.19)2.34 (0.21)2.17 (0.17)2.33 (0.20)2.29 (0.24)2.19 (0.18)2.33 (0.19)2.17 (0.17)2.35 (0.17)2.26 (0.19)
Weight/Capacitance153.3 (14.1)158.3 (14.3)153.9 (15.0)153.0 (11.6)160.2 (16.1)153.3 (14.2)158.8 (12.6)154.3 (15.1)152.9 (10.6)159.0 (14.0)
R (%)43.7 (0.9)44.7 (1.1)43.7 (0.9)44.0 (0.9)45.4 (0.8)43.8 (0.9)44.7 (0.9)43.6 (0.9)44.0 (0.7)45.4 (0.7)
G (%)41.0 (0.9)40.5 (0.3)41.1 (0.9)40.5 (0.5)40.7 (0.3)41.0 (0.9)40.5 (0.3)41.1 (0.9)40.5 (0.4)40.7 (0.2)
B (%)15.4 (1.3)14.8 (1.2)15.4 (1.2)15.6 (1.3)13.9 (0.8)15.4 (1.3)14.8 (1.1)15.4 (1.2)15.6 (1.0)13.9 (0.6)
The values are the averages, with their standard deviations in the brackets.
Table
Table 7. Performance of three ML models for two-class classification using original data.
Table 7. Performance of three ML models for two-class classification using original data.
4-Fold CrossValidation for Two Classes
ModelClassPrecision AvgPrecision StdAccuracy AvgAccuracy Std
GNBUnripe0.8370.1160.7300.210
Ripe0.4000.339
SVMUnripe0.8110.0780.7500.183
Ripe0.3750.479
FANNUnripe0.9170.1670.8500.300
Ripe0.7500.500
Table
Table 8. Performance of three ML models for three-class classification using original data.
Table 8. Performance of three ML models for three-class classification using original data.
4-Fold CrossValidation for Three Classes
ModelClassPrecision AvgPrecision StdAccuracy AvgAccuracy Std
GNBUnripe0.6460.1540.5700.165
Ripe0.3290.273
Overripe0.6250.479
SVMUnripe0.6170.0490.5500.060
Ripe0.3080.217
Overripe0.2080.250
FANNUnripe0.9130.1360.7900.266
Ripe0.7140.323
Overripe0.7710.315
Table
Table 9. Performance of three ML models for two-class classification using oversampling data.
Table 9. Performance of three ML models for two-class classification using oversampling data.
4-Fold CrossValidation for Two Classes (Oversampling)
ModelClassPrecision AvgPrecision StdAccuracy AvgAccuracy Std
GNBUnripe0.8770.0550.8100.035
Ripe0.7800.087
SVMUnripe0.9400.0460.9110.068
Ripe0.9100.122
FANNUnripe0.9790.0420.9360.112
Ripe0.9140.142
Table
Table 10. Performance of three ML models for three-class classification using oversampling data.
Table 10. Performance of three ML models for three-class classification using oversampling data.
4-Fold CrossValidation for Three Classes (Oversampling)
ModelClassPrecision AvgPrecision StdAccuracy AvgAccuracy Std
GNBUnripe0.8520.1710.6660.061
Ripe0.5620.085
Overripe0.7820.141
SVMUnripe0.8480.1370.8450.044
Ripe0.7970.089
Overripe0.9340.054
FANNUnripe0.8520.1030.8960.102
Ripe0.8650.180
Overripe0.9840.031
Table
Table 11. Results of the performance of the FANN model after 4-fold cross validation in ripeness classification were tested on the external unseen 20 mangoes for 4 different sets: 80, 90, 100, and 110 days after fruit set. Each set of mangoescontained five mangoes, which were labeled as 1, 2, 3, 4, and 5.
Table 11. Results of the performance of the FANN model after 4-fold cross validation in ripeness classification were tested on the external unseen 20 mangoes for 4 different sets: 80, 90, 100, and 110 days after fruit set. Each set of mangoescontained five mangoes, which were labeled as 1, 2, 3, 4, and 5.
DAFSDay after HarvestUnripeRipeOverripe
8011, 2, 3, 4, 5
31, 2, 3, 4, 5
51, 2, 3, 4, 5
72, 3, 4, 5 1
92, 3, 4, 5 1
9012, 3, 41, 5
31, 2, 3, 4, 5
51, 2, 3, 4, 5
71, 2, 3, 4, 5
941, 32, 5
10011, 42, 3, 5
31, 42, 3, 5
51, 42, 3, 5
71, 42, 3, 5
91, 42, 53
1101 1, 2, 3, 4, 5
3 1, 2, 3, 4, 5
5 1, 2, 3, 4, 5
73, 4, 5 1, 2
9 1, 2, 3, 4, 5
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Worasawate, D.; Sakunasinha, P.; Chiangga, S. Automatic Classification of the Ripeness Stage of Mango Fruit Using a Machine Learning Approach. AgriEngineering 2022, 4, 32-47. https://doi.org/10.3390/agriengineering4010003

AMA Style

Worasawate D, Sakunasinha P, Chiangga S. Automatic Classification of the Ripeness Stage of Mango Fruit Using a Machine Learning Approach. AgriEngineering. 2022; 4(1):32-47. https://doi.org/10.3390/agriengineering4010003

Chicago/Turabian Style

Worasawate, Denchai, Panarit Sakunasinha, and Surasak Chiangga. 2022. "Automatic Classification of the Ripeness Stage of Mango Fruit Using a Machine Learning Approach" AgriEngineering 4, no. 1: 32-47. https://doi.org/10.3390/agriengineering4010003

APA Style

Worasawate, D., Sakunasinha, P., & Chiangga, S. (2022). Automatic Classification of the Ripeness Stage of Mango Fruit Using a Machine Learning Approach. AgriEngineering, 4(1), 32-47. https://doi.org/10.3390/agriengineering4010003

Article Metrics

Back to TopTop