Scalable Data-Driven EV Charging Optimization Using HDBSCAN-LP for Real-Time Pricing Load Management
Abstract
Highlights
- Advanced Behavioral Segmentation: HDBSCAN segmented 72,856 EV charging sessions into nine clusters (Davies-Bouldin score: 0.355, noise: 1.62%), capturing temporal and seasonal patterns.
- Enhanced Load Optimization: HDBSCAN-LP integration with RTP achieved 23.10–25.41% peak load reductions (321.87–555.15 kWh) and 2.87–5.31% cost savings ($27.35–$50.71), improving load factors by up to 17.14%.
- Provides a scalable, data-driven approach for precise EV load management adaptable to seasonal and behavioral dynamics, enhancing grid stability and economic efficiency.
- Enables utility planners and policymakers to implement targeted and effective demand-response strategies, supporting sustainable urban energy transitions.
Abstract
1. Introduction
1.1. Background and Problem Context
1.2. Literature Survey
1.3. Research Gaps and Proposed Contributions
- (i)
- The absence of clustering-based demand profiles in optimization frameworks restricts tailored interventions for diverse user behaviors, as in deterministic models.
- (ii)
- Inadequate adaptation to seasonal and temporal charging variations, essential for aligning loads with grid conditions, is often overlooked in static analyses.
- (iii)
- Insufficient balance between aggregator constraints, such as grid capacity and charger scheduling requirements, and user heterogeneity, leading to suboptimal load balancing in real-world scenarios. These gaps necessitate a robust, data-driven framework to dynamically optimize EV charging, ensuring grid stability, cost efficiency, and user satisfaction.
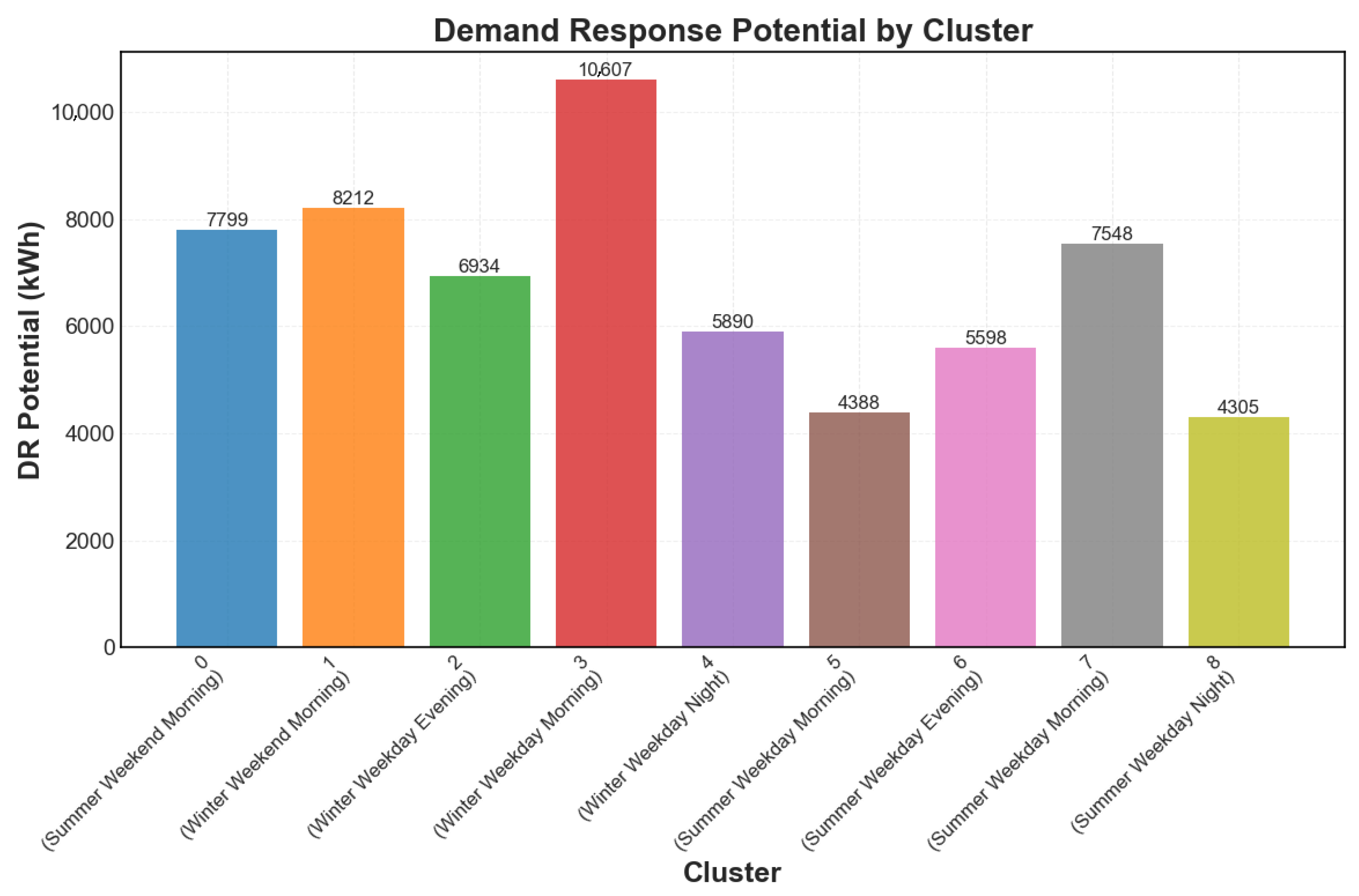
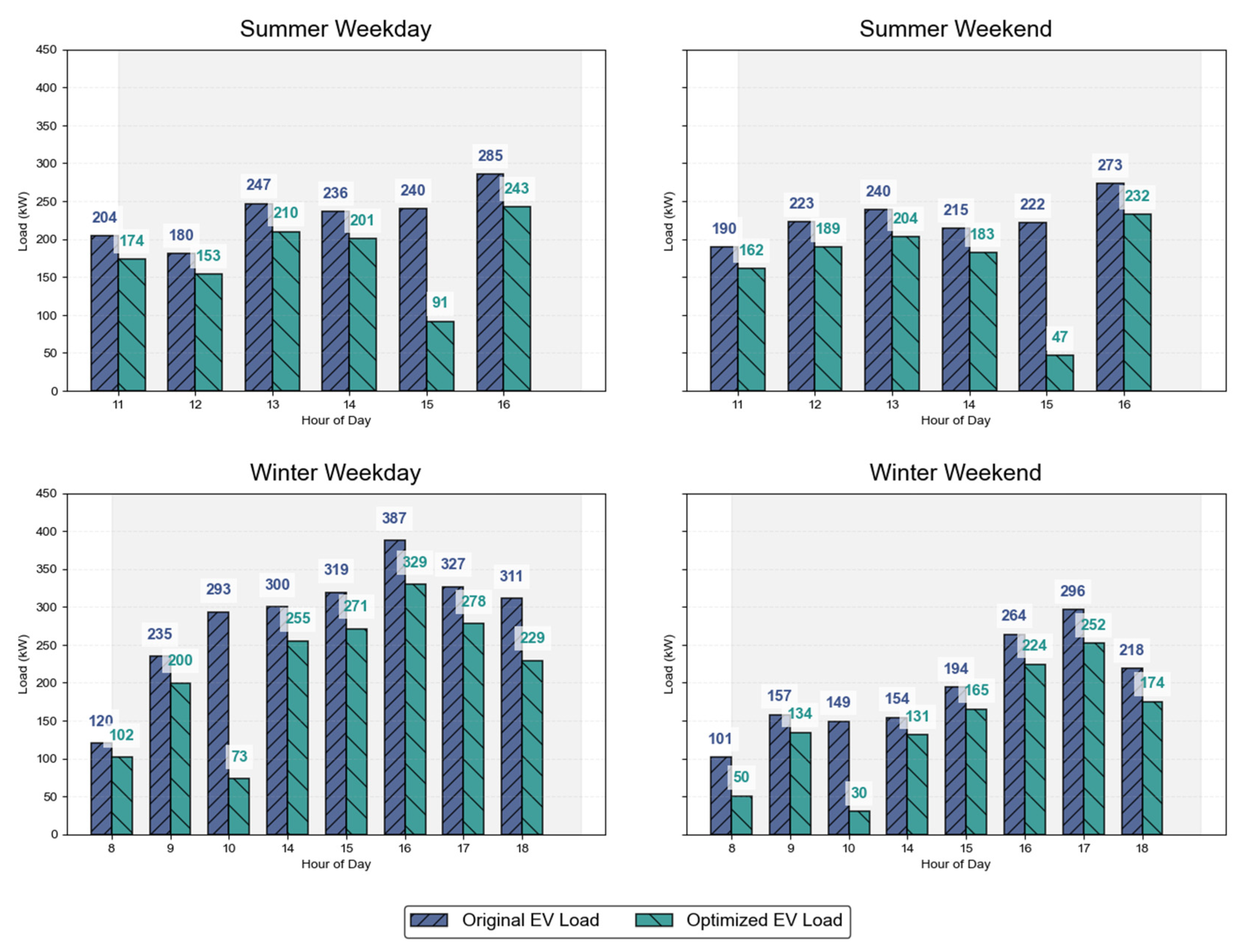
- Cluster-Specific Load Management: Pioneers HDBSCAN-derived demand profiles within optimization loops, enabling tailored DR strategies that outperform non-segmented models, as demonstrated by Winter Weekday’s 250 kW load shift within its 555.15 kWh/day DR limit.
- Seasonal and Temporal Adaptation: Achieves robust adaptation to charging variability through scenario-based profiling, yielding peak reductions of 321.87–555.15 kWh (23.10–25.41%) across diverse conditions, surpassing studies lacking dynamic modelling.
- Scalable Operational Feasibility: Balances grid capacity, charger constraints, and user heterogeneity under RTP, improving load factors by 14.29–17.14% (e.g., Summer Weekday: 0.70 to 0.82) and securing cost savings of $27.35–$50.71 (2.87–5.31%).
1.4. Organization of the Paper
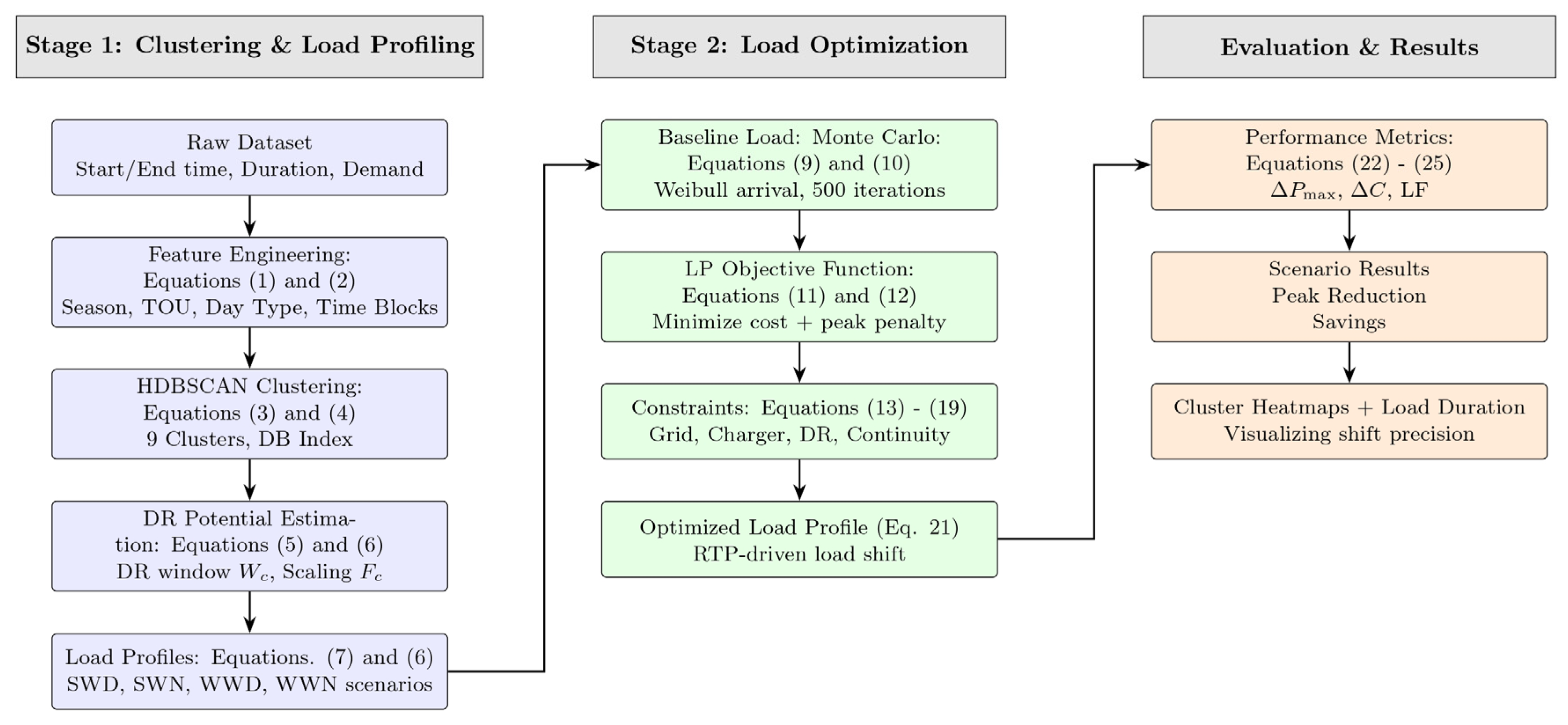
2. Methodology
2.1. Pattern Identification and Load Profiling
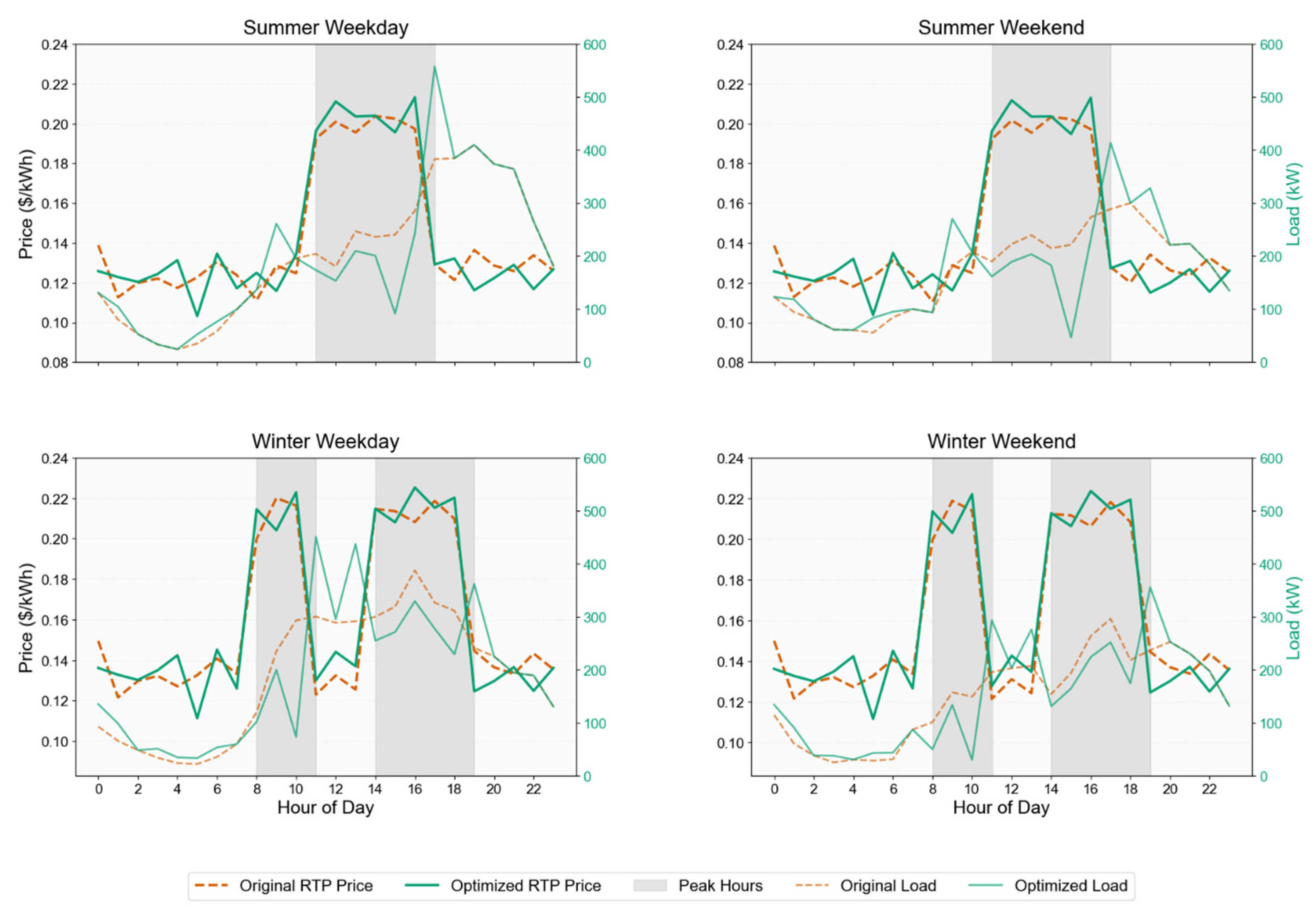
2.2. Load Optimization and Demand Response
- (a)
- Energy Balance (Equation (13)): This ensures energy delivery stays within of , allowing DR flexibility while meeting demand, a tolerance typical in smart grid studies (10–25%) [5]:
- (b)
- (c)
- Load Continuity (Equation (15)): This balances load shifts proportionally across clusters, ensuring energy conservation, as per scheduling principles [41]:
- (d)
- DR Constraint (Equation (16)): Load shifts are capped at of , reflecting realistic DR participation rates (5–15%) [41]:
- (e)
- Peak Load Cap (Equation (17)): A peak reduction mitigates grid stress, aligning with targets in DR literature [43]:
- (f)
- Non-Peak Load Limit (Equation (18)): The The limit prevents off-peak over-shifting, consistent with load management bounds (1.52) [44]:
- (g)
- Charger Capacity (Equation (19)): This reflects Level 2 charger limits, a standard in EV studies:
- (h)
3. Results
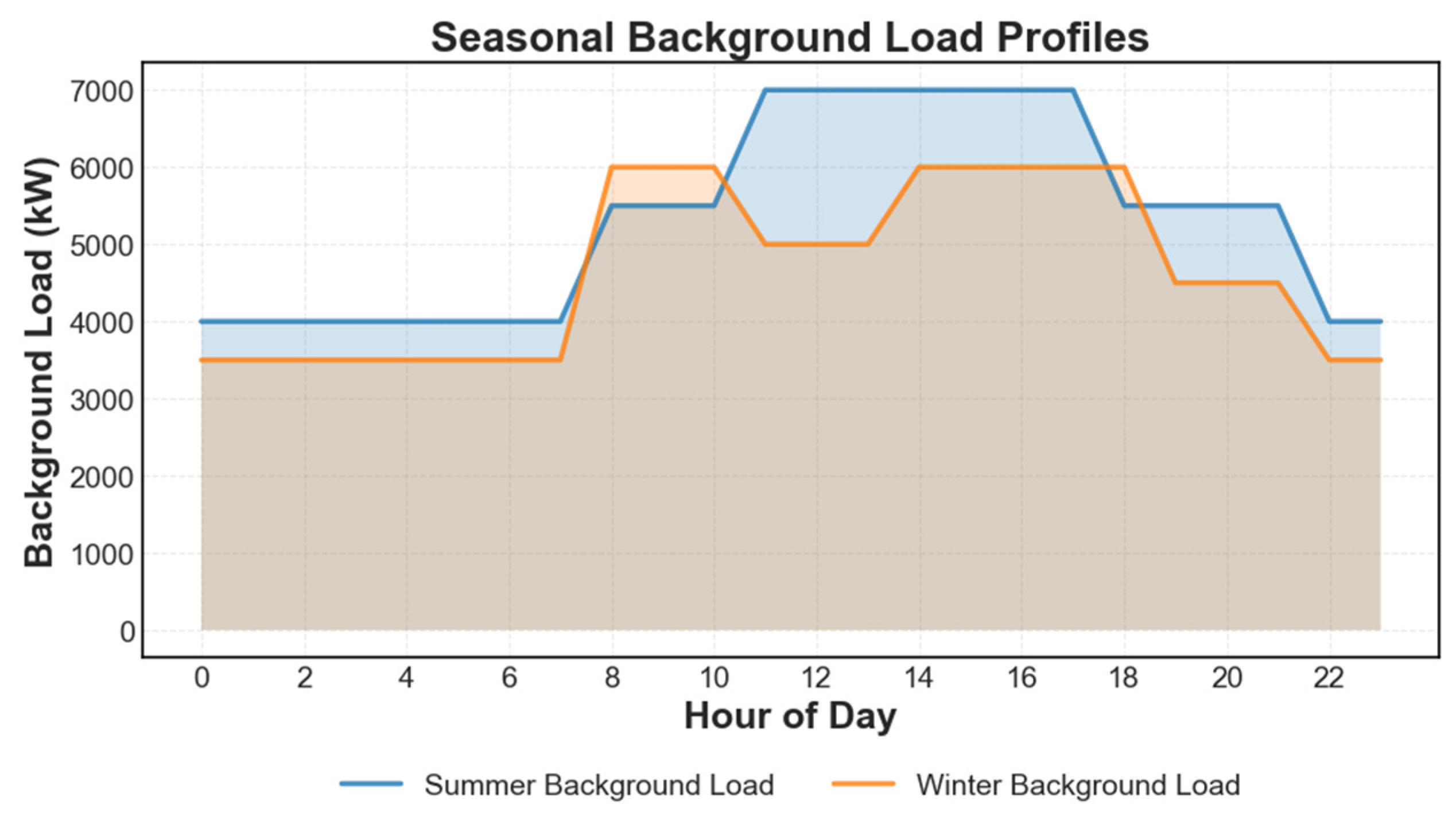
3.1. Seasonal Background Load Analysis
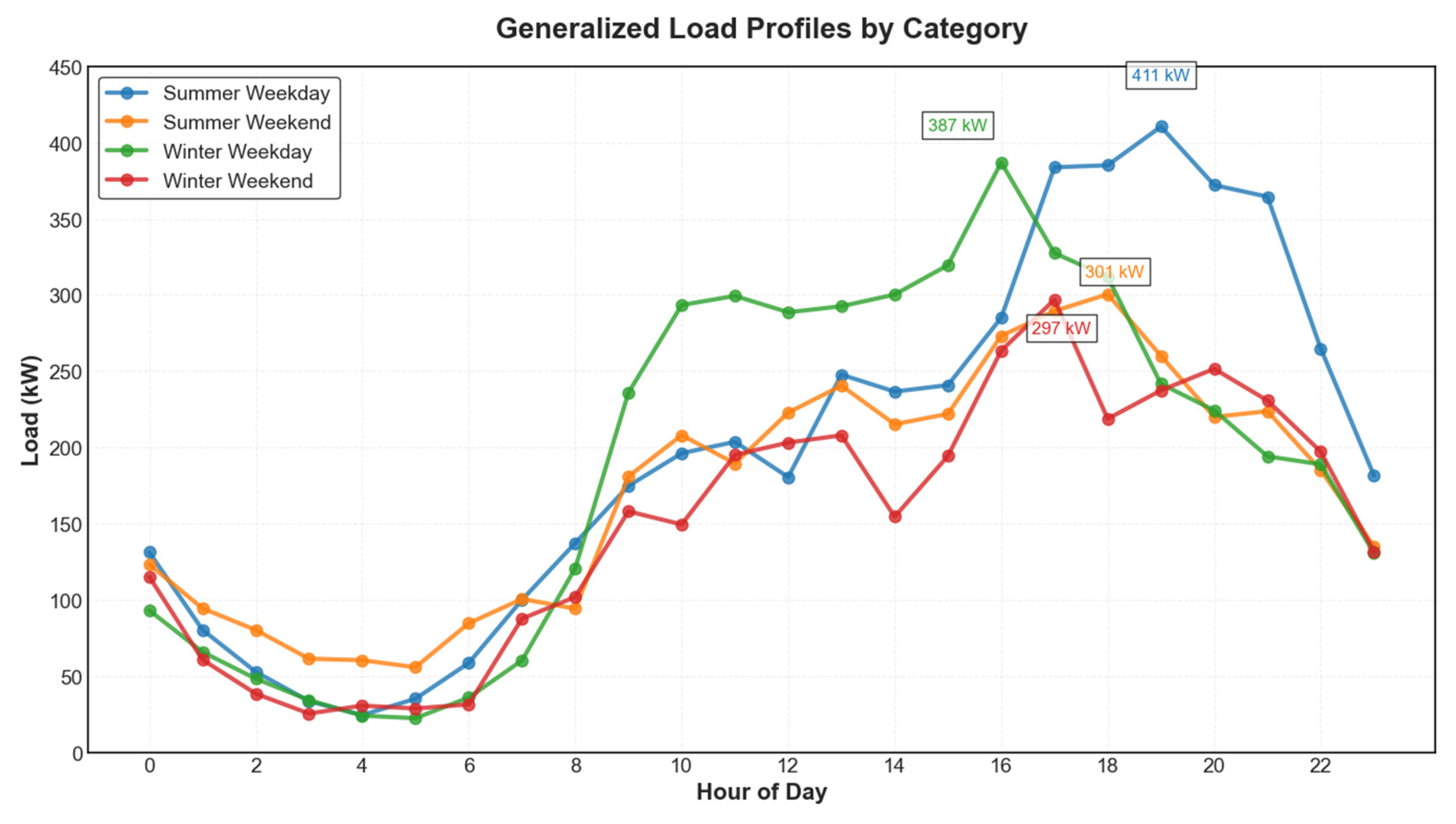
3.2. EV Load Profiling and Clustering
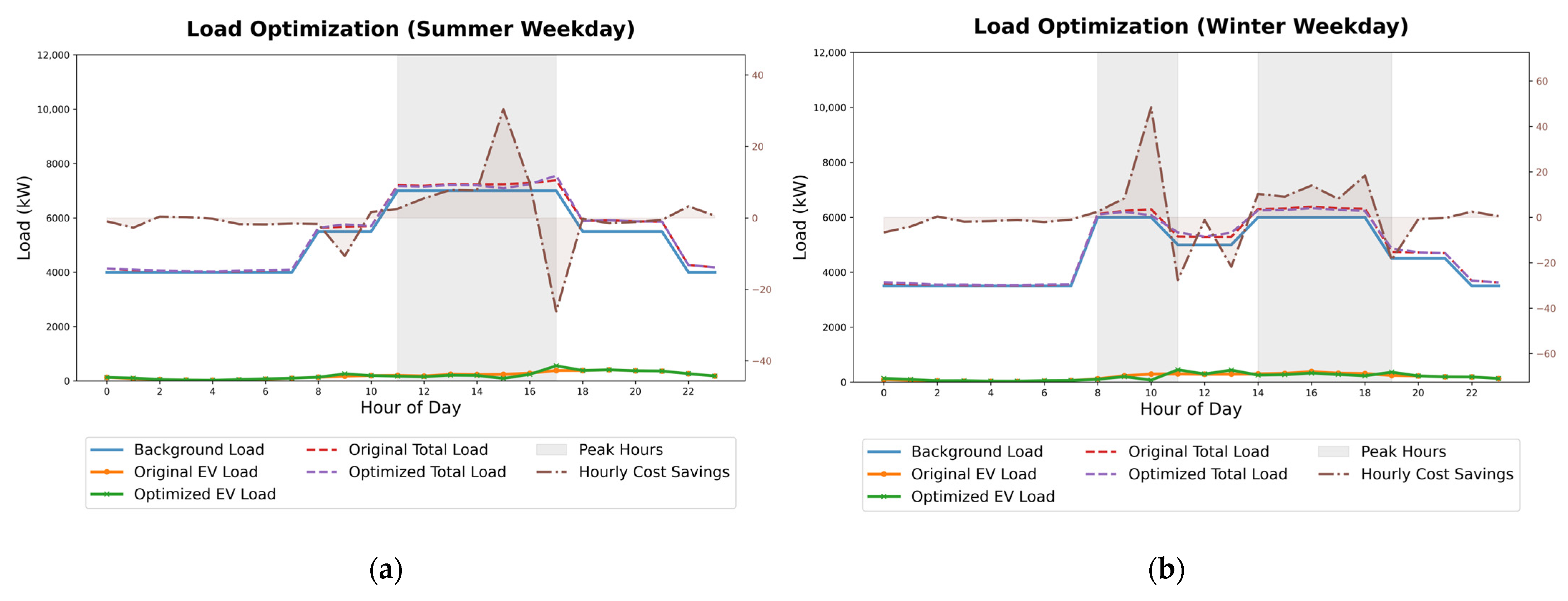
3.3. Load Optimization Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACDC | Alternating Current/Direct Current charger type indicator |
| AI | Artificial Intelligence |
| DBCV | Davies-Bouldin Cluster Validity Score |
| DR | Demand Response |
| DSM | Demand-Side Management |
| GPS | Global Positioning System |
| HDBSCAN | Hierarchical Density-Based Spatial Clustering of Applications with Noise |
| K | Number of clusters |
| k | Number of nearest neighbors used in HDBSCAN mutual reachability |
| kW | Kilowatt |
| kWh | Kilowatt-hour |
| LP | Linear Programming |
| LSTM | Long Short-Term Memory |
| MAPE | Mean Absolute Percentage Error |
| MIP | Mixed Integer Programming |
| ML | Machine Learning |
| mclust | Minimum cluster size |
| msamp | Minimum sample size |
| N | Number of charging sessions |
| PCA | Principal Component Analysis |
| RTP | Real-Time Pricing |
| Scat | Per-day session count (sessions per category per day) |
| ToU | Time-of-Use (tariff segmentation of hours) |
| Wc | Shift window for cluster c (in hours) |
| Xnorm | Normalized feature matrix |
| V2G | Vehicle-to-Grid |
References
- Dimanchev, E.; Qorbani, D.; Korpås, M. Electric vehicle adoption dynamics on the road to deep decarbonization. In The 4Ds of Energy Transition: Decarbonization, Decentralization, Decreasing Use and Digitalization; Wiley: Hoboken, NJ, USA, 2022; pp. 177–205. [Google Scholar]
- Saklani, M.; Saini, D.K.; Yadav, M.; Gupta, Y.C. Navigating the Challenges of EV Integration and Demand-Side Management for India’s Sustainable EV Growth. IEEE Access 2024, 12, 143767–143796. [Google Scholar] [CrossRef]
- Ejuh Che, E.; Roland Abeng, K.; Iweh, C.D.; Tsekouras, G.J.; Fopah-Lele, A. The Impact of Integrating Variable Renewable Energy Sources into Grid-Connected Power Systems: Challenges, Mitigation Strategies, and Prospects. Energies 2025, 18, 689. [Google Scholar] [CrossRef]
- Senol, M.; Bayram, I.S.; Naderi, Y.; Galloway, S. Electric vehicles under low temperatures: A review on battery performance, charging needs, and power grid impacts. IEEE Access 2023, 11, 39879–39912. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Mohanty, S.; Panda, S.; Parida, S.M.; Rout, P.K.; Sahu, B.K.; Bajaj, M.; Zawbaa, H.M.; Kumar, N.M.; Kamel, S. Demand side management of electric vehicles in smart grids: A survey on strategies, challenges, modeling, and optimization. Energy Rep. 2022, 8, 12466–12490. [Google Scholar] [CrossRef]
- Sultan, V.; Aryal, A.; Chang, H.; Kral, J. Integration of EVs into the smart grid: A systematic literature review. Energy Inform. 2022, 5, 65. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Tamoor, M.; Liaqat, R.; Rasool, A.; Salam, Z.; Ali, A.; Sherefa, A. Electric vehicle charging stations and the employed energy management schemes: A classification based comparative survey. Discov. Appl. Sci. 2024, 6, 503. [Google Scholar] [CrossRef]
- Gerritsma, M.K.; AlSkaif, T.A.; Fidder, H.A.; van Sark, W.G.J.H.M. Flexibility of Electric Vehicle Demand: Analysis of Measured Charging Data and Simulation for the Future. World Electr. Veh. J. 2019, 10, 14. [Google Scholar] [CrossRef]
- Yang, X.; Peng, Z.; Wang, P.; Zhuge, C. Seasonal variance in electric vehicle charging demand and its impacts on infrastructure deployment: A big data approach. Energy 2023, 280, 128230. [Google Scholar] [CrossRef]
- Naderi, E.; Asrari, A. Integrated power and transportation systems targeted by false data injection cyberattacks in a smart distribution network. In Electric Transportation Systems in Smart Power Grids; CRC Press: Boca Raton, FL, USA, 2023; pp. 447–472. [Google Scholar]
- Naderi, E.; Asrari, A.; Fajri, P. False data injection cyberattacks targeting electric vehicles in smart power distribution systems. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Rosemont, IL, USA, 19–21 June 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Chhetri, A.; Saini, D.K.; Yadav, M. Applications of BESS in Electrical Distribution Network with Cascading Failures Study—A Review. IEEE Access 2024, 12, 188267–188295. [Google Scholar] [CrossRef]
- Elghanam, E.; Abdelfatah, A.; Hassan, M.S.; Osman, A.H. Optimization Techniques in Electric Vehicle Charging Scheduling, Routing and Spatio-Temporal Demand Coordination: A Systematic Review. IEEE Open J. Veh. Technol. 2024, 5, 1294–1313. [Google Scholar] [CrossRef]
- Sayarshad, H.R. Optimization of electric charging infrastructure: Integrated model for routing and charging coordination with power-aware operations. npj Sustain. Mobil. Transp. 2024, 1, 4. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal Charging Strategies for Unidirectional Vehicle-to-Grid. IEEE Trans. Smart Grid 2011, 2, 131–138. [Google Scholar] [CrossRef]
- Carrasco, C.A.; Hernandez-Del-Valle, A. Energy intensity, economic structure, and capital goods imports in upper-middle income countries: Insights from HDBSCAN clustering. J. Environ. Manag. 2023, 339, 117840. [Google Scholar] [CrossRef]
- Kreft, M.; Brudermueller, T.; Fleisch, E.; Staake, T. Predictability of electric vehicle charging: Explaining extensive user behavior-specific heterogeneity. Appl. Energy 2024, 370, 123544. [Google Scholar] [CrossRef]
- Çakıl, F.; Aksoy, N. Reinforcement learning-based multi-objective smart energy management for electric vehicle charging stations with priority scheduling. Energy 2025, 322, 135475. [Google Scholar] [CrossRef]
- Hassan, M. Machine learning optimization for hybrid electric vehicle charging in renewable microgrids. Sci. Rep. 2024, 14, 13973. [Google Scholar] [CrossRef] [PubMed]
- Paudel, A.; Pinthurat, W.; Marungsri, B. Impact of Large-Scale Electric Vehicles’ Promotion in Thailand Considering Energy Mix, Peak Load, and Greenhouse Gas Emissions. Smart Cities 2023, 6, 2619–2638. [Google Scholar] [CrossRef]
- Aldossary, M. Enhancing Urban Electric Vehicle (EV) Fleet Management Efficiency in Smart Cities: A Predictive Hybrid Deep Learning Framework. Smart Cities 2024, 7, 3678–3704. [Google Scholar] [CrossRef]
- Muthusamy, T.; Meyyappan, U.; Thanikanti, S.B.; Khishe, M. Enhancing distribution system performance by optimizing electric vehicle charging station integration in smart grids using the honey badger algorithm. Sci. Rep. 2024, 14, 27341. [Google Scholar] [CrossRef]
- Singh, A.R.; Kumar, R.S.; Madhavi, K.R.; Alsaif, F.; Bajaj, M.; Zaitsev, I. Optimizing demand response and load balancing in smart EV charging networks using AI integrated blockchain framework. Sci. Rep. 2024, 14, 31768. [Google Scholar] [CrossRef]
- Xu, P.; Wang, X.; Li, Z. Impact and optimization of vehicle charging scheduling on regional clean energy power supply network management. Energy Inform. 2025, 8, 13. [Google Scholar] [CrossRef]
- Fescioglu-Unver, N.; Yıldız Aktaş, M. Electric vehicle charging service operations: A review of machine learning applications for infrastructure planning, control, pricing and routing. Renew. Sustain. Energy Rev. 2023, 188, 113873. [Google Scholar] [CrossRef]
- Panda, S.; Samanta, I.S.; Sahoo, B.; Rout, P.K.; Sahu, B.K.; Bajaj, M.; Blazek, V.; Prokop, L.; Misak, S. Comprehensive framework for smart residential demand side management with electric vehicle integration and advanced optimization techniques. Sci. Rep. 2025, 15, 9948. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Liu, F.; Xie, N.; Guo, W.; Wu, W. Dynamic Pricing Strategy of Charging Station Based on Traffic Assignment Simulation. Sustainability 2022, 14, 14476. [Google Scholar] [CrossRef]
- Jauhar, S.K.; Sethi, S.; Kamble, S.S.; Mathew, S.; Belhadi, A. Artificial intelligence and machine learning-based decision support system for forecasting electric vehicles’ power requirement. Technol. Forecast. Soc. Change 2024, 204, 123396. [Google Scholar] [CrossRef]
- Fayyazbakhsh, A.; Kienberger, T.; Vopava-Wrienz, J. Comparative Analysis of Load Profile Forecasting: LSTM, SVR, and Ensemble Approaches for Singular and Cumulative Load Categories. Smart Cities 2025, 8, 65. [Google Scholar] [CrossRef]
- The Scikit-Learn Developers. Time-Related Feature Engineering. Available online: https://scikit-learn.org/stable/auto_examples/applications/plot_cyclical_feature_engineering.html (accessed on 1 August 2020).
- Jiang, W.; Zhen, Y. A real-time EV charging scheduling for parking lots with PV system and energy store system. IEEE Access 2019, 7, 86184–86193. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Y.; Zhang, Y.; Cai, L. Intelligent parking garage EV charging scheduling considering battery charging characteristic. IEEE Trans. Ind. Electron. 2017, 65, 2806–2816. [Google Scholar] [CrossRef]
- Campello, R.J.; Moulavi, D.; Sander, J. Density-based clustering based on hierarchical density estimates. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Gold Coast, Australia, 14–17 April 2013; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Campello, R.J.; Kröger, P.; Sander, J.; Zimek, A. Density-based clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2020, 10, e1343. [Google Scholar] [CrossRef]
- Darabi, Z.; Ferdowsi, M. Aggregated impact of plug-in hybrid electric vehicles on electricity demand profile. IEEE Trans. Sustain. Energy 2011, 2, 501–508. [Google Scholar] [CrossRef]
- Kikusato, H.; Fujimoto, Y.; Hanada, S.-I.; Isogawa, D.; Yoshizawa, S.; Ohashi, H.; Hayashi, Y. Electric vehicle charging management using auction mechanism for reducing PV curtailment in distribution systems. IEEE Trans. Sustain. Energy 2019, 11, 1394–1403. [Google Scholar] [CrossRef]
- McShane, B.; Adrian, M.; Bradlow, E.T.; Fader, P.S. Count models based on Weibull interarrival times. J. Bus. Econ. Stat. 2008, 26, 369–378. [Google Scholar] [CrossRef]
- Wang, S.; Zang, Y.; Ge, W.; Wang, A.; Li, D.; Tang, J. Data-driven real-time pricing strategy and coordinated optimization of economic load dispatch in electricity market. Front. Energy Res. 2021, 9, 714951. [Google Scholar] [CrossRef]
- Nam, S.; Shin, J.; Hong, B.I. How consumers value improving energy efficiency policy in the electricity market: A contingent valuation experiment in South Korea. Energy Environ. 2024, 35, 3144–3164. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, X.; Yu, X.; Yun, J.; Zhang, J. Electric vehicle participation in regional grid demand response: Potential analysis model and architecture planning. Sustainability 2023, 15, 2763. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2009, 25, 371–380. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Jang, H. Lessons from residential electricity demand analysis on the time of use pricing experiment in South Korea. Energy Econ. 2022, 113, 106224. [Google Scholar] [CrossRef]
- Baek, K.; Lee, E.; Kim, J. A dataset for multi-faceted analysis of electric vehicle charging transactions. Sci. Data 2024, 11, 262. [Google Scholar] [CrossRef]

| Clustering Method | Silhouette Score | Calinski-Harabasz Score | DBCV Score | Noise Fraction (%) | Number of Clusters | Notes |
|---|---|---|---|---|---|---|
| HDBSCAN | 0.225 | 356.130 | 0.355 | 1.62 | 9 | Best separation, low noise, interpretable clusters |
| K-means (k = 9) | 0.217 | 514.720 | N/A | N/A | 9 | Spherical clusters are less meaningful for temporal data |
| GMM (k = 9) | 0.206 | 392.186 | N/A | N/A | 9 | Gaussian assumption, moderate performance |
| DBSCAN | 0.007 | 93.059 | 0.244 | 35.12 | 25 | Over-segmentation, high noise despite tuning |
| Cluster ID | Description | Sessions | Avg Start Hour | Avg Duration (hrs) | Avg Demand (kWh) | % Weekday | % Winter | User Profile | Charging Period |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Summer Weekend Morning Chargers | 387 | 14:32 | 2.41 | 17.71 | 0.0% | 0.0% | Residential | Off-peak (0:00–9:00) |
| 1 | Winter Weekend Morning Chargers | 336 | 14:81 | 2.41 | 16.98 | 0.0% | 100.0% | Residential | Off-peak (0:00–9:00) |
| 2 | Winter Weekday Evening Chargers | 277 | 18:38 | 2.68 | 18.63 | 100.0% | 100.0% | Commercial | Peak (14:00–19:00) |
| 3 | Winter Weekday Morning Chargers | 429 | 12:65 | 1.78 | 13.61 | 100.0% | 100.0% | Commercial | Off-peak (9:00–13:00) |
| 4 | Winter Weekday Night Chargers | 241 | 13:82 | 3.27 | 22.15 | 100.0% | 100.0% | Residential | Off-peak (13:00–17:00) |
| 5 | Summer Weekday Morning Chargers | 216 | 10:41 | 1.68 | 15.11 | 100.0% | 0.0% | Commercial | Off-peak (9:00–13:00) |
| 6 | Summer Weekday Evening Chargers | 266 | 14:60 | 1.81 | 15.66 | 100.0% | 0.0% | Commercial | Peak (13:00–17:00) |
| 7 | Summer Weekday Morning Chargers | 379 | 18:84 | 2.96 | 19.45 | 100.0% | 0.0% | Residential | Peak (17:00–22:00) |
| 8 | Summer Weekday Night Chargers | 209 | 10:18 | 2.90 | 20.37 | 100.0% | 0.0% | Residential | Off-peak (20:00–23:00) |
| Scenario | Summer Weekday | Summer Weekend | Winter Weekday | Winter Weekend |
|---|---|---|---|---|
| Original Cost ($) | 720.00 | 626.41 | 802.36 | 613.08 |
| Optimized Cost ($) | 699.11 | 605.13 | 768.65 | 591.17 |
| Cost Savings ($) | 27.35 | 30.97 | 50.71 | 32.76 |
| Cost Savings (%) | 2.87 | 4.12 | 5.31 | 4.62 |
| Original Max Peak (kW) | 285.33 | 273.45 | 387.38 | 296.18 |
| Optimized Max Peak (kW) | 242.53 | 232.43 | 329.27 | 251.75 |
| Max Peak Reduction (kW) | 42.80 | 41.02 | 58.11 | 44.43 |
| Original Total Peak (kWh) | 1393.39 | 1362.18 | 2292.45 | 1534.59 |
| Optimized Total Peak (kWh) | 1071.52 | 1016.12 | 1737.31 | 1160.21 |
| Total Peak Reduction (kWh) | 321.87 | 346.07 | 555.15 | 374.38 |
| Total Peak Reduction (%) | 23.10 | 25.41 | 24.22 | 24.40 |
| Load Factor (Original) | 0.70 | 0.63 | 0.49 | 0.51 |
| Load Factor (Optimized) | 0.82 | 0.74 | 0.57 | 0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saklani, M.; Saini, D.K.; Yadav, M.; Siano, P. Scalable Data-Driven EV Charging Optimization Using HDBSCAN-LP for Real-Time Pricing Load Management. Smart Cities 2025, 8, 139. https://doi.org/10.3390/smartcities8040139
Saklani M, Saini DK, Yadav M, Siano P. Scalable Data-Driven EV Charging Optimization Using HDBSCAN-LP for Real-Time Pricing Load Management. Smart Cities. 2025; 8(4):139. https://doi.org/10.3390/smartcities8040139
Chicago/Turabian StyleSaklani, Mayank, Devender Kumar Saini, Monika Yadav, and Pierluigi Siano. 2025. "Scalable Data-Driven EV Charging Optimization Using HDBSCAN-LP for Real-Time Pricing Load Management" Smart Cities 8, no. 4: 139. https://doi.org/10.3390/smartcities8040139
APA StyleSaklani, M., Saini, D. K., Yadav, M., & Siano, P. (2025). Scalable Data-Driven EV Charging Optimization Using HDBSCAN-LP for Real-Time Pricing Load Management. Smart Cities, 8(4), 139. https://doi.org/10.3390/smartcities8040139






